Control of Particle Size in the Self-Assembly of Amphiphilic Statistical Copolymers

Abstract

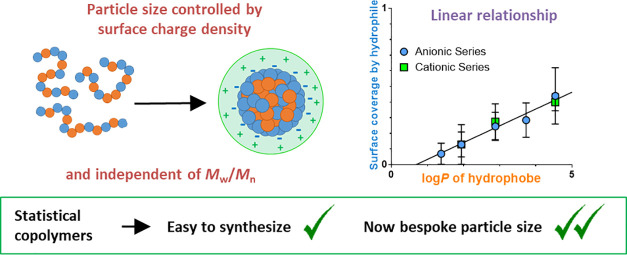
A range of amphiphilic statistical copolymers is synthesized where the hydrophilic component is either methacrylic acid (MAA) or 2-(dimethylamino)ethyl methacrylate (DMAEMA) and the hydrophobic component comprises methyl, ethyl, butyl, hexyl, or 2-ethylhexyl methacrylate, which provide a broad range of partition coefficients (log P). Small-angle X-ray scattering studies confirm that these amphiphilic copolymers self-assemble to form well-defined spherical nanoparticles in an aqueous solution, with more hydrophobic copolymers forming larger nanoparticles. Varying the nature of the alkyl substituent also influenced self-assembly with more hydrophobic comonomers producing larger nanoparticles at a given copolymer composition. A model based on particle surface charge density (PSC model) is used to describe the relationship between copolymer composition and nanoparticle size. This model assumes that the hydrophilic monomer is preferentially located at the particle surface and provides a good fit to all of the experimental data. More specifically, a linear relationship is observed between the surface area fraction covered by the hydrophilic comonomer required to achieve stabilization and the log P value for the hydrophobic comonomer. Contrast variation small-angle neutron scattering is used to study the internal structure of these nanoparticles. This technique indicates partial phase separation within the nanoparticles, with about half of the available hydrophilic comonomer repeat units being located at the surface and hydrophobic comonomer-rich cores. This information enables a refined PSC model to be developed, which indicates the same relationship between the surface area fraction of the hydrophilic comonomer and the log P of the hydrophobic comonomer repeat units for the anionic (MAA) and cationic (DMAEMA) comonomer systems. This study demonstrates how nanoparticle size can be readily controlled and predicted using relatively ill-defined statistical copolymers, making such systems a viable attractive alternative to diblock copolymer nanoparticles for a range of industrial applications.

Introduction

Self-assembled copolymers have applications in a wide range of diverse fields, including healthcare,¹⁻⁷ energy,^8,9 and coatings.¹⁰⁻¹² The assembly of diblock copolymers in solution has been studied extensively and is driven by minimization of the energetically unfavorable interactions between the solvent and the solvophobic block.¹³ The morphology of diblock copolymer nano-objects depends on the relative volume fractions of solvophilic and solvophobic blocks and can be rationalized in terms of the fractional packing parameter.¹⁴⁻¹⁶ For a fixed diblock composition, the nano-object dimensions depend on both the overall copolymer molecular weight and also the aggregation number, with the latter parameter depending on the processing conditions.^17,18

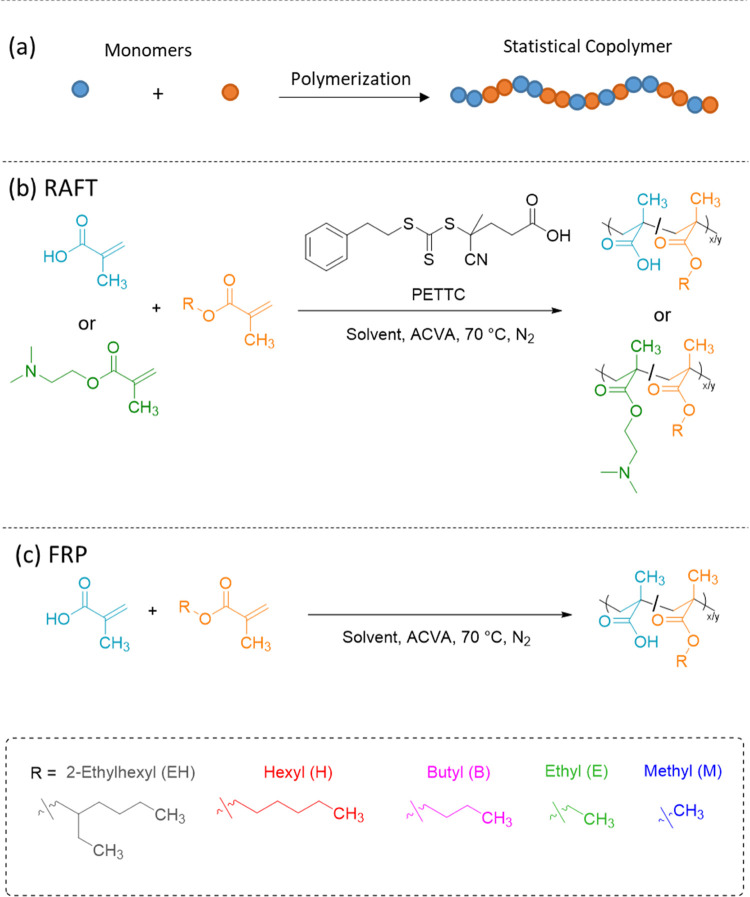
In contrast to amphiphilic diblock copolymers, amphiphilic statistical copolymers (ASC) comprise hydrophilic and hydrophobic comonomers that are distributed throughout each copolymer chain rather than being spatially segregated. More importantly, such copolymers are readily synthesized without using the controlled/living polymerization techniques that are required for the synthesis of diblock copolymers. As such, they are routinely prepared on an industrial scale (i.e., millions of tonnes per annum) using conventional free-radical copolymerization.¹⁹ Like diblock copolymers, ASCs can self-assemble to form a range of copolymer morphologies, including spheres,²⁰⁻²² rods/worms,²³⁻²⁵ and vesicles.^22,26 Furthermore, Liu et al. reported that statistical copolymers comprising styrene and methacrylic acid could form a remarkable “bowl-like” morphology in an aqueous solution.²⁷ It has also been demonstrated by Zhu and Liu that statistical copolymers of N-acryloyl-l-glutamic acid and N-dodecyl acrylamide can self-assemble to form either spheres or vesicles depending on the choice of solvent.²⁸ Statistical distribution of the solvophobic groups along the copolymer backbone also enables microphase separation on shorter length scales (<10 nm) than that typically achieved for block copolymers.²⁹ Moreover, both copolymer composition and solvophobe type can affect the domain size of the nanoparticles.²⁹⁻³¹ Recently, Imai et al. showed that ASCs composed of poly(ethylene glycol) methacrylate statistically copolymerized with either n-butyl methacrylate or n-dodecyl methacrylate self-assembled in an aqueous solution to form structures in which copolymer chains were self-sorted both in terms of their composition and choice of hydrophobic comonomer.³² Matsumoto et al. found that block copolymers consisting of two different statistical blocks with a common hydrophilic poly(ethylene glycol) methacrylate component self-organize to yield nano-objects with distinct compartments.³¹

Despite these advances, the rationalization and understanding of nano-object dimensions and morphology formed by ASCs has been rather limited. Sato et al. found that higher degrees of ASC polymerization lead to lower aggregation numbers of molecules assembling in nanoparticles.³³ Similarly, it was recently reported that the size of self-assembled nanoparticles formed by amphiphilic poly(butyl methacrylate-stat-methacrylic acid) [P(BMA-stat-MAA)] copolymers depends on the copolymer composition but is independent of the copolymer molecular weight.³⁴ To describe the observed particle size behavior, a particle surface charge density (PSC) model based on the ionized surface charge density arising from the anionic MAA units was proposed.³⁴ Herein, this model is generalized for charged nanoparticles formed by various ASC systems comprising either positively or negatively charged ionic comonomers. More specifically, this PSC model has been validated for a series of MAA-based statistical copolymers comprising a range of hydrophobic alkyl methacrylate comonomers synthesized using either reversible addition–fragmentation chain transfer (RAFT) polymerization or conventional free-radical polymerization (FRP) (Scheme 1). These anionic ASCs are complemented by an analogous series of cationic ASCs prepared using 2-(dimethylamino)ethyl methacrylate (DMAEMA) as the hydrophilic comonomer. Importantly, it is demonstrated that (i) the particle size is correlated with the partition coefficient (log P) of the hydrophobic comonomer and (ii) this model can be used to predict the nanoparticle size for a given hydrophobic comonomer and target copolymer composition.

Scheme 1. (a) Representative Diagram of a Statistical Copolymerization; (b) RAFT Solution Copolymerization of Either MAA or DMAEMA (B) with EHMA, HMA, BMA, EMA, or MMA (A) to Form a Range of P(A-stat-B) ASCs; and (c) Standard Free-Radical Copolymerization of MAA and a Hydrophobic Methacrylate Monomer.

Copolymerization of BMA with MAA was performed in 1,4-dioxane at 50% w/w, whereas all other copolymerizations were performed in IPA at the same concentration.

Experimental Section

Materials

Methyl methacrylate (MMA, 99%), ethyl methacrylate (EMA, 99%), n-butyl methacrylate (BMA, 99%), n-hexyl methacrylate (HMA, 99%), DMAEMA (99%), and MAA (99.5%) were purchased from Sigma-Aldrich (Gillingham, U.K.) and were passed through a basic alumina column to remove inhibitor prior to polymerization. 2-Ethylhexyl methacrylate (EHMA, 98%) was purchased from Alfa Aesar (Heysham, U.K.), and its inhibitor was removed using an alumina column. Isopropanol (IPA, 99.9%), triethanolamine (TEA, 99%), 4,4′-azobis(4-cyanovaleric acid) (ACVA), 1,4-dioxane (99.5%), trimethylsilyldiazomethane solution (2.0 M in diethyl ether), benzyl bromide (BzBr, 98%), and deuterated acetone were purchased from Sigma-Aldrich. Deuterated chloroform (CDCl₃) and deuterated dimethyl sulfoxide (DMSO-d₆) for NMR spectroscopy measurements were purchased from VWR (Lutterworth, U.K.). Deionized water was obtained using an Elgastat Option 3A water purifier (Elga, High Wycombe, U.K.). 4-Cyano-4-(2-phenylethanesulfanylthiocarbonyl)sulfanylpentanoic acid (PETTC) used for RAFT polymerization was prepared and purified in-house, as reported previously.³⁵ Unless stated otherwise, all materials were used as received.

¹H NMR Spectroscopy

¹H NMR spectra were recorded in either DMSO-d₆ or CDCl₃ using a Bruker AV1-400 or AV3HD-400 MHz spectrometer. These spectra were analyzed using Bruker Topspin 3.5pl7 software and chemical shifts are reported relative to a residual solvent peak. Copolymer compositions were calculated using ¹H NMR spectra of alkylated copolymers where methacrylic acid repeat units were alkylated prior to the measurements using either trimethylsilyldiazomethane to form methyl methacrylate residues³⁶ or BzBr to form benzyl methacrylate residues. In the former reaction, excess trimethylsilyldiazomethane was added dropwise to a 5% w/w copolymer solution in THF (5 mL) with a few drops of methanol (approx. 0.1 mL) until the solution turned a persistent yellow color. The reaction solution was stirred overnight allowing all solvent to evaporate leaving a residue of methylated copolymer. The latter reaction was performed at 5% w/w in DMF with CsCO₃ being added to deprotonate the methacrylic acid repeat units, followed by BzBr addition. This alkylation reaction was allowed to proceed for 24 h, then the solvent was removed under vacuum and the derivatized copolymer product was purified by washing with water.

Gel Permeation Chromatography (GPC)

Molecular weight distributions were assessed by GPC in THF containing 0.025% w/v butyl hydroxytoluene (BHT) and either 4% v/v acetic acid or 1% v/v triethylamine. The MAA-based copolymers were analyzed using the acidic eluent, whereas DMAEMA-based copolymers were analyzed using the basic eluent. Measurements were performed at a flow rate of 1.0 mL min^–1 using an Agilent PL-GPC50-integrated GPC system equipped with a refractive index detector. Separations were carried out using a pair of PLgel Mixed-C columns (7.8 mm internal diameter, 300 mm length, and 5 μm bead size) equipped with a PLgel guard column (7.8 mm, 50 mm, and 5 μm). Calibration was achieved using a set of 10 low-dispersity poly(methyl methacrylate) (PMMA) standards (Agilent, U.K.) with peak molecular weight values ranging from 550 to 1 568 000 Da.

Small-Angle X-ray Scattering (SAXS)

SAXS patterns were recorded using laboratory SAXS instruments [either a Bruker AXS Nanostar equipped with a two-dimensional (2D) Hi-STAR multiwire gas detector, and modified with a Xenocs GeniX 3D microfocus X-ray source (Cu Kα radiation, wavelength λ = 1.54 Å) and motorized collimating scatterless slits or a Xeuss 2.0 laboratory beamline (Xenocs, Grenoble, France) equipped with a 2D Pilatus 1M pixel detector (Dectris, Baden-Daettwil, Switzerland) and a MetalJet X-ray source (Ga Kα radiation, λ = 1.34 Å; Excillum, Kista, Sweden)]. Samples were run in either an open top- or a sealed flow-through borosilicate glass capillary (Capillary Tube Supplies Ltd, Cornwall, U.K.) of 2 mm diameter. Patterns were collected over a scattering vector range of 0.008 Å^–1 < q < 0.16 Å^–1, where 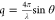and θ is half the scattering angle. 2D X-ray scattering patterns were reduced to one-dimensional curves using the Nika SAS macro (version 1.74) for Igor Pro³⁷ or software supplied by the SAXS instrument manufacturers. Background subtraction and further data analysis were performed using Irena SAS macro (version 2.61) for Igor Pro.³⁸ The scattering of pure water was used for the absolute intensity calibration of the SAXS patterns.

Small-Angle Neutron Scattering (SANS)

SANS measurements were performed on the LOQ diffractometer at the ISIS Spallation Neutron Source (Didcot, U.K.)³⁹ using the contrast variation technique. The sample-to-detector distance was 4.1 m and the beam diameter was 10 mm. The solutions were pipetted into either 1 or 2 mm path length PTFE-stoppered quartz cuvettes (Hellma UK) depending on the solvent (either H₂O or H₂O/D₂O mixtures, respectively). Cuvettes were mounted on a computer-controlled sample changer maintained at a fixed temperature of 25 °C. Scattering patterns were recorded using an Ordela 2D multiwire gas detector, and each data set was corrected for the incident neutron wavelength distribution, the detector efficiency and spatial linearity, and the measured transmission and cuvette path length, before being radially averaged and converted to coherent elastic differential scattering cross-section per unit sample volume data (∂∑/∂Ω) as a function of q using the Mantid software framework.⁴⁰ In the following text, ∂∑/∂Ω is referred to as the intensity, I. A partially deuterated polymer blend standard of known molecular weight was used to scale the reduced SANS data to an absolute intensity scale in accordance with well-established protocols.⁴¹ Background subtraction and some data analysis was performed using the Irena SAS macro for Igor Pro.³⁸

Transmission Electron Microscopy (TEM)

TEM imaging was performed on 0.1% w/w copolymer dispersions. Copper/palladium TEM grids (Agar Scientific, U.K.) surface-coated in-house by a thin film of amorphous carbon were used as sample substrates. Before a sample deposition, the substrate surface was treated by plasma glow discharge for 30 s to make it hydrophilic. A copolymer solution (0.1% w/w, 9 μL) was pipetted onto a freshly glow discharged grid for 20 s and then blotted to remove the excess using filter paper. These were negatively stained using an aqueous solution of uranyl formate (0.75% w/w, 9 μL). The sample-loaded grid was exposed to the stain for 30 s before removing the excess by blotting. Grids were dried using a vacuum hose. Imaging was performed at 120 kV using a FEI Tecnai G2 Spirit TEM instrument equipped with a Gatan 1kMS600CW CCD camera.

Synthesis of Statistical Copolymers

The copolymerization protocol for producing a P(A-stat-B) amphiphilic statistical copolymer, where A is hydrophobic comonomer and B is hydrophilic comonomer, is illustrated here for all cases by a synthesis of P(EMA-stat-MAA) with EMA to MAA molar ratio of 80:20 (EH₈₀₂₀, see Table 1).

Table 1. Summary of Experimental Data Obtained for P(A-stat-B) Copolymers, Where synth Denotes the Polymerization Method Used, (A:B) is the Molar Ratio of A and B Comonomers, M_n, M_w, and M_w/M_n are the Number-Average Molecular Weight, Weight-Average Molecular Weight, and Copolymer Dispersity Determined from GPC Analysis, Respectively (See Figure S5 for Representative GPC Traces).

				composition (A:B)a		GPCb
synth.	B	A	copolymer name	targeted	actual	Mn, kDa	Mw, kDa	Mw/Mn
RAFT	MAA (M)	MMA (M)	MM6040	60:40	62:38	21.5	30.4	1.42
			MM7030	70:30	71:29	28.0	39.8	1.42
			MM8020	80:20	81:19	25.6	31.0	1.21
			MM8812	88:12	88:12	27.3	32.8	1.19
			MM9010	90:10	90:10	23.6	29.6	1.25
			MM9505	95:05	95:05	23.1	28.7	1.24
			MM9802	98:02	97:03	21.7	26.8	1.24
		EMA (E)	EM6040	60:40	60:40	33.5	44.4	1.33
			EM7030	70:30	70:30	33.0	42.8	1.30
			EM8020	80:20	80:20	27.3	33.2	1.22
			EM8119	81:19	81:19	30.7	38.3	1.25
			EM8416	84:16	84:16	22.6	28.8	1.27
			EM8614	86:14	86:14	24.1	30.1	1.25
			EM9010	90:10	90:10	26.2	32.5	1.24
		BMA (B)	BM6040	60:40	61:39	37.9	44.6	1.18
			BM7030	70:30	71:29	36.4	45.4	1.25
			BM7525	75:25	76:24	35.2	44.9	1.28
			BM8020	80:20	80:20	39.0	48.8	1.25
			BM8515	85:15	86:14	33.6	40.6	1.21
			BM9010	90:10	90:10	27.1	30.1	1.11
		HMA (H)	HM5050	50:50	49:51	28.6	34.4	1.20
			HM6040	60:40	61:39	28.3	33.6	1.19
			HM7030	70:30	68:32	31.1	37.2	1.19
			HM8020	80:20	76:24	33.5	40.1	1.20
		EHMA (EH)	EHM3070	30:70	31:69	34.7	57.9	1.66
			EHM4060	40:60	41:59	37.0	48.8	1.31
			EHM5050	50:50	49:51	37.5	47.3	1.26
			EHM6040	60:40	61:39	40.8	54.7	1.34
			EHM7030	70:30	71:29	25.5	32.6	1.28
			EHM8020	80:20	80:20	29.8	33.0	1.11
	DMAEMA (D)	EMA (E)	ED8515	85:15	85:15	22.8	27.4	1.20
			ED9010	90:10	90:10	22.5	27.2	1.21
			ED9307	93:07	93:07	23.1	27.7	1.20
			ED9505	95:05	95:05	23.4	28.1	1.20
		BMA (B)	BD6040	60:40	61:39	26.9	34.4	1.28
			BD7030	70:30	68:32	28.7	36.4	1.27
			BD7525	75:25	73:27	28.9	36.4	1.26
			BD8020	80:20	78:22	29.4	35.6	1.21
			BD8515	85:15	84:16	26.0	32.0	1.23
		EHMA (EH)	EHD5050	50:50	51:49	31.1	38.6	1.31
			EHD6040	60:40	61:39	24.5	33.0	1.35
			EHD7030	70:30	71:29	22.2	28.2	1.27
FRP	MAA (M)	BMA (B)	BM7030(FRP)	70:30	69:31	13.2	23.9	1.81
			BM8020(FRP)	80:20	78:22	16.5	31.2	1.89
			BM9010(FRP)	90:10	88:12	11.5	21.2	1.85

^aCopolymer compositions were determined by ¹H NMR spectroscopy analysis of the respective alkylated copolymers.

^bThe GPC measurements were performed using THF eluent containing 0.025% w/v butyl hydroxytoluene (BHT) and either 4% v/v acetic acid or 1% v/v triethylamine against PMMA standards.

EMA (monomer A, 1.26 g, 11.1 mmol), MAA (monomer B, 0.238 g, 2.76 mmol), ACVA (4.70 mg, 0.017 mmol), and PETTC (17.1 mg, 0.050 mmol) were mixed in IPA (1.52 g) [1,4-dioxane was used instead of IPA for the P(BMA-stat-MAA) series] creating a 50% w/w monomer solution and placed in an ice bath to cool. The mixture was degassed with N₂ for 20 min and then heated to 70 °C to initiate the reaction. The copolymerization was allowed to proceed for 24 h before quenching by cooling to ambient temperature with concomitant exposure to air. The product was purified by precipitation from petroleum ether and then dried in a 30 °C vacuum oven overnight to give a pale-yellow powder.

Results and Discussion

Synthesis of Amphiphilic Statistical Copolymers

A series of methacrylic P(A-stat-B) ASCs was synthesized (Scheme 1a) in which the hydrophobic comonomer and the overall copolymer composition were systematically varied. Either anionic (MAA) or cationic (DMAEMA) monomers were used as the hydrophilic component (B) to examine whether the polarity of the surface charge had any influence. Five different alkyl methacrylates (e.g., MMA, EMA, BMA, HMA, or EHMA) were used in turn as the hydrophobic comonomer (A) to target a wide range of log P values, which is a commonly used parameter to quantify hydrophobicity/hydrophilicity (see Table S1).⁴²

P(A-stat-B) copolymers were synthesized via RAFT solution copolymerization (Scheme 1) targeting a consistent overall molecular weight (ca. 30 kDa) while varying the copolymer composition. With the exception of the P(BMA-stat-MAA) copolymer series, all of the RAFT-synthesized copolymers were prepared in IPA at 50% w/w. Kinetic studies of such batch copolymerization suggested that the instantaneous rate of consumption of the two comonomers was comparable throughout the course of the reaction (Figures S1 and S2). Thus, an approximately statistical distribution of the hydrophobic and hydrophilic comonomers within each copolymer chain can be assumed, and the final copolymer composition is close to that targeted. Recently, it was reported that copolymerization of BMA and MAA at 20% w/w in IPA produces somewhat “blocky” copolymer chains with an undesirable BMA-rich terminus caused by a significant reduction in the rate of consumption of the acidic comonomer toward the end of the reaction.³⁴ To avoid this problem, IPA was replaced with 1,4-dioxane while performing the copolymerization at the same 50% w/w concentration; this strategy resulted in both comonomers being consumed at comparable rates throughout the copolymerization (Figure S1c).

Each series forms stable colloidal dispersions of copolymer nanoparticles at different acid/amine contents depending on the nature of the hydrophobic alkyl methacrylate comonomer. For example, P(EHMA-stat-MAA) copolymers require a higher acid content to produce stable colloidal dispersions compared to P(MMA-stat-MAA) because EHMA is significantly more hydrophobic than MMA (Table 1).

Copolymer compositions were determined by ¹H NMR spectroscopy (after exhaustive alkylation in the case of the MAA-based copolymers; see Figures S3 and S4). As suggested by the kinetic analysis, the final copolymer compositions were always in good agreement with the initial comonomer feed ratios (Table 1). A consistent molecular weight was targeted for each copolymer to minimize the number of variables for a given copolymer type and composition. Copolymers within each comonomer series exhibited similar M_w values by GPC, but some discrepancies were observed between series (Table 1). Molecular weight data are expressed relative to PMMA calibration standards; thus, systematic differences between copolymer series are expected as each of the different hydrophobic components and compositions will result in different hydrodynamic volumes for a given chain length compared to the PMMA standards in the GPC eluent (THF).⁴³ Where the MAA weight fraction was high (e.g., MM₆₀₄₀, EHM₃₀₇₀), increased M_w/M_n was observed (Table 1), which is attributed to reduced solubility in the GPC eluent leading some aggregation. Previous research suggests little or no correlation between copolymer molecular weight and nanoparticle size for relatively high aggregation numbers.^33,34 Thus, minor inconsistencies between molecular weights are unlikely to adversely affect the particle size formed within this regime. However, for relatively low aggregation numbers, when copolymer interactions are mainly intramolecular in nature, the copolymer molecular weight may affect the particle size. In particular, this aspect should be taken into account when considering the formation of single-chain nanoparticles (for which the aggregation number is one).

One significant advantage of statistical copolymers is that they can be readily prepared by free-radical polymerization (FRP), which is a relatively simple and inexpensive process. Since FRP inevitably produces broad molecular weight distributions, a small series of P(BMA-stat-MAA) copolymers (Scheme 1c) comprising 10–30 mol % MAA was prepared using FRP (M_w/M_n > 1.85) instead of RAFT polymerization (M_w/M_n < 1.50) to assess the effect of the polymerization method and copolymer dispersity on the self-assembly behavior, see Table 1.

Self-Assembly of Amphiphilic Statistical Copolymers

Aqueous dispersions of ASC nanoparticles were obtained using a solvent-switch method. Each copolymer was initially dissolved at 50% w/w in a good solvent (IPA) and then diluted slowly using water. Dilution of MAA-based copolymers was performed in the presence of triethanolamine (TEA; 1.1 equiv relative to MAA residues). This organic base deprotonates the MAA comonomer units, thereby producing the anionic surface charge required to stabilize the copolymer nanoparticles. Conversely, dilution of the DMAEMA-based copolymers was performed in the presence of sufficient acetic acid to protonate the pendent tertiary amine groups and hence confer a cationic surface charge. In each case, slow addition of water drives in situ intramolecular and intermolecular self-assembly of the strongly amphiphilic copolymer chains. The hydrophobic alkyl methacrylate repeat units self-assemble to form nanoparticles that are stabilized by the charged hydrophilic groups. Copolymer dispersions were diluted to 1.0% w/w to (i) minimize the volume fraction of the remaining water-miscible good solvent (IPA) and (ii) reduce the interparticle interactions that are present at higher copolymer concentrations. The pH of the 1.0% w/w anionic dispersions was measured to be around 8, which is much higher than the pK_a of MAA (pK_a ∼ 4–5)⁴⁴ providing evidence that all (99.9%) of the MAA units are deprotonated. Likewise, the pH of the cationic dispersions were approximately 4, which is much lower than the pK_a of DMAEMA (pK_a ∼ 7)⁴⁵ verifying that the all (99.9%) DMAEMA units are protonated.

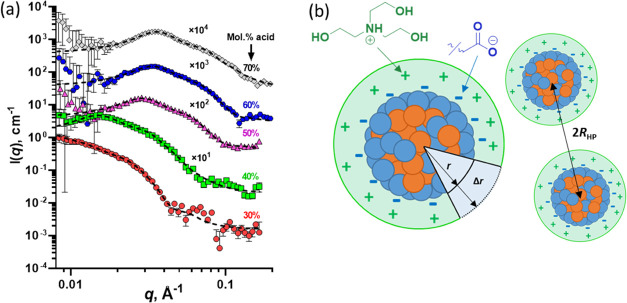
SAXS was utilized to investigate the copolymer morphology of the colloidal dispersions. SAXS patterns recorded for 1.0% w/w dispersions of the MAA-based copolymers indicated the formation of spherical nanoparticles (Figures 1a and S6), which is consistent with prior studies of closely related copolymers.³⁴ Additionally, well-defined spherical particles were observed by TEM (Figure S7) further validating the self-assembly of these copolymers. However, TEM is not an ideal structural analysis method for this study as the particle dimensions are often below the reliable resolution of the microscope. Moreover, the particle shape might be distorted during the sample preparation. Especially, when the glass transition temperatures (T_g) of both PHMA and PEHMA are below room temperature and particles formed by the associated copolymers will not retain the structure once dried. Instead, SAXS was chosen as particles can be assessed in their dispersed state in situ and nanoparticle dimensions can be measured with a high degree of accuracy. In addition, SAXS is a much more statistically reliable method in a comparison with microscopy techniques as scattering data are collected from a relatively large sample volume and, therefore, are averaged over millions of particles. The scattering patterns can be satisfactorily fitted using an intensity equation (see the Supporting Information, eqs S1, S34, or S35) incorporating a spherical core–shell form factor (eqs S8–S11), which accounts for a “shell” of cations (protonated TEA molecules) that are associated with the anionic nanoparticles (Figure 1b). This structural feature cannot be ignored in the scattering analysis because the scattering length density (SLD) of TEA is substantially greater than that of water (ξ_TEA = 10.54 × 10¹⁰ cm^–2 and ξ_water = 9.42 × 10¹⁰ cm^–2), which produces significant contrast. The mean thickness of the TEA cationic shell (Δr, Figure 1b) is fixed at 6 Å during the fitting. This value corresponds to the approximate length of a single TEA unit within the shell (eq S12). Furthermore, the SLD of this cationic TEA shell is highly dependent on the volume fraction of water molecules within it. Following the earlier PSC model,³⁴ it was assumed that all of the MAA repeat units are located at the surface of the nanoparticles (i.e., k = 1, where k is the fraction of surface-confined MAA units relative to all available MAA units). Further, it was assumed that every surface-confined anionic MAA unit has an associated protonated TEA cation. Based on these assumptions, the relative volumes of TEA and water within the cationic shell can be estimated for the core–shell model (eqs S13–S16), enabling the shell SLD to be calculated from the nanoparticle size when fitting the SAXS patterns. According to prior studies of a closely related ASC system, the solvent concentration within the nanoparticle cores is close to zero (about a few vol %).³⁴ Thus, to simplify the SAXS model, it is assumed in the SAXS analysis that the solvent volume fraction in the particle core, x_sol, equals zero.

Figure 1.

(a) SAXS patterns recorded for 1.0% w/w aqueous dispersions of P(EHMA-stat-MAA) copolymer nanoparticles (symbols) using a Bruker AXS Nanostar instrument. A core–shell form factor (dotted lines; eqs S8–S11) was fitted to determine the mean size of nanoparticles formed by copolymers comprising 30, 40, 50, 60, or 70 mol % MAA. Patterns are shifted upwards by arbitrary numerical factors (indicated on the plot) to aid clarity. (b) Schematic cartoon of the core–shell model used to fit the SAXS patterns accounting for the hydrated shell of TEA cations surrounding each nanoparticle, where r is the nanoparticle radius, Δr is the thickness of the cation shell, and 2R_HP is the interparticle distance determined using the Hayter–Penfold approximation for the charged sphere structure factor. A protonated TEA molecule (cation, green) and an ionized MAA unit in its anionic carboxylate form (anion, blue) are also shown.

A high q plateau (q > 0.1 Å^–1) is observed in the scattering patterns recorded for most of the copolymer dispersions (Figures 1a, 2a, S6, and S9). This structural feature has been observed for similar ASC systems^34,46 and is possibly associated with electron density fluctuations within the nanoparticles owing to the statistical distribution of comonomer repeat units and/or thermal motion of the copolymer chains. A linear background intensity was incorporated into the intensity equation to account for this feature (eq S34). In some cases, there is an upturn at low q (q < 0.015 Å^–1) caused by nanoparticle clusters formed as a result of their strong charges fixing them in space with respect to each other so they appear as a larger coherent structure. This feature requires a power law function to be incorporated into the intensity equation (eq S35). Fitting the modified intensity equation (either eqs S34 or S35) to the SAXS patterns enabled calculation of the mean nanoparticle radius (R, Table 2). However, similar results were obtained if the low q upturn intensity region was excluded from the analysis and each SAXS pattern was fitted with the unmodified intensity equation (eq S1).

Figure 2.

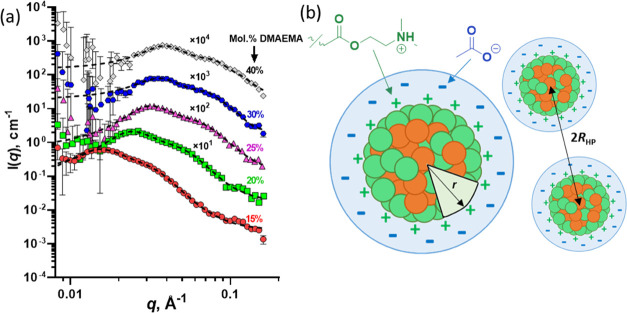
(a) SAXS patterns recorded using a Bruker AXS Nanostar instrument for 1.0% w/w aqueous dispersions of P(BMA-stat-DMAEMA) copolymer nanoparticles (symbols) fitted using a sphere model (eq S7) (dotted lines) to calculate the mean nanoparticle radius for copolymers comprising 15, 20, 25, 30, or 40 mol % DMAEMA. Some patterns are shifted upwards by arbitrary numerical factors to aid clarity. (b) Schematic cartoon showing how the anions surround the cationic nanoparticles to form a hydrated anionic shell, where r is the nanoparticle radius and 2R_HP is the interparticle distance determined using the Hayter–Penfold approximation for the charged sphere structure factor. A protonated DMAEMA unit (cation, green) and an ionized acetate (anionic, blue) are also shown. Since the SLD of acetic acid is close to that of water and the SLD contrast between the copolymer and water is high, these SAXS measurements are not sensitive to the anionic shell. Thus, SAXS patterns are satisfactorily fitted using a simplified sphere form factor (eq S7) rather than the more complicated core–shell form factor required for anionic copolymer dispersions (Figure 1).

Table 2. Summary of Structural Characteristics Obtained from SAXS Analysis of 1.0% w/w Dispersions of Anionic P(A-stat-MAA) Amphiphilic Statistical Copolymers (Where A Denotes MMA, EMA, BMA, HMA, or EHMA): the Mean Particle Radius (R) and Its Corresponding Standard Deviation (σ_R), the Mean Aggregation Number (N_agg) as Calculated Using eq S6 and Rounded to the Nearest Integer, and the Spheroidal Particle Aspect Ratio (α).

	form factor parameters
copolymer	R (Å)	σR (Å)	Nagg	α
MM6040	13	1	1a,b	3.96
MM7030	13	1	1a,b	3.95
MM8020	12	9	1b	1
MM8812	19	14	1b	1
MM9010	24	20	2	1
MM9505	40	20	7	1
MM9802	87	19	71	1
EM6040	15	1	1a,b	3.18
EM7030	14	8	1b	1
EM8020	20	11	1b	1
EM8119	28	13	2	1
EM8416	34	11	4	1
EM8614	39	12	6	1
EM9010	68	21	30	1
BM6040	26	6	2	1
BM7030	35	7	4	1
BM7525	51	10	12	1
BM8020	49	11	11	1
BM8515	78	13	43	1
BM9010c
HM5050	26	5	2	1
HM6040	35	6	4	1
HM7030	48	9	10	1
HM8020	72	13	32	1
EHM3070	37	10	5	1
EHM4060	47	13	9	1
EHM5050	58	18	27	1
EHM6040	88	23	58	1
EHM7030	105	20	97	1
EHM8020c
BM7030(FRP)	35	13	5	1
BM8020(FRP)	66	16	25	1
BM9010(FRP)	137	33	281	1

^aFitted using a spheroid model for anisotropic particles with an aspect ratio greater than unity.

^bAssigned to single-chain nanoparticles, although their N_agg is not exactly one.

^cThese copolymer compositions did not form stable colloidal dispersions when diluted with water.

Despite the relatively low copolymer concentration used for these measurements, each SAXS pattern exhibits a structure peak at low q (0.01 Å^–1 < q < 0.05 Å^–1), indicating interactions between neighboring particles (Figures 1a and S6). This phenomenon was observed in previous work³⁴ and is well known in dispersions of charged copolymer nanoparticles in aqueous media,⁴⁷ where the interaction distance is controlled by the copolymer concentration, the nanoparticle surface charge, and the dielectric constant of the solvent.^35,36 Accordingly, the Hayter–Penfold approximation for the charged sphere structure factor⁴⁸ (eq S33) was incorporated into the intensity equation (eqs S1, S34, or S35) to describe the particle interactions. This structure factor includes the effective radius equivalent to half of the mean interparticle distance from the center of one particle to the center of another (R_HP), the effective volume fraction (f_HP), the ionic strength of the solvent (M), the absolute temperature (T), and the solvent dielectric constant (ε) and the particle charge expressed in electrons (Q). However, the structure factor function is mainly used in this study as an analytical expression for the scattering analysis, and it is shown that the obtained form factor results (in particular, the particle radius) are virtually independent of the structure factor used [i.e., Hayter–Penfold or a hard-sphere structure factor solved with the Percus–Yevick closure relation^49,50 (commonly used in scattering models for counting an effect of particle interactions)] within the intensity equation for a wide range of copolymer dispersions (Table S2). SAXS analysis indicates that larger nanoparticles are always obtained as the MAA content is reduced for all five series of copolymer compositions, regardless of the type of hydrophobic comonomer (Table 2). For example, the particle size increases from 37 to 105 Å in the EHM series as the acid content is reduced from 70 to 30 mol %, while the particle size increases from 20 to 68 Å in the EM series as the acid content is lowered from 20 to 10 mol %. This finding is consistent with data obtained earlier for closely related systems.³⁴ Furthermore, an approximate mean aggregation number (N_agg) can be calculated by dividing the mean volume of a spherical nanoparticle by the volume occupied by a single copolymer chain (eq S6). Since the molecular weight and thus the volume occupied are similar for all of the copolymers, N_agg increases for larger particles (Table 2). Moreover, for an aggregation number of one, the nanoparticle volume is simply equal to that of an individual copolymer chain. The finding that the size of the dispersion is fundamentally determined by the copolymer acid (solvophilic component) content and is independent of the copolymer molecular weight³⁴ offers very simple design rules for controlling the size of spherical particles formed by statistical copolymers. These design rules can also be considered substantially simpler than the established relationships for diblock copolymer particle size based on scaling factors^13,51,52 and packing parameters.^14,53

A stabilization limit was observed within the BMA and EHMA series, whereby the BM₉₀₁₀ and EHM₈₀₂₀ copolymers form macroscopic precipitates rather than colloidally stable nanoparticles (Table 2 and Figure S8). Presumably, the acid content of such copolymers is insufficient to confer colloidal stability. This suggests that the nanoparticle formation is confined to a finite range of copolymer compositions, whereby the surface charge density is sufficient to ensure the nanoparticle stabilization.

In the MMA and EMA copolymer series (abbreviated to MM and EM, respectively), SAXS analysis indicates that N_agg becomes one at higher MAA contents (Table 2). This means that the copolymer chains no longer self-assemble via intermolecular hydrophobic interactions but instead form single-chain nanoparticles (SCNP) or self-folded chains through intramolecular hydrophobic interactions.⁵⁴⁻⁵⁸ The critical acid content at which SCNPs are formed depends on the alkyl methacrylate comonomer. Thus, SCNPs are formed at (or above) 12 mol % MAA for the MM series, whereas the EMA series requires an acid content of at least 20 mol %. However, the BMA, HMA, and the EHMA series do not form SCNPs within the compositional range studied herein (Table 2), presumably owing to the greater hydrophobic character conferred by the larger alkyl groups.

When SCNPs are formed, SAXS analysis indicates that the particles become anisotropic. In this case, satisfactory data fits to the scattering patterns could only be obtained using a spheroidal form factor (eqs S2–S5) that incorporates an aspect ratio parameter for elongated (ellipsoidal) nanoparticles (Figure S12). This is because higher acid contents lead to more hydrophilic copolymer chains that eventually become molecularly dissolved in aqueous media. Moreover, it is well known that poly(methacrylic acid) forms either an extended structure in its highly ionized form or a relatively compact, globular structure in its neutral form.⁵⁹⁻⁶² Thus, given that these MAA-rich copolymers are dispersed at around pH 8, such elongated structures are consistent with the behavior observed for highly ionized poly(methacrylic acid).⁵⁹⁻⁶² Furthermore, this nanoparticle anisotropy is consistent with studies performed by Stals et al. on hydrogen-bonded SCNPs, which fold to produce asymmetric structures.⁶³ Like the majority of the anionic nanoparticles (Table 2), SAXS analysis of cationic P(A-stat-DMAEMA) ASC systems indicate the formation of spherical nanoparticles (Figures 2 and S10). However, in this case, the hydrated cationic shell should have an SLD similar to the background solvent (ξ_acid = 9.32 × 10¹⁰ cm^–2 and ξ_water = 9.42 × 10¹⁰ cm^–2) and the copolymers have relatively high SLDs compared to water, so such SAXS measurements should not be particularly sensitive to the ionic shell. Thus, the SAXS patterns could be satisfactorily fitted using a simplified sphere form factor (eq S7) that does not account for the hydrated shell of counterions, rather than a core–shell model. The sphere model is simply described by the nanoparticle radius (r) corresponding to the core where the additional shell is ignored (Figure 2b).

Like the anionic nanoparticles, a structure factor peak is observed in the SAXS patterns recorded for the cationic nanoparticles (Figures 2a and S10). This feature indicates that there is a relatively strong interaction between neighboring nanoparticles. As before, the Hayter–Penfold structure factor (eq S33) was incorporated into the intensity function (eqs S1, S34, or S35) to account for this interaction. Structural analysis of all three copolymer series indicates that larger nanoparticles are always obtained as the DMAEMA content is reduced, regardless of the type of hydrophobic comonomer (Table 3); this finding is fully consistent with the SAXS data obtained for the P(A-stat-MAA) copolymer series (Table 2). Moreover, this result further validates the conclusion that the size of the particles formed by an amphiphilic statistical copolymer can be controlled simply by the solvophobic component content.

Table 3. Summary of the Structural Characteristics of 1.0% w/w Aqueous Dispersions of P(A-stat-DMAEMA) Amphiphilic Statistical Copolymers (Where A Denotes EMA, BMA, or EHMA) Obtained from SAXS Analysis: the Mean Particle Radius (R) and its Corresponding Standard Deviation (σ_R), and the Mean Aggregation Number (N_agg) Calculated Using Eq S6, and Rounded to the Nearest Integer.

	form factor
copolymer	R (Å)	σR (Å)	Nagg
ED8515	26	10	2
ED9010	36	20	4
ED9307	43	21	7
ED9505	53	21	13
BD6040	25	7	1a
BD7030	31	3	3
BD7525	34	4	3
BD8020	43	9	7
BD8515	60	31	19
EHD5050	37	5	4
EHD6040	44	3	8
EHD7030	62	2	21

^aAssigned to single-chain nanoparticles, although their N_agg is not exactly one.

SAXS analysis indicates that most of the amphiphilic copolymers self-assemble to form spherical nanoparticles when using the solvent-switch method regardless of the polarity of the surface charge conferred by the hydrophilic comonomer. Moreover, the particle size is strongly dependent on both the copolymer composition and also on the nature of the alkyl methacrylate comonomer. Relatively hydrophobic copolymers form macroscopic precipitates, rather than stable colloidal dispersions. Furthermore, relatively hydrophilic copolymers form distinctly anisotropic single-chain nanoparticles similar to that expected for highly ionized homopolymers.

Relationship between Nanoparticle Size and Copolymer Composition

SAXS analysis has shown that the nanoparticle size is strongly dependent on the hydrophilic comonomer content of these amphiphilic statistical copolymers (Tables 2 and 3). This is consistent with the previously proposed PSC model.³⁴ This simple model assumes (i) perfectly spherical particles, (ii) a constant surface charge density across a copolymer series regardless of the copolymer composition, and (iii) that there is no solvent present within the nanoparticle (i.e., x_sol = 0). In this prior study, it was found that a critical fractional surface coverage (SA_frac.) by anionic (B) units is required for colloidal stability.

The spherical nanoparticle surface area can be calculated from the particle radius (R). Thus, if SA_frac. is independent of the nanoparticle size, the mean number of anionic B groups per nanoparticle (N_B,p) can be estimated using

1

where CS_B is the cross-sectional area of a single B repeat unit calculated from the approximate volume of a single B unit, V_B (CS_B = V_B^2/3) and k is the fraction of the B groups located at the particle surface. k equals 1 when all of the anionic B groups are located at the nanoparticle surface. Alternatively, if all of the B units are buried within the nanoparticle cores, k equals 0. In the latter case, the nanoparticles are not colloidally stable (N_B,p tends to infinity, suggesting that an infinitely large particle would be required to form a stable dispersion). Since the size of particles formed by statistical copolymers is independent of their molecular weight, the chosen definition of N_B,p (eq 1) enables the molecular weight to be excluded from the calculation.

The mean number of hydrophobic alkyl methacrylate (A) repeat units can be obtained from the volume of the hydrophobic domain within a nanoparticle, which is equal to the difference between the overall nanoparticle volume and the volume occupied by the B repeat units in the same nanoparticle, divided by the approximate volume of a single hydrophobic unit (V_A)

2

Using both N_B,p and N_A,p, the mole fraction of B groups in a nanoparticle, x_B, can be calculated

3

This parameter is equivalent to the B mole fraction in the copolymer so eqs 1–3 provide a relationship between the particle radius and the copolymer composition. If the B content is sufficiently high, then the amphiphilic copolymer chains undergo intramolecular hydrophobic interactions to form SCNPs or self-folded chains. At this point, the particle volume is simply equal to the volume of a single copolymer chain. Hence, the corresponding copolymer compositions do not fit the PSC model (eqs 1–3) because the condition that the particle size is independent of polymer molecular weight is no longer valid. It follows that the data points corresponding to SCNPs should be excluded from any analysis based on this model. Furthermore, if the ionic comonomer content is sufficiently high, then the individual copolymer chains will be molecularly dissolved. Conversely, as the mole fraction of B tends toward zero then R tends to infinity, with infinitely large particles corresponding to the macroscopic precipitation that is observed when the mole fraction of B is insufficient to confer colloidal stability (Figure S8).

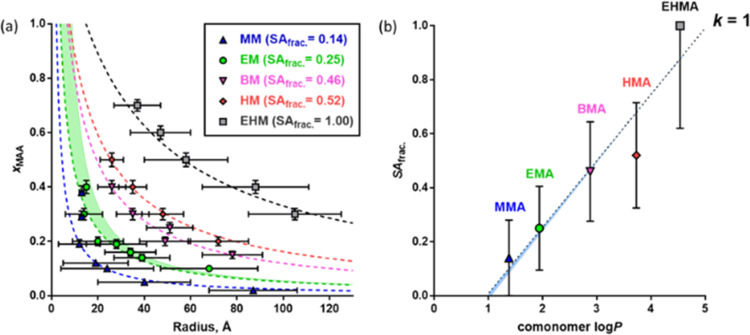
Bearing these important caveats in mind, the proposed PSC model was initially used to fit the mean particle radius for each anionic ASC series (Table 2) and hence predict the mean surface area fraction for the MAA repeat units (Figure 3a). Initially, it was assumed that all of the MAA units were located on the nanoparticle surface, i.e., k = 1. This simple model provided a good fit to all of the experimental data, with larger nanoparticles always being formed by copolymers with lower acid contents. Such good agreement between the experimental data and the model fit for the five series of anionic copolymers (Figure 3a) validates the assumption that a constant surface charge density is required for a particular pair of comonomers to form self-assembled nanoparticles, regardless of their molar ratio. Furthermore, the PSC model provided good data fits regardless of whether the copolymerization has pseudo-living or nonliving character (i.e., RAFT polymerization vs FRP, Figure S11). This indicates that this model is insensitive to the copolymer molecular weight distribution.

Figure 3.

(a) Relationship between the mole fraction of MAA units in the amphiphilic statistical copolymer chains, x_MAA, and the corresponding mean radius of the nanoparticles formed by the self-assembly of such copolymers in aqueous solution: experimental data (symbols) fitted by the PSC model (dashed lines) assuming that k = 1 (eqs 1–3). Color-coded values of the MAA fractional surface coverage (SA_frac.) obtained by the PSC model fitting are given for each series. The green shaded area indicates the effect of nanoparticle hydration on the PSC model. The bars plotted for each point in the direction of the x-axis correspond to the standard deviation in the mean nanoparticle radius. (b) Plot of SA_frac. values obtained by fitting the PSC model for each copolymer series (symbols) against log P for the respective alkyl methacrylate comonomers: a linear fit to the data (dotted line) was obtained using the equation SA_frac. = 0.246 × log P – 0.237. The narrow blue shaded area indicates the minimal effect of nanoparticle hydration on the linear relationship. The bars plotted for each point indicate the range of SA_frac. values estimated from the standard deviation in the nanoparticle radius.

The PSC model assumes that there is no solvent present within the nanoparticles. This has been confirmed for the BM series³⁴ and is also likely to be the case for the more hydrophobic comonomers (i.e., HMA and EHMA). However, it may not necessarily be true for less hydrophobic comonomers such as MMA and EMA. In this latter case, the effect of nanoparticle hydration on the PSC model can be explored by assuming that x_sol is proportional to x_B (i.e., x_sol = γ × x_B). Even for an extreme scenario, where the x_sol is equal to x_B (γ = 1), the effect of nanoparticle hydration on this simple PSC model is minimal (Figure 3a, green shaded area), so any deviation from the modeled SA_frac. is negligible [EM SA_frac. = 0.25 (γ = 0) and 0.23 (γ = 1)].

For the copolymer series with differing hydrophobic A units (Figure 3a), incorporating a more hydrophobic comonomer at a given (fixed) MAA content always produces larger nanoparticles. This is because of the difference in critical surface charge density required for colloidal stability. For example, the PSC model indicates that the HM copolymer series requires 52% surface coverage of the nanoparticles by MAA units, whereas only 14% surface coverage is required for the MM copolymer series (Figure 3a). These observations are consistent with the greater hydrophobic character of HMA compared to MMA. To achieve a higher surface charge density for the same mole fraction of MAA units, the copolymer aggregation number must increase to reduce the particle surface-to-volume ratio and hence increase the number of surface-confined MAA units. This leads to a larger overall copolymer volume per nanoparticle and hence a corresponding increase in the mean nanoparticle radius (Figure 3a, compare nanoparticle radii observed for copolymers with comparable MAA contents). For the EHM series, the modeled SA_frac. reaches the PSC model’s theoretical limit of 1 (i.e., the entire nanoparticle surface is covered with MAA units), which is not physically realistic. It is rather unlikely that all of the MAA units are simultaneously co-located at the nanoparticle surface owing to the statistical distribution of this comonomer along the copolymer backbone. Hence, the earlier assumption that k = 1 may not be valid. If k < 1, then the modeled SA_frac. will be reduced accordingly so the EHM series will no longer achieve the maximum SA_frac. of 1. It should also be noted that the dispersions were formulated so that the MAA units were fully ionized (pH ∼ 8). However, it is probable that a reduction of MAA ionization will lead to a higher SA_frac. being required for stabilization and could eventually lead to mass precipitation due to insufficient charge stability. Although this simple PSC model provides good fits to the experimental data, it would be more useful to relate the model parameters to the hydrophobic character of the alkyl methacrylate comonomer. The partition coefficient (log P) is commonly used to rank the hydrophobic character of compounds: it is defined as the concentration distribution of a compound between two immiscible solvents, typically water and n-octanol, and can be used to quantify the hydrophobicity of methacrylic monomers.⁶⁴⁻⁶⁷ Recently, this approach has also been used to predict suitable water-miscible monomers for RAFT aqueous dispersion polymerization formulations.⁶⁷ The relationship between log P for the hydrophobic comonomer and SA_frac., as determined from the PSC model fitting assuming that all of the MAA units are located at the nanoparticle surface (k = 1) (Figure 3a), can be satisfactorily fitted using a linear function: [SA_frac. = 0.246 × log P – 0.237; R² = 0.91] (Figure 3b). This equation can be used to predict the self-assembly behavior of other methacrylic ASCs: given the log P of the hydrophobic comonomer, a corresponding SA_frac. may be estimated and then the nanoparticle size is determined using the PSC model (eqs 1–3).

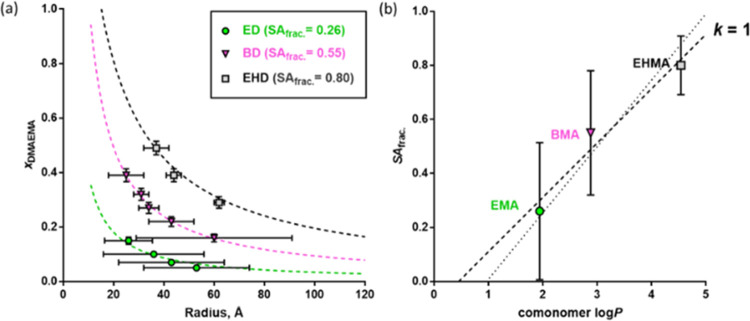
The PSC model was also used to establish the size-composition relationship for the cationic copolymer series (Table 3). Good data fits are obtained (Figure 4a), justifying the hypothesis that the nanoparticle size is determined by achieving the critical surface charge density required for a stable colloidal dispersion. Furthermore, the critical surface charge density or fraction of the nanoparticle surface area covered by DMAEMA repeat units (SA_frac.) can be determined using the PSC model. In agreement with the anionic copolymer series, SA_frac. increases when using more hydrophobic alkyl methacrylate comonomers. If k = 1, only 26% of the nanoparticle surface needs to be covered by DMAEMA repeat units to form stable colloidal dispersions for the ED series. On the other hand, 80% coverage is required for the EHD series (Figure 4a) since EHMA is a much more hydrophobic comonomer than EMA.

Figure 4.

(a) Relationship between the mole fraction of DMAEMA repeat units in the amphiphilic statistical copolymer chains, x_DMAEMA, and the corresponding mean radius of nanoparticles formed by their self-assembly in an aqueous solution: experimental data (symbols) are fitted by the PSC model (dashed lines) assuming that k = 1 (eqs 1–3). Color-coded DMAEMA fractional surface coverages (SA_frac.) obtained by PSC model fits are given for each series. The bars plotted for each point in the direction of the x-axis correspond to the standard deviation in the nanoparticle radius. (b) Plot of SA_frac. values obtained by fitting the PSC model for each copolymer series (symbols) against log P for the respective alkyl methacrylate comonomers: a linear fit to the data (dotted line) was obtained using the equation SA_frac. = 0.201 × log P – 0.091. The linear trend of the anionic series (from Figure 3b) is also shown for comparison (dotted line). The bars plotted for each point indicate the range of SA_frac. estimated from the standard deviation in the nanoparticle radius.

The log P values for the hydrophobic comonomers were plotted against SA_frac, as determined from the PSC model by assuming k = 1. In analogy with the anionic copolymer series, a linear function could be fitted to the data [SA_frac. = 0.201 × log P – 0.091; R² = 0.96] (Figure 4b). This relationship between log P and SA_frac. can be used to predict the behavior of other P(A-stat-DMAEMA) amphiphilic copolymers. Furthermore, a strong correlation between the linear fits is observed for the anionic and cationic copolymer series (Figure 4b, dashed line vs solid line). Thus, the PSC model appears to be universal for describing the aqueous self-assembly behavior of charged amphiphilic statistical copolymers that comprise a pair of hydrophilic and hydrophobic comonomers.

Determination of Internal Particle Structure Using Contrast Variation SANS

Since the ionic comonomer repeat units are statistically distributed along each copolymer chain, the formation of well-defined hydrophilic and hydrophobic domains within the nanoparticles seems unlikely. Indeed, satisfactory fits to the scattering patterns recorded for these amphiphilic copolymer nanoparticles can be obtained when they are described as homogeneous spheres (Figures 1, 2, S6, and S10). However, according to the PSC model analysis (Figures 3 and 4), the MAA (or DMAEMA) repeat units should be located preferentially at the nanoparticle surface to confer sufficient surface charge density for colloidal stability. Therefore, it is likely that such nanoparticles actually comprise a thin “shell-like” surface layer enriched with the ionic comonomer and a “core-like” region composed mainly of the hydrophobic alkyl methacrylate comonomer (Figure 5a). In the initial analysis (Figures 3a and 4a), it was assumed that all of the ionic comonomer repeat units were located at the nanoparticle surface (k = 1). However, their statistical distribution along the copolymer chains suggests that at least some of these ionic groups may be located within the interior of the nanoparticles (i.e., k < 1). In this respect, experimental determination of the mole fraction of the ionic comonomer repeat units at the nanoparticle surface would enable the refinement of the PSC model.

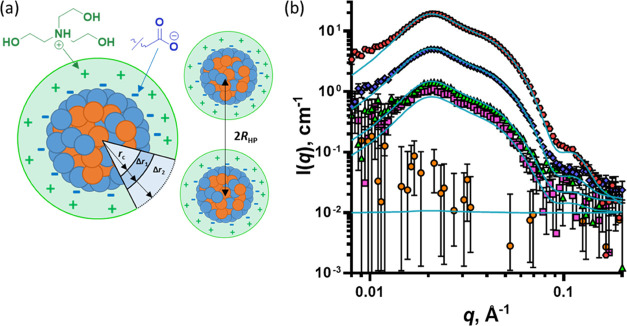
Figure 5.

(a) Schematic cartoon describing the core–shell–shell model used to fit the SANS data that accounts for the preferential location of the BMA units within the core, the preferential location of the MAA units at the particle surface (inner shell), and the hydrated outer shell of TEA cations surrounding the nanoparticles, where r_c is the nanoparticle core radius, Δr₁ is the thickness of the MAA-rich inner shell, Δr₂ is the thickness of the cation outer shell, and 2R_HP is the mean interparticle distance. (b) SANS patterns recorded for 2.0% w/w aqueous dispersions of BM₈₀₂₀ in five different H₂O/D₂O binary mixtures (symbols). For this contrast variation experiment, the solvent SLD corresponds to −0.56 × 10¹⁰ cm^–2 (H₂O; pink squares), 0.58 × 10¹⁰ cm^–2 (83.5:16.5 H₂O/D₂O; orange circles), 2.20 × 10¹⁰ cm^–2 (60:40 H₂O/D₂O; green triangles), 3.58 × 10¹⁰ cm^–2 (40:60 H₂O/D₂O; blue diamonds), and 6.33 × 10¹⁰ cm^–2 (D₂O; red hexagons). All five data sets were fitted simultaneously using a spherical core–shell–shell nanoparticle model (eqs S17–S29) (turquoise solid lines).

Accordingly, contrast variation SANS experiments were performed on nanoparticles formed by one of the anionic copolymers (BM₈₀₂₀) to examine their internal structure. This particular copolymer was chosen for SANS measurements because it is representative: BMA exhibits an intermediate log P value and BM₈₀₂₀ lies in the middle of the BMA copolymer series. In addition, it was previously demonstrated that the solvent (water) does not penetrate the BM nanoparticles,³⁴ which should simplify the SANS analysis. Since H₂O and D₂O exhibit differing neutron SLDs (−0.56 × 10¹⁰ and 6.33 × 10¹⁰ cm^–2, respectively),⁶⁸⁻⁷⁵ H₂O/D₂O mixtures can be used to adjust the SLD of the solvent environment (ξ_sol) to highlight any hydrophilic or hydrophobic domains that may be present in the copolymer nanoparticles. Thus, 2% w/w dispersions of BM₈₀₂₀ were prepared in H₂O, D₂O, and several H₂O/D₂O mixtures (comprising 83.5:16.5, 60:40, and 40:60 compositions by volume, which correspond to ξ_sol values of 0.58 × 10¹⁰, 2.20 × 10¹⁰, and 3.58 × 10¹⁰ cm^–2, respectively, see eq S23). TEA was added during the formulation of the dispersions so that all MAA units were ionized (pH 8). SANS patterns were recorded for all five dispersions (Figure 5b). Following the general approach and principles adopted for the SAXS data analysis (Figure 1), each SANS pattern could be fitted reasonably well using a core–shell model.

Assuming that the MAA comonomer is preferentially located near the nanoparticle surface, a more sophisticated spherical core–shell–shell model (Figure 5a) should be more appropriate for analyzing the SANS patterns. Thus, all patterns were fitted using the core–shell–shell model (eqs S17–S29) where the core corresponds to a BMA-rich region, the inner shell is the MAA-rich anionic surface layer, and the outer shell represents the protonated TEA counterions (Figure 5). To account for interactions between such anionic nanoparticles, the Hayter–Penfold approximation for a charged sphere structure factor (eq S33) was included in the intensity equation (eq S34). To ensure that the model was physically realistic, a number of constraints were incorporated. The 80:20 BMA/MAA copolymer composition was fixed, and the overall nanoparticle composition should be identical to that of the copolymer. Thus, the SLDs of the core and the first shell, which are each formed by redistribution of the comonomer repeat units within the nanoparticles, were related to each other via the copolymer composition (eqs S24–S29). In other words, if the nanoparticle shell is MAA-rich, then the particle core must be depleted in MAA to the same extent. Furthermore, the inner shell thickness (Δr₁) was fixed at 5 Å, which corresponds to the approximate dimensions of a single MAA repeat unit (eq S30). Finally, like the SAXS analysis, the outer shell thickness was fixed at 6 Å, which corresponds to the approximate dimensions of an individual protonated TEA counterion, and the SLD of this cationic shell was calculated from the fraction of MAA repeat units located at the nanoparticle surface.

It is worth noting that analysis of the SANS and SAXS patterns recorded for the BM₈₀₂₀ dispersion using a simple sphere model (eq S7) yielded apparently inconsistent nanoparticle dimensions. More specifically, SAXS indicated a mean radius of 58 Å while SANS suggested a mean radius of 49 Å. This difference is attributed to the presence of the TEA cation shell as its SLD contrast in respect to the surrounding solvent is significantly higher for X-rays than for neutrons. This observation highlights the presence of the cationic TEA shell surrounding the anionic nanoparticles. Using a core–shell model to fit the SAXS pattern of BM₈₀₂₀ dispersions, a nanoparticle mean radius of 49 Å was calculated (Table 2). This is in good agreement with the mean radius reported by SANS, which is less sensitive to the cationic TEA shell. Initial analysis of the contrast variation SANS data performed for the five patterns individually indicated that the SLD of the first shell was always higher than that of the core. This suggests that the MAA residues (which have a higher neutron SLD than the BMA residues) are preferentially located at (or near) the surface. However, the first shell SLDs obtained for each of the measurements were spread over a relatively broad range of values. Thus, all contrast variation SANS patterns were fitted simultaneously to provide more statistically robust and reliable information. To achieve this, it was assumed that all copolymer dispersions differ only in terms of their SLD contrast relative to the aqueous continuous phase. Thus, SANS patterns were fitted simultaneously using certain global parameters for the contrast series such as mean nanoparticle radius (and its associated standard deviation), inner shell thickness, outer shell thickness, degree of hydration of the outer shell (calculated based on the proportion of surface MAA units as for the SAXS analysis), and the mean SLD for the nanoparticle core and shell components. A plugin describing the structural model (eqs S17–S29) has been coded for the SASfit package⁷⁶ to perform this analysis. Satisfactory fits were obtained for all five SANS scattering patterns (Figure 5b), allowing the mean radius for the nanoparticle core and SLDs for the nanoparticle core and shell to be determined (R_c = 41 Å, ξ_core = 0.61 × 10¹⁰ cm^–2, and ξ_shell = 0.72 × 10¹⁰ cm^–2, respectively).

According to this SANS analysis, the nanoparticle core has a lower neutron SLD than the shell (ξ_core < ξ_shell). By comparing these values with those obtained for ξ_BMA and ξ_MAA (0.55 × 10¹⁰ and 1.38 × 10¹⁰ cm^–2, respectively), calculated using respective mass densities of PBMA and PMAA (ρ_BMA = 1.05 g cm^–3 and ρ_MAA = 1.25 g cm^–3), it can be concluded that approximately half of the MAA residues are located within the nanoparticle cores while the remainder are within the thin shell at the nanoparticle surface (eqs S36–S38). Thus, the copolymer nanoparticle surface is certainly enriched with anionic MAA residues, but only about 50% of the available MAA groups are actually located there (i.e., k ∼ 0.5). This is physically reasonable as the statistically distributed MAA residues are constrained within the copolymer chains; this reduces their mobility and results in a significant proportion remaining within the nanoparticle cores.

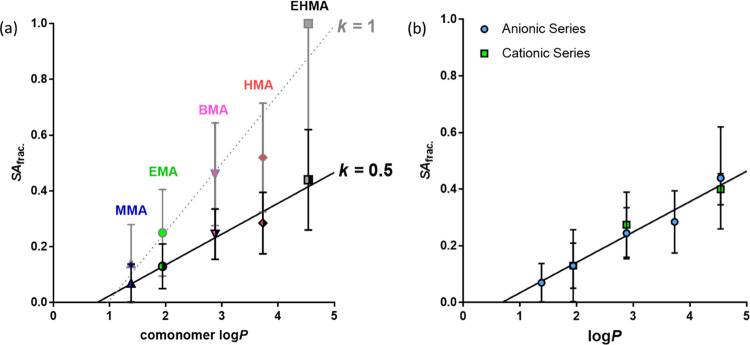
These SANS results enable (i) the core–shell model used for analyzing the SAXS data to be adjusted and (ii) the PSC model (eqs 1–3, Figure 3) to be calibrated with a realistic estimate of the proportion of ionic comonomer residues actually located at the nanoparticle surface. Accordingly, the numerical value of k used in the core–shell model was reduced from 1 to 0.5 to calculate a more realistic SLD for the cation shell. The entire anionic series was appropriately remodeled for k = 0.5, and new particle sizes were calculated (Table S3). Similarly, the PSC model (eqs 1–3) was adjusted using k = 0.5. This dual approach produced new SA_frac. values based on the real composition of the particle surfaces measured by SANS. Moreover, the linear relationship between log P and SA_frac. remained valid for the new data (Figure 6a). A new linear regression was fit to the data, yielding SA_frac. = 0.110 × log P – 0.085. This new equation can be used to predict particle size if it is assumed that k remains constant in the PSC model.

Figure 6.

(a) Linear relationship between the log P values for the hydrophobic alkyl methacrylate comonomers and the SA_frac. evaluated by PSC model fitting. The open symbols correspond to the previously assumed scenario³⁴ (Figure 3b) in which the MAA units are exclusively located at the nanoparticle surface (k = 1), while the half closed symbols correspond to the more physically realistic scenario indicated by contrast variation SANS experiments (k = 0.5). These two data sets were fitted using SA_frac. = 0.246 × log P – 0.237 (dotted line) and SA_frac. = 0.110 × log P – 0.085 (solid line) linear functions, respectively. (b) Linear relationship between the log P values for the various hydrophobic alkyl methacrylate comonomers and the SA_frac. evaluated by PSC model fitting, where k = 0.5. The blue circle symbols correspond to the anionic (MAA) copolymer series, and the green square symbols correspond to the cationic (DMAEMA) copolymer series. The black line shows the linear relationship obtained when combining these two series [SA_frac. = 0.107 × log P – 0.073, R² = 0.96]. The bars plotted for each point indicate the range of SA_frac. values estimated using the standard deviation for the nanoparticle radius.

The cationic copolymer series was similarly reanalyzed. Combining the data obtained for the anionic and cationic series (Figure 6b) produces a linear relationship (R² = 0.96) between log P and the modeled SA_frac. (k = 0.5). This highlights the self-consistency of the refined PSC model. Finally, the linear equation representing the relationship between log P for the hydrophobic comonomer and the modeled SA_frac. for the MAA copolymers crosses the x-axis (i.e., SA_frac. = 0) at a log P value of between 0.5 and 1. This suggests that, at this log P value, the nanoparticles would require no ionic comonomer to be located at the surface to confer colloidal stability. Alternatively, a comonomer exhibiting a log P of between 0.5 and 1, or below 0.5, would not be sufficiently hydrophobic to induce self-assembly, hence, such copolymers would remain molecularly dissolved in an aqueous solution.

Conclusions

A series of five alkyl methacrylates were statistically copolymerized in turn with either anionic MAA or cationic DMAEMA via RAFT polymerization to generate a library of amphiphilic statistical copolymers with varying MAA (or DMAEMA) content and tunable hydrophobic character. Additionally, a series of P(BMA-stat-MAA) copolymers were prepared using conventional free-radical polymerization to examine the effect of a relatively broad molecular weight distribution on statistical copolymer self-assembly. Kinetic studies confirmed that the hydrophobic and hydrophilic comonomers react at similar rates when copolymerizations were performed in concentrated solution in either IPA or dioxane. This indicates that an approximately statistical distribution of hydrophilic comonomer within the copolymer chains can be achieved using a one-shot batch synthesis protocol.

A solvent-switch technique was used to obtain aqueous dispersions of self-assembled copolymer nanoparticles, whereby each copolymer was first molecularly dissolved in IPA and then slowly diluted using either an alkaline or acidic aqueous solution depending on the type of hydrophilic comonomer. SAXS analysis confirmed that alkyl methacrylate-rich statistical copolymers formed larger nanoparticles, regardless of the nature of the hydrophilic comonomer. On the other hand, if the copolymer chains have a sufficiently high hydrophilic comonomer content, distinctly anisotropic single-chain nanoparticles can be obtained via intramolecular hydrophobic interactions. When targeting a fixed copolymer composition, using a more hydrophobic comonomer produced larger spherical nanoparticles. Contrast variation SANS studies performed on P(BMA-stat-MAA) copolymer nanoparticles enabled their internal structure to be determined. Such nanoparticles possess a core–shell-like morphology in which anionic MAA residues are preferentially located within the shell, thus conferring colloidal stability. However, owing to their statistical distribution along the copolymer chains, only about 50% of the available MAA residues can access the nanoparticle surface, with the remaining anionic residues being trapped within the nanoparticle cores.

The previously proposed particle surface charge model³⁴ was applied to the wide range of statistical copolymer dispersions prepared in this study. This revealed a strong correlation between the chemical structure of the hydrophobic comonomer and the surface charge density required to stabilize the copolymer nanoparticles. This model is remarkably consistent with the experimental SAXS data obtained for each copolymer, regardless of the type of hydrophilic comonomer or the molecular weight distribution. Importantly, it enables the nanoparticle size to be reliably predicted for a given copolymer composition. SANS studies indicate that approximately 50% of the hydrophilic comonomer repeat units is preferentially located at the nanoparticle surface. There is a linear relationship between SA_frac. (the fraction of the nanoparticle surface covered by the hydrophile component) calculated using the PSC model and the log P value for the hydrophobic comonomer. Moreover, this PSC model is valid for both cationic and anionic amphiphilic statistical copolymers and is remarkably insensitive to the breadth of the copolymer molecular weight distribution. The PSC model offers a clear set of design rules for controlling statistical copolymer particle size, which can be adjusted via the copolymer composition in a highly convenient one-shot one-pot synthesis. This is significantly simpler than the control of diblock copolymer particle size based on copolymer composition and molecular weight and also requiring a multistage synthesis of the molecules. In summary, this study provides important new insights regarding the aqueous self-assembly of amphiphilic statistical copolymers: the reproducible and predictable control over nanoparticle size that is observed even for relatively ill-defined chains means that such copolymers should be considered as an attractive alternative to diblock copolymers for a range of industrial applications.

Glossary

Abbreviations

SAXS

small-angle X-ray scattering

SANS

small-angle neutron scattering

PSC

particle surface charge (model)

ASC

amphiphilic statistical copolymers

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.macromol.0c02341.

• Kinetic data for the polymerizations, TEM images, further SAXS analysis, and SAXS models (PDF)

Author Contributions

The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.