Abstract
The alignment of arterial endothelial cells (ECs) with the mean wall shear stress (WSS) vector is the prototypical example of their responsiveness to flow. However, evidence for this behaviour rests on experiments where many WSS metrics had the same orientation or where they were incompletely characterized. In the present study, we tested the phenomenon more rigorously. Aortic ECs were cultured in cylindrical wells on the platform of an orbital shaker. In this system, orientation would differ depending on the WSS metric to which the cells aligned. Variation in flow features and hence in possible orientations was further enhanced by altering the viscosity of the medium. Orientation of endothelial nuclei was compared with WSS characteristics obtained by computational fluid dynamics. At low mean WSS magnitudes, ECs aligned with the modal WSS vector, while at high mean WSS magnitudes they aligned so as to minimize the shear acting across their long axis (transverse WSS). Their failure to align with the mean WSS vector implies that other aspects of endothelial behaviour attributed to this metric require re-examination. The evolution of a mechanism for minimizing transverse WSS is consistent with it having detrimental effects on the cells and with its putative role in atherogenesis.
Keywords: endothelium, haemodynamics, multidirectional flow, mechanotransduction, transWSS, atherosclerosis
1. Introduction
Endothelial cells (ECs) transduce mechanical stimuli into biochemical signals that change their behaviour [1–3]. Such mechano-responsiveness is critical for normal physiology and is key to several pathologies: for example, the non-uniform distribution of atherosclerosis within the arterial tree has been attributed to anatomical variation in the magnitude of time-averaged wall shear stress (WSS), oscillatory WSS and multidirectional WSS, among other factors [4–7]. Perhaps the most basic behaviour of this type is that ECs and their nuclei elongate and align with one another under high WSS, whereas under static conditions they show no alignment and exhibit a cobblestone morphology [8,9].
In an early in vivo study [10], a section of the canine descending thoracic aorta was removed, cut open longitudinally, sutured into a tube at 90° to its original axis and inserted back into the aorta. After several days, nuclei had turned through 90° to align with the expected flow direction. In experiments where a stenosis was introduced into the canine aorta, EC elongation increased in the convergent region and decreased in the divergent region, returning to the prestenotic value further downstream, a pattern that correlated with laser Doppler velocity measurements [11]. In vitro, experiments employing a cone-and-plate device showed that ECs align with the direction of flow when exposed to a WSS of 0.8 Pa but not 0.1–0.5 Pa [12]. (The term WSS is used to refer to shear stress acting on cultured ECs by analogy to the haemodynamic stresses occurring in vivo.) In studies where WSS was increased to 8.5 Pa using a parallel-plate flow chamber, alignment and elongation increased over time and were essentially complete by 24 h [9].
These studies and others investigated the effects on ECs of flow that was unidirectional or pulsatile along one axis. In the complex geometry of the arterial system, especially in areas predisposed to disease, flow can change axis during the cardiac cycle [4], but the effects of multidirectional flow on elongation and alignment have been investigated less extensively. Complex patterns of nuclear orientation were observed in early studies of areas of arterial curvature and branching [10], but the in vivo flow was not characterized and hence could not be compared with these observations. Complex in vivo flows have been mimicked in vitro by using an orbital shaker to swirl the medium in multiwell culture plates [13,14]; this system exposes ECs to multidirectional WSS at the centre of the well and to more uniaxial WSS towards the edge [15,16]. Cells in the centre of the well had a cobblestone morphology and a random orientation, whereas cells away from the centre elongated and oriented at an angle that diverged from the tangent to the edge of the well [13,14]; the orientation was attributed to the direction of flow but that was not proven.
The present study aimed to improve understanding of EC orientation under multidirectional flow. The swirling well methods of Ghim et al. [17,18] were used and were also modified by increasing the viscosity of the fluid up to that of blood; patterns of WSS were obtained by computational fluid dynamics (CFD) and compared with the orientation of cell nuclei.
2. Methods
2.1. Cell culture and application of flow
Human aortic ECs (PromoCell) were cultured in EC growth medium (ECGM; PromoCell). At passage 4, they were seeded in gelatin-coated 12-well plates at 21 000 cells cm−2 with a medium depth of 2 mm. Once confluence had been reached (3–4 days), the plates were placed on the horizontal platform of an orbital shaker (PSU-10i; Grant Instruments) translating at 150 r.p.m. in a circular orbit of 5 mm radius in the plane of the platform (electronic supplementary material, figure S1). They were incubated at 37°C under 5% CO2 for 4 days in ECGM with or without modified viscosity. Cells from three different aortas were used for each viscosity. Cells from the same aortas were also incubated under static conditions.
2.2. Modifying the viscosity of the culture medium
Dextran from Leuconostoc sp. (2 MDa; Sigma Aldrich) was dissolved in phosphate-buffered saline (PBS) at a concentration of 20% by autoclaving. This stock solution was further diluted in the culture medium to 2%, 3% and 5%.
The viscosity of distilled water and culture media (ECGM and Dulbecco's modified Eagle medium (DMEM) with and without dextran) was measured in triplicate using Ostwald U-tube viscometers. The viscometer was immersed vertically in an oil bath at 37°. DMEM-based media were supplemented with 10% fetal bovine serum, 10 000 U ml−1 penicillin, 100 µg ml−1 streptomycin, 5 µg ml−1 gentamicin, 250 µg ml−1 amphotericin, 250 µg ml−1 EC growth factor and 200 mM L-glutamine.
2.3. Staining and imaging
Following exposure to shear, cells were fixed with 4% paraformaldehyde for 15 min, permeabilized with 0.1% Triton-X for 5 min, blocked with 1% bovine serum albumin in PBS for 1 h and stained with DRAQ5 nuclear stain (1 : 1000; BioStatus, UK). Cells were washed three times in PBS before each step. Cells cultured under static conditions were subjected to the same procedures.
Wells were imaged using an inverted Leica SP5 confocal microscope with 10 × 0.4 NA objective and motorized stage using the methods of Ghim et al. [17]. Briefly, three-dimensional (3D) image volumes having a depth of 100 µm were obtained from the centre to the edge of the well with 1024 × 1024 pixels per plane in each tile. The nuclear stain was excited at 633 nm and its emission was recorded at 675–725 nm.
2.4. Image analysis and calculation of nuclear orientation
Matlab (r2016a) was used for post processing. A two-dimensional maximum projection image was computed from the 3D dataset and was binarized by thresholding the pixel intensity histogram. Area thresholding was then used to remove artefacts such as speckles of stain or pairs of nuclei that were too close to be resolved into individual objects. Ellipses were fitted to the remaining nuclei. A vector was then plotted which connected the centre of the well to the centroid of each ellipse. Nuclear orientation was defined as the angle between this reference axis and the major axis of the fitted ellipse, viewed from above. Angles clockwise from the reference axis were defined as positive. Since the polarity of the cells was not determined, the range was limited to ±90°. Means were determined by doubling the angles, calculating a circular mean and then halving the result.
2.5. Computational simulations of flow
Flow in the swirling well was simulated using STAR-CCM+ (v. 11.02.010-r8). Only one well was modelled since the motion experienced by all wells in a plate is identical. The geometry consisted of a cylinder with 22.1 mm diameter, 10 mm height and an open surface; it was discretized into 652 000 grid elements. The simulation was initiated from a static state, with 2 mm depth of liquid assigned a density of 1003 kg m−3 and, in the control model, a kinematic viscosity of 0.78 mm s−2. The remaining space was filled with air of density 1.1115 kg m−3 and kinematic viscosity 16.8 × 10−6 mm s−2.
The base of the cylinder and side walls were defined as no-slip boundaries, while the open surface was defined as a pressure outlet. An acceleration of [Aω2cos(ωt), Aω2sin(ωt), − 9.81] was applied in the x, y and z planes, where A is the orbital radius and ω the angular velocity. The free surface was defined where the fractional function, C, was 50%. Time was discretized into steps of 5 × 10−5 s, giving a Courant–Friedrichs–Lewy number less than 0.5. Surface tension was modelled using the continuum surface force model [19]. The fluid was assigned a surface tension of 72 mN m−1. An interface momentum dissipation model with a value of 3.0 and a contact angle of 71° was used. Further details will be published elsewhere.
This control model was modified for the presence of 2%, 3% and 5% dextran by using the measured kinematic viscosities. Even at the highest concentration, dextran was expected to increase the density of the solution by only ≈2% [20], and this was consequently ignored.
Simulations were run for a minimum of seven cycles. The instantaneous WSS components at each mesh point on the base of the well were extracted at every 10th time step to ensure a periodic state had been achieved. Data from the last cycle are reported.
2.6. Calculation of wall shear stress metrics
Metrics were calculated using a custom Matlab script. Time-averaged wall shear stress (TAWSS) is the average of the magnitudes of the instantaneous WSS vectors over one cycle of the shaker, and the magnitude of the mean wall shear stress (MagMeanWSS) is the magnitude of the mean WSS vector for one cycle,
| 2.1 |
and
| 2.2 |
τx, τy and τz are the x, y and z components of the instantaneous WSS vector τw, τmean is the mean WSS vector, t is time and T is the time to complete one cycle. For flow of constant speed oriented in the positive x direction for half the cycle and the negative x direction for the other half of the cycle, TAWSS would be non-zero, whereas MagMeanWSS would be zero.
The oscillatory shear index (OSI) [6,21] indicates if WSS is purely forward or not but cannot distinguish between pulsatile uniaxial WSS and truly multidirectional WSS. Transverse wall shear stress (transWSS) [7] is the magnitude of the components of the instantaneous WSS vectors perpendicular to the mean WSS direction, averaged over one cycle. It characterizes multidirectional WSS but, unlike the OSI, it does not include pulsatile uniaxial WSS,
| 2.3 |
and
| 2.4 |
where n is the unit vector perpendicular to the base of the well.
For flow of constant speed oriented in the positive x direction for half of the cycle and the negative x direction for the other half of the cycle, the OSI would be 0.5 since MagMeanWSS = 0. The transWSS would be indeterminate in this artificial case because there is no mean flow direction; however, if the flow were slightly greater in the positive than the negative x direction, allowing a mean to be defined, then the transWSS would be zero since there are no components perpendicular to the mean direction.
TransWSS is dependent on the mean WSS direction; a more generalized metric, termed the transverse wall shear stress minimum (transWSSmin), is the transWSS that would occur if cells oriented so as to minimize it, instead of orienting in the direction of the mean WSS vector [17],
| 2.5 |
where is the angle associated with the axis that minimizes transWSS components, averaged over the cycle.
A metric termed the cross-flow index (CFI) characterizes the multidirectionality of WSS without taking its magnitude into consideration. It is the average over the cycle of the absolute value of the sine of the angle between the instantaneous WSS component and the mean WSS direction [22]. Like transWSS, it only includes components of instantaneous vectors perpendicular to the mean WSS vector and not those at 180° to it. By analogy with the transWSSmin, a metric termed the CFImin can be calculated. It is the average over the cycle of the absolute value of the sine of the angle between the instantaneous WSS component and the axis that minimizes the average. That is, it is equivalent to the transWSSmin but takes into account only the magnitudes of instantaneous WSS vectors, not their direction,
| 2.6 |
and
| 2.7 |
Note that transWSS, transWSSmin, the CFI and CFImin remain undefined for any motion where the TAWSS is zero.
2.7. Statistics
The χ2 test for variance was used to assess differences in the histogram of nuclear alignments between static and sheared data. Changes in the number of nuclei per unit area with radial location and viscosity were assessed by two-way ANOVA. A value of p < 0.05 was used as the criterion of significance.
3. Results
3.1. Kinematic viscosity of the media
The viscosity obtained for distilled water was 0.695 mm2 s−1, while values for DMEM and ECGM were within 1% of each other, at 0.763 and 0.758 mm2 s−1, respectively. Adding dextran to DMEM at concentrations from 1% to 5% gave viscosities of 1.5 to 4.0 mm2 s−1 (electronic supplementary material, figure S2).
Reynolds numbers, computed as previously described [16] for the four viscosities used in subsequent experiments, were 2466 at the control viscosity, 874 at 2.2 mm2 s−1, 566 at 3.4 mm2 s−1 and 481 at 4.0 mm2 s−1. Note that the critical Reynolds number obtained for pipe flow, in the absence of a liquid–air interface, cannot be applied to the swirling well; stability, especially with regard to wave breaking and resonance (both of which were avoided here), is discussed in [16].
3.2. Shear stress patterns in swirling wells with control and modified media
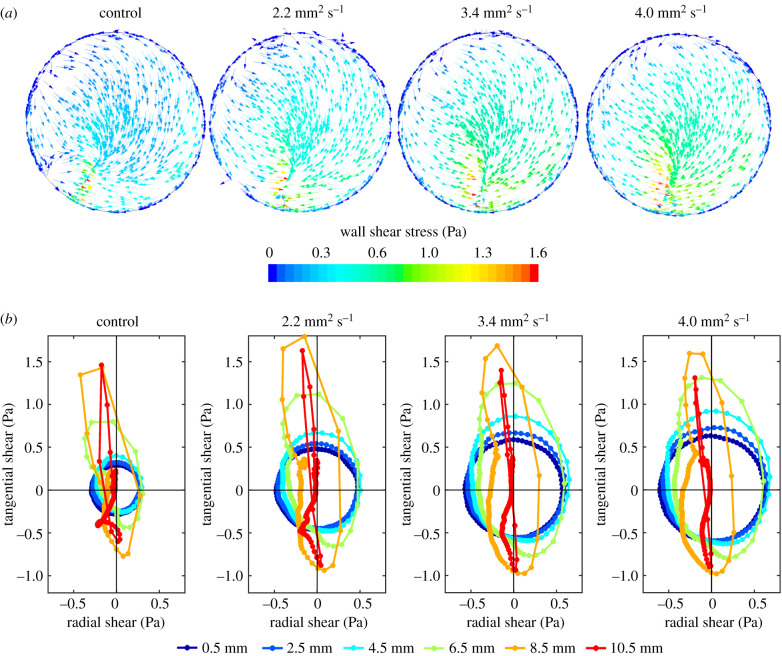
In all models, the orbital shaker produced a wave which rotated around the well. Figure 1 shows the magnitude and direction of WSS vectors on the base of the well at one instant, and throughout the cycle for six radial positions in the well, for the four viscosities. At a radial distance of 0.5 mm from the centre of the well, the vector rotated through 360° at a nearly constant rate and with a nearly constant magnitude, leading to a nearly circular plot with equidistant points. With increasing radial distance from the centre of the well, the plot became more elongated, and the vector rotated more rapidly at some points in the cycle than at others. By 10.5 mm, close to the edge of the well, the plot is essentially a line through the origin, indicating flow that was pulsatile along one axis. The shapes of the plots are broadly similar at all four viscosities. However, the magnitudes of the instantaneous vectors vary; those near the centre of the well increased with each increase in viscosity, whereas those nearer the edge increased and then decreased.
Figure 1.
(a) Pattern of shear stress on the base of a swirling well for all four viscosities at one time step, viewed from above. The direction of the arrows shows the direction of the shear stress, while the colour of the arrows shows its magnitude, as indicated by the colour bar. Like the wave, this pattern rotates clockwise with time but otherwise does not change, giving multidirectional shear of constant magnitude at the centre and uniaxial but pulsatile shear of fluctuating magnitude at the edge. (b) Polar plots showing the instantaneous WSS magnitude and direction over one cycle at points 0.5–10.5 mm from the centre of the well along a single radius. Panels from left to right show the control model (i.e. no dextran) and the models with increased viscosity. The plots show the location over time of the tip of the instantaneous WSS vector, which has its origin at 0.0. (Note that 0.0 does not designate the same real position for each differently coloured line, but the point along the radius for which the vectors were calculated.) The filled circles on each plot are spaced at equal time intervals of 5 ms. Negative radial values indicate vector components pointing to the left of the well and negative tangential values indicate components in the direction of the swirling wave when viewed from above.
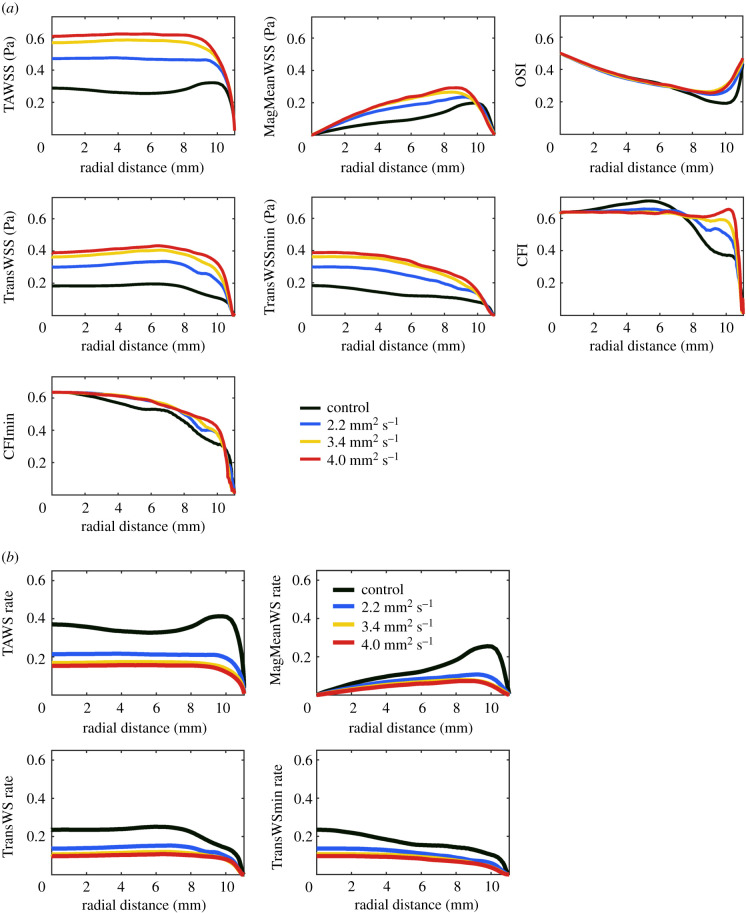
WSS metrics as a function of radial position and the effects on them of increasing viscosity are shown in figure 2a. Maps and alternative graphical presentations are shown in electronic supplementary material, figures S3 and S4. Plots of TAWSS, MagMeanWSS, transWSS and transWSSmin retained the same general shape as viscosity increased, but the magnitude of the metrics increased. (The changes in TAWSS from the centre to the edge of the well became less pronounced, suggesting that increased viscosity dampens the wave, which has a larger amplitude towards the edge.) OSI, CFI and CFImin showed little or no effect of increased viscosity up to radial distances of 6–7 mm. At larger radial distances, the magnitude increased for all three, suggesting that flow characteristics were altered in these regions. This is again consistent with an alteration of the wave.
Figure 2.
(a) WSS metrics from the centre to the edge of the well for the control model and the models with increased viscosity. (b) Wall shear rate metrics from the centre to the edge of the well for the control model and the models with increased viscosity. OSI, CFI and CFImin are not shown because the plots for these dimensionless metrics are identical to those in (a).
To determine whether increasing the viscosity of the medium altered velocity gradients perpendicular to the base of the well, the metrics were replotted as shear rates rather than shear stresses. Wall shear rate is the velocity gradient next to the wall. WSS is the wall shear rate multiplied by the viscosity. If changing the viscosity does not alter the flow, and the velocity gradient therefore stays the same, then WSSs will differ between viscosities (they will be scaled by the viscosity), whereas wall shear rates will be the same across viscosities. If altering viscosity does lead to a change in the near-wall velocity gradient, then the wall shear rate will also change. OSI, CFI and CFImin are dimensionless—they do not have viscosity as a multiplier, unlike metrics based on WSS—and are not shown.
For the other metrics, figure 2b shows that shear rates decreased with increasing viscosity. This trend is the opposite of the trend seen for shear stresses and demonstrates an increase in boundary layer thickness; the direct effect of viscosity on frictional forces overrides this effect when shear stresses are calculated.
3.3. Nuclear orientation under shear and static conditions
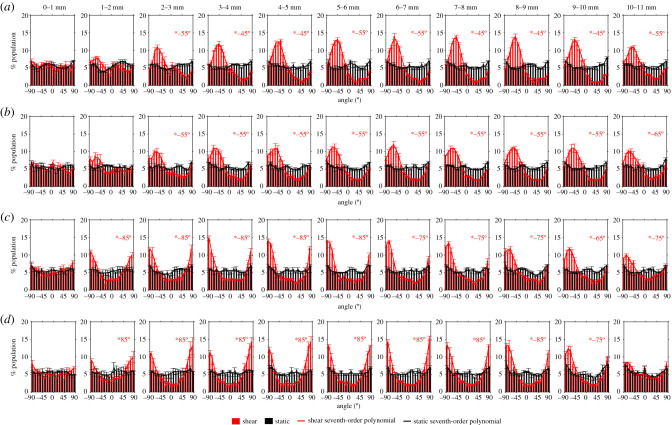
To examine the pattern of nuclear orientation within the well, orientations were divided into 10° bins, and were also binned in 1 mm intervals from the centre to the edge of the well. Figure 3 shows the resulting frequency histograms for cells under static conditions and applied shear for each of the four viscosities. Where there was a significant difference between data for static and sheared culture, the modal orientation (i.e. the angle corresponding to the bin with the highest frequency) is also given.
Figure 3.
Frequency histograms of nuclear orientation from the centre to the edge of the well in 1 mm increments. 0° is the radial orientation. Orientations of +90° and −90° are tangential to the side wall of the well and are equivalent: the histograms wrap around so that the left and right ends of the x-axis are continuous with each other. The lines are best-fit seventh-order polynomials. At radial locations where there was a significant difference between profiles for static and sheared conditions, the modal nuclear orientation under shear is indicated. Viscosities were (a) 0.8 mm2 s−1 (control model), (b) 2.2 mm2 s−1, (c) 3.4 mm2 s−1 and (d) 4.0 mm2 s−1. Mean ± s.e.m., n = 3.
Under static conditions, all orientations were approximately equally represented at each location, and this finding was unaffected by viscosity.
There was no significant difference between static and sheared cell orientations for radial distances of 0–2 mm from the centre at the two lowest viscosities and of 0–1 mm at the two highest viscosities. This presumably reflects the absence of a preferred flow direction in these central regions. A currently unexplained outlier is that there was also no preferred orientation at a radial distance of 10–11 mm, near the edge of the well, at the highest viscosity.
For all other combinations of radial distance and viscosity, there was a statistically significant difference between static and sheared conditions; the modal orientation varied between −45° and −5° (where +90 and −90 are tangent to the wall of the well and 0° is the radial direction). Almost all of these histograms had a single peak. Nuclei in the control (dextran-free) model had orientations in the range of −45° to −55°. As the viscosity was increased to 2.2, 3.4 and 4.0 mm s−2, the nuclei aligned more closely with the wall of the well, with modal angles of −55° to −65°, −65° to −85° and −75° to 85°, respectively.
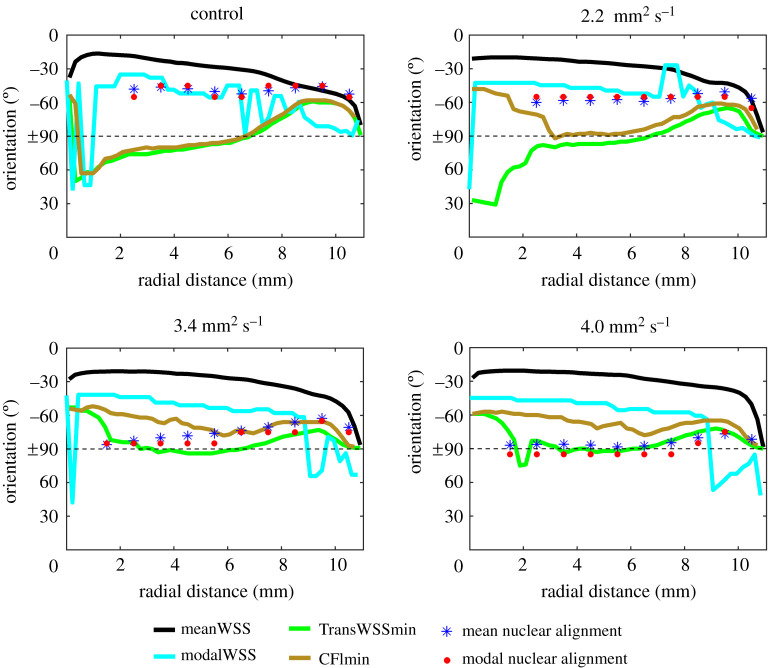
The four lines in figure 4 show the orientations that would be expected if nuclei aligned with the mean WSS vector, the modal WSS vector or so as to minimize transWSS or the CFI.
Figure 4.
The mean and modal orientation of cell nuclei measured from the centre to the edge of the well (symbols), and lines showing the orientation that would have been observed if the nuclei aligned with the mean WSS vector, the modal WSS vector or the axis that minimizes transWSS or the CFI. The four panels show the dextran-free control model and the models with increased viscosity. Angles are explained in the legend to figure 3. To produce the lines, the orbital period was split into thirty 15-ms bins, and the data were plotted every 0.22 mm from the centre to the edge.
There was almost no effect of viscosity on the mean and modal WSS orientation curves, but the transWSSmin and CFImin orientations were affected. The nuclear data are included for cases where there was a significant difference in orientation between sheared and static conditions. The mean and modal nuclear orientations align best with the orientation of the modal WSS vector at the two lowest viscosities. (The agreement with the modal WSS direction is less good close to the edge of the well, and the agreement with the mean WSS direction is better, especially at the lowest viscosity; nevertheless, even in the absence of dextran, the data do not support a consistent alignment with the mean WSS vector.) The mean and modal nuclear orientations align best with the orientation that minimizes transWSS at the two highest viscosities; at the highest viscosity—and hence highest TAWSS and transWSS—the agreement is excellent at every radial distance. (A vector representation of the data is given in electronic supplementary material, figure S5, and the average discrepancy in angle between the modal measurements and the numerical data is given in electronic supplementary material, table S1.)
4. Discussion
Early in vitro studies appeared to confirm the impression gained from in vivo observations that arterial ECs align with the mean WSS vector. However, they were restricted to steady or pulsatile uniaxial flow, where the directions of the mean and modal WSS vector and the directions associated with transWSSmin and CFImin are all the same; hence, any one of them could have determined the orientation of the ECs. Here, we tested which one of them actually does so, using the swirling well system. This method produces purely multidirectional and nearly uniaxial flows, gives shear magnitudes and frequencies of directional change that are physiological and allows chronic experiments with high throughput; it has been used in numerous previous studies [23]. The present work corrected an error [18] in the study of Ghim et al. [17], considered additional metrics, incorporated surface tension and wetting to improve the accuracy of the CFD model and used dextran to increase viscosity. Dextran had no effect on the nuclear orientation of ECs in static culture (figure 3), so its influence in swirled wells was attributed to alteration of WSS rather than direct effects on the cells.
Polar plots in figure 1 show instantaneous WSS vectors throughout the cycle at various radial locations from the centre. As in all other such representations of flow in the swirling well, the plots changed from circular, representing multiaxial flow, at the centre to almost linear, representing uniaxial flow, at the edge. Figure 2 shows the magnitude of all the WSS metrics for different radial distances from the centre of the well and different viscosities. A detailed explanation of the trends in these magnitudes is given in electronic supplementary material, appendix.
Data for the modal nuclear orientation obtained in the control model (i.e. with no added dextran) were almost identical to those obtained by Ghim et al. [17], obtained using a culture medium of normal viscosity. Modal nuclear orientations were also essentially identical to the mean nuclear orientations, reflecting the nearly symmetrical distribution of nuclear orientation (figure 3) at most radial locations and viscosities. Figure 4 compares both measures of nuclear orientation with the orientation of the mean and modal WSS vectors and the angle required to minimize transWSS or the CFI. For the control model and for viscosity = 2.2. mm2 s−1, the data align best with the direction of the modal WSS vector, apart from anomalous behaviour near the edge of the well. It is perhaps surprising that cells exposed to these flow regimes aligned with a metric that captures the direction of instantaneous WSS vectors but not their magnitude. This implies a mechanosignalling system which integrates signals from a transducer behaving like a weather vane: one that can change direction but does not bend or stretch with the flow.
With further increases in viscosity and hence in the TAWSS and transWSS, the nuclear data aligned with the transWSSmin curve; the fit is good at 3.4 mm2 s−1 and excellent at 4.0 mm2 s−1. This switch occurred when TAWSS over the majority of the well was between ≈0.5 and ≈0.6 Pa.
Since nuclei aligned with the modal rather than the mean WSS vector at lower viscosities, we defined a new metric—the CFImin—that is independent of WSS magnitude and hence bears the same relation to the transWSSmin as the modal WSS vector does to the mean WSS vector. Nuclei did not align with this new metric: the data clearly support the transWSSmin hypothesis under some flow regimes. The implication is that the mechanosignalling responsible for this behaviour integrates signals from a transducer that responds to magnitude as well as direction.
At the edge of the well, the directions of the mean and modal WSS vectors and the directions associated with the transWSSmin and CFImin are degenerate, as in flow systems that produce only unidirectional or uniaxial flows. At the higher viscosities, cells in this region aligned with the direction that minimizes transWSS but also, for example, with the direction of the mean WSS vector. We cannot determine whether cell alignment is governed by the same metrics at the edge of the well as in other regions of it, but that would be the most economical assumption.
An interesting feature of endothelial alignment is that different cell structures show different orientations. Kim et al. [24] found in vivo that the stress fibres distributed through the central regions of the cell did not always match cell orientation; there was a discrepancy of up to 30°. The swirling well data of Ghim et al. [17] show a consistent discrepancy of 10–20° between the direction of nuclei and of the cells themselves, with the cell orientation being more negative (i.e. shifted in the direction of the transWSSmin line). Future studies should examine cellular and stress fibre orientation under the conditions used in the present work.
We examined nuclear orientation because modelling studies suggest that it determines, and is determined by, the distribution of WSS at the cellular level. Yamaguchi et al. [25] developed a computational model to mimic cultured ECs under flow. The cells were modelled with a Gaussian shape to reflect the protrusion of the nucleus; WSS at the cell surface was greatest at the highest point of the ‘nucleus’. When the cells were able to continuously move and deform, and were given the aim of minimizing WSS under unidirectional flow, the protrusions aligned with the flow and elongated. In a similar study, Hazel & Pedley [26] found that the aspect ratio of nuclei which minimized WSS over the cell in their model was similar to that seen in vivo. Barbee et al. [27] found that ECs align and reduce their nuclear height under flow, resulting in a lower peak shear and lower maximum spatial gradient of shear, both of which occurred over the nucleus. Of particular relevance to the present study, they also tested flow at right angles to aligned cells: there was a 13% increase in peak shear and an 80% increase in peak spatial gradient, compared with flow in the direction that produced the alignment.
The latter result suggests one way in which cells might be influenced by transWSS, and why they might minimize it. The same can be said of the studies of Wang et al. [28], which show that transverse flow reduces activation of endothelial nitric oxide synthase and increases activation of NF-κB. The mechanotransduction and signalling events remain to be elucidated, but KLF2, syndecan 4 and JNK2 have been implicated [29–31]. Note that ECs are not homogeneous: ECs from aortic valves align perpendicular to steady flow, as do lymphatic ECs exposed to the types of flow expected in nascent lymphatic valves; different signalling molecules appear to be involved in these cases [32,33].
Metrics of multidirectionality other than transWSS have been proposed. One is the ratio of the magnitude of circumferential to axial WSS projections, devised by Morbiducci et al. [34]. A second is the directional OSI of Chakraborty et al. [14], which uses principal component analysis to determine orthogonal axes of WSS in the swirling well and then computes the ratio of the OSI along these axes. A third is the anisotropy ratio of Vamsi Krishna et al. [35], which uses principal component analysis of the polar plot to obtain the axes, followed by calculation of the aspect ratio of a bounding rectangle that has its long axis parallel to the principal axis. The last two appear to identify the same axis as the transWSSmin calculation, but then compute different metrics comparing that axis with the orthogonal axis—either the ratio of the OSIs or the ratio of the WSS maxima.
Our own metrics are based on assumptions about the responses of the ECs themselves. TransWSS [7] assumes that cells align with the mean WSS vector and are adversely affected by flows across their long axis. TransWSSmin [17] assumes that transWSS is sufficiently detrimental to the cells that they have evolved a mechanism for orienting themselves so as to minimize it. In the present study, it appeared to predict cell orientation when the viscosity and hence the WSS and transWSS were high.
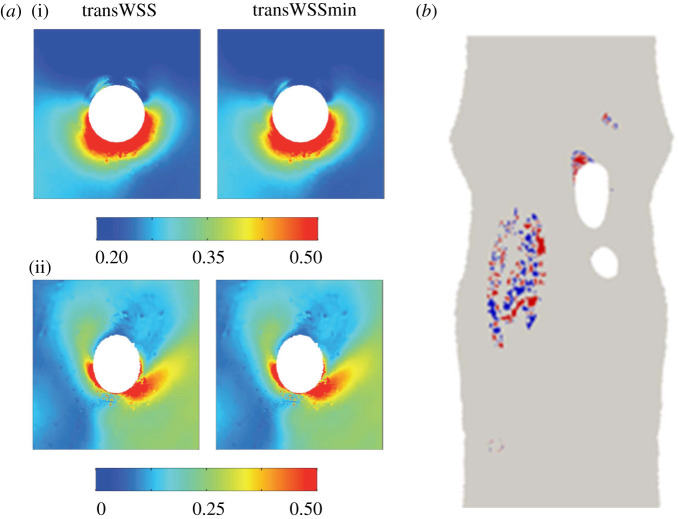
We have previously shown that the distribution of diet-induced atherosclerosis at branch points in the rabbit aorta correlates better with the pattern of transWSS than it does with low TAWSS or the OSI [36]. We have also shown [36] that the magnitudes and patterns of transWSS and transWSSmin are essentially identical around these branches (figure 5a); for this reason, it is not possible to determine from the pattern of lesions whether it is transWSSmin rather than transWSS that is the most likely trigger of disease, as the present data suggest. However, it may be possible to determine the relative importance of the two metrics by looking at the orientation of ECs. Using the methods documented by Mohamied [37], we have shown that the two metrics predict measurably different orientations in the inner curvature of the aortic arch and the inflow tract of the brachiocephalic artery (figure 5b). Hence, comparing actual EC orientation with CFD-derived WSS metrics in vivo—a comparison analogous to the in vitro one shown in figure 4—would indicate which metric dominates endothelial behaviour. The data from such a study could be clinically important if mechanotransduction and the mechanosignalling pathways relevant to atherogenesis may become targets for therapeutic intervention.
Figure 5.
(a) TransWSS and transWSSmin around the origin of an intercostal artery in the rabbit aorta. (i) and (ii) show, respectively, the average of all individual branches and a representative individual branch. (The white circle represents the ostium itself and has a diameter of approximately 0.5 mm.) Values are in pascal (from [36], with permission). (b) En face map of a rabbit aortic arch that has been opened to show regions where CFD simulations of blood flow indicate greater than 20° discrepancy between the direction of the mean WSS vector and the direction that minimizes transWSS. (Areas are coded red or blue depending on whether the discrepancy is rotated clockwise or anticlockwise relative to the mean vector.) Simulations in eight additional animals show essentially the same pattern. In all cases, mean aortic flow is from top to bottom of the map.
Supplementary Material
Data accessibility
This article has no additional data.
Authors' contributions
M.A. conducted experimental and numerical work and contributed to the design, interpretation and writing. M.G. conducted experimental work and contributed to the design and interpretation. Y.M. conducted numerical work and contributed to the design and interpretation. S.J.S. contributed to the design and interpretation. P.D.W. contributed to the design, interpretation and writing.
Competing interests
We declare we have no competing interests.
Funding
M.A. and Y.M. were funded by studentships from the Imperial College BHF Centre of Research Excellence. M.G. was supported by a BHF project grant awarded to P.D.W.
References
- 1.Davies PF 1995. Flow-mediated endothelial mechanotransduction. Physiol. Rev. 75, 519–560. ( 10.1152/physrev.1995.75.3.519) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chien S, Li S, Shyy YJ. 1998. Effects of mechanical forces on signal transduction and gene expression in endothelial cells. Hypertension 31, 162–169. ( 10.1161/01.hyp.31.1.162) [DOI] [PubMed] [Google Scholar]
- 3.Givens C, Tzima E. 2016. Endothelial mechanosignaling: does one sensor fit all? Antioxid. Redox Signal. 25, 373–388. ( 10.1089/ars.2015.6493) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fry DL 1969. Certain chemorheologic considerations regarding the blood vascular interface with particular reference to coronary artery disease. Circulation 40, IV-38–IV-57. ( 10.1161/01.CIR.40.5S4.IV-38) [DOI] [Google Scholar]
- 5.Caro CG, Fitz-Gerald JM, Schroter RC. 1971. Atheroma and arterial wall shear. Observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proc. R. Soc. Lond. B 177, 109–133. ( 10.1098/rspb.1971.0019) [DOI] [PubMed] [Google Scholar]
- 6.Ku DN, Giddens DP, Zarins CK, Glagov S. 1985. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low and oscillating shear stress. Arteriosclerosis 5, 293–302. ( 10.1161/01.ATV.5.3.293) [DOI] [PubMed] [Google Scholar]
- 7.Peiffer V, Sherwin SJ, Weinberg PD. 2013. Computation in the rabbit aorta of a new metric—the transverse wall shear stress—to quantify the multidirectional character of disturbed blood flow. J. Biomech. 46, 2651–2658. ( 10.1016/j.jbiomech.2013.08.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dewey CJ 1984. Effects of fluid flow on living vascular cells. J. Biomech. Eng. 106, 31–35. ( 10.1115/1.3138453) [DOI] [PubMed] [Google Scholar]
- 9.Levesque MJ, Nerem RM. 1985. The elongation and orientation of cultured endothelial cells in response to shear stress. J. Biomech. Eng. 107, 341–347. ( 10.1115/1.3138567) [DOI] [PubMed] [Google Scholar]
- 10.Flaherty JT, Pierce JE, Ferrans VJ, Patel DJ, Tucker WK, Fry DL. 1972. Endothelial nuclear patterns in the canine arterial tree with particular reference to hemodynamic events. Circ. Res. 30, 23–33. ( 10.1161/01.RES.30.1.23) [DOI] [PubMed] [Google Scholar]
- 11.Dewey CF, Bussolari SR, Gimbrone MA, Davies PF. 1981. The dynamic response of vascular endothelial cells to fluid shear stress. J. Biomech. Eng. 103, 177–185. ( 10.1115/1.3138276) [DOI] [PubMed] [Google Scholar]
- 12.Levesque MJ, Liepsch D, Moravec S, Nerem RM. 1986. Correlation of laser-Doppler-velocity measurements and endothelial cell shape in a stenosed dog aorta. Arteriosclerosis 6, 220–229. ( 10.1161/01.ATV.6.2.220) [DOI] [PubMed] [Google Scholar]
- 13.Dardik A, Chen L, Frattini J, Asada H, Aziz F, Kudo FA, Sumpio BE, Haven N, Haven W. 2005. Differential effects of orbital and laminar shear stress on endothelial cells. J. Vasc. Surg. 41, 869–880. ( 10.1016/j.jvs.2005.01.020) [DOI] [PubMed] [Google Scholar]
- 14.Chakraborty A, Chakraborty S, Jala VR, Haribabu B, Sharp MK, Berson RE. 2012. Effects of biaxial oscillatory shear stress on endothelial cell proliferation and morphology. Biotechnol. Bioeng. 109, 695–707. ( 10.1002/bit.24352) [DOI] [PubMed] [Google Scholar]
- 15.Berson RE, Purcell MR, Sharp MK. 2008. Computationally determined shear on cells grown in orbiting culture dishes. Adv. Exp. Med. Biol. 614, 189–198. ( 10.1007/978-0-387-74911-2_22) [DOI] [PubMed] [Google Scholar]
- 16.Alpresa P, Sherwin S, Weinberg PD, van Reeuwijk M. 2018. Orbitally shaken shallow fluid layers. I. Regime classification. Phys. Fluids 30, 032107 ( 10.1063/1.4996916) [DOI] [Google Scholar]
- 17.Ghim M, Alpresa P, Yang SW, Braakman ST, Gray SG, Sherwin SJ, van Reeuwijk M, Weinberg PD. 2017. Visualization of three pathways for macromolecule transport across cultured endothelium and their modification by flow. Am. J. Physiol. Heart Circ. Physiol. 313, H959–H973. ( 10.1152/ajpheart.00218.2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ghim M, Alpresa P, Yang SW, Braakman ST, Gray SG, Sherwin SJ, van Reeuwijk M, Weinberg PD. 2020. Visualization of three pathways for macromolecule transport across cultured endothelium and their modification by flow. Am. J. Physiol. Heart Circ. Physiol. 319, H359 10.1152/ajpheart.zh4-3151-corr.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Brackbill JU, Kothe DB, Zemach C. 1992. A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354. ( 10.1016/0021-9991(92)90240-Y) [DOI] [Google Scholar]
- 20.Snyder CF, Isbell HS, Dryden MR, Holt NB. 1954. Optical rotations, refractive indices, and densities of dextran solutions. J. Res. Natl Bur. Stand. 53, 131 ( 10.6028/jres.053.016) [DOI] [Google Scholar]
- 21.He X, Ku DN. 1996. Pulsatile flow in the human left coronary artery bifurcation: average conditions. J. Biomech. Eng. 118, 74–82. ( 10.1115/1.2795948) [DOI] [PubMed] [Google Scholar]
- 22.Mohamied Y, Sherwin SJ, Weinberg PD. 2017. Understanding the fluid mechanics behind transverse wall shear stress. J. Biomech. 50, 102–109. ( 10.1016/j.jbiomech.2016.11.035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Warboys CM, Ghim M, Weinberg PD. 2019. Understanding mechanobiology in cultured endothelium: a review of the orbital shaker method. Atherosclerosis 285, 170–177. ( 10.1016/j.atherosclerosis.2019.04.210) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kim DW, Langille BL, Wong MKK, Gotlieb AI. 1989. Patterns of endothelial microfilament distribution in the rabbit aorta in situ. Circ. Res. 64, 21–31. ( 10.1161/01.RES.64.1.21) [DOI] [PubMed] [Google Scholar]
- 25.Yamaguchi T, Yamamoto Y, Liu H. 2000. Computational mechanical model studies on the spontaneous emergent morphogenesis of the cultured endothelial cells. J. Biomech. 33, 115–126. ( 10.1016/S0021-9290(99)00159-1) [DOI] [PubMed] [Google Scholar]
- 26.Hazel AL, Pedley TJ. 2000. Vascular endothelial cells minimize the total force on their nuclei. Biophys. J. 78, 47–54. ( 10.1016/S0006-3495(00)76571-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Barbee KA, Mundel T, Lal R, Davies PF. 1995. Subcellular distribution of shear stress at the surface of flow-aligned and nonaligned endothelial monolayers. Am. J. Physiol. Heart Circ. Physiol. 268, H1765–H1772. ( 10.1152/ajpheart.1995.268.4.h1765) [DOI] [PubMed] [Google Scholar]
- 28.Wang C, Baker BM, Chen CS, Schwartz MA. 2013. Endothelial cell sensing of flow direction. Arterioscler. Thromb. Vasc. Biol. 33, 2130–2136. ( 10.1161/ATVBAHA.113.301826) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dekker RJ, et al. 2005. Endothelial KLF2 links local arterial shear stress levels to the expression of vascular tone-regulating genes. Am. J. Pathol. 167, 609–618. ( 10.1016/S0002-9440(10)63002-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Boon RA, Leyen TA, Fontijn RD, Fledderus JO, Baggen J, Volger OL, van Nieuw Amerongen GP, Horrevoets AJ. 2010. KLF2-induced actin shear fibers control both alignment to flow and JNK signaling in vascular endothelium. Blood 115, 2533–2542. ( 10.1182/blood-2009-06-228726) [DOI] [PubMed] [Google Scholar]
- 31.Hahn C, Wang C, Orr AW, Coon BG, Schwartz MA. 2011. JNK2 promotes endothelial cell alignment under flow. PLoS ONE 6, e24338 ( 10.1371/journal.pone.0024338) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Butcher JT, Penrod AM, García AJ, Nerem RM. 2004. Unique morphology and focal adhesion development of valvular endothelial cells in static and fluid flow environments. Arterioscler. Thromb. Vasc. Biol. 24, 1429–1434. ( 10.1161/01.ATV.0000130462.50769.5a) [DOI] [PubMed] [Google Scholar]
- 33.Michalaki E, Surya VN, Fuller GG, Dunn AR. 2020. Perpendicular alignment of lymphatic endothelial cells in response to spatial gradients in wall shear stress. Commun. Biol. 3, 57 ( 10.1038/s42003-019-0732-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Morbiducci U, Gallo D, Cristofanelli S, Ponzini R, Deriu MA, Rizzo G, Steinman DA. 2015. A rational approach to defining principal axes of multidirectional wall shear stress in realistic vascular geometries, with application to the study of the influence of helical flow on wall shear stress directionality in aorta. J. Biomech. 48, 899–906. ( 10.1016/j.jbiomech.2015.02.027) [DOI] [PubMed] [Google Scholar]
- 35.Vamsi Krishna C, Chandran Suja V, Watton PN, Arakeri JH, Gundiah N. 2020. Shear stress rosettes capture the complex flow physics in diseased arteries. J. Biomech. 104, 109721 ( 10.1016/j.jbiomech.2020.109721) [DOI] [PubMed] [Google Scholar]
- 36.Mohamied Y, Rowland EM, Bailey EL, Sherwin SJ, Schwartz MA, Weinberg PD. 2015. Change of direction in the biomechanics of atherosclerosis. Ann. Biomed. Eng. 43, 16–25. ( 10.1007/s10439-014-1095-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mohamied Y 2017. Multidirectional near-wall flow in arteries and its spatial correlation with atherosclerosis. PhD thesis, Imperial College London, London, UK; ( 10.25560/44374) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This article has no additional data.