Are all models wrong?

Mathematical modeling in cancer is enjoying a rapid expansion (Brady & Enderling, 2019). For collegial discussion across disciplines, many -if not all of us- have used the aphorism that “All models are wrong, but some are useful” (George Box 1976). This has been a convenient approach to justify and communicate the praxis of modeling. This is to suggest that the usefulness of a model is not measured by the accuracy of representation but how well it supports the generation, testing and refinement of hypotheses. A key insight is not to focus on the model as an outcome, but to consider the modeling process and simulated model predictions as “ways of thinking” about complex nonlinear dynamical systems (Apweiler 2018). Here, we discuss the convoluted interpretation of models being wrong in the arena of predictive modeling.

“All models are wrong, but some are useful” emphasizes the value of abstraction in order to gain insight. While abstraction clearly implies misrepresentation, it allows to explicitly define model assumptions and interpret model results within these limitations - Truth emerges more readily from error than from confusion (Francis Bacon c. 1610). It is thus the process of modeling and the discussions about model assumptions that are often considered most valuable in interdisciplinary research. They provide a way of thinking about complex systems and mechanisms underlying observations. Abstractions are being made in cancer biology for every experiment in each laboratory around the world. In vitro cell lines or in vivo mouse experiments are abstractions of complex adaptive evolving human cancers in the complex adaptive dynamic environment called the patient. These ‘wet lab’ experiments akin to ‘dry lab’ mathematical models offer confirmation or refutation of hypotheses and results, which have to be prospectively evaluated in clinical trials before conclusions can be generalized beyond the abstracted assumptions. The key for any model -mathematical, biological, or clinical- to succeed is an iterative cycle of data-driven modeling and model-driven experimentation (Khan 2018, Aherne 2020). The value of such an effort lies in the insights about mechanisms that can then be attributed to the considered variables (Singh 2020). With simplified representations of a system one can learn about the emergence of general patterns, like the occurrence of oscillations, bistability, or chaos (Stamper 2010; Tyson 2003; Nikolov 2014).

In this context, Alan Turing framed the purpose of a mathematical model in his seminal paper about “The chemical basis of morphogenesis” (Turing 1952) with “This model will be a simplification and an idealization, and consequently a falsification. It is to be hoped that the features retained for discussion are those of greatest importance in the present state of knowledge.” For many mathematical biology models that are built to explore, test and generate hypotheses about emerging dynamics this remains true. “Wrong models” allow us to reevaluate our assumptions, and the lessons learned from these discussions can help formulate revised models and improve our understanding of the underlying dynamics.

However, mathematical oncology models are deployed not only to simulate emergent properties of complex systems to generate, test and refine hypotheses, but increasingly also with the intent to make predictions - often how an individual cancer patient will respond to a specific treatment (Brady 2019). For predictive modeling, the aphorism “All models are wrong” becomes awkward. In the predictive modeling arena, a useful model should not be wrong. A major hurdle in the application of predictive modeling, in general and in oncology in particular, is communication of model purpose and prediction uncertainty, and how likelihood and risks are interpreted by the end user. With limited data available about a complex adaptive evolving system, “forecasting failures” are common when events that are not represented in the data dominate the subsequent behavior (such as emergence of treatment resistance not being represented in pre-treatment dynamics). If predictive models are trained on historic data but with little patient-specific data over multiple time points, what role could predictive models play in oncology?

Computer simulations of mathematical models that are based on limited data are merely visualizing plausible disease trajectories forward in time. Predictions could then be made from analyzing the possible trajectories using multiple plausible parameter combinations, from either a single model or multiple models with competing assumptions and different weighting of likely important factors. While in some domains, such as hurricane trajectory forecasts, we trust mathematical models and accept their inherent, well-documented prediction uncertainties (Yankeelov et al., 2015), it is imperative to improve the communication of what models can and cannot do when it comes to personal health. “Nothing is more difficult to predict than the future¹”, and while the uncertainty linked to predictions rises quickly, we may still find use in the model.

For clinical purpose, predictive models may not need to accurately describe the complex biology of cancer, but to provide a trigger for decision making, often upon binary endpoints. For many years, we have set ourselves the lofty goal of predicting the tumor burden evolution during treatment with ever decreasing error to the actual data (Prokopiou 2015; Poleszczuk 2018; Sunassee 2019); yet the clinical endpoint for patients is often not the actual tumor volume dynamics but binary endpoints such as continuous response or cancer progression, tumor control or treatment failure. Machine learning approaches (or simple statistics) can identify threshold values for tumor burden at different time points during therapy that stratify patients into the different outcomes (Latifi 2017, Brady-Nicholls 2020, Byun 2020). Then, the model purpose becomes to accurately predict whether a tumor will shrink below this threshold or not. A larger error to the data but a correct outcome classification becomes an acceptable tradeoff for better fits but incorrect predictions. With this understanding we have seen unprecedented model prediction accuracy for individual patients from few response measurements early during therapy (Brady-Nicholls 2020). The dilemma is visualized in Figure 1. For both patients, one head and neck cancer patient treated with radiotherapy and one prostate cancer patient treated with intermittent hormone therapy, only a few of the 100 predicted disease trajectories each mimic the eventual clinically-observed dynamics. Yet, the majority of the simulations accurately predict disease burden to be above or to be below the learned thresholds for tumor control or treatment resistance.

Figure 1.

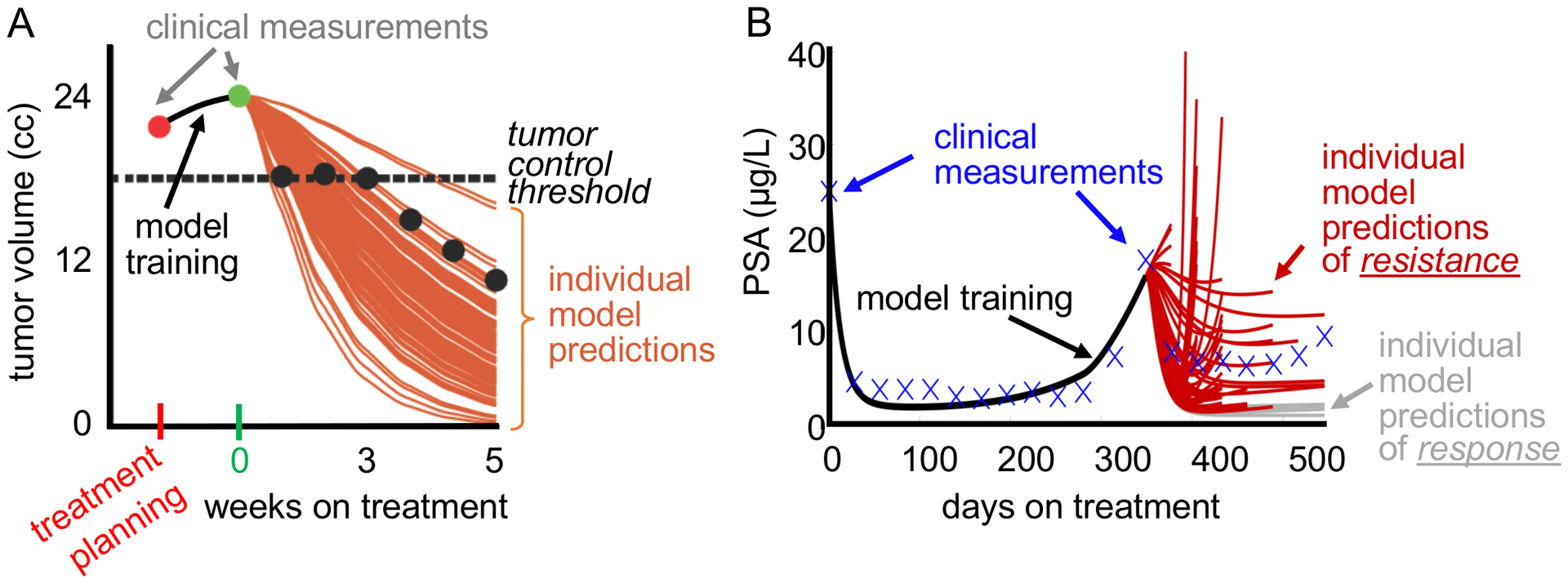
A. Example of the evolution of a head and neck tumor volume from treatment planning (red) to just before the delivery of the first radiation dose (green) and during fractionated radiotherapy (black circles). The 100 mathematical model training-derived tumor response predictions (brown curves) accurately project the final tumor volume to be below the threshold for local tumor control despite collectively missing the observed data. B. Example of the evolution of prostate-specific antigen (PSA) concentration during intermittent hormone therapy for prostate cancer. Data in the first treatment cycle are used to train a mathematical model. Only one of the 100 individual model predictions accurately forecasts the data in the second treatment cycle. However, the number of individual model predictions of resistance (red curves) is sufficiently high compared to response predictions (grey curves) to correctly predict the outcome that the patient will become resistant in the next treatment cycle.

Modeling efforts support various goals, linked to different expectation as to what modeling provides to a specific project. For the application of mathematical modeling for personalized medicine, further discussions about what models can and cannot contribute are necessary. For predictive modeling, right or wrong may not be how well the predicted disease dynamics based on uncertain parameter combinations mimic the clinically observed responses and their underlying biology, but the interpretation and actionability of model predictions and their uncertainty. While mathematical models may not be right, they don’t have to be wrong. Thusly, we may just adopt the philosophy of Assistant Director of Operations Domingo “Ding” Chavez, who taught the young Jack Ryan, Jr., in Tom Clancy’s Oath of Office to “Don’t practice until you get it right. Practice until you don’t get it wrong” (Cameron 2018).