Bayesian Zero-Inflated Negative Binomial Regression Based on Pólya-Gamma Mixtures

Abstract

Motivated by a study examining spatiotemporal patterns in inpatient hospitalizations, we propose an efficient Bayesian approach for fitting zero-inflated negative binomial models. To facilitate posterior sampling, we introduce a set of latent variables that are represented as scale mixtures of normals, where the precision terms follow independent Pólya-Gamma distributions. Conditional on the latent variables, inference proceeds via straightforward Gibbs sampling. For fixed-effects models, our approach is comparable to existing methods. However, our model can accommodate more complex data structures, including multivariate and spatiotemporal data, settings in which current approaches often fail due to computational challenges. Using simulation studies, we highlight key features of the method and compare its performance to other estimation procedures. We apply the approach to a spatiotemporal analysis examining the number of annual inpatient admissions among United States veterans with type 2 diabetes.

1. Introduction

Count data with an abundance of zeros arise commonly in many scientific fields, including ecology, infectious disease epidemiology, and health services research. Consider, for example, our motivating application, which examines the number of inpatient hospitalizations among United States (US) veterans with type 2 diabetes. The majority of patients had no inpatient admissions, resulting in a count of zero, while some had a handful of admissions and a small fraction had numerous admissions. When the number of zeros is greater than expected under a standard count model, the data are said to be zero inflated relative to the standard model. Zero-inflated count data often require flexible two-part mixture models to address both the excess zeros and the heterogeneous distribution of nonzero counts. A common choice is the zero-inflated model (Lambert, 1992), which is a mixture of a point mass that accounts for the excess zeros and a count distribution for the remaining values. The zero-inflated negative binomial (ZINB) model is a popular choice for modeling zero-inflated data because it simultaneously accommodates zero inflation and overdispersion in the count portion of the model.

Frequentist inference for the ZINB model is carried out using Newton-Raphson routines or the EM algorithm, where the excess zeros are treated as a type of missing data. However, frequentist procedures become computationally challenging for complex data structures, including longitudinal, spatial and spatiotemporal data that incorporate multivariate random effects. This has prompted increased interest in tractable Bayesian approaches to fitting zero-inflated models (Ghosh et al., 2006; Neelon et al., 2010; Zurr et al., 2012). Bayesian inference for the ZINB model is typically implemented in prepackaged Bayesian software such as WinBUGS (Lunn et al., 2014). While such programs are suitable for relatively simple models, they become computationally infeasible for fitting zero-inflated models with high-dimensional random effects. In our motivating application, for example, WinBUGS was incapable of fitting a ZINB model with spatially correlated random intercepts and slopes.

To allow for additional flexibility, we propose a computationally efficient Bayesian approach to fitting ZINB models that is specifically designed to handle high-dimensional data where existing methods often fail. We augment the data by introducing two latent variables, each following a mixture of normal distributions with independent Pólya-Gamma precision terms (Polson et al., 2013a). As such, our model extends the approach of Polson et al. (2013a) and Pillow and Scott (2012) to the zero-inflated setting. Because the latent variables are conditionally normal, they admit the convenient posterior distributions available under standard Bayesian linear model theory. This leads to efficient Gibbs sampling routines, and enables closed-form updates for various random effect models.

The remainder of the paper is organized into four sections. Section 2 describes the proposed ZINB model, outlines the Bayesian model fitting approach, and discusses extensions to mixed effects models for longitudinal and spatial data. Section 3 presents numerical examples that highlight salient properties of the model and the proposed Gibbs sampler. In Section 4, we apply the model to a study examining spatiotemporal patterns in inpatient admissions among US veterans residing in three southeastern states from 2011–2015. The final section provides a discussion and offers directions for future research.

2. Bayesian Zero-Inflated Negative Binomial Model

2.1. The Zero-Inflated Negative Binomial Model

Zero-inflated models are mixtures of a point mass at zero, representing the excess zeros, and a count distribution for the remaining values. The term “excess” denotes the fact that the data contain more zeros than expected under a standard count model. By construction, zero-inflated models partition zeros into two types. The first type, typically referred to as a “structural” zero, corresponds to individuals who are not at risk for an event, and therefore have no opportunity for a positive count. The second type, termed the “at-risk” or “chance” zero, applies to a latent class of individuals who are at risk for an event but nevertheless have an observed response of zero. For example, in our application examining the number of inpatient hospitalizations, the structural zeros might represent patients who are in good health or can be treated through outpatient care, and thus have no recorded inpatient days. In contrast, the at-risk zeros might correspond to patients with more serious chronic conditions who, for various reasons, have had no inpatient admissions in a given year. Thus, zero-inflated models can be viewed as latent class models in which the classes are formed by the two types of zeros.

The ZINB model is a common choice for modeling zero-inflated data because it addresses not only zero inflation, but also overdispersion among the counts in the at-risk class. In its generic form, the ZINB model is expressed as

$$y_i\sim (1-{\pi }_i)1_{({\mathrm{w}}_i=0\wedge y_i=0)}+{\pi }_i\text{NB}({\mu }_i,r)1_{({\mathrm{w}}_i=1)},i=1,\dots ,n,$$ (1)

where y_i is the count response for individual i, $1_{(\cdot )}$ is the indicator function, and w_i is a latent “at-risk” indicator variable such that with probability 1 – π_i, w_i = y_i = 0 implying a structural zero, and with probability π_i, w_i = 1 and y_i is in turn drawn from a negative binomial distribution with mean μ_i and dispersion parameter r > 0. Thus, π_i denotes the probability of being in the at-risk class while μ_i denotes the mean count among the at-risk population.

The at-risk indicators, w₁, … , w_n, are typically modeled using a logistic model of the form

$$\mathrm{logit}({\pi }_i)=\mathrm{logit}[\text{Pr}({\mathrm{w}}_i=1\mid {\beta }_1)]={\mathit{x}}_i^T{\beta }_1={\eta }_{1i},$$ (2)

where x_i is a p × 1 vector of covariates and β₁ is a vector of regression parameters. Equation (2) is commonly referred to as the binary or logistic component of the ZINB model, which we denote with the subscript “1” in equation (2). Next, for reasons discussed below, we follow Pillow and Scott (2012) and parameterize the negative binomial component (conditional on w_i = 1) as

$$\begin{gathered} p(y_i\mid r,{\beta }_2,{\mathrm{w}}_i=1)\stackrel{d}{=}\frac{\Gamma (y_i+r)}{\Gamma (r)y_i!}(1-{\psi }_i{)}^r{\psi }_i^{y_i}\forall i\text{s.t.}{\mathrm{w}}_i=1,\text{where} \\ {\psi }_i=\frac{\text{exp}\left({\mathit{x}}_i^T{\beta }_2\right)}{1+\text{exp}\left({\mathit{x}}_i^T{\beta }_2\right)}=\frac{\text{exp}({\eta }_{2i})}{1+\text{exp}({\eta }_{2i})}. \end{gathered}$$ (3)

Equation (3) is often referred to as the count or negative binomial component of the ZINB model, which we denote with the subscript “2”. The expected value and variance among the counts in the at-risk class are

$$\begin{gathered} \mathrm{E}(y_i\mid r,{\beta }_2,{\mathrm{w}}_i=1)=\frac{r{\psi }_i}{1-{\psi }_i}=r\text{exp}({\eta }_{2i})={\mu }_i, \\ \text{Var}(y_i\mid r,{\beta }_2,{\mathrm{w}}_i=1)=\frac{r{\psi }_i}{(1-{\psi }_i{)}^2}=r\text{exp}({\eta }_{2i})[1+\text{exp}({\eta }_{2i})] \\ ={\mu }_i(1+{\mu }_i∕r). \end{gathered}$$ (4)

The marginal mean, averaged over w_i, is E(y_i) = π_iμ_i. The parameter α = 1/r captures the overdispersion in at-risk class, so that as α → ∞, the at-risk counts become increasingly dispersed relative to the Poisson. Above, we have assumed the same set of covariates x_i for both the binary and count components, but in general this is not necessary.

2.2. Bayesian Inference for the ZINB Model

We now outline the posterior sampling algorithm for the fixed effects ZINB model. The details are presented in the following sub-sections, but in brief, the algorithm proceeds in four steps:

1. Given current parameter values, update the latent at-risk indicators, w₁, … , w_n, from their discrete full conditional distributions

2. Update β₁ using the Gibbs sampler proposed by Polson et al. (2013a) for logistic regression

3. Conditional on w_i = 1, update β₂ using the negative binomial Gibbs sampler proposed by Pillow and Scott (2012)

4. Update r using either a random-walk Metropolis-Hastings step or the two-stage Gibbs sampler proposed by Zhou and Carin (2015)

Steps 1, 2 and 3 involve Gibbs updates that admit closed-form full conditionals, and Step 4 involves either a straightforward Metropolis-Hastings update or a Gibbs update.

Step 1: Update the Latent At-Risk Indicators

In Step 1 of the sampler, we update the at-risk indicators, w₁, …, w_n. As outlined in the online supplement (Neelon, 2018), the full conditional for w_i is a discrete distribution with probabilities that depend on whether the observed count, y_i, is zero or non-zero. If y_i > 0, then subject i belongs to the at-risk class, and hence by definition, w_i = 1 with probability 1. Conversely, if y_i = 0, then we observe either a structural zero (implying that w_i = 0) or an at-risk zero (implying w_i = 1). Here, we draw w_i from a Bernoulli distribution with probability

$$\begin{gathered} {\theta }_i=\text{Pr}({\mathrm{w}}_i=1\mid y_i=0,\text{rest})=\text{Pr(at-risk zero}\mid \text{at risk or structural zero)} \\ =\frac{{\pi }_i{\upsilon }_i^r}{1-{\pi }_i(1-{\upsilon }_i^r)}, \end{gathered}$$ (5)

where, from equation (2), π_i = exp(η_1i)/[1 + exp(η_1i)] is the unconditional probability that w_i = 1, and v_i = 1 – ψ_i, where ψ_i is the negative binomial event probability defined in equation (3). The result follows from a direct application of Bayes’ Theorem. The proof is presented in Appendix A of the supplement.

Step 2: Update β₁

To implement Step 2, we employ the data-augmentation Gibbs sampler proposed by Polson et al. (2013a). The approach introduces a vector of latent variables that are scale mixtures of normals with independent Pólya-Gamma precision terms. A random variable ω is said to have a Pólya-Gamma distribution with parameters b > 0 and $c\in \Re$, if

$$\omega \sim \text{PG}(b,c)\stackrel{d}{=}\frac{1}{2{\pi }^2}\sum _{k=1}^{\infty }\frac{g_k}{(k-1∕2{)}^2+c^2∕(4{\pi }^2)},$$ (6)

where the g_k’s are independently distributed according to Ga(b, 1).

Poison et al. (2013a) establish two important properties of the PG(b, c) density. First, for $a\in \Re$ and $\eta \in \Re$, it follows that

$$\frac{({\mathrm{e}}^{\eta }{)}^a}{(1+{\mathrm{e}}^{\eta }{)}^b}=2^{-b}{\mathrm{e}}^{\kappa \eta }{\int }_0^{\infty }{\mathrm{e}}^{-\omega {\eta }^2∕2}p(\omega \mid b,0)\mathrm{d}\omega ,$$ (7)

where κ = a – b/2 and p(ω∣b, 0) denotes a PG(b, 0) density. Next, the conditional distribution p(ω∣b, c) ~ PG(b, c) arises from an “exponential tilting” of the PG(b, 0) density:

$$\begin{gathered} p(\omega \mid b,c)=\frac{\text{exp}(-c^2\omega ∕2)p(\omega \mid b,0)}{{\mathrm{E}}_{\omega }[\text{exp}(-c^2\omega ∕2)]} \\ =\frac{\text{exp}(-c^2\omega ∕2)p(\omega \mid b,0)}{{\int }_0^{\infty }{\mathrm{e}}^{-c^2\omega ∕2}p(\omega \mid b,0)\mathrm{d}\omega }. \end{gathered}$$ (8)

Under the logistic model in equation (2), the Bernoulli likelihood for the at-risk indicators w = (w₁, … , w_n)^T is

$$\begin{gathered} p(\mathbf{w}\mid {\beta }_1)=\prod _{i=1}^{n}p({\mathrm{w}}_i\mid {\beta }_1) \\ =\prod _{i=1}^n{\left(\frac{\text{exp}({\eta }_{1i})}{1+\text{exp}({\eta }_{1i})}\right)}^{{\mathrm{w}}_i}{\left(\frac{1}{1+\text{exp}({\eta }_{1i})}\right)}^{1-{\mathrm{w}}_i} \\ =\prod _{i=1}^n\frac{{\left({\mathrm{e}}^{{\eta }_{1i}}\right)}^{{\mathrm{w}}_i}}{1+{\mathrm{e}}^{{\eta }_{1i}}}, \end{gathered}$$ (9)

where ${\eta }_{1i}={\mathit{x}}_i^T{\beta }_1$. The i-th element of the Bernoulli likelihood has the same form as the left-hand expression in equation (7), with a_i = w_i and b = 1. Thus, we can re-write the Bernoulli likelihood in terms of the Pólya-Gamma random variables ω₁ = (ω₁₁, … , ω_1n)^T according to equation (7):

$$p({\mathrm{w}}_i\mid {\beta }_1)\propto {\mathrm{e}}^{{\kappa }_i{\eta }_{1i}}{\int }_0^{\infty }{\mathrm{e}}^{-{\omega }_{1i}{\eta }_{1i}^2∕2}p({\omega }_{1i}\mid 1,0)\mathrm{d}{\omega }_{1i},$$ (10)

where κ_i = w_i – 1/2. Let ω_1i (i = 1, … , n) be independently distributed according to PG(1, η_1i). By appealing to the above properties the Pólya-Gamma distribution, Polson et al. (2013a) show that the full conditional distribution of β₁, given w and ω₁, is

$$p({\beta }_1\mid \mathbf{w},{\omega }_1)\propto \pi ({\beta }_1)\text{exp}\left[-\frac{1}{2}({\mathit{z}}_1-\mathit{X}{\beta }_1{)}^T{\Omega }_1({\mathit{z}}_1-\mathit{X}{\beta }_1)\right],$$ (11)

where π(β₁) is the prior distribution for β₁; for i = 1, … , n, $z_{1i}=\frac{{\mathrm{w}}_i-1∕2}{{\omega }_{1i}}$ with z₁ = (z₁₁, … , z_1n)^T; Ω₁ = diag(ω₁) is an n × n precision matrix; and X is an n × p design matrix. It is clear that, given β₁ and Ω₁, z₁ is normally distributed with mean η₁ = Xβ₁ and diagonal covariance ${\Omega }_1^{-1}$. Thus, assuming a N_p(β₀, Σ₀) prior for β₁, the full conditional for β₁ given z₁ and Ω₁ is N_p(μ, Σ), where

$$\begin{gathered} \Sigma ={\left({\Sigma }_0^{-1}+{\mathit{X}}^T{\Omega }_1\mathit{X}\right)}^{-1}, \\ \mu =\Sigma \left({\Sigma }_0^{-1}{\beta }_0+{\mathit{X}}^T{\Omega }_1{z}_1\right). \end{gathered}$$ (12)

The derivation can be found in Polson et al. (2013a); for convenience, we provide a summary in Appendix A of the online supplement.

Given these results, the Gibbs sampler for Step 2 proceeds by selecting initial values for β₁ and w and iterating through the following steps:

1. For i = 1, … , n, update ω_1i from a PG(1, η_1i) density, where ${\eta }_{1i}={\mathit{x}}_i^T{\beta }_1$

2. For i = 1, …, n, define $z_{1i}=\frac{{\mathrm{w}}_i-1∕2}{{\omega }_{1i}}$

3. Conditional on z₁, update β₁ from N_p(μ, Σ), where μ and Σ are given in (12).

An efficient accept-reject algorithm is used to sample from the Pólya-Gamma distribution and can be implemented in the R package BayesLogit (Polson et al., 2013b).

Step 3: Update β₂

The update for β₂ is similar to the one for β₁. Adopting the parameterization of the negative binomial in equation (3), the conditional likelihood of y_i given w_i = 1 is

$$\begin{gathered} p(y_i\mid r,{\beta }_2,{\mathrm{w}}_i=1)\propto (1-{\psi }_i{)}^r{\psi }_i^{y_i} \\ =\frac{\text{exp}({\eta }_{2i}{)}^{y_i}}{[1+\text{exp}({\eta }_{2i}){]}^{r+y_i}}, \end{gathered}$$ (13)

where ${\eta }_{2i}={\mathit{x}}_i^T{\beta }_2$. Exploiting property 1 of the Pólya-Gamma distribution in equation (7), it follows that

$$p(y_i\mid r,{\beta }_2,{\mathrm{w}}_i=1)\propto {\mathrm{e}}^{{\kappa }_i{\eta }_{2i}}{\int }_0^{\infty }{\mathrm{e}}^{-{\omega }_{2i}{\eta }_{2i}^2∕2}p({\omega }_{2i}\mid r+y_i,0)\mathrm{d}{\omega }_{2i},$$ (14)

where κ_i = (y_i – r)/2. If we let ω_2i be distributed according to PG(y_i + r, η_2i), then following Pillow and Scott (2012), the full conditional for β₂ is

$$p({\beta }_2\mid {\mathit{y}}^{\ast },r,\mathbf{w},{\omega }_2)\propto \pi ({\beta }_2)\text{exp}\left[-\frac{1}{2}({\mathit{z}}_2-{\mathit{X}}^{\ast }{\beta }_2{)}^T{\Omega }_2({\mathit{z}}_2-{\mathit{X}}^{\ast }{\beta }_2)\right],$$ (15)

where y* is the n* × 1 subvector of y corresponding to w_i = 1; $n^{\ast }={\sum }_{i=1}^n{\mathrm{w}}_i$ is the number of individuals in the at-risk class (i.e., for whom w_i = 1); ω₂ is a vector of length n* with elements ω_2i; z₂ is a vector of length n* with elements $z_{2i}=\frac{y_i-r}{2{\omega }_{2i}}$; Ω₂ = diag(ω₂) is an n* × n* precision matrix; and X* is an n* × p design matrix. From (15), it is clear that z₂ is normally distributed with mean η₂ = X* β₂ and diagonal covariance ${\Omega }_2^{-1}$. Thus, assuming a N_p(β₀, Σ₀) prior for β₂, the conjugate full conditional for β₂ given z₂ and Ω₂ is N_p (μ, Σ), where

$$\begin{gathered} \Sigma ={\left({\Sigma }_0^{-1}+{\mathit{X}}^{\ast T}{\Omega }_2{\mathit{X}}^{\ast }\right)}^{-1}, \\ \mu =\Sigma \left({\Sigma }_0^{-1}{\beta }_0+{\mathit{X}}^{\ast T}{\Omega }_2{z}_2\right). \end{gathered}$$ (16)

The proof can be found in Pillow and Scott (2012) and is summarized in the context of the ZINB model in Appendix A of the online supplement. Thus, given current values for β₂, w, and r, the Gibbs sampler for Step 3 proceeds as follows:

1. For w_i = 1, draw ω_2i from its PG(y_i + r, η_2i) distribution, where ${\eta }_{2i}={\mathit{x}}_i^T{\beta }_2$

2. For w_i = 1, define $z_{2i}=\frac{y_i-r}{2{\omega }_{2i}}$

3. Update β₂ from its N(μ, Σ) distribution, where μ and Σ are given in (16).

Step 4: Update r

In the final step, we update r using either a Metropolis-Hastings step or a conjugate Gibbs update. For the Metropolis update, we select a uniform prior with positive support and draw candidate values of r from a zero-truncated normal proposal centered at the current value of r. Alternatively, one can adopt the two-stage Gibbs update proposed by Zhou and Carin (2015) and discussed more recently by Dadaneh et al. (2018). In stage 1, latent counts are introduced according to a Chinese restaurant table distribution; in stage 2, r is sampled from a conjugate Gamma distribution given the latent counts. Details are provided in the online supplement. In our experience, the Metropolis-Hastings update works well in practice, and we therefore present Metropolis-based results in the sections below.

To complete the prior specification for the ZINB model, we assign weakly informative N_p(0, 100I_p) priors to β₁ and β₂. These choices work well for the analyses presented in Sections 3 and 4. More generally, we expect little sensitivity to prior specification, except perhaps in cases where there is an extremely high or low percentage of zeros (e.g., > 95% or < 5%). In the former case, there are relatively few nonzero values, resulting in a small at-risk sample; in the latter, there tend to be very few structural zeros, in which case a standard (non-inflated) negative binomial model provides adequate fit. However, these are instances in which maximum likelihood methods also break down. In general, the proposed sampling algorithm works well for scenarios commonly encountered in practice, as illustrated by the numerical examples presented in Section 3.

The MCMC algorithm cycles through Steps 1–4 until convergence, which can be assessed using standard Markov chain Monte Carlo (MCMC) diagnostics such as trace plots, Geweke z-statistics (Geweke, 1992) and Monte Carlo standard errors. These diagnostics can be obtained from the R packages coda (Plummer et al., 2006) and mcmcse (Flegal et al., 2017). In our experience, convergence for fixed effects models is almost immediate with excellent mixing. Even for more complex models, we typically observe rapid convergence, as illustrated by the simulated examples presented in Section 3.

2.3. Extensions to Longitudinal and Spatial Data

Equipped with the latent normal variables z₁ and z₂, the ZINB model can easily be extended to accommodate longitudinal, spatial, and time series data — essentially any setting where the model parameters are linear in z₁ and z₂. Suppose, for example, we have count responses, y_ij, measured at occasions j = 1, …, n_i for individual i. We can model the data using a longitudinal version of the ZINB model, which is expressed as

$$y_{ij}\sim (1-{\pi }_{ij})1_{({\mathrm{w}}_{ij}=0\wedge y_{ij}=0)}+{\pi }_{ij}\text{NB}({\mu }_{ij},r)1_{({\mathrm{w}}_{ij}=1)},$$ (17)

where, for the ij-th observation, w_ij denotes the at-risk indicator taking value 1 with probability π_ij, and μ_ij is the negative binomial mean analogous to the one presented in line 1 of equation (4). As before, we model π_ij using a logit link

$$\mathrm{logit}({\pi }_{ij})=\mathrm{logit}[\text{Pr}({\mathrm{w}}_{ij}=1\mid {\beta }_1,{\varphi }_{1i})]={\mathit{x}}_{ij}^T{\beta }_1+{\mathit{v}}_{ij}^T{\varphi }_{1i}={\eta }_{1ij},$$ (18)

where x_ij is a p × 1 vector of covariates including appropriate functions of time (e.g., linear or polynomial time trends); β₁ is a p × 1 vector of fixed effect coefficients; ${\mathit{v}}_{ij}^T$ is a q × 1 random effect design vector that includes functions of time; and ϕ_1i ~ N_q(0, G₁) is a q × 1 vector of random effects for the binary component, with q × q prior covariance G₁. Similarly, the negative binomial component (conditional on w_ij = 1) is modeled as

$$\begin{gathered} p(y_{ij}\mid r,{\beta }_2,{\varphi }_{2i},{\mathrm{w}}_{ij}=1)\stackrel{d}{=}\frac{\Gamma (y_{ij}+r)}{\Gamma (r)y_{ij}!}(1-{\psi }_{ij}{)}^r{\psi }_{ij}^{y_{ij}},\forall i,j\text{s.t.}{\mathrm{w}}_{ij}=1, \\ {\psi }_{ij}=\frac{\text{exp}\left({\mathit{x}}_{ij}^T{\beta }_2+{\mathit{v}}_{ij}^T{\varphi }_{2i}\right)}{1+\text{exp}\left({\mathit{x}}_{ij}^T{\beta }_2+{\mathit{v}}_{ij}^T{\varphi }_{2i}\right)}=\frac{\text{exp}({\eta }_{2ij})}{1+\text{exp}({\eta }_{2ij})}, \end{gathered}$$ (19)

where ϕ_2i × N_q (0, G₂) is a q × 1 vector of random effects for the count component with q × q covariance G₂. Often it is reasonable to retain the same random effect structure for both components, although in general this is not necessary. For example, we might include only a random intercept in the binary component but a random intercept and slope in the count component. Without loss of generality, we assume throughout that q is the same for both components; however, the proposed models can be easily modified to accommodate separate dimensions q₁ and q₂ for the two parts of the ZINB model.

To facilitate posterior computation, we again augment the data with latent normal variables for each component. Let z_1ij = (y_ij – 1/2)/ω_1ij be the latent normal variable for the binary component of the ZINB at occasion ij, and let z_2ij = (y_ij – r)/(2ω_2ij) be the latent normal variable for the count component conditional on w_ij = 1, where ω_1ij and ω_2ij follow independent Pólya-Gamma distributions. We model the n_i × 1 vector z_1i = (z_1i1, … , z_1ini)^T as

$${\mathit{z}}_{1i}\mid {\eta }_{1i},{\Omega }_{1i}\sim {\mathrm{N}}_{n_i}\left({\eta }_{1i},{\Omega }_{1i}^{-1}\right),$$ (20)

where, for subject i, η_1i = (η_1i1, … , η_1ini)^T = X_iβ₁ + V_iϕ_1i is the n_i × 1 linear predictor for the binary component; X_i and V_i are, respectively, n_i × p and n_i × q fixed and random effect design matrices; Ω_1i = diag(ω_1i) is an n_i × n_i diagonal precision matrix; and ω_1i = (ω_1i1, … , ω_1ini)^T. Similarly, for the count component, we have

$${\mathit{z}}_{2i}\mid {\eta }_{2i},{\Omega }_{2i}\sim {\mathrm{N}}_{n_i^{\ast }}\left({\eta }_{2i},{\Omega }_{2i}^{-1}\right)$$ (21)

Here, z_2i is a vector of length $n_i^{\ast }$, where $n_i^{\ast }={\sum }_{j=1}^{n_i}{\mathrm{w}}_{ij}$ is the number of at-risk observations for subject i; ${\eta }_{2i}={\mathit{X}}_i^{\ast }{\beta }_2+{\mathit{V}}_i^{\ast }{\varphi }_{2i}$ is the $n_i^{\ast }\times 1$ linear predictor for the count component, where ${\mathit{X}}_i^{\ast }$ and ${\mathit{V}}_i^{\ast }$ are $n_i^{\ast }\times p$ and $n_i^{\ast }\times q$ fixed and random effect design matrices; Ω_2i = diag(ω_2i) is an $n_i^{\ast }\times n_i^{\ast }$ precision matrix; and ω_2i is an n* × 1 vector of PG precisions for the count component.

Note that if $n_i^{\ast }=0$, then none of the observations fall into the at risk class – that is, w_ij = 0 for all j = 1, …, n_i. This is unlikely to occur unless n_i is small or ϕ_ij is low for j = 1, … , n_i, leading to few at-risk observations for subject i. When $n_i^{\ast }$ is small, we must rely more heavily on the multivariate normal prior for ϕ_2i to shrink the random effects toward a global population mean of zero, thus stabilizing the random effect predictions. As we illustrate in Section 3, the proposed random effect ZINB model performs well even for small $n_i^{\ast }$.

In many cases, it is reasonable to assume that the binary and count components are correlated, thus allowing for dependence between the at-risk probability and the count distribution among those at risk. In our motivating application, for example, patients who are at high risk for inpatient hospitalizations may also have a greater number of re-admissions compared to those with low risk of inpatient hospitalizations. Recent work suggests that ignoring this association can lead to biased inferences in zero-inflated models (Su et al., 2009). We can accommodate this dependence by allowing ϕ_1i and ϕ_2i to be correlated according to a multivariate normal distribution. Let ${\varphi }_i=({\varphi }_{1i}^T,{\varphi }_{2i}^T{)}^T$ denote the 2q × 1 vector comprising the random effects for both the binary and count components. We assume the following multivariate normal distribution for ϕ_i:

$$\begin{gathered} {\varphi }_i\mid \Gamma \sim {\mathrm{N}}_{2q}(0,\Gamma ), \\ \text{where}\Gamma =\left(\begin{array}{cc}\hfill {\mathit{G}}_1\hfill & \hfill {\mathit{G}}_{12}\hfill \\ \hfill {\mathit{G}}_{21}\hfill & \hfill {\mathit{G}}_2\hfill \end{array}\right) \end{gathered}$$ (22)

is a 2q × 2q positive-definite covariance matrix under the default assumption that q is the same for the binary and count components. The covariance between the components is captured by the q × q off-diagonal elements ${\mathit{G}}_{12}={\mathit{G}}_{21}^T$.

The correlated random effects model is especially attractive because it allows the level of shrinkage imposed on the random effects to be correlated across components. By applying two related sources of shrinkage to the random effects, the correlated model improves inference in the presence of small $n_i^{\ast }$. In particular, when there are few at-risk observations, so that $n_i^{\ast }$ is small, the correlated model allows the random effects ϕ_2i in the count component to borrow information from ϕ_1i in the binary component, which typically has a greater sample size (i.e., $n_i\ge n_i^{\ast }$) and hence more information available for prediction.

The model can further extend to areal spatial and spatiotemporal data by assigning a multivariate conditionally autoregressive (CAR) prior to ϕ_i in equation (22). For example, an intrinsic CAR prior (Banerjee et al., 2014) takes the form

$${\varphi }_i\mid {\varphi }_{(-i)},\Gamma \sim {\mathrm{N}}_{2q}\left(\frac{1}{m_i}\sum _{l\in {\partial }_i}{\varphi }_{il},\frac{1}{m_i}\Gamma \right),$$ (23)

where m_i is the number of neighbors for i-th areal unit, ∂_i is the set of neighbors for unit i, and Γ is the 2q × 2q conditional covariance matrix given the remaining spatial random effects, ϕ(−i). Whereas the multivariate normal prior in equation (22) permits “global” shrinkage to a population mean of zero, the CAR prior borrows information across neighboring spatial regions, resulting in “localized” shrinkage that yields a spatially smoothed map.

As the dimension of q increases, the joint posterior update for ϕ_i can become unmanageable. Consider, for example, a spatiotemporal intercept and slope model, where each component includes a random intercept and linear time trend. Here, each component includes q = 2 random effects, resulting in a 4 × 4 covariance matrix Γ in equation (23). Let ϕ₁₁ = (ϕ₁₁₁, … , ϕ_1n1)^T and ϕ₁₂ = (ϕ₁₁₂, … , ϕ_1n2)^T denote, respectively, the n × 1 vectors of random intercepts and slopes for the binary component. Similarly, define ϕ₂₁ = (ϕ₂₁₁, … , ϕ_2n1)^T and ϕ₂₂ = (ϕ₂₁₂, … , ϕ2n2)^T to be the intercept and slope vectors for the count component. Finally, let $\varphi =({\varphi }_{11}^T,\dots ,{\varphi }_{22}^T{)}^T$, be the 4n × 1 collection of all random effects. Following Brook’s Lemma (Banerjee et al., 2014), the joint prior for ϕ is given by

$$p(\varphi \mid \Gamma )\propto \text{exp}\left[-\frac{1}{2}{\varphi }^T({\Gamma }^{-1}\otimes \mathit{Q})\varphi \right],$$ (24)

where Q = M – A is an n × n “structure” matrix of rank n – 1; M = diag(m₁, … , m_n) with diagonal elements equal to the number of neighbors for each spatial unit; and A is an n × n adjacency matrix with a_ii = 0, a_il = 1 if spatial units i and l are neighbors, and a_il = 0 otherwise. Because Q is rank-deficient — and hence p(ϕ∣Γ) is improper — a sum-to-zero constraint is typically applied to ϕ as part of the MCMC algorithm to ensure an identifiable model (Banerjee et al., 2014).

From expression (24), the joint prior for ϕ is proportional to a multivariate normal density with 2qn × 2qn precision matrix Γ⁻¹ ⊗ Q, which in many applications is too unwieldy for efficient posterior inference. It is therefore convenient to partition expression (24) into univariate conditional priors for each vector ϕ_kk (k = 1, … , q) given the remaining random effects. This leads to efficient Gibbs sampling by permitting separate updates for each n × 1 vector ϕ_kk. For instance, under the spatiotemporal intercept/slope model described above, the conditional prior for ϕ₁₁, the n × 1 vector of random intercepts for the binary component, is

$$\begin{gathered} p({\varphi }_{11}\mid {\varphi }_{12},{\varphi }_{21},{\varphi }_{22},\Gamma )\propto \text{exp}\left[-\frac{1}{2}({\varphi }_{11}-{\mu }_{11}{)}^T{\Sigma }_{11}({\varphi }_{11}-{\mu }_{11})\right],\text{where} \\ {\Sigma }_{11}={\left[{\Gamma }_{11}-{\Gamma }_{(1,-1)}{\Gamma }_{(-1,-1)}^{-1}{\Gamma }_{(-1,1)}\right]}^{-1}\mathit{Q}, \\ {\mu }_{11}=\left[\left({\Gamma }_{(1,-1)}{\Gamma }_{(-1,-1)}^{-1}\right)\otimes {\mathit{I}}_n\right]{\varphi }_{(-1)}, \end{gathered}$$ (25)

where Γ is the 4 × 4 covariance of ϕ_i Γ₁₁ denotes the first element of Γ, Γ_{(−1, −1}) is the 1 × 3 vector comprising the first row of Γ with element 1 removed, Γ_{(−1, −1}) is the 3 × 3 submatrix of Γ after removing row 1 and column 1, Γ_(−1,1) is the 3 × 1 vector comprising the first column of Γ with element 1 removed, and ${\varphi }_{(-1)}=({\varphi }_{12}^T,{\varphi }_{21}^T,{\varphi }_{22}^T{)}^T$ is a 3n × 1 vector of the remaining random effects. Equation (25) follows directly from conditional multivariate normal theory. Similar expressions hold for ϕ₁₂, ϕ₂₁ and ϕ₂₂.

The conditional prior specification in (25) leads to efficient Gibbs updates for the spatial effects. Consider once again the spatial intercept/slope model. As detailed in the Appendix B of the online supplement, the updates for ϕ₁₁ and ϕ₁₂ in the binary component depend on the likelihood contributions from all $N={\sum }_{i=1}^n{n}_i$ observations, whereas the updates for ϕ₂₁ and ϕ₂₂ in the count component rely only on contributions from the $N^{\ast }={\sum }_{i=1}^n{n}_i^{\ast }\le N$ “at-risk” observations for which w_ij = 1 (i = 1, … , n; j = 1, … , n_i). This sample-size imbalance prevents a joint Gibbs update for $\varphi =({\varphi }_{11}^T,\dots ,{\varphi }_{22}^T{)}^T$ based on prior (24). The conditional prior (25) avoids this problem by providing separate univariate updates for ϕ₁₁, ϕ₁₂, ϕ₂₁ and ϕ₂₂, the first two based on all N observations and the latter two based on the N* at-risk observations. The approach can easily be generalized to q > 2 random effects for each component, as well as to non-spatial longitudinal data, where Q = I_n is of full rank. Additional details on the conditional prior specification can be found in Appendix B of the supplement.

Prior specification for the spatial and non-spatial correlated ZINB models is completed by assigning conditionally conjugate N_p(β₀, Σ₀) priors to the fixed effects and an inverse-Wishart(2q, Λ) prior to Γ, where Λ is 2q × 2q scale matrix. By default, we set β₀ = 0, Σ₀ = 100I_p, and Λ = I_2q. To implement the MCMC for random effect ZINB models, we initialize the model parameters and then cycle through the following steps:

1. For all i, j, update the latent at-risk indicators, w_ij, according to the discrete probability distribution

   $$\text{Pr}({\mathrm{w}}_{ij}=1\mid \text{rest})=\{\begin{array}{cc}1,\hfill & \text{if}{y}_{ij}=1\hfill \\ \frac{{\pi }_{ij}{\upsilon }_{ij}^r}{1-{\pi }_{ij}(1-{\upsilon }_{ij}^r)},\hfill & \text{if}{y}_{ij}=0\hfill \end{array}\phantom{\}},$$ (26)

   where π_ij = exp(η_1ij)/[1 + exp(η_1ij)] is the unconditional probability that w_ij = 1 given in equation (18), v_ij = 1 – ψ_ij, and ${\psi }_{ij}=\frac{\text{exp}({\eta }_{2ij})}{1+\text{exp}({\eta }_{2ij})}$ is the negative binomial event probability defined in equation (19).

2. Update the parameters for the binary component:

   1. For all i, j, sample ω_1ij from PG(1, η_1ij), where η_1ij is defined in equation (18)
   2. For all i, j, define z_1ij = (y_ij — 1/2)/ω_1ij
   3. Update β₁ from its normal full conditional
   4. For k = 1, …, q, update each n × 1 vector ϕ_1k from its normal full conditional based on the conditional prior specification given in (25); apply sum-to-zero constraints as needed
3. Update the parameters for the count component:

   1. For w_ij = 1, sample ω_2ij from PG(1, η_2ij), where η_2ij is defined in equation (19)
   2. For w_ij = 1, define z_2ij = (y_ij – r)/(2ω_2ij)
   3. Update β₂ from its normal full conditional
   4. For k = 1, … , q, update each n × 1 vector ϕ_2k from its normal full conditional based on the conditional prior specification given in (25); apply sum-to-zero constraints as needed
   5. Update r using a random-walk Metropolis-Hastings step or the two-stage Gibbs sampler analogous to the ones outlined in Section 2.2

4. Update the 2q × 2q covariance matrix Γ from its conjugate inverse-Wishart full conditional.

Appendix B of the supplement derives the full conditionals for the spatial intercept/slope ZINB model implemented in Sections 3.3 and 4.

3. Simulated Examples

3.1. Simulation 1: Fixed Effects ZINB Model

To illustrate the properties of the model, we conducted a series of simulations of increasing model complexity. First, we generated data from fixed effects ZINB model and compared the results to maximum likelihood estimates (MLEs) obtained using the SAS^® software procedure NLMIXED (SAS Institute, Cary, North Carolina). The aim was to determine whether the proposed Bayesian approach with weakly informative priors yielded regression estimates and uncertainty intervals similar to those obtained under a classical, frequentist approach. To do so, we generated 1000 observations according to the following ZINB model:

$$\begin{gathered} y_i\sim (1-{\pi }_i)1_{({\mathrm{w}}_i=0\wedge y_i=0)}+{\pi }_i\text{NB}({\mu }_i,r)1_{({\mathrm{w}}_i=1)}, \\ \log \text{it}({\pi }_i)=\mathrm{logit}[\text{Pr}({\mathrm{w}}_i=1\mid {\beta }_1)]={\eta }_{1i}={\beta }_{10}+{\beta }_{11}{x}_{i1}+{\beta }_{12}{x}_{i2}+{\beta }_{13}{x}_{i3}, \\ p(y_i\mid r,{\beta }_2,{\mathrm{w}}_i=1)\stackrel{d}{=}\frac{\Gamma (y_i+r)}{\Gamma (r)y_i!}(1-{\psi }_i{)}^r{\psi }_i^{y_i}, \\ {\psi }_i=\frac{\text{exp}({\eta }_{2i})}{1+\text{exp}({\eta }_{2i})}, \\ {\eta }_{2i}={\beta }_{20}+{\beta }_{21}{x}_{i1}+{\beta }_{22}{x}_{i2}+{\beta }_{23}{x}_{i3}, \end{gathered}$$ (27)

where x_i1 was simulated from an N(0, 1) distribution, x_i2 was simulated from a Bernoulli(0.5) distribution, x_i3 was simulated from a discrete uniform distribution taking values {0, 1, 2}, β₁ = (β₁₀, … , β₁₃)^T = (0.5, −0.5, −0.25, 0.25)^T, β₂ = (β₂₀, … , β₂₃)^T = (0.5, −1, 0.75, −0.25)^T and r = 1. These values resulted in 60% zeros, a mean count of 2.8, and the five-number summary (0, 0, 0, 2, 68). Figure S1 in Appendix C of the online supplement presents a full histogram of the count distribution.

We assigned independent N(0, 100) priors to the regression coefficients and a Unif(0, 10) prior to r. To update r, we used a zero-truncated normal proposal with variance 0.025 centered at the current value, resulting in a Metropolis-Hastings acceptance rate of 36%. Initial values were set at β₁ = β₂ = 0, and r = 1. We ran 50,500 iterations of the MCMC algorithm described in Section 2, discarding the first 500 as burn-in. Figure S2 of the supplement presents trace plots, Monte Carlo standard errors and p-values from the Geweke diagnostics for selected parameters. Non-significant p-values are indicative of convergence. The p-values for simulation 1 ranged from 0.10 to 0.47, indicating reasonable convergence. The trace plots showed satisfactory mixing. The algorithm took 6.20 minutes to run on a Dell^® Precision T3610 workstation, compared to 0.50 seconds for SAS. However, a shorter run of 1500 iterations took approximately 11 seconds to run and produced similar results (Figure S3), indicating that the proposed Bayesian method is comparable to SAS in terms of run time.

Watanabe (Watanabe, 2010) Information Criteria (WAIC) values for the ZINB and negative binomial models were 3011 and 3067, respectively, indicating superior fit for the ZINB model. We based our model comparisons on WAIC rather than the more commonly used Deviance Information Criteria (DIC) because the DIC penalty term can yield negative values for mixture models, such as the ZINB, when the posterior mean deviates from the posterior mode (Celeux et al., 2006; Gelman et al., 2014). For a detailed discussion of WAIC and its comparison to other information criteria, please see Gelman et al. (2014).

Table 1 presents the parameter estimates and 95% intervals for the ZINB model under Bayesian and maximum likelihood estimation. In all cases, the Bayesian estimates were as or more accurate than the maximum likelihood estimates (MLEs). For both methods, the 95% intervals encompassed the simulated values. These results suggest that even for moderate sample sizes with a large percentage of zeros, the proposed Bayesian approach provides a suitable alternative to frequentist estimation for fixed effects ZINB models. The Bayesian approach might prove particularly attractive when prior data can be incorporated into the analysis to improve inferences, as frequentist approaches do not accommodate such information.

Table 1:

Parameter estimates and 95% intervals for fixed effects ZINB model in simulation study 1.

Model Component	Parameter	Simulated Value	Estimate (95% Interval)
			Proposed Model†	MLE‡
Binary	β10	0.50	0.51 (−0.00, 1.18)	0.39 ( 0.12, 0.90)
	β11	0.50	0.47 ( 0.18, 0.85)	0.41 ( 0.12, 0.70)
	β12	−0.25	−0.03 (−0.46, 0.38)	−0.01 (−0.41, 0.38)
	β13	0.25	0.09 (−0.15, 0.35)	0.09 (−0.15, 0.32)
Count	β20	0.50	0.37 ( 0.04, 0.72)	0.33 (−0.01, 0.67)
	β21	−1.00	−0.95 (−1.09, −0.82)	−0.95 (−1.08, −0.81)
	β22	0.75	0.62 ( 0.40, 0.84)	0.62 ( 0.40, 0.83)
	β23	−0.25	−0.11 (−0.24, 0.02)	−0.11 (−0.24, 0.02)
	r	1.00	1.18 ( 0.77, 1.68)	1.25 ( 0.78, 1.73)

^†Posterior means and 95% credible intervals for proposed Bayesian ZINB model.

^‡MLEs and 95% confidence intervals obtained using SAS Proc NLMIXED.

3.2. Simulation 2: Correlated Random Intercept ZINB Model

For the second simulation study, we generated data for 1000 subjects from the following correlated random intercept model analogous to the one given in equation (17):

$$\begin{gathered} y_{ij}\sim (1-{\pi }_{ij})1_{({\mathrm{w}}_{ij}=0\wedge y_{ij}=0)}+{\pi }_{ij}\text{NB}({\mu }_{ij},r)1_{({\mathrm{w}}_{ij}=1)}, \\ \log \text{it}({\pi }_{ij})=\mathrm{logit}[\text{Pr}({\mathrm{w}}_{ij}=1\mid {\beta }_1,{\varphi }_{1i})] \\ ={\eta }_{1ij}={\beta }_{10}+{\beta }_{11}{x}_i+{\beta }_{12}{t}_{ij}+{\varphi }_{1i}, \\ p(y_{ij}\mid r,{\beta }_2,{\varphi }_{2i},{\mathrm{w}}_{ij}=1)\stackrel{d}{=}\frac{\Gamma (y_{ij}+r)}{\Gamma (r)y_{ij}!}(1-{\psi }_{ij}{)}^r{\psi }_{ij}^{y_{ij}}, \\ {\psi }_{ij}=\frac{\text{exp}({\eta }_{2ij})}{1+\text{exp}({\eta }_{2ij})}, \\ {\eta }_{2ij}={\beta }_{20}+{\beta }_{21}{x}_i+{\beta }_{22}{t}_{ij}+{\varphi }_{2i}, \\ {\varphi }_i=({\varphi }_{1i},{\varphi }_{2i}{)}^T\sim {\mathrm{N}}_2(0,\Gamma ), \end{gathered}$$ (28)

where, for i = 1, … , 1000 and j = 1, … , n_i, y_ij denotes the count for individual i at occasion j; w_ij is the “at-risk” indicator for observation ij; π_ij is the corresponding at-risk probability; x_i ~ Bern(0.5) is a time-invariant binary covariate (e.g., gender); t_ij ~ N(0, 2) denotes the timing of observation ij (after centering, say); and ϕ_i is a bivariate normal vector of random intercepts for the i-th individual, with mean zero and covariance Γ. As with simulation 1, the goal was to compare the Bayesian estimates under weakly informative priors to the corresponding MLEs. Maximum likelihood was implemented using SAS Proc NLMIXED, which combines Gaussian quadrature for numerical integration with Newton-Raphson for maximization.

For simulation 2, we generated n_i according to a discrete uniform distribution ranging from 1 to 10, resulting in a total sample size of N = 5585 with a mean of 5.59 observations per subject. Seven percent of the subjects had no at-risk observations ($n_i^{\ast }=0$), and another 17% had only one at-risk observation. Thus, we were able to evaluate the performance of our model when approximately one quarter of the sample had few (or no) at-risk observations. We assigned the following values to the model parameters: β₁ = (β₁₀, β₁₁, β₁₂)^T = (0.25, −0.25, 0.25)^T, β₂ = (β₂₀, β₂₁, β₂₂)^T = (0.50, −.25, 0.25)^T, r = 1.25, and $\Gamma =\left(\begin{array}{cc}\hfill 0.50\hfill & \hfill 0.25\hfill \\ \hfill 0.25\hfill & \hfill 0.75\hfill \end{array}\right)$. These values resulted in 52% zeros, a mean count of 3.34, and a five-number summary of (0, 0, 0, 4, 220). Figure S4 of the online supplement presents a full histogram of the counts for simulation 2.

As in simulation 1, we assigned independent N(0, 100) priors to the fixed effects and a Unif(0, 10) prior to r. We reparameterized the bivariate normal prior for ϕ_i using the conditional specification described in equation (25), leading to a conditional prior for ϕ_1i of the form

$$\begin{gathered} {\varphi }_{1i}\mid {\varphi }_{2i}\sim \mathrm{N}(m,v), \\ v={\Gamma }_{11}-\frac{{\Gamma }_{12}{\Gamma }_{12}}{{\Gamma }_{22}}=(1-{\rho }^2){\Gamma }_{11}, \\ m=\frac{{\Gamma }_{21}}{{\Gamma }_{22}}{\varphi }_{2i}=\rho \sqrt{\frac{{\Gamma }_{11}}{{\Gamma }_{22}}}{\varphi }_{2i}, \end{gathered}$$ (29)

where Γ₁₁ and Γ₂₂ are the marginal variances of ϕ_1i and ϕ_2i, respectively, and $\rho =\frac{{\Gamma }_{12}}{\sqrt{{\Gamma }_{11}{\Gamma }_{22}}}=\text{Corr}({\varphi }_{1i},{\varphi }_{2i})$. The conditional prior for ϕ_2i follows a similar expression. Finally, we assigned an inverse-Wishart(2, I₂) prior to Γ.

For posterior inference, we implemented the MCMC algorithm described at the end of Section 2. Starting values for β₁, β₂ and r were identical to those in simulation 1. Initial values for ϕ_1i and ϕ_2i were drawn from independent standard normal distributions, and Γ was initialized to I₂. To update r, we used a zero-truncated normal proposal with variance 0.003, resulting in an acceptance rate of 42%. We ran the sampler for 50,500 iterations, discarding the first 500 as burn-in. Figure S5 of the supplement presents trace plots, Geweke diagnostic p-values and Monte Carlo standard errors for selected parameters. The results indicate excellent mixing. For comparison, we re-ran the algorithm for 2500 iterations (Figure S6 and Table S1), which took 78 seconds to run, compared to 55 seconds for SAS. An even shorter run of 1500 iterations yielded similar results and took only 44 seconds to complete, confirming that the proposed model is competitive with SAS in terms of computation time.

Table 2 presents the parameter estimates and 95% intervals under Bayesian and maximum likelihood estimation. The estimates for the two procedures were nearly identical, with 95% intervals encompassing the true parameter values. These results suggest that the proposed Bayesian approach performs similarly to maximum likelihood for commonly used mixed models with relatively few observations per subject, thus offering an appropriate Bayesian alternative to frequentist estimation in such cases.

Table 2:

Parameter estimates and 95% intervals for random effects ZINB model in simulation study 2.

Model Component	Parameter	Simulated Value	Estimate (95% Interval)
			Proposed Model†	MLE‡
Binary	β10	0.25	0.06 (−0.17, 0.30)	0.05 (−0.19, 0.28)
	β11	−0.25	−0.27 (−0.47, −0.08)	−0.27 (−0.47, −0.08)
	β12	0.25	0.29 ( 0.21, 0.38)	0.29 ( 0.20, 0.38)
Count	β20	0.50	0.39 ( 0.20, 0.58)	0.39 ( 0.20, 0.58)
	β21	−0.25	−0.11 (−0.27, 0.03)	−0.12 (−0.27, 0.03)
	β22	0.25	0.26 ( 0.21, 0.31)	0.26 ( 0.21, 0.30)
	r	1.25	1.32 ( 1.17, 1.54)	1.35 ( 1.19, 1.53)
Random Effects	Γ11 = Var(ϕ1i)	0.50	0.54 ( 0.33, 0.79)	0.52 ( 0.28, 0.76)
	Γ22 = Var(ϕ2i)	0.75	0.77 ( 0.64, 0.90)	0.76 ( 0.63, 0.89)
	Γ12 = Cov(ϕ1i, ϕ2i)	0.25	0.30 ( 0.18, 0.41)	0.31 ( 0.19, 0.42)

^†Posterior means and 95% credible intervals for proposed Bayesian ZINB model.

^‡MLEs and 95% confidence intervals obtained using SAS Proc NLMIXED.

3.3. Simulation 3: Spatiotemporal ZINB Model

For the final simulation, we generated data from a spatiotemporal intercept/slope model analogous to the one described in Section 2. To emulate the spatial layout of our application, we used the US Census county-level adjacency matrix for South Carolina, Georgia, and Alabama U.S. Census Bureau (2014). This matrix contains n = 272 counties and 1528 pairwise adjacencies. We simulated 50 observations per county over five years — the study time frame for our application — for a total of N = 50 × 272 × 5 = 68, 000 observations. We simulated the data from the following spatiotemporal ZINB model:

$$\begin{gathered} y_{ij}\sim (1-{\pi }_{ij})1_{({\mathrm{w}}_{ij}=0\wedge y_{ij}=0)}+{\pi }_{ij}\text{NB}({\mu }_{ij},r)1_{({\mathrm{w}}_{ij}=1)}, \\ \log \text{it}({\pi }_{ij})=\mathrm{logit}[\text{Pr}({\mathrm{w}}_{ij}=1\mid {\beta }_1,{\varphi }_{1i})] \\ ={\eta }_{1ij}={\beta }_{10}+{\beta }_{11}{t}_{ij}+{\varphi }_{1i1}+{\varphi }_{1i2}{t}_{ij}, \\ p(y_{ij}\mid r,{\beta }_2,{\varphi }_{2i},{\mathrm{w}}_{ij}=1)\stackrel{d}{=}\frac{\Gamma (y_{ij}+r)}{\Gamma (r)y_{ij}!}(1-{\psi }_{ij}{)}^r{\psi }_{ij}^{y_{ij}}, \\ {\psi }_{ij}=\frac{\text{exp}({\eta }_{2ij})}{1+\text{exp}({\eta }_{2ij})}, \\ {\eta }_{2ij}={\beta }_{20}+{\beta }_{21}{t}_{ij}+{\varphi }_{2i1}+{\varphi }_{2i2}{t}_{ij}, \\ {\varphi }_i\mid {\varphi }_{(-i)},\Gamma \sim {\mathrm{N}}_4\left(\frac{1}{m_i}\sum _{l\in {\partial }_i}{\varphi }_{il},\frac{1}{m_i}\Gamma \right) \end{gathered}$$ (30)

where t_ij ∈ {0, 1, 2, 3, 4} denotes study year, with 0 as baseline; ϕ_1i = (ϕ_1i1, ϕ_1i2)^T is a vector comprising the i-th random intercept (ϕ_1i1) and slope (ϕ_1i2) for the binary component; ϕ_2i = (ϕ_2i1, ϕ_2i2)^T is the corresponding vector of random effects for the count component; ϕ_i = (ϕ_1i1, ϕ_1i2, ϕ_2i1, ϕ_2i2)^T is modeled as multivariate ICAR distribution with conditional covariance Γ; and m_i denotes the number of counties adjacent to county i. The true parameter values are given in Table 3. These values resulted in a count distribution containing 70% zeros with a five number summary of (0, 0, 0, 1, 158). Figure S7 presents a full histogram of the counts. Unlike the models in simulations 1 and 2, the correlated spatial model (30) cannot be readily fit using existing frequentist or Bayesian software. In WinBUGS, for example, we immediately encountered unavoidable “trap” errors when fitting the model. This may be due to the fact that the ZINB model relies on the so-called “zeros trick” for implementation in WinBUGS, which may contribute to numerical instability. Thus, the proposed approach offers a convenient method for fitting complex ZINB models that cannot be easily accommodated by other means.

Table 3:

Parameter estimates and 95% credible intervals (CrIs) for the spatiotemporal ZINB model in simulation study 3.

Model Component	Parameter	Simulated Value	Posterior Mean (95% CrI)
Binary	β10	−0.25	−0.27 (−0.33, −0.19)
	β11	0.25	0.22 ( 0.19, 0.26)
Count	β20	0.50	0.49 ( 0.43, 0.54)
	β21	−0.25	−0.24 (−0.26, −0.22)
	r	1.00	1.03 ( 0.96, 1.09)
Random	Γ11 = Var(ϕ1i1)	0.50	0.61 ( 0.42, 0.84)
Effects	Γ12 = Cov(ϕ1i1, ϕ1i2)	0.10	0.03 (−0.05, 0.11)
	Γ13 = Cov(ϕ1i1, ϕ2i1)	0.10	0.09 (−0.02, 0.20)
	Γ14 = Cov(ϕ1i1, ϕ2i2)	−0.10	−0.07 (−0.13, −0.01)
	Γ22 = Var(ϕ1i2)	0.15	0.21 ( 0.14, 0.29)
	Γ23 = Cov(ϕ1i2, ϕ2i1)	0.10	0.12 ( 0.05, 0.20)
	Γ24 = Cov(ϕ1i2, ϕ2i2)	0.10	0.08 ( 0.04, 0.12)
	Γ33 = Var(ϕ2i1)	0.50	0.55 ( 0.42, 0.71)
	Γ34 = Cov(ϕ2i1, ϕ2i2)	0.10	0.06 ( 0.01, 0.11)
	Γ44 = Var(ϕ2i2)	0.15	0.17 ( 0.13, 0.22)

As before, we assumed independent N(0, 100) priors for the fixed effects and a Unif(0, 10) prior for r. Following equation (25), we partitioned the multivariate intrinsic CAR prior for ϕ_i into separate univariate priors. We completed the prior specification by assigning an inverse-Wishart(4, I₄) prior to Γ. Starting values for β₁, β₂ and r were identical to those in simulations 1 and 2. Initial values for the random effects were drawn from independent standard normal distributions, and Γ was initialized to I₄. To update r, we used a zero-truncated normal proposal with variance 0.0002, resulting in an acceptance rate of 43%. To improve efficiency of the algorithm, we used the R package spam (Furrer and Sain, 2010; Gerber and Furrer, 2015) to convert the CAR structure matrix Q in equation (24) to a sparse matrix object. This avoids computationally intensive matrix operations designed for dense matrices. We ran the sampler for 50,500 iterations with a burn-in of 500. Trace plots, Geweke diagnostics and Monte Carlo standard errors were indicative of convergence and showed reasonable mixing for a range of model parameters (Figure S8). For comparison, we re-ran the analysis for 2,500 iterations (Figure S9 and Table S2), as well as for 1500 iterations with a run time of 9 minutes. We obtained similar results for all scenarios.

Table 3 presents the posterior means and 95% credible intervals (CrIs) for the model parameters. Overall, the estimates were close to the true value with 95% intervals that overlapped the simulated value. Figure 1 presents maps of the true values and posterior mean predictions for ϕ_1i1 and ϕ_1i2 (i = 1, … , n), the random intercepts and slopes for the binary component of the spatiotemporal ZINB model. In each case, the spatial pattern for the estimated effects closely mirrored the true spatial distribution, suggesting the proposed model accurately recovered the underlying spatial pattern in the data. Figure 2 presents the corresponding maps for the count component. Again, the predicted spatial pattern is similar to the true pattern, but with increased smoothing. The additional smoothing is not surprising, as the count component conditions on the at-risk class, and therefore has fewer observations available for spatial prediction than the binomial component. As a result, it relies more heavily on the CAR smoothing prior for prediction.

Figure 1:

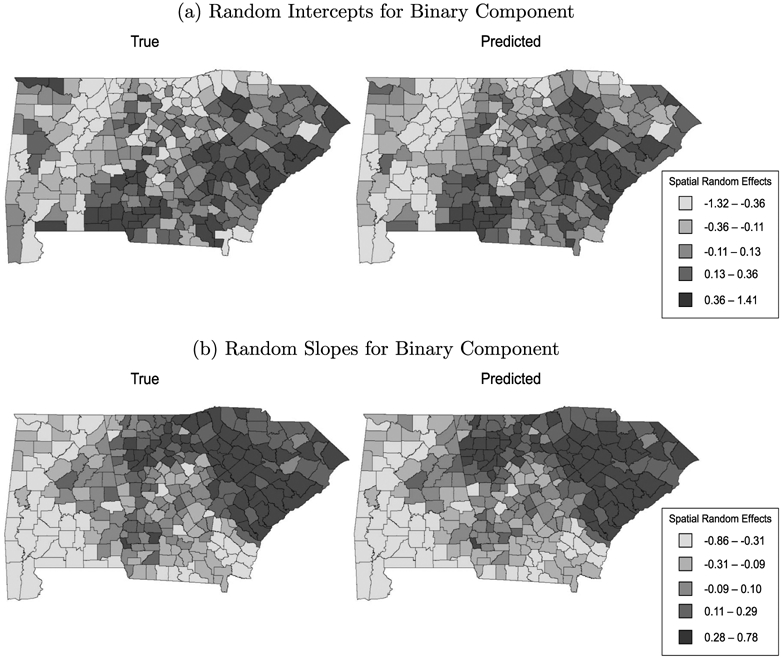
Simulated and predicted (a) random intercepts and (b) random slopes for the binary component of the ZINB model in simulation study 3. Top Left: Simulated random intercepts. Top Right: Predicted random intercepts. Bottom Left: Simulated random slopes. Bottom Right: Predicted random slopes.

Figure 2:

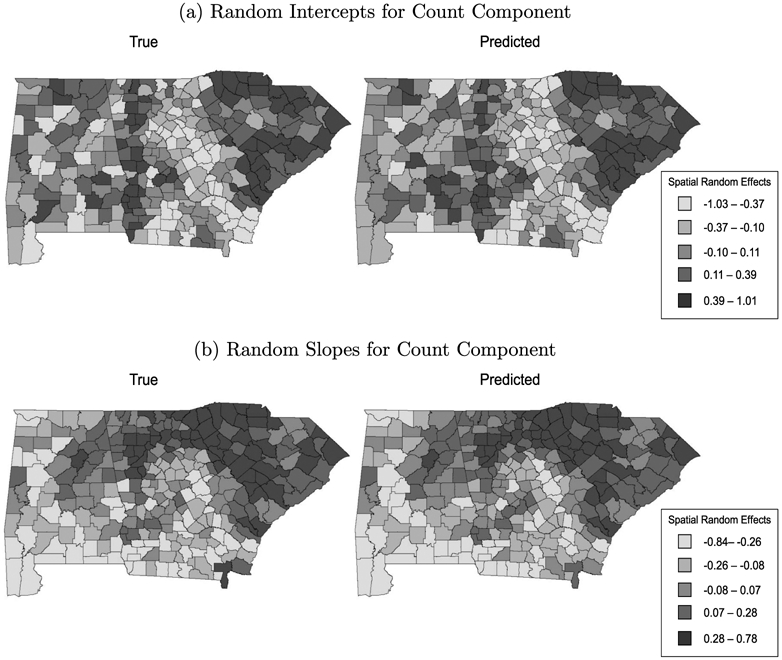
Simulated and predicted (a) random intercepts and (b) random slopes for the count component of the ZINB model in simulation study 3. Top Left: Simulated random intercepts. Top Right: Predicted random intercepts. Bottom Left: Simulated random slopes. Bottom Right: Predicted random slopes.

As a final comparison, we fitted two additional models. First, we fit a “partially correlated” model that assumed independence between the binary and count components — that is, we assumed Γ in equation (22) to be block diagonal with G₁₂ = G₂₁ = 0. For this model, we assigned independent inverse-Wishart(2, I₂) priors to G₁ and G₂. Second, we fit an uncorrelated model that assumed no correlation among any of the random effects — i.e., we assumed Γ to be strictly diagonal. Here we assigned independent inverse-Gamma(0.001,0.001) priors to the random effect variances. The WAIC values were 143, 456 for the fully correlated model, 143, 480 for the partially correlated model, and 143, 653 for the uncorrelated model, indicating superior predictive accuracy for the fully correlated model. Because WAIC relies on a conditionally independent partitioning of the data, which can be problematic for spatially correlated data (Gelman et al., 2014), we additionally compared models based the root mean square predictive errors (RMSPEs) for each random effect vector, ϕ₁₁, ϕ₁₂, ϕ₂₁, ϕ₂₂, using the expression

$${\text{RMSPE}}_{kk}=\sqrt{\frac{1}{n}\sum _{i=1}^n({\varphi }_{kik}-{\widehat{\varphi }}_{kik}{)}^2},k=1,2,$$ (31)

where ϕ_kik denotes the simulated value of random effect kk for subject i, and ${\widehat{\varphi }}_{kik}$ is the corresponding predicted value. Table S3 in the supplement presents the posterior mean RMSPEs for each random effect under the three models. In all cases, the fully correlated model produced the smallest RMSPEs, particularly in contrast to the uncorrelated model. In addition, the parameter estimates for the uncorrelated model showed extreme bias (Table S4). These results suggest that ignoring even modest association among the random effects can result in diminished predictive performance and imprecise estimates. These model comparison methods could also be used to test for other types of model misspecification, such as the choice of link function for the binary component. Taken together, the three simulations suggest that the proposed approach is comparable to maximum likelihood for relatively simple models, but can accommodate more complex scenarios where existing methods are impractical.

4. Analysis of Inpatient Admissions

We applied the spatiotemporal ZINB model to an analysis of inpatient hospital stays among 23, 533 diabetic veterans residing in Alabama, Georgia, and South Carolina from 2011 to 2015. We modeled the annual number of inpatient admissions using a model analogous to equation (30). Covariates included patient age (centered), sex, and race (non-Hispanic white vs other); Elixhauser score (Quan et al., 2005), a measure of comorbidity burden; and an indicator for service connected disability medical coverage, with 1 implying full medical coverage and 0 implying partial coverage. The sample comprised 68% zeros, an average of 1.24 admissions annually, and a five-number summary of (0, 0, 0, 1, 235). Figure S10 in Appendix D of the supplement provides a histogram of the counts, and Table S5 presents sample summary statistics. Prior distributions and MCMC specifications were identical to those for simulation 3. We ran the algorithm for a 50,000 iterations with a conservative burn-in of 25,000. We additionally thinned the chain by 25 to conserve disc space on the VA central server. Trace plots and Geweke statistics suggested MCMC convergence with adequate mixing (Figure S11). Generally speaking, shorter MCMC runs and burn-ins should be adequate for most applications. For example, a run of 5500 iterations with a burn-in of 500 yielded nearly identical results in the current case study (Figure S12 and Table S6). Table 4 presents the posterior means and 95% CrIs for the model parameters. The negative fixed effects estimates for year (β₁₁ and β₂₁) suggest that there was a general decline in admissions over time. This finding is consistent with recent VA efforts to reduce inpatient admissions through improved outpatient services (Kaboli et al., 2012). Additionally, patients with full disability coverage had fewer admissions. This finding supports recent studies showing that patients with full disability coverage are more likely to seek outpatient care because their copays are fully covered (Chuan-Fen et al., 2012). Not surprisingly, higher comorbidity scores were associated with increased admissions. The random effect covariances showed modest heterogeneity across counties in both components of the model.

Table 4:

Parameter estimates and 95% credible intervals (CrIs) for the spatiotemporal ZINB model in the VA inpatient study. NHW: Non-Hispanic white.

Model Component	Parameter	Variable	Posterior Mean (95% CrI)
Binary	β10	Intercept	0.11 (−0.10, 0.34)
	β11	Year	−0.07 (−0.09, −0.06)
	β12	Age	0.00 (−0.002, 0.002)
	β12	Male Gender	−0.02 (−0.12, 0.09)
	β12	NHW Race	0.03 (−0.01, 0.08)
	β12	Full Disability Coverage	−0.12 (−0.17, −0.07)
	β12	Elixhauser Score	0.43 ( 0.41, 0.45)
Count	β20	Intercept	0.86 ( 0.72, 1.00)
	β21	Year	−0.04 (−0.05, −0.03)
	β22	Age	0.003 ( 0.002, 0.005)
	β22	Male Gender	0.05 (−0.01, 0.12)
	β22	NHW Race	−0.04 (−0.07, −0.01)
	β22	Full Disability Coverage	−0.04 (−0.09, −0.01)
	β22	Elixhauser Score	0.16 ( 0.15, 0.17)
	r	Dispersion	0.77 ( 0.72, 0.83)
Random	Γ11	Var(ϕ1i1)	0.04 (0.03, 0.05)
Effects	Γ12	Cov(ϕ1i1, ϕ1i2)	0.01 (0.001, 0.01)
	Γ13	Cov(ϕ1i1, ϕ2i1)	0.01 (0.002, 0.02)
	Γ14	Cov(ϕ1i1, ϕ2i2)	0.01 (0.001, 0.01)
	Γ22	Var(ϕ1i2)	0.02 (0.01, 0.02)
	Γ23	Cov(ϕ1i2, ϕ2i1)	0.01 (0.001, 0.01)
	Γ24	Cov(ϕ1i2, ϕ2i2)	0.003 (0.001, 0.01)
	Γ33	Var(ϕ2i1)	0.06 (0.05, 0.09)
	Γ34	Cov(ε2i1, ϕ2i2)	0.01 (0.01, 0.02)
	Γ44	Var(ϕ2i2)	0.02 (0.01, 0.02)

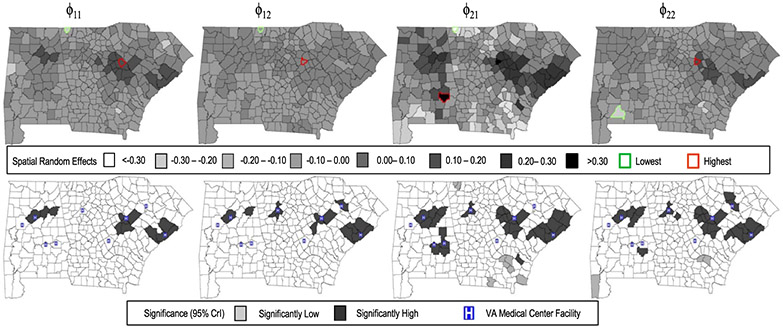
Figure 3 maps the spatial random effects for each component. The upper panels show the predicted random effect values, while the lower panels map the posterior significance, with the white shade representing non-significant effects (i.e., a 95% CrI overlapping zero), the dark shade corresponding to positive significance (95% CrI > 0), and light shade denoting counties with significantly negative effects (95% CrI < 0). VA medical centers are superimposed on the maps. The random intercept for the count component (upper panel, map 3) showed the greatest variability, confirming the result found in Table 4 for Γ₃₃. In general, the maps show a band of elevated spatial effects extending from southeast South Carolina through central Georgia and Alabama, with several hotspots of elevated random effects in urban areas such as Charleston and Columbia, SC; Augusta and Atlanta, GA; and Birmingham, AL. These areas are home to large VA facilities. Thus, after controlling for other factors, including comorbidity burden, patients residing near urban VA facilities tend to have more annual admissions compared to those in more rural areas. Recent studies have shown that urban medical facilities typically have larger bed capacities compared to rural facilities; as a result, increased admissions may be a byproduct of “discretionary” factors such as hospital capacity rather than clinical factors such as severity of illness (Fisher et al., 2000). Our findings appear to support this conclusion.

Figure 3:

County maps of predicted spatial random effects (top panel) and posterior significance (lower panel) for the VA inpatient study. From left to right, the maps correspond to the random intercepts and slopes for the binary component, and the random intercepts and slopes for the count component. For lower panel, dark gray denotes significantly high random effect, light gray denotes significantly low, and white denotes non-significant.

Table 5 presents the predicted marginal mean number of admissions, E(y_ij) = π_ijμ_ij, for patients residing in three hypothetical counties in years 2011 and 2015, along with accompanying multiplicative ratios. All three patients were from the reference covariate population. The first county corresponded to an “average” county in which spatial random effects were set to zero. The spatial random effects for the remaining two counties were one standard deviation above and one standard deviation below average, respectively. As Table 5 indicates, there was a decrease in expected counts for patients in the average and below-average counties. This is consistent with the negative fixed effect coefficients for year (β₁₁ and β₂₁) found in Table 4. In contrast, for the above-average county, there was an increase over time, reflecting the fact that the positive random slope standard deviations ($\sqrt{0.02}=0.14$) were larger than the negative fixed effect coefficients for year, resulting in a net increase over time. The multiplicative ratios comparing an average county to a below-average county were 1.42 (1.35, 1.46) in 2011 and 3.37 (3.05, 3.77) in 2015. Thus, in 2015, patients in the average county had 3.37 times more admissions on average than patients in the below-average county. The multiplicative ratios comparing above- and below-average counties were 1.98 (1.83, 2.18) in 2011 and an impressive 10.17 (8.35, 12.46) in 2015. These results suggest that while there is an overall decline in admissions over time for patients residing in average or below-average counties, there appears to be substantial spatial heterogeneity in the magnitude of the trend across counties.

Table 5:

Mean number of annual admissions per patient and corresponding multiplicative ratios for patients residing in 3 hypothetical counties. 95% credible intervals are given in parentheses. Estimates are for the reference covariate group. Random effects for the average county were set to 0. Random effects for the remaining counties were set to 1 standard deviation (SD) above and 1 SD below average.

	Year
Mean No. of Admissions	2011	2015
Average County	0.97 (0.85, 1.10)	0.71 (0.62, 0.81)
1 SD Above Average	1.36 (1.19, 1.54)	2.12 (1.82, 2.46)
1 SD Below Average	0.68 (0.59, 0.78)	0.21 (0.17, 0.25)
Multiplicative Ratios
Average vs. Below-Average	1.42 (1.35, 1.48)	3.37 (3.05, 3.77)
Above-Average vs. Average	1.40 (1.34, 1.46)	3.00 (2.74, 3.31)
Above-Average vs. Below-Average	1.98 (1.83, 2.18)	10.17 (8.35, 12.46)

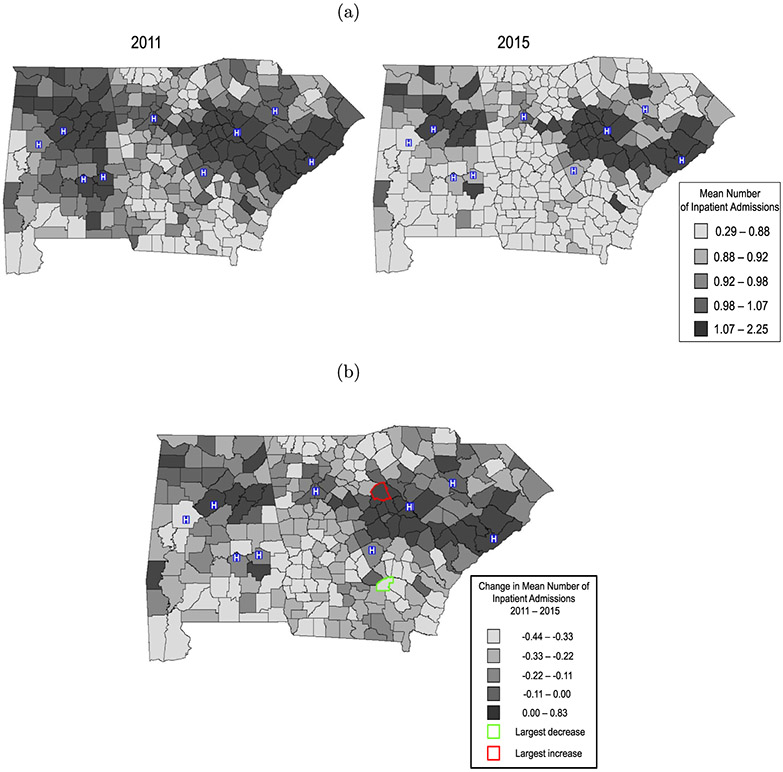
The space-time interaction is highlighted more prominently in Figures 4(a) and 4(b). Figure 4(a) presents the mean number of admissions per patient for each county in 2011 and 2015, while Figure 4(b) displays the net change over time in expected admissions per patient for each county. Estimates correspond to a patient in the reference covariate group. Approximately 12% of the counties had increasing trends over time. These counties were concentrated in urban areas such as Charleston, Augusta and Birmingham, which again are home to large VA medical centers. These counties could be targeted for policy initiatives, such as improved outpatient services, to reduce inpatient admissions. Such efforts also have important cost-saving implications: a recent VA report estimates the per-patient daily cost of inpatient care to be $3300 (Health Economic Resource Center, 2017). By pinpointing facilities associated with frequent inpatient admissions, the VA can help manage overhead costs while minimizing the burden imposed on both patients and hospital staff.

Figure 4:

Panel (a): Predicted per-patient admissions by county. Panel (b): Change in mean number of admissions per patient from 2011–2015. Both figures correspond to a patient in the reference covariate group. In Figure (b), the darkest shade shows counties with net increase in admissions. “H” denotes VA medical center.

5. Conclusion

We have proposed an efficient Bayesian approach to fitting ZINB models. The proposed data-augmented Gibbs sampler makes use of easily sampled Pólya-Gamma random variables; conditional on these latent variables, inference proceeds via straightforward Bayesian inference for linear models. As such, the model can be easily extended to more complex settings, including those involving multivariate, longitudinal and spatiotemporal data. Our simulations showed that the approach performs well across a range of scenarios, even in the case of few at-risk observations. For simpler models, the approach yields estimates similar to maximum likelihood, but can accommodate more complex data that are not amenable to current methods. In terms of computation time, our simulations suggest that the approach is comparable to existing software when such comparisons are available.

There are a number of potential areas for future work. Although the ZINB is among the most common choices for modeling zero-inflated data, it cannot accommodate underdispersion, which occurs when there are fewer counts than expected under a standard count model. Future work might consider alternative count distributions that permit underdispersion, such as the generalized Poisson (Consul, 1989), while preserving the convenient Gibbs updates presented here. The model could also be extended to accommodate high-dimensional geostatistical data through the use of reduced rank and predictive process models (Banerjee, 2017). Restricted spatial regression could further be used to address spatial confounding due to collinearity between spatial random effects and spatially varying, cluster-level covariates (Hodges and Reich, 2010). Other extensions include finite mixture ZINB models to study underlying subgroups in the population, and shrinkage priors for high-dimensional predictors. More generally, the proposed method should prove useful in settings where interest lies in modeling zero-inflated count data within a Bayesian inferential framework.