Abstract
The novel photosensitizer [Ru(S–Sbpy)(bpy)2]2+ harbors two distinct sets of excited states in the UV/Vis region of the absorption spectrum located on either bpy or S–Sbpy ligands. Here, we address the question of whether following excitation into these two types of states could lead to the formation of different long-lived excited states from where energy transfer to a reactive species could occur. Femtosecond transient absorption spectroscopy identifies the formation of the final state within 80 fs for both excitation wavelengths. The recorded spectra hint at very similar dynamics following excitation toward either the parent or sulfur-decorated bpy ligands, indicating ultrafast interconversion into a unique excited-state species regardless of the initial state. Non-adiabatic surface hopping dynamics simulations show that ultrafast spin–orbit-mediated mixing of the states within less than 50 fs strongly increases the localization of the excited electron at the S–Sbpy ligand. Extensive structural relaxation within this sulfurated ligand is possible, via S–S bond cleavage that results in triplet state energies that are lower than those in the analogue [Ru(bpy)3]2+. This structural relaxation upon localization of the charge on S–Sbpy is found to be the reason for the formation of a single long-lived species independent of the excitation wavelength.
Short abstract
We investigate selective excitation in two types of ligands present in [Ru(S−Sbpy)(bpy)2]2+. Femtosecond transient absorption spectroscopy identifies the formation of the same final state within 80 fs for both excitation wavelengths. Surface hopping simulations reveal ultrafast mixing of singlet and triplet states within less than 50 fs. Energy lowering due to S−S bond cleavage is identified as the driving factor for convergence to a single final state.
1. Introduction
Natural photocatalytic systems include a light-harvesting complex, where absorption occurs, covalently linked to a site of catalytic activity. Energy transfer from the absorptive to the reactive site is achieved via a multitude of proton-coupled electron transfers that form a complicated network of single- and multi-step subreactions themselves.1−4 The efficiency of these energy and electron transfers is increased in biological photosynthesis by a supramolecular arrangement, which connects the light-harvesting unit to the catalytic site via a cascade of electron transporters operating near the thermodynamical optimum.5,6 Selectivity in this directional transfer is of utmost importance as other pathways could lead to the formation of reactive oxygen species and other harmful products. One challenge in building artificial photocatalytic systems is to identify suitable photosensitizers that not only efficiently harness the photon energy but also transfer it conveniently to the actual catalytic entity or act themselves as catalysts.
A prototypical photosensitizer that has seen decades of experimental and theoretical investigations7−15 and advancements in the form of modifications is [Ru(bpy)3]2+ (bpy = 2,2′-bipyridine). The prominence of this and other ruthenium complexes featuring polypyridine ligands is credited to their visible-light absorption in the blue end, allowing for selective absorption via the complex in the presence of most organic compounds and solvents, as well as photostability and capability to be directly attached to an acceptor functionality. Recently, the bpy ligand itself has been found to exhibit both π-donating and π-accepting features in iron complexes.16 The low-energy photon absorption leads to excitation of a singlet state of metal-to-ligand charge-transfer (1MLCT) character, oxidizing the ruthenium center and reducing the ligands whereto the electrons are excited. From this initial 1MLCT excited state, ultrafast intersystem crossing into the triplet manifold is observed in less than 50 fs17−19 followed by a descent into the lowest 3MLCT state from which phosphorescence is observed or an electron could be transferred to another species. Population of the same 3MLCT state has been observed independent of the excitation wavelength resulting in a stable hot precursor for energy or electron transfer to other reagents.20 The phosphorescence decays in hundreds of nanoseconds,21 providing ample time for interaction with other species whereto the energy or electron is transferred.
Rooted in [Ru(bpy)3]2+, other ruthenium complexes capable of harboring multiple charges at once without loss of stability22−25 have been investigated. Recently, we synthesized and characterized [Ru(S–Sbpy)(bpy)2](PF6)2, a complex containing two bipyridine ligands and a modified bipyridine ligand decorated by a bridging disulfide moiety (S–Sbpy; Figure 1).21,26 Other ruthenium complexes with constrained bipyridyl-type ligands, viz., with 3,3′-methylene or -ethylene bridged bipyridine, have been investigated decades ago, but time-resolved studies of their ultrafast excited-state dynamics are lacking so far.27−30 In contrast to those previous systems with a peripheral aliphatic bridge, the present [Ru(S–Sbpy)(bpy)2]2+ has a disulfide linkage in the constrained bpy ligand, which represents a redox-active switch imparting distinct electronic structure modulations of the [Ru(bpy)3]2+-type complex. In-depth electrochemical studies showed that S–Sbpy can reversibly accommodate two electrons at moderate potentials (−1.1 V vs Fc+/0), making it appealing to mediate novel excited-state proton-coupled multielectron-transfer reactions.21 Furthermore, it was theoretically predicted21 that solvation in acetonitrile shifts the excited states located at the S–Sbpy ligand to lower energies that allows for selective charge transfer from the metal to either the bpy or S–Sbpy ligand. From these two different excitations to the bpy or S–Sbpy ligands, two different relaxation pathways are then conceivable, which might result in the formation of two triplet states from which energy or an electron could be transferred. The question arises whether a small change in excitation energy might be able to induce these different deactivation pathways creating different long-lived triplet states. In this paper, we address this question by investigating the early excited-state dynamics of [Ru(S–Sbpy)(bpy)2]2+ both experimentally and theoretically. Specifically, we are interested to see whether [Ru(S–Sbpy)(bpy)2]2+ shows the ability to form different final triplet excited states upon excitation to different excitation bands or whether despite the availability of two different ligands, only one triplet state is populated, and if so from where the energy would be subsequently transferred. To this aim, time-resolved transient absorption spectra at different wavelengths were collected and then interpreted with the help of non-adiabatic dynamics simulations.
Figure 1.
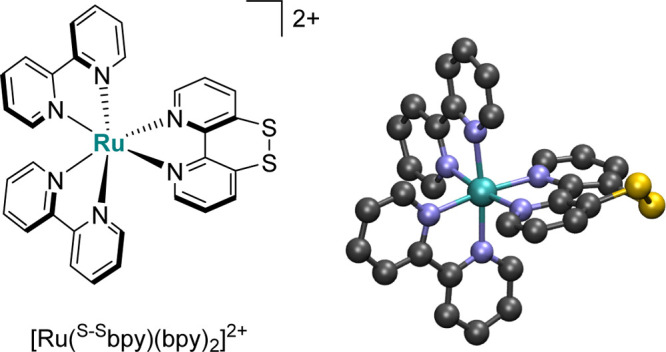
Schematic and three-dimensional representation of [Ru(S–Sbpy)(bpy)2]2+.
2. Methodology
2.1. Femtosecond Transient Absorption Spectroscopy
[Ru(S–Sbpy)(bpy)2](PF6)2 has been synthesized as described earlier.21 Femtosecond transient absorption spectroscopy was carried out on a setup similar to the one described in ref (31). The 35-fs laser output centered at 800 nm (Solstice Ace, Spectra physics) was split into two pulses. One pulse served as input for an optical parametric amplifier (TOPAS Prime+, Spectra Physics) and a subsequent frequency mixer (NirUVis, Spectra Physics), generating pump pulses at 430 and 520 nm. The other pulse (∼3 μJ) passed a translational stage (max 1.1 ns delay) and was focused into a 4 mm CaF2 crystal for white light continuum generation. The generated white light was further split into two pulses of equal energies. One of them was overlapped with the pump pulse and served as the probe beam, and the other pulse served as the reference beam. The sample was sealed in a quartz cuvette (2 mm in optical path length) equipped with a magnetic stirrer for refreshing the solution between laser shots. The plane of polarization of pump and probe pulses was set to 54.7° (magic angle). Energies of pump pulses were typically 0.5–1 μJ to avoid multiphoton excitation. Probe and reference spectra were measured using two spectrometers equipped with 256 element linear image sensors.
2.2. Non-adiabatic Excited-State Dynamics
The propagation of nuclei and electronic state populations has been performed in the framework of surface hopping31 using the SHARC method,32,33 which can include non-adiabatic and spin–orbit couplings (SOCs) on the same footing.34 Electronic properties for every time-step of a trajectory have been obtained from a parameterized linear vibronic coupling (LVC)35−37 model that included 21 singlet states and the lowest lying 20 triplet electronic states, calculated as described below. All simulations are based on a set of 10,000 initial conditions created from a ground-state Wigner sampling.38 Two sets of simulations have been done, exciting into the two parts of the low-energy absorption peak, featuring different charge-transfer character, assuming instantaneous δ-pulse excitation. One excitation window (EW) allows populating exclusively excited states falling inside the high-energy side (2.85–3.05 eV, EW-I) and another into the low-energy (2.4–2.6 eV, EW-II) side of the peak. The choice of the initially populated states and initial conditions inside each EW is based upon a stochastic selection process rooted in the relative oscillator strength within the corresponding EW. This process resulted in 5125 and 3838 excited initial conditions for EW-I and EW-II, respectively. All so-obtained initial conditions are propagated for 250 fs using nuclear time-steps of 0.5 fs in a fully diagonal basis for propagation.34 Propagation of the electronic wave function is interpolated using 0.002 fs time-steps. The overcoherence problem inherent to surface hopping trajectories is tackled by applying the energy-based decoherence correction by Granucci and Persico39 with the suggested value of 0.1 Eh for the C parameter. Nuclear velocities are rescaled after every hopping event to conserve the total energy of the ensemble by enforcing energy conservation inside each trajectory. All simulations have been conducted using the SHARC program suite.40 The obtained trajectories and the corresponding state populations are analyzed employing a spin-pure adiabatic set of states when the lowest triplet state populations are discussed, and a diabatic representation based on the reference states in the LVC model when the charge-transfer character of the wave function is presented. In both cases, a mixed quantum-classical transformation of the obtained populations has been conducted.41
2.3. Parameterized Potential Energy Surfaces
The excited-state dynamics of [Ru(S–Sbpy)(bpy)2]2+ has been simulated on parameterized potential energy surfaces (PESs) obtained from a LVC35−37 model up to the first order. The LVC model describes the PES along every vibrational normal mode in the proximity of a chosen reference point—which in this case is the optimized ground-state geometry—via the diabatic Hamiltonian V, written as
Here, 1 is the unit matrix, W is the matrix that contains all interstate (κ) and intrastate (λ) couplings, and V0 is the ground-state potential. It is obtained as
with ωi and Qi being the calculated frequency and mass-weighted normal mode coordinate of mode i, respectively. To obtain the κ and λ values, for every one of the 177 vibrational normal modes present in the complex, two molecular structures were generated. These structures correspond to the optimized structure ±0.05 times the corresponding normal mode in mass-weighted coordinates. On these structures, the κ values are obtained as numerical gradients, while the λ values are approximated via a change in the state-to-state overlap of wave functions. Overlaps have been truncated at 99.9% of the norm. SOCs between the singlet and triplet states have been approximated using the program PySOC,42 which is based on MolSOC.43 An estimation for the effective charge of ruthenium44 was added to the existing code to allow the evaluation of the SOC elements. The SOC elements between triplet states have been disregarded as the triplet–triplet interactions are governed by the respective non-adiabatic coupling elements with only small contributions from the respective triplet–triplet SOCs. Both, SOCs and transition dipole moments, are taken from the optimized geometry and no linear scaling parameters have been determined for these properties.
2.4. Quantum Chemical Calculations
The electronic excited states of the absorption spectrum and the parametrization of the LVC model of [Ru(S–Sbpy)(bpy)2]2+ have been calculated employing time-dependent density functional theory (TD-DFT)45,46 employing the B3LYP47,48 functional with the D3 dispersion correction.49 The LANL2DZ50 basis set was used at the ruthenium center, while the 6-311G(d)51 basis set was employed for all other atoms (B3LYP/6-311G(d)-LANL2DZ). The geometries were optimized at the same level of theory (see Section S1 of the Supporting Information). The inclusion of relativistic effects in all the calculations is taken into account via Douglas–Kroll–Hess integrals.52 Solvation of the complex in acetonitrile was mimicked by the integral equation formalism polarized continuum model53 using the default set of parameters for this solvent in Gaussian09.54 This level of theory is the same as that employed previously,21 which was able to successfully reproduce the experimental electronic absorption spectrum of the complex. The latter is theoretically simulated using ab initio calculations of 21 singlet excited states on a set of 200 geometries obtained from a zero-point energy Wigner sampling.38,55 Every excited state is convoluted with a Gaussian function with a full width at half maximum (FWHM) of 0.1 eV to move from discrete absorption toward a continuous one. For the parametrization of the LVC template, 21 singlet and 20 triplet states have been calculated using the same computational setup.
The wave functions of the resulting 4200 electronic states are characterized in terms of charge-transfer numbers56 using the TheoDORE57 program package. For this purpose, [Ru(S–Sbpy)(bpy)2]2+ is fragmented into the central ruthenium atom (M), two bipyridine ligands (L), and the bipyridine ligand that is functionalized by a S–S bridge (S). Depending on where the electron is excited from (hole) and to (electron), the following classification scheme for every excited state can be devised: If both the hole and the electron are located at Ru, a metal-centered state (MC) is obtained. A charge-transfer (CT) state is characterized by a difference in the hole and electron fragments. In this work, the hole fragment is noted in front of the electron fragment; hence, an excitation of a metal-based electron to the sulfur-substituted ligand is called an MSCT state. In this framework, a set of 10 different labels is available to investigate the excited-state dynamics: MC, SC, LC, MSCT, MLCT, SMCT, LMCT, SLCT, LSCT, and LLCT. Contributions toward and from the two bpy ligands are added up for simplicity, see Section S2 for more details.
3. EXPERIMENTAL RESULTS
Pump–probe UV–vis absorption spectroscopy was carried out to investigate the excited-state dynamics of [Ru(S–Sbpy)(bpy)2](PF6)2. Figure 2 shows the transient difference spectra measured in acetonitrile solution. Different pump wavelengths of 430 and 520 nm were used to preferentially excite the complex either to the parent bpy ligands’ charge-transfer states (MLCT states) or to the metal-to-ligand charge-transfer states that are predominantly associated with the sulfur-decorated S–Sbpy ligand (MSCT states), respectively. The spectra show ground-state bleaches between 400 and 550 nm superimposed by excited-state absorption resulting in a positive peak at 370 nm and a plateau at >570 nm. The excited-state absorption around 370 nm is assigned to spin-allowed π–π* transitions in the transient bpy radical anion. The ground-state bleach in the lower energy region can be assigned to the vanishing 1MLCT transition in the excited state of the complex.20 All the transients in Figure 2 show striking similarities to those measured recently with ns time resolution and which were unequivocally assigned to the triplet excited state of [Ru(S–Sbpy)(bpy)2]2+ with a lifetime of 109 ns.21 It is therefore not possible to experimentally differentiate the excited-state absorptions associated with the parent bpy and the sulfurated S–Sbpy ligand. Furthermore, no dependence on the pump wavelength is observed within the pump–probe delay range (0.05–100 ps) of these measurements.
Figure 2.
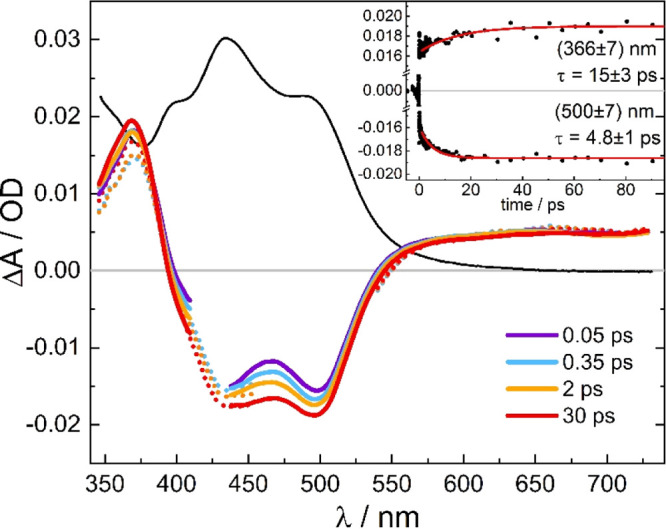
Pump pulse-induced difference spectra of [Ru(S–Sbpy)(bpy)2](PF6)2 (1.2 × 10–4 M in acetonitrile) at pump–probe delays, as indicated (solid colored lines: λpump = 430 nm, dotted lines: λpump = 520 nm, black line: scaled linear absorption spectrum). The insert shows time traces at (366 ± 7) and (500 ± 7) nm with exponential fits giving time constants of (15 ± 3) and (4.8 ± 1) ps, respectively.
Within the time resolution of our experiment, the data do not show any evidence of a precursor state, which means that the triplet state is formed in <80 fs. Afterwards, the spectra exhibit slight amplitude changes on a tens of picosecond timescale, as illustrated in the inset of Figure 2. At the peak of the π–π* transitions of the transient bpy radical anion band (370 nm), there is a minor increase in absorption, whereas in the bleach region (400–500 nm), a drop is observed. After that, no further spectral changes appear up to 1 ns, indicating the formation of a long-lived excited state. The minor amplitude modulations seen in Figure 2 have further been analyzed by estimating the spectral evolution of the triplet state (AT(t)) from the sum of the transient spectra (ΔA(t)) and the linear absorption spectrum (AGS), AT(t) = ΔA(t) + a·AGS. The scaling factor a was chosen such that the drop in absorption seen in the transients at 500–550 nm arising from the ground state bleach just disappeared. The resultant spectra shown in Figure 3 are initially broadened with enhanced absorption at the red wing and less absorption in the center of the π–π* band, which subsequently contract to the relaxed spectrum of the triplet state. This behavior along with the observed relaxation time of about 10 ps is a clear indication of a vibrationally hot electronic state. From the pump photon energy (430 nm) and the onset of phosphorescence spectrum (650 nm),21 an excess vibrational energy of 7900 cm–1 in the triplet state directly after excitation and intersystem crossing is estimated giving rise to hot bands and subsequent vibrational cooling. Similar behavior was observed for related complexes such as [Os(bpy)3]2+58 and [Ru(bpy)3]2+.59
Figure 3.
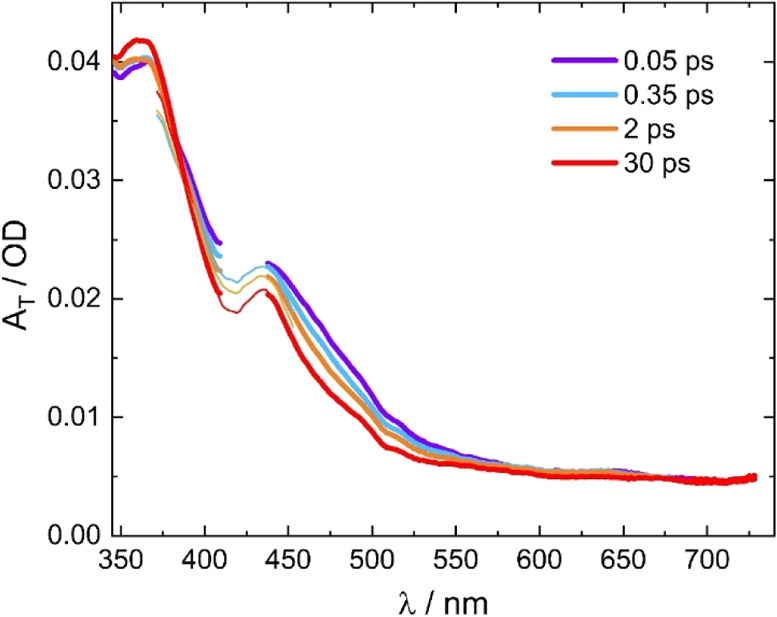
Time-dependent spectra of the triplet state of [Ru(S–Sbpy)(bpy)2](PF6)2 derived from the transients of Figure 2 by adding the scaled ground-state absorption spectrum (thick lines: λpump = 430 nm, thin lines: λpump = 520 nm).
Since the relaxation processes leading toward the long-lived triplet state are obviously very fast and no experimental evidence of a precursor state or different deactivation pathways could be obtained via pump–probe spectroscopy with the present setup, we turned to computations to shed light on the excited-state dynamics of the complex.
4. Computational Results
4.1. Absorption Spectrum and Model Potentials
The TD-DFT calculated electronic absorption spectrum of [Ru(S–Sbpy)(bpy)2]2+ in acetonitrile, decomposed in terms of different types of excitations, is shown in Figure 4a.
Figure 4.
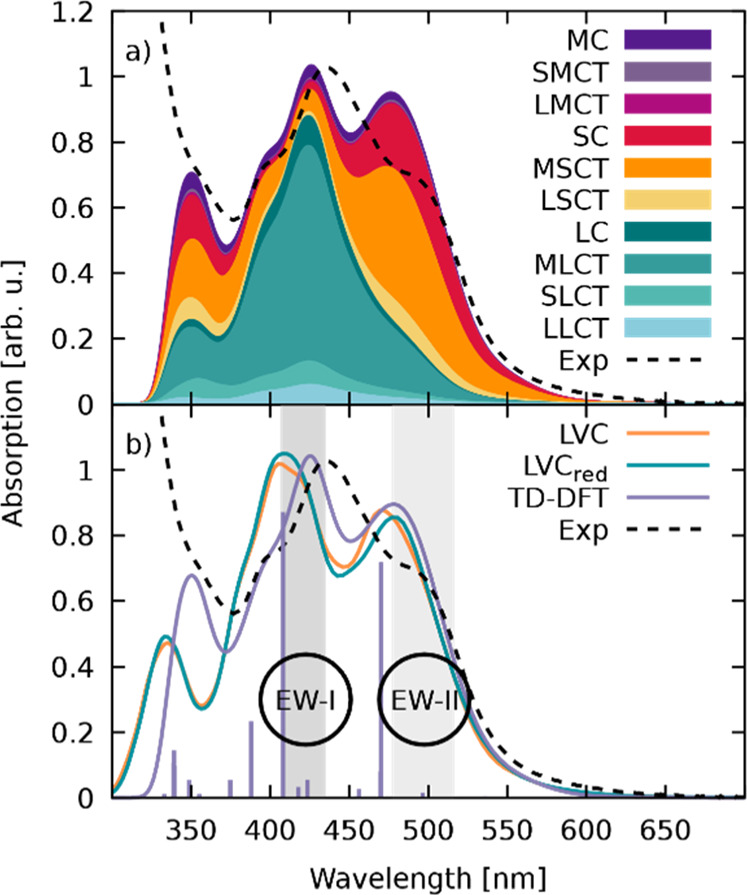
(a) Experimental21 (dashed, black) and TD-DFT calculated (solid, black) absorption spectra of [Ru(S–Sbpy)(bpy)2]2+ in acetonitrile decomposed into different types of excitations. The scheme for labeling the types of excitation denotes the ruthenium atom as M, the S–Sbpy ligand as S, and each bpy ligand as L. From this, excitations within each fragment are written as MC, SC, and LC, while the electron transfer between fragments is denoted XYCT, where X represents the fragment from which the electron is excited and Y the fragment to which it is excited. (b) Absorption spectra calculated with the full-parametrized LVC template (LVC), the reduced LVC template (LVCred), the ab initio TD-DFT absorption spectrum (TD-DFT), and the experimental one (exp). The electronically excited states at the optimized equilibrium geometry are indicated by bars at the corresponding energy with the relative height given by a normalized oscillator strength. EWs I and II used in the dynamics simulations are highlighted in gray.
Two distinct features of the CT character-dominated spectrum can be observed: (i) predominant excitations to the sulfur-decorated S–Sbpy ligand (MSCT states) at lower energies around 500 nm and (ii) excitations to the parent bpy ligands (MLCT states) dominating at high energies around 420 nm with almost no (<10%) contribution of CT toward the S–Sbpy ligand.21 As shown in Figure 4b, the bright states obtained from the optimized geometry (lavender sticks) are found at higher energies than the respective experimental absorption maxima. This indicates vibronic intensity borrowing when moving away from the optimized structure, resulting in a transfer of oscillator strength toward lower lying electronic states in the ensemble of structures.
The dynamics ensuing after excitation toward the bpy and S–Sbpy ligands is calculated using an LVC template, which approximates the real PES. In order to estimate the quality of the employed LVC Hamiltonian, we rely on two verifications. The first involves using the TD-DFT absorption spectrum (Figure 4a) as a quality check. Figure 4b shows (orange line) an absorption spectrum calculated with the LVC template from a set of 1000 geometries. The LVC spectrum shows a slightly blue-shifted onset of the first absorption band and a small shift of 0.12 eV for the main absorption peak around 420 nm, as compared with the TD-DFT one. However, the agreement of the two spectra can be considered very satisfactory considering the crude approximations present in the LVC model. The small deviations are due to the fact that the transition dipole moments in the LVC model are taken from the optimized geometry alone. Therefore, changes in the transition dipole moment only occur via mixing of the excited states with no explicit geometry dependence of these properties when using the LVC template. This results in absorption peaks centered on the absorption energy of the corresponding states.
The second validation of the LVC template refers to its ability to describe the subsequent excited-state dynamics adequately, for example, by testing how well the LVC model potential is able to locate a point likely to be encountered within the dynamics, for instance, the T1 minimum structure. The optimized T1 geometry at the B3LYP/6-311G(d)-LANL2DZ level of theory is very similar to the S0 geometry, except for the drastically elongated S–S bond in the T1 structure (2.57 Å, an increase of 0.46 Å). When performing a T1 optimization using the LVC template, an S–S bond of only 2.43 Å is observed. This is little surprising as a harmonic model is expected to be capable of describing adequately the region close to the reference point but deteriorates at larger distances. With the reference being the S0 geometry, leaving the Frank–Condon (FC) region and simulating the S–S bond elongation to this extent goes beyond the capabilities of this LVC setup. Besides the S–S bond being too short, the LVC optimization of the T1 minimum leads to non-planar bpy ligands with the two pyridine rings twisted against each other, in disagreement with the TD-DFT results where the two bpy ligands are found to be planar to support extended π-conjugation. This indicates that some artificial energy lowering occurs in the LVC optimization due to coupling of a low-frequency bpy-twisting mode with a large λ value. This is reflected in a very low energy of the LVC T1 (0.87 eV) when compared to the ab initio T1 (1.41 eV) with respect to the ground-state energy at the S0 optimized geometry.
The disagreement between the LVC-optimized T1 minimum energy structure and the B3LYP/6-311G(d)-LANL2DZ-optimized structure is due to the inability of the LVC model to correctly describe large-scale displacements in the molecule. This stems from the harmonic approximation used for calculating the basic shape of the PES of the molecule and the inclusion of only linear coupling terms in the definition of the Hamiltonian. Hence, this model is not suited to describe anharmonic motion such as rotation and can lead to computational artifacts if strong movement along such specific normal mode occurs. In order to identify problematic normal modes, 60 different T1 optimizations have been conducted where 60 different numbers of normal modes have been removed from the template file. The reduction is done by removing all κ and λ values related to the lowest x vibrational normal modes, with x ranging from 0 to 59. The so-obtained T1 geometries have been then analyzed with regard to the S–S bond length, the adiabatic energy gap, and the root-mean-square deviation (RMSD) of the full structure as compared to those of the ab initio one. Figure 5 (see also Figure S2) collects values from which multiple trends are apparent: (i) The more the low-frequency modes are neglected, the smaller the obtained S–S bond length is, converging almost to the initial ground state S–S bond length of 2.11 Å as more and more modes that involve the sulfur atoms are removed. Unfortunately, none of the optimized T1 geometries shows an S–S bond length longer than 2.43 Å, pointing to a general shortcoming of the LVC model to describe large amplitude motion. (ii) The adiabatic S0–T1 energy gap displays the opposite trend: the energy difference increases with decreasing number of considered modes. It starts out at 0.87 eV and increases up to 1.93 eV upon removal of 60 normal modes, showing its strong sensitivity. Finally, (iii) the RMSD value decreases rapidly and is almost converged at 0.09 Å after omitting the lowest 16 vibrational modes.
Figure 5.
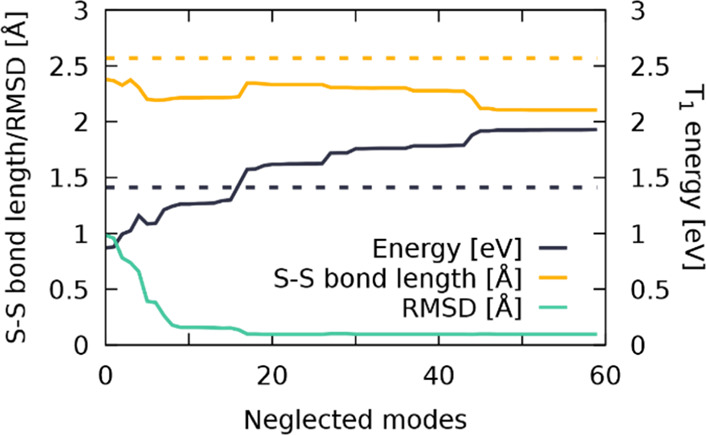
S–S bond length (Å, yellow), T1 energy (eV, dark blue), and the RMSD (Å, teal) of the LVC-optimized T1 geometry as a function of the number of neglected normal modes. Values for the full-dimensional geometry optimization at the B3LYP/6-311G(d)-LANL2DZ level of theory are shown in dashed lines.
The previous results evidence that including all the normal modes into the LVC template will yield unreasonable results once the dynamics simulation approaches structures close to the T1 minimum energy structure, as both the RMSD values and T1 energy of the ab initio optimization are not reproducible with the LVC model. As a remedy, specific normal modes that were found to have the largest impact on the observed deviations from the desired properties have been removed from the simulations. Accordingly, a “reduced-LVC” model was created, where 16 vibrational modes (v1–v10, v16, v17, v20, v23, v26, and v28, see Table S1) from a total of 177 have been removed. The absorption spectrum calculated with this reduced LVC model is shown for comparison in Figure 4b (green line). As it can be seen, the impact of these 16 normal modes in the absorption spectrum is negligible, so this reduced template is now used to simulate the excited-state dynamics of [Ru(S–Sbpy)(bpy)2]2+ in acetonitrile.
Initial excited-state simulations revealed that including the diabatic T17 state forms a low-lying triplet minimum, which is not reproducible with TD-DFT. Given the unphysical presence of this state and its ability to warp the excited-state dynamics, we excluded this state from the diabatic LVC Hamiltonian, resulting in a final template with 161 modes, 21 singlet and 19 triplet states; this is denoted LVCred. The influence of the T17 state is thoroughly discussed in Section S3.2 of the Supporting Information.
4.2. Non-adiabatic Dynamics
Two separate sets of excited-state dynamics simulations have been carried out to initially excite into the MLCT- or MSCT-dominated regions of the low-energy absorption band, recall Figure 4b. First, the results for excitation into the MLCT region of the EW-I band (2.85–3.05 eV) will be discussed. After excitation into low-energy singlet states (S4–S11 are initially populated), ultrafast intersystem crossing to the triplet manifold is observed. Figure 6a shows the time evolution over 250 fs of all the singlet and triplet states grouped together for simplicity. To fit the retained populations, a kinetic model was employed that features a fast and a slow reacting singlet component, termed hot and cold singlets for the remainder, and the manifold of all triplet states combined. Population can be transferred between the two singlet components via kIC, and ISC can occur from both of these. This results in two different ISC crossing rates to the triplet manifold, kISC,fast and kISC,slow, one from the hot- and one from the cold-singlet component. Using this model, a perfect fit of the observed populations was possible, resulting in a kISC,fast of 46 fs, indicating an initial ultrafast transfer via spin mixing, followed by a transfer with a time constant, kISC,slow, of 337 fs. Transfer from the hot-singlet component to the cold one occurred with kIC = 72 fs. This fast transfer via kISC,fast toward the triplet states is not surprising as the initially excited states are embedded in a multitude of energetically close triplet states with strong SOCs, as seen in other Ru complexes.19 The transfer to the triplet states is present from the very first time step, indicating that this is an electronically driven ISC process, which does not depend strongly on structural changes, similar to recent observations in a ReI metal complex.60 In this ReI complex, this electronic, ultrafast ISC is related to the excitation, in that case, simulated with a δ-pulse that excites pure singlet states, from which the system undergoes almost instantaneous spin-mixing due to substantial SOC. Such electronic spin-mixing can be verified by carrying out a separate simulation that employs the same set of initial conditions but with frozen nuclear coordinates where all momenta in all time steps are set to zero. In doing so, any structural relaxation beyond the original zero-point energy sampling of the wavepacket is omitted, allowing the separation of ISC induced by nuclear motion from the electronic coupling of states in the initial distribution of geometries. The resulting plot of the diabatic populations of this frozen dynamics for [Ru(S–Sbpy)(bpy)2]2+ in acetonitrile is shown in Figure 6b. Employing an identical fitting scheme, kISC,fast amounts to 49 fs, while the slow component kISC,slow is now at −3189 fs. Hence, preventing the nuclei to move results in an almost identical fast ISC component (46 vs 49 fs) but completely stops any delayed ISC. The fast ISC component is therefore attributed to electronic spin-mixing, while the slow ISC is clearly driven by nuclear relaxation, as in the ReI complex.60
Figure 6.
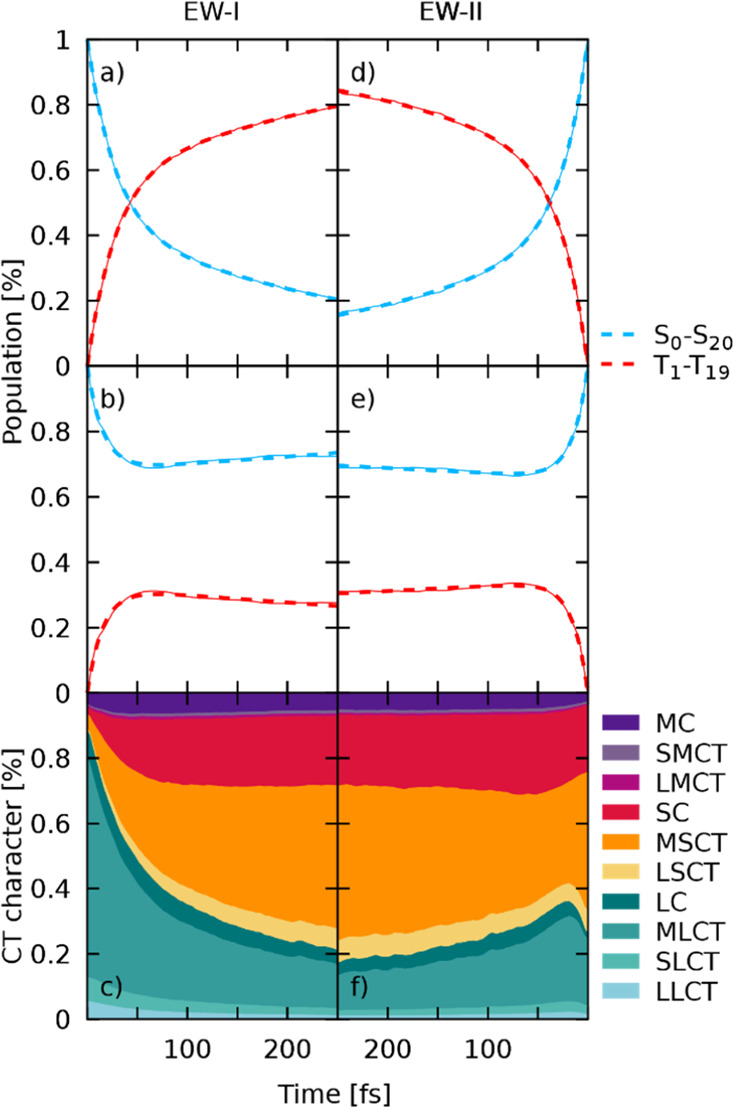
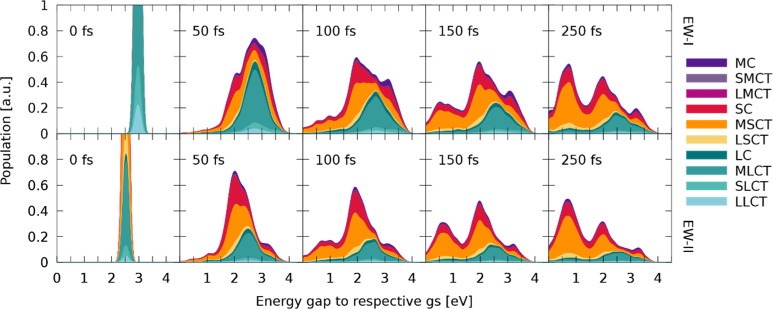
Excited-state dynamics simulations of [Ru(S–Sbpy)(bpy)2]2+ for both EWs. Note the inverted time axis for the right-hand side plots. Results for simulations starting in EW-I and EW-II are shown on the left- and right-hand side, respectively. (a,d) Sum of singlet and triplet populations for excitation in EW-I and EW-II, respectively. Thin lines represent the sum of all trajectories and thick dashed lines represent fits of populations. (b,e) Sum of singlet and triplet populations for frozen nuclear dynamics after excitation in EW-I and EW-II, respectively. (c,f) Evolution of charge-transfer character along the simulations for the non-frozen dynamics shown in (a,d), respectively.
Following the initial crossing into the triplet manifold, a rapid cascading down the ladder of states occurs. At the end of the simulation, 47% of the population ends up in the lowest triplet state. From there, the population could either decay to the initial ground state via emission of a photon or via a conical intersection with the ground state PES. The process of phosphorescence is not modeled in the present dynamics, which is not supposed to have any influence on the current simulations, considering the simulated time scale of only 250 fs, while luminescence was experimentally observed with a lifetime of 109 ns. On the basis of this longevity, an accessible crossing to the singlet ground state is unlikely.
The investigation of the nature of the wave function throughout the dynamics is straightforward as the LVC template is diabatic by construction. Therefore, the wave function at each point of dynamics is already expressed in terms of states at the optimized geometry. With this information, the wave function of the ensemble of all trajectories can be understood in terms of CT characters and is plotted in Figure 6c. Initially, the character of the complete wave function represents the partitioning of oscillator strengths in the initial EW-I (see Figure 4) and is predominantly of MLCT character with very small contributions of excited states located at the central metal atom or the S–Sbpy ligand. This prevalence of MLCT changes almost instantaneously with the onset of dynamics, where transfer toward excited states where the electron is located at the S–Sbpy ligand increases. The time scale of the observed decay in bpy-directed excitations (MLCT, SLCT, and LLCT) coincides with the ISC crossing rate, indicating that spin-mixing with triplet states of strong SC and MSCT character is responsible for the speed of this transfer. During the total 250 fs, a continuous increase in MSCT character is observed. The final composition of the wave function amounts to about 44% MSCT, 21% SC, 13% MLCT, and 6% MC. The T1 state is populated with 47% of the total population at the end of the simulation. It has to be noted that a small number of trajectories (∼1%) were found in the lowest state. Since the coupling between S0 and all other singlet states is zero per construction and only SOCs are included that couple to this lowest state, these transitions to S0 will be considered erroneous.
The results obtained upon excitation to the low-energy band of the absorption spectrum (EW-II) are presented in Figure 6d–f. In this energy range, the lowest seven excited-singlet states are initially populated. From them, ultrafast decay from the hot singlet population is observed with fitted time constants of kISC,fast = 43 fs and kIC = 74 fs, almost identical to the ones obtained for EW-I. Larger differences in time constants are found for kISC,slow, which amount to 256 fs for the low-energy excitation. The similarity in the crossing rates for the fast part highlights the fact that this initial ISC is driven by state-mixing alone without any need for approaching crossing points between the singlet and triplet energy surfaces. It is therefore independent of the excitation wavelength as even at this lower energy range, an abundance of triplet states is close to the initially excited singlet states. For simulations in EW-II, a high accumulation of population is found in the adiabatic T1 (57%) state at the end of the dynamics. The analysis of CT character of the wave function reveals that most of the initial population starts in MSCT (41%) or SC (19%) states. However, after few fs, there is transfer from MSCT to MLCT and LC states, followed by a decrease in MLCT and an increase in SC states. After 100 fs, only the MSCT character increases at the expense of states located at the bare bpy ligands. Thus, almost identical ending points in the CT picture are reached after 250 fs for simulations in EW-I and EW-II, and it can be concluded that dynamics starting from both EWs converge toward identical final states. To verify whether this could be a mere coincidence, the energy with respect to the lowest state of every trajectory is plotted with its current CT character for both EWs against time. The few snapshots shown at selected times in Figure 7 illustrate that the nuclear wavepackets disperse soon and strive toward lower potential energy gaps while descending the ladder of states, which is expected. Two facts can be deduced from the presented figure. First, it is evident that a lower potential energy gap is directly connected to an increase in MSCT and SC character. This emphasizes the importance of the S–Sbpy ligand, which accommodates these low-lying states, and therefore, favors this fast decrease in potential energy by S–S bond elongation. Second, both the dynamics starting in EW I and II show almost identical final distributions both in energy and the corresponding CT character. Despite the initial localization of the excited electron on a specific fragment, the excitation evolves toward the S–Sbpy ligand in the dynamics due to the corresponding lowering of energy, which seems to dominate all other deactivation pathways restricted to the pure bpy ligands. Therefore, it can be concluded that the same deactivation pathways are triggered for both excitation wavelengths.
Figure 7.
Evolution of the excited-state wavepacket for different time-steps throughout the dynamics starting from EWs I (top) and II (bottom). Each panel contains information about the active state at the given time-step for each trajectory to provide an overview of the distribution of energy gaps for each time frame. The CT character of every trajectory is plotted against the energy gap to the S0 state at the corresponding geometry. For this, the character of the diabatic quantum population of a trajectory is transformed into the corresponding CT characters and then depicted at the energy gap of the currently active state to the S0 energy of this trajectory at this state. All these values are then convoluted to yield the shown wavepackets.
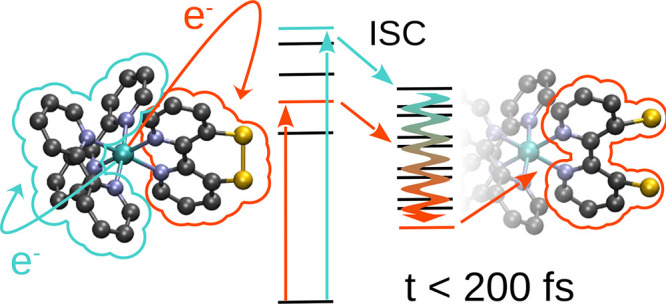
The importance of states located at the S–Sbpy ligand for the excited-state dynamics has surfaced at multiple parts throughout this discussion. In an attempt to further investigate the influence of the sulfur bond on the excited-state dynamics, a geometric analysis of all trajectories has been conducted. For this, pairs of S–S bond lengths and energy gaps of the currently active state to the lowest singlet state have been collected along each trajectory across both ensembles of EWs. These time-resolved data points have been convoluted both in space and energy by Gaussian functions to give Figure 8, employing FWHM values of 0.025 Å and 0.1 eV, respectively. An animated collection across the complete dynamics can be found in the Supporting Information. Figure 8 shows the distribution of energies and bond lengths at the initial state of simulations. Both EWs are clearly visible, and the S–S bond lengths correspond to the Wigner-sampled S–S bond lengths of the ground-state geometry. From this initially small distribution in both energy and space, broadening in populated energy gaps and bond lengths is observed in the first steps of dynamics. Already after 50 fs, a slight elongation of the S–S bond is evident for the trajectories that underwent energy gap lowering and are now found in the region of energy gaps between 1.5 and 2.5 eV. The corresponding plot of the character of the wave function indicates that population of this low energy gap region between 1.5 and 2.5 eV is predominantly linked to SC and MSCT states, which facilitate S–S bond elongation. At 100 fs, this minimum is even more pronounced, with most of the wavepacket being located in this region of bond lengths and energies. This energy lowering is directly correlated to destabilization of the singlet ground state that lowers the energy gap, while the active state is stabilized or hopping to lower states takes place. When going beyond 100 fs, quantitative population of T1 accompanied by further sulfur bond elongation is observed, as more and more trajectories populate the energy region between 0.2 and 1 eV. In this region, the wave function comprised almost exclusively of states that locate the excited electron on the sulfur-decorated bpy ligand. At the final time-step of the simulation, most of the trajectories are found in this T1 minimum from where the population depletes via radiative emission, as has been shown in the experiment.21 Plotting the energy gaps with respect to the S–S bond length shows that three hot spots are populated throughout the dynamics. First, there is a high energy population at moderate S–S bond lengths indicating trajectories in higher lying states where the sulfur bond is of no consequence. The electronic character at these states is a mixture of all considered types of excitations and features the highest amount of MC character. From these high-lying states, stabilization can occur either via occupation of predominantly MLCT or MSCT states centered around energy gaps of 2.5 and 2.0 eV, respectively. It can be seen that population of the MSCT states is associated with a slightly increased bond length. Trajectories can be trapped for a short amount of time in these two quasi-minima before ending up in a state that further promotes elongation of the S–S bond upon which energy gaps are decreased and the T1 minimum is reached. We note that in the first 150 fs of the dynamics, coherent motion of the S–S bond length is observable due to the initial population of non-equilibrium states that all seem to favor bond elongation compared to the ground-state bond length61 (Figure S4). The presence of S–Sbpy modification results in the stabilization of charge on the corresponding ligand due to a dynamical energy-lowering of the associated states as the S–S bond is lengthened. This additional dynamical stabilization of the excited electron is not observed in some modifications to the [Ru(bpy)3]2+ complex where selective metal-to-modified ligand excitation is possible.62,63 Similarly to the S–Sbpy ligand, selective excitation is possible here due to lowering of the absorption energy of bright states that are characterized by charge transfer to the modified ligand. The additional dynamical stabilization within the S–Sbpy ligand is assumed to decrease the reversibility of the localization process on this ligand, resulting in a stronger trapping of the electron on the S–Sbpy ligand in comparison to more rigid modifications of the bpy ligand. The availability for both further relaxing and rather rigid ligands that can be selectively excited enables the synthesis of tailored complexes and opens up the avenue to a set of interesting questions regarding competitive pathways if both types of ligands are present.
Figure 8.
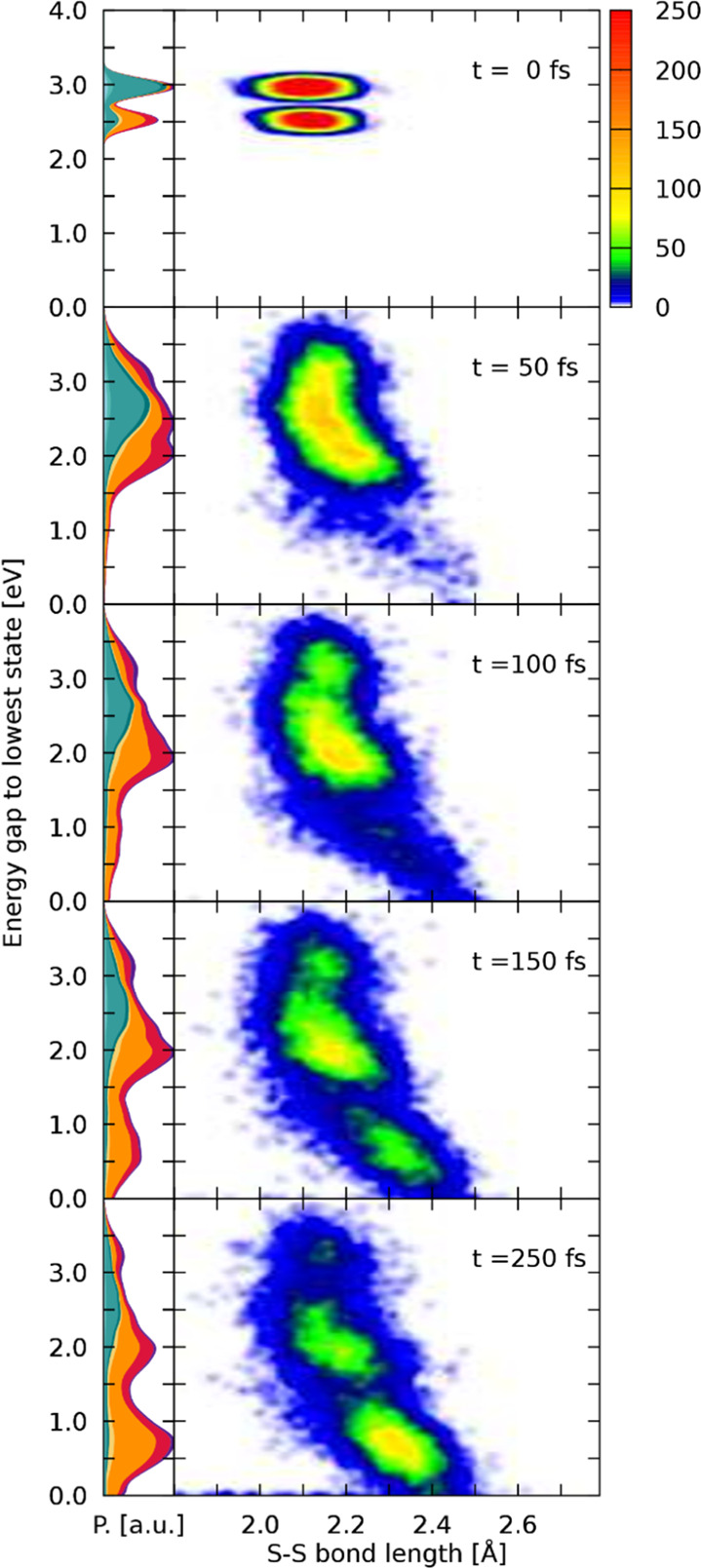
Left-hand side panels show the distribution of the wave function character against the energy gap between the classical active state and the lowest singlet state, similar to Figure 7, with the difference being that trajectories from both EWs are combined. The nuclear density is normalized in every time-step. On the right-hand side, a convoluted scatter plot of the S–S bond length with the corresponding energy gaps to the lowest state is given.
5. Summary
A time-resolved investigation of the nuclear and electronic dynamics of [Ru(S–Sbpy)(bpy)2]2+ in acetonitrile following excitations with green (520 nm) to blue (430 nm) light has been conducted. Two different sets of excited states are initially populated via absorption, each reminiscent of transferring an electron from the ruthenium center to one of the two types of ligands present: the parent bpy ligands or the modified S–Sbpy ligand, which are experimentally accessible at 430 and 520 nm, respectively. From these diverging sets of initially populated states, formation of a unique localized long-lived triplet state is observed from where radiative decay can occur.
After formal oxidation of the metal atom and reduction of the respective ligands via metal-to-ligand charge transfer, ultrafast time-resolved UV/Vis pump–probe spectroscopy reveals an excitation wavelength-independent behavior of the observed complex, where the absence of precursor states unequivocally identifies the formation of the lowest energy state within less than 80 fs. Excess vibrational energy in the T1 state is transferred to the solvent on a 10 ps timescale.
A direct insight into the molecular dynamics occurring in the early times is obtained with surface-hopping trajectory simulations, using a TD-DFT-fitted LVC model. The general validity of this LVC model to describe the ensuing dynamics was verified using the absorption spectrum as a reference. Furthermore, it was found that 16 vibrational modes and one triplet state had to be removed from the LVC Hamiltonian to allow the correct formation of the minimum energy structure of the lowest triplet state. The non-adiabatic dynamics was then performed with a Hamiltonian containing 78 states and 161 vibrational degrees of freedom, where a total of 8983 trajectories were propagated during 250 fs each to unravel the mechanisms of ultrafast formation of the emissive state.
The non-adiabatic dynamics show that ultrafast intersystem crossing into the triplet manifold occurs on two time scales, a fast intersystem crossing component kISC,fast and a slow one kISC,slow. Simulations starting in an energy range of 2.85–3.05 eV delivered kISC,fast = 46 fs and kISC,slow = 337 fs. Similar time constants have been obtained for the low-energy excitation (2.4 to 2.6 eV) with kISC,fast = 43 fs and kISC,slow = 256 fs. The fast ISC component persists if the dynamics are repeated while keeping all nuclei in every trajectory frozen, proving it to be due to electronic spin-mixing that does not rely on any structural rearrangement beyond the zero-point energy sampling of the ground-state geometry. Contrarily, the slow component completely vanishes in the absence of structural relaxation. At the end of the 250-fs simulation time, half of the population is found in the lowest triplet state for both excitation wavelengths. When looking at the electronic wave functions of the two ensembles of structures, the character of the total wave function changes toward increased contribution of MSCT states during the dynamics, regardless of the initial population of states. Therefore, during the very first few fs, the excited electron gets more localized on the sulfur-decorated ligand, forming a [RuIII(S–Sbpy•–)(bpy)2]2+ species, where an electron has been excited from the central metal to the S–Sbpy ligand. This early dominance of MSCT states is due to their lower energy in comparison to the MLCT counterparts. Another reason that drives the prevalence of MSCT states during the dynamics is the energetic stabilization of some MSCT states upon elongating—and essentially breaking—the attached S–S bond resulting in a further energetic separation between MSCT and other MLCT states where parent bpy ligands are involved. During the dynamics, a decrease in the S0–T1 energy gap was found to directly correlate with an increase of the S–S bond length.
Both experimental observations and theoretical predictions reveal an ultrafast ISC coupled with the formation of an excited triplet state minimum from where emission has been observed with a timescale of 109 ns.21 While the formation of this state is independent of the excitation wavelength in the visible region of the spectrum, the final state is solely located on one ligand (S–Sbpy), opening up the possibility of directed energy transfer to another reactive species. Furthermore, the excited-state geometric evolution, viz., the elongation/rupture of the S–S bond, is reminiscent of the ground-state changes of the S–Sbpy ligand upon reduction, and thus, renders this photosensitizer a promising candidate for investigation on excited-state proton-coupled multielectron-transfer reactivity via the peripheral disulfide/dithiol switch.
Acknowledgments
L.G. is grateful to the Göttingen Academy of Sciences for awarding a Gauss Professorship that allowed for an extended research stay in Göttingen. The Vienna Scientific Cluster is gratefully acknowledged for generous computational resources.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c03163.
Optimized geometry and Cartesian coordinates of optimized S0 and T1 minima; labeling of the charge-transfer states used for the classification of electronic states; and reduction of the employed LVC Hamiltonian; mode reduction; S–S bond lengths; and T17 state; exemplary input file for the gaussian calculations (PDF)
Full and reduced LVC templates and the corresponding frequency files in Molden format to set up initial conditions (ZIP)
Author Contributions
All authors have given approval to the final version of the manuscript.
L.G., D.S., and F.M. are grateful to the Deutsche Forschungsgemeinschaft (DFG) for financial support of this work (projects Go1059/8-1, SCHW 661/4-1, and Me1313/15-1 within the SPP 2102 “Light-Controlled Reactivity of Metal Complexes”).
The authors declare no competing financial interest.
Supplementary Material
References
- Gagliardi C. J.; Westlake B. C.; Kent C. A.; Paul J. J.; Papanikolas J. M.; Meyer T. J. J. Integrating Proton Coupled Electron Transfer (PCET) and Excited States. Coord. Chem. Rev. 2010, 254, 2459–2471. 10.1016/j.ccr.2010.03.001. [DOI] [Google Scholar]
- Wenger O. S. Proton-Coupled Electron Transfer with Photoexcited Metal Complexes. Acc. Chem. Res. 2013, 46, 1517–1526. 10.1021/ar300289x. [DOI] [PubMed] [Google Scholar]
- Pannwitz A.; Wenger O. S. Proton-Coupled Multi-Electron Transfer and Its Relevance for Artificial Photosynthesis and Photoredox Catalysis. Chem. Commun. 2019, 55, 4004–4014. 10.1039/C9CC00821G. [DOI] [PubMed] [Google Scholar]
- Hammes-Schiffer S. Theory of Proton-Coupled Electron Transfer in Energy Conversion Processes. Acc. Chem. Res. 2009, 42, 1881–1889. 10.1021/ar9001284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roach T.; Krieger-Liszkay A. Regulation of Photosynthetic Electron Transport and Photoinhibition. Curr. Protein Pept. Sci. 2014, 15, 351–362. 10.2174/1389203715666140327105143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wherland S.; Pecht I. Controlling Time Scales for Electron Transfer through Proteins. Perspect. Sci. 2015, 6, 94–105. 10.1016/j.pisc.2015.06.005. [DOI] [Google Scholar]
- Crosby G. A. Spectroscopic Investigations of Excited States of Transition-Metal Complexes. Acc. Chem. Res. 1975, 8, 231–238. 10.1021/ar50091a003. [DOI] [Google Scholar]
- Thompson D. W.; Ito A.; Meyer T. J. [Ru(bpy)3]2+* and Other Remarkable Metal-to-Ligand Charge Transfer (MLCT) Excited States. Pure Appl. Chem. 2013, 85, 1257–1305. 10.1351/PAC-CON-13-03-04. [DOI] [Google Scholar]
- Müller P.; Brettel K. [Ru(bpy)3]2+ as a Reference in Transient Absorption Spectroscopy: Differential Absorption Coefficients for Formation of the Long-Lived 3MLCT Excited State. Photochem. Photobiol. Sci. 2012, 11, 632–636. 10.1039/C2PP05333K. [DOI] [PubMed] [Google Scholar]
- Bock C. R.; Connor J. A.; Gutierrez A. R.; Meyer T. J.; Whitten D. G.; Sullivan B. P.; Nagle J. K. Estimation of Excited-State Redox Potentials by Electron-Transfer Quenching. Application of Electron-Transfer Theory to Excited-State Redox Processes. J. Am. Chem. Soc. 1979, 101, 4815–4824. 10.1021/ja00511a007. [DOI] [Google Scholar]
- Ito A.; Meyer T. J. The Golden Rule. Application for Fun and Profit in Electron Transfer, Energy Transfer, and Excited-State Decay. Phys. Chem. Chem. Phys. 2012, 14, 13731–13745. 10.1039/C2CP41658A. [DOI] [PubMed] [Google Scholar]
- Kober E. M.; Meyer T. J. Concerning the Absorption Spectra of the Ions M(bpy)32+ (M = Fe, Ru, Os; bpy = 2,2’-bipyridine). Inorg. Chem. 1982, 21, 3967–3977. 10.1021/ic00141a021. [DOI] [Google Scholar]
- Soupart A.; Dixon I. M.; Alary F.; Heully J.-L. DFT Rationalization of the Room-Temperature Luminescence Properties of Ru(bpy)32+and Ru(tpy)22+: 3MLCT–3MC Minimum Energy Path from NEB Calculations and Emission Spectra from VRES Calculations. Theor. Chem. Acc. 2018, 137, 37. 10.1007/s00214-018-2216-1. [DOI] [Google Scholar]
- Prier C. K.; Rankic D. A.; MacMillan D. W. C. Visible Light Photoredox Catalysis with Transition Metal Complexes: Applications in Organic Synthesis. Chem. Rev. 2013, 113, 5322–5363. 10.1021/cr300503r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kober E. M.; Meyer T. J. An Electronic Structural Model for the Emitting MLCT Excited States of Ru(bpy)32+ and Os(bpy)32+. Inorg. Chem. 1984, 23, 3877–3886. 10.1021/ic00192a009. [DOI] [Google Scholar]
- Ashley D. C.; Jakubikova E. Tuning the Redox Potentials and Ligand Field Strength of Fe(II) Polypyridines: The Dual π-Donor and π-Acceptor Character of Bipyridine. Inorg. Chem. 2018, 57, 9907–9917. 10.1021/acs.inorgchem.8b01002. [DOI] [PubMed] [Google Scholar]
- Damrauer N. H.; Cerullo G.; Yeh A.; Boussie T. R.; Shank C. V.; McCusker J. K. Femtosecond Dynamics of Excited-State Evolution in [Ru(bpy)3]2+. Science 1997, 275, 54–57. 10.1126/science.275.5296.54. [DOI] [PubMed] [Google Scholar]
- Bräm O.; Messina F.; El-Zohry A. M.; Cannizzo A.; Chergui M. Polychromatic Femtosecond Fluorescence Studies of Metal–Polypyridine Complexes in Solution. Chem. Phys. 2012, 393, 51–57. 10.1016/j.chemphys.2011.11.022. [DOI] [Google Scholar]
- Atkins A. J.; González L. Trajectory Surface-Hopping Dynamics Including Intersystem Crossing in [Ru(bpy)3]2+. J. Phys. Chem. Lett. 2017, 8, 3840–3845. 10.1021/acs.jpclett.7b01479. [DOI] [PubMed] [Google Scholar]
- Arias-Rotondo D. M.; McCusker J. K. The Photophysics of Photoredox Catalysis: A Roadmap for Catalyst Design. Chem. Soc. Rev. 2016, 45, 5803–5820. 10.1039/C6CS00526H. [DOI] [PubMed] [Google Scholar]
- Hua S.-A.; Cattaneo M.; Oelschlegel M.; Heindl M.; Schmid L.; Dechert S.; Wenger O. S.; Siewert I.; González L.; Meyer F. Electrochemical and Photophysical Properties of Ruthenium(II) Complexes Equipped with Sulfurated Bipyridine Ligands. Inorg. Chem. 2020, 59, 4972–4984. 10.1021/acs.inorgchem.0c00220. [DOI] [PubMed] [Google Scholar]
- Whittemore T. J.; White T. A.; Turro C. New Ligand Design Provides Delocalization and Promotes Strong Absorption throughout the Visible Region in a Ru(II) Complex. J. Am. Chem. Soc. 2018, 140, 229–234. 10.1021/jacs.7b09389. [DOI] [PubMed] [Google Scholar]
- Rau S.; Walther D.; Vos J. G. Inspired by Nature: Light Driven Organometallic Catalysis by Heterooligonuclear Ru(II) Complexes. Dalton Trans. 2007, 915–919. 10.1039/B615987G. [DOI] [PubMed] [Google Scholar]
- Kinoshita T.; Nonomura K.; Joong Jeon N.; Giordano F.; Abate A.; Uchida S.; Kubo T.; Seok S. I.; Nazeeruddin M. K.; Hagfeldt A.; Grätzel M.; Segawa H. Spectral Splitting Photovoltaics Using Perovskite and Wideband Dye-Sensitized Solar Cells. Nat. Commun. 2015, 6, 1–8. 10.1038/ncomms9834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagfeldt A.; Grätzel M. Molecular Photovoltaics. Acc. Chem. Res. 2000, 33, 269–277. 10.1021/ar980112j. [DOI] [PubMed] [Google Scholar]
- Cattaneo M.; Schiewer C. E.; Schober A.; Dechert S.; Siewert I.; Meyer F. 2,2′-Bipyridine Equipped with a Disulfide/Dithiol Switch for Coupled Two-Electron and Two-Proton Transfer. Chem.—Eur. J. 2018, 24, 4864–4870. 10.1002/chem.201705022. [DOI] [PubMed] [Google Scholar]
- Taffarel E.; Chirayil S.; Kim W. Y.; Thummel R. P.; Schmehl R. H. Coexistence of Ligand Localized and MLCT Excited States in a 2-(2′-Pyridyl)Benzo[g]Quinoline Complex of Ruthenium(II). Inorg. Chem. 1996, 35, 2127–2131. 10.1021/ic9412973. [DOI] [Google Scholar]
- Henderson L. J.; Cherry W. R. Dynamics of Ligand Field Excited States in Polypyridine Ruthenium(II) Complexes. Chem. Phys. Lett. 1985, 114, 553–556. 10.1016/0009-2614(85)85140-X. [DOI] [Google Scholar]
- Henderson L. J.; Fronczek F. R.; Cherry W. R. Selective Perturbation of Ligand Field Excited States in Polypyridine Ruthenium(II) Complexes. J. Am. Chem. Soc. 1984, 106, 5876–5879. 10.1021/ja00332a020. [DOI] [Google Scholar]
- Thummel R. P.; Lefoulon F.; Korp J. D. Polyaza Cavity-Shaped Molecules. 12. Ruthenium(II) Complexes of 3,3’-Annelated 2,2’-Bipyridine: Synthesis, Properties, and Structure. Inorg. Chem. 1987, 26, 2370–2376. 10.1021/ic00262a007. [DOI] [Google Scholar]
- Tully J. C. Molecular Dynamics with Electronic Transitions. J. Chem. Phys. 1990, 93, 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
- Richter M.; Marquetand P.; González-Vázquez J.; Sola I.; González L. SHARC: Ab Initio Molecular Dynamics with Surface Hopping in the Adiabatic Representation Including Arbitrary Couplings. J. Chem. Theory Comput. 2011, 7, 1253–1258. 10.1021/ct1007394. [DOI] [PubMed] [Google Scholar]
- Mai S.; Marquetand P.; González L. Nonadiabatic Dynamics: The SHARC Approach. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1370 10.1002/wcms.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mai S.; Marquetand P.; González L. A General Method to Describe Intersystem Crossing Dynamics in Trajectory Surface Hopping. Int. J. Quantum Chem. 2015, 115, 1215–1231. 10.1002/qua.24891. [DOI] [Google Scholar]
- Köppel H.; Domcke W.; Cederbaum L. S.. Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation. Advances in Chemical Physics; John Wiley & Sons, Ltd., 2007; pp 59–246. [Google Scholar]
- Worth G. A.; Cederbaum L. S. Beyond Born-Oppenheimer: Molecular Dynamics Through a Conical Intersection. Annu. Rev. Phys. Chem. 2004, 55, 127–158. 10.1146/annurev.physchem.55.091602.094335. [DOI] [PubMed] [Google Scholar]
- Plasser F.; Gómez S.; Menger M. F. S. J.; Mai S.; González L. Highly Efficient Surface Hopping Dynamics Using a Linear Vibronic Coupling Model. Phys. Chem. Chem. Phys. 2018, 21, 57–69. 10.1039/C8CP05662E. [DOI] [PubMed] [Google Scholar]
- Wigner E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. 10.1103/PhysRev.40.749. [DOI] [Google Scholar]
- Granucci G.; Persico M. Critical Appraisal of the Fewest Switches Algorithm for Surface Hopping. J. Chem. Phys. 2007, 126, 134114. 10.1063/1.2715585. [DOI] [PubMed] [Google Scholar]
- Mai S.; Richter M.; Heindl M.; Menger M. F. S. J.; Atkins A.; Ruckenbauer M.; Plasser F.; Ibele L. M.; Kropf S.; Oppel M.; Marquetand P.; González L.. SHARC2.1: Surface Hopping Including Arbitrary Couplings—Program Package for Non-adiabatic Dynamics, http://Sharc-Md.Org (2019).
- Landry B. R.; Falk M. J.; Subotnik J. E. Communication: The Correct Interpretation of Surface Hopping Trajectories: How to Calculate Electronic Properties. J. Chem. Phys. 2013, 139, 211101. 10.1063/1.4837795. [DOI] [PubMed] [Google Scholar]
- Gao X.; Bai S.; Fazzi D.; Niehaus T.; Barbatti M.; Thiel W. Evaluation of Spin-Orbit Couplings with Linear-Response Time-Dependent Density Functional Methods. J. Chem. Theory Comput. 2017, 13, 515–524. 10.1021/acs.jctc.6b00915. [DOI] [PubMed] [Google Scholar]
- Chiodo S. G.; Leopoldini M. MolSOC: A Spin–Orbit Coupling Code. Comput. Phys. Commun. 2014, 185, 676–683. [Google Scholar]
- Koseki S.; Schmidt M. W.; Gordon M. S. Effective Nuclear Charges for the First- through Third-Row Transition Metal Elements in Spin–Orbit Calculations. J. Phys. Chem. A 1998, 102, 10430–10435. 10.1021/jp983453n. [DOI] [Google Scholar]
- Runge E.; Gross E. K. U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. 10.1103/PhysRevLett.52.997. [DOI] [Google Scholar]
- Casida M. E.; Jamorski C.; Casida K. C.; Salahub D. R. Molecular Excitation Energies to High-Lying Bound States from Time-Dependent Density-Functional Response Theory: Characterization and Correction of the Time-Dependent Local Density Approximation Ionization Threshold. J. Chem. Phys. 1998, 108, 4439–4449. 10.1063/1.475855. [DOI] [Google Scholar]
- Becke A. D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Hay P. J.; Wadt W. R. Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for K to Au Including the Outermost Core Orbitals. J. Chem. Phys. 1985, 82, 299–310. 10.1063/1.448975. [DOI] [Google Scholar]
- Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. 10.1063/1.438955. [DOI] [Google Scholar]
- Hess B. A. Relativistic Electronic-Structure Calculations Employing a Two-Component No-Pair Formalism with External-Field Projection Operators. Phys. Rev. A 1986, 33, 3742–3748. 10.1103/PhysRevA.33.3742. [DOI] [PubMed] [Google Scholar]
- Cancès E.; Mennucci B.; Tomasi J. A New Integral Equation Formalism for the Polarizable Continuum Model: Theoretical Background and Applications to Isotropic and Anisotropic Dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. 10.1063/1.474659. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Cheeseman J. R.; Scalmani G.; Caricato M.; Hratchian H. P.; Li X.; Barone V.; Bloino J.; Zheng G.; Vreven T.; Montgomery J. A.; Petersson G. A.; Scuseria G. E.; Schlegel H. B.; Nakatsuji H.; Izmaylov A. F.; Martin R. L.; Sonnenberg J. L.; Peralta J. E.; Heyd J. J.; Brothers E.; Ogliaro F.; Bearpark M.; Robb M. A.; Menucci B.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Rendell A.; Gomperts R.; Zakrzewski V. G.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H. A.. Gaussian09, 1. 2197; Gaussian Inc.: Wallingford CT, 2009.
- Crespo-Otero R.; Barbatti M. Spectrum Simulation and Decomposition with Nuclear Ensemble: Formal Derivation and Application to Benzene, Furan and 2-Phenylfuran. Theor. Chem. Acc. 2012, 131, 1237. 10.1007/s00214-012-1237-4. [DOI] [Google Scholar]
- Mai S.; Plasser F.; Dorn J.; Fumanal M.; Daniel C.; González L. Quantitative Wave Function Analysis for Excited States of Transition Metal Complexes. Coord. Chem. Rev. 2018, 361, 74–97. 10.1016/j.ccr.2018.01.019. [DOI] [Google Scholar]
- Plasser F.TheoDORE: A Package for Theoretical Density Orbital Relaxation and Exciton Analysis. Available at Http://Theodore-Qc.Sourceforge.Net/ (accessed January 09, 2021).
- Shaw G. B.; Styers-Barnett D. J.; Gannon E. Z.; Granger J. C.; Papanikolas J. M. Interligand Electron Transfer Dynamics in [Os(Bpy)3]2+: Exploring the Excited State Potential Surfaces with Femtosecond Spectroscopy. J. Phys. Chem. A 2004, 108, 4998–5006. 10.1021/jp0363850. [DOI] [Google Scholar]
- Wallin S.; Davidsson J.; Modin J.; Hammarström L. Femtosecond Transient Absorption Anisotropy Study on [Ru(Bpy)3]2+ and [Ru(Bpy)(Py)4]2+. Ultrafast Interligand Randomization of the MLCT State. J. Phys. Chem. A 2005, 109, 4697–4704. 10.1021/jp0509212. [DOI] [PubMed] [Google Scholar]
- Mai S.; González L. Unconventional Two-Step Spin Relaxation Dynamics of [Re(CO)3(Im)(Phen)]+ in Aqueous Solution. Chem. Sci. 2019, 10, 10405–10411. 10.1039/C9SC03671G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mai S.; González L. Identification of Important Normal Modes in Nonadiabatic Dynamics Simulations by Coherence, Correlation, and Frequency Analyses. J. Chem. Phys. 2019, 151, 244115. 10.1063/1.5129335. [DOI] [PubMed] [Google Scholar]
- McCusker C. E.; McCusker J. K. Synthesis and Spectroscopic Characterization of CN-Substituted Bipyridyl Complexes of Ru(II). Inorg. Chem. 2011, 50, 1656–1669. 10.1021/ic102085b. [DOI] [PubMed] [Google Scholar]
- Brown A. M.; McCusker C. E.; Carey M. C.; Blanco-Rodríguez A. M.; Towrie M.; Clark I. P.; Vlček A.; McCusker J. K. Vibrational Relaxation and Redistribution Dynamics in Ruthenium(II) Polypyridyl-Based Charge-Transfer Excited States: A Combined Ultrafast Electronic and Infrared Absorption Study. J. Phys. Chem. A 2018, 122, 7941–7953. 10.1021/acs.jpca.8b06197. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.