Nanoscale Hydration in Layered Manganese Oxides

Abstract

Birnessite is a layered MnO₂ mineral capable of intercalating nanometric water films in its bulk. With its variable distributions of Mn oxidation states (Mn^IV, Mn^III, and Mn^II), cationic vacancies, and interlayer cationic populations, birnessite plays key roles in catalysis, energy storage solutions, and environmental (geo)chemistry. We here report the molecular controls driving the nanoscale intercalation of water in potassium-exchanged birnessite nanoparticles. From microgravimetry, vibrational spectroscopy, and X-ray diffraction, we find that birnessite intercalates no more than one monolayer of water per interlayer when exposed to water vapor at 25 °C, even near the dew point. Molecular dynamics showed that a single monolayer is an energetically favorable hydration state that consists of 1.33 water molecules per unit cell. This monolayer is stabilized by concerted potassium–water and direct water–birnessite interactions, and involves negligible water–water interactions. Using our composite adsorption–condensation–intercalation model, we predicted humidity-dependent water loadings in terms of water intercalated in the internal and adsorbed at external basal faces, the proportions of which vary with particle size. The model also accounts for additional populations condensed on and between particles. By describing the nanoscale hydration of birnessite, our work secures a path for understanding the water-driven catalytic chemistry that this important layered manganese oxide mineral can host in natural and technological settings.

Introduction

Birnessite (MnO₂) is a layered manganese oxide (Figure 1) occurring as fine-grained poorly crystalline nanoparticles or coatings in soils, sediments, and ferromanganese deposits.¹⁻³ This phyllomanganate has the notable quality of accommodating nanometric water films within its structure. These films contribute to birnessite stability^4,5 and host important solvent-driven processes, including ionic exchange and electron transfer reactions. Understanding the behavior of this hydration environment is essential for applications as varied as contaminant transport and redox geochemistry,⁶⁻⁹ catalysis,^10,11 energy storage solutions,¹² and even potentially harvesting atmospheric water in arid areas.¹³ Examples of knowledge required for these various applications include molecular configurations¹⁴ of intercalated water layers and of their thermal stabilities^4,15

Figure 1.

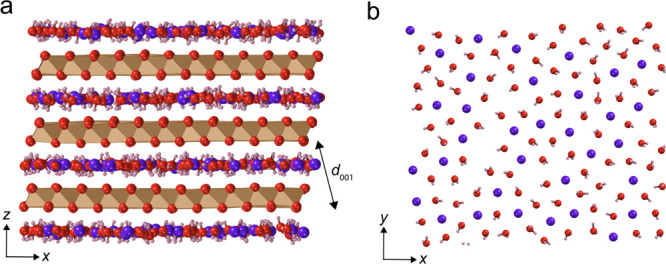
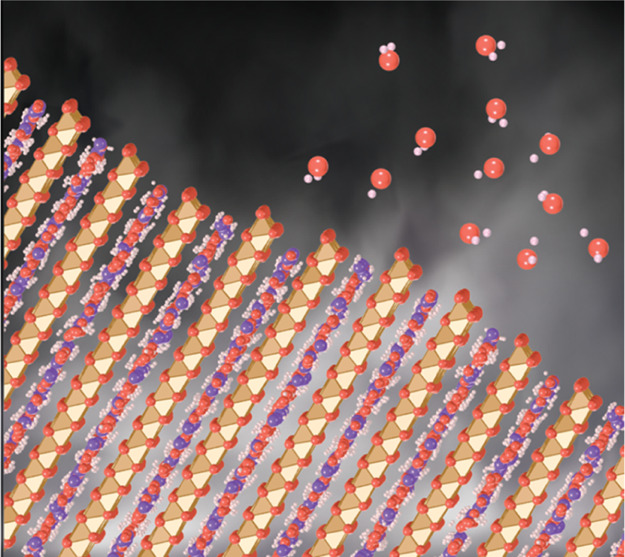
(a) Side view of the birnessite structure with an idealized 1-layer (1 W) interlayer hydration state of 1.33 H₂O (red/pink) per unit cell. Sheets of Mn octahedra (brown/beige) are connected through edge-sharing basal oxygens (red). Charge imbalance caused by Mn^III and Mn^II is compensated by interlayer countercations (purple) and/or vacancies (not shown). (b) Basal face view of a single water layer, also partially hydrating interlayer countercations, in this case, K⁺. These images were generated by a snapshot of a molecular dynamics simulations and then edited for illustration purposes.

The MnO₂ structure of birnessite is formally composed of stacked sheets of edge-sharing MnO₆ octahedra (Figure 1)¹⁶⁻¹⁸ and forms ultrathin nanoplatelets with a surface dominated with its basal face.^19,20 It has a formal average oxidation state (AOS) of 4.0, but synthetic and natural forms commonly contain a mixture of Mn oxidation states (Mn^IV, Mn^III, and Mn^II).²¹⁻²⁴ In nature, birnessite or vernadite with AOS values as low as ∼3.5 is probably more common because natural organic matter has a strong propensity to reduce Mn^IV.^21,25−28 Cationic vacancies represent an additional source of charge imbalance with, for example, previously reported populations of 12% in birnessite prepared in acidic and 6% in alkaline media.^21,29,30 Countercations (e.g., Na⁺, K⁺, and Mn²⁺) in the interlayer region counterbalance the missing charges resulting from the mixed Mn-oxidation states and vacancies. These can collectively alter the structure and the chemical reactivity of intercalated water. For example, manganese oxides with well-defined crystallographic sites host structured water layers, while those of lower crystallinity host relatively more disordered water.³¹ Understanding the forms of water trapped in the interlayer region when birnessite is exposed to moist air is especially central for understanding how they mediate reactions of natural and technological importance. Of note, resolving this chemistry can also be challenged by the coexistence of water condensed in pores between particles.

Building upon our recent work on water vapor binding on minerals,³²⁻³⁸ we here resolved the humidity-dependent loadings of water achieved on birnessite nanoparticles, alongside their resulting vibrational spectral profiles and the interlayer expansion they generate. We predict the microscopic hydration states of birnessite using a composite adsorption–condensation–intercalation model that we recently developed for layered minerals. Our model accounts for water intercalated in the internal and external basal faces of birnessite (Figure 1).³⁸ We also provide additional insight into the structure and dynamics of the intercalated water by molecular dynamics simulations of a representative form of birnessite. This work should facilitate future studies following the solvent-driven chemistry of this important nanolayered manganese oxide when exposed to moist air.^39,40

2. Materials and Methods

2.1. Synthesis and Experimental Characterization

The birnessite samples used in this work are important analogues to the most common vernadite and biogenic Mn oxides in nature and thus especially informative to understand natural and technological processes.^21,25,41,42 To this end, we prepared birnessite formed in acidic (AcidBir) and alkaline (δ-MnO₂) solutions, which are two synthetic representative isomorphs of layered MnO₂ with a hexagonal structure.²⁵ Here, we follow the classification of Villalobos et al.,²⁵ where AcidBir is synthesized by reduction¹⁶ of a permanganate solution under acidic conditions, and δ-MnO₂ is synthesized from a redox reaction of permanganate with Mn²⁺ under alkaline conditions.

AcidBir was prepared by the dropwise addition of 166 mL of 12 M HCl to a vigorously stirred 2.5 L solution of 0.4 M KMnO₄ kept in a water bath at 90 °C.¹⁶ The resulting solution was reacted for an additional 10 min after completion of the titration. The precipitate was then washed with ultrapure water by repeated cycles of centrifugation/decantation until the conductivity was close to 0 μS/cm. δ-MnO₂ was, in contrast, prepared by adding an 80 mL solution of 0.1 M KMnO₄ and a 160 mL solution of 0.1 M KOH to 1640 mL of ultrapure water at 25 °C. An aliquot of 120 mL of a 0.1 M MnCl₂ solution was thereafter added dropwise to this solution under vigorous stirring. All synthesis procedures were carried out in polypropylene bottles, and all washed precipitates were stored as aqueous suspensions in polyethylene bottles at 4 °C for a 2 month period prior the onset of this work.

A portion of the precipitates was oven-dried at 60 °C for particle characterization, a detailed account of which is in the Supplementary Section. Crystalline MnO₂ phase purity was confirmed by X-ray diffraction (XRD; PANalytical X’Pert Pro X-ray diffractometer; Figure S1). B.E.T.²⁵ specific surface areas of 59.2 m²/g for AcidBir and 204 m²/g for δ-MnO₂ were obtained from 90-point adsorption/desorption N₂(g) isotherms (Micromeritics). The surface Mn:O:K compositions of 1.00:1.49:0.20 for AcidBir, “MnO₂ (0.20 K)”, and 1.00:1.38:0.17 for δ-MnO₂, “MnO₂ (0.17 K)”, were resolved by X-ray photoelectron spectroscopy (XPS; Kratos Axis Ultra DLD electron spectrometer; see the text in the Supporting Information and Figures S2–S4). The O/Mn ratios were lower than the stoichiometrically expected value of 2, and could result from (i) the near surface composition of birnessite surfaces probed by XPS (i.e., within the first ∼10 nm of the topmost region), and (ii) the loss of chemisorbed water to vacuum.

Surface Mn AOS values of AcidBir (AOS = 3.69; 72% Mn^IV, 25% Mn^III, and 3% Mn^II) and δ-MnO₂ (AOS = 3.52; 58% Mn^IV, 36% Mn^III, and 6% Mn^II) were resolved by fitting of the Mn 3s region according to the method of Ilton et al.(43) Of note, these oxidation states are highly similar to those of Ling et al.(44) obtained using the same analysis method of a birnessite synthesized by reduction of permanganate under acidic conditions (AOS = 3.69; 68% Mn^IV, 22% Mn^III, and 4% Mn^II), as in AcidBir, and for another birnessite by a redox reaction at high pH (AOS = 3.69; 60% Mn^IV, 38% Mn^III, 2% Mn^II), as in δ-MnO₂. See the supplementary section for a discussion on the fitting procedure and results, in Figures S2–S4 and Table S1.

2.2. Water Vapor Uptake

Binding of water vapor on birnessite during dynamic vapor sorption (DVS)⁴⁵ was monitored by (1) microgravimetry, (2) Fourier transform infraRed (FTIR) spectroscopy, and (3) basal spacing (d₀₀₁) obtained by powder XRD.

2.2.1. Microgravimetry

Microgravimetric measurements of water vapor uptake by birnessite were obtained using a DVS Advantage ET 2 instrument (Surface Measurement Systems). A 21-point isotherm cycle occurred between 0 and 98% relative humidity (RH) at 25 °C, and we used ∼30 mg samples initially dried at 110 °C for 3 h. The equilibrium criterion for each stepwise increase in % RH was set to a change in mass of less than 0.001 wt % per minute. A complete adsorption–desorption isotherm cycle took up to ∼3 days (Figure S5).

2.2.2. Adsorption–Condensation–Intercalation Modeling

Water loadings (w_tot) obtained by microgravimetry were predicted using our composite adsorption–condensation–intercalation model,³⁸ which was implemented in a MATLAB R2019b (The Mathworks, Inc.) code. The model accounts for coexisting water populations (i) on the external basal faces (adsorption; w_ads), (ii) condensed between particle (condensation; w_cond) water, and (ii) on the internal basal face (intercalation; w_int), such that

1

These populations were expressed in terms of the number of H₂O bound per unit cell (UC). We note that a single UC consists of two MnO₂ units. Additionally, the conversion of the experimentally obtained “mass of bound H₂O per mass of MnO₂” to “H₂O/UC” is made using the molar masses (m_MnO2) of MnO₂ (0.20 K) for AcidBir and of MnO₂ (0.17 K) for δ-MnO₂.

In this work, one complete monolayer (1 W) on the basal face of birnessite corresponds to W_1,int = 1.33 H₂O/UC or ρ_Wads = 9 H₂O/nm², which are values determined by our molecular dynamics simulations to be presented in the latter part of this paper. We determined the total populations associated to the external basal faces in terms of H₂O/UC with

2

where s_s is the total B.E.T. specific surface area. Incidentally, we do not explicitly account for water populations at particle edges, which represent a low proportion of the particle surface area.

Predictions of internal water loadings (w_int) achieved by intercalation were treated using Dubinin–Asthakhov theory⁴⁶ with

3

Here, the binding strength of water (E) and the pore size distribution (e.g., i = 2 for Gaussian) are adjustable parameters. These two adjustable parameters account for the humidity-dependence shape of the water uptake curve.⁴⁷ The water vapor pressure dependence on binding in eq 3 is expressed through the adsorption potential (A)

4

where p is the partial pressure of water vapor and p_o is the saturation (dew point) pressure. As the results from XRD will show, a maximum of only one water layer (1 W) is accommodated in each interlayer region of birnessite.

Predictions of water binding on the external surface were made with a theory first developed by Do and Do,⁴⁸ but here adapted for minerals to account for coexisting adhesive adsorption (w_ads) and cohesive water–water condensation (w_cond) interactions, respectively, with

5

and

6

The adsorption term (eq 5) makes use of a fixed total binding density of W_1,ads (eq 2), a fixed bond order (β=0), and an adjustable binding constant (K_f). The condensation term (eq 6) involves the condensable water density (C_μs), the condensation constant (K_μ), and the critical number of water molecules in a nanocluster needed to trigger condensation.

2.2.3. Vibrational Spectroscopy

Water vapor binding to birnessite was also monitored by FTIR spectroscopy. All FTIR spectra were collected with a Bruker Vertex 70/V FTIR spectrometer, equipped with a DLaTGS detector. The spectra were collected in the 600–4000 cm^–1 range at a resolution of 4.0 cm^–1 and at a forward/reverse scanning rate of 10 kHz. Each spectrum was an average of 500 scans.

Centrifuged wet pastes of birnessite were deposited on a diamond window of an attenuated total reflectance (ATR) cell (Golden Gate, single-bounce). They were dried with a heat gun to ∼110 °C, then to a hot stream of dry N₂(g), and then covered with a lid enabling the passage of a flow of 250 mL/min N₂(g) over the sample set to 25 °C. FTIR spectra were collected during the drying period to monitor the loss of water until the intensities of the O–H stretching and bending bands became constant. Accordingly, exposure of our sample to 0.4% RH, our driest N₂(g) gas at 25 ± 1 °C, revealed residual levels of intercalated water (Figure S6). See the Supplementary Section for additional experiments providing information on the conditions necessary for fully removing these most recalcitrant water molecules from birnessite (Figure S7).

Water vapor adsorption and desorption experiments were carried out by exposing the resulting mineral film to 0.4–95% RH in the reaction cell at 25 ± 1 °C. A 250 mL/min flow of water vapor of controlled pressure was first generated by mixing predetermined proportions of humid N₂(g) and dry N₂(g) using a humidity generator module (proUmid MHG32). Water vapor pressures were continuously monitored by a sensor equipped with the module and a nondispersible infraRed device (LI-7000, Licor Inc). A separate deuteration exchange experiment (Figure S6), in which birnessite was suspended in D₂O(l) for 3 days, showed that the intercalated water populations were all responsive to changes in chemical gradient.

Spectra sets from each DVS experiments were analyzed using the multivariate curve resolution-alternating least square (MCR-ALS) method.⁴⁹ Absorbance data, represented in the matrix format A_m×n of m wavenumbers and n water vapor pressures, were decomposed into their MCR spectral components (ε), and their respective concentration profiles (C), according to the Beer–Lambert law (A = ε·C). A singular value decomposition of matrix A_m×n was used to estimate the dimensionality of spectral components required to reproduce a given variance of the data. All calculations were performed in the computational environment of MATLAB R2019b (The Mathworks, Inc.).

2.2.4. d₀₀₁ Spacing by X-ray Diffraction

Interlayer expansion and collapse, respectively, resulting from the intercalation and withdrawal of water, were monitored by powder X-ray diffraction (XRD). AcidBir and δ-MnO₂ powders were first heated to 105 °C for 3 h under a dry N₂(g) flow to remove all interlayer water. This was confirmed by the resulting XRD-derived d-spacing. After cooling to 25 °C under the same dry N₂(g) flow, humidity was then incrementally increased to 98% during an adsorption leg and then incrementally decreased during the desorption leg. The samples were allowed to equilibrate at each preselected RH value for 30 min prior to collecting the diffractograms. The data were acquired using a PANalytical X’Pert³ Powder instrument (1.54187 Å CuKα̅ beam at 45 kV and 40 mA) at a resolution of 0.0334° in the 2–50° 2θ range.

Due to the low signal-to-noise ratio obtained in the transmission mode, humidity-dependent d₀₀₁ values were determined with Bragg’s law after fitting a Gaussian function of the background-corrected 001 reflection. These analyses produced d₀₀₁ data for AcidBir only. Diffractograms of the considerably smaller δ-MnO₂ particles were of insufficient quality to extract reliable d₀₀₁ values, and are therefore not reported.

2.2.5. Molecular Dynamics

To gain direct molecular-scale insight into the hydration of birnessite, molecular dynamics (MD) simulations of K⁺-saturated birnessite at different water loadings were also undertaken. The lattice of one UC¹⁴ was expanded into a system containing 6 × 12 × 4 UCs, with a composition of K₁₄₄[Mn₅₇₆O₁₁₅₂] × (H₂O)₃₈₄₀. This initial composition corresponded to an average of 0.25 K⁺ ions and 13.333 water molecules per UC. After energy minimization and 2 ns of volume and pressure optimization, 61 × 3 ns successive production runs in the isobaric–isothermal ensemble (NPT) were performed at decreasing water loadings. This was realized by successively evaporating a constant number of randomly selected water molecules (0.22 water molecules per UC per step) from each interlayer region, while preserving the same d₀₀₁ of each interlayer at each step. Each evaporation step was followed by a 100 ps of pre-equilibration run not included in the analysis.

All simulations were carried out using GROMACS⁵⁰ with a 1 fs time step and a 1.0 nm cutoff for the direct van der Waals and for Coulombic interactions. Long-range Coulombic interactions were accounted for by the particle-mesh Ewald (PME) method. For practical reasons, the birnessite lattice was modeled with Mn^3.75+ as in Cygan et al.(39) but with Lennard-Jones forcefield parameters recently reported by Newton and Kwon.⁵¹ Water was described with the SPC/E model,⁵² and K⁺ ions were described with SPC/E compatible ion-pair potentials from Joung and Cheatham.⁵³

MD simulation results were analyzed for d₀₀₁ along the UC c axis, hydrogen bonding, K⁺–O coordination, and K⁺ and water diffusion coefficients. The energetics of stable hydration states were analyzed with^54,55

7

Q(N) is the hydration immersion energy (J/g) relative to a reference hydration state N^o, N is the number of water molecules per birnessite unit cell (H₂O/UC), U is the time-averaged potential energy, and U_bulk (46.8 kJ/mol) is the mean interaction energy of a bulk SPC/E water molecule. In a second set of simulations, we replaced K⁺ by Na⁺ to compare with the MD results of Newton and Kwon⁵¹ (Figure S8).

3. Results and Discussion

3.1. Water Intercalation Causes Interlayer Expansion

The humidity-dependent water loadings on AcidBir and δ-MnO₂ are characteristic of a Type II adsorption/desorption isotherm,⁵⁶ with some hysteresis in the desorption leg. The isotherms became nearly congruent when expressed on a mass per mass (mg H₂O/g birnessite) or unit cell (H₂O/UC) basis (Figure 2) and reached ∼1.5–1.6 H₂O/UC just below the dew point of water. This congruency for both materials indicates that the majority of bound water was associated to the birnessite bulk.

Figure 2.

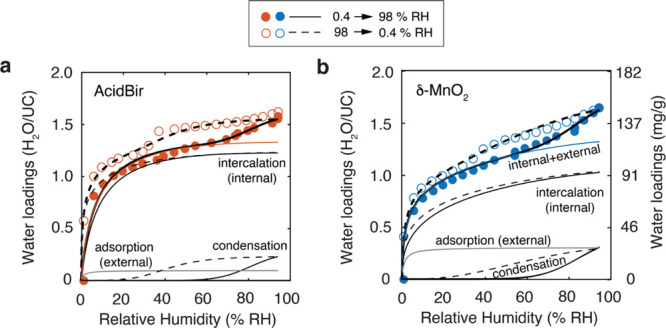
Gravimetrically derived water loadings on (a) AcidBir (59.2 m²/g) and (b) δ-MnO₂ (204 m²/g), collected as adsorption (closed symbols) and desorption (open symbols) isotherms at 25 °C. Loadings are shown in terms of bound water molecules per unit cell (H₂O/UC) and birnessite mass-normalized (left ordinate axis) mass of H₂O (mg/g). Lines (see labels) are predictions of water binding during the adsorption (full) and desorption (dashed) leg of the data collection and generated using the composition adsorption–condensation–intercalation model of this study. The orange line in (a) and the blue line in (b) show the sum of internally and externally bound water to the basal faces of birnessite.

XRD-derived d₀₀₁ spacing values of AcidBir (Figure 3) revealed a sharp increase in d_001, from 0.690 nm at 5% RH, where the interlayer region is chiefly dehydrated (0 W), to 0.735 nm at 98% RH. As the 001 diffraction peak intensity remained relatively unchanged, no significant change in the stacking of MnO₂ sheets is likely to have been induced by humidity. The interlayer expansion of 0.045 nm corresponds to the intercalation of no more than a single monolayer (1 W), as will be confirmed further by the simulations of the last section of this paper. These results also revealed a population of intercalated water resilient to outgassing below ∼40% RH. The population responsible for the microgravimetrically measured hysteresis above this value must therefore arise from the surface and interparticle water as the d₀₀₁ spacing values are fully reversible at these higher levels of humidity.

Figure 3.

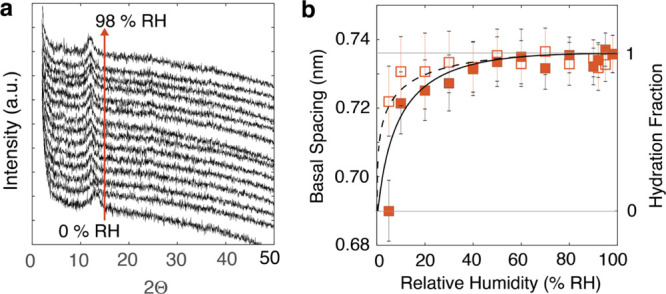
(a) Transmission-mode XRD diffractograms of AcidBir exposed to 0–98% RH and (b) result of d₀₀₁ basal spacing (left ordinate axis) analyses from these data (filled square = adsorption; open square = desorption), also showing uncertainties. The model predictions of d₀₀₁ in (b) (full line for adsorption; dashed for desorption) were taken from the Dubinin–Asthakhov theory⁴⁶ term derived from the microgravimetric water binding data (Figure 2a). This model prediction of the hydration fraction (right ordinate axis) was scaled such that d₀₀₁ = 0.690 nm at 0 W (0 H₂O/UC) and d₀₀₁ = 0.735 nm at 1 W (1.33 H₂O/UC). Diffractograms for δ-MnO₂ were of insufficient quality to be shown here, due to the small particle size.

Using a maximal water population of 1.33 H₂O/UC (e.g., 121 mg of H₂O per g MnO₂ (0.17 K) for δ-MnO₂) on the internal and external basal faces of birnessite, we modeled the microgravimetric data of Figure 2 with our adsorption–condensation–intercalation model (Table 1). The model accounts for constant proportions of internally and externally bound water on AcidBir and δ-MnO₂, and this assumption is justified by the constant intensities of the 001 diffraction peaks of Figure 3. The model involves a single set of values to predict adsorption on external basal faces, as well as highly comparable values for the intercalation term, except for differing pore size distributions (parameter i in eq 3) in AcidBir and δ-MnO₂. We must consider that the sum of the intercalation (internal) and adsorption (external) terms (orange line in Figure 2a and blue line in Figure 2b) represents the total amount of water associated to the basal faces of birnessite, regardless of whether the dry particles are stacked in such a way that a portion of the particle surface area (s_s, determined by B.E.T.) is no longer accessible for direct adsorption in the water vapor binding experiments. We make this statement because our estimate of external site densities from B.E.T. values may be too high for δ-MnO₂, and this could explain the lowered contributions of the intercalation term. It does not, however, explain the different pore size distributions, which are obtained even by removing the adsorption term from the model. Still, the intercalation term of our model reproduces the humidity dependence of the experimentally derived d₀₀₁ values of AcidBir, when scaled as described in Figure 3b. Additionally, the model explains the greater portion of the hysteresis of the microgravimetric data in terms of liquid water populations between particles, which we find by vibrational spectroscopy in the following section. Our model provides, as such, an insightful depiction of the distribution of water on and within birnessite particles exposed to moist air and almost up to the dew point of water.

Table 1. Adsorption–Condensation–Intercalation Modeling Parameters of the Microgravimetric Data.

		adsorptiona			condensationb			intercalationc
sample	experiment	W1,adsd	log10Kf	β	Cμsd	log10Kμ	α	W1,intd	log10E	i
δ-MnO2	0 → 98% RH	0.30	1.90	0	0.46	0.48	8.4	1.33	3.90	1.2
δ-MnO2	98 → 0% RH	0.30	1.90	0	0.40	0.48	2.9	1.33	3.98	1.2
AcidBir	0 → 98% RH	0.09	1.90	0	0.32	0.61	8.5	1.33	3.91	2.0
AcidBir	98 → 0% RH	0.09	1.90	0	0.22	0.55	4.2	1.33	4.08	2.0

^aEquation 5.

^bEquation 6.

^cEquation 3.

^dH₂O/UC.

3.2. Vibrational Spectral Profile of Intercalated Water

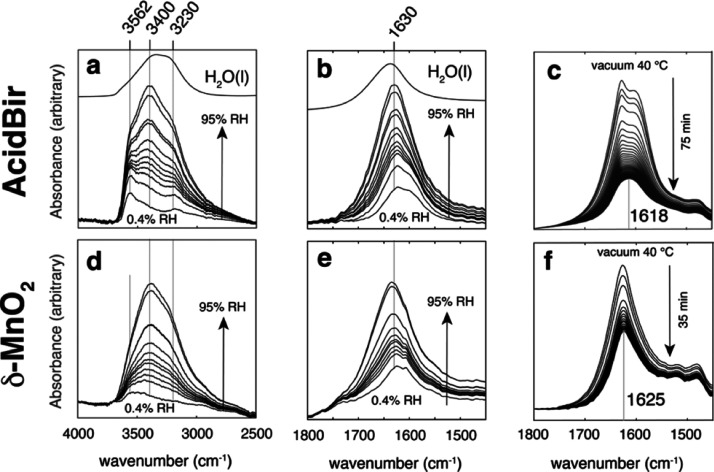
The vibrational spectroscopic response of bound water was monitored in thin birnessite films exposed to water vapor (Figure 4). First, we note that the O–H stretching (ν₁) region (Figure 4a,d) responds to water uptake through the development of (i) a 3230 cm^–1 band from O–H stretches with strong intermolecular coupling and from the Fermi resonance (2·ν₂) of the bending mode (ν₂ ≈ 1630 cm^–1), (ii) a 3400 cm^–1 band from water involved in a hydrogen bonding network with other water molecules, and (iii) a ∼3562 cm^–1 band from water molecules that are directly hydrogen-bonded with oxygens of the basal faces of the interlayer region. This latter assignment is supported by our previous work on layered aluminosilicates, as by our molecular simulations to be presented in the following section.⁵⁷ The water bending (ν₁) region of intercalated water (Figure 4 b,e) also acquired a shape comparable to that of liquid water at high humidity at ∼1630 cm^–1. Low humidity (e.g., 0.4% RH) and outgassing experiments (Figure 4c,f; S6), however, revealed residual water populations of relatively blue-shifted bending frequencies that likely arise from potassium and perhaps vacancy-bound water molecules pointed out by Ling et al.(44) For example, a double-band for AcidBir during outgassing (Figure 4c) could be evidence for coexisting water populations under low water loadings. We will, however, not focus on this aspect of hydration in this study.

Figure 4.

FTIR spectra of (a–c) AcidBir and (d–f) δ-MnO₂. Samples were collected in ATR mode for experiments in the 0.4–95% RH range (adsorption leg) at 25 °C (a,b,d,e) and in transmission mode for samples exposed to vacuum at 40 °C (c,f). Note that the intensities in c and f are lower than those at 0.4% RH, and represent very low hydration states.

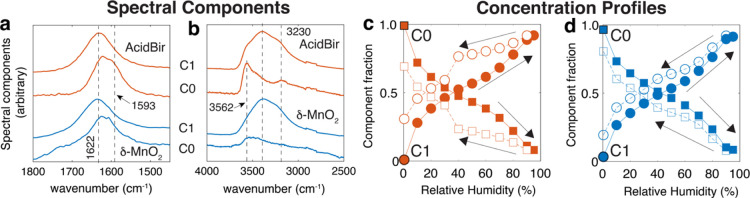
The humidity dependence on interlayer water populations was resolved further by extracting spectral components (Figure 5a,b) and concentration profiles (Figure 5c,d) of the most dehydrated (C0) and hydrated (C1) forms of birnessite from the spectra of Figure 4a,b,d,e.⁴⁹ These chemometric analyzes revealed that only two spectral components accounted for over 96% of the variance of the spectra over the 0–98% RH range. Because additional components could not be extracted from these data, contributions from intercalated, adsorbed, and condensed interparticle water are implicitly overlapped in component C1. We ascribe the difficulties that arise in separating these contributions to the lack of variance in the spectra resulting from the concurrent binding of different water populations of highly comparable spectral profiles.

Figure 5.

Chemometric analysis of FTIR spectra of AcidBir (orange) and δ-MnO₂ (blue) from the adsorption (Figure 4a,b,d,e) and desorption (not shown) legs. The analysis decomposed the spectra into spectral components (a,b) and relative concentration profiles (c,d). Concentration profiles show both adsorption (filled) and desorption (open) legs.

The resulting concentration profiles (Figure 5c,d) revealed systematic and reversible changes in the adsorption and removal of water. The steep change in C1 in the adsorption leg within the 0–10% RH range correlates with the increase in d₀₀₁ values (Figure 3b). Changes at larger humidity relate, in contrast, to a combination of a smaller change intercalation and binding to the external basal face and of a more dominant contribution from the condensation regime. Finally, we note that the desorption leg reveals a stronger hysteresis for AcidBir than in δ-MnO₂ in the 30–90% RH range. These results confirm that the hysteresis seen in the microgravimetric data (Figure 1) is from condensed interparticle water, as little hysteresis was observed in the d₀₀₁ spacing data.

3.3. Molecular Structure and Dynamics of Intercalated Water

To gain further insight into the molecular controls on the formation and stability of the intercalated water, we performed MD simulations on an idealized birnessite with intercalated K⁺ ions (Figure 1). We also explored hydration states larger than 1 W to evaluate whether these could have been reached in the laboratory.

The dependence of d₀₀₁ with water loading and the corresponding immersion energy data, derived from these simulations, indicate a stable 1 W hydration state at 0.705 nm (Figure 6). This d₀₀₁ value is slighter below our experimentally derived value of ∼0.735 nm. It corresponds to 1.33 H₂O/UC (5.33 H₂O/K⁺), which is the intercalation density chosen for modeling the microgravimetric data (Figure 2). Simulations also identified higher hydration states at 1.02 nm (2 W), 1.36 nm (3 W), and 1.68 nm (4 W), but none of these d₀₀₁ values correspond to our experimental values, which strongly indicate that the highest hydration state that can be achieved by birnessite in moist air is 1 W. This is consistent with previous accounts showing that the 2 W state, informally known as buserite, is only stable in liquid water.^1,58,59

Figure 6.

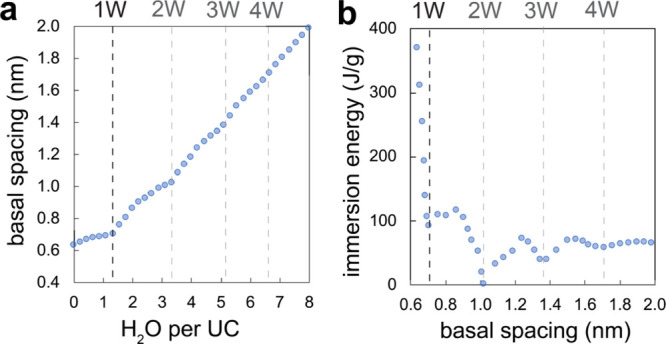
(a) Predicted d₀₀₁ (along the UC c axis) as a function of water loading, here expressed as the water molecule per UC of K⁺-birnessite. (b) Corresponding immersion energy profiles vs d₀₀₁. Here, 0.705 nm = 1 W and 1.02 nm = 2 W. Note that the immersion energy curve indicates possible higher and quasi-stable hydration states at 1.36 (3 W) and 1.68 (4 W) nm. See Figure S8 for comparison with Na-birnessite, which was also reported in the literature.³⁰ Dashed vertical lines indicate the loci of hydration states.

Our simulated stable 1 W hydration state was nearly monoclinic, with average UC dimensions of a = 0.511, b = 0.295, and c = 0.705 nm and angles of α = 90.0, β = 104.0, and γ = 89.8°. These results are in line with reported dimensions of Na-birnessite by Newton and Kwon⁵¹ and are within 4% of the values of two previous studies.^60,61 We also find that K⁺ and water oxygens were positioned in the center interlayer region (Figure 7), in between basal oxygens of the birnessite lattice. This symmetric interlayer structure deviates from previous simulation studies,³⁹ possibly due to contrasting water contents and forcefield parameters. Still, our results show similar positions of K⁺ and its coordinating water, as was previously shown with MD for Na-birnessite.^39,51

Figure 7.

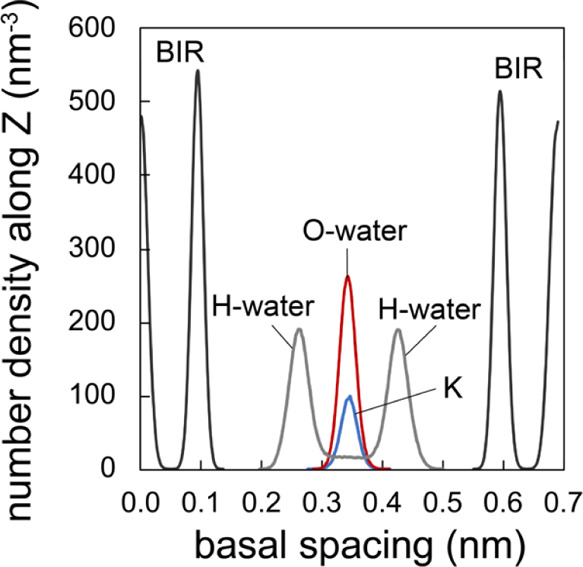
Density profile data binned over a single 6 × 12 1 W birnessite layer with the composition K₃₆[Mn₁₄₄O₂₈₈] × (H₂O)₉₆, demonstrating the position of the K⁺ counterions and water oxygens being fully centered in the interlayer region. This contrasts with water hydrogens, which are almost exclusively oriented toward the basal oxygens of the birnessite lattice.

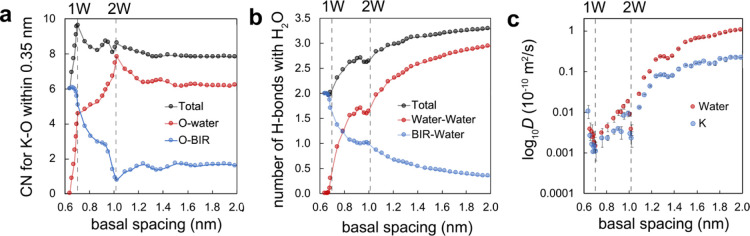
Our simulations also revealed (i) the coordination number of interlayer K⁺, (ii) hydrogen bond populations, and (iii) the diffusion coefficients (D) of K⁺ and water in birnessite (Figure 8). In particular, the 1 W state displayed a local maximum in the number of K⁺–oxygen interactions (Figure 8a), with ∼10 O within 0.35 nm, ∼5 of which are O-sites from the basal face and ∼5 from water oxygen. It is a hydration state with the maximum number of donating hydrogen bonds (2 per O) to birnessite basal oxygen groups (observed at 3562 cm^–1 in Figure 5b) and the least number of water–water interactions (Figure 8b). This latter observation thus implies that the hydrogen-bonded water populations seen by vibrational spectroscopy must arise from condensed water between the particles, not from the interlayer region. Finally, our simulations also show that the 1 W state is also the one with the lowest diffusion coefficients for both K⁺ and water and even the lowest of all simulated hydration states (Figure 8c). For comparison, the diffusion coefficient of liquid water (D = 2.68 × 10^–9 m²/s)⁵⁵ is four orders of magnitude larger than that of the 1 W state. These findings consequently underscore the singular attributes of water molecules intercalated in the interlayer region of birnessite.

Figure 8.

MD simulation results showing the basal spacing dependence (d₀₀₁) on (a) the coordination environment of K⁺, (b) hydrogen bond populations, and (c) diffusion coefficients of water. (a) First-shell coordination of K⁺ to oxygens, belonging to either water (O-water, red) or birnessite (O-BIR, blue).The coordination numbers were calculated from the radial distribution functions up to the minima of the first coordination shell at 0.35 nm (Figure S9). (b) Number of hydrogen bonds between water and birnessite. (c) Diffusion coefficients of water (red) and K⁺ (blue). Dashed vertical lines indicate ideal 1 W and 2 W hydration states.

4. Conclusions

By combining evidence from microgravimetry, vibrational spectroscopy, X-ray diffraction, and adsorption modeling, we showed that birnessite exposed to water vapor accommodates no more than a single monolayer of water in its interlayer region at 25 °C. The 2 W state of birnessite, known as buserite, is therefore not achieved by exposure of water vapor under ambient pressure and temperature.^14,62,63

The 1 W hydration state of K⁺-intercalated birnessite contains 1.33 water molecules per unit cell. This population can be distributed in the internal and external basal faces of the nanoparticles, the proportions of which vary with particle size. Condensed water on and between particle surfaces appears at ∼50% RH during adsorption but disappears below ∼20% RH during desorption. The 1 W state expands the basal spacing to d₀₀₁ = 0.735 nm and consists of a single layer of water molecules simultaneously hydrating interlayer K⁺ and donating hydrogen bonds to O-sites on the basal face. Unlike liquid water, those in the 1 W state of birnessite form almost no intermolecular hydrogen bonds, and their diffusion coefficient is four orders of magnitude lower than that of liquid water. This explains the distinct solvation environment offered by water intercalated in the birnessite bulk. The combined macroscopic, structural, and molecular information gathered for this work should provide new opportunities for exploring catalytic reactions driven by birnessite that are of great importance to nature and technology.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.0c02592.

• Reflection-mode XRD diffractograms; Mn 2p and Mn 3s XPS spectra; O(1s) spectrum; Mn 3s region; temperature-programmed desorption of water; evacuation of residual water from d-MnO2 and AcidBir in vacuum; molecular dynamics simulations of water intercalation in birnessite; radial distribution functions; and X-ray photoelectron spectroscopy results (PDF)

The authors declare no competing financial interest.