Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 15;37(4):1511–1520. doi: 10.1021/acs.langmuir.0c03050

Nucleotide Interaction with a Chitosan Layer on a Silica Surface: Establishing the Mechanism at the Molecular Level

Tetyana M Budnyak †,‡,*, Nataliya N Vlasova ‡, Lyudmila P Golovkova ‡, Olga Markitan ‡, Glib Baryshnikov §,∥, Hans Ågren §,#, Adam Slabon †
PMCID: PMC7880576  PMID: 33449701

Abstract

graphic file with name la0c03050_0009.jpg

The growing interest in gene therapy is coupled with the strong need for the development of safe and efficient gene transfection vectors. A composite based on chitosan and fumed silica has been found to be a prospective gene delivery carrier. This study presents an investigation of the nature of the bonds between a series of nucleotides with a chitosan layer deposited on a fumed silica surface. Experimentally measured surface complex formation constants (logK) of the nucleotides were found to be in the range of 2.69–4.02, which is higher than that for the orthophosphate (2.39). Theoretically calculated nucleotide complexation energies for chitosan deposited on the surface range from 11.5 to 23.0 kcal·mol–1, in agreement with experimental data. The adsorption of nucleotides was interpreted using their calculated speciation in an aqueous solution. Based on the structures of all optimized complexes determined from quantum-chemical PM6 calculations, electrostatic interactions between the surface-located NH3+ groups and −PO3H––/–PO32– fragments of the nucleotides were identified to play the decisive role in the adsorption mechanism. The saccharide fragment of monophosphates also plays an important role in the binding of the nucleotides to chitosan through the creation of hydrogen bonds.

1. Introduction

Gene therapy has proved to be an effective solution for most known diseases. The increased interest in gene therapy has called for proper materials to serve as safe and efficient gene transfection vectors.1 Among biopolymers, chitosan and its derivatives represent perspective materials for a large number of applications, especially in the pharmaceutical, environmental, and industrial fields.2−6 These biopolymers, originating from marine waste, have attracted much attention as nonviral vectors due to their valuable properties as well as a high positive charge density in low-pH solution localized on the primary amino groups. Deoxyribonucleic acid (DNA) plasmids are nonviral vectors that can be delivered to the target cells as naked DNA or in association with different compounds such as liposomes, gelatin, or polyamine nanospheres.7 Their positively charged character enables chitosan to bind with the negatively charged DNA and ribonucleic acid (RNA).8 These beneficial features give chitosan the capability as gene carriers.9,10 Some studies have reported the modification of chitosan to improve the transfection efficiency of chitosan formulations.11,12 However, the interaction mechanism between chitosan and DNA is still unclear at the molecular level.

It has been proved that the activity of chitosan could even be increased when it is part of organic–inorganic composites.13,14 Chitosan–silica composites deserve here special attention due to the complementary properties of silica toward polymers, e.g., resistance to the influence of microorganisms and high specific surface area.2,15−19

Defining the interaction of a chitosan–silica composite with a biological medium is an extremely complex task. This is due to the formation of many different-in-nature bonds, involving numerous groups of biomolecules and surface functional groups of chitosan and silica. The interaction of the composite surfaces with monomeric biomolecules—nucleotides, which are the structural units of nucleic acids—can serve as a subject for model studies. This work aims to study the adsorption of nucleotides from an aqueous solution onto chitosan–silica surfaces and to quantitatively estimate experimental data in terms of surface complexation theory. The study is supported by quantum-chemical calculations that provide an understanding of the impact and the nature of bonds between the nucleotides (heterocyclic base, saccharide, and phosphate groups) and chitosan.

2. Experimental Part

2.1. Materials

Chitosan (Sigma Aldrich, no. 417963; molecular weight from 190 to 370 kDa, degree of deacetylation not less than 75%, and solubility of 10 g·L–1) and fumed silica (specific surface area of 150 m2·g–1, obtained from State Enterprise “Kalush Test Experimental Plant of Institute of Surface Chemistry of National Academy of Sciences of Ukraine”) were used for the synthesis. Nucleotides as sodium salts (adenosine-5′-monophosphate (Reanal), adenosine-5′-diphosphate (Alfa Aesar), adenosine-5′-triphosphate (Alfa Aesar), guanosine-5′-monophosphate (Reanal), inosine-5′-monophosphate (Sigma Aldrich), cytidine-5′-monophosphate (Reanal), uridine-5′-monophosphate (Reanal), and orotidine-5′-monophosphate (Sigma Aldrich)), sodium dihydrophosphate (Merck), and sodium chloride (Merck) were used without additional purification. The standard solutions of HCl and NaOH (Titrisol, Merck) were used for pH adjustment.

2.2. Synthesis of the Chitosan–Fumed Silica Composite

The chitosan–silica composite was synthesized under a technique reported in our previous study.20 Briefly, 10 g of fumed silica (A150) was impregnated with 100 mL of 1% chitosan solution in 2% acetic acid and stirred for a day. The obtained sample was dried at 50 °C overnight.

2.3. Potentiometric Titration

Potentiometric titration of the chitosan–silica composite suspension (1 g·L–1) with an acid and base was performed at 20 °C (±1 °C) in gas-tight 50 mL centrifuge tubes (Falcon) in a thermostated water bath shaker. To each centrifuge tube, 0.02 g of composite and 20 mL of 0.01 M NaCl solution were placed, and then some amounts of HCl or NaOH solutions were added. After 24, 48, and 72 h of shaking, the pH values were measured using an Inolab Level 2P pH meter (WTW) equipped with a combination electrode (SenTix81) and temperature probe. The electrode was calibrated using three-point calibration with commercial pH buffers (CertiPur, Merck) to a precision of pH 0.02 units. It was found that acid–base equilibrium was achieved in 48 h. Electrode readings were taken when a drift of less than 0.002 pH units in 10 min was attained.

2.4. Sorption Experiments

Nucleotide adsorption was studied at 20 °C (±1 °C). To each centrifuge tube, 0.02 g of composite and 20 mL of 0.1 mmol·L–1 nucleotide solution (in 0.01 M NaCl) were placed. The pH was adjusted to the desired value between 2 and 9 with HCl or NaOH solutions. All suspensions were stirred for 2 days, the final pH was measured, and then the solid phase was separated by centrifugation (8000 rpm, 10 min). It was preliminarily found that 2 days was a sufficient time to reach adsorption equilibrium. Nucleotide concentrations were determined from the UV absorption spectra (Specord M40 spectrophotometer, Carl Zeiss Jena). All components were characterized by the absorption bands near 260 nm. The pH dependencies of the positions and intensities of the bands were determined beforehand. Orthophosphate concentrations in the solutions were determined as phosphoric molybdenum blue using a Phosphate Test reagent kit (Spectroquant, Merck).

The amounts of adsorbed nucleotides and phosphates (as % of adsorption) were calculated as the difference between initial and equilibrium concentrations. Experimental adsorption values are shown in the figures as symbols, and the calculated adsorption curves are shown as lines. The effect of initial AMP, ADP, and ATP nucleotide concentration on the adsorption capacity of the composite surface was studied in acidic media (pH 3.5) in the range of initial nucleotide concentration from 0.02 to 0.5 mmol·L–1.

Langmuir, Freundlich, and Temkin isotherm models were applied to analyze the adsorption of ATP by chitosan deposited on the silica surface. The linear form of the Langmuir model is21

2.4.

where ce is the equilibrium concentration of molecules (mmol·L–1), qe is the amount of the adsorbed molecules (mmol·g–1), and q0 and KL are the Langmuir constants related to the adsorption capacity (mmol·g–1) and the equilibrium constant (L·mg–1), respectively.

The Freundlich model is22

2.4.

where KF and n are the Freundlich constants related to the sorption capacity and the sorption intensity, respectively.

The Temkin model is

2.4.

where cs is the concentration of the molecule in the solid phase (mol·g–1), KT is the model constant (L·g–1), R is the gas constant (8.314 J·mol–1·K–1), T represents the absolute temperature (K), and ceq denotes the equilibrium concentration of molecules (mol·L–1) in the aqueous phase.

2.5. Model Calculations

The basic Stern surface complexation model23 and GRFIT software24 were used for the quantitative interpretation of experimental data. The GRFIT program is very convenient because the fitting of adjustable parameters is accompanied by a graphic drawing of an adsorption curve, from which one can immediately judge how successful the choice of reaction equations and initial values of the adjustable parameters is. The first step of the work was to choose the components of the solution, solid, and charge on different planes of the interface. The components of the solution were the initial species of a biomolecule, a proton, and electrolyte ions. The surface components are considered to be an initial amino group of chitosan (≡S—NH2) and the electrical components (exp0 and exp1), which correspond to the values of the charges of the species in the 0 and 1 planes of the interface. They were expressed as coefficients of the potentials at the respective planes of the electric double layer (EDL). The next step is a creation of a matrix in which the species present in the solution (all forms of biomolecules other than the initial one) and surface species (neutral and protonated amino groups of chitosan), ion pairs with background electrolyte ions, and surface complexes with biomolecules were defined as combinations of components. It should also be noted that the program requires knowledge of the characteristics of a solid, i.e., the specific surface area and concentration of functional groups or site density. The concentration of functional groups can be set as an adjustable parameter or is selected on the basis of data.

2.6. Quantum-Chemical Calculations

To help explain the mechanism of nucleotide adsorption on the chitosan–silica composite, quantum-chemical calculations were employed. A model chitosan–silica substrate was chosen as a fragment of a chitosan chain containing four elementary units, one acetyl (CH3CO–) group, and one protonated amino (−NH3+) group. The edge −CH2–O– vacancies were terminated by methyl groups (i.e., −CH2–OCH3). The whole substrate model was considered as a positively charged (1+) cation (denoted next as Ch+). The nucleotide species were simulated following the structures in Table 1. Optimization of individual chitosan fragment, nucleotide species, and their complexes was performed by the semiempirical PM6 method,25 accounting for the solvent effect (water) employing the polarizable continuum model (PCM).26 The cationic chitosan fragment was optimized first (an optimized structure is presented in the Supporting Information). After that, we optimized each nucleotide presented in Table 1 (optimized geometries are also presented in the Supporting Information). The initial structures for the optimization of nucleotides were taken from the sample database of the GaussView 6 program.27 For PM6-optimized structures, we checked the localization of positive and negative charges responsible for electrostatic interaction between the chitosan fragment and the nucleotide. We have found that positive charge in the chitosan fragment is predominantly localized on the protonated amino group (i.e., on the −NH3+ group), while the negative charge in the nucleotides is localized on the phosphate fragments (even when considering the neutral nucleotides, the phosphate groups possess partially negative charge). Thus, we constructed initial chitosan–nucleotide complexes to provide the best electrostatic interaction between the positively and negatively charged sides of chitosan and nucleotide counterparts. Several other initial structures of chitosan–nucleotide dimers were tested, but all of them finally relaxed into the structures presented in the Supporting Information, meaning that these structures are the most energetically favorable ones.

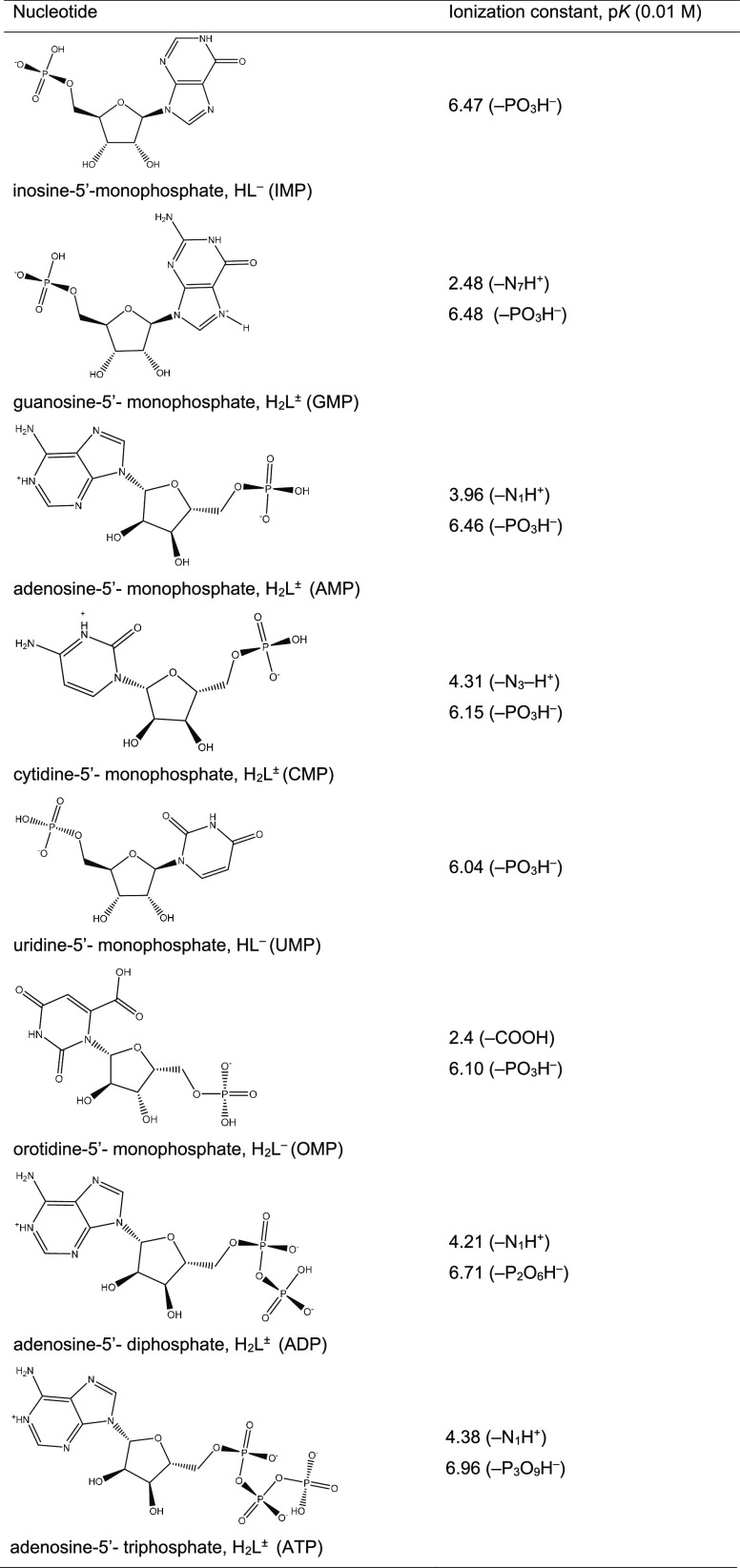
Table 1. Ionization Constants of Nucleotides.

2.6.

Open in a new tab

The silica–chitosan interface was not considered in this paper computationally, while only chitosan–nucleotide interactions were described. Calculated complexation energies correlate well with experimental complex formation constants. It means that silica–chitosan interactions are similar (i.e., nonspecific) for all considered chitosan–nucleotide complexes, but such a limitation of the model is systematic and does not affect the general conclusions on the chitosan–nucleotide binding mechanism.

For all optimized structures, the vibrational frequencies were calculated. No imaginary frequencies were found in the simulated vibrational spectra, meaning that the optimized structures correspond to real energy minima on the potential energy surface of the singlet ground electronic state. Complexation energies (Ecom) were calculated by the direct method, accounting for zero-point energy (EZPE) correction

2.6.

where E0 denotes the total energy of the corresponding complex (Ch+HnLm–) and the individual [Ch+] and [HnLm–] counterparts. All the calculations were performed using the Gaussian 16 software.28

3. Results and Discussion

3.1. Synthesis and Characterization of the Chitosan–Silica Material

Chitosan combined with an inorganic oxide such as silica could have the potential for concentrating molecules of different nature: extended specific surface, accessibility of functional groups, and thermal stability.13,14,20 The impregnation of fumed silica with a slightly acidic chitosan solution is a rapid, effective, and sustainable way of composite preparation. This approach of composite processing is in agreement with the principles of Green Chemistry.29,30 The synthesized composite belongs to a hybrid material of class I, where the organic (chitosan) and inorganic (silica) parts are combined through weak interactions, such as hydrogen bonds between the amine, acetamid, or hydroxyl groups of the biopolymer and silanol groups of silica or electrostatic forces between protonated amino groups and dissociated hydroxyl groups.14,31−33

A detailed characterization of the chitosan–silica composite was accomplished in our previous work.20 The chitosan layer on the silica surface was confirmed by the characteristic bands in the FTIR spectra of the composite (Figure S1): 1640–1548 cm–1: ν(C=O) in NHCOCH3, amid I; 1600–1400 cm–1: δ(N–H) in NH3+; 1420 cm–1: δ(CH2) in CH2OH; 1380 cm–1: δs(CH3) in NHCOCH3; along with the bands related to the silica-based materials: 1097, 967 cm–1: ν(Si–O) of Si–O–Si; 810 cm–1: δ(Si–O) of Si–O–Si (Table S1). Based on the results of thermogravimetrical analysis (Figure S2), the concentration of chitosan in the composite is 100 mg·g–1 (10%). This serves as an additional confirmation for a high yield (close to 100%) of the composite material. As this is well correlated with the mass ratio of pristine chitosan and fumed silica used for synthesis, it can be assumed that the Atom Economy principle of Green Chemistry was successfully achieved.30 The main thermal parameters and decomposition regions determined from TG and DTG curves are summarized in Table S2. According to the SEM micrographs, the synthesized composite is characterized by a homogeneous overlayer of chitosan (Figure S3). The relatively high specific surface area (170 m2·g–1) for a biopolymer-based hybrid material and its mesoporosity with an average diameter of pores around 30 nm make it reasonable to assume that the material can be successfully applied as a carrier for a concentration of even relatively large organic molecules (Figure S4). The high potential as a sorbent from aqueous solutions is also confirmed by its good stability in acidic conditions according to the conducted tests.20

3.2. Chitosan Surface Basicity

Chitosan is a partially deacetylated derivative of chitin, a naturally occurring amino polysaccharide.34,35 Chitosan is a linear copolymer of 2-acetoamido-2-deoxy-β-d-glucopyranose and 2-amino-2-deoxy-β-d-glucopyranose (Scheme S1). Due to the presence of a primary amine on the glucosamine residues, which can be protonated in a wide range of pH, chitosan behaves in an aqueous solution as a cationic polyelectrolyte. The acid–base properties of chitosan as a function of the degree of deacetylation, molecular weight, and ionic strength have been investigated by several groups.36−39 The protonation constants (logK) of chitosan in an aqueous solution vary from 6.3 to 7.3 depending on the degree of deacetylation and the molecular weight of the polymer. It can be assumed that chitosan attached to the surface of silica retains its ability to attach protons. According to surface complexation theory,40−42 the charging of composite surfaces as a result of their interaction with protons of an aqueous solution gives rise to an electrical double layer. This affects the complexation reactions with inorganic and organic molecules. Surface complexation models have been successfully used to describe the binding of protons and chemical species by active groups of oxide surfaces. As far as we know, the principles of surface complexation theory have not previously been used to quantify acid–base and adsorption properties of polymers attached to the surface of a carrier. Regardless, the study of the adsorption interaction of organic or inorganic compounds dissolved in water must be preceded by a detailed investigation of the protolytic properties of the polymer surface groups.23,40−42

We assumed that the surface charge of the composite under investigation is determined by the interaction of chitosan’s primary amino groups with protons. We therefore treated the potentiometric titration data of the composite as adsorbed proton concentrations as dependence of pH

3.2.

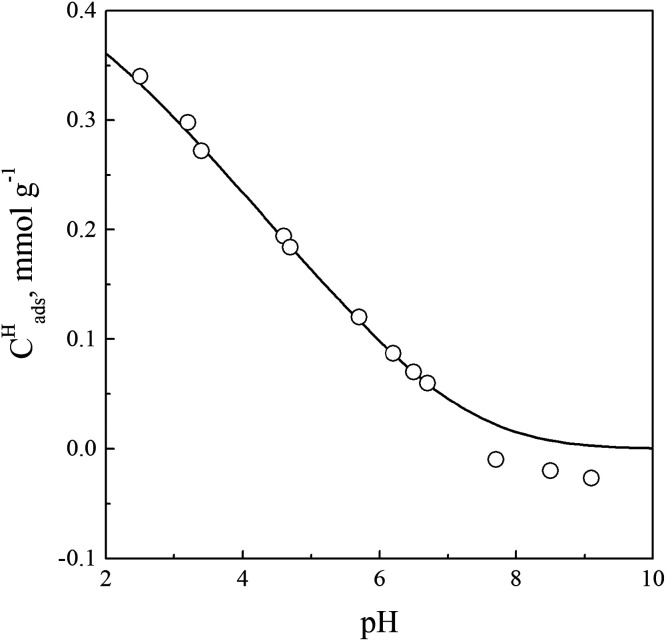
where CHCl and CNaOH are the concentrations of the added acid and base, and [H+] and [OH–] are the equilibrium proton (measured as pH) and hydroxyl concentrations. These data are presented in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Concentrations of protons adsorbed on a chitosan–composite surface as a function of pH: Ccomp = 1 g·L–1, 0.01 M NaCl. Symbols are the experimental data, and the full line is the calculated curve.

These experimental data were used for surface complexation modeling to estimate the deprotonation constant of chitosan protonated amino groups according to the following reaction:

3.2.
3.2.

where [S–NH2] and [S–NH3+] are the equilibrium concentrations of neutral and protonated chitosan amino groups (mol·L–1), Ψ0 is the potential of plane 0 of the electric double layer, F is the Faraday constant (96,485 C/mol), R is the universal gas constant, and T is the temperature (K).

First, we used the diffuse double layer model23,41 and GRFIT software for fitting of the surface site density and the deprotonation constant, leading to the following values: the surface site density is 0.4 mmol·g–1 and logKSH = −6.93 ± 0.05. The concentration of active groups on the surface, calculated on the basis of the amount of chitosan, the average molecular weight of the monomer unit, and the degree of deacetylation of 75%, is 0.4 mmol·g–1. The deprotonation constant of the protonated amino groups is comparable with these constants obtained for chitosan in an aqueous solution.37−39

Subsequently, we used these values for fitting of the capacitance of the electric double layer with the constant capacitance model,23,40,42 which is related to surface charge (σ0) and surface potential (Ψ0)

3.2.

to obtain C1 = 0.9 F·cm–2. All these values are required for modeling of acid–base and adsorption properties of immobilized chitosan with the basic Stern model (BSM).23 The latter makes it possible to distinguish inner- and outer-sphere complexes. According to this model, the interface is divided into two regions: the compact region (extending up to several angstroms from surface) and the diffuse one, where the counterions accumulate to compensate the surface charge (Figure 2). The compact region involves two charged planes: the surface (or plane 0) of the active surface groups and the head end of the diffuse layer of the interface (or plane 1). Potential-determining ions are adsorbed in one of them (zero plane), while weakly bound counterions are adsorbed in another plane (plane 1). These counterions form electrostatic outer-sphere complexes (or ions pairs) with the surface groups of opposite charge.

Figure 2.

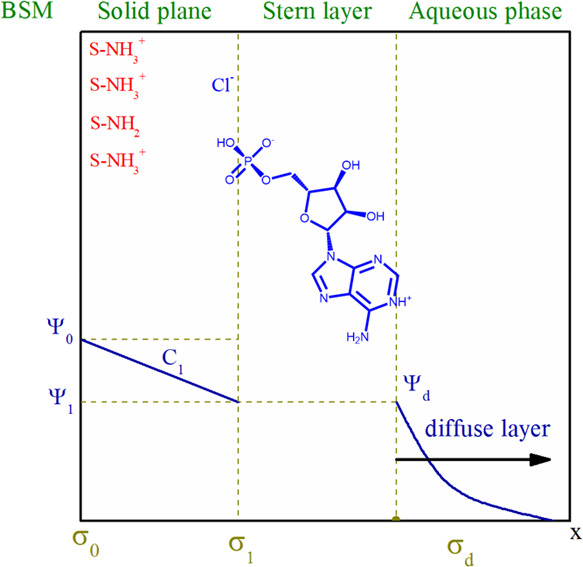
Figure 2

Open in a new tab

Structure of the electrical double layer (BSM) at the chitosan–silica/aqueous electrolyte solution interface: Ψ is the potential, σ is the surface charge, and charge symbols of σ0 and σ1 correspond to planes 0 and 1, respectively.

Thus, we should take into account the interaction of protonated amino groups of chitosan with electrolyte anions according to the reaction

3.2.

which is characterized by the following constant

3.2.

where Ψ0 and Ψ1 are the potentials in planes 0 and 1, respectively. The fitting of experimental potentiometric data with all obtained values of surface site density, deprotonation constant, and capacitance of EDL gives the ion pair formation constant logKSCl = 1.35 ± 0.05. In Figure 1, the calculated curve is shown as a line. It should be noted that this calculated line is in good agreement with experimental data. In the region of pH > 7, small negative charge values are observed. Most likely, ionization of silanol groups of silica used as a substrate is manifested in this region. It is difficult to quantify the contribution of the ionization of silanol groups since their exact concentration is unknown. The further calculations, studying the nucleotide adsorption, we have neglected the possible ionization of the silanol groups.

3.3. Nucleotide Adsorption

The interaction of nucleotides with the surface of the chitosan–silica composite in an aqueous electrolyte solution was interpreted as the formation of adsorption complexes. To select possible complexation reactions, it is necessary to take into account not only the state of the functional groups of the solid but also the forms in which the solutes being adsorbed are present in solution depending on pH. Nucleotides consist of a heterocyclic base (purine or pyrimidine), in which a hydrogen atom at one of the nitrogen atom (N-1 for pyrimidine or N-9 for purine bases) is replaced by a phosphorylated carbohydrate residue. Apart from the common bases adenine and guanine (purine) and cytosine and uracil (pyrimidine), nucleic acids may contain the “minor” base hypoxanthine (the corresponding nucleotide is inosine phosphate) and orotic acid (nucleotide is orotidine phosphate). All these nucleotides were tested at the adsorption study from an aqueous solution.

The structures of the studied nucleotides as monophosphates and their ionization constants are presented in Table 1. Considering the acid–base properties of the nucleotides in more detail, we note that the phosphate groups in the nucleoside monophosphates are characterized by two ionization constants: the primary group dissociates at pH < 2, while the secondary one is ionized at pH > 6.43,44 In the studied purine and pyrimidine nucleotides, nitrogen atoms of the heterocyclic ring differ significantly in their basicity. Proton releases from the N1–H+ group of adenosine-5′-monophosphate and from N3–H+ of cytidine-5′-monophosphate occur at pH ≈ 4. The deprotonation of the N7–H+ group of guanosine-5′-monophosphate is observed at pH > 2.3, while the N7 nitrogen atom of inosine-5′-monophosphate is protonated in a highly acidic solution. The pyrimidine heterocycle of orotidine-5′-monophosphate contains an additional carboxyl group, which is ionized at pH > 2.4.

All these acid–base properties of the nucleotides under investigation are reflected in the solution speciation diagrams presented in Figure 3. The solution speciations show in which forms, depending on pH, the studied nucleotides are present in the solution. At pH 2, initial forms of AMP and CMP are zwitterionic (NH+ and PO3H–). The fraction of zwitterions for GMP is smaller due to the lower value of the deprotonation constant of the N7–H+ group in comparison with these values for AMP and CMP. The initial forms of IMP and UMP are monoanionic. In an acid solution, the OMP exists as a dianion due to ionization of the additional carboxyl group (COO– and PO3H–). The initial forms of adenosine-5′-diphosphate and triphosphate are doubly and triply charged anions, respectively. With increasing pH, further ionization of the initial forms is observed with the formation of the corresponding anions with higher charges.

Figure 3.

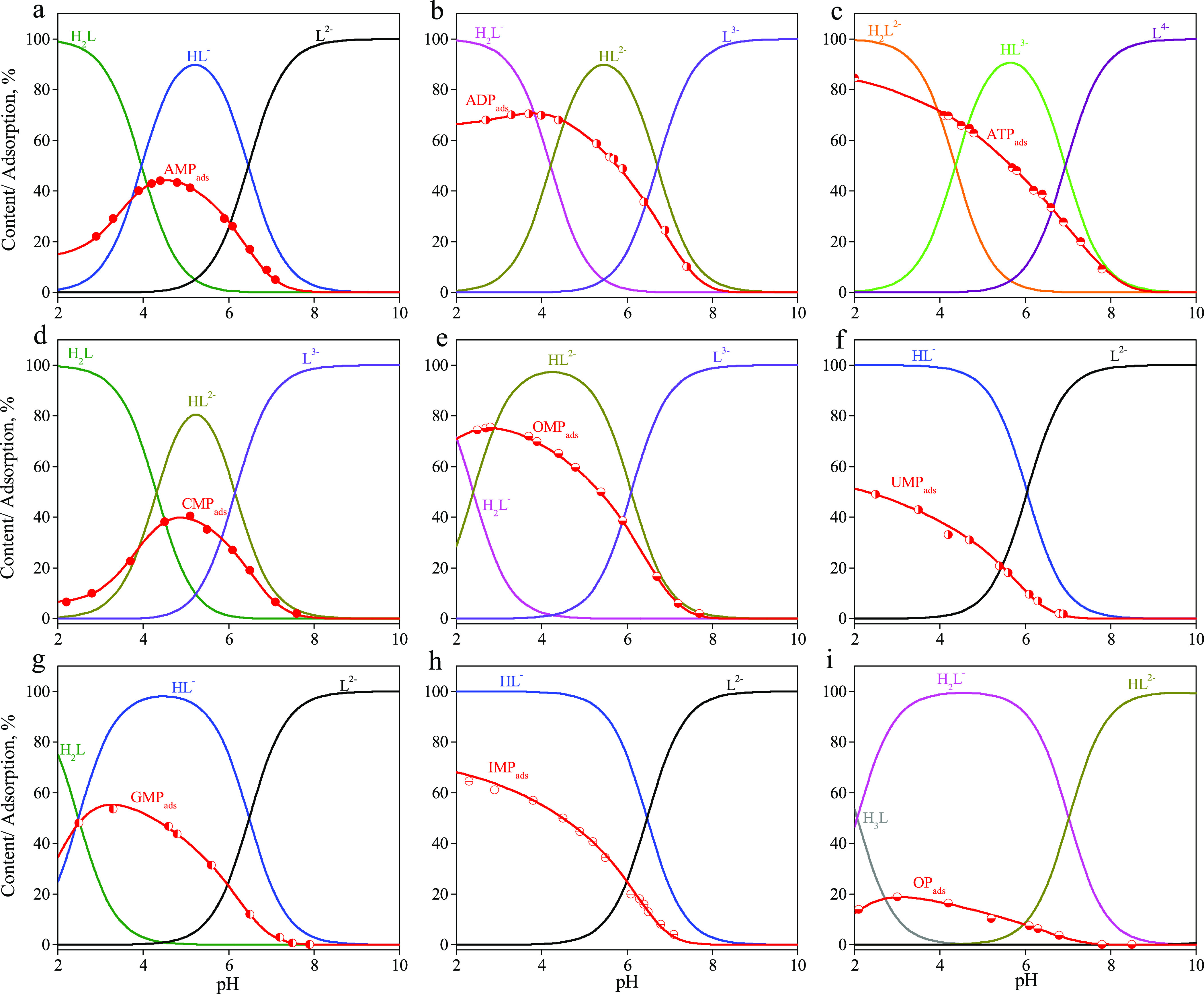
Figure 3

Open in a new tab

Solution speciations and adsorption curves of nucleotides: (a) AMP, (b) ADP, (c) ATP, (d) CMP, (e) OMP, (f) UMP, (g) GMP, (h) IMP, and (i) OP. Csorbate = 0.1 mmol·L–1 and Ccomposite = 1 g·L–1. Symbols are the experimental adsorption data, and lines are the calculated adsorption curves.

Adsorption of all nucleotides from 0.01 M NaCl solution was studied as a function of pH (Figure 3). The adsorption of all nucleotides decreases with increasing pH. The adsorption curves of AMP, GMP, and CMP pass through a maximum whose position on the pH scale corresponds to the ionization constant of the zwitterion. The presence of anionic forms of nucleotides in solutions suggests that the main contribution to the adsorption on the composite surface comes from the electrostatic interaction with positively charged amino groups of chitosan according to

3.3.
3.3.

where HnLm– is the initial form of nucleotide, and n and m are dependent on the nature of nucleotides (for details, see Table 2).

Table 2. Experimentally Measured Surface Complex Formation Constants of Nucleotides and Orthophosphate (in logK Units) vs Theoretically Calculated Complexation Energies (Ecom).

nucleotide surface reactions logK ± 0.05 Ecom (kcal·mol–1)
AMP ≡S—NH3+ + H2L± ↔ ≡S—NH3 H2L± 3.18 –15.3
≡S—NH3+ + HL– ↔ ≡S—NH3 HL– 3.31 –15.4
CMP ≡S—NH3+ + H2L± ↔ ≡S—NH3 H2L± 2.96 –14.1
≡S—NH3+ + HL– ↔ ≡S—NH3 HL– 3.28 –14.0
GMP ≡S—NH3+ + HL– ↔ ≡S—NH3 HL– 3.22 –16.1
IMP ≡S—NH3+ + HL– ↔ ≡S—NH3 HL– 3.27 –16.6
UMP ≡S—NH3+ + HL– ↔ ≡S—NH3 HL– 2.69 –11.5
OMP ≡S—NH3+ + HL2– ↔ ≡S—NH3 HL2– 3.03 –16.6
ADP ≡S—NH3+ + H2L– ↔ ≡S—NH3 H2L– 3.21 –16.1
≡S—NH3+ + HL2– ↔ ≡S—NH3 HL2– 3.52 –20.8
ATP ≡S—NH3+ + H2L2– ↔ ≡S—NH3 H2L2– 3.38 –22.9
≡S—NH3+ + HL3– ↔ ≡S—NH3 HL3– 4.02 –23.0
OP ≡S—NH3+ + H2L– ↔ ≡S—NH3 H2L– 2.39 –12.0
Open in a new tab

The modeling of the acid–base properties of solid and adsorption curves with the GRFIT program begins with a matrix of components. This interaction leads to the formation of all species in the systems. The active surface sites of the solid, protons, an adsorbate, and background electrolyte ions are among the material components. The matrix of components is supplemented with exp0 and exp1 electric components corresponding to the particle charge in planes 0 and 1, respectively. It is important to choose an appropriate initial form of the adsorbate because any form of nucleotide present in the solution can be chosen as the initial one. The surface complexation reactions and their equilibrium constants may be written in a different manner depending on the choice of an initial particle. The best agreement between experimental data and calculated adsorption curves was achieved for complex formation reactions presented in Table 2. These calculated adsorption curves for all nucleotides are shown in Figure 3 as solid lines connected to experimental points.

The nucleotide anions and zwitterions (of AMP and CMP only) form outer-sphere electrostatic complexes with protonated amino groups of chitosan. The values of the complex formation constants of the singly charged anion of all nucleotides are almost the same regardless of the nucleotide nature. This can be explained by the fact that a phosphate group of the nucleotides takes part in the electrostatic interaction. The protolytic properties are practically the same for all nucleotides. The higher the charge of an anion forming a complex with a protonated group, the higher the stability constant of the complex, a regularity that is typical for electrostatic interactions. Therefore, ATP complexes are stronger than AMP complexes. The same observation was made in the study by De Stefano et al.45 devoted to the interaction of ATP and AMP with chitosan in an aqueous solution.

The orthophosphate (OP) adsorption on the surface of the chitosan–silica composite was studied for comparison with the nucleotides. As can be seen from Table 2, the complex formation constant of the orthophosphate monoanion is much smaller than the nucleotide constants. This indicates that not only the phosphate group determines the strength of the nucleotide binding to the surface but it also seems that the heterocyclic base and saccharide can form other types of bonds.

Indeed, as follows from our quantum-chemical PM6 calculations, the saccharide fragment forms quite short H-bonds with the chitosan substrate (Ch+, Figure 4), while the heterocyclic bases are quite far from the chitosan surface and do actually not interact with it. We also observe a clear correlation between the experimentally estimated complex formation constant and calculated complexation energies (Table 2). We find that the OP and UMP species demonstrate the smallest complex formation constants (logK = 2.39 and 2.69, respectively) and smallest calculated complexation energies (Ecom = −12.0 and −11.5 kcal·mol–1). Multicharged nucleotides, like ADP in HL2– form, ATP in HL3– form, and ATP in HL2– form, generally demonstrate higher complex formation constants (logK = 3.52, 3.38, and 4.03) than the zwitterionic and anionic nucleotides (logK varies within the short range of 2.69–3.31). Such a trend is also reproduced in our PM6 calculations—complexation energies are the highest for ADP in HL2– form (−20.8 kcal·mol–1), ATP in HL3– form (−23.0 kcal·mol–1), and ATP in HL2– form (−22.9 kcal·mol–1). This is due to the stronger electrostatic interaction between the positive charge localized on the −NH3+ group of the Ch+ substrate model and multiple negative charges localized on the phosphate groups of the studied nucleotides (Figure 4). An exception is the OMP dianion where the complex formation constant is quite small (logK = 3.03) as well as the calculated Ecom value being in a moderate region (−16.6 kcal·mol–1). This is because OMP possesses a two-center dianionic structure in which one negative charge is localized on the PO3H– group, while the second one is localized on the COO– moiety. The latter does not directly interact with the chitosan substrate (Figure 4). For the remaining monoanionic and zwitterionic nucleotides, a calculated complexation energy varied only within the range of −11.5 to −16.6 kcal·mol–1, in agreement with experimental observations (logK = 2.69–3.31).

Figure 4.

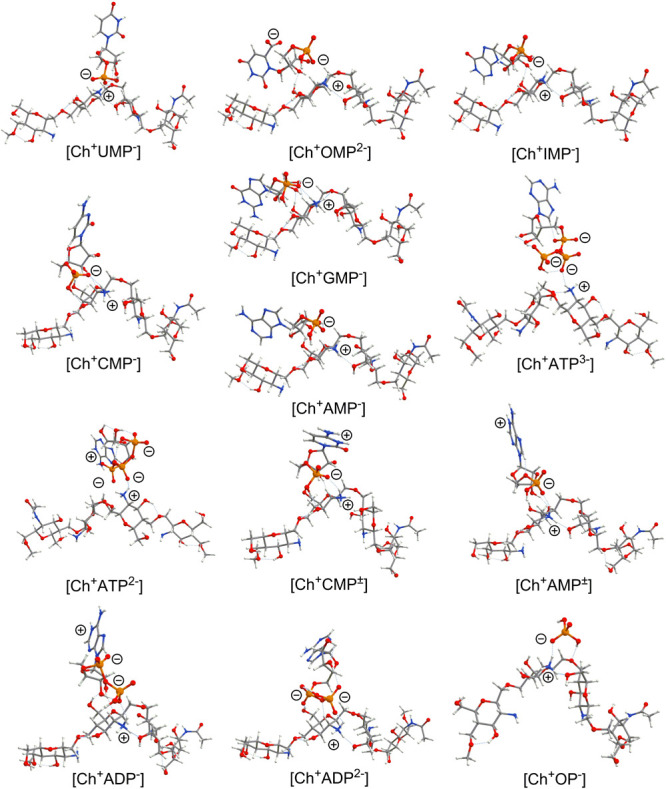
Figure 4

Open in a new tab

PM6 method-optimized structures of chitosan–nucleotide complexes. Predominant localizations of positive and negative charges are also marked for each complex.

The analysis of the structures for all optimized complexes reveals that for all monophosphates (OMP, UMP, CMP, AMP, GMP, and IMP) and for the only one diphosphate (ADP in monoanionic form), the saccharide fragment plays an important role in the binding of the nucleotides to the chitosan surface. For the dianionic ADP and both studied triphosphates (ATP in HL3– and HL2– forms), the saccharide unit is far from the chitosan substrate and does not directly interact with it (Figure 4). This fact additionally confirms the key role of the electrostatic interactions between the surface-located NH3+ groups and −PO3H––/–PO32– fragments of the nucleotides in the adsorption mechanism of ADP (HL2–) and ATP (HL2– and HL3–) nucleotides.

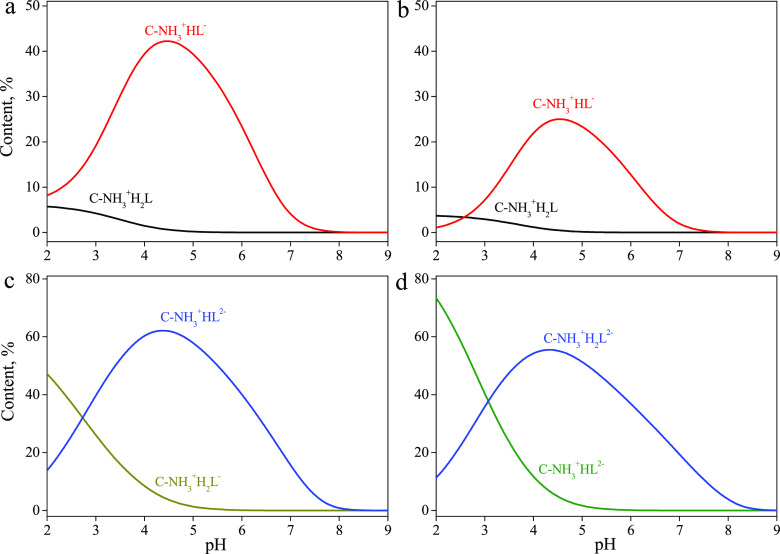
The adsorption of most of the studied nucleotides is determined by the formation of one surface complex. Figure 5 shows distribution diagrams of the surface complexes of those nucleotides forming two surface species. The concentrations of the complexes containing the zwitterionic forms of AMP and CMP are significantly lower than those of the anionic complexes. The content of the complexes of the various anions of ADP and ATP in the surface layer is determined by their distribution in the aqueous solution.

Figure 5.

Figure 5

Open in a new tab

Distribution diagrams of complexes of (a) AMP, (b) CMP, (c) ADP, and (d) ATP formed on the surface of chitosan-containing silica.

We carried out a study of the adsorption isotherms of adenine nucleotides with different phosphate chain lengths. Since it was assumed that the phosphate groups are involved in the formation of electrostatic bonds with the protonated amino groups of chitosan, it was relevant to compare the adsorption isotherms of adenosine mono-, di-, and triphosphates. The pH-adsorption edges of these phosphates and the calculated complexation constants indicate that the stability of the surface complexes enhances with an increase in the anion charge. Adsorption isotherms are well described by the Langmuir equation (R2 higher than 0.99). The nucleotide binding constants increase in the series AMP < ADP < ATP; they practically coincide with the surface complex formation constants calculated by the Stern model (Table 2). The maximum adsorption values change in the opposite order AMP > ADP > ATP and do not exceed the surface site density of protonated groups of chitosan (0.4 mmol·g–1). It should be noted that the Langmuir constants are conditional since they are valid only for certain conditions, for example, pH. At the same time, the constants calculated within the framework of surface complexation theory can be used to estimate the adsorption values under conditions that differ from those used in the experiment; i.e., they allow calculation of the adsorption values for other pH values, ionic strengths, and adsorbate concentrations.

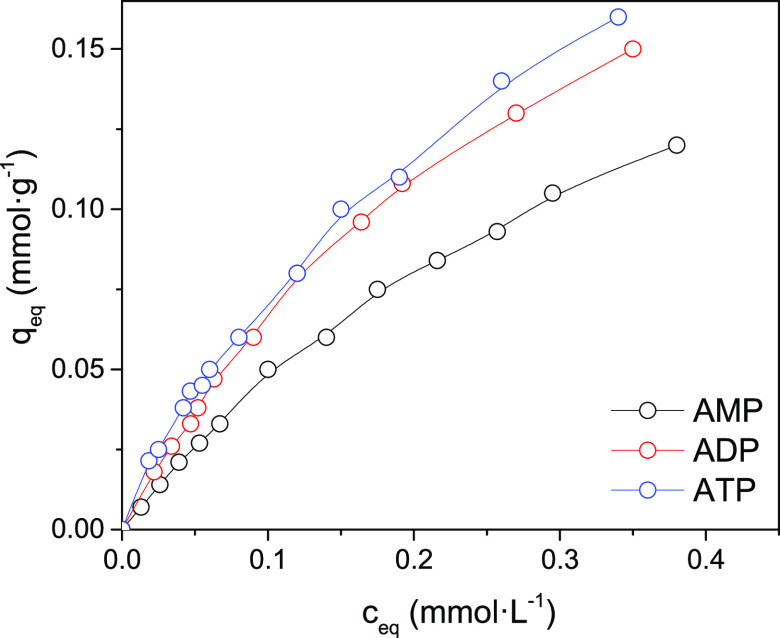
The isotherms of adsorption of AMP, ADP, and ATP nucleotides by the composite surface in acidic media (pH 3.5) are presented in Figure 6. Calculated parameters from the Langmuir, Freundlich, and Temkin isotherm models for the adsorption of AMP, ADP, and ATP nucleotides on a synthesized chitosan–silica composite are summarized in Table 3. Based on the obtained values of the correlation coefficient, Langmuir and Freundlich isotherm models are consistent with the experimental data for the chosen range of initial nucleotide concentrations. The monolayer capacities were found to be 0.324, 0.29, and 0.198 mmol·g–1 for the AMP, ADP, and ATP nucleotides, respectively. The heat of adsorption (bT) of ATP on the composite was found to be higher (140.9–134.7 kJ·mol–1) than for other complex organic molecules, for example, bile acids.20

Figure 6.

Figure 6

Open in a new tab

Isotherms of adsorption of AMP, ADP, and ATP by the chitosan–silica composite (concentration of composite, 1 g·L–1; pH 3.5).

Table 3. Langmuir, Freundlich, and Temkin Isotherm Model Parameters for Adsorption of AMP, ADP, and ATP by the Chitosan–Silica Composite (Concentration of Composite, 1 g·L–1; pH 3.5).

isotherm model parameter AMP ADP ATP
Langmuir q0, mol·g–1 0.324 0.290 0.198
KL, L·mol–1 1709 2947 6742
logK 3.23 3.47 3.83
R2 0.9998 0.9986 0.9926
Freundlich KF, mmol·g–1 1.70 1.70 1.78
n 1.014 1.058 1.154
1/n 0.987 0.945 0.866
R2 0.9546 0.9546 0.9497
Temkin bT, kJ·mol–1 140.9 139.4 134.7
KT, L·g–1 181.03 371.85 411.70
R2 0.2780 0.1657 0.1805
Open in a new tab

4. Conclusions

A composite based on chitosan and silica was found to be a prospective carrier for mono-, di-, and triphosphate nucleotides. The measured surface complex formation constants of the nucleotides were found to be higher than for the orthophosphate. These experimental observations were confirmed by high values of theoretically computed nucleotide complexation energies for chitosan deposited on the surface compared to the system chitosan:ortophosphate. It was determined from quantum-chemical PM6 calculations that the electrostatic interactions between the surface-located protonated amino groups and the negatively charged P-containing fragments of the nucleotides play a decisive role in their adsorption. In the case of nucleotides in the monoanionic form, the saccharide fragment could take part in the adsorption through creation of hydrogen bonds. These results demonstrate that chitosan–silica composites are highly promising materials as biocarriers in gene therapy.

Acknowledgments

T.M.B. acknowledges financial support from the ÅForsk Foun-dation (grant number 19-676). A.S. thanks the financial support from MISTRA (project: SafeChem). H.Å. and G.B. thank the support from Olle Engkvist Byggmästare Foundation (contract no. 189-0223). G.B. also thanks for the support from the Ministry of Education and Science of Ukraine (project no. 0117U003908). The quantum-chemical calculations were performed with computational resources provided by the High Performance Computing Center North (HPC2N) in Umeå, Sweden, through the project “Multiphysics Modeling of Molecular Materials” SNIC 2019/2-41.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.0c03050.

  • Scheme of chemical structure of chitosan; FTIR spectra; thermal analysis; SEM micrographs; surface area and average pore size measurements for the surface of the chitosan–silica composite; theoretical calculations and modeling (PDF)

The authors declare no competing financial interest.

Supplementary Material

la0c03050_si_001.pdf (498.1KB, pdf)

References

  1. Cao Y.; Tan Y. F.; Wong Y. S.; Liew M. W. J.; Venkatraman S. Recent Advances in Chitosan-Based Carriers for Gene Delivery. Mar. Drugs 2019, 17, 381. 10.3390/md17060381. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Varma A. J.; Deshpande S. V.; Kennedy J. F. Metal Complexation by Chitosan and Its Derivatives: A Review. Carbohydr. Polym. 2004, 55, 77–93. 10.1016/j.carbpol.2003.08.005. [DOI] [Google Scholar]
  3. Kumar M. N. V. R. A Review of Chitin and Chitosan Applications. React. Funct. Polym. 2000, 46, 1–27. 10.1016/S1381-5148(00)00038-9. [DOI] [Google Scholar]
  4. Babel S.; Kurniawan T. A. Low-Cost Adsorbents for Heavy Metals Uptake from Contaminated Water: A Review. J. Hazard. Mater. 2003, 97, 219–243. 10.1016/S0304-3894(02)00263-7. [DOI] [PubMed] [Google Scholar]
  5. Crini G. Recent Developments in Polysaccharide-Based Materials Used as Adsorbents in Wastewater Treatment. Prog. Polym. Sci. 2005, 30, 38–70. 10.1016/j.progpolymsci.2004.11.002. [DOI] [Google Scholar]
  6. Dodane V.; Vilivalam V. D. Pharmaceutical Applications of Chitosan. Pharm. Sci. Technol. Today 1998, 1, 246–253. 10.1016/S1461-5347(98)00059-5. [DOI] [Google Scholar]
  7. Ramamoorth M.; Narvekar A. Non Viral Vectors in Gene Therapy-an Overview. J. Clin. diagn. Res. 2015, 9, GE01. 10.7860/JCDR/2015/10443.5394. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Shen J.-W.; Li J.; Zhao Z.; Zhang L.; Peng G.; Liang L. Molecular Dynamics Study on the Mechanism of Polynucleotide Encapsulation by Chitosan. Sci. Rep. 2017, 7, 1–9. 10.1038/s41598-017-05197-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Mao S.; Sun W.; Kissel T. Chitosan-Based Formulations for Delivery of DNA and SiRNA. Adv. Drug Delivery Rev. 2010, 62, 12–27. 10.1016/j.addr.2009.08.004. [DOI] [PubMed] [Google Scholar]
  10. Lee M.-K.; Chun S.-K.; Choi W.-J.; Kim J.-K.; Choi S.-H.; Kim A.; Oungbho K.; Park J.-S.; Ahn W. S.; Kim C.-K. The Use of Chitosan as a Condensing Agent to Enhance Emulsion-Mediated Gene Transfer. Biomaterials 2005, 26, 2147–2156. 10.1016/j.biomaterials.2004.07.008. [DOI] [PubMed] [Google Scholar]
  11. Shu X. Z.; Zhu K. J. The Influence of Multivalent Phosphate Structure on the Properties of Ionically Cross-Linked Chitosan Films for Controlled Drug Release. Eur. J. Pharm. Biopharm. 2002, 54, 235–243. 10.1016/S0939-6411(02)00052-8. [DOI] [PubMed] [Google Scholar]
  12. Gao Y.; Xu Z.; Chen S.; Gu W.; Chen L.; Li Y. Arginine-Chitosan/DNA Self-Assemble Nanoparticles for Gene Delivery: In Vitro Characteristics and Transfection Efficiency. Int. J. Pharm. 2008, 359, 241–246. 10.1016/j.ijpharm.2008.03.037. [DOI] [PubMed] [Google Scholar]
  13. Blachnio M.; Budnyak T. M.; Derylo-Marczewska A.; Marczewski A. W.; Tertykh V. A. Chitosan-Silica Hybrid Composites for Removal of Sulfonated Azo Dyes from Aqueous Solutions. Langmuir 2018, 34, 2258–2273. 10.1021/acs.langmuir.7b04076. [DOI] [PubMed] [Google Scholar]
  14. Budnyak T. M.; Blachnio M.; Slabon A.; Jaworski A.; Tertykh V. A.; Derylo-Marczewska A.; Marczewski A. W. Chitosan Deposited onto Fumed Silica Surface as Sustainable Hybrid Biosorbent for Acid Orange 8 Dye Capturing: Effect of Temperature in Adsorption Equilibrium and Kinetics. J. Phys. Chem. C 2020, 124, 15312–15323. 10.1021/acs.jpcc.0c04205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Vakili M.; Rafatullah M.; Salamatinia B.; Abdullah A. Z.; Ibrahim M. H.; Tan K. B.; Gholami Z.; Amouzgar P. Application of Chitosan and Its Derivatives as Adsorbents for Dye Removal from Water and Wastewater : A Review. Carbohydr. Polym. 2014, 113, 115–130. 10.1016/j.carbpol.2014.07.007. [DOI] [PubMed] [Google Scholar]
  16. Ngah W. S. W.; Teong L. C.; Hanafiah M. a. K. M. Adsorption of Dyes and Heavy Metal Ions by Chitosan Composites: A Review. Carbohydr. Polym. 2011, 83, 1446–1456. 10.1016/j.carbpol.2010.11.004. [DOI] [Google Scholar]
  17. Julkapli N. M.; Akil H. M.; Ahmad Z. Preparation , Properties and Applications of Chitosan-Based Biocomposites / Blend Materials : A Review. Compos. Interfaces 2011, 18, 449–507. 10.1163/156855411X610232. [DOI] [Google Scholar]
  18. El-sherbiny I. M.; El-baz N. M.. A Review on Bionanocomposites Based on Chitosan and Its Derivatives for Biomedical Applications. In Eco-friendly Polymer Nanocomposites; Springer: 2015. 10.1007/978-81-322-2473-0. [DOI] [Google Scholar]
  19. Kyzas G.; Bikiaris D. Recent Modifications of Chitosan for Adsorption Applications: A Critical and Systematic review. Mar. Drugs 2015, 312–337. 10.3390/md13010312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Budnyak T. M.; Vlasova N. N.; Golovkova L. P.; Slabon A.; Tertykh V. A. Bile Acids Adsorption by Chitoan-Fumed Silica Enterosorbent. Colloid Interface Sci. Commun. 2019, 32, 100194. 10.1016/j.colcom.2019.100194. [DOI] [Google Scholar]
  21. Langmuir I. The Constitution and Fundamental Properties of Solids and Liquids. Part I. Solids. J. Am. Chem. Soc. 1916, 38, 2221–2295. 10.1021/ja02268a002. [DOI] [Google Scholar]
  22. Freundlich H. Über Die Adsorption in Lösungen. Z. Phys. Chem. 1907, 57U, 385. 10.1515/zpch-1907-5723. [DOI] [Google Scholar]
  23. Westall J.; Hohl H. A Comparison of Electrostatic Models for the Oxide/Solution Interface. Adv. Colloid Interface Sci. 1980, 12, 265–294. 10.1016/0001-8686(80)80012-1. [DOI] [Google Scholar]
  24. Ludwig C.GRFIT, a Program for Solving Speciation Problems: Evaluation of Equilibrium Constants, Concentrations and Other Physical Parameters; Internal Report of Univ. of Bern, 1992. [Google Scholar]
  25. Stewart J. J. P. Optimization of Parameters for Semiempirical Methods V: Modification of NDDO Approximations and Application to 70 Elements. J. Mol. Model. 2007, 13, 1173–1213. 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Miertuš S.; Scrocco E.; Tomasi J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilizaion of AB Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981, 55, 117–129. 10.1016/0301-0104(81)85090-2. [DOI] [Google Scholar]
  27. Dennington R.; Keith T. A.; Millam J. M. GaussView. Version 6.1. Semichen Inc., Shawnee Mission, KS 2016.
  28. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016. [Google Scholar]
  29. Anastas P. T.; Zimmerman J. B. Peer Reviewed: Design through the 12 Principles of Green Engineering. Environ. Sci. Technol. 2003, 95A–101A. [DOI] [PubMed] [Google Scholar]
  30. Anastas P. T.; Warner J. C.. Green Chemistry: Theory and Practice; Oxford University Press: New York, 1998. [Google Scholar]
  31. Puchol V.; El Haskouri J.; Latorre J.; Guillem C.; Beltran A.; Beltran D.; Amoros P. Biomimetic Chitosan-Mediated Synthesis in Heterogeneous Phase of Bulk and Mesoporous Silica Nanoparticles. Chem. Commun. 2009, 19, 2694–2696. [DOI] [PubMed] [Google Scholar]
  32. Zou H.; Wu S.; Shen J. Polymer/Silica Nanocomposites: Preparation, Characterization, Properties, and Applications. Chem. Rev. 2008, 108, 3893–3957. 10.1021/cr068035q. [DOI] [PubMed] [Google Scholar]
  33. Chassary P.; Vincent T.; Guibal E. Metal Anion Sorption on Chitosan and Derivative Materials: A Strategy for Polymer Modification and Optimum Use. React. Funct. Polym. 2004, 60, 137–149. 10.1016/j.reactfunctpolym.2004.02.018. [DOI] [Google Scholar]
  34. Roberts G. A. F.Chitin Chemistry; Macmillan International Higher Education, 1992, 10.1007/978-1-349-11545-7. [DOI] [Google Scholar]
  35. Muzzarelli R. A. A.; Peter M. G.. Chitin Handbook; Atec, 1997. [Google Scholar]
  36. Sorlier P.; Denuzière A.; Viton C.; Domard A. Relation between the Degree of Acetylation and the Electrostatic Properties of Chitin and Chitosan. Biomacromolecules 2001, 2, 765–772. 10.1021/bm015531+. [DOI] [PubMed] [Google Scholar]
  37. Filion D.; Lavertu M.; Buschmann M. D. Ionization and Solubility of Chitosan Solutions Related to Thermosensitive Chitosan/Glycerol-Phosphate Systems. Biomacromolecules 2007, 8, 3224–3234. 10.1021/bm700520m. [DOI] [PubMed] [Google Scholar]
  38. Cataldo S.; Crea F.; Gianguzza A.; Pettignano A.; Piazzese D. Solubility and Acid-Base Properties and Activity Coefficients of Chitosan in Different Ionic Media and at Different Ionic Strengths, at T= 25 C. J. Mol. Liq. 2009, 148, 120–126. 10.1016/j.molliq.2009.07.006. [DOI] [Google Scholar]
  39. Wang Q. Z.; Chen X. G.; Liu N.; Wang S. X.; Liu C. S.; Meng X. H.; Liu C. G. Protonation Constants of Chitosan with Different Molecular Weight and Degree of Deacetylation. Carbohydr. Polym. 2006, 65, 194–201. 10.1016/j.carbpol.2006.01.001. [DOI] [Google Scholar]
  40. Stumm W.Aquatic Surface Chemistry: Chemical Processes at the Particle-Water Interface; John Wiley & Sons, 1987; Vol. 87. [Google Scholar]
  41. Dzombak D. A.; Morel F. M. M.. Surface Complexation Modeling: Hydrous Ferric Oxide; John Wiley & Sons, 1990. [Google Scholar]
  42. Davis J. A. Surface Complexation Modeling in Aqueous Geochemistry. Miner.-Water Interface Geochem. 1990, 23, 177–259. [Google Scholar]
  43. Smith R. M.; Martell A. E.; Chen Y. Critical Evaluation of Stability Constants for Nucleotide Complexes with Protons and Metal Ions and the Accompanying Enthalpy Changes. Pure Appl. Chem. 1991, 63, 1015–1080. 10.1351/pac199163071015. [DOI] [Google Scholar]
  44. Saenger W.Principles of Nucleic Acid Structure; Springer Science & Business Media, 2013. [Google Scholar]
  45. De Stefano C.; Gianguzza A.; Piazzese D.; Sammartano S. Speciation of Chitosan–Phosphate and Chitosan–Nucleotide Systems in NaCI Aqueous Solution. Chem. Speciation Bioavailability 2010, 22, 99–107. 10.3184/095422910X12692701255297. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la0c03050_si_001.pdf (498.1KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES