Graphical abstract
Keywords: SARS-CoV-2, COVID-19, R0, Epidemic growth rate, Vaccination
Abstract
SARS-CoV-2 rapidly spread from a regional outbreak to a global pandemic in just a few months. Global research efforts have focused on developing effective vaccines against COVID-19. However, some of the basic epidemiological parameters, such as the exponential epidemic growth rate and the basic reproductive number, R0, across geographic areas are still not well quantified. Here, we developed and fit a mathematical model to case and death count data collected from the United States and eight European countries during the early epidemic period before broad control measures were implemented. Results show that the early epidemic grew exponentially at rates between 0.18 and 0.29/day (epidemic doubling times between 2.4 and 3.9 days). We found that for such rapid epidemic growth, high levels of intervention efforts are necessary, no matter the goal is mitigation or containment. We discuss the current estimates of the mean serial interval, and argue that existing evidence suggests that the interval is between 6 and 8 days in the absence of active isolation efforts. Using parameters consistent with this range, we estimated the median R0 value to be 5.8 (confidence interval: 4.7–7.3) in the United States and between 3.6 and 6.1 in the eight European countries. We further analyze how vaccination schedules depend on R0, the duration of protective immunity to SARS-CoV-2, and show that individual-level heterogeneity in vaccine induced immunity can significantly affect vaccination schedules.
1. Introduction
SARS-CoV-2 is the infectious agent that causes the COVID-19 pandemic. It was first detected in Wuhan city, China in Dec 2019 (WHO, 2020), and has spread rapidly causing the ongoing global pandemic. Two key epidemiological parameters for understanding the dynamics of the COVID-19 outbreak are the early epidemic growth rate, defined as the rate of early exponential growth of an epidemic in the absence of control measures, and the basic reproductive number R0, defined as the number of secondary infections when an index case is introduced into a fully susceptible population. Accurate estimations of these two fundamental parameters of infectious disease dynamics across geographic areas are crucial for many aspects of policy making, from outbreak preparedness to rational design of epidemic intervention and exit strategies (Thompson et al., 2020). For example, in the wake of second waves of COVID-19 outbreak (Kissler et al., 2020), they allow for accurate forecasting the country specific epidemic trajectory, and the burden on health care systems (Grasselli et al., 2020, Li et al., 2020b) and potential health and economic damage. They set the baseline for evaluation of effectiveness of country specific public health intervention strategies (Dehning et al., 2020, Flaxman et al., 2020, Pellis et al., 2020). Finally, accurate estimation of R0 is crucial for predicting the herd immunity threshold needed to stop transmission (Britton et al., 2020, Gomes et al., 2020, Lipsitch et al., 2003, Park et al., 2020, Sanche et al., 2020). This is particularly pertinent to the development of appropriate vaccination strategies (Jackson et al., 2020).
Initial estimates of the rate of early epidemic spread in Wuhan, China suggested that the epidemic grew at 0.1–0.14/day, leading to an epidemic doubling time of 5–7 days (Kucharski et al., 2020, Li et al., 2020a, Riou and Althaus, 2020, Wu et al., 2020a). However, using domestic travel data and two distinct approaches, we estimated that the epidemic in Wuhan grew much faster than initially estimated, and the growth rate is likely to be between 0.21 and 0.3/day before lock-down was implemented, translating to a doubling time between 2.3 and 3.3 days, and an R 0 approximately at 5.7 with a confidence interval between 3.8 and 8.9 (Sanche et al., 2020). A high epidemic growth rate and a high R 0 of the outbreak in Wuhan were also reported by another study (Tang et al., 2020).
The early epidemic growth rate and R 0 likely vary across different geographic regions, because transmission of infectious agents depends on not only biological factors, but also social factors and population structure. Several works addressed the need to estimate the early epidemic growth rates in Europe and other countries across the globe during initial COVID-19 pandemic (Dehning et al., 2020, Flaxman et al., 2020, Pellis et al., 2020, Romero-Severson et al., 2020), including a preprint version of this work posted online in early April 2020 (Ke et al., 2020). In general, these works found that SARS-CoV-2 outbreaks grew at very fast rates (with a short doubling time), similar to what we have estimated for the outbreak in Wuhan. However, the basic reproductive number R 0 has not been well quantified, and refinement is needed especially in light of the recent new understanding of the duration of the serial interval (Ali et al., 2020), i.e. a key parameter used to estimate R 0 from the epidemic growth rate.
Here, we fit mechanistic models to both case and death count data collected from the United States (US) and eight European countries in March 2020 before broad interventions were established. By considering the joint distribution of COVID-19 cases and deaths, our inference approach gives a more accurate assessment of early COIVD-19 dynamics and will help minimize biases as a result of systemic underreporting of cases and/or deaths. Importantly, we provide estimates of the basic reproductive numbers across the US and eight European countries, using the current best estimates of basic epidemiological parameters, such as the serial interval (see Section 4 for details). We show that in most countries, COVID-19 spreads very rapidly, leading to high estimated R 0 values and consequently high herd immunity thresholds in these countries. We further explore how vaccination schedules depend on the value of R 0 and the distribution of the duration of vaccine-induced immunity in a population, in the context of the durations of protective immunity reported for SARS-CoV-2 (Long et al., 2020, Seow et al., 2020), as well as other coronaviruses such as HCoV-OC43 and HCoV-HKU1 (Callow et al., 1990, Kissler et al., 2020), SARS-CoV-1 (Cao et al., 2007, Chan et al., 2013, Le Bert et al., 2020) and MERS-CoV (Payne et al., 2016).
2. Methods
2.1. Data
We collected daily case confirmation and death count data from the John Hopkins CSSE (Center for Systems Science and Engineering) database (https://github.com/CSSEGISandData/COVID-19). The data is accessed and extracted on March 31, 2020. The data consists of time series of the cumulative number of case confirmations and deaths by country. Daily incidences were derived from the cumulative counts. We included data from the United States (US) and eight most affected European countries where the total deaths exceed 150 by March 31, 2020. The total deaths threshold is to ensure that the number of deaths is high enough for statistical inference. The eight European countries are France (FR), Italy (IT), Spain (SP), Germany (GR), Belgium (BE), Switzerland (SW), Netherlands (NT), United Kingdom (UK).
We included a subset of case and death count data for inference based on the two following criteria. First, to minimize the impact of stochasticity and uncertainty in early data collection, we used case confirmation incidence data starting from the date when the cumulative number of cases was greater than 100, and used daily new death count data starting from the date when the cumulative death count is greater than 20 in each country (see Table S1 and Fig. 1 for the period from which data is included). Second, to estimate the early outbreak growth in each country before control measures were implemented, we included case count data up to the date of lockdown in each country. For death counts, we included a maximum of 15 days of data points starting from the date when the cumulative death count is greater than 20 in each country. We tested the sensitivity of model predictions against variations in the number of data points used for inference. In this analysis, we included the 15, 13 or 10 days of data points prior to the date when lockdown was implemented in each country. Overall, we found that the results are consistent across the different numbers of data points used (Table S1).
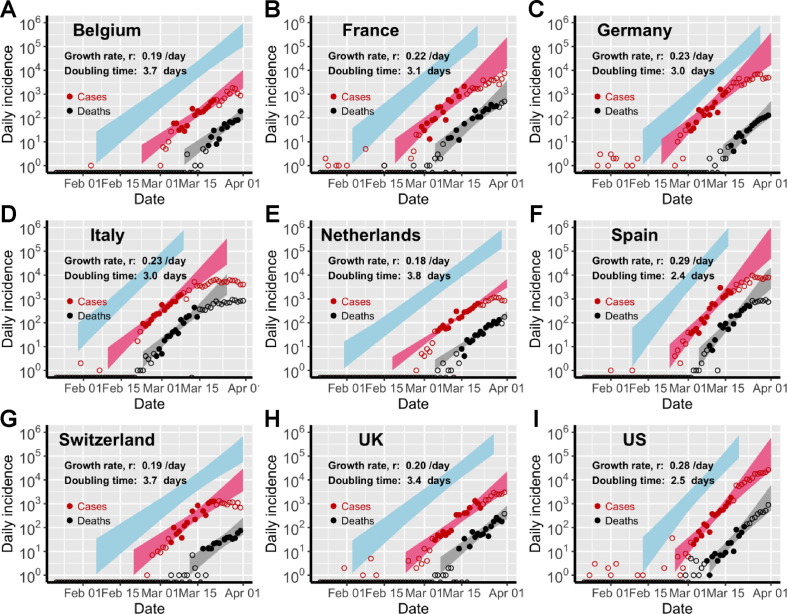
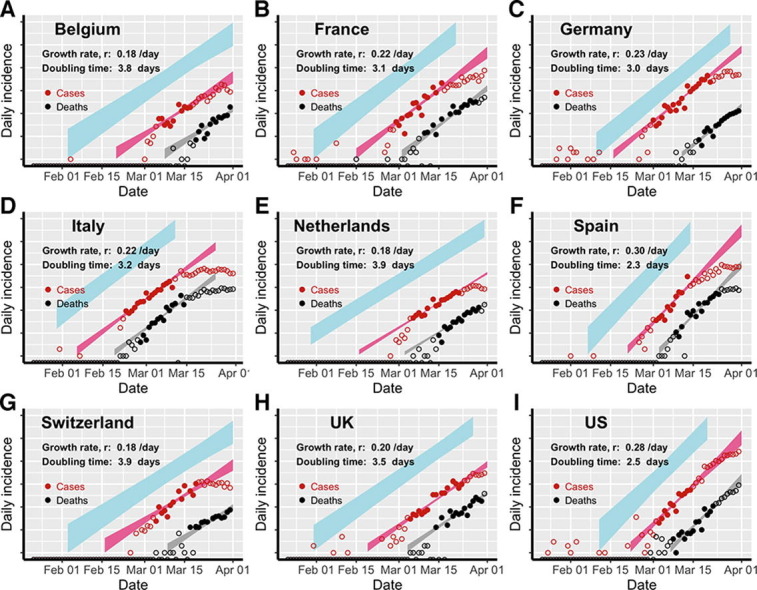
Fig. 1.
Estimation of the exponential growth rate and the doubling time of epidemics in eight European countries and the US. Red and black symbols show the daily counts of new cases and new deaths, respectively. Closed dots denote data used for parameter inference; whereas open circles denote data that are not used for parameter inference. We simulated the model using sampled parameter combinations that are able to explain the data shown in dots (see Uncertainty quantification in Section 2). The colored bands denote the area between the lower and upper bounds of simulated/predicted true daily infection incidence (blue), daily cases (red) and daily deaths (grey) assuming no intervention efforts nor changes in surveillance intensity. Deviations of open circles from the corresponding bands thus indicate either changes in surveillance intensity or impacts of control measures.
2.2. Model
We construct a SEIR type model using ordinary differential equations (ODEs; see Supplementary Text). We consider the exponentially growing phase of the outbreak and thus make the common assumption that the susceptible population is constant over time. Then, the total number of infected individuals can be expressed as:
| (1) |
where is the exponential growth rate of the epidemic (the growth rate for short below), and is the number of total infected individuals at time 0, set arbitrarily as January 20, 2020. Note the choice of the date of time 0 does not affect our estimation.
We solve the ODE model and derive the following expressions for the key quantities for model inference (see Supplementary Text). The descriptions and values used for the parameters in the ODE model are summarized in Table 1 .
Table 1.
Description of parameter and their values. See the Supplementary Text for discussions of choice of parameter values.
| Parameters | Description | Value | Ranges used in uncertainty analysis | References |
|---|---|---|---|---|
| Exponential growth rate | Estimated from data | 0.1–0.35 /day | ||
| is the number of total infected individual at time 0 (Jan. 20) | Estimated from data | 0.0001–10 on a log scale | ||
| detection probability | Estimated from data | 0.001–1 on a log scale | ||
| Infectivity in the SEIR model | Calculated from | See Supplementary Text | ||
| The mean latent period, i.e. from infection to becoming infectious | 3 days | 3–4 days | He et al., 2020, Lauer et al., 2020, Sanche et al., 2020 | |
| The mean duration from infection to case confirmation | 12 days | 10–14 days | Ng et al., 2020, Sanche et al., 2020 | |
| Shape parameter for the duration from infection to symptom onset | 3 | 2–4 | Sanche et al. (2020) | |
| Shape parameter for the duration from symptom onset to death. | 4 | 3–5 | Sanche et al. (2020) | |
| Mean duration from infection to death | 21.5 days | 20.5–23.5 days | Sanche et al., 2020, Zhou et al., 2020 | |
| Infection fatality ratio | 0.01 | 0.004–0.014 | Dorigatti et al., 2020, Wu et al., 2020b |
The true daily incidence of infected individuals, , can be expressed as:
| (2) |
where and 1/ are the transmission parameter of the virus and the latent period of infection, respectively.
The daily new confirmed case count, , is related to the true daily incidence, as:
| (3) |
where is the detection probability, i.e. the fraction of newly individuals at time who are later detected among all infected individuals. We assumed an Erlang distribution for the period between infection and case confirmation (Sanche et al., 2020), where and are the mean and the shape parameter for the distribution.
The daily new death count, , is related to the true daily incidence, as:
| (4) |
where is the infection fatality ratio. Again, we assumed an Erlang distribution for the period between infection and death (Sanche et al., 2020), where and are the mean and the shape parameter for the distribution.
We tested three different scenarios for surveillance intensity changes over time, modeled as the detection probability, :
-
1)
is a constant, i.e. no change over time;
-
2)
, i.e. is a Hill-type function of ;
-
3)
is equal to before , increases linearly to between and and stay constant at after , i.e. is a semi-linear function of .
Note that the time from infection to case confirmation, , can be a time dependent function as we and others have shown previously (Ng et al., 2020, Sanche et al., 2020). To keep the model simple, we implicitly assume that the time dependent changes in can be included in the estimation of .
2.3. Parameter estimation
We fit the daily case count function and the death count function to incidence data and daily death data to infer the exponential growth rate of the infection , the initial number of total infected individuals at time, and the detection probability (). Other parameter values are fixed according to previous estimates (see Table 1). We assumed that the data were negative binomial distributed conditional on the model and inferred parameters by maximizing the likelihood function using standard methods.
To compare between models, we calculate the Akaike Information Criterion (AIC) score for each model as (Burnham and Anderson, 2002):
| (5) |
where is the number of fitted parameters and LL is the log likelihood of the model. The model with the lowest AIC score is the best model. A model is significantly worse than the best model if the difference between their AIC scores is greater than 2 (Burnham and Anderson, 2002).
2.4. Uncertainty quantification
To evaluate uncertainties in the estimated parameters , and , we sampled 108 parameter combinations of all fixed parameters and estimated parameters by drawing parameters randomly from uniform distributions over the ranges specified in Table 1. We calculate the LL for each parameter combination. We accepted a parameter combination if the likelihood of this parameter combination was not statistically different from the best-fit parameter combinations using the log-likelihood ratio test. The upper and lower bounds reported were summarized using simulation results of all accepted parameter combinations.
2.5. Estimation of R0
We calculated R 0 according to the equation derived by Wearing et al. (2005):
| (6) |
where and are the mean latent and infectious periods, respectively, and and are the shape parameters for the gamma distributions for the latent and the infectious periods, respectively.
We set the mean latent period, , to vary between 3 and 4 days. This is based on that the incubation period is estimated to be between 5 and 6 days (Backer et al., 2020, Lauer et al., 2020, Sanche et al., 2020) and infected individuals become infectious approximately 2 days before symptom onset (He et al., 2020).
We set the mean infectious period, , to be between 6 and 8 days to be consistent with the estimated mean serial interval, i.e. the mean time interval between symptom onsets of an index case and secondary cases in transmission pairs, of 6–8 days (Bi et al., 2020, Lavezzo et al., 2020, Thompson et al., 2020). See the Section 4 for a discussion of the estimates of the serial interval. We note that this range of infectious period is also consistent with the findings that infectious viruses can be recovered during the first week of symptom onset (and up to 9 days post symptom onset) (Payne et al., 2016, Wolfel et al., 2020).
To quantify the uncertainty of , we assumed that m = 4 and n = 3 similar as in our previous work (Sanche et al., 2020). We assume that the exponential growth rate, , varies in the range estimated from the data. The parameters are assumed to be mutually independent and we generate random samples from uniform distributions according to ranges of variations defined above to compute the resulting . We generated parameters, and then computed their respective using Eq. (6). We used the 97.5% and 2.5% percentile of the generated data to quantify the 95% confidence interval.
2.6. Calculation of the level of population immunity after mass vaccination
We assume a gamma distribution for the duration of protective immunity induced by a hypothetical vaccine to SARS-CoV-2 in a population. Let be the mean duration, and s be the shape parameter of the gamma distribution. For simplicity, we assume that the durations of the immunity induced by natural infection and vaccination are the same. We further assume that the percentage of protected population reaches to 85% after every mass vaccination with the hypothetical vaccine. Note that this is likely to be an optimistic scenario (Mello et al., 2020). The fraction of population that are immune to SARS-CoV-2 at time after a mass vaccination can then be expressed as , where is the cumulative density function of the gamma distribution for the duration of population immunity. Based on this expression, we calculate the time when the population immunity reaches to the herd immunity threshold value by solving for . The solution for is the maximum time interval between two vaccinations to maintain herd immunity in a population.
3. Results
3.1. Estimation of the epidemic growth rate and surveillance intensity
Using our simplified SEIR-type (susceptible-exposed-infected-recovered) model (see Section 2 and Supplementary Text for details), we fit both the case incidence data and the daily death count data to estimate the epidemic growth rate and the detection probability, i.e. the probability that an infected person is identified, before interventions were implemented in eight European countries and the US. The exponential growth rates of early outbreaks, r, range between 0.19 and 0.29/day in the nine countries, translating to doubling times between 2.4 and 3.7 days (Fig. 1). Spain and the US had the highest estimated growth rates, at 0.29/day and 0.28/day, respectively; whereas Switzerland and Netherlands had the lowest estimates at 0.19/day and 0.18/day, respectively. Evaluating uncertainties in these estimates (see Section 2), we found that the epidemic growth rates are highly constrained by the time series data despite variations in parameter values in the model (Fig. 2 A).
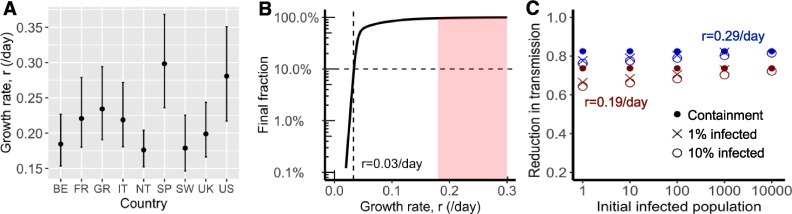
Fig. 2.
Fast spread of SARS-CoV-2 and its implications for public health interventions. (A) Point estimates and confidence interval ranges of the exponential growth rate, in each country. See Table 2 for country name abbreviations. (B) Final fraction of infected individuals after 12 months of outbreak. A growth rate less than 0.03/day, i.e. a doubling time of 23 days, is needed to achieve the goal that less than 10% of individuals are infected (dashed lines). However, the benefit, i.e. fraction of uninfected individuals, increases exponentially when the growth rate is further reduced beyond the threshold. (C) High levels of control efforts, measured as fractions of transmission reduction (y-axis), are needed to achieve containment, i.e. reverting epidemic growth (dots), or mitigation, i.e. the final fraction of infected individuals is 1% (x) or 10% (open circle) after a year. We assumed initial infected population as shown in x-axis and epidemic growth rates of 0.19 (red) or 0.29/day (blue).
We estimated that the detection probability, i.e. the fraction of infected individuals who are detected by surveillance, was likely to be low (<30%) across the countries examined except for Germany. The point estimate of the detection probability in the US is 12%, i.e. approximately 1 in 8 infected individuals were detected, similar to a recent estimate using influenza like illness data (Silverman et al., 2020). This is likely due to the high percentage of infected individuals with no or mild-to-moderate symptoms (Mizumoto et al., 2020, Zou et al., 2020), which are difficult to detect through passive surveillance systems. The detection probability is higher in Germany (with a point estimate of 58%) than in other countries, providing an explanation of the high number of reported cases compared to the relative low number of deaths in Germany during March 2020. Overall, there exist large uncertainties in our estimation of the detection probability (Fig. S1) due to the uncertainties in the fixed parameter values assumed in the model, such as the infection fatality ratio.
Changes to the detection probability over time, e.g. as a result of changes in testing, could lead to an apparent increase or decrease in case count and biases in inference. We considered two scenarios involving increases in testing over the study period (see Section 2 for the mathematical formulations), and found no statistical evidence that case counts during the relatively short period for which we perform inference are strongly impacted by changes in surveillance intensity (Table S2). While it is highly likely that the probability of a case being detected increased over the period where testing was becoming available, our analysis excluded data from that period. As shown in Fig. 1, the red, open circles indicate data outside of the study period. Most countries show a pattern of very rapid increase in detected cases in the very early epidemic period that is likely the result of both a growing epidemic and increasing availability and use of testing.
3.2. Implications of fast epidemic growth for public health intervention strategies
Using our empirical estimates of the growth rates, we explored the implications for public health efforts to control the COVID-19 outbreak. We considered an outbreak scenario in a large city with a population of 10 million. We first calculated the total fraction of infected individuals after a year, assuming only one infected individual at day 0. If our goal is that the total fraction of infected individuals is less than 10% after a year, the growth rate has to be reduced from 0.2 to 0.3/day to less than 0.03/day (Fig. 2B). This suggests that moderate social distancing efforts will be insufficient to prevent the virus to infect a large fraction of the population. On the other hand, if the targeted growth rate, i.e. 0.03/day, is achieved through very strong public health interventions, then a lower rate may also be attainable. The benefits of a small decrease below the threshold are significant, as the total infected fraction decreases exponentially when r decreases beyond 0.03/day as shown in Fig. 2B.
To corroborate the results above, we calculated the intervention efforts needed for three hypothetical goals: 1) containment (i.e. the size of epidemic decreases), 2) 1% of the population is infected one year after the intervention, and 3) 10% of the population is infected one year after the intervention. Efforts needed for each goal are similarly high, especially when the population of infected individuals is already more than 1000 (Fig. 2C). For example, when an outbreak grows at rate 0.29/day (as we estimated for the US), the levels of efforts needed to achieve the three goals are between 80% and 82% reduction in transmission; whereas when the growth rate is 0.19/day, the levels of effort needed are between 70% and 73% reduction. Regardless of the heterogeneity in the growth rates, the force of infection must be significantly reduced, arguing for strong and comprehensive intervention efforts.
3.3. Estimating the basic reproductive number, R0
We computed the basic reproductive number, R 0, for each country following the approach of Wearing et al. (2005), which uses as input the estimated growth rate, and the durations of the latent and infectious periods. We assumed that the duration of the latent period (i.e. the period between infection and becoming infectious) and the infectious periods to be 3–4 days and 6–8 days, respectively (see Section 2 for justification of these parameter ranges). These choices of parameters are consistent with the estimated mean serial intervals of 6–8 days (Bi et al., 2020, Lavezzo et al., 2020, Thompson et al., 2020). Note that some estimates of the mean serial intervals are shorter (Du et al., 2020, Ganyani et al., 2020, He et al., 2020, Nishiura et al., 2020). These shorter serial intervals are a result of intensive intervention efforts to rapidly isolate infected individuals (Ali et al., 2020, Bi et al., 2020), and can be useful in estimating effective reproductive numbers in places where intensive isolation efforts are implemented. However, for the purpose of estimating the basic reproductive number, R 0, and the herd immunity threshold (in the next section), the mean serial interval in the absence of isolation effort, i.e. 6–8 days, shall be used. In the Section 4, we present a more complete argument that for the choice of the duration of the mean serial interval.
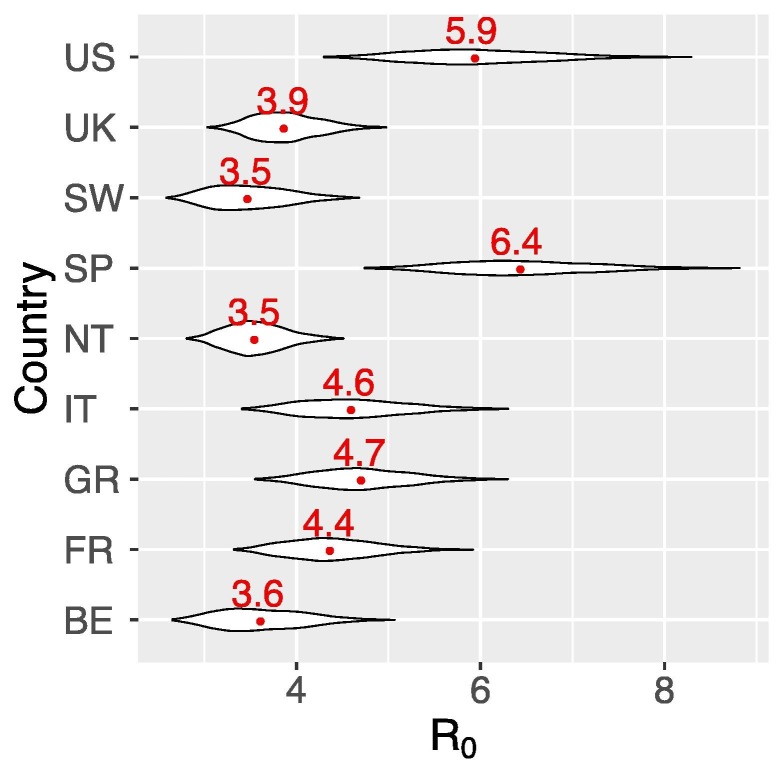
Using the estimated ranges of the growth rates for each country, we estimated that the US and Spain had highest median R 0s at 5.9 (CI: 4.7–7.5) and 6.4 (5.2–8.0), respectively (Fig. 3 and Table 2 ). For the other countries, we estimated the median R 0 ranges between 3.5 and 4.7 (Fig. 3 and Table 2).
Fig. 3.
Estimates of the median and ranges of the reproductive number R0 in each country. Median R0 were shown in red numbers. See Table 2 for country name abbreviations.
Table 2.
Estimated medians and confidence intervals of the basic reproductive number, R0, and their corresponding herd immunity thresholds for eight European countries and the US.
| Country | Abbreviation | Median R0 | Confidence interval – R0 | Classical herd immunity threshold | Confidence interval – herd immunity |
|---|---|---|---|---|---|
| Belgium | BE | 3.6 | (2.9, 4.6) | 72% | (65%, 78%) |
| France | FR | 4.4 | (3.6, 5.4) | 77% | (72%, 81%) |
| Germany | GR | 4.7 | (3.8, 5.8) | 79% | (74%, 83%) |
| Italy | IT | 4.6 | 3.7, 5.8) | 78% | (73%, 83%) |
| Netherlands | NT | 3.5 | (3.0, 4.2) | 72% | (67%, 76%) |
| Spain | SP | 6.4 | (5.2, 8.0) | 84% | (81%, 88%) |
| Switzerland | SW | 3.5 | (2.8, 4.3) | 71% | (63%, 77%) |
| United Kingdom | UK | 3.9 | (3.3, 4.6) | 74% | (69%, 78%) |
| United States | US | 5.9 | (4.7, 7.5) | 83% | (79%, 86%) |
3.4. Implications for vaccination strategies
From the range of median R 0 estimated above, we first calculated the fraction of individuals needed to be immune in a homogenous population such that an outbreak stops growing. This fraction is given by the classical result, 1–1/R 0 (Anderson and May, 1991). We refer to this term as the ‘classical herd immunity threshold’, which spanned between 71% and 84% for the countries considered here (Table 2). We note that recent works show that due to population heterogeneity, the herd immunity threshold induced by disease transmission may be lower than the classical threshold predicted by 1–1/R 0 (Britton et al., 2020, Gomes et al., 2020). However, the herd immunity threshold through random vaccination stays at 1 − 1/R 0.
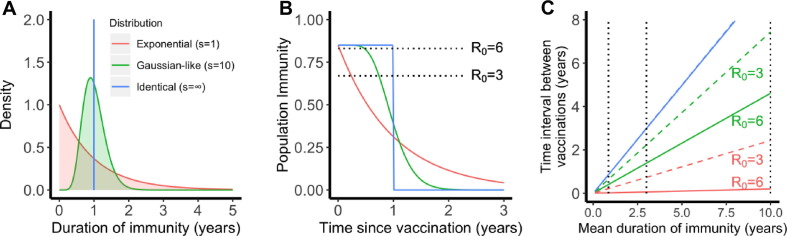
Multiple lines of evidence suggest that the protective immunity may not be long lived for SARS-CoV-2 (Long et al., 2020, Seow et al., 2020). Thus, we further considered how a vaccine with waning protection could be used to combat COVID-19 given our estimated levels of R 0 (see Section 2). We assumed that vaccination achieves 85% population immunity in a population. This is an optimistic scenario. For example, with a protective efficacy of 94%, the coverage has to be greater than 90% to achieve 85% population immunity. If this level of immunity is not achieved, for example, due to low vaccination coverage (Mello et al., 2020) or low protective efficacy, we may not reach herd immunity through vaccination for places where R 0 is estimated to be around 6, e.g. the US and Spain. In the model, we assumed a gamma distribution for the duration of protective immunity induced by a hypothetical vaccine in a population, where s is the shape parameter of the gamma distribution (Fig. 4 A).
Fig. 4.
The importance of the distribution of the duration of vaccine-induced immunity in maintaining herd immunity in a population. (A) Three scenarios for the distribution: exponential (shape parameter ), Gaussian-like () and identical (). All three distributions have the same mean, i.e. 1 year. The color code applies to all panels. (B) The fraction of individuals who are immune in a population over time. We assumed that 85% of population are immune after a mass vaccination at time 0. The dotted lines show the heard immunity thresholds, i.e. 83% (for R0 = 6) and 67% (for R0 = 3). (C) The time when the population immunity decreases to the threshold value (predicted for each R0) for the three scenarios. We assumed R0 = 3 (dashed lines) or 6 (solid lines) in the calculations. Note the dashed blue line overlaps with the solid blue line. The dotted lines show mean durations of immunity of 45 weeks, 3 years and 10 years.
If the duration of protective immunity from the vaccine follows an exponential distribution, (i.e. when ), a sizable fraction of individuals lose immunity rapidly, leading to a loss of herd immunity shortly after the initial vaccination program, especially when R 0 is large and the herd immunity threshold is high (Fig. 4B). Consequently, the time between vaccinations required to maintain herd immunity is much shorter than the mean duration of protective immunity (Fig. 4C). For example, even if the mean duration of protective immunity is 10 years, vaccination must occur every 2.4 month and 2.4 years to maintain herd immunity when R 0 is 6 and 3, respectively (see the red lines in Fig. 4C). On the other extreme, when s is very large (Fig. 4A, ), individuals in the population have identical durations of protective immunity. In this case, herd immunity persists for a long period of time before the fraction of immune individuals suddenly drops to a very low level (Fig. 4B). In this case, herd immunity can be kept at a duration similar to the mean duration of protective immunity irrespective of R 0 (see blue lines in Fig. 4C).
The reality of an imperfect vaccine is likely to be between these two extremes. When we assume , the distribution becomes more Gaussian-like (Fig. 4A) where some people lose protective immunity faster than others, but that heterogeneity is relatively low. If a mass vaccination achieves 85% immunity in a population and protective immunity lasts on-average around 45 weeks to 1 year (Long et al., 2020) (consistent with the duration of immunity induced by endemic coronaviruses (Callow et al., 1990, Kissler et al., 2020)), then vaccination will need to occur once a few months (Fig. 4C). If the mean duration of protective immunity is around 3 years as observed for the antibody response to SARS-CoV-1 or MERS-CoV (Payne et al., 2016), vaccination once a year or once two years will be sufficient, if R 0 is 6 or 3, respectively (Fig. 4C). If the mean duration of protective immunity is greater than 10 years (for example, a long T cell immunity to SARS-CoV-1 is observed in individuals recovered from SARS-CoV-1 infection (Le Bert et al., 2020)), the time interval between repeated vaccinations becomes longer than 4 years or 7 years when R 0 is 6 or 3, respectively.
4. Discussion
In this work, we report rapid COVID-19 epidemic spread before broad control measures were implemented in the US and in the eight most affected countries in Europe during March 2020. We further estimated that R 0 values range between 3.5 and 6.4 in these countries, which means high herd immunity thresholds between 71% and 84%. Together with our previous estimates for the outbreak in Wuhan (Sanche et al., 2020), these results are consistent with SARS-CoV-2 being highly transmissible irrespective of heterogeneities in geographic and social settings and emphasize the necessity of strong control measures, such as social distancing. A high level of coverage of effective vaccines are needed to achieve herd immunity. We further show that the heterogeneity of individual-level protection provided by a vaccine is an important factor in determining the frequency of vaccinations.
Awareness of the extraordinary high rates of COVID-19 spread in the absence of control measures is critically important for epidemic preparedness. The short doubling times of the epidemic means that health care systems can be overwhelmed in a couple of weeks rather than several months in the absence of control (Li et al., 2020b). For example, a report shows that the number of COVID-19 patients admitted to intensive care units in Italy during February and early March 2020 grew at a rate of approximately 0.25/day during early epidemic (Grasselli et al., 2020). We estimated that the SARS-CoV-2 outbreaks grew extremely rapidly at rates between 0.18 and 0.29/day, in eight European countries and the US. These estimates for European countries are in general consistent with other studies using different approaches and different sources of data (Dehning et al., 2020, Flaxman et al., 2020, Pellis et al., 2020). We further show that because of the high transmissibility of the virus, moderate control efforts will not sufficiently slow the virus spread to achieve measurable public health benefits. This may explain the continuous growth of the outbreak in some countries despite measures, such as work and school closures, were in place. To delay the peak or to reverse the growth of the epidemic with non-pharmaceutical interventions, strong and comprehensive intervention efforts, such as wide-spread testing, isolation and quarantine, use of personal protective equipment, and social distancing, may be needed.
While we found remarkably high rates of epidemic growth in all the examined countries, we caution that our inference is largely driven by data collected from highly populated areas, such as Wuhan in China, Lombardy in Italy, and New York city in the US. Heterogeneities in the growth rate almost certainly exist among different areas within each country. For example, recent works suggest that the rate of spread is positively associated with population densities (Rader et al., 2020). Therefore, the estimates we provide may represent good estimates in highly populated areas such as in cities.
One limitation of our inference (as well as in other works (Dehning et al., 2020, Flaxman et al., 2020, Pellis et al., 2020, Romero-Severson et al., 2020)) arises from the case and death count data. Case confirmation data is influenced by many factors, including underreporting (Li et al., 2020c). Death and the cause of death are usually recorded more reliably and are less affected by surveillance intensity changes than case counts. However, COVID-19 death counts may also underestimate the true COVID deaths. For example, it is possible that deaths from COVID-19 are underreported when people are unaware of community transmission of COVID-19 (Kong et al., 2020) or when health care system is overwhelmed (Li et al., 2020b). In addition, factors including changes in definitions and protocols for ascertaining COVID deaths, updating prior deaths may also impact on COVID death reporting.
Calculation of the basic reproductive number requires knowledge of the distribution of the length of serial interval (SI), which in turn is determined by the latent and the infectious periods. Similar to our earlier work (Sanche et al., 2020), we assumed parameter values that are consistent with a mean SI of 6–8 days, based on estimates using transmission-pair data from Wuhan, China and Vo, Italy (Ali et al., 2020, Lavezzo et al., 2020, Thompson et al., 2020). This led to higher estimates of R 0 for the European countries than other studies (Flaxman et al., 2020, Salje et al., 2020). For example, Flaxman et al. assumed a mean serial interval of 6.5 days according to Bi et al. (2020). However, Bi et al. demonstrated that when the transmission pair is not isolated rapidly after symptom onset, the mean serial interval is estimated to be 8 days (Bi et al., 2020).
Shorter mean SIs were frequently reported in the literature, for example, 4.0 days in Du et al. (2020), 5.8 days in He et al. (2020), 4–5 days in Nishiura et al. (2020), 4–5.2 days in Ganyani et al. (2020). However, these estimates were based on data reported in locations outside of Wuhan, Hubei province, and other Asian countries and territories neighboring China, and thus were strongly impacted by active surveillance and isolation effort as demonstrated by Ali et al. (2020) and discussed in Bar-On et al. (2020). Indeed, we previously estimated that in provinces outside of Hubei province, the mean time from symptom onset to hospitalization/isolation, was as short as 1.5 days after Jan 18th (Sanche et al., 2020), suggesting an exceptionally active surveillance effort. For the purpose of estimating the basic reproductive number, R 0, and the herd immunity threshold, the mean serial interval in the absence of isolation effort is the relevant quantity to use. Therefore, we believe our estimation of R 0 represent a more accurate estimate. Further work characterizing the heterogeneities of the distribution of serial intervals and measuring serial intervals from individuals who are asymptomatic may help to improve the estimation of R 0 (Park et al., 2020).
We calculated the classical herd immunity thresholds 1 − 1/R 0, derived from models assuming a homogenous population (Anderson and May, 1991), to be between 71% and 84% in China (Sanche et al., 2020), the US and the eight European countries. These are very high thresholds for random vaccination even with an effective vaccine. A recent survey showed that only approximately 50% of Americans plan to get a COVID-19 vaccine (Mello et al., 2020). Assuming 90% efficacy, 50% coverage only leads to a population immunity of 45%. This is much lower than the herd immunity required to stop transmission. This highlights the importance of public education about COVID-19 vaccination to ensure high vaccine coverage to achieve herd immunity (Mello et al., 2020). Other intervention efforts including both non-pharmaceutical, i.e. effective test, trace and isolation, and pharmaceutical interventions, i.e. therapeutics, are likely needed in addition to vaccination. If the herd immunity threshold is not achieved, i.e. a likely scenario given the high herd immunity thresholds, transition to endemicity will be expected (Lavine et al., 2021).
We note that the herd immunity thresholds derived from the classical formula, 1 − 1/R 0, represent good estimates in the context of random vaccinations and recent works pointed out that the disease induced herd immunity threshold may be lower due to heterogeneity in population structure, such as age structure and contact activity levels (Britton et al., 2020), and individual susceptibility and exposure (Gomes et al., 2020). This is because individuals with a high level of contacts are more likely to be infected and once these individuals are recovered/vaccinated and immune, the infectious agent is much less likely to spread. This may be true when there exists substantial heterogeneity in the population and risk behavior is static, i.e. low risk persons never engage in high-risk behaviors over time. However, the extent of heterogeneity and whether contact structure changes over time for SARS-CoV-2 spread are yet to be quantified through rigorous epidemiological studies. Therefore, cautions need to be made when disease induced immunity thresholds are used for public health policy making.
Recent COVID-19 vaccine trials show that they are highly efficacious in preventing disease (Moderna, 2020, Pfizer, 2020); however, it is still not known how effective they protect from infection and how long the protective immunity lasts. We found that if the duration of immunity is relatively short as suggested in Long et al., 2020, Seow et al., 2020, and similar to the durations of protective immunity against other endemic coronaviruses (Callow et al., 1990, Kissler et al., 2020) or MERS-CoV (Payne et al., 2016), a frequent vaccination schedule once every couple of years to multiple times per year is needed to maintain herd immunity. Furthermore, we found that in addition to the mean duration of vaccine-induced protective immunity, the distribution of the duration is an important factor in determining vaccination frequency. A vaccine that induces a more uniform response in a population is better than a vaccine that induces a heterogeneous response in maintaining population immunity. Studies of the kinetics of antibody dynamics in individuals, such as Antia et al., 2018, Seow et al., 2020, will help making more precise predictions of vaccine schedules.
Overall, our work shows that SARS-CoV-2 has high R 0 values and spread very rapidly in the absence of strong control measures across different countries. This implies very high herd immunity thresholds, and thus highly effective vaccines with high levels of population coverage will be needed to prevent sustained transmission. If the protective immunity induced by vaccination is not long lasting, understanding the full distribution of the duration of protective immunity in the population is crucial to determine the frequency of vaccinations.
Author contributions
RK and NH conceived the project; RK performed literature search and designed the study; SS collected data; RK, SS and ERS performed analyses; RK, SS, ERS and NH wrote and edited the manuscript.
CRediT authorship contribution statement
Ruian Ke: Conceptualization, Methodology, Formal analysis, Supervision, Funding acquisition, Writing - original draft, Writing - review & editing. Ethan Romero-Severson: Methodology, Formal analysis, Writing - original draft, Writing - review & editing. Steven Sanche: Methodology, Formal analysis. Nick Hengartner: Methodology, Formal analysis.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We would like to thank Alan Perelson for suggestions and critical reading of the manuscript. The work is partially funded by the Laboratory Directed Research and Development (LDRD) Rapid Response Program through the Center for Nonlinear Studies at Los Alamos National Laboratory. RK and SS would like to acknowledge funding from DARPA (HR0011938513) and the Center for Nonlinear Studies. ERS was funded through the NIH grant (R01AI135946).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jtbi.2021.110621.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- Ali S.T., Wang L., Lau E.H.Y., Xu X.K., Du Z., Wu Y., Leung G.M., Cowling B.J. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science. 2020 doi: 10.1126/science.abc9004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., May R.M. Oxford University Press; 1991. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
- Antia A., Ahmed H., Handel A., Carlson N.E., Amanna I.J., Antia R., Slifka M. Heterogeneity and longevity of antibody memory to viruses and vaccines. PLoS Biol. 2018;16 doi: 10.1371/journal.pbio.2006601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Backer J.A., Klinkenberg D., Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 January 2020. Eur. Surveill. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.5.2000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-On, Y.M., Sender, R., Flamholz, A.I., Philips, R., Milo, R., 2020. A quantitative compendium of COVID-19 epidemiology. arXiv preprint arXiv:2006.01283.
- Bi Q., Wu Y., Mei S., Ye C., Zou X., Zhang Z., Liu X., Wei L., Truelove S.A., Zhang T., Gao W., Cheng C., Tang X., Wu X., Wu Y., Sun B., Huang S., Sun Y., Zhang J., Ma T., Lessler J., Feng T. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britton T., Ball F., Trapman P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science. 2020 doi: 10.1126/science.abc6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham K.P., Anderson D.R. Springer; 2002. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. [Google Scholar]
- Callow K.A., Parry H.F., Sergeant M., Tyrrell D.A. The time course of the immune response to experimental coronavirus infection of man. Epidemiol. Infect. 1990;105:435–446. doi: 10.1017/s0950268800048019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao W.C., Liu W., Zhang P.H., Zhang F., Richardus J.H. Disappearance of antibodies to SARS-associated coronavirus after recovery. N. Engl. J. Med. 2007;357:1162–1163. doi: 10.1056/NEJMc070348. [DOI] [PubMed] [Google Scholar]
- Chan K.H., Chan J.F., Tse H., Chen H., Lau C.C., Cai J.P., Tsang A.K., Xiao X., To K.K., Lau S.K., Woo P.C., Zheng B.J., Wang M., Yuen K.Y. Cross-reactive antibodies in convalescent SARS patients' sera against the emerging novel human coronavirus EMC (2012) by both immunofluorescent and neutralizing antibody tests. J. Infect. 2013;67:130–140. doi: 10.1016/j.jinf.2013.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehning J., Zierenberg J., Spitzner F.P., Wibral M., Neto J.P., Wilczek M., Priesemann V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science. 2020;369 doi: 10.1126/science.abb9789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorigatti I., Okell L., Cori A., Imai N., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-Dannenburg G., FitzJohn R., Xi X., Donnelly C., Ghani A., Neil F. 2020. Severity of 2019-novel Coronavirus (nCoV)https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-severity-10-02-2020.pdf (accessed Mar 30, 2020) [Google Scholar]
- Du Z., Xu X., Wu Y., Wang L., Cowling B.J., Meyers L.A. Serial interval of COVID-19 among publicly reported confirmed cases. Emerg. Infect. Dis. 2020;26:1341–1343. doi: 10.3201/eid2606.200357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., Whittaker C., Zhu H., Berah T., Eaton J.W., Monod M., Imperial College C.-R.-T., Ghani A.C., Donnelly C.A., Riley S.M., Vollmer M.A.C., Ferguson N.M., Okell L.C., Bhatt S. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020 doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- Ganyani T., Kremer C., Chen D., Torneri A., Faes C., Wallinga J., Hens N. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Euro. Surveill. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.17.2000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomes, M.G.M., Corder, R.M., King, J.G., Langwig, K.E., Souto-Maior, C., Carneiro, J., Goncalves, G., Penha-Goncalves, C., Ferreira, M.U., Aguas, R., 2020. Individual variation in susceptibility or exposure to SARS-CoV-2 lowers the herd immunity threshold. medRxiv, 2020.04.27.20081893. Doi: 10.1101/2020.04.27.20081893. [DOI] [PMC free article] [PubMed]
- Grasselli G., Pesenti A., Cecconi M. Critical care utilization for the COVID-19 outbreak in Lombardy, Italy: early experience and forecast during an emergency response. JAMA. 2020 doi: 10.1001/jama.2020.4031. [DOI] [PubMed] [Google Scholar]
- He X., Lau E.H.Y., Wu P., Deng X., Wang J., Hao X., Lau Y.C., Wong J.Y., Guan Y., Tan X., Mo X., Chen Y., Liao B., Chen W., Hu F., Zhang Q., Zhong M., Wu Y., Zhao L., Zhang F., Cowling B.J., Li F., Leung G.M. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020;26:672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- Jackson L.A., Anderson E.J., Rouphael N.G., Roberts P.C., Makhene M., Coler R.N., McCullough M.P., Chappell J.D., Denison M.R., Stevens L.J., Pruijssers A.J., McDermott A., Flach B., Doria-Rose N.A., Corbett K.S., Morabito K.M., O'Dell S., Schmidt S.D., Swanson P.A., 2nd, Padilla M., Mascola J.R., Neuzil K.M., Bennett H., Sun W., Peters E., Makowski M., Albert J., Cross K., Buchanan W., Pikaart-Tautges R., Ledgerwood J.E., Graham B.S., Beigel J.H. An mRNA vaccine against SARS-CoV-2 – preliminary report. N. Engl. J. Med. 2020 doi: 10.1056/NEJMoa2022483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ke, R., Sanche, S., Romero-Severson, E., Hengartner, N., 2020. Fast spread of COVID-19 in Europe and the US suggests the necessity of early, strong and comprehensive interventions. medRxiv, 2020.04.04.20050427. Doi: 10.1101/2020.04.04.20050427.
- Kissler S.M., Tedijanto C., Goldstein E., Grad Y.H., Lipsitch M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science. 2020;368:860–868. doi: 10.1126/science.abb5793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong W.H., Li Y., Peng M.W., Kong D.G., Yang X.B., Wang L., Liu M.Q. SARS-CoV-2 detection in patients with influenza-like illness. Nat. Microbiol. 2020;5:675–678. doi: 10.1038/s41564-020-0713-1. [DOI] [PubMed] [Google Scholar]
- Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Centre for Mathematical Modelling of Infectious Diseases C.-W.G. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 2020;20:553–558. doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 2020;172:577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavezzo E., Franchin E., Ciavarella C., Cuomo-Dannenburg G., Barzon L., Del Vecchio C., Rossi L., Manganelli R., Loregian A., Navarin N., Abate D., Sciro M., Merigliano S., De Canale E., Vanuzzo M.C., Besutti V., Saluzzo F., Onelia F., Pacenti M., Parisi S., Carretta G., Donato D., Flor L., Cocchio S., Masi G., Sperduti A., Cattarino L., Salvador R., Nicoletti M., Caldart F., Castelli G., Nieddu E., Labella B., Fava L., Drigo M., Gaythorpe K.A.M., Imperial College C.-R.T., Brazzale A.R., Toppo S., Trevisan M., Baldo V., Donnelly C.A., Ferguson N.M., Dorigatti I., Crisanti A. Suppression of a SARS-CoV-2 outbreak in the Italian municipality of Vo'. Nature. 2020 doi: 10.1038/s41586-020-2488-1. [DOI] [PubMed] [Google Scholar]
- Lavine J.S., Bjornstad O.N., Antia R. Immunological characteristics govern the transition of COVID-19 to endemicity. Science. 2021 doi: 10.1126/science.abe6522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Bert N., Tan A.T., Kunasegaran K., Tham C.Y.L., Hafezi M., Chia A., Chng M.H.Y., Lin M., Tan N., Linster M., Chia W.N., Chen M.I., Wang L.F., Ooi E.E., Kalimuddin S., Tambyah P.A., Low J.G., Tan Y.J., Bertoletti A. SARS-CoV-2-specific T cell immunity in cases of COVID-19 and SARS, and uninfected controls. Nature. 2020 doi: 10.1038/s41586-020-2550-z. [DOI] [PubMed] [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S.M., Lau E.H.Y., Wong J.Y., Xing X., Xiang N., Wu Y., Li C., Chen Q., Li D., Liu T., Zhao J., Liu M., Tu W., Chen C., Jin L., Yang R., Wang Q., Zhou S., Wang R., Liu H., Luo Y., Liu Y., Shao G., Li H., Tao Z., Yang Y., Deng Z., Liu B., Ma Z., Zhang Y., Shi G., Lam T.T.Y., Wu J.T., Gao G.F., Cowling B.J., Yang B., Leung G.M., Feng Z. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., Rivers C., Tan Q., Murray M.B., Toner E., Lipsitch M. Estimated demand for US hospital inpatient and intensive care unit beds for patients with COVID-19 based on comparisons with Wuhan and Guangzhou, China. JAMA Netw. Open. 2020;3 doi: 10.1001/jamanetworkopen.2020.8297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368:489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipsitch M., Cohen T., Cooper B., Robins J.M., Ma S., James L., Gopalakrishna G., Chew S.K., Tan C.C., Samore M.H., Fisman D., Murray M. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300:1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long Q.X., Tang X.J., Shi Q.L., Li Q., Deng H.J., Yuan J., Hu J.L., Xu W., Zhang Y., Lv F.J., Su K., Zhang F., Gong J., Wu B., Liu X.M., Li J.J., Qiu J.F., Chen J., Huang A.L. Clinical and immunological assessment of asymptomatic SARS-CoV-2 infections. Nat. Med. 2020 doi: 10.1038/s41591-020-0965-6. [DOI] [PubMed] [Google Scholar]
- Mello M.M., Silverman R.D., Omer S.B. Ensuring uptake of vaccines against SARS-CoV-2. N. Engl. J. Med. 2020 doi: 10.1056/NEJMp2020926. [DOI] [PubMed] [Google Scholar]
- Mizumoto K., Kagaya K., Zarebski A., Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eur. Surveill. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.10.2000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moderna I. 2020. Moderna’s COVID-19 Vaccine Candidate Meets its Primary Efficacy Endpoint in the First Interim Analysis of the Phase 3 COVE Study.https://investors.modernatx.com/news-releases/news-release-details/modernas-covid-19-vaccine-candidate-meets-its-primary-efficacy (accessed: 11/24/2020) [Google Scholar]
- Ng Y., Li Z., Chua Y.X., Chaw W.L., Zhao Z., Er B., Pung R., Chiew C.J., Lye D.C., Heng D., Lee V.J. Evaluation of the effectiveness of surveillance and containment measures for the first 100 patients with COVID-19 in Singapore – January 2–February 29, 2020. MMWR Morb. Mortal Wkly. Rep. 2020;69:307–311. doi: 10.15585/mmwr.mm6911e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, S.W., Bolker, B.M., Champredon, D., Earn, D.J.D., Li, M., Weitz, J.S., Grenfell, B.T., Dushoff, J., 2020. Reconciling early-outbreak estimates of the basic reproductive number and its uncertainty: framework and applications to the novel coronavirus (SARS-CoV-2) outbreak. medRxiv, 2020.01.30.20019877. Doi: 10.1101/2020.01.30.20019877. [DOI] [PMC free article] [PubMed]
- Payne D.C., Iblan I., Rha B., Alqasrawi S., Haddadin A., Al Nsour M., Alsanouri T., Ali S.S., Harcourt J., Miao C., Tamin A., Gerber S.I., Haynes L.M., Al Abdallat M.M. Persistence of antibodies against middle east respiratory syndrome coronavirus. Emerg. Infect. Dis. 2016;22:1824–1826. doi: 10.3201/eid2210.160706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellis, L., Scarabel, F., Stage, H. B., Overton, C.E., Chappell, L.H.K., Lythgoe, K.A., Fearon, E., Bennett, E., Curran-Sebastian, J., Das, R., Fyles, M., Lewkowicz, H., Pang, X., Vekaria, B., Webb, L., House, T.A., Hall, I., 2020. Challenges in control of Covid-19: short doubling time and long delay to effect of interventions. medRxiv, 2020.04.12.20059972. doi: 10.1101/2020.04.12.20059972. [DOI] [PMC free article] [PubMed]
- Pfizer I. 2020. Pfizer and Biontech Conclude Phase 3 Study of Covid-19 Vaccine Candidate, Meeting all Primary Efficacy Endpoints.https://www.pfizer.com/news/press-release/press-release-detail/pfizer-and-biontech-conclude-phase-3-study-covid-19-vaccine (accessed: 11/24/2020) [Google Scholar]
- Rader, B., Scarpino, S., Nande, A., Hill, A., Reiner, R., Pigott, D., Gutierrez, B., Shrestha, M., Brownstein, J., Castro, M., Tian, H., Pybus, O., Kraemer, M.U.G., 2020. Crowding and the epidemic intensity of COVID-19 transmission. medRxiv, 2020.04.15.20064980. Doi: 10.1101/2020.04.15.20064980.
- Riou J., Althaus C.L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eur. Surveill. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.4.2000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romero-Severson E.O., Hengartner N., Meadors G., Ke R. Change in global transmission rates of COVID-19 through May 6 2020. PLoS One. 2020;15 doi: 10.1371/journal.pone.0236776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salje H., Tran Kiem C., Lefrancq N., Courtejoie N., Bosetti P., Paireau J., Andronico A., Hoze N., Richet J., Dubost C.L., Le Strat Y., Lessler J., Levy-Bruhl D., Fontanet A., Opatowski L., Boelle P.Y., Cauchemez S. Estimating the burden of SARS-CoV-2 in France. Science. 2020;369:208–211. doi: 10.1126/science.abc3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanche S., Lin Y.T., Xu C., Romero-Severson E., Hengartner N., Ke R. High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2. Emerg. Infect. Dis. 2020;26:1470–1477. doi: 10.3201/eid2607.200282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seow, J., Graham, C., Merrick, B., Acors, S., Steel, K.J.A., Hemmings, O., O'Bryne, A., Kouphou, N., Pickering, S., Galao, R., Betancor, G., Wilson, H.D., Signell, A.W., Winstone, H., Kerridge, C., Temperton, N., Snell, L., Bisnauthsing, K., Moore, A., Green, A., Martinez, L., Stokes, B., Honey, J., Izquierdo-Barras, A., Arbane, G., Patel, A., Oconnell, L., O Hara, G., MacMahon, E., Douthwaite, S., Nebbia, G., Batra, R., Martinez-Nunez, R., Edgeworth, J.D., Neil, S.J.D., Malim, M.H., Doores, K., 2020. Longitudinal evaluation and decline of antibody responses in SARS-CoV-2 infection. medRxiv, 2020.07.09.20148429. Doi: 10.1101/2020.07.09.20148429.
- Silverman J.D., Hupert N., Washburne A.D. Using influenza surveillance networks to estimate state-specific prevalence of SARS-CoV-2 in the United States. Sci. Transl. Med. 2020 doi: 10.1126/scitranslmed.abc1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang B., Wang X., Li Q., Bragazzi N.L., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020;9 doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson R.N., Hollingsworth T.D., Isham V., Arribas-Bel D., Ashby B., Britton T., Challenor P., Chappell L.H.K., Clapham H., Cunniffe N.J., Dawid A.P., Donnelly C.A., Eggo R.M., Funk S., Gilbert N., Glendinning P., Gog J.R., Hart W.S., Heesterbeek H., House T., Keeling M., Kiss I.Z., Kretzschmar M.E., Lloyd A.L., McBryde E.S., McCaw J.M., McKinley T.J., Miller J.C., Morris M., O'Neill P.D., Parag K.V., Pearson C.A.B., Pellis L., Pulliam J.R.C., Ross J.V., Tomba G.S., Silverman B.W., Struchiner C.J., Tildesley M.J., Trapman P., Webb C.R., Mollison D., Restif O. Key questions for modelling COVID-19 exit strategies. Proc. Biol. Sci. 2020;287:20201405. doi: 10.1098/rspb.2020.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wearing H.J., Rohani P., Keeling M.J. Appropriate models for the management of infectious diseases. PLoS Med. 2005;2 doi: 10.1371/journal.pmed.0020174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO . 2020. Pneumonia of Unknown Cause – China. (accessed January 30, 2020) [Google Scholar]
- Wolfel R., Corman V.M., Guggemos W., Seilmaier M., Zange S., Muller M.A., Niemeyer D., Jones T.C., Vollmar P., Rothe C., Hoelscher M., Bleicker T., Brunink S., Schneider J., Ehmann R., Zwirglmaier K., Drosten C., Wendtner C. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581:465–469. doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.T., Leung K., Bushman M., Kishore N., Niehus R., de Salazar P.M., Cowling B.J., Lipsitch M., Leung G.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat. Med. 2020;26:506–510. doi: 10.1038/s41591-020-0822-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Xiang J., Wang Y., Song B., Gu X., Guan L., Wei Y., Li H., Wu X., Xu J., Tu S., Zhang Y., Chen H., Cao B. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet. 2020 doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou L., Ruan F., Huang M., Liang L., Huang H., Hong Z., Yu J., Kang M., Song Y., Xia J., Guo Q., Song T., He J., Yen H.L., Peiris M., Wu J. SARS-CoV-2 viral load in upper respiratory specimens of infected patients. N. Engl. J. Med. 2020;382:1177–1179. doi: 10.1056/NEJMc2001737. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.