Mathematical modeling with optimal control analysis of social media addiction

Abstract

In this paper, we developed a deterministic mathematical model of social media addiction (SMA) with an optimal control strategy. Major qualitative analysis like the social media addiction free equilibrium point (E₀), endemic equilibrium point (E∗), basic reproduction number $\left({\mathcal{R}}_0\right)$, were computed. From the stability analysis, we found that the social media addiction free equilibrium point (SMAFEP) is locally asymptotically stable if ${\mathcal{R}}_0<1$. The global asymptotic stablity of SMAFEP is stablished using Castillo-Chavez theorem. If ${\mathcal{R}}_0>1$ the unique endemic equilibruim is locally assymptotically stable. Also using Center Manifold theorem, the model exhabits a forward bifurcation at ${\mathcal{R}}_0=1$. The sensitivity of model parameters is done using the normalized forward sensitivity index definition. Secondly, we introduced two time dependent controls on the basic model and formulated an optimal control model. Then, we used the Pontryagin’s maximum principle to find the optimal system of the model. Numerical simulations, on the optimal control problem using the fourth-order Range-Kutta forward-backward sweep method, on the suggested strategies for SMA is performed. We found that to effectively control SMA at a specified period of time, stakeholders and policymakers must apply the integrated control strategies C.

1. Introduction

In recent decades, the forms of social communication have fundamentally changed due to the advancement of information technology, in particular the rapid growth of social media with the internet (Anise et al., 2013; Deborah et al., 2019; Guedes et al., 2016; Siddiqui & Sigh, 2016). When appropriately used, social media is an important technology that provides people with vital skills, such as access to information, problem-solving, business, self-directed learning and others (Ali et al., 2019; Hou et al., 2019; Shek et al., 2008; Siddiqui & Sigh, 2016). However, individuals that are using it improperly affect them negatively (Monacis et al., 2017; Shek et al., 2008; Siddiqui & Sigh, 2016). From the negative effects, the most significant is addiction of social media (Ali et al., 2019; Monacis et al., 2017; Shek et al., 2008). Like gambling, alcohol and drugs, social media addiction seems to be harmless, but it is a growing epidemic that needs to be addressed (Chakraborty et al., 2010). Social media addiction is a term that is often used to refer to someone who spends too much time on social media like Instagram, Twitter, Facebook, YouTube or other forms of social media (Hou et al., 2019).

Social media addiction is a growing problem in the 21st century (Ali et al., 2019; Guedes et al., 2016; Kolan & Dzandza, 2018). Consequently, a number of studies on this subject have been conducted in different countries (Ali et al., 2019; Anise et al., 2013; Deborah et al., 2019; Kolan & Dzandza, 2018; Monacis et al., 2017; Shek et al., 2008). This addiction activities can lead to serious problems at school, work, and home in turn affecting the society at large (Guedes et al., 2016; Siddiqui & Sigh, 2016). This problem must be mitigated until it has any more serious effects than we are looking now (Chakraborty et al., 2010; Kolan & Dzandza, 2018). The best way to do so is to consider the consequences of social media addiction. Like all other diseases and problems, there are treatments and approaches to social media addiction. Advertisements and education about the negative effects of social media is taken as a control technique. The other strategy is using treatment approachs such us; turning off the notifications, limit your time spent on social media, deleted the apps, disconnect and unplug yourself, never bring your smartphone into your bedroom and others (ALRushaidan et al., 2018; Brevers & Turel, 2019; Hou et al., 2019; Shek et al., 2008).

Mathematical modelling plays an important role in comprehending and providing useful techniques to predict and control the dynamics of infectious disease (Murray, 2007). Many scholars have applied infectious disease dynamics model to smoking, alcoholism, drug addiction, game addiction, social media addition and other issues. From these authors, some were applied modeling for alcoholic addiction (Adu et al., 2017; Hou et al., 2019; Khajji et al., 2020; Ma et al., 2015; Sharma & Samanta, 2013), some were used modeling for online game addiction (Guo & Li, 2020; Li & Guo, 2019), others for social media impact on academic performance (Ishaku et al.,). Authors were applied optimal control techniques in order to understand how the spread of above addictions may be controlled with optimal implementation costs (Guo & Li, 2020; Li & Guo, 2019; Wang et al., 2014). However, to the best of our knowledge, no one has investigated social media addiction with an optimal control model. Therefore, in this paper we are interested in filling this gap.

The structure of the paper is organized as follows. In Section 2, we describe and formulate the mathematical model. Section 3 is dedicated to investigate model analysis including the basic reproduction number, the stability analysis, bifurcation & sensitivity analysis of model. Section 4 is devoted to formulation of optimal control problem & drived the optimality system. On the other hand, numerical simulations are presented in Section 5. Finally, we give conclusions in Section 6.

2. Model construction

In this section, we consider a deterministic mathematical model for the construction of a mathematical model for SMA with the following assumptions: the SMA epidemic occurs in a closed environment, sex, race and social status do not affect the probability of becoming addicted to the social media, members mix homogeneously (have the same interaction to the same degree) and social media addictive’s transmite to non-addictive’s when they are in contact with peer pressure of addictive.

In this model we divide the human population into five subpopulations representing addiction status. Susceptible individuals (denoted by S) are those who are not addicted but susceptible to social media addiction. Exposed individuals (Denoted by E) are those who use social media less frequently but do not grow to the addicted stage. Addicted individuals (denoted by A) are individuals who are addicted to social media and spent most of their time on it. Recovered individuals (denoted by R) are those individuals who recovered from the SMA. Those who permanently do not use and quit using social media are denoted by Q.

Susceptible individuals are recruited into the population at rate π. These individuals start using social media by the peer pressure contact rate of β from addicted with probability of transmission σ and move to the exposed compartment. Some susceptible individuals join to subpopulation who do not permanently use social media at a rate k. The exposed individuals become addicted and join the addicted compartment at rate αδ and the remaining proportion of this exposed individuals recovered through treatments at a rate (1 − α)δ. Either through education and/or treatment the addicted individuals move to the recovered compartment at a rate of ϵ, or died due to addiction at a rate of ρ. The recovered individuals become again susceptible to the SMA at a rate of γη or totally stop using social media at a rate (1 − γ)η. The whole population have an average death rate of μ. The parameters are described in Table 2. The flow diagram of the model is shown in Fig. 1.

Table 2.

Description of parameters of the SMA model (1).

parameter	Description	Value	Source
π	Recruitment rate of subseptible individuals	0.5	Assumed
μ	Natural death rate	0.25	Wang et al. (2014)
β	Transmission rate of addiction to the susceptible individuals	0.6	Wang et al. (2014)
σ	Contact rate of subseptible individuals with addicted individuals	0.5	Wang et al. (2014)
α	Proportion of exposed individuals that join addicted class	0.7	Guo and Li (2020)
ρ	Induce death rate	0.01	Assumed
δ	Individuals that leave exposed class	0.25	Guo and Li, (2020)
ϵ	Addicted individuals that join recovered class due to the treatment	0.7	Huo and Wang, (2014)
k	subseptible individuals that don’t use and/or quit from using social media	0.01	Assumed
γ	Proportion of recovered individuals susceptible to SMA	0.35	Li and Guo, (2019)
η	Individuals that leave recovered class	0.4	Huo and Wang, (2014)

Fig. 1.

Compartmental diagram for the transmission dynamics of SMA.

Setting the above considerations together and flow diagram shown in Fig. 1 the following system of nonlinear differential equations describe the dynamics of SMA in human population:

$$\begin{array}{cc}\frac{dS}{dt}& =\pi +\gamma \eta R-\beta \sigma AS-\left(k+\mu \right)S\\ \frac{dE}{dt}& =\beta \sigma AS-\left(\delta +\mu \right)E\\ \frac{dA}{dt}& =\alpha \delta E-\left(\mu +ϵ+\rho \right)A\\ \frac{dR}{dt}& =\left(1-\alpha \right)\delta E+ϵA-\left(\mu +\eta \right)R\\ \frac{dQ}{dt}& =kS+\left(1-\gamma \right)\eta R-\mu Q,\end{array}$$ (1)

with the initial condition

$$S\left(0\right)>0,E\left(0\right)\ge 0,A\left(0\right)\ge 0,R\left(0\right)\ge 0,Q\left(0\right)\ge 0.$$

3. Model analysis

3.1. Invariant region

The following theorem ensures the boundedness of the model (1).

Theorem 3.1

If the initial conditions of the model(1) are with in

$$\mathrm{\Omega }=\left\{\left(S,E,A,R,Q\right)\in {\mathcal{R}}_{+}^5:0<N\left(t\right)\le \left(\frac{\pi }{\mu }\right)\right\}$$

then all solutions of the system equations of the model enter and remain in Ω.

Proof

Given the set (S(t), E(t), A(t), R(t), Q(t)) with any solution of the system(1), and

$$N=S+E+A+R+Q.$$

Then we have

$$\frac{dN}{dt}\le \pi -\mu N-\rho A.$$ (2)

If there is no death due to the SMA, equation (2) becomes

$$\frac{dN}{dt}\le \pi -\mu N.$$ (3)

The solution of equation (3) given by, $N\left(t\right)\le N\left(0\right){\exp }^{-\mu t}+\frac{\pi }{\mu }\left(1-{\exp }^{-\mu t}\right)$. Then, as t → ∞, $N\left(t\right)\to \frac{\pi }{\mu }$. Hence the model positively invariant region is given by:

$$\mathrm{\Omega }=\left\{\left(S,E,A,R,Q\right)\subset {\mathcal{R}}_{+}^5:0<N\left(t\right)\le \left(\frac{\pi }{\mu }\right)\right\}$$

3.2. Positivity of solutions

It is necessary to prove that all solutions of system (1) with non negative initial data should remain non negative for future time t > 0. This will be established with the following theorem:

Theorem 3.2

Given that the initial values S(0) > 0, E(0) > 0, A(0) > 0, R(0) > 0, Q(0) > 0. Then the solutions S(t), E(t), A(t), R(t), Q(t) of system (1) are positive for all t ≥ 0.

Proof

From the first equation of the system (1)

$$\frac{dS}{dt}=\pi +\gamma \eta R-\beta \sigma AS-\left(k+\mu \right)S$$

$$\le \pi -\left(k+\mu \right)S$$

Then we have

$$\frac{dS}{\pi -\left(k+\mu \right)S}\le dt$$

⇒

$$S\left(t\right)\le S\left(0\right){\exp }^{-\left(k+\mu \right)t}+\frac{\pi }{k+\mu }\left(1-{\exp }^{-\left(k+\mu \right)t}\right)$$

As t → ∞, we obtain $0\le S\left(t\right)\le \frac{\pi }{k+\mu }$. By the same procedure, we obtained

$$E\left(t\right)\ge E\left(0\right){\exp }^{-\left(\mu +\delta \right)t}\ge 0,$$

$$A\left(t\right)\ge A\left(0\right){\exp }^{-\left(\mu +ϵ+\rho \right)t}\ge 0,$$

$$R\left(t\right)\ge R\left(0\right){\exp }^{-\left(\mu +\eta \right)t}\ge 0,$$

$$Q\left(t\right)\ge Q\left(0\right){\exp }^{-\mu t}\ge 0.$$

Hence all feasible solutions of system (1) lies in the region Ω. Thus the model is epidemiologically meaningful and mathematically well posed. □

3.3. Social media addiction free equilibrium Point(SMAFEP)

In absence of the addiction of social media, we assume that E = A = 0. Therefore the SMAFEP is given by:

$$E_0=\left(\frac{\pi }{k+\mu },0,0,0,\frac{k\pi }{\mu \left(\mu +k\right)}\right).$$ (4)

3.4. Basic reproduction number

To analyze the stability of the equilibrium points, the basic reproduction number ${\mathcal{R}}_0$ of the model is important. It is obtained by the next-generation matrix method and by the principle then system (1) can be written as:

$$\begin{array}{cc}\frac{dE}{dt}& =\beta \sigma AS-\left(\delta +\mu \right)E\\ \frac{dA}{dt}& =\alpha \delta E-\left(\mu +ϵ+\rho \right)A\\ \frac{dR}{dt}& =\left(1-\alpha \right)\delta E+ϵA-\left(\mu +\eta \right)R\end{array}$$ (5)

Then, we have

$$F=\left(\begin{array}{c}\beta \sigma AS\\ 0\\ 0\end{array}\right)andV=\left(\begin{array}{c}\left(\delta +\mu \right)E-\alpha \delta E+\left(\mu +ϵ+\rho \right)A-\left(1-\alpha \right)\delta E-ϵA+\left(\mu +\eta \right)R\end{array}\right)$$ (6)

The jacobian matrices at SMAFEP of the matrices in equation (6) is given as:

$$\mathcal{F}=\left(\begin{array}{ccc}0& \frac{\beta \pi \sigma }{k+\mu }& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)and\mathcal{V}=\left(\begin{array}{c}\delta +\mu 00-\alpha \delta -\left(\alpha -1\right)\delta \\ \mu +ϵ+\rho 0-\left(\alpha -1\right)\delta -\left(\alpha -1\right)\delta \\ & -ϵ& \eta +\mu \end{array}\right)$$ (7)

Hence, the basic reproduction number is obtained as:

$${\mathcal{R}}_0=\frac{\beta \pi \alpha \delta \sigma }{\left(k+\mu \right)\left(\delta +\mu \right)\left(\mu +ϵ+\rho \right)}$$ (8)

3.5. Local stability of DFE

Theorem 3.3

The SMAFEP is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable otherwise.

Proof

The linearization of the model (1) is given by:

$$J=\left(\begin{array}{ccccc}-\beta \sigma A-\kappa -\mu & 0& -\beta S\sigma & \gamma \eta & 0\\ \beta \sigma A& -\delta -\mu & \beta S\sigma & 0& 0\\ 0& \alpha \delta & -\epsilon -\rho -\mu & 0& 0\\ 0& \left(1-\alpha \right)\delta & \epsilon & -\eta -\mu & 0\\ \kappa & 0& 0& \left(1-\gamma \right)\eta & -\mu \end{array}\right)$$ (9)

Evaluating equation (9) at the SMAFEP $E_0=\left(\frac{\pi }{k+\mu },0,0,0,\frac{k\pi }{\mu \left(k+\mu \right)}\right)$, we get:

$$J=\left(\begin{array}{ccccc}-k-\mu & 0& -\frac{\beta \pi \sigma }{\kappa +\mu }& \gamma \eta & 0\\ 0& -\delta -\mu & \frac{\beta \pi \sigma }{\kappa +\mu }& 0& 0\\ 0& \alpha \delta & -\epsilon -\rho -\mu & 0& 0\\ 0& \left(1-\alpha \right)\delta & \epsilon & -\eta -\mu & 0\\ k& 0& 0& \left(1-\gamma \right)\eta & -\mu \end{array}\right)$$ (10)

From the matrix in equation (10), some of the negative eigen values are

$$-\mu ,-\left(\mu +k\right),-\left(\mu +\eta \right),-\left(\mu +\delta \right),$$

the other eigenvalues are obtained from the quadratic equation:

$${\lambda }^2+{\psi }_1\lambda +{\psi }_2=0,$$ (11)

where ψ₁ = ϵ + ρ + δ + 2μ and ${\psi }_2=\left(\delta +\mu \right)\left(ϵ+\rho +\mu \right)-\frac{\beta \pi \alpha \delta \sigma }{k+\mu }$.

To see the negativity of the two roots, we used Routh-Hurwitz criteria and by the principle equation (11) has strictly negative real root iff ψ₁ > 0, ψ₂ > 0 and ψ₁ψ₂ > 0. It is clear that ψ₁ > 0 and ψ₂ can be written as

$$\begin{array}{cc}{\psi }_2& =\left(\delta +\mu \right)\left(ϵ+\rho +\mu \right)\left(1-\frac{\beta \pi \alpha \delta \sigma }{\left(k+\mu \right)\left(\delta +\mu \right)\left(ϵ+\rho +\mu \right)}\right)\\ & =\left(\delta +\mu \right)\left(ϵ+\rho +\mu \right)\left(1-{\mathcal{R}}_0\right)>0.\end{array}$$

Hence the SMAFEP is locally asymptotically stable if ${\mathcal{R}}_0<1$. □

3.6. Global stability of SMAFEP

In this paper we investigate global asymptotic stability of the SMAFEP using Castillo-Chavez theorem (Castillo-Chavez et al., 2002). We rewrite model (1) in the form:

$$\left\{\begin{array}{c}\frac{dX}{dt}=F\left(X,Y\right),\\ \frac{dY}{dt}=G\left(X,Y\right),G\left(X,0\right)=0\end{array}\right)$$ (12)

where $X=\left(S,R,Q\right)\in {\mathcal{R}}^3$ denotes uninfected populations and $Y=\left(E,A\right)\in {\mathcal{R}}^2$ denotes the infected population. Let E₀ = (X∗, 0) represents the SMAFEP of the system.

E₀ to be globally asymptotically stable equilibrium for the model, the conditions (H₁) and (H₂) below should be satisfied:

H₁: For $\frac{dX}{dt}=F\left(X,0\right),X^{\ast }$ is globally asymptotically stable.

H₂: $\frac{dZ}{dt}=D_{Z}G\left(X^{\ast },0\right)Z-\widehat{G}\left(X,Z\right),\widehat{G}\left(X,Z\right)\ge 0forall\left(X,Z\right)\in \mathrm{\Omega }$.where D_ZG(X∗, 0) is the Jacobian of G(X,Z) taken in (E, I, P) and evaluated at (X∗, 0) = (K, 0, 0, 0). If the system in equation (12) satisfies the above conditions, then according to (Castillo-Chavez et al., 2002) the following theorem holds true.

Theorem 3.4

The equilibrium point E₀ = (X∗, 0) of the system (12) is globally asymptotically stable if ${\mathcal{R}}_0<1$ and the conditions (i) and (ii) are satisfied.

Proof

We start the proof by defining new variables and dividing the system into subsystems. X = (S, R, Q) and Y = (E, A). From equation (12) we have two functions G(X, Y) and F(X, Y) given by:

$$F\left(X,Y\right)=\left(\begin{array}{c}\pi +\gamma \eta R-\beta \sigma AS-\left(k+\mu \right)S\\ \left(1-\alpha \right)\delta E+ϵA-\left(\eta +\mu \right)R\\ kS+\left(1-\gamma \right)\eta R-\mu Q\end{array}\right)$$

and

$$G\left(X,Y\right)=\left(\begin{array}{c}\beta \sigma AS-\left(\delta +\mu \right)E\\ \alpha \delta E-\left(\mu +ϵ+\rho \right)A\end{array}\right)$$

Now consider the reduced system $\frac{dX}{dt}=F\left(X,0\right)$ from condition H₁

$$\left\{\begin{array}{c}\frac{dS}{dt}=\pi -\left(k+\mu \right)S,\\ \frac{dR}{dt}=0\\ \frac{dQ}{dt}=kS-\mu Q\end{array}\right)$$ (13)

We note that this asymptomatic dynamics is independent of the initial conditions in Ω, therefore the convergence of the solutions of the reduced system equation (13) is global in Ω.

Now we compute

$$D_{Y}G\left(X^{\ast },0\right)=\left(\begin{array}{cc}-\left(\mu +\delta \right)& \frac{\beta \sigma \pi }{k+\mu }\\ \alpha \delta & -\left(\mu +ϵ+\rho \right)\end{array}\right),$$

From the expression in condition H₂, we get

$$\widehat{G}\left(X,Y\right)=\left(\begin{array}{c}\beta \sigma A\left(\frac{\pi }{k+\mu }-S\right)\\ 0\end{array}\right).$$

Here, since $X^{\ast }=\frac{\pi }{k+\mu }\ge S$, it is clear that $\widehat{G}\left(X,Y\right)\ge 0$ for all (X, Y) ∈Ω. Therefore, by LaSalle’s invariance principle (LaSalle, 1976) this proves that SMAFEP is globally asymptotically stable. □

3.7. The endemic equilibrium point

If SMA persists with in the population (i.e S(t) ≥ 0, E(t) ≥ 0, A(t) ≥ 0, R(t) ≥ 0, Q(t) ≥ 0), the model has an equilibruim point called endemic equilibrium point denoted by E∗ = (S∗, E∗, A∗, R∗, Q∗)≠0. It can be obtained by equating each equation of the system equal to zero. I.e

$$\frac{dS}{dt}=\frac{dE}{dt}=\frac{dA}{dt}=\frac{dR}{dt}=\frac{dQ}{dt}=0,$$

Then, we obtain

$$\begin{array}{cc}{S}^{\ast }& =\frac{\left(\mu +\delta \right)\left(\mu +ϵ+\rho \right)}{\alpha \beta \delta \sigma },\\ E^{\ast }& =\frac{\left(\epsilon +\rho +\mu \right){\varphi }_1}{\beta \delta \alpha \sigma {\varphi }_2},\\ A^{\ast }& =\frac{{\varphi }_1}{\beta \sigma {\varphi }_2},\\ R^{\ast }& =\frac{\left(\alpha \mu +\alpha \rho -\epsilon -\mu -\rho \right)\left[\pi \alpha \beta \delta \sigma -\left(\mu +\delta \right)\left(k+\mu \right)\left(\mu +ϵ+\rho \right)\right]}{\alpha \beta \sigma {\varphi }_2},\\ Q^{\ast }& =\frac{k{S}^{\ast }+\left(1-\gamma \right)\eta R^{\ast }}{\mu },\end{array}$$

where

$$\begin{array}{cc}{\varphi }_1& =\pi \alpha \delta \beta \sigma \left(\eta +\mu \right)-\left(k+\mu \right)\left(\delta ϵ\eta +\delta ϵ\mu +ϵ\eta \mu \right)-\left(\rho +\mu \right)\left(k+\mu \right)\left(\mu +\delta \right)\left(\mu +\eta \right)-ϵ{\mu }^2\left(\mu +k\right).\\ {\varphi }_2& =\alpha \delta \gamma \eta \left(\rho +\mu \right)-\delta \gamma \eta \left(ϵ+\eta +\mu \right)+\left(ϵ+\rho +\mu \right)\left(\delta +\mu \right)\left(\eta +\mu \right).\end{array}$$

3.8. Bifurcation & local stability of endemic equilibrium point

To investigate the local stablity of endemic equilibrium point and the nature of bifurcation, we used the method introduced in (Castillo-Chavez & Song, 2004), as explained in (Alemneh et al., 2019a, 2019b).

Theorem 3.5

If ${\mathcal{R}}_0>1$, then the endemic equilibrium E∗ of system (1) is locally asymptotically stable in Ω and the system(1) exhibits forward bifurcation at ${\mathcal{R}}_0=1$.

Proof

Let S = x₁, E = x₂, A = x₃, R = x₄ and Q = x₅. Then model in equation (1) can be written:

$$\begin{array}{cc}\frac{d{x}_1}{dt}& =\pi +\gamma \eta x_4-\beta \sigma x_3{x}_1-\left(k+\mu \right)x_1\\ \frac{d{x}_2}{dt}& =\beta \sigma x_3{x}_1-\left(k+\mu \right)x_2\\ \frac{d{x}_3}{dt}& =\alpha \delta x_2-\left(\mu +ϵ+\rho \right)x_3\\ \frac{d{x}_4}{dt}& =\left(1-\alpha \right)\delta x_2+ϵx_3-\left(\mu +\eta \right)x_4\\ \frac{d{x}_5}{dt}& =k{x}_1+\left(1-\gamma \right)\eta x_4-\mu x_5\end{array}$$ (14)

We consider the transmission rate β as a bifurcation parameters so that ${\mathcal{R}}_0=1$ iff

$$\beta ={\beta }^{\ast }=\frac{\left(k+\mu \right)\left(\mu +\delta \right)\left(\mu +ϵ+\rho \right)}{\pi \delta \alpha \sigma }$$

The SMAFEP $\left(x_1=\frac{\pi }{k+\mu },x_2=0,x_3=0,x_4=0,x_5=\frac{k\pi }{\mu \left(k+\mu \right)}\right)$. Then the linearizion matrix of equation (14) at SMAFEP is given by:

$$J=\left(\begin{array}{ccccc}-k-\mu & 0& -\frac{\beta \pi \sigma }{k+\mu }& \gamma \eta & 0\\ 0& -\delta -\mu & \frac{\beta \pi \sigma }{k+\mu }& 0& 0\\ 0& \alpha \delta & -\epsilon -\rho -\mu & 0& 0\\ 0& \left(1-\alpha \right)\delta & \epsilon & -\eta -\mu & 0\\ k& 0& 0& \left(1-\gamma \right)\eta & -\mu \end{array}\right)$$ (15)

To compute the right eigenvector, $w={\left(w_1,w_2,w_3,w_4,w_5\right)}^T$, we consider the system Jw = 0. Then the system becomes

$$\begin{array}{c}-\left(k+\mu \right)w_1-\frac{\beta \sigma \pi }{k+\mu }{w}_3+\gamma \eta w_4=0-\left(\mu +\delta \right)w_2+\frac{\beta \sigma \pi }{k+\mu }{w}_3-\left(\mu +\delta \right)w_2+\frac{\beta \sigma \pi }{k+\mu }{w}_3\\ & =& 0\\ \alpha \delta w_2-\left(\mu +ϵ+\rho \right)w_3& =& 0\\ \left(1-\alpha \right)\delta w_2+ϵw_3-\left(\mu +\eta \right)w_4& =& 0\\ k{w}_1+\left(1-\gamma \right)\eta w_4-\mu w_5& =& 0\end{array}$$ (16)

Solving equation (16), we obtain

$$\begin{array}{cc}{w}_1& =-\frac{\delta \gamma \eta \left(1-\alpha \right)\left(\mu +ϵ+\rho \right)+\gamma \delta ϵ\alpha \eta -\left(\delta +\mu \right)\left(\mu +\eta \right)\left(\mu +ϵ+\rho \right)}{\left(k+\mu \right)\left(\eta +\mu \right)\left(\mu +ϵ+\rho \right)}{w}_2,\\ w_3& =\frac{\alpha \delta }{\mu +ϵ+\rho }{w}_2,\\ w_4& =\frac{\left(1-\alpha \right)\left(\mu +ϵ+\rho \right)\delta +\alpha \delta ϵ}{\left(\eta +\mu \right)\left(\mu +ϵ+\rho \right)}{w}_2,\\ w_5& =\frac{\phi -k\gamma \delta ϵ\alpha \eta +\mu \left(k+\mu \right)ϵ\alpha \delta }{\mu \left(k+\mu \right)\left(\eta +\mu \right)\left(\mu +ϵ+\rho \right)}{w}_2,\end{array}$$

Where $\phi =\left(\mu +ϵ+\rho \right)\left(-k\delta \gamma \eta \left(1-\alpha \right)+k\left(\delta +\mu \right)\left(\mu +\eta \right)+\mu \delta \left(k+\mu \right)\left(1-\gamma \right)\left(1-\alpha \right)\right)$.

The left eigenvector, v = (v₁, v₂, v₃, v₄, v₅) computed from vJ = 0 and we obtain

$$v_1=v_4=v_5=0,v_3=\frac{\mu +\delta }{\alpha \delta }{v}_2.$$

where v₂ is calculated to ensure that the eigenvectors satisfy the condition v.w = 1. From the derivatives of f₂ and f₃, the only ones that are nonzero are:

$$\frac{{\partial }^2{f}_2}{\partial x_1\partial x_3}=\frac{{\partial }^2{f}_2}{\partial x_3\partial x_1}={\beta }^{\ast }\sigma$$

with

$$\frac{{\partial }^2{f}_2}{\partial x_3\partial \beta }=\sigma x_1^{\ast }$$

The direction of the bifurcation at ${\mathcal{R}}_0=1$ is determined by the signs of the bifurcation coefficients a and b, obtained from the above partial derivatives, given respectively by:

$$\begin{array}{cc}a=& 2v_2{w}_1{w}_3\beta \sigma <0.\\ b=& v_2{w}_2{\sigma }_2>0.\end{array}$$

Therefore, system (1) exhibits forward bifurcation at ${\mathcal{R}}_0=1$ and the unique endemic equilibruim is locally assymptotically stable for ${\mathcal{R}}_0>1$, which also mean that the SMAFEP and the endemic equilibrium point does not co-exist when ${\mathcal{R}}_0<1$. □

3.9. Sensitivity analysis

We performed sensitivity analysis, to show the effect of each parameter to the SMA transmission. To go through, we followed the approach defined in (Blower & Dowlatabadi, 1994) as done in (Alemneh et al., 2019a, 2019b; Alemneh & Telahun, 2020) which used the definition of normalized forward sensitivity index defined as a variable, ${\mathcal{R}}_0$, that depends differentiably on a parameter, p, is defined as:

$${\Lambda }_p^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial p}\times \frac{p}{{\mathcal{R}}_0},$$

where p represents all the basic parameters and ${\mathcal{R}}_0=\frac{\beta \pi \alpha \delta \sigma }{\left(k+\mu \right)\left(\delta +\mu \right)\left(\mu +ϵ+\rho \right)}$. Then

$$\begin{array}{cc}{\Lambda }_{\beta }^{{\mathcal{R}}_0}& =\frac{\partial {\mathcal{R}}_0}{\partial \beta }\times \frac{\beta }{{\mathcal{R}}_0}=1>0.\\ {\Lambda }_{\delta }^{{\mathcal{R}}_0}& =\frac{\partial {\mathcal{R}}_0}{\partial \delta }\times \frac{\delta }{{\mathcal{R}}_0}=\frac{\mu }{\delta +\mu }>0.\\ {\Lambda }_{\rho }^{{\mathcal{R}}_0}& =\frac{\partial {\mathcal{R}}_0}{\partial \rho }\times \frac{\rho }{{\mathcal{R}}_0}=-\frac{\rho }{ϵ+\rho +\mu }<0.\\ {\Lambda }_{ϵ}^{{\mathcal{R}}_0}& =\frac{\partial {\mathcal{R}}_0}{\partial ϵ}\times \frac{ϵ}{{\mathcal{R}}_0}=-\frac{ϵ}{ϵ+\rho +\mu }<0.\end{array}$$

And it is similar with respect to the remaining parameters.

The sensitivity indices of the basic reproductive number with respect to main parameters are found in Table 1. Examining the sensitivity analysis, it is reasonable to suggest that the treating addicted individuals (ϵ) and the educating susceptible to use social media for positive purpose with in quiet subclass (k) should be increased in order to control the disease. The other possible sensitive parameters that are important for effective control of the disease are contact rate of susceptible with addicted individuals (σ), rate of change from exposed to addicted (δ) should be decreased.

Table 1.

Sensitivity indecies table.

Parameter symbol	Sensitivity indecies
β	+ve
σ	+ve
α	+ve
δ	+ve
ϵ	-ve
ρ	-ve
k	-ve
μ	-ve

4. An optimal control model

In this section, to achieve the minimized social media addiction we reconsider the model (1) and formulate an optimal control problem with two control variables u₁(t) and u₂(t). The control u₁(t) represents efforts intended to prevent the susceptible from contacting with the addictives, by an advertisements and educating the population about the negative impact of social media. The control variable u₂(t) used to control SMA individuals to give an appropriate treatment measures mentioned in the introduction to recover from the addiction. After incorporating the control variables u₁(t) and u₂(t) in the model (1), the optimal control model looks:

$$\begin{array}{cc}\frac{dS}{dt}& =\pi +\gamma \eta R-\left(1-u_1\right)\beta \sigma AS-\left(k+u_1+\mu \right)S\\ \frac{dE}{dt}& =\left(1-u_1\right)\beta \sigma AS-\left(\delta +u_2+\mu \right)E\\ \frac{dA}{dt}& =\alpha \left(\delta +u_2\right)E-\left(ϵ+u_2+\rho +\mu \right)A\\ \frac{dR}{dt}& =\left(1-\alpha \right)\left(\delta +u_2\right)E+\left(ϵ+u_2\right)A-\left(\eta +\mu \right)R\\ \frac{dQ}{dt}& =\left(k+u_1\right)S+\left(1-\gamma \right)\eta R-\mu Q\end{array}$$ (17)

The control variables u₁ and u₂ minimizes the objective functional defined in equation (18) subject to optimal control model (17):

$$J=\underset{0}{\overset{t_f}{\int }}\left[b_{1}E+b_{2}I+\frac{1}{2}\left(w_1{u}_1^2+w_2{u}_2^2\right)\right]dt$$ (18)

where t_f is the final time, b₁ and b₂ are weight constants of the exposed and addicted population respectively while w₁ and w₂ are weight coefficients for each individual control measure. We make the cost expression $\left(\frac{1}{2}{w}_i{u}_i^2\right)$ quadratic, due to the fact that cost is not linear in its nature (Alemneh et al., 2020; Alemneh & Telahun, 2020; Osman et al., 2020; Tilahun et al., 2017). Next, we will investigate the existence of the optimal control of the above-mentioned problem using the woke of Fleming and Rishel (Fleming & Rishel, 1976).

Theorem 4.1

There exists an optimal control pair $u^{\ast }=\left(u_1^{\ast },u_2^{\ast }\in U\right)$ such that.

$$J\left(u_1^{\ast },u_2^{\ast }\right)=min\left\{J\left(u_1,u_2\right)|u_1\left(t\right),u_2\left(t\right)\in U\right\}$$ (19)

where $U=\left\{\left(u_1,u_2\right)|u_i\left(t\right)\right)$ is measurable on [0, t_f], $\left(0\le u_i\left(t\right)\le 1,i=1,2\right\}$ is the closed set. subject to the control system (17) with initial conditions

Proof

To prove the existence of an optimal control, according to the classic literature (Fleming & Rishel, 1976), we have to show the following.

• (1)The control and state variables are nonnegative values.
• (2)The control set U is convex and closed.
• (3)The right side of the state system is bounded by linear function in the state and control variables.
• (4)The integrand of the objective functional is concave on U.
• (5)There exist constants d₁ > 0, d₂ > 0 and c > 1 such that the integrand

$$L\left(t;u_1;u_2\right)\triangleq E\left(t\right)+A\left(t\right)+\frac{1}{2}{u}_1^2\left(t\right)+\frac{1}{2}{u}_2^2\left(t\right)$$

of the objective functional satisfies

$$L\left(t;u_1;u_2\right)\ge d_1{\left({\left|u_1\right|}^2+{\left|u_2\right|}^2\right)}^{\frac{c}{2}}-d_2$$

The state and the control variables of the system (17) are positive values. The control set U is closed and convex. The integrand of the objective cost function J stated by (17) is a convex function of (u₁, u₂) on the control set U. The Lipschitz property of the state system with regard to the state variables is fulfilled since the state solutions are bounded. I.e

$$\begin{array}{cc}\frac{dS}{dt}& \le \mathrm{\Pi },\frac{dE}{dt}\le \left(1-u_1\right)\beta \sigma AS,\frac{dA}{dt}\le \alpha \left(\delta +u_2\right)E,\\ & \frac{dR}{dt}\le \left(1-\alpha \right)\left(\delta +u_2\right)E+\left(ϵ+u_2\right)A,\frac{dQ}{dt}\le \left(k+u_1\right)S+\left(1-\gamma \right)\eta R\end{array}$$

For the last condition,

$$L\left(t;u_1;u_2\right)\ge d_1{\left({\left|u_1\right|}^2+{\left|u_2\right|}^2\right)}^{\frac{c}{2}}-d_2$$

is also true, when we choose $d_1=min\left\{\frac{b_1}{2},\frac{b_2}{2}\right\}$ and for all $d_2\in {\mathcal{R}}^{+},c=2$. The Proof is complete. □

4.1. The Hamiltonian and optimality system

According to the Pontryagin’s maximum principle (Pontryagin, 1987), the Hamiltonian $\left(\mathcal{H}\right)$, obtained from system of equation (17) and equation (18) as follows:

$$\begin{array}{cc}\mathcal{H}& =c_{1}E+c_{2}A+\frac{1}{2}{w}_1{u_1}^2+\frac{1}{2}{w}_2{u_2}^2\\ & +{\lambda }_1\left[\mathrm{\Pi }+\gamma \eta r-\left(1-u_1\right)\beta \sigma AS-\left(\kappa +u_1+\mu \right)S\right]\\ & +{\lambda }_2\left[\left(1-u_1\right)\beta \sigma AS-\left(\delta +u_2+\mu \right)E\right]\\ & +{\lambda }_3\left[\alpha \left(\delta +u_2\right)E-\left(\epsilon +u_2+\rho +\mu \right)A\right]\\ & +{\lambda }_4\left[\left(1-\alpha \right)\left(\delta +u_2\right)E+\left(\epsilon +u_2\right)A-\left(\eta +\mu \right)R\right]\\ & +{\lambda }_5\left[\left(\kappa +u_1\right)S+\left(1-\gamma \right)\eta R-\mu Q\right]\end{array}$$

Where, λ_i, i = 1, …, 5 are the adjoint variable functions to be determined.

Theorem 4.2

Given optimal control pair ($u_1^{\ast }$, $u_2^{\ast }$) and S(t), E(t), A(t), R(t), Q(t) and solutions of the respective state system, there exist adjoint variables, λ_i, i = 1, …, 5 that satisfy the equation below:

$$\begin{array}{cc}\frac{d{\lambda }_1}{dt}& =-\frac{\partial \mathcal{H}}{\partial S}\left(t\right)\\ \frac{d{\lambda }_2}{dt}& =-\frac{\partial \mathcal{H}}{\partial E}\left(t\right)\\ \frac{d{\lambda }_3}{dt}& =-\frac{\partial \mathcal{H}}{\partial A}\left(t\right)\\ \frac{d{\lambda }_4}{dt}& =-\frac{\partial \mathcal{H}}{\partial R}\left(t\right)\\ \frac{d{\lambda }_5}{dt}& =-\frac{\partial \mathcal{H}}{\partial Q}\left(t\right)\end{array}$$

With transversality conditions, λ_i(t_f) = 0, i = 1, …, 5 and control set $\left(u_1^{\ast },u_2^{\ast }\right)$ characterized by

$$\begin{array}{cc}{u}_1^{\ast }& =max\left\{0,min\left(1,\frac{\left({\lambda }_1-{\lambda }_5\right)S+\beta \sigma AS\left({\lambda }_2-{\lambda }_1\right)}{w_1}\right)\right\}\\ u_2^{\ast }& =max\left\{0,min\left(1,\frac{\left({\lambda }_2-{\lambda }_4\right)E+\left({\lambda }_4-{\lambda }_3\right)\left(\alpha E-A\right)}{w_2}\right)\right\}\end{array}$$

Proof

By the principle Pontryagin’s maximum (Pontryagin, 1987), we differentiate the Hamiltonian and got the adjoint system which can be written as:

$$\begin{array}{cc}\frac{d{\lambda }_1}{dt}& =-\frac{\partial \mathcal{H}}{\partial S}={\lambda }_1\left(\left(1-u_1\right)\beta \sigma A+\kappa +u_1+\mu \right)-{\lambda }_2\left(\left(1-u_1\right)\beta \sigma A\right)-{\lambda }_5\left(\kappa +u_1\right)\\ \frac{d{\lambda }_2}{dt}& =-\frac{\partial \mathcal{H}}{\partial E}=-b_1+{\lambda }_2\left(\delta +u_2+\mu \right)-{\lambda }_3\alpha \left(\delta +u_2\right)-{\lambda }_4\left(1-\alpha \right)\left(\delta +u_2\right)\\ \frac{d{\lambda }_3}{dt}& =-\frac{\partial \mathcal{H}}{\partial A}=-b_2+{\lambda }_1\left(\left(1-u_1\right)\beta \sigma S\right)-{\lambda }_2\left(1-u_1\right)\beta \sigma S+{\lambda }_3\left(\epsilon +u_2+\rho +\mu \right)-{\lambda }_4\left(\epsilon +u_2\right)\\ \frac{d{\lambda }_4}{dt}& =-\frac{\partial \mathcal{H}}{\partial R}=-{\lambda }_1\gamma \eta +{\lambda }_4\left(\eta +\mu \right)-{\lambda }_5\left(\left(1-\gamma \right)\eta \right)\\ \frac{d{\lambda }_5}{dt}& =-\frac{\partial \mathcal{H}}{\partial Q}=\mu {\lambda }_5\end{array}$$

With transversality conditions, λ_i(t_f) = 0, i = 1, …, 5. The control set $\left(u_1^{\ast },u_2^{\ast }\right)$ satisfies the condition

$$\frac{\partial \mathcal{H}}{\partial u_i}=0,i=1,2$$

By solving the above equations, the Proof is completed. □

The optimality system is formed from the optimal control system (the state system) and the adjoint variable system by incorporating the characterized control set under initial and transversal condition:

$$\left\{\begin{array}{cc}\frac{dS}{dt}& =\pi +\gamma \eta R-\left(1-u_1^{\ast }\right)\beta \sigma AS-\left(k+u_1^{\ast }+\mu \right)S\\ \frac{dE}{dt}& =\left(1-u_1^{\ast }\right)\beta \sigma AS-\left(\delta +u_2^{\ast }+\mu \right)E\\ \frac{dA}{dt}& =\alpha \left(\delta +u_2^{\ast }\right)E-\left(ϵ+u_2^{\ast }+\rho +\mu \right)A\\ \frac{dR}{dt}& =\left(1-\alpha \right)\left(\delta +u_2^{\ast }\right)E+\left(ϵ+u_2^{\ast }\right)A-\left(\mu +\eta \right)R\\ \frac{dQ}{dt}& =\left(k+u_1^{\ast }\right)S+\left(1-\gamma \right)\eta R-\mu Q\\ \frac{d{\lambda }_1}{dt}& ={\lambda }_1\left(\left(1-u_1^{\ast }\right)\beta \sigma A+\kappa +u_1^{\ast }+\mu \right)-{\lambda }_2\left(\left(1-u_1^{\ast }\right)\beta \sigma A\right)-{\lambda }_5\left(\kappa +u_1^{\ast }\right)\\ \frac{d{\lambda }_2}{dt}& =-b_1+{\lambda }_2\left(\delta +u_2^{\ast }+\mu \right)-{\lambda }_3\alpha \left(\delta +u_2^{\ast }\right)-{\lambda }_4\left(1-\alpha \right)\left(\delta +u_2^{\ast }\right)\\ \frac{d{\lambda }_3}{dt}& =-b_2+{\lambda }_1\left(\left(1-u_1^{\ast }\right)\beta \sigma S\right)-{\lambda }_2\left(1-u_1^{\ast }\right)\beta \sigma S+{\lambda }_3\left(\epsilon +u_2^{\ast }+\rho +\mu \right)-{\lambda }_4\left(\epsilon +u_2^{\ast }\right)\\ \frac{d{\lambda }_4}{dt}& =-{\lambda }_1\gamma \eta +{\lambda }_4\left(\eta +\mu \right)-{\lambda }_5\left(\left(1-\gamma \right)\eta \right)\\ \frac{d{\lambda }_5}{dt}& =\mu {\lambda }_5\\ u_1^{\ast }& =max\left\{0,min\left(1,\frac{\left({\lambda }_1-{\lambda }_5\right)S+\beta \sigma AS\left({\lambda }_2-{\lambda }_1\right)}{w_1}\right)\right\}\\ u_2^{\ast }& =max\left\{0,min\left(1,\frac{\left({\lambda }_2-{\lambda }_4\right)E+\left({\lambda }_4-{\lambda }_3\right)\left(\alpha E-A\right)}{w_2}\right)\right\}\\ {\lambda }_i\left(t_f\right)& =0,i=1,\dots ,5,S\left(0\right)=S_0,E\left(0\right)=E_0,A\left(0\right)=A_0,R\left(0\right)=R_0,Q\left(0\right)=Q_0\end{array}\right)$$ (20)

5. Numerical simulations and discussions

In this section, we performed numerical simulation of the optimality system. We have used Maple 18, for simulation. To simulate the optimality system in (20), which consists of the state system and the adjoint system, we used an iterative technique called Forward fourth-order Runge-Kutta method. We used the forward fourth-order Runge–Kutta method to solve the state system and the backward fourth-order Runge–Kutta method for solving the adjoint system.Then, the controls are updated by means of convex combination of the previous controls and the values computed in the characterizations process. The solution of the state and adjoint system is repeated by the updated controls. The iteration continued until a predefined convergence criterion is met (Alemneh, 2020; LenhartJiongmin, 1992). For simulation, we used parameter values in Table 2 and the initial conditions S(0) = 1000, E(0) = 10, A(0) = 50, R(0) = 0, Q(0) = 100. Also the following weight constants were used: b₁ = 1, b₂ = 2, w₁ = 10, w₂ = 10.

We considered the following three strategies for numerical simulation of the SMA model:

• (i)Strategy A: Advertising and educating the negative effects of social media (u₁≠0 &u₂ = 0)
• (ii)Strategy B: Treating the addicted individuals (u₁ = 0 & u₂≠0).
• (iii)Strategy C: Combination of both strategies A and B (u₁≠0 and u₂≠0).

5.1. Strategy A: Eduacting the negative effects of social media

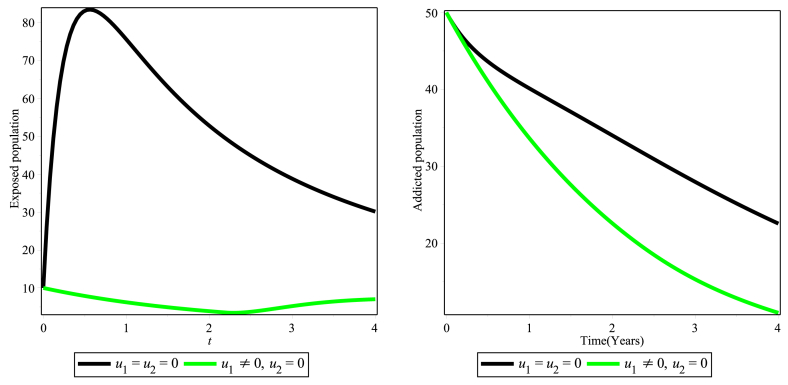
In this strategy, setting the control u₂ to zero, we used control u₁ to optimize the objective function J. In Fig. 2, we see that exposed and addicted population significantly reduced when there is control compared to situation with no control. However, Fig. 2 shows that the number exposed population seems eliminated in the first two year but the exposed individuals relapse using the social media due to lack of effectiveness of the strategy. Hence it is not effective strategy to combat SMA from the population.

Fig. 2.

Simulations of the SMA model showing the effect of the optimal strategies u₁≠0.

5.2. Strategy B: Treating the addicted individuals

In the second case, we preform simulation of control system in the absence of the first strategy u₁. It is evident from Fig. 3 that, the number of exposed individuals and addicted individuals reduced using the strategy as compared with no control. Here, the applied strategy seems effective in reducing the addiction burden within the intervention period and thus can be consider as optimal candidate to manage the burden of SMA.

Fig. 3.

Simulations of the SMA model showing the effect of the optimal strategies u₂≠0.

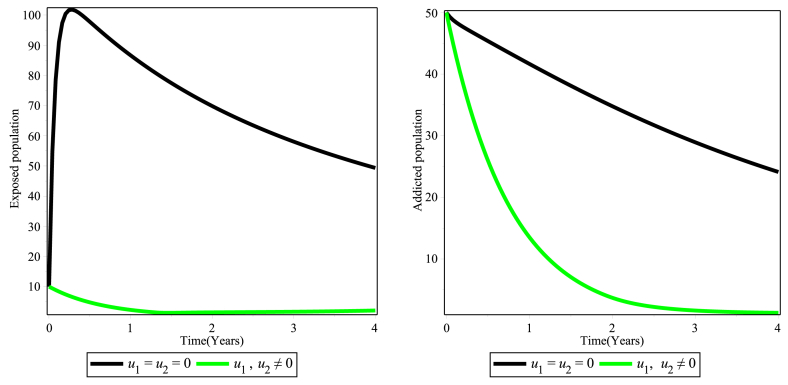
5.3. Strategy C: Combination of both strategies A and B

Finally, we present the effects of implementing the combined controls strategies in optimizing the objective function. The corresponding simulation results are illustrated in Fig. 4. From this Figure one can easily see that the number of exposed and addicted individuals are highly reduced due to the control strategy as compare with no control. Therefore, the intervention strategy is effective in bringing down the exposed and addicted population in the specified period of time. Thus, the policy makers may choose this integrated strategy in combating the addiction.

Fig. 4.

Simulations of the SMA model showing the effect of the optimal strategies u₁≠0 & u₂≠0.

6. Conclusions

In this paper, we formulated a mathematical model for the transmission dynamics of SMA with an optimal control model. The analysis shows that the disease-free equilibrium of the model is locally asymptotically stable whenever the associated reproduction number is less than unity and unstable otherwise. The basic reproduction number ${\mathcal{R}}_0$ was computed and the stability of equilibria points was investigated. The model exhibits forward bifurication at ${\mathcal{R}}_0=1$, from bifurcation analysis. Using the definition of normalized forward sensitivity, the sensitivity parameters were determined. Then, the optimal control model was formulated by adding two time-dependent controls (u₁ ≡ advertisement & education strategy and u₂ ≡ treatment strategy). The optimality system was established with the help of Pontryagin’s Maximum Principle. From the results of the numerical simulation, the integrated control strategy C is an optimal policy to fight against SMA. Therefore, we recommend for stakeholders and policymakers to use the integrated strategy in combating SMA effect on the population.

Data availability

The data supporting this deterministic model are from previous published articles and they have been duly cited in this paper.

Declaration of competing Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Handling Editor: Dr Y. Shao