Mortality containment vs. Economics Opening: Optimal policies in a SEIARD model

Abstract

We extend the classic approach (SIR) to a SEAIRD model with policy controls. A social planner’s objective reflects the trade-off between mortality reduction and GDP, featuring its perception of the value of statistical life (PVSL). We introduce realistic and drastic limitations to the control available to it. Within this setup, we explore the results of various control policies. We notably describe the joint dynamics of infection and economy in different contexts with unique or multiple confinement episodes. Compared to other approaches, our contributions are: (i) to restrict the class of functions accessible to the social planner, and in particular to impose that they remain constant over some fixed periods; (ii) to impose implementation frictions, e.g. a lag in their implementation; (iii) to prove the existence of optimal strategies within this set of possible controls; iv) to exhibit a sudden change in optimal policy as the statistical value of life is raised, from laissez-faire to a sizeable lockdown level, indicating a possible reason for conflicting policy proposals.

1. Introduction

A COVID-19 outbreak has begun in China at the end of 2019 (HWO, 2020), later spreading to most other countries and causing a large number of infected individuals and deaths. In Italy, the first country to be hit after China, the first confirmed autochthonous case was recorded on February 21, and the first death on February 22 (Statista, 2020); the first death in US was recorded on February 28th (Times, 2020).1 The outbreak has so far caused at least $50$ million recorded cases, and $1,260,000$ recorded deaths (Worldometer, 2020), with real numbers estimated at much higher values. In New York City there have been at this time at least 27,000 deaths, corresponding to 0.335% of the population.

Massive regulatory responses have been put in place by most local and central governments. Efforts to try to mitigate the outbreak have been multidimensional, from mobility restrictions, imposition of masks, sanitation, distancing, to the halting of educational, economic and social activities. The most severe restrictions have been named lockdowns.

The assessment of the effect of these measures is not simple, due to a variety of factors including non-linearities, random clustering of outbreaks, superspreading events etc. In addition, favorable situations at a certain time might hide later epidemic resurgence. In any case, there is a general consensus that the combination of all the above mentioned measures has reduced the spread of the virus and the potential mortality.2

Although it might not be easy to assess the direct economic effects of containment measures, it is clear that direct restrictions, and indirect effects on demand have had a large economic costs. As of October 2020, the IMF economic projections predict a loss in real GDP in 2020 of 4.4% worldwide, as opposed to ＋3.45% in the four years before (2016–2019). Even with the IMF forecast for the rebound of 5.2% in 2021, the cumulated loss over 2020 and 2021 relative to the World 2016–2019 trend is expected to reach 6.1% of World GDP. In advanced economies, these losses, calculated relative to specific regional trends, would have been 5.95%, including 8.15% in the European Union and 5% in the United States, similar in Emerging Market and Developing Economy (−5.95%) or Sub-Saharan Africa (−5.3%). These are massive numbers, quite different by areas of the world, and updated regularly with likely higher GDP losses.

In this paper, we are agnostic about the relative weight of the various restrictions, but argue that the combination of different measures jointly determines an economic loss as well as a containment of the epidemic. We call the measures “interventions”; sometimes, for convenience or when describing country measures, we refer to them as “lockdowns”, still referring to the combination of all measures. We provide here a framework to think about costs and benefits; we then simulate the initial scenario of the spreading of COVID-19 in western countries in March 2020 and evaluate several optimal policies.

As indicators of the effects of the epidemic we adopt the number of COVID-19 fatalities, while GDP loss is used as a proxy for the economic effects of containment measures. The two indicators have been selected for their reliability: GDP is a standard economic indicator, while COVID-19 mortality is regularly monitored and made public in many countries; excess mortality would be an even more reliable indicator, where available.

For a functional description of the epidemic, we consider a compartmental model; models of this type are, in fact, relatively simple to set up and analyze, they provide reliable approximations of various epidemic features (Bertozzi et al., 2020), and are widely used in modeling and relied upon in policy planning (Acemoglu et al., 2020, Bethune and Korinek, 2020, Berger et al., 2020, Eichenbaum et al., 2020). In particular, we develop in Section 3 a SEAIRD model, in which susceptibles become pre-symptomatic at contact; they then might remain asymptomatic or develop symptoms, and then recover or die; natural death is included, as well as birth to stabilize the population. The model is considered in fixed time interval $[0,T]$, representing the expectation of an available vaccine: in some prototypical simulations we take $T$ as the end of the first quarter 2021. We then consider a proxy for containment policies that, as mentioned, encompasses all possible restrictions: the measures are summarized by a function $c\left(t\right)\in [c_0,1],t\in [0,T]$, $c=1$ being absence of any restriction and $c=c_0>0$ being the complete shutdown of all non vital activities; $c\left(t\right)$ simultaneously reduces the chances of infection and GDP. As a normalization, $c$ will be assumed to linearly affect the infection rate and has a concave effect on GDP.

We then focus on the social planner’s objective of containing both COVID-19 fatalities, evaluated in terms of an attributed value of life, and GDP loss over the estimated time frame. For both dimensions, the objective of the social planner discounts the future and optimizes the combined loss functional over the available lockdown policies. While the infection has started at some earlier time, $t=0$ for convenience, the planner determines policies and acts at some time $T_0>0$; in addition, the planner selects a time frame $[T_0,T]$ for the evaluation, based on assessment of future technological development. The choice of $T$ might seem restrictive at first, but the validity of our original guess of a decisive attenuation of the epidemic at the end of the first quarter 2021 indicates that the possibility of such a guess was actually well founded.3

One of the main novelties of our research is that, to the contrary of the usual assumption that control policies can instantly vary with time (see Grigorieva et al., 2020 and various economic papers cited below), we restrict to more realistic policies that are constant over reasonably long periods of time (of the order of weeks, for instance): no shorter period is, in fact, allowed for the measures to be successfully implemented (Yan and Zou, 2008). In addition, since aggregate variables such as average behavior or total production cannot change instantaneously, we assume that there is some friction in implementing life changing policies, so that the lockdown level moves continuously during transitions (which last a few days). These restrictions are usually not considered in theoretical analysis but are first order constraints of policy making. We assume that a specific class of such intervention policies is available for the social planner.

Another novelty of our paper is that we carry out in Section 4 a detailed mathematical analysis showing the existence of at least one minimum in classes of realistic controls. Standard results in Optimal Control Theory, e.g. Fleming and Rishel (2012), show, in general, existence of an overall optimal control in terms of possibly irregular functions, and then show some continuity properties of the control; we take a direct approach showing existence of a control $c\left(t\right)$ which is optimal within the preassigned class of realistic controls available to the social planner; we use for this a lower bound on the rate of change of the openness function $c\left(t\right)$.

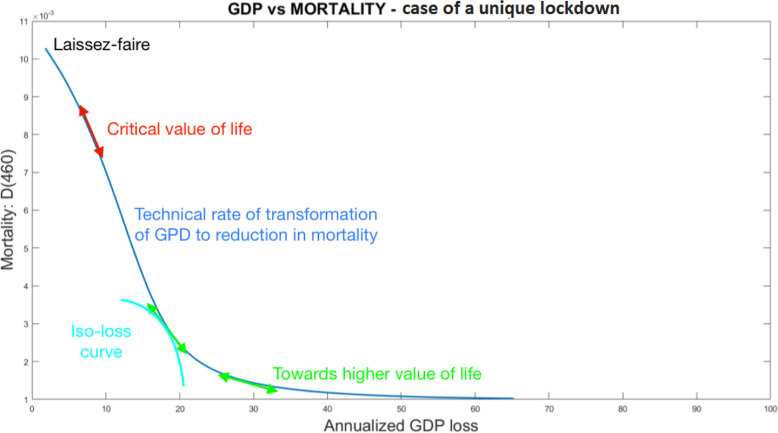
To illustrate the main arbitrage present in our set up, Fig. 1 shows GDP loss and mortality of a single lockdown level $c$ kept constant for the entire observation period, see Kaplan et al. (2020) for a similar assessment of the trade-offs involved, implicit or explicit in most economic works discussed in next Section. The blue curve $\mathcal{C}$ is parametrized by the lockdown level, from laissez-faire $c=1$ to $c=c_0$, and represents the various options for the social planner: it can be thought of as a technical rate of transformation between economic activity and health safety. Generally speaking, it is best to be close to the origin, as otherwise very little advantage is gained in one variable, at a huge cost in the other. A specific choice of the intervention level, however, can be determined as optimal solution for each given value of life through the social planner welfare function: the indifference curves of the welfare function (light blue curve) define an optimal rule, when it exists. Its slope reflects the marginal rate of substitution (MRS) between mortality reduction and GDP losses and under simplifying assumptions, it is the inverse of the statistical value of life, as we will explain later.

Fig. 1.

Mortality and production loss with one single, long lasting intervention. The optimal choice, see Online Material, reduces mortality to 0.34% with a 18.13% GDP loss: the intervention realizes a sharp containment of mortality, but the constraint of protracted measures causes a dramatic GDP loss. This policy has not been followed by any country. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

There is, however, a surprising feature: in some scenarios, laissez-faire is the optimal solution for all values of life below a certain threshold, while immediately above the threshold a sizeable restriction policy is optimal. This determines that at the threshold itself two different optimal policies coexist (due to the non convexity of $\mathcal{C}$ for large $c$). This situation, which we see appearing for various policy classes, is indicative of the variety of optimal responses depending on the value attributed to statistical life; it also clarifies some of the differences in the proposed policies (among which laissez-faire has been initially advocated by some governments). Although such discontinuity in the optimal policy takes place presumably only at isolated values of the value of life, we argue that a social planner particularly responsive to the population diverse views might be inclined to act according to a value of life near the critical one. In addition, discontinuity of controls around the critical value can have relevant social consequences in terms on how to evaluate potential alternatives to a given containment policy. We then provide some arguments indicating that, in general, the optimal control is likely to depend smoothly on the statistical value of life, provided that either the social cost attributed to COVID-19 mortality or the discount rate for future events is large enough.

In Section 5, we finally consider some intervention classes, each with a combination of possible closing and reopening times and/or levels. Parameters are realistically taken from the observations at the early stages of the COVID-19 epidemic, and validated by reproducing observed mortality and GDP reductions due to first intervention periods. All examples are explicitly simulated and optimal controls are numerically determined. We then carry out a sensitivity analysis to evaluate the sensitivity of the results to errors and fluctuations in parameters selection. We also compare the optimal policies with those obtained with interventions varying continuously in time, and we observe that these would not determine a substantial improvement, see Table 4.

Table 4.

Comparison between the numerical results given by the continuous and piecewise linear optimal controls.

	Continuous Opt. control Fig. 5	Piecewise linear Opt. control Fig. 5
Mortality at day 85	0.028%	0.028%
Total mortality at Day 460	0.16%	0.19%
Total mortality reduction	84.47%	81.97%
Annualized 1st quarter GDP loss	3.91%	2.82%
Total annualized GDP loss	16.69%	17.40%
Value loss functional	121	130.25

In one prototypical case the social planner imposes a lockdown on March $25$, Day $85$, till May $29$, Day $250$, and then a reopening level till the end of the period on April $4$, 2021, Day $460$, at levels to be decided (cf. Fig. 6). With no restrictions the GDP loss of the four quarters would have been 1.41% with a 1.05% Covid-19 mortality. An optimization is then carried out assuming a value of life, in relation to Covid mortality, of around $2$ (in Europe) to $3$ (in US) million dollars; the optimal solution determines a 17.40% GDP loss and reduces mortality by 81.97%, see Table 3. Although the limitation to two lockdown levels in this specific simulation is unrealistic, the values we obtain are comparable with those observed at the end of Quarter $2$ with a 13% GDP contraction in France and a 31.4% GDP reduction in US. The actual level of reopening in most countries has been much higher than that in our optimal solution, with the consequence of an exceptional economic rebound, but also a deadly second (and even third) wave: a situation described by a non optimal reopening level in our second simulation of Section 5.

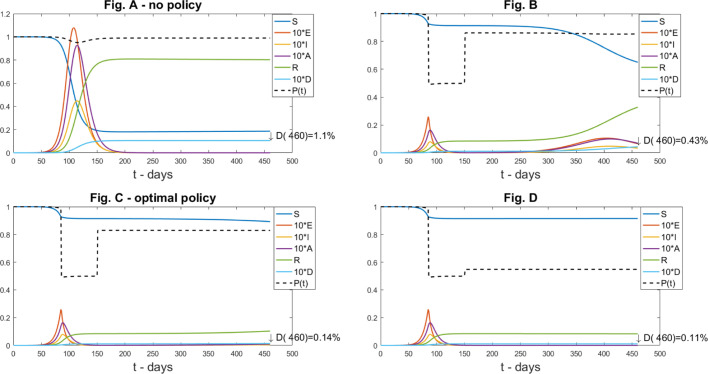
Fig. 6.

The numerical results of the experiment where a first lockdown at day 85 is fixed to $\underset{\_}{c}=0.5$ and a reopening level at day 150 has to be determined. Fig. 6.A, Top left: no policy. Fig. 6.B, Top right: high reopening. Fig. 6.C, Bottom left: optimal policy. Fig. 6.D, Bottom right: a limited reopening level.

Table 3.

Two level restrictions.

	Epidemic	Excessive restrictions	Optimal Fig. 4.C	Insufficient restrictions
	Fig. 4.A - No policy	Fig. 4.B		Fig. 4.D
Opening and reopening levels [$\underset{\_}{c}$, $\overline{c}$]	[100%,100%]	[12.5%,12.5%]	[27.5%,55.1%]	[72.9%,85.7%]
Mortality at day 85	0.028%	0.028%	0.028%	0.028%
Total mortality at day 460	1.054%	0.106%	0.19%	0.83%
Total mortality reduction	0%	89.98%	81.97%	21.06%
Annualized 1st quarter GDP loss	1.22%	3.73%	2.82%	1.74%
Total annualized GDP loss	1.41%	40.91%	17.40%	6.04%
Value loss functional	189.21	379.43	130.25	171.19

In Section 6, we further show how to extend the approach to capital accumulation in a Solow and a Ramsey approach, and relegate their mathematical analysis in Appendix A, Appendix B.

2. Previous works and limitations

2.1. Brief literature review

The number of papers adapting the SIR model to various economic contexts is large and rapidly evolving and it is impossible to make justice to the literature. In addition to the papers cited in introduction, one can cite Jones et al. (2020) who derive an optimal strategy where the social planner can affect both the contacts from consumption and contacts from production, each of them contributing to a third on the diffusion parameter $\beta$. They study the optimal policy using a standard growth model with leisure-consumption trade-offs. Agents react too little to the epidemics because they do not contemplate the impact of their behavior on other agents’ infection rate and a lockdown seriously reduces infection and fatalities in flattening the curve, and avoid congestion of ICU units that would increase the fatality rate.

Eichenbaum et al. (2020) study a standard DSGE model with a SIR contagion. They find that the epidemic causes per se a moderate recession, with aggregate consumption falling down by 0.7% within the year. Optimal containment would lead to a more drastic loss in consumption by 22%. They also discuss the model with various health policies including vaccines, preparedness and other dimensions.

Acemoglu et al. (2020) develop a multi-SIR model with infection, hospitalization and fatality rate depending on age, with three classes of individuals (young, middle-aged and old). They find that targeted containment policies are most efficient. For the same loss in GDP ($-$24%), the targeted policies reduce mortality by 0.7 to 1.8 percentage points. They also include a stochastic vaccine arrival, not known for sure by the policy maker, and the stochastic process evolves over time. They assume as in Alvarez et al. (2020) that full lockdown is not feasible, as we also assume. Alvarez et al. (2020) have a SIR model embedded in the growth model. Their optimal policy is to implement a severe lockdown 2 weeks after 1% of the population is infected, to cover 60% of the population, and then gradually reduce the intensity of the lockdown to 20% of the population after 3 months. The absence of testing reduces the welfare. With testing and under the optimal policy, the welfare loss is equivalent to 2% of GDP. Another paper on sequential lockdown with heterogeneous population is Rampini (2020). In particular, he uses a fatality rate of 0.06–0.08% for younger agents and 2.67 to 3.65% for older workers. Caulkins et al. (2021) analyse, as us, how optimal lockdown policies can differ drastically from small differences in parameters using a SIR model due to Skiba points and non-convexities.

Hall et al. (2020) study a variant with the minimization of an objective function and Hamilton–Jacobi-Bellman equations. Basing their fatality rate on 0.8% from the Imperial college study, they argue that the optimal decline in consumption is approximately 1/3rd for one year. They then consider more recent estimates of the fatality rate, around 0.3% across age groups, and argue that the optimal decline in consumption is still around 18%. Our numbers are in line with these numbers.

Gollier (2020b), similar to us assumes that a vaccine is ready after a few months (52 weeks in his case). He uses a $R_0$ around 2 (1.85 on the slides available online) prior to containment, and the containment policy drives it down to 1, as we do. He uses a value of statistical life of 1 million euros and studies confinement scenarii under notably periodic reinfection rates. In Gollier, 2020c, Gollier, 2020a, he further explores the ethics of herd immunity and elaborates on lockdowns differentiated by age groups. In particular, he uses (Table 4 of Gollier, 2020c) a valuation of statistical lives depending on age, with the population between 60 and 69 representing 37% of that of individuals below 19, the population between 70 and 79 representing 23% and those above 80% being slightly less than 10% of that maximum value. He further discusses the critical moral hazard issues associated with the epidemic.

Economic consequences associated with demand and transmission mechanisms have been studied in Guerrieri et al. (2020): they show that in the presence of multi-sector production, with or without imperfect insurance, it is possible and plausible to have demand shocks in the second round going beyond the initial supply (shutdown shock). They study various aspects such as labor hoarding and bankruptcy cascades. Gregory et al. (2020) study the response of the economy in a search framework. The existence of search frictions slows down the recovery, and under reasonable parameter values, the initial lockdown strategy is likely to have long-lasting effects. In their baseline scenario, unemployment increases by 12 percentage points of the labor force for a year, and it takes 4 years to get back to 3 percentage points above the starting point before the lockdown. They find, interestingly, that it is better to have a longer initial lockdown (6 months) and no uncertainty than a shorter lockdown with the risk during 9 to 12 months to face a second lockdown. Farboodi et al. (2020) estimate a SIR model in which the decline in activity comes from the optimal response of agents without intervention, and where immediate distancing in a discontinuous way, until a treatment is found, is a superior policy, to contain the reproduction number. In contrast, Krueger and Uhlig (2020) calibrate a model similar to Eichenbaum et al. (2020) in introducing goods that can be consumed at home rather than in public places and show that a Swedish-type policy of no-lockdown but strong behavioral response by agents reduces the socio-economic costs of Covid by up to 80%. Another estimation of various epidemiology models has been done by Palma et al. (2020) for five countries, with in particular estimates of the basic reproduction number. They then assess the different lockdown policies.

Last and most related to us, Garibaldi et al. (2020) analyze the existence of a SIR-matching decentralized equilibrium and analyze the inefficiencies stemming from matching externalities to determine the optimal way to reach herd immunity.

To conclude, in most of the papers cited above, there is an explicit focus on the optimal policy and the difference between the laissez-faire and the optimal policy is important, due to the externality of contagion. What our paper adds is a formal treatment of existence and a discussion of the potential multiplicity of solutions and phase transitions due to the non-linearity in the transmission mechanisms of the epidemic. Another paper in this spirit by Łukasz (2020) finds explicit optimal solutions in a set of constrained policy functions and characterizes in particular the optimal starting date of the intervention and discusses time-consistency issues.

2.2. Limitations

Our results are only a first indication of a modeling methodology for the search of an optimal trade off between containment of fatalities and reduced loss in welfare. While the parameters of the SEAIR model are related to the current outbreak, a more detailed model needs to consider stratified and geographically dispersed populations, and more elaborate intervention policies, targeted to regions, industries and population that are more at risk. The following points are in order.

• (1)As discussed above, several papers have recently addressed similar questions, with a particular focus on the optimal lockdown policy in the presence of behavioral response of agents on production, on investment or on consumption, of heterogeneity of the population and on learning on the underlying parameters of the economy. Here, as usual in most current literature on COVID-19, we use an extension of the SIR model, hence assuming that each individual has the same chance of meeting every other individual in the population.4 More realistically, one would need to consider geographically dispersed populations with long range interactions and communities (in the spirit of Gandolfi and Cecconi, 2016 for instance).
• (2)In this paper, in order to have an accurate model of the dynamics of the pandemic with several classes (susceptible, exposed, asymptomatic, symptomatic, recovered, fatality, natural demographic turnover), and yet be able to prove existence and discuss conditions for uniqueness of an optimal response function, we treat the simpler case where the social planner can directly control the contagion parameter with an instrument that also affects GDP, either influencing the behavior of agents or closing markets.
• (3)The simulations we provide are based on parametersknown at the time of this study, which are also the parameters perceived by policy makers at the time of decision making. With these parameters, and using a statistical value of a human life that is consistent with the value employed in actuarial sciences, we replicate levels of policy intervention that are in line with what was observed in many Western countries.
• (4)Given the nature of the virus and its novelty, there is some uncertainty surrounding the parameters, and these are likely to evolve as medical and epidemiological research progresses. The final numbers will only be available gradually, with large testings currently being implemented. Our approach will therefore only allow us to reassess current policies retrospectively, in one way or another, when the uncertainty at the time of decisions will have dissipated.
• (5)Similarly, the parameters connecting the spread of the diffusion of the virus to the loss of GDP from intervention are uncertain. We choose a median way in the numbers in our simulations.
• (6)We remain agnostic in our conclusions and provide sensitivity analysis in describing a range of alternative parameters. The shape of the optimal response in time is relatively invariant to those parameters, but warn that the intensity of the optimal intervention relies a lot on exact numbers chosen in our simulations.
• (7)On the economic side, one dimension not analyzed yet is the fact that the loss of GDP – a supply shock here – is likely to produce second round demand effects, leading to a persistence in the recession that our model does not take into account. Another limitation, of a similar spirit, is the ability of the intervention to be reversible in the short-run, that is, once stopped, assembly lines may need a lag to resume.
• (8)Another limitation in the benchmark exercise is that the fatality rates vary enormously by age and morbidity, and in particular, the fatality rate is 10 times higher at least between the population below 60 and above 60. Since the intervention mostly acts through adjustment of the labor force in our model, more analysis is needed to draw consequences about the overall intervention strategy. We cannot deliver conclusions about the opportunity of the observed intervention .
• (9)Another limitation is that our model does not focus on the behavioral response of agents who may have learned about the parameters of the diffusion of the epidemics and reduced the infectivity of the virus independently of the lockdown. We do however believe that there are behavioral responses, but as in Jones et al. (2020), we also believe that there are strong externalities in the contagion process that the purely-selfish individual behavior would not internalize. In that sense, the non-behavioral approach we follow is a proxy for the inefficiency of the decentralized equilibrium approach that leads to excessive contamination of the population. Future work should however relax the lack of behavioral response and investigate the size and sign of the interaction between government regulations and individual responses.
• (10)Last but not least, contrary to other studies, we limit our welfare analysis to a fixed period of time of the pandemic, one year and one quarter in the simulations. The implicit assumption is that after one year, treatments will have improved and vaccines may be possible. This acts as an extreme capitalization effect: in the future, technology will have improved and this is already integrated in economic calculation of the present time. It is easy to do a sensitivity analysis where the length of time periods is augmented, and investigate whether a new cycle of pandemic and intervention is needed. The solution we exhibit for the optimal intervention are therefore useful not only to rationalize the current experience, but also to prepare to the next wave or the next virus. We however introduce this assumption of a fixed and short period of time over which the smoothing occurs because the hope of a vaccine was present in public discussion.

In the Appendix, we present optimal control problems that would address some of these limitations.

3. A simple SEAIRD model with containment

3.1. Epidemic model

We consider SEAIRD, a version of the SIR model (Chowell et al., 2009 (25) Page 20), with some realistic features taken from observations of the Covid-19 outbreak. The population is divided into: susceptible (S), exposed (E) (sometimes called presymptomatic throughout the paper), asymptomatic (A), infected (I), recovered (R), Covid related deceased (D), and natural deaths (ND). Variables are normalized so that $S+E+A+I+R+D=1$. Overall, we consider a natural death rate $n$. This is compensated by a natural birth rate, that can be considered as the rate of inclusion into the labor force; the natural birth rate is reduced by a factor that can be interpreted as a Covid related slowdown.

We assume that affected individuals become first exposed (E), a phase in which they have contracted the virus and are contagious, without showing symptoms. A contagious transmission can occur when a susceptible encounters an individual from the virus carrying categories; these encounters are assumed uniform, as in each compartmental model, but reduced by quarantine measures: in particular, a fraction $s$ of the symptomatic infected is encountered, with $s$ small due to their almost complete seclusion; while fractions $s_1$ and $s_2$ of exposed and asymptomatic, respectively, due to testing. Upon encounter, there is a rate $\beta$ of transmission. Exposed individuals either develop symptoms at a constant rate $ϵ\kappa$, becoming infected, or progress into being asymptomatic with rate $(1-ϵ)\kappa$. Those who are symptomatically infected recover at rate $\gamma$, or do not recover and die at rate $\delta$; $\delta ∕\gamma$ is the deaths to recovered ratio to be estimated from current available observations. Asymptomatic recover at rate $\gamma$.

$$\text{Susceptible:}\frac{dS}{dt}=-\beta Sc\left(t\right)(sI+s_{1}E+s_{2}A)-nS+n(1-D)$$ (1)

$$\text{Exposed:}\frac{dE}{dt}=\beta c\left(t\right)S(sI+s_{1}E+s_{2}A)-(\kappa +n)E$$ (2)

$$\text{Asymptomatic:}\frac{dA}{dt}=(1-ϵ)\kappa E-(\gamma +n)A$$ (3)

$$\text{Infected:}\frac{dI}{dt}=ϵ\kappa E-(\gamma +\delta +n)I$$ (4)

$$\text{Recovered:}\frac{dR}{dt}=\gamma (A+I)-nR$$ (5)

$$\text{Covid deceased:}\frac{dD}{dt}=\delta I$$ (6)

$$\text{Natural deaths:}\frac{d{D}_N}{dt}=n(S+E+A+I+R)$$ (7)

The initial population at the onset of the outbreak of a previously unknown virus consists primarily of susceptible, $S\left(0\right)\approx 1$, and a small fraction of exposed, so that $S\left(0\right)+E\left(0\right)=1$. For the model under consideration the reproduction number has the following expression

$$\mathcal{R}\left(t\right)=\beta S\left(t\right)c\left(t\right)\left(\frac{s_1}{\kappa +n}+\frac{\kappa }{\kappa +n}\frac{s_2(1-ϵ)}{\gamma +n}+\frac{\kappa }{\kappa +n}\frac{sϵ}{\gamma +\delta +n}\right)=c\left(t\right)S\left(t\right)\frac{\beta \kappa }{\kappa +n}\left(\frac{s_1}{\kappa }+\frac{s_2(1-ϵ)}{\gamma +n}+\frac{sϵ}{\gamma +\delta +n}\right)$$ (8)

with basic reproduction number ${\mathcal{R}}_0=\mathcal{R}\left(0\right)$. Notice that the population $S+E+A+I+R+D$ is preserved. This is a consequence of the fact that by including the term $n$ demography replaces all deaths except Covid deaths.5

3.2. Containment policies

Containment policies are aimed at reducing the spread of the epidemic by reducing the chances of contacts among individuals. This is reflected in the model by a coefficient $c\left(t\right)$ that modulates the encounters between susceptible and either exposed, infected or asymptomatic individuals. We assume that the reduction is the same for all groups, as we have already included the effect of symptoms and testing. This justifies the factor $c\left(t\right)$ in (1).

The opening level function $c\left(t\right)$ takes values in $[c_0,1]$ $c_0>0$; $c\left(t\right)=1$ indicates that there is full opening, and no intervention measures have been taken; this is, by default, the status at the early stages of the outbreak. The lower bound $c_0$ corresponds to the infeasibility of a complete shutdown; this features the fact that there will always be a minimum amount of productive activity (e.g. via internet for home production) from private agents that cannot be interrupted. Provided $c_0$ is small enough, all our results are insensitive to the precise value. Further, to model concrete feasibility of the policy, controls can only take the form of continuous, piece-wise linear function, with the additional constraints of being constant for long enough time intervals $\overline{\delta }$; the transitions between the various constant levels are taken to be linear and last at least some $\underset{\_}{\delta }$ to model non-negligible friction in policies implementation. Further details on the admissible $c\left(t\right)$’s are given in Section 4.1.

We assume that the social planner can select the control in some specific subclass of the controls described above, that depends on the specific situation. Several examples of such sub-classes are presented in Section 5. The containment policies considered in this work are in sharp contrast with other choices, such as Grigorieva et al. (2020), in which all continuous functions are considered as possible controls. Our work is in the spirit of other applied papers (Rahimov and Ashrafova, 2010), focused on more realizable controls.

For example, since the presence of the virus went substantially unnoticed in the early stages in most locations, and then some time we needed to pass the required legislation, we assume that all interventions begin on day 85; this corresponds to March 25.6 When considering reopening, we use Day $150$, which corresponds to May 29. This is an indicative period of the first lockdown period of about two months that has been implemented by many countries.

3.3. Economic effects of epidemic and intervention

3.3.1. Social planner’s objective

We investigate optimal containment policies balancing the effect of overall death vs. loss of production. This entails performing an a-priori evaluation of the social cost of Covid deaths, embodied in a constant $a$. The social planner minimizes then a loss functional $\mathcal{L}$ (the negative of its utility), which combines production $P$ and number of Covid deaths,7 between an initial period $T_0$, when the first intervention takes place, and a final period $T$, the supposedly predictable end date of the epidemic. If $\mathcal{V}\left(P\right)$ is a decreasing convex function of $P$, the social planner’s objective is represented as

$$\mathcal{L}={\int }_{T_0}^T{e}^{-r(t-T_0)}\left[\mathcal{V}\left(P\left(t\right)\right)-\mathcal{V}\left(1\right)+a{D}^{\prime }\left(t\right)\right]dt$$ (9)

Assuming that the loss function is zero for full capacity, $\mathcal{V}\left(1\right)=0$, a typical function would be:

$$\mathcal{V}\left(P\right)=-\frac{P^{1-\sigma }-1}{1-\sigma }$$

with $\sigma >0,\sigma \ne 1$, and $\mathcal{V}\left(P\right)=-log\left(P\right)$ if $\sigma =1$. In our analysis we will assume $\sigma >1$ (our choice in the numerical simulations hereafter will be 2), so that ${lim}_{P\to 0}\mathcal{V}\left(P\right)=-\infty .$ We have ${\mathcal{V}}^{\prime }\left(P\right)=-P^{-\sigma }$ and ${\mathcal{V}}^{\prime \prime }\left(P\right)=\sigma P^{-\sigma -1}>0.$

Observe that with a linear loss function corresponding to $\sigma =0$, the parameter $a$ can directly be linked to the value of a marginal life with respect to GDP and in a static sense. Indeed, $a$ is the number of units of GDP (in the simulations, daily GDP) that can be sacrificed to maintain constant the expression inside integrals (the loss function) to save one additional life. With higher values of $\sigma$, the calculation is slightly richer and involves the aversion to intertemporal fluctuations in GDP that is characterized by the inverse of the elasticity of intertemporal substitution $\sigma$ which is also the risk-aversion parameter. Differentiating the integrand along the iso-loss curve, the slope of the iso-loss (indifference) curve is exactly:

$$\frac{dP}{d{D}^{\prime }}=\frac{a}{-{\mathcal{V}}^{\prime }\left(P\right)}=\frac{a}{P^{-\sigma }}=a{P}^{\sigma }$$ (10)

hence the adjustment factor with respect to the linear case is of the order of magnitude of actual level of GDP $P$ below 1, to the square.

Another way to gauge the value of $a$ is to compare the value of one life saved at time $T_0$ with the permanent change in GDP from $T_0$ to $T$, taking discounting into consideration. The ex-post loss function would then be

$$\tilde{\mathcal{L}}=\frac{{\int }_{T_0}^T{e}^{-r(t-T_0)}\left[\mathcal{V}\left(P\left(t\right)\right)-\mathcal{V}\left(1\right)\right]dt}{{\int }_{T_0}^T{e}^{-r(t-T_0)}dt}+\tilde{a}{\int }_{T_0}^T{e}^{-r(t-T_0)}\left[D^{\prime }\left(t\right)\right]dt$$ (11)

where we have normalized the total production of the observed period, and $\tilde{a}$ represents the fraction of GDP related welfare that the social planner is willing to renounce to save an actuarized 1% of Covid mortality. It follows that $\tilde{a}=a(1-e^{-r(T-T_0)})∕r$. We re-discuss the value of $a$ in the parameter selection Section 5.1

3.3.2. Production and welfare

We take the overall production $P$ to be a linear function of labor. At any given time, the labor force is $S+s_{1}E+s_{2}A+R$, but its effective availability for production is determined by the current opening policy $c\left(t\right)$. The link between $c\left(t\right)$ and GDP is captured by a function

$$\mathcal{G}\left(c\left(t\right)\right)$$

and it affects GDP as:

$$P\left(t\right)=\mathcal{G}\left(c\left(t\right)\right)L\left(t\right)=\mathcal{G}\left(c\left(t\right)\right)\left[S+s_{1}E+s_{2}A+R\right].$$ (12)

Labor availability in the presence of the intervention is not assumed to be linear, as the effects of socio-economic restrictions can be contained by work force substitution or increased productivity. We assume an iso-elastic control

$$\mathcal{G}\left(c\left(t\right)\right)=c{\left(t\right)}^{\theta }$$ (13)

with $\theta \in (0,1)$ for reasons discussed in the parameter selection Section 5.1. We think of $\theta$ as a reduced form parameter that connects the infection spread and the change in GDP.

With these assumptions, the loss functional becomes

$$\mathcal{L}=\mathcal{L}\left(c\right)={\int }_{T_0}^T{e}^{-r(t-T_0)}\left[-\frac{{\left\{c{\left(t\right)}^{\theta }\left[S+s_{1}E+s_{2}A+R\right]\right\}}^{1-\sigma }-1}{1-\sigma }\right)\left(+a{D}^{\prime }\left(t\right)\right]dt.$$ (14)

4. Mathematical results

We address the issues of existence and uniqueness (or lack thereof) of the optimal control for the system (1)–(7) with loss functional (14).

4.1. Existence of a global minimum of the loss functional

We discuss existence of at least one control $c$ minimizing $\mathcal{L}\left(c\right)$, when the minimum is taken over specific classes of possible controls.

The most general version is minimizing over integrable controls; existence of a minimizer in this case is guaranteed by standard results in Optimal Control Theory via the Pontryagin minimum principle (see Theorem 4.2 of Fleming and Rishel, 1975); in particular, System (1)–(7) and loss functional (14) satisfy the sufficient conditions to ensure that such optimal control is continuous (see Theorem 6.2 of Fleming and Rishel, 1975). The optimal control can be determined in theory via the Pontryagin first order conditions that we derive in Appendix B; the software Bocop 2.2.1, see Team Commands (2017) and Bonnans et al. (2017), computes a numerically effective approximation of the optimal control.

On the other hand, as argued before, controls continuously varying with time are not realistic: we, therefore, restrict to a class of more implementable policies, and use the absolute minimum as benchmark for the efficiency of the optimal control in the restricted classes. Optimal control theory does not seem suitable to verify the existence of minimizers in the restricted classes (Fleming and Rishel, 1975), so we take a different route, based on a variational method. By itself, this method would not allow to prove existence of the optimal continuous control, as the set of continuous functions is not compact, but it is sufficient for our purposes. Results are stated here and proofs are in Appendix A.

For mathematical convenience, controls are extended to be defined on $[0,T]$ by taking $c\left(t\right)=1$ for $0\le t\le T_0$.

Theorem 4.1

The functional $\mathcal{L}$ is continuous on the set of continuous controls on $[0,T]$ with respect to the uniform convergence.

We now show that several classes of controls are compact, so that Weierstrass Theorem guarantees existence of a minimizer in each class.

The first class is that of uniformly Lipschitz continuous functions: we say that $f$ is uniformly Lipschitz continuous if $\frac{|f\left(t_1\right)-f\left(t_2\right)|}{|t_1-t_2|}\le M$ for any $t_1,t_2\in [0,T],t_1\ne t_2$. Let us indicate by ${\mathcal{K}}_M$ the set of uniformly Lipschitz continuous functions in $[0,T]$ with values in $[c_0,1]$. It follows immediately as a consequence of Ascoli Arzelá Theorem that

Corollary 4.2

${\mathcal{K}}_M$ is compact in the space of continuous functions on $[0,T]$ taking values in $[c_0,1]$ with uniform convergence.

The class of controls we consider is further restricted by constraints on the time intervals: fix two values $\overline{\delta },\underset{\_}{\delta }$ with $\overline{\delta }>2\underset{\_}{\delta }>0$, and let ${\mathcal{K}}^{\ast }$ be the collection of continuous functions

$$c:[0,T]\to [c_0,1],$$

such that there exist $k\in \mathbb{N}$, times ${\alpha }_1<\cdots <{\alpha }_{k-1}\in [0,T]$ and opening levels $c_0\le {\beta }_1,\dots ,{\beta }_k\le 1$, with ${\alpha }_{i+1}-{\alpha }_i\ge \overline{\delta }$ for all $i=1,\dots ,k-1$, such that $c\left(t\right)$ is continuous and

$$c\left(t\right)=\left\{\begin{array}{c}{\beta }_1\text{ if }t\in [0,{\alpha }_1]\hfill \\ {\beta }_i\text{ if }t\in [{\alpha }_{i-1}+\underset{\_}{\delta },{\alpha }_i],i=1,\dots ,k\hfill \\ {\beta }_i+({\beta }_{i+1}-{\beta }_i)(t-{\alpha }_i)∕\underset{\_}{\delta }\text{ if }t\in [{\alpha }_i,{\alpha }_i+\underset{\_}{\delta }],\hfill \end{array}\right)$$ (15)

where we have taken ${\alpha }_0=0,{\alpha }_k=T$. Notice that ${\mathcal{K}}^{\ast }$ is a class of Lipschitz continuous functions with Lipschitz constant bounded uniformly by $(1-c_0)∕\underset{\_}{\delta }$ on $[0,T]$, as exemplified by the red function in Fig. 5 (notice the non constant linear sections).

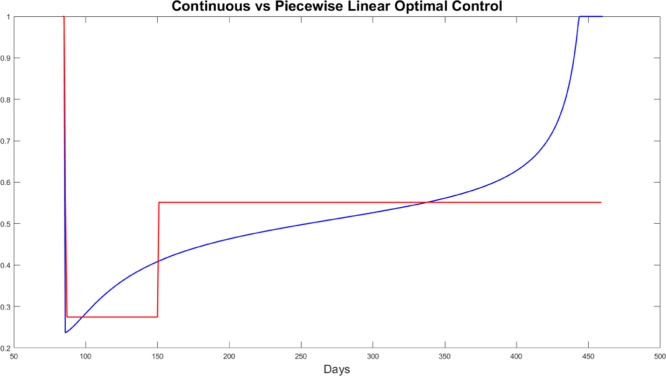
Fig. 5.

Overall optimal control obtained by using BOCOP (Team Commands, 2017, Bonnans et al., 2017) and the piecewise linear optimal control with two level restrictions . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Theorem 4.3

${\mathcal{K}}^{\ast }$ is closed in ${\mathcal{K}}_M$ for $M\ge (1-c_0)∕\underset{\_}{\delta }$ .

In practice, the social planner might be further restricted to take action only at specific times or adopt only specific opening levels. Existence of the minimum there is guaranteed by

Corollary 4.4

Any subset ${\mathcal{K}}_0$ of ${\mathcal{K}}^{\ast }$ with $k$ fixed, or with $k$ fixed and ${\alpha }_i$ ’s also fixed, is closed in ${\mathcal{K}}_M$ , and hence the optimal value of ${min}_{c\in {\mathcal{K}}_0}\mathcal{L}\left(c\right)$ belongs to ${\mathcal{K}}_0$ .

4.2. On uniqueness and continuous dependence of the optimal control

The functional $\mathcal{L}$ in (14) is in general not convex, and there are no reasons to expect uniqueness of the optimal control in ${\mathcal{K}}_M$ and in any subclass of it, nor continuity of the optimal control in the social cost of COVID-19 death $a$. In fact, in some cases the cost functional appears to undergo a first order phase transition in $a$. Typically, real valued functions of systems undergoing a phase transition are convex in one phase and concave in the other (see, e.g., the percolation probability as function of its intensity parameter, Gandolfi, 2013, Figure 2.3). In addition, at the critical value of $a$ there is a jump discontinuity of some functions (in first order transitions, or of their derivatives in second order), and multiple optimal controls can appear.

To show this, we present numerical evidence of this phenomenon for two of the classes of controls that are discussed in detail in Section 5. Note that the value of $a$ here is not the one retained for the policy scenario of next Section: this is just an example illustrating the possibility of phase transition phenomenon, while we argue later in Section 5.1 that observed values of $a$ are mostly above the critical values.

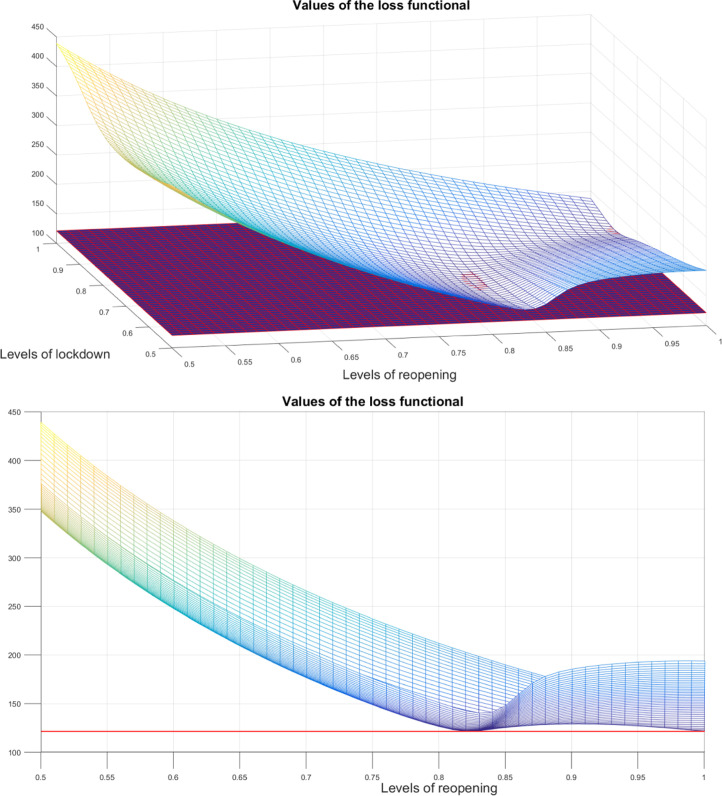
In the first example, a single intervention (called lockdown hereafter for convenience) can be imposed at Day $85$ at a fixed opening level $\underset{\_}{c}$, assumed to be $\underset{\_}{c}=12.5\text{\%}$, till Day 150 where a reopening strategy occurs. The aim of this experiment is to identify the optimal reopening level $\overline{c}$. For each hypothetical value of $a$, the optimization carried out in Section 5.3 is with respect to the value of $\overline{c}$. In order to show the bifurcation phenomenon, we vary the value of $a$ while all other parameters are as in Section 5.1. Indeed, for low values of $a$, laissez-faire, i.e. $\overline{c}=1$, is the optimal policy. For values of $a$ which seem to better reflect current valuations (see Section 5.1), the minimum is instead likely to occur in the phase in which $\mathcal{L}\left(\overline{c}\right)$, is convex, which is at lower values of $\overline{c}$, and therefore it is unique and continuously dependent of $a$. At the largest of the values of $a$ for which laissez-faire is an optimal policy, which is $a\approx 6436.98$, the functional $\mathcal{L}$ admits two optimal policies: one is $\overline{c}=1$, and the other $\overline{c}\approx 0.84$, see the $\mathcal{L}$-$\overline{c}$ plot in Fig. 2. For smaller values of $a$ the graph of Fig. 2 is tilted to the right, and hence laissez-faire is optimal, for larger values it is tilted leftward, and hence the best opening level is around $\overline{c}\approx 0.84$. This discontinuity may help explaining why radically different policies have been advocating for the same situation, such as, for instance, the initial resistance of some administrations to imposing any lock down measure.

Fig. 2.

An example of two minima. $\mathcal{L}$ as function of the reopening intensity $\overline{c}$ applied from day $150$ to $460$. The social cost of Covid death is fixed at $a\approx 6436.98$. See Section 5.1 for the interpretation of this parameter.

We have the same evidence in a class in which two intervention levels can be selected, $\underset{\_}{c}$ from Day 85 till Day 150, followed by a higher reopening level $\overline{c}$ until Day 460, see Section 5.2. For a value of $a$ of about 12907.85 the loss functional $\mathcal{L}$ is plotted in Fig. 3. In one of the two optimal policies, laissez-faire is the selected option after reopening while much more stringent measures are taken in the other optimal strategy. Again, there are discontinuities in the optimal strategy as $a$ goes across the critical value.

Fig. 3.

An example of two minima. Front and side plots of $\mathcal{L}$ as function of the opening level $\underset{\_}{c}$ from Day 85 till Day 150 and reopening intensity $\overline{c}$ applied from day $150$ to $460$. The social cost of Covid death is set at $a\approx 12907.85$.

5. Examples of constrained optimal policies

In this section we select realistic values of the model parameters, and then present three examples of optimal policies subject to tight time constraints. More examples are presented in online material.8

5.1. Parameter selection

In order to simulate several realistic scenarios the parameters of the epidemic model have been selected from available data and suitable inferences. The details are described in Appendix C. For the parameters whose determination is more likely to be subject to limited studies or ad-hoc inferences a sensitivity analysis is carried out in Appendix D. A recap of epidemic parameters is in Table 1.

Table 1.

Recap of the model parameters and their selected values.

Parameter	Selected value
$\beta$	0.25	$\left[h^{-1}\right]$
$\kappa$	0.2	$\left[h^{-1}\right]$
$ϵ$	$1∕3$
$\gamma$	0.14	$\left[h^{-1}\right]$
$\delta$	0.0056	$\left[h^{-1}\right]$
$n$	$3\times 10^{-5}$	$\left[h^{-1}\right]$
$s$	0.1
$s_1$	0.88
$s_2$	0.79

With these assumptions, the equations become

$$\frac{dS}{dt}=-0.25Sc\left(t\right)(0.1I+0.88E+0.79A)-0.00003S+0.00003(1-D)$$ (16)

$$\frac{dE}{dt}=0.25S(0.1I+0.88E+0.79A)-(0.2+0.00003)E$$ (17)

$$\frac{dA}{dt}=0.4∕3E-(0.14+0.00003)A$$ (18)

$$\frac{dI}{dt}=0.2∕3E-(0.14+0.00563)I$$ (19)

$$\frac{dR}{dt}=0.14(A+I)-0.00003R$$ (20)

$$\frac{dD}{dt}=0.0056I$$ (21)

$$\frac{d{D}_N}{dt}=0.00003(S+E+A+I+R)$$ (22)

As we take as initial time a very early stage of the epidemic outbreak (for all countries except China), we assume that the number of initial exposed is very small, in the order of one in a million; hence we take $S\left(0\right)=1-10^{-6},E\left(0\right)=10^{-6},A\left(0\right)=I\left(0\right)=R\left(0\right)=D\left(0\right)=0$. A more accurate model, taking care of the geographical dispersion of the population would include different contact rates for individual living in far away areas (Gatto et al., 2020). As a verification of parameter selection, one can observe the plot of mortality (see Figure 1) in the Online Material.

We now discuss the parameters appearing in the loss function. The yearly discount rate is an annual 3.65%, corresponding to a daily $r=10^{-4}$. In the sensitivity analysis we check the impact of a wide range of alternative assumptions. The exponent $\sigma$ of the function $\mathcal{V}$ is taken to be $\sigma =2$, leading to an intertemporal elasticity of substitution within the year of 1/2.

The elasticity parameter $\theta$ is evaluated as follows. Given that the reproduction number (8) has been estimated in various countries before and after a lockdown, as well as the GDP losses around the first lockdown, one has at each point in time that

$$logP=\theta \left(logc\left(t\right)\right)+log(S+s_{1}E+s_{2}A+R)$$

so that, considering two times, $t^{-}$ shortly before, and $t^{+}$ shortly after a lockdown, we have

$$log\frac{P\left(t^{+}\right)}{P\left(t^{-}\right)}\approx \theta \left(log\frac{c\left(t^{+}\right)}{c\left(t^{-}\right)}\right)\approx \theta log\frac{\mathcal{R}\left(t^{+}\right)}{\mathcal{R}\left(t^{-}\right)},$$

where in the first approximation, we neglected the variation in the potential labor force $S+s_{1}E+s_{2}A+R$, since between $t^{-}$ and $t^{+}$, the labor force available for production is assumed to be only impacted by the variations in $c$; the second approximation follows from (8) again neglecting variations in $S\left(t\right)$ in the short interval. This gives the estimate

$$\theta \approx log\frac{P\left(t^{+}\right)}{P\left(t^{-}\right)}∕log\frac{\mathcal{R}\left(t^{+}\right)}{\mathcal{R}\left(t^{-}\right)}.$$ (23)

In Appendix, we display Table 7 which gives an order of magnitude for $\theta$ based on Eq. (23). We will select an indicative value of $\theta =1∕3$.

In order to identify the time horizon of our analysis, we make several assumptions about the evolution of the epidemic. In particular, we assume that the policy assessment can be made with a specific time frame in mind, after which technological advancements like a therapy or a vaccine will drastically reduce the negative effects of the infection: HHS (2020) and Le et al. (2020) predict a vaccine in early 2021, and challenge trials will anticipate things even further. We then assume a prototypical situation in which the epidemic has started unobserved in January 2020, and we assume that it will resolve at the end of the first quarter of 2021, hence we take $T=460$ days. Clearly, these periods are only indicative, and one can adapt the time frame when more reliable perspectives are identifiable. This was the foreseeable situation in early 2020, but still, in Fall 2020, vaccine development and testing is progressing at the expected rate, so it still seems plausible that a sufficiently widespread vaccination will be completed by the end of the first quarter 2021.

The choice of the social cost $a$ of deaths depends on a variety of socio-political and economic factors, specific to each country. Using the interpretation from Eq. (10), the static value of a life evaluated at full GDP, a benchmark value of $a=18000$ in daily terms leads to a value of life equal to 18 000 the value of daily GDP. In France, this would correspond, with a GDP per capita of $\$41400$, to a statistical value of life of $\$41400∕365\ast 18000\approx \$2.04M$. Applied to the US, the same value for $a$ would lead to a higher statistical value of a life, around $\$3.22M$.9 Using (11) with $r=10^{-4}$, $365$ is replaced by $(1-e^{-365r})∕r\approx 358.4$, with minor changes in the estimates. Such value of $a$ is large enough that the optimal control functions determine an effective containment of the spread of the virus; this implies that the minimum of $\mathcal{L}$ occurs where the total mortality is also likely to be convex as function of the control, and that the minimum is likely to be unique and continuously varying in $a$ (see Section 4.2).

Table 2 summarizes the selected values.

Table 2.

Recap of the loss function parameters and their selected values.

Parameter	Selected value
$r$	$10^{-4}$
$\sigma$	2
$\theta$	$1∕3$
$T_0$	85	Days
$T$	460	Days
$a$	18,000

5.2. Optimal two level restrictions

The first example assumes that two levels of restrictions are imposed, one, denoted by $\underset{\_}{c}$, at Day $85$ till Day $150$, and another level, denoted by $\overline{c}$, up to $T=460$. The policy maker can only determine the levels $\underset{\_}{c}$ and $\overline{c}$, while the dates are fixed. Fig. 4 shows epidemic and economic indicators in four different situations: no restrictions, the optimal policy, and two non optimal ones. This is the same setting that determines two minima in Fig. 3, there with a smaller value of $a$. It is seen in Table 3 that the optimal policy determines almost 82% reduction in mortality at the cost of about 17.40% reduction in GDP.

Fig. 4.

Optimization over two opening levels, the first at Day $85$, and the second at Day $150$, planned in advance. The social cost of Covid death is fixed at $a=18000$ and $r=10^{-4}$. Fig. 4.A, Top left: no policy. Fig. 4.B, Top right: Excessive restrictions. Fig. 4.C, Bottom left: optimal policy. Fig. 4.D, Bottom right: Insufficient restrictions.

The next exercise is to compare the distance between our optimal policy that is constrained at a constant level between Days 85 and 150, and an unconstrained policy simulated by BOCOP. BOCOP uses a direct method to solve the optimal control problem, see Team Commands (2017) and Bonnans et al. (2017). We observe that the continuous optimal control is rather close to the optimal solution with two containment levels, in spite of the restrictions on the policies available to the social planner; see Table 4 for a comparison of the numerical results, and Fig. 5 for a plot of the openness levels in the two policies.

5.3. Optimal reopening level

Most countries have imposed severe restrictions around Day $85$, followed by a sizeable reopening after about two months. To simulate this situation, we assume that at Day $85$ the opening level has been fixed at $\underset{\_}{c}=0.125$; the containment is then relaxed to a level $\overline{c}$, to be optimized, at Day $150$. A loss of production is incurred with the initial containment, and we have selected the opening level $\underset{\_}{c}=0.125$ that reproduces the observed loss of GDP in the first quarter at an annual rate of $3$–5%, see Table 5, Line 5.

Table 5.

One reopening after a lockdown.

	Epidemic Fig. 6.A - No policy	High reopening Fig. 6.B	Opt. reopening Fig. 6.C	Limited reopening Fig. 6.D
Reopening level $\overline{c}$	100%	64.3%	57.2%	16.6%
Mortality at day 85	0.028%	0.028%	0.028%	0.028%
Total mortality at day 460	1.06%	0.43%	0.14%	0.11%
Mortality reduction	0%	59.34%	87.12%	89.54%
Annualized 1st quarter GDP loss	1.22%	3.73%	3.73%	3.73%
Total annualized GDP loss	1.41%	16.82%	18.82%	37.63%
Value loss functional	187.82	183.95	145.88	326.67

We then numerically determine the optimal level of reopening, which turns out to be at $\overline{c}\approx 57.2\text{\%}$. Fig. 6 compares the optimal solution with non-optimal ones, and the case where no policy is adopted. A detailed comparison of some of the outcomes is carried out in Table 5.

Notice that the optimal reopening level achieves a control of the epidemic, with a mortality reduction of about 87%, but with a sizeable annualized GDP loss of almost 19%. On the other hand, the suboptimal policy with an excessive reopening leads to a second epidemic outbreak, the so-called second wave: this is apparently the situation most countries are facing now (in some cases even a third wave in under way).

5.4. Optimal two level restrictions with testing

The sensitivity analysis carried out in Appendix D has shown that, among the most influential parameters, the only ones that are still at disposal to the social planner refer to testing. In the simulations of this section we have assumed the level of testing currently observed in several countries, as this is an endogenous variable unless the social planner explicitly decides to invest in extensive testing.

We present now a simulation with expanded testing, in order to explore its efficacy. Instead of assuming the observed 12% of presymptomatic and 21% of asymptomatic cases detected, we assume that extensive testing is capable of detecting 50% of presymptomatic and 60% of asymptomatic. Considering that a few of the $5$–$7$ days periods are likely to go by before actual testing takes place and results are available, these numbers reflect an almost complete detection of the individuals infected by the virus. We assume a two-level policy, as in Section 5.2.

The results of these simulations reported in Table 6 show a drastic improvement compared to the previous policy. In the optimal policy the GDP loss is less than 1% and mortality is reduced by more than 60%, with a very mild closure at level 88.5% for the first period, and subsequent complete reopening. The loss functional is down to about $5$, while without expanded testing the minimum was at $130$.

Table 6.

Two level restrictions with a high testing.

	Epidemic	Excessive restrictions	Optimal	Sub-optimal restrictions
	Fig. 4.A - No policy	Fig. 4.B	Fig. 4.C	Fig. 4.D
Opening and reopening levels [$\underset{\_}{c}$, $\overline{c}$]	[100%,100%]	[12.5%,12.5%]	[88.5%,100%]	[73%,85.7%]
Mortality at Day 85	$2.89\cdot 10^{-5}$%	$2.89\cdot 10^{-5}$%	$2.89\cdot 10^{-5}$%	$2.89\cdot 10^{-5}$%
Total mortality at Day 460	0.04%	$3.9647\cdot 10^{-5}$%	0.016%	0.00012%
Total mortality reduction	0%	99.90%	61.02%	99.69%
Annualized 1st quarter GDP loss	1.1%	3.57%	1.25%	1.54%
Total annualized GDP loss	0.24%	40.82%	0.80%	4.97%
Value loss functional	7.20	364.45	5.44	22.90

In a sub-optimal policy, with only about 5% GDP loss the mortality is completely eradicated.

6. Extension: Capital accumulation and Ramsey problem

Instead of having GDP directly in the social planner’s objective as in Eq. (9), we modify the problem slightly in allowing the social planner’s utility $\mathcal{W}$ to now combine consumption $C$ and lives, minimizing the loss functional:

$$\mathcal{L}={\int }_{T_0}^T{e}^{-rt}\left[\hat{\mathcal{V}}\left(C\left(t\right)\right)+a{D}^{\prime }\left(t\right)\right]dt$$

with

$$\hat{\mathcal{V}}\left(C\left(t\right)\right)=\frac{1-C{\left(t\right)}^{1-\sigma }}{1-\sigma }$$

6.1. Introducing capital accumulation

Production combines labor, capital and the lockdown control strategy:

$$P=F[c,L,K]$$

Appendix E develops the necessary restrictions on themarginal product of capital necessary to adapt the proof’s strategy to this problem, which in particular requires that $F_K^{\prime }<+\infty$ over the period, which is in particular satisfied with conventional production function as long as aggregate capital does not vanish entirely over the time horizon considered.

In a Solow model, consumers save an exogenous fraction $\xi$ of output and use it to invest in capital. They also consume the rest, that is,

$$C\left(t\right)=(1-\xi )P\left(t\right)$$

Capital stock is accumulated thanks to savings and depreciates at rate $\Psi$ say 10% yearly and so capital is governed by the following ode:

$$\frac{dK}{dt}=-\Psi K+\xi F[c,L,K]$$

The system governing the epidemics is kept the same but we add one additional variable, the capital $K$ being governed by the aforementioned ode. Since consumption is function of the lockdown control $c\left(t\right)$ and is proportional to production the optimization problem reduces again to a minimization over the controls $c\in {\mathcal{K}}^{\ast }$. See Appendix E for further details showing that the Solow problem can be solved as the case treated in the paper, with an additional multiplier on capital accumulation.

6.2. A Ramsey first best problem

If the saving rate is added as a control for the social planner, the saving rate $\xi$ is no longer constant. The social planner minimizes the same loss function as before

$${\mathcal{L}}_{C,c}={\int }_{T_0}^T{e}^{-rt}\left[\hat{\mathcal{V}}\left(C\left(t\right)\right)+a{D}^{\prime }\left(t\right)\right]dt$$

but now has two instruments: one is the lockdown control $c\left(t\right)$, the second one is the saving rate $\xi \left(t\right)$ to control consumption

$$C\left(t\right)=(1-\xi \left(t\right))P\left(t\right)$$

The first order optimality conditions are derived in the form of Pontryagin minimum principle, Pontryagin (2018), for the constrained optimization problem

$$\underset{(\xi ,c)\in {\mathcal{K}}_L\times {\mathcal{K}}^{\ast }}{min}\mathcal{L}(\xi ,c)=\underset{(\xi ,c)\in {\mathcal{K}}_L\times {\mathcal{K}}^{\ast }}{min}{\int }_{T_0}^T{e}^{-rt}\left[\frac{1-{\left((1-\xi \left(t\right))F[c,L,K]\right)}^{1-\sigma }}{1-\sigma }+a{D}^{\prime }\left(t\right)\right]dt$$

under the constraint

$${\overrightarrow{X}}^{\prime }=\overrightarrow{F}(c,\overrightarrow{X}),\overrightarrow{X}\left(0\right)={\overrightarrow{X}}_0.$$

$$\frac{dK}{dt}=-\Psi K+\xi F[c,L,K],K\left(0\right)=K_0.$$ (24)

and Appendix F shows the full optimality conditions.

7. Conclusions

In this paper, we have formalized the trade-offs involved in the decision making between preserving economic activity and reducing the speed of diffusion of the pandemic. Our premise is that individual agents, as well as governments, want to contain and, possibly, postpone the infection and therefore the risk of a greater number of potential deaths to a later stage (“flatten the curve”) in the expectation of better treatments, or a weakening of the virus, or a vaccine, and hence impose restriction measures for relatively long periods. Our second working assumption is that there is a strong link between the containment measures and the intensity of the economic shock, with an elasticity that varies in time and across countries but seems to be in a range around 1/3. This elasticity is the result of all changes in behavior of agents, from the economic lockdown itself to the greater precautions of consumers who reduce their consumption and firms who favor drastic reductions in working time. We have modeled containment measures by a function describing the level of opening, which we have taken to be piece-wise linear, with additional regularities, to include feasibility; we then formally described, in the form of a loss functional, the trade-off between mortality reduction and limitation of economic loss which includes an estimation of the social cost $a$ of COVID-19 mortality, and a discount rate which intensifies the effect of early deaths and early economic losses. We assume that actions are planned over a fixed time horizon, that we choose to be 460 days after reviewing plausible targets for widespread vaccination.

We discussed the mathematical set-up and proved the existence of at least one optimal containment strategy in each class of available strategies; as benchmark, we showed how to determine the overall optimal strategy, that we argue is not realistically implementable. A parametric representation of mortality vs. economic losses illustrates the potentialities of the optimization approach.

We then uncovered the possibility of a discontinuity in the optimal strategy as function of the parameter $a$ describing the social cost of COVID-19 mortality, very likely due to the non convexity of the loss functional. In some examples, a first order phase transition takes place as $a$ varies: at and below the bifurcation point, laissez-faire is optimal, but a substantially different policy is preferred when the statistical value of a life is larger than the critical value.

Given that, for most countries, the implied value of the social cost of COVID-19 death $a$ is in a range in which laissez-faire is not a viable solution. We discussed the optimal policies in a restricted set where the opening level can vary only a very limited number of times and where the solution turns out to be unique. Parameters have been estimated from available data, and a sensitivity analysis has been carried out on the main ones. We have analyzed various examples. In the first example, two lockdown levels are admitted between fixed dates. We propose the same simulation even with a higher level of testing. In the second example, a more severe lock has been decided in the first period, and we optimize on the level of reopening. Further examples are one unique lockdown to be extended till the presumed end of the epidemic at the end of the first quarter 2021; and some alternation of containment and reopening after the current one, which is a plausible outcome if the regained activity leads to recurrence of the virus (see Online Material). One of the outcomes of these simulations is that containment policies could be very effective if planned properly; on the other hand, most countries have not been able to implement them, as all optimal policies end up preventing a second wave, which is instead taking place almost everywhere.

Finally, the sensitivity analysis has pointed out that the most relevant parameters on which the social planner could direct its intervention concern testing. With a substantially expanded testing optimal and sub-optimal policies almost completely eliminate mortality with extremely mild economic losses.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Manuscript handled by Editor Aditya Goenka

Appendix A. Proofs

Proof of Theorem 4.1

To prove continuity we use the well-posedness of the S-E-A-I-R-D model. In fact, let $\overrightarrow{X}=(S,E,A,I,R,D)$ and denote by $\overrightarrow{F}(c,\overrightarrow{X})$ the vector-valued function having as components the right-hand sides of the S-E-A-I-R-D differential equations.

Then we can rewrite the system in vector form

$${\overrightarrow{X}}^{\prime }=\overrightarrow{F}(c,\overrightarrow{X}),\overrightarrow{X}\left(0\right)={\overrightarrow{X}}^0.$$

where by assumption the norm10 of the solution $\overrightarrow{X}$ is such that $\Vert \overrightarrow{X}\Vert \le 1$ and $\overrightarrow{F}$ is smooth in both variables. Let now $c_n$ be a sequence of continuous functions on $[0,T]$ converging uniformly in $[0,T]$ to a continuous function $c$. Consider now the solution ${\overrightarrow{X}}_n\in C^1[0,T]$ of

$${\overrightarrow{X}}^{\prime }=\overrightarrow{F}(c_n,\overrightarrow{X}),\overrightarrow{X}\left(0\right)={\overrightarrow{X}}^0$$

and denote by $\overrightarrow{X}\in C^1[0,T]$ the solution to

$${\overrightarrow{X}}^{\prime }=\overrightarrow{F}(c,\overrightarrow{X}),\overrightarrow{X}\left(0\right)={\overrightarrow{X}}^0$$

Then ${\overrightarrow{W}}_n={\overrightarrow{X}}_n-\overrightarrow{X}$ is solution to

$${\overrightarrow{W}}_n^{\prime }=\overrightarrow{F}(c_n,{\overrightarrow{X}}_n)-\overrightarrow{F}(c,\overrightarrow{X}),\overrightarrow{W}\left(0\right)=\overrightarrow{0}$$

Now observe that

$$\overrightarrow{F}(c_n,{\overrightarrow{X}}_n)-\overrightarrow{F}(c,\overrightarrow{X})=\overrightarrow{F}(c_n,{\overrightarrow{X}}_n)-\overrightarrow{F}(c,{\overrightarrow{X}}_n)+\overrightarrow{F}(c,{\overrightarrow{X}}_n)-\overrightarrow{F}(c,\overrightarrow{X})$$

and by the smoothness of $\overrightarrow{F}$, the boundness of ${\overrightarrow{X}}_n$ and $\overrightarrow{X}$ and the linear dependence of $\overrightarrow{F}$ on $c$ we have the following bounds

$$\Vert \overrightarrow{F}(c_n,{\overrightarrow{X}}_n)-\overrightarrow{F}(c,{\overrightarrow{X}}_n)\Vert \le C\Vert c_n-c\Vert$$

and

$$\Vert \overrightarrow{F}(c,{\overrightarrow{X}}_n)-\overrightarrow{F}(c,\overrightarrow{X})\Vert \le K\Vert {\overrightarrow{W}}_n\Vert$$

From these last two inequalities we get the differential inequality

$$\Vert {\overrightarrow{W}}_n^{\prime }\Vert \le K\Vert {\overrightarrow{W}}_n\Vert +C\Vert c_n-c\Vert ,\overrightarrow{W}\left(0\right)=\overrightarrow{0}$$

which implies

$$\underset{[0,T]}{max}\Vert {\overrightarrow{W}}_n\Vert \le C\underset{[0,T]}{max}|c_n-c|e^{KT}$$

Hence,

$$\underset{[0,T]}{max}\Vert {\overrightarrow{W}}_n\Vert \to 0$$

as $n\to \infty$ i.e. 

$$\underset{[0,T]}{max}\Vert {\overrightarrow{X}}_n-\overrightarrow{X}\Vert \to 0$$

as $n\to \infty$. Finally, noting that

$$\mathcal{L}\left(c_n\right)={\int }_{T_0}^{T}f(t,c_n,{\overrightarrow{X}}_n)dt$$

and since $f$ is continuous in all variables ($a{D}^{\prime }=\delta X_4$), ${max}_{[0,T]}\Vert {\overrightarrow{X}}_n-\overrightarrow{X}\Vert \to 0$ and ${max}_{[0,T]}|c_n-c|\to 0$ we finally obtain

$$\mathcal{L}\left(c_n\right)\to \mathcal{L}\left(c\right)$$

as $n\to \infty$. □

Proof of Theorem 4.3

For each sequence $\left\{c_n\right\},c_n\in {\mathcal{K}}^{\ast }$, we have $c_n\le 1$ and $|c_n\left(x\right)-c_n\left(y\right)|\le \frac{(1-c_0)}{\underset{\_}{\delta }}|x-y|$; by Ascoli–Arzela Theorem, the sequence converges uniformly in $[0,T]$, possibly up to a subsequence, to a continuous function $c$. Clearly the function $c$ has range in $[c_0,1]$ and is Lipschitz continuous with Lipschitz constant bounded by $(1-c_0)∕\underset{\_}{\delta }$. Let us prove that it must be piece-wise linear of the form (15).

Consider $\eta \le \underset{\_}{\delta }$ and points of the form $x_h=h\eta$ for $h=1,\dots ,\lfloor T∕\eta \rfloor$. Take $h_1$ and $h_2$ such that $|h_1-h_2|<\underset{\_}{\delta }∕\eta$. We consider the two possible cases.

• (1)
  Suppose $c\left(x_{h_1}\right)=c\left(x_{h_2}\right)$. Since $|x_{h_1}-x_{h_2}|<\underset{\_}{\delta }$, any $c_n$ has the extreme values in the interval $[x_{h_1},x_{h_2}]$ exactly at $x_{h_1}$ and $x_{h_2}$; for small $ϵ$ and large enough $n$, assuming, without loss of generality, that $c_n\left(x_{h_1}\right)\le c_n\left(x_{h_2}\right)$, we have

  $$c\left(x_{h_1}\right)-ϵ\le c_n\left(x_{h_1}\right)\le c_n\left(x\right)\le c_n\left(x_{h_2}\right)\le c\left(x_{h_2}\right)+ϵ=c\left(x_{h_1}\right)+ϵ$$

  for all $x\in [x_{h_1},x_{h_2}]$. Hence, in the limit for $n\to \infty$, we have $c\left(x\right)=c\left(x_{h_1}\right)$ for all $x\in [x_{h_1},x_{h_2}]$.
• (2)If $c\left(x_{h_1}\right)\ne c\left(x_{h_2}\right)$, then take $x_{h_2}+\underset{\_}{\delta }$ and $x_{h_2}+\underset{\_}{\delta }+(\overline{\delta }-\underset{\_}{\delta })∕2$: it must be $c(x_{h_2}+\underset{\_}{\delta })=c(x_{h_2}+\underset{\_}{\delta }+(\overline{\delta }-\underset{\_}{\delta })∕2)$; in fact, for $ϵ<|c\left(x_{h_1}\right)-c\left(x_{h_2}\right)|∕3$ and $n$ large enough, $|c_n\left(x_{h_1}\right)-c_n\left(x_{h_2}\right)|>|c\left(x_{h_1}\right)-c\left(x_{h_2}\right)|∕3>0$, hence $c_n$ must have a non constant part in $[x_{h_1},x_{h_2}]$ and must thus be constant in $[x_{h_2}+\underset{\_}{\delta },x_{h_2}+\underset{\_}{\delta }+(\overline{\delta }-\underset{\_}{\delta })∕2]$. For the same reason, $c(x_{h_1}-\underset{\_}{\delta })=c(x_{h_1}-\underset{\_}{\delta }-(\overline{\delta }-\underset{\_}{\delta })∕2)$. Let ${\overline{x}}_1$ be the sup of the points $x\le x_{h_2}$ such that $c\left(x\right)=c(x_{h_1}-\underset{\_}{\delta })$, and let ${\overline{x}}_2$ be the inf of the points $x\ge x_{h_1}$ such that $c\left(x\right)=c(x_{h_2}+\underset{\_}{\delta })$. For $ϵ$ small enough and $n$ large enough, $c_n$ must be constant in $[x_{h_1}-\underset{\_}{\delta },{\overline{x}}_1-ϵ]$ and in $[{\overline{x}}_2+ϵ,x_{h_2}+\underset{\_}{\delta }]$, and linear in some interval of length $\underset{\_}{\delta }$ included in $[{\overline{x}}_1-ϵ,{\overline{x}}_2+ϵ]$; moreover, taking ${\overline{x}}_1<{\tilde{x}}_1<{\overline{x}}_1+ϵ$ and ${\overline{x}}_2-ϵ<{\tilde{x}}_2<{\overline{x}}_2$ such that $c\left({\overline{x}}_1\right)<c\left({\tilde{x}}_1\right)<c\left({\overline{x}}_1\right)+(c\left({\overline{x}}_2\right)-c\left({\overline{x}}_1\right))∕4$ and $c\left({\overline{x}}_2\right)+(c\left({\overline{x}}_2\right)-c\left({\overline{x}}_1\right))∕4<c\left({\tilde{x}}_2\right)<c\left({\overline{x}}_2\right)$, we have that $c_n$ is connecting two values at distance at most $ϵ$ from $c\left({\overline{x}}_1\right)$ and $c\left({\overline{x}}_2\right)$, being nowhere constant in $[{\overline{x}}_1+ϵ,{\overline{x}}_2-ϵ]$. Since this holds for all small $ϵ$, it implies that $|{\overline{x}}_1-{\overline{x}}_2|=\underset{\_}{\delta }$, and that $c$ must be linear in between these points, connecting $c\left({\overline{x}}_1\right)$ and $c\left({\overline{x}}_2\right)$ by continuity.

Pairs of points in which $\left(2\right)$ happens cannot overlap, hence indicate ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{k-1}$ be the smallest points of each pair, arranged in increasing order; let ${\alpha }_0=0,{\alpha }_k=T$; and let $c_0\le {\beta }_1,\dots ,{\beta }_k\le 1$ be the such that $c\left(x\right)={\beta }_i$ for $x\in [{\alpha }_{i-1}+\underset{\_}{\delta },{\alpha }_i]$ for $i=1,\dots ,k$. We have shown that $c\left(t\right)$ satisfies (15) for these values of $\alpha$’s and $\beta$’s. This finishes the proof.  □

Proof of Corollary 4.4

It is seen in the proof of Theorem 4.3 that if $c_n\in {\mathcal{K}}^{\ast }$ is a sequence of controls, where $c_n$ has $k\left(n\right)$ intervals and subdivisions ${\alpha }_i\left(n\right)$, converging to a control $c$ with $k$ intervals and subdivisions ${\alpha }_i$, then

$$k\le lim\; infk\left(n\right)$$

since for $ϵ<{min}_i\{{\beta }_{i+1}-{\beta }_i\}∕2$ and $n$ large enough, any $c_n$ such that $\Vert c_n-c\Vert <ϵ$ has at least $k$ different level $\beta$’s; therefore, each ${\mathcal{K}}_0$ with $k$ fixed is closed.

In addition, each ${\alpha }_i$ is accumulation point of some sequence ${\alpha }_{i_n}\left(n\right)$ by Part (2) of the proof of Theorem 4.3, so that each ${\mathcal{K}}_0$ with $k$ fixed and ${\alpha }_i$’s also fixed is closed as well. □

Appendix B. First order optimality conditions

We derive the first order Pontryagin conditions for loss functional (9)

Let ${\overrightarrow{X}}^{\ast }$ and $c^{\ast }$ be the optimal pair for the above constrained minimization problem.

Then the augmented Hamiltonian is

$$\mathcal{H}=e^{-rt}\left(\frac{1-{\left(c^{\theta }\left[S+s_{1}E+s_{2}A+R\right]\right)}^{1-\sigma }}{1-\sigma }+a\delta I+e^{rt}\overrightarrow{\lambda }\cdot \overrightarrow{F}\right)\left(+e^{rt}{w}_1(1-c)+e^{rt}{w}_{2}c\right)$$

and considering now

$$\tilde{\mathcal{H}}=e^{rt}\mathcal{H}=\frac{1-{\left(c^{\theta }\left[S+s_{1}E+s_{2}A+R\right]\right)}^{1-\sigma }}{1-\sigma }+a\delta I+e^{rt}\overrightarrow{\lambda }\cdot \overrightarrow{F}+e^{rt}{w}_1(1-c)+e^{rt}{w}_{2}c$$

where $\overrightarrow{\lambda }=({\lambda }_S,{\lambda }_E,{\lambda }_A,{\lambda }_I,{\lambda }_R,{\lambda }_D)$, $w_1$ and $w_2$ are two non-negative functions. Set $\overrightarrow{\mu }=e^{rt}\overrightarrow{\lambda }$ and $v_1=e^{rt}{w}_1$, $v_2=e^{rt}{w}_2$, we can express the optimality conditions in terms of the Hamiltonian $\tilde{\mathcal{H}}$, i.e., 

$${\tilde{\mathcal{H}}}_c^{\ast }=0$$

where ${\tilde{\mathcal{H}}}_c^{\ast }$ indicates the derivative with respect to $c$ of $\tilde{\mathcal{H}}(c,{\overrightarrow{X}}^{\ast },{\overrightarrow{\mu }}^{\ast },v^{\ast })$, i.e. 

$$-\theta c^{\theta (1-\sigma )-1}{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{1-\sigma }-{\mu }_S^{\ast }\beta S^{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast })+{\mu }_E^{\ast }\beta S^{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast })-v_1^{\ast }+v_2^{\ast }=0$$

where $v_1^{\ast },v_2^{\ast }\ge 0$ and the vectors ${\overrightarrow{X}}^{\ast }$ and $\overrightarrow{{\mu }^{\ast }}$ are respectively the solution of the direct problem and of the adjoint linear problem along the optimal solution $c=c_{\ast }\left(t\right)$, that is

$$\left\{\begin{array}{ccc}\hfill {\mu }_S^{\prime }-r{\mu }_S& \hfill =\hfill & c_{\ast }^{(1-\sigma )\theta }{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{-\sigma }\hfill \\ \hfill & \hfill \hfill & +{\mu }_S(n+\beta c_{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }))\hfill \\ \hfill & \hfill \hfill & -{\mu }_E\beta c_{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast })\hfill \\ \hfill {\mu }_E^{\prime }-r{\mu }_E& \hfill =\hfill & s_1{c}_{\ast }^{(1-\sigma )\theta }{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{-\sigma }+{\mu }_S{s}_1\beta c^{\ast }{S}^{\ast }\hfill \\ \hfill & \hfill \hfill & -{\mu }_E(s_1\beta c^{\ast }{S}^{\ast }-(\kappa +n))-{\mu }_A(1-ϵ)\kappa -{\mu }_I\kappa ϵ\hfill \\ \hfill {\mu }_A^{\prime }-r{\mu }_A& \hfill =\hfill & s_2{c}_{\ast }^{(1-\sigma )\theta }{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{-\sigma }+{\mu }_S{s}_2\beta c_{\ast }{S}^{\ast }\hfill \\ \hfill & \hfill \hfill & -{\mu }_E{s}_2\beta c_{\ast }{S}^{\ast }+{\mu }_A(\gamma +n)-{\mu }_R\gamma \hfill \\ \hfill {\mu }_I^{\prime }-r{\mu }_I& \hfill =\hfill & -a\delta +{\mu }_S\beta s{c}_{\ast }{S}^{\ast }-{\mu }_E\beta s{c}_{\ast }{S}^{\ast }+{\mu }_I(\gamma +\delta +n)\hfill \\ \hfill & \hfill \hfill & -{\mu }_R\gamma -{\mu }_D\delta \hfill \\ \hfill {\mu }_R^{\prime }-r{\mu }_R& \hfill =\hfill & c_{\ast }^{(1-\sigma )\theta }{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{-\sigma }+{\mu }_{R}n\hfill \\ \hfill {\mu }_D^{\prime }-r{\mu }_D& \hfill =\hfill & {\mu }_{S}n\hfill \\ \hfill \overrightarrow{\mu }\left(T\right)& \hfill =\hfill & 0\hfill \end{array}\right)$$

One can use the optimality conditions to compute the optimal control in a larger class of continuous functions and use it as benchmark for the suboptimal control that we find in the class ${\mathcal{K}}^{\ast }$.

Appendix C. Epidemic parameters selection

There is a large variability in the estimations of the COVID-19 infection rate $\beta$ (Toda, 2020); we adopt the average value of $\beta \approx 0.25$.

Duration of the latency period, after infection and before symptoms are developed, has been estimated in about $5$ days (see for example Li et al., 2020 and Kai-Wang et al., 2020), so that $\kappa \approx 0.2$. The fraction of asymptomatic is also quite problematic, with estimates ranging from 15% to 80%; as it is likely that a proportion of asymptomatic is missed from the testing, we take a recently reported high value of $(1-ϵ)=2∕3$, Al-Qahtani et al. (2020). Similarly, the average recovery period is about $7$ days, for mild cases (Byrne et al., 2020), suggesting $\gamma \approx 0.14$ for the recovery rate of an asymptomatic; in general, more severe cases worsen after about $7$ days, requiring hospitalization, which completely excludes them from the possibility of transmission: for this reason, we also use the same value of $\gamma \approx 0.14$ for moving these cases from the infected to recovered, where most of them eventually will be; one fraction eventually dies, with the rate discussed now. The death to recovery rate is a highly controversial value, as both the recorded number of infected and deaths are affected by error which could range to 1000%. We take $\delta ∕\gamma \approx 0.04$ in such a way that the overall mortality rate in the population if the epidemics spreads without control ends up being about 1.06%; this is in line with several studies and observations: Basu (2020) estimates a US mortality of 1.3%; the Institute Pasteur indicates 0.53% (Salje et al., 2020); and several locations have observed an increase of overall mortality up to six-fold (ISTAT, 2020); this is compatible with a COVID-19 death rate of about 1.06% spread over the two months very likely needed for the uncontrolled virus to infect everyone in a limited area. Finally, the natural mortality rate is taken to be $3\times 10^{-5}$ corresponding to about 12 death per year per $1000$, which is an average natural mortality rate in industrialized countries.11

Next, we discuss the coefficients $s$, indicating the fraction of the affected population that is not in isolation. Symptomatic individuals are mostly isolated as soon as symptoms appear, even before testing: we assume, therefore, that only about 10% are at the onset of symptoms or do not follow the protocols, which is, we take a factor $s=0.1$. Pre- and asymptomatic are mostly isolated as effect of testing; according to various estimates, e.g. Böhning et al. (2020), the undetected fraction of people affected by Covid-19 exceeds 67% at the current level of testing in several European countries; moreover, it is reported in Woodhill (2020) that about 21% of the individuals being tested have symptoms, and that another 12% develops symptoms later, indicating that they were in the presymptomatic phase $E$ at testing; assuming the above percentages, that also a fraction $12∕33$ of the asymptomatic are in the presymptomatic phase at testing, and that the other cases are asymptomatic, as discussed before, one gets that testing at the current level reveals the following percentages: the fraction of cases revealed at the presymptomatic stage is about ${(1∕3)}^{2}12∕33$ for those who will be symptomatic and $2{(1∕3)}^{2}12∕33$ for those who will be asymptomatic; combining these two estimates, this makes about 12% of cases revealed at presymptomatic stage; since all cases went through such stage we take $s_1=0.88$. Asymptomatics are about 67% of those affected, and $1∕32∕321∕33\approx 0.14$ are detected, this is $0.14{(0.67)}^{-1}\approx 0.21$ of the asymptomatic are detected, and hence so we take $s_2=0.79$. We then carry out a sensitivity analysis of all these parameters.

Table 7 shows various examples of co-variations of $\mathcal{R}$ and instantaneous GDP variations in various countries, estimated from now-casting studies from various economic and statistical institutions after a lockdown. The displayed values derive from data based estimates, simulations of epidemiological models, and calibrations of economic papers, whose diversity of methods determines the variability in the values of $\theta$. The range is between 0.14 and 0.52, with an average of 0.27 and a s.d. of 0.12. We select an indicative value of $1∕3$.12

Table 7.

Alternative values of $\theta$, from various studies and variants.

Country/Region	GDP loss (Instantan. or monthly)	$log\frac{P\left(t^{+}\right)}{P\left(t^{-}\right)}$	Source	$\mathcal{R}\left(t\right)$	$log\frac{\mathcal{R}\left(t^{+}\right)}{\mathcal{R}\left(t^{-}\right)}$	Source	Implied $\theta$
France	−36%	−0.405	(A)	From 3 to 1	−1.099	(0)	0.369
France (2)	–	–	–	From 3 to 0.5	−1.792	(b)	0.226
France (3)	–	–	–	From 3.15 to 0.27	−2.457	(a)	0.165
Italy	−36%	−0.405	(B)	From 3.54 to 0.19	−2.925	(a)	0.139
Germany	−30%	−0.357	(B)	From 3 to 1	−1.099	(c)	0.325
Germany (2)				From 3.34 to 0.52	−1.860	(a)	0.192
Sweden	−20%	−0.223	(B)	From 3.04 to 2.02	−0.409	(a)	0.545
US (late March)	−10.0%	−0.105	(C)	From 1.50 (to 1)	−0.405	(d)	0.260
US (2) (late March)	–	–	–	From 2,20 (to 1)	−0.788	(e)	0.134
US (3) (late March)	−10%	–	–	From 2 to 1	−0.693	(f)	0.152
US (4) (May)	−31.0%	−0.371	(C)	From 3 to 1	−1.099	(0)	0.338
US (5) (May)	−34.9%	−0.430	(D)	From 3 to 1	−1.099	(0)	0.391
Our preferred benchmark	−23.3%	−0.265	–	From 2 to 0.8	−0.916	(*)	1/3

Notes: specification and sources.

(0): Priors; (*): our simulated benchmark outcome.

(a): Bryant and Elofsson (2020).

(b): Dimdore-Miles and Miles (2020).

(c): Hamouda et al. (2020).

(d): Eichenbaum et al. (2020).

(e): Riou and Althaus (2020).

(f): Jones et al. (2020).

(A) INSEE, April 2020, Point conjoncture.

(B) OECD Nowcasts, Coronavirus: The world economy in freefall, http://www.oecd.org/economy/.

(C) Fed Atlanta GDPNow tracker (8/10/2020).

(D) New York Fed Staff Nowcast https://www.forexlive.com/centralbank/!/the-ny-fed-nowcast-tracks-2q-growth-at-3122-20200508.

(E) Sweden: Forecast for 2020 are estimated to be between −6.9% and 9.7% by Statistics Sweden and the Riskbank, approx. 2/3rd of the decline in France. https://www.cnbc.com/2020/04/30/coronavirus-sweden-economy-to-contract-as-severely-as-the-rest-of-europe.html.

Appendix D. Sensitivity analysis

We provide, in this section, a Sensitivity Analysis (SA) to evaluate how some of the parameters affect the minimum of the loss functional in the case of two level restrictions of Section 5.2. Initially, SA is performed by a global sensitivity analysis approach using the Sensitivity Analysis tool of Matlab. Then, we also provide a local sensitivity analysis where we calculate the optimal policy varying one parameter at a time.

The global sensitivity approach uses a representative set of samples of parameters to evaluate the loss functional, which also includes the level of opening and reopening. The workflow is as follows:

• (1)For each parameter, including the opening level $\underset{\_}{c}$ during containment and the reopening level $\overline{c}$, we generate multiple values that the parameters can assume, namely we define the parameter sample interval by specifying a uniform probability distribution for each parameter. We create 800 combinations of these parameters.
• (2)Then, we find the solution of the SEAIRD model and evaluate the loss functional at each combination of parameter values and choose the combination which gives the minimum value of the loss functional.
• (3)Fixing the “best outcome” combination found in (2), except the opening level $\underset{\_}{c}$ and the reopening level $\overline{c}$, we run again the optimization procedure, used in the previous sections, to find the optimal value of the opening and reopening levels for that combination of parameters.

Table 8 indicates the ranges for each parameter.

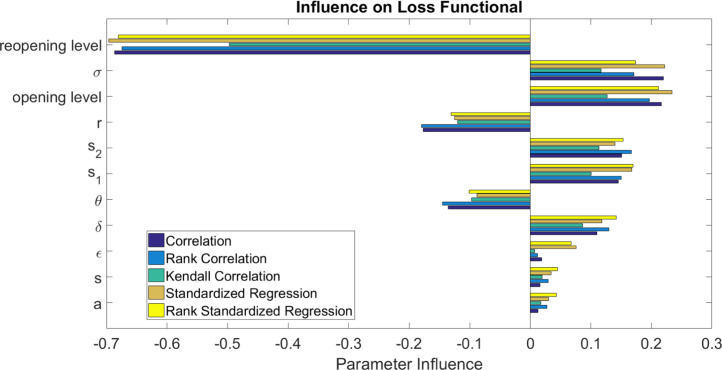
As expected, parameters that carry a greater weight on the functional value are $\sigma ,r,s_1$ and $s_2$. Especially, the sensitivity analysis suggests to use the smallest possible value for $s_1$ and $s_2$. In fact, this is clear in Fig. 7, where, as a result of the sensitivity analysis, a tornado plot is displayed. The coefficients are plotted in order of influence of parameters on the loss functional, starting with those with greatest magnitude of influence from the top of the chart. One can appreciate the influence of $s_1$ and $s_2$ on the results of the optimization process by the numerical outcomes in Table 6, where $s_1=0.5$ and $s_2=0.4$, comparing them with the optimal opening and reopening levels obtained by the sensitivity analysis in Table 9.

Table 8.

Parameter ranges in sensitivity analysis.

Parameter	Range
$ϵ$	$[0.3,0.6]$
$\delta$	$[0.004,0.008]$
$s$	$[0,0.3]$
$s_1$	$[0.5,1]$
$s_2$	$[0.4,1]$
$r$	$[0,0.0001]$
$\sigma$	$[1.5,3.5]$
$\theta$	$[\frac{1}{4},\frac{5}{12}]$
$a$	$[15000,20000]$

Fig. 7.

An example of the influence of the parameters on the loss functional for the numerical experiment with two restrictions.

We provide below a table comparing results from the optimal case determined with our methods, and the optimal case after the SA described in (2), (3) above. For completeness, we also provide a local sensitivity analysis which is a technique to analyze the effect of one parameter on the cost function, and especially on the optimal policy. See Table 10.

Table 9.

Comparison of the optimal values of Section 5.2 with the result of the global sensitivity analysis.

	Optimal case - Section 5.2	Optimal case - SA
Optimal Opening and reopening levels [$\underset{\_}{c},\overline{c}$]	[27.5%,55.1%]	[85.7%,94.1%]
Mortality at Day 85	0.028%	3.946e−05%
Total mortality at day 460	0.19%	0.017996%
Mortality reduction	81.97%	94.08%
Annualized 1st quarter GDP loss	2.82%	1.3136%
Total annualized GDP loss	17.40%	2.2875%
Value loss functional	130.25	10.8296

Table 10.

Local sensitivity analysis for the numerical experiment with two restrictions, see Section 5.2.

Parameter	Range	Optimal Opening and reopening levels $[\underset{\_}{c},\overline{c}]$
		At min range	At max range
$ϵ$	$[0.3,0.6]$	[28.8%,55.1%]	[35.8%,59.3%]
$\delta$	$[0.004,0.008]$	[32.9%,55.1%]	[23.8%,55.1%]
$s$	$[0,0.3]$	[28.8%,55.1%]	[27.5%,57.2%]
$s_1$	$[0.5,1]$	[53.1%,68.2%]	[51.2%,1%]
$s_2$	$[0.4,1]$	[43.9%,65.9%]	[55.1%,1%]
$r$	$[0,0.0001]$	[27.5%,55.1%]	[27.5%,55.1%]
$\sigma$	$[1.5,3.5]$	[25%,55.1%]	[35.8%,55.1%]
$\theta$	$[\frac{1}{4},\frac{5}{12}]$	[34.3%,63.6%]	[63%,78%]
$a$	$[15000,20000]$	[30.1%,55.1%]	[26.2%,55.1%]

Appendix E. A problem with capital and consumption with fixed saving rate (Solow type)

Social planner’s objective

The social planner’s utility $\mathcal{W}$ combines now consumption defined below. The social planner minimizes a loss function between an initial period $t=0$ and final period $T$ which could be infinity:

$$\mathcal{L}={\int }_{T_0}^T{e}^{-rt}\left[\hat{\mathcal{V}}\left(C\left(t\right)\right)+a{D}^{\prime }\left(t\right)\right]dt$$

with

$$\hat{\mathcal{V}}\left(C\left(t\right)\right)=\frac{1-C{\left(t\right)}^{1-\sigma }}{1-\sigma }$$

Economy

Production combines labor, capital and the lockdown control strategy:

$$P=F[c,L,K]$$

with $F_K^{\prime }<+\infty$ e.g. with production functions of the form

• (1)$F(c,L,K)=c^{\theta }{(a{K}^{\rho }+b{L}^{\rho })}^{1∕\rho }$ for $\rho <0$, or $\rho \ge 0$ but capital strictly positive over the time horizon analyzed,13
• (2)$F(c,L,K)=\left(a{c}^{\theta }L+bK\right)$ or of the form,
• (3)$F(c,L,K)=A{c}^{\theta }{L}^{\alpha }{(K+a)}^{1-\alpha }$ with $a>0,\alpha \in (0,1)$.

In all cases the marginal product of capital stays bounded uniformly in $(c,L,K)$.

Consumers save an exogenous fraction $\xi$ of output and use it to invest in capital. They also consume the rest, that is,

$$C\left(t\right)=(1-\xi )P\left(t\right)$$

Capital stock is accumulated thanks to savings and depreciates at rate $\Psi$ say 10% yearly and so capital is governed by the following ode:

$$\frac{dK}{dt}=-\Psi K+\xi F[c,L,K]$$

Optimal control problem

The system governing the epidemics is kept the same but we add one additional variable, the capital $K$ being governed by the aforementioned ode. Since consumption is function of the lockdown control $c\left(t\right)$ and is proportional to production the optimization problem reduces again to a minimization over the controls $c\in {\mathcal{K}}^{\ast }$

$$\underset{c\in {\mathcal{K}}^{\ast }}{min}\mathcal{L}\left(c\right)=\underset{c\in \mathcal{K}}{min}{\int }_{T_0}^T{e}^{-rt}\left[\frac{1-{\left[(1-\xi )F(c,L,K)\right]}^{1-\sigma }}{1-\sigma }+a{D}^{\prime }\left(t\right)\right]dt$$ (25)

under the constraints

$${\overrightarrow{X}}^{\prime }=\overrightarrow{F}(c,\overrightarrow{X}),\overrightarrow{X}\left(0\right)={\overrightarrow{X}}_0.$$

$$\frac{dK}{dt}=-\Psi K+\xi F[c,L,K],K\left(0\right)=K_0.$$ (26)

and where ${\mathcal{K}}^{\ast }$ is the same class of controls defined in the text. So, by the assumptions on the nonlinearity $F$ governing production as function of labor and capital the Solow problem can be solved as the case treated in the paper.

Appendix F. A Ramsey first best problem

Now, let consumption be endogenous too, so that the saving rate $\xi$ is not constant.

The social planner’s utility $\mathcal{L}$ combines now consumption defined below. The social planner minimizes the same loss function as before, between an initial period $0$ and a final period $T$ which could be infinity:

$${\mathcal{L}}_{C,c}={\int }_{T_0}^T{e}^{-rt}\left[\hat{\mathcal{V}}\left(C\left(t\right)\right)+a{D}^{\prime }\left(t\right)\right]dt$$

but now has two instruments: one is the lockdown control $c\left(t\right)$, the second one is the saving rate $\xi \left(t\right)$ to control consumption

$$C\left(t\right)=(1-\xi \left(t\right))P\left(t\right)$$

which determines at which rate the capital can be accumulated, namely:

$$\frac{dK}{dt}=-\Psi K+F[c,L,K]-C\left(t\right),K\left(0\right)=K_0$$

So, the problem reduces to determine

$${\mathcal{L}}_{\xi ,c}={\int }_{T_0}^T{e}^{-rt}\left[\hat{\mathcal{V}}\left((1-\xi \left(t\right))P\left(t\right)\right)+a{D}^{\prime }\left(t\right)\right]dt$$

Existence of an optimal control can be shown similarly as for the case treated in the paper assuming now that $(\xi ,c)\in {\tilde{\mathcal{K}}}_L\times {\mathcal{K}}^{\ast }$ where ${\tilde{\mathcal{K}}}_L=L_M([0,T];[0,1])$ using the regularity properties of the functions $F(c,L,K)$ in (1) and (2) introduced for the Solow model in Appendix 1.

We can write first order optimality conditions in the form of Pontryagin minimum principle, Pontryagin (2018), for the constrained optimization problem

$$\underset{(\xi ,c)\in {\mathcal{K}}_L\times {\mathcal{K}}^{\ast }}{min}\mathcal{L}(\xi ,c)=\underset{(\xi ,c)\in {\mathcal{K}}_L\times {\mathcal{K}}^{\ast }}{min}{\int }_{T_0}^T{e}^{-rt}\left[\frac{1-{\left((1-\xi \left(t\right))F[c,L,K]\right)}^{1-\sigma }}{1-\sigma }+a{D}^{\prime }\left(t\right)\right]dt$$

under the constraint

$${\overrightarrow{X}}^{\prime }=\overrightarrow{F}(c,\overrightarrow{X}),\overrightarrow{X}\left(0\right)={\overrightarrow{X}}_0.$$

$$\frac{dK}{dt}=-\Psi K+\xi F[c,L,K],K\left(0\right)=K_0.$$ (27)

Fixing our attention on the case where $F(c,L,K)=a{c}^{\theta }L+bK$ the optimality conditions

$${\tilde{\mathcal{H}}}_{c_{\ast }}=0$$

where ${\tilde{\mathcal{H}}}_{c_{\ast }}$ indicates the derivative with respect to $c$ of $\tilde{\mathcal{H}}(c,{\xi }^{\ast },{\overrightarrow{X}}^{\ast },K^{\ast },{\overrightarrow{\mu }}^{\ast },{\overrightarrow{v}}^{\ast },{\overrightarrow{w}}^{\ast })$ has the form

$$-a{(1-\xi )}^{1-\sigma }\theta c_{\ast }^{\theta -1}{\left(a{c}_{\ast }^{\theta }{L}^{\ast }+b{K}^{\ast }\right)}^{-\sigma }+{\mu }_K^{\ast }\xi \theta c_{\ast }^{\theta -1}a{L}^{\ast }-{\mu }_S^{\ast }\beta S^{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast })+{\mu }_E^{\ast }\beta S^{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast })-v_1^{\ast }+v_2^{\ast }=0$$ (28)

and

$${\tilde{\mathcal{H}}}_{{\xi }_{\ast }}=0$$

where ${\tilde{\mathcal{H}}}_{{\xi }_{\ast }}$ indicates the derivative with respect to $\tilde{\sigma }$ of $\tilde{\mathcal{H}}(c_{\ast },\xi ,{\overrightarrow{X}}^{\ast },{\overrightarrow{\mu }}^{\ast },{\overrightarrow{v}}^{\ast },{\overrightarrow{w}}^{\ast })$ has the form

$${\left((1-{\xi }_{\ast }\left(t\right))(a{c}_{\ast }^{\theta }{L}^{\ast }+b{K}^{\ast })\right)}^{-\sigma }(a{c}_{\ast }^{\theta }{L}^{\ast }+b{K}^{\ast })+{\mu }_{K^{\ast }}(a{c}_{\ast }^{\theta }{L}^{\ast }+b{K}^{\ast })-w_1^{\ast }+w_2^{\ast }=0$$

where $w_1^{\ast },w_2^{\ast }\ge 0$ are the Lagrange multipliers to constraint $\xi \in [0,1]$ and the vectors ${\overrightarrow{X}}^{\ast }$, $K^{\ast }$ and $\overrightarrow{{\mu }^{\ast }}$ are respectively the solution of the direct problem and of the adjoint linear problem along the optimal solution $c=c_{\ast }\left(t\right),\xi ={\xi }_{\ast }\left(t\right)$, that is

$$\left\{\begin{array}{ccc}\hfill {\mu }_S^{\prime }-r{\mu }_S& \hfill =\hfill & (1-\xi )a{c}_{\ast }^{\theta }\left((1-\xi )(a{c}_{\ast }^{\theta }(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })\right)\hfill \\ \hfill & \hfill +\hfill & {\left(b{K}^{\ast })\right)}^{-\sigma }+{\mu }_S(n+\beta c_{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }))\hfill \\ \hfill & \hfill -\hfill & {\mu }_E\beta c_{\ast }(s{I}^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast })-{\mu }_K{c}_{\ast }^{\theta }a\hfill \\ \hfill {\mu }_E^{\prime }-r{\mu }_E& \hfill =\hfill & s_1(1-\xi )a{c}_{\ast }^{\theta }\left((1-\xi )(a{c}_{\ast }^{\theta }(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })\right)\hfill \\ \hfill & \hfill +\hfill & {\left(b{K}^{\ast })\right)}^{-\sigma }\hfill \\ \hfill & \hfill +\hfill & {\mu }_S{s}_1\beta c_{\ast }{S}^{\ast }-{\mu }_E(s_1\beta c_{\ast }{S}^{\ast }-(\kappa +n))\hfill \\ \hfill & \hfill -\hfill & {\mu }_A(1-ϵ)\kappa -{\mu }_I\kappa ϵ-{\mu }_K{c}_{\ast }^{\theta }a\hfill \\ \hfill {\mu }_A^{\prime }-r{\mu }_A& \hfill =\hfill & s_2{c}_{\ast }^{(1-\sigma )\theta }{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{-\sigma }+{\mu }_S{s}_2\beta c_{\ast }{S}^{\ast }\hfill \\ \hfill & \hfill -\hfill & {\mu }_E{s}_2\beta c_{\ast }{S}^{\ast }+{\mu }_A(\gamma +n)-{\mu }_R\gamma -{\mu }_K{c}_{\ast }^{\theta }a\hfill \\ \hfill {\mu }_I^{\prime }-r{\mu }_I& \hfill =\hfill & -a\delta +{\mu }_S\beta s{c}_{\ast }{S}^{\ast }-{\mu }_E\beta s{c}_{\ast }{S}^{\ast }+{\mu }_I(\gamma +\delta +n)\hfill \\ \hfill & \hfill -\hfill & {\mu }_R\gamma -{\mu }_D\delta \hfill \\ \hfill {\mu }_R^{\prime }-r{\mu }_R& \hfill =\hfill & c_{\ast }^{(1-\sigma )\theta }{(S^{\ast }+s_1{E}^{\ast }+s_2{A}^{\ast }+R^{\ast })}^{-\sigma }+{\mu }_{R}n-{\mu }_K{c}_{\ast }^{\theta }a\hfill \\ \hfill {\mu }_D^{\prime }-r{\mu }_D& \hfill =\hfill & {\mu }_{S}n,\hfill \\ \hfill {\mu }_K^{\prime }\text{-r}{\mu }_K& \hfill =\hfill & {\mu }_K\left(\Psi -{\xi }^{\ast }b\right)\hfill \\ \hfill \overrightarrow{\mu }\left(T\right)& \hfill =\hfill & 0\hfill \end{array}\right)$$

In other problems, such as the Ramsey second best problem, the social planner may not be able to allocate consumption properly. Instead, private agents in a market economy choose themselves their consumption, maximizing their own utility function, leading to an arbitrage between consumption in different dates, corresponding to the traditional Euler equation in macroeconomics. his constraint is an additional constraint to the social planner and at this stage, our results do not apply to them.

Appendix G. Data appendix

See Table 11.

Table 11.

Fatality rates by age.

Fatality rates per age (in %)
Age groups	China (Verity et al., 2020)	France (Salje et al., 2020)
0–9	0.00161	0.001
10–19	0.00695	(For 0–19)
20–29	0.0309	0.007
30–39	0.0844	0.02
40–49	0.161	0.05
50–59	0.595	0.2
60–69	1.93	0.8
70–79	4.28	2.2
80$+$	7.8	8.3
Less than 60	0.145	Na
More than 60	3.28	Na
Overall	0.657	0.53

Note: These figures refer to the ratio of probable deaths to infected population.

Appendix H. Supplementary data

The following is the Supplementary material related to this article.