A new approximation of mean-time trends for the second wave of COVID-19 pandemic evolving in key six countries

Abstract

We have presented in the current analytic research the generating formulae and results of direct mathematical modelling of non-classical trends for COVID-19’s evolution in world which, nevertheless, can be divided into two types: (1) the general trends for European countries such as Germany presented by the curve of modified sigmoid-type with up-inclination of the upper limit of saturation (at the end of first wave of pandemic) as well as for other cases of key countries that suffered from pandemic such as USA, India, Brazil, Russia (we conclude that the same type of coronavirus pandemic is valid for most of the countries in world with similar scenarios of the same type for general trends); (2) non-classical general trends for Middle East countries (such as Iran), with the appropriate bulge on graphical plots at the beginning of first wave of pandemic. We expect that the second wave of pandemic will pass its peak at the end of December 2020 for various countries. Moreover, the second wave of pandemic will have come to end at first decade of January 2021 in Germany and Iran (but at the end of January 2021 in India as well), so we should restrict ourselves in modelling the first and second waves of pandemic within this time period for these countries. Thus, the model of first approximation is considered here which allows to understand the mean-time trends of COVID-19 evolution for the first + second waves of pandemic for USA, Brazil and Russia, or predict the approximated time period of the upcoming third wave of pandemic in cases of India, Germany and Iran.

Introduction, basic approach

In this paper, we present a new interpretation of a semi-analytical research with respect to analysis of the COVID-19 virus evolution [1] over the world up to date [2]. This article continues modelling study as presented earlier [1].

We have presented previously a heuristic mathematical model of the outcome of outbreak, which differs from most of the existing theories for describing the evolution of the viruses in human society (mainly, from those which are based on dynamics by modelling with the help of ordinary differential equations or well-known stochastic methods). Namely, the theory of finite recurrent sets or finite chains of recurrent sequences was applied for describing how population evolves over time.

One of the classical examples of using such an approach in theoretical biology is the modelling sunflower patterns in the plant biology via Fibonacci or Lucas numbers [3] (in 1202, Fibonacci published book for learning the Arabic system of math which included Fibonacci’s solution to a puzzle focused on predicting the number of bunnies born in one year to a huge family started simply with by two bunnies), or modelling dynamics of population in biology via Tribonacci [4] sequences for animals, sea organisms, insects, plants or trees.

Following by the aforementioned classical traditions, the approach suggested in [1] determines a nonlinear dependence of self-similar rate of evolution process (or dynamics of infected population) in regard to the proper residual capacity of non-infected part of all the humankind to overcome the pandemic. The last is assumed to be associated with “potential of the niche for absorbing the infection”, defining a catastrophic acceleration (or optimistic deceleration) of the dynamics of the infected part of population, as below:

$$x_{n+30}=(1-\mathrm{\alpha })·x_n+\mathrm{\beta }·x_{n+5}+\mathrm{\gamma }·x_{n+11}$$ *

where n ∈ N, x_n is the number of alive and (presumably) healthy population at the beginning of the current month (α is the coefficient of migration to other regions [1]); x_n+30 is the number of alive population at the end of month (30 days); x_n+5 is the number of alive population on 5th day (β is the coefficient for those who have been detected as having been infected after passing the 5-day period); x_n+11 is the number of alive population on 11th day (γ is the coefficient for those who have been detected as not infected after passing the 11-day period of quarantine).

Then afterwards, semi-analytical algorithm has been proposed in [1] for solving finite difference Eq. (*) along with additional reasonable criterion in the absence of migration of population from the considered country to other regions. The results are formulae of a type (1) or (2) presented for calculating the modified sigmoid curve with inclination for cases of Russia (1) or Germany (2).

For brevity, we do not mention here many classical models often used in epidemiology models, like SIR method and its variants [5]. As for the obvious but important disadvantage of the classical SIR-like models [6–9], the population of alive creatures or humans could not be adequately described by differential approaches in case of middle size (or small amount) of population, because all beings should be accounted as sum of separated units (i.e., of those who could not be presented as infinitesimal differential quantity). Otherwise, ansatz suggested in [1] is based on investigation of equations of a type (*), left part of which is a linear combination of sequences of recurrent finite sets or finite chains of recurrent sequences. Thus, such approach can naturally be applied for describing how population (living organisms or humans) evolves over time. We have suggested absolutely novel theory which describes such epidemiological processes by recurrent finite sets or finite chains of recurrent sequences via semi-analytical algorithm. As for the purpose (and motivation) of the current research, we can formulate it as follows: the main aim is to find a kind of the semi-analytical solving algorithm (preferably, presented by analytical formulae) which describes evolution of pandemic in chosen key six countries with accuracy less than 10% for the chosen time period. Namely, each obtained semi-analytical algorithm can clarify the structure, intrinsic code and features for the variety of possible solutions (from mathematical point of view) depending on initial data.

As for other similar works, there are no other available models of this type (excluding those where modelling with the help of ordinary differential equations or well-known stochastic methods was carried out). It means the originality and importance of the suggested approach and obtained results coinciding with the data of really observed and confirmed cases of coronavirus pandemic with sufficiently good level of approximation (less than 10% for the chosen time period for most of the key six countries, namely USA, India, Brazil, Russia, Iran or Germany).

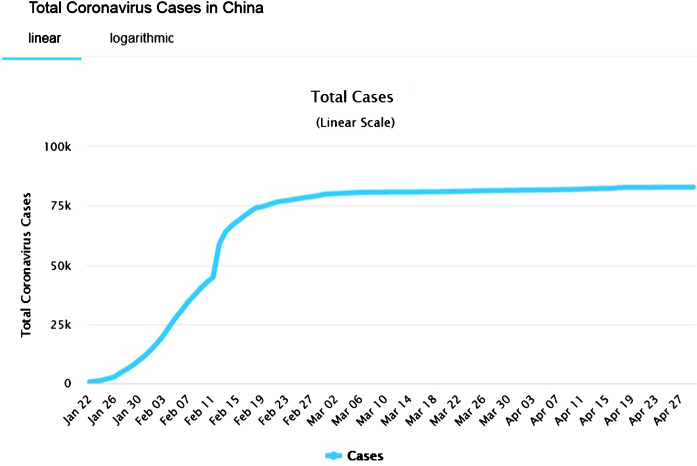
Moreover, emphasizing the main contribution of the study, we will proceed from practical point of view for investigating here the countries where the pandemic evolves by non-classic scenario, for example as it happens in case of USA, India, Brazil, Russia, Iran or Germany. The classical general trend is the simple sigmoid or logistic curve (which stems from our model [1]); it can be seen in slightly locally changed form in case of China (Fig. 1).

Fig. 1.

Dynamics of total COVID-19 cases for China

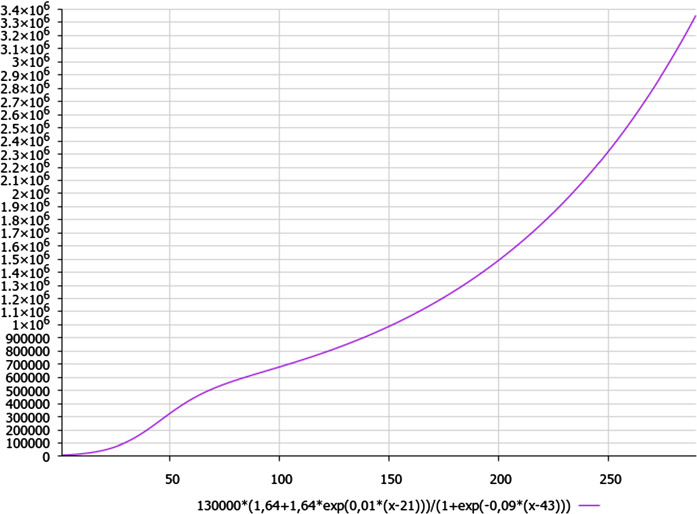
Otherwise, discussing non-classic scenario, we can interpolate the maximal level of cases of illness, e.g. for Russia, according to formula (1).

As we can see from Fig. 2, there is no classic horizontal trend of sigmoidal type at the end of the first wave of pandemic; it is presented in a form of modified sigmoid curve with inclination. The same conclusion should be made for most of the countries in the world, including Iran (and similar countries from Middle East) or USA, India, Brazil, Russia or Germany.

Fig. 2.

A schematic dynamics of COVID-19 cases for Russia. Beginning is 1 April 2020 (here we designate x = t, in days, just for presenting the plot)

Let us explain such a non-classical trend of COVID-19 outbreak in case of various countries: as each country imposed and relaxed non-pharmaceutical interventions at different stages of the pandemic, it is difficult to believe that algorithm (1) in [1] with fixed parameter values has any predictive power except classical trend of COVID-19’s evolving in human society presented by sigmoidal type of curve (in ideal case of isolated islands countries, for example).

All in all, it means for the cases of non-classical trends of COVID-19’s evolving in various countries that we should take into consideration the additional correcting coefficients in the numerators of formulae for the aforementioned modified sigmoid curves.

We should note that formula (1) has been slightly corrected in the current research, according to the updated data regarding the confirmed cases of illness in Russia for the combined first and the second (current) wave of pandemic, with respect to previous formula which was published earlier in [1] only for the first wave of pandemic:

$$x_{n_{(\text{Russia})}}=\frac{130,000\left(1.64+1.64exp(0.01(n-21))\right)}{\left(1+exp(-0.09(n-43))\right)},$$ 1

where n is the current day from 1 April 2020, which yields Fig. 2. (Meanwhile, the relative deviation between the calculated vs. real data of the COVID-19 dynamics is less than 9% for the data, presented in [2] for the case of Russia, except first 17 days from the beginning of pandemic.)

The approach, suggested previously in [1] by applying chains of recurrent sequences to algorithm of modelling the COVID-19 pandemic, let us obtain the partial discrete solution (of exponential type as in [10, 11]) which directly stems from such an analytical algorithm and, furthermore, it lets us obtain the general trend of a type of modified sigmoid curve in case of Russia (as mentioned above).

But we should especially note that it is very important for obtaining the appropriate algorithm of COVID-19’s evolution in world to adjust accordingly the curve stemming from the theoretical calculations with respect to the real cases of observed dynamics. (Or, in other words, our basic model [1] needs substantial adjustment to match the actual reported data in each country.)

We present in the next sections such examples of the direct mathematical modelling in case of Germany, Iran, USA, Brazil and India. Albeit the basis for such a modelling should be the recurrent sequences, nonetheless we leave constructing the chains of recurrent sequences for theoretical sociology (or mathematical biology) and will concentrate our efforts on the direct mathematical modelling of the pandemic in case of these countries.

We expect that the second wave of pandemic will pass its peak at the end of December 2020 for various countries, so all the approximated formulae for COVID-19’s evolution in human society should be corrected afterwards, according to the updated dynamics for the confirmed cases of illness. The main reason is that predicting the future with such a model will obviously have a limited planning horizon due to the unavoidable uncertainty of the future. All coefficients in analytical formulae remain statistically the same if only both the disease characteristics and the societal ones will be in future as they were in the past, which seems unrealistic given the efforts around the globe to diminish the prevalence of COVID-19. One of the obvious ways to diminish the spreading of the current pandemic is the early diagnostic of those who have been infected [12].

Direct mathematical modelling of the COVID-19’s cases in Germany

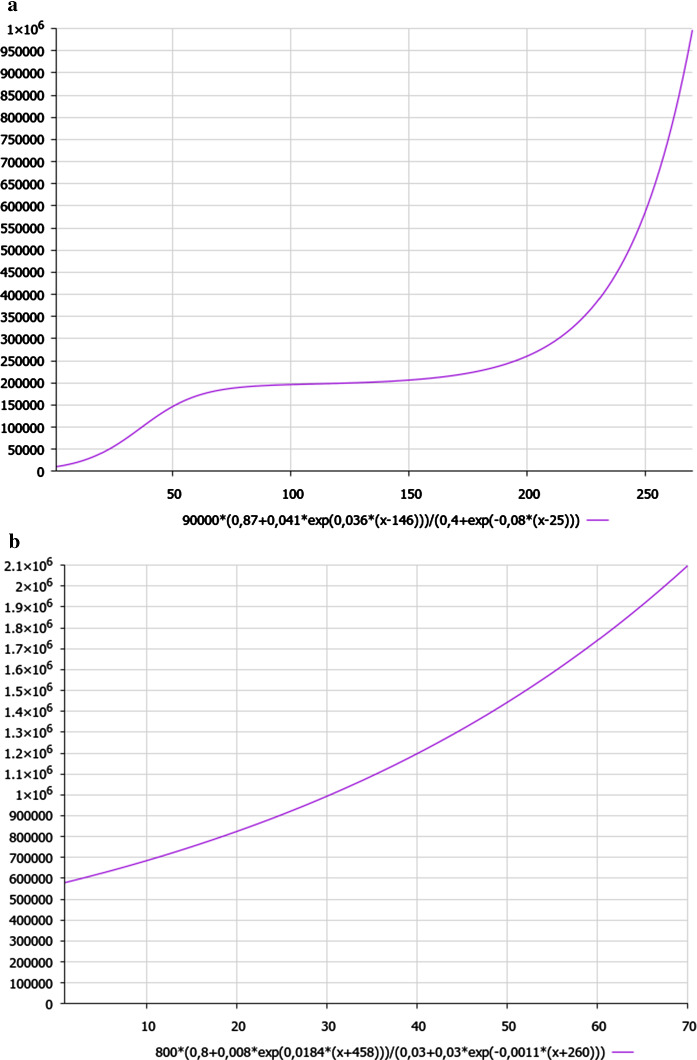
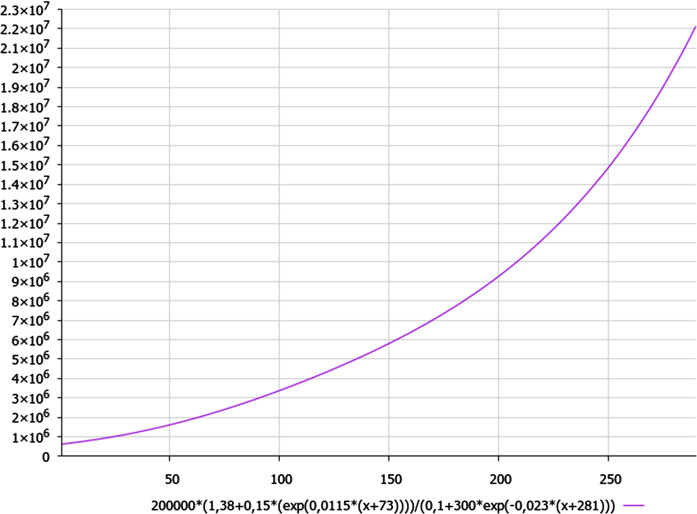
Let us discuss the non-classical trends of COVID-19’s evolution in case of Germany. It is worth to note that coefficients in formula (2a) have also been slightly corrected (according to the updated set of data of coronavirus cases in Germany) with respect to previous formula which was published earlier in [1] for the first wave of pandemic, but such a corrected formula (2a) has been generating correctly the approximated results of calculations during first 8 months up to the end of first wave of pandemic at the end of October 2020

$$x_{n_{(\text{Germany})}}=\frac{90,000\left(0.87+0.041exp(0.036(n-146))\right)}{0.4+exp(-0.08(n-25))},$$ 2a

where n is the current day from 1 March 2020, which yields Fig. 3a. (We should note that the relative deviation between the calculated by formula (2a) and real data of the COVID-19 dynamics is less than 8% for the data, presented in [2] for the case of Germany, except first 30 days from the beginning of pandemic.)

Fig. 3.

a A schematic dynamics of coronavirus cases in Germany for the first wave of pandemic. The start is 1 March 2020 (here we designate x = t, in days). b A schematic dynamics of coronavirus cases in Germany for second wave of pandemic. The start is 1 November 2020 (here we designate x = t, in days)

As we can see from Fig. 3a, the schematic dynamics of coronavirus cases in Germany demonstrates the trend of classical sigmoid curve up to circa 150th day of pandemic (till the beginning of August 2020), whereas the numerator in formula (2a) yields the modified sigmoid curve with up-inclination at the end of first wave of pandemic (at the beginning of November 2020, i.e. up to the circa 250th day of pandemic).

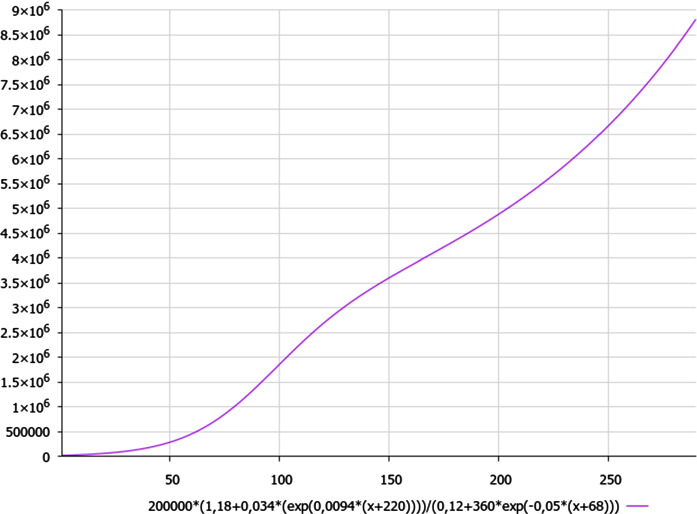
Then afterwards, the second wave of pandemic has been born (among the relatively stable dynamics of outcome of the first wave) with the generating, best-fitting formula (2b):

$$x_{n_{(\text{Germany})}}=\frac{800\left(0.8+0.008exp(0.0184(n+458))\right)}{0.03+0.03exp(-0.0011(n+260))},$$ 2b

where n is the current day from 1 November 2020, which yields Fig. 3b. (We should note that the relative deviation between the calculated by formula (2b) and real data of the COVID-19 dynamics is less than 9% for the data, presented in [2] for the case of Germany.)

As we can see from Fig. 3b, the schematic dynamics of coronavirus cases in Germany for the second wave of pandemic demonstrates the trend of classical sigmoid curve close up to its end at the beginning of January 2021, whereas the contribution of numerator in formula (2b) into the final result appears to be negligible till the end of second wave of pandemic in Germany. It is worth to note that we expect that the second wave of pandemic will come to the end at the first decade of January 2021 in Germany, so we should suggest revolving scheme for calculating algorithm with respect to the cascade of waves of pandemic: at each calculation step, the final solution value of the previous stage of pandemic (e.g. at the end of second wave) should be considered to be the initial condition for the next calculation step (at the beginning of the third wave of pandemic).

As for the considerable deviation (in amount circa 35,000 of people) between final solution value of the first wave of pandemic (ending 31st of October) and initial condition for the next calculation step, 1st day of second wave of pandemic started by agreement from 1 November 2020; this fact can be explained by hidden statistics of non-registered cases of illness without obvious symptoms of the disease (COVID-19).

Direct mathematical modelling of the COVID-19’s cases in Iran

Let us present the non-classical trend of COVID-19’s evolution in Iran, where we should take into consideration the additional (of other type) correcting coefficients for formulae of a type (1) or (2).

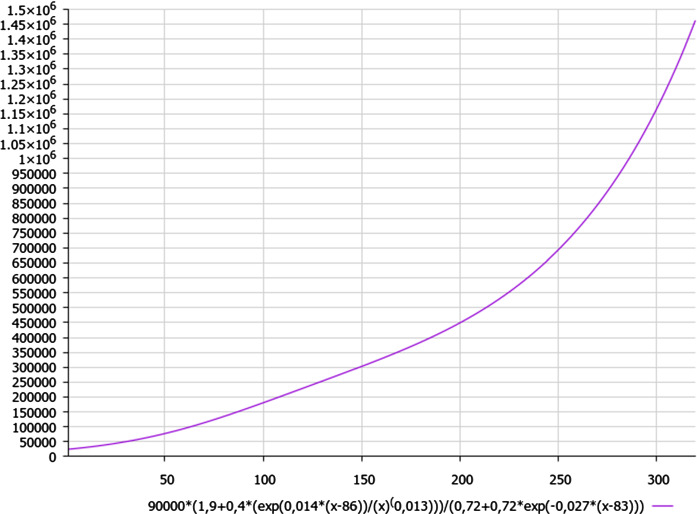
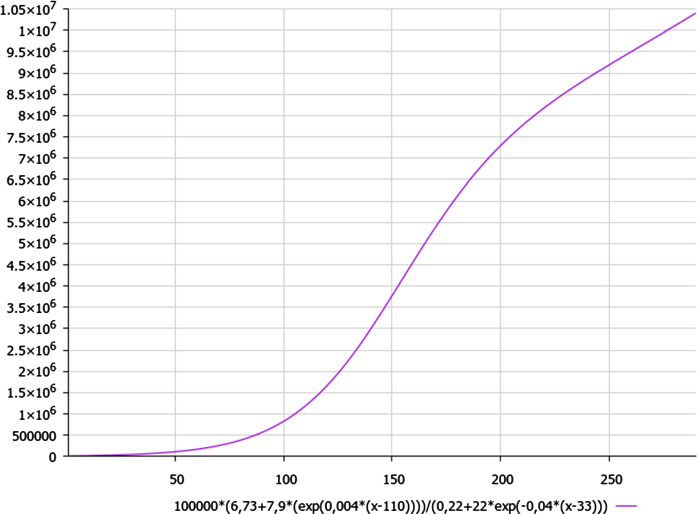
The aforementioned non-classical trend could be presented by the best-fitting formula (3) for mathematical modelling of COVID-19 dynamics in Iran:

$$x_{n_{(\text{Iran})}}=\frac{90,000\left(1.9+\left\{\frac{0.4exp(0.014(n-86))}{n^{0.013}}\right\}\right)}{0.72+0.72exp(-0.027(n-83))},$$ 3

where n is the current day, starting from 25 February 2020, which yields Fig. 4.

Fig. 4.

A schematic dynamics of coronavirus cases in Iran

As we can see from Fig. 4, the end of first wave of pandemic seems to be at the second half of May 2020 in Iran (as in Russia), but there is no horizontal trend at the end of first wave of pandemic.

Moreover, there is a bulge on a plot of the first wave of pandemic, determined by additional coefficient ~ (1/n^(0.013)) in the numerator of formula (3).

As we can see from Table 1, the deviation of the calculated vs. real data of the COVID-19 dynamics is less than 10% for most of the days in case of Iran (except the first 32 days from the start of the pandemic, 31 of which have been deleted from Table 1 as non-informative).

Table 1.

Calculated versus real data for coronavirus cases in Iran

Days	Real data, see [2]	Key points (calculated data)	Difference in %% (calculated vs. real data)	Difference current vs. previous day (real data)	Calculated data	Difference in %% (calculated vs. real data)
32	47,593			2988	52,376	9
33	50,468			2875	53,578	6
34	53,183			2715	54,801	3
35	55,743	56,047	0.5	2560	56,047	1
36	58,226			2483	57,315	− 2
37	60,500			2274	58,605	− 3
38	62,589			2089	59,917	− 4
39	64,586			1997	61,252	− 5
40	66,220	62,610	− 5.8	1634	62,610	− 6
41	68,192			1972	63,990	− 7
42	70,029			1837	65,393	− 7
43	71,686			1657	66,819	− 7
44	73,303			1617	68,268	− 7
45	74,877	69,739	− 7.4	1574	69,739	− 7
46	76,389			1512	71,234	− 7
47	77,995			1606	72,751	− 7
48	79,494			1499	74,292	− 7
49	80,868			1374	75,855	− 7
50	82,211	77 441	− 6.2	1343	77,441	− 6
51	83,505			1294	79,050	− 6
52	84,802			1297	80,681	− 5
53	85,996			1194	82,335	− 4
54	87,026			1030	84,011	− 4
55	88,194	85,710	− 2.9	1168	85,710	− 3
56	89,328			1134	87,431	− 2
57	90,481			1153	89,175	− 1
58	91,472			991	90,940	− 1
59	92,584			1112	92,726	0
60	93,657	94,535	0.9	1073	94,535	1
61	94,640			983	96,364	2
62	95,646			1006	98,215	3
63	96,448			802	100,086	4
64	97,424			976	101,978	4
65	98,647	103,890	5.0	1223	103,890	5
66	99,970			1323	105,823	6
67	101,650			1680	107,775	6
68	103,135			1485	109,746	6
69	104,691			1556	111,736	6
70	106,220	113,745	6.6	1529	113,745	7
71	107,603			1383	115,772	7
72	109,286			1683	117,817	7
73	110,767			1481	119,880	8
74	112,725			1958	121,960	8
75	114,533	124,057	7.7	1808	124,057	8
76	116,635			2102	126,170	8
77	118,392			1757	128,299	8
78	120,198			1806	130,443	8
79	122,492			2294	132,603	8
80	124,603	134,777	7.5	2111	134,777	8
81	126,949			2346	136,966	7
82	129,341			2392	139,168	7
83	131,652			2311	141,383	7
84	133,521			1869	143,612	7
85	135,701	145 853	7.0	2180	145,853	7
86	137,724			2023	148,105	7
87	139,511			1787	150,369	7
88	141,591			2080	152,644	7
89	143,849			2258	154,930	7
90	146,668	157,226	6.7	2819	157,226	7
91	148,950			2282	159,531	7
92	151,466			2516	161,846	6
93	154,445			2979	164,169	6
94	157,562			3117	166,501	5
95	160,696	168,840	4.8%	3134	168,840	5
96	164,270			3574	171,187	4
97	167,156			2886	173,541	4
98	169,425			2269	175,902	4
99	171,789			2364	178,269	4
100	173,832	180 642	3.8	2043	180,642	4
101	175,927			2095	183,020	4
102	177,938			2011	185,403	4
103	180,156			2218	187,791	4
104	182,525			2369	190,184	4
105	184,955	192,580	4.0	2430	192,580	4
106	187,427			2472	194,981	4
107	189,876			2449	197,385	4
108	192,439			2563	199,792	4
109	195,051			2612	202,202	4
110	197,647	204,615	3.4	2596	204,615	3
111	200,262			2615	207,030	3
112	202,584			2322	209,448	3
113	204,952			2368	211,868	3
114	207,525			2573	214,289	3
115	209,970	216,713	3.1	2445	216,713	3
116	212,501			2531	219,138	3
117	215,096			2595	221,564	3
118	217,724			2628	223,992	3
119	220,180			2456	226,421	3
120	222,669	228,851	2.7	2489	228,851	3
121	225,205			2536	231,282	3
122	227,662			2457	233,715	3
123	230,211			2549	236,149	3
124	232,863			2652	238,583	2
125	235,429	241,019	2.3	2566	241,019	2
126	237,878			2449	243,456	2
127	240,438			2560	245,894	2
128	243,051			2613	248,333	2
129	245,688			2637	250,774	2
130	248,379	253,217	1.9	2691	253,217	2
131	250,458			2079	255,660	2
132	252,720			2262	258,106	2
133	255,117			2397	260,554	2
134	257,303			2186	263,003	2
135	259,652	265,455	2.2	2349	265,455	2
136	262,173			2521	267,909	2
137	264,561			2388	270,366	2
138	267,061			2500	272,826	2
139	269,440			2379	275,289	2
140	271,606	277,756	2.2	2166	277,756	2
141	273,788			2182	280,226	2
142	276,202			2414	282,701	2
143	278,827			2625	285,179	2
144	281,413			2586	287,663	2
145	284,034	290,151	2.1	2621	290,151	2
146	286,523			2489	292,645	2
147	288,839			2316	295,144	2
148	291,172			2333	297,650	2
149	293,606			2434	300,162	2
150	296,273	302,680	2.1	2667	302,680	2
151	298,909			2636	305,206	2
152	301,530			2621	307,740	2
153	304,204			2674	310,282	2
154	306,752			2548	312,832	2
155	309,437	315,392	1.9	2685	315,392	2
156	312,035			2598	317,960	2
157	314,786			2751	320,539	2
158	317,483			2697	323,128	2
159	320,117			2634	325,728	2
160	322,567	328,340	1.8	2450	328,340	2
161	324,692			2125	330,963	2
162	326,712			2020	333,599	2
163	328,844			2132	336,247	2
164	331,189			2345	338,909	2
165	333,699	341,585	2.3	2510	341,585	2
166	336,324			2625	344,275	2
167	338,825			2501	346,981	2
168	341,070			2245	349,702	2
169	343,203			2133	352,439	3
170	345,450	355,193	2.7	2247	355,193	3
171	347,835			2385	357,965	3
172	350,279			2444	360,754	3
173	352,558			2279	363,562	3
174	354,764			2206	366,389	3
175	356,792	369,235	3.4	2028	369,235	3
176	358,905			2113	372,102	4
177	361,150			2245	374,990	4

We should additionally note that the second wave of pandemic seems to come to its end at the first decade of January 2021 in Iran (as in case of Germany). So, all the calculations for the combined first + second waves of pandemic should be interrupted in case of Iran within the pointed time period for the reason the third wave will come (with its specific features of evolving in time).

Direct mathematical modelling of the COVID-19’s cases in USA

Let us present non-classical trend of COVID-19’s evolution in USA, where we should take into consideration the additional correcting coefficients for formulae of a type (1) or (2).

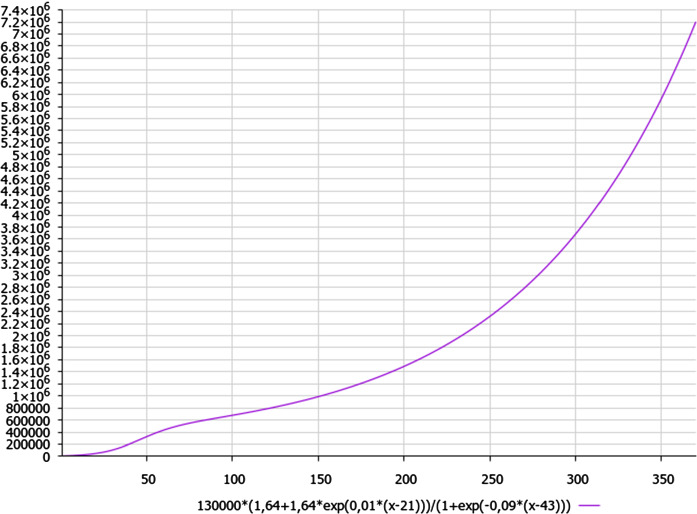
The aforementioned non-classical trend could be presented by the best-fitting formula (4) for the direct mathematical modelling of the burst of expansion of COVID-19 cases in USA:

$$x_{n_{(\text{USA})}}=\frac{200,000\left(1.38+0.15exp(0.0115(n+73))\right)}{0.1+300exp(-0.023(n+281))},$$ 4

where n is the current day, starting from 1 April 2020, which yields Fig. 5. (Let us note that the relative deviation between the calculated and real data of the COVID-19 dynamics is less than 10% for the data, presented in [2] for the case of USA, except first 20 days from the beginning of pandemic.)

Fig. 5.

Schematic dynamics of coronavirus cases in USA

Such large 10% deviation can be explained by accounting of those who may have been migrating into the USA during previous period of pandemic without strict accounting, across the board, e.g. from Brazil or via flight-communicating with other countries, including China, because USA did not restrict the flights at the beginning of pandemic sufficiently as it was reasonably required.

As we can see from Fig. 5, there is also no horizontal trend at the curve of pandemic. But, nevertheless, there is no bulge on a plot of the pandemic curve, determined by additional coefficient in the numerator of formula (4) [as e.g. in case of Iran, formula (3)].

We should especially note that modelling of the dynamics of COVID-19 pandemic in USA is not an easy matter because the statistic data for USA, reported in [2], are questionable (starting from 131 day of pandemic, official data have been changed several times a week: namely, data for all period of pandemic have been changed after 131, 138, 143, 150, 152, 154, 155, 159 days of pandemic, etc.). Anyone can check this fact personally by online visiting [2] every day.

Such ambiguity at accounting the data of officially confirmed coronavirus cases could explain relatively large deviating in amount of 10% as stated above if we compare calculated vs. real data of the COVID-19 dynamics in the USA. (The aforementioned deviation in amount of 10% is much more than 8–9% in most cases of other countries.) The aforesaid manipulating of statistic data is a worst basis for the correct mathematical modelling of COVID-19’ pandemic dynamics; no one country even Brazil (see the next section) does allow such a significant manipulation by COVID-19’s official data of pandemic as it happened in the USA. It is worth noting that we cannot trust statistic data of COVID-19’s pandemic in the USA (and Brazil) after 159 day of pandemic (6 September 2020). Nevertheless, we should note that the second wave of pandemic seems losing its power in USA with coming to its end at first decade of March 2021 (much more later than in cases of Germany or Iran).

Direct mathematical modelling of the COVID-19’s cases in Brazil

Let us present non-classical trend of COVID-19’s evolution in Brazil, where we should take into consideration the additional correcting coefficients for formulae of a type (1) or (2).

The aforementioned non-classical trend could be presented by the best-fitting formula (5) for the direct mathematical modelling of the coronavirus cases in Brazil:

$$x_{n_{(\text{Brazil})}}=\frac{200,000\left(1.18+0.034exp(0.0094(n+220))\right)}{0.12+360exp(-0.05(n+68))},$$ 5

where n is the current day, starting from 1 April 2020, which yields Fig. 6. (It is worth noting that the relative deviation between the calculated and real data of the COVID-19 dynamics is less than 9% for most of the days in data, presented in [2] for the case of Brazil, except the first 42 days from the start of pandemic.)

Fig. 6.

Schematic dynamics of coronavirus cases in Brazil

Such deviation (9%) can be considered as a good result, taking into consideration that most of the statistic data for Brazil are questionable due to a permanent interrupting in the process of reporting the amount of officially registered cases of illness (by political reasons). An interesting fact is that the level of epidemiological contamination by COVID-19 in Brazil is less for last day of previous and first day of current week during all the period of pandemic. This can be explained by weekend at offices which have been officially registering the cases of illness in Brazil.

As we can see from Fig. 6, there is also no horizontal trend on the curve of pandemic. Moreover, there is no any deviation (from general trend) or essential bulge on a plot at the beginning of pandemic, which is determined in case of, for example, Iran by additional coefficient ~ 1/(n^(0.013)) in the numerator of formula (3). Last but not least, let us note that the second wave of pandemic seems losing its power in Brazil with coming to its end at the middle of February 2021 (later than in cases of Germany or Iran).

Direct mathematical modelling of the COVID-19’s cases in India

Let us present non-classical trend of COVID-19’s evolution in India, where we should take into consideration the additional correcting coefficients for formulae of a type (1) or (2). The aforementioned non-classical trend could be presented by the best-fitting formula (6) for the direct mathematical modelling of the COVID-19 dynamics in India:

$$x_{n_{(\text{India})}}=\frac{100,000\left(6.73+7.9exp(0.004(n-110))\right)}{0.22+22exp(-0.04(n-33))},$$ 6

where n is the current day, starting from 1 April 2020, which yields Fig. 7

Fig. 7.

Schematic dynamics of coronavirus cases in India

As we can see from Fig. 7, there is also no horizontal trend hereafter on the curve of pandemic.

As we can see from Table 2, the deviation of the calculated vs. real data of the COVID-19 dynamics is not more than 8% for most of the days in India, except the first 43 days from the start of the pandemic in India (40 of which have been deleted from Table 2 as non-informative).

Table 2.

Calculated versus real data for coronavirus cases in India

Days	Real data, Ref. [2]	Key points (calculated data)	Difference in %% (calculated vs. real data)	Difference current vs. previous day (real data)	Calculated data	Difference in %% (calculated vs. real data)
41	70,768			3607	78,570	10
42	74,292			3524	81,885	9
43	78,055			3763	85,339	9
44	81,997			3942	88,937	8
45	85,784	92,685	7.4	3787	92,685	7
46	90,648			4864	96,588	6
47	95,698			5050	100,654	5
48	100,328			4630	104,889	4
49	106,475			6147	109,298	3
50	112,028	113,891	1.6	5553	113,891	2
51	118,226			6198	118,673	0
52	124,794			6568	123,653	− 1
53	131,423			6629	128,838	− 2
54	138,536			7113	134,236	− 3
55	144,950	139,856	− 3.6	6414	139,856	− 4
56	150,793			5843	145,707	− 3
57	158,086			7293	151,797	− 4
58	165,386			7300	158,136	− 5
59	173,491			8105	164,734	− 5
60	181,827	171,601	− 6.0	8336	171,601	− 6
61	190,609			8782	178,746	− 7
62	198,370			7761	186,181	− 7
63	207,191			8821	193,917	− 7
64	216,824			9633	201,964	− 7
65	226,713	210 336	− 7.8	9889	210,336	− 8
66	236,184			9471	219,044	− 8
67	246,622			10,438	228,101	− 8
68	257,486			10,864	237,520	− 8
69	265,928			8442	247,313	− 8
70	274,780	257 495	− 6.7	8852	257,495	− 7
71	287,155			12,375	268,081	− 7
72	298,283			11,128	279,084	− 7
73	309,603			11,320	290,519	− 7
74	321,626			12,023	30,403	− 6
75	332,783	314,750	− 5.7	11,157	314,750	− 6
76	343,026			10,243	327,578	− 5
77	354,161			11,135	340,902	− 4
78	367,264			13,103	354,741	− 4
79	381,091			13,827	369,110	− 3
80	395,812	384,030	− 3.1	14,721	384,030	− 3
81	411,727			15,915	399,516	− 3
82	426,910			15,183	415,590	− 3
83	440,450			13,540	432,269	− 2
84	456,115			15,665	449,573	− 1
85	472,985	467,522	− 1.2	16,870	467,522	− 1
86	491,170			18,185	486,136	− 1
87	509,446			18,276	505,436	− 1
88	529,577			20,131	525,442	− 1
89	549,197			19,620	546,176	− 1
90	567,536	567,659	0.0	18,339	567,659	0
91	585,792			18,256	589,913	1
92	605,220			19,428	612,960	1
93	627,168			21,948	636,821	2
94	649,889			22,721	661,520	2
95	673,904	687,077	1.9	24,015	687,077	2
96	697,836			23,932	713,516	2
97	720,346			22,510	740,858	3
98	743,481			23,135	769,127	3
99	769,052			25,571	798,344	4
100	794,842	828,531	4.1	25,790	828,531	4
101	822,603			27,761	859,710	4
102	850,358			27,755	891,902	5
103	879,466			29,108	925,130	5
104	907,645			28,179	959,413	5
105	937,487	994,771	5.8	29,842	994,771	6
106	970,169			32,682	1,031,225	6
107	1,005,637			35,468	1,068,794	6
108	1,040,457			34,820	1,107,495	6
109	1,077,864			37,407	1,147,346	6
110	1,118,107	1,188,365	5.9	40,243	1,188,365	6
111	1,154,917			36,810	1,230,565	6
112	1,194,085			39,168	1,273,962	6
113	1,239,684			45,599	1,318,570	6
114	1,288,130			48,446	1,364,399	6
115	1,337,022	1,411,461	5.3	48,892	1,411,461	5
116	1,385,494			48,472	1,459,764	5
117	1,436,019			50,525	1,509,316	5
118	1,482,503			46,484	1,560,124	5
119	1,532,135			49,632	1,612,190	5
120	1,584,384	1,665,518	4.9	52,249	1,665,518	5
121	1,639,350			54,966	1,720,107	5
122	1,697,054			57,704	1,775,956	4
123	1,751,919			54,865	1,833,061	4
124	1,804,702			52,783	1,891,416	5
125	1,855,331	1,951,013	4.9	50,629	1,951,013	5
126	1,906,613			51,282	2,011,842	5
127	1,963,239			56,626	2,073,888	5
128	2,025,409			62,170	2,137,138	5
129	2,086,864			61,455	2,201,573	5
130	2,152,020	2,267,174	5.1	65,156	2,267,174	5
131	2,214,137			62,117	2,333,918	5
132	2,267,153			53,016	2,401,780	6
133	2,328,405			61,252	2,470,733	6
134	2,395,471			67,066	2,540,746	6
135	2,459,613	2,611,788	5.8	64,142	2,611,788	6
136	2,525,222			65,609	2,683,824	6
137	2,589,208			63,986	2,756,817	6
138	2,647,316			58,108	2,830,728	6
139	2,701,604			54,288	2,905,517	7
140	2,766,626	2,981,139	7.2	65,022	2,981,139	7
141	2,835,822			69,196	3,057,550	7
142	2,904,329			68,507	3,134,704	7
143	2,973,368			69,039	3,212,550	7
144	3,043,436			70,068	3,291,040	8
145	3,105,185	3,370,122	7.9	61,749	3,370,122	8
146	3,164,881			59,696	3,449,742	8

Such an initial significant deviation can be explained by hidden migration from other surrounding countries directly into India without accounting of those people who have been infected outside the India at previous time period of pandemic (from China, Bangladesh, Pakistan, etc.).

Last but not least, it is worth to note that the second wave of pandemic seems to come to its end at the end of January 2021 in India (later than in cases of Germany and Iran). So, all calculations for the combined first + second waves of pandemic should be interrupted in case of India within this time period.

Discussion

First, we should mention that the governments of a lot of countries [1] are applying extraordinary efforts to overcome pandemic with the aim to protect the citizens of these countries. (So, they have demonstrated the classical general trends of a type of sigmoid curve at the end of first wave of COVID-19 pandemic.) But there are also obviously two types of non-classical general trends of COVID-19′s evolving in the world:

• Tendency such as in Germany (2) (but, nevertheless, it means successful efforts of government) from the one hand and Russia (1) from the other hand (unsuccessful case), or e.g. USA (4), Brazil (5), India (6) (let us mention that this type of coronavirus pandemic is valid for all countries in Europe and most of the countries in world with various scenarios of the same type for general trends);

• Non-classical general trends (3) as in Iran’s case, with the appropriate bulge on graphical plots (Fig. 4) at the beginning of first wave of pandemic.

As we can see from Figs. 4, 5, 6 and 7, there are no horizontal trends at the end of first wave of pandemic in USA, India, Brazil or Iran. Moreover, we should note that there is the appropriate bulge on the graphical plot of first + second wave of pandemic in Iran, which is determined by additional coefficient ~ 1/(n^(0.013)) in the numerator of formula (3).

We expect that the second wave of pandemic will pass its peak at the end of December 2020 for various countries, so all the approximated formulae for COVID-19’s evolution in human society should be corrected afterwards, according to the updated dynamics for the confirmed cases of illness in these countries. Videlicet, the second wave of pandemic will come to the end at the first decade of January 2021 in Germany and Iran (but at the end of January 2021 in India as well), so we should restrict ourselves in modelling first and second waves of pandemic within this period of time for these countries.

Let us note that the same conclusion (as in case of Iran) can be made for most of the countries from Middle East such as Iraq (we can see a little bulge at the beginning of the graphical plot of coronavirus cases in this country [2]), Azerbaijan (a little bulge), Saudi Arabia (a little bulge at the end of first wave of pandemic), Uzbekistan (bulge of middle size), Kazakhstan (a little bulge, but nevertheless), Lebanon (a huge bulge at the beginning of pandemic), Jordan (the same huge bulge as in case of Lebanon), State of Palestine (a huge bulge at the middle of pandemic), Libya (bulge of a little size but during a long time period), Syria (a middle-sized bulge at the beginning of pandemic) and, unexpectedly, such countries as Djibouti (bulge of middle size), Niger (a more huge bulge than in other countries), Ghana (oscillating curve of bulge of middle size close to the middle of first wave of pandemic), Rwanda (a middle-sized bulge at the end of first wave of pandemic), Costa Rica (a big-sized bulge), Madagascar (bulge of middle size but during a long time period), Malta (combination of two bulges: a middle-sized bulge at the beginning along with the second huge bulge at the end of first wave of pandemic), Singapore (a middle-sized bulge), North Macedonia (bulge of middle size but during a long time period), Sri Lanka (a middle-sized bulge close to the end of the first wave of pandemic), Paraguay (a middle-sized bulge at the end of first wave of pandemic), Jamaica (a huge bulge at the middle of pandemic), Myanmar (a huge bulge during a long time period at the end of pandemic), Cayman Islands (bulge of middle size) and also a negligible bulge we can see on curve of coronavirus cases in Denmark.

As for the possible deviations in the data of registered cases of COVID-19 [2] in various countries (due to reporting bias, censoring due to lack of testing availability and asymptomatic infection), we based our research on the data which have been cross-checked and verified from various sources, including data from COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) [13]. We should especially note that correct modelling of the dynamics of COVID-19 pandemic in USA is impossible because the statistic data for USA are questionable (starting from 131st day of pandemic, where 1st day of pandemic is 1 April 2020, official data have been changed several times a week).

Last but not least, let us note that the well-developed epidemic spread over spatially extended regions (such as the USA and Russia) cannot be considered within a local model with the complete mixing that leads to the logistic cumulative curve. So, we have considered here the model of first approximation which allows to understand the mean-time trends of COVID-19 evolution for the first + second waves of pandemic for USA, Brazil and Russia, or predict the approximated time period of the upcoming third wave of pandemic in cases of India, Germany and Iran.

Ending discussion, one more (but important) remark should be added regarding the reason why the obtained results are achieved in the process of self-developing of coronavirus pandemic in all the world. Namely, why this had happened or is there any reasonable (physical) reason why the current pandemic has not lost his death power up during a year after its beginning in January of 2020 in China? Indeed, most of the previous pandemics have been exhausting their power with further tending to the classical general trend or the simple sigmoid curve like in case of China (Fig. 1).

But in case of COVID-19 pandemic, we conclude that the same type of coronavirus pandemic is valid for most of the countries in world with similar scenarios of the same type for general trends presented by the curve of modified sigmoid type with up-inclination of the upper limit of saturation (at the end of first wave of pandemic). There are no horizontal trends at the curves of pandemic in most countries in the world. (The horizontal trend could be associated with the exhausting of pandemic power in this or that country.)

Our assumption in this regard that “charging potential” of COVID-19 is in a manner more related to the host than virus [1] makes the aforementioned a catastrophic acceleration scenario to be realistic insofar as possible. In other words, virus (spreading successfully inside the human society) gains its energy for self-developing from humankind directly as collective vampire. The only way to overcome the pandemic in future is, obviously, the total vaccination [9] of all the humankind or the total local quarantine (by the same way as China government launched at the beginning in January of 2020 in China's Hubei Province), in addition to social distancing (and wearing a masks), of course. These are the rules of the COVID-19, which have been dictated to humankind by novel coronavirus.

Conclusion

We have presented in the current analytic research the results of direct mathematical modelling of the non-classical trends of COVID-19’s evolution in world which can be divided into two types: European countries (such as Germany or from the other hand, unexpectedly, India) versus Middle East countries (the most typical represented by Iran).

Basing on the presented results, we can estimate mean-time perspectives of evolution of COVID-19 pandemic in various countries. For example, if we proceed the general trend of a type (1), (2) for the modified sigmoid curve (or logistic curve) which stems from our model [1], we will obtain that scenario of pandemic in Russia is worse than in Germany, alas! (Fig. 8). Nevertheless, we should note that the second wave of pandemic seems losing its power in Russia with its ending at last decade of February 2021 (later than in cases of Germany, Iran, or India). We can see from Fig. 8 that we will obtain more than 5 million of coronavirus’ cases (taking into account vaccination by Russia's “Sputnik V” coronavirus vaccine) in Russia during 1 year at the current stable (catastrophic) scenario of COVID-19’s evolution. So, efforts of Russian government to overcome the pandemic should be considered as unsuccessful due to a lot of strategic mistakes they have made at the beginning of the current catastrophic pandemic of COVID-19’s evolving in Russia.

Fig. 8.

A schematic prognosis for the dynamics of total coronavirus cases in Russia during 1 year. The start is 1 April 2020

We expect that the second wave of pandemic will pass its peak at the end of December 2020 for cases of USA, India, Brazil, Russia, Iran, Germany and other countries, so all the approximated formulae for COVID-19’s evolution in human society should be corrected afterwards, according to the updated dynamics for the confirmed cases of illness. The main reason is that predicting the future with such a model will obviously have a limited planning horizon due to the unavoidable uncertainty of the future.

Thus, for each stage of pandemic we should derive appropriate approximated formula which will correspond to the main dynamical features of the pandemic at the current stage (in accordance with both the disease characteristics and the societal ones that stem from the governmental efforts to decrease the pandemic rate). It means that we should suggest revolving scheme for calculating algorithm with respect to the cascade of waves of pandemic: at each calculation step, the final solution values of the previous stage of pandemic should be considered to be the initial conditions for the next calculation step (next wave of pandemic). In [1], we have suggested approximated formulae for the first wave of pandemic in case of Russia and Germany; in the current research, we decode the second wave of pandemic for the key six countries (including USA, India, Brazil, Russia, Iran and Germany).

Thus, in this article we suggest approach how to estimate the evolution of COVID-19 pandemic in time for the restricted chosen period of time associated with the second wave of pandemic. This is definitely new insight for presenting clear mathematical algorithm of modelling pandemic in a form which allows us to gain new useful information about mean-time and also long-term COVID-19 evolution with respect to critical level of the aforementioned epidemiological contamination in human society. Meanwhile, it obviously means that suggested method should enrich our knowledge about evolution of COVID-19 from mathematical point of view. Indeed, such a novel approach differs from most of the existing theories for describing the evolution of the viruses in human society (which are based mainly on modelling such a dynamics with the help of appropriate systems of ODEs or by the stochastic methods).

According to our understanding, the suggested approach is the significant theoretical tool (with practical application of mathematical algorithms) for the analysis of the global evolution of various pandemics and it can be used in future researches for determining the extent of the biological hazard that poses a threat to the health of living organisms, primarily humans, at the chosen step of evolving pandemic.

Also, remarkable articles [14–20] should be cited, which concern the problem under consideration.

Remarks (with highlights)

• Analytic modelling of humankind amount infected by COVID-19 has been developed.

• Finite chains of recurrent sequences describe how population evolve over time.

• Semi-analytical ansatz is suggested for such a recurrent solving procedure.

• The proper formulae for COVID-19 evolving inside human population are obtained.

• Formulae for non-classical trends of pandemic are presented for six countries.

• Modified sigmoid curves with up-inclination at the end of first wave are obtained.

• Plots for such formulae can be divided into two types: with bulge or no at beginning.

• Second wave of pandemic will pass its peak at the end of December 2020 for six countries.

• Second wave will come to end at the first decade of January in 2021 for Germany and Iran.

• Second wave will come to end at the end of January 2021 in India, 3^rd wave will be born.

• Trends of pandemic for USA, India, Brazil, Russia, Iran and Germany are presented.

Let us explain or clarify how each of the parameters influences the performance of the proposed approach. Denominators in formulae (1), (2), (3), (4), (5) and (6) yield the trends of classical sigmoid curves (Fig. 1), whereas numerators yield the modified sigmoid curves with up-inclination at the end of first wave of pandemic (Figs. 2, 3, 4, 5, 6, 7, 8). In addition, if in the numerator of formula there is an polynomial extent of the current day of pandemic (e.g., in formula (3) for Iran) it should mean the presence of the appropriate bulge (Fig. 4 at zoom) at the beginning of the graphical plot of coronavirus curve as in case of Iran (or other Middle East countries).

There is only one variable parameter for each formulae, namely the number of days from the start of the pandemic (in this or that countries). Also, geometry of the modified sigmoid curves strongly depends on the initial data (the amount of infected people officially registered at the 1st day of pandemic).

Author contributions

In this research, SE is responsible for the results of the article, the obtaining of exact solutions, simple algebra manipulations, calculations, the representation of a general ansatz and calculations of graphical solutions, approximation and also is responsible for the search of approximate solutions. AR was responsible for approximated solving of the algebraic Eqs. (6) and (7) in [1] by means of advanced numerical methods as well as, videlicet, is responsible for applying numerical data of calculations to the current research.

Funding

Not applicable.

Availability of data and materials

The data for this paper are available by contacting the corresponding author.

Code availability

To obtain graphical results, online software package was used: http://grafikus.ru/.

Compliance with ethical standards

Conflict of interest

The authors declare that there is no conflict of interests regarding publication of article.