RLDOCK: A new method for predicting RNA-ligand interactions

Abstract

The ability to accurately predict the binding site, binding pose, and binding affinity for ligand-RNA binding is important for RNA-targeted drug design. Here we describe a new computational method, RLDOCK, for predicting the binding site and binding pose for ligand-RNA binding. By developing an energy-based scoring function, we sample exhaustively all the possible binding sites with flexible ligand conformations for a ligand-RNA pair based on the geometric and energetic scores. The model distinguishes from other approaches in three notable features. First, the model enables exhaustive scanning of all the possible binding sites, including multiple alternative or coexisting binding sites, for a given ligand-RNA pair. Second, the model is based on a new energy-based scoring function developed here. Third, the model employs a novel multi-step screening algorithm to improve computational efficiency. Specifically, first, for each binding site, we use a gird-based energy map to rank the binding sites according to the minimum Lennard-Jones potential energy for the different ligand poses. Second, for a given selected binding site, we predict the ligand pose using a two-step algorithm. In the first step, we quickly identify the probable ligand poses using a coarse-grained simplified energy function. In the second step, for each of the probable ligand poses, we predict the ligand poses using a refined energy function. Tests of the RLDOCK for a set of 230 RNA-ligand bound structures indicate that RLDOCK can successfully predict ligand poses for 27.8%, 58.3%, and 69.6% of all the test cases with the root-mean-square deviation within 1.0, 2.0, and 3.0 Å, respectively, for the top-three predicted docking poses. The computational method presented here may enable the development of a new, more comprehensive framework for the prediction of ligand-RNA binding with an ensemble of RNA conformations and the metal ions effects.

Graphical Abstract

1. Introduction

RNA molecules can fold into complicated tertiary structures that contain various motifs such as pseudoknots, kissing loops, and deep major groove.¹ Such a plethora of tertiary structural motifs can lead to a variety of ideal binding sites for small molecules and hence make RNAs potential drug targets.² The RNA druggability is particularly important as protein druggability is severely limited by the lack of proper binding pockets.^3,4 Furthermore, RNA is critical to gene expression,⁵ thus inhibiting RNA function may lead to the termination of the production of dozens or more proteins.^6,7 A notable example for the effect of ligand-RNA binding is riboswitch,^8–12 where ligand binding results in the termination or go-through for transcription or translation.¹² Furthermore, because RNAs can directly participate in the protein syntheses⁶ through the formation of specific active sites in the ribosome,¹³ or ligand-RNA binding can directly impact gene expression and viral replication in viral gene regulation.¹⁴

In recent years, computational docking/scoring methods, such as such as rDOCK,^15,16 DrugScore^RNA,^18,19 LigandRNA,¹⁷ DOCK6,²⁰ and MORDOR,²¹ have been developed to predict RNA-ligand interactions. These docking/scoring methods can be classified into two types:

1. Knowledge-based methods. DrugScore^RNA18,19 uses a set of distance-dependent knowledge-based potentials to score and rank the ligand poses for an RNA target. The potentials used in DrugScore^RNA18,19 are described by the distance between a pair of atoms in the ligand and the RNA, respectively. The potentials are derived from 670 crystallographic RNA-ligand and RNA-protein complexes. However, only 50 of them are RNA-ligand. LigandRNA¹⁷ is another knowledge-based method. Its potentials consider not only the distances but also the angles between RNA atom pairs and ligand atoms. The potentials used in LigandRNA¹⁷ are derived from 251 RNA-ligand complexes. rDOCK¹⁶ is an open-source software that can predict ligand binding poses in nucleic acids and proteins. The (empirical) scoring functions in rDOCK¹⁵ account for specific RNA-ligand interactions such as those involving aromatic groups.

2. Physics-based methods. MORDOR²¹ applies all-atom CHARMM27 force field²² to the target and general AMBER force field²³ to the ligand. This model allows both ligand and target to be flexible. DOCK6²⁰ is another typical physics-based docking procedure. In DOCK6, AMBER force field^23,24 is applied to both ligand and RNA, and the scoring function contains the solvent and (sodium) ion effects on docking. In comparison, MORDOR may provide higher accuracy in predictions of a specific ligand database, while DOCK6 has higher efficiency and be applicable to a broader database.²⁰ In addition to MORDOR and DOCK6, other physics-based scoring/docking methods focus mainly on special types of ligand such as aminoglycoside antibiotics,²⁵ or targets such as purine riboswitch.²⁶

The applications of the existing scoring/docking methods have been successful at different levels.²⁷ The accuracy of the knowledge-based methods is dependent on the training database of RNA-ligand complexes. Compared with protein-ligand complexes,²⁸ we have much less experimentally determined structures available for the RNA-ligand complexes. Nevertheless, with the development of rigorous physical models, we can realistically expect that with the expansion of the RNA-ligand complex structure family, the accuracy of the predictions can be continuously improved.²⁹ Moreover, given the limited dataset of available structures, physics-based docking/scoring methods are particularly needed. Despite the significant efforts devoted to the development of physics-based algorithms, limitations of the current approaches remain. For example, DOCK6²⁰ requires expert knowledge to choose the various parameter options for reliable calculations.

Here we report a new RNA-ligand docking (RLDOCK) model. The model has three key novel ingredients. First, we develop a new scoring function based on ligand-RNA energetics,²⁷ including the van der Waals (VDW) interaction, electrostatic interaction, polar and nonpolar hydration effects, and hydrogen bond effect. Second, we employ a novel global search algorithm to identify all the potential docking sites for a given ligand. Third, the model enables docking with an ensemble of ligand conformers. To derive the scoring function, we use a total of 230 RNA-ligand complexes that have been experimentally determined (Table S1 in the Supplemental Information (SI)), among which 30 are the training set for the extraction of the statistical potential and 200 are the test set. Comparisons between other existing models suggest that RLDOCK can give better predictions for ligand docking pose.

2. Model and methods

2.1. Preparations for RNA and ligand

We download all the (totally 230) experimentally determined RNA-ligand complex structures, from the protein data bank (PDB).³⁰ For the NMR structures that contain multiple models, we select the first model. If an RNA-ligand complex contains multiple types of ligands, we select the ligand that has the largest number of heavy atoms and ignore the other ligands. For example, the RNA-ligand complex of PDB identifier (ID) 3DIL³¹ has five ligand molecules, a lysine with 8 heavy atoms, three fragments of pentaethylene glycol with 3, 3, and 5 heavy atoms, respectively, and an isopropyl alcohol with 4 atoms. We keep only the lysine for the docking prediction. For a ligand with rotatable bonds, we generate an ensemble of ligand conformers. Specifically, we use the cheminformatics toolkit Open Babel 3.0³² to generate at least 200 distinct conformers. The generated ligand conformers along with the native (crystal) conformer are classified into at least 30 clusters based on the RMSDs between the different conformations. The centroid structures of the clusters are selected to form the conformational ensemble of a ligand. For a cluster that contains the crystal structure of the ligand, the crystal structure is used. To cover a broad range of conformations, we adopt an adaptive method for conformational clustering. A larger RMSD cut-off between the conformations would lead to a smaller number of clusters and hence a less diverse conformational ensemble. In our calculation, we gradually reduce the RMSD cut-off value until the number of the resultant clusters is no less than 30. We then select the largest 30 clusters for ligand conformers. To further test the reliability of the model, we also generate conformational ensembles of ligands by excluding all the native poses. The ensembles are used to test the ability of the model to predict the (near-native) binding poses without prior knowledge about the (experimental) native poses.

We use RMSD with respect to the native pose to assess the accuracy of the theoretical predictions for the ligand poses. The detailed information about the RNA-ligand complexes, such as the experiment method (NMR or X-ray) and the ligand name, are listed in Table S2 in the SI.

To calculate the electrostatic interaction energy, we assign partial charges using the “Dock prep” module in Chimera.³³ For a given RNA or ligand, we implement the “Dock prep” module for alternate location deletion (keeping the highest occupancy), hydrogen addition, partial charges addition, and output with Mol2 format. Here we apply the hydrogen addition to generate possible protonation states at the physiological pH. In the step of partial charges addition, we use AMBER ff14SB (with Parm99) to assign charges^34,35 of standard RNA residues. For the ligand and nonstandard residues in RNA, we first calculate the partial charges using ANTECHAMBER with the AM1-BCC (AM1 for short) method.^36,37 If AM1 fails to assign the partial charges, we then use Gasteiger (GAS for short)³⁸ to calculate the partial charges. Both AM1 (by default) and GAS are included in the “Prep Dock” module. See Table S2 in the SI for a summary of the methods that we use to assign partial charges.

2.2. The RLDOCK model and the scoring function

The procedure above for an RNA-ligand complex results in two files of the RNA and the ligands in the format of Mol2 that contain the information about the atomic coordinates and partial charges. In our model, the different types of atoms are treated as spheres with specific VDW radii (listed in Table S3 in the SI). We describe a ligand pose using four variables (R,L,A,O), where R denotes the coordinate of the candidate binding site (an effective anchor point for the ligand), L represents the ligand conformer used for docking, A refers to the ligand atom to be placed at site R, and O denotes the three-dimensional orientation of the ligand. We use Euler angles (α,β,γ) about the anchor point R to represent the ligand orientation O.

To efficiently sample the ligand binding pose for a given RNA structure, we first sample the possible binding sites R and the different ligand atoms A to be placed at the binding site R for all the different ligand conformers, then generate all the possible ligand orientations through 3D rotation about the ligand atom at the site. We configure the RNA in a box such that the six boundaries of the box are 3 Å away from the outermost atoms of the RNA, and discretize the space using a simple cubic lattice of grid 0.5 Å. We note that the distance 3 Å is slightly larger than the hydration layer, which has a decay length around 1.4 Å. To sample the binding configurations for a given binding sites R, we place a ligand (heavy) atom A in a conformer L at R. For each give set of (R,L,A), we sample ligand poses through 3D rotation around atom A. We generate the rotation through the Euler angles O with 10^◦ increment for each angle in each step. In the next step, we score each binding pose (R,L,A,O) using a novel energy-based scoring function described below.

The RLDOCK scoring function is based on the physical interaction energies between RNA and ligand, including the VDW interaction, electrostatic interaction, polar and nonpolar hydration interactions, hydrogen-bond interaction, and ligand intramolecular van der Waals (VDW) interaction. We use the generalized Born approximation with solvent-accessible surface area (GB/SA model)^39–44 to treat the polar and nonpolar hydration interactions. In the energy calculation, we neglect the hydrogen atoms in RNA and ligand and add their charges to the directly connected heavy atoms. For a given ligand pose (R,L,A,O), the energy score is given by:

$$\begin{gathered} S(R,L,A,O)=c_{lj}\times \mathrm{\Delta }{U}_{lj}+c_e\times \mathrm{\Delta }{U}_e+c_h\times \mathrm{\Delta }{U}_h+c_{sa}\times \mathrm{\Delta }{U}_{sa}+ \\ {c}_{pol}\times \mathrm{\Delta }{U}_{pol}+c_{self}^{\text{R}}\times \mathrm{\Delta }{U}_{self}^{\text{R}}+c_{self}^{\text{L}}\times \mathrm{\Delta }{U}_{self}^{\text{L}}+c_{internal}^{\text{L}}\times \mathrm{\Delta }{U}_{internal}^{\text{L}}, \end{gathered}$$ (1)

where we use the weight coefficients⁴⁵ c to account for the correlation (nonadditivity) effects for the different interactions. In what follows, we illustrate the calculation of each energy term in the scoring function above.

We use the Lennard-Jones (LJ) potential ΔU_lj to represent VDW interaction:

$$\mathrm{\Delta }{U}_{lj}=\sum _r\sum _l\left[{\left(\frac{{\sigma }_{rl}}{r_{rl}}\right)}^{12}-{\left(\frac{{\sigma }_{rl}}{r_{rl}}\right)}^6\right].$$ (2)

Here the subscripts r and l denote the atom r in the RNA and the atom l in the ligand. r_rl represents the distance between the two atoms and σ_rl = 0.8(R_r + R_l) is the equilibrium distance, where R_r and R_l are the radii of atom r and l, respectively. We apply a cut-off distance r_cut = 2.5(R_r + R_l) in the LJ potential calculation.

We calculate the electrostatic interaction ΔU_e between the ligand and RNA using the following formula:

$$\mathrm{\Delta }{U}_e=\sum _r\sum _l\frac{Z_r{Z}_l{e}^2}{{\epsilon }_c{r}_{rl}}.$$ (3)

Here Z_r and Z_l are the electric charges of the atoms r in RNA and l in ligand, respectively, e is the electronic charge, ε_c (=20 in our calculation) is the dielectric constant of the RNA-ligand complex.

We evaluate the hydrogen-bond interaction energy ΔU_h between the RNA and ligand as:

$$\mathrm{\Delta }{U}_h=\sum _r\sum _l{u}_h\left(r_{rl}\right),$$ (4)

where u_h(r_rl) is the hydrogen-bond energy of an RNA-ligand atom pair. We apply an empirical formula¹⁵ to evaluate the hydrogen-bond energy:

$$u_h\left(r_{rl}\right)=\{\begin{array}{cc}-1& r_{rl}\le r_{\min }\\ -1+\frac{r_{rl}-r_{\min }}{r_{\max }-r_{\min }}& r_{\min }<r_{rl}<r_{\max }\\ 0& r_{rl}\ge r_{\max }\end{array}$$ (5)

Here r_min = 0.8(R_r + R_l) and r_max = 1.3(R_r + R_l).

To account for the change of the hydration energy upon ligand-RNA binding, we consider a hydration layer of width 1.4 Å around the surface ^46,47 of the RNA, ligand, and ligand-RNA complex structures. We evaluate the nonpolar hydration energy ΔU_sa according to the change in the solvent-accessible surface area (SASA):^48–50

$$\mathrm{\Delta }{U}_{sa}=\sigma \times \mathrm{\Delta }SA.$$ (6)

where ΔSA is the total SASA change before and after the ligand docking.

$$\mathrm{\Delta }SA=S{A}_{\text{complex}}-\left(S{A}_{\text{RNA}}+S{A}_{\text{ligand}}\right).$$ (7)

Here SA_complex denotes the SASA of the RNA-ligand complex with the pose (R, L, A, O). SA_RNA and SA_ligand are the SASA of the RNA alone and ligand alone, respectively (see Fig. S1 in SI). We choose σ = 0.0054kcal/(mol·Å² for the empirical atomic solvation parameter σ in Eq. 6.⁵¹

We decompose the polar hydration interaction into three parts:⁵² the self-polarization energy changes $\mathrm{\Delta }{U}_{\mathit{\text{self}}}^{\text{R}}$ for the RNA and $\mathrm{\Delta }{U}_{\mathit{\text{self}}}^{\text{L}}$ for the ligand, and the mutual polarization energy change ΔU_pol induced by other atoms:

$$\mathrm{\Delta }{U}_{pol}=U_{pol}^{\text{complex}}-\left(U_{pol}^{\text{RNA}}+U_{pol}^{\text{ligand}}\right),$$ (8)

where $U_{pol}^{\text{complex}},U_{pol}^{\text{RNA}}$, and $U_{pol}^{\text{ligand}}$ are the mutual polarization of the complex, the RNA alone, and the ligand alone, respectively. We estimate the three mutual polarization energies from the GB model:^39–44

$$U_{pol}=\frac{1}{2}\left(\frac{1}{{\epsilon }_w}-\frac{1}{{\epsilon }_c}\right)\sum _{ij}\frac{Z_i{Z}_j{e}^2}{\sqrt{r_{ij}^2+B_i{B}_j\exp \left(-\frac{r_{ij}^2}{4B_i{B}_j}\right)}},$$ (9)

where ε_w (=78) denotes the dielectric constant of water. We assume the same dielectric constant ε_c for the bound and the unbound RNA and ligand. The subscripts i and j $(i\ne j)$ represent respective molecule (complex, RNA alone, or ligand alone). r_ij denotes the distance between these two atoms. B_i and B_j are the Born radii of atoms i and j (see Eqs. S1-S4 in the SI). We compute The self-polarization energies $\mathrm{\Delta }{U}_{\mathit{\text{self}}}^{\text{R}}$ of the RNA and $\mathrm{\Delta }{U}_{\mathit{\text{self}}}^{\text{L}}$ of the ligand as the following:

$$\begin{gathered} \mathrm{\Delta }{U}_{\mathit{\text{self}}}^{\text{R}}=\left(\frac{1}{{\epsilon }_w}-\frac{1}{{\epsilon }_c}\right)\sum _r\left(\frac{1}{B_r^a}-\frac{1}{B_r^b}\right)Z_r^2{e}^2 \\ \mathrm{\Delta }{U}_{\mathit{\text{self}}}^{\text{L}}=\left(\frac{1}{{\epsilon }_w}-\frac{1}{{\epsilon }_c}\right)\sum _l\left(\frac{1}{B_l^a}-\frac{1}{B_l^b}\right)Z_l^2{e}^2 \end{gathered}$$ (10)

Here $B_{r(\text{or}l)}^b$ and $B_{r(\text{or}l)}^a$ denote the Born radius of atom r (or l) in the RNA (or ligand) before and after the ligand-RNA docking, respectively.

For a given conformer L, we use the intra-molecular LJ potential $\mathrm{\Delta }{U}_{internal}^{\text{L}}$ within ligand to characterize its energy:

$$\mathrm{\Delta }{U}_{internal}^{\text{L}}=\sum _i^L\sum _{j(j\ne i)}^L\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right].$$ (11)

Here i and j denote a non-bonded atom pair in the ligand, r_ij is the distance between the two atoms, and σ_ij = 0.8(R_i + R_j) is the equilibrium distance, where R_i and R_j are the radii of atom i and j, respectively. A cut-off distance r_cut = 2.5(R_i + R_j) is applied here for the LJ potential.

The total number of the ligand poses generated in the sampling algorithm above is equal to (the number of grid points) × (the number of ligand conformers) × (the number of ligand atoms) × (the number of orientations). The complete enumeration of all these possible ligand docking poses and the evaluation of their energy scores are computationally demanding. To enhance the computational efficiency, we develop a novel approach.

2.3. Global sampling and search for binding mode (R, L, A)

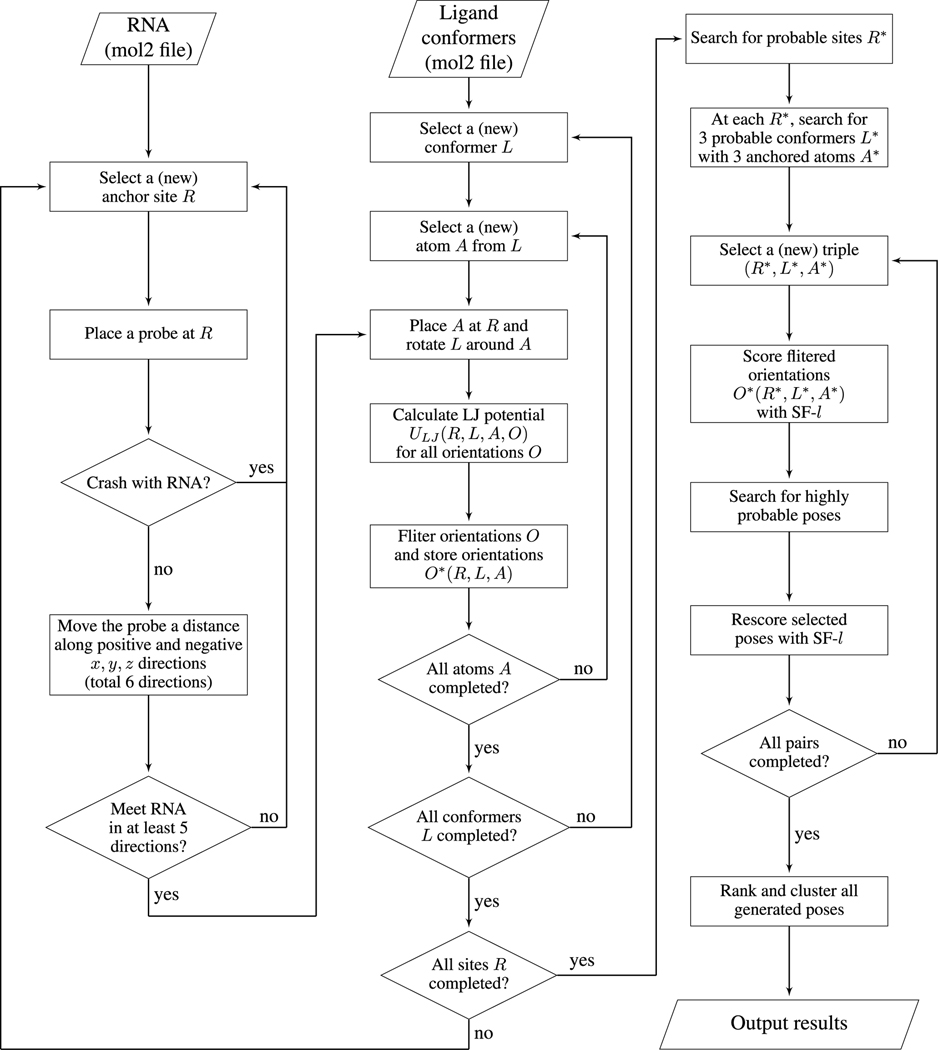
To enhance the efficiency in the sampling of the ligand poses, we develop the following multi-step screening approach (see the flowchart in Fig. 1).

Figure 1:

The flowchart of the RLDOCK model.

First, we remove all the grid points R that can cause steric clashes between the ligand and the RNA. We determine the steric clash using a spherical probe of radius r_ball = 2Å, which is slightly larger than the largest atom phosphor (of radius 1.9Å shown in table S3 in SI). For a given site R = (x, y, z), if the probe centered at R touches RNA heavy atoms, i.e., the distance between R and an RNA atom is within r_ball + r_atom, where r_atom is the radius of the atom, we exclude the grid site R from the sampling space of the binding site (anchor point for the ligand).

Second, we search for all the pocket regions on RNA surface. These regions are potential RNA binding sites. To identify the binding pockets, we move the probe sphere a distance (6 Å) along the positive and negative x, y, and z directions (a total of 6 directions). If this probe sphere in the above movements meets the heavy atom(s) of RNA in at least 5 directions, we keep the site R. Otherwise, the site is not in an RNA pocket and is removed from further sampling steps.

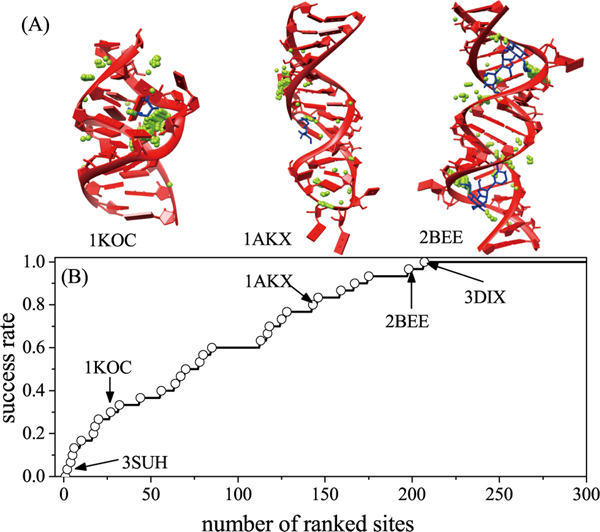
The above two-step screening results in a significant reduction in the available number of grid points R as candidate binding sites; See Fig. 2A for three examples (PDB IDs: 1KOC, 1AKX, and 2BEE) and Table S4 in the SI for the resultant number of candidate binding sites.

Figure 2:

(A) The binding sites after the probe detect. The RNAs and ligands are marked by red and blue. The green points represent the candidate binding sites. (B) The success rate of the global search as a function of the number of the ranked sites for the 30 RNA-ligand cases in training set.

After generating the putative binding sites, we sample the different ligand configurations at each candidate binding site. The sampling involves two steps. First, for each candidate binding site R(anchor points) sampled above, we place the different atoms A from conformer L at the site R. Second, for a given assignment of the atom A, we sample the ligand orientation by rotating the conformer L about the atom A (anchored at R). We use Euler angles for the 3D rotation about R to generate an ensemble of ligand orientations. This step results in an ensemble of ligand pose (and RNA-ligand complex structure) described by (R, L, A, O).

We employ a crude, computationally efficient method to further sieve the ensemble of ligand binding poses above. We prepare a grid energy map with grid spacing of 0.2 Å for common atom types (C, N, O, P, S, etc) in advance. For each atom type placed at the different grid sites, we calculate and tabulate the LJ potential energy values between the atom and the RNA. For an arbitrary binding configuration (R, L, A, O), some atoms may not be positioned exactly on grid sites. For the off-grid atoms, we use the LJ energy values on the nearest grid sites. With the pre-tabulated grid energy data, we can quickly calculate ΔU_ij(R, L, A, O) (see Eq. 2) by simply adding the corresponding numbers in the energy table. Among the different orientations, we call the one with the lowest LJ potential as the “geometrically preferred orientation” and the corresponding LJ potential energy as the geometric compatibility score SCORE_LJ(R, L, A). Similarly, for a given binding site R, among all the different conformers L and all the different assignments of the ligand (bound) atom A at R, we identify the conformer L* and the corresponding atom A* that has the best (lowest) SCORE_LJ(R, L, A).

We evaluate the success of the global search algorithm above for the potential binding site R and the binding atom A using the experimentally determined RNA-ligand complex structure. We rank the candidate binding sites R according to SCORE_LJ(R, L, A) and consider a prediction for the candidate site R to be successful if R is the closest to the atom A(R, L^exp) in the experimental structure (here L^exp denotes the experimental conformer) and the distance is within 0.5Å (grid spacing). As shown in Fig. 2B for the success rate for the 30 RNA-ligand complexes as the training set (see also Table S4 in the SI), we find that the most poorly predicted case is (PDB ID) 3DIX, for which the most native-like ligand binding pose is ranked the 207th in list of the candidate poses. Among the 30 cases, 3DIX has the largest RNA (174-nt) and the ligand has a relatively simple structure with only 10 heavy atoms. Predicting the binding sites for large RNAs and small ligands is challenging because a larger RNA usually has a larger number of potential anchor points and a smaller ligand is less sensitive to the geometric compatibility scores at the different anchor points.

After generating the above ensemble of binding poses (R,L,A,O) on the basis of the LJ potential, we apply a more refined energy function to score the candidate poses. To reach the optimal balance between the computational efficiency and the accuracy, we keep the top 300 ranked binding sites R*, and for each R* we keep 3 conformers L* each with 3 different assignments of the bound ligand atom A* according to the SCORE_LJ(R*, L*, A*) score.

Although the above procedure leads to a drastic reduction in the number of the candidate binding sites and the binding atoms in each site, for a given set of binding site R*, conformer L*(R*), and atom A*(R*, L*), there exist a huge number (> 10⁵) of ligand orientations. Because a slight change in the ligand orientation may incur a notable change in the SASA of the RNA-ligand complex SA_complex (see Eq. 7) and new Born radii of the atoms in complex(see Eqs. S1-S4 in SI), we need to update the SASA and Born radii for each ligand orientation sampled. SASA and Born radii calculations involve all the atoms in the RNA-ligand complex, thus, an exhaustive computation for all the possible orientations can be time-consuming (several seconds per orientation). To speed-up the overall computational efficiency, before applying the complete (high-resolution) scoring function (Eqs. 1–11; denoted as SF-h for the high-resolution scoring function), we first use a computationally efficient, simplified (low-resolution) scoring function (denoted as SF-l for the low-resolution scoring function) to select the highly probable ligand orientations for a given (R*, L*, A*).

2.4. The simplified scoring function

In the simplified scoring function(SF-l), we employ a fast method to estimate the GB/SA energy terms.^39–44

1. Simplified in SASA. When considering the SASA change for a pair of ligand-RNA atoms, we ignore the effect from other atoms (see Fig. S1 in SI), and estimate the SASA change ΔSA using the following approximation:

   $$\mathrm{\Delta }SA=\sum _r\sum _l-2\pi \left(R_r^{*}\times H_r^{*}+R_l^{*}\times H_l^{*}\right).$$ (12)

   Here $R_r^{*}\left(=R_r+1.4\mathrm{\AA }\right)$ and $R_l^{*}\left(R_l+1.4\mathrm{\AA }\right)$ denote the radii of the RNA atom r (with a hydration shell) and the ligand atom l (with a hydration shell). $H_r^{*}$ and $H_l^{*}$ are the heights of the overlapping spherical crown of the atoms (see Fig. S1 in SI).

2. Simplified Born radii. Ignoring the changes in the Born radii for the RNA upon ligand docking, we assume $\mathrm{\Delta }{U}_{self}^{\text{R}}=0$ in the Eq. 10 and neglect the changes in the RNA-RNA mutual polarization interactions $U_{pol}^{\text{complex}}$ and $U_{pol}^{\text{RNA}}$ in Eq. 9. For the ligand atoms before docking, we estimate the Born radii using the VDW radii $\left(B_l^b=r_{\text{atom}}\right)$. For a ligand atoms, we estimate the post-docking Born radii by placing the atom at the binding site R*. For example, for a ligand consisting of three types of atoms N, C, and O, we position atoms N, C, and O one by one at the binding site R* and calculate their Born radii separately. With the above approximations, we can assume atoms in a ligand bound at a given site with different orientations to have the same Born radii.

Compared to the original full scoring function, the above simplified scoring function (SF-l) can lead to thousands-fold reduction in computational time.

2.5. Refined scoring function

We first employ the SF-l above to perform a quick screening of ligand orientations in a binding site, then apply the rigorous SF-h (Eqs. 1–11) to refine the ranking of the ligand poses. We use the aforementioned 30 RNA-ligand complexes to train the weight coefficients in the scoring function. The training set covers a wide variety of ligands from the totally 230 RNA-ligand structures. In the training process, each coefficient varies from 0.02 to 5.00 with a step 0.02. As shown below, we repeat the coordinate descent method to find out the different quasi-optimal sets of the weight coefficients and then determine the optimal values of the weight coefficients by minimizing the heavy-atom RMSD between the predicted ligand pose and the native pose (in the PDB structure). The resultant weight coefficients can give the heavy-atom RMSD within 2 Å for the top-three ranked poses. In detail, the computation for the weight coefficients involves three steps.

First, we use the crude SF-l to calculate the seven interaction terms in Eq. 1 for a quick estimation of the coefficients by the coordinate descent method; See Table 1. Because $\mathrm{\Delta }{U}_{self}^{\text{R}}=0$ in SF-l, the corresponding coefficient is not included in the calculation.

Table 1:

The coefficients in the simplified and precise scoring functions

coefficients	clj	ce	ch	csa	cpol	$c_{self}^{\text{R}}$	$c_{self}^{\text{L}}$	$c_{vdw}^{\text{L}}$
simplified	3.30	1.32	0.10	0.30	0.36	—	0.58	0.66
precise	3.30	1.32	0.10	1.26	1.38	4.98	2.78	0.66

Second, we apply the rigorous SF-h to refine the predicted weight coefficients. Specifically, we run the calculation for the top-five poses predicted in the first step above for each set of the binding site R, conformer L, and atom A. In this step, the coefficients of the VDW interaction, electrostatic interaction, hydrogen-bond interaction, and ligand internal intramolecular VDW interaction remain the same as those obtained in the first step because these ligand-RNA interactions are the same in the SF-l and SF-h. The refined results for the coefficients are shown in Table 1. This step leads to the final scoring function.

Third, we start from the top-ranked pose and group the ligand poses into clusters using a heavy-atom RMSD cut-off 2 Å. In each cluster, the pose with the best score is chosen to represent the cluster. This step leads to a new list of ranked poses, each representing a cluster.

3. Results

The prediction of a ligand-RNA bound structure involves five steps in the RLDOCK model: (1) search for the possible binding sites R using the spherical probe; (2) determine the binding atoms A of conformer L through the geometric fit; (3) select the binding orientations O using the crude, simplified scoring function; (4) rank the ligand docking poses using the original, refined scoring function; and (5) generate the final rank list after the cluster calculation. Our test results are shown in Table S2 in the SI.

3.1. Success rate of RLDOCK

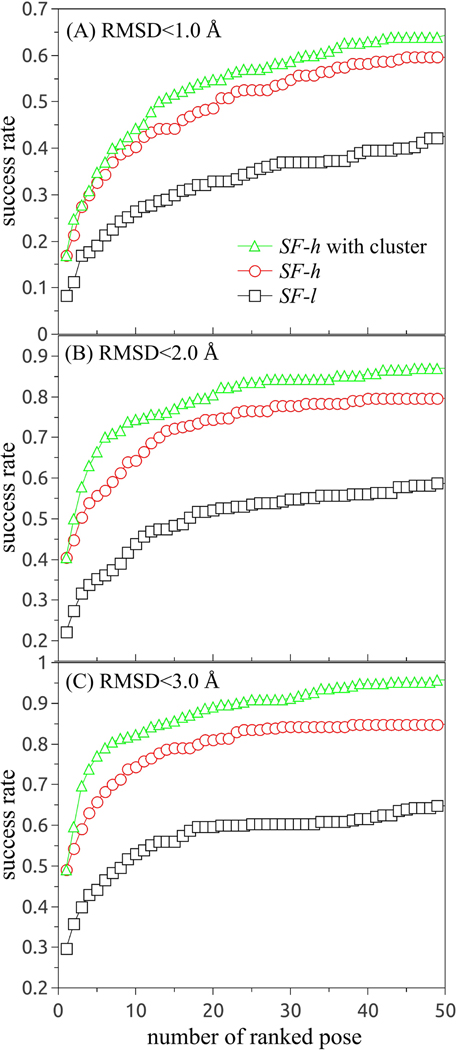
Success rates using multiple RMSD thresholds are necessary for the evaluation of a ligand pose prediction model.⁵³ We measure the accuracy for the prediction of the ligand binding pose in terms of the heavy-atom RMSD to the ligand pose in the crystal structure. Fig. 3 shows the success rate with the increased RMSD cutoff from (A) < 1 Å, (B) < 2 Å, and (C)< 3 Å for all 230 RNA-ligand complexes. In Fig. S2 of the SI, we show the success rates for the training set (30 complexes) and the test set (200 complexes), respectively. If we use only the crude SF-l (without using the more accurate SF-h) in the RLDOCK model, the model can successfully predict 8.3%, 22.2%, and 29.6% of all the cases within RMSD thresholds 1 Å, 2 Å, and 3 Å, respectively. The use of SF-h (after the SF-l-based quick, initial screening) would increase the fractions to 17%, 40.4%, and 49.1%, respectively, for the top-ranked pose.

Figure 3:

The success rate as a function of the number of the top-ranked poses with RMSD within 1 Å (A), 2 Å (B), and 3 Å (C) for all 230 RNA-ligand binding cases. In the statistic of the success rate for RMSD within 1 Å, we use the cut-off RMSD = 1Å in the cluster calculations.

Because RLDOCK uses the top-ranked pose as the starting point for clustering, the success rates of the SF-h-based predictions with and without clustering are the same for the top-ranked pose. However, for the results that include the top-10 poses, the use of clusters can cause a notable increase in the success rate by 3.9% (from 40.4% to 44.3%), 10.0% (from 64.3% to 74.3%), and 7.9% (from 74.3% to 82.2%) for RMSD within 1 Å, 2 Å, and 3 Å, respectively. According to the results shown in Fig. 3, within the top-50 ligand docking poses, the RLDOCK model based on SF-h (after applying SF-l) and the cluster of the poses can give successful predictions for 64.3% (RMSD <1 Å), 87.0% (RMSD <2 Å), and 95.7% (RMSD <3 Å) of all the RNA-ligand complexes, respectively.

3.2. Predictions for ligand binding with multiple binding sites

Among all the 230 RNA-ligand complexes, there are 51 cases that contain multiple ligands, each bound to different binding sites (PDB IDs listed in Table S5 in the SI). The novel global search method for all the possible binding sites enables the RLDOCK model to find out the multi-ligand poses in these (51) cases (also see Table S5 in SI).

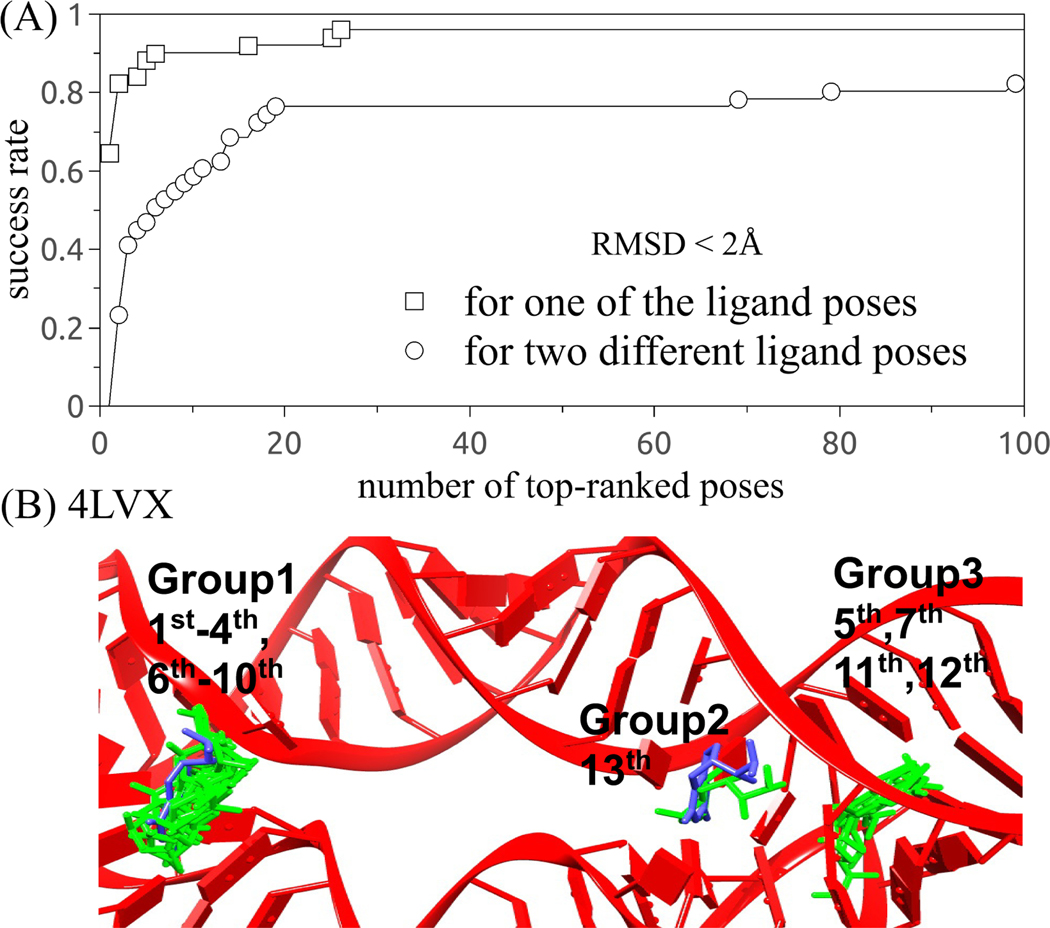
Our test results show that RLDOCK can successfully predict 62.7% of the 51 cases, where the top ranked pose is an experimental pose within 2 Å RMSD; See Fig. 4A. The success rate is increased to 84.3% and 86.3% if we consider the top-three and top-five poses, respectively. For 10 out of the 51 (19.6%) cases, the top-two ranked poses correspond exactly to the two experimental ligand poses. The apparent low success rate (19.6%) is due to our strict criteria that the top-two poses correspond exactly to the experimentally observed two alternative binding poses. In fact, the top few ranked poses often cluster around the top-one binding site before the second, distinct, binding pose/site emerges in the ranked list. Indeed, the success rate for the prediction of the multiple binding poses rises rapidly to 37.3% and 60.8% if we include the top-three and top-ten poses, respectively. Moreover, the success rate increases to 82.4% cases if we include the top-100 ranked poses. These 100 predicted poses form less than ten clusters, demonstrating the reliability of RLDOCK in predicting multiple docking poses.

Figure 4:

The success rate as a function of the number of the top-ranked poses with RMSD within 2 Å from the 51 cases containing multiple binding sites.

3.3. Comparisons to other models

Here we compare our RLDOCK model to other models, such as the original version of rDOCK reported in 2004,¹⁵ LigandRNA,^17,29 DrugScore^RNA,^18,19 DOCK6,²⁰ and MORDOR.²¹ In the comparisons, we use a collection of 42 RNA-ligand complexes reported in Ref. 17 as the test set (see Table S6 and S7 in the SI). Among the 42 test cases, 1FJG, 1HNW, 1XPB, and 2OGN (PDB id) are ribosomal complexes. RLDOCK may not provide accurate predictions for these systems because the proteins in the complexes may influence ligand binding and the huge number (> 10⁵) of the potential binding sites in these large systems (> 2000 nts) may render the sampling and scoring for the binding poses computationally infeasible.

Using the top-ranked pose with RMSD ≤ 2Å as the criteria for a successful prediction, out of the 42 test cases, LigandRNA, DrugScoreRNA, and DOCK6 can successfully predict 15, 13, and 15 cases, respectively (see Table S6 in SI). The combination of the LigandRNA and DOCK6 can find 20 cases. Our RLDOCK model alone finds 21 out of 38 cases. Furthermore, the original version of rDOCK, the original DrugScoreRNA, and MODDOR can predict 5 out of 10, 12 out of 21 cases, and 20 out of 32 cases, respectively. Considering the 38 cases that RLDOCK can treat, we find that RLDOCK outperforms the other models listed in Table 2 for both the top-one ranked poses and the top-three poses (see the details in Table S7 in SI).

Table 2:

The success rate of various docking models^a

	LigandRNA17	DrugscoreRNA 18,19	DOCK620	ligandRNA+DOCK617	RLDOCK
top 1b	39.5%(35.7%)	28.9%(31.0%)	36.8%(35.7%)	50.0%(47.6%)	55.3%(40.4%)
top 3c	47.4%(45.2%)	39.5%(42.9%)	44.7%(42.9%)	57.9%(47.6%)	60.5% (57.8%)

^athe percentage without parenthesis is calculated for the 38 RNA-ligand cases in Ref. (17). the value with parenthesis is calculated for the 42 test cases in Ref. (17) and the 230 complexes in the present study.

^bthe success rate of the top-ranked poses.

^cthe success rate (measured by the best RMSD) of the three top-ranked poses. the best results are indicated in bold.

4. Discussions

RLDOCK is a physics-based model for ligand-RNA binding. The model has three key ingredients: (a) a global search algorithm for the potential binding sites, (b) a scoring function for ligand-RNA interactions, and (c) conformational sampling of flexible ligands. Our tests indicate that the RLDOCK model can identify the native ligand pose with an improved success rate. Moreover, the score versus RMSD plot supports a positive discerning ability of the scoring function; See Figs. 5A-C.

Figure 5:

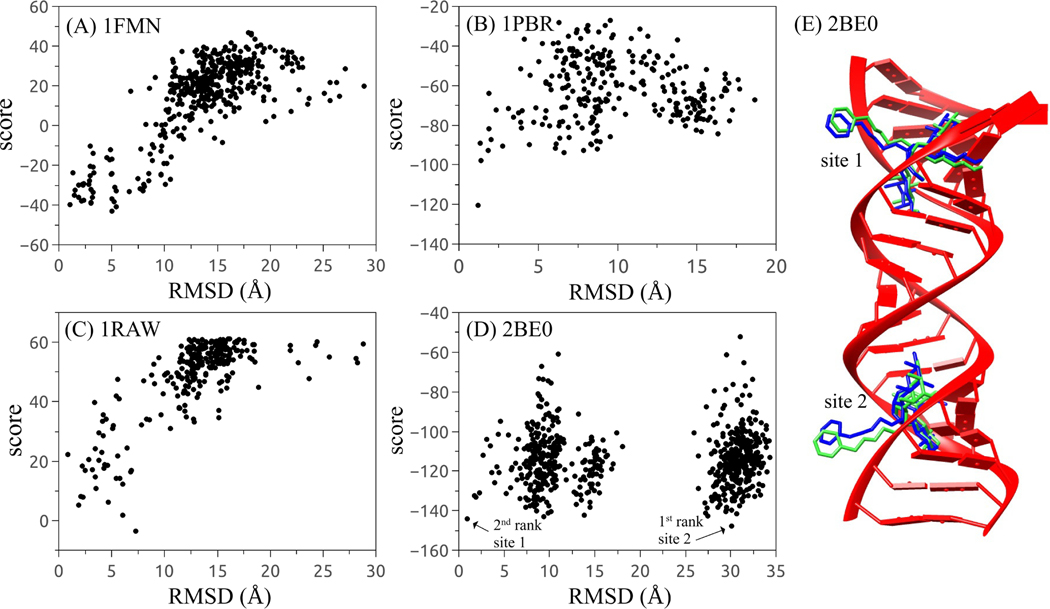
(A)-(D) score-RMSD dependence for the four selected RNA-ligand complexes with PDB IDs 1FMN (A), 1PBR (B), 1RAW (C), and 2BE0 (D), respectively. (E) The structure of RNA-ligand complex with PDB ID 2BE0. The experimental ligands and the predicted ligands are depicted in blue and green.

Furthermore, for the cases in Figs. 5A-C, we also plot the Receiver Operating Characteristic (ROC) curve for the top 100 poses and calculate the corresponding Area Under Curve (AUC) of each ROC curve (see Fig. S3 in SI). The value of AUC is a binary identifier evaluation indicator and it varies between 0.5 and 1, where 0.5 denotes a random guess and 1 denotes to a perfect identifier.⁵⁴ The AUC-ROC results further support RLDOCK as a good identifier. Even for the case that a ligand has two binding sites in the RNA receptor, the RLDOCK model can find both ligand poses/sites, such as the case of PDB ID 2BE0 as shown in Fig. 5D. Here, in order to discriminate the predicted ligand poses in Fig. 5D, we use the native ligand pose in site 1 as the reference ligand pose to calculate the RMSD (same for the case of PDB ID 2BEE in Fig. 6A3). The first and the second top-ranked poses correspond to the native ligand pose in site 2 and site 1 respectively, as shown in Fig. 6E.

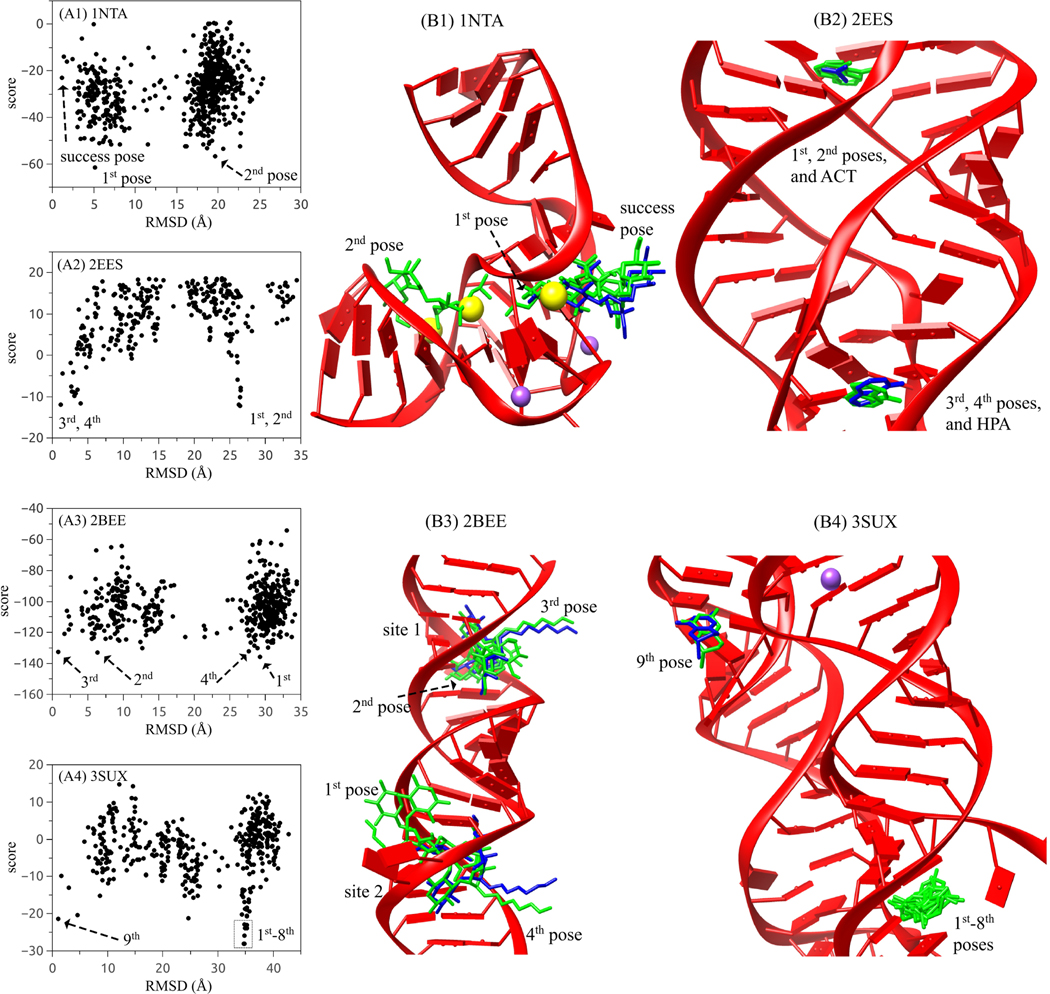
Figure 6:

(A1)-(A4) score-RMSD dependence for the four selected RNA-ligand complexes with PDB IDs 1NTA (A1), 2EES (A2), 2BEE (A3), and 3SUX (A4), respectively. (B1)-(B4) The structures of RNA-ligand complexes corresponding to the four cases in (A1)-(A4). The experimental ligands and the predicted ligands are depicted in blue and green. Yellow and purple balls represent the Ba²⁺ and Na⁺ ions observed in crystal structures.

However, due to the fact that ligand pose prediction is based on the global search around the given RNA receptor, we find that the first or the first few high-ranked poses could be located in a false binding pocket in the RNA (see the four selected examples in Fig. 6). A close examination of such cases suggests other potentially important factors that need to be considered for ligand-RNA docking.

1. Ligand flexibility. The current RLDOCK can treat flexible ligand conformations. Combined with exhaustive 3D rotation of the ligand conformations, we generate a large ensemble of binding configurations. A limited sampling of the ligand conformations can impact the accuracy of the model prediction. Taking the ligand streptomycin (with 16 rotatable bonds) in PDB ID 1NTA as an example, the furanose and pyranose rings are positioned outside the RNA pocket and are less well defined than the streptidine anchored inside the binding pocket.⁵⁵ Although the streptidine part of the top-ranked pose is also buried deep inside the pocket with other two rings outside, the predicted configuration shows a relatively large RMSD of 5.1 Å, as shown in Fig. 6A1 and B1. In addition, the streptidine has two guanidino and three hydroxyl groups which cause many possible ways of inter-molecular interactions. Thus, more binding configurations need to be considered in order to predict more accurate top-ranked poses. Moreover, we only consider the intramolecular VDW interaction (see Eq. 11) for each ligand conformer. For a ligand with many rotatable bonds, however, the highly flexible conformations may cause other important interactions beyond the VDW.

2. Metal ion binding. The metal ions play an essential roles in RNA folding and stability.^56,57 The metal ions can be trapped at specific binding sites in RNAs.²⁷ The bound ions, especially multivalent ions, can exclude ligand binding in the same pocket region. As shown in Figs. 6A1 and B1 for the 1NTA case, poses with large RMSDs represented by the second-ranked pose are located at the pocket that is actually occupied by two Ba²⁺ ions (yellow balls) in the crystal structure. Moreover, other ions such as Na⁺ ions (purple balls) can also influence the ligand docking pose. In the current version of RLDOCK, effects from such specifically bound ions are ignored. In fact, our test calculation shows that if we consider the bound ions (by keeping them in the RNA mol2 file), the first successfully predicted pose would move up in the ranking system from the 200^th to the 40^th.

3. Competition between the different types of ligands. In some cases, the crystal structure contains different types of ligands bound to the RNA. For example, the structure of PDB ID 2EES contains two types of ligands (ACT and HPA), as shown in Fig. 6B2. In RLDOCK, only the ligand with the most heavy atoms (HPA in this example) is used for the prediction (see the subsection 2.1). The experimental structure shows that the RLDOCK-predicted top two poses are located in the RNA pocket occupied by the ACT ligand (Fig. 6A2 and B2). The result suggests that ACT out-competes HPA in the binding to this pocket.

4. Correlation between the same type of ligands. For the cases of a ligand having two or more binding sites, the current RLDOCK model dock ligands one by one as if the different ligands bind to RNA independently. The model neglects the correlation between the different ligand binding events and may cause false predictions. For example, in the case of PDB ID 2BEE as shown in Fig. 6A3 and B3, the crystal structure shows two ligands bound at site 1 and 2, respectively. Although the top-two poses predicted from RLDOCK are located not far from the two native poses, the ligand (ID: JS4) is an antibiotics after amination from paromomycin with a physiological charge is +7.⁵⁸ So the ligand is very sensitive to the charged environment, therefore, the correlation between the two ligands cannot be ignored. If the correlation is considered by placing a ligand in site 1 (or site 2), the RLDOCK model can successfully predict the top-ranked pose with RMSD = 0.805 Å at site 2 (or RMSD = 0.861 Å at site 1).

5. Other RNA-ligand interactions neglected in the scoring function. We find that in some cases, such as 3SUX (see Fig. 6A4 and B4) and 4LVX (see group 3 in Fig. 4B), a few top-ranked poses will be located at the “false” binding pockets. The result may be attributed to RNA-ligand interactions that are neglected in the scoring function, such as the attractive lipophilic interaction and aromatic stacking interaction.¹⁵

Further refinement of the RLDOCK model can also come from an improved computational efficiency. The computational efficiency is limited by the sampling of all the possible binding sites; See Table S4 in the SI for the computer time of the global search of binding sites. The complexity of global search is correlated to the square of the number of ligand atoms. This is because for a given binding site R, all the ligand atoms are tried at the binding site and for each binding pose, the calculation for the VDW intra-molecular interaction energy involves the sum over all the ligand atom pairs. RLDOCK computations with larger ligands such as those in PDB structures 1ET4, 2BE0, 2BEE, and 2FD0 are much more demanding in computation time due to the sampling of a much larger ensemble of flexible ligand conformers. In addition, the complexity of global search is also correlated to the number of candidate binding sites. Therefore, global search for the binding sites on a large RNA such as ribosome can be time demanding and memory intensive.

5. Conclusions

We here present a newly developed model, RLDOCK, to predict the ligand docking pose in a ligand-RNA complex. In the prediction, the structures and partial charges for the RNA and an ensemble of ligand conformers are used as the input information, RLDOCK predicts the ligand binding poses in the following steps: (a) To select the candidate binding sites over the entire RNA using a sphere probe; (b) To determine the ligand atom to be placed at the selected binding sites according to the geometric compatibility between the RNA and ligand, (c) To choose the probable ligand orientations through quick computation by applying the simplified scoring function (SF-l); (d) To score the (hundreds to thousands) ligand poses using the rigorous scoring function (SF-h); (e) To rank the poses with cluster analysis.

Currently the database of the experimentally determined RNA-ligand complex structures is relatively limited compared with the protein-ligand complexes.²⁸ Therefore, a physics-based approach such as RLDOCK is highly needed. We note that the RLDOCK model developed here has several unique advantages.

1. The novel multi-step sieving algorithm for the global search of the binding sites and poses (section 2.3) can optimize the balance between efficiency and robustness. In particular, the global search method enables the RLDOCK model to predict multiple binding sites/poses.

2. The RLDOCK scoring function (see Eq. 1) consists of various RNA-ligand interactions, such as the VDW interaction, electrostatic interaction, polar and nonpolar solvent effects, the hydrogen-bond interaction, and ligand internal VDW interactions.

3. With the sampling of ligand conformers, RLDOCK can account for a broad sampling space for the conformations and binding sites, which leads to an improved performance as compared with other models.

The model, which is trained using only 30 known complexes, can successfully predict other 200 test complexes (Table 3 and Fig. S2). The result suggests that the parameters are transferable and the model may be robust. In fact, even the “false” predicted poses by the RLDOCK may provide useful information (see the example in Fig. 6A3 and B3). Future development of the RLDOCK model should address several significant issues such as computational efficiency, effects from metal ions and other ligands, and a more accurate scoring function.

Table 3:

The comparisons of the success rate between the training set and test set

	training set			test set
RMSD	top 1	top 3	top 10	top 1	top 3	top 10
< 1Å	20.0%	23.3%	36.7%	16.5%	28.5%	45.5%
< 2Å	50.0%	70.0%	86.7%	39.0%	56.5%	72.5%
< 3Å	63.3%	76.7%	90.0%	47.0%	68.5%	81.5%