Survival prediction algorithms for COVID‐19 patients admitted to a UK district general hospital

Abstract

Objective

To collect and review data from consecutive patients admitted to Queen’s Hospital, Burton on Trent for treatment of Covid‐19 infection, with the aim of developing a predictive algorithm that can help identify those patients likely to survive.

Design

Consecutive patient data were collected from all admissions to hospital for treatment of Covid‐19. Data were manually extracted from the electronic patient record for statistical analysis.

Results

Data, including outcome data (discharged alive/died), were extracted for 487 consecutive patients, admitted for treatment. Overall, patients who died were older, had very significantly lower Oxygen saturation (SpO2) on admission, required a higher inspired Oxygen concentration (IpO2) and higher CRP as evidenced by a Bonferroni‐corrected (P < 0.0056). Evaluated individually, platelets and lymphocyte count were not statistically significant but when used in a logistic regression to develop a predictive score, platelet count did add predictive value. The 5‐parameter prediction algorithm we developed was:

$$P_{\left(\text{death}\right)}=\frac{1}{1+e^{‐1(‐22.8449+4.1124\text{LN}(\text{age})+2.0421\text{LN}(\text{IpO}2)+0.2770\text{LN}(\text{CRP})‐0.7738\text{LN}(\text{Plt})+0.7625\#\text{consolidated}\_\text{lungs})}}$$

Conclusion

Age, IpO2 on admission, CRP, platelets and number of lungs consolidated were effective marker combinations that helped identify patients who would be likely to survive. The AUC under the ROC Plot was 0.8129 (95% confidence interval 0.0.773 ‐ 0.853; P < .001).

What’s known

• Covid‐19 is a novel viral infection that causes a significant risk of death in those patients who need hospital treatment.

• Many prediction algorithms have already been written but more data are required to further improve algorithm performance.

What’s new

• We have developed a survival prediction algorithm that uses admission blood results, and two clinical factors to identify risk of death from Covid‐19.

• We used data from a single location to remove the confounding effects of different policies in different healthcare systems.

1. INTRODUCTION

SARS‐CoV‐2 (Covid‐19) is a novel coronaviral infection that emerged in Wuhan, China in December 2019. The clinical characteristics showed that disease severity was linked to age (mean age of non‐severe cases 45.0, compared with severe cases, 52.0 years). ¹ Of these only a small proportion developed the primary composite endpoint (admission to ICU, use of mechanical ventilation or death).

By 5th August 2020, the UK had 306 000 confirmed cases and 46 299 deaths. Of these, 27 361 cases were in the West Midlands and 23 770 were in the East Midlands (https://www.statista.com/statistics/1102151/coronavirus‐cases‐by‐region‐in‐the‐uk/). Queen’s Hospital, Burton on Trent is a hospital in the University Hospitals of Derby and Burton NHS Foundation Trust. Queen’s Hospital is in the west Midlands and Derby is in the East Midlands. Internal hospital reports show that for the UHDB Trust, between March 20th and 2nd August 1687, patients have been admitted for treatment of Covid‐19, of whom 1163 have been discharged alive and 524 have died. This gives a large potential dataset that allows evaluation of factors that may allow prediction of those patients who will be likely to survive.

A large number of prediction algorithms have already been described ² but of those reported, only one reported study deals with prediction of hospital mortality in patients from the UK, but that UK data are combined with data from China. ³ That report was based on 653 patients of whom the outcome was known in just 58 patients. We also note a BMJ Editorial that stated that all models are wrong but better reporting and data sharing could improve this. ⁴ Therefore, we reviewed the case notes of patients with known outcomes seen at Queen’s Hospital Burton (QHB). To ensure consistency of data collection, only QHB data were used because the UHDB Trust has only been recently formed by merger of two individual Trusts and the two parts of the group use different patient records software. We then identified an algorithm that may help to predict which patients will survive Covid‐19 infection, based on their initial investigation results.

2. METHODS

Data were manually extracted from the Meditech hospital computer system for 487 consecutive patient admissions for Covid‐19 infection at Queen’s Hospital, Burton‐on‐Trent, UK into an excel spreadsheet. Anonymised data were used for this evaluation project.

We carried out two rounds of algorithm development. The first was based on laboratory data only and the second included clinical information.

2.1. Statistical analysis

2.1.1. First analysis round

Demographics (Age, gender, ethnicity) and Initial investigation results (Oxygen saturation on admission (SpO2), platelets, total white cell count, neutrophil count, lymphocyte count, CRP, ALT, ALP bilirubin and d‐Dimers) were collated and since the data were not normally distributed, statistical analysis was non‐parametric using the Mann‐Whitney rank test for unpaired data (http://vassarstats.net/index.html). Due to the multiple possible correlations for each set of blood results, a Bonferroni correction was used (to P < .0056) for blood results. For age and initial SpO2, the standard threshold (P < .05) was used.

Gender, ethnicity, ALT, ALP, bilirubin and d‐dimers were all excluded from further analysis because Mann‐Whitney statistic showed there were no significant differences between those who survived and those who died.

Multivariate logistic regression of age, admission SpO2, admission CRP, admission platelets and admission lymphocytes (X variables) against survival (0)/death (1) (Y variable) was carried out using an internet calculator (http://stats.blue/Stats_Suite/logistic_regression_calculator.html), and IBM SPSS. Platelets and lymphocytes were included in this analysis because although they were non‐significant using the Bonferroni corrected P threshold, they met the standard significance threshold, and because the stepwise logistic regression process assesses whether data are significant or not for the regression and non‐significant contributors are excluded. Lymphocytes were then excluded because they were shown to be non‐significant in the logistic regression, leading to a 4‐parameter regression model.

2.1.2. Second analysis round

Data used in the first analysis round were supplemented by clinical data on Inspired O2 concentration required by the patient on admission [IpO2] (Room air (20%)/24%/28%/35%/40%/60%), number of lungs showing consolidation by X‐ray (0/1/2), comorbidities (obesity, COPD, hypertension, Ischaemic heart disease) and prior use of ACE inhibitors or ACE receptor blocking drugs. Only IpO2 was shown to be significant.

A 6‐parameter multivariate logistic regression of age, admission SpO2, admission IpO2, admission CRP, admission platelets and number of consolidated lungs (X variables) against survival (0)/death (1) (Y variable) was carried out. This revealed that SpO2 was no longer significant so it was excluded in the final 5‐parameter regression.

In both stages of data analysis, logistic regression was attempted using a variety of different normalisation transforms (Square root, inverse, and logarithm) for all variables and the transform that worked best for each analyte was used for the final version of the algorithm. For age, SpO2, IpO2, platelets and CRP, the appropriate transform was the natural logarithm.

2.1.3. Model validation

The second regression model gave a significantly greater area under the ROC curve. Therefore, validation analysis was carried out only on the 5‐parameter regression model. This analysis was carried out by boot‐strapping using 20 replicates. For each replicate, the data were separated into two roughly equal groups (regression and validation) by assigning a random number (0‐1) to each row of data, with values <0.5 assigning the data to the regression group and ≥0.5, to the validation group. The data were then regressed using a 5‐parameter model and the AUC was estimated using the validation data.

2.2. Ethical review

Data were collected retrospectively, and the study had no impact on the care of the patient during their admission. Furthermore, it was anonymised before statistical analysis. This met the definition of service evaluation and therefore did not require review by a research ethics committee (http://www.hra‐decisiontools.org.uk/research/).

3. RESULTS

After exclusion of patients for whom the full dataset was not available, there were 166 patients who had died and 250 who had survived whose data were used to derive the 4‐parameter prediction algorithm (416 patients in total). During the collation of the extra clinical data, nine extra sets of patient data were collected resulting in 259 patients who had survived and 166 who had died being used for the second analysis round (425 patients in total).

Ethnicity was not shown to be significant but this may be due to the population distribution (88.6% white, 2.26% Indian sub‐continent, 0.4% Black, 9.97% unspecified).

Table 1 shows ages and initial blood results for patients who left the hospital alive, and those who died with the two‐tailed P value for difference. Overall, patients who died were older, had very significantly lower SpO2 on admission and higher CRP. No other differences met Bonferroni‐corrected statistical significance. Platelets and lymphocyte counts did meet the “standard” statistical significance threshold of P < .05.

TABLE 1.

Admission blood results

		Mean ± SD	Median	IQR	Mann‐Whitney two‐tailed P
Age (years)	Dead	79.2 ± 10.9	82	74‐87	<.0001
	Alive	70.1 ± 17.3	74	59‐84
Adm SpO2 (%)	Dead	91.6 ± 11.8	94	91‐96	.0044
	Alive	94.2 ± 6.6	95	93‐97
Platelets (×109/L)	Dead	203.1 ± 88.5	188	142.5‐245	.0232 (NS)
	Alive	225.8 ± 106.4	208	161.25‐264
WCC (×109/L)	Dead	9.04 ± 4.98	7.7	5.5‐10.95	.3524 (NS)
	Alive	8.59 ± 4.61	7.7	5.3‐10.8
Neutrophils (×109/L)	Dead	7.34 ± 4.64	6.2	4.15‐9.15	.0588 (NS)
	Alive	6.57 ± 4.29	5.7	3.5‐8.33
Lymphocytes (×109/L)	Dead	1.07 ± 1.05	0.9	0.6‐1.3	.0074 (NS)
	Alive	1.19 ± 0.85	1	0.7‐1.5
CRP (mg/L)	Dead	116.0 ± 100.4	91	38‐167	<.0001
	Alive	80.0 ± 91.1	52	16‐108
ALT (IU/L)	Alive	37.6 ± 108.8	19	13‐30	.4413 (NS)
	Dead	31.6 ± 37.9	21	13‐36
ALP (IU/L)	Dead	116.6 ± 140.1	87	66‐121.5	.6818 (NS)
	Alive	111.3 ± 151.4	82	67‐112
Bilirubin (μmol/L)	Dead	12.7 ± 10.57	10	6‐15	.0151 (NS)
	Alive	10.1 ± 8.69	8	6‐12
d‐Dimer (μg/L)	Dead	2768 ± 6920.0	565.5	315.5‐1022.7	.246 (NS)
	Alive	1348 ± 2390.1	406	256‐793

For blood test results, Bonferroni‐corrected P threshold = .0056. For age and SpO2, P < .05 was treated as significant.

Abbreviation: NS, not significant.

Table 2 shows the blood results after 6 days. In the patients who died, the platelets, neutrophils and CRP were statistically significantly higher. Further analysis of blood results of patients for whom paired data at days 0 and 6 were available did not reveal any significant differences in the changes in results between the dead and alive groups (data not shown).

TABLE 2.

Day 6 blood results

		Mean ± SD	Median	IQR	Mann‐Whitney two‐tailed P
Platelets (×109/L)	Dead	229.3 ± 124.5	211.5	143.5‐285.5	.0034
	Alive	268.7 ± 138.4	249	170.3‐329.8
WCC (×109/L)	Dead	10.2 ± 5.8	8.9	6.3‐12.8	.0078 (NS)
	Alive	8.47 ± 5.15	7.9	5.5‐10
Neutrophils (×109/L)	Dead	8.42 ± 5.20	7.8	4.7‐10.2	.0004
	Alive	6.52 ± 5.03	5.5	3.8‐8.0
Lymphocytes (×109/L)	Dead	1.051 ± 0.91	0.8	0.5‐1.3	.0588 (NS)
	Alive	1.07 ± 0.52	1.0	0.7‐1.3
CRP (mg/L)	Dead	151.2 ± 121.9	128.5	56‐208.3	<.0001
	Alive	90.2 ± 100.0	57	20‐117
ALT (IU/L)	Dead	68.2 ± 151.4	26	16‐33	.7642 (NS)
	Alive	44.0 ± 40.0	25	18.5‐62.5
ALP (IU/L)	Dead	171.2 ± 163.6	137	82.8‐179.8	.385 (NS)
	Alive	117.8 ± 85.3	100	68‐124
Bilirubin (μmol/L)	Dead	26.8 ± 42.2	11	6‐25.8	.3222 (NS)
	Alive	20.8 ± 40.6	8	6‐14
d‐Dimer (μg/L)	Dead	5931 ± 3661	5841.5	3012‐9074.8	.101 (NS)
	Alive	2881 ± 3015	2119	394.2‐4919.2

For blood test results, Bonferroni‐corrected P threshold = .0056. For age and SpO2, P < .05 was treated as significant.

Abbreviation: NS, not significant.

After testing different transforms in the first data analysis round, it was found that optimum normalisation was achieved using the natural logarithm of all X variables. On the first pass of the logistic regression using normalised variables, Age, SpO2, CRP and platelet count were statistically significant contributors but lymphocyte count was shown to be non‐significant (P = .435), so a second pass excluding lymphocytes was completed. This gave the following prediction algorithm, which was statistically significant (Goodness of fit by Hosmer and Lemeshow Test P = .018).

3.1. 4‐parameter dataset

$$P_{\left(\text{survival}\right)}=\frac{1}{1+e^{‐1(‐16.7104‐3.3810\text{LN(age)}+6.\text{5592LN(SpO2)}‐0.\text{4584LN(CRP)}+0.\text{7183LN(Plt)})}}$$

where LN is natural logarithm.

For this 4‐parameter algorithm, the ROC curve AUC was 0.737 (95% Conf. Interval 0.689‐0.784; P < .001).

In the second data analysis round, IpO2 was shown to be statistically significant but this rendered SpO2 non‐significant (P0.3913), so it was excluded. The resultant algorithm was as follows:

3.2. 5‐parameter dataset

$$P_{(\text{death})}=\frac{1}{1+e^{‐1(‐22.8449+4.\text{1124LN(age)}+2.0\text{421LN(IpO2)}+0.2770\text{LN(CRP)}‐0.\text{7738LN(Plt)}+0.7625\#\text{consolidated}\_\text{lungs})}}$$

For this 5 ‐parameter algorithm, the ROC curve AUC was 0.8129 (95% Conf. Interval 0.0.773‐0.853; P < .001). The difference between the AUCs for the 4‐parameter and 5‐parameter curves was tested (www.vassarstats.net/roc_comp.html) and was shown to be significant (P = .021 two‐tailed).

Table 3 shows the coefficients and AUC estimated using the full 5‐parameter dataset, and the mean ± SD derived from the 20 replicates of split regression/validation datasets. The deviation of the full dataset coefficient from the mean of the split dataset means was evaluated by calculating the number of standard deviations between them (Z score). In all cases, the Z score was < ± 0.4 indicating no statistically significant difference.

TABLE 3.

Coefficients from full dataset and split datasets for 5‐parameter model

Coefficient	Full dataset	Split dataset (Mean ± SD)	Z
β 0 (intercept)	−22.8449	−23.0442 ± 3.645276	0.054669
β 1 (Age)	4.1124	4.086625 ± 0.649164	0.039705
β 2 (IpO2)	2.0421	2.169965 ± 0.340298	−0.37574
β 3 (CRP)	0.277	0.291305 ± 0.123649	−0.11569
β 4 (Plt)	−0.7738	−0.8149 ± 0.312639	0.131462
β 5 (#consolidated)	0.7625	0.78894 ± 0.172615	−0.15317
AUC	0.817392	0.800234 ± 0.018473

Figure 1 shows a ROC plot for the 4‐ and 5‐parameter prediction algorithms.

FIGURE 1.

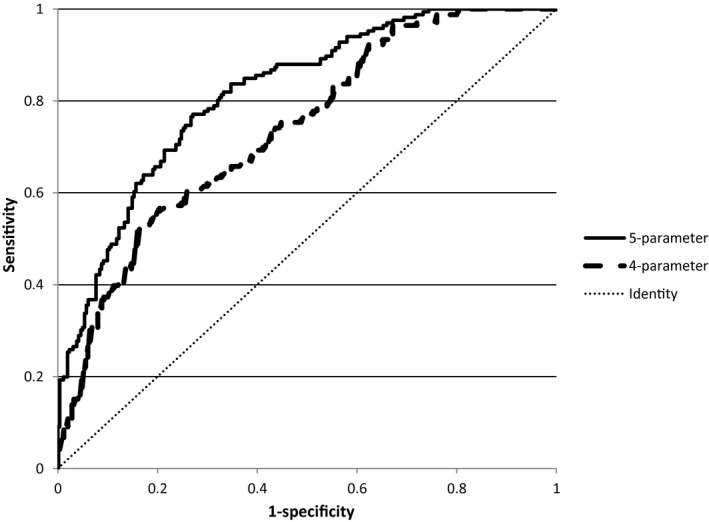
ROC plot for 4‐parameter algorithm [AUC = 0.737 (95% confidence interval 0.689‐0.784; P < .001)] and 5‐parameter algorithm [AUC 0.8129 (95% confidence interval 0.0.773‐0.853; P < .001)]

4. DISCUSSION

Covid‐19 represents a new threat to health and we are still learning to deal with it. The only way to improve our knowledge about how to deal with this threat quickly is to share the data we have as openly and rapidly as possible. ⁴ A large number of algorithms evaluating Covid‐19 patients have already been published but we were unable to identify any that use admission data from a single source to predict outcome. Furthermore, many algorithms used data from multiple centres in different countries which may have significantly different healthcare systems.

The two algorithms we have developed use parameters that have been reported to work in other predictive algorithms ² but only use four parameters (Age, Admission SpO2, CRP and platelet count) or five parameters (age, admission inspired pO2, CRP, platelet count and number of consolidated lungs) because other data that we evaluated were shown not to have significant differences between those who survived admission for Covid‐19, and those who did not. All of the parameters used are simple tests that should be available within 60‐90 minutes of arrival at hospital. The importance of having a tool that helps predict survival is that it can also be used to predict which patients may need more complex interventions to assist them, that is, patients with a lower survival probability may benefit from earlier consideration for intensive care.

There are clearly limitations to the data we have presented.

• Our dataset is relatively small (416 patients, of whom 166 died) but represents the total data available from the first wave of Coronavirus patients passing through our doors, so is as complete a dataset as we can collect.

• We were unable to get data from any independent source to verify the algorithm but boot‐strapping analysis shows that the overall estimate for the better 5‐parameter algorithm are robust.

• The population served by our hospital is predominantly white British, so data on other ethnicities were too limited to be useful.

Despite the limitations, our 5‐parameter model has similar effectiveness to other published algorithms:

The PANDEMYC score ⁵ based on 1104 cases, of whom 325 died had an AUC of 0.808 in its validation samples, which is comparable to the AUC of 0.80 that we had in our boot‐strapping validation stage. The score used nine key features: age, oxygen saturation, smoking, serum creatinine, lymphocytes, haemoglobin, platelets, C‐reactive protein and sodium at admission to create a risk score (approximate range 100‐400) to estimate a probability of death.

The Italian score ⁶ based on 516 patients, of whom 120 died had an AUC of 0.9. The score used six features: age, No of comorbidities, breathing rate (breaths/minute), PaO2/FiO2 ratio, creatinine and platelets to generate a score (range 6‐18) to estimate probability of death, with patients being grouped into three cohorts: low, intermediate and high risk.

Another study ⁷ has reviewed the effectiveness of 22 published algorithms by testing them against a dataset of 411 patients. This showed that oxygen saturation was an important discriminatory factor in predicting survival or in‐hospital deterioration.

We note that our dataset and the other datasets described above are all relatively small. We would be very happy to share our data with any other researcher to allow the development of better clinical tools for survival prediction. Also, having derived our algorithm during the first wave of the epidemic, further studies to identify whether survival is improved in second and subsequent waves would be very useful.

5. CONCLUSION

We have developed an algorithm to predict the probability of survival/death from Covid‐19 in patients admitted to a single UK District General Hospital. We recognise that our algorithm is “wrong” because it is based on a particular set of data which has the inherent assumptions of the UK healthcare system and local factors that may influence the way that treatment, including escalation/de‐escalation to critical care, is provided ⁴ or may make our population less representative of the populations elsewhere (ethnic diversity, test frequency, etc.). Thus, our result may not be directly translatable to other health systems where the threshold for hospital admission may be lower. In that situation, our estimate could be excessively pessimistic. Similarly, in systems where admission to hospital is less easy than in the UK, our estimate may be too optimistic. It may not even be translatable to other hospitals in the UK, but regardless of how precise the estimates it makes, it may provide useful prognostic information to admitting teams and does provide a baseline against which other algorithms can be compared.

DISCLOSURES

TMR is currently in the receipt of project grants from Genzyme Therapeutics, Oxford, UK (now Sanofi Genzyme, Oxford, UK); Shire Pharmaceuticals, Basingstoke, UK, now Takeda Pharmaceutical Ltd; and Synageva BioPharma, Watford, UK (now Alexion Pharma UK, Uxbridge, UK).

AUTHOR CONTRIBUTIONS

Data Collection: AF/AH/JK. Statistical Analysis: TR. Paper writing/Approval: AF/AN/NO/TR.

Fernandez A, Obiechina N, Koh J, Hong A, Nandi A, Reynolds TM. Survival prediction algorithms for COVID‐19 patients admitted to a UK district general hospital. Int J Clin Pract. 2021;75:e13974. 10.1111/ijcp.13974

DATA AVAILABILITY STATEMENT

All data available from the authors and has been uploaded as supplemental files with this submission.