Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Feb 3;125(5):2918–2925. doi: 10.1021/acs.jpcc.0c09062

Going beyond Pentacene: Photoemission Tomography of a Heptacene Monolayer on Ag(110)

Marie S Sättele †,‡, Andreas Windischbacher §, Larissa Egger §, Anja Haags ∥,⊥,#, Philipp Hurdax §, Hans Kirschner ∇, Alexander Gottwald ∇, Mathias Richter ∇, François C Bocquet ∥,⊥, Serguei Soubatch ∥,⊥, F Stefan Tautz ∥,⊥,#, Holger F Bettinger ‡, Heiko Peisert †, Thomas Chassé †, Michael G Ramsey §, Peter Puschnig §, Georg Koller §,*
PMCID: PMC7883341  PMID: 33603943

Abstract

graphic file with name jp0c09062_0007.jpg

Longer acenes such as heptacene are promising candidates for optoelectronic applications but are unstable in their bulk structure as they tend to dimerize. This makes the growth of well-defined monolayers and films problematic. In this article, we report the successful preparation of a highly oriented monolayer of heptacene on Ag(110) by thermal cycloreversion of diheptacenes. In a combined effort of angle-resolved photoemission spectroscopy and density functional theory (DFT) calculations, we characterize the electronic and structural properties of the molecule on the surface in detail. Our investigations allow us to unambiguously confirm the successful fabrication of a highly oriented complete monolayer of heptacene and to describe its electronic structure. By comparing experimental momentum maps of photoemission from frontier orbitals of heptacene and pentacene, we shed light on differences between these two acenes regarding their molecular orientation and energy-level alignment on the metal surfaces.

Introduction

π-Conjugated molecules have gained a crucial role in the development of organic electronic technologies. Among compounds that have attracted ongoing interest is the class of acenes, i.e., polycyclic aromatic hydrocarbons consisting of n linearly fused benzene rings, which we are going to notate as nA in the following. Here, the commercially available tetracene (4A, n = 4) and pentacene (5A, n = 5) are the most prominent members, which have been studied extensively over the years.1,2 Longer acenes are attractive due to their narrow band gap between the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO, respectively),3 low reorganization energy,4 and high charge carrier mobility.5 These optical and electronic properties strongly depend on the number of benzene units and can thus be tuned by the number of fused rings.6,7 More importantly, longer acenes may serve as the atomically precise model systems for the narrowest possible zigzag-edge graphene nanoribbons with potential applications in spintronics and plasmonics.8,9 However, the experimental study and application of acenes longer than 5A have so far been limited by their poor solubility and their pronounced tendency toward degradation,10−12 making synthesis and handling under conventional conditions difficult. Carried out within a solid matrix, the production of acenes from hexacene upwards has been demonstrated.3,13−15 In the last decade, on-surface synthesis has been established as an alternative approach toward the generation of compounds hard to access otherwise.16−19 Linear acenes up to dodecacene20−26 have recently been generated in this way, but on-surface synthesis of acenes is mainly restricted to submonolayer coverages on crystalline surfaces. The largest acene, for which film formation on crystalline surfaces was achieved and adequately characterized, is hexacene.27,28 Its next higher neighbor heptacene 3 can be obtained from thermally induced cycloreversion of a D2h symmetrical 1 and a Cs symmetrical 2 diheptacene isomer mixture (Scheme 1), which can be synthesized via a modified Meerwein–Ponndorf–Verley (MPV) reduction29 (cf. Supporting Information (SI)). It was shown that thermolysis of the diheptacene (D7A) mixture results in sublimation of 7A, and it was suggested that this may enable the deposition of 7A films on various substrates via organic vapor deposition under ultrahigh-vacuum conditions.29 To date, however, heptacene (7A) monolayers on monocrystalline surfaces have never been reported.

Scheme 1. Synthesis of Heptacene (7A) by Thermal Cycloreversion of Diheptacenes (D7A).

Scheme 1

Open in a new tab

1 and 2 denote D2h symmetrical and Cs symmetrical D7A, respectively; 3 denotes 7A.

In general, applications in organic-based electronic devices rely on well-defined interfaces between organic films and inorganic substrates and on a detailed knowledge of the electronic structure at the interface,30 which can be acquired by angle-resolved photoemission experiments (ARPES), in particular using photoemission tomography (PT).31,32 The momentum maps of photoemission, i.e., intensity of photoemission as a function of kx, ky at fixed binding energy (Eb), reflect the square of the Fourier transform of the molecular orbitals, from which the electrons were emitted.33 Thus, they allow not only the emissions to be assigned to particular orbitals but also the identification of molecules and their orientation on the surface.34,100 Here, we have applied PT to confirm that indeed a well-oriented 7A monolayer can be grown on Ag(110) via thermal evaporation from D7A powder. This allows us to investigate the adsorption geometry of the prepared monolayer and orbital structure of 7A in great detail.

Methods

Sample preparation and photoemission experiments were conducted in an ultrahigh-vacuum vessel (10–10 mbar). The Ag(110) substrate was prepared by cycles of sputtering (Ar+ ions at 1 kV) and annealing (450 °C). Diheptacene loaded into a Knudsen-type molecular evaporator decomposed at 300 °C, resulting in molecular heptacene evaporating in vacuum and adsorbing on Ag(110) located in front of the evaporator and kept at room temperature. The molecular flux of heptacene was calibrated using a quartz microbalance. Photoemission experiments were performed at the Metrology Light Source of the Physikalisch-Technische Bundesanstalt (Berlin, Germany) at the insertion device beamline using a toroidal electron-energy analyzer.35 A photon energy of 35 eV and an incidence angle of χ = 40° with respect to the surface normal were used. The light polarization direction is in the specular plane. The toroidal analyser registers the photoelectrons with trajectories in this plane and for emission angles of ±80° with respect to the surface normal. To measure the momentum maps at chosen binding energies, the sample was rotated in the azimuthal direction in 2° steps, which results in a full photoelectron distribution in the (kx, ky) plane perpendicular to the sample normal. The energy distribution curves (EDC) were obtained by integration of photoemission intensity over the available k∥ range in forward emission.

All calculations were performed within the framework of density functional theory (DFT) using the Vienna Ab Initio Simulation Package (VASP) version 5.4.4.36,37 Exchange–correlation effects were described by the functional of Perdew–Burke–Ernzerhof (PBE)38 and van der Waals contributions treated with the D3 dispersion correction.39 We utilized the projector augmented wave (PAW) method40 together with an energy cutoff of 400 eV. The ionic positions of all structures were optimized within 10–6 eV with a Gaussian smearing of 0.01 eV. We performed two types of calculations: first for the isolated heptacene molecule and its most stable dimer41 and second for a monolayer of heptacene on Ag(110). The isolated molecules were simulated in supercells with a minimum of 15 Å vacuum between periodic replicas. To model the monolayer of 7A on Ag(110), two orthogonal unit cells containing 7A oriented either along or across the close-packed Ag rows have been considered (cf. SI p. 4ff). The unit cell with the long axis of 7A along the [001] is based on the experimentally observed low-energy electron diffraction (LEED) structure of 5A on Ag(110),42 while the unit cell in which 7A lies along the [11̅0] direction was adapted from the experimental LEED structure of 4A on Ag(110).43 The surface is simulated within the repeated-slab approach using five metallic layers and a 30 Å vacuum layer. To avoid spurious electrical fields, a dipole layer is inserted in the vacuum region.44 The structure is optimized on a Monkhorst–Pack 5 × 2 × 1 grid of k-points constraining the coordinates of the two bottom Ag layers of the slab.45 Subsequent to the geometry relaxation, the Kohn–Sham energies and orbitals are calculated non-self-consistently on a denser k-point mesh of 12 × 5 × 3, which is required for the simulation of the photoemission data. The momentum maps of photoemission intensity are calculated within the one-step model of photoemission46 approximating the final state as a plane wave,42 modified by an exponential damping factor introduced between the substrate and the organic molecule to mimic the mean free path of the photoemitted electrons.47

Results and Discussion

Using a Knudsen-type molecular evaporator, we have deposited heptacene onto the Ag(110) surface, which was kept at room temperature. Figure 1a shows the momentum map of emission from a molecular state located ∼0.8 eV below the Fermi level, namely, the HOMO of 7A, as will be unambiguously identified below. As a start, we compare the experimental momentum maps to the theoretical ones simulated for the HOMOs of isolated heptacene molecules as a superposition of two perpendicular orientations (Figure 1b). The simulated momentum maps of the HOMOs for a single orientation of 7A and the D2h symmetrical diheptacene molecule 1 (D7A, Scheme 1) are shown in Figure 1c,d, respectively.

Figure 1.

Figure 1

Open in a new tab

(a) Experimental momentum map of 7A/Ag(110) measured at a binding energy of 0.85 eV. (b) Simulated momentum map of the HOMO emission of two isolated heptacene molecules as a superposition of two perpendicular orientations, with a 1:1 ratio. (c) Simulated momentum map of the HOMO emission for a single heptacene orientation. (d) Simulated momentum map of the HOMO emission of a single D7A molecule (1). Note that y is parallel to the long molecular axis.

The simulated HOMO map of 7A is characterized by four major lobes similar to HOMOs of other acenes (e.g., tetracene48 and pentacene42). In contrast, the map of D7A shows a splitting of the major lobes of the HOMO emission, which leads to four major lobes with much lower ky values than for 7A and additional minor lobes (Figure 1d). Such a splitting originates from the breaking of the extended π-conjugated system into two smaller π subsystems (one per each 7A moiety of D7A), due to the formation of C–C single bonds. However, no such splitting is observed in the experimental momentum map in Figure 1b (and the experimental maps of other molecular emissions; see below). Instead, the k-positions of the photoemission lobes (Figure 1a) perfectly agree with those of the simulated momentum map of the 7A HOMO (Figure 1c), which confirms the formation of 7A molecules on Ag(110). Moreover, as PT is an area-averaging technique, we measure the accumulated photoemission response of an ensemble of molecules on a macroscopic scale proving high reaction yield. The quality of the experimental momentum map demonstrates the chemical purity of our synthesized 7A. However, a closer look at the experimental momentum map of Figure 1a reveals a peculiar star-shaped structure of the emission pattern, instead of the elongated features expected from the simulated HOMO of 7A. Such a shape can be rationalized by superimposing HOMO maps for two different orientations rotated by 90° with respect to each other. Note that the coexistence of two different adsorption configurations, i.e., orientation along both principal azimuths [11̅0] and [001], has been reported for shorter acenes on Ag(110) earlier.48,49 Closer inspection reveals that the orientation of 7A along [11̅0] and [001] in a ratio of 3:1 yields the best agreement with the experiment (cf. SI Figure S8), which is demonstrated by the corresponding simulated map in Figure 1b. After clarifying the chemical nature and geometrical structure of the adsorbate layer, we want to analyze its electronic properties in more detail. To this end, we have recorded energy distribution maps (band maps, i.e., photoemission intensity vs (Eb, kII)) for two different orientations of the sample ([11̅0] and [100] + 45°; cf. combined band map in Figure 2a).

Figure 2.

Figure 2

Open in a new tab

(a) Energy distribution map (band map) in [100] + 45° → Γ and Γ → [11̅0] directions; the white circles and crosses mark the binding energies with respect to Fermi energy at which momentum maps have been recorded. (b) Energy distribution curve obtained by integration of photoemission intensity of (a). (c) MOPDOS calculated for 7A/Ag(110). Red: orbitals of the apex band; blue: orbitals of the linking band.

We have chosen these directions due to the nodal symmetry of the orbitals and molecular orientation on the surface; the LUMO and HOMO-3 of 7A have their maximal emission intensities in the [11̅0] direction, and the HOMO, HOMO-1, and HOMO-2 in the [100] + 45° direction. Molecular emissions observed in experiment along these directions are marked with white symbols in Figure 2a.

Note that the π-orbitals of planar organic molecules derived from pz-states of carbon atoms can be assigned to different π-bands of intra-molecular dispersion depending on their symmetry, i.e., nodal structure (cf. SI).50 The symmetry of the orbital nodal structure in real space is reflected in reciprocal space. The π-band lowest in energy consists of orbitals concentrated at the linking and terminal carbon pairs and will further be denoted as the linking band. The π-band next in energy consists of orbitals from the pairs of apex carbons (apex band) and features a characteristic node along the long molecular axis.

The photoemission features of 7A in Figure 2a can accordingly be assigned to these π-bands. To do so, we, first, compare the energy distribution curve (EDC) in Figure 2b with DFT results for a 7A monolayer on Ag(110). For comparison, we have computed the density of states projected onto the molecular orbitals (MOPDOS) (Figure 2c). From the MOPDOS in Figure 2c, we also expect to observe several molecular emissions in the energy range from the Fermi level to the onset of the d-band of silver. The calculation also suggests at least partial filling of the former LUMO of 7A. Indeed, the corresponding emission feature in the experimental band map is clearly observed below the Fermi energy. Note that after including the Hartree–Fock exchange in the exchange–correlation functional (cf. SI), the computed molecular states shift toward higher binding energies, thereby increasing the agreement with experimental results. Emissions attributed to orbitals of the linking band are colored in red; those belonging to the apex band are in blue.

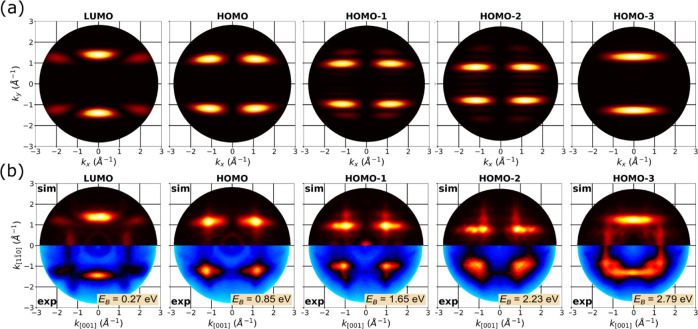
To definitively assign the photoemission features in Figure 2a,b to populated molecular orbitals of 7A, we have measured and simulated momentum maps at the binding energies marked in Figure 2a. Figure 3a shows the simulated momentum maps for an isolated heptacene molecule. In Figure 3b, the experimental maps (lower halves) are compared to theoretical momentum maps simulated for the complete 7A/Ag(110) interface (upper halves) at the binding energies corresponding to the respective peaks in the MOPDOS (Figure 2c). To mimic the experimental situation, the simulated maps are taken as a superposition of maps calculated for two heptacene orientations, along and across the silver rows in a ratio of 3:1 (see the discussion above). The agreement between experimental and simulated maps allows us to unambiguously identify five molecular emissions within a small energy window from the Fermi edge to the d-band of silver. In particular, we observe a population of the LUMO, which peaks at 0.4 eV below the Fermi edge. Note that strong interactions between metal surfaces and organic molecules may change the electronic structure of the molecule at the interface, resulting in charge transfer from the metal into the molecule, which results in a population of the formerly unoccupied molecular states. We note that also the profile of the C1s core-level spectrum measured for 7A/Ag(110) (cf. SI) indicates a redistribution of electrons at the interface presumably due to charge transfer from metal to the molecule.

Figure 3.

Figure 3

Open in a new tab

(a) Simulated photoemission momentum maps of the π-orbitals for an isolated heptacene molecule. (b) Comparison of simulated (sim) and experimental (exp) photoemission momentum maps of the π-orbitals. Note that the simulated maps are superpositions of two distinct heptacene/Ag(110) azimuthal orientations in the monolayer, [11̅0] and [001], with a weighting ratio of 3:1.

At first glance, the HOMO, HOMO-1, and HOMO-2 of 7A have similar emission patterns. However, they can clearly be distinguished as their intensity maxima appear at different k-values. The HOMO has a maximum at k∥ = 1.7 Å–1, HOMO-1 at k∥ = 1.6 Å–1, and HOMO-2 at k∥ = 1.5 Å–1, which is a direct consequence of the decreasing number of nodes along the long molecular axis. Following the orbitals, their measured momentum maps can also be assigned to the corresponding π-bands: LUMO and HOMO-3 belong to the linking band, while HOMO, HOMO-1, and HOMO-2 have the characteristic node along the molecular axis and thus belong to the apex band (see the color code in Figures 2c and 4).

Figure 4.

Figure 4

Open in a new tab

π-Orbitals of 5A and 7A separated in two different π-bands, linking band and apex band, according to their symmetry and the corresponding experimental momentum maps of 5A/Ag(110) and 7A/Ag(110). To plot molecular orbitals, isosurfaces 10% of the maximum electron density have been used.

It is important to note that, although ARPES is an area-averaging technique, we can exploit the angular dependence of the molecular emissions to shed light on differences in the electronic structure of 7A oriented parallel or perpendicular to the close-packed Ag rows. In case of 7A/Ag(110), this can be shown best for the LUMO emission. Scanning the binding energy close to the energy of LUMO maximum and looking at the corresponding momentum maps, one notes that the partial contribution of the two perpendicularly oriented molecules varies. Namely, the LUMO of 7A molecules aligned across the Ag rows, i.e., in the [001] direction, peaks at a binding energy of about 0.1 eV lower than the LUMO of those aligned along the Ag rows ([11̅0] direction). Deconvolution of the photoemission intensity I(E, kx, ky) datacube41 using two theoretical maps of the 7A LUMO of molecules oriented perpendicular to each other confirms this finding (cf. SI), pointing at slightly different occupations of the LUMO for those two species. Note that the energy difference derived from such deconvolution should be taken with care because of proximity to the Fermi edge. Nonetheless, we note that our DFT results for 7A molecules oriented along the [001] and [11̅0] directions on Ag(110) have also revealed a shift of 0.08 eV between corresponding LUMO energies (cf. SI), where the molecules oriented along [001] have the lower energy. This indicates that the adsorption site (orientation) has small but not negligible influence on the electronic interaction between 7A and Ag(110). It also demonstrates the ability of photoemission tomography to draw a link between binding energies of molecules and their geometric orientation.33,51−54

When comparing our results for 7A/Ag(110) with a previous PT study of 5A/Ag(110),42 one can clearly recognize strong similarities, which are expected since smaller acenes develop similar orbital structures owing to their common symmetry and topology. Despite the similarities, there are some interesting differences to discuss. Geometrically, the preferred orientations for 7A and 5A are different, with 7A lying predominantly along the Ag substrate rows, i.e., in [11̅0] orientation, while the preferred orientation of 5A molecules is across the Ag rows i.e., along [100] and thus rotated by 90°. This has been accounted for in Figure 4 to facilitate comparison.

Electronically, the LUMO of 7A adsorbed on Ag(110) appears fully occupied, while only partial LUMO occupation has been observed for 5A/Ag(110).42 This is expected taking into account the trend in the electron affinities, which, in the gas phase, increases from 1.01 eV for 5A to 1.57 eV for 7A.55 Moreover, the energy difference between the HOMO and LUMO for 7A has shrunk to only about 0.4 eV (cf. Figure 2b) compared to 1.3 eV for 5A. This is a result of the more extended aromatic system in 7A, which leads to a smaller energy spacing between electronic levels in 7A and correspondingly a reduction of the HOMO–LUMO gap. Additionally, increasing the length of the conjugated π-system leads to a reduction of the k-width of the features reflecting the number of scatterers in general. This can indeed be observed by comparing the LUMOs of 5A and 7A (Figure 4).

Finally, the overall number of π-orbitals is also increased when increasing the number of benzene units from 5A to 7A. While gas phase 5A features five occupied orbitals in the apex band and six orbitals in the linking band (cf. SI), the two additional rings of 7A give rise to four more orbitals in each band (two occupied and two unoccupied). We have measured and assigned all emissions of molecular π-states of 7A (Figure 4, right column) on Ag(110) and compared them to those of 5A (Figure 4, left column). For comparison, we also included the real space orbitals, which highlight the different nodal structures of the π-bands. The first observed patterns below the Fermi energy belong to the former LUMOs of 5A and 7A, respectively, which can be classified into the linking band. The next molecular state (and corresponding momentum map) of the same linking band is HOMO-3 in the case of 7A and HOMO-2 in the case of 5A. Framed by these orbitals of the linking band, the topmost orbitals of the apex band are observed. Note that for 5A, PT shows the HOMO and HOMO-1 in this energy window, while for 7A, three orbitals can be unambiguously distinguished: HOMO, HOMO-1, and HOMO-2 (vide supra).

Conclusions

To summarize, by combining ARPES experiments with ab initio electronic structure calculations, we have demonstrated the successful preparation of a well-defined monolayer of 7A on Ag(110) via organic vapor deposition. We have utilized the power of PT not only to clearly identify intact 7A molecules and their orientations on the surface but also to disentangle the electronic structure of the two prominent 7A adsorbate species, which differ in their azimuthal alignment on the Ag(110) substrate. We find the LUMO of 7A to be occupied upon charge transfer from the Ag(110) surface and we have further characterized the electronic structure within a binding energy window from the Fermi energy down to the d-band of silver, thereby identifying four more orbitals. As an outlook, succeeding in the growth of heptacene monolayers and, thus, understanding their interactions with metal contact interfaces is a prerequisite for possible applications in organic electronics. Moreover, the present results constitute a basis for future research on substituted heptacene derivatives exhibiting higher stability.

Acknowledgments

This work was funded by the Austrian Science Fund (FWF) I4145-N36 and I3731. The computations have been performed on the Vienna Scientific Computer (VSC) and the HPC facilities of the University of Graz. Financial support from the Deutsche Forschungsgemeinschaft (DFG), through projects BE 3183/4–2, Po 2226/2–1, Ri 804/8–1, GO 1812/2–1, and the SFB 1083 “Structure and Dynamics of Internal Interfaces” (projects A4, A12, and A13) is gratefully acknowledged. The authors thank Hendrik Kaser (PTB, Berlin) and John Riley (La Trobe, Australia) for the experimental support. They also thank Peter Grüninger for his preliminary work with longer acenes on crystalline surfaces that has been beneficial for these experiments.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.0c09062.

  • Synthesis of diheptacenes; Kohn–Sham orbitals assigned to the molecular π-bands of heptacene and pentacene in the gas phase; calculated adsorption configurations of heptacene on Ag(110); experimental EDCs compared to the density of states of heptacene/Ag(110) projected onto the molecular orbitals of a freestanding monolayer of heptacene for four different adsorption sites; deconvolution of the experimental photoemission intensity I(Eb, kx, ky) datacube with two theoretical maps of heptacene; and C 1s core-level spectra of monolayers of heptacene and pentacene on Ag(110) (PDF)

The authors declare no competing financial interest.

Notes

Raw data are available at the Jülich DATA public repository (https://doi.org/10.26165/JUELICH-DATA/D8GNJM).

Supplementary Material

jp0c09062_si_001.pdf (1,002.2KB, pdf)

References

  1. Anthony J. E. Functionalized acenes and heteroacenes for organic electronics. Chem. Rev. 2006, 106, 5028–5048. 10.1021/cr050966z. [DOI] [PubMed] [Google Scholar]
  2. Voz C.; Puigdollers J.; Martin I.; Muñoz D.; Orpella A.; Vetter M.; Alcubilla R. Optoelectronic devices based on evaporated pentacene films. Sol. Energy Mater. Sol. Cells 2005, 87, 567–573. 10.1016/j.solmat.2004.07.039. [DOI] [Google Scholar]
  3. Shen B.; Tatchen J.; Sánchez-García E.; Bettinger H. F. Evolution of the optical gap in the acene series: Undecacene. Angew. Chem., Int. Ed. 2018, 57, 10506–10509. 10.1002/anie.201802197. [DOI] [PubMed] [Google Scholar]
  4. Deng W. Q.; Goddard W. A. Predictions of hole mobilities in oligoacene organic semiconductors from quantum mechanical calculations. J. Phys. Chem. B 2004, 108, 8614–8621. 10.1021/jp0495848. [DOI] [Google Scholar]
  5. Cheng Y. C.; Silbey R. J.; da Silva D. A.; Calbert J. P.; Cornil J.; Brédas J. L. Three-dimensional band structure and bandlike mobility in oligoacene single crystals: A theoretical investigation. J. Chem. Phys. 2003, 118, 3764–3774. 10.1063/1.1539090. [DOI] [Google Scholar]
  6. Houk K. N.; Lee P. S.; Nendel M. Polyacene and cyclacene geometries and electronic structures: Bond equalization, vanishing band gaps, and triplet ground states contrast with polyacetylene. J. Org. Chem. 2001, 66, 5517–5521. 10.1021/jo010391f. [DOI] [PubMed] [Google Scholar]
  7. Brédas J.-L.; Beljonne D.; Coropceanu V.; Cornil J. Charge-transfer and energy-transfer processes in π-conjugated oligomers and polymers: A molecular picture. Chem. Rev. 2004, 104, 4971–5003. 10.1021/cr040084k. [DOI] [PubMed] [Google Scholar]
  8. Han W.; Kawakami R. K.; Gmitra M.; Fabian J. Graphene spintronics. Nat. Nanotechnol. 2014, 9, 794–807. 10.1038/nnano.2014.214. [DOI] [PubMed] [Google Scholar]
  9. Bursi L.; Calzolari A.; Corni S.; Molinari E. Light-induced field enhancement in nanoscale systems from first-principles: The case of polyacenes. ACS Photonics 2014, 1, 1049–1058. 10.1021/ph500269q. [DOI] [Google Scholar]
  10. Biermann D.; Schmidt W. Diels-Alder reactivity of polycyclic aromatic hydrocarbons. 1. Acenes and benzologs. J. Am. Chem. Soc. 1980, 102, 3163–3173. 10.1021/ja00529a046. [DOI] [Google Scholar]
  11. Schleyer P. V.; Manoharan M.; Jiao H. J.; Stahl F. The acenes: Is there a relationship between aromatic stabilization and reactivity?. Org. Lett. 2001, 3, 3643–3646. 10.1021/ol016553b. [DOI] [PubMed] [Google Scholar]
  12. Reddy A. R.; Fridman-Marueli G.; Bendikov M. Kinetic and thermodynamic stability of acenes: Theoretical study of nucleophilic and electrophilic addition. J. Org. Chem. 2007, 72, 51–61. 10.1021/jo061552o. [DOI] [PubMed] [Google Scholar]
  13. Mondal R.; Adhikari R. M.; Shah B. K.; Neckers D. C. Revisiting the stability of hexacenes. Org. Lett. 2007, 9, 2505–2508. 10.1021/ol0709376. [DOI] [PubMed] [Google Scholar]
  14. Mondal R.; Shah B. K.; Neckers D. C. Photogeneration of heptacene in a polymer matrix. J. Am. Chem. Soc. 2006, 128, 9612–9613. 10.1021/ja063823i. [DOI] [PubMed] [Google Scholar]
  15. Tönshoff C.; Bettinger H. F. Photogeneration of octacene and nonacene. Angew. Chem., Int. Ed. 2010, 49, 4125–4128. 10.1002/anie.200906355. [DOI] [PubMed] [Google Scholar]
  16. Cai J. M.; Ruffieux P.; Jaafar R.; Bieri M.; Braun T.; Blankenburg S.; Muoth M.; Seitsonen A. P.; Saleh M.; Feng X. L.; et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 2010, 466, 470–473. 10.1038/nature09211. [DOI] [PubMed] [Google Scholar]
  17. Otero G.; Biddau G.; Sánchez-Sánchez C.; Caillard R.; López M. F.; Rogero C.; Palomares F. J.; Cabello N.; Basanta M. A.; Ortega J.; et al. Fullerenes from aromatic precursors by surface-catalysed cyclodehydrogenation. Nature 2008, 454, 865–868. 10.1038/nature07193. [DOI] [PubMed] [Google Scholar]
  18. Grill L.; Dyer M.; Lafferentz L.; Persson M.; Peters M. V.; Hecht S. Nano-architectures by covalent assembly of molecular building blocks. Nat. Nanotechnol. 2007, 2, 687–691. 10.1038/nnano.2007.346. [DOI] [PubMed] [Google Scholar]
  19. Di Giovannantonio M.; El Garah M.; Lipton-Duffin J.; Meunier V.; Cardenas L.; Revurat Y. F.; Cossaro A.; Verdini A.; Perepichka D. F.; Rosei F.; et al. Insight into organometallic intermediate and its evolution to covalent bonding in surface-confined Ullmann polymerization. ACS Nano 2013, 7, 8190–8198. 10.1021/nn4035684. [DOI] [PubMed] [Google Scholar]
  20. Urgel J. I.; Mishra S.; Hayashi H.; Wilhelm J.; Pignedoli C. A.; Di Giovannantonio M.; Widmer R.; Yamashita M.; Hieda N.; Ruffieux P.; et al. On-surface light-induced generation of higher acenes and elucidation of their open-shell character. Nat. Commun. 2019, 10, 861 10.1038/s41467-019-08650-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zugermeier M.; Gruber M.; Schmid M.; Klein B. P.; Ruppenthal L.; Müller P.; Einholz R.; Hieringer W.; Berndt R.; Bettinger H. F.; et al. On-surface synthesis of heptacene and its interaction with a metal surface. Nanoscale 2017, 9, 12461–12469. 10.1039/C7NR04157H. [DOI] [PubMed] [Google Scholar]
  22. Krüger J.; García F.; Eisenhut F.; Skidin D.; Alonso J. M.; Guitián E.; Pérez D.; Cuniberti G.; Moresco F.; Peña D. Decacene: On-surface generation. Angew. Chem., Int. Ed. 2017, 56, 11945–11948. 10.1002/anie.201706156. [DOI] [PubMed] [Google Scholar]
  23. Zuzak R.; Dorel R.; Kolmer M.; Szymonski M.; Godlewski S.; Echavarren A. M. Higher acenes by on-surface dehydrogenation: From heptacene to undecacene. Angew. Chem., Int. Ed. 2018, 57, 10500–10505. 10.1002/anie.201802040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zuzak R.; Dorel R.; Krawiec M.; Such B.; Kolmer M.; Szymonski M.; Echavarren A. M.; Godlewski S. Nonacene generated by on-surface dehydrogenation. ACS Nano 2017, 11, 9321–9329. 10.1021/acsnano.7b04728. [DOI] [PubMed] [Google Scholar]
  25. Colazzo L.; Mohammed M. S. G.; Dorel R.; Nita P.; Fernández C. G.; Abufager P.; Lorente N.; Echavarren A. M.; Oteyza D. G. On-surface synthesis of heptacene on Ag(001) from brominated and non-brominated tetrahydroheptacene precursors. Chem. Commun. 2018, 54, 10260–10263. 10.1039/C8CC04402C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Eisenhut F.; Kühne T.; García F.; Fernández S.; Guitián E.; Pérez D.; Trinquier G.; Cuniberti G.; Joachim C.; Peña D.; Moresco F. Dodecacene generated on surface: Reopening of the energy gap. ACS Nano 2020, 14, 1011–1017. 10.1021/acsnano.9b08456. [DOI] [PubMed] [Google Scholar]
  27. Grüninger P.; Greulich K.; Karstens R.; Belser A.; Ovsyannikov R.; Giangrisostomi E.; Bettinger H. F.; Batchelor D.; Peisert H.; Chassé T. Highly oriented hexacene molecules grown in thin films on Cu(110)-(2 × 1)O. J. Phys. Chem. C 2019, 123, 27672–27680. 10.1021/acs.jpcc.9b08837. [DOI] [Google Scholar]
  28. Grüninger P.; Polek M.; Ivanović M.; Balle D.; Karstens R.; Nagel P.; Merz M.; Schuppler S.; Ovsyannikov R.; Bettinger H. F.; et al. Electronic structure of hexacene and interface properties on Au(110). J. Phys. Chem. C 2018, 122, 19491–19498. 10.1021/acs.jpcc.8b04274. [DOI] [Google Scholar]
  29. Einholz R.; Fang T.; Berger R.; Grüninger P.; Früh A.; Chassé T.; Fink R. F.; Bettinger H. F. Heptacene: Characterization in solution, in the solid state, and in films. J. Am. Chem. Soc. 2017, 139, 4435–4442. 10.1021/jacs.6b13212. [DOI] [PubMed] [Google Scholar]
  30. Yang J. L.; Yan D. H.; Jones T. S. Molecular template growth and its applications in organic electronics and optoelectronics. Chem. Rev. 2015, 115, 5570–5603. 10.1021/acs.chemrev.5b00142. [DOI] [PubMed] [Google Scholar]
  31. Offenbacher H.; Lüftner D.; Ules T.; Reinisch E. M.; Koller G.; Puschnig P.; Ramsey M. G. Orbital tomography: Molecular band maps, momentum maps and the imaging of real space orbitals of adsorbed molecules. J. Electron Spectrosc. Relat. Phenom. 2015, 204, 92–101. 10.1016/j.elspec.2015.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Weiss S.; Lüftner D.; Ules T.; Reinisch E. M.; Kaser H.; Gottwald A.; Richter M.; Soubatch S.; Koller G.; Ramsey M. G.; et al. Exploring three-dimensional orbital imaging with energy-dependent photoemission tomography. Nat. Commun. 2015, 6, 8287 10.1038/ncomms9287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Puschnig P.; Berkebile S.; Fleming A. J.; Koller G.; Emtsev K.; Seyller T.; Riley J. D.; Ambrosch-Draxl C.; Netzer F. P.; Ramsey M. G. Reconstruction of Molecular Orbital Densities from Photoemission Data. Science 2009, 326, 702–706. 10.1126/science.1176105. [DOI] [PubMed] [Google Scholar]
  34. Yang X. S.; Egger L.; Hurdax P.; Kaser H.; Lüftner D.; Bocquet F. C.; Koller G.; Gottwald A.; Tegeder P.; Richter M.; Ramsey M. G.; et al. Identifying surface reaction intermediates with photoemission tomography. Nat. Commun. 2019, 10, 3189 10.1038/s41467-019-11133-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Haags A.; Reichmann A.; Fan Q.; Egger L.; Kirschner H.; Naumann T.; Werner S.; Vollgraff T.; Sundermeyer J.; Eschmann L.; et al. Kekulene: On-surface synthesis, orbital structure, and aromatic stabilization. ACS Nano 2020, 14 (11), 15766–15775. 10.1021/acsnano.0c06798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Broekman L.; Tadich A.; Huwald E.; Riley J.; Leckey R.; Seyller T.; Emtsev K.; Ley L. First results from a second generation toroidal electron spectrometer. J. Electron Spectrosc. Relat. Phenom. 2005, 144–147, 1001–1004. 10.1016/j.elspec.2005.01.022. [DOI] [Google Scholar]
  37. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  38. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  39. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple (vol 77, pg 3865, 1996). Phys. Rev. Lett. 1997, 78, 1396. 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  40. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  41. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  42. Zade S. S.; Zamoshchik N.; Reddy R. A.; Fridman-Marueli G.; Sheberla D.; Bendikov M. Products and mechanism of acene dimerization. A computational study. J. Am. Chem. Soc. 2011, 133, 10803–10816. 10.1021/ja106594v. [DOI] [PubMed] [Google Scholar]
  43. Ules T.; Lüftner D.; Reinisch E. M.; Koller G.; Puschnig P.; Ramsey M. G. Orbital tomography of hybridized and dispersing molecular overlayers. Phys. Rev. B 2014, 90, 155430 10.1103/PhysRevB.90.155430. [DOI] [Google Scholar]
  44. Takasugi K.; Yokoyama T. Coverage induced structural transformations of tetracene on Ag(110). J. Chem. Phys. 2016, 144, 104702 10.1063/1.4943576. [DOI] [PubMed] [Google Scholar]
  45. Neugebauer J.; Scheffler M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys. Rev. B 1992, 46, 16067–16080. 10.1103/PhysRevB.46.16067. [DOI] [PubMed] [Google Scholar]
  46. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  47. Feibelman P. J.; Eastman D. E. Photoemission spectroscopy—Correspondence between quantum theory and experimental phenomenology. Phys. Rev. B 1974, 10, 4932–4947. 10.1103/PhysRevB.10.4932. [DOI] [Google Scholar]
  48. Lüftner D.; Weiss S.; Yang X. S.; Hurdax P.; Feyer V.; Gottwald A.; Koller G.; Soubatch S.; Puschnig P.; Ramsey M. G.; Tautz F. S. Understanding the photoemission distribution of strongly interacting two-dimensional overlayers. Phys. Rev. B 2017, 96, 125402 10.1103/PhysRevB.96.125402. [DOI] [Google Scholar]
  49. Yang X. S.; Egger L.; Fuchsberger J.; Unzog M.; Lüftner D.; Hajek F.; Hurdax P.; Jugovac M.; Zamborlini G.; Feyer V.; et al. Coexisting charge states in a unary organic monolayer film on a metal. J. Phys. Chem. Lett. 2019, 10, 6438–6445. 10.1021/acs.jpclett.9b02231. [DOI] [PubMed] [Google Scholar]
  50. Wang Y. L.; Ji W.; Shi D. X.; Du S. X.; Seidel C.; Ma Y. G.; Gao H. J.; Chi L. F.; Fuchs H. Structural evolution of pentacene on a Ag(110) surface. Phys. Rev. B 2004, 69, 075408 10.1103/PhysRevB.69.075408. [DOI] [Google Scholar]
  51. Berkebile S.; Puschnig P.; Koller G.; Oehzelt M.; Netzer F. P.; Ambrosch-Draxl C.; Ramsey M. G. Electronic band structure of pentacene: An experimental and theoretical study. Phys. Rev. B 2008, 77, 115312 10.1103/PhysRevB.77.115312. [DOI] [Google Scholar]
  52. Stadtmüller B.; Lüftner D.; Willenbockel M.; Reinisch E. M.; Sueyoshi T.; Koller G.; Soubatch S.; Ramsey M. G.; Puschnig P.; Tautz F. S.; et al. Unexpected interplay of bonding height and energy level alignment at heteromolecular hybrid interfaces. Nat. Commun. 2014, 5, 3685 10.1038/ncomms4685. [DOI] [PubMed] [Google Scholar]
  53. Stadtmüller B.; Willenbockel M.; Reinisch E. M.; Ules T.; Bocquet F. C.; Soubatch S.; Puschnig P.; Koller G.; Ramsey M. G.; Tautz F. S.; et al. Orbital tomography for highly symmetric adsorbate systems. Epl 2012, 100, 26008 10.1209/0295-5075/100/26008. [DOI] [Google Scholar]
  54. Schönauer K.; Weiss S.; Feyer V.; Lüftner D.; Stadtmüller B.; Schwarz D.; Sueyoshi T.; Kumpf C.; Puschnig P.; Ramsey M. G.; et al. Charge transfer and symmetry reduction at the CuPc/Ag(110) interface studied by photoemission tomography. Phys. Rev. B 2016, 94, 205144 10.1103/PhysRevB.94.205144. [DOI] [Google Scholar]
  55. Willenbockel M.; Lüftner D.; Stadtmüller B.; Koller G.; Kumpf C.; Soubatch S.; Puschnig P.; Ramsey M. G.; Tautz F. S. The interplay between interface structure, energy level alignment and chemical bonding strength at organic-metal interfaces. Phys. Chem. Chem. Phys. 2015, 17, 1530–1548. 10.1039/C4CP04595E. [DOI] [PubMed] [Google Scholar]
  56. Horn S.; Lischka H. A comparison of neutral and charged species of one- and two-dimensional models of graphene nanoribbons using multireference theory. J. Chem. Phys. 2015, 142, 054302 10.1063/1.4906540. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c09062_si_001.pdf (1,002.2KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES