Controlling the Photostability of Pyrrole with Optical Nanocavities

Abstract

Strong light-matter coupling provides a new strategy to manipulate the non-adiabatic dynamics of molecules by modifying potential energy surfaces. The vacuum field of nanocavities can couple strongly with the molecular degrees of freedom and form hybrid light-matter states, termed as polaritons or dressed states. The photochemistry of molecules possessing intrinsic conical intersections can be significantly altered by introducing cavity couplings to create new conical intersections or avoided crossings. Here, we explore the effects of optical cavities on the photo-induced hydrogen elimination reaction of pyrrole. Wave packet dynamics simulations have been performed on the two-state, two-mode model of pyrrole, combined with the cavity photon mode. Our results show how the optical cavities assist in controlling the photostability of pyrrole and influence the reaction mechanism by providing alternative dissociation pathways. The cavity effects have been found to be intensely dependent on the resonance frequency. We further demonstrate the importance of the vibrational cavity couplings and dipole-self interaction terms in describing the cavity-modified non-adiabatic dynamics.

Introduction

Photochemistry involves the interaction of matter with light and plays an important role in synthetic chemistry, biology, and material sciences.¹⁻³ Photochemical reactions are crucial in processes such as photosynthesis,⁴ vision,⁵ and storage of solar energy,⁶ but they can also possess detrimental effects such as DNA damage⁷ and modification of the efficiency of solar cells.⁸ Therefore, photochemical reactions need to be either accelerated or suppressed depending on their applications. These manipulations can be achieved by chemical modifications and classical laser fields.⁹⁻¹² In recent times, strong light-matter coupling introduced by the optical cavities has evolved as a new tool to control the photochemical processes.¹³⁻¹⁷ The light-matter interaction can be considered to be strong when the energy exchange rate between matter and the cavity mode outpaces all incoherent decay processes. This strong cavity coupling results in the formation of hybrid field-matter states called dressed states or polaritons and consequently modifies the energy landscape of the molecules involved in the chemical process.^14−16,18 Tuning the resonance frequency of an optical nanocavity may in turn be used as a control knob for tuning the spectroscopic and dynamical properties of the molecular systems.¹⁹⁻³¹ Notable examples of their potential applications include modifying the branching ratio between multiple reaction pathways,³² controlling the photochemical reaction rates,²³⁻²⁵ and improving Raman signals.³³ The field of polaritonic chemistry has also seen several theoretical developments including quantum optics and ab initio approaches to investigate and understand the cavity-modified dynamics.^{14,15,19,22,26,34−42}

The cavity-modified photochemistry significantly differs from that of the bare molecule when entering a strong coupling regime. In the absence of a cavity, many of the photochemical reactions are governed by the conical intersections (CIs) through which the molecule can decay non-radiatively to a lower electronic state.^43,44 The strong coupling enables mixing the cavity mode with the molecular degree of freedom and manipulates the potential energy surfaces (PESs) by creating additional CIs. These modified PESs correspond to the polaritonic states and determine the dynamics of the coupled cavity-molecular system.

The photochemistry of light-induced CIs is well explored^27,45 and recent studies have started to investigate the phenomena of cavity-field induced CIs.^13,14,46 Studies investigating the direct coupling of quantized light fields with the non-adiabatic dynamics of avoided crossings¹⁵ or intrinsic CIs^16,47 are still limited. Previous studies have mainly considered polaritons formed by electronic states. In this work, we theoretically investigate the effect of the optical nanocavities on the non-adiabatic dynamics of the molecule possessing an intrinsic CI. Wave-packet dynamics calculations have been performed on the two-state, two-mode model of the pyrrole coupled to the cavity mode. In addition to the electronic–cavity interactions, we have also incorporated vibrational cavity couplings and dipole self-energy (DSE, which was found to be important in the ultrastrong cavity regime⁴⁸) terms in the Hamiltonian used for the simulations. Our study involves exploring the influences of strong light-matter interaction on the photochemistry of pyrrole. The goal is to understand how an optical cavity controls the molecular photostability and affects the reaction mechanism. We have also attempted to assess the importance of vibrational cavity couplings and DSE terms in describing cavity-modified photochemistry.

Pyrrole and related compounds can be considered as interesting model systems for investigating the excited-state dynamics.⁴⁹⁻⁵⁶ The lowest-energy intense bands in the absorption spectrum of pyrrole appear around 6 eV.^57,58 The assignment of these bands has become quite challenging due to the presence of a large number of electronic states in this energy range.^59,60 Broad peaks in the UV absorption spectrum and small fluorescence quantum yields are also responsible for the ambiguity in assigning the spectral bands.^59,60

Upon interacting with UV radiation, pyrrole undergoes dissociation along the NH bond. Based on previous theoretical studies, four lowest singlet excited states, ¹A₂(πσ*), ¹B₁(πσ*), ¹B₂(ππ*), and ¹A₁(ππ*), have been found to be involved in the photolysis reaction.^55,61 Among these, ππ* states are the bright states, which correspond to the intense bands around 6 eV in the absorption spectrum. The molecule from the initially excited ππ* state relaxes to the πσ* state within an ultrafast time scale (≈20 fs).⁵¹ Because of the significant antibonding character of the σ* orbital, the latter state becomes repulsive in nature with respect to the NH bond.⁵¹ Consequently, the molecule dissociates and forms a conical intersection between the πσ* state and the ground state. In this paper, the photodissociation dynamics of pyrrole on the ¹B₁(πσ*), hereafter referred to as just πσ*, state has been considered for the study. Previous studies reveal NH stretching and out-of-plane bending modes as the tuning and the coupling mode coordinates for πσ*–S₀ states, respectively.⁵⁵ Thus, we here considered the two-state, two-mode model of pyrrole along with the cavity mode to unravel the influences of the strong light-matter interaction on the photo-dynamics of pyrrole. Nuclear wave-packet dynamics are used to simulate the coupled dynamics of electronic, vibrational, and photon mode by including all relevant cavity coupling terms—electronic, vibrational, and DSE—in the corresponding Hamiltonian. Since the primary objective here is to explore the cavity effects on the dynamics involving intrinsic CIs, we restricted ourselves to consider the ground and πσ* states, and their vibronic interactions to the other excited states have been ignored. It should be noted that these effects, which may influence the photodissociation dynamics of pyrrole, are not included in the current model.

Theory and Model

Hamiltonian

The Hamiltonian describing the system of a molecule considered in an optical cavity comprises the molecular Hamiltonian Ĥ_M, the Hamiltonian of the cavity mode Ĥ_C, and the molecule–cavity interaction term Ĥ_I(15,62,63)

1

where we assume that the dressed states can be expressed in field-free molecular electronic states.⁶⁴ The molecular Hamiltonian includes two electronic states in a diabatic basis and the nuclear degrees of freedom q = (q₁,q₂)^T

2

where m_i are the reduced masses of the respective nuclear coordinates q_i. The operators σ = |g⟩⟨e| and σ^† = |e⟩⟨g| annihilate and create an excitation in the electronic subspace, respectively. The ground and first excited-state PESs are V_gg(q) and V_ee(q), respectively, and Ŝ_ge(q) is the diabatic coupling. The quantized cavity mode is described by

3

where â^(†) is the annihilation (creation) operator of the cavity photon with mode frequency ω_c. The coupling between the photon field and the molecule in the dipole approximation is given as

4

where g_ij are the cavity couplings given by the vacuum Rabi frequency

5

and ⟨μ̂²⟩_ij = ⟨i|μ̂²|j⟩ is the electronic matrix of the squared dipole operator, which describes the influence of the DSE interaction.⁶⁴ Here 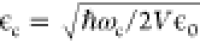is the vacuum field amplitude of the cavity mode with cavity mode volume V and μ_ij are dipole functions for the permanent dipoles (i = j) and transition dipole moments (i ≠ j). The term g_ge is responsible for coupling the electronic states, and the terms g_gg and g_ee include the coupling of the vibrational levels to the cavity.

For a more convenient numerical treatment, we use photon displacement coordinates,^15,25 which are obtained by expressing the corresponding ladder operators for the cavity mode in terms of a pseudo spatial coordinate x̂ and a conjugate momentum , where

6

The Hamiltonian for the cavity mode then reads

7

and the light-matter coupling can be rewritten to read

8

Note that in this form, the counter-rotating terms aσ and a^†σ^† from eq 4 are preserved.

In the present study, two nuclear coordinates corresponding to the NH bond are considered to be the active modes affecting the ground and the πσ* states of pyrrole (see below for more discussion). Consequently, the system under consideration becomes three-dimensional after adding the photon displacement coordinate x̂ as the third coordinate.

Potential Energy Surfaces

Based on the ab initio and quantum dynamics calculations, it is now well established that the πσ* state dynamics of pyrrole mainly involves NH stretching and out-of-plane bending modes.^55,61 The former coordinate tunes the energy difference between the ground and the πσ* state, whereas the latter couples the two states. Consequently, these modes were referred to as the tuning and coupling modes, respectively. In the current work, we used Cartesian coordinate displacements for modeling the two-dimensional PESs. This choice simplifies the kinetic operator at the expense of grid points that are required to describe the nuclear wave packet. The tuning mode is considered to be the in-plane displacement of the hydrogen atom attached to the nitrogen atom, and the coupling mode is the vertical out-of-plane displacement (Figure 1a). These two coordinates are denoted as DIP (displacement in-plane) and DOP (displacement out-of-plane), respectively. Figure 1b shows the diabatic PESs of the ground and πσ* states as a function of DIP and DOP coordinates. It is observed that the two diabatic energy surfaces vary smoothly along the abovementioned displacement coordinates. There is a shallow well on the πσ* state from which the intersection between the ground and πσ* state around r_NH = 2.1 Å is accessible by surmounting a small barrier.

Figure 1.

(a) Definition of tuning (DIP) and coupling (DOP) modes corresponding to S₀–πσ* CI of pyrrole. (b) Two-dimensional diabatic PESs, highlighting the location of the curve crossing of ground (grey) and πσ* (red) states of pyrrole along DIP and DOP coordinates computed at the CASSCF(8,7)/aug-cc-pVDZ level of theory.

Our calculations predict the NH dissociation barrier on the πσ* state to be 0.19 eV. The vertical excitation energy from the ground state to the πσ* state is 4.9 eV. The computed dissociation limits for the S₀ and πσ* states of pyrrole radical are 3.5 and 4.8 eV, respectively. These energetics are found to be lower than the values reported in the previous theoretical studies at more accurate levels of theory such as CASPT2 and MRCI.⁶¹ A maximum deviation of 0.8 eV has been observed in the case of vertical excitation energy. This underestimation of the energies with the CASSCF method is already pointed out by Domcke and co-workers in their theoretical study on the photochemistry of pyrrole.⁵⁵ Furthermore, the energy ordering of the three states (S₀, πσ* (¹A₂), and πσ* (¹B₁)) considered in our calculation and the location of the CI (r_NH = 2.1 Å) are consistent with those in the earlier reports.^54,55,61 Therefore, the computed PESs provide us a qualitative picture of the hydrogen detachment process in pyrrole.

Methods

Electronic Structure Methods

The reference geometry used to construct the PESs has been optimized at the DFT/B3LYP/aug-cc-pVDZ level of theory. Single point energies on the two-dimensional nuclear coordinate grid have been calculated using the 3-state-averaged CASSCF method along with the aug-cc-pVDZ basis set. The three states included in the state-averaging are S₀, πσ* (¹A₂), and πσ* (¹B₁). A similar rigid scan methodology that does not consider the effect of the reaction coordinate displacement on the remaining molecular coordinates has also been applied successfully to describe the excited-state dynamics of pyrrole.⁵⁵ The active space used for the CASSCF calculation consists of three π-orbitals, two π*-orbitals, and a pair of σ/σ*-orbitals corresponding to NH bond (Figure S1 of the Supporting Information). This active space can be denoted as CAS(8,7), which indicates the distribution of 8 electrons among 7 orbitals. All orbitals, including the core shells, were optimized in the CASSCF calculation. It is worth mentioning that the current active space yields small discontinuities around DOP ≈ −1.5 Å for DIP ≈ 0 to 1 Å  (Figure 1b). However, this does not affect the dynamics because the wave packet has been observed to be never going beyond 1 Å along the DOP mode (more details in the results and discussion section). The other necessary electronic properties for the dynamics calculations are also obtained using the CASSCF method and are presented in the Supporting Information. These include diabatic couplings (Figure S2 of the Supporting Information), transition dipole moments (Figure S3 of the Supporting Information), and permanent dipole moments (Figures S4 and S5 of the Supporting Information). The diabatic PESs are used in time-dependent dynamics simulations. To obtain the diabatic states and the corresponding couplings, we employed the quasi-diabatization procedure of Simah et al. as implemented in MOLPRO-2019.⁶⁵ The transformation matrix has been used to transform the remaining electronic properties such as permanent dipole moments and transition dipole moments from adiabatic to diabatic basis. All electronic structure calculations have been performed using the MOLPRO-2019 program package.^66,67 The expectation value of the squared dipole operator ⟨μ̂²⟩_ij(q) was obtained using the dipole moments. By inserting the resolution of identity, ⟨μ̂²⟩_ij(q) takes the following form

9

Here, i, j, and k refer to the electronic eigenstates. A truncated subspace for the intermediate state k that includes the relevant electronic states involved in the dynamics has been used here.⁶⁸ In the present case, the subset includes ground and excited electronic states of pyrrole⁵⁵ and the sum in eq 9 then runs over g and e.

Polariton Non-Adiabatic Dynamics

The excited-state dynamics of the pyrrole-cavity coupled system has been simulated by numerically solving the time-dependent Schrödinger equation with the Hamiltonian given in eq 1, which uses eqs 7 and 8 for Ĥ_C and Ĥ_I, respectively. Here, we consider the H atom Cartesian displacements in evaluating the molecular kinetic energy term in eq 2. This approximation is valid because of the much smaller H atom mass than that of the remaining molecular entity. The coupled nuclear-wave packet is propagated according to the Arnoldi propagation scheme⁶⁹ on the PESs of pyrrole. These PESs are represented by a three-dimensional numerical grid with 256 points along DIP, 128 points along DOP, and 32 points for the photon displacement coordinate x̂. The initial condition of the system is prepared by vertically placing the ground electronic state with the lowest vibrational level on the πσ* state. This vertical excitation model, which has also been employed to investigate the photodissociation dynamics of pyrrole,⁵⁵ can be justified as follows. According to Kasha’s rule, the initially populated ππ* state rapidly decays to the πσ* state after which the hydrogen-detachment process starts.⁷⁰ Furthermore, the computed transition dipole moments suggest that the direct electronic excitation from the ground to the πσ* state should also be possible due to the nonzero dipole values along the symmetry breaking DOP mode (Figure S3 of the Supporting Information). Therefore, investigating the cavity-modified dynamics on the πσ* state is essential to understand the polaritonic effects on the photodissociation reaction of pyrrole. The vibrational ground state of the S₀ potential is obtained by employing the imaginary time propagation method.⁷¹ Four different cavity mode frequencies, ω_c = 0.28, 0.56, 1.56, and 3.54 eV, have been considered for the study (Figure 2). The nuclear wave packet has been evolved for 726 fs with a time step of 48 as using our in-house quantum dynamics code (QDng). The perfect matched layer (PML) has been placed adjacent to the edges of the DIP and DOP coordinates, as the absorbing boundary conditions.⁷²

Figure 2.

One-dimensional potential energy curves of ground (black) and πσ* (red) states of pyrrole along NH in-plane displacement computed at CASSCF/aug-cc-pVDZ level of theory. Vertical arrows with green color represent the cavity mode frequencies ω_c, considered in the current study.

The two-dimensional PES is separated by a radial dividing surface located slightly above the surface crossing region (Figure S6 of the Supporting Information). The areas before and after the dividing surface of the PES are designated as the bonding and dissociative regions, respectively. In other words, the molecule reaching the region beyond the intersection in the vicinity of DIP = 1 Å has been considered dissociative. The population probability in the bonding region can be obtained by the expectation value of the elliptical step function with the time-dependent nuclear wave function.

10

where q₁ and q₂ refer to the DIP and DOP coordinates, respectively. The elliptical step function f(q₁, q₂) is defined as

11

The dynamics results discussed in the main article are obtained by considering the cavity field along the y-component of the molecular dipole moments. The other components (x and z) are found to be very small, and the corresponding dynamics are very similar to that of the bare molecule (Figures S7 and S8 of the Supporting Information).

Results and Discussion

To investigate the effects of the cavity coupling on the photolysis reaction of pyrrole, wave packet dynamics calculations were performed. Here we have assumed a vertical excitation from the ground electronic state, starting with a product wave function comprising the respective cavity, electronic, and vibrational subsystems: Ψ(t = 0) = |0⟩⊗|πσ*⟩⊗|v_X = 0⟩. The quantized cavity field was included in the Hamiltonian (eq 1) used for the simulations. Figure 2 displays the 1-D potential energy profile of ground and πσ* states as a function of NH in-plane displacement (r_DOP= 0). There exist a conical intersection (at r_N–H ≈ 2.1 Å) between the ground and πσ* states along the DIP coordinate and is accessible for the excited-state molecule by surmounting a small barrier (Figure 2). As a result, pyrrole undergoes hydrogen-dissociation reaction upon photo-excitation. The branching ratio between the ground and excited-state dissociative channels was found to be dependent on the preparation of the initial state.⁵⁵ The study by Domcke and co-workers considers different initial states with different vibrational levels of the ground electronic state and suggests that the vibrational excitation of NH modes (DIP and DOP) influences the branching ratio between different dissociation channels.⁵⁵ The present work aims to understand the influences of the cavity coupling on the photo-induced hydrogen-elimination reaction of pyrrole.

The impact of the light-matter interaction on modifying the dynamics not only depends on the strength of the cavity coupling but also on the region of the PES in which the cavity is in resonance with the electronic states. We have considered different cavity mode frequencies ω_c that range from coupling near the Franck–Condon (FC) region to coupling in the CI vicinity (Figure 2). The molecular-cavity couplings corresponding to electronic and vibrational polaritons, and DSE terms are included in the Hamiltonian (eq 8) to describe the photon–matter interaction. The photonic-molecular PESs are represented by a three-dimensional numerical grid, including the two molecular degrees of freedom and the photon field coordinate.

We have analyzed the time evolution of the overall population probabilities (P_g^br + P_e) of the molecule in the bonding region, which will be referred to as the survival probabilities hereafter. Figure 3a–d shows the variation of these probabilities by increasing the cavity vacuum field strength ϵ_c at different cavity frequencies ω_c. The black curve in each plot represents the survival probability for the bare molecule (ϵ_c = 0.00 GV/m), which decays with a dissociation rate of 0.02 fs^–1 and fully dissociates within 200 fs. This scenario changes markedly when the cavity field is added to the Hamiltonian. The observed influence is distinct for some cavity parameters (Figure 3a–d) and will be discussed for each cavity resonance frequency separately in the following. The excited-state lifetimes of the molecule in the bonding region are obtained by exponential fitting of the corresponding survival probability decay curves and presented in Figure 4.

Figure 3.

Time evolution of the survival probabilities upon excitation to the πσ* state of pyrrole under the influence of different cavity field strengths (ϵ_c) with cavity frequency (ω_c), 0.28 eV (a), 0.54 eV (b), 1.36 eV (c), and 3.54 eV (d).

Figure 4.

Lifetimes of pyrrole in the bonding region following vertical excitation as a function of the cavity field strength ε_c. The inset figure is to show the lifetime reduction for the smallest cavity frequency ω_c = 0.28 eV.

At the smallest cavity frequency ω_c = 0.28 eV, the cavity couples 0.1 Å before the wave packet reaches the CI. The two lowest cavity field strengths (ϵ_c = 0.78 and 1.96 GV/m) show only minimal effects on the time evolution of the survival probability (Figure 3a). For the two higher field strengths (ϵ_c = 3.92 and 5.87 GV/m), the dynamics is significantly altered and the photodissociation reaction is accelerated, reducing the lifetime from ≈50 fs (bare molecule) to ≈10 fs (Figure 4). Consequently, the bonding region’s population diminishes to zero much more quickly than the other cavity field strengths and resonance frequencies.The expectation value for the square of the DIP and DOP coordinates with the full polaritonic wave function, ⟨q_i²⟩, is computed using time-dependent wave functions. This yields the spread of the wave packet in DIP and DOP modes as a function of time (Figures S9 and S10 of the Supporting Information). Upon increasing the cavity field strength at 0.28 eV resonance frequency, the spread of DOP coordinate on the excited state increases from ≈0.1 Å (bare molecule) to ≈0.8 Å for ϵ_c = 5.87 GV/m (Figure S10a of the Supporting Information), which suggests the involvement of out-of-plane mode for the dissociation. Unlike the field-free molecule case, the hydrogen detachment process here proceeds along both DIP and DOP coordinates, and multiple pathways are possible.

In the case of ω_c = 0.54 eV, the time evolution of the survival probability curves is similar at all cavity field strengths, except for 3.92 GV/m where the probability increases slightly (Figure 3b). The out-of-plane dissociation becomes significant with this frequency too, although the contribution is only ≈30% to that of the previous cavity frequency of 0.28 eV (Figure S10b of the Supporting Information). The lifetime is maximized for a field strength of ϵ_c = 3.92 GV/m with ≈300 fs and drops when the field strength is further increased (Figure 4).

The nature of the decay curves changes again with the next higher cavity resonance frequency 1.56 eV, but in contrast to 0.28 eV, we observe a significant increase in the lifetime (Figure 3c) for higher field strengths. The photoreaction is suppressed drastically for stronger cavity fields (ϵ_c = 3.92 and 5.87 GV/m), which leads to a huge rise in the survival probability and increases the lifetime to ≈1500 fs (Figure 4). At the end of the simulation time scale (726 fs), more than 50% of the wave packet remains in the bonding region due to the massive suppression of the hydrogen-elimination reaction at ϵ_c = 5.87  GV/m. By further increasing the resonance frequency ω_c to 3.54 eV, the influence of the cavity mode on the dynamics is decreased (Figure 3d). Analyzing the population dynamics at the abovementioned cavity frequencies (Figure 3a–d), it becomes clear that there is an optimum resonance that allows for maximizing and minimizing excited-state lifetimes, respectively.

To gain more insight into the effects of the cavity on the photolysis of pyrrole, we have evaluated the influence of the light-matter coupling terms such as g_ii (vibrational cavity couplings) and ⟨μ̂²⟩_ij (DSE interactions) for the description of the dynamics. For this purpose, two more sets of wave packet dynamics calculations were performed, where we have dropped coupling terms from the calculation. The corresponding reduced Hamiltonians, Ĥ_red2 and Ĥ_red1, have the following form

12

13

Figure 5a–d displays the corresponding survival probabilities of these two calculations along with those of the full Hamiltonian for the strongest cavity field ϵ_c = 5.87 GV/m. Excluding both, the DSE and the coupling to the vibrational motion, leaves the dynamics nearly unaffected, when compared to the field-free case (cyan curve in Figure 5a–d). This highlights the importance of the vibrational cavity couplings, especially at higher field strengths. On the other hand, ignoring only the DSE interaction terms, ⟨μ²⟩_ij, results in the survival probability to remain significant at all resonance frequencies (blue curve in Figure 5a–d), overestimating the stabilizing effect of the cavity field. Interestingly, these cavity terms were also observed to be playing a role in the cavity-modified dynamics of pyrrole for other cavity field strengths, except ϵ_c = 0.78 GV/m (Figures S11, S12, and S13 of the Supporting Information). This emphasizes the necessity to consider the cavity coupling to the vibrational motion and the DSE when investigating the cavity-induced modifications on the dynamics of the molecule.

Figure 5.

Time evolution of the survival probabilities upon excitation to the πσ* state of pyrrole under the influence of the cavity field strength, ϵ_c = 5.87 GV/m, with different resonance frequencies, ω_c. Full Hamiltonian represents the Hamiltonian in eq 8, whereas Ĥ_red1 and Ĥ_red2 refer to the reduced Hamiltonians. DSE term, ⟨μ²⟩_ij, is excluded in the former reduced Hamiltonian, and both DSE and g_ii terms are excluded in the latter.

The results discussed above suggest that the hydrogen-dissociation dynamics on the πσ* state of pyrrole coupled to an optical cavity are largely determined by the light-matter coupling terms g_ii and ⟨μ̂²⟩_ii which depend on the molecular permanent dipole moments. Since these two terms appear in the diagonal part of the electronic Hamiltonian, their magnitudes corresponding to the different electronic states must be considerably different to affect the overall dynamics. Thus, there should be a significant jump in the permanent dipole moments going from the ground electronic state to the πσ* state of pyrrole. The excited-state dipole moments of pyrrole are indeed higher than those of the ground state, which can be attributed to the diffused/Rydberg-type nature of the σ* orbital involved in the electronic transition (Figures S1, S4, and S5 of the Supporting Information). In order to discern the factors controlling the dissimilar dynamics (Figures 3a–d and 5a–d), one-dimensional cuts of the polaritonic PESs are obtained by diagonalizing the Hamiltonian in the basis of the Fock states (Figure 6a–c). We would like to emphasize here that the displayed polaritonic curves are along only the DIP coordinate and are obtained within rotating wave approximation where the counter-rotating terms in eq 4 are ignored. On the other hand, the simulations were performed on a three-dimensional surface (DIP, DOP, and x̂), and no further approximations were made to the Hamiltonian. Thus, the polaritionic curves shown here are meant to deliver a qualitative understanding of the mechanisms, especially for the higher field strengths.

Figure 6.

One dimensional cuts of polaritonic PESs for highest cavity field strength ϵ_c = 5.87 GV/m. Full Hamiltonian represents the Hamiltonian in eq 8, whereas Ĥ_red1 and Ĥ_red2 refer to the reduced Hamiltonians. DSE term, ⟨μ²⟩_ij, is excluded in the former Hamiltonian and both DSE and g_ii terms are excluded in the latter.

Based on the analysis of the polaritonic curves at different cavity frequencies, two quantities have been found to be significantly affected. One is the dissociation barrier (ΔE_bar) on the excited-state PES and the other is the energy gap (ΔE_gap) between the upper and lower polaritons at the new avoided crossing formed by the hybrid field-matter states. These energetics are compiled in Table 1. In the full Hamiltonian case, the dissociation barrier gradually increases going from ω_c = 0.28 to 3.54 eV (Figure 6a). At the two lowest resonance frequencies (0.28 and 0.54  eV), the curves exhibit negligible dissociation barriers with a moderate energy gap. Though the two curves possess similar ΔE_bar and ΔE_gap, they mainly differ by the energy of the excited-state minimum, around 6 eV for the former and 4.5 eV for the latter. In the field-free case, the FC is around 1 eV above the CI. The higher energy difference with respect to the CI causes the wave packet to reach the crossing region with higher kinetic energy. Combined with the minuscule barrier, this explains the short lifetimes for ω_c = 0.28 eV (Figure 4). Furthermore, the paltry dissociation barrier makes the excited-state minimum very flat and allows the wave packet to evolve in all directions of the surface. As a result, multiple dissociation paths, along DIP or DOP or any combination of them, become accessible. The presence of these competing pathways rationalizes the increased DOP contributions for the dissociation process at the two lowest resonance frequencies (Figure S10 of the Supporting Information). This process is also responsible for the sudden drop in the lifetimes observed at the strongest cavity field for ω_c = 0.54 eV (blue curve in (Figure 4). An increase in the cavity field strength leads to an increased Rabi splitting between the polaritonic curves, separating the upper polariton states, thus stabilizing it.¹⁴ The final field strength (ϵ_c = 5.87 GV/m) however reduces the lifetime by allowing the molecule to dissociate via another competing pathway. For ω_c = 1.56 eV, the barrier and energy gap become quite significant. Consequently, molecular photostability increases greatly. The energy gap again decreases at the highest resonance frequency 3.54 eV. Here, the polaritonic states (see Figure 6a) are not well separated, and a vertical excitation leads to a partial population of the lower polariton state, thus reducing the stabilizing effect that has been observed for ω_c = 1.56 eV.

Table 1. Excited-State Dissociation Barriers, ΔE_bar (eV), Energy Gap between Upper and Lower Polaritonic States ΔE_gap (eV) at the Avoided Crossing for Three Different Hamiltonians.

	full Hamiltonian		Ĥred1 (no ⟨μ2⟩ij)		Ĥred2 (no gii + ⟨μ2⟩ij)
cavity freq (eV)	ΔEbar	ΔEgap	ΔEbar	ΔEgap	ΔEbar	ΔEgap
ωc = 0.28	0.05	0.24	0.60	0.20	0.19	0.02
ωc = 0.54	0.06	0.28	0.60	0.35	0.19	0.09
ωc = 1.56	0.28	0.40	0.60	0.42	0.19	0.35
ωc = 3.54	0.46	0.13	0.56	0.33	0.00	0.64

We now turn to discuss the dynamics of the reduced Hamiltonians, Ĥ_red1 and Ĥ_red2, using the corresponding polaritonic curves (Figure 6b,c). Upon excluding the self-interaction term from the Hamiltonian, the curves exhibit high barriers with significant energy gaps at all four frequencies (Table 1). Furthermore, the FC-minimum on the excited state is energetically similar to the avoided crossing, which is unlike the full Hamiltonian case resulting in a wave packet that reaches the crossing region with less kinetic energy. Accordingly, the dissociation process becomes less efficient, and the survival probability remains large. With Ĥ_red2, on the other hand, the barriers are similar to the bare molecule for all frequencies except for ω_c = 3.54 eV, which exhibits no significant barrier. The minimal energy gaps at 0.28 and 0.54 eV are consistent with the corresponding dynamics that are identical to those of the molecule without the cavity field. The higher energy gaps for the next two frequencies do not explain the observed dynamics. However, the energy difference between the FC-minimum and the avoided crossing for ω_c = 1.56 eV and the absence of the barrier for ω_c = 3.54 eV may lead to an efficient dissociation process.

The role of the collective light-matter couplings on the photodissociation dynamics of pyrrole has not been considered in the present work. In a recent study by Pérez-Sánchez and Yuen-Zhou on polariton-assisted down-conversion of photons, collective coupling effects have been shown to be less significant.⁷³ The smaller collective effects were due to the cavity resonating the molecules far away from the FC region. As a result, the coupling of the cavity with the initially excited single molecule is possible only after sufficient progress of the reaction, while the other molecules at the FC region remain off-resonant. The resonating frequencies employed in the present work are also not very close to the FC region, so similar collective coupling effects can be expected. However, an extensive study with a detailed account of such collective cavity couplings is necessary to ascertain their effects on the photolysis of pyrrole.

Additionally, the leakages of cavity photons may also play a role in altering the dynamics of the polariton states. More recently, the influence of photon loss on the excited-state dynamics has been addressed by several authors:⁷⁴⁻⁷⁷ certain reaction channels, such as dissociation, may actually be suppressed by short photon life times. Along with these effects, other molecular modes and the vibronic interactions of πσ* with the remaining excited states could also be important in describing the photodissociation dynamics of pyrrole. A detailed investigation by considering all these effects is beyond the scope of this paper and deferred to future work.

Conclusions

In summary, the optical cavity can either accelerate or inhibit the photodissociation reaction of pyrrole depending on their frequency and coupling strength. The longest lifetime (1.5 ps) has been observed for a cavity frequency of 1.56 eV (at ϵ_c = 5.87 GV/m), which we found to be an optimum for stabilizing the photodissociation dynamics of pyrrole. The shortest lifetime that has been observed is ≈10 fs (at ω_c = 0.28 eV with ϵ_c = 5.87 GV/m), whereas the value is ≈50 fs for the field-free molecule (Figure 4). Subsequently, the hydrogen elimination reaction proceeds along an alternative pathway involving DOP mode in addition to the in-plane dissociation. Therefore, the cavity allows the molecule to dissociate along multiple reaction pathways. These modifications are mainly due to the cavity coupling with the vibrational modes and self-polarization terms (Figure 5a–d). The rapid local changes of the permanent dipoles in the vicinity of the CI and their difference between the two electronic states are responsible for the stark difference in the simulations. They further add to the mixing between electronic and vibrational degrees of freedom in the vicinity of the CI. A second factor that has been found to be important is the change of the PES in the FC region; varying the resonance frequency of the cavity affects barriers and the relative energy shift with respect to the crossing region. For an intrinsic CI, the electronic and vibrational degrees are already heavily mixed, thus making the inclusion of the full dipole matrix into light-matter couplings essential. While this may be expected, the strong influence of the self-polarization terms has so far mainly been considered in the context of vibrational strong coupling in the ground state.⁷⁸ This highlights the importance of these couplings and their consideration for studying the cavity-modified photochemistry of molecules with intrinsic CIs.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c09252.

• Molecular orbitals involved in the active space, diabatic couplings, transition dipole moments, permanent dipole moments correspond to ground and πσ* states, bonding and dissociative regions, survival probability plots corresponding to the dynamics where x- and z-components of dipole moments are considered, the expectation value for the spread of DIP and DOP coordinates, and comparison of survival probabilities obtained using full and reduced Hamiltonians (PDF)

The authors declare no competing financial interest.