Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 27;21(3):1320–1326. doi: 10.1021/acs.nanolett.0c04014

Enhancing Vibrational Light–Matter Coupling Strength beyond the Molecular Concentration Limit Using Plasmonic Arrays

Manuel Hertzog †, Battulga Munkhbat ‡, Denis Baranov ‡, Timur Shegai ‡,*, Karl Börjesson †,*
PMCID: PMC7883392  PMID: 33502874

Abstract

graphic file with name nl0c04014_0005.jpg

Vibrational strong coupling is emerging as a promising tool to modify molecular properties by making use of hybrid light–matter states known as polaritons. Fabry–Perot cavities filled with organic molecules are typically used, and the molecular concentration limits the maximum reachable coupling strength. Developing methods to increase the coupling strength beyond the molecular concentration limit are highly desirable. In this Letter, we investigate the effect of adding a gold nanorod array into a cavity containing pure organic molecules using FT-IR microscopy and numerical modeling. Incorporation of the plasmonic nanorod array that acts as artificial molecules leads to an order of magnitude increase in the total coupling strength for the cavity with matching resonant frequency filled with organic molecules. Additionally, we observe a significant narrowing of the plasmon line width inside the cavity. We anticipate that these results will be a step forward in exploring vibropolaritonic chemistry and may be used in plasmon based biosensors.

Keywords: Vibropolariton, Strong coupling, Plasmonic, Polaritonic chemistry

Introduction

Strong light–matter coupling has attracted considerable attention in the past couple of years due to the potential applications it offers in physical and chemical sciences.1−4 For example, strong coupling of organic molecules has been shown to modify the rate of a photoisomerization reaction,5,6 increase electronic transport,7 and expand the length scale of Förster energy transfer.8−10 Not to mention other effects of strong coupling such as selective manipulation of excited states,11 suppression of photo-oxidation,12 or reducing photodegradation in polymers.13 Recently, vibrational strong coupling has come into focus as a promising physical tool to control molecular properties. Since the first experimental evidence of vibrational strong coupling (VSC) in both solid14−16 and liquid states,17 the field has expanded considerably18−25 and it has been shown to alter reaction kinetics,26−29 control reaction selectivity,30 allow for intermolecular energy transfer,31 and modification of enzyme activity.32 Recent progress in chemical reactions making use of polaritons was summarized by Hirai et al.33 In order to significantly impact chemical reactivity, theoretical investigations have demonstrated that a high coupling strength is required34,35 and a recent experimental study has shown a nonlinear relationship between the coupling strength and thermodynamics of a chemical reaction.29

Strong light–matter coupling is achieved by interfacing molecules with confined electromagnetic field of resonant cavities tuned to a molecular transition. When a molecular vibrational transition is in the strong coupling regime, two new hybrid states, known as polaritons, are formed,36 separated in energy by the so-called Rabi splitting ℏΩR. Traditionally, polaritons have been engineered with the use of planar cavities, such as Fabry–Perot (FP) resonators confining the electromagnetic fields between two mirrors.14 Reaching large coupling strengths usually requires saturating the cavity volume with the molecular material, and additionally aligning the transition dipole moments with the cavity vacuum field.37−39

Plasmonics offers an alternative route to strong coupling by confining light down to subwavelength scales with the use of metallic nanoparticles and nanocavities.40−42 Only a tight region of space around the metallic cavity needs to be filled with molecules in order to form polaritons.43 Plasmon resonances of nanoparticles are tunable from the UV to the IR range and can be used for molecular sensing in the IR range due to nanoscale mode volumes.44−47 However, to improve the sensitivity, new approaches for narrowing the plasmon line width are desirable.

The magnitude of the Rabi splitting for a given molecular transition is proportional to the square root of the molecular concentration and the filling factor. Furthermore, the maximal achievable magnitude of the Rabi splitting in the case of saturated mode volume is ultimately bound by the bulk Rabi splitting 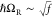Inline graphic (with f being the transition oscillator strength48), which is independent of the cavity type.49−51 Therefore, new approaches are required to increase the Rabi splitting in order to maximize the effect of the confined electromagnetic field onto molecules, as shown by theoretical studies.34,52,53

In this Letter, we utilize a hierarchical coupling between a Fabry–Perot cavity, a vibrational absorption band of an organic molecule, and a localized surface plasmon resonance in the mid-IR regime to go beyond the Rabi splitting imposed by the maximal concentration limit.54 First, we show that the coupling of the plasmon and the FP cavity results in an order of magnitude decrease in the plasmon’s line width which is an observation rationalized by reduced radiative losses from the plasmon in the cavity.55 Then, by using numerical and analytical modeling in conjunction to our experimental data, we show a 5–9-fold increase in the total coupling strength, indicating that the plasmon acts as an artificial molecule that increases the molecular coupling strength.

Results and Discussions

In this study, we report a method to increase the coupling strength above the limit of Inline graphic using a hybrid system composed of a Fabry–Perot (FP) cavity, an organic molecule, and a localized surface plasmon in a fashion similar to the one introduced by Bisht et al.54 using two-dimensional transition metal dichalcogenides in the visible regime. All three entities are tuned to the same resonance frequency, thereby coupled amidst themselves, creating hybrid polaritons (Figure 1a). The Fabry–Perot cavities used in the following experiments are composed of IR-transparent substrates (CaF2 and ZnSe) coated with 10 nm of gold (Figure 1b; see SI for experimental methods). The physical distance between the gold mirrors, ranging from 11 to 16 μm, was controlled using a polymer spacer. The cavities were designed with two inlets to inject liquids. The quality factor of an empty cavity was 28, and the free spectral range was 496 cm–1 (Figure 2a). We choose hexanal and 4-butylbenzonitrile as the organic molecules for this study (Figure 1c). Both are liquids at room temperature and were processed in neat form. The molecular vibrations of interest are the C=O stretching mode of hexanal and the C≡N stretching mode of 4-butylbenzonitrile. These are strong absorption bands centered around 1724 and 2225 cm–1 with full width at half maxima (fwhm) of 27 and 10 cm–1, respectively (Figure 2b,c). The surface plasmon was provided by gold nanorod arrays (size about 100 μm2), which were deposited on top a spacer composed of 450 nm of SiO2 to minimize interference from the gold mirror (Figure 1b). Five different arrays were made with all having equal thickness and spacing but with lengths ranging from 1100 to 1500 nm, which gave plasmon resonances covering the energy of both two molecular vibrations and the Fabry–Perot mode (Figure 2d). The plasmon resonances were broad (fwhm = 621–1120 cm–1) due to radiative losses. This is an intrinsic feature of plasmon arrays in the mid-IR, hampering its use.

Figure 1.

Figure 1

Open in a new tab

(a) Conceptual diagram of the system in this study. (b) Schematic view of the Fabry–Perot cavity. Fourier transform infrared spectroscopy microscopy was used to either probe the small area where gold nanorods were deposited (beam 1) or where no rods were present (beam 2). (c) Molecular structure of 4-butylbenzonitrile (top) and hexanal (bottom). Highlighted in orange are the functional groups responsible for the vibrational band coupled to the FP cavity. (d) SEM picture of the gold nanorods deposited on a glass substrate.

Figure 2.

Figure 2

Open in a new tab

(a) Transmission spectrum of an empty Fabry–Perot cavity. (b) ATR spectrum of hexanal (purple) showing the C=O absorption band around 1724 cm–1, and transmission spectrum of the FP cavity filled with hexanal (orange). The value of ℏΩR is 101 cm–1. (c) ATR spectrum of 4-butylbenzonitrile (purple) showing the C≡N absorption band around 2225 cm–1, and transmission spectrum of the FP cavity filled with 4-butylbenzonitrile (orange). The value of ℏΩR is 46 cm–1. (d) Reflection map of the five different gold nanorod arrays.

We will first describe the coupling between the cavity and the two organic compounds, then the cavity and plasmonic nanorods, and finally the complete coupled system with the FP cavity, the plasmonic nanorods, and the organic molecules. Figure 2b,c shows a clear normal mode splitting of the vibrational absorption band of the two molecules when placed inside the FP cavity at resonant conditions. This indicates strong coupling between the cavity mode and the carbonyl group of hexanal (Figure 2b) as well as the cavity mode and the nitrile group of 4-butylbenzonitrile (Figure 2c). The resulting formation of vibro-polaritons gives a measured Rabi splitting of 101 and 46 cm–1 for the C=O mode and the C≡N mode with the cavity, respectively. The Rabi splittings are larger than both the fwhm of the bare molecular vibrations and the cavity mode, which constitutes further evidence that our system is indeed in the strong-coupling regime. Furthermore, the ratio between the coupling strength and the bare transition energy of the vibrations are 2.93% for the C=O band and 1.03% for the C≡N band.

Let us now consider the plasmonic arrays inside the FP cavity. With increasing rod length, the plasmon resonance shifts to lower energies (Figure 2d), and the nanorod length therefore provides a way of controlling the cavity–plasmon detuning. Moreover, due to intrinsic anisotropy of the rods the microcavity–plasmon polaritons are observed only along the long axis of the rods, whereas along the short axis the bare cavity is recovered. This polariton anisotropy can be probed using polarization-resolved transmission spectroscopy. As shown in Figure 3a, the two original FP cavity modes that can be observed in the given spectral range couple to the plasmonic array mode, forming exactly 2 + 1 = 3 microcavity–plasmon polaritonic states, denoted with dot-dashed lines. These new modes exhibit almost linear dispersive behavior because of the underlying dispersion of the plasmonic mode with the nanorod length.

Figure 3.

Figure 3

Open in a new tab

(a–c) Transmission maps of the gold rods inside the Fabry–Perot cavity, containing air, hexanal, or 4-butylbenzonitrile, respectively. All three were measured with a polarizer along the long axis of the rods. The blue dash-dot lines highlight the newly formed polaritonic states, the residual vertical modes are artifact due to nonideal polarization alignment. (d–f) Simulated spectra of the same systems (with the cavity thicknesses of 10.8, 8.5, and 10.4 μm, respectively). The gray dashed line indicates the absorption band of interest of the molecules, and the gray dots indicate the plasmon absorption maximum.

Furthermore, we observe an order of magnitude decrease in the line width of the resulting polariton compared to the bare plasmon. Similar narrowing was observed in our previous experiments with plasmonic arrays ultrastrongly coupled with FP cavities in the visible to mid-IR range.55 The line width of closely packed metallic nanorods in the IR region is dominated by radiative losses; however, when placed inside a closed cavity the radiation from the nanorods does not instantaneously leave the cavity, instead bouncing between the mirrors and thus reducing the total resonance line width. Consequently, the fwhm of the plasmon polaritons drops to about 70 cm–1 for all of the rods’ lengths, as a result of significantly suppressed radiative damping. Observing that the fwhm of the FP modes are 84 ± 7.3 cm–1, the line width of the cavity is the main limitation of the line width of the plasmon polariton (Table S2).

By adding molecules into the cavity, a third resonant component is introduced to the hybrid system. The hexanal C=O band is on resonance with the longest nanorods (Figure 3b), whereas the 4-butylbenzonitrile C≡N band is on resonance with the shortest nanorods (Figure 3c). This time, more FP modes are present in the same spectral range due to the larger background refractive index of the molecular solution compared to air. Dot-dashed lines indicate the dispersions of the resulting cavity–plasmon–molecule polaritonic modes, whereas the dashed vertical lines indicate the respective molecular resonances. In the next section, we will uncover the polaritonic origin of these linearly dispersing modes with the use of the analytical Hamiltonian formalism. Furthermore, the polaritonic line widths are again reduced by the cavity mirrors, showing that the FP cavity mode limits the polariton line width irrespectively of the medium inside the cavity.

In order to gain further understanding of the experimental results, we performed numerical modeling of the coupled systems with the use of the finite-difference time domain (FDTD) method in a commercial software (Lumerical Figure 3d–f and Figures S1–3). Simulated normal-incidence transmission spectra demonstrate a good agreement with the experimental spectra for both plasmonic structures and composite plasmon–molecule ones. Specifically, the observed polaritonic modes linearly disperse with the rod’s length, however, the dispersion is less pronounced than for uncoupled rods (gray dots). This is a consequence of intermixing between highly dispersive plasmonic modes and nondispersive FP modes (all arrays were placed in the same FP cavity).

Generally, a system of N distinct oscillators produces N polaritonic modes upon coupling (as long as the system is not exactly at an exceptional point). In our case, we start with M bare cavity modes, the plasmonic array mode, and the molecular resonance so that one could expect emergence of M + 2 new eigenstates. However, the simulated spectra strongly suggest that the molecules and the plasmons join in a single effective oscillator, which adds only one additional polaritonic mode to the system, as one can clearly see from the transmission dispersions in Figure 3 (aside from the parasitic uncoupled FP modes). This confirms that even a system with slightly detuned plasmons and molecules does behave as a system with a single additional compound plasmonic–molecular oscillator.

Next, to ensure that the observed dispersions are a result of the interaction between the three components in the hybrid system, transmission spectra of the system with a polarizer perpendicular to the nanorods’ long axis were measured. The results are shown in Figure S5 (numerical modeling in Figure S1). As expected, when the contribution of the plasmonic array is removed by the polarizer, the transmission spectra are the same as when probing the system beside the array (Figure 2b,c). Likewise, the values of ℏΩR with a perpendicular polarizer are 46 and 101 cm–1 for the C≡N and C=O vibrations, respectively, which are the same values as we observed when probing next to the plasmonic array.

Theoretical Analysis

In order to extract coupling strengths and confirm that the plasmonic array acts as an artificial molecule enhancing the total coupling strength of the system, we turn to theoretical analysis of the experimental data. This analysis is essentially based on the coupled harmonic oscillator algebra in the simplest possible implementation. Furthermore, this analysis requires several rather crude assumptions, which may be false in general, but are satisfactory for the goal of extracting the collective coupling constants.

In view of the above remark, we describe the cavity by a set of M orthogonal Fabry–Perot eigenmodes, each coupling to the molecular resonance with a certain coupling constant. As we are far from the ultrastrong coupling regime in this case, the interacting system can be described by a multimode coupled-harmonic oscillator Hamiltonian, which under the rotating wave approximation takes the form (see Methods)

graphic file with name nl0c04014_m003.jpg 1

where â and b̂ are the annihilation operators of the mth cavity mode and that of the molecular resonance, respectively, and gm is the coupling constant.

The coupled Fabry–Perot system exhibits transmission peaks at its polaritonic resonances, corresponding to the eigenvalues of the Hamiltonian (eq 1). Therefore, we estimate the cavity–molecule coupling strength by fitting the energies of the transmission peaks by the eigenvalues of Hamiltonian eq 1 accounting for M = 20 lowest cavity modes (see Methods for the details of the fitting procedure). Since in the multimode system the coupling strength is dependent on the FP mode order and the frequency, to make a reasonable comparison we estimate the coupling strength at zero detuning, that is, with the particular FP mode, (near-)resonant with the molecular transition.

By fitting the Hamiltonian eigenvalues to the positions of measured transmission peaks (see Figure S6), we obtain the hexanal-cavity system zero-detuning coupling strength (with the seventh FP mode of a 14.25 μm thick cavity) of about 41 cm–1. Remarkably, this value is close to the bulk polariton coupling strength of hexanal Inline graphic cm–1, which describes the photon–molecule interaction strength in an unbounded homogeneous molecular medium.56 Similarly, for the 4-butylbenzonitrile-cavity system we obtain the zero-detuning coupling strength (with the 11th mode of a 16.15 μm thick cavity) of about 18 cm–1, which is also comparable to the respective bulk coupling strength of 4-butylbenzonitrile (21 cm–1).

In a similar way, we analyze the cavity–nanorod system by replacing the single collective molecular resonance with a single mode plasmonic mode (see Methods). By fitting the measured dispersion of transmission peaks with the Hamiltonian eigenvalues, we obtain the energy spectrum of the coupled system, Figure 4a. For as long as the plasmonic array is located in a specific horizontal plane z = z0 of the cavity, the coupling strength strongly disperses with the mode order m as the result of alternating electric field nodes and antinodes of the cavity’s standing wave (see Methods). Considering the fourth FP mode of a 9.7 μm thick cavity resonant at about 2000 cm–1 (which is close to both molecular resonances), we obtain the nanorod array coupling strength to that cavity mode of about 172 cm–1. To help appreciate the appearance of anticrossings in this multimode system, we present the resulting dispersion of the Hamiltonian eigenvalues in a shorter spectral range in Figure S7, which also demonstrate a set of anticrossings between the polaritonic states.

Figure 4.

Figure 4

Open in a new tab

Hamiltonian analysis of the experimental data. (a) Fitting of the measured transmission peaks of the coupled nanorod-cavity system (circles) with eigenvalues of the multimode JC Hamiltonian (lines). (b) The same as (a) for the hybrid hexanal-nanorod system. (c) The same as (a) for the hybrid 4-butylbenzonitrile-nanorod system.

Finally, we switch to the complete cavity–plasmon–molecule systems. The key idea of our experiment is to show that plasmonic nanorods can act as artificial molecules with the oscillator strength significantly exceeding molecular ones, joining the real molecules in a single collective oscillator, and thus boosting the coupling strength and Rabi splitting. Therefore, we model the full three-component structures with the same Jaynes-Cummings Hamiltonian in which the plasmon–molecule hybrid is described as a single collective oscillator (see Methods). By fitting the measured dispersion of transmission peaks of the hybrid plasmon–hexanal-cavity system with the Hamiltonian eigenvalues, Figure 4b, we obtain a resonant coupling strength (with the fifth FP mode of a 8.0 μm thick cavity and z = 500 nm) of about 220 cm–1. Despite the number of assumptions made in the analysis, the Hamiltonian fit shows a good agreement with measured transmission peaks. Similarly, for the hybrid plasmon-4-butylbenzonitrile-cavity system we obtain a resonant coupling strength of 202 cm–1 (with the eigth FP mode of a 10.1 μm thick cavity), Figure 4c.

The simple analysis performed above suggests that the molecules and the nanorods act indeed as a collective oscillator with the effective coupling strength very approximately given by the sum of the two individual coupling strengths, geff ∼ gpl + gmol. Thus, the presence of the plasmon boosts the effective coupling strength of 4-butylbenzonitrile and hexanal with the cavity mode by 10 times and 5 times, respectively. The results of our experiment and its subsequent analysis suggest that using the plasmon resonance with large oscillator strength indeed boosts the effective coupling strength beyond the bulk limit bound by the molecular concentration. Of course, this addition of the plasmonic meta-atoms does not modify the molecular oscillator strength per se but rather modifies the effective polaritonic spectrum of the hybrid system in the vibrational strong coupling regime. This in turn may potentially affect chemical reactions whose rate was claimed to depend on the vacuum Rabi splitting in the recent literature.30

Conclusion

In summary, our hybrid Fabry–Perot cavities show that the addition of a plasmonic array to the standard molecular vibro-polaritonic system increases the total coupling strength by almost an order of magnitude for a nitrile absorption band and five times for a carbonyl absorption band. Increasing the coupling strength beyond the molecular concentration limit dismantles the crucial obstacle for reaching the ultrastrong coupling regime using organic molecules. Furthermore, precisely controlling the coupling strength, not only with the molecular concentration but also with the density of the plasmonic array, allows molecules at small concentrations to reach the strong coupling limit in a complementary fashion than the cooperating vibrational strong coupling reported by Lather et al.26 One can in a sense view the plasmonic array as a form of “catalyst” that enables any on-resonance molecular transition, regardless of molecular concentration and transition dipole moment strength, to reach the strong coupling regime. Furthermore, the cavity reduces the radiative damping from the plasmon, sharpening the polariton line width with more than an order of magnitude. Together with the spectral tuning ability, such sharp line widths may allow for mode-selective chemical sensing in the mid-IR. The approach described here is not limited to infrared transitions but can also be transposed to electronic transitions. For these reasons, we suggest that our hybrid system will be an ideal platform to explore the promising potential of polaritonic chemistry, the ultrastrong coupling regime, as well as provide an approach to mode-selective mid-IR sensing.

Acknowledgments

B.M., D.B., and T.S. acknowledge financial support from the Swedish Research Council (under VR Miljö project, Grant 2016-06059) and the Knut and Alice Wallenberg Foundation (KAW 2019.0140). K.B. and M.H. acknowledge financial support from the European Research council (ERC-2017-StG-757733) and the Knut and Alice Wallenberg Foundation (KAW 2017.0192).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c04014.

  • Methods and additional figures (PDF)

The authors declare no competing financial interest.

Supplementary Material

nl0c04014_si_001.pdf (1.2MB, pdf)

References

  1. Ebbesen T. W. Hybrid Light–Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
  2. Ribeiro R. F.; Martínez-Martínez L. A.; Du M.; Campos-Gonzalez-Angulo J.; Yuen-Zhou J. Polariton chemistry: controlling molecular dynamics with optical cavities. Chem. Sci. 2018, 9, 6325–6339. 10.1039/C8SC01043A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Flick J.; Rivera N.; Narang P. Strong light-matter coupling in quantum chemistry and quantum photonics. Nanophotonics 2018, 7, 1479–1501. 10.1515/nanoph-2018-0067. [DOI] [Google Scholar]
  4. Hertzog M.; Wang M.; Mony J.; Börjesson K. Strong light–matter interactions: a new direction within chemistry. Chem. Soc. Rev. 2019, 48, 937–961. 10.1039/C8CS00193F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Schwartz T.; Hutchison J. A.; Genet C.; Ebbesen T. W. Reversible Switching of Ultrastrong Light-Molecule Coupling. Phys. Rev. Lett. 2011, 106, 196405. 10.1103/PhysRevLett.106.196405. [DOI] [PubMed] [Google Scholar]
  6. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  7. Orgiu E.; George J.; Hutchison J. A.; Devaux E.; Dayen J. F.; Doudin B.; Stellacci F.; Genet C.; Schachenmayer J.; Genes C.; Pupillo G.; Samorì P.; Ebbesen T. W. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 2015, 14, 1123–1129. 10.1038/nmat4392. [DOI] [PubMed] [Google Scholar]
  8. Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
  9. Zhong X.; Chervy T.; Wang S.; George J.; Thomas A.; Hutchison J. A.; Devaux E.; Genet C.; Ebbesen T. W. Non-Radiative Energy Transfer Mediated by Hybrid Light-Matter States. Angew. Chem. 2016, 128, 6310–6314. 10.1002/ange.201600428. [DOI] [PubMed] [Google Scholar]
  10. Zhong X.; Chervy T.; Zhang L.; Thomas A.; George J.; Genet C.; Hutchison J. A.; Ebbesen T. W. Energy Transfer between Spatially Separated Entangled Molecules. Angew. Chem., Int. Ed. 2017, 56, 9034–9038. 10.1002/anie.201703539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Stranius K.; Hertzog M.; Börjesson K. Selective manipulation of electronically excited states through strong light–matter interactions. Nat. Commun. 2018, 9, 2273. 10.1038/s41467-018-04736-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Munkhbat B.; Wersäll M.; Baranov D. G.; Antosiewicz T. J.; Shegai T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Sci. Adv. 2018, 4, eaas9552 10.1126/sciadv.aas9552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Peters V. N.; Faruk M. O.; Asane J.; Alexander R.; Peters D. A.; Prayakarao S.; Rout S.; Noginov M. A. Effect of strong coupling on photodegradation of the semiconducting polymer P3HT. Optica 2019, 6, 318–325. 10.1364/OPTICA.6.000318. [DOI] [Google Scholar]
  14. Shalabney A.; George J.; Hutchison J.; Pupillo G.; Genet C.; Ebbesen T. W. Coherent coupling of molecular resonators with a microcavity mode. Nat. Commun. 2015, 6, 5981. 10.1038/ncomms6981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Long J. P.; Simpkins B. S. Coherent Coupling between a Molecular Vibration and Fabry–Perot Optical Cavity to Give Hybridized States in the Strong Coupling Limit. ACS Photonics 2015, 2, 130–136. 10.1021/ph5003347. [DOI] [Google Scholar]
  16. Simpkins B. S.; Fears K. P.; Dressick W. J.; Spann B. T.; Dunkelberger A. D.; Owrutsky J. C. Spanning Strong to Weak Normal Mode Coupling between Vibrational and Fabry–Pérot Cavity Modes through Tuning of Vibrational Absorption Strength. ACS Photonics 2015, 2, 1460–1467. 10.1021/acsphotonics.5b00324. [DOI] [Google Scholar]
  17. George J.; Shalabney A.; Hutchison J. A.; Genet C.; Ebbesen T. W. Liquid-Phase Vibrational Strong Coupling. J. Phys. Chem. Lett. 2015, 6, 1027–1031. 10.1021/acs.jpclett.5b00204. [DOI] [PubMed] [Google Scholar]
  18. Hertzog M.; Börjesson K. The Effect of Coupling Mode in the Vibrational Strong Coupling Regime. ChemPhotoChem. 2020, 4, 612–617. 10.1002/cptc.202000047. [DOI] [Google Scholar]
  19. Menghrajani K. S.; Fernandez H. A.; Nash G. R.; Barnes W. L. Hybridization of Multiple Vibrational Modes via Strong Coupling Using Confined Light Fields. Adv. Opt. Mater. 2019, 7, 1900403. 10.1002/adom.201900403. [DOI] [Google Scholar]
  20. Dunkelberger A. D.; Grafton A. B.; Vurgaftman I.; Soykal O. O.; Reinecke T. L.; Davidson R. B.; Simpkins B. S.; Owrutsky J. C. Saturable Absorption in Solution-Phase and Cavity-Coupled Tungsten Hexacarbonyl. ACS Photonics 2019, 6, 2719–2725. 10.1021/acsphotonics.9b00703. [DOI] [Google Scholar]
  21. Pietron J. J.; Fears K. P.; Owrutsky J. C.; Simpkins B. S. Electrochemical Modulation of Strong Vibration–Cavity Coupling. ACS Photonics 2020, 7, 165–173. 10.1021/acsphotonics.9b01339. [DOI] [Google Scholar]
  22. Xiang B.; Ribeiro R. F.; Li Y.; Dunkelberger A. D.; Simpkins B. B.; Yuen-Zhou J.; Xiong W. Manipulating optical nonlinearities of molecular polaritons by delocalization. Sci. Adv. 2019, 5, eaax5196 10.1126/sciadv.aax5196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Menghrajani K. S.; Nash G. R.; Barnes W. L. Vibrational Strong Coupling with Surface Plasmons and the Presence of Surface Plasmon Stop Bands. ACS Photonics 2019, 6, 2110–2116. 10.1021/acsphotonics.9b00662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Menghrajani K. S.; Barnes W. L. Strong coupling beyond the light-line. ACS Photonics 2020, 7, 2448–2459. 10.1021/acsphotonics.0c00552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Takele W. M.; Wackenhut F.; Piatkowski L.; Meixner A. J.; Waluk J. Multimode Vibrational Strong Coupling of Methyl Salicylate to a Fabry–Pérot Microcavity. J. Phys. Chem. B 2020, 124, 5709–5716. 10.1021/acs.jpcb.0c03815. [DOI] [PubMed] [Google Scholar]
  26. Lather J.; Bhatt P.; Thomas A.; Ebbesen T. W.; George J. Cavity Catalysis by Cooperative Vibrational Strong Coupling of Reactant and Solvent Molecules. Angew. Chem., Int. Ed. 2019, 58, 10635–10638. 10.1002/anie.201905407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hirai K.; Takeda R.; Hutchison J. A.; Uji-i H. Modulation of Prins Cyclization by Vibrational Strong Coupling. Angew. Chem. 2020, 132, 5370–5373. 10.1002/ange.201915632. [DOI] [PubMed] [Google Scholar]
  28. Pang Y.; Thomas A.; Nagarajan K.; Vergauwe R. M. A.; Joseph K.; Patrahau B.; Wang K.; Genet C.; Ebbesen T. W. On the Role of Symmetry in Vibrational Strong Coupling: The Case of Charge-Transfer Complexation. Angew. Chem. 2020, 132, 10522–10526. 10.1002/ange.202002527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Thomas A.; Jayachandran A.; Lethuillier-Karl L.; Vergauwe R. M.; Nagarajan K.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Ground state chemistry under vibrational strong coupling: dependence of thermodynamic parameters on the Rabi splitting energy. Nanophotonics 2020, 9, 249–255. 10.1515/nanoph-2019-0340. [DOI] [Google Scholar]
  30. Thomas A.; Lethuillier-Karl L.; Nagarajan K.; Vergauwe R. M. A.; George J.; Chervy T.; Shalabney A.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 2019, 363, 615–619. 10.1126/science.aau7742. [DOI] [PubMed] [Google Scholar]
  31. Xiang B.; Ribeiro R. F.; Du M.; Chen L.; Yang Z.; Wang J.; Yuen-Zhou J.; Xiong W. Intermolecular vibrational energy transfer enabled by microcavity strong light–matter coupling. Science 2020, 368, 665–667. 10.1126/science.aba3544. [DOI] [PubMed] [Google Scholar]
  32. Vergauwe R. M. A.; Thomas A.; Nagarajan K.; Shalabney A.; George J.; Chervy T.; Seidel M.; Devaux E.; Torbeev V.; Ebbesen T. W. Modification of Enzyme Activity by Vibrational Strong Coupling of Water. Angew. Chem., Int. Ed. 2019, 58, 15324–15328. 10.1002/anie.201908876. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Hirai K.; Hutchison J. A.; Uji-i H. Recent Progress of Vibropolaritonic Chemistry. ChemPlusChem 2020, 85, 1981. 10.1002/cplu.202000411. [DOI] [PubMed] [Google Scholar]
  34. Galego J.; Climent C.; Garcia-Vidal F. J.; Feist J. Cavity Casimir-Polder Forces and Their Effects in Ground-State Chemical Reactivity. Phys. Rev. X 2019, 9, 021057. 10.1103/PhysRevX.9.021057. [DOI] [Google Scholar]
  35. Hiura H.; Shalabney A.. A Reaction Kinetic Model for Vacuum-Field Catalysis Based on Vibrational Light-Matter Coupling. 2019, chemrxiv.9275777.v1. ChemRxiv. (accessed Jan 22, 2021).
  36. Khitrova G.; Gibbs H. M.; Kira M.; Koch S. W.; Scherer A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2006, 2, 81–90. 10.1038/nphys227. [DOI] [Google Scholar]
  37. Hertzog M.; Rudquist P.; Hutchison J. A.; George J.; Ebbesen T. W.; Börjesson K. Voltage-controlled switching of strong light–matter interactions using liquid crystals. Chem. - Eur. J. 2017, 23, 18166–18170. 10.1002/chem.201705461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Berghuis A. M.; Serpenti V.; Ramezani M.; Wang S.; Rivas J. G. Light–Matter Coupling Strength Controlled by the Orientation of Organic Crystals in Plasmonic Cavities. J. Phys. Chem. C 2020, 124, 12030–12038. 10.1021/acs.jpcc.0c00692. [DOI] [Google Scholar]
  39. Le Roux F.; Taylor R. A.; Bradley D. D. C. Enhanced and Polarization-Dependent Coupling for Photoaligned Liquid Crystalline Conjugated Polymer Microcavities. ACS Photonics 2020, 7, 746–758. 10.1021/acsphotonics.9b01596. [DOI] [Google Scholar]
  40. Savasta S.; Saija R.; Ridolfo A.; Di Stefano O.; Denti P.; Borghese F. Nanopolaritons: Vacuum Rabi Splitting with a Single Quantum Dot in the Center of a Dimer Nanoantenna. ACS Nano 2010, 4, 6369–6376. 10.1021/nn100585h. [DOI] [PubMed] [Google Scholar]
  41. Manjavacas A.; Garcia de Abajo F. J.; Nordlander P. Quantum Plexcitonics: Strongly Interacting Plasmons and Excitons. Nano Lett. 2011, 11, 2318–2323. 10.1021/nl200579f. [DOI] [PubMed] [Google Scholar]
  42. Schlather A. E.; Large N.; Urban A. S.; Nordlander P.; Halas N. J. Near-Field Mediated Plexcitonic Coupling and Giant Rabi Splitting in Individual Metallic Dimers. Nano Lett. 2013, 13, 3281–3286. 10.1021/nl4014887. [DOI] [PubMed] [Google Scholar]
  43. Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Rodrigo D.; Limaj O.; Janner D.; Etezadi D.; Garcia de Abajo F. J.; Pruneri V.; Altug H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. 10.1126/science.aab2051. [DOI] [PubMed] [Google Scholar]
  45. Limaj O.; Etezadi D.; Wittenberg N. J.; Rodrigo D.; Yoo D.; Oh S.-H.; Altug H. Infrared Plasmonic Biosensor for Real-Time and Label-Free Monitoring of Lipid Membranes. Nano Lett. 2016, 16, 1502–1508. 10.1021/acs.nanolett.5b05316. [DOI] [PubMed] [Google Scholar]
  46. Singh P. SPR Biosensors: Historical Perspectives and Current Challenges. Sens. Actuators, B 2016, 229, 110–130. 10.1016/j.snb.2016.01.118. [DOI] [Google Scholar]
  47. Leitis A.; Tittl A.; Liu M.; Lee B. H.; Gu M. B.; Kivshar Y. S.; Altug H. Angle-multiplexed all-dielectric metasurfaces for broadband molecular fingerprint retrieval. Sci. Adv. 2019, 5, eaaw2871 10.1126/sciadv.aaw2871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Novotny L.; Hecht B.. Principles of Nano-Optics; Cambridge University Press: Cambridge, 2006. [Google Scholar]
  49. Törmä P.; Barnes W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 2015, 78, 013901. 10.1088/0034-4885/78/1/013901. [DOI] [PubMed] [Google Scholar]
  50. Pino J. d.; Feist J.; Garcia-Vidal F. J Quantum theory of collective strong coupling of molecular vibrations with a microcavity mode. New J. Phys. 2015, 17, 053040. 10.1088/1367-2630/17/5/053040. [DOI] [Google Scholar]
  51. Baranov D. G.; Wersäll M.; Cuadra J.; Antosiewicz T. J.; Shegai T. Novel Nanostructures and Materials for Strong Light–Matter Interactions. ACS Photonics 2018, 5, 24–42. 10.1021/acsphotonics.7b00674. [DOI] [Google Scholar]
  52. Climent C.; Galego J.; Garcia-Vidal F. J.; Feist J. Plasmonic Nanocavities Enable Self-Induced Electrostatic Catalysis. Angew. Chem., Int. Ed. 2019, 58, 8698–8702. 10.1002/anie.201901926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Triana J.; Herrera F.. Self-Dissociation of Polar Molecules in a Confined Infrared Vacuum. 2020, chemrxiv.12702419.v1. ChemRxiv. (accessed Jan 22, 2021).
  54. Bisht A.; Cuadra J.; Wersäll M.; Canales A.; Antosiewicz T. J.; Shegai T. Collective Strong Light-Matter Coupling in Hierarchical Microcavity-Plasmon-Exciton Systems. Nano Lett. 2019, 19, 189–196. 10.1021/acs.nanolett.8b03639. [DOI] [PubMed] [Google Scholar]
  55. Baranov D. G.; Munkhbat B.; Zhukova E.; Bisht A.; Canales A.; Rousseaux B.; Johansson G.; Antosiewicz T. J.; Shegai T. Ultrastrong coupling between nanoparticle plasmons and cavity photons at ambient conditions. Nat. Commun. 2020, 11, 5561. 10.1038/s41467-020-16524-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Hopfield J. J. Theory of the Contribution of Excitons to the Complex Dielectric Constant of Crystals. Phys. Rev. 1958, 112, 1555–1567. 10.1103/PhysRev.112.1555. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c04014_si_001.pdf (1.2MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES