Generalized SIR (GSIR) epidemic model: An improved framework for the predictive monitoring of COVID-19 pandemic

Abstract

Novel coronavirus respiratory disease COVID-19 has caused havoc in many countries across the globe. In order to contain infection of this highly contagious disease, most of the world population is constrained to live in a complete or partial lockdown for months together with a minimal human-to-human interaction having far reaching consequences on countries’ economy and mental well-being of their citizens. Hence, there is a need for a good predictive model for the health advisory bodies and decision makers for taking calculated proactive measures to contain the pandemic and maintain a healthy economy. This paper extends the mathematical theory of the classical Susceptible–Infected–Removed (SIR) epidemic model and proposes a Generalized SIR (GSIR) model that is an integrative model encompassing multiple waves of daily reported cases. Existing growth function models of epidemic have been shown as the special cases of the GSIR model. Dynamic modeling of the parameters reflect the impact of policy decisions, social awareness, and the availability of medication during the pandemic. GSIR framework can be utilized to find a good fit or predictive model for any pandemic. The study is performed on the COVID-19 data for various countries with detailed results for India, Brazil, United States of America (USA), and World. The peak infection, total expected number of COVID-19 cases and thereof deaths, time-varying reproduction number, and various other parameters are estimated from the available data using the proposed methodology. The proposed GSIR model advances the existing theory and yields promising results for continuous predictive monitoring of COVID-19 pandemic.

1. Introduction

There are many mathematical approaches for the modeling and analysis of the spread of infectious, contagious, or both types of diseases in the human population. The mathematical models provide important information such as the basic reproduction number, threshold values, contact, removal and death rates. These models help in the estimation of key parameters and evaluation of the sensitivities to changes in these parameters on the pandemic spread or containment. This information about any contagious disease in regions, communities, countries, and across the globe can help in devising better strategies for controlling the transmission. Epidemic models have been used for the analysis of disease spread, forecast, identifying trends, planning, evaluation, implementation, optimizing various resources for testing, detection and prevention using the therapy, medication, and other disease control programs [1]. Studies [1], [2], [3], [4] have developed a number of epidemic models and have also derived the epidemic threshold value, namely the reproduction number, that if exceeded beyond a critical value leads to an epidemic outbreak. These models can analyze and predict an outbreak of a specific disease. The classic Susceptible–Infected–Removed (SIR) model and its variants such as Susceptible–Exposed–Infected–Removed (SEIR), Susceptible–Exposed–Infected–Recovered–Susceptible (SEIRS), passively immune SEIR (MSEIR), Susceptible–Infected–Recovered–Dead (SIRD) and many more models such as SIRS, SEIS, SI, SIS have been widely used in the literature for epidemic modeling and prediction.

The classical SIR model, proposed by Kermack–McKendrick [2], consists of a set of three coupled differential equations which describe the dynamics of the pandemic over time using the $S$, $I$, and $R$ compartments. It has been utilized to describe the variations of the infected individuals from the epidemics of severe acute respiratory syndrome (SARS), middle east respiratory syndrome (MERS) and influenza A virus subtype (H1N1) [5], [6], [7], [8], [9]. The SIR model allows a one-way movement from susceptible to infectious to removed. This seems reasonable for an infectious disease that is transmitted from human to human, while the recovery provides a lasting resistance [10], [11]. Recently, the SIR model and its variants have been used to model the COVID-19 pandemic [10], [12], [13], [14].

COVID-19 is a viral disease rapidly spreading to various parts of the globe. It has many symptoms such as cough, sore throat, fever, and difficulty in respiration. Initially, some cases of COVID-19 were reported from Wuhan, China in December 2019. Subsequently, it spread rapidly to other countries. Millions of people have been infected by this virus globally and many more have lost their jobs, livelihoods, and businesses. There is a continuous struggle for medical and other basic necessities, particularly, in countries where COVID-19 reached initially because the countries were not prepared for its lethal impact and rapid spread. Such an emergency in this pandemic now or later for any other disease requires immediate corrective actions for humans. COVID-19 is a highly contagious disease and is known to spread by coming in contact with viruses through air and other common surfaces contaminated by infected persons. It is believed that this virus may survive over air and on many surfaces for several hours and, therefore, utmost precautions are required to avoid the spread of the disease. Since the onset of the disease, the World Health Organization (WHO) has been providing advisories and detailed information from time-to-time [15].

Resumption of the travel, economic, and other activities, along with high stress on the healthcare facilities can be better managed and utilized by developing suitable mathematical models for understanding, estimating and predicting the spread of pandemic. The classical SIR model is used in [16] to understand the outbreak of COVID-19 in China. In order to predict the expected number of deaths by considering data from India, a regression analysis approach is used in [17]. An autoregressive integrated moving average model is used in [18] for the prediction of infected cases in Italy. The long short-term memory (LSTM) model is employed in [19] for estimating the number of cases and analyzing the efficacy of the lockdown and social isolation. The numbers of daily cases of infection and death vary due to multiple reasons including the highly random nature of the pandemic, the number of testing, and the reporting mechanism. Hence, the trend and variability analysis of the data using the discrete cosine transform (DCT) based Fourier decomposition method (FDM) [20], [21] followed by Gaussian mixture model (GMM) for COVID-19 prediction has been used recently in [22]. The FDM is based on DCT that works as an optimal transform for the first order Gauss–Markov random signals and has been proved useful in various applications [23], [24], [25], [26]. Authors in [27] presented predictions related to the spread of COVID-19 disease in Italy, France, and China. In order to help the authorities respond to COVID-19 epidemics, a case study is performed in [28] for the identification of situational information from the social media. In [29], a data-driven SIR model is implemented to estimate various parameters in order to predict the size and end-dates of COVID-19 pandemic in different parts of the globe. Modeling of COVID-19 epidemic and study of the implementation of population-wide interventions in Italy is performed in [30]. Using LSTM networks, forecasting of COVID-19 transmission is performed for Canada in [31]. The estimation of the duration of outbreaks and its turning point in various countries is performed using the gamma mixture model ($\Gamma$MM) in [32], while the logistic growth model is used for the predictions of pandemic size and end-dates in [29], [33]. Recently, some studies [10], [12], [13] have been performed to model the reproduction number as a time-varying parameter using the SIR model.

This work advances the mathematical theory of SIR modeling of pandemic and proposes a Generalized SIR (GSIR) model. The classical SIR model is a special case of the proposed GSIR model which encompasses many distinct features. The main contributions of this study are as follows:

• 1.This study identifies the limitations of the classical SIR model (refer Section 2) and proposes a new GSIR model as a solution to these. Although the present study focuses on only improvising the SIR model, the proposed methodology can be easily extended for the other variants of the SIR model.
• 2.GSIR model is an integrative model that captures the pandemic data via distinct waves that emerge and vanish during the time period studied.
• 3.Although GMM, $\Gamma$MM, and logistic growth functions have been used for COVID-19 modeling and prediction, their connection with the SIR model is not established so far. In fact, the solution of the classical SIR model is computed numerically using the available epidemic data. We demonstrate that the logistic, GMM, $\Gamma$MM and other growth functions are the special solutions of the constituent waves of the proposed GSIR model.
• 4.Unlike the classical SIR model, the GSIR solution leads to time-varying parameters that grow or decay over time. Furthermore, the GSIR model presents a closed form solution of all the system parameters, which is not available in the SIR model. The dynamic profile of these parameters captures the impact of policy decisions and awareness such as social or physical distancing (sotancing), lockdown, medication, vaccination, and other measures.
• 5.The classical SIR model is an initial-value problem and does not ensure end/final boundary conditions for different functions of susceptible, infected, and removed. The proposed GSIR model ensures both initial and final conditions and overcomes this limitation of the SIR model.
• 6.The proposed modeling approach can also be easily extended for the other variants of the classical SIR model such as SEIR, SEIRS, MSEIR, SIRS, SIRD, SEIS, SI, and SIS.

We have used the proposed GSIR model to predict the total number of cases, deaths, end-dates and other parameters for the pandemic in India, Brazil, and USA. The rest of this study is organized as follows. Section 2 presents the classical SIR epidemic model. Section 3 discusses the model proposed in this work and defines various parameters associated with the GSIR model. Results and discussions are presented in Section 4. Finally, Section 5 presents the conclusion and future scope of the study.

2. The classical SIR epidemic model

In this section, we discuss the classical Susceptible–Infected–Removed (SIR) model. The classical SIR epidemic model [1], [2], as shown via a block diagram in Fig. 1, is defined by the following initial-value problem

$$\frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=\frac{-\beta I\left(t\right)S\left(t\right)}{N},S\left(0\right)=S_0\ge 0,$$ (1a)

$$\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}=\frac{\beta S\left(t\right)I\left(t\right)}{N}-\gamma I\left(t\right),I\left(0\right)=I_0\ge 0,$$ (1b)

$$\frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\gamma I\left(t\right),R\left(0\right)=R_0\ge 0,$$ (1c)

where $S\left(t\right)$, $I\left(t\right)$, and $R\left(t\right)$ are the numbers of susceptible, infected, and removed (recovered and deaths) cases, respectively, $\beta$ is the contact/infection rate, and $\gamma$ is the removal rate ($1/\gamma$ represents the average infectious period). The total population size (a constant number) is obtained as

$$S\left(t\right)+I\left(t\right)+R\left(t\right)=N.$$ (2)

Fig. 1.

Block diagram of the classical SIR model.

It is evident from (1) that $\frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}+\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}+\frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=0$. The SIR model parameters $\beta$ and $\gamma$ along with the initial values $S_0,I_0,R_0$ can be estimated by minimizing ${\Vert F\left(t\right)-\hat{F}(t,\beta ,\gamma ,S_0,I_0,R_0)\Vert }^2$, where $F\left(t\right)=I\left(t\right)+R\left(t\right)$ is the given total number of cases and $\hat{F}\left(t\right)$ is the total number of estimated cases by the SIR model at times $t_1,t_2,\dots ,t_m$.

In addition to the above parameters, another important parameter is the attack rate that is used to indicate the pace of the spread of the viral disease. This parameter is represented by the reproduction number and is denoted as ${\mathfrak{R}}_0$. The value ${\mathfrak{R}}_0>1$ indicates that the infection growth (1b) is positive, ${\mathfrak{R}}_0=1$ indicates flattening of the infection, while ${\mathfrak{R}}_0<1$ indicates that the outbreak will gradually disappear. This value depends on the sign of ${\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}|}_{t=0}$. From (1b), it is evident that if $\frac{\beta S_0}{N\gamma }-1$ is greater than zero, ${\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}|}_{t=0}$ will be positive indicating an increase in the number of cases reported daily over time, leading to epidemic. Thus, ${\mathfrak{R}}_0=\frac{\beta S_0}{N\gamma }$ with a value greater than 1 indicates epidemic.

In reality, both $\beta$ and $\gamma$ are functions of time because they change with awareness, hygiene, social distancing, lockdown, medication, vaccination, and other measures. However, the classical SIR model assumes these parameters to be constant, which is one of the biggest limitations of this model. Likewise, it is worthwhile to compute and track the reproduction number at all time points instead of computing only at the beginning. This tracking can be very helpful because policy related changes will eventually translate into this number showing whether the pandemic is increasing (${\mathfrak{R}}_0\left(t\right)>1$) or decreasing (${\mathfrak{R}}_0\left(t\right)<1$) and hence, corrective measures can be taken.

We enumerate the following limitations of the classical SIR model:

• 1.Generally, SIR model assumes all parameters $\beta$, $\gamma$, and ${\mathfrak{R}}_0$ to be constant, while in real scenario, these parameters would be changing with time.
• 2.The solution to the model is computed numerically and hence, the model has limited tracking and prediction ability.
• 3.Initial infected population $I\left(0\right)$ is small at the beginning of the pandemic. At the end of the pandemic, its final value should be zero, i.e., $I\left(\infty \right)=0$, which is not ensured in the classical SIR model.
• 4.Initial removed population, $R\left(0\right)=0$, because there is no recovery at the very beginning of the pandemic. Once the pandemic is over, there must be complete removal by recovery and deaths. Thus, $R\left(\infty \right)=K$, where $K={\int }_0^{\infty }I\left(t\right)\mathrm{d}t$, is the total number of population infected over the entire period of the pandemic. However, this is also not ensured in the classical SIR model.
• 5.Initial susceptible population, $S\left(0\right)=N-I\left(0\right)$, is close to the total population $N$. Since $\frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}$ is a negative-valued function of time, $S\left(t\right)\ge 0$ is also a decreasing function of time. Therefore, its final value must be zero, i.e., $S\left(\infty \right)=0$. However, this is not ensured in the classical SIR model.

From the theory of differential calculus, it is well-known that an $n$th order differential equation satisfies $n$ boundary conditions. The classical SIR model depicted by (1) is a set of three first-order differential equations. Hence, this model can satisfy only three conditions. In this model, these boundary conditions have been chosen to be the three initial conditions ($S\left(0\right)=S_0,I\left(0\right)=I_0$ and $R\left(0\right)=R_0$). Thus, the SIR model is also known as the initial-value problem. The final conditions are not satisfied in the classical SIR model. Our proposed GSIR model ensures both initial and final conditions. Further, we assert that the initial susceptible population $S_0$ is continuously interacting or coming in contact with the infected cases. Hence, in the long run, almost all susceptible persons will get infected and thus, $N=K$. In other words, practically, the susceptible population does not include those (i) who are not coming in contact (or interacting) with the infected cases, and (ii) who are immune and may be interacting with the infected cases.

The proposed GSIR model addresses all the above limitations of the classical SIR model, is a much more generic model, and can help with better modeling and tracking ability.

3. The proposed generalized SIR (GSIR) model

In this section, we present the proposed GSIR model. During COVID-19, the number of cases kept increasing and decreasing over time. The daily reported cases change with different measures being taken by the governments. Hence, in the GSIR model, we assume that multiple waves of varying peak amplitude and shape emerge and vanish over time. The following equations capture the $P$ number of waves in the GSIR model as

$$\frac{\mathrm{d}S\left(t\right)}{\mathrm{d}t}=-\sum _{i=1}^P\frac{{\beta }_i{I}_i\left(t\right)S_i\left(t\right)}{N_i},S\left(0\right)=S_0\ge 0,$$ (3a)

$$\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}=\sum _{i=1}^P\left(\frac{{\beta }_i{I}_i\left(t\right)S_i\left(t\right)}{N_i}-{\gamma }_i{I}_i\left(t\right)-{\ell }_i\right),I\left(0\right)=I_0\ge 0,$$ (3b)

$$\frac{\mathrm{d}R\left(t\right)}{\mathrm{d}t}=\sum _{i=1}^P\left({\gamma }_i{I}_i\left(t\right)+{\ell }_i\right),R\left(0\right)=R_0\ge 0,$$ (3c)

where ${\ell }_i$ is a constant and,

$$S\left(t\right)=\sum _{i=1}^P{S}_i\left(t\right),I\left(t\right)=\sum _{i=1}^P{I}_i\left(t\right),$$ (4a)

$$R\left(t\right)=\sum _{i=1}^P{R}_i\left(t\right),N=\sum _{i=1}^P{N}_i.$$ (4b)

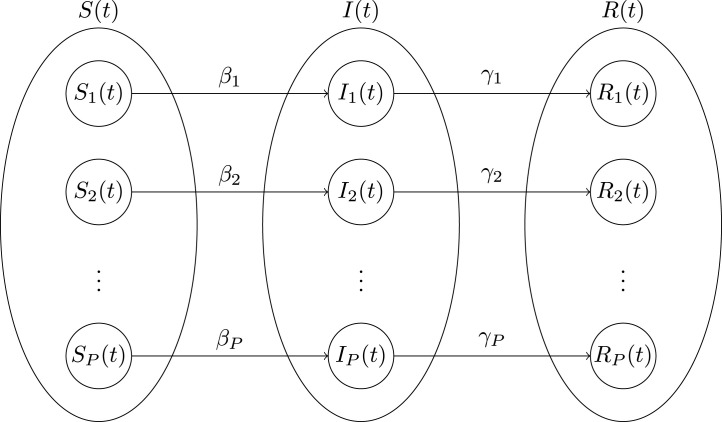
The block diagram of this proposed GSIR model is shown in Fig. 2.

Fig. 2.

A block diagram of the proposed GSIR, where susceptible, infected, and removed populations of $P$ number of waves of an outbreak of disease are presented.

3.1. GSIR model using the logistic growth model

First, we present the framework with a single wave, i.e., with $P=1$ and its modeling via the logistic growth model. We use the GSIR model equations in (3) and present the theory that presents the closed form solutions of all the system parameters.

Logistic growth model (LGM) is often used in epidemiology to model the spread of the infection. Here, the number of infections initially grow exponentially, but later decline as the numbers approach the population’s carrying-capacity, where the carrying capacity is denoted as the number of people that can be infected eventually in a population. The cumulative number of infections on the $t$th day, denoted as $C\left(t\right)$, using the LGM [34], [35], can be written as

$$C\left(t\right)=\frac{K}{1+A{e}^{-rt}},$$ (5)

where $K$ is the carrying capacity, $A$ denotes the number of persons initially infected, and $r$ is the growth rate. Corresponding to this model, the number of infected persons on the $t$th day, $I\left(t\right)$, is given by

$$I\left(t\right)=\frac{\mathrm{d}C\left(t\right)}{\mathrm{d}t}=\frac{KAr{e}^{-rt}}{{(1+A{e}^{-rt})}^2}.$$ (6)

For any country, the numbers reported on day-0 (day of reference) are those that are active on that day. Hence, these are the cumulative numbers until that day and are equal to $C\left(0\right)$. Substituting $t=0$ in (5), (6), we obtain $C\left(0\right)=C_0=\frac{K}{1+A}$ that implies $A=\frac{K}{C_0}-1$, while $C_{\infty }=K$. Also, $C\left(0\right)-\epsilon =I\left(0\right)$. $I\left(0\right)=\frac{KAr}{{(1+A)}^2}$, and $A=\frac{K}{C_0}-1$. The values of $K$, $A$, $r$, $C_0$ and $I_0$ are determined from the curve fitting of the available data. Further, we assume that $R_0=0$ and hence, $S_0=N-I_0$.

Solving for $\text{d}I\left(t\right)/\text{d}t$ from (6) above and equating to the R.H.S. of (3b), we obtain

$$\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}=\frac{\beta }{N}S\left(t\right)I\left(t\right)-\gamma I\left(t\right)-\ell =\frac{2}{K}(1+A{e}^{-rt})I^2\left(t\right)-rI\left(t\right).$$ (7)

Rearranging terms in (7), we obtain the number of susceptible persons as

$$S\left(t\right)=\frac{2N}{K\beta }\left(1+A{e}^{-rt}\right)I\left(t\right)+\left(\gamma +\frac{\ell }{I\left(t\right)}-r\right)\frac{N}{\beta },$$ (8)

where

$${\gamma }_e\left(t\right)=\gamma +\frac{\ell }{I\left(t\right)}$$ (9)

is the effective removal rate that is a function of time. The first term $\gamma$ is a constant and the second term is inversely proportional to $I\left(t\right)$. As the number of infections decrease and approach zero at large $t$, the removal rate ${\gamma }_e\left(t\right)$ increases to a large value because every person in the population is either recovered or removed by this time. In other words, at very large $t=T$ for $T$ equivalent to $\infty$, $R_T=K$ and $I_T=S_T=0$. The susceptible population at any time $t$ can be written as

$$S\left(t\right)=N-I\left(t\right)-R\left(t\right).$$ (10)

Thus, from (8), (10), we obtain the expression of $\beta$ as a function of time

$$\beta \left(t\right)=\frac{N\left[\frac{2}{K}\left(1+A{e}^{-rt}\right)I\left(t\right)+{\gamma }_e\left(t\right)-r\right]}{N-I\left(t\right)-R\left(t\right)}.$$ (11)

The initial behavior of the epidemic depends on whether the numbers decline or increase, or on the sign of ${\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}|}_{t=0}$, i.e., 

$${\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}|}_{t=0}=\frac{{\beta }_0{S}_0{I}_0}{K}-\gamma I_0-\ell =\left(\frac{{\beta }_0{S}_0}{K}-{\gamma }_{e0}\right)I_0,$$ (12)

where ${\beta }_0$ and ${\gamma }_{e0}$ denote the values of $\beta \left(t\right)$ and ${\gamma }_e\left(t\right)$, respectively, at $t=0$. For pandemic, ${\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}|}_{t=0}>0$. This implies that ${\gamma }_{e0}<\frac{{\beta }_0{S}_0}{K}$ or the reproduction number ${\mathfrak{R}}_0=\frac{{\beta }_0{S}_0}{N{\gamma }_{e0}}>1$. In general, it is worthwhile to track the sign of ${\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}|}_{t=0}$ or the value of the reproduction number ${\mathfrak{R}}_0\left(t\right)$ at time $t$ for the monitoring of pandemic. Since for pandemic $\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}>0$, we obtain the below expression of the reproduction number, from (3b), (7), as a function time

$${\mathfrak{R}}_0\left(t\right)=\frac{\beta \left(t\right)S\left(t\right)}{N{\gamma }_e\left(t\right)}=\frac{\frac{2}{K}(1+A{e}^{-rt})I\left(t\right)+{\gamma }_e\left(t\right)-r}{{\gamma }_e\left(t\right)}.$$ (13)

Next, we solve for the removed person $R\left(t\right)$ from (3c) and obtain

$$R\left(t\right)=\int \left(\gamma I\left(t\right)+\ell \right)\mathrm{d}t=\gamma C\left(t\right)+\ell t+b.$$ (14)

Substituting the initial condition $R\left(0\right)=0$ and the final condition $R\left(T\right)=K$ in (14), we obtain $b=-\gamma C_0$, $\ell =(K-\gamma K+\gamma C_0)/T$. To derive $N$, we evaluate (10) at $T$, i.e., $0=N-0-K$ and obtain $N=K$.

We utilize the above GSIR model to fit the data. In the above equations, $\gamma$ is the only free parameter. The value of $1/\gamma$ can be set to be equal to the mean infection time as known for the disease. In general, the number of infections $I\left(t\right)$ for any country will fit into multiple waves. Once the data is fitted and the number of waves extracted, we will substitute those waves individually in the GSIR model (3) and estimate the parameters for every $i\text{th}$ constituent wave.

The composite logistic growth model can be written as [34], [35]

$$C\left(t\right)=\sum _{i=1}^P\frac{K_i}{1+A_i{e}^{-r_i(t-{\tau }_i)}},$$ (15)

where the number of waves $P$, and the four parameters ($K_i,A_i,r_i,{\tau }_i$) for each wave are estimated by minimization of the objective function, which is the sum of squares of residuals [29], [33], [36]. The minimization uses the simplex search method [37] to estimate optimal values of these unknown model parameters.

3.2. GSIR model using the Gaussian growth function

Next, we model $I\left(t\right)$ using the Gaussian growth function. Here, the number of infected persons $I\left(t\right)$ on the $t$th day is given by

$$I\left(t\right)=\alpha e^{-\frac{{(t-\mu )}^2}{2{\sigma }^2}},$$ (16)

where $\mu$ denotes the mean and ${\sigma }^2$ denotes the variance of the Gaussian function, while $I_0=\alpha e^{-\frac{{\mu }^2}{2{\sigma }^2}}$. Thus, using (3b), we obtain a solution of $I\left(t\right)$, which is the GMM, as follows

$$I\left(t\right)=\sum _{i=1}^P{I}_i\left(t\right)=\sum _{i=1}^P{\alpha }_{i}exp\left(-\frac{{(t-{\mu }_i)}^2}{2{\sigma }_i^2}\right),$$ (17)

where regression parameters ${\alpha }_i$, ${\mu }_i$ and ${\sigma }_i$ are the amplitude, mean and standard deviation, respectively. The removed population $R\left(t\right)$ is obtained from (3c), similar to (14), as

$$R\left(t\right)=\sum _{i=1}^P{R}_i\left(t\right)=\sum _{i=1}^P\left(\int \left({\gamma }_i{I}_i\left(t\right)+{\ell }_i\right)\mathrm{d}t\right)=\sum _{i=1}^P\left({\gamma }_i{G}_i\left(t\right)+{\ell }_{i}t+b_i\right),$$ (18)

where $G_i\left(t\right)={\int }_{-\infty }^t\alpha e^{-\frac{{(\tau -{\mu }_i)}^2}{2{\sigma }_i^2}}\mathrm{d}\tau$. Substituting the initial condition, $R_i\left(0\right)=0$, and the final condition, $G_i\left(T\right)=N_i=R_i\left(T\right)$, in (18), we obtain $b_i=-\gamma G_i\left(0\right)$, ${\ell }_i=(N_i-{\gamma }_i{N}_i+{\gamma }_i{G}_i\left(0\right))/T$.

The susceptible population is obtained from (2), (17), (18) as

$$S\left(t\right)=\sum _{i=1}^P{S}_i\left(t\right)=\sum _{i=1}^P\left[N_i-I_i\left(t\right)-R_i\left(t\right)\right].$$ (19)

This shows that as $t\to \infty$, $I_i\left(t\right)\to 0$, $R_i\left(t\right)\to N_i$ and $S_i\left(t\right)$ reduces to zero.

Solving for $\text{d}I\left(t\right)/\text{d}t$ from (16) and equating to the R.H.S. of (3b), we obtain

$$\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}t}=\left(\frac{\beta \left(t\right)}{N}S\left(t\right)-{\gamma }_e\left(t\right)\right)I\left(t\right)=\left(\frac{\mu -t}{{\sigma }^2}\right)I\left(t\right).$$ (20)

On simplifying (20), we obtain the expression of the number of susceptible persons $S\left(t\right)$ on the $t$th day as

$$S\left(t\right)=\left(\frac{\mu +{\sigma }^2{\gamma }_e\left(t\right)-t}{{\sigma }^2\beta \left(t\right)/N}\right).$$ (21)

For the case with multiple waves, i.e., $P>1$, we can write

$$S\left(t\right)=\sum _{i=1}^P{S}_i\left(t\right)=\sum _{i=1}^P\left(\frac{{\mu }_i+{\sigma }_i^2{\gamma }_{ei}\left(t\right)-t}{{\sigma }_i^2{\beta }_i\left(t\right)/N_i}\right),$$ (22)

where ${\beta }_i\left(t\right)$ and ${\gamma }_{ei}\left(t\right)$ are the infection and removal rates, respectively, of the $i$th wave. This implies that the overall susceptible population $S\left(t\right)$ is a superposition of multiple waves ${\left\{S_i\left(t\right)\right\}}_{i=1}^P$ that are emerging and vanishing over time. From (19), (22), time-varying ${\beta }_i\left(t\right)$ is obtained as

$${\beta }_i\left(t\right)=\left(\frac{{\mu }_i+{\sigma }_i^2{\gamma }_{ei}\left(t\right)-t}{N_i-I_i\left(t\right)-R_i\left(t\right)}\right)\frac{N_i}{{\sigma }_i^2}.$$ (23)

Finally, similar to (13), time-varying reproduction number is obtained as

$${\mathfrak{R}}_{0ic}\left(t\right)=\frac{{\beta }_i\left(t\right)S_i\left(t\right)}{{\gamma }_{ei}\left(t\right)N_i},$$ (24)

where from (9)

$${\gamma }_{ei}\left(t\right)={\gamma }_i+\frac{{\ell }_i}{I_i\left(t\right)},$$ (25)

and for each $i$, ${\gamma }_i$ is a free parameter that affects all parameters, waves $R\left(t\right)$ and $S\left(t\right)$, but does not affect $I\left(t\right)$.

3.3. GSIR model using the gamma growth function

Next, we attempt to find the solution for the Gamma growth function into the GSIR model. Here, the number of infected period on the $t$th day, $I\left(t\right)$, is given by

$$I\left(t\right)=\rho t^{\kappa -1}{e}^{-\lambda t},\kappa >0,\lambda >0,$$ (26)

where $\rho$, $\lambda$, and $\kappa$ are the regression parameters of the gamma growth function. Physically, $\lambda$ and $\kappa$ represent the rate and shape, respectively, of the gamma function. For $P$ waves, we obtain $I\left(t\right)$ in terms of the Gamma mixture model ($\Gamma$MM) as

$$I\left(t\right)=\sum _{i=1}^P{I}_i\left(t\right)=\sum _{i=1}^P{\rho }_i{t}^{{\kappa }_i-1}{e}^{-{\lambda }_{i}t},{\kappa }_i>0,{\lambda }_i>0.$$ (27)

The Erlang (${\kappa }_i\in {\mathbb{Z}}_{+}$, a positive integer), exponential (${\kappa }_i=1$), and chi-squared (replacing ${\kappa }_i-1$ with $k_i/2-1$ and ${\lambda }_i=1/2$) distributions are special cases of the gamma distribution. Further, by modeling each wave in the R.H.S. of (3b) as $\left(\frac{{\beta }_i\left(t\right)S_i\left(t\right)}{N}-{\gamma }_{ei}\left(t\right)\right)=\left(\frac{{\kappa }_i-1}{t}-{\lambda }_i\right)⟹S_i\left(t\right)=\left({\gamma }_{ei}\left(t\right)-{\lambda }_i+\frac{{\kappa }_i-1}{t}\right)\frac{N}{{\beta }_i\left(t\right)}$ with $t>0$.

General comments: Another interesting model, namely, the Gaussian-Gamma mixture model (G$\Gamma$MM) can be obtained by combining (17), (27) piecewise or group-wise or both as

$$I\left(t\right)=\sum _{i=1}^{P_1}{\rho }_i{t}^{{\kappa }_i-1}{e}^{-{\lambda }_{i}t}+\sum _{i=P_1+1}^P{\alpha }_{i}exp\left(-\frac{{(t-{\mu }_i)}^2}{2{\sigma }_i^2}\right).$$ (28)

Following the above procedure, various other mixture model of the distributions (e.g., beta, Kumaraswamy, Irwin–Hall, Gumbel, Fréchet and Weibull) can be easily obtained, simply because solution of the differential equation (3b) depends on the modeling of the individual waves.

3.4. Computation of the composite parameters with multiple waves

So far, we have observed that there could be multiple waves. Hence, we computed the composite parameters for $P$ waves. From (1) and (3), (1) and (3), we observe that the composite (overall) infection rate ${\beta }_c\left(t\right)$, removal rate ${\gamma }_c\left(t\right)$ and reproduction number ${\mathfrak{R}}_{0c}\left(t\right)$ can be obtained as

$${\beta }_c\left(t\right)=\frac{\sum _{i=1}^P\frac{{\beta }_i\left(t\right)S_i\left(t\right)I_i\left(t\right)}{N_i}}{S\left(t\right)I\left(t\right)/N},$$ (29a)

$${\gamma }_c\left(t\right)=\frac{\sum _{i=1}^P\left({\gamma }_i{I}_i\left(t\right)+{\ell }_i\right)}{I\left(t\right)},$$ (29b)

$$\text{ and }{\mathfrak{R}}_{0c}\left(t\right)=\frac{{\beta }_c\left(t\right)\sum _{i=1}^P{S}_i\left(t\right)}{{\gamma }_c\left(t\right)\sum _{i=1}^P{N}_i}$$ (29c)

respectively, where composite $S\left(t\right)$, $I\left(t\right)$, and $N$ are presented in (4). The computation of the above parameters is valid for any growth function or for any general mixture growth model, where the constituent waves can be modeled using different types of growth functions.

4. Results and discussion

In this section, we present the results of the GSIR model using the Logistic growth model for COVID-19 infection. We have presented results related to daily cases for Brazil, India, USA, World, and daily World deaths. First, we analyze the data of Brazil. We present the comparative results of SIR modeling (Fig. 3) and GSIR modeling (Fig. 4) on the data of Brazil. The root mean squared value (RMSE) in fitting the data with SIR model (RMSE$=$22986) is more than twice than that obtained (RMSE$=$10983) with the GSIR

Fig. 3.

SIR model fitting for Brazil (actual data: March 6 to July 28, 2020). Top subfigure: modeling of the total number of people infected; middle subfigure: modeling of new cases reported on daily basis—the middle red curve shows the fitted data, while the outer and inner red curves are at two standard deviation away from the middle curve; and bottom subfigure: predicted versus actual value of growth factor of daily cases computed as $\frac{\text{d}C\left(t\right)/\text{d}t}{C\left(t\right)}\times 100\text{\%}$. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

(a) Logistic model fitting for Brazil (actual data: March 6 to July 28, 2020) which shows there are four COVID-19 waves; (b) corresponding plots of $I_i\left(t\right)$, $S_i\left(t\right)$ and $R_i\left(t\right)$ using the proposed GSIR model and; (c) the corresponding ${\mathfrak{R}}_{0c}\left(t\right)$. In (a): Top subfigure: modeling of the total number of people infected; middle subfigure: modeling of new cases reported on daily basis $I\left(t\right)$–the middle black curve shows the fitted data, while the outer and inner red curves are at two standard deviation away from the middle curve; and bottom subfigure: predicted versus actual value of growth factor of daily cases computed as $\frac{\text{d}C\left(t\right)/\text{d}t}{C\left(t\right)}\times 100\text{\%}$.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

model. In addition, the GSIR model of Fig. 4 shows multiple pandemic waves in Brazil data, while the SIR model is not able to do so. As we observe from Fig. 3, the SIR model fits the daily new cases data with only one wave. Since the surge of new cases emerge and vanish as the policy decisions of lockdown or partial lockdown are taken to control the pandemic, it seems inappropriate to fit the entire data within one wave. This is also the reason that the RMSE is very high with the SIR model compared to the GSIR model. Hence, overall, the GSIR model is performing better than the SIR model.

As shown by the GSIR model, there are four pandemic waves in Brazil with the total number of expected cases to be approximately 3.37 million, estimated from the data as of 28 July, 2020. First wave has 142,942 cases with $r_1=0.1756$, second wave is significantly stronger than the first one with 1.1208e$+$06 cases and $r_2=0.1068$, third wave is also strong (1.65e$+$06 cases) with $r_3=0.0932$, and the estimated final wave is the weakest with 457 644 cases and $r_4=0.1563$ as shown in Fig. 4(a), while the parameters are presented in Table 1. Plots of $S_i\left(t\right)$, $I_i\left(t\right)$, $R_i\left(t\right)$, the corresponding reproduction number waves ${\mathfrak{R}}_{0ic}\left(t\right)$, and the composite reproduction number wave ${\mathfrak{R}}_{0c}\left(t\right)$ obtained from the proposed model are shown in Fig. 4(b) and (c). Currently, the overall growth factor of daily cases for Brazil is 1.69%.

Table 1.

Estimated parameters of multiple waves of integrative GSIR model shown in Eq. (15).

S.N.	Parameters	India, P $=$ 2	Brazil, P $=$ 4	USA, P $=$ 4	World, P $=$ 4	World deaths, P $=$ 4
1	$K_1$	438 003	142 942	808 921	2.6723e＋06	181 988
2	$r_1$	0.0615	0.1756	0.1675	0.1083	0.1357
3	$C_{01}$	890	9.0231	6.8432	63.9908	1.6932
4	${\tau }_1$	0	0	0	0	0
5	$K_2$	4.068e＋06	1.121e＋06	3.2131e＋06	3.8634e＋06	145 878
6	$r_2$	0.063	0.1068	0.0830	0.08162	0.10580
7	$C_{02}$	145.1	7.3187	7.2230	51.9018	1.1222
8	${\tau }_2$	0.840	0.0022	11.4938	0.0529	1.544e−05
9	$K_3$	–	1.6500e＋06	505 948	4.5714e＋06	193 723
10	$r_3$	–	0.0932	0.1209	0.0953	0.0831
11	$C_{03}$	–	5.2979	3.6811	38.5677	0.9406
12	${\tau }_3$	–	9.9547	22.2229	50.2243	2.4858
13	$K_4$	–	457 644	612 172	1.0164e＋07	206 070
14	$r_4$	–	0.1563	0.1614	0.0918	0.0962
15	$C_{04}$	–	5.8998	7.9578	24.4083	0.8063
16	${\tau }_4$	–	11.0474	24.7327	65.0202	58.7741

Next, we present the results of India, USA, and World in Fig. 5, Fig. 6, Fig. 7, Fig. 8, while the estimated parameters are presented in Table 1. We have used the MATLAB codes [29], [33], [38] for the estimation of logistic model parameters, and downloaded COVID-19 data from [39].

Fig. 5.

(a) Logistic model fitting for India (actual data: March 3 to July 28, 2020) which shows there are four COVID-19 waves; (b) corresponding plots of $I_i\left(t\right)$, $S_i\left(t\right)$ and $R_i\left(t\right)$ using the proposed GSIR model and; (c) the corresponding ${\mathfrak{R}}_{0c}\left(t\right)$. In (a): Top subfigure: modeling of the total number of people infected; middle subfigure: modeling of new cases reported on daily basis $I\left(t\right)$–the middle black curve shows the fitted data, while the outer and inner red curves are at two standard deviation away from the middle curve; and bottom subfigure: predicted versus actual value of growth factor of daily cases computed as $\frac{\text{d}C\left(t\right)/\text{d}t}{C\left(t\right)}\times 100\text{\%}$.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

(a) Logistic model fitting for USA (actual data: February 15 to July 28, 2020) which shows there are four COVID-19 waves; (b) corresponding plots of $I_i\left(t\right)$, $S_i\left(t\right)$ and $R_i\left(t\right)$ using the proposed GSIR model and; (c) the corresponding ${\mathfrak{R}}_{0c}\left(t\right)$. In (a): Top subfigure: modeling of the total number of people infected; middle subfigure: modeling of new cases reported on daily basis $I\left(t\right)$–the middle black curve shows the fitted data, while the outer and inner red curves are at two standard deviation away from the middle curve; and bottom subfigure: predicted versus actual value of growth factor of daily cases computed as $\frac{\text{d}C\left(t\right)/\text{d}t}{C\left(t\right)}\times 100\text{\%}$.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

(a) Logistic model fitting for World (actual data: December 31, 2019 to July 28, 2020) which shows there are four COVID-19 waves; (b) corresponding plots of $I_i\left(t\right)$, $S_i\left(t\right)$ and $R_i\left(t\right)$ using the proposed GSIR model and; (c) the corresponding ${\mathfrak{R}}_{0c}\left(t\right)$. In (a): Top subfigure: modeling of the total number of people infected; middle subfigure: modeling of new cases reported on daily basis $I\left(t\right)$–the middle black curve shows the fitted data, while the outer and inner red curves are at two standard deviation away from the middle curve; and bottom subfigure: predicted versus actual value of growth factor of daily cases computed as $\frac{\text{d}C\left(t\right)/\text{d}t}{C\left(t\right)}\times 100\text{\%}$.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 8.

Logistic model fitting for World deaths (actual data: January 9 to July 28, 2020) that shows there are four COVID-19 death waves. Top subfigure: modeling of the total number of deaths; middle subfigure: modeling of new deaths reported on daily basis–the middle black curve shows the fitted data, while the outer and inner red curves are at two standard deviation away from the middle curve; and bottom subfigure: predicted versus actual value of growth factor of daily deaths. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

India has the world’s second largest population. There are two pandemic waves in India and the total number of expected cases are approximately 4.5 millions, estimated from the data as of 28 July, 2020. The first wave is relatively small (438,003 cases), while the second wave is significantly strong (4.0681e$+$06 cases) as shown in Fig. 5(a) and Table 1. Infection growth rate of the first wave ($r_1=0.061$) is similar to the second wave ($r_2=0.063$). Plots of $S_i\left(t\right)$, $I_i\left(t\right)$, $R_i\left(t\right)$, the corresponding reproduction number waves ${\mathfrak{R}}_{0ic}\left(t\right)$, and the composite reproduction number wave ${\mathfrak{R}}_{0c}\left(t\right)$ obtained from the proposed model are shown in Fig. 5(b) and (c). Currently, the overall growth factor of daily cases for India is 3.4% (from the blue line of the bottom third subfigure of Fig. 5(a)), which is highest among the considered countries.

Further, we observe from Fig. 5(b) and (c) that India attained its first peak of daily reported cases on May 6, 2020 (64th day from March 3) when the value of ${\mathfrak{R}}_{01c}\left(t\right)=1.05>1$, the second peak of daily reported cases on July 9, 2020 (129th day from March 3) when the value of ${\mathfrak{R}}_{02c}\left(t\right)=1.054>1$, and the composite peak of daily reported cases on July 18, 2020 (137th day from March 3) when the value of ${\mathfrak{R}}_{0c}\left(t\right)=1.04>1$. Our analysis predicts that the composite ${\mathfrak{R}}_{0c}\left(t\right)$ will decline below one on the 164th day, i.e., August 13, 2020, when the predicted value of daily reported cases is also going to attain its peak. Hence, although the second wave of $I_2\left(t\right)$ is still picking up as on 28th July, the trend of ${\mathfrak{R}}_{0c}\left(t\right)$ indicates that the downward journey of the pandemic began on 18th July, 2020. Further, the current trends predict that ${\mathfrak{R}}_{0c}\left(t\right)$ will attain its minimum with a value of 0.945 on the 200th day, i.e., on September 19, 2020. Thus, policymakers need to ensure that trend does not pick up from this ebb beyond Sep 19, 2020. Since another wave has not started yet, it shows that the pandemic can be controlled if people follow precautions as advertised.

On further studying the pattern of ${\mathfrak{R}}_{0c}\left(t\right)$Fig. 5(c) in the context of policy decisions taken and the predicted parameters, we note that the two waves emerged in early March 2020. While the first wave (with ${\tau }_0=0$ day) picked up immediately, the second wave (with ${\tau }_1=0.8$ day) took off very slowly. The first wave did not attain a very high peak because the spread of corona was contained by the national lockdown announced shortly, i.e., on March 22, 2020. Since the lockdown continued and there were stringent restrictions in the areas where the first few corona cases appeared, these lockdown duration and restrictions forced this wave to die out. The value of ${\mathfrak{R}}_{01c}\left(t\right)$ attained its peak around May 06, but started declining afterwards and fell below the value of 1 somewhere around 30th May 2020. It appears that a complete lockdown from March to early May yielded the desired results.

Interestingly, some relaxations in lockdown were provided on May 30, 2020. Around this time, the second wave took off from ground. In May, Shramik trains were also started by the Government of India and road transport was opened partially for inter-state movement of people within India to facilitate return to their respective home states. It is estimated that about 25 million people moved inter-state within India. This movement might have led to the spread of the disease to other regions and hence, led to the second wave that took off from very low numbers in the first week of June. At the same time, the number of tests per day grew from 0.05 million per day to around 0.13 million per day in the first week of June. By 16th July 2020, the number of tests per day were more than 0.35 million per day. Hence, the number of corona cases grew much bigger than the first wave owing to (1) the movement of people and (2) due to the growing number of tests and hence, detection of corona. Moreover, while people in initially affected areas took more precautions, people of less affected areas were relatively relaxed.

Unlock 1.0 was announced on June 08, 2020 and Unlock 2.0 was announced for July 01 to July 31 at the national level. As a consequence, major restrictions and closure of all shopping malls, cinema halls, schools, colleges, offices (work from home) continued in July. Thus, we observe from the ${\mathfrak{R}}_{02c}\left(t\right)$ wave that the downward journey from peak started on July 18, 2020 (137th day), somewhere during the middle of the Unlock 2.0 phase. From the above discussion, it is clear that the pandemic trends vis-à-vis policy are easy to interpret with waves of ${\mathfrak{R}}_{0ic}\left(t\right)$ instead of the waves of $I\left(t\right)$. Hence, it is worthwhile to track ${\mathfrak{R}}_{0ic}\left(t\right)$ instead of only computing the constant value ${\mathfrak{R}}_{0c}$ at the beginning of any pandemic.

Similar to India, four pandemic waves are observed in the data of USA. The total number of expected cases are approximately 5.14 million, estimated from the data as of 28 July, 2020. First wave has 808,921 cases with $r_1=0.1675$, the second wave is around four times stronger than the first one with 3.2131e$+$06 cases and $r_2=0.083$, while the third wave is weaker with 505,948 cases and $r_3=0.120923$. The estimated final wave is also weak with 612 172 cases and $r_4=0.1614$ (Fig. 6(a) and Table 1). Plots of $S_i\left(t\right)$, $I_i\left(t\right)$, $R_i\left(t\right)$, the reproduction number waves ${\mathfrak{R}}_{0ic}\left(t\right)$, and the composite reproduction number wave ${\mathfrak{R}}_{0c}\left(t\right)$ obtained from the GSIR model are shown in Fig. 6(b) and (c). Currently, the overall growth factor of the daily cases for USA is 1.16%.

For the world data, there are four pandemic waves and a total number of expected cases are approximately 21.27 millions, estimated from the data as of 28 July, 2020. First wave is strong with 2.67232e$+$06 cases and $r_1=0.1083$, second wave is stronger than the first one with 3.8634e$+$06 cases and $r_2=0.0816$, third wave is stronger than the first two waves with 4.571e$+$06 cases $r_3=0.0953$, and the estimated final wave is the strongest one with 1.0164e$+$07 cases and $r_4=0.0918$ as shown in Fig. 7(a) and Table 1. Plots of $S_i\left(t\right)$, $I_i\left(t\right)$, $R_i\left(t\right)$, the corresponding reproduction number waves ${\mathfrak{R}}_{0ic}\left(t\right)$, and the composite reproduction

number wave ${\mathfrak{R}}_{0c}\left(t\right)$ obtained from the proposed model are shown in Fig. 7(b) and (c). Currently, the overall growth factor of daily cases for the World is 1.49%. Similarly, there are four pandemic waves across the world for deaths, and the total number of expected deaths are approx. 727,659, estimated from the data as of 28 July, 2020. First wave has 181,988 deaths with $r_1=0.1357$, second wave is weaker than the first one with 145,878 deaths and $r_2=0.1058$, third wave is stronger than first two waves with 193,723 deaths with $r_3=0.0831$, and the estimated final wave is strongest with 206,070 deaths and $r_4=0.09625$ as shown in Fig. 8(a) and Table 1. Currently, the overall growth factor of daily deaths for World is 0.74%.

5. Conclusions and future scope

The important conceptual innovations and fundamental contributions of the study are as follows. First of all, we identified the limitations of the classical SIR model and provided the solutions for the same. Next, we extended the mathematical theory of the classical Susceptible–Infected–Removed (SIR) epidemic model and proposed Generalized SIR (GSIR) model that satisfies six boundary conditions (the three existing initial conditions and the three new final conditions) without modeling the SIR model with a set of second-order differential equations. We have shown that the existing growth function models of epidemics such as the logistic, Gaussian and gamma functions are the special cases of the GSIR model. The GSIR solution led to time-varying parameters that grow or decay over time. Closed-form expressions are presented for all the system waves of susceptible, infected and removed populations as well as for the parameters of infection rate, removal rate, and the reproduction number. The second order modeling allows control on the terminal conditions, i.e., to achieve the expected goal at a certain time, while the time varying parameters show a better tractability with policies. Thus, the pandemic controlling agencies can utilize this model and specify terminal conditions of pandemic with appropriate policies in place that can help achieve those targets while tracking this model.

In this study, the GSIR framework is utilized as a data-driven approach for predictive monitoring of COVID-19 pandemic, although it can be used to model any pandemic. Using the proposed model, study is performed on the COVID-19 data of various countries with detailed results for Brazil, India, USA, and World. The proposed GSIR model advances the existing theory of SIR model and provides better results compared to the SIR model. GSIR model can be utilized for continuous predictive monitoring of COVID-19 pandemic across the world. With a closer study of the lockdown periods of India during COVID-19 pandemic and the trends of the corresponding reproduction number waves, it is emphasized that tracking of these time-varying parameters can prove very helpful for decision makers to control any pandemic.

We have considered three well-known and widely-usedgrowth models, namely logistic, Gaussian and gamma functions to derive explicit mathematical relations for the GSIR model. However, the proposed model is generic and one can choose any function (e.g., beta, Kumaraswamy, Irwin–Hall, Gumbel, Fréchet, and Weibull, etc.) to model the infected population that satisfies the initial and final conditions. In the literature, there are many probability density functions. In this work, we have carried out explicit derivations for three growth functions, and implemented one of these (the logistic function) to obtain results through MATLAB coding. Therefore, two interesting future directions of the study are: (i) to consider various possible functions and develop a mathematical method or an algorithm to select the best one and (ii) to extend the proposed study for the other variants of the classical SIR model such as SEIR, SEIRS, MSEIR, SIRS, SIRD, SEIS, SI, and SIS.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.