Abstract

The accurate and systematically improvable frozen natural orbital (FNO) and natural auxiliary function (NAF) cost-reducing approaches are combined with our recent coupled-cluster singles, doubles, and perturbative triples [CCSD(T)] implementations. Both of the closed- and open-shell FNO-CCSD(T) codes benefit from OpenMP parallelism, completely or partially integral-direct density-fitting algorithms, checkpointing, and hand-optimized, memory- and operation count effective implementations exploiting all permutational symmetries. The closed-shell CCSD(T) code requires negligible disk I/O and network bandwidth, is MPI/OpenMP parallel, and exhibits outstanding peak performance utilization of 50–70% up to hundreds of cores. Conservative FNO and NAF truncation thresholds benchmarked for challenging reaction, atomization, and ionization energies of both closed- and open-shell species are shown to maintain 1 kJ/mol accuracy against canonical CCSD(T) for systems of 31–43 atoms even with large basis sets. The cost reduction of up to an order of magnitude achieved extends the reach of FNO-CCSD(T) to systems of 50–75 atoms (up to 2124 atomic orbitals) with triple- and quadruple-ζ basis sets, which is unprecedented without local approximations. Consequently, a considerably larger portion of the chemical compound space can now be covered by the practically “gold standard” quality FNO-CCSD(T) method using affordable resources and about a week of wall time. Large-scale applications are presented for organocatalytic and transition-metal reactions as well as noncovalent interactions. Possible applications for benchmarking local CCSD(T) methods, as well as for the accuracy assessment or parametrization of less complete models, for example, density functional approximations or machine learning potentials, are also outlined.
1. Introduction
Well-converged coupled-cluster (CC) computations, due to their
beneficial size-extensive and systematically improvable properties,
have been repeatedly found in agreement with experiments for various
properties of matter at the atomic scale.1−4 For single-reference cases, the
CC model with single and double excitations (CCSD) augmented with
perturbative triples correction [CCSD(T)]5 is widely regarded as the “gold standard” of quantum
chemistry. Although the CC treatment of multireference systems remains
actively investigated,6 the applicability
domain of single-reference closed- and open-shell CCSD(T) covers a
large portion of the current chemical questions including reaction
mechanisms and catalysis, molecular interactions, and partly also
processes involving radicals, ions, or excited states. The main technical
limitations of conventional CCSD(T) implementations are the steep 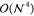 - and
- and 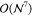 -scaling data storage and operation
count
complexity with system size
-scaling data storage and operation
count
complexity with system size 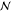 , restricting
the reach of conventional
implementations to systems of up to 20–25 atoms.
, restricting
the reach of conventional
implementations to systems of up to 20–25 atoms.
The 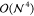 -scaling storage challenges posed
by the
two-electron four-center electron repulsion integrals (ERIs) have
been addressed via density fitting (DF, or resolution-of-identity)7−12 or Cholesky decomposition (CD)7,13,14 techniques, and further improvements are expected from promising
tensor factorization ideas.15−22 The benefits of a DF-based reconstruction of the four-center ERI
have been demonstrated by DePrince and Sherrill,9 which was developed further to exploit graphics processing
units (GPUs).23,24 The DF-CCSD(T) implementations
of Peng, Valeev, and co-workers10,25 and of Scheffler, Shen,
and co-workers11 also reassemble some of
the ERIs to reduce disk and network use. Our recent DF-CCSD(T) implementation
also exploits DF-based reassembly of all ERIs needed for the integral-direct t1-transformed CCSD iteration and for our integral-direct
(T) algorithm.12 Further technical details
of these implementations were discussed in previous reports.9−12,24
-scaling storage challenges posed
by the
two-electron four-center electron repulsion integrals (ERIs) have
been addressed via density fitting (DF, or resolution-of-identity)7−12 or Cholesky decomposition (CD)7,13,14 techniques, and further improvements are expected from promising
tensor factorization ideas.15−22 The benefits of a DF-based reconstruction of the four-center ERI
have been demonstrated by DePrince and Sherrill,9 which was developed further to exploit graphics processing
units (GPUs).23,24 The DF-CCSD(T) implementations
of Peng, Valeev, and co-workers10,25 and of Scheffler, Shen,
and co-workers11 also reassemble some of
the ERIs to reduce disk and network use. Our recent DF-CCSD(T) implementation
also exploits DF-based reassembly of all ERIs needed for the integral-direct t1-transformed CCSD iteration and for our integral-direct
(T) algorithm.12 Further technical details
of these implementations were discussed in previous reports.9−12,24
Regarding the operation
count bottleneck, recent developments have
successfully exploited the tools of modern high-performance computing,
such as various accelerators,10,23,24,26,27 shared-memory intranode (Open Multi-Processing, OpenMP) and/or multinode
(Message Passing Interface, MPI) parallelism.10−13,25,28−35 However, parallelization alone can only moderately deal with the 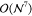 -scaling operation count of CCSD(T).
For
this reason, reduced-cost and reduced-scaling CCSD(T) approaches are
also intensively developed. Here, we employ frozen natural orbitals
(FNOs) to compress the space spanned by the virtual molecular orbitals
(MOs). This is beneficial for both the CCSD and the (T) components
for which the rate-determining operations scale with the fourth power
of the number of virtual MOs.
-scaling operation count of CCSD(T).
For
this reason, reduced-cost and reduced-scaling CCSD(T) approaches are
also intensively developed. Here, we employ frozen natural orbitals
(FNOs) to compress the space spanned by the virtual molecular orbitals
(MOs). This is beneficial for both the CCSD and the (T) components
for which the rate-determining operations scale with the fourth power
of the number of virtual MOs.
In our recent MPI/OpenMP DF-CCSD(T) implementation, (i) disk I/O and network use are rigorously avoided during both the CCSD iterations and the (T) step, (ii) the operation count and the memory requirement are fully optimized by exploiting the permutational symmetry of all amplitude, residual, and ERI tensors, and (iii) all terms of the CCSD equations are optimized and parallelized with the same efficiency, not only the usually considered particle–particle–ladder (PPL) term.12 The latter is surprisingly important also in the FNO context as the PPL term experiences fourth-power scaling cost reduction, while the non-PPL terms benefit only from at most third-power scaling cost reduction. For that reason, the combination of our integral-direct DF-CCSD(T) implementation with FNOs is expected to be highly competitive.
Additional cost reduction is realized here by compressing the auxiliary basis set used for the DF approximation, exploiting the so-called natural auxiliary functions (NAFs).36 The NAFs, discussed in detail in Section 2.3, are analogous to FNOs in the sense that they are combined from the original auxiliary functions (AFs) via unitary transformations. Moreover, these unitary rotations are determined so that the four-center ERIs assembled in the truncated NAF basis will approximate the exact DF integrals optimally in the least-squares sense.36 As the number of different orbital product densities decreases quadratically with the number of dropped FNOs, a considerable portion of the original auxiliary basis, which is responsible for the description of the discarded FNO pair densities, can also be dropped. In the context of our integral-direct DF-CCSD(T) implementation, the NAF approach is thus beneficial to reduce the cost of repeated ERI assembly steps in both the CCSD and (T) parts.
Interestingly, in spite of the active development of high-performance CCSD(T) implementations10−13,25,28−35 and the reliability of the FNO approach, there appears to be only a surprisingly small number of large-scale CCSD(T) applications in the literature, especially originating outside of the developer community.37,38 Conventional CCSD(T) computations have been presented so far with up to about 1000 atomic orbitals (AOs), and about 20–40 atoms, in triple- and quadruple-ζ basis sets.10−13,31,32,34,39 Recently, we demonstrated that systems with up to 1500 AOs can also be tackled using affordable resources12 and without relying on a high level of spatial symmetry34 or hundred thousand cores.40 To the best of our knowledge, multinode parallelization and orbital space truncation techniques were combined in the CCSD(T) context at the largest scale for 36 atoms, about 1300 AOs, and 750 retained MOs.13
Here, we demonstrate that the FNO approach is a powerful tool to extend the reach of CCSD(T) to a much broader range of systems. For that goal, we explored potential reasons that could hinder the wider adaptation of the FNO-CCSD(T) method for molecules of current chemical interest and addressed these concerns in our method development and benchmarking efforts presented here:
-
(i)
Although impressive scaling performance has been reported with recent parallel CCSD(T) codes,10−13,30,31,34 it is challenging to maintain high peak performance utilization for thousands of cores. We find that, on easily accessible computer clusters, it is simpler to obtain access to a small number of nodes with recent many core CPUs than to obtain thousands of cores and exploit the outstanding peak performance utilization and parallel scaling of our DF-CCSD(T) implementation.12 The issue of the longer runtimes potentially exceeding wall time limits has also been effectively overcome in our code by frequent checkpointing. We expect that the combination of more manageable hardware requirements and reduced arithmetic demand because of the use of FNOs and NAFs will make highly accurate CCSD(T) benchmarks accessible for a wider audience.
-
(ii)
We have revisited and benchmarked best practices regarding the correction scheme employed for the frozen orbitals, the variable choice governing the truncation process, and extrapolation schemes toward truncation-free CCSD(T). The best performing correction and extrapolation approaches facilitate the use of almost an order of magnitude looser truncation thresholds compared to the uncorrected results and thereby increase the efficiency of FNO-CCSD(T) even further.
-
(iii)
We have also extended the benchmark data available for the accuracy of the FNO method41−47 for frequently employed test sets covering complicated reactions with multiple bond breaking,48,49 as well as atomization and ionization processes including open-shell species.50,51 We also show that conservative truncation thresholds performing well for relatively small systems and large basis sets up to quadruple-ζ quality also yield highly accurate correlation and reaction energies (max. 1 kJ/mol error) up to the largest conventional CCSD(T) reference data available to date in the 30–40-atom range.12 Thus, FNO-CCSD(T) is expected to remain highly accurate also for the 50–75 atoms targeted here.
-
(iv)
The rapid development of local CCSD(T) methods could also play a role in the moderate popularity of FNO-CCSD(T) methods. Indeed, highly efficient implementations39,52−54 and extensive benchmarks reporting thousands of examples55,56 demonstrate the applicability of these local approximations for various chemical systems. Latest implementations can utilize sufficiently large basis sets and were shown to scale up to the range of a few hundred53,54 or even to a few thousand39,56 atoms. However, considering the moderate number of local CCSD(T) applications so far, these methods have not yet reached their full potential in solving chemical problems. For instance, there is still more to learn about the performance of current local approximations on particularly challenging systems exhibiting extended π-systems54,56,57 and/or moderate nondynamic correlation.54,57,58 However, assessing the accuracy of such methods against CCSD(T) benchmarks is hindered by the scarcity of reliable reference data above the 30-atom range.56 Thus, well-converged FNO-CCSD(T) results are also valuable for the assessment of local approximations for extended systems often targeted using local CCSD(T) methods.
-
(v)
The relatively slow basis set convergence of CCSD(T) requires the use of at least triple- and quadruple-ζ basis sets, and thus practical applications face various CPU time and storage bottlenecks already in the 20–30-atom range. Here, we show that well-converged FNO-CCSD(T) computations can be performed for systems of up to 75 atoms with triple-ζ and up to 51 atoms (2124 AOs) with quadruple-ζ basis sets. While only a small fraction of modern chemistry fits into 20–30 atoms, by doubling the size of the computable systems the covered chemical space increases tremendously. The capabilities of our implementation for systems in the 50–75-atom range are demonstrated for organocatalytic and transition-metal reactions of recent interest, as well as for the noncovalent interaction energies (NCIEs) of molecular complexes. Considering that these computations required wall times of only a few days to about a week with 112 CPU cores, the presented FNO-CCSD(T) implementation can contribute significantly to the wider adoption of accurate CCSD(T) references in computational chemistry.
The paper is organized as follows. Sections 2 and 3 provide theoretical background and algorithmic and computational details for CCSD(T), FNOs, and NAFs. Sections 4.1–4.3 illustrate the truncation threshold dependence of the FNO and NAF errors and explores various truncation and extrapolation ideas to decrease the above sources of error. A statistical analysis of the compound FNO and NAF errors is carried out in Section 4.4 for benchmark sets collecting small- to medium-sized molecules with both closed- and open-shell character. Large-scale applications and timings are presented in Sections 4.5 and 4.6.
2. Theoretical Background and Algorithms
The CCSD(T)5 model is considered assuming a single-reference determinant. Indices i, j, k, ... (a, b, c, ...) will refer to the occupied (virtual) orbitals, whereas p, q, r, and s are generic MO indices and P and Q will denote auxiliary basis functions. N will refer to the total number of orbitals and no, nv, and na will denote the dimension of the occupied, virtual, and auxiliary spaces, respectively.
2.1. CCSD(T) Method
Here, we recapitulate the relevant aspects of CCSD(T) and refer to the literature for additional details.1−5,12,59 The CCSD correlation energy in a spin–orbital basis reads as
| 1 |
where the summation indices run over occupied (i and j) and virtual (a and b) spin orbitals, fai denotes the elements of the Fock matrix, tia and tij stand for the singles and doubles cluster amplitudes, respectively, and (pq|rs) is a two-electron integral in Mulliken notation.
The evaluation of the CCSD equations
determining the singles and doubles amplitudes requires a number of
sixth power-scaling operations. For instance, the PPL term requires
∑cdtijcd(ac|bd) type of
matrix multiplications exhibiting 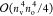 -scaling. In the case of relatively small nv/no ratios of 5–10,
which occurs with double- or triple-ζ basis sets or compressed
FNO virtual subspaces, the computational cost of the
-scaling. In the case of relatively small nv/no ratios of 5–10,
which occurs with double- or triple-ζ basis sets or compressed
FNO virtual subspaces, the computational cost of the 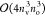 -scaling terms are also comparable to that
of the PPL term.12 Finally, the rate-determining
step of the perturbative triples correction is dominated by
-scaling terms are also comparable to that
of the PPL term.12 Finally, the rate-determining
step of the perturbative triples correction is dominated by 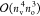 -scaling terms [see Section
S1 of the Supporting Information].
-scaling terms [see Section
S1 of the Supporting Information].
2.2. Frozen Natural Orbitals
Orbital transformation techniques have been particularly successful to compress the space spanned by the virtual MOs. Optimized virtual orbitals (OVOs) were introduced by Adamowicz and Bartlett60,61 and also adopted by Neogrády, Pitoňák, Urban, and co-workers,13,62 while FNOs proposed by Löwdin63 were introduced into the CC context by Taube and Bartlett.41,42 Both OVOs and FNOs can be obtained using the cost-efficient second-order Møller–Plesset (MP2) model and exhibited similar accuracy in previous comparisons.46,47 We find the FNO method more beneficial as the FNO construction is simpler to scale up to thousands of orbitals, especially with reduced scaling one-particle density matrix (OPDM) approximations,64−67 and it has been extended also for analytic gradients42 and various excited-state methods.43,44,68−70
The NOs are defined as the eigenvectors of the OPDM, D. In practice, the OPDM is approximated at the level of MP2, although density matrix expressions depending on the CCSD amplitudes could potentially provide a more compact NO basis for applications in the CCSD(T) context.71 The MP2 OPDM expression reads in the spin–orbital basis as
| 2 |
where ϵp denotes the canonical orbital energy of orbital p. The MP2 OPDM of eq 2 and its closed-shell counterpart are evaluated using the efficient DF-MP2 implementation of the MRCC suite, which can handle systems with more than 5000 AOs.72 A reduced cost NO construction option is discussed in Section S2 of the Supporting Information, but it is not employed in the presented computations.
The NOs and the natural occupation numbers are obtained as the eigenvectors and eigenvalues of D. Then, n̅v pieces of active virtual NOs are selected, while the remaining FNOs are not treated at the CCSD(T) level. The active virtual NOs are transformed into a semi-canonical representation by diagonalizing the virtual–virtual block of the Fock matrix.
For the selection of the active virtual NOs, one assumes that NOs with larger occupation numbers are more important for the accurate representation of the wavefunction and for well-converged correlation energies. A frequently employed method for the selection of the retained NOs is to sum up the largest occupation numbers in decreasing order until a certain threshold is reached relative to the sum of all occupation numbers. The cutoff parameter governing this procedure will be referred to as the cumulative occupation threshold (COT). Alternatively, an occupation number threshold (ONT) can be employed for the selection of the retained or frozen NOs based on their OPDM eigenvalues. The active NOs can also be determined by fixing the percentage of virtual orbitals (PVO), that is, by keeping a fixed ratio of the NOs with the largest possible occupation numbers. The performance of the three alternatives will be compared in Section 4.1.
The truncation error caused in the CCSD(T) correlation energy can be straightforwardly reduced by utilizing the MP2 energies computed with the entire virtual space and with the FNO basis. The difference of these MP2 correlation energies estimate the truncation error of CCSD(T) at the MP2 level.41 This approach will be referred to as ΔMP2. Alternatively, the FNO errors can also be decreased by exploiting the systematic convergence of the correlation energies toward the approximation free value as the truncation threshold is tightened. There are again several promising possibilities for the extrapolation, and in Section 4.2, we compare techniques taken from the literature43,45 with some novel ideas presented here.
Note that the above FNO construction and energy correction methods also rely on the applicability of the single-reference MP2 ansatz. An additional benefit of using FNOs over, for example, OVOs, is that they can be straightforwardly extended to multireference cases invoking well-established multireference second-order methods, although this avenue is yet to be explored.
The rate-determining steps of both CCSD and (T) scale with the fourth power of the number of virtual orbitals, nv. Consequently, a theoretical speedup of (nv/n̅v)4 is anticipated for the PPL contraction and ERI assembly steps of CCSD, and for the most demanding steps of the triples amplitude contraction in (T). The next most operation intensive terms scale with the third power of nv; hence, the overall theoretical speedup in FNO-CCSD(T) is expected to be (nv/n̅v)s with 3 < s < 4. Because the operations scaling with nv4 dominate the computational costs for large basis sets, the operation count reduction should approach (nv/n̅v)4 with increasing AO basis sets. Additionally, the memory requirement of the three-center ERI integrals required for the DF method and the double amplitudes also decreases by a factor of (nv/n̅v)2, while a factor of (nv/n̅v)3 compression is realized for intermediates required for the “ijkabc” (T) algorithm.12,59,73−75 The data compression has an additional positive effect on our integral-direct CCSD(T) algorithm because more memory remains for the storage of the blocks of the four-center ERIs and fewer ERI assembly steps have to be repeated.
2.3. Natural Auxiliary Functions
In the DF approximation,76,77 the fourth-order two-electron integral tensor is approximated as the product of third-order tensors
| 3 |
DF-CCSD(T) algorithms usually assemble
the four-center ERIs from the three-center integral-dependent J matrices because the 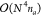 scaling of the assembly is smaller than
the six- and seventh-power scaling cost of CCSD and (T). In our integral-direct
DF-CCSD algorithm, integral assembly is performed in each iteration,
which can still be demanding in realistic applications with large
basis sets. The ratio of operation counts of the PPL and assembly
steps scales about as
scaling of the assembly is smaller than
the six- and seventh-power scaling cost of CCSD and (T). In our integral-direct
DF-CCSD algorithm, integral assembly is performed in each iteration,
which can still be demanding in realistic applications with large
basis sets. The ratio of operation counts of the PPL and assembly
steps scales about as 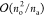 and thus decreases with the increasing
AO basis set size for a given molecule. In spite of the decreasing
relative cost of the ERI assembly with the number of electrons, for
the largest systems considered here, it could require up to 30–40
and 40–70% of a single FNO-CCSD iteration with triple-ζ
and quadruple-ζ basis sets, respectively.
and thus decreases with the increasing
AO basis set size for a given molecule. In spite of the decreasing
relative cost of the ERI assembly with the number of electrons, for
the largest systems considered here, it could require up to 30–40
and 40–70% of a single FNO-CCSD iteration with triple-ζ
and quadruple-ζ basis sets, respectively.
Because of this potentially sizable integral assembly cost, it would be beneficial to compress the auxiliary basis, especially when the FNO method is invoked. To that end, we successfully employed the combination of FNOs and NAFs previously to reduce the costs of the direct random phase approximation (dRPA) method,72 as well as those of the linear-response second-order CC (CC2)68 and second-order algebraic-diagrammatic construction [ADC(2)]65 approaches. FNOs and NAFs are also vital in the context of our local correlation methods.39,56,59,72,78 The gain in operation count is obvious for these applications as the rate-determining steps in MP2, CC2, and ADC(2) calculations scale linearly36,65,68 with the number of AFs, while a quadratic-scaling speedup can be achieved for dRPA.72 In the context of integral-direct DF-CCSD(T), the ERI assembly of both the CCSD and the (T) steps benefits from the compression of the auxiliary space.
Moreover, in combination with the FNO approach, the number of different orbital product densities decreases considerably when only the active NOs are correlated at the CCSD(T) level. Consequently, AF combinations required for the fitting of the product densities involving the frozen NOs can also be discarded. The optimal AF combinations for that purpose are determined by the singular value decomposition (SVD) of J̅,36 where J̅ holds the J tensor transformed into the active NO basis, as
| 4 |
Unitary matrices M and N collect the left and right singular vectors and the diagonal Σ matrix contains the singular values of J̅. Because of the large memory requirement of SVD, J̅ is not used directly, but the right singular vectors are obtained as the eigenvalues of
| 5 |
where W has eigenvalues equal to the singular values of J̅ squared.
The elements of N are called the NAFs36 because of the analogy with NOs. Moreover, the eigenvalues of W can be used to truncate the NAF basis because the r largest eigenvalues of W, or equivalently the r largest singular values of J̅, and the corresponding singular vectors define the best rank r approximation of J̅. Here, we employ an occupation number like threshold for the truncation of the NAF basis according to the eigenvalues of W, and the Eh2 unit of the NAF threshold will be omitted for the sake of simplicity.
Let us briefly note that the NAF approach combines the benefits associated with both the DF and the CD techniques. NAFs provide a systematically improvable and system specifically compact expansion in resemblance to the properties of the Cholesky vectors7,13,14 of the CD method. At the same time, the construction of NAFs from ERIs in any of the AO, MO, or FNO bases remains relatively straightforward with efficient, fourth-power scaling algorithms. On the other hand, it would be challenging to employ CD on ERIs in the MO or FNO basis at the 1000 orbital range because of the highly expensive and data intensive four-center integral transformation steps.
In practice, matrix W should contain contributions from every independent generalized product density exactly once, that is, the summation in the matrix product of eq 5 runs over only the J̅pqP elements, where p ≥ q. In the case of an unrestricted MO basis, the spin-dependent construction of NAFs would be problematic, for instance, because four-center ERIs with both spin up and spin down orbital indices also have to be assembled. For this reason, spin independent NAFs are constructed using W = (Wα + Wβ)/2, where Wα and Wβ are built from the spin up and spin down J̅ tensors, respectively.
For the correction of the NAF truncation error, we can combine two cost-effective approaches.36 First, the ΔMP2 correction introduced for the FNO approach can also reduce the NAF error. To that end, the MP2 energies obtained with the full MO and AF bases as well as with the active NO and NAF bases are employed. Additionally, the two-external four-center ERIs needed for the correlation energy expression of eq 1 are computed and stored using the complete AF basis. These NAF error-free ERIs can be contracted with the MP2 and CCSD amplitudes obtained with the active NO and NAF bases, which circumvents any NAF error contribution to the correlation energies from the integrals. In other words, only the amplitudes are affected by the NAF approximation. Note that the second NAF error reduction technique would be significantly more demanding and would bring smaller improvement in accuracy for the (T) term, and thus it is not employed beyond CCSD.
Considering the benefits of the NAF approach from the operation count perspective, a theoretical speedup scaling linearly with the NAF compression ratio is achieved for the four-center integral assembly step. However, for large AO basis sets and in combination with the FNO approximation 50% or more of the NAFs can be discarded with a negligible error in the correlation energies. For such cases, the NAF approximation alone can reduce the number of operations required for a CCSD iteration by up to 30–40%. For the (T) part, in general modest improvements can be expected, but there is a noticeable increase in performance when limited memory is available. First, more memory can be allocated to the storage of the three-external ERIs because of the compression of the three-center integral tensor transformed into the NAF basis. Second, the repeated assembly of the three-external ERIs, which cannot be stored during the (T) part, also benefit from a speedup proportional to the NAF compression ratio.
3. Computational Details
The presented FNO and NAF basis set compression approaches have been implemented in the closed- and open-shell CCSD(T) codes of the MRCC suite of quantum chemical programs.79,80 The programs will be made available in a forthcoming release of the package.
Benchmark calculations were performed on the reaction energy test sets assembled by Adler and Werner (AW)48 as well as by Neese, Wennmohs, and Hansen (NWH)49 for closed-shell molecules. Additionally, atomization energies taken from the “high-accuracy extrapolated ab initio thermochemistry” (HEAT)50 compilation as well as vertical ionization potentials (VIP)51 are also used containing both closed- and open-shell species.
The benchmark timings were measured on Intel Xeon E5-2670 v3 CPUs containing 12 physical cores, Intel Xeon Platinum 8180M processors equipped with 28 physical cores, 8-core Intel Xeon E5-2609 v4 CPUs, and Intel Xeon Gold 6138 CPUs containing 20 physical cores. The corresponding theoretical peak performances of those CPUs in giga floating point operations per second (GFLOP/s) are 441.6, 1523.2, 217.6, and 832, respectively.
The Cartesian coordinates of the species of Table 5 are available in the Supporting Information of ref (12). The coordinates of the largest species of Table 7 are taken from the original publications: GC-dDMP-B system,30 ruthenium-complex,81 organocatalytic reaction,82 and corannulene dimer.83
Table 5. Wall Times and Corresponding Peak Performance Utilizations Measured for Medium-Sized Systems.
| wall
time |
%
performance |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| species | atoms | no. of AOs | no. of AFs | FNO threshold | % NOa | % NAFb | CCSD [min]c | (T) [h] | CCSD | (T) |
| FLPOd | 41 | 1037 | 2500 | 5 × 10–5 | 60 | 39 | 13 | 15 | 47 | 50 |
| 10–5 | 81 | 53 | 40 | 57 | 53 | 45 | ||||
| TSAddd | 43 | 1071 | 2578 | 5 × 10–5 | 59 | 38 | 15 | 16 | 47 | 55 |
| 10–5 | 81 | 53 | 47 | 74 | 53 | 42 | ||||
| FLPAd | 43 | 1071 | 2578 | 5 × 10–5 | 59 | 38 | 15 | 16 | 47 | 55 |
| 10–5 | 81 | 53 | 45 | 75 | 55 | 41 | ||||
| OOe | 40 | 1089 | 2620 | 5 × 10–5 | 63 | 41 | 5 | 4.6 | 35 | 55 |
| 10–5 | 82 | 53 | 13 | 13 | 37 | 58 | ||||
| TS1e | 40 | 1089 | 2620 | 5 × 10–5 | 63 | 41 | 5 | 4.9 | 34 | 53 |
| 10–5 | 83 | 54 | 13 | 16 | 38 | 46 | ||||
| ABPe | 31 | 1569 | 3671 | 5 × 10–5 | 41 | 31 | 4 | 2.6 | 35 | 51 |
| 10–5 | 65 | 48 | 17 | 13 | 44 | 60 | ||||
Percentage of active virtual NOs.
Percentage of retained NAFs with the threshold set to 5 × 10–2.
Time of one iteration.
Performed on two 12-core Intel Xeon E5-2670 v3 CPUs clocked at 2.3 GHz.
Performed on four 28-core Intel Xeon Platinum 8180M CPUs clocked at 1.7 GHz.
Table 7. Dimensions of the Various Orbital Spaces Employed for the Largest Systems of 47–75 Atoms, As Well As the Corresponding FNO-CCSD(T) Correlation Energies.
| species | atoms | basis set | no. of AOs | no. of AFs | % NOa | % NAFb | ECCSD(T) [Eh] |
|---|---|---|---|---|---|---|---|
| ED28 | 47 | def2-QZVP | 1978 | 4469 | 66 | 50 | –4.1527 |
| PR28 | 51 | def2-QZVP | 2124 | 4745 | 65 | 49 | –4.2185 |
| enamine | 57 | def2-TZVP | 998 | 2478 | 86 | 52 | –4.6411 |
| Corannulene dimer | 60 | def2-TZVPPD | 1820 | 4460 | 66 | 42 | –6.6704 |
| GC-dDMP-B | 63 | 6-311++G(d,p) | 1042 | 5320 | 80 | 23 | –6.6211 |
| TSCCRS | 75 | def2-TZVP | 1381 | 3419 | 86 | 53 | –6.7300 |
Percentage of active virtual NOs. For the ED28 and the PR28 molecules 10–5, for the other species 5 × 10–5 NO threshold was set.
Percentage of retained NAFs with the threshold set to 5 × 10–2.
Correlation consistent basis sets, cc-pVXZ84 with the corresponding DF auxiliary bases, cc-pVXZ-RI85 and triple- and quadruple-ζ valence basis sets (def2-TZVP and def2-QZVP), including polarization86 and diffuse functions87 (def2-TZVPPD and def2-QZVPPD) with the corresponding auxiliary basis sets,88 were utilized. The 28-electron Stuttgart–Köln effective core potential developed for the def2 basis sets89 were employed for the Ru atom. The calculation for the GC-dDMP-B molecule was performed with the 6-311++G(d,p) basis set according to ref (30) and the aug-cc-pVTZ-RI auxiliary basis. The core electrons were not correlated in any of the presented cases. The extrapolation to the complete basis set (CBS) limit was performed using the formula of Helgaker and co-workers.90
The accuracy of the approximations will be characterized by the mean absolute error (MAE), the root mean square error (RMS), and the maximum absolute error (MAX) of the computed quantities.
4. Results and Discussion
In this section, we analyze the accuracy and efficiency of the FNO and NAF approximations. First, we explore the convergence of both approximations toward the truncation free reference and suggest default thresholds yielding sub-kJ/mol accuracy and considerable cost reduction. Various extrapolation and error correction schemes are also considered to increase the rate of convergence toward conventional CCSD(T). The combined error of the FNO and NAF approximations is characterized on a set of challenging reaction energies containing both closed- and open-shell species48−50 as well as on ionization potentials. The scaling of the truncation errors and the gains in efficiency are also assessed on some of the largest systems for which conventional CCSD(T) is still feasible,12 containing 31–43 atoms. Finally, several large-scale applications illustrate the current domain of applicability of the implementation in the 50–75 atom range.
4.1. Relationship of the Various Truncation Strategies
The truncation of both the virtual and the auxiliary subspaces can be carried out as a function of various measures, but there is no clear consensus in the literature on which variable to choose. Thus, here, we explore the relation of multiple possibilities: COT, ONT, and PVO. The left panel of Figure 1 plots the PVO and COT criteria as a function of the ONT, that is, the corresponding data points represent the numerical value of the three measures with an identical number of frozen NOs averaged over the AW compilation. As expected, the percentage of the retained virtual NOs tends to 100% more steeply for the cc-pVQZ basis set than for cc-pVTZ, indicating the potential to achieve larger savings in computation time in the case of the larger cc-pVQZ basis. Especially with the cc-pVQZ basis set, ONT and COT show an almost linear dependence for the AW test set, suggesting that similar performance can be expected from both measures. This relation is not obvious as the distribution of the occupation numbers is not known and may also be nonuniversal because of the basis set and molecule dependence. An additional consequence of this observation is that the conclusions of previous COT-based studies on extrapolation toward the complete virtual space results43 could potentially be transferable to the ONT criterion using the appropriate quasi-linear transformation between them. On the other hand, the steep nonlinear shape of the PVO curve suggests that a stronger system dependence and consequently less robustness can be expected from this measure, especially with a larger basis set. Indeed, in contrast to ONT and COT, PVO is not system specific and thus can be expected to adapt to the electronic structure worse than ONT and COT.
Figure 1.

Relationship of the various truncation strategies for the FNO (left panel) and the NAF (right panel) approximations. The values were averaged over the molecules of the AW test set.
In the case of the NAF truncations, it is straightforward to consider an ONT-type variable because of the analogy between the NAF eigenvalues and the NO occupation numbers. Unlike the case of the NOs, the percentage of the retained NAFs depends almost linearly on the NAF truncation threshold, as shown in the right panel of Figure 1. Compared to that, the cumulative eigenvalue threshold (CET, i.e., the analogue of COT for the NAF approximation) shown in Figure 1 exhibits a more pronounced nonlinear dependence on the NAF truncation threshold, especially with the cc-pVTZ basis set around the 5 × 10–2 value, which is recommended as a suitable default NAF threshold choice below. For these reasons, primarily the ONT criterion and its NAF analogue will be employed in the rest of the present study.
4.2. Error Correction and Extrapolation Techniques
The most straightforward way to correct the NO and NAF approximations is to use an additive correction obtained at the MP2 level (ΔMP2), as introduced in Sections 2.2 and 2.3. In both cases, the difference of the MP2 correlation energies obtained with the complete and the truncated orbital spaces is added to the CCSD(T) results. This way the second-order energy remains unaffected and only the higher-order energy corrections are subject to the approximations.
Additionally, the systematic convergence of the CCSD(T) correlation energies with tighter and tighter thresholds can also be exploited via extrapolation approaches. To date, two alternatives have been investigated to extrapolate the CCSD(T) correlation energy toward the limit of the complete virtual space relying on either linear extrapolation43 or nonlinear sequence transformations.45 The choice of the transformation technique is far from obvious because the form of the extrapolated function, that is, the dependence of the CCSD(T) correlation energy on the truncation threshold is not known. Moreover, the rate of convergence can also be system dependent, and different extrapolation techniques perform best for sequences with different convergence properties.
Besides the choice of the extrapolation method, there are also several possibilities for the selection of the independent variable. It has been demonstrated that the COT criterion exhibits a close to linear relationship with the truncation error over a wider range than PVO.43 Because the occupation number-based thresholds (COT and ONT) exhibit an almost linear relationship with each other as shown above, they are both expected to be more suitable for extrapolation than PVO. In order to provide data comparable to previous studies, the case of the COT criterion will be presented in this section.
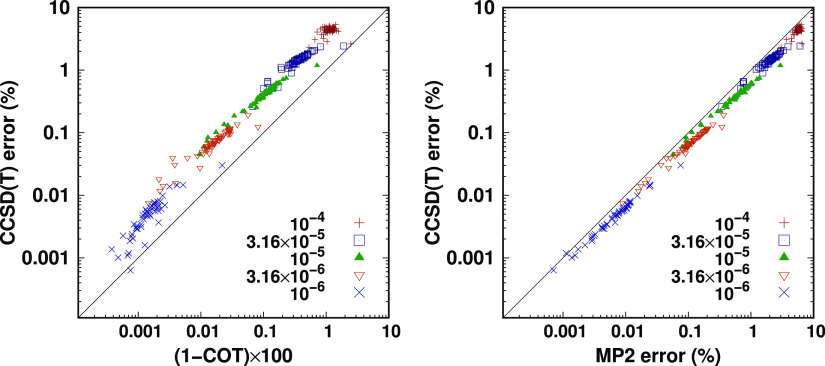
Additionally, we propose the use of correlation energy-based quantities as an alternative variable to be employed in the extrapolation. The motivation is that the convergence, for example, of the MP2 correlation energy with the FNO and NAF thresholds might exhibit a similar pattern as the targeted CCSD(T) correlation energy, which could be beneficial for the extrapolation. To assess the performance of correlation energy-based independent variables, we compare these to the occupation number-based alternative employed so far. The left and right panels of Figure 2 plot the percentage error of the CCSD(T) correlation energy as a function of the COT value and the MP2 correlation energy error, respectively, for all entries of the AW compilation. In order to make the MP2 correlation energies scattered over a wide range more comparable to the COT, the part missing from the 100% MP2 correlation energy and the part missing from the 100% cumulative occupation number are compared for the same five ONTs. The correlation of the CCSD(T) correlation energy with the MP2 correlation energy evaluated using the same approximations (right panel of Figure 2) appears clearly superior compared to the case of COT. It is important to point out that the relation with the approximated MP2 correlation energy is still neither completely linear nor universal but gets much closer to ideal than COT in these aspects.
Figure 2.
Percentage error of the CCSD(T) correlation energy as a function of the discarded cumulative occupation (1-COT) (left panel) and the percentage error of the MP2 correlation energy (right panel). Symbols and colors refer to five ONT thresholds ranging from 10–4 to 10–6, while individual points mark a single species of the AW test set with the cc-pVQZ basis.
Furthermore, the correlation of the MP2 and CCSD(T) errors collected in Figure 2 indicates that simple linear extrapolations using the MP2 energy as an independent variable might perform significantly better than previous attempts relying on the occupation number type variables. Besides the linear extrapolations, we will also explore frequently employed sequence transformations, namely, the Shanks transformation45 and the Richardson extrapolation.91 An advantage of these transformation methods is that they can be repeated by performing them on the extrapolated values themselves. This repeated extrapolation could improve the extrapolated results even further by taking into account deviations from the linear behavior.
The sequence transformation methods map a sequence, a, to a new sequence [for example, the S(Ak) for Shanks and Rn(h,t) for Richardson transformations defined below] that is expected to converge faster than the original one. The Shanks transformation operates on the kth partial sums of the original sequence, Ak = ∑i=0kai, as
| 6 |
For the Shanks transformation of correlation energies, respective terms of the Taylor series of the correlation energy, that is, aiS = F(i)(h)(h0 – h)i, form the sequence that is subjected to sequence transformation. Here, F(i) denotes the ith derivative of the correlation energy as a function of the truncation threshold h, and h0 stands for the value of the threshold with no truncation, for example, h0 = 1 for COT. For instance, the correlation energies obtained with three different thresholds provide the partial sums of A0 = F(h), A1 = F(h) + F′(h)(h0 – h), A2 = F(h) + F′(h)(h0 – h) + 1/2F″(h)(h0 – h)2, and the corresponding S(A1) is the updated approximation of the correlation energy provided by the Shanks transformation.
In the case of the Richardson
extrapolation, the a sequence is assumed to be a
function of a small parameter, h: 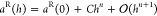 , where, in our case, aR(0) is the truncation-free correlation energy, Chn is the nth order error
term, and C is a constant. The nth order error term is assumed to vanish in the Richardson
extrapolated sequence expressed from aR obtained at two different threshold values, h and h/t
, where, in our case, aR(0) is the truncation-free correlation energy, Chn is the nth order error
term, and C is a constant. The nth order error term is assumed to vanish in the Richardson
extrapolated sequence expressed from aR obtained at two different threshold values, h and h/t
| 7 |
where Rn(h,t) is the Richardson extrapolated approximation of the correlation energy. Because the form of the correlation energy as a function of the truncation threshold, that is, aR(h) is not known, the threshold-dependent error term of Chn is assumed to be linear (n = 1) for the first Richardson extrapolation, yielding R1(h,t). The Richardson extrapolation can be repeated according to eq 7 with n = 2 by replacing the original aR(h) sequence with R1(h,t), which is referred to as “Richardson 2” below.
These various extrapolation methods are compared to the uncorrected and not extrapolated results for the AW test set with the cc-pVQZ and the aug-cc-pVTZ basis sets in Tables 1 and S1 of the Supporting Information for the correlation energies as well as in Tables 2 and S2 of the Supporting Information for the reaction energies, respectively. The general trends are similar for the two basis sets, only the overall uncertainties are lower for the aug-cc-pVTZ basis. Therefore, only the results for the cc-pVQZ basis set will be presented in detail. The considered correction methods are the additive MP2 correction (ΔMP2), the linear extrapolation with the independent variables of COT (COT linear) and with the MP2 correlation energy (MP2 linear), the three-point Shanks transformation as discussed in the previous example (Shanks), and the repeated Richardson extrapolation (Richardson 2) as the function of the MP2 energy. The Shanks transformation was performed on the terms of the Taylor series as in ref (45), with the modification that the CCSD(T) correlation energy was expressed as the function of the MP2 energy instead of COT. Note that the first Richardson extrapolation as the function of the MP2 energy is identical to a linear extrapolation (MP2 linear), if n = 1 is assumed in eq 7. Note also that the linear extrapolation of the ΔMP2 corrected correlation energies is equal to the extrapolation of the uncorrected values because the linear extrapolation of the MP2 correction term is zero at the truncation-free limit. In other words, the linear extrapolation of the ΔMP2 results would be identical to the ones labeled “MP2 linear”. Because the error term is assumed to be linear, the same holds for the Richardson extrapolation as well. In the case of the Shanks transformation, the extrapolation of the ΔMP2 corrected and the uncorrected correlation energies are not necessarily the same, but in practice, they did yield essentially identical results. For each column, that is, each ONT value of Tables 1 and 2, the corresponding threshold and one (for COT linear and MP2 linear) or two (for Shanks and Richardson 2) looser thresholds were employed for the extrapolation.
Table 1. Average Relative (Maximum) Error of Correlation Energies as the Percentage of the Conventional CCSD(T) Correlation Energy for the AW Test Set with the cc-pVQZ Basis Set and Various FNO Truncation Thresholdsa.
| threshold |
|||||
|---|---|---|---|---|---|
| technique | 10–4 | 3.16 × 10–5 | 10–5 | 3.16 × 10–6 | 10–6 |
| uncorrected | 4.22 (5.32) | 1.41 (2.43) | 0.40 (1.18) | 0.07 (0.19) | 0.00 (0.03) |
| ΔMP2 | 0.93 (2.72) | 0.51 (2.55) | 0.20 (1.23) | 0.04 (0.16) | 0.00 (0.03) |
| COT linear | 0.14 (1.79) | 0.03 (0.43) | 0.01 (0.02) | 0.00 (0.01) | |
| MP2 linear | 0.22 (0.37) | 0.05 (0.12) | 0.00 (0.02) | 0.00 (0.00) | |
| Shanks | 0.04 (0.10) | 0.00 (0.02) | 0.00 (0.00) | ||
| Richardson 2 | 0.03 (0.09) | 0.00 (0.02) | 0.00 (0.00) | ||
The best performing methods are highlighted in bold for each ONT value.
Table 2. Average (Maximum) Error of Reaction Energies [in kJ/mol] Compared to Conventional CCSD(T) Calculations for the AW Test Set with the cc-pVQZ Basis Set and Various FNO Truncation Thresholdsa.
| threshold |
|||||
|---|---|---|---|---|---|
| technique | 10–4 | 3.16 × 10–5 | 10–5 | 3.16 × 10–6 | 10–6 |
| uncorrected | 4.31 (14.81) | 1.90 (6.55) | 0.61 (2.65) | 0.28 (1.15) | 0.05 (0.17) |
| ΔMP2 | 0.71 (2.24) | 0.45 (1.62) | 0.13 (0.55) | 0.13 (0.52) | 0.03 (0.12) |
| COT linear | 1.62 (6.49) | 0.30 (1.58) | 0.09 (0.67) | 0.03 (0.09) | |
| MP2 linear | 0.78 (2.96) | 0.22 (1.18) | 0.03 (0.13) | 0.01 (0.03) | |
| Shanks | 0.23 (1.22) | 0.03 (0.13) | 0.01 (0.08) | ||
| Richardson 2 | 0.21 (0.97) | 0.03 (0.11) | 0.01 (0.03) | ||
The best performing methods are highlighted in bold for each ONT value.
Both the correlation energies and the reaction energies converge to the exact values for every method as the threshold gets tighter, which indicates the stability of all extrapolation strategies. Consequently, every technique improves the correlation energies compared to the uncorrected values. The same holds for the reaction energies.
Considering the correlation energies, the ΔMP2 correction
usually improves upon the uncorrected results as much as tightening
the ONT by a factor of 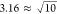 . Similarly, linear extrapolation
as a function
of the MP2 correlation energy is as good as or slightly better than
the ΔMP2 results obtained with
. Similarly, linear extrapolation
as a function
of the MP2 correlation energy is as good as or slightly better than
the ΔMP2 results obtained with 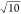 -times tighter thresholds. All extrapolation
strategies eliminate the error almost completely when 10–5 or tighter thresholds are employed. When applicable, the repeated
Richardson extrapolation performs slightly but consistently better
than the alternatives, although this benefit is probably not sufficient
to outweigh the need for three data points instead of the two required
for the linear methods. In the case of the 3.16 × 10–5 threshold, the “MP2 linear” extrapolation, equivalent
to the first Richardson extrapolation, appears to perform best because
of its excellent maximum error value. It is worth noting that for
correlation energies, every extrapolation method surpasses the ΔMP2
correction in accuracy.
-times tighter thresholds. All extrapolation
strategies eliminate the error almost completely when 10–5 or tighter thresholds are employed. When applicable, the repeated
Richardson extrapolation performs slightly but consistently better
than the alternatives, although this benefit is probably not sufficient
to outweigh the need for three data points instead of the two required
for the linear methods. In the case of the 3.16 × 10–5 threshold, the “MP2 linear” extrapolation, equivalent
to the first Richardson extrapolation, appears to perform best because
of its excellent maximum error value. It is worth noting that for
correlation energies, every extrapolation method surpasses the ΔMP2
correction in accuracy.
In the case of the reaction energies, the “MP2 linear” extrapolation method as well as the three-point extrapolations are again the best performers with thresholds below 10–5. Interestingly, for the ONTs of 10–5 and above, the ΔMP2 correction outperforms all other methods and yields results almost as good as the “uncorrected” values obtained with an order of magnitude tighter threshold. The exceptional accuracy of the ΔMP2 correction over the alternatives for reaction energies does not follow from the ranking observed for the correlation energies and can be attributed to the fortuitous cancellation of errors. This can be understood better by inspecting the individual reaction energy errors, which are plotted for all entries of the AW set in Figure S1 of the Supporting Information. In contrast to the case of ΔMP2 (left panel of Figure S1), the linear extrapolated errors of the right panel decrease systematically with a tighter FNO threshold and thus exhibit a more reliable overall convergence pattern. Compared to that, the oscillatory convergence of ΔMP2 leads to smaller reaction energy errors on the average above the 10–5 ONT value. Because, in the remaining sections, we consider the accuracy of energy differences, mostly of reaction energies, and employ 5 × 10–5 to 10–5 ONT thresholds; we will utilize the ΔMP2 correction.
Let us briefly note that similar trends can be observed with the cc-pVTZ basis set as with the cc-pVQZ basis described above. The only difference is that the ONT values corresponding to similar levels of NO truncation and the error measures shift to higher ONT values. For instance, the performance of ONT = 5 × 10–5 with the triple-ζ basis is comparable to that of ONT = 10–5 at the quadruple-ζ level.
Considering the choice of the independent variable, the MP2 energy-based extrapolation is found to perform better than the ones carried out with occupation-based thresholds. The extrapolation as a function of COT gives similar or slightly lower average deviations than the MP2 energy-based extrapolation, but the corresponding maximum errors are 1.5–5 times higher, that is, this scheme is less consistent. For reaction energies, the MP2 energy-based extrapolation performs best in all statistical measures.
Finally, let us point to further applications of the correlation energy-based extrapolations. Because the linear as well as the nonlinear sequence transformation techniques are found to perform better for correlation energies, they might be superior to MP2-based corrections for different molecular properties, where error cancellations cannot occur, such as nuclear gradients, dipole moments, or polarizabilities. These avenues will be explored in a forthcoming study.
4.3. Convergence of Reaction Energies with the FNO and NAF Approximations
Next, the convergence of the correlation energies and the reaction energies with the FNO and NAF truncation thresholds are inspected in order to determine the default settings for practical use. Error measures are reported using the ΔMP2 correction for the FNO truncation and both correction techniques described in Section 2.3 for the NAF approximation. Relative errors are evaluated compared to conventional DF-CCSD(T), while statistical measures are reported for the AW test set, containing 58 closed-shell species of up to 18 atoms.
The two panels of Figure 3 show the absolute error of reaction energies separately for the FNO and the NAF approximations. The plotted numerical data are collected in Tables S4 and S7 of the Supporting Information. The accuracy of both approximations is highly satisfactory. Concerning the FNO truncation, both the MAE and RMS measures are below the 1 kJ/mol mark already with 10–4 ONT values, while MAX errors are lower than 0.5 kJ/mol using 5 × 10–5 for the cc-pVTZ and 10–5 for the cc-pVQZ basis set. The latter two threshold-basis set combinations correspond to 0.22 and 0.13 kJ/mol MAE in the reaction energies and about 0.2% relative correlation energy errors (see Table S3). As expected from the results of Section 4.2, the absolute correlation energy errors are larger than the error of their contribution to the reaction energies, there is a noticeable error compensation, especially with the looser thresholds. Thus, anticipating the size-extensive growth of correlation energy errors and some error compensation in reaction energies, thresholds 5 × 10–5 and 10–5 can be expected to maintain the about 1 kJ/mol or better accuracy for cc-pVTZ and cc-pVQZ, respectively, at least up to the targeted range of 50–75 atoms.
Figure 3.

Errors of CCSD(T) reaction energies [in kJ/mol] for the AW test set with various basis sets and truncation thresholds separately for the FNO (left panel) and NAF (right panel) approximations. For clarity, the 3.69 kJ/mol RMS and 15.68 kJ/mol MAX errors obtained with the 10–1 NAF threshold are not shown.
The basis set-dependent progression of the FNO errors can be understood looking at the ratio of the retained NOs (left panel of Figure 4). Clearly, there are barely any NOs that can be dropped from the most compact cc-pVDZ basis, thus one cannot expect significant computational saving with double-ζ or smaller basis sets. There is more room to compress the system independently optimized larger basis sets using molecule-specific FNOs. The similar performance of the 5 × 10–5 and 10–5 thresholds for the triple- and quadruple-ζ basis sets is explained by the different slopes of the trends in the retained NO ratios and by the fact that a similar portion of the NOs (77 and 72%, respectively) is kept for the two basis sets with these truncations.
Figure 4.
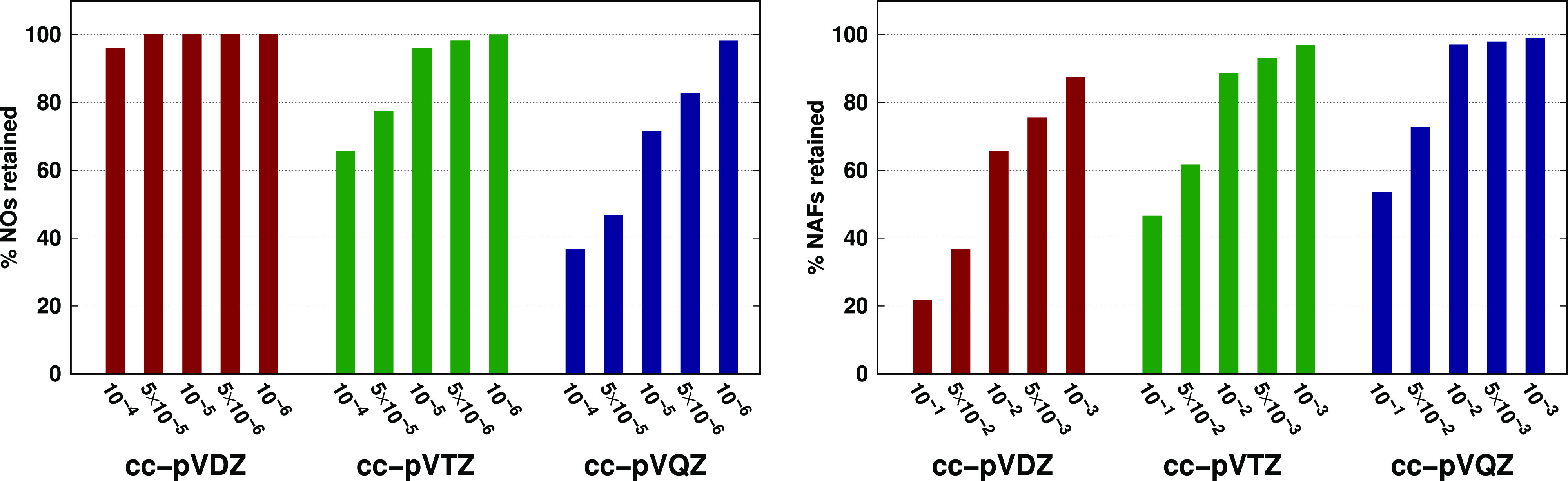
Average percentage of retained virtual NOs (left panel) and NAFs (right panel) for the AW test set with various basis sets and truncation thresholds. The plotted numerical data are collected in Tables S5 and S8 of the Supporting Information.
The convergence of the reaction energies with the NAF threshold (see Figure 3) is even more rapid, the MAE (MAX) values are already below 0.1 (0.25) kJ/mol with the 5 × 10–2 threshold for both cc-pVTZ and cc-pVQZ. However, the trend in the ratio of retained NAFs as a function of the basis set is quite the opposite of the trend observed for the FNOs (cf. the two panels of Figure 4). Because the number of terms yielding a single element of the W matrix of eq 5 scales quadratically with the number of AOs, the same NAF threshold introduces a more severe truncation in the auxiliary space corresponding to the smaller basis sets. This property explains the small number of retained NAFs and relatively large truncation errors observed for the cc-pVDZ basis set. However, the recommended 5 × 10–2 threshold performs similarly well for the two larger basis sets because of the comparable portion of retained NAFs (62 and 73%). Because the NAF approach provides smaller gains in the computational cost, it is beneficial to keep the NAF errors smaller than the FNO error. Indeed, the relative inaccuracies in the correlation energies with the 5 × 10–2 threshold are, in average, 0.08 and 0.02% for the cc-pVTZ and cc-pVQZ bases, respectively (see Table S6). Similarly to the case of the DF approximation, the NAF errors compensate excellently in reaction energies.36 In the present case, a factor of 20 and 7 reduction is observed in the NAF reaction energy errors compared to the corresponding correlation energy errors.
4.4. Accuracy of the Combined FNO and NAF Approximations
The simultaneous use of the FNO and NAF approximations is assessed on four test compilations. The NWH set, containing 47 species of up to 36 atoms, is chosen to test how the truncation errors change with the system size compared to the case of the AW set collecting roughly twice smaller molecules. Much less is known about the accuracy of the FNO and NAF approximations for open-shell molecules, thus we also examine the HEAT and the VIP test sets. The atomization energies of the HEAT suite are expected to be highly challenging because of the increased number of chemical bond breakings and the presumably smaller error compensation. The ionization potentials of the VIP list pose a different challenge because the IPs resulting from the difference of two large numbers being about 700–1300 kJ/mol could be more sensitive to the relative errors.
Absolute reaction energy errors obtained with the suggested 10–5 FNO and 5 × 10–2 NAF thresholds are collected for the AW and NWH sets in Table 3. The cumulative FNO and NAF errors are roughly the sum of the individual errors found in Section 4.3 for the AW test molecules, a minor compensation can be observed for the cc-pVQZ basis. In accord with our expectations, the ratio of the retained NAFs decreases further by about 5–15% when used in combination with the FNO approach without noticeable additional inaccuracy. Consequently, the MAE (MAX) deviations remain below the highly satisfactory 0.2 (0.8) kJ/mol for both cc-pVTZ and cc-pVQZ. Furthermore, the accuracy appears to be well balanced for the triple- and quadruple-ζ bases, and consequently, the average (maximum) errors of the CBS(T,Q) scheme increase only by 0.1 (0.5) kJ/mol compared to cc-pVQZ when the basis set extrapolation is employed.
Table 3. Combined FNO and NAF Truncation Errors (in kJ/mol) Including all MP2-Based Corrections for the Reaction Energies of the AW and the NWH Test Sets Using 10–5 FNO and 5 × 10–2 NAF Thresholds.
| test set | basisa | MAE | MAX | RMS |
|---|---|---|---|---|
| AW | cc-pVDZ | 0.75 | 2.85 | 1.02 |
| cc-pVTZ | 0.19 | 0.75 | 0.24 | |
| cc-pVQZ | 0.18 | 0.67 | 0.24 | |
| CBS(D,T) | 0.41 | 1.93 | 0.55 | |
| CBS(T,Q) | 0.30 | 1.18 | 0.41 | |
| NWH | cc-pVTZ | 0.10 | 0.37 | 0.14 |
CBS(X,X+1) denotes results obtained with the basis set extrapolation using the cc-pVXZ and cc-pV(X+1)Z basis sets.
Interestingly, the error measures are twice as small when comparing the larger species of the NWH set to those of AW on the same cc-pVTZ basis set. The smaller uncertainties obtained for NWH can be explained by the relatively large number of isomerization reactions in the NWH set, which benefit more from error cancellation. The remaining (i.e., not isomerization) reactions exhibit significantly larger errors than the isomerization reactions (0.34 kJ/mol on average compared to 0.08 kJ/mol obtained for the isomerizations), which resemble the average errors of the AW test set more closely. Therefore, it can be concluded that the error of the simultaneous NO and NAF basis set compressions does not increase significantly for larger molecules even if the isomerization reactions of the NWH compilation are not considered.
The analogous performance measures obtained for the HEAT and the VIP test sets are collected in Table 4. The ionization potentials exhibit absolute errors comparable to the case of the closed-shell molecules and, consequently, show exceptionally small relative errors. It is worth noting that the number of retained functions is found to be lower for diffuse basis sets. At least for the aug-cc-pV(T+d)Z basis and the VIP test set, it was sufficient to retain only about 65–70% of the virtual orbitals and 50% of the AFs with the same 10–5 FNO and 5 × 10–2 NAF thresholds.
Table 4. Combined FNO and NAF Truncation Errors (in kJ/mol) Including All MP2-Based Corrections for the Atomization Energies of the HEAT and the Ionization Potentials of the VIP Test Sets Using 10–5 FNO and 5 × 10–2 NAF Thresholds.
| all
reactions |
no hydrogena |
||||||
|---|---|---|---|---|---|---|---|
| test set | basis | MAE | MAX | RMS | MAE | MAX | RMS |
| HEAT | cc-pVTZ | 0.84 | 1.99 | 0.98 | 1.12 | 1.99 | 1.21 |
| cc-pVQZ | 0.96 | 2.71 | 1.20 | 0.30 | 0.88 | 0.39 | |
| CBS(T,Q) | 1.34 | 3.96 | 1.73 | 0.57 | 1.46 | 0.74 | |
| VIP | aug-cc-pV(T+d)Z | 0.24 | 0.97 | 0.37 | |||
Calculated from atomization energies excluding hydrogen-containing species.
The case of the HEAT test set appears to differ from the previous results, at least if only the same error measures are considered. The significantly increased deviations found for the atomization energies are somewhat unexpected in light of the fact that the largest species of the HEAT suite contains only 4 atoms. More detailed analysis uncovers that these higher errors for the case of the cc-pVQZ basis set can mostly be attributed to the complete lack of error cancellation in the atomization energies of hydrogen-containing species because of the zero correlation energy of the hydrogen atom. Indeed, the average (maximum) error for the cc-pVQZ basis set obtained without the hydrogen-containing molecules of HEAT is 0.30 (0.88) kJ/mol, in accordance with the error statistics of the other three test sets. In other words, the atomization energies of the hydrogen-containing species exhibit an average error of 0.87 kJ/mol per hydrogen atom, which is almost exactly the half of the 1.72 kJ/mol absolute error obtained for H2. Obviously, the FNO and NAF errors affect all other atom types too, but the large performance deviation of the HEAT set compared to the other three ones can mostly be explained by the missing error cancellation for hydrogen. Because atomization energies of molecules with dozens of atoms are not in the focus of practical interest, this shortcoming of the method can be accepted and taken into account in the rare cases when it is relevant. A different trend is observed for the case of the cc-pVTZ basis set, where the truncation of the smaller AO basis sets leads to somewhat higher errors for the non-hydrogen elements, and thus for the atomization of the molecules without hydrogen content. One should also point out that the CBS-extrapolated results again preserve well the accuracy obtained for the cc-pVTZ and cc-pVQZ bases.
Sherrill and DePrince previously invested significant effort into the assessment of the FNO-CCSD(T) method on noncovalent interaction energies.9,92 These authors found that the average (maximum) FNO error does not exceed 0.4 (0.9) kJ/mol with the aug-cc-pVTZ basis set and 0.1 (0.4) kJ/mol with aug-cc-pVDZ for the S22 test set even with a looser 10–4 ONT. Compared to this, our tighter FNO thresholds are expected to perform better even in combination with the NAF approach.
The test sets considered so far contain only a handful of molecules reaching 30 atom due to the high computational cost of obtaining CCSD(T) references. To further demonstrate that the performance does not deteriorate for extended systems, we consider other test cases lying in the 31–43-atom range, for which we have previously performed some of the largest conventional CCSD(T) computations using triple- and quadruple-ζ quality basis sets.12 First, the reaction energy and the corresponding barrier height are examined for a cyclic dihydrooxazine N-oxide (OO) intermediate formed from β-nitrostyrene (NS) and an enamine derivative (en-trans)82 as depicted in Figure 10 of ref (12). Second, an alternative reaction energy and barrier height are computed for the H2 activation by a frustrated Lewis pair type catalyst (FLPO)93 (see Figure 11 of ref (12)). The third reaction involves a palladium catalyzed C–H bond activation94 as depicted in Figure 12 of ref (12). The corresponding errors in reaction energies and barrier heights depicted in Figure 5 and gathered in Table S9 of the Supporting Information are excellent being in the range of −0.01 to 0.48 kJ/mol with the 10–5 threshold. Furthermore, the deviation from the exact reference remains below 1 kJ/mol even for the somewhat looser 5 × 10–5 threshold. While the remarkable accuracy of 0.01 kJ/mol obtained for the C–H activation reaction can be at least partly attributed to fortuitous error cancellation, these examples suggest that we can still expect 1 kJ/mol accuracy for large systems, at least in the 30–40 atom range. Even more interestingly, the FNO and NAF errors in energy differences appear to grow sub-linearly with system size indicating that similar performance can be expected for our largest applications with about twice as many atoms.
Figure 5.
FNO-CCSD(T) reaction energy errors compared to the conventional DF-CCSD(T) reference for medium-sized molecules of 31–43 atoms with two FNO thresholds and 5 × 10–2 as NAF threshold. Notations: “FLP TS” stands for FLPO + H2 → TSAdd, “FLP reac.” for FLPO + H2 → FLPA, “orgcat. TS” for en-trans + nitrostyrene → TS1, “orgcat. reac.” for en-trans + nitrostyrene → OO, and “Pd reac.” for AA + BA + TBHP → ABP + TBP + H2O. The plotted data are collected in Table S9 of the Supporting Information.
4.5. Timings and Computational Efficiency
The largest species involved in the reactions of Figure 5 and Table S9 of the Supporting Information are denoted by OO, TS1, FLPO, TSAdd, FLPA, and ABP and contain 40, 40, 41, 43, 43, and 31 atoms, respectively. The results of the corresponding wall time measurements are collected in Table 5. The performance values of Table 5 are obtained from the measured wall times divided by the estimates for the optimal wall time corresponding to the theoretical peak performance utilization of the employed CPUs. The measurements demonstrate that highly accurate FNO-CCSD(T) results became feasible with our implementation for systems of about 40 atoms and 1000 AOs almost overnight (cca. 18–20 h) using 24 cores of two 6-year-old 12-core CPUs and at most 100 GB memory. Such hardware resources should be available to almost everyone in the computational chemistry community.
Moreover, if very large basis sets are required to approach the CBS limit of CCSD(T), quadruple-ζ level FNO-CCSD(T) computations can also be performed in about a day at the 30 atom range. For that, we employed 112 cores of four many-core CPUs resulting in about 17 h of runtime for the ABP molecule because of the almost 60% peak performance utilization. Compared to our previous measurements [performed with the same DF-CCSD(T) implementation as was employed also in the FNO-CCSD(T) context and for the same species (OO, TS1, ABP) using the complete MO and auxiliary bases,12 here, we find that the peak performance utilization does not change significantly upon the compression of the MO and auxiliary spaces. Note that for the FLPO, FLPA, and TSAdd systems, we employed a considerably older CPU, which does not support AVX-512 instructions. Moreover, we utilized less memory for these cases leading to some redundant ERI assembly steps for both CCSD and (T). All in all, the 34–55 and 41–60% peak performance utilizations measured in these cases for CCSD and (T), respectively, are still highly competitive compared to currently available (reduced-cost) CCSD(T) implementations. Most interestingly, we observe a two- and an eight-fold reduction in the CPU time requirement for the OO (or TS1) and the ABP molecules, respectively, because of the NAF and FNO (with the tighter 10–5 threshold) approaches. These speedups match the theoretical operation count reductions of 2.3 and 7.3 almost perfectly. An even higher speedup factor of 38 is obtained for the ABP molecule using the still practically error-free 5 × 10–5 FNO threshold.
The performance of the closed-shell DF- and FNO-CCSD(T) implementations is also demonstrated on the guanine–cytosine deoxydinucleotide monophosphate (GC-dDMP-B) molecule (see Figure 6), which has become one of the standard benchmark systems to assess the performance of parallel CC programs. Wall time measurements performed with the present implementation of the MRCC suite,12 as well as with the CCSD(T) programs of the NWChem30 and MPQC10 packages and the CCSD code of TeraChem,24 are collected in Table 6. The CCSD program of NWChem30 introduced pioneering algorithmic developments to overcome the severe communication bottleneck related to the numerous four-center ERIs needed during the CCSD iteration. The massively parallel (T) implementation of NWChem30 has also achieved impressive parallel scaling on 160,000 cores of 20,000 CPUs and, consequently, surpassed the 1 PFLOP/s performance milestone. Recent optimization efforts in MPQC10 include the utilization of DF in the CCSD part and the permutational symmetry of the (T) energy expression. The latter is probably the largest contributing factor to the noticeable jump in the performance increase of MPQC over NWChem for the (T) term (cf. the 10 and 44% efficiencies). The most recent CCSD implementation of TeraChem represents a significant step toward a large-scale utilization of GPUs.24 Even though this GPU code has been developed for a single node equipped with 1 TB memory and 8 of the most advanced V100 GPUs, the 14% peak performance utilization appears to be highly advanced considering the additional data transfer needed between the main memory and the GPUs.
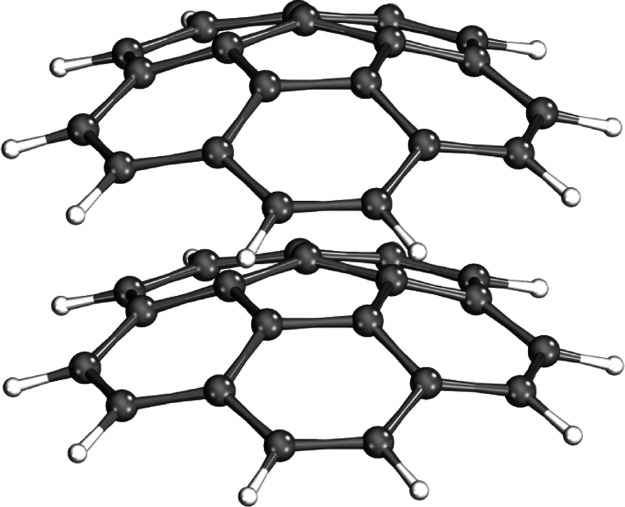
Figure 6.
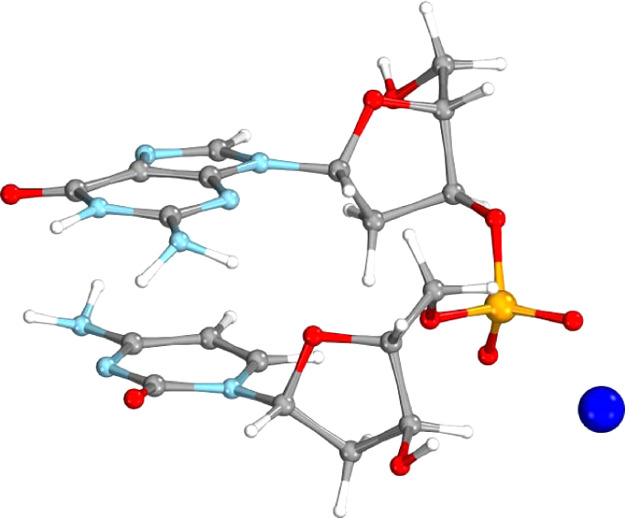
Guanine–cytosine deoxydinucleotide monophosphate (GC-dDMP-B) system: 63 atoms, 1042 AOs.30
Table 6. Wall Times for CCSD(T) Calculations for the GC-dDMP-B Molecule Performed with the NWChem,30 MPQC,10 and MRCC Suites,12 as well as the CCSD Program of TeraChem24.
| no. of CPUs | no. of cores | CCSD it. [min] | (T) [day] | % CCSD performancea | % (T) performanceb | |
|---|---|---|---|---|---|---|
| NWChem30 | 1100c | 1100 | 72 | 11 | ||
| NWChem30 | 20,000c | 160,000d | 13 | 0.06 | 3.4 | 10 |
| MPQC10 | 128e | 1024 | 43 | 1.98 | 24 | 44 |
| TeraChem(24) | 8f | 40,960f | 25 | 14 | ||
| MRCC | 4g | 112 | 67 | 5.48 | 47 | 53 |
| MRCC (FNO & NAF)h | 4g | 112 | 31 | 2.27 | 39 | 54 |
Efficiency based on the operation count of an optimal CCSD algorithm estimated as the sum of the operation counts of the sixth-power scaling terms, and in the case of a DF algorithm, the assembly of the four-external two-electron integrals utilizing the full permutational symmetry.
Efficiency based on the operation count of an optimal (T) algorithm estimated as the operation count of the seventh-power scaling terms utilizing the full permutational symmetry.
Performed with 8-core AMD 6276 Interlagos CPUs clocked at 2.3 GHz.
The CCSD calculation utilized one core per node.
Performed with 8-core Intel Xeon E5-2670 CPUs clocked at 2.6 GHz.
The calculation was performed on 8 Tesla V100 GPUs. The “no. of CPUs” column contains the number of GPUs, the “no. of cores” corresponds to the number of CUDA cores.
Performed with four 28-core Intel Xeon Platinum 8180M CPUs clocked at 1.7 GHz.
Calculated with a FNO threshold of 5 × 10–5 and a NAF threshold of 5 × 10–2.
Compared to these advanced implementations, the efficiency of our code facilitates the computation of the same system in a comparable time using a fraction of compute cores, namely, only 112 cores. This markedly smaller hardware requirement in this example can be attributed to the excellent 47 and 53% peak performance utilization of our CCSD and (T) algorithms, respectively. Note that, because of a lack of dedicated auxiliary basis sets corresponding to the 6-311++G(d,p) basis, we employed the aug-cc-pVTZ-RI basis, which contains about 5.1 times more AFs than the number of AOs in 6-311++G(d,p) (cf. Table 7 below). In the case of Dunning and Ahlrichs basis sets with dedicated RI fitting bases, this ratio is usually much smaller, around 2.5 at the triple-ζ level. This resulted in an unnecessarily high ERI assembly cost and decreased the efficiency compared to NWChem, while the RI fitting basis choice was not documented in ref (10).
In comparison with the above results, the present FNO and NAF approximations further decrease the wall times by a factor of 2.2–2.4, which now closely approach the runtime of the highly optimized MPQC code using an order of magnitude more cores for the considered approximation-free DF-CCSD(T) computation.10 The truncation error of the correlation energy introduced by the FNO and NAF basis set compressions is about 0.3%. This value is in close agreement with the average correlation energy deviations obtained for the much smaller systems of the AW set with triple-ζ basis set (see Table S3 of the Supporting Information). Moreover, there are a number of possible applications of the present FNO-CCSD(T) approach, where, especially above 50 atoms, truncation errors above the 1 kJ/mol mark are equally sufficient because of the increase of the uncertainty, for instance, in the relevant conformers, as well as thermal, entropic, or solvent contributions. Thus, the use of looser thresholds in such cases could further reduce the required computational efforts, making the FNO and NAF approximation pair highly beneficial for large-scale and accurate CCSD(T) computations.
4.6. Large-Scale Applications
In this section, we illustrate the capabilities of the presented FNO-CCSD(T) implementation on current chemical questions, which would otherwise be well out of the scope of conventional CCSD(T) implementations. Special attention was paid during the selection of the demonstrative applications to keep the required resources in the range of 100 compute cores and few days of runtime. Our motivation was to present examples which can be relatively routinely accessible for a broad audience supposing a widely available number of cores and compute time quotas. Besides the GC-dDMP-B system30 representing a small model of biochemical systems, the three other examples include a ligand exchange reaction of a ruthenium complex81 (Figure 7), a barrier height in an organocatalytic reaction82 (Figure 8), and the NCIE of the corannulene dimer83,95 (Figure 9).
Figure 7.

Ligand exchange reaction of a Ru-complex (reaction 28 of the MOR41 test set81).
Figure 8.
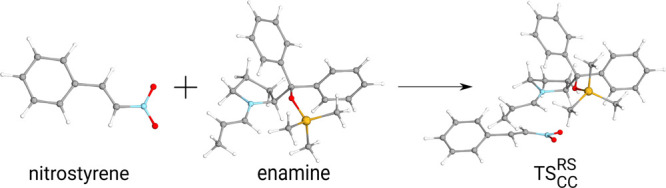
C–C bond formation step of the Michael addition reaction via the transition state labeled TSCCRS in ref (82).
Figure 9.
Concave–convex, eclipsed conformer of the corannulene dimer taken from ref (83).
The organometallic ligand exchange reaction is taken from the recent metal organic reaction (MOR41) test compilation of Checinski and co-workers.81 This reaction, number 28 of the MOR41 set, contains two Ru-complexes related by the exchange of 1,2-bis(dimethylphosphino)ethane (dmpe) and 1,5-cyclooctadiene (COD) ligands. The educt and product Ru-complexes, labeled ED28 and PR28, contain 47 and 51 atoms, respectively, and these are the largest systems considered in the present work using quadruple-ζ basis sets. Table 7 collects the dimensions of the corresponding orbital spaces reaching 2124 AOs and 4745 AFs for the PR28 system. To the best of our knowledge, these are by far the largest orbital spaces ever involved in a CCSD(T) computation without relying on local approximations. The PR28 computation has clearly become feasible on 112 cores by compressing the virtual MO (with the tighter 10–5 threshold) and the AF dimensions to about 65 and 49% of the original, which correspond to a theoretical speedup of 5.8.
The MOR41 reference energies were evaluated using local CCSD(T) methods, and the authors of ref (81) also found it important to estimate the accuracy of the employed local approximations compared to conventional CCSD(T). However, the computation of such reference energies is challenging using quadruple-ζ basis sets, and the limitations of the CCSD(T) implementation employed in ref (81) emerged already for reaction 5 containing species with at most 14 atoms. Thus, in such cases the present FNO-CCSD(T) implementation can triple the size of the accessible systems in similar state-of-the-art benchmark studies, where the accuracy assessment of local CCSD(T) methods is also of interest. The CBS-extrapolated local CCSD(T) reaction energy of ref (81) was reported to be −36.3 kcal/mol, which, considering the remaining basis set incompleteness as well as FNO, NAF, and local errors, is consistent with our FNO-CCSD(T)/def2-QZVP result of −35.1 kcal/mol (see Figure 10 and Table S10 of the Supporting Information).
The motivation for the consideration of the remaining two examples is similar, namely, to provide reliable references for particularly challenging systems that we encountered during the development and application of our local CCSD(T) method.39,56 One step of an organocatalytic Michael addition reaction is selected leading to a transition state (TSCCRS) along the C–C bond formation between NS and an enamine formed from the propanal reactant and a diphenylprolinol silyl ether catalyst.82 As sizable noncovalent interactions between the reactant and the catalyst contribute considerably to the energetics and thus to the overall stereochemistry, well-converged local CCSD(T) results were used to benchmark the employed density functional approximation (DFA).56,82 Previously, we closely studied an analogous but slightly larger system, the complex of TSCC with the p-nitrophenol cocatalyst,56,82 and we have found an unexpectedly large (T) contribution of −7.8 kcal/mol to the barrier height. Here, the CBS extrapolation using aug-cc-pVTZ and aug-cc-pVQZ basis sets performed previously with the LNO-CCSD(T) method56,82 is unfeasible, but the FNO-CCSD(T) approach facilitated the use of the def2-TZVP basis set. The resulting calculation for the 75 atoms of TSCCRS is still demanding but benefited from the theoretical speedup of 2 provided by the FNO and NAF approaches. Furthermore, approximately −7 kcal/mol is found for the (T) contribution to the barrier height (see Figure 10 and Table S10 of the Supporting Information), which, considering the presence of the co-catalyst in the previous study and the different level of basis set convergence, indicates that the local approximations provided a realistic result.
Figure 10.

Reaction and NCIEs of extended molecules using the FNO and NAF thresholds specified in Table 7. Notation: “Ru reac.” for ED28 + dmpe → PR28 + COD,81 “organocat. TS” for NS + enamine → TSCCRS,82 and “NCIE (no CP)” and “NCIE (CP)” for the NCIE of the corannulene dimer without and with CP correction, respectively. The plotted data are collected in Table S10 of the Supporting Information.
The third example focuses more closely on complicated noncovalent interactions, namely, the interaction energy of the corannulene dimer is evaluated. The relatively long-range and large number of the π–π interactions involved in complexes held together by such delocalized π-systems pose a significant challenge on all local correlation methods.54,56,57,95 The difficulty for local CC methods is that only a small portion of distant π–π interactions can be treated at an approximate, for example, MP2 level. Consequently, accurate local CCSD(T) computations require tight thresholds and could become highly demanding. Recently, we have performed LNO-CCSD(T) computations aiming at highly converged interaction energies for extended supramolecular complexes with significant π–π interactions.95 The LNO-CCSD(T) interaction energies were compared to fixed-node diffusion Monte Carlo (FN-DMC) results for the L7 set96 and an additional supramolecular complex.95 FN-DMC is one of the handful wavefunction-based methods which was repeatedly found to provide highly reliable interaction energies in agreement with CCSD(T) and can be employed for large complexes above 100 atoms.97−99 Interestingly, LNO-CCSD(T) and FN-DMC were consistent within their error estimates only for five of the eight complexes studied in ref (95), while notable differences remained especially for systems interacting through extended and curved π-electron systems.95 Thus, it would be helpful moving toward an explanation for this disagreement to obtain alternative and reliable interaction energies for such systems, which are free from the approximations employed in LNO-CCSD(T) and FN-DMC.
Here, we employ the presented FNO-CCSD(T) method to provide such reference data without relying on local approximations. The corannulene dimer is one of the largest complexes (60 atoms) that contains extended and curved π-systems and could be targeted by FNO-CCSD(T) using a reasonably large AO basis set equipped with diffuse functions. The size of the def2-TZVPPD basis set resulting in 1820 AOs and 4460 AFs still makes FNO-CCSD(T) highly challenging, and it only becomes treatable on 160 CPU cores after reducing the operation count by a factor of 5.3 using the FNO and NAF techniques. While the interaction energies are not converged with the def2-TZVPPD basis set, the basis set superposition error can be decreased using counterpoise (CP) corrections100 (see Figure 10 and Table S10 of the Supporting Information). The CP corrected FNO-CCSD(T) result of −14.3 kcal/mol is consistent with the pioneering QCISD(T)/aug-cc-pVDZ computation of Janowski et al.,83 who reported −15.5 kcal/mol after the inclusion of an MP2/aug-cc-pVTZ level basis set correction.
Finally, let us consider the wall time requirements and corresponding peak performance utilizations for the largest presented examples collected in Table 8. The enamine molecule and the corannulene dimer were computed with four MPI tasks and two outermost OpenMP threads. The remaining computations of Table 8 are performed using four MPI tasks, four outer OpenMP threads, and threaded BLAS routines in the innermost OpenMP layer. This setup was found to be the most efficient for the (T) part of CCSD(T) in our previous measurements. We refer to that work for further technical details.12 The measured efficiency in terms of peak performance utilization is again consistently high. The best performance is measured for the enamine system exhibiting 55 and 71% efficiency for the CCSD and (T) parts, respectively. The factors contributing to this close to optimal efficiency are the relatively small number of innermost OpenMP threads, the sufficiently high, 120 GB/node memory allocation, and the more fortunate arithmetic performance per data transfer rate ratio of the employed processors. Some deterioration of performance is observed for the larger systems using many core processors. These CPUs perform 4–7 times more operations per second and thus pose more challenges from the data transfer point of view. Additionally, the number of occupied and virtual MOs, and hence, the memory requirement of these molecules are considerably larger here than for the enamine system or in the measurements of ref (12). Consequently, more ERI assembly steps have to be repeated in our integral-direct CCSD and (T) algorithms. However, the expressions employed for the optimal performance measure guarantee that each ERI assembly step is counted precisely once in order to avoid any bias toward algorithms relying on disk I/O or distributed memory. Let us note that for PR28, the data size of the symmetry-packed four-center ERI tensor would be 18.5 TB in the complete basis of 2124 orbitals and 3.3 TB in the compressed NO space. Such large four-center ERI arrays would lead to serious complications in alternative algorithms relying on disk I/O, semi-integral-direct contractions, and so forth and point to DF factorization as a particularly effective way to circumvent such data bottlenecks.
Table 8. Wall Times and Corresponding Peak Performance Utilizations Measured for Large Systems of 47–75 Atoms with the FNO-NAF Thresholds Specified in Table 7.
| wall
time |
% performance |
|||||||
|---|---|---|---|---|---|---|---|---|
| species | atoms | no. of AOs | no | no. of cores | CCSD [min]a | (T) [day] | CCSD | (T) |
| ED28b | 47 | 1978 | 57 | 112 | 60 | 3.4 | 48 | 54 |
| PR28b | 51 | 2124 | 60 | 112 | 76 | 5.1 | 49 | 50 |
| enaminec | 57 | 998 | 69 | 32 | 74 | 4.7 | 55 | 71 |
| corannulene dimerd | 60 | 1820 | 90 | 160 | 80 | 13.5 | 28 | 33 |
| GC-dDMP-Bb | 63 | 1042 | 103 | 112 | 31 | 2.3 | 39 | 54 |
| TSCCRSb | 75 | 1381 | 97 | 112 | 87 | 9.9 | 46 | 50 |
Time of one iteration.
Performed with four 28-core Intel Xeon Platinum 8180M CPUs clocked at 1.7 GHz.
Performed with four 8-core Intel Xeon E5-2609 v4 CPUs clocked at 1.7 GHz.
Performed with eight 20-core Intel Xeon Gold 6138 CPUs clocked at 1.3 GHz.
Let us also highlight the relatively affordable computational cost of these calculations. The entire FNO-CCSD iteration was completed in a day for all six examples of Table 8. However, the convergence pattern of Figure 10 clearly indicates that the (T) correction is required for chemical accuracy. The full FNO-CCSD(T) computation required only 4.7 days for the enamine system of 57 atoms using four four-year-old, 8-core CPUs. Similar resources should be accessible in almost all computer clusters. The remaining examples required only 4–8 many-core processors and less than 1-2 weeks of wall time. For PR28, the corannulene dimer, and TSCCRS, the 6, 14.4, and 9.9 days even include a restart step as these computations took longer than the 5–7-day wall time limit enforced in the utilized computer clusters. We find that better compute quota efficiencies and preferable times to solution can be obtained using a relatively small number of nodes for multiple reasons: (i) smaller performance loss because of imperfect parallel scaling with a large number of nodes, (ii) shorter queuing times, and (iii) smaller and more crowded computer clusters can also be utilized, where it would be practically impossible to request several hundred or thousand cores.
5. Summary and Outlook
The accurate, efficient, and systematically
improvable FNO and
NAF approximations are implemented and benchmarked within both the
closed- and open-shell single-reference DF-CCSD(T) formulations. Both
DF-CCSD(T) algorithms are hand-optimized, OpenMP-parallel, fully or
partially integral direct, as well as operation count- and memory-economic
by exploiting the full permutational symmetry of contractions and
symmetry-packed storage formats. Additionally, both the closed- and
open-shell DF-CCSD(T) codes benefit from frequent checkpointing, the 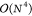 -scaling cost reduction resulting from the
FNO scheme and the reduced-cost four-center ERI assembly performed
in the compressed FNO and NAF bases. On top of that, the hybrid MPI/OpenMP
parallel closed-shell DF-CCSD(T) implementation requires negligible
disk I/O and network bandwidth and exhibits excellent parallel scaling
and peak performance utilization (50–70%) up to a few hundred
cores.12 Because the relative cost of the
non-PPL terms increase when the virtual space is compressed in the
FNO basis, our t1-transformed CCSD algorithm
with optimized non-PPL terms is especially well suited for the FNO-CCSD(T)
approach. Analogously, the time required for the integral-direct ERI
assembly may grow up to 50–70% of a CCSD iteration performed
in the compressed FNO and original auxiliary bases, which is accelerated
by up to 50–80% using the NAF approximation.
-scaling cost reduction resulting from the
FNO scheme and the reduced-cost four-center ERI assembly performed
in the compressed FNO and NAF bases. On top of that, the hybrid MPI/OpenMP
parallel closed-shell DF-CCSD(T) implementation requires negligible
disk I/O and network bandwidth and exhibits excellent parallel scaling
and peak performance utilization (50–70%) up to a few hundred
cores.12 Because the relative cost of the
non-PPL terms increase when the virtual space is compressed in the
FNO basis, our t1-transformed CCSD algorithm
with optimized non-PPL terms is especially well suited for the FNO-CCSD(T)
approach. Analogously, the time required for the integral-direct ERI
assembly may grow up to 50–70% of a CCSD iteration performed
in the compressed FNO and original auxiliary bases, which is accelerated
by up to 50–80% using the NAF approximation.
Extensive benchmarks are performed for challenging reactions, isomerizations, as well as atomization and ionization processes involving both closed- and open-shell species. Various energy correction as well as linear and nonlinear extrapolation schemes are explored, which decrease both the FNO and the NAF errors and allow for the use of significantly looser thresholds in return for larger performance gains. Rigorous FNO and NAF threshold combinations are determined yielding at most 1–2 kJ/mol errors even for the most challenging atomization energies obtained with triple- and quadruple-ζ basis sets. This accuracy is maintained upon both basis set extrapolation and significant increase in system size. Maximum errors remained below 1 kJ/mol when tested against the largest accessible conventional CCSD(T) references in the 31–43 atom region. Even these highly conservative thresholds yield up to 8–38-fold speedup and up to 3–14-fold reduction in memory requirements. This cost reduction opens the possibility to explore a considerably larger portion of chemical space up to about 50–75 atoms (2124 AOs) while retaining the reliability of CCSD(T).
Using widely accessible computational resources, that is, at most 112–160 cores of a few CPUs, we presented some of the largest CCSD(T) computations ever performed without relying on local approximations. The same computational performance is now available, for example, in a single, dual-socket node with 128 cores of two recent AMD CPUs. The demonstrative benchmark FNO-CCSD(T) results obtained for organocatalytic and organometallic reactions, as well as noncovalent interactions have immediate use in the accuracy assessment of local CCSD(T) schemes right within or much closer to their intended scope of application. The increasing interest in the utilization of the more and more affordable local CCSD(T) methods also uncovered systems of an unexpectedly complicated electronic structure54,56−58,95 for which benchmarking local approximations remains highly challenging. The presented FNO-CCSD(T) method is thus expected to assist the characterization of such local approximations, which can be practically inactive for small systems but may become significant with increasing system size.
Furthermore, the more reliable sampling of real-life chemical questions motivated recent compilations of CCSD(T) benchmark data,57,81,101−104 evaluated with either local approximations or composite methods with lower level basis set corrections, in the size range just became reachable also by our FNO-CCSD(T) scheme. However, the average deviation of the best performing DFAs from these references is becoming more and more comparable to the error estimates corresponding to local and/or basis set incompleteness errors of the benchmark data. Thus, the presented FNO-CCSD(T) code could also be useful to narrow the error estimates of such CCSD(T) references. Moreover, current data sets employed for the parametrization or assessment of DFAs105,106 and for the training step in machine learning approaches107−115 often contain thousands or more CC results. The construction of such CCSD(T) references could also benefit from the presented FNO-CCSD(T) code optimized for the effective use of compute resource quotas in commodity computer clusters or in cloud environments. Finally, the presented developments represent the first steps toward an effective and parallel FNO-based reduced-cost, and eventually an LNO-based, reduced-scaling CCSD(T) gradient implementation.
Acknowledgments
The authors are grateful for the financial support from the National Research, Development, and Innovation Office (NKFIH, grant no. KKP126451). The research reported in this paper was also supported by the BME Biotechnology TKP2020 IE grant of NKFIH Hungary (BME IE-BIO TKP2020). The work of PRN is supported by the ÚNKP-19-4 and ÚNKP-20-5 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. The computing time granted on the Hungarian HPC Infrastructure at NIIF Institute, Hungary and the DECI resource Saga based in Norway at Trondheim with support from the PRACE aisbl (NN9914K) are gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c01077.
The authors declare no competing financial interest.
Supplementary Material
References
- Crawford T. D.; Schaefer H. F. III. An Introduction to Coupled Cluster Theory for Computational Chemists. Reviews in Computational Chemistry; John Wiley & Sons, Ltd., 1999; Vol. 14, p 33. [Google Scholar]
- Helgaker T.; Jørgensen P.; Olsen J.. Molecular Electronic Structure Theory; Wiley: Chichester, 2000. [Google Scholar]
- Shavitt I.; Bartlett R. J.. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory; Cambridge Molecular Science; Cambridge University Press, 2009. [Google Scholar]
- Bartlett R. J.; Musiał M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291. 10.1103/revmodphys.79.291. [DOI] [Google Scholar]
- Raghavachari K.; Trucks G. W.; Pople J. A.; Head-Gordon M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479. 10.1016/s0009-2614(89)87395-6. [DOI] [Google Scholar]
- Evangelista F. A. Perspective: Multireference coupled cluster theories of dynamical electron correlation. J. Chem. Phys. 2018, 149, 030901. 10.1063/1.5039496. [DOI] [PubMed] [Google Scholar]
- Epifanovsky E.; Zuev D.; Feng X.; Khistyaev K.; Shao Y.; Krylov A. I. General implementation of the resolution-of-the-identity and Cholesky representations of electron repulsion integrals within coupled-cluster and equation-of-motion methods: Theory and benchmarks. J. Chem. Phys. 2013, 139, 134105. 10.1063/1.4820484. [DOI] [PubMed] [Google Scholar]
- Bozkaya U.; Sherrill C. D. Analytic energy gradients for the coupled-cluster singles and doubles with perturbative triples method with the density-fitting approximation. J. Chem. Phys. 2017, 147, 044104. 10.1063/1.4994918. [DOI] [PubMed] [Google Scholar]
- DePrince A. E.; Sherrill C. D. Accuracy and Efficiency of Coupled-Cluster Theory Using Density Fitting/Cholesky Decomposition, Frozen Natural Orbitals, and a t1-Transformed Hamiltonian. J. Chem. Theory Comput. 2013, 9, 2687. 10.1021/ct400250u. [DOI] [PubMed] [Google Scholar]
- Peng C.; Calvin J. A.; Valeev E. F. Coupled-cluster singles, doubles and perturbative triples with density fitting approximation for massively parallel heterogeneous platforms. Int. J. Quantum Chem. 2019, 119, e25894 10.1002/qua.25894. [DOI] [Google Scholar]
- Shen T.; Zhu Z.; Zhang I. Y.; Scheffler M. Massive-parallel Implementation of the Resolution-of-Identity Coupled-cluster Approaches in the Numeric Atom-centered Orbital Framework for Molecular Systems. J. Chem. Theory Comput. 2019, 15, 4721. 10.1021/acs.jctc.8b01294. [DOI] [PubMed] [Google Scholar]
- Gyevi-Nagy L.; Kállay M.; Nagy P. R. Integral-direct and parallel implementation of the CCSD(T) method: Algorithmic developments and large-scale applications. J. Chem. Theory Comput. 2020, 16, 366. 10.1021/acs.jctc.9b00957. [DOI] [PubMed] [Google Scholar]
- Pitoňák M.; Aquilante F.; Hobza P.; Neogrády P.; Noga J.; Urban M. Parallelized implementation of the CCSD(T) method in MOLCAS using optimized virtual orbitals space and Cholesky decomposed two-electron integrals. Collect. Czech. Chem. Commun. 2011, 76, 713–742. 10.1135/cccc2011048. [DOI] [Google Scholar]
- Boström J.; Pitoňák M.; Aquilante F.; Neogrády P.; Pedersen T. B.; Lindh R. Coupled Cluster and Møller–Plesset Perturbation Theory Calculations of Noncovalent Intermolecular Interactions using Density Fitting with Auxiliary Basis Sets from Cholesky Decompositions. J. Chem. Theory Comput. 2012, 8, 1921. 10.1021/ct3003018. [DOI] [PubMed] [Google Scholar]
- Kinoshita T.; Hino O.; Bartlett R. J. Singular value decomposition approach for the approximate coupled-cluster method. J. Chem. Phys. 2003, 119, 7756. 10.1063/1.1609442. [DOI] [Google Scholar]
- Hummel F.; Tsatsoulis T.; Grüneis A. Low rank factorization of the Coulomb integrals for periodic coupled cluster theory. J. Chem. Phys. 2017, 146, 124105. 10.1063/1.4977994. [DOI] [PubMed] [Google Scholar]
- Schutski R.; Zhao J.; Henderson T. M.; Scuseria G. E. Tensor-structured coupled cluster theory. J. Chem. Phys. 2017, 147, 184113. 10.1063/1.4996988. [DOI] [PubMed] [Google Scholar]
- Peng B.; Kowalski K. Highly Efficient and Scalable Compound Decomposition of Two-Electron Integral Tensor and Its Application in Coupled Cluster Calculations. J. Chem. Theory Comput. 2017, 13, 4179. 10.1021/acs.jctc.7b00605. [DOI] [PubMed] [Google Scholar]
- Parrish R. M.; Sherrill C. D.; Hohenstein E. G.; Kokkila S. I. L.; Martínez T. J. Communication: Acceleration of coupled cluster singles and doubles via orbital-weighted least-squares tensor hypercontraction. J. Chem. Phys. 2014, 140, 181102. 10.1063/1.4876016. [DOI] [PubMed] [Google Scholar]
- Parrish R. M.; Zhao Y.; Hohenstein E. G.; Martínez T. J. Rank reduced coupled cluster theory. I. Ground state energies and wavefunctions. J. Chem. Phys. 2019, 150, 164118. 10.1063/1.5092505. [DOI] [PubMed] [Google Scholar]
- Benedikt U.; Böhm K.-H.; Auer A. A. Tensor decomposition in post-Hartree-Fock methods. II. CCD implementation. J. Chem. Phys. 2013, 139, 224101. 10.1063/1.4833565. [DOI] [PubMed] [Google Scholar]
- Lesiuk M. Implementation of the Coupled-Cluster Method with Single, Double, and Triple Excitations using Tensor Decompositions. J. Chem. Theory Comput. 2020, 16, 453. 10.1021/acs.jctc.9b00985. [DOI] [PubMed] [Google Scholar]
- DePrince A. E.; Kennedy M. R.; Sumpter B. G.; Sherrill C. D. Density-fitted singles and doubles coupled cluster on graphics processing units. Mol. Phys. 2014, 112, 844. 10.1080/00268976.2013.874599. [DOI] [Google Scholar]
- Fales B. S.; Curtis E. R.; Johnson K. G.; Lahana D.; Seritan S.; Wang Y.; Weir H.; Martínez T. J.; Hohenstein E. G. Performance of Coupled-Cluster Singles and Doubles on Modern Stream Processing Architectures. J. Chem. Theory Comput. 2020, 16, 4021–4028. 10.1021/acs.jctc.0c00336. [DOI] [PubMed] [Google Scholar]
- Peng C.; Calvin J. A.; Pavošević F.; Zhang J.; Valeev E. F. Massively Parallel Implementation of Explicitly Correlated Coupled-Cluster Singles and Doubles Using TiledArray Framework. J. Phys. Chem. A 2016, 120, 10231. 10.1021/acs.jpca.6b10150. [DOI] [PubMed] [Google Scholar]
- Eriksen J. J. Efficient and portable acceleration of quantum chemical many-body methods in mixed floating point precision using OpenACC compiler directives. Mol. Phys. 2017, 115, 2086. 10.1080/00268976.2016.1271155. [DOI] [Google Scholar]
- Aprà E.; Kowalski K. Implementation of High-Order Multireference Coupled-Cluster Methods on Intel Many Integrated Core Architecture. J. Chem. Theory Comput. 2016, 12, 1129. 10.1021/acs.jctc.5b00957. [DOI] [PubMed] [Google Scholar]
- Deegan M. J. O.; Knowles P. J. Perturbative corrections to account for triple excitations in closed and open shell coupled cluster theories. Chem. Phys. Lett. 1994, 227, 321. 10.1016/0009-2614(94)00815-9. [DOI] [Google Scholar]
- Kobayashi R.; Rendell A. P. A direct coupled cluster algorithm for massively parallel computers. Chem. Phys. Lett. 1997, 265, 1–11. 10.1016/s0009-2614(96)01387-5. [DOI] [Google Scholar]
- Anisimov V. M.; Bauer G. H.; Chadalavada K.; Olson R. M.; Glenski J. W.; Kramer W. T. C.; Aprà E.; Kowalski K. Optimization of the Coupled Cluster Implementation in NWChem on Petascale Parallel Architectures. J. Chem. Theory Comput. 2014, 10, 4307–4316. 10.1021/ct500404c. [DOI] [PubMed] [Google Scholar]
- Asadchev A.; Gordon M. S. Fast and Flexible Coupled Cluster Implementation. J. Chem. Theory Comput. 2013, 9, 3385–3392. 10.1021/ct400054m. [DOI] [PubMed] [Google Scholar]
- Deumens E.; Lotrich V. F.; Perera A.; Ponton M. J.; Sanders B. A.; Bartlett R. J. Software design of ACES III with the super instruction architecture. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 895–901. 10.1002/wcms.77. [DOI] [Google Scholar]
- Kaliman I. A.; Krylov A. I. New algorithm for tensor contractions on multi-core CPUs, GPUs, and accelerators enables CCSD and EOM-CCSD calculations with over 1000 basis functions on a single compute node. J. Comput. Chem. 2017, 38, 842–853. 10.1002/jcc.24713. [DOI] [PubMed] [Google Scholar]
- Janowski T.; Pulay P. Efficient Parallel Implementation of the CCSD External Exchange Operator and the Perturbative Triples (T) Energy Calculation. J. Chem. Theory Comput. 2008, 4, 1585–1592. 10.1021/ct800142f. [DOI] [PubMed] [Google Scholar]
- Solomonik E.; Matthews D.; Hammond J. R.; Stanton J. F.; Demmel J. A massively parallel tensor contraction framework for coupled-cluster computations. J. Parallel Distr. Comput. 2014, 74, 3176. 10.1016/j.jpdc.2014.06.002. [DOI] [Google Scholar]
- Kállay M. A systematic way for the cost reduction of density fitting methods. J. Chem. Phys. 2014, 141, 244113. 10.1063/1.4905005. [DOI] [PubMed] [Google Scholar]
- Kruse H.; Šponer J. Revisiting the Potential Energy Surface of the Stacked Cytosine Dimer: FNO-CCSD(T) Interaction Energies, SAPT Decompositions, and Benchmarking. J. Phys. Chem. A 2019, 123, 9209–9222. 10.1021/acs.jpca.9b05940. [DOI] [PubMed] [Google Scholar]
- Paulechka E.; Kazakov A. Efficient Estimation of Formation Enthalpies for Closed-Shell Organic Compounds with Local Coupled-Cluster Methods. J. Chem. Theory Comput. 2018, 14, 5920. 10.1021/acs.jctc.8b00593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy P. R.; Samu G.; Kállay M. Optimization of the linear-scaling local natural orbital CCSD(T) method: Improved algorithm and benchmark applications. J. Chem. Theory Comput. 2018, 14, 4193. 10.1021/acs.jctc.8b00442. [DOI] [PubMed] [Google Scholar]
- Yoo S.; Aprà E.; Zeng X. C.; Xantheas S. S. High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H2O)16 and (H2O)17: A New Global Minimum for (H2O)16. J. Phys. Chem. Lett. 2010, 1, 3122–3127. 10.1021/jz101245s. [DOI] [Google Scholar]
- Taube A. G.; Bartlett R. J. Frozen natural orbitals: Systematic basis set truncation for coupled-cluster theory. Collect. Czech. Chem. Commun. 2005, 70, 837–850. 10.1135/cccc20050837. [DOI] [Google Scholar]
- Taube A. G.; Bartlett R. J. Frozen natural orbital coupled-cluster theory: Forces and application to decomposition of nitroethane. J. Chem. Phys. 2008, 128, 164101. 10.1063/1.2902285. [DOI] [PubMed] [Google Scholar]
- Landau A.; Khistyaev K.; Dolgikh S.; Krylov A. I. Frozen natural orbitals for ionized states within equation-of-motion coupled-cluster formalism. J. Chem. Phys. 2010, 132, 014109. 10.1063/1.3276630. [DOI] [PubMed] [Google Scholar]
- Pokhilko P.; Izmodenov D.; Krylov A. I. Extension of frozen natural orbital approximation to open-shell references: Theory, implementation, and application to single-molecule magnets. J. Chem. Phys. 2020, 152, 034105. 10.1063/1.5138643. [DOI] [PubMed] [Google Scholar]
- Segarra-Martí J.; Garavelli M.; Aquilante F. Converging many-body correlation energies by means of sequence extrapolation. J. Chem. Phys. 2018, 148, 034107. 10.1063/1.5000783. [DOI] [PubMed] [Google Scholar]
- Sosa C.; Geertsen J.; Trucks G. W.; Bartlett R. J.; Franz J. A. Selection of the reduced virtual space for correlated calculations. An application to the energy and dipole moment of H2O. Chem. Phys. Lett. 1989, 159, 148. 10.1016/0009-2614(89)87399-3. [DOI] [Google Scholar]
- Rolik Z.; Kállay M. Cost-reduction of high-order coupled-cluster methods via active-space and orbital transformation techniques. J. Chem. Phys. 2011, 134, 124111. 10.1063/1.3569829. [DOI] [PubMed] [Google Scholar]
- Adler T. B.; Werner H.-J. An explicitly correlated local coupled cluster method for calculations of large molecules close to the basis set limit. J. Chem. Phys. 2011, 135, 144117. 10.1063/1.3647565. [DOI] [PubMed] [Google Scholar]
- Neese F.; Wennmohs F.; Hansen A. Efficient and accurate local approximations to coupled-electron pair approaches: An attempt to revive the pair natural orbital method. J. Chem. Phys. 2009, 130, 114108. 10.1063/1.3086717. [DOI] [PubMed] [Google Scholar]
- Tajti A.; Szalay P. G.; Császár A. G.; Kállay M.; Gauss J.; Valeev E. F.; Flowers B. A.; Vázquez J.; Stanton J. F. HEAT: High accuracy Extrapolated Ab initio Thermochemistry. J. Chem. Phys. 2004, 121, 11599. 10.1063/1.1811608. [DOI] [PubMed] [Google Scholar]
- Ma Q.; Werner H.-J. Scalable Electron Correlation Methods. 7. Local Open-Shell Coupled-Cluster Methods Using Pair Natural Orbitals: PNO-RCCSD and PNO-UCCSD. J. Chem. Theory Comput. 2020, 16, 3135. 10.1021/acs.jctc.0c00192. [DOI] [PubMed] [Google Scholar]
- Schmitz G.; Hättig C. Perturbative triples correction for local pair natural orbital based explicitly correlated CCSD(F12*) using Laplace transformation techniques. J. Chem. Phys. 2016, 145, 234107. 10.1063/1.4972001. [DOI] [PubMed] [Google Scholar]
- Riplinger C.; Pinski P.; Becker U.; Valeev E. F.; Neese F. Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. 10.1063/1.4939030. [DOI] [PubMed] [Google Scholar]
- Ma Q.; Werner H.-J. Explicitly correlated local coupled-cluster methods using pair natural orbitals. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1371 10.1002/wcms.1371. [DOI] [Google Scholar]
- Liakos D. G.; Guo Y.; Neese F. Comprehensive Benchmark Results for the Domain Based Local Pair Natural Orbital Coupled Cluster Method (DLPNO-CCSD(T)) for Closed- and Open-Shell Systems. J. Phys. Chem. A 2020, 124, 90–100. 10.1021/acs.jpca.9b05734. [DOI] [PubMed] [Google Scholar]
- Nagy P. R.; Kállay M. Approaching the basis set limit of CCSD(T) energies for large molecules with local natural orbital coupled-cluster methods. J. Chem. Theory Comput. 2019, 15, 5275. 10.1021/acs.jctc.9b00511. [DOI] [PubMed] [Google Scholar]
- Sylvetsky N.; Banerjee A.; Alonso M.; Martin J. M. L. Performance of Localized Coupled Cluster Methods in a Moderately Strong Correlation Regime: Hückel–Möbius Interconversions in Expanded Porphyrins. J. Chem. Theory Comput. 2020, 16, 3641. 10.1021/acs.jctc.0c00297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallick S.; Roy B.; Kumar P. A comparison of DLPNO-CCSD(T) and CCSD(T) method for the determination of the energetics of hydrogen atom transfer reactions. Comput. Theor. Chem. 2020, 1187, 112934. 10.1016/j.comptc.2020.112934. [DOI] [Google Scholar]
- Nagy P. R.; Kállay M. Optimization of the linear-scaling local natural orbital CCSD(T) method: Redundancy-free triples correction using Laplace transform. J. Chem. Phys. 2017, 146, 214106. 10.1063/1.4984322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adamowicz L.; Bartlett R. J. Optimized virtual orbital space for high-level correlated calculations. J. Chem. Phys. 1987, 86, 6314. 10.1063/1.452468. [DOI] [Google Scholar]
- Adamowicz L.; Bartlett R. J.; Sadlej A. J. Optimized virtual orbital space for high-level correlated calculations. II. Electric properties. J. Chem. Phys. 1988, 88, 5749. 10.1063/1.454721. [DOI] [Google Scholar]
- Neogrády P.; PitoňáK M.; Urban M. Optimized virtual orbitals for correlated calculations: An alternative approach. Mol. Phys. 2005, 103, 2141. 10.1080/00268970500096251. [DOI] [Google Scholar]
- Löwdin P.-O. Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction. Phys. Rev. 1955, 97, 1474. 10.1103/physrev.97.1474. [DOI] [Google Scholar]
- Grüneis A.; Booth G. H.; Marsman M.; Spencer J.; Alavi A.; Kresse G. Natural Orbitals for Wave Function Based Correlated Calculations Using a Plane Wave Basis Set. J. Chem. Theory Comput. 2011, 7, 2780–2785. 10.1021/ct200263g. [DOI] [PubMed] [Google Scholar]
- Mester D.; Nagy P. R.; Kállay M. Reduced-cost second-order algebraic-diagrammatic construction method for excitation energies and transition moments. J. Chem. Phys. 2018, 148, 094111. 10.1063/1.5021832. [DOI] [Google Scholar]
- Ramberger B.; Sukurma Z.; Schäfer T.; Kresse G. RPA natural orbitals and their application to post-Hartree–Fock electronic structure methods. J. Chem. Phys. 2019, 151, 214106. 10.1063/1.5128415. [DOI] [PubMed] [Google Scholar]
- Segarra-Martí J.; Garavelli M.; Aquilante F. Multiconfigurational Second-Order Perturbation Theory with Frozen Natural Orbitals Extended to the Treatment of Photochemical Problems. J. Chem. Theory Comput. 2015, 11, 3772. 10.1021/acs.jctc.5b00479. [DOI] [PubMed] [Google Scholar]
- Mester D.; Nagy P. R.; Kállay M. Reduced-cost linear-response CC2 method based on natural orbitals and natural auxiliary functions. J. Chem. Phys. 2017, 146, 194102. 10.1063/1.4983277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folkestad S. D.; Koch H. Multilevel CC2 and CCSD Methods with Correlated Natural Transition Orbitals. J. Chem. Theory Comput. 2020, 16, 179–189. 10.1021/acs.jctc.9b00701. [DOI] [PubMed] [Google Scholar]
- Kumar A.; Crawford T. D. Frozen Virtual Natural Orbitals for Coupled Cluster Linear-Response Theory. J. Phys. Chem. A 2017, 121, 708. 10.1021/acs.jpca.6b11410. [DOI] [PubMed] [Google Scholar]
- Clement M. C.; Zhang J.; Lewis C. A.; Yang C.; Valeev E. F. Optimized Pair Natural Orbitals for the Coupled Cluster Methods. J. Chem. Theory Comput. 2018, 14, 4581–4589. 10.1021/acs.jctc.8b00294. [DOI] [PubMed] [Google Scholar]
- Kállay M. Linear-scaling implementation of the direct random-phase approximation. J. Chem. Phys. 2015, 142, 204105. 10.1063/1.4921542. [DOI] [PubMed] [Google Scholar]
- Rendell A. P.; Lee T. J.; Komornicki A. A parallel vectorized implementation of triple excitations in CCSD(T): application to the binding energies of the AlH3, AlH2F, AlHF2 and AlF3 dimers. Chem. Phys. Lett. 1991, 178, 462. 10.1016/0009-2614(91)87003-t. [DOI] [Google Scholar]
- Lee T. J.; Rendell A. P.; Taylor P. R. Comparison of the quadratic configuration interaction and coupled-cluster approaches to electron correlation including the effect of triple excitations. J. Phys. Chem. 1990, 94, 5463. 10.1021/j100377a008. [DOI] [Google Scholar]
- Rendell A. P.; Lee T. J.; Komornicki A.; Wilson S. Evaluation of the contribution from triply excited intermediates to the fourth-order perturbation theory energy on Intel distributed memory supercomputers. Theor. Chem. Acc. 1993, 84, 271. 10.1007/bf01113267. [DOI] [Google Scholar]
- Whitten J. L. Coulombic potential energy integrals and approximations. J. Chem. Phys. 1973, 58, 4496. 10.1063/1.1679012. [DOI] [Google Scholar]
- Dunlap B. I.; Connolly J. W. D.; Sabin J. R. On some approximations in applications of Xα theory. J. Chem. Phys. 1979, 71, 3396. 10.1063/1.438728. [DOI] [Google Scholar]
- Mester D.; Nagy P. R.; Kállay M. Reduced-scaling correlation methods for the excited states of large molecules: Implementation and benchmarks for the second-order algebraic-diagrammatic construction approach. J. Chem. Theory Comput. 2019, 15, 6111. 10.1021/acs.jctc.9b00735. [DOI] [PubMed] [Google Scholar]
- Kállay M.; Nagy P. R.; Mester D.; Rolik Z.; Samu G.; Csontos J.; Csóka J.; Szabó P. B.; Gyevi-Nagy L.; Hégely B.; Ladjánszki I.; Szegedy L.; Ladóczki B.; Petrov K.; Farkas M.; Mezei P. D.; Ganyecz Á. The MRCC program system: Accurate quantum chemistry from water to proteins. J. Chem. Phys. 2020, 152, 074107. 10.1063/1.5142048. [DOI] [PubMed] [Google Scholar]
- Mrcc, a quantum chemical program suite written by Kállay M.; Nagy P. R.; Rolik Z.; Mester D.; Samu G.; Csontos J.; Csóka J.; Szabó P. B.; Gyevi-Nagy L.; Ladjánszki I.; Szegedy L.; Ladóczki B.; Petrov K.; Farkas M.; Mezei P. D.; Hégely B.. See https://www.mrcc.hu/ (accessed Oct 1, 2020). [DOI] [PubMed]
- Dohm S.; Hansen A.; Steinmetz M.; Grimme S.; Checinski M. P. Comprehensive thermochemical benchmark set of realistic closed-shell metal organic reactions. J. Chem. Theory Comput. 2018, 14, 2596–2608. 10.1021/acs.jctc.7b01183. [DOI] [PubMed] [Google Scholar]
- Földes T.; Madarász Á.; Révész Á.; Dobi Z.; Varga S.; Hamza A.; Nagy P. R.; Pihko P. M.; Pápai I. Stereocontrol in Diphenylprolinol Silyl Ether Catalyzed Michael Additions: Steric Shielding or Curtin-Hammett Scenario?. J. Am. Chem. Soc. 2017, 139, 17052. 10.1021/jacs.7b07097. [DOI] [PubMed] [Google Scholar]
- Janowski T.; Pulay P.; Sasith Karunarathna A. A.; Sygula A.; Saebø S. Convex-concave stacking of curved conjugated networks: Benchmark calculations on the corannulene dimer. Chem. Phys. Lett. 2011, 512, 155–160. 10.1016/j.cplett.2011.07.030. [DOI] [Google Scholar]
- Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. 10.1063/1.456153. [DOI] [Google Scholar]
- Weigend F.; Köhn A.; Hättig C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175. 10.1063/1.1445115. [DOI] [Google Scholar]
- Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Rappoport D.; Furche F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. 10.1063/1.3484283. [DOI] [PubMed] [Google Scholar]
- Hellweg A.; Rappoport D. Development of new auxiliary basis functions of the Karlsruhe segmented contracted basis sets including diffuse basis functions (def2-SVPD, def2-TZVPPD, and def2-QVPPD) for RI-MP2 and RI-CC calculations. Phys. Chem. Chem. Phys. 2015, 17, 1010. 10.1039/c4cp04286g. [DOI] [PubMed] [Google Scholar]
- Andrae D.; Häußermann U.; Dolg M.; Stoll H.; Preuß H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chem. Acc. 1990, 77, 123. 10.1007/bf01114537. [DOI] [Google Scholar]
- Helgaker T.; Klopper W.; Koch H.; Noga J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639. 10.1063/1.473863. [DOI] [Google Scholar]
- Brezinski C.; Zaglia M.. Extrapolation Methods: Theory and Practice; Elsevier Science, 2013. [Google Scholar]
- DePrince A. E.; Sherrill C. D. Accurate Noncovalent Interaction Energies Using Truncated Basis Sets Based on Frozen Natural Orbitals. J. Chem. Theory Comput. 2013, 9, 293. 10.1021/ct300780u. [DOI] [PubMed] [Google Scholar]
- Chernichenko K.; Kótai B.; Pápai I.; Zhivonitko V.; Nieger M.; Leskelä M.; Repo T. Intramolecular Frustrated Lewis Pair with the Smallest Boryl Site: Reversible H2 Addition and Kinetic Analysis. Angew. Chem., Int. Ed. 2015, 54, 1749. 10.1002/anie.201410141. [DOI] [PubMed] [Google Scholar]
- Szabó F.; Daru J.; Simkó D.; Nagy T. Z.; Stirling A.; Novák Z. Mild Palladium-Catalyzed Oxidative Direct ortho-C-H Acylation of Anilides under Aqueous Conditions. Adv. Synth. Catal. 2013, 355, 685. 10.1002/adsc.201200948. [DOI] [Google Scholar]
- Al-Hamdani Y. S.; Nagy P. R.; Barton D.; Kállay M.; Brandenburg J. G.; Tkatchenko A.. Interactions between Large Molecules: Puzzle for Reference Quantum-Mechanical Methods. 2020, arXiv:2009.08927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sedlak R.; Janowski T.; Pitoňák M.; Řezáč J.; Pulay P.; Hobza P. Accuracy of Quantum Chemical Methods for Large Noncovalent Complexes. J. Chem. Theory Comput. 2013, 9, 3364. 10.1021/ct400036b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubecký M.; Mitas L.; Jurečka P. Noncovalent Interactions by Quantum Monte Carlo. Chem. Rev. 2016, 116, 5188–5215. 10.1021/acs.chemrev.5b00577. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Hobza P. Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications. Chem. Rev. 2016, 116, 5038–5071. 10.1021/acs.chemrev.5b00526. [DOI] [PubMed] [Google Scholar]
- Al-Hamdani Y. S.; Tkatchenko A. Understanding non-covalent interactions in larger molecular complexes from first principles. J. Chem. Phys. 2019, 150, 010901. 10.1063/1.5075487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boys S. F.; Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553. 10.1080/00268977000101561. [DOI] [Google Scholar]
- Iron M. A.; Janes T. Evaluating Transition Metal Barrier Heights with the Latest Density Functional Theory Exchange–Correlation Functionals: The MOBH35 Benchmark Database. J. Phys. Chem. A 2019, 123, 3761–3781. 10.1021/acs.jpca.9b01546. [DOI] [PubMed] [Google Scholar]
- Kruse H.; Mladek A.; Gkionis K.; Hansen A.; Grimme S.; Sponer J. Quantum Chemical Benchmark Study on 46 RNA Backbone Families Using a Dinucleotide Unit. J. Chem. Theory Comput. 2015, 11, 4972–4991. 10.1021/acs.jctc.5b00515. [DOI] [PubMed] [Google Scholar]
- Řezáč J.; Bí D.; Gutten O.; Rulíšek L. Toward Accurate Conformational Energies of Smaller Peptides and Medium-Sized Macrocycles: MPCONF196 Benchmark Energy Data Set. J. Chem. Theory Comput. 2018, 14, 1254–1266. 10.1021/acs.jctc.7b01074. [DOI] [PubMed] [Google Scholar]
- Wappett D. A.; Goerigk L. Toward a Quantum-Chemical Benchmark Set for Enzymatically Catalyzed Reactions: Important Steps and Insights. J. Phys. Chem. A 2019, 123, 7057–7074. 10.1021/acs.jpca.9b05088. [DOI] [PubMed] [Google Scholar]
- Mardirossian N.; Head-Gordon M. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315. 10.1080/00268976.2017.1333644. [DOI] [Google Scholar]
- Goerigk L.; Hansen A.; Bauer C.; Ehrlich S.; Najibi A.; Grimme S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184. 10.1039/c7cp04913g. [DOI] [PubMed] [Google Scholar]
- Cheng L.; Welborn M.; Christensen A. S.; Miller T. F. A universal density matrix functional from molecular orbital-based machine learning: Transferability across organic molecules. J. Chem. Phys. 2019, 150, 131103. 10.1063/1.5088393. [DOI] [PubMed] [Google Scholar]
- McGibbon R. T.; Taube A. G.; Donchev A. G.; Siva K.; Hernández F.; Hargus C.; Law K.-H.; Klepeis J. L.; Shaw D. E. Improving the accuracy of Møller–Plesset perturbation theory with neural networks. J. Chem. Phys. 2017, 147, 161725. 10.1063/1.4986081. [DOI] [PubMed] [Google Scholar]
- Bartók A. P.; De S.; Poelking C.; Bernstein N.; Kermode J. R.; Csányi G.; Ceriotti M. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 2017, 3, e1701816 10.1126/sciadv.1701816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nudejima T.; Ikabata Y.; Seino J.; Yoshikawa T.; Nakai H. Machine-learned electron correlation model based on correlation energy density at complete basis set limit. J. Chem. Phys. 2019, 151, 024104. 10.1063/1.5100165. [DOI] [PubMed] [Google Scholar]
- Chmiela S.; Sauceda H. E.; Müller K.-R.; Tkatchenko A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 2018, 9, 3887. 10.1038/s41467-018-06169-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mezei P. D.; von Lilienfeld O. A. Non-covalent quantum machine learning corrections to density functionals. J. Chem. Theory Comput. 2020, 16, 2647. 10.1021/acs.jctc.0c00181. [DOI] [PubMed] [Google Scholar]
- Montavon G.; Rupp M.; Gobre V.; Vazquez-Mayagoitia A.; Hansen K.; Tkatchenko A.; Müller K.-R.; von Lilienfeld O. A. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 2013, 15, 095003. 10.1088/1367-2630/15/9/095003. [DOI] [Google Scholar]
- Ramakrishnan R.; Dral P. O.; Rupp M.; von Lilienfeld O. A. Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput. 2015, 11, 2087. 10.1021/acs.jctc.5b00099. [DOI] [PubMed] [Google Scholar]
- Smith J. S.; Nebgen B. T.; Zubatyuk R.; Lubbers N.; Devereux C.; Barros K.; Tretiak S.; Isayev O.; Roitberg A. E. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 2019, 10, 2903. 10.1038/s41467-019-10827-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.