Abstract
A simple and robust range-separated (RS) double-hybrid (DH) time-dependent density functional approach is presented for the accurate calculation of excitation energies of molecules within the Tamm–Dancoff approximation. The scheme can be considered as an excited-state extension of the ansatz proposed by Toulouse and co-workers [J. Chem. Phys. 2018, 148, 164105], which is based on the two-parameter decomposition of the Coulomb potential, for which both the exchange and correlation contributions are range-separated. A flexible and efficient implementation of the new scheme is also presented, which facilitates its extension to any combination of exchange and correlation functionals. The performance of the new approximation is tested for singlet excitations on several benchmark compilations and thoroughly compared to that of representative DH, RS hybrid, and RS DH functionals. The one-electron basis set dependence and computation times are also assessed. Our results show that the new approach improves on standard DHs in most cases, and it can provide a more robust and accurate alternative. In addition, on average, it noticeably surpasses the existing RS hybrid and RS DH functionals.
1. Introduction
Electronic excitations are cardinal phenomena in many areas of chemistry, physics, and biology. Accordingly, the appropriate description of electronic transitions is necessary. One of the most reliable choices is the coupled-cluster (CC)1 approach relying on the equation-of-motion2,3 or the linear-response4−6 theories. The hierarchical CC methods, such as the CC singles and doubles (CCSD),2 the CC singles, doubles, and triples (CCSDT),3 etc., enable an arbitrary level of accuracy, but their computational expenses scale as a high power of the system size. To reduce the eighth-order scaling of the CCSDT method and also improve the results of CCSD, several approximate CCSDT approaches have been proposed. These include, for example, the CC3,7 the CCSDR(3),8 and the CCSDT-39 approaches, in which an iterative or perturbative triple excitation correction is added to CCSD. However, the aforementioned methods still have too steep of a scaling for practical applications, which is also true for CCSD itself. The most common choice to investigate extended molecular systems with wave function-based methods is to use even less expensive models, such as the iterative second-order approximate CCSD (CC2)10 approach developed by Christiansen and co-workers as well as the second-order algebraic-diagrammatic construction [ADC(2)] approach11 of Schirmer et al., or the configuration interaction singles with perturbative second-order correction [CIS(D)]12 method of Head-Gordon and co-workers, which scale as the fifth power of the system size.
An alternative solution for avoiding the high computational expenses is time-dependent density functional theory (TDDFT), which can be derived from density functional theory (DFT) through the linear-response formalism.13−17 However, for molecular systems, it is well-known that adequate results cannot be expected from TDDFT using pure exchange-correlation (XC) functionals. For semiquantitative accuracy, at least hybrid functionals are recommended, where the XC energy contains a Hartree–Fock (HF) exchange contribution as well. The hybrid TDDFT excitation energies are quite good for valence excitations; however, the results are frequently in question18−21 for some challenging cases, such as Rydberg and charge transfer (CT) states, or π → π* excitations of conjugated systems. A particular hybrid functional could give reasonable results for only one family of the aforementioned transitions, nevertheless, their general usage requires further developments. To improve the results obtained, for both the ground- and excited-state properties, numerous approaches were developed. The two most noteworthy ones are the range-separated (RS) and double hybrid (DH) theories.
The wrong long-range (LR) behavior of standard XC functionals is a known problem. In the range separation scheme, the Coulomb operator is split into LR and short-range (SR) components.22 The most common partition is the
| 1 |
form,23 where r12 is the distance between two electrons, erf is the standard error function, and μ stands for the range-separation parameter. For RS hybrid functionals, such as LC-BOP,24−27 LC-ωPBE,28 ωPBEh,29,30 CAM-B3LYP,31 ωB97,32 and M11,33 the LR HF exchange is dominantly used for the LR part of the exchange energy, while SR DFT exchange accounts for the SR counterpart. The correlation energy is not range-separated and contains solely a full-range (FR) DFT contribution. It has been demonstrated in several studies that the range separation significantly improves the results over the standard hybrid methods.34−40
In the DH approach,41 hybrid functionals are further improved by combining them with second-order wave function methods. In most cases, a hybrid Kohn–Sham (KS) calculation is carried out, and a second-order Møller–Plesset (MP2)-like correction evaluated on the KS orbitals is added to the XC energy. Several approaches with empirical42,43 and nonempirical44−49 parametrizations were proposed, and spin-scaled variants were also introduced.50−52 The DH approximation was also extended to excited-states by Grimme and Neese.53 In their approach, a hybrid TDDFT calculation is performed, and subsequently, the second-order contribution is added a posteriori relying on the CIS(D) method. Later, several DH functionals were adapted to excited-state calculations,54,55 and the most encouraging ones were also combined with spin-scaling techniques by Schwabe and Goerigk.56 The performance of DH functionals for both the ground- and excited-state properties has been benchmarked in excellent studies.39,40,50,57−63
The RS and DH approaches can also be utilized together. The first attempts in this direction were made by Ángyán, Toulouse, Savin et al.,64,65 while the theory of the calculation of the SR DFT correlation contributions was elaborated by Toulouse and co-workers,66,67 as well as by Stoll et al.68−70 Inspired by these studies, several outstanding RS-DH approaches were proposed in which the LR correlation energy is evaluated at the MP2 level71,72 or beyond.73−76 Unfortunately, standalone SR DFT correlation functionals are not widely available; however, an alternative and simple solution was introduced by Scuseria and co-workers76 where a so-called local-scaling approximation is invoked to enable the straightforward construction of SR functionals. Nonetheless, in most cases, a more approximate form of the RS XC energy is employed where solely the exchange contributions are range-separated.77−80 The connection between the fraction of the exact exchange in the RS XC energy and the optimal range-separation parameter for the nonempirical functionals was presented by Adamo et al.78 Later, it was demonstrated that these parameters are in line with the results obtained by relying on the so-called optimally tuned procedure.79 The only excited-state RS-DH approach proposed81 and carefully benchmarked82,83 recently by Goerigk and co-workers also originated from this scheme.
In this paper, we go even further and extend the completely RS ansatz to excited states relying on the work of Toulouse and co-workers.71 We present a flexible implementation of the new approach, and finally, we demonstrate its advantages through numerous benchmark calculations.
2. Theory
2.1. Double-Hybrid Density Functional Theory
In the DH approach,41 the XC energy of a ground-state system can be obtained as
| 2 |
where EXHF is the exact (HF) exchange energy, EC stands for the MP2 correlation energy, and EXDFT and EC denote the DFT exchange and correlation energy contributions, respectively. The ratio of the HF and MP2 contributions is handled by the mixing factors αX and αC, respectively. Supposing a closed-shell system and spatial orbitals, the MP2 correlation energy is defined by
| 3 |
where (ia|jb) is a four-center two-electron electron repulsion integral (ERI) in the Mulliken notation, tijab stands for an MP2 doubles amplitude, and Tij denotes the so-called antisymmetrized amplitudes. The notation follows the convention that i, j, ..., a, b, ..., and p, q, ... are occupied, virtual, and general molecular orbital indices, respectively. The MP2 amplitudes can be expressed as
| 4 |
where εp is the corresponding orbital energy. In this scheme, a calculation starts with solving the self-consistent KS equations including the DFT exchange and correlation potentials, as well as the HF exchange contribution, and thereafter the MP2 correction is evaluated on the KS orbitals obtained.
Computationally favorable algorithms can be designed with the aid of the density-fitting (DF) approach, where the ERIs are written in an approximate form as the products of two- and three-center arrays. In this case, four-center ERIs can be recast in the form
| 5 |
where P and Q stand for the elements of the auxiliary basis, whereas IpqP and VPQ are three- and two-center Coulomb integrals, respectively, and VPQ is a simplified notation for the corresponding element of the inverse of the two-center Coulomb integral matrix. Usually, the matrix K with elements Kpq,rs = (pq|rs) is factorized as K = IV–1IT = BIT or K = IV–1/2V–1/2IT = JJT. Using the latter notation, the MP2 correlation energy can be expressed in the following simple form:
| 6 |
where the intermediate YiaQ is defined by the contraction of the three-center integrals and the antisymmetrized amplitudes.
Since several excited-state extensions of DFT and the MP2 method exist,11,12 one has different options to evaluate the excitation energy in the DH approach.53,84 One of the most common schemes is utilized here, which is based on the Tamm–Dancoff approximation (TDA).85 Numerous benchmark studies have shown that significant differences cannot be observed between the TDA- and “full” TDDFT approaches for singlet excitation energies,83,85,86 while only TDA-TDDFT is recommended for triplet transitions due to the triplet instability of TDDFT.17,83 In this scheme, the first step of the calculation is to solve the symmetric eigenvalue equation as
| 7 |
where c is the singles excitation vector, ωTDA is the TDA excitation energy, and the matrix elements of the Jacobian A are defined by
| 8 |
where fpq stands for the corresponding Fock-matrix element. The DFT exchange term is written in the following form:
| 9 |
where ρ(r) denotes the electron density, and r is a vector for electron coordinates. A similar expression holds for the DFT correlation. The second-order correction is calculated perturbatively relying on the CIS(D) method12 using the singles excitation amplitudes and excitation energy obtained from eq 7. The final DH excitation energy53 is defined by
| 10 |
where the second-order correction for a singlet excitation is given as
| 11 |
In this expression, the intermediate Vijab can be written in the
 |
12 |
form, and the double excitation amplitudes are obtained as cijab = Vij/(Dijab + ωTDA), while the elements of the intermediate σia read explicitly as
 |
13 |
2.2. DH Ansatz Using Range Separation
Our proposition is based on the two-parameter Coulomb-attenuating method (CAM)-like decomposition31 of the Coulomb potential and the DH ansatz of Toulouse et al.,71 where both the exchange and correlation contributions are range-separated. In this approach, the XC energy is defined by
| 14 |
where EXSR-DFT and EC are the SR DFT exchange and correlation contributions, respectively, and EXLR-HF denotes the LR HF exchange, while EC stands for the LR MP2 correlation energy. Similar notation is used for the SR counterpart of the latter two quantities. The parameter λ can be interpreted as the weight of the wave function methods in the XC energy. Since the MP2 energy is nonlinear in the Coulomb potential, a mixed LR-SR contribution, ECLR- SR-MP2, also appears in the expression. The decomposition of the exact SR DFT XC energy as EXC(μ) ≈ (1 – λ)EXSR-DFT(μ) + (1 – λ2)EC(μ) utilized here is referred to as “approximation1” in ref (71).
To evaluate the SR DFT contributions, we adapted the local-scaling approximation of Scuseria and co-workers.76 In this scheme, the SR DFT correlation energy is calculated as
| 15 |
where εCSR-LDA and εC are the SR and FR correlation energy densities within the local-density approximation (LDA), respectively, and εCGGA is the analogue of the latter within the generalized gradient approximation (GGA). A similar expression holds for the exchange contribution. The major advantage of the above functional form is that the SR contribution calculation can simply be extended to any GGA functional or beyond. Note also that the functional derivatives required for the solution of the KS or response equations can also be straightforwardly derived and implemented if the corresponding formulas and program codes are available for the GGA functional.
The mixed ECLR-SR-MP2 correlation energy can be simply expressed in the
| 16 |
form, where the LR MP2 correlation energy reads as
| 17 |
and the LR MP2 doubles amplitudes can be evaluated
as 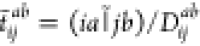 . Hereafter, the tilded
symbols will refer
to LR quantities, and the working equations will be given solely for
them. The SR quantities can be easily put down analogously to their
LR counterpart.
. Hereafter, the tilded
symbols will refer
to LR quantities, and the working equations will be given solely for
them. The SR quantities can be easily put down analogously to their
LR counterpart.
The DF approach can also be used for the RS MP2 and CIS(D) equations including the LR/SR interaction. However, it is not recommended to apply the conventional DF formulas together with the modified Coulomb potentials since they may result in large errors and can even be singular for small values of parameter μ. Hence, the usual Coulomb metric should be employed along with robust fitting formulas.75,87 Relying on them, matrix K̃ can be decomposed as
| 18 |
Accordingly, the DF form of the LR doubles amplitudes is given by
| 19 |
Substituting this results into eq 17, the final expression for the LR MP2 correlation energy reads as
| 20 |
Compared to the expression for the FR MP2 correlation energy, eq 6, it is obvious that the working equations are rather similar, only the number of the terms is higher in this case.
2.3. Range-Separated DH Ansatz for Excited States
Here, we extend the above RS ansatz to the excited-state calculations. For that purpose, the Jacobian A in eq 7 is modified according to eq 14 to include the LR and SR exact exchange terms, as well as the SR DFT exchange and correlation contributions. For the sake of simplicity, the singles excitation vector and excitation energy obtained as a solution of the modified TDA equations will be denoted by c̃ and ωTDA(μ), respectively. For the final RS DH excitation energy, analogously to eq 14, we propose the form
| 21 |
where ωLR-(D)(μ) and ωSR-(D)(μ) are the LR and SR perturbative second-order corrections, respectively. The mixed LR-SR contribution similar to the MP2 counterpart can be calculated as
| 22 |
There is only one question left: how can we evaluate the LR/SR correlation contributions, ωLR-(D)(μ) and ωSR-(D)(μ)? A fully consistent theory would require the solution of the TDA equations with the FR, LR, and SR Coulomb interactions, and the resulting single excitation amplitudes should be used in the second-order expressions. However, this would be rather impractical as it would necessitate the solution of four TDA-like equations, the modified as well as the FR, LR, and SR ones. This would be not only expensive, but it would also be cumbersome in particular cases as the iterations might converge to different excited-state solutions. Therefore, we take a more pragmatic choice and use the singles excitation coefficients c̃ from the modified TDA equations together with the FR/LR/SR Coulomb integrals. Consequently, in this approximation, the LR (D) correction reads explicitly as
| 23 |
where the elements of the intermediate Ṽ can be expressed as
 |
24 |
the LR double excitation amplitudes are obtained as c̃ijab = Ṽij/[Dijab + ωTDA(μ)], and the intermediate σ̃ia can be written in the
 |
25 |
form. Note that it also means that in eq 22 not the true ω(D) defined by eq 11 is used, but this contribution is also evaluated with the c̃ coefficients. Again, the structure of the excited-state RS expressions is very similar to that of the corresponding FR terms, only the number of intermediates is twice as many. In other words, an existing FR implementation can be easily modified for a RS calculation.
When the equations are inspected, a couple of important observations can be made about special cases. First, the standard KS-based TDA-TDDFT is recovered if one sets μ = 0 and λ = 0. In this case, the HF and second-order contributions vanish; furthermore, the SR DFT contributions are equal to the corresponding FR contributions. In the μ → ∞ or λ = 1 limits, the DFT contributions go to zero, and the approach simplifies to the standard CIS(D) method. In addition, the one-parameter RS ansatz proposed by Ángyán et al.64 is recovered in the 0 < μ < ∞ and λ = 0 case. In this scheme, the SR HF exchange and second-order contributions are omitted, and the remaining quantities are not scaled. Finally, a standard DH-like approach is recovered for μ = 0 and 0 < λ < 1 because the SR contributions are equal to the corresponding FR quantities and the LR contributions vanish.
To the best of our knowledge, only one attempt has been made so far to combine the DH approach with range separation for excited-state calculations, namely the ωB2(GP)PLYP functionals.81 In this scheme, the original form of the functional is retained, and it can be considered as an extension of the standard DH approach utilizing range separation for the exchange contributions. The amounts of the SR HF and DFT exchange contributions are controlled by factors αX and 1 – αX, respectively, and the total LR HF exchange energy contribution is added to the XC energy. The mixing factors for the DFT and second-order correlation energies are unchanged, and no range separation is applied to those contributions. Accordingly, the XC energy formula contains only one adjustable parameter and is equal to the expression presented by Adamo and co-workers77,78 for ground-state calculations, namely the RSX-QIDH and RSX0-DH functionals. This approach recovers the standard DH excitation energies in the μ = 0 limit, however, in the μ → ∞ limit, no other ansatz is recovered. Extensive benchmark calculations have shown that the ansatz improves the accuracy of the ωB2(GP)PLYP functionals in most cases, however, it is less efficient for the RSX-QIDH and RSX0-DH methods.83 For the sake of completeness, we note that the range-separation parameter was tuned for excited-state properties for the former, which is also true in our case.
The ansatz proposed herein differs from the approach of ref (81) in that it exploits range separation for both the exchange and the correlation contributions. Thus, needless to say that the evaluation of the second-order corrections is more demanding in this case. However, these steps are not the bottleneck of the entire procedure.53,84 In addition, our method is based on the consistent DH ansatz of Toulouse, the property of which is also inherited by the excited-state theory. Our implementation utilizing the local-scaling approximation for the SR DFT functional is also more flexible allowing for the rapid testing of arbitrary combinations of exchange and correlation functionals. Finally, as it will be demonstrated below, our approach in most cases improves on DHs not using the range separation approximation.
3. Results
3.1. Computational Details
The new approach has been implemented in the Mrcc suite of quantum chemical programs and will be available in the next release of the package.88,89
In our study, Dunning’s correlation consistent basis sets (cc-pVXZ, where X = T, Q, 5),90,91 their diffuse function augmented variants (aug-cc-pVXZ),92 as well as Ahlrichs’ TZVP,93 def2-TZVPP, and def2-QZVPP94 basis sets were used. In all calculations, the DF approximation was applied for both the ground and the excited states, and the corresponding auxiliary bases of Weigend et al.95−97 were employed. In all the post-KS/HF calculations, the core orbitals were kept frozen. The convergence threshold for the energies was set to 10–6 Eh, while the default adaptive integration grid of the Mrcc package was used for the DFT contributions.
The exchange and correlation functionals of Perdew, Burke, and Ernzerhof (PBE),98 Becke’s 1988 exchange functional (B88),99 the correlation functional of Lee, Yang, and Parr (LYP),100 and Perdew’s 1986 correlation functional (P86)101 were used to compare our ansatz with common DH functionals. In eq 15, the Slater–Dirac exchange102−104 and the Perdew–Wang 1992 correlation105 functionals were applied as LDA functionals together with their SR extensions proposed by Savin106 and Paziani et al.107 For RS hybrids, such as CAM-B3LYP31 and ωB97X,32 the Libxc library108,109 was used, while for the ωB2(GP)PLYP81 calculations, the modified version of Libxc was employed.
Our training and validation sets were taken from the literature, but only the singlet excitations are assessed in this paper. The training set was the well-balanced benchmark set of Gordon and co-workers,110 which includes 32 valence (π → π*, n → π*, σ → π*, n → σ*) and 31 Rydberg excitations for 14 molecules. For this test set, the reoptimized geometries and the composite CC3-CCSDR(3)/aug-cc-pVTZ reference excitation energies of Schwabe and Goerigk (SG)56 were taken. To briefly assess the effects on the ground-state properties, adiabatic electron affinities (G21EA set)111 and ionization potentials (G21IP set)111 were taken from the GMTKN5540 set using the def2-QZVPP basis set. Cross-validation was performed on several test sets. The training set of SG56 is a compilation of CCSDR(3) excitation energies obtained with the aug-cc-pVTZ basis set and includes 38 excitation energies for 22 molecules. The latter compilation, which is hereafter referred to as the SG set, comprises 32 valence (π → π*, n → π*, σ → π*), and 6 Rydberg transitions. The comprehensive CT benchmark set recently proposed by Szalay et al.112 contains 14 excitation energies for 8 molecular complexes, such as ammonia–fluorine, acetone–fluorine, pyrazine–fluorine, ammonia–oxygen-difluoride, acetone–nitromethane, ammonia–pyrazine, pyrrole–pyrazine, and tetrafluoroethylene–ethylene systems. The reference energies were calculated at the CCSDT-3 level using the cc-pVDZ basis sets. Another compilation of CT excitations was presented by Goerigk and co-workers,83 which contains relatively standard organic molecules. The reference energies were obtained at different levels of theory, detailed information can be found in ref (83). As it can be assumed that the former CT set is a more challenging compilation, we only briefly discuss the results regarding the latter. One of the most popular benchmark sets was suggested by Thiel and co-workers113,114 and later reconsidered by Szalay et al.115 This set contains CC3/TZVP reference values, and 121 excitations of 24 molecules were selected in order to retain the consistency with the previous DH studies.56,84 This test set only incorporates valence excitations of type π → π*, n → π*, and σ → π*. Two different benchmark compilations were presented by Loos, Jacquemin, and co-workers.116,117 From their first set,116 55 excited states (29 Rydberg and 26 valence) were taken for 18 molecules (LJ1), and CC3/aug-cc-pVTZ excitation energies were used as reference in this study. Their second benchmark set (LJ2)117 consists of 19 excitation energies of 14 so-called “exotic” molecules evaluated at the CC3 level with the aug-cc-pVTZ basis set. In addition, a test set on the 1La and 1Lb excitations of the linear polycyclic aromatic hydrocarbons (PAHs) from naphthalene to hexacene is also assessed. The reference values118 were calculated at the completely renormalized equation-of-motion CCSD(T) [CR-EOM-CCSD(T)]119 level using the cc-pVTZ basis set. These challenging transitions have been inspected in several comprehensive studies.20,81,120−122
The errors utilized for the evaluation of the excitation energies are calculated by subtracting the reference from the computed value. The statistical error measures presented in the tables and figures are the mean error (ME), the mean absolute error (MAE), and the maximum absolute error (MAX). All the computed excitation energies and statistical error measures are available in the Supporting Information. In addition, further measures, such as the root-mean-square errors, standard deviations, and deviation spans are also included. These numbers are only discussed if the order of the methods significantly changes when evaluating their performance using the latter measures instead of the former ones.
3.2. Determination of the Parameters
The main focus of this study is to compare the most successful DH and RS functionals, namely PBE0-2,47 PBE-QIDH,49 the spin-component scaled DSD-PBEP86,52 B2PLYP,53 B2GPPLYP,43 ωB2PLYP,81 ωB2GPPLYP,81 CAM-B3LYP,31 and ωB97X,32 with our ansatz for singlet–singlet transitions. Since the mixing factors of these functionals cannot be retained in our approach (cf. eqs 2 and 14), we have to define various alternatives which contain the same exchange and correlation functionals as the aforementioned popular ones. Accordingly, we introduce the RS-PBE-PBE, RS-PBE-P86, and RS-B88-LYP functionals, in which the second and third part of the acronyms refer to the exchange and correlation functionals, respectively, used in eq 14. These DHs are the analogues of the PBE0-2/PBE-QIDH, DSD-PBEP86, and B2(GP)PLYP/ωB2(GP)PLYP functionals, respectively. To help the reader, the attributes of the functionals considered in our study are collected in Table 1.
Table 1. Functionals Assessed in This Paper.
| functional | exchange | correlation | level | range separation | spin scaling |
|---|---|---|---|---|---|
| PBE0-QIDH | PBE | PBE | double hybrid | no | no |
| PBE0-2 | PBE | PBE | double hybrid | no | no |
| DSD-PBEP86 | PBE | P86 | double hybrid | no | yes |
| B2PLYP | B88 | LYP | double hybrid | no | no |
| B2GPPLYP | B88 | LYP | double hybrid | no | no |
| ωB2PLYP | B88 | LYP | double hybrid | yes | no |
| ωB2GPPLYP | B88 | LYP | double hybrid | yes | no |
| CAM-B3LYP | B88 | LYP | hybrid | yes | no |
| ωB97X | B97 | B97 | hybrid | yes | no |
| RS-PBE-PBE | PBE | PBE | double hybrid | yes | no |
| RS-PBE-P86 | PBE | P86 | double hybrid | yes | no |
| RS-B88-LYP | B88 | LYP | double hybrid | yes | no |
First, we determined the ideal values of the parameters λ and μ for the new functionals. For this purpose, we minimized the MAE for the Gordon benchmark set using the aug-cc-pVTZ basis set. To analyze the individual effect of the parameters, we scanned one of parameters, while the other was fixed at λ = 0.5 or μ = 0.5 bohr–1, which are fairly appropriate choices for the ground-state energy.71 The results are presented in Figure 1.
Figure 1.

MAE for the Gordon test set as a function of the parameters μ (left) and λ (right) using various functionals and the aug-cc-pVTZ basis set with the corresponding auxiliary bases.
Foremost, we inspected the fixed λ case. As it can be seen, the performance of the RS-PBE-PBE and RS-PBE-P86 functionals is almost identical. The largest deviation between the MAEs is only 0.03 eV, whereas the MAE is at most 0.01 eV lower for RS-PBE-P86 in the practically important range. In the first region, the errors decrease rapidly until μ = 0.4 bohr–1. The minimum errors, which are 0.15 and 0.14 eV for the RS-PBE-PBE and RS-PBE-P86, respectively, are fairly constant in the range of 0.4 ≤ μ ≤ 0.8 bohr–1. Thereafter, the errors start to converge asymptotically to somewhat higher values. The shape of the curve for RS-B88-LYP is similar to the other two; however, the error is consistently higher. The minimum is shallow again and can be found between the μ = 0.7 bohr–1 and μ = 0.9 bohr–1 values. In these cases, the MAE is 0.18 eV. On the basis of this numerical experience, it is assumed that the optimal value for the range-separation parameter will be at around 0.7 bohr–1.
Next, we assessed the fixed μ case. Similar conclusions can be drawn about the performance of the functionals. The best results are obtained with the RS-PBE-P86 functional, and RS-PBE-PBE is very close to it, while the RS-B88-LYP variant is less satisfactory. The shapes of the RS-PBE-PBE and RS-PBE-P86 curves are almost identical, while it is a bit different for RS-B88-LYP. The one-parameter variants of the ansatz,64 that is, the RS DHs with λ = 0, provide quite good results; however, the errors for all three functionals decrease with increasing λ parameter until 0.3–0.4. Thereafter, the errors increase monotonically for RS-PBE-P86 and RS–PBE-PBE. This behavior is more unbalanced for the RS-B88-LYP, and the error fluctuates within a narrow range. In the λ = 1 limit, the CIS(D) method is recovered, and the MAE is 0.21 eV. The minimal MAEs are 0.12 and 0.13 eV for the RS-PBE-P86 and RS-PBE-PBE functionals, respectively, and can be found at λ = 0.3. The same measure is 0.18 eV for the RS-B88-LYP functional at λ = 0.4.
Finally, the simultaneous optimization of the parameters was carried out. Taking into consideration the above results, our first intention was to minimize the MAE in the ranges of 0.6 ≤ μ ≤ 0.8 bohr–1 and 0.2 ≤ λ ≤ 0.4. Although very promising results were obtained for this benchmark set on the average, the performances of the methods were not satisfactory for particular excited states since the MAXs were somewhat higher. We found that the quality of the corresponding excitation energies can be boosted if the proportion of the HF and MP2 contributions is slightly increased. We notice that smaller values of λ could be favorable from the point of view of the one-electron basis set dependence, but as we will see in the following subsection, the basis set dependence of the excitation energies is moderate. In addition, a large λ value also has the benefit that it can decrease the self-interaction error. Accordingly, the range for the search of the optimal value was extended to 0.4 ≤ λ ≤ 0.6 to gain more robust approaches. In this manner, our numerical experiments showed that all three functionals have an optimal behavior at λ = 0.5 and μ = 0.7 bohr–1, which is greatly in line with the ground-state results.71 In addition, these results confirm the trend that the optimal parameter μ is higher when the correlation part is also range-separated71,73−76 than if only the exchange contributions are.78,79,81
To assess the effects on the ground-state properties, we compared the performance of the two-parameter RS DHs to the existing functionals. Please note that, since ground-state properties are out of the scope of our study, only the most important findings are discussed here; more information is available in the Supporting Information. For the ionization potentials, DSD-PBEP86 and B2GPPLYP have the best performance with MAEs of around 2.00 kcal/mol. Among the RS DHs, the lowest values, precisely, 2.37 and 2.55 kcal/mol can be attained by the ωB2GPPLYP and RS-B88-LYP approaches, respectively. For the remaining RS DHs, the MAE is uniformly lower than 2.70 kcal/mol. The RS hybrids are inferior, the MAE is 2.97 and 3.87 kcal/mol for the ωB97X and CAM-B3LYP functionals, respectively. When the electron affinities are inspected, the order changes dramatically. In this case, the best performers are the RS hybrids with MAEs of 2.96 and 3.43 kcal/mol for the CAM-B3LYP and ωB97X approaches, respectively. The first standard DH is DSD-PBEP86, while the two best RS DHs are the ωB2PLYP and RS-PBE-P86 methods. For these approaches, the MAE is 4.26, 4.18, and 4.39 kcal/mol, respectively. In contrast to the former set, the performance of the ωB2GPPLYP, B2GPPLYP, and RS-B88-LYP approaches are not satisfying as the MAE is 5.66 kcal/mol for the latter. On the basis of these numerical experiences, we can conclude that the performance of the RS DHs is not outstanding; however, they can compete with the standard functionals despite the fact that they are tuned for excited-state properties.
The MAEs with the default parameters for various types of excitations of the Gordon test set are visualized in Figure 2.
Figure 2.
MAEs for the calculated excitation energies of all, valence, and Rydberg states of the Gordon test set110 (63, 32, and 31 states, respectively) using the aug-cc-pVTZ basis sets with the corresponding auxiliary bases.
Inspecting the bars, we can observe that the lowest overall MAE, 0.11 eV, is attained, not surprisingly, by the CCSD method. The next two methods are the RS-PBE-P86 and RS–PBE-PBE functionals with 0.14 and 0.15 eV, respectively. The standard DH functionals DSD-PBEP86, PBE-QIDH, and PBE0-2 seem reliable as well, and the error is less than 0.20 eV for two further methods, namely the RS-B88-LYP and CC2 approaches. The performance of the available RS functionals is inferior, especially for ωB97X. This trend somewhat changes when the excitations are separated. In the case of the valence excitations, the former best approaches are still rather well-balanced. Their MAEs are around 0.18 eV; however, the DSD-PBEP86 and CC2 results are outstanding, while PBE-QIDH and PBE0-2 perform a bit worse. In contrast, these approaches are two of the best performers for the Rydberg excitations together with the CCSD method. The RS DH functionals are also reliable, while the RS hybrids, just as B2(GP)PLYP are not recommended. The MAEs for the Rydberg states are usually lower than those for the valence excitations for the most accurate methods.
The compilations of the further statistical error measures for the Gordon set can be found in Table 2. The lowest MEs are achieved by the CIS(D), DSD-PBEP86, and the present RS-DH approaches; however, the ME has an opposite sign for the valence and Rydberg excitations. From this point of view, the RS-PBE-P86 and RS-PBE-PBE functionals are somewhat more balanced. The lowest MAX, which is 0.49 eV, is attained by the CCSD method. Several approaches, such as CC2, ωB2(GP)PLYP, PBE0-2, PBE-QIDH, DSD-PBEP86, and our RS-DH methods, have acceptable performance in this regard. The MAX is around 0.60 eV in these cases. For the CC2, DSD-PBEP86, and PBE-QIDH methods, the MAX belonging to a Rydberg excitation, while it is affiliated with a valence excitation for the others. It is also interesting to realize that our RS-DH ansatz slightly but consistently improves upon the corresponding “genuine” DHs irrespective of the underlying DFT functionals. That is, the MAEs for the RS-B88-LYP, RS-PBE-PBE, and RS-PBE-P86 approaches are somewhat lower than those for B2(GP)PLYP, PBE0-2/PBE-QIDH, and DSD-PBEP86, respectively.
Table 2. Error Measures for the Calculated Excitation Energies (in eV) of All, Valence, and Rydberg States of the Gordon Test Set110 (63, 32, and 31 States, Respectively).
| all |
valence |
Rydberg |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| method | MAE | ME | MAX | MAE | ME | MAX | MAE | ME | MAX |
| CCSDa | 0.11 | 0.10 | 0.49 | 0.17 | 0.17 | 0.49 | 0.04 | 0.04 | 0.14 |
| CC2 | 0.18 | –0.11 | 0.64 | 0.13 | –0.01 | 0.53 | 0.24 | –0.22 | 0.64 |
| CIS(D) | 0.21 | –0.01 | 1.04 | 0.23 | 0.11 | 1.04 | 0.19 | –0.15 | 0.57 |
| CAM-B3LYPa | 0.23 | –0.09 | 0.89 | 0.15 | 0.10 | 0.64 | 0.32 | –0.31 | 0.89 |
| ωB97Xa | 0.30 | 0.26 | 0.74 | 0.30 | 0.29 | 0.68 | 0.30 | 0.23 | 0.74 |
| B2PLYPa | 0.33 | –0.28 | 0.98 | 0.19 | –0.09 | 0.61 | 0.50 | –0.50 | 0.98 |
| B2GPPLYPa | 0.24 | –0.12 | 0.71 | 0.15 | 0.06 | 0.59 | 0.33 | –0.32 | 0.71 |
| ωB2PLYPa | 0.21 | 0.12 | 0.61 | 0.25 | 0.25 | 0.61 | 0.16 | –0.01 | 0.57 |
| ωB2GPPLYPa | 0.20 | 0.13 | 0.73 | 0.26 | 0.26 | 0.73 | 0.14 | –0.01 | 0.57 |
| RS-B88-LYP | 0.18 | –0.02 | 0.61 | 0.18 | 0.11 | 0.61 | 0.18 | –0.16 | 0.39 |
| PBE-QIDHa | 0.16 | 0.13 | 0.52 | 0.22 | 0.22 | 0.49 | 0.09 | 0.02 | 0.52 |
| PBE0-2 | 0.16 | 0.12 | 0.64 | 0.22 | 0.20 | 0.64 | 0.10 | 0.02 | 0.55 |
| RS-PBE-PBE | 0.15 | 0.03 | 0.61 | 0.18 | 0.13 | 0.61 | 0.11 | –0.07 | 0.42 |
| DSD-PBEP86 | 0.16 | –0.04 | 0.59 | 0.11 | 0.08 | 0.39 | 0.21 | –0.18 | 0.59 |
| RS-PBE-P86 | 0.14 | 0.04 | 0.60 | 0.18 | 0.13 | 0.60 | 0.10 | –0.05 | 0.44 |
Values were taken from ref (83).
3.3. Benchmark Calculations
Numerous calculations were carried out to assess the performance and to verify the robustness of our approaches for singlet excitations using the default parameters determined. First, we consider the SG test set. The relevant error measures are visualized in Figure 3.
Figure 3.
Error measures for the calculated excitation energies for the SG test set56 using the aug-cc-pVTZ basis sets with the corresponding auxiliary bases. The PBE-QIDH, B2(GP)PLYP, ωB2(GP)PLYP, CAM-B3LYP, and ωB97X values were taken from ref (83), while the CCSD results come from ref (56).
As it can be seen, the average performances of DSD-PBEP86 and CCSD are the best. However, it is not unexpected for the former since the set is dominated by valence excitations, for which this approach was also the best performer in the case of the Gordon set. The success of the CCSD method is somewhat more surprising. The MAE is only slightly higher, 0.12 eV, for our two-parameter RS functionals and for the CC2 method. The PBE0-2, B2GPPLYP, PBE-QIDH, and CIS(D) methods yield acceptable results as well with a MAE of around 0.15 eV. The lowest MAX is also obtained for these approaches; however, it is surprisingly high for the CCSD method. It is interesting to see that the performances of the B88-LYP-based functionals are relatively poor, except for RS-B88-LYP. This is also true for the ωB2PLYP and ωB2GPPLYP functionals, which were trained for this test set, although the range-separation parameter was optimized for full TDDFT calculations. The ME is almost perfect for DSD-PBEP86 and B2GPPLYP, furthermore, the wave function-based methods and the CAM-B3LYP functional have a small ME. However, the latter is not recommended because of its relatively high maximum error. The MEs of our approaches are around 0.07 eV, which is also appropriate. The MAX errors, apart from the B88-LYP-based methods and CCSD, are very close to each other and acceptable. The lowest deviation span, around 0.6 eV, can be attained by the two-parameter RS functionals and the PBE0-2 method, while it is under 0.8 eV for the CC2, DSD-PBEP86, and ωB2GPPLYP approaches.
Next, we study CT excitations, which present a well-known problem in TDDFT theory. The numerical results for the CT benchmark set of Szalay et al. are presented in Figure 4.
Figure 4.
Error measures for the calculated excitation energies for the CT test set112 using the cc-pVDZ basis sets with the corresponding auxiliary bases. For clarity, the bars for the rightmost four methods are not proportional to the corresponding error measures, but the relevant values are displayed on the bars. The CCSD values were taken from ref (112).
Inspecting the errors, we can state that it is difficult to compete with the iterative wave function-based methods, namely with CCSD and CC2. However, significant improvement can be realized in the case of the RS-DH functionals over other DHs and RS hybrid functionals. Our RS-PBE-PBE and RS-PBE-P86, as well as ωB2GPPLYP are better than the CIS(D) method, while the performance of RS-B88-LYP is almost identical to it. The MAE for these methods is below 0.45 eV. A somewhat larger value, precisely, 0.51 eV can be achieved with the ωB2PLYP functional, which is still acceptable. It is instructive to realize that the performance of the RS hybrids is far from what is expected. The MAE for the ωB97X and CAM-B3LYP functionals is 0.92 and 1.68 eV, respectively, while it is higher than 1.0 eV for DSD-PBEP86 as well. All the methods underestimate the excitation energies, except for CCSD. If the MAXs are considered, the order does not change significantly for the best approaches. The CCSD and CC2 methods are outstanding with 0.44 and 0.76 eV, respectively. The MAX for the best RS DHs is around 1.0 eV, while it is 1.30 eV for ωB2PLYP. It is definitely a surprising fact that the error can be about 3 eV for an RS hybrid functional or with the B2PLYP DH. This order somewhat changes if the deviation span is considered. The CCSD and CC2 methods are still the superior ones. In these cases, the deviation spans are 0.29 and 0.65 eV, respectively. It is around 1.1 eV for our approaches, while the span is 1.33 and 1.58 eV for the PBE0-2 and DSD-PBEP86 standard DH functionals, respectively. This measure is 1.52 (1.62) eV for ωB2GPPLYP (ωB2PLYP), while those for the remaining RS hybrids are still the worst, being around 2.4 eV. A similar order can be determined if the standard deviations or root-mean-square errors are considered.
The excitation energies for the additional CT test set proposed by Goerigk and co-workers83 were also assessed. As could be assumed, these excitations are less challenging for TDA-TDDFT calculations. That is, the standard DHs have similar performance compared to the RS functionals, and no systematic underestimation can be observed. The best performance can be achieved, not surprisingly, with the CC2 method. In this case, the MAE is 0.18 eV. The standard DHs, such as PBE0-2, DSD-PBEP86, and PBE-QIDH seem to be reliable as well with MAEs of 0.22, 0.24, and 0.24 eV, respectively. The error is identically about 0.25 eV for almost all the RS functionals, while their MAXs are systematically lower compared to the best standard DHs, being around 0.50 eV. The most inaccurate results are attained by the B2(GP)PLYP approaches. The MAE is 0.51 eV, while the MAX is 1.16 eV in the worst case. More statistical measures can be found in the Supporting Information.
Thereafter, we compare the methods using the Thiel test set. The obtained error measures are presented in Figure 5. Since the benchmark set only contains valence excitations, the best performances are attained by the CC2 and DSD-PBEP86 approaches. Surprisingly, B2(GP)PLYP has a fairly low MAE. The MAE is under 0.30 eV together with the CCSD method, while it is around 0.30 eV for the CIS(D), all the two-parameter RS DHs, the CAM-B3LYP, the PBE0-2, and the PBE-QIDH approaches. For ωB2(GP)PLYP and ωB97X, it exceeds 0.40 eV. The excitation energies are systematically overestimated, except for B2PLYP, where the ME is close to zero. The MAXs are well-balanced for the complete list, but the CC2, B2PLYP, and CCSD methods have a somewhat lower error. Inspecting the MAEs and MEs, our RS approaches are consistently better than the ωB2(GP)PLYP RS DHs and, concerning DFT approximations, are only outperformed by the DSD-PBEP86 and B2(GP)PLYP methods. However, the root-mean-square errors and standard deviations are slightly higher compared to the PBE0-2 and PBE-QIDH approaches.
Figure 5.
Error measures for the calculated excitation energies for the Thiel test set113 using the TZVP basis sets with the def2-QZVPP-RI(-JK) auxiliary bases. The CCSD values were taken from ref (115).
The first set of Loos, Jacquemin, and co-workers (LJ1) incorporates 55 excited states with various types of excitations. For this comparison, the reference energies calculated at the CC3 level with the aug-cc-pVTZ basis set are used. The results are visualized in Figure 6. The lowest overall MAE, 0.09 eV, is attained by the CCSD method. Thereafter, several methods have almost the same accuracy. The lowest MAE among them, which is 0.17 eV, can be achieved with the ωB2(GP)PLYP and DSD-PBEP86 functionals. The performances of our approaches are excellent as well, with MAEs of 0.18 eV. For the ωB97X, PBE0-2, and PBE-QIDH functionals, it is still below 0.20 eV. The standard deviation and the root-mean-square error are lower for PBE-based functionals than for ωB97X. Beyond them, the error starts to increase. The sign of the errors fluctuates since the MEs are rather low for almost all the methods. The best results are obtained with the B88-LYP-based RS DHs and the CC2 method. The MAX is also well-balanced being around 0.60 eV, except for CCSD, where it is much lower. In this regard, the DSD-PBEP86 and ωB2(GP)PLYP approaches are also excellent.
Figure 6.
Error measures for the calculated excitation energies for the LJ1 test set116 using the aug-cc-pVTZ basis sets with the corresponding auxiliary bases. The CCSD values were taken from ref (116).
The second benchmark compilation of Loos, Jacquemin, and co-workers (LJ2) consists of the so-called “exotic” molecules. The error measures are shown in Figure 7. Inspecting the bars, it can be stated that the excitations considered are not a big challenge to these methods. The MAEs are reasonably low for all the approaches. The best performances are achieved with our RS DH approaches, B2GPPLYP, DSD-PBEP86, and CCSD. The MAE is uniformly 0.07 eV for them; however, the ME is lower for the former. The MAE is somewhat worse for the available RS functionals since it exceeds 0.10 eV. The MAX is under 0.25 eV for the best approaches except for DSD-PBEP86, while it is around 0.40 eV for the less satisfactory functionals.
Figure 7.
Error measures for the calculated excitation energies for the LJ2 test set117 using the aug-cc-pVTZ basis sets with the corresponding auxiliary bases. The PBE-QIDH, B2PLYP, B2GPPLYP, ωB2PLYP, ωB2GPPLYP, CAM-B3LYP, and ωB97X values were taken from ref (83).
The last benchmark set for the cross-validation tests the lowest two excitations and their splitting for the linear PAHs from naphthalene to hexacene. The MAEs are visualized in Figure 8. As it can be seen, inspecting the 1La excitations, the standard DHs systematically outperform, apart from CAM-B3LYP, the RS functionals. The most reliable results can be attained by the DSD-PBEP86 and B2GPPLYP approaches, as well as the CC2 method with a MAE of around 0.05 eV. The best performers among the RS functionals are the CAM-B3LYP and the two-parameter RS DHs, where this measure is 0.10 and 0.19 eV, respectively. Almost the same order can be determined for the 1Lb excitations; however, the MAEs are noticeably higher. That is, the error is around 0.30 eV for the best DHs, while it is 0.42 eV for the most reliable RS functionals, which are our approaches. It is interesting to note that the most accurate excitation energies were obtained by the ωB2(GP)PLYP approaches relying on full TDDFT,81 but their performances are relatively poor taking into account the present TDA-TDDFT results. This can be explained by the fact that the excitation energies are overestimated for all the functionals in ref (81), and a systematic blue-shift of 0.20–0.25 eV can be observed between the TDA- and full TDDFT results. Nevertheless, this effect somewhat vanishes when the splitting of the two excitations is considered. In this respect, the most remarkable results are surprisingly attained by the CIS(D) method with a MAE of 0.13 eV, while the most reliable functionals are the DSD-PBEP86 and the two-parameter RS DH approaches. In these cases, the MAEs are around 0.23 eV. For the rest of the functionals, the error is noticeably higher; however, they do not seem to be less reliable than the CC2 method, where the MAE is 0.29 eV.
Figure 8.
MAEs for the calculated lowest two excitations for the linear PAHs and their splitting118 using the cc-pVTZ basis sets with the corresponding auxiliary bases.
We have also tested the one-electron basis set dependence of the approaches. This phenomenon can be assessed from many aspects, but it is well-known that the effects of the basis set applied are rather unpredictable for excited-state properties.114,116,123−127 Nevertheless, we think that one of the most robust and important measures for these effects is the deviation from the basis set limit within a given method. Accordingly, we determined the MAEs for the LJ1 compilation applying the aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ basis sets for all the approaches using the corresponding results with the aug-cc-pV5Z basis set as reference. The results are presented in Figure 9.
Figure 9.

MAEs for the LJ1 test set116 as a function of the applied basis sets. The aDZ, aTZ, and aQZ denote the aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ basis sets, respectively. The reference energies are the aug-cc-pV5Z values for the corresponding approach.
As it can be seen, the largest basis set effects can be observed for the wave function-based methods using the aug-cc-pVDZ basis set. The MAE is 0.19 and 0.16 eV for the CIS(D) and CC2 methods, respectively. The TDA-TDDFT methods have a somewhat lower error; however, the difference between wave function and density functional methods is relatively smaller than that for the ground-state energy.71 This is at least partly explained by the fact that, in general, the errors of the calculated ground- and excited-state energies cancel each other. The standard DHs and ωB97X have practically identical performance, with MAEs of around 0.16 eV. The gain for the RS DHs and CAM-B3LYP is more significant, while the best performance is attained by ωB2PLYP with a MAE of 0.13 eV. The benefit of the TDA-TDDFT methods reduces for the aug-cc-pVTZ basis, while it almost disappears for aug-cc-pVQZ. The largest deviation between the MAEs is only 0.02 eV for the triple-ζ basis set. The two extremes are 0.08 and 0.06 eV for the B2PLYP and RS-PBE-P86 functionals, respectively. It is interesting to see that the basis set effect on the B2PLYP approach is larger than that for the wave function-based methods. The results for the aug-cc-pVQZ basis set are even more balanced with MAEs of about 0.04 eV. Four salient errors can be found for all the approaches using the quadruple-ζ basis set, which are two Rydberg excitations for the N2 and NH3 molecules, with MAEs of around 0.20 eV. In general, we can conclude that the best performances are achieved by the RS DHs, however, the benefit is far from what is expected taking into account the corresponding ground-state tendencies and decreases with increasing the quality of the basis set. Upon closer inspection of the excitation energies of ref (126), similar findings can be observed for the first- and second-row atoms using nonempirical standard DHs.
Finally, we measured computation times to gain some insight in what computational resources are required by the various methods. The timing benchmarks were performed for the most extended system of our test sets, the anthracene molecule with 24 atoms and 94 electrons. The aug-cc-pVTZ basis set and the corresponding auxiliary bases were used in these calculations resulting in 874 atomic orbitals and 1916 (1944) auxiliary functions for the KS (post-KS) calculations. For the self-consistent field (SCF) procedure and for the TDA equations, a completely integral-direct algorithm was executed, while a semi-integral-direct one was executed for the second-order corrections. The latter means that the contributions of the virtual–virtual block of the three-center integral list are evaluated with an integral-direct algorithm, while the remaining blocks are kept in the main memory and their contributions are calculated in an “in-core” manner. This algorithm is almost identical to the “Algorithm 3” approach of ref (53). It is clear that the RS methods are more costly because of the increased number of terms in the XC energy and the use of robust fitting formulas. This effect is, of course, different for each step of a calculation and depends on the number of the contributions. Consequently, we selected a standard DH, an RS hybrid, and two RS DHs with different ansatze to compare. The most obvious choices are the B88- and LYP-based approaches, such as the B2PLYP, CAM-B3LYP, ωB2PLYP, and RS-B88-LYP functionals. The wall-clock times for the various steps of the calculations determined on a machine with an 8-core 3.0 GHz Intel Xeon E5-1660 v3 processor are collected in Table 3. Inspecting the results, we can conclude that the genuine DH is the least demanding approach. For the B2PLYP functional, the SCF and TDA parts take 13 min, while the second-order corrections including the integral transformation are roughly 1.5 min. It means that the MP2 and (D) corrections increase the wall-clock time by about 10%. The HF exchange contribution for an SCF and a TDA iteration takes the same amount of time; the overhead can be explained by the increased costs of the evaluation of the XC terms as higher derivatives of the XC functional are required. The CAM-B3LYP calculation takes 4 min longer since it requires the evaluation of the LR and FR HF terms, as well as a SR DFT contribution. The ωB2PLYP functional contains LR and SR HF contributions as well; however, the FR integrals are also required due to the robust fitting formulas. Accordingly, the time required is somewhat higher but still acceptable. The total wall-clock time is 24.5 min, which is almost twice as much compared to the standard DH. The SCF and TDA parts are uniformly 23.7 min for the ωB2PLYP and RS-B88-LYP functionals. The second-order corrections are obviously more costly for the latter; however, they take just about 4 min. It means that the total wall-clock time is higher only by about 10% compared to that of the ωB2PLYP approach. We note that this overhead could be more unfavorable for larger systems as the perturbative step scales more steeply than the SCF and TDA steps with respect to system size. However, it cannot be expected that the calculation of the second-order correction will become the bottleneck for practical applications even with the robust-fitting formulas. In addition, the memory demand is not higher than that of the standard DHs since the evaluation of the different range-separated terms is carried out consecutively. For larger systems, only the number of the input–output operations could be somewhat higher. On the basis of the above findings, we can conclude that the evaluation of the second-order corrections is not the bottleneck of the DH schemes, and the range-separation of the second-order terms does not increase the total wall-clock times significantly.
Table 3. Computation Times (in min) and Number of Iterations for the Lowest Singlet Excited State of the Anthracene Molecule Using the aug-cc-pVTZ basis set.
| functional |
||||
|---|---|---|---|---|
| B2PLYP | CAM-B3LYP | ωB2PLYP | RS-B88-LYP | |
| SCF iterationa | 0.37 | 0.55 | 0.69 | 0.69 |
| TDA iterationa | 0.73 | 0.94 | 1.11 | 1.11 |
| integral transformationb | 0.73 | – | 0.73 | 0.73 |
| second-order correctionsc | 0.78 | – | 0.78 | 3.98 |
| no. of the SCF iterations | 13 | 13 | 14 | 14 |
| no. of the TDA iterations | 11 | 12 | 12 | 12 |
| total wall-clock time | 14.4 | 18.4 | 24.5 | 27.7 |
Wall-clock time per iteration step.
Wall-clock time for the occupied–occupied and occupied–virtual blocks of the three-center integral list.
Wall-clock time for the second-order corrections.
4. Conclusions
A robust two-parameter RS-DH TDA-TDDFT approach has been proposed for excited-state calculations, which is based on the CAM-like decomposition of the Coulomb potential utilizing the ansatz introduced by Toulouse et al.71 for the ground-state XC energy. In contrast to the existing RS-DH functional,81 the range separation was invoked for both the exchange and the correlation contributions. The detailed working equations were also presented for the perturbative LR/SR second-order corrections for singlet excitations using the numerically stable robust fitting formulas87 supposing a closed-shell system. A flexible local-scaling approximation for the SR DFT contributions76 was adapted as well, which enables the rapid testing of an arbitrary combination of exchange and correlation functionals. Utilizing this infrastructure, the RS analogues of the most popular standard DHs were introduced and tested.
The two adjustable parameters of the ansatz were determined using the well-balanced benchmark set of Gordon and co-workers.110 In addition to the excellent results obtained, it is also noteworthy that all three functionals introduced here have an optimal behavior with the same parameter set. The value of the parameters is greatly in line with the ground-state results of ref (71). Cross-validation was performed on several test sets using the default parameters, such as the benchmark compilation of Schwabe and Goerigk,56 a CT set of Szalay and co-workers,112 another CT set of Goerigk et al.,81 the widely used compilation of Thiel and co-workers,113 a set on the two lowest excitations of linear PAHs from naphthalene to hexacene,118 as well as two additional sets of Loos, Jacquemin, and co-workers.116,117 Our numerical results show that the new RS-DH functionals are the most robust ones among the density functional approximations studied, yielding reliable excitation energies for all kinds of singlet excitations. The best performances for the valence excitations were attained by the DSD-PBEP86 and the two-parameter RS-DH approaches. The PBE0-2 and RS-DH functionals can be recommended for the Rydberg excitations, while only the RS-DH approaches can be used reliably for the challenging CT excitations. The performances of all three two-parameter RS DHs proposed herein were very similar regardless of the exchange and correlation functionals applied. On average, the results for the recently proposed ωB2(GP)PLYP approaches were noticeably inferior compared to the RS-B88-LYP functional. The one-electron basis set dependence and computation times were also assessed. It was shown that, with the use of the aug-cc-pVDZ basis set, the results are closer to the basis set limit for the RS DHs, though this gain is moderate compared to the ground-state results and decreases with increasing basis set size. In addition, it has also been demonstrated that the evaluation of the second-order corrections is not the bottleneck of the DH schemes even if the range-separation approximation is invoked.
Acknowledgments
The authors are grateful for the financial support from the National Research, Development, and Innovation Office (NKFIH, Grant No. KKP126451). The work of D.M. is supported by the ÚNKP-20-4 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund. The research reported in this paper and carried out at BME has been supported by the NRDI Fund (TKP2020 IES, Grant No. BME-IE-BIO) based on the charter of bolster issued by the NRDI Office under the auspices of the Ministry for Innovation and Technology. The computing time granted on the Hungarian HPC Infrastructure at NIIF Institute, Hungary, is gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c01135.
Computed excitation energies (XLSX)
The authors declare no competing financial interest.
Supplementary Material
References
- C̆ížek J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256. 10.1063/1.1727484. [DOI] [Google Scholar]
- Stanton J. F.; Bartlett R. J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029. 10.1063/1.464746. [DOI] [Google Scholar]
- Watts J. D.; Bartlett R. J. The inclusion of connected triple excitations in the equation-of-motion coupled-cluster method. J. Chem. Phys. 1994, 101, 3073. 10.1063/1.467620. [DOI] [Google Scholar]
- Koch H.; Jørgensen P. Coupled cluster response functions. J. Chem. Phys. 1990, 93, 3333. 10.1063/1.458814. [DOI] [Google Scholar]
- Koch H.; Jensen H. J. A.; Jørgensen P.; Helgaker T. Excitation energies from the coupled cluster singles and doubles linear response function (CCSDLR). Applications to Be, CH+, CO, and H2O. J. Chem. Phys. 1990, 93, 3345. 10.1063/1.458815. [DOI] [Google Scholar]
- Rico R. J.; Head-Gordon M. Single-reference theories of molecular excited states with single and double substitutions. Chem. Phys. Lett. 1993, 213, 224. 10.1016/0009-2614(93)85124-7. [DOI] [Google Scholar]
- Christiansen O.; Koch H.; Jørgensen P. Response functions in the CC3 iterative triple excitation model. J. Chem. Phys. 1995, 103, 7429. 10.1063/1.470315. [DOI] [Google Scholar]
- Christiansen O.; Koch H.; Jørgensen P. Perturbative triple excitation corrections to coupled cluster singles and doubles excitation energies. J. Chem. Phys. 1996, 105, 1451. 10.1063/1.472007. [DOI] [Google Scholar]
- Watts J. D.; Bartlett R. J. Iterative and non-iterative triple excitation corrections in coupled-cluster methods for excited electronic states: the EOM-CCSDT-3 and EOM-CCSD(T) methods. Chem. Phys. Lett. 1996, 258, 581. 10.1016/0009-2614(96)00708-7. [DOI] [Google Scholar]
- Christiansen O.; Koch H.; Jørgensen P. The second-order approximate coupled cluster singles and doubles model CC2. Chem. Phys. Lett. 1995, 243, 409. 10.1016/0009-2614(95)00841-Q. [DOI] [Google Scholar]
- Schirmer J.; Trofimov A. B. Intermediate state representation approach to physical properties of electronically excited molecules. J. Chem. Phys. 2004, 120, 11449. 10.1063/1.1752875. [DOI] [PubMed] [Google Scholar]
- Head-Gordon M.; Rico R. J.; Oumi M.; Lee T. J. A doubles correction to electronic excited states from configuration interaction in the space of single substitutions. Chem. Phys. Lett. 1994, 219, 21. 10.1016/0009-2614(94)00070-0. [DOI] [Google Scholar]
- Runge E.; Gross E. K. U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997. 10.1103/PhysRevLett.52.997. [DOI] [Google Scholar]
- Gross E. K. U.; Kohn W. Local density-functional theory of frequency-dependent linear response. Phys. Rev. Lett. 1985, 55, 2850. 10.1103/PhysRevLett.55.2850. [DOI] [PubMed] [Google Scholar]
- Appel H.; Gross E. K. U.; Burke K. Excitations in Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 2003, 90, 043005. 10.1103/PhysRevLett.90.043005. [DOI] [PubMed] [Google Scholar]
- Casida M. E. In Computational Chemistry: Reviews of Current Trends; Chong D. P., Ed.; World Scientific: Singapore, 1999; Vol. 1. [Google Scholar]
- Casida M. E.; Huix-Rotllant M. Progress in Time-Dependent Density-Functional Theory. Annu. Rev. Phys. Chem. 2012, 63, 287. 10.1146/annurev-physchem-032511-143803. [DOI] [PubMed] [Google Scholar]
- Dreuw A.; Head-Gordon M. Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009. 10.1021/cr0505627. [DOI] [PubMed] [Google Scholar]
- Dreuw A.; Head-Gordon M. Failure of Time-Dependent Density Functional Theory for Long-Range Charge-Transfer Excited States: The Zincbacteriochlorin-Bacteriochlorin and Bacteriochlorophyll-Spheroidene Complexes. J. Am. Chem. Soc. 2004, 126, 4007. 10.1021/ja039556n. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Parac M. Substantial Errors from Time-Dependent Density Functional Theory for the Calculation of Excited States of Large Π Systems. ChemPhysChem 2003, 4, 292. 10.1002/cphc.200390047. [DOI] [PubMed] [Google Scholar]
- Prlj A.; Curchod B. F. E.; Fabrizio A.; Floryan L.; Corminboeuf C. Qualitatively Incorrect Features in the TDDFT Spectrum of Thiophene-Based Compounds. J. Phys. Chem. Lett. 2015, 6, 13. 10.1021/jz5022087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savin A.; Flad H.-J. Density functionals for the Yukawa electron-electron interaction. Int. J. Quantum Chem. 1995, 56, 327. 10.1002/qua.560560417. [DOI] [Google Scholar]
- Leininger T.; Stoll H.; Werner H.-J.; Savin A. Combining long-range configuration interaction with short-range density functionals. Chem. Phys. Lett. 1997, 275, 151. 10.1016/S0009-2614(97)00758-6. [DOI] [Google Scholar]
- Iikura H.; Tsuneda T.; Yanai T.; Hirao K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540. 10.1063/1.1383587. [DOI] [Google Scholar]
- Tawada Y.; Tsuneda T.; Yanagisawa S.; Yanai T.; Hirao K. A long-range-corrected time-dependent density functional theory. J. Chem. Phys. 2004, 120, 8425. 10.1063/1.1688752. [DOI] [PubMed] [Google Scholar]
- Chiba M.; Tsuneda T.; Hirao K. Excited state geometry optimizations by analytical energy gradient of long-range corrected time-dependent density functional theory. J. Chem. Phys. 2006, 124, 144106. 10.1063/1.2186995. [DOI] [PubMed] [Google Scholar]
- Tsuneda T.; Hirao K. Long-range correction for density functional theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 375. 10.1002/wcms.1178. [DOI] [Google Scholar]
- Vydrov O. A.; Scuseria G. E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. 10.1063/1.2409292. [DOI] [PubMed] [Google Scholar]
- Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. 10.1063/1.1564060. [DOI] [Google Scholar]
- Vydrov O. A.; Heyd J.; Krukau A. V.; Scuseria G. E. Importance of short-range versus long-range Hartree-Fock exchange for the performance of hybrid density functionals. J. Chem. Phys. 2006, 125, 074106. 10.1063/1.2244560. [DOI] [PubMed] [Google Scholar]
- Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Chai J.-D.; Head-Gordon M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- Peverati R.; Truhlar D. G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810. 10.1021/jz201170d. [DOI] [Google Scholar]
- Mardirossian N.; Head-Gordon M. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315. 10.1080/00268976.2017.1333644. [DOI] [Google Scholar]
- Brémond É.; Savarese M.; Su N. Q.; Pérez-Jiménez Á. J.; Xu X.; Sancho-García J. C.; Adamo C. Benchmarking Density Functionals on Structural Parameters of Small/Medium-Sized Organic Molecules. J. Chem. Theory Comput. 2016, 12, 459. 10.1021/acs.jctc.5b01144. [DOI] [PubMed] [Google Scholar]
- Peverati R.; Truhlar D. G. Quest for a universal density functional: The accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. R. Soc., A 2014, 372, 20120476. 10.1098/rsta.2012.0476. [DOI] [PubMed] [Google Scholar]
- Mardirossian N.; Head-Gordon M. ωB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Phys. Chem. Chem. Phys. 2014, 16, 9904. 10.1039/c3cp54374a. [DOI] [PubMed] [Google Scholar]
- Najibi A.; Goerigk L. The Nonlocal Kernel in van der Waals Density Functionals as an Additive Correction: An Extensive Analysis with Special Emphasis on the B97M-V and ωB97M-V Approaches. J. Chem. Theory Comput. 2018, 14, 5725. 10.1021/acs.jctc.8b00842. [DOI] [PubMed] [Google Scholar]
- Martin J. M. L.; Santra G. Empirical Double-Hybrid Density Functional Theory: A ‘Third Way’ in Between WFT and DFT. Isr. J. Chem. 2020, 60, 1. 10.1002/ijch.201900114. [DOI] [Google Scholar]
- Goerigk L.; Hansen A.; Bauer C.; Ehrlich S.; Najibi A.; Grimme S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184. 10.1039/C7CP04913G. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
- Tarnopolsky A.; Karton A.; Sertchook R.; Vuzman D.; Martin J. M. L. Double-Hybrid Functionals for Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 3. 10.1021/jp710179r. [DOI] [PubMed] [Google Scholar]
- Karton A.; Tarnopolsky A.; Lamere J.-F.; Schatz G. C.; Martin J. M. L. Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 12868. 10.1021/jp801805p. [DOI] [PubMed] [Google Scholar]
- Sharkas K.; Toulouse J.; Savin A. Double-hybrid density-functional theory made rigorous. J. Chem. Phys. 2011, 134, 064113. 10.1063/1.3544215. [DOI] [PubMed] [Google Scholar]
- Toulouse J.; Sharkas K.; Brémond É.; Adamo C. Rationale for a new class of double-hybrid approximations in density-functional theory. J. Chem. Phys. 2011, 135, 101102. 10.1063/1.3640019. [DOI] [PubMed] [Google Scholar]
- Brémond É.; Adamo C. Seeking for parameter-free double-hybrid functionals: The PBE0-DH model. J. Chem. Phys. 2011, 135, 024106. 10.1063/1.3604569. [DOI] [PubMed] [Google Scholar]
- Chai J.-D.; Mao S.-P. Seeking for reliable double-hybrid density functionals without fitting parameters: The PBE0–2 functional. Chem. Phys. Lett. 2012, 538, 121. 10.1016/j.cplett.2012.04.045. [DOI] [Google Scholar]
- Hui K.; Chai J.-D. SCAN-based hybrid and double-hybrid density functionals from models without fitted parameters. J. Chem. Phys. 2016, 144, 044114. 10.1063/1.4940734. [DOI] [PubMed] [Google Scholar]
- Brémond É.; Sancho-García J. C.; Pérez-Jiménez Á. J.; Adamo C. Double-hybrid functionals from adiabatic-connection: The QIDH model. J. Chem. Phys. 2014, 141, 031101. 10.1063/1.4890314. [DOI] [PubMed] [Google Scholar]
- Goerigk L.; Grimme S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals - Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291. 10.1021/ct100466k. [DOI] [PubMed] [Google Scholar]
- Kozuch S.; Gruzman D.; Martin J. M. L. DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction. J. Phys. Chem. C 2010, 114, 20801. 10.1021/jp1070852. [DOI] [Google Scholar]
- Kozuch S.; Martin J. M. L. DSD-PBEP86: in search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104. 10.1039/c1cp22592h. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Neese F. Double-hybrid density functional theory for excited electronic states of molecules. J. Chem. Phys. 2007, 127, 154116. 10.1063/1.2772854. [DOI] [PubMed] [Google Scholar]
- Goerigk L.; Moellmann J.; Grimme S. Computation of accurate excitation energies for large organic molecules with double-hybrid density functionals. Phys. Chem. Chem. Phys. 2009, 11, 4611. 10.1039/b902315a. [DOI] [PubMed] [Google Scholar]
- Meo F. D.; Trouillas P.; Adamo C.; Sancho-García J. C. Application of recent double-hybrid density functionals to low-lying singlet-singlet excitation energies of large organic compounds. J. Chem. Phys. 2013, 139, 164104. 10.1063/1.4825359. [DOI] [PubMed] [Google Scholar]
- Schwabe T.; Goerigk L. Time-Dependent Double-Hybrid Density Functionals with Spin-Component and Spin-Opposite Scaling. J. Chem. Theory Comput. 2017, 13, 4307. 10.1021/acs.jctc.7b00386. [DOI] [PubMed] [Google Scholar]
- Brémond É.; Ciofini I.; Sancho-García J. C.; Adamo C. Nonempirical Double-Hybrid Functionals: An Effective Tool for Chemists. Acc. Chem. Res. 2016, 49, 1503. 10.1021/acs.accounts.6b00232. [DOI] [PubMed] [Google Scholar]
- Kozuch S.; Martin J. M. L. Spin-Component-Scaled Double Hybrids: An Extensive Search for the Best Fifth-Rung Functionals Blending DFT and Perturbation Theory. J. Comput. Chem. 2013, 34, 2327. 10.1002/jcc.23391. [DOI] [PubMed] [Google Scholar]
- Su N. Q.; Xu X. The XYG3 Type of Doubly Hybrid Density Functionals. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 721. 10.1002/wcms.1274. [DOI] [Google Scholar]
- Goerigk L.; Grimme S. Calculation of Electronic Circular Dichroism Spectra with Time-Dependent Double-Hybrid Density Functional Theory. J. Phys. Chem. A 2009, 113, 767. 10.1021/jp807366r. [DOI] [PubMed] [Google Scholar]
- Goerigk L.; Grimme S. Assessment of TD-DFT methods and of various spin scaled CIS(D) and CC2 versions for the treatment of low-lying valence excitations of large organic dyes. J. Chem. Phys. 2010, 132, 184103. 10.1063/1.3418614. [DOI] [Google Scholar]
- Sancho-García J. C.; Adamo C. Double-hybrid density functionals: Merging wavefunction and density approaches to get the best of both worlds. Phys. Chem. Chem. Phys. 2013, 15, 14581. 10.1039/c3cp50907a. [DOI] [PubMed] [Google Scholar]
- Goerigk L.; Grimme S. Double-hybrid density functionals. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 576. 10.1002/wcms.1193. [DOI] [Google Scholar]
- Ángyán J. G.; Gerber I. C.; Savin A.; Toulouse J. van der Waals forces in density functional theory: Perturbational long-range electron-interaction corrections. Phys. Rev. A: At., Mol., Opt. Phys. 2005, 72, 012510. 10.1103/PhysRevA.72.012510. [DOI] [Google Scholar]
- Toulouse J.; Gerber I. C.; Jansen G.; Savin A.; Ángyán J. G. Adiabatic-Connection Fluctuation-Dissipation Density-Functional Theory Based on Range Separation. Phys. Rev. Lett. 2009, 102, 096404. 10.1103/PhysRevLett.102.096404. [DOI] [PubMed] [Google Scholar]
- Toulouse J.; Colonna F.; Savin A. Long-range-short-range separation of the electron-electron interaction in density-functional theory. Phys. Rev. A: At., Mol., Opt. Phys. 2004, 70, 062505. 10.1103/PhysRevA.70.062505. [DOI] [Google Scholar]
- Toulouse J.; Colonna F.; Savin A. Short-range exchange and correlation energy density functionals: Beyond the local-density approximation. J. Chem. Phys. 2005, 122, 014110. 10.1063/1.1824896. [DOI] [PubMed] [Google Scholar]
- Goll E.; Werner H.-J.; Stoll H. A short-range gradient-corrected density functional in long-range coupled-cluster calculations for rare gas dimers. Phys. Chem. Chem. Phys. 2005, 7, 3917. 10.1039/b509242f. [DOI] [PubMed] [Google Scholar]
- Goll E.; Leininger T.; Manby F. R.; Mitrushchenkov A.; Werner H.-J.; Stoll H. Local and density fitting approximations within the short-range/long-range hybrid scheme: application to large non-bonded complexes. Phys. Chem. Chem. Phys. 2008, 10, 3353. 10.1039/b804672g. [DOI] [PubMed] [Google Scholar]
- Goll E.; Ernst M.; Moegle-Hofacker F.; Stoll H. Development and assessment of a short-range meta-GGA functional. J. Chem. Phys. 2009, 130, 234112. 10.1063/1.3152221. [DOI] [PubMed] [Google Scholar]
- Kalai C.; Toulouse J. A general range-separated double-hybrid density-functional theory. J. Chem. Phys. 2018, 148, 164105. 10.1063/1.5025561. [DOI] [PubMed] [Google Scholar]
- Benighaus T.; DiStasio R. A. Jr; Lochan R. C.; Chai J.-D.; Head-Gordon M. Semiempirical Double-Hybrid Density Functional with Improved Description of Long-Range Correlation. J. Phys. Chem. A 2008, 112, 2702. 10.1021/jp710439w. [DOI] [PubMed] [Google Scholar]
- Zhu W.; Toulouse J.; Savin A.; Ángyán J. G. Range-separated density-functional theory with random phase approximation applied to noncovalent intermolecular interactions. J. Chem. Phys. 2010, 132, 244108. 10.1063/1.3431616. [DOI] [PubMed] [Google Scholar]
- Kalai C.; Mussard B.; Toulouse J. Range-separated double-hybrid density-functional theory with coupled-cluster and random-phase approximations. J. Chem. Phys. 2019, 151, 074102. 10.1063/1.5108536. [DOI] [PubMed] [Google Scholar]
- Mezei P. D.; Kállay M. Construction of a range-separated dual-hybrid direct random phase approximation. J. Chem. Theory Comput. 2019, 15, 6678. 10.1021/acs.jctc.9b00891. [DOI] [PubMed] [Google Scholar]
- Garza A. J.; Bulik I. W.; Henderson T. M.; Scuseria G. E. Range separated hybrids of pair coupled cluster doubles and density functionals. Phys. Chem. Chem. Phys. 2015, 17, 22412. 10.1039/C5CP02773J. [DOI] [PubMed] [Google Scholar]
- Brémond É.; Savarese M.; Pérez-Jiménez Á. J.; Sancho-García J. C.; Adamo C. Range-Separated Double-Hybrid Functional from Nonempirical Constraints. J. Chem. Theory Comput. 2018, 14, 4052. 10.1021/acs.jctc.8b00261. [DOI] [PubMed] [Google Scholar]
- Brémond É.; Pérez-Jiménez Á. J.; Sancho-García J. C.; Adamo C. Range-separated hybrid density functionals made simple. J. Chem. Phys. 2019, 150, 201102. 10.1063/1.5097164. [DOI] [PubMed] [Google Scholar]
- Brémond É.; Pérez-Jiménez Á. J.; Sancho-García J. C.; Adamo C. Range-separated hybrid and double-hybrid density functionals: A quest for the determination of the range-separation parameter. J. Chem. Phys. 2020, 152, 244124. 10.1063/5.0010976. [DOI] [PubMed] [Google Scholar]
- Chai J.-D.; Head-Gordon M. Long-range corrected double-hybrid density functionals. J. Chem. Phys. 2009, 131, 174105. 10.1063/1.3244209. [DOI] [PubMed] [Google Scholar]
- Casanova-Páez M.; Dardis M. B.; Goerigk L. ωB2PLYP and ωB2GPPLYP: The First Two Double-Hybrid Density Functionals with Long-Range Correction Optimized for Excitation Energies. J. Chem. Theory Comput. 2019, 15, 4735. 10.1021/acs.jctc.9b00013. [DOI] [PubMed] [Google Scholar]
- Goerigk L.; Casanova-Páez M. The Trip to the Density Functional Theory Zoo Continues: Making a Case for Time-Dependent Double Hybrids for Excited-State Problems. Aust. J. Chem. 2020, 93. 10.1071/CH20093. [DOI] [Google Scholar]
- Casanova-Páez M.; Goerigk L. Assessing the Tamm-Dancoff approximation, singlet-singlet, and singlet-triplet excitations with the latest long-range corrected double-hybrid density functionals. J. Chem. Phys. 2020, 153, 064106. 10.1063/5.0018354. [DOI] [PubMed] [Google Scholar]
- Mester D.; Kállay M. Combined density functional and algebraic-diagrammatic construction approach for accurate excitation energies and transition moments. J. Chem. Theory Comput. 2019, 15, 4440. 10.1021/acs.jctc.9b00391. [DOI] [PubMed] [Google Scholar]
- Hirata S.; Head-Gordon M. Time-dependent density functional theory within the Tamm-Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291. 10.1016/S0009-2614(99)01149-5. [DOI] [Google Scholar]
- Chantzis A.; Laurent A. D.; Adamo C.; Jacquemin D. Is the Tamm-Dancoff Approximation Reliable for the Calculation of Absorption and Fluorescence Band Shapes?. J. Chem. Theory Comput. 2013, 9, 4517. 10.1021/ct400597f. [DOI] [PubMed] [Google Scholar]
- Dunlap B. I. Robust and variational fitting: Removing the four-center integrals from center stage in quantum chemistry. J. Mol. Struct.: THEOCHEM 2000, 529, 37. 10.1016/S0166-1280(00)00528-5. [DOI] [Google Scholar]
- Kállay M.; Nagy P. R.; Mester D.; Rolik Z.; Samu G.; Csontos J.; Csóka J.; Szabó P. B.; Gyevi-Nagy L.; Hégely B.; Ladjánszki I.; Szegedy L.; Ladóczki B.; Petrov K.; Farkas M.; Mezei P. D.; Ganyecz Á.. MRCC, a quantum chemical program suite. https://www.mrcc.hu/ (accessed 2020-10-01). [DOI] [PubMed]
- Kállay M.; Nagy P. R.; Mester D.; Rolik Z.; Samu G.; Csontos J.; Csóka J.; Szabó P. B.; Gyevi-Nagy L.; Hégely B.; Ladjánszki I.; Szegedy L.; Ladóczki B.; Petrov K.; Farkas M.; Mezei P. D.; Ganyecz Á. The MRCC program system: Accurate quantum chemistry from water to proteins. J. Chem. Phys. 2020, 152, 074107. 10.1063/1.5142048. [DOI] [PubMed] [Google Scholar]
- Dunning T. H. Jr Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. 10.1063/1.456153. [DOI] [Google Scholar]
- Woon D. E.; Dunning T. H. Jr Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358. 10.1063/1.464303. [DOI] [Google Scholar]
- Kendall R. A.; Dunning T. H. Jr; Harrison R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796. 10.1063/1.462569. [DOI] [Google Scholar]
- Schäfer A.; Huber C.; Ahlrichs R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829. 10.1063/1.467146. [DOI] [Google Scholar]
- Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy integrals over Gaussian functions. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Weigend F.; Köhn A.; Hättig C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175. 10.1063/1.1445115. [DOI] [Google Scholar]
- Weigend F.; Häser M.; Patzelt H.; Ahlrichs R. RI-MP2: optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998, 294, 143. 10.1016/S0009-2614(98)00862-8. [DOI] [Google Scholar]
- Weigend F. Hartree-Fock Exchange Fitting Basis Sets for H to Rn. J. Comput. Chem. 2008, 29, 167. 10.1002/jcc.20702. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 33, 8822. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- Dirac P. A. M. Quantum mechanics of many-electron systems. Proc. R. Soc. (London) A 1929, 123, 714. [Google Scholar]
- Slater J. C. A simplification of the Hartree-Fock method. Phys. Rev. 1951, 81, 385. 10.1103/PhysRev.81.385. [DOI] [Google Scholar]
- Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Perdew J. P.; Chevary J. A.; Vosko S. H.; Jackson K. A.; Pederson M. R.; Singh D. J.; Fiolhais C. Atoms, molecules, solids and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46, 6671. 10.1103/PhysRevB.46.6671. [DOI] [PubMed] [Google Scholar]
- Savin A.Recent Developments and Applications of Modern Density Functional Theory; Elsevier: Amsterdam, 1996. [Google Scholar]
- Paziani S.; Moroni S.; Gori-Giorgi P.; Bachelet G. B. Local-spin-density functional for multideterminant density functional theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 155111. 10.1103/PhysRevB.73.155111. [DOI] [Google Scholar]
- Lehtola S.; Steigemann C.; Oliveira M. J. T.; Marques M. A. L. Recent developments in LIBXC - A comprehensive library of functionals for density functional theory. SoftwareX 2018, 7, 1. 10.1016/j.softx.2017.11.002. [DOI] [Google Scholar]
- Lehtola S.; Steigemann C.; Oliveira M. J. T.; Marques M. A.. Recent developments in Libxc-A comprehensive library of functionals for density funtional theory; Software X7, 1; 2018; See https://www.tddft.org/programs/libxc/.
- Leang S. S.; Zahariev F.; Gordon M. S. Benchmarking the performance of time-dependent density functional methods. J. Chem. Phys. 2012, 136, 104101. 10.1063/1.3689445. [DOI] [PubMed] [Google Scholar]
- Curtiss L. A.; Raghavachari K.; Trucks G. W.; Pople J. A. Gaussian-2 theory for molecular energies of first-and second-row compounds. J. Chem. Phys. 1991, 94, 7221. 10.1063/1.460205. [DOI] [Google Scholar]
- Kozma B.; Tajti A.; Demoulin B.; Izsák R.; Nooijen M.; Szalay P. G. A New Benchmark Set for Excitation Energy of Charge Transfer States: Systematic Investigation of Coupled Cluster Type Methods. J. Chem. Theory Comput. 2020, 16, 4213. 10.1021/acs.jctc.0c00154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber M.; Silva-Junior M. R.; Sauer S. P. A.; Thiel W. Benchmarks for electronically excited states: CASPT2, CC2, CCSD, and CC3. J. Chem. Phys. 2008, 128, 134110. 10.1063/1.2889385. [DOI] [PubMed] [Google Scholar]
- Silva-Junior M. R.; Sauer S. P. A.; Schreiber M.; Thiel W. Basis set effects on coupled cluster benchmarks of electronically excited states: CC3, CCSDR(3) and CC2. Mol. Phys. 2010, 108, 453. 10.1080/00268970903549047. [DOI] [PubMed] [Google Scholar]
- Kánnár D.; Szalay P. G. Benchmarking Coupled Cluster Methods on Valence Singlet Excited States. J. Chem. Theory Comput. 2014, 10, 3757. 10.1021/ct500495n. [DOI] [PubMed] [Google Scholar]
- Loos P.-F.; Scemama A.; Blondel A.; Garniron Y.; Caffarel M.; Jacquemin D. A Mountaineering Strategy to Excited States: Highly Accurate Reference Energies and Benchmarks. J. Chem. Theory Comput. 2018, 14, 4360. 10.1021/acs.jctc.8b00406. [DOI] [PubMed] [Google Scholar]
- Loos P.-F.; Scemama A.; Boggio-Pasqua M.; Jacquemin D. Mountaineering Strategy to Excited States: Highly Accurate Energies and Benchmarks for Exotic Molecules and Radicals. J. Chem. Theory Comput. 2020, 16, 3720. 10.1021/acs.jctc.0c00227. [DOI] [PubMed] [Google Scholar]
- Lopata K.; Reslan R.; Kowalska M.; Neuhauser D.; Govind N.; Kowalski K. Excited-State Studies of Polyacenes: A Comparative Picture Using EOMCCSD, CR-EOMCCSD(T), Range-Separated (LR/RT)-TDDFT, TD-PM3, and TD-ZINDO. J. Chem. Theory Comput. 2011, 7, 3686. 10.1021/ct2005165. [DOI] [PubMed] [Google Scholar]
- Kowalski K.; Piecuch P. New coupled-cluster methods with singles, doubles, and noniterative triples for high accuracy calculations of excited electronic states. J. Chem. Phys. 2004, 120, 22. 10.1063/1.1632474. [DOI] [PubMed] [Google Scholar]
- Parac M.; Grimme S. A TDDFT study of the lowest excitation energies of polycyclic aromatic hydrocarbons. Chem. Phys. 2003, 292, 11. 10.1016/S0301-0104(03)00250-7. [DOI] [Google Scholar]
- Goerigk L.; Grimme S. Double-Hybrid Density Functionals Provide a Balanced Description of Excited 1La and 1Lb States in Polycyclic Aromatic Hydrocarbons. J. Chem. Theory Comput. 2011, 7, 3272. 10.1021/ct200380v. [DOI] [PubMed] [Google Scholar]
- Richard R. M.; Herbert J. M. Time-Dependent Density-Functional Description of the 1La State in Polycyclic Aromatic Hydrocarbons: Charge-Transfer Character in Disguise?. J. Chem. Theory Comput. 2011, 7, 1296. 10.1021/ct100607w. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Izgorodina E. I. Calculation of 0–0 excitation energies of organic molecules by CIS(D) quantum chemical methods. Chem. Phys. 2004, 305, 223. 10.1016/j.chemphys.2004.06.050. [DOI] [Google Scholar]
- Laurent A. D.; Blondel A.; Jacquemin D. Choosing an atomic basis set for TD-DFT, SOPPA, ADC(2), CIS(D), CC2 and EOM-CCSD calculations of low-lying excited states of organic dyes. Theor. Chem. Acc. 2015, 134, 76. 10.1007/s00214-015-1676-9. [DOI] [Google Scholar]
- Giner E.; Scemama A.; Toulouse J.; Loos P.-F. Chemically accurate excitation energies with small basis sets. J. Chem. Phys. 2019, 151, 144118. 10.1063/1.5122976. [DOI] [PubMed] [Google Scholar]
- Hernández-Martínez L.; Brémond E.; Pérez-Jiménez A. J.; San-Fabián E.; Adamo C.; Sancho-García J. C. Nonempirical (double-hybrid) density functionals applied to atomic excitation energies: A systematic basis set investigation. Int. J. Quantum Chem. 2020, 120, e26193 10.1002/qua.26193. [DOI] [Google Scholar]
- Hoyer C. E.; Gagliardi L.; Truhlar D. G. Multiconfiguration Pair-Density Functional Theory Spectral Calculations Are Stable to Adding Diffuse Basis Functions. J. Phys. Chem. Lett. 2015, 6, 4184. 10.1021/acs.jpclett.5b01888. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.