Abstract

Hill coefficients, which provide a measure of cooperativity in ligand binding, can be determined for equilibrium (or steady-state) data by measuring fractional saturation (or initial reaction velocities) as a function of ligand concentration. Hill coefficients can also be determined for transient kinetic data from plots of the observed rate constant of the ligand-promoted conformational change as a function of ligand concentration. Here, it is shown that the ratio of the values of these two Hill coefficients can provide insight into the allosteric mechanism. Cases when the value of the kinetic Hill coefficient is equal to or greater than the value of the equilibrium coefficient indicate concerted transitions whereas ratios smaller than one indicate a sequential transition. The derivations in this work are for symmetric dimers but are expected to have general applicability for homo-oligomers.
Introduction
Insights into reaction mechanisms are often obtained through identifying and characterizing reaction intermediates. Consequently, various criteria have been proposed, for example, for determining the validity of the two-state approximation of protein folding reactions. Examples include a calorimetric criterion for two-state folding according to which the measured calorimetric enthalpy change upon unfolding should be equal to the van’t Hoff enthalpy change calculated assuming a two-state transition.1−3 Another criterion is that the m-value (i.e., the slope of the plot of the change in free energy vs denaturant concentration) for equilibrium denaturation should be equal to the sum of m-values for folding and unfolding obtained from transient kinetic data.4 In contrast, there has been surprisingly little consideration of such criteria for the legitimacy of the two-state approximation of allosteric transitions as assumed, for example, in the classic Monod–Wyman–Changeux (MWC) model.5 Here, we show that the ratio between the values of the Hill coefficients obtained for equilibrium binding data and transient kinetic data can provide such a criterion.
Cooperativity in the function of multisubunit proteins is often reflected in sigmoidal plots of fractional saturation of ligand binding sites as a function of ligand concentration. Such plots can be fitted to the Hill equation:
| 1 |
where Y̅ and K designate the fractional saturation and apparent binding constant, respectively, [S] is the ligand concentration, and ne is the Hill coefficient, which provides a measure for the extent of cooperativity under equilibrium or steady-state (when Y̅ is replaced by initial enzyme velocity divided by the maximal initial velocity, V/Vmax) conditions. Cooperativity in ligand binding by multimeric proteins is often due to ligand-promoted conformational changes, which can be concerted, sequential, or probabilistic.6 Regardless of the allosteric mechanism, plots of the rate of the conformational change, k, as a function of the ligand concentration are often also sigmoidal. Such plots can be fitted to a kinetic version of the Hill equation:7
| 2 |
where k0 and kmax are the respective rate constants of conformational change in the absence of ligand and at saturating ligand concentration, nk is the Hill coefficient for transient kinetic data, and K and [S] are defined as before. In previous work,8 it was shown that nk/ne ≠ 1 can indicate that the allosteric transition is sequential. Other reasons for a deviation from a value of one were, however, not excluded. Here, such scenarios are considered in the case of a symmetric dimer (i.e., with identical subunits and no pre-existing asymmetry in the unbound state).
The Hill Constant for Equilibrium Data
The relationship between the Hill coefficient for equilibrium data, ne, and the ligand binding constants of a symmetric dimer has been derived before9 as follows.
Rearranging eq 1 yields the following expression for the Hill coefficient:
| 3 |
It follows from eq 3 that the Hill coefficient at 50% saturation, ne, 0.5, is given by
| 4 |
where [S]e.0.5 is the substrate concentration at the midpoint of the plot. The fractional saturation, in the case of a symmetric dimer, is given by
| 5 |
where K1 and K2 are the statistically corrected intrinsic
association constants for the respective first and second binding
events. Hence, 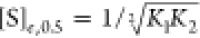 (i.e., when Y̅ =
0.5). Combining this relationship with eqs 4 and 5 results in the
following expression for the Hill coefficient:9
(i.e., when Y̅ =
0.5). Combining this relationship with eqs 4 and 5 results in the
following expression for the Hill coefficient:9
| 6 |
It can be seen that when K1 = K2, i.e., in the absence of cooperativity, ne,0.5 = 1. In the presence of strong positive cooperativity (K2 ≫ K1) or strong negative cooperativity (K2 ≪ K1), ne,0.5 → 2 and ne,0.5 → 0, respectively.
In the case of concerted conformational changes, which are described by the Monod–Wyman–Changeux (MWC) model,5 cooperativity is due to an equilibrium between two unliganded states: a tense (T) state with relatively low affinity for the ligand, which is the predominant form in the absence of ligand, and a relaxed (R) state with a higher affinity for the ligand. In this model, the extent of cooperativity is determined by the equilibrium constant L (=[T]/[R]) and by the relative affinities of the ligand for the T and R states (c = KT/KR). In the case of the MWC model, it is straightforward to show that ne,0.5 is given by
| 7 |
Inspection of eq 7 shows that the value of ne,0.5 for the MWC model cannot be less than one. According to this model, cooperativity is absent (ne,0.5 = 1) when c = KT/KR = 1, i.e., when the T and R states are, in practice, indistinguishable from each other and no allosteric transition can be observed. It is also absent when L = ∞ or L = 0 in which cases the T or R states, respectively, are so stable that no allosteric transition takes place.
Comparing the Hill Constants for Equilibrium and Kinetic Data in the Concerted Case
Next, we consider the relationship between the Hill coefficient for transient kinetic data, nk, and the ligand binding constants of a symmetric dimer. Equation 2 can be rearranged (by analogy to eq 3) as follows:
| 8 |
It is important to note that eq 8 does not change when the substrate-independent reverse rate constant is included in eq 2 (because it cancels out in the three differences in eq 8 and because dk/d[S] does not change since the reverse rate constant is substrate-independent). Consequently, the reverse rate constants do not need to be considered in the analyses here. In the case of the concerted model,5 the forward rate constant, k, of the conformational change of a symmetric dimer, as a function of the ligand concentration, can be expressed, as follows (Figure 1):
| 9 |
where k0, k1, and k2 are the
respective forward rate constants of conformational changes of the
unbound, singly and double bound species and the other symbols are
defined as before. This equation is derived by assuming that the conformational
changes are slow relative to binding so that the latter can be described
by equilibrium constants. Equation 9 corresponds to the concerted model because symmetry
is implicitly maintained and the apo state can also undergo conformational
switching. Substituting 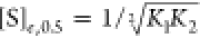 into eq 9 yields
into eq 9 yields
 |
10 |
where k0.5 is the observed rate constant of conformational change at [S]e, 0.5. Combining eqs 8–10 (where kmax = k2) yields the following expression for the Hill coefficient of a symmetric dimer for transient kinetic data:
 |
11 |
Figure 1.

Scheme showing different states of a dimer in the case of a concerted conformational change. The apo protein is in equilibrium between two conformational states, E and E′, with low and high affinities, respectively, for the ligand (S). The ligand can bind to both states. In accordance with the concerted model, the allosteric switch can take place either in the absence or presence of bound ligand via a mechanism of conformational selection.
Combining eqs 6 and 11, therefore, yields an expression for the ratio between the Hill coefficients for the transient kinetic data and equilibrium (or steady-state) data for a symmetric dimer in the concerted case:
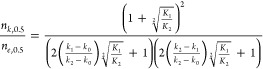 |
12 |
It is useful to rewrite eq 12 as follows:
| 13 |
where 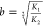 and
and  . Inspection of eq 13 shows that nk,0.5/ne,0.5 = 1 when a = 0.5 (i.e., when k1 = (k2 + k0)/2) and that nk,0.5/ne,0.5 > 1 when a ≠ 0.5. It also
shows that the value of nk,0.5/ne,0.5 cannot be less than one in the case of
the concerted model described by eq 9.
. Inspection of eq 13 shows that nk,0.5/ne,0.5 = 1 when a = 0.5 (i.e., when k1 = (k2 + k0)/2) and that nk,0.5/ne,0.5 > 1 when a ≠ 0.5. It also
shows that the value of nk,0.5/ne,0.5 cannot be less than one in the case of
the concerted model described by eq 9.
Equation 13 can be further interpreted by considering a kinetic scheme (Figure 2) in which the symmetry argument of the MWC model is applied also to the transition state, ‡, and reverse reactions from R to T are ignored as before (eq 9). In such a case, the rate constants for the conformational changes promoted by i bound ligand molecules can be expressed as follows:
| 14 |
where x = K‡/KT (K‡ is the ligand association constant of the transition state). Hence, it follows from eq 13 that nk,0.5/ne,0.5 = 1 when x = 1 (i.e., when the affinities of the T state and transition state for the ligand are equal) and that nk,0.5/ne,0.5 > 1 when x ≠ 1.
Figure 2.

Scheme showing extension of the symmetry argument of the MWC model to the transition state, ‡, of the T to R allosteric switch. The association constants of the ligand for the T, ‡, and R states are designated KT, K‡, and KR, respectively. The forward rate constants of the T to R conformational changes, in the presence of 0, 1, and 2 bound ligand molecules, are designated by k0, k1, and k2, respectively.
The Hill Constant for Kinetic Data in the Sequential Case
In the Koshland-Némethy-Filmer (KNF) sequential model,10 symmetry is not conserved. In other words, the ligand-promoted conformational switch in a multisubunit protein does not take place in an all-or-none fashion as in the MWC model (the states in the left and right columns in Figure 3). Instead, ligand binding induces (see also ref (11)) a conformational change only in the ligand-bound subunit (the states on the diagonal in Figure 3) and asymmetric states are allowed. In the case of the sequential model for a symmetric dimer, the rate constant of the conformational change, k, as a function of the ligand concentration can, therefore, be expressed, as follows:
| 15 |
where A and B stand for the respective ligand-free and ligand bound conformational states of a subunit (without bound ligand), [S] is the ligand (substrate) concentration, K1 is the apparent binding constant for the first binding step and ka and kb are the rate constants for the conformational changes AAS → ABS and ASBS → BSBS, respectively (see Figure 3). It is important to note that the right-hand side of eq 15 is reached by dividing the nominator and denominator by [S]. Equation 15 is, therefore, not defined for [S] = 0. The derivative of k in eq 15 with respect to [S] is given by
| 16 |
Figure 3.

Scheme highlighting different states of a dimer in the case of a sequential conformational change. Each subunit of the dimer can be in two conformations designated A and B. In the case of sequential allostery, ligand binding (designated by the subscript S) induces the conformational switching, and therefore, only the highlighted states on the diagonal are considered.
Combining eqs 8 and 16, one obtains:
| 17 |
Given that k0 = 0 (by definition) and kmax = kb (as may be seen by inspecting eq 15), one obtains:
| 18 |
Substituting 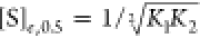 into eq 18, therefore, yields
into eq 18, therefore, yields
 |
19 |
Interestingly, nk,0.5 ≤ 1 for a sequential transition (given the assumptions that were made) and its value is, thus, smaller than ne,0.5. The value of nk,0.5 approaches one when kb ≫ ka as expected.
Concluding Remarks
In this work, we explored whether the ratio of the Hill coefficients
for transient and equilibrium (or steady-state) data,  , can provide insight into the allosteric
mechanism. We showed that
, can provide insight into the allosteric
mechanism. We showed that 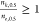 and
and 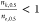 indicate concerted and sequential transitions,
respectively.
indicate concerted and sequential transitions,
respectively.  for concerted transitions is expected since
they lack intermediates, which reduce cooperativity (step functions,
therefore, correspond to maximum cooperativity). Consequently, it
is also expected, as found here, that
for concerted transitions is expected since
they lack intermediates, which reduce cooperativity (step functions,
therefore, correspond to maximum cooperativity). Consequently, it
is also expected, as found here, that  for sequential transitions will be lower
than for concerted ones. It is less intuitive, however, that
for sequential transitions will be lower
than for concerted ones. It is less intuitive, however, that 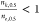 for sequential transitions. This implies
a lower variance in the binding numbers of the kinetic vs equilibrium
intermediates at [S]e,0.5. The derivations in this work
were obtained for symmetric dimers but are expected to have general
applicability for homo-oligomers. For example, the values of ne and nk for the
transition of the first ring of F44W GroEL were found to be 2.85 (±0.46)12 and 2.75 (±0.12),13 respectively. These similar values of ne and nk are in line with biochemical14 and computational15 evidence for the concerted nature of the intraring allosteric transitions
in GroEL. Future work should test the applicability of the criteria
derived here for homo-oligomers larger than dimers.
for sequential transitions. This implies
a lower variance in the binding numbers of the kinetic vs equilibrium
intermediates at [S]e,0.5. The derivations in this work
were obtained for symmetric dimers but are expected to have general
applicability for homo-oligomers. For example, the values of ne and nk for the
transition of the first ring of F44W GroEL were found to be 2.85 (±0.46)12 and 2.75 (±0.12),13 respectively. These similar values of ne and nk are in line with biochemical14 and computational15 evidence for the concerted nature of the intraring allosteric transitions
in GroEL. Future work should test the applicability of the criteria
derived here for homo-oligomers larger than dimers.
Acknowledgments
This work was supported by the Minerva Foundation with funding from the Federal German Ministry for Education and Research and the Kimmelman Center for Biomolecular Structure and Assembly. A.H. is the incumbent of the Carl and Dorothy Bennett Professorial Chair in Biochemistry. We thank Drs. Hagen Hoffman and Attila Szabo for critical reading of an earlier draft of this manuscript and helpful comments.
The authors declare no competing financial interest.
Special Issue
Published as part of The Journal of Physical Chemistry virtual special issue “Dave Thirumalai Festschrift”.
This paper was published on January 5, 2021. Three in-text equations were corrected to use a product rather than a quotient. The revised version was published on the Web on February 11, 2021.
References
- Jackson W. M.; Brandts J. F. Thermodynamics of protein denaturation. Calorimetric study of the reversible denaturation of chymotrypsinogen and conclusions regarding the accuracy of the two-state approximation. Biochemistry 1970, 9, 2294–2301. 10.1021/bi00813a011. [DOI] [PubMed] [Google Scholar]
- Privalov P. L. Stability of proteins: small globular proteins. Adv. Protein Chem. 1979, 33, 167–241. 10.1016/S0065-3233(08)60460-X. [DOI] [PubMed] [Google Scholar]
- Zhou Y.; Hall C. K.; Karplus M. The calorimetric criterion for a two-state process revisited. Protein Sci. 1999, 8, 1064–1074. 10.1110/ps.8.5.1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson S. E.; Fersht A. R. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry 1991, 30, 10428–10435. 10.1021/bi00107a010. [DOI] [PubMed] [Google Scholar]
- Monod J.; Wyman J.; Changeux J. P. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 1965, 12, 88–118. 10.1016/S0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- Gruber R.; Horovitz A. Unpicking allosteric mechanisms of homo-oligomeric proteins by determining their successive ligand binding constants. Philos. Trans. R. Soc., B 2018, 373, 20170176. 10.1098/rstb.2017.0176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammes G. G.; Schimmel P. R. Chemical relaxation spectra: calculation of relaxation times for complex mechanisms. J. Phys. Chem. 1966, 70, 2319–2324. 10.1021/j100879a039. [DOI] [Google Scholar]
- Horovitz A.; Yifrach O. On the relationship between the Hill coefficients for steady-state and transient kinetic data: a criterion for concerted transitions in allosteric proteins. Bull. Math. Biol. 2000, 62, 241–246. 10.1006/bulm.1999.0150. [DOI] [PubMed] [Google Scholar]
- Levitzki A.Quantitative aspects of allosteric mechanisms; Springer-Verlag: Berlin, 1978. [DOI] [PubMed] [Google Scholar]
- Koshland D. E. Jr.; Némethy G.; Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry 1966, 5, 365–385. 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- Vogt A. D.; Di Cera E. Conformational selection or induced fit? A critical appraisal of the kinetic mechanism. Biochemistry 2012, 51, 5894–5902. 10.1021/bi3006913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yifrach O.; Horovitz A. Transient kinetic analysis of adenosine 5-triphosphate binding-induced conformational changes in the allosteric chaperonin GroEL. Biochemistry 1998, 37, 7083–7088. 10.1021/bi980370o. [DOI] [PubMed] [Google Scholar]
- Yifrach O.; Horovitz A. Nested cooperativity in the ATPase activity of the oligomeric chaperonin GroEL. Biochemistry 1995, 34, 5303–5308. 10.1021/bi00016a001. [DOI] [PubMed] [Google Scholar]
- Dyachenko A.; Gruber R.; Shimon L.; Horovitz A.; Sharon M. Allosteric mechanisms can be distinguished using structural mass spectrometry. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 7235–7239. 10.1073/pnas.1302395110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J.; Sigler P. B.; Xu Z.; Karplus M. A dynamic model for the allosteric mechanism of GroEL. J. Mol. Biol. 2000, 302, 303–313. 10.1006/jmbi.2000.4014. [DOI] [PubMed] [Google Scholar]


