Transferred-Rotational-Echo Double Resonance

Abstract

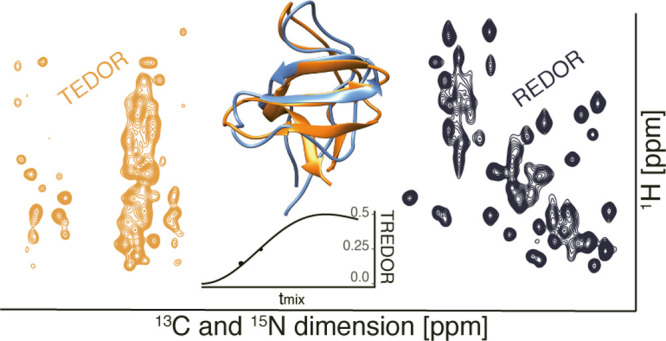
Internuclear distance determination is the foundation for NMR-based structure calculation. However, high-precision distance measurement is a laborious process requiring lengthy data acquisitions due to the large set of multidimensional spectra needed at different mixing times. This prevents application to large or challenging molecular systems. Here, we present a new approach, transferred-rotational-echo double resonance (TREDOR), a heteronuclear transfer method in which we simultaneously detect both starting and transferred signals in a single spectrum. This co-acquisition is used to compensate for coherence decay, resulting in accurate and precise distance determination by a single parameter fit using a single spectrum recorded at an ideal mixing time. We showcase TREDOR with the microcrystalline SH3 protein using 3D spectra to resolve resonances. By combining the measured N–C and H–C distances, we calculate the structure of SH3, which converges to the correct fold, with a root-mean-square deviation of 2.1 Å compared to a reference X-ray structure. The TREDOR data used in the structure calculation were acquired in only 4 days on a 600 MHz instrument. This is achieved due to the more than 2-fold time saving afforded by co-acquisition of additional information and demonstrates TREDOR as a fast and straightforward method for determining structures via magic-angle spinning NMR.

Introduction

Distance determination is the foundation for determination of 3D molecular structures via NMR, both in solution and in solid samples. Multidimensional spectra, in combination with homonuclear recoupling or spin diffusion methods, have been developed for structure determination with applications to biological molecules¹⁻⁶ and materials.⁷⁻⁹ Typically, a large set of internuclear distances, often categorized as imprecise distance ranges, are used as an input to simulated annealing protocols that converge to the correct protein fold. These structural representations are improved with more precise distance information.^6,10,11 However, determination of precise distances is still extremely challenging for proteins, particularly for large proteins in the solid state where multiple dimensions are required to resolve resonances. Improved distance precision typically requires many such multidimensional data sets, each acquired with a different mixing time such that distance-dependent buildup of magnetization can be recorded precisely. This dramatically increases the required measurement time.

Commonly, homonuclear recoupling or spin diffusion methods¹²⁻¹⁵ such as RFDR,¹⁶ DARR,^17,18 and DREAM¹⁹ are employed for distance determination and subsequent 3D structure calculation. These have the drawback of yielding only rough distance bounds,²⁰⁻²² while for solution NMR, experiments for the precise determination of these have been developed.^10,11 Only recently, attempts at determining precise distances in the solid state using RFDR have been made.⁶

Recoupling of heteronuclear dipole interactions in magic-angle spinning (MAS) NMR is a well-established method to measure distances^23,24 and order parameters.²⁵⁻³¹ Due to a favorable scaling factor and relatively low radio frequency (rf) power requirement, one of the earlier recoupling sequences, rotational echo double resonance (REDOR),^32,33 remains widely applied to both materials and biological samples. Since the spin part of the recoupled Hamiltonian is identical to the J-coupling Hamiltonian, a transferred sequence analogous to the solution HSQC sequence was developed soon after and is referred to as transferred-echo double resonance (TEDOR).³⁴ The REDOR and TEDOR sequences were originally devised for isolated spin pairs. Application to uniformly labeled samples by addition of z-filters³⁵ or insertion of selective pulses³⁶ has extended the applicability of the method. The REDOR and TEDOR pulse sequences have also been combined sequentially with other recoupling sequences to construct multidimensional pulse sequences for assignment and distance determination.³⁷⁻³⁹

A key advantage of the REDOR pulse sequence is that a reference spectrum is interleaved with the dephased spectrum in order to remove the effects of transverse coherence decay. On the other hand, a key advantage of TEDOR is that the dephasing nucleus is frequency encoded, and it is possible to separate the effects of multiple dephasing spins. This has been used for the simultaneous determination of multiple distances.^35,40 A major disadvantage in the use of TEDOR for precise distance determination is that unlike REDOR, there is no reference spectrum to account for transverse coherence decay. To make matters worse, there is a second parameter needed to fit TEDOR data, which is an overall amplitude scaling factor. The amplitude scale is not evident from TEDOR alone but can often be approximately determined based on TEDOR peaks arising from strong couplings or from a separate reference spectrum.^35,41,42 In practice, this means that when precise distances are needed, typical TEDOR data are recorded to sufficient time so as to observe a dipolar oscillation, and when only a partial oscillation can be recorded, or when the signal is over-damped due to coherence decay, free variation of the two fit parameters (amplitude scaling and coherence decay) results in fits to the data for a wide range of dipolar couplings.⁴⁰ The case of over-damping (transverse coherence decay rates of comparable magnitude to the couplings) occurs for weak couplings that encode useful structural information in protein samples, particularly for noncrystalline samples such as membrane proteins, which are of great biological interest. The ¹⁵N T₂ time, relevant during REDOR periods, is reported to be around 10 ms for non-exchanging backbone amide nitrogens in M2 protein from the influenza virus⁴³ and around 31 ms in perdeuterated SH3 microcrystals (100% back exchanged) without decoupling.⁴⁴ In the case of deuterated proteins or ultrafast MAS, proton T₂ can also reach ∼5 ms or more, long enough to acquire REDOR data,⁴⁵ suggesting that complementary H–C distances could be recorded. In addition to T₂ decay, the effects of multiple spin interactions, as well as pulse imperfections, can lead to faster signal loss during REDOR periods.^35,46 This results in lower signal-to-noise and less precise distance determination, particularly for uniformly labeled samples. Ideally, we would like to apply a sequence that can precisely determine distances using short mixing times (less than a dipolar oscillation) where the signal is still strong. At the same time, the sequence should identify both the dephased and the dephasing spins such that it can be applied to uniformly labeled samples.

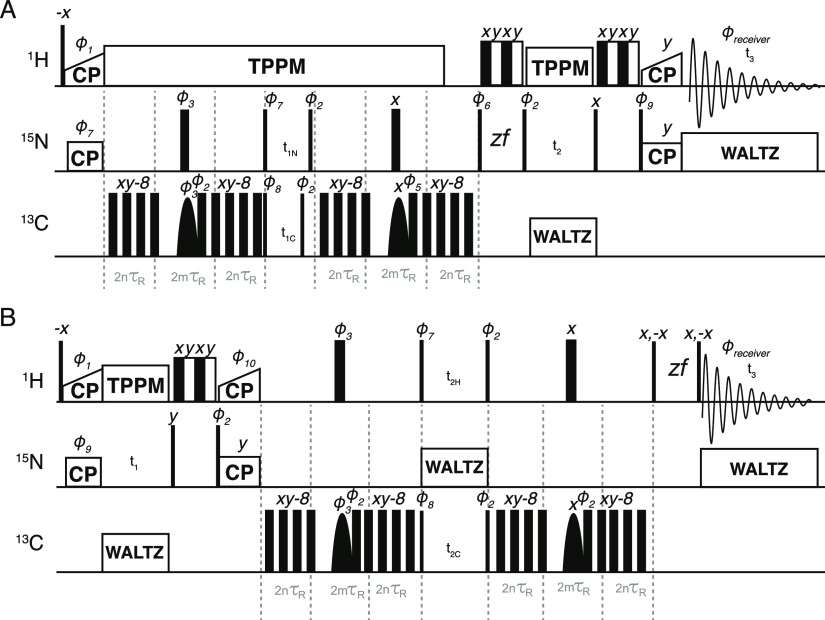
We took inspiration from transfer sequences used for the measurement of homonuclear J-couplings⁴⁷⁻⁴⁹ and for protein assignment⁵⁰ in order to design a heteronuclear sequence that retains both the starting signal (REDOR) and the transferred signal (TEDOR). The resulting transferred-rotational-echo double resonance pulse sequence (TREDOR) co-acquires the chemical shifts of both dipolar coupled nuclei (here ¹³C and ¹⁵N or ¹³C and ¹H) in one indirect dimension. Pulse sequences for two implementations of TREDOR are shown in Figure 1. By tracking both the original and transferred signal, it is possible to account for coherence decay at each mixing time and in so doing to remove two fit parameters of amplitude scaling and transverse coherence decay. The result is a single parameter fit to determine the dipolar coupling.

Figure 1.

Pseudo-4D TREDOR (H)(N)CNH and (H)N(H)CH pulse sequences shown in (A,B), respectively. Narrow and wide filled rectangles represent hard π/2 and π pulses, respectively, while soft selective pulses on the carbon channel are shown as parabolas. The REDOR periods are implemented with the usual two hard π pulses^32,33 per rotor period applied to the carbon channel. REDOR pulses were cycled according to the xy-8 scheme.⁵⁵ In the middle of each REDOR period, a REBURP⁵⁹-shaped pulse is used to select the ¹³C chemical shifts of interest. For ¹⁵N–¹³C_α TREDOR, the bandwidth of this pulse is set to 40–70 ppm; for ¹⁵N–¹³Cx TREDOR, the bandwidth of this pulse is set to 5–53 ppm, which should refocus all side-chain ¹³C shifts except for that of the C_β of serine and threonine; for H–CO TREDOR, the bandwidth of this pulse is set to 154–254 ppm. In (A), water suppression⁵⁷ is split before and after acquisition of the second dimension (t₂). This doubles as two z-filter elements, allowing a reduced phase cycle. Pulses were phase cycled as Φ₁ = 11333311, Φ₂ = 00222200, Φ₃ = 01, Φ₅ = 0022, Φ₆ = 1133, Φ₇ = 0022, Φ₈ = 2200, Φ₉ = 0022, Φ₁₀ = 2, Φ_rec′r = 02202002, where 0 = x, 1 = y, 2 = −x, 3 = −y. Unless indicated, other pulses have phase 0. To conveniently encode a correct ppm scale during acquisition of the first indirect dimension in (A) for both ¹⁵N and ¹³C, the increment of the ¹³C shifts t_1C is set to t_1N × (γ¹⁵N/γ¹³C), where γ is the gyromagnetic ratio, so that ¹⁵N and ¹³C will share the same ppm scale. Hypercomplex data were acquired by shifting Φ₇, Φ₈, Φ₁₀ by −90°, and Φ₉ by +90° in a separate acquisition to acquire pure phases, according to the procedure of Ruben and co-workers.⁷²

Materials and Methods

SH3 Sample Preparation

Perdeuterated chicken brain α-spectrin SH3 was expressed, purified, and crystallized based on previous publications.^51,52 Transformed Escherichia coli BL21(DE3) cells were grown in 250 mL of D₂O-based M9 minimal medium with 3 g/L ¹³C-d₇-glucose and 1 g/l ¹⁵N–NH₄Cl at 37 °C with shaking at 120 rpm. At OD_600nm 0.7, the temperature was switched to 30 °C until the OD_600nm reached ∼0.8 before induction with 1 mM isopropyl β-d-1-thiogalactopyranoside (IPTG). After overnight expression, SH3 was purified by anion exchange chromatography (HiTrap Q XL, GE Healthcare, 20 mM Tris, pH 8.0, 1 mM ethylenediaminetetraacetic acid (EDTA), gradient 0–1 M NaCl), gel filtration (Superdex 75, GE Healthcare, 20 mM citric acid, pH 3.5, 200 mM NaCl, 1 mM EDTA), followed by dialysis against H₂O–HCl (pH 3.5). Lyophilized protein was resuspended in H₂O–HCl (pH 3.5) at ∼20 mg/mL, and the same volume of 200 mM (NH₄)₂SO₄ (pH 3.5, 0.04% NaN₃) was added. Crystallization was induced by shifting the pH to ∼7.0 with gaseous NH₃. Samples were subsequently kept for 3 days at 4 °C before packing into a Bruker zirconia 1.3 mm NMR rotor using a centrifugation protocol introduced previously.

Opa60 Sample Preparation

The protocol for the purification of Opa60 is based on a previously published procedure.⁵³ A pET-28b(+) plasmid containing the Opa60 sequence with a C-terminal hexa-His-tag was transformed into E. coli BL21(DE3) cells. ¹³C-/¹⁵N-labeled Opa60 was expressed in M9 medium containing 4 g/L ¹³C-glucose and 1 g/L ¹⁵N–NH₄Cl. Cells were grown to an OD_600nm of 0.8 at 37 °C. Before induction, the temperature was decreased to 25 °C. Expression was induced overnight with 1 mM IPTG. Cells were harvested for 20 min at 5000g and 4 °C. The pellet was resuspended in 35 ml of lysis buffer (50 mM Tris, 150 mM NaCl, 1 mM MgCl₂, pH 8.0, cOmplete EDTA-free protease inhibitor cocktail (Roche)). Bacteria were lysed by sonication (Sonopuls HD 2200 (Bandelin), 6 × 60% power for 20 s, 1 min pause, on ice). The suspension was centrifuged for 1 h at 22,000g and 4 °C. The pellet, containing Opa60 inclusion bodies, was resuspended in 30 ml of lysis buffer with 1% w/v Triton X-100 and again centrifuged for 1 h at 22,000g and 4 °C. This step was repeated without Triton X-100, and the pellet was resuspended in 50 mL of solubilization buffer (50 mM Tris, 150 mM NaCl, 6 M guanidinium hydrochloride (Gu-HCl), pH 8.0). Nonsolubilized particles were removed by centrifugation for 45 min at 25,000g and 22 °C. 2 mM imidazole was added to the solubilized part, and this was loaded at room temperature onto a 5 mL column volume (CV) TALON resin (Takara Bio), equilibrated in loading buffer (20 mM sodium phosphate, 150 mM NaCl, 6 M Gu-HCl, 2 mM imidazole, pH 7.8). The resin was washed with 3 CV wash buffer (same as loading buffer, but 10 mM imidazole), and finally, Opa60 was eluted with 4 CV of elution buffer (same as loading buffer, but 250 mM imidazole). Opa60 was refolded for 2.5 days at room temperature by 40-fold dilution from ∼1 mg/mL protein concentration into refolding buffer [20 mM Tris, 500 mM NaCl, 0.25% w/v dodecylphosphocholine (DPC, Avanti Polar Lipids), pH 8.0, cOmplete EDTA-free protease inhibitor cocktail (Roche)]. Folding success was assessed with SDS-PAGE shift.⁵⁴ Refolded protein was concentrated and purified by size exclusion chromatography [SEC, Superdex 200 Increase 10/300 GL (GE Healthcare), SEC buffer (20 mM sodium phosphate, 150 mM NaCl, 0.15% w/v DPC, pH 6.2)]. Opa60-containing fractions were pooled. Opa60 was reconstituted into 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, Avanti Polar Lipids) lipid bilayers by dialysis against dialysis buffer (20 mM sodium phosphate, 100 mM NaCl, 20 mM MgCl₂, pH 6.2). Protein was added together with DMPC (lipid-to-protein mass ratio 0.25) into a dialysis cassette (cutoff 3500 Da), and over a course of 4–5 days, the buffer was changed each day. Methyl-β-cyclodextrin was added in between but was not in the final sample. After successful reconstitution (white precipitate), 0.02% w/v NaN₃ was added to the final sample. Opa60 was packed into a Bruker 0.7 mm MAS rotor.

NMR Spectroscopy

All TREDOR SH3 spectra were recorded on a Bruker AVIIIHD 600 UltraShield spectrometer with a field strength of 14.1 T, with a MASDVT600W2 BL1.3 HXY probe. The MAS frequency was set 55.555 kHz, and the temperature was set to 240 K (1000 L/h cooling gas). Proton and ¹³C hard pulse powers were both 100 kHz, and ¹⁵N hard pulse power was 83.3 kHz. REDOR pulses were applied on the carbon channel, employing the xy-8 scheme.⁵⁵ TPPM heteronuclear proton decoupling⁵⁶ was 12 kHz, MISSISSIPPI water suppression⁵⁷ was applied for 100 ms with 13.9 kHz, and WALTZ-16 heteronuclear decoupling⁵⁸ was 10 kHz.

Pseudo-4D TREDOR N–Cx spectra were recorded with 8 scans and a recycle delay of 1 s, with a total acquisition time of ∼2 days and 1 h for each mixing time (4, 6, 10 ms). For ¹H, the carrier frequency was set to 4.5 ppm, the acquisition time was 20.5 ms, and the spectral width was 41.7 ppm. For ¹³C (the combined dimension), the carrier frequency was 40 ppm, the acquisition time was 8 ms (making the ¹⁵N acquisition time in this dimension 19.9 ms), and the spectral width was 130.7 ppm. For ¹⁵N, the carrier was 90 ppm, the acquisition time was 16.5 ms, and the spectral width was 30 ppm. ¹H to ¹⁵N cross polarization (CP) was 700 μs long, with a ¹⁵N power of 45 kHz and a linear power ramp on proton from 89.6 to 112 kHz. ¹⁵N to ¹H CP was 500 μs long, with a ¹⁵N power of 45 kHz and a linear power ramp on proton from 112 to 89.6 kHz. The selective Reburp⁵⁹ pulse during the REDOR period was adjusted to have a bandwidth of 48 ppm, with an offset placing the center at 28 ppm.

Pseudo-4D TREDOR H–CO spectra were recorded with 4 scans and a recycle delay of 1.5 s, with a total acquisition time of ∼1 day and 20 h for each mixing time (0.6 and 1.2 ms). For ¹H, the carrier frequency was set to 4.5 ppm, the acquisition time was 20.5 ms, and the spectral width was 41.7 ppm. For ¹³C (the combined dimension), the carrier frequency was 203.7 ppm to place the double quantum artifacts away from the signal of interest (Supporting Information Figure S2). The acquisition time is 7.2 ms for both ¹³C and ¹H, such that only ¹³C has the correct ppm scale. The spectral width was 184.4 ppm. For ¹⁵N, the carrier was 118 ppm, the acquisition time was 16.5 ms, and the spectral width was 30 ppm. ¹H to ¹⁵N CP was 1700 μs long with a ¹⁵N power of 41 kHz and a linear power ramp on proton from 85.6 to 107 Hz. ¹⁵N to ¹H CP was 600 μs long with a ¹⁵N power of 45 kHz, and a linear power ramp on proton from 110 to 88 Hz was applied. The selective Reburp⁵⁹ pulse during the REDOR period was adjusted to have a bandwidth of 100 ppm, with an offset placing the center at 203.7 ppm.

Pseudo-4D Opa60 H–CO spectrum was recorded on a BRUKER ASCEND 1.2 GHz magnet equipped with a MASDVT1200S6 BL0.7 NCH probe. The MAS frequency was set to 100 kHz and the temperature to 265 K (425 l/h cooling gas). Proton hard pulse power was set to 147 kHz, ¹³C to 114 kHz, and ¹⁵N to 78 kHz. TPPM heteronuclear⁵⁶ proton decoupling was 23 kHz, and MISSISSIPPI⁵⁷ water suppression was 25 kHz applied for 80 ms. The spectrum was recorded with 4 scans at two mixing times (0.64 and 0.96 ms), and the measurement time totaled 1 day and 7 h for each mixing time. The interscan delay was set to 0.9 s. The ¹H dimension had a carrier frequency at 4.72 ppm, an acquisition time of 21 ms, and a spectral width of 40.4 ppm. The ¹³C dimension (the combined TREDOR dimension) has a spectral width of 331.3 ppm and an acquisition time of 3 ms with a carrier frequency at 203.7 ppm. The ¹⁵N dimension’s carrier frequency was set to 120 ppm, with a spectral width of 30 ppm and an acquisition time of 6.3 ms. ¹H to ¹⁵N CP was 1400 μs long with a ¹⁵N power of 65.6 kHz and a linear power ramp on proton from 158 to 197 kHz. ¹⁵N to ¹H CP was 350 μs long with a ¹⁵N power of 65.6 kHz, and a linear power ramp on proton from 197 to 158 kHz was applied. Additionally, due to the large field drift of the newly charged magnet, we applied linear drift correction⁶⁰ to the spectra before analysis. All other parameters were the same as the H–CO TREDOR acquired for SH3.

SH3 Data Analysis and Structure Calculation

SH3 TREDOR spectra were processed with Bruker Topspin 3.5 and analyzed with CcpNmr.^61,62 Side-chain carbon and backbone carbonyl resonances were assigned using the pseudo-4D N–Cx and H–CO TREDOR at short mixing time and verified against published chemical shifts.⁴⁴ Extracted peak intensities were fit with eq 9 using MATLAB R2016b⁶³ to determine internuclear distances. The root-mean-square noise level was used to estimate the error in the fits. Since the random error always corresponded to less than 10%, and 10% deviation can occur due to geometrical considerations,³⁵ the imposed error for the calculation was always 10%. The SH3 structure was calculated using CYANA 3.98.13.⁶⁴ Specifically, 100 structures were calculated to satisfy the TREDOR distance restraints, entered as upper and lower distance boundaries, as well as TALOS-N torsion angle restraints (generated from all assigned residues which include Cα, Cβ chemical shifts).⁶⁵ Only TALOS-N “strong” predictions were included (see Supporting Information Table S3). The final restraint list can be found in the Supporting Information. After an initial structure calculation, two TALOS-N torsion angle restraints (psi of residue 38 and phi of residue 39) were observed to violate by more than 50° on average. These were removed from the restraint list. For root-mean-square deviation (rmsd) calculations, all heteroatoms of residues 11–58 were compared. Images of protein structures were prepared using UCSF Chimera 1.11.2.⁶⁶

Simulations

TREDOR simulations were performed with in-house MATLAB scripts by numerical solutions of the von Neumann equations of motion.⁶⁷ The numerical solution was obtained using a previously described method⁶⁸ where each of the Dyson-dependent propagators was divided in a series of N Dyson-independent propagators with the first-order Hamiltonian approximation.^69,70 For each of N propagators, the analytical integration of the time-dependent functions of the first-order Hamiltonian was applied, and N propagators in the matrix form were multiplied on each other, keeping the order. This converges to the exact solution for large enough N. The simulated signals represent the powder integration of the product of the trigonometric functions with power 2. 1154 angles were used in the powder integrations according to ZCW1. The Bessel function simulation was also performed with in-house MATLAB scripts according to the previously published Bessel approximation.⁷⁵

TREDOR Fitting

TREDOR curves were fit in a MATLAB script (available upon request) based on the Bessel function approximation of TREDOR described in this paper. The best fit dipolar coupling was found by minimization of the reduced χ² (eq 1).

1

The fit curves were plotted with the ggplot package in R.⁷¹ The experimental error is estimated by propagating spectral noise (taken at one standard deviation). Fitting error was generated by Monte Carlo error analysis with 100 Monte Carlo runs assuming a Gaussian noise distribution.

Results and Discussion

Pulse Program and Sequence Analysis

Shown in Figure 1 are the pulse programs for pseudo-4D TREDOR. The pulse sequence analysis for the TREDOR period will exclusively focus on the pseudo-4D (H)(N)CNH, as the pseudo-4D (H)N(H)COH experiment requires only replacing N with H.

The TREDOR pulse sequence resembles that of the 3D zf-TEDOR introduced previously^35,36 and modified later for proton detection⁷³ except for four major distinctions. First, during acquisition of the indirect (carbon) dimension, TREDOR co-acquires the untransferred (nitrogen) signal. These spectral regions can be placed in the spectrum relative to one another by appropriate placement of the offset and need not have the same sampling rate. Additional phases and appropriate processing of sum and differences could also be used to separate the two pathways.⁷⁴ We used a dwell time ratio of ∼2.48, such that both carbon and nitrogen peaks display correctly in ppm after Fourier transformation. Second, TREDOR removes the first z-filter, since it is incompatible with storing both transferred and dephased signals that lie along x and y after the first REDOR period. The second z-filter can be retained and doubles as water suppression. Third, our implementation of TREDOR begins with CP to nitrogen, since ¹⁵N–¹⁵N J couplings are negligible, and therefore, antiphase terms associated with homonuclear J-couplings do not build up during the first REDOR period. This allows the removal of the z-filter without significant spectral artifacts even at long mixing times. Fourth, rather than detecting a heteronucleus, the TREDOR sequence is implemented here with a final CP to proton for detection in order to improve sensitivity and to resolve the resonances in an additional dimension. For the case of two spins, the pulse program can be understood with a product operator analysis as follows, where we start with transverse nitrogen magnetization generated by CP from the protons

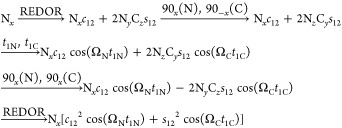2

with

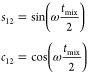All terms not converted to observable magnetization are ignored. The analysis presented here follows the real part of the signal in t₁, that is, the cosine-modulated part of the signal. Since the spin part of the Hamiltonian is identical to a J-coupling, the analysis is essentially identical to the “in-phase COSY”⁴⁸ with the only difference being the orientation dependence of the coupling frequency ω, as in REDOR and TEDOR. The first REDOR period creates antiphase carbon coherence with respect to nitrogen (N_yC_z), which is frequency labeled in t_1C with the ¹³C chemical shift after coherence transfer (N_zC_y) with two π/2 pulses. The second REDOR period then converts it back to in-phase nitrogen magnetization, which is subsequently frequency labeled in t₂ with the ¹⁵N chemical shift. The remaining untransferred nitrogen magnetization (N_x) stays the same during both REDOR periods; it is frequency labeled in both t_1N and t₂ with the ¹⁵N chemical shift and will thus appear as diagonal peaks in the t₁ and t₂ dimensions. Fortunately, there are relatively few untransferred nitrogen signals, one for each residue, while there are potentially many transferred signals that are resolved in an additional dimension. It should also be noted that during acquisition of the first indirect dimension, the carbon spins (−2N_zC_y) have a 180° phase shift with respect to the untransferred ¹⁵N shifts (N_x). They will thus appear with opposite sign in the spectrum and are easily distinguishable.

In proteins, spin systems typically contain multiple couplings, which has the potential to generate multiple quantum terms. For such cases, the product operator analysis for an NC₂ spin system with the nitrogen coupled to two carbon spins can be considered explicitly, as follows, again starting from nitrogen transverse magnetization

3

with

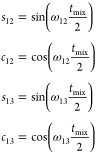All multiple quantum terms not converted to the detectable signal are ignored in the analysis; however, one multiple quantum term survives. There is a 3-spin term, 4N_xC_2yC_3y during t₁ evolution, that could appear in the first dimension with a frequency that is dependent on the chemical shifts of all spins. The term is modulated by a sine squared function of both active coupling strengths, such that it builds up more slowly. We identified such multiple quantum signals for H–C TREDOR as weak peaks placed at the sum of the three chemical shifts and at the proton shift minus the sum of the carbon offsets (see Figure S2). These produce artifacts in the spectrum, similar to those detailed previously,³⁵ but the position of the artifacts can be placed away from the peaks of interest such that they do not degrade the spectrum.

For a N₁–C_i spin pair with an active dipolar coupling of ω_1i, its cross-peak intensity V_1i(t_mix) in a TEDOR-type spectrum with mixing time t_mix is given as

4

We follow the notation previously introduced³⁵ in which V₁(0) is the intensity of the N₁ spin at 0 ms mixing time and n_i is the number of ¹³C nuclei that are simultaneously coupled to N₁ within the same spin system with a passive coupling of ω_1k. The ⟨⟩ symbols indicate a powder average. The parameter Γ₁ gives the coherence decay rate of the spin coherence, which can be modeled as a single exponential. The corresponding REDOR-type nitrogen signal, dephased by all multiple couplings inside the system, is

5

6

In the pseudo-4D TREDOR spectrum, since the intensity of the untransferred part of the magnetization is also recorded, the following ratio ζ_ij(t_mix) of REDOR and TREDOR terms approximately removes the influence of coherence decay and passive couplings

7

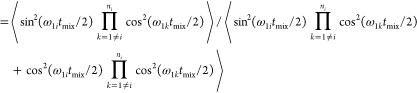8

9

10

The TREDOR parameter ζ_1i(t_mix) is free of the impact of coherence decay, if both the transferred and the total magnetization follow the same decay properties during the REDOR periods. This is found to be true for SH3 spectra, even though ¹⁵N T₂ is not the dominant source of signal loss, as discussed later. The ratio ζ_1i(t_mix) does not depend on the starting signal or need correction for experimental imperfections as both signals are acquired simultaneously. Similar to REDOR, the buildup of ζ_1i(t_mix) is sensitive to the strength of the dipolar coupling and follows an absolute amplitude scale such that dipolar coupling measurements can be performed with short mixing times before the first dipolar oscillation. A good approximation based on the expansion of Bessel functions was derived previously⁷⁵ to describe the powder averaged dipolar recoupling signal under MAS. Only the zeroth-order Bessel function expansion J₀(x) is needed to describe the observed signal buildup, and the error introduced by ignoring the relative orientations of the active and passive dipolar couplings was shown to be less than 5–10%.³⁵ The ratio ζ_1i(t_mix) can then be approximated as

11

where J₀ is the 0th-order Bessel function. This applies for any spin pair 1i in which the spin 1 is coupled to an arbitrary number of heteronuclei i. Formally, this means that the TREDOR curve will build up to a maximum value of 0.5 in a fully labeled sample. Partial labeling of the dephasing nucleus would result in a predictable down-scaling of the TREDOR curve. In a standard TEDOR fit,³⁵ to extract the dipolar couplings, one needs to additionally fit the overall coherence decay rate and an arbitrary amplitude scaling factor since the starting signal is typically not recorded. This consequently puts a high demand on the data density, that is, many mixing times recorded. In comparison to TEDOR, TREDOR reduces the number of fit parameters by two, which as shown in the later sections allows determination of the dipolar couplings, and therefore C–N distances, with a single mixing time. The two fit parameters that are removed by TREDOR are an amplitude scaling factor and a relaxation parameter, namely, V₁(0) and Γ₁ in eq 4.

Buildup of the Multiple Quantum Terms

For a multiple spin system with the spin 1 coupled to more than one I spin, the product operator analysis showed that there exists a multiple quantum term that is modulated by two couplings (eq 3). This term is eliminated in zf-TEDOR by the first z-filter but not removed in TREDOR. It could be detected by an appropriate phase cycle to select double or zero quantum coherences; however, the term builds up slower than the antiphase TEDOR terms (Figure 2) and will therefore be more difficult to detect. In TREDOR, it represents a mechanism for total signal loss, and we observe artifacts from this term in the H–CO TREDOR spectrum at the expected offsets for the component that is double quantum in carbon (see Figure S2). The artifacts are similar in appearance to those seen before for carbon-detected TEDOR.³⁵ We simulated the buildup of this term for an NC₂ spin system with similar couplings (Figure 2A) and found that it is negligible when the mixing time is smaller than 8 ms. However, when the two couplings are different, the buildup of this term can be as fast as the desired TEDOR term (Figure 2B),⁷⁶ which explains the observation of artifacts in the H–CO spectra. (The artifacts can be placed such that they do not obscure the desired peaks, see the Materials and Methods and Supporting Information.) However, for mixing times smaller than 4 ms, the contribution of this term is in all cases negligible for N–C TREDOR. Multiple quantum terms with even higher coherence orders coming from systems with more than three spins are not considered, as they will build up even more slowly than the double quantum terms. The influence of passive couplings in a multispin system is also revealed by the exact simulation (Figure 2C). For the coupling of interest, the modulation by passive couplings in the system leads to a slight damping of the buildup compared with simulation of an isolated spin pair which could bias the fitting toward a slightly larger distance (4.1 Å instead of 4 Å). This bias could be reconciled by fitting TREDOR curves in a system-wide way, taking into account the modulation by other couplings (Supporting Information). However, for us, the analysis with the single curve fit method (eq 11) produced the same results within the experimental error.

Figure 2.

Buildup of multiple quantum terms in pseudo-4D TREDOR as a function of mixing time. In (A,B), an NC₂ system was simulated by an exact numerical method, with distances of r_NC1 = 3 Å and r_NC2 = 3.5 Å and of r_NC1 = 2.5 Å and r_NC2 = 4 Å, respectively. The black line shows buildup of the transferred signal via the 2N_yC_z1 operator, the thick red line shows the buildup of the 2N_yC_z2 term, and the blue dotted line shows the buildup of the 4N_xC_z1C_z2 term. The area indicated with a yellow rectangle is expanded in the inset to show the difference in initial buildup rates. In (C), exact simulation of the TREDOR signal for a nitrogen–carbon spin pair with a distance of 4 Å in a NC₄ system (black line) and for isolated nitrogen–carbon spin pairs with distances of 4 Å (thin red dashed line), 4.1 Å (red dashed line), and 4.2 Å (thick red dashed line) is shown.

TREDOR Fitting

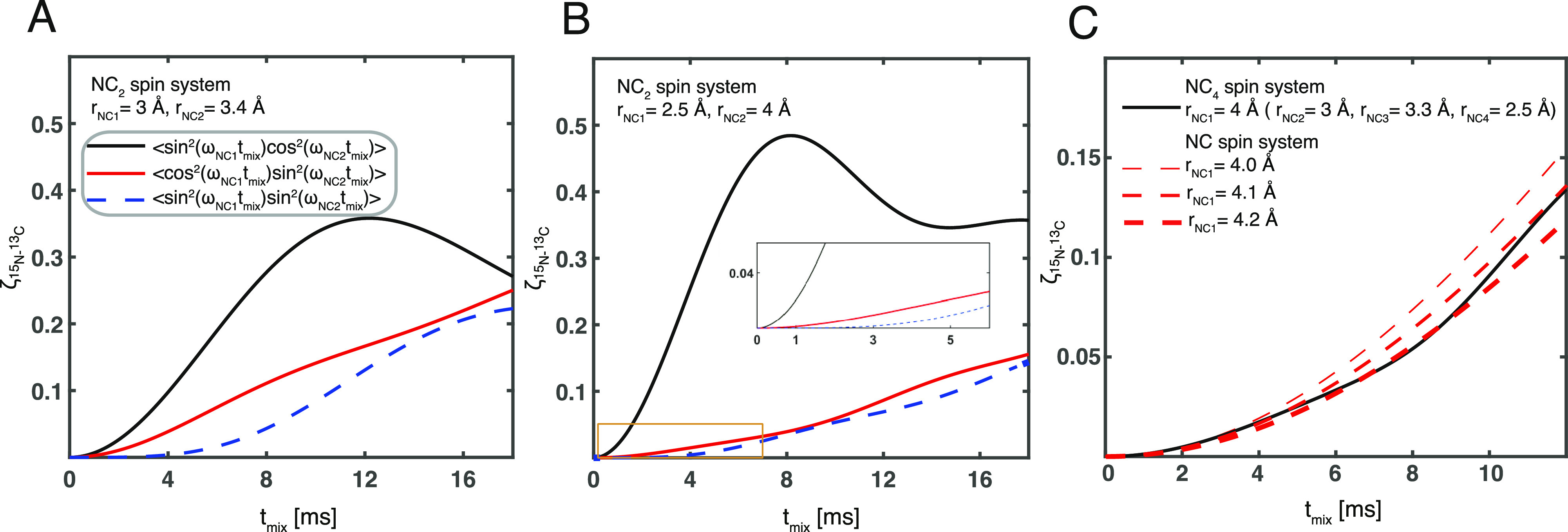
To test the performance of TREDOR in measuring accurate distance information in a protein, spectra were acquired at different mixing times for the microcrystalline protein SH3. Since pulse imperfections and rf inhomogeneity impact the apparent dipolar oscillation, we used the one bond N_H–C_α distance of Glycine 51 to calibrate the fit dipolar coupling (Figure 3). Since in our spectrum, both dimensions are undersampled, both ¹³C and ¹⁵N have approximately the same lineshape such that the use of peak amplitude was a good measure of the intensity. In other cases, it may be necessary to integrate peaks or scale amplitudes according to the linewidths. The theoretical dipolar coupling for a rigid one-bond distance of 1.45 Å⁷⁷ between ¹⁵N and ¹³C is 1005 Hz when delta pulses are assumed, compared with the coupling value of 810 or 798 Hz measured using TREDOR, giving us an overall scaling factor of 0.8. One contribution to scaling is the result of non-perfect coherence transfer caused by non-ideal pulses. These imperfections include rf inhomogeneity,^46,78 pulse miscalibration, and finite pulse effects,⁷⁹ all of which can be simulated. Under our experimental conditions, the finite pulse effect accounts for a scaling of the dipolar coupling by 0.93. The remaining scaling comes from inhomogeneity, as well as a true scaling, which is a result of fast molecular motions at ambient temperature,⁸⁰⁻⁸² compared with a low-temperature crystal. This factor can be approximated by the order parameter which is reported to be about 0.9 at the protein backbone.^25,83−85 Combining the two factors, finite pulses and order parameter, already comes close to the measured scaling factor of 0.8. This value was used to calibrate all other measured distances.

Figure 3.

Pseudo 4D N–C_α TREDOR and determination of scaling factor. The 2D carbon(nitrogen)-proton plane of pseudo 4D N–C_α TREDOR at 5.8 ms TREDOR mixing is shown in (A). Positive signals from ¹³C resonances are contoured in orange, while the negative ¹⁵N signals are shown in black. The peaks of Glycine 51 of the untransferred ¹⁵N and transferred carbon resonances are indicated with black crosses. (B) Signal modulation of dephased and transferred magnetization of Glycine 51 N–C_α, shown as 1D carbon (nitrogen) dimension traces at different mixing times. The relevant peaks are as labeled. (C) Fitting of the experimental TREDOR signal to two spin simulations ζ_N–Cα with Bessel approximation (black) and exact numerical simulation (brown). The dipolar coupling is fit to 810 Hz with the Bessel approximation and to 798 Hz with the exact numerical simulation, which corresponds to a N–C_α distance of 1.45 Å⁷⁷ in the crystal structure (inset), revealing a scaling factor of 0.8 (details in text). Asterisks indicate overlapped signals from residues K18, K59, I30, and E45, which are separated in the pseudo-4D spectrum.

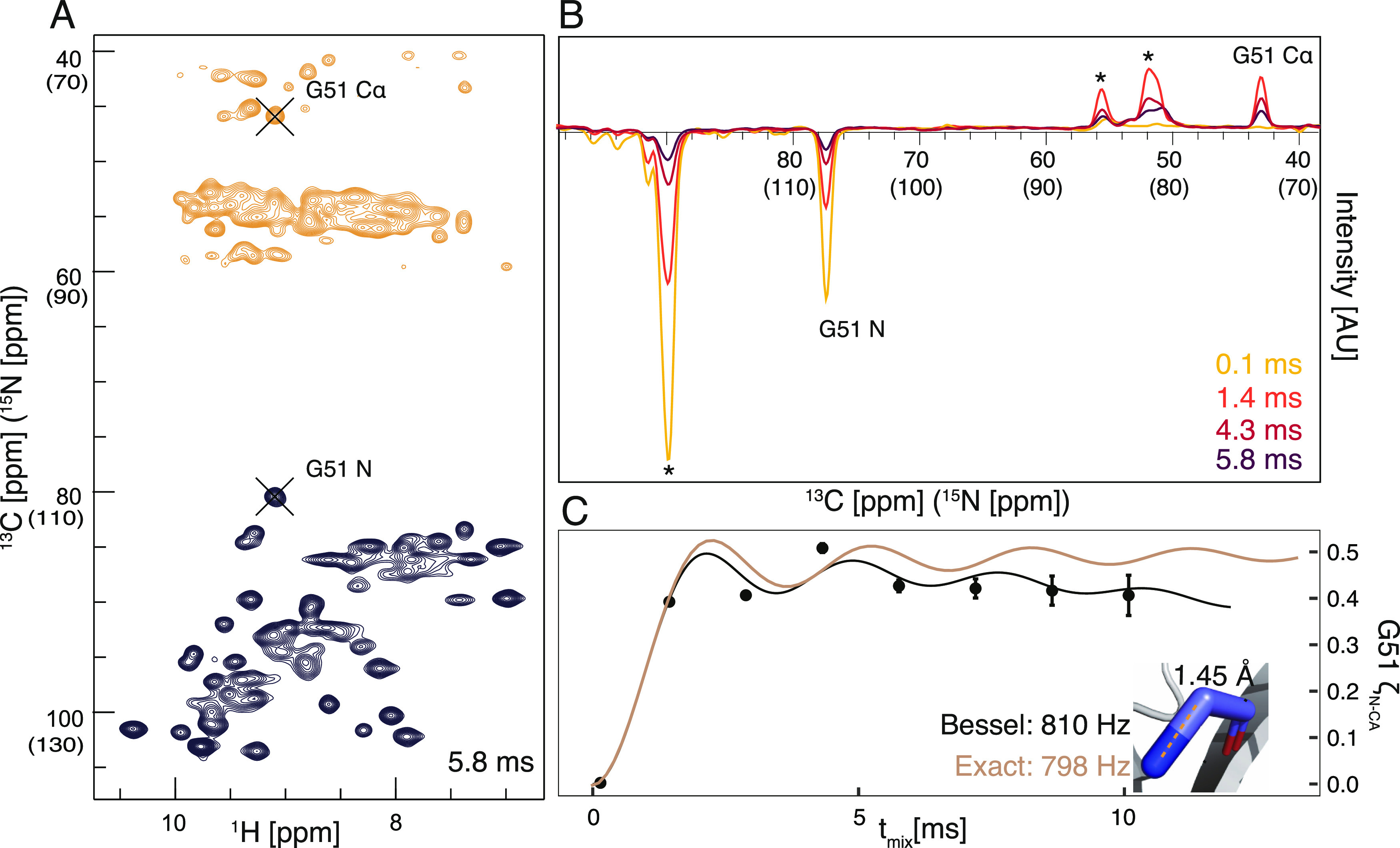
Since TREDOR extracts dipolar couplings by fitting a single parameter, in principle, only one data point is needed for fitting each curve. Figure 4 shows TREDOR distance determination for structurally important distances using 1, 2, or 3 mixing points. The full set of distances (above 3-bonds separated) are shown in Figure 4A. All two point fits correctly reported the same distance as the three point fits. However, in some cases, single points with very short (4 ms) or very long mixing time (10 ms) lead to deviation from the fitting with the full set, while the 6 ms mixing time provided faithful fitting. To some degree, this is expected, in particular for stronger couplings, due to the nonmonotonous nature of the dipolar oscillation curve; without prior knowledge of the range of reasonable coupling values, a single point might result in an unstable fit. However, such a case can be easily recognized, since it will only occur when the measured point reaches close to the maximum value of 0.5. Importantly, site-specific distance information was readily determined with short mixing times of 4 and 6 ms, which suggests that the method will be applicable to samples with a wide range of relaxation properties. In Figure 4B–E, both intra-residue (Val9N to Val9C_β and C_γ) and inter-residue (Trp42N_ϵ to Ala55C_β) distances are highlighted. Since these distances are well isolated in pseudo-4D TREDOR spectra and have known dipole couplings, we chose them to show in detail how TREDOR faithfully reproduces their N to C distance even with sparse data. The Trp42N_ϵ to Ala55C_β distance is of particular interest for three-dimensional protein structure determination and was investigated previously using REDOR in a specifically labeled sample.⁸⁶ We found the same dipolar coupling using TREDOR but in a uniformly labeled sample. The TREDOR measured value after scaling of 55.3 ± 1.4 Hz is equivalent to the previously reported 53 ± 8 Hz within the experimental error. Figure 4F shows resolved cross-peaks in the pseudo-4D H−CO TREDOR spectrum.

Figure 4.

Dipolar couplings extracted from pseudo-4D N–Cx and H–CO TREDOR with different sets of mixing times. (A) All contacts found in SH3, with dipole coupling measured by fitting subsets of one mixing time (black) and two mixing times (blue) plotted against the fit with the complete set. Site-specific TREDOR fitting for (B,D) Val9 N (C,E) Trp42N_ϵ, with distances from the crystal structure as an inset. Bessel function fits are shown with three mixing times (solid line), sets of two mixing times (dashed lines), and single mixing time (dotted lines). (F) Exemplary TREDOR H–CO strips for Trp42N_ϵ, Val9 N, and Gly51 N with a mixing time of 1.2 ms.

Coherence Decay under TREDOR and Choice of Mixing Time

As TREDOR fitting with a single point is possible (Figure 4A), it makes sense to choose the optimal mixing time that will provide the most precise fitting. Two opposing factors must be taken into consideration. First, the mixing time needs to be sufficiently long so that the signal can build up, and second, the overall intensity should not relax beyond detection. Since TREDOR measures multiple couplings simultaneously, there will not be a single optimum. Nevertheless, a single mixing point is near optimal for the range of structurally relevant couplings below about 100 Hz, as detailed below. The trade-off between the two factors can be modeled by scaling the TREDOR curve by an exponential decay as in eq 12, taking again the Bessel approximation of powder averaged dipolar recoupling. Additionally, the uncertainty in the TREDOR curve is not constant but is reduced for later mixing times due to the additional information detected in the REDOR part of the signal. Combining both factors,

12

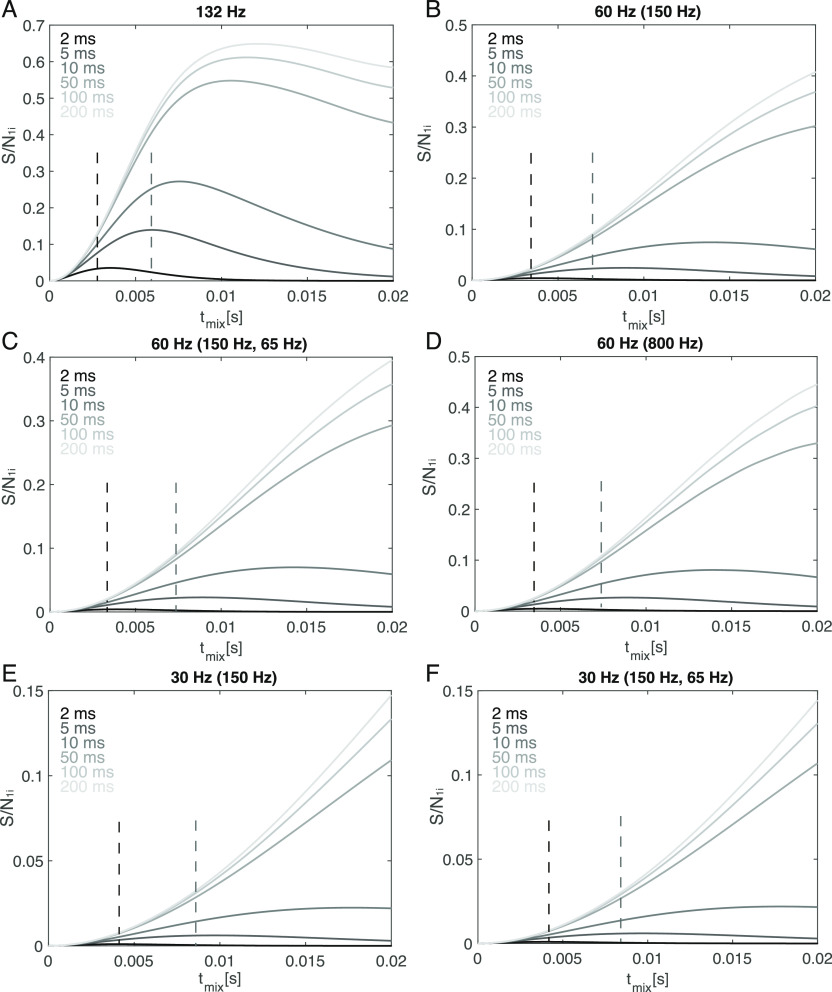
The optimal mixing time is found when S/N_1i(t_mix) is at its maximum. This represents a “transfer efficiency” that takes into consideration the signal available from both the REDOR and TEDOR components. We simulated several combinations of active and passive couplings that are representative of typical spin systems relevant for protein structure determination (Figure 5). We found that for a microcrystalline sample such as SH3, this optimal mixing time is around 8 ms for a typical N_H–C_β coupling of 132 Hz, when the coherence decay time is 10 ms (Figure 5A). For coupling strengths relevant for structure calculation, which are around 30–60 Hz for measuring torsion angles or long-range distances in proteins, the optimal mixing time is below 8 ms when the transverse decay time is smaller than 10 ms. However, in practice, it is advisable to use mixing times slightly smaller than that. This is not only to observe spins with short site-specific transverse coherence lifetime but also to more accurately fit those that have a larger N_H–C_β coupling. This explains our observation that a mixing time of 6 ms leads to the most stable fitting. The effect of other passive couplings in the system is seen by comparing the buildup of similar couplings with varying number and strength of passive couplings. When a relatively weak dipolar coupling (30 or 60 Hz) is modulated by two passive couplings (150, 65 Hz), the absolute intensity is only slightly smaller than when there is only one passive coupling (150 Hz). In the extreme case, when a weak coupling (60 Hz) is modulated by a very large passive coupling (800 Hz) (Figure 5D), the overall profile of the buildup is similar to a smaller passive coupling (Figure 5D) but with slightly reduced intensity. This shows that the optimal mixing time is mostly determined by the coherence decay rate and the active coupling.

Figure 5.

Bessel approximation of the TREDOR “transfer efficiency” shown as signal-to-noise S/N_1i in spin systems with different combinations of active and passive dipolar coupling. Typical active C–N dipole coupling strengths for proteins are indicated, with passive coupling(s) in brackets. Different site-specific coherence decay rates are also included; the system with one spin (A), two (B,D,E), and three (C,F) coupled spins all have an optimal mixing time between 4 and 16 ms when T₂ is smaller than 10 ms. The maximum TREDOR signal-to-noise when the decay time is short (<10 ms) is around 5% of the starting signal for a 60 Hz coupling and around 2% for 30 Hz coupling. Optimal mixing times when the decay time is 5 ms (gray dashed lines) and 2 ms (black dashed lines) are indicated.

Equation 7 assumes that the decay of both the REDOR and TEDOR parts of the magnetization is dominated by a single exponential decay, which would follow if it is dominated by ¹⁵N T₂. This can be checked experimentally by comparing the decay of total signal in TREDOR for each residue in SH3. Indeed, one single exponential decay rate results in a good fit to the total signal decay (Figure 6). Surprisingly though, the coherence decay under TREDOR is much faster than the ¹⁵N T₂ measured site-specifically via the dephased signals in the (H)NH spectrum. This potentially originates from relaxation of the multiple quantum terms generated during the REDOR periods from non-ideal pulses. One potential origin is the rf inhomogeneity of the hard pulses during REDOR which will cause incomplete inversion of antiphase terms 2N_yC_z. In that case, the additional undesired operators—2N_yC_x and 2N_yC_y are created. The effects are minimized with xy phase cycling⁵⁵ but not removed. The quantitative description of the influence of the rf inhomogeneity on the TREDOR signal is complicated with the additional influences of the carbon offset, the external field inhomogeneity, the carbon chemical shift anisotropy interaction, the carbon spin–spin relaxation, and non-ideal long selective pulses. All these effects can be approximately replaced with the influence of the apparent spin–spin coherence decay, that is, the measured decay of the combined REDOR and TEDOR parts of the signal. The REDOR pulses on the carbon channel could also result in decoherence through a T2ρ process. We measured the bulk T2ρ of Cα and C′ with various spin lock offsets and power (Supporting Information Tables S4 and S5). However, T2ρ values of interest are significantly longer than the apparent relaxation rate in TREDOR, eliminating T2ρ as the major contributor to signal losses. The dramatic increase in decay rates further justifies the need for a dipolar recoupling measurement that only requires a short mixing time. Figure 6 indicates coherence decay times of about 5–10 ms. Note that several residues deviate from the average, but this is likely the result of fitting only 3 time points. A typical TREDOR decay time of 5–10 ms indicates an ideal TREDOR mixing time of around 6 ms (Figure 5), and the stable fits for 4 and 6 ms suggest that TREDOR will also be useful in the case of faster decay.

Figure 6.

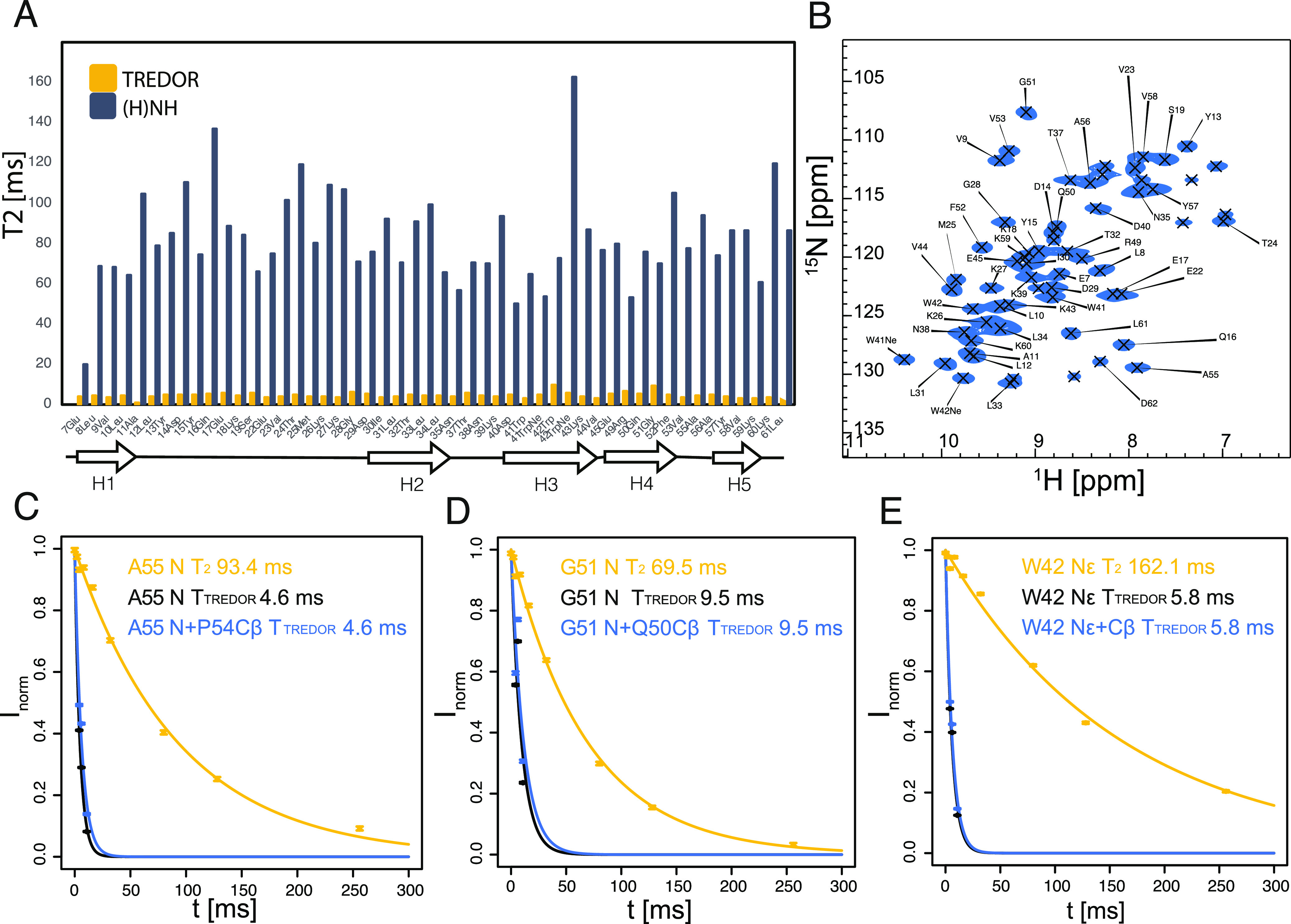
Site-specific ¹⁵N T₂ rate during TREDOR [(A) yellow] and (H)NH [(A) dark blue] and (H)NH spectrum at 0 ms delay (B). The topology of SH3 is plotted under (A); there is no obvious correlation of the size of the ¹⁵N T₂ with the secondary structure of the residue. The coherence decay rate under TREDOR is significantly higher than that under (H)NH (Supporting Information Table S1); but for all residues, a single exponential decay well predicts the total signal decay [examples of decay of residues A55, G51, and W42 are shown in (C–E)].

Structure Calculation

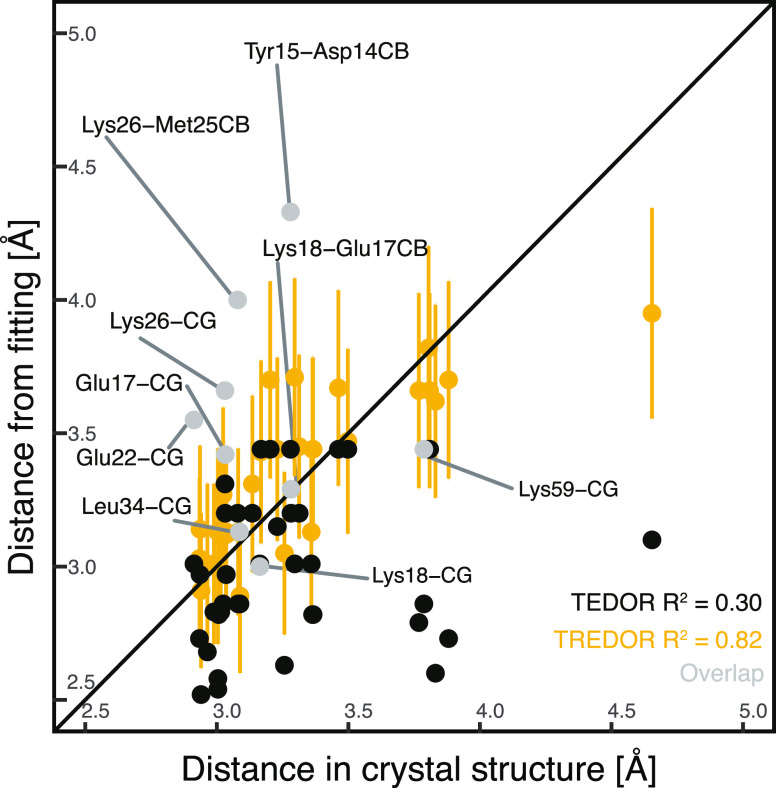
We recorded site-specific TREDOR data on a microcrystalline SH3 sample and performed a structure calculation. The structure of SH3 has previously been calculated⁸⁷ using ¹³C-detected solid-state NMR based largely on restraints derived from a set of PDSD spectra with a range of mixing times. The distances determined from pseudo-4D TREDOR (full fitting information available in Supporting Information Figure S1) are in good agreement with a previously published crystal structure of the SH3 domain (PDB-code 2NUZ). Discrepancies are mostly due to spectral overlap or ambiguous assignments. The fit dipolar couplings were multiplied with the previously determined scaling factor of 1.25 and converted to distances. Unambiguous pseudo-4D N–Cx TREDOR restraints relevant for torsion angle determination can be compared with distances in the crystal structure (Figure 7). Compared with TEDOR data alone, TREDOR determines the χ1 and ψ angle more accurately as indicated by comparison of the corresponding distances with the crystal structure (correlation coefficient of 0.82 for TREDOR compared with 0.30 for TEDOR using 3 data points). For the comparison, only isolated peaks were considered. Where peak overlap occurs, the TREDOR distance tends to be too large, since the overlap mainly increases the intensity of the REDOR signal. Avoiding this problem would require a more sophisticated peak deconvolution or extension to higher dimensional spectra. This is also seen from the fit curves: most cases where fit curves deviate from the experimental data significantly are due to spectral overlap (Supporting Information Figure S1). However, TREDOR still performed better in predicting the precise distance when overlapped peaks in the 2D (H)NH spectra (Figure 6B) are included for the analysis (correlation coefficient of 0.57 for TREDOR compared with 0.21 for TEDOR). All distances extracted from the pseudo-4D N–C TREDOR and the pseudo-4D H–CO TREDOR were subsequently used as restraints for a CYANA⁶⁴ structure calculation (see Materials and Methods). The pseudo-4D H–CO TREDOR spectra provide orthogonal contacts to define the beta-fold of SH3 better and are particularly suitable for determination of inter-strand contacts in anti-parallel beta sheet structures.

Figure 7.

Comparison of NMR-derived distances that define χ1 and ψ torsion angles for residues with a single conformer in the crystal structure. Distances are compared with those of the crystal structure 2NUZ either fitting with pseudo-4D TREDOR data (yellow and gray) or only the N–C TEDOR component (black). Long-range contacts or ambiguous torsion angle restraints are not included in the analysis to exclude potential assignment errors. Contacts with overlapped nitrogen signals are shown in gray and were not included in the determination of R². Pseudo-4D TREDOR predicts distances (R² 0.82) more accurately than TEDOR (R² 0.30) with data from 3 mixing times. Yellow error bars are indicated at ±10% to indicate the expected error from ignoring relative orientations.³⁵

As input, we used 5 (N–Cx) + 12 (H–CO) medium (contacts 2–4 residues apart) and 18 (N–Cx) + 16 (H–CO) long-range restraints (contacts greater than 4 residues apart) from the N–Cx and H–CO spectra (details in the Supporting Information Figure S1). In addition, we input 83 (N–Cx) + 26 (H–CO) intra-residue or sequential restraints that help define torsion angles. These include not only the ψ angle that is already defined by the chemical shifts for most residues but also the χ1 angle that is not. The 10% distance error estimates used here results in large errors in angles, and further improvement would be needed for true angle determination. Nevertheless, the information excludes part of the Ramachandran space, which is helpful particularly for glycine residues where TALOS does not always provide confident predictions. Considering that the short mixing time TREDOR was used primarily for assignments, four days of experiments are enough to determine the distances used in the structure calculation. Additionally, we enforced backbone torsion angles predicted by TALOS-N.⁶⁵ The resulting structured ensemble (20 lowest energy structures, residues 11–58) is shown in Figure 8, alongside an overlay of the average structure with the reference crystal structure (PDB-code 2NUZ). Distance information from the TREDOR method faithfully reproduced the overall fold of the SH3 domain with a backbone ensemble rmsd of 1.8 Å in the structured part (residues 11–58). This covers nearly the range of assigned residues (7–62), which coincides with the range of residues determined by X-ray diffraction. The TREDOR calculated structure differs from the crystal structure by 2.1 Å (again comparing residues 11–58) mainly on the ends of the sequence due to lack of contacts and the very dynamic loop region. Additionally, we measured N–CA, N–CO, and H–CA distances with TREDOR. However, we found very few structurally interesting long-range distances, which is likely due to the presence of very strong 1-bond dipole couplings for the N–CA and N–CO cases and to somewhat longer distances for the H–CA case as compared with H–CO distances. Mostly, we observed intra-residue or sequential contacts. We therefore used only the N–Cx and H–CO data during structure calculation. Figure 8C shows the per-residue rmsd as compared to the crystal structure. In the loop regions, TREDOR side-chain to side-chain contacts (see Supporting Information Table S2, last 7 contacts, for details) improve the rmsd and thus aid in accurately determining the structure. Since the N–Cx TREDOR data contains a multitude of backbone to side-chain contacts, it is surprisingly valuable in defining the structure of the RT-loop, which is particularly challenging using backbone data alone.^20,22 This is obvious, as in the loop region, the all atom rmsd is improved by 2–4 Å (Figure 8C).

Figure 8.

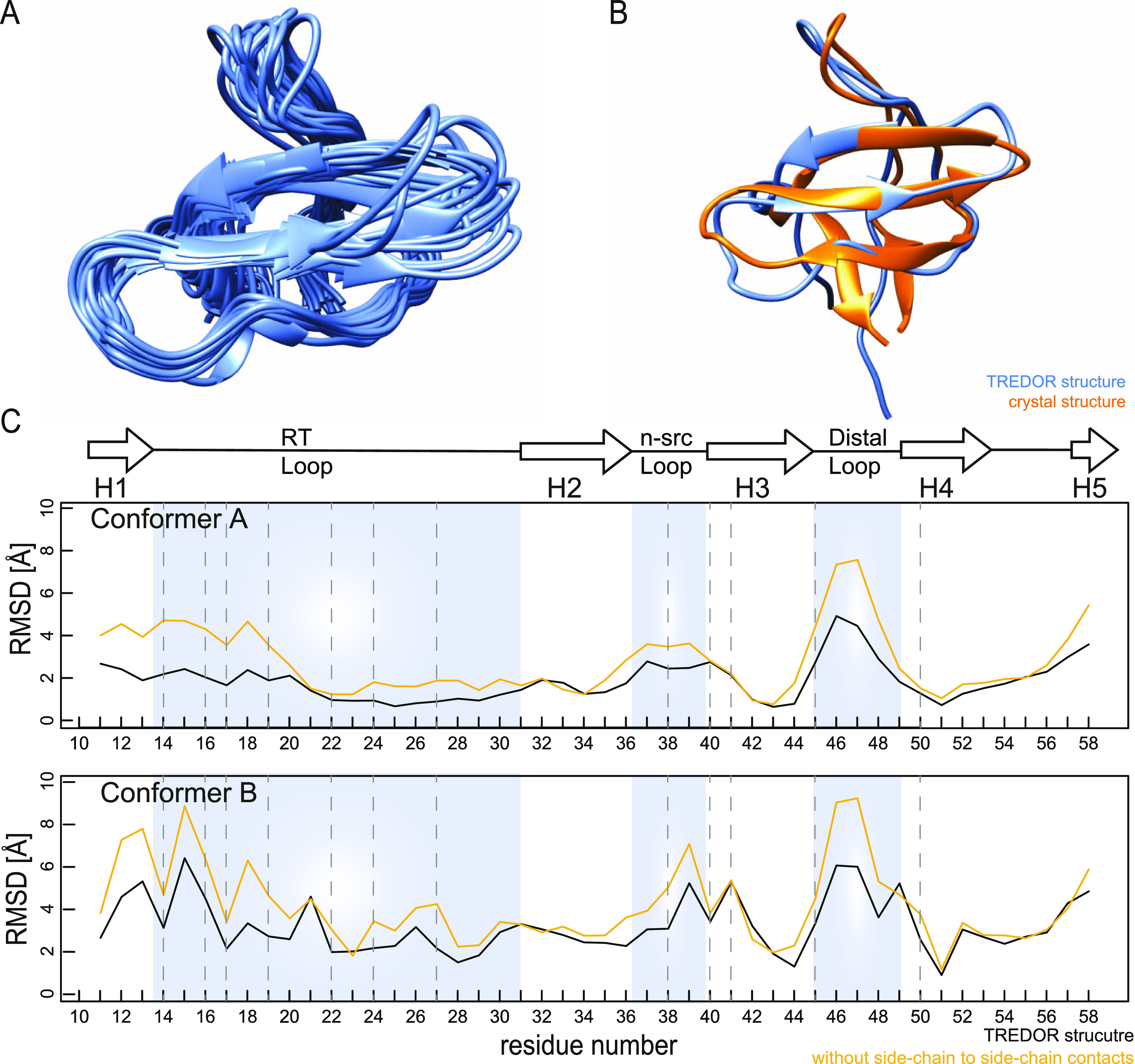
Structure of SH3 obtained from TREDOR distances and TALOS-N backbone dihedral angle restraints. (A) 20 lowest energy structures of 100 calculated structures from a CYANA calculation. The structurally defined region from residues 11–58 is shown. The backbone ensemble rmsd of 20 structures is 1.8 Å for these residues. (B) Comparison of the lowest-energy TREDOR structure with the reference crystal structure (PDB-code 2NUZ, orange), revealing the correct overall fold of SH3. The rmsd of the TREDOR-calculated structure vs the crystal structure A (upper panel) is 2.1 Å. (C) TREDOR-derived restraints faithfully reproduced the crystal SH3 structure, as shown by the low residue specific all-atom rmsd values across the sequence to both conformations in the crystal structure (conformers A and B). Including side-chain to side-chain contacts (black line), which are a unique feature of TREDOR, increases the accuracy in the loop region (blue shading) compared with the structure calculated without (yellow line). Dashed lines indicate residues with side-chain proton to side-chain carbon contacts.

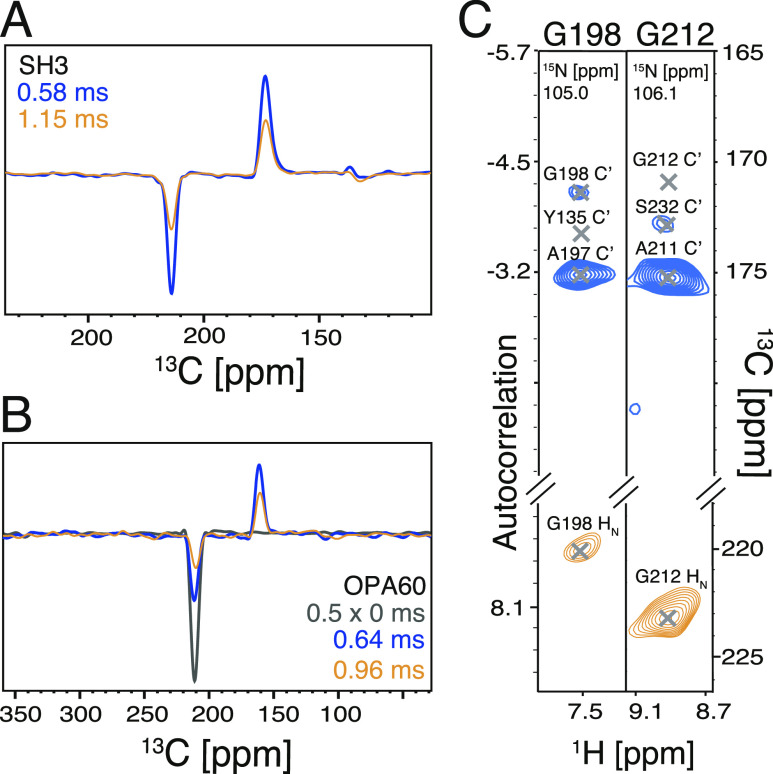
To showcase the application of TREDOR for a more challenging regime of membrane proteins, which typically exhibit faster coherence decay, a pseudo-4D H−CO TREDOR spectrum was measured for the 28 kDa membrane protein Opa60 at 100 kHz MAS frequency with a 1.2 GHz magnet. Even with the shorter ¹H T2′ of 2.5 ms and the higher power demand at ultrafast MAS, the total signal of Opa60 decayed only slightly faster than that of SH3 (Figure 9A,B), with time constants of 0.75 and 0.85 ms for Opa60 and SH3, respectively. A brief analysis of the spectrum revealed a structurally interesting long-range contact in Opa60 (Figure 9C) between G212 and S232.

Figure 9.

Pseudo-4D H−CO TREDOR shows long-range contacts in the membrane protein Opa60 without significant loss in sensitivity compared with that of SH3. At 1 ms mixing time [yellow lines in (A,B)], both the REDOR (negative peaks) and TEDOR (positive peaks) parts of the magnetization decay similarly for SH3 (A) and Opa60 (B). Though the contact between Gly198 and Tyr135 is missing [(C), left panel], a long-range contact can be identified between Gly212 and Ser232 [(C), right panel].

In conclusion, we demonstrate TREDOR as a fast and robust method to precisely measure site-specific internuclear distances using MAS NMR. We show that the 2-fold increased information in TREDOR leads to accurate distance determination by stabilizing the dipolar oscillation fitting even for the extreme limit of a single point fit. This allows acquisition at the optimal mixing time where signal-to-noise is maximized, which together with the simultaneous acquisition inherent to the TREDOR method leads to an order of magnitude improvement. We demonstrate TREDOR in two variants, pseudo-4D N–Cx and H–CO. The data results in efficient protein structure determination. We expect that adaptations of TREDOR, including extension to other spin 1/2 nuclei, will be useful for a variety of applications in materials science, chemistry, and biology. While we demonstrate TREDOR with deuterated protein and fast spinning of 55 kHz, or with fully protonated protein and 100 kHz spinning, the relatively low rf requirement of REDOR will allow extension to even faster spinning, so long as the hardware allows the Rabi frequency of the REDOR pulses to exceed the MAS frequency.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c09033.

• Detailed distance fitting, residue specific coherence decay times, restraints used in the structure calculation, multiple curve TREDOR fitting, multiple quantum term artifacts, and ¹³C T_2ρ values (PDF)

Author Contributions

^† X.C.Z. and M.C.F. contributed equally.

The authors declare no competing financial interest.