Combined Computational and Experimental Investigation on the Nature of Hydrated Iodoplumbate Complexes: Insights into the Dual Role of Water in Perovskite Precursor Solutions

Abstract

Water is generally considered an enemy of metal halide perovskites, being responsible for their rapid degradation and, consequently, undermining the long-term stability of perovskite-based solar cells. However, beneficial effects of liquid water have been surprisingly observed, and synthetic routes including water treatments have shown to improve the quality of perovskite films. This suggests that the interactions of water with perovskites and their precursors are far from being completely understood, as water appears to play a puzzling dual role in perovskite precursor solutions. In this context, studying the basic interactions between perovskite precursors in the aqueous environment can provide a deeper comprehension of this conundrum. In this context, it is fundamental to understand how water impacts the chemistry of iodoplumbate perovskite precursor species, PbI_x^2–x. Here, we investigate the chemistry of these complexes using a combined experimental and theoretical strategy to unveil their peculiar structural and optical properties and eventually to assign the species present in the solution. Our study indicates that iodide-rich iodoplumbates, which are generally key to the formation of lead halide perovskites, are not easily formed in aqueous solutions because of the competition between iodide and solvent molecules in coordinating Pb²⁺ ions, explaining the difficulty of depositing lead iodide perovskites from aqueous solutions. We postulate that the beneficial effect of water when used as an additive is then motivated by its behavior being similar to high coordinative polar aprotic solvents usually employed as additives in one-step perovskite depositions.

1. Introduction

Lead halide perovskites have been subjected to great research from the global scientific community in the last decades in virtue of their outstanding optoelectronic properties.^1,2 These allowed their employment as innovative materials for photovoltaics, leading to amazing efficiencies up to 25% reported in state-of-the-art devices.^3,4 On the other hand, the stability of these materials can be strongly affected by factors such as UV light, temperature, water, and ambient humidity.⁵ In particular, the origin of water-induced instability has been investigated from different points of view, ranging from the dissolution mechanism of methylammonium lead iodide (CH₃NH₃PbI₃)⁶⁻⁸ to formation of defects⁹ and the interaction of water with perovskite surfaces.¹⁰ The detrimental action of water on perovskites can be summarized by the degradation pathway reported in eq 1

1

leading to the intermediated (CH₃NH₃)₄PbI₆ hydrated phase and PbI₂. Nevertheless, the role of water is not limited to this: interestingly enough, the beneficial effects of water have been recently reported.^11,12 In particular, it has been proved that if the degradation pathway of eq 1 is blocked at the first stage, that is, the reversible formation of the monohydrate phase, the crystallization process of the perovskite film is enhanced with increased grain size and nonradiative recombination centers are deactivated.^12,13 Moreover, controlled concentrations of water have been proven to passivate defects.¹³⁻¹⁵ Therefore, the nature of the water–perovskite interaction appears to also depend on the actual amount of water in contact with the material, thus potentially being a game-changing factor in perovskite synthesis. In this regard, however, the wide literature of studies on this subject is far from reaching a unanimous consensus.¹⁶⁻²⁹ Conings et al. reported that the presence of a fraction of water up to 10% volume in the precursor solution does not affect the photovoltaic performance of the prepared perovskite thin film.¹⁶ In contrast, Clegg and Hill observed that low concentration of water can be simultaneously detrimental for the photovoltaic performances but beneficial for the long-term stability of the device.¹⁷ In contrast to these studies, controlled amounts of water and humidity have improved the performances of perovskite solar cells: small amounts of H₂O as an additive in the perovskite precursor solution improves film crystallization and, consequently, photovoltaic performances.¹⁸⁻²² Similar effects are encountered considering ambient moisture²³⁻²⁸ directly interacting in the precursor solution, during the annealing stage or in post-treatment processes. Zhang et al. recently reported a prenucleation method for the fabrication of perovskite solar cells in ambient conditions, in which water promotes the formation of lead complexes.²⁹ In this context, it is evident that the dual nature of water when involved in the interaction with perovskites is a consequence of its rich chemistry, which brings to bear a plethora of possible reaction pathways.

As metal halide perovskites can be easily synthesized in solution, for example, through spin-coating and blade-coating,³⁰⁻³² the solvent has a crucial role in determining the final perovskite quality. This directly affects the type and amount of precursors in solution, usually in the form of iodoplumbate species, that is, Pb²⁺ and I^– complexes such as PbI⁺, PbI₂, PbI₃^–, PbI₄^2–, PbI₅^3–, and PbI₆^4–, which are forerunner species to the perovskite formation.³³⁻³⁸ Solvent and processing conditions are in turn linked to the presence of defects incorporated in the perovskite film,^{33,34,38−41} with possible serious consequences on both material stability and overall optoelectronic quality. Highly coordinating solvents generally employed in synthetic routes, such as dimethyl sulfoxide (DMSO) and N,N-dimethylformamide (DMF), are toxic and harmful for the environment, raising an issue for safe and sustainable development of perovskite manufacturing.^42,43 In this sense, water would be an environmentally friendly solution to this problem, but because of the abovementioned stability problems and the general low solubility of precursor lead salts (e.g., PbI₂) in this solvent, it has only rarely been employed for perovskite synthesis as a precursor. For example, the use of Pb(NO₃)₂ as a precursor has been attempted owing to its enhanced water solubility:⁴⁴⁻⁴⁶ Hsieh et al. reported on the formation of CH₃NH₃PbI₃ starting from Pb(NO₃)₂ in aqueous solution. Through this synthesis method, they were able to achieve materials with cell performances close to those obtained with a standard PbI₂/DMF solution.⁴⁴ Following this work, Sveinbjörnsson et al. produced perovskites with Pb(NO₃)₂ and CsNO₃ obtaining good results,⁴⁵ while Zhai et al. employed Pb(NO₃)₂ to manufacture perovskite solar cells on plastic.⁴⁶ Mixed halide perovskite nanocrystals were also successfully prepared by Geng et al. through synthesis in an aqueous environment in acidic conditions.⁴⁷ Therefore, it has been proven that it is not impossible to synthesize a perovskite using water as the principal solvent, but the numerous reports on its detrimental effect and the low solubility of some of the common precursors generally employed certainly suggest that it is not a straightforward process.

To gain insights into this peculiar chemistry and to understand how water can impact the synthesis of perovskite through interaction with precursors, we here investigate the nature of iodoplumbates in aqueous solutions. We aim, in particular, to obtain information on how water influences the stability and optical properties of these complexes and on the possible differences with other more common solvent environments such as DMSO, DMF, γ-butyrolactone (GBL), and acetonitrile (ACN). Formation of complex iodoplumbate species, such as PbI₃^– and PbI₄^2–, has already been tracked in a typical synthetic solution environment by many studies, mainly by means of UV–vis spectroscopy,^{11,33,35,40,41,48} highlighting how these species are preferentially produced in a low coordinating solvent environment, that is, following the general trend ACN > GBL > DMF > DMSO well described by the increasing Gutmann’s donor number with the corresponding values of 14.1, 18.0, 26.6, and 29.8 kcal/mol, respectively.^34,49 In this sense, being transparent to UV and visible radiations because of its large optical energy gap,⁵⁰⁻⁵³ water is an ideal solvent to explore the spectroscopic properties of iodoplumbates in a spectral range larger than those accessible with the solvents commonly employed for the synthesis of perovskites. Here, we investigate the nature of iodoplumbate precursors in aqueous solution by studying the PbI₂ + CH₃NH₃I (MAI) solutions by means of UV–vis spectroscopy, ab initio molecular dynamics (MD) simulations, and time-dependent density functional theory (TDDFT) excited-state calculations including relativistic effects. By supporting experiments with high-level quantum mechanical simulations, we achieve a deeper comprehension of the chemistry of iodoplumbates in aqueous solutions in terms of structure, coordination number, and equilibria. We find that formation of iodoplumbates containing a high number of coordinated iodide ions is hindered in aqueous environments and it only takes place when a very high quantity of MAI is added in the solution. This is interesting if we only consider the low donor number of water (18.0 kcal/mol),⁴⁹ for which a favorable formation of iodoplumbates would be expected, confirming the uncertainties that affect this quantity when it comes to protic solvents and suggesting, at the same time, that other factors such as the high polarity of water molecules and the strong solvation of I^– are acting on these complex equilibria.

2. Computational Details

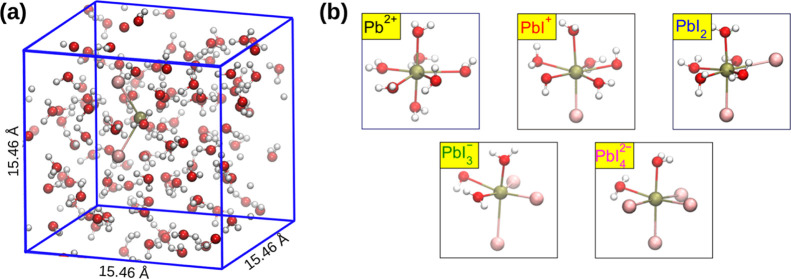
To simulate Pb²⁺ and the iodoplumbates in aqueous solutions, we first consider a structural configuration of a previously performed MD simulation of liquid water.⁵⁴ In particular, we consider a periodic cubic cell of length 15.46 Å, containing 128 H₂O molecules, Figure 1a, corresponding to the experimental density. Then, we replace a water molecule with a Pb²⁺ ion and we carry out a DFT-based Born-Oppenheimer MD simulation in the NVT ensemble. A time step of 0.48 fs is employed. A production run of ∼15 ps follows an equilibration run of 5 ps. The target temperature of the simulations, controlled with a Nosé–Hoover thermostat,^55,56 is set at 350 K, in order to achieve liquid-like behavior and to approximately take into account nuclear quantum motion.^57,58 A similar computational strategy is adopted to study aqueous I^–. The simulation of aqueous iodoplumbates (PbI⁺, PbI₂, PbI₃^–, and PbI₄^2–) is carried out by replacing a water molecule within the first coordination shell of aqueous Pb²⁺ with a I^– ion for each I^– of the considered species. The same computational setup used to simulate aqueous Pb²⁺ is then employed. DFT-based MD simulations are carried out with the rVV10 functional,^59,60 which accounts for van der Waals interactions. In particular, the analytic expression of the rVV10 functional depends on an empirical parameter b, which governs the short-range interactions.⁵⁹ We adopt the value of b = 9.3, as this has been shown to reproduce the experimental mass density in the case of liquid water.⁶¹ The freely available CP2K/QUICKSTEP package is used to perform the MD simulations.⁶² This suite of programs features a combined atomic basis set/plane-wave approach: atom-centered Gaussian-type basis functions are used to describe the orbitals and an auxiliary plane-wave basis set is employed to re-expand the electron density. For all the calculations, we use a triple-ζ correlation-consistent polarized basis set (cc-pVTZ) for O and H atoms⁶³ and double-ζ polarized basis sets for the wave functions for Pb and I. A cutoff of 600 Ry is used for the plane waves.⁶⁴ Core electrons are described by the analytical Goedecker–Teter–Hutter pseudopotentials.⁶⁵ The following convergence criteria for the wave function optimization are employed: 10^–7 a.u. for the electronic gradient and 10^–12 a.u. for the energy difference between the final self-consistent field (SCF) cycles. This computational setup has been found to provide structural and dynamical properties of liquid water and aqueous solutes in good agreement with the experiment.^54,66

Figure 1.

(a) Model of PbI₂ in aqueous solution employed for the MD calculations. (b) Optimized structures of the complexes formed in aqueous solution by Pb²⁺, PbI⁺, PbI₂, PbI₃^–, and PbI₄^2–. O atoms in red, H in white, Pb in brown, and I in pink.

DFT calculations for the optimization of selected iodoplumbate structures are run with the Gaussian 09 software package,⁶⁷ employing the B3LYP exchange–correlation functional,^68,69 Grimme’s dispersion interactions DFT-D3,⁷⁰ CPM polarizable continuum model for implicit solvation effects, and LANL2DZ basis sets for heavy Pb and I atoms together with the LANL2 pseudopotentials for the core electrons, while for light atoms (C, H, N, O, and S), the 6-31G* basis sets are chosen. Relative energy differences for optimized solvated lead complexes are evaluated following eq 2

2

where E_tot is the total energy of the iodoplumbate with n explicit coordinating solvent molecules and E_solute and E_solv are the total energies of the bare Pb²⁺/iodoplumbate and the solvent molecule, respectively.

TDDFT calculations are carried out with the ADF 2014.04 program package.⁷¹⁻⁷³ We employ the B3LYP exchange–correlation functional,^68,69 a ZORA Hamiltonian to include relativistic spin–orbit coupling (SOC) effects^74,75 and the COSMO implicit solvation model.⁷⁶ A Slater-type TZP basis is used for all the atoms (the cores 1s-2s, 1s-4p, and 1s-4d are kept frozen, respectively, for S, I, and Pb). The absorption spectra are simulated by interpolating the computed transitions by Gaussian functions with a broadening σ = 0.1. To obtain the thermally averaged UV–vis optical absorption spectra of the various investigated species, ∼30 snapshots equally spaced in time from the last 5 ps of each MD simulation of aqueous iodoplumbates were subjected to TDDFT calculations retaining the closest 1–8 water molecules (i.e., the first coordination sphere for each complex) and adding a polarizable continuum solvation model.

Equilibrium chemical composition of solutions are simulated with Spana/Database (version 2020-06-19), a freely available software⁷⁷ based on the HALTAFALL algorithm^78,79 and partially inspired by SOLGASWATER.⁸⁰

For the theory on calculation of equilibrium dissociation constants of iodoplumbates in aqueous solutions through the thermodynamic integration method, the reader is referred to Section S1, Supporting Information.

3. Experimental Details

PbI₂ solutions with concentrations ranging from 2.00 × 10^–3 to 6.04 × 10^–1 mM in H₂O are prepared from a 1.00 mM PbI₂ stock solution. A volume of MAI corresponding to a concentration range between 2.00 and 3.76 × 10² mM is added to a 3.00 × 10^–2 mM PbI₂ solution prepared from the same 1.00 mM stock solution. UV–vis absorption spectra are recorded with a double-beam spectrophotometer Perkin-Elmer Lambda 800 employing quartz cuvettes with two optical walls and an optical path of 0.5 cm.

4. Results and Discussion

To unveil the structural properties of hydrated iodoplumbates, we first carried out MD simulations of the Pb²⁺, PbI⁺, PbI₂, PbI₃^–, and PbI₄^2– complexes in an aqueous environment, employing models such as the one reported for PbI₂ in Figure 1a. One of the advantages of using MD simulations for water systems over cluster models is that because of the protic nature of water, employing larger solvation shells is a way to take into account the formation of hydrogen bonds between water molecules, thus making it easier to unveil the structure of coordination complexes. Because iodoplumbates with higher iodide content, such as PbI₅^3– and PbI₆^4–, are difficult to find in the diluted solutions generally employed for the investigation of the spectral properties of these systems,^{33,34,40,41,48} we did not consider these complexes in our analysis.

Pb²⁺ in aqueous solution is found to occur, on average, as an heptacoordinated complex, Pb(H₂O)₇²⁺, with the oxygen water atoms pointing toward the metal cation. The complex features a pentagonal-bipyramidal structure, Figure 1b, and is dynamically holodirected with water molecules surrounding the cation from all the directions in line with a previous first-principles simulation.⁸¹ The average Pb–O distance of 2.56 Å is consistent with those inferred from X-ray measurements (2.53⁸² and 2.50 Å⁸³). Consistently, integration of the first peak of the Pb–O radial distribution function (RDF), Figure 2a, provides a Pb–O coordination number n_O = 6.91. Further analysis of the distribution reveals not only a majority sevenfold coordination (69% of configurations) but also sixfold coordination (21%) and eightfold coordination (10%) were found in line with the larger coordination numbers usually observed when accounting for van der Waals interactions in the simulations.^54,61

Figure 2.

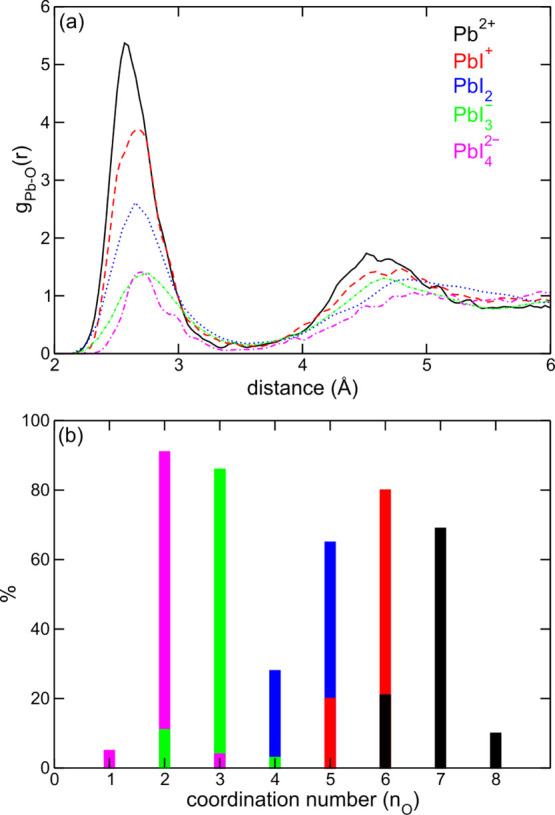
(a) Pb–O RDF for aqueous Pb²⁺ (black), PbI⁺ (red), PbI₂ (blue), PbI₃^– (green), and PbI₄^2– (magenta). (b) Average number of water molecules (%) coordinating Pb²⁺ in the considered aqueous species. The same color code used for panel a) is adopted.

Noteworthy, previous ¹H NMR⁸⁴ and X-ray⁸² studies report an average sixfold coordination for aqueous Pb²⁺. However, we note that experimental techniques could be unable to probe loosely coordinated water molecules⁸¹ that, instead, we inherently take into account within our approach. For example, the protons belonging to such remote water molecules are likely to not be subject to the influence of the metal cation, thus being not probed by ¹H NMR. In this regard, we note that the NMR estimate was questioned because it was found to underestimate the coordination of other metal cations.⁸⁴ Furthermore, Persson et al.⁸² predicted the coordination number of aqueous Pb²⁺ by coupling the experiment with inferred average Pb–O bond lengths (2.5–2.6 Å, in line with this work). Again, such an estimate may not account for all water molecules within the first shell. In fact, n_O = 6.00 in our simulation corresponds to integration of the first peak of the RDF up to a distance of 2.9 Å, a value ∼0.4 Å shorter than that corresponding to the first minimum of the RDF.

The sevenfold coordination and the pentagonal-bipyramidal structure are retained for PbI⁺ and PbI₂ in aqueous solution with iodide ions replacing water molecules in the first coordination shell, Figure 1b, as evidenced by calculated n_O = 5.90 and 4.65 for PbI⁺ and PbI₂, respectively. However, solvation of the iodide/water complexes is somehow more rigid than that of the bare Pb²⁺ ion. In fact, an eightfold coordination (iodide + water) is not observed during MD simulations for PbI⁺ and PbI₂. Furthermore, we notice an average elongation of the Pb–O distance from 2.56 Å of Pb²⁺ to 2.65 Å and to 2.68 Å of PbI⁺ and PbI₂, respectively, Figure 2a. We address both the difference in the coordination number and the increase in Pb–O bond distances to the reduced positive charge on the lead cation as a consequence of the strong interaction with the iodide anions, which makes Pb²⁺ less available to bond with other water molecules and partially prevents their interaction because of steric hindrance. This effect becomes even more apparent when considering PbI₃^– and PbI₄^2–, which instead show a sixfold coordination and an octahedral structure, Figure 1b, with n_O = 2.93 and 1.99, respectively, thus indicating that a reduced number of water molecules can interact with the metal cation. For a detailed structural description of these complexes, the reader is referred to Section S2, Supporting Information.

It is also interesting to comment on the coordination of iodide by surrounding water molecules in the aqueous iodoplumbates. Analysis of the I–H RDF indicates that three water molecules coordinate, on average, with I^– for each complex, Figure S2, Supporting Information. We also notice that the average distance between iodide and hydrogen atoms is reduced from PbI⁺ (2.74 Å) to PbI₄^2– (2.61 Å). In fact, as the interaction with the central metal cation involves more iodide anions, their partial negative charge increases, becoming available for a stronger hydrogen bond interaction with water molecules. To sum up, in Table 1, we report the average Pb–O and I–H coordination number, n_O and n_H, along with the average Pb–O and I–H bond distances. As we go down the table, that is, passing from Pb²⁺ to PbI₄^2–, the number of coordinating water molecules is decreased from ca. 7 to 2, according to the increasing presence of iodide anions. In contrast with this, the number of water molecules coordinating iodide anions is essentially constant for all the studied iodoplumbates (∼3), for a total fourfold coordination, in line with the solvation of the aqueous iodide, Figure S2, Supporting Information. At the same time, we can see that the Pb–O bonds moves from Pb²⁺ to PbI₄^2–, while for the I–H bonds, we see an opposite trend, which is motivated by the weakening and the strengthening of Pb–O and I–H bonds, respectively.

Table 1. Calculated Values of the Average Number of Water Molecules Coordinating Pb²⁺ (n_O) and Hydrogen Atoms Coordinating I^– (n_H) in the Considered Iodoplumbates^a.

species	nO	nH	r(Pb–O)	r(I–H)
Pb2+	6.91		2.56
PbI+	5.90	3.09	2.68	2.74
PbI2	4.65	3.14	2.65	2.68
PbI3–	2.93	3.00	2.75	2.65
PbI42–	1.99	3.04	2.75	2.61

^aAverage Pb–O and I–H distances, r(Pb–O) and r(I–H), respectively, are also reported (Å).

We next investigate the optical properties of solvated iodoplumbates by measuring their UV–vis spectra. We start by analyzing the spectra of bare PbI₂ at different concentrations. PbI₂ is poorly soluble in water (solubility limit around 1.66 × 10^–3 mol PbI₂/Kg H₂O at 298.15 K, corresponding to 0.76 g PbI₂/l H₂O), with a solubility product, K_ps, ranging from 6.3 × 10^–9 to 1.2 × 10^–8 at room temperature⁸⁵ (in the following, we are using the default value implemented in Spana, 7.94 × 10^–9). We prepared solutions with concentrations ranging from 2.00 × 10^–3 to 6.04 × 10^–1 mM, by dilution of a 1.00 mM stock solution. At such concentrations, PbI₂ is almost completely dissociated and one retrieves the spectrum of the solvated Pb²⁺ ion overlapping with that of iodide at ∼226 nm, Figure 3a. By increasing the PbI₂ concentration, we observe the emergence of a band at 270 nm, which can be assigned to the lowest energy absorption feature of solvated PbI⁺, Figure 3a. Further increasing the concentration of the solution, one may expect to observe higher coordinated iodoplumbates. At the highest considered concentration of 6.04 × 10^–1 mM, PbI₂ amounts to ca. 0.2% of the total, Table S1, Supporting Information, thus essentially not contributing to the overall solution absorbance. Formation of PbI₃^– and PbI₄^2– complexes is negligible in the concentration range here considered.

Figure 3.

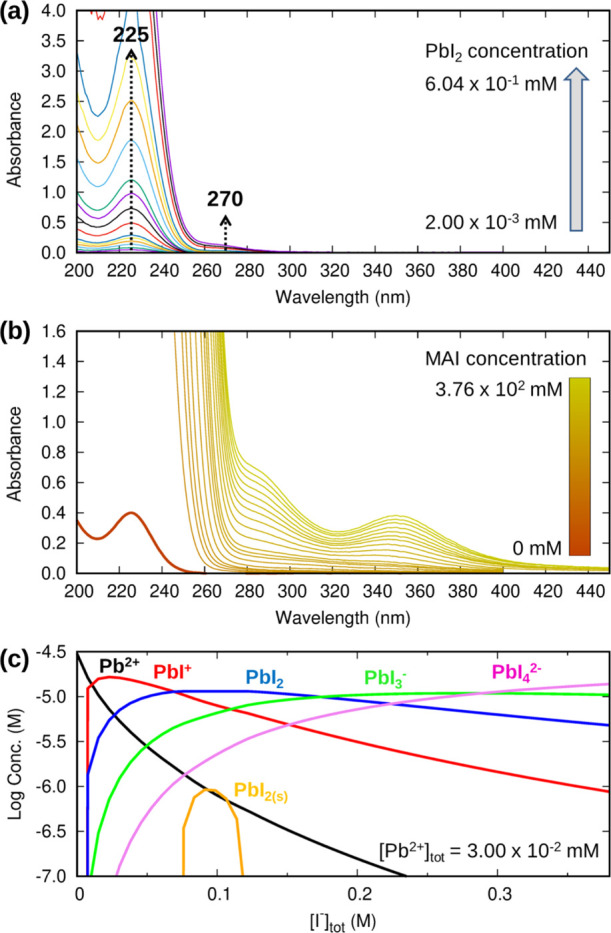
(a) Experimental UV–vis spectra of PbI₂ at different concentrations. (b) Experimental UV–vis spectra of PbI₂ 3.00 × 10^–2 mM + MAI (from 2.00 to 3.76 × 10² mM). (c) Estimated concentration diagram of aqueous iodoplumbates for a 3.00 × 10^–2 mM PbI₂ solution upon addition of MAI with a maximum concentration of 3.76 × 10² mM. The concentration of I^– is out of range.

On the basis of this preliminary analysis, we chose to start from a PbI₂ solution with a concentration of 3.00 × 10^–2 mM, for which we are confidently in a range dominated by fully dissociated PbI₂. Upon the first addition of MAI to this solution, we can see an increase of absorbance at 226 nm (with the detector that quickly gets saturated) and in the region between 250 and 280 nm, Figure 3b. The increase in absorption at 226 nm is mainly due to I^–.⁸⁶ Upon addition of ∼40 mM of MAI, corresponding to a 1333 [PbI₂]/[MAI] ratio, we see the rise of absorbances at 287 and 345 nm. These signals increase with further addition of MAI, taking a shoulder-like and band-like spectral shape, respectively, starting at an MAI concentration of ∼131 mM. Interestingly, in the case of the 345 nm band, we can see that the absorption maximum is gradually shifted toward longer wavelengths, from 345 to 351 nm. This shift is likely indicative of the formation of PbI₂, PbI₃^–, and PbI₄^2– species. Notably, the absence of scattering signals even at such high concentrations of MAI suggests that no aggregates are present in the solution. We then simulate the concentration profile for the Pb²⁺, PbI⁺, PbI₂, PbI₃^–, PbI₄^2–, and I^– species, solving the corresponding equilibria with the Spana software by employing the equilibrium formation constants at zero ionic strength reported by Tur’yan.^85,87 The results, reported in Figure 3c, confirm that a large quantity of MAI is needed to induce the formation of iodine-rich iodoplumbates, thus implying that it is not easy for the iodide anion to displace water molecules interacting with the Pb²⁺ center.¹⁴ We also note that the amount of solid PbI₂ as evaluated by Spana is negligible, thus indicating that metal halide is almost completely dissolved. Although the diluted PbI₂ solutions we employ here are not representative of the deposition conditions used for perovskites, they are still useful to probe the relative strength of formation of iodoplumbates. In particular, this means that it is difficult to form iodide-rich iodoplumbates, such as PbI₅^3– and PbI₆^4–, that are considered necessary for the formation of good-quality perovskites.^33−35,88

To assign the observed optical features to the specifically investigated complexes, we resort to a direct comparison between experiment and calculated optical spectra. To evaluate the optical properties of aqueous iodoplumbates, the thermally averaged structures of solvated Pb²⁺, PbI⁺, PbI₂, PbI₃^–, and PbI₄^2– species extracted from MD simulations were considered. Here, we explicitly include in the excited-state calculations the first solvation sphere considering a cutoff distance for a Pb–O bond length of 3.25 Å, corresponding to the first minimum of the RDF, and we represent the bulk solvent by an implicit solvation model, see Computational Details. Time-averaged spectra obtained for each species are compared with experimental UV–vis spectra of PbI₂ with increasing amounts of added MAI. Because of the limited number of simulated optical transitions, we are only able to describe the lowest absorption band for each solvated species. Additional TDDFT simulations including an extended number of excited states are reported in Figure S3, Supporting Information. The results obtained by the thermally averaged TDDFT calculations are reported in Figure 4a. As one may notice, the calculated spectra follow the experimental trend quite accurately. Starting with solvated Pb²⁺, we calculate an absorption maximum at 218 nm, in good agreement with the experimental maximum at 226 nm, which, as stated before, is also related to the absorption of I^–. Absorption maxima at 294 – 314, 336, 349, and 361 nm are respectively calculated for PbI⁺, PbI₂, PbI₃^–, and PbI₄^2– and reported, together with the experimental maxima as per Figure 3b, in Table 2.

Figure 4.

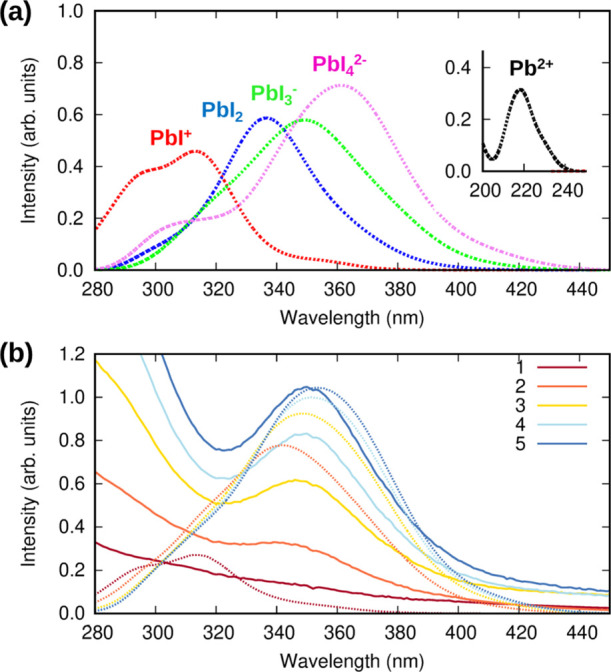
(a) Time-averaged spectra of solvated Pb²⁺ (black), PbI⁺ (red), PbI₂ (blue), PbI₃^– (green), and PbI₄^2– (magenta) complexes. The inset shows the spectrum of the solvated Pb²⁺ complex. (b) Selected UV–vis spectra of PbI₂ 3.00 × 10^–2 mM + MAI (continuous lines) compared with time-averaged spectra of simulated iodoplumbates weighted for their concentrations as evaluated by Spana software (dotted lines) in the 280–450 nm region. Each color corresponds to a specific MAI concentration: 1–57 mM, 2–131 mM, 3–231 mM, 4–311 mM, and 5–376 mM. Experimental intensities were scaled to compare with the calculated ones.

Table 2. Theoretical Absorption Maxima for the Investigated Iodoplumbates Compared with the Experimental Absorption Peaks from PbI₂ + MAI Solutions at Different Concentrations of MAI (C_MAI).

species (theo.)	abs. max (nm)	solutions (exp.)	abs. max (nm)
Pb2+	218	PbI2	226
PbI+	294	PbI2 + MAI (CMAI < 40 mM)	∼270
	314	PbI2 + MAI (40 mM < CMAI < 131 mM)	287, 345
PbI2	336	PbI2 + MAI (131 mM < CMAI < 167 mM)	345–351
PbI32–	349
PbI4–	361

Considering the complexity of the involved equilibria with multiple overlapping absorptions from different species, a global approach for comparing theory and experiment is required. To this end, we analyze the absorption profile obtained by multiplying the concentrations determined through the Spana software, Figure 3c, by the calculated thermally averaged absorption profiles of the various species. Results, reported in Figure 4b, show a good agreement between the variation of the experimental absorbance as a function of MAI additions and the calculated absorption profile, especially for high added MAI amounts. Because of the limited number of excitation energies calculated here, we are only able to reproduce the longest wavelength absorption band centered at ∼350 nm and the emergence of a shoulder at ∼315 nm, which, however, trustfully reproduce the experimental spectra. The main feature at ∼350 nm is dominated by the absorption of PbI₃^– and PbI₄^2– with a residual contribution from PbI₂, these being the only species which absorb at such long wavelength.

Interestingly, these absorptions are quite different from those found for iodoplumbates in organic solvents, such as GBL, for which the absorption maxima lie around 330, 370, and 423 nm for PbI₂, PbI₃^–, and PbI₄^2–, respectively.^33,34,41,48 This behavior is unexpected if one only considers Gutmann’s donor number (D.N.), or donicity, as a metric of solvent coordination strength to Pb²⁺: with a value of 18.0 kcal/mol,⁴⁹ the same as GBL, one would expect a similar coordination to Pb²⁺ by water. In fact, the experimental D.N. trend is in agreement with the relative formation energies of the Pb²⁺(solv)_n complexes, evaluated for n = 1–7 and solv = DMSO, DMF, GBL, ACN, and H₂O as per eq 2, see Table 3. Following the work of Hamill et al.,⁸⁹ we also consider the relative formation energy for the PbI₂(solv)_n adducts with n = 1 as a supplementary indicator, c.f. Table 3, the observed trend being consistent with that provided by the energetics of Pb²⁺–solvent interactions. Notably, GBL and H₂O shares the same D.N. but the calculations show that hydrated Pb²⁺ complexes with low number of coordinated solvent molecules are less stable compared to GBL ones, while the energetics tends to equalize for highly solvated complexes, that is, for n > 3. From this analysis, we can conclude that, while D.N. has been proved to correctly describe the coordination to Pb²⁺ of commonly employed organic solvents, this seems not to be the case for water, which again has to be treated as a special case. In this regard, we pinpoint that the D.N. is determined by the heat of the 1:1 reaction between SbCl₅ and the compound of interest dissolved in dichloroethane. However, because of the interactions with SbCl₅, D.N. has been determined by indirect methods for protic solvents.^90,91

Table 3. Relative Formation Energies (in eV) of Solvated Pb²⁺(solv)_n, with n = 1–7, and PbI₂(solv) Complexes, for solv (D.N., kcal/mol) = DMSO (29.8), DMF (26.6), GBL (18.0), H₂O (18.0), and ACN (14.1).

	DMSO	DMF	GBL	H2O	ACN
Pb2+(solv)	–2.412	–2.166	–1.781	–1.494	–1.400
Pb2+(solv)2	–2.108	–1.904	–1.599	–1.409	–1.278
Pb2+(solv)3	–1.883	–1.712	–1.488	–1.343	–1.185
Pb2+(solv)4	–1.680	–1.502	–1.305	–1.198	–1.031
Pb2+(solv)5	–1.483	–1.340	–1.177	–1.083	–0.912
Pb2+(solv)6	–1.366	–1.221	–1.091	–1.021	–0.818
Pb2+(solv)7	–1.295	–1.108	–1.027	–0.953	–0.738
PbI2(solv)	–1.273	–1.084	–0.863	–0.827	–0.648

The difference between the optical properties of iodoplumbates in water and organic solvents is indicative that such properties are highly dependent on both the coordination number and donor strength of the solvent. Increasing the coordination number generally leads to an absorption blue shift, see the calculated absorption spectra of Pb²⁺(H₂O)_n and PbI₂(H₂O)_n complexes at varying n, Figure S4, Supporting Information. Increasing the solvent donor strength at a fixed number of coordinated solvent molecules (n = 2, n = 3) in Pb²⁺(solv)_n complexes leads, on the other hand, to an absorption red shift, see Figure S5, Supporting Information.

Because of the small size of the water molecule and its high polarity and dielectric constant, lead complexes are surrounded by large water coordination spheres, which are difficult to move. This means that the D.N. could not be sufficient to describe the coordination strength of solvents to lead ions in some particular cases. Furthermore, the more pronounced tail in the distribution of Pb–I bonds in all iodoplumbates, Figure S1, Supporting Information, clearly indicates the weakening of Pb–I interactions at increasing contents of iodide in the iodoplumbate complex. This translates in lower energies for iodide removal from the complex and higher dissociation constants. In this regard, starting from MD simulations, we estimate the dissociation constants for each considered iodoplumbate through a grand-canonical formulation of solutes in aqueous solution and the thermodynamic integration method,^54,92 see Section S1 in the Supporting Information. The calculated values of dissociation constants for the aqueous iodoplumbates are consistent with the physical picture arising from the structural analysis of the MD simulations, that is, larger iodoplumbates show a stronger tendency to dissociate, in agreement with the trend experimentally observed, cf. Section S1 in the Supporting Information.

Finally, we discuss the solvation of the I^– species, which is another aspect worth considering. Integration of the first peak of the I–H RDF indicates that five water molecules coordinate, on average, with the solvated iodide, Figure S6 and Figure S7, Supporting Information. As a polar protic solvent, water better solvates anions than polar aprotic solvents through hydrogen bonding.^93,94 This can also be seen from the Mayer’s acceptor number (A.N.), a measure of the strength of a molecule as a Lewis acid. Organic solvents commonly employed in the synthesis of perovskites show an A.N. around 20 ppm (18.9, 17.3, 16.0, and 19.3 ppm for ACN, GBL, DMF, and DMSO, respectively),^90,95 while water, with a value of 54.80 ppm,⁹⁰ is likely to better coordinate with I^– (see Section S6 of the Supporting Information for a detailed analysis of iodide solvation), which then becomes less available to interact with Pb²⁺. We note that A.N. is based on the ³¹P NMR shift that triethylphosphine oxide shows when dissolved in the compound of interest. In this case, measurements on protic compounds do not suffer from the same issues that are affecting D.N. measurements.^96,97

Therefore, because the formation of iodide-rich iodoplumbates is an important step to obtain perovskites, the low propensity to produce these complexes in aqueous environment is indeed a symptom of the possible problems related to using water as a unique solvent for perovskites. Nevertheless, this can partially explain why water can be successfully implemented as an additive to enhance the crystallization of perovskites, as it shows a behavior similar to that typical of high coordinative polar aprotic solvents that are generally employed as an additive in one-step perovskite depositions.

5. Conclusions

We have reported on the study of hydrated perovskite precursors, unveiling their peculiar structural and optical properties by means of a combined theoretical and experimental strategy. The structure and average coordination number of different iodoplumbates have been revealed thanks to ab initio MD simulations. Then, combining the information extracted from excited-state TDDFT calculations and UV–vis spectroscopy has allowed us to characterize the optical properties of iodoplumbates and, consequently, their equilibrium behavior. Compared to other common solvents for perovskite precursors as DMSO, DMF, GBL and ACN, water turns out to be an interesting exception: because of its poor ability to solvate PbI₂ and its modest donor number, it cannot be classified as a strongly coordinating solvent to lead ions; nevertheless, it is also difficult to produce iodide-rich iodoplumbates because of the high polarity of water molecules and to the preferential solvation of I^– compared to other solvents. With this analysis, we propose an explanation on why it is difficult to deposit perovskites from aqueous solutions and at the same time why water is sometimes employed as an additive for the deposition of perovskites because iodoplumbates species, necessary precursors for the synthesis of perovskite, are hardly formed in this environment. Water is then a very peculiar solvent for the PbI₂ + MAI system and an exception to the low donor number/low coordination correlation usually found for organic solvents commonly employed for the synthesis of perovskites.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c08624.

• Equilibrium dissociation constants of aqueous iodoplumbates from a grand-canonical formulation of solutes in aqueous solution, structural analysis of aqueous iodoplumbates, concentration of species in PbI₂ solutions evaluated with the Spana software, extended spectra of aqueous iodoplumbates, absorption spectra versus number of water molecules and comparison with other solvents, and structural analysis of aqueous iodide (PDF)

The authors declare no competing financial interest.