Relative Information Gain: Shannon entropy-based measure of the relative structural conservation in RNA alignments

Abstract

Structural characterization of RNAs is a dynamic field, offering many modelling possibilities. RNA secondary structure models are usually characterized by an encoding that depicts structural information of the molecule through string representations or graphs. In this work, we provide a generalization of the BEAR encoding (a context-aware structural encoding we previously developed) by expanding the set of alignments used for the construction of substitution matrices and then applying it to secondary structure encodings ranging from fine-grained to more coarse-grained representations. We also introduce a re-interpretation of the Shannon Information applied on RNA alignments, proposing a new scoring metric, the Relative Information Gain (RIG). The RIG score is available for any position in an alignment, showing how different levels of detail encoded in the RNA representation can contribute differently to convey structural information. The approaches presented in this study can be used alongside state-of-the-art tools to synergistically gain insights into the structural elements that RNAs and RNA families are composed of. This additional information could potentially contribute to their improvement or increase the degree of confidence in the secondary structure of families and any set of aligned RNAs.

INTRODUCTION

Graphical representation of the secondary structure of RNA molecules is a field in continuous evolution. For decades, RNA secondary structure was encoded with the dot-bracket notation, in which dots and brackets represent, respectively, unpaired and paired bases. This 3-character string encoding model has been fundamental for the design of core algorithms predicting RNA secondary structure (1–3). Other commonly used representations include (but are not limited to) circle plots, graph representations (4,5) or context free grammars (6), whose applicability and usefulness depend on the task specifically addressed. However, to our knowledge, there are no frameworks to compare the performance on specific tasks of different encodings for RNA secondary structure. To give an example, graph representation performs well in secondary structure motif search when dealing with small datasets (7), yet it remains a computationally expensive representation to address the same task using RNA-binding protein datasets such as high-throughput sequencing of RNA isolated by crosslinking immunoprecipitation (HITS-CLIP) or photoactivatable ribonucleoside-enhanced crosslinking and immunoprecipitation (PAR-CLIP). For these tasks, string representations (8) or mixed models (9–11) perform better.

RNA secondary structure representation models not only allow for a simple, intuitive illustration of a complex 2D geometry of the RNA (9,10,12), but can also be exploited to extract information from the data (7,8,13). These representations are important for two main reasons. First, they ensure data visualization, thus improving communication. Second, they can be used as a means to do ‘feature engineering’. However, RNA structure representations are usually unbalanced towards data visualization or feature engineering, which can be a limitation as these two tasks cover aspects that are not mutually exclusive. As an example, the dot-bracket encoding is commonly used for structure visualization but does not excel in feature engineering. This is due to the fact that algorithms require to look at the whole string before understanding if a dot is a hairpin loop or an internal loop (14,15). Along similar lines, graph modelling of the RNA secondary structure (16,17) is almost exclusively used for feature encoding, but is not suitable for data visualization as it lacks an immediate communication (18), and is computationally too expensive to be used for large datasets (19–21).

Alternative representation models developed in recent years depict RNA secondary structure as multiple alphabetic character strings. Among them, the Brand nEw Alphabet for RNA (BEAR) efficiently encodes the 2D RNA structure into a linear string, thus lowering algorithm complexity, which is crucial for large-scale data (22–24). Moreover, secondary structures (and pseudoknots) can be successfully represented by graphs. Of relevance, beyond describing secondary structures, enhanced alphabets were also applied to tasks such as in vitro short motif discovery (25,26) and post-transcriptional regulation characterization (27). Nonetheless, these models have some limitations. Although performing well in terms of usability and performance (28), the standard BEAR encoding lacks communication of other string-based structural representations (24,26,29–31) because the high number of different characters does not allow researchers to immediately grasp the represented structures. Instead, other string representations developed so far lack usability and are mostly used for visualization.

These considerations and limitations call for the design of a well-balanced representation of the RNA secondary structure. Driven by this aim, in this study, we established a framework that can be used by researchers to move in this direction. In particular, we considered three different RNA secondary structure encodings and tested their efficacy using specifically built structural substitution matrices to solve the problems of pairwise structural alignments and structural conservation retrieval. Moreover, we introduced a new measure of structural conservation that can be computed on any RNA alignment for all its positions, and used it to assess structural conservation also in condition of insufficient base pair covariance.

MATERIALS AND METHODS

All the encodings described in this work represent the RNA secondary structure as a string with length equal to its underlying sequence, that is, one character per nucleotide. In more detail, the original BEAR encoding describes the structural context of a single nucleotide along with its length, and it is made up of 83 characters (28). The quickBEAR (qBEAR) encoding was previously developed as a means to represent the logo of a secondary structure motif (23). This encoding divides the structural contexts in three groups each based on the distribution of context lengths (see Supplementary Data—Encodings), resulting in an 18-character alphabet. The zipBEAR (zBEAR) encoding, which is introduced in this work, is inspired by the few-characters alphabets used in previous works (24,29). In such simpler encoding only the high-level structural contexts (e.g. hairpin loops, stems, but not their length) are considered, resulting in an alphabet composed of eight characters.

To derive the secondary structures, we applied the method devised in (28). In particular, Rfam seed members were each folded using hard constraints derived from the corresponding ‘consensus’ primary and secondary structure (32). In this way, an enhanced structure prediction was obtained as described in the original paper.

RNA Blocks

To build a framework from which derive different substitution matrices, we followed the classical formulation of BLOcks SUbstitution Matrix (BLOSUM) Blocks, with some relaxations (33,34). In more detail, for each Rfam seed alignment, we removed redundant primary sequences up to 90% of identity and considered the underlying alignments of secondary structures. First, we converted the RNA secondary structures using the BEAR, qBEAR or zBEAR encodings. Then, we selected each column of the alignments as a part of an RNA Block of that family on conditions that (i) no gaps were present and (ii) a structural consensus, dependent on the chosen alphabet, existed (i.e. there must be a character with a relative frequency >50%). The relaxation with respect to the classical formulation is the non-necessity to have contiguous columns to form an RNA Block. Finally, for each encoding, we derived the substitution matrix from a set of RNA Blocks, as described in (28,35) (Figure 1). Using all the RNA Blocks together, we build the substitution matrix as:

where MBR stands for Matrix of Bear encoded RNA, is a pseudocount (in this work 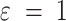), and 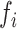, are, respectively, the relative frequency of the encoded character 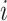among all RNA Blocks and co-occurrences of characters 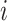and in any possible pair of RNA Blocks.

Figure 1.

RNA Block generation in zBEAR. From a given seed alignment, the secondary structure alignment is retrieved upon filtering from sequence redundancy, gaps and non-conserved positions to form a block (columns with the red circle on the top are filtered out). All the RNA Blocks are then used to compute the substitution matrix. RNA Block generation in zBEAR. From a given seed alignment, the secondary structure alignment is retrieved upon filtering from sequence redundancy, gaps and non-conserved positions to form a block (columns with the crossed circle on the top are filtered out). All the RNA Blocks are then used to compute the substitution matrix.

Rfam PSSMs as family models

A given encoding can be used to build a model from any RNA multiple alignment. We started off with Position Specific Scoring Matrices (PSSMs) as defined in the original formulation of Eisenberg (36). In particular, given an RNA Multiple Sequence Alignment (MSA), a mirroring Multiple Secondary Structure Alignment (MSSA) can be created by using available structures and by applying one possible encoding. In this way, for each encoding we obtained a 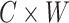matrix, where is the size of the alphabet and 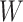is the length of the alignment. As this matrix encodes structural information, we call it structural PSSM (sPSSM).

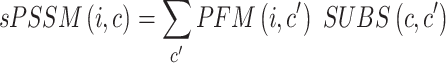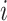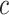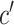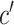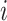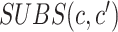In the formula is the position index, and run over all the alphabet’s characters of the selected encoding, is the frequency of character in position , and is the substitution matrix score of characters and . The values of an sPSSM are based on the structural context scores of the underlying substitution matrix, highlighting relations between different structural elements.

RESULTS

Here, we provided a generalization of our previous work (28), showing how distinct levels of detail encoded in RNA secondary structure representations contribute differently to depict useful information. In particular, by introducing a re-interpretation of the classical Shannon Information applied on sPSSMs, we showed how to extract information from the comparison of different encodings, revealing that detailed structural encoding can bring out information hidden by more a generic one and vice versa.

Substitution matrices for secondary structure elements

Using the described framework, we built a BEAR MBR (83 × 83), a qBEAR MBR (18 × 18) and a zBEAR MBR (8 × 8), with 90% primary sequence identity removal, and tested the ability of those encodings to communicate structural characteristics and information that can be used to derive quantitative measures. A color-coded representation of the MBRs is shown in Figure 2. In particular, we expected to see a trade-off between visual interpretability of the encoding used and the amount of structural information that can be retrieved using different models. A rich encoding like BEAR is expected to work better in fine-grained tasks, such as the alignment of two sequences. Indeed, this task involves summation of many terms and the differences can be defined by a single character. So, we expected a complex encoding to be more functional. Simpler encodings like qBEAR and zBEAR, instead, should be able to catch general properties of the data, such as distribution-dependent measures (e.g. Information Content and Structural neighbouring), while at the same time being easily interpretable in a visual context.

Figure 2.

Graphical representation of the MBRs. The MBR matrices are built applying different encodings (from left to right, BEAR, qBEAR and zBEAR), and with 90% sequence identity removal. Rows and columns represent RNA secondary structure elements (83 for BEAR, 18 for qBEAR and 8 for zBEAR), and each cell stores the log2-odds score for the substitution of one element with another element, from lower (blue) to higher (red) values. Each graphic element on the left represents one structural context (in order: stems, loops, internal loops, branching stems, branching internal loops, bulges and the generic unpaired branching). The lines connecting the matrices show the mapping between the secondary structure elements in the different encodings (see Supplementary Table S2 for the detailed mapping).

To test the performances of the newly created matrices on a pairwise alignment task, we compared these data with the results presented in our previous work (28). To this aim, BEar Alignment Global and Local (Beagle) algorithm (22) was used to compute pairwise alignments of benchmarks and between RNA secondary structure consensus (see Supplementary Materials—BEar Alignment Global and Local algorithm). We observed that the structural alignments performed using these new versions of the BEAR matrices have comparable performances with respect to the original MBRs in terms of sequence Sum of Pairs Scores (SPS) (Supplementary Figure S1).

Relative information gain

Each sPSSM contains information about the conservation of certain structural contexts, but this information is not directly available. To extract this feature, we used the Shannon entropy, defined as:

where 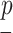is a probability distribution and 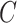is the number of available characters that is dependent on the chosen encoding in the current structural context. The Shannon entropy can be seen as the number of extra-bits needed to describe the distribution of a given sPSSM column. This measure is 0 when the distribution is completely unimodal (i.e. if a single character is present in the column, then no extra-bits are needed to completely understand the distribution), and is equal to 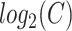(its maximum value) when the distribution is uniform (i.e. we need to specify every single character with bits each). However, an sPSSM column distribution is not normalized as a probability distribution, therefore we applied a transformation which first linearizes the quantities by applying the exponential function (an sPSSM cell is proportional to a log-odd), and then renormalized the values such that the sum of the values in a given position were 1:

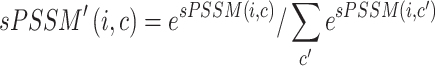In this way, the ordering between values is preserved and the added value of an sPSSM, which is the information contained in the substitution matrix, is brought forth in the probability distribution. High values for a character 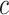in position 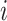can be due to structural context conservation, to contexts’ high substitution values in the matrix, or both.

To build a framework able to generalize between different encodings, we developed a measure of the relative structural conservation of an alignment position that is applicable to any encoding without changing its formulation. The proposed score is the Relative Information Gain (RIG):

where is .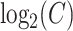

This formula ensures that (i) the measure is normalized between 0 and 1 for every possible encoding, and (ii) the measure is 1 when the structure is conserved in the column in each of the alignment members and 0 when the structure is not conserved at all. This means that the RIG score highlights strongly conserved structural motifs in multiple alignments, such as Rfam families’ seeds, but taking into consideration the structural variability given by the substitution matrix. In particular, thanks to this matrix, it is possible to enhance the difference in structural contexts present at a certain position when the substitution is unfavourable, while similar structural elements will yield higher RIG scores. RIG scores can be used to estimate the relative contribution of the structure to the conservation of an alignment. By analysing all Rfam 14.1 families, 810 out of 3016 resulted in stretches of higher structure contribution by applying the BEAR encoding; the structure contexts represented are evenly distributed between major structural categories (stems, hairpin loops, bulge/internal loops, pseudoknots and unpaired bases, see Supplementary Materials—Secondary Structure Dominance). Notably, the distribution of contiguous stretches of higher structural contribution is biased towards short stretches, as expected by the fact that the primary sequence carries stronger information in Rfam alignments (i.e. covariance models rely strongly on primary sequence conservation).

In general, higher RIG scores mean higher structural conservation of the alignment, but, depending on the underlying encoding, different conclusions can be drawn. A high RIG score in a coarse-grained encoding (like zBEAR) indicates a conservation of structural contexts (e.g. a hairpin loop), disregarding the length of those structures (e.g. the aligned hairpin loops may be of different lengths). A high RIG score in a fine-grained encoding (like BEAR) indicates a less strict structural conservation, allowing different structural contexts, or same contexts with different lengths, with favourable substitution rates to emerge as ‘conserved’. Moreover, by comparing different RIG scores obtained on the same alignments, other information can be deduced. For example, if an alignment position has a high zBEAR RIG score and a low BEAR RIG score, this discrepancy indicates a conserved structural element in that position, but with different and unfavourable lengths (in terms of the substitution matrices) in the alignment. With this in mind, we explored several Rfam alignments taken as examples to show how to interpret the RIG scores and how to gain useful information not directly available using a single encoding. The next paragraphs will explore some of the insights that can be extracted using RIG by taking some families as examples.

The family RF02021, which is the pre-miRNA family mir-3179, has a highly conserved structure with a central hairpin loop that is more variable in size. The small internal loop is similarly variable, but we can infer that is usually substituted with more favourable structural contexts with respect to the substitution scores (Figure 3). There are multiple possible cases: when a more coarse grained encoding (like zBEAR) has higher RIG scores compared to a more detailed alphabet, the underlying alignment has a set of positions that are conserved in the simplest level of abstraction (e.g. those positions are occupied by nucleotides in a stem context) but the finer-level details are not favourable in terms of substitution (e.g. there are multiple stem lengths aligned but the lengths of the stems involved are not frequently found together). In the opposite situation (low RIG scores with coarse-grained encodings and high RIG scores with fine-grained encodings), the structural contexts are not conserved because there are multiple different contexts involved in those positions (e.g. internal loops, stems and hairpin loops), yet their substitution score at a finer level of detail is favourable (e.g., it can be the case for the 5′ of hairpin loops, which can be aligned with the 3′ of the corresponding 5′ stem when different hairpin lengths are involved).

Figure 3.

z/q/BEAR90 RIG of RF02021. The color on the background represents the structural elements from the structural consensus reported in the covariance model, which simplifies the interpretation. The less conserved hairpin loop is shown as a depression in the RIG plot for BEAR and qBEAR. This should be interpreted as a conservation in the structural context (hairpin loop, high RIG scores for zBEAR), where the individual RNAs have different hairpin loop lengths (lower RIG scores for BEAR and qBEAR).

In each RFAM family, the RIG score can be compared to the (normalized) sequence entropy, in order to assess which element (primary or secondary structure) contributes the most to the conservation of a section of the family. The sequence entropy 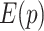used in this work is rescaled in a way similar to RIG in order to compare them in a more intuitive way:

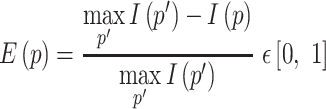where the maximum of 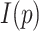in the case of the primary sequence is .

The representation in Figure 4 maps the ‘consensus’ structure elements (on the bottom) along with the difference between the RIG score and the sequence entropy (on the top). The resulting measure can take values in the range [-1, 1]: 1 represents a case where the structure has a full conservation and the primary sequence is more random, while -1 is for the opposite case. In the reported example, the RF02230 family shows a stem towards the 3′ end that is more conserved in structural elements than its underlying primary sequence.

Figure 4.

Difference between qBEAR90 RIG and sequence entropy in RF02230 (Xanthomonas sRNA sX11). In the upper part of the figure, a graphical representation of the difference between the RIG score and the sequence entropy is reported, with cells storing the difference for each position of the alignment, from lower (blue) to higher (red) values. In the lower part of the figure, a colour mapping representing the consensus structure of the family is shown. In this case, the stem towards the 3′ end is more conserved in structure than in sequence throughout the family members.

In addition, the RIG score can be also used alongside well-established tools like R-scape (37) to gain insights in the structural elements that RNA families are composed of. R-scape is the state-of-the-art method to evaluate the statistical significance of covariation support for conserved RNA base pairs. For paired bases, R-scape reports the estimation of the statistical power (i.e. the expected sensitivity of detecting significant covariation) but it does not give information on unpaired sections. By supporting the R-scape power with the RIG scores, we can gain more insight in the nature of a certain alignment, as shown for the U5 spliceosomal RNA (RF00020) family (Figure 5). Indeed, besides informing on stem structures, R-scape gives information on base-pair covariation, with RIG reflecting in a minor way similar aspects. As a main difference, RIG highlights structural conservation based on the substitution matrix instead of covariation. For example, positions from 8 to 16 have a high R-scape power; these positions are in fact part of a highly conserved stem with covariation support (bases paired with positions 59–67; the structural context can be derived from the RIG plot of the same family, see Availability). RIG scores are low in those regions and this reflects a low substitution score for stems of that size. Instead, positions 35–45 are unpaired, and represent a hairpin loop where terminal positions (35–37,43–45) yield a higher RIG score. This is a strong signal, indicating higher substitution scores between the terminal bases, and is due to the fact that the local structure favours a longer stem with a bulge of size 1 in position 36 (and 44), ending in position 37 (and 43). This can be seen by looking at the structural alignments (made available in the GitHub repository, see Availability): considering the gaps, position 77 in the alignment (which corresponds to position 36 in Figure 5) is predicted to be a bulge in the majority of the RNAs of that family. The same can be found in position 87 in the alignment (position 44 in Figure 5). Interestingly, the current version of Rfam (version 14.3) shows two different structures that emphasize this aspect, even if not showing the bulges.

Figure 5.

Comparative analyses of RIG scores alongside R-scape values in RF00020 (U5 spliceosomal RNA). For R-scape, the ‘power’ is reported. Both metrics can take values in range [0, 1]. Green bands represent areas where R-scape has no value because they contain unpaired elements. High RIG scores represent structural conservation, independently of base-pair covariation.

These results show that the RIG is unrelated to the classical measures of sequence conservation and base-pair covariation that can be found within Rfam. Especially in the context of sequence conservation, it is true that it is closely tied to structural conservation, but base pair covariance and mid-to-long-range interactions with other nucleotides (causing different folding although with the same central sequence (38)) can lead to a detachment of the two aspects.

The same type of plot as Figure 4 can have more or less pronounced peaks, depending on the level of complexity of the encoding used (see Supplementary Materials—RIG versus RIG). A region of high RIG scores in a zBEAR RIG plot indicates a conserved context, but should the region have lower RIG scores in the standard BEAR RIG plot, the structural context would be less conserved as the single elements of the family have no dominant length for that structure. On the other hand, a conserved area in a BEAR RIG plot would indicate a conserved context with a constant length, or with a highly favourable substitution, depending on the matrix used.

In general, we see a higher mean RIG score for more compact encodings. This was expected, since it is easier to find accordance in structure mappings when a single character encodes for more secondary structure elements (SSE), yet a more accurate scenario is described by more rich alphabets (e.g. it becomes clear, by comparing the RIG plots of different encodings, when a certain structure is fully conserved in its elements’ length or only contextually conserved). By comparing RIG data with sequence entropy, regions of structural importance may be derived (see Supplementary Materials—secondary structure dominance).

DISCUSSION

The RNA secondary structure representation is more than a simple means of visualization as it can be used to enrich features applicable to study those molecules. In this context, the encodings described in this work move towards a balanced representation, where both communication and usability are at good levels. In particular, we developed a pipeline for a custom construction of secondary structure elements similarity matrices, inspired by classical formulations of BLOSUM Blocks. This pipeline is suitable for large-scale applications, allowing also an easy integration with other existing pipelines and tools. We also demonstrated that the substitution matrices we can obtain with such approach are more than just a means to improve alignments where structural information is present, since the information value they bring can emerge by exploiting other measures. At this regard, we introduced the scoring metric RIG, a Shannon-based measure to exploit the structural information embedded in such matrices and highlight conserved structural motifs in multiple alignments. Importantly, we showed that RIG is unrelated to other well-established measures (sequence entropy and base-pair covariation), and so it can add useful information that could potentially contribute to improve the degree of confidence in the secondary structure elements that RNAs and RNA families are composed of. Here, we used the RIG metric on Rfam alignments as a use case, but the same idea can be applied to explore any set of aligned RNAs for which a hypothesis of conserved structure can be made as a means to gain insight into the nature of locally conserved structural elements.

DATA AVAILABILITY

Precalculated RNA Blocks, MBRs, sPSSMs, RIG scores and plots calculated for 3016 Rfam 14.1 families are made available via Zenodo at http://doi.org/10.5281/zenodo.4299601. All the scripts to build the data present in this work are available at https://github.com/helmercitterich-lab/RIG.

Notes

Present address: Marta Adinolfi, Department of Experimental Oncology, IEO, European Institute of Oncology IRCCS, Milan, Italy.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

AIRC [project [to MHC] (grant number IG 23539).

Conflict of interest statement. None declared.