Statistical considerations for medication adherence research

Abstract

Objective

Medication non-adherence is a widespread problem and has been known to be associated with worse health outcomes and increased healthcare costs. Although many measures of adherence have been developed, their usage is not consistent across studies. Furthermore, statistical methods for analyzing adherence measures have not been rigorously evaluated.

Methods

Using Proportion of Days Covered (PDC), a commonly used adherence measure, we examine the variability inherent to study inclusion criteria and several variations of the PDC calculation method using a motivating data example. We illustrated via sensitivity analyses the potential for flawed inference when modeling PDC as an outcome measure. We also performed simulation studies to investigate the statistical properties of three statistical models: logistic regression, negative binomial, and ordinal logistic regression models.

Results

Our sensitivity analysis showed that parameter estimates can vary greatly depending on the rules for determining the study end date in calculating PDC, or the minimum number of fills in defining the cohort. In simulation studies, logistic regression had lower power than ordinal logistic and negative binomial regression models. Naivete to treatment was an important predictor of adherence and omitting it from statistical models can lead to inflated type I errors.

Conclusions

We discourage dichotomizing adherence data as it results in low power. The negative binomial model offers advantages in modeling adherence data, as it avoids the problematic use of a ratio in regression models. The ordinal logistic regression is robust to distributional assumptions with greater power, but naivete to treatment should be adjusted to reserve type I error rate. We also provide a recommendation for defining the observation window in calculating PDC.

Introduction

In the United States, more than half of all adults are on at least one prescription drug [1]. Patient adherence to medication is defined as the extent to which a patient takes prescribed medications according to the dosage and frequency recommended by the provider [2]. Medication non-adherence is a widespread problem and has been associated with worse health outcomes, more hospitalizations and increased healthcare costs [3–5]. Uniform measurements, calculations and operational definitions are not consistently implemented in the area of adherence research, and some adherence-related publications do not carefully define their terminology or methodology, leading to much confusion about the chosen metrics [6]. Without a uniform conceptual framework, medication adherence research is not generalizable [7]. Better adherence research is predicated on a standardized definition of adherence, a transparent method of calculation, and robust statistical modeling methods.

There have been efforts to summarize and standardize measures of medication adherence [2, 7–9]. A notable study investigated properties of continuous multiple-interval measures of medication availability [10]. This term refers to the large class of medication adherence measures calculated by taking the ratio of days’ supply of medication obtained within some observation period divided by its duration [11]. Vollmer et al. identified eight variants based on different study aims and assumptions. The eight measures differ based on how the start and end of the observation window are determined, whether or not to cap the ratio at 100%, and whether oversupply should be accounted for in a time-forward manner. The list of calculations is not exhaustive, but it does illustrate the fact that adherence can be calculated in many different ways. Dima and Dediu have done important work on adapting these measures for standardization using the R programming language [12].

Although many measures of adherence have been developed, their definitions and calculations are not transparent, nor consistent across studies [13, 14]. Proportion of Days Covered (PDC) is a commonly used method for claims-based adherence measurement [15]. The PDC is expressed as a ratio of the number of days covered by the prescription fills over the duration of the observation window. Here, “covered” denotes that prescription fills are entered as time arrays in the PDC calculation, and if one array of medication overlaps with the next one (i.e., the patient refills the prescription before the current supply is exhausted), the new array is shifted to begin once the older prescription has been used up. Thus, a maximum of one daily dose is counted per day. As such, the PDC can provide more granular information with respect to the timing of the sequence of fills than other measures.

The problematic usage of ratios in regression models aside [16], there are myriad challenges in analyzing adherence data. Adherence measures are a summary statistic that obscures the chronology of patient behavior, as well as the length of time the patient was observed. Furthermore, they do not account for the different amounts of drug supply patients may receive (i.e., 30 vs. 90 days’ worth of supply). Medication switching and polypharmacy can further compound those issues [17]. Loss to follow up can be a major source of bias: patients who are non-adherent are indistinguishable from those who switch pharmacy or stop using the medication for legitimate reasons. The source of the data (i.e. pharmacy claims data vs. insurance claims data) can obscure true adherence patterns if information such as medically advised drug holidays or patients moving to a new pharmacy system are not available. Perhaps most importantly, there is no consensus on how PDC data should be used in statistical analysis, though previous simulation studies have suggested viable methods [18].

In order to analyze PDC data, it is better to fully understand the structure underlying this distribution. Figure 1A shows the distribution of PDC measurements obtained from a motivating data example. There is a high proportion of patients with a PDC value of 100%, and a long tail of patients with low adherence. Such a non-normal distribution, which is common for PDC values, is part of the reason why applying statistical models to the data presents a challenge.

Figure 1.

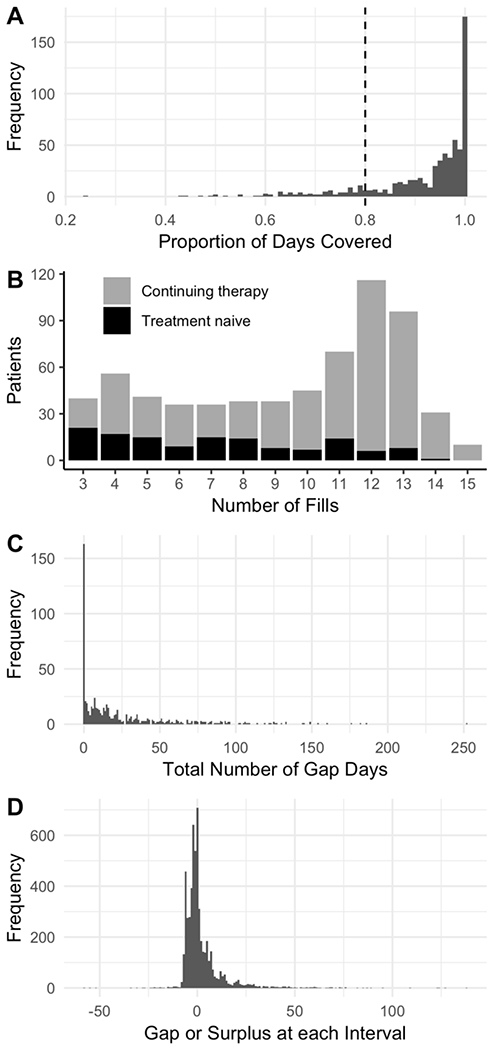
Exploratory data analysis from a motivating data example, using the one-year fill history of 653 patients who were prescribed medication to treat multiple sclerosis. A minimum of three fills was required for inclusion into the study. (A) Histogram of PDC, which shows a highly skewed distribution with a large portion of the study population with 100% PDC. The dashed line indicates a threshold of 80% PDC, which is often used as an arbitrary cut point to classify non-adherent vs. adherent patients. The last fill plus method was used to determine the end date for this plot. (B) Histogram of number of fills for each patient. The most common number of fills was 12, indicating patients who started treatment before or near the study start date and were followed through to the end. Treatment naive patients make up a larger portion of the patients with low fill numbers, as patients were enrolled continuously throughout the year. (C) Total number of cumulative gap days per patient. Similar to the distribution of PDC, gap days have a high density of patients with zero gap days (which is equivalent to having a PDC of 100%), and has a long tail reaching out beyond 250 gap days. (D) Timing of fills at each interval. Positive values represent length of time between the exhaustion of supply and refilling of the medication (gap days). Negative values represent the number of days the prescription was filled early (medication surplus).(Note: this figure omits a 252-day gap in order to provide more detail where the majority of the data lie.)

The goal of this study is to systematically investigate the fundamental issues of PDC definition and its usage as a metric for medication adherence. We aim to illustrate the importance of defining the end of the observation window (end date) when calculating PDC, and to find the best statistical method for determining predictors of PDC using a motivating data example. We consider three methods: logistic, ordinal logistic, and negative binomial regressions. We perform sensitivity analyses on the motivating data, and end with a simulation study to evaluate the performance of each statistical model.

Methods

Motivating data example

The data consist of pharmacy records for 653 patients who received dispensations of medication from the Vanderbilt Specialty Pharmacy to treat Multiple Sclerosis [19]. Once prescribed, medication should be taken continuously and filled at regular intervals. Prescription records for this study were restricted to the calendar year 2016, and patients were excluded from the study if they had fewer than 3 fills. Most fills were for either 28 or 30 days (95%). One goal of this study was to determine if patients who were new to therapy (i.e., treatment naive) had different adherence as measured by PDC compared to those who were continuing therapy (non-naive). In this study, 79% of patients were non-naive, and thus could be observed for almost the full year. The remainder of patients were treatment naive and were enrolled continuously until October 2016. As shown in Figure 1B not all patients had the same number of fills, and a large proportion of the patients with fewer than nine fills were treatment naive. Other predictors of interest were age, race, gender and whether or not the patient received copayment assistance to reduce patient out-of-pocket costs (copay).

Calculation of PDC

Definition of PDC:

PDC is commonly defined by: PDC = (Sum of days covered in observation period) / (length of observation period) [15], which involves two major components: the number of days covered and the duration of the observation window. In order to measure these two components, the beginning and the end of the observation window need to be defined for each patient. Often it is not transparent how this window was defined, and there are substantial variations in its definition if defined. Furthermore, little research on the effect of this window on adherence measures has been performed. For this motivating study, the date of the patient’s first fill within the study period was considered the beginning of the observation window, which is reasonable choice for both treatment naive and non-naive patients. Here, we focus on the end of the observation window to investigate its effect on PDC measurements. The main reason we investigate an end date rule is that the adherence profile of patients who are lost to follow-up prior to the end of the study period can be greatly misrepresented. Compare a patient who switches pharmacy systems to one who stops taking the medication at the same point in the study: both patients could have the same adherence profile, yet one is censored from the study while the other patient is considered to be non-adherent. To account for this unknown censoring, it is incumbent on researchers to select a method which fairly summarizes the actual capacity of the data to measure adherence.

Defining the end rule for PDC:

In determining the end of the observation window, we consider four options. The first is to use the end of the study period for all patients, called “fixed end date”, or “Fixed”. This is the method recommended by the Pharmacy Quality Alliance [15], and assumes all patients should be taking the medication through the end of the study period, making this the most conservative approach. The next method is to select the earlier occurrence of either the study end date or the date the last fill is exhausted, called “last fill plus”, or “LFP”. This may bias estimates of PDC high, as it assumes all discontinuations were medically advised (i.e., no one was non-adherent after their last fill). An extension to the LFP method is to use the earlier occurrence of the study end date or the date the last fill was exhausted plus 30 days, called, “last fill plus plus”, or “LFPP”. This allows for the possibility that people were non-adherent after their last fill, but caps this gap at 30 days. Finally, we can disregard the decision of a censoring rule altogether and use the last fill as the final date in the study, called “last fill”, or “LF”. The impact of applying each end date rule is illustrated in Figure 2, wherein supply diaries for all four methods are displayed for one patient. Depending on the end date rule applied, the PDC can be as low as 64.7% (using a fixed end date) or 100% (using either LFP or LF).

Figure 2.

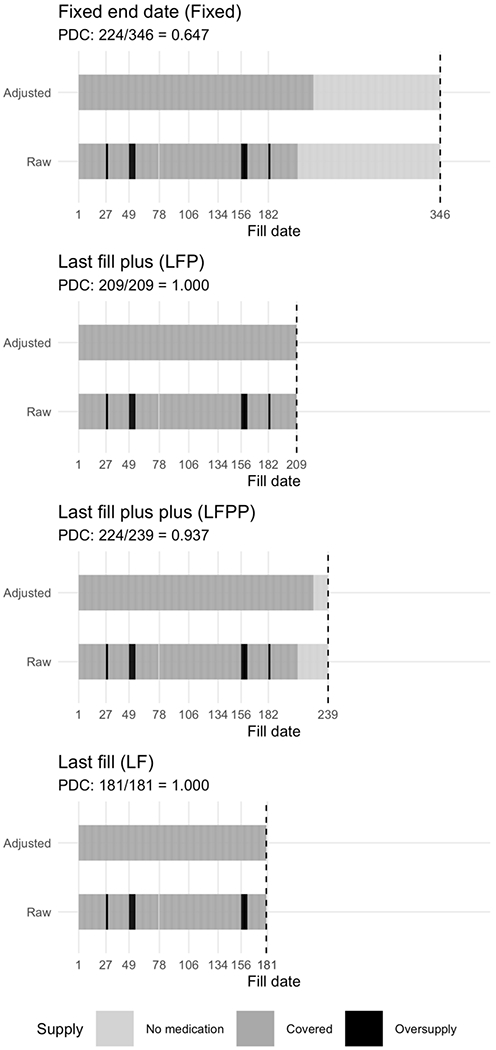
Case study of a single patient’s adherence profile detailing the calculation of PDC based on different end date rules. The “Raw” bar indicates the medication adherence supply diary, where grey bars indicate normal supply (“Covered”), black bars indicate a surplus of medication (caused by an early fill, “Oversupply”), while the light grey bars indicate days where the patient is not covered by medication (gap days, “No medication”). The “Adjusted” bar represents the supply diary after the oversupply has been shifted forward in time according the rules for calculating PDC. Conceptually, the black bars can be thought to slide forward in time until a gap in medication occurs, then the excess supply provides coverage for otherwise uncovered days. Here we present supply diaries for the same patient data according to four different end date rules: Fixed end date (Fixed), Last fill plus (LFP), Last fill plus plus (LFPP), and Last fill (LF). This patient was lost to follow-up, and hence the last fill date is before the end of the study period, thus the observation window is more variable than a patient who was followed through to the end. PDC calculations are displayed above each plot. Note that last fill and last fill plus methods arrive at the same PDC result, but with different lengths of the observation window.

Determination of study cohort

In addition to determining the best method for defining the observation window, we also investigate how the results would be impacted by defining the cohort in terms of complete follow-up and the number of fills. Because three fills (the current inclusion criteria, i.e., the full cohort; Cohort ≥ 3 fills) may not provide enough time to effectively assess a patient’s medication refilling behavior, as discussed in Vollmer et al. [10], we also restrict the cohort to patients with at least six fills (Cohort ≥ 6 fills) as well as at least nine (Cohort ≥ 9 fills). While this may result in the exclusion of patients who are less compliant, it does allow for a more equitable comparison of adherence propensity within the cohort. Last, we limit the study population to patients who were covered through the last day of the study, thus removing the ambiguity on how to handle patients who may or may not have dropped out (Cohort “complete follow-up”), and effectively disentangling the question of persistence from adherence. The cohort reduction without clear justification would not be recommended in practice, but this may provide insight into the properties of PDC in actual data.

Statistical models for assessing predictors of PDC

The choice of which statistical model may be the most appropriate for the data is broad in scope. Here, we present a representative model for each of three outcome types: dichotomized PDC, continuous PDC values, and gap days.

Model for PDC as dichotomous outcome:

The logistic regression (LR) model is a common method for modeling patient adherence to medication [20–22]. This is accomplished by dichotomizing a continuous measure of adherence and classifying patients above some threshold (usually 80% [23]) as adherent and those below it as non-adherent. There are numerous reasons why dichotomization should be avoided [24]. Most importantly, much of the information will be lost. Such a method of classification implies patients just above the 80% threshold are expected to have different clinical outcomes compared to a patient just below the threshold, or that patients far below the threshold exhibit the same patterns of behavior as those just below it. While we do not advise modeling adherence by dichotomizing the continuous measure, it is included for comparison.

Model for continuous PDC values:

We examine the cumulative probability ordinal regression model as a potential method for analyzing adherence data. Unlike the linear model which assumes a normal distribution for the outcome, Y, conditional on covariates, X, the ordinal regression is based on the ranks of Y rather than the values, thus no distributional assumptions are required [24]. This can be particularly advantageous when the distribution of adherence measures is highly skewed. Furthermore, this method is robust to outliers (e.g., patients with very high or low adherence relative to typical values). Cumulative probability models can be constructed with various link functions; here we consider the logit link, which is called the ordinal logistic regression (OLR) model. Proportional odds is an assumption of this type of model, however this assumption may be overstressed, for even when the assumption is not met, estimates and inferences of the overall odds will still be valid [25].

Model for gap days:

Instead of directly using PDC, we also consider the number of gap days defined by the difference between the denominator and numerator. The distribution of this outcome using our motivating data example can be seen in Figure 1C. In this setting, a PDC of 100% is the same as having zero gap days. Gap days can be considered as count data that can be analyzed using a Poisson or negative binomial (NB) model. We choose NB to fit gap days as it can account for overdispersion due to a high proportion of zeroes. To account for the length of the observation window, the denominator in the PDC calculation can be included as an offset in the model.

Sensitivity analyses

Sensitivity analyses are crucial in determining how robust methods are to changes in the structure of the data, and can aid in the assessment of key assumptions, influential observations as well as different modeling methods. We compare different derivations of PDC based on the observation window (Fixed, LF, LFP, and LFPP) and patient inclusion criteria (Cohorts ≥ 3 fills, ≥ 6 fills, ≥ 9 fills, and complete follow-up) as well as the LR, OLR and NB models. Each of the three models was fit on combinations of the four end date rules and four cohort criteria, for a total of 48 models. The covariates included in each model are: treatment naive, copay assistance, race, age and gender.

Simulation study

Data generation model:

Instead of simulating PDC values directly, we mimic the actual data-generating process by simulating the timing of each refill, and then calculate PDC. Unless a patient refills a prescription the day after the previous fill is exhausted, it affects the overall PDC calculation in one of two ways: the addition of gap days if the fill is later than the target date, or the addition of surplus medication if the refill occurs before the target date. To approximate the distribution of gap and surplus days as observed in our motivating data example (Figure 1D), we applied a non-central t-distribution-normal random-effects model as follows. For ith patient, i =1, …, N and jth fill, j = 1, …, m_i, where N is the total number of patients and m_i is the number of fills for patient i,

$$\begin{gathered} {\mathrm{Y}}_{\mathrm{ij}}\sim {\mathrm{T}}_{\mathrm{v}}({\mathrm{\delta }}_{\mathrm{i}}|{\mathrm{X}}_{\mathrm{i}},{\mathrm{m}}_{\mathrm{i}}), \\ {\mathrm{\delta }}_{\mathrm{i}}={\mathrm{\beta }}_{0\mathrm{i}}+{\mathrm{\beta }}_1{\mathrm{X}}_{1\mathrm{i}}+{\mathrm{\beta }}_2{\mathrm{X}}_{2\mathrm{i}}+{\mathrm{\beta }}_3{\mathrm{X}}_{3\mathrm{i}}, \\ {\mathrm{\beta }}_{0\mathrm{i}}\sim \mathrm{N}(0,{\mathrm{\sigma }}^2), \end{gathered}$$

where Yij is the timing of refills in the number of days, following a non-central t-distribution, T_v(δ). Positive Y_ij value corresponds to a gap in medication coverage in days, while negative Y_ij value corresponds to an early refill and a surplus of |Y_ij| days’ supply, δ_i, is the non-centrality parameter for patient i; v is the degrees of freedom set at 2.3; X_i = (X_1i, X_2i, X_3i) is the covariate matrix for patient i; β_0i, is the patient-specific random effect, with the variance σ² fixed at 12. We used a non-central t-distribution with v = 2.3 to mimic the observed gaps and surplus days as close as possible to the motivating data example. The non-centrality parameter determines the skewness of the distribution, and larger δ increases the likelihood of a larger gap between fills.

Simulation scenario:

Under the described PDC-generating framework, we examined the impact of multiple parameters in our simulation study (summarized in Table 1). Each patient is assumed to have his or her own propensity for the timing of their refills. This subject-specific propensity for filling is modeled as a random effect following a normal distribution with mean β₁X_1i + β₂X_2i+ β₃X_3i. We considered three binary covariates; X₁ is a real predictor on non-adherence with β₁ = 2 (i.e., late refills), whereas X₂ is not associated with adherence, thus β₂ = 0. In our setting, β₃ corresponds to the impact naivete to treatment on adherence, and can take the value of −1, 0, or 1, where negative values correspond to a better adherence. The covariate matrix X is allowed to have different correlation structures. We examine the setting of corr(X₁, X₂) = corr(X₁, X₃) = corr(X₂, X₃) = 0, as well as the scenario where corr(X₁, X₂) = corr(X₁, X₃) = corr(X₂, X₃) = 0.5.

Table 1.

Simulation Conditions

Component	Levels	Rationale
β1	β1 = 2	Assess the impact of a true covariate effect on adherence (evaluate type II error)
β2	β2 = 0	Assess the impact of a null covariate effect on adherence (evaluate type I error)
β3	β3 = −1 β3 = 0 β3 = 1	Explore the effect treatment naivete may have on adherence
Sample size	N = 200 N = 600	Understand simulation conditions in low and high-powered settings
Correlation among covariates	Correlation = 0 Correlation = 0.5	Assess the impact on closely related covariates
Adjustment for naivete	With Without	Determine the effect of failing to adjust for treatment naivete
Cohort inclusion criteria	≥ 3 fills ≥ 6 fills ≥ 9 fills Complete follow-up	Understand the impact of different inclusion criteria

To distinguish treatment naive from non-naive patients, different start dates were randomly assigned. Non-naive patients (70%) were given a start data based on an exponential distribution: t_0C ~ Exp(0.075); this made the start date for most of these patients within the first 30 days of the study. Treatment naive patients (30%) were assigned a start date based on a uniform distribution: t_0N ~ U(15, 275); that is these patients were randomly enrolled throughout the first nine months of the study period. All patients were assigned 30 days of supply at each fill. To address the possibility for improbably early fills, any large surplus was truncated at 15 days.

Under this simulation condition, 5,000 replicated datasets were generated with either 200 or 600 subjects. The correlation among covariates was set to 0.0 or 0.5, and the covariate of treatment naivete was either included or excluded in the model. Four types of inclusion criteria were applied to the data: a minimum of either three, six or nine fills, as well as complete follow-up. The PDC outcome was defined using the LF rule. The outcomes and corresponding models are as follows: the attainment of the 80% threshold of PDC (LR), the PDC value (OLR), and the number of gap days (NB). Analyses were performed with R statistical software [26].

Results

Summary of PDC calculation by observation window and cohort

Table 2 provides summary statistics of PDC based on the combination of the end date rules with each of the cohort restrictions. Of the four cohort restrictions, the full cohort (≥ 3 fills) results in the most variable mean PDC, which suggests that the exclusion criteria applied in the other cohorts is removing the patients with lower adherence. Thus, the smaller cohort size makes the mean and median measures more uniform across the different end date rules applied. The PDC for ≥ 3 fills using the Fixed method results in the lowest mean and median PDC, as well as the highest proportion of patients below 80%. The number of patients not meeting the threshold is highly variable within the ≥ 3 fills and ≥ 6 fills cohorts, which illustrates that the choice of the end date rule applied to the data can have drastic effects on the dichotomized PDC measures.

Table 2.

Summary Statistics of PDC Calculated by the End Date Rule of the Observation Window Variations and Cohort Restrictions

End Date Rule	Mean PDC (SD)	Interquartile Range (0.25 0.5 0.75)	N < 0.80 PDC (%)
Cohort ≥ 3 Fills (N = 653)
Fixed	0.87 (0.18)	0.82 0.95 0.99	148 (23%)
LF	0.91 (0.12)	0.88 0.96 1.00	99 (15%)
LFP	0.92 (0.11)	0.89 0.96 1.00	90 (14%)
LFPP	0.90 (0.12)	0.86 0.95 0.99	117 (18%)
Cohort ≥ 6 Fills (N = 516)
Fixed	0.90 (0.13)	0.86 0.95 0.99	95 (18%)
LF	0.92 (0.11)	0.88 0.96 0.99	71 (14%)
LFP	0.92 (0.10)	0.89 0.96 0.99	67 (13%)
LFPP	0.91 (0.11)	0.88 0.95 0.99	76 (15%)
Cohort ≥ 9 Fills (N = 406)
Fixed	0.93 (0.08)	0.90 0.96 0.99	34 (8%)
LF	0.94 (0.08)	0.91 0.96 0.99	32 (8%)
LFP	0.94 (0.07)	0.91 0.96 0.99	29 (7%)
LFPP	0.94 (0.08)	0.90 0.96 0.99	31 (8%)
Complete Follow-up (N = 516)
Fixed	0.92 (0.10)	0.90 0.96 1.00	61 (12%)
LF	0.92 (0.11)	0.89 0.96 1.00	66 (13%)
LFP	0.92 (0.10)	0.90 0.96 1.00	61 (12%)
LFPP	0.92 (0.10)	0.90 0.96 1.00	61 (12%)

Fixed: fixed end date; LF: last fill; LFP: last fill plus; LFPP: last fill plus plus

Sensitivity analysis

The estimates of the regression coefficients (β) and 95% confidence intervals from 48 analyses are shown in Figure 3. Depending on the model, the β has a different interpretation. Thus, we only compared the results within each model. In the LR model, copay assistance was significant in eight models. Race was significant in ten of the OLR models, and treatment naive significant in five. Only one of the NB models found any significance, which was copay assistance with the full cohort using LFPP. Across all three models, β estimates were the most variable for the treatment naive coefficient. Because of the reduction in sample size, estimates within Cohort ≥ 9 fills had the most variation compared to the other cohorts.

Figure 3.

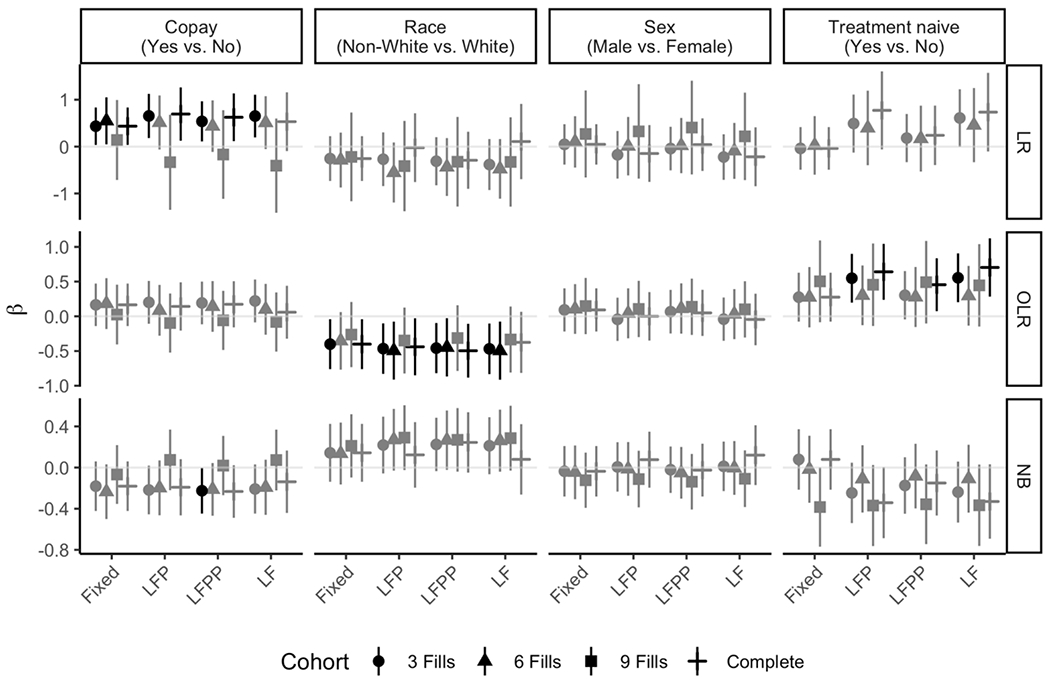
Sensitivity analyses for each of the three statistical models applied each of the four end date rules and four cohort restrictions. Significant results are denoted with black points (the estimates) and lines (the 95% confidence intervals), while non-significant estimates are shown in grey. (Note: for the LR case of ≥ 9 fills, the estimates and the 95% confidence intervals are not shown because of quasi-separation within the treatment naive variable, i.e., too few patients are below 80% PDC to obtain reliable estimates.)

Simulation results

We calculate the power and type I error rate (at the 0.05 level) of each model for each simulation scenario summarized in Table 1. The primary results with the full cohort are shown in Tables 3A and 3B. With a smaller sample size, the LR model has low power. The OLR and NB models have power greater than 80%, with OLR having a slightly greater power. Both the OLR and NB models show a reduction in power when the covariates are correlated; the trend is exacerbated when naivete with a positive effect on adherence (β₃ = −1) is not adjusted for in the model. When naivete has a non-null effect on adherence and the covariates are correlated, the type I error is inflated for both OLR and NB, with greater degree in the OLR model. This inflation is increased in the larger sample size.

Table 3A.

Simulation Results Using the Full Cohort (≥ 3 Fills) (N = 200)

					Power			Type I Error Rate
Naive Effect	Correlation b/w Covariates	Average Sample Size	Naive N (%)	Adjustment of Naive	LR	OLR	NB	LR	OLR	NB
Higher adherence (β3 = −1)	0.0	200	59.8 (30%)	with	59.4	95.1	90.6	4.46	5.46	5.64
				without	59.3	94.9	90.8	4.52	5.26	5.56
	0.5	200	59.9 (30%)	with	52.3	91.4	85.8	4.90	6.00	6.14
				without	44.6	85.0	82.9	5.54	7.32	6.34
Null (β3 = 0)	0.0	200	59.8 (30%)	with	62.3	95.4	91.6	4.78	5.32	5.66
				without	62.1	95.2	91.7	4.96	5.28	5.46
	0.5	200	59.8 (30%)	with	54.1	91.7	87.0	5.10	5.90	6.02
				without	55.3	92.8	87.1	5.08	5.38	6.10
Lower adherence (β3 = 1)	0.0	200	59.7 (30%)	with	64.9	95.3	91.8	4.72	5.34	5.42
				without	65.0	95.0	91.9	4.46	5.28	5.38
	0.5	200	59.8 (30%)	with	56.1	91.8	87.3	4.44	6.00	5.94
				without	66.3	96.4	89.7	5.16	7.28	6.24

Table 3B.

Simulation Results Using the Full Cohort (≥ 3 Fills) (N = 600)

					Power			Type I Error Rate
Naive Effect	Correlation b/w Covariates	Average Sample Size	Naive N (%)	Adjustment of Naive	LR	OLR	NB	LR	OLR	NB
Higher adherence (β3 = −1)	0.0	600	179.8 (30%)	with	97.6	100	100	5.38	5.20	5.48
				without	97.6	100	100	5.34	5.08	5.56
	0.5	600	179.9 (30%)	with	94.8	100	100	4.76	5.40	5.04
				without	90.6	100	100	7.32	10.84	6.54
Null (β3 = 0)	0.0	600	179.7 (30%)	with	98.4	100	100	5.60	5.18	5.62
				without	98.3	100	100	5.58	5.20	5.68
	0.5	599	179.8 (30%)	with	95.6	100	100	5.28	5.38	5.16
				without	96.5	100	100	5.46	5.42	4.98
Lower adherence (β3 = 1)	0.0	599	179.5 (30%)	with	98.7	100	100	5.52	5.06	5.46
				without	98.6	100	100	5.56	5.16	5.24
	0.5	599	179.5 (30%)	with	96.6	100	100	5.12	5.34	5.14
				without	99.0	100	100	7.04	9.78	5.46

The reported trends replicate in different formulations of the cohort inclusion criteria (Supplementary tables). Restricting the size of the cohort by complete follow-up or the number of fills, results in reduced power compared to the full data set. Under these cohort restrictions, the percentage of naive patients is reduced, as they are less likely to meet the inclusion criteria.

Discussion

Simulation studies show LR is not a good option for modeling adherence data, and we advocate abandoning the dichotomization of adherence measures in future studies. OLR and NB models perform comparably well, however, the NB model has a slight advantage in controlling type I error when the covariates are correlated. If treatment naive is controlled for, then the OLR model has the advantage of being more powerful. The NB model may be preferable to the OLR model because the length of the observation window (the PDC denominator) can be controlled for in the regression model as the numerator and the denominator of PDC measure are separated, thus avoiding the use of a ratio in regression models which has been criticized [16].

We found no benefit to restricting the cohort greater than 3 minimum number of fills, or by limiting the cohort only to patients with complete follow-up. We recommend the LF end date rule, as this method accounts for the fact that some patients can be lost to follow-up while others can be non-adherent after their last fill. Also, the same rule is applied to all patients regardless of their filling behavior. Further rationale for recommending this method is since medication taking can only be assumed [11], a refill suggests a higher likelihood that the medication for the previous fill was taken than it does for the current fill. The LF method allows researchers to assess predictors of PDC when the patient is known to be on medication, effectively separating the question of persistence into a distinct theoretical framework.

Our sensitivity analysis showed parameter estimates can vary greatly depending on the rules for determining the study end date, or the minimum number of fills, with the greatest variability being observed for the treatment naive covariate.

Using our example data, we showed the variability in PDC outcomes when different end date rules and cohort inclusion criteria are applied. The proportion of patients < 80% PDC can be especially sensitive, as a change in just a few days in either the numerator or denominator can change the PDC value enough to cross the threshold.

The findings of our study are subject to some limitations. First, the sensitivity and simulation studies were based on one motivating study. Although this data is representative of adherence data encountered previously, it may not be generalizable to other drug classes, pharmacy systems or study periods. The covariates selected for our model are not exhaustive for the potential factors contributing to medication adherence, and different studies may be limited in which variables are available for analysis. While we recommend treatment naivete be included in statistical models, we realize that this information may not be available for some studies. Second, our choice of statistical models is not exhaustive nor definitive on the matter. While there may be better methods to analyze the dichotomized outcome, such as log-binomial regression [27] or robust Poisson regression [28], especially when estimating risk ratios for binary outcomes, we did not investigate them further as we do not recommend dichotomizing continuous outcome in adherence research. In modeling gap days, there are other potential models which may be better suited to the task. Another simulation study investigated the performance of two-part models such as the zero-inflated negative binomial model and reported promising results [18]. However, when the proportion of zeroes is moderate, the NB model can handle the excess zeroes fairly well as a part of overdispersion; we did confirm that the NB model was sufficient to handle the proportion of zeroes observed in our data (approximately 20% - 30%). In addition, the NB model has better interpretability, as two-part models are more challenging to understand, and the structural component of inflated zeroes may not provide a realistic mechanism of the actual data generating process. However, when the proportion of zeroes is unusually high, we recommend that researchers see if zero-inflated models would provide a better fit. Third, we only studied the case of simple medication taking and did not investigate the effects of differential days’ supply, drug switching or polypharmacy. These would add more complexity to an already challenging problem, and present opportunities for future studies.

Given the varied difficulties in modeling adherence, researchers should consider which strategies are most apt to answer their scientific questions. Additional future work would include the investigation of alternate methods for modeling adherence data. Furthermore, while the date of the first fill is traditionally used as the study start date, the effect of a lookback period to account for medication stockpiling may impact the adherence profiles of non-naive patients, and therefore, the selection of the study start date may warrant a similar investigation. Lastly, it is our opinion that alternative adherence measures to ratios such as PDC should be considered, as they may not provide the most accurate portrayal of medication adherence.

Statistical modeling is an important aspect of medication adherence research. Here, we present sensitivity analyses and simulation studies showing that covariate selection and model choice can have large impacts on results. Our simulations provide strong evidence that PDC dichotomization and LR methods should be abandoned in this line of research. We present two viable alternatives to this approach with the OLR and NB methodologies, and note a slight advantage to using NB. Additionally, we provide recommendations for determining the end date when calculating PDC.