Melanoma Detection Using Spatial and Spectral Analysis on Superpixel Graphs

Abstract

Melanoma is the most fatal type of skin cancer. Detection of melanoma from dermoscopic images in an early stage is critical for improving survival rates. Numerous image processing methods have been devised to discriminate between melanoma and benign skin lesions. Previous studies show that the detection performance depends significantly on the skin lesion image representations and features. In this work, we propose a melanoma detection approach that combines graph-theoretic representations with conventional dermoscopic image features to enhance the detection performance. Instead of using individual pixels of skin lesion images as nodes for complex graph representations, superpixels are generated from the skin lesion images and are then used as graph nodes in a superpixel graph. An edge of such a graph connects two adjacent superpixels where the edge weight is a function of the distance between feature descriptors of these superpixels. A graph signal can be defined by assigning to each graph node the output of some single-valued function of the associated superpixel descriptor. Features are extracted from weighted and unweighted graph models in the vertex domain at both local and global scales and in the spectral domain using the graph Fourier transform (GFT). Other features based on color, geometry and texture are extracted from the skin lesion images. Several conventional and ensemble classifiers have been trained and tested on different combinations from those features using two datasets of dermoscopic images from the International Skin Imaging Collaboration (ISIC) archive. The proposed system achieved an AUC of $99.91\%$, an accuracy of $97.40\%$, a specificity of $95.16\%$ and a sensitivity of $100\%$.

Introduction

In normal human cell growth, cells divide to meet the needs of the human body in replacing any damaged or dead cells to preserve the body functions [1]. When cancer develops, this normal division is broken down and the cells are needlessly produced in huge numbers. In particular, skin cancer occurs when a group of abnormal skin cells grow and divide uncontrollably. Malignant melanoma, hereafter melanoma, is the deadliest skin cancer of the three known types of skin cancer [2]. Melanoma is characterized by malignant tumors of melanocytes [3] which are cells that produce melanin that gives the skin its color. The seriousness of the melanoma skin cancer emerges from the fact that it can spread throughout other parts of the body [4, 5]. These cancer cells can diffuse for example to the lung and develop there [5]. This process of outgrowth development from the primary cancer site is called metastasis.

Melanoma incidence and prevalence rates have been quite high. According to the World Health Organization (WHO), currently about 132,000 new cases of melanoma and between 2 and 3 millions of non-melanoma cases are diagnosed worldwide each year [6, 7]. In some countries, particularly in the Western ones, melanoma has been emerging more widely. The highest incidence rates of melanoma are in Australia and New Zealand. In fact, the rates there are almost twice the rate in North America according to the AIM at Melanoma Foundation [8]. Those relatively high rates may be due to the closeness of those two countries to the equator and their greatly eroded ozone layer [8]. According to the Australian government statistics, it is estimated that there will be 16,221 new cases diagnosed with melanoma in 2020 as well as 1,375 melanoma-related deaths [9]. In the USA, the proportion of people with melanoma has nearly doubled in the past 30 years [10]. According to the Skin Cancer Foundation, it is estimated that there will be 196,060 new skin cancer cases in the USA in 2020. Moreover, the USA will have in 2020 an estimate of 6,850 deaths, $67\%$ of which are men [11].

Before the 1980s, skin cancer detection was based mainly on the presence of some symptoms like hard swelling parts on the body, ulcerations, irregular markings on the skin and bleeding [12]. In 1985, the ABCD technique was first introduced for the diagnosis of melanoma [12]. This technique is based on some morphological characteristics of a melanoma lesion which are asymmetry (A), border irregularity (B), color variegation (C) and having a diameter of more than 6 mm (D).

In the 1980s, dermoscopy was first used in the diagnosis of melanoma through acquiring some subsurface features [13]. Dermoscopy (also known as dermatoscopy, incident light microscopy or skin-surface microscopy) is a noninvasive imaging technique used to acquire images of the pigmented skin lesions for further visualization and examination [14]. This imaging technique helps dermatologists with early detection of lesions that are not visible to the naked eye. However, the process of manual examination of the dermoscopic images depends mainly on the dermatologist’s experience. Even for experienced dermatologists, this examination is a non-trivial time-consuming task whose outcomes can be easily compromised by the inter-observer variability [15]. Also, in early stages, melanoma cases are most probably confused with non-melanoma nevi. As melanoma is still incurable and inflicts a high cost on human lives [16], methods for early diagnosis and treatment are indispensible.

Since 1987, numerous computer systems have been developed to assist dermatologists in achieving accurate and fast detection of skin cancer [17–24]. Each system is composed mainly of an imaging module, an image processing module, and a lesion detection module. However, automatic melanoma detection is still a challenging task and requires more improvements [21]. The challenges come mainly from the large variations in skin lesion color, texture, and geometric properties. Those variations complicate the task of differentiating between benign and malignant lesions.

To advance the state of the art in automated melanoma detection, the International Skin Imaging Collaboration (ISIC) created a database of 10,000 dermoscopic images and organized a challenge on “Skin Lesion Analysis Towards Melanoma Detection” in conjunction with the International Symposium on Biomedical Imaging (ISBI) in 2016. The challenge focused on three relevant tasks, namely skin lesion segmentation, dermoscopic feature extraction and lesion classification. The best classification accuracy achieved in this challenge was $85.5\%$ [26]. In 2017, a similar challenge was announced with the same tasks and a larger dataset. The best classification accuracy achieved in the ISBI 2017 challenge was $88.8\%$, [27]. In the next section, we summarize some results based on these datasets for developing automated melanoma detection systems.

In this paper, we propose and evaluate graph-theoretic representations of skin lesion images for melanoma detection. Specifically, each lesion image region is segmented into superpixels using the simple linear iterative clustering (SLIC) algorithm [28]. Then, the generated superpixel map is used to construct a superpixel graph, where each node represents one superpixel and each edge represents a neighborhood relation between adjacent superpixels. Using superpixels instead of individual pixels as graph nodes certainly reduces the memory usage and improves the computational efficiency. We compare the features derived from graph-theoretic representations to conventional global features based on texture, color and shape analyses. Our work differs in several aspects from the earlier graph approaches of [29, 30] (outlined below in Section 2). In the proposed technique, we focus on classification rather than segmentation. Moreover, our approach exploits different graph signal representations, while the graph models of [29] and [30] use only graph structures without nodal graph signals.

In summary, our contributions in this paper are of three folds. Firstly, we propose a superpixel graph representation of skin lesion images for melanoma detection. Several spatial-domain features are computed based on this representation. Secondly, we investigate spectral graph features based on the graph Fourier transform (GFT) [31]. Thirdly, we compare melanoma detection performance outcomes using spatial and spectral superpixel graph features as well as global lesion features. Our feature representation is neither local, nor global, but can be considered to be of a hybrid nature. Indeed, the proposed representation includes local superpixel features at the graph vertices, in addition to global color, texture and geometry features extracted from the superpixel graph.

The remainder of this paper is organized as follows. In Section 2, we review the state-of-the-art computational approaches for melanoma detection. Section 3 describes the ISIC 2017 dataset and explains the preprocessing steps. Section 4 gives the details of the construction of the weighted and unweighted superpixel graphs and the associated graph signals from skin lesion images. Section 5 introduces the local and global graph metrics, as well as the graph Fourier transform (GFT). Section 6 reviews other conventional image features extracted from skin lesion images. The design of the proposed melanoma detection system is explained in Section 7. In Section 8, we describe the experimental setup and evaluation of our system, discuss the experimental results and compare them against relevant methods. Finally, conclusions and future directions are outlined in Section 9.

Related Work

We review here recent state-of-the-art techniques for computerized melanoma detection. Rastgoo et al. [32] proposed an automated technique for binary classification of skin lesions into benign and melanoma ones. Color, texture and shape features were extracted, and three classifiers were trained and tested using different feature combinations. The experimental results show a sensitivity and a specificity of $98\%$ and $70\%$, respectively. Celebi et al. [33] extracted morphological, color and texture features from a surface microscopy image atlas of pigmented skin lesions [34]. Each dermoscopic image was subdivided into separate clinically significant segments using the Euclidean distance transform. The experimental evaluation resulted in a sensitivity and a specificity of $93.33\%$ and $92.34\%$, respectively. Schaefer et al. [35] employed an automated lesion segmentation technique on the same atlas data. Then, hand-crafted color, texture and geometric features were extracted and used to train an ensemble classifier for melanoma detection. This classifier achieved an accuracy, a sensitivity and a specificity of $93.83\%$, $93.76\%$ and $93.84\%$, respectively. Oliveira et al. [36] proposed a system for melanoma diagnosis based on different combinations of shape and texture features, as well as color features based on different color spaces. This system was evaluated on the ISIC 2016 dataset of the ISBI 2016 challenge and achieved an accuracy of $92.3\%$. Abbas et al. [37] developed a system that identifies seven types of dermoscopic patterns based on color and texture features extracted in a CIECAM02 (JCh) uniform color space. A sensitivity of $89.28\%$ and a specificity of $93.75\%$ were reported on 1039 color images from the EDRA-CDROM interactive atlas [38].

Lee et al. [22] proposed new contour irregularity indices of skin lesions to differentiate between melanoma and benign lesions. In particular, two such indices were computed by combining texture and structure irregularities. Dermoscopic images were collected from patients in the Pigmented Lesion Clinics of the Division of Dermatology in Vancouver, BC, Canada. The results showed that the two indices agreed well with the clinical evaluation of experienced dermatologists and outperformed other shape descriptors. Schmid−Saugeon [23] evaluated the symmetry of a pigmented lesion according to the lesion geometry, texture and color information. The evaluation was carried out on 100 dermoscopic lesion images evenly distributed among the benign and melanoma types. The symmetry analysis was exploited to address skin cancer diagnosis and achieve an accuracy of $72\%$ and a sensitivity of $78\%$.

Some registration and tracking techniques have been also developed to detect skin lesions and track their variations over time. For example, Mirzaalian et al. [24] developed a system for detecting and tracking pigmented skin lesions. For each patient, lesions were detected and tracked by analyzing the degree of matching between dermoscopic images captured at different times. Specifically, this process involved identifying some anatomical lesion landmarks, encoding the spatial landmark distribution in a structured graphical model and then matching models of image pairs. A detection sensitivity of $80\%$ was achieved.

Deep learning architectures, especially convolutional neural networks (CNN), have been recently used in tasks of dermoscopic image analysis such as lesion detection, segmentation, feature extraction and classification [25]. Majtner et al. [39] extracted RSurf, local binary pattern (LBP) and CNN-based feature descriptors from the ISIC 2016 dataset. These features were used to train a support vector machine (SVM) classifier and get an accuracy of $82.6\%$ and an area under the receiver operating characteristic curve (AUC) of $78\%$. Gutman et al. [26] reviewed the ISIC 2016 challenge outcomes where all participants used deep learning methods. The best method achieved an AUC of $86\%$. Lopez et al. [40] adopted variants of the VGG16 CNN architecture for melanoma detection and achieved an accuracy of $81.33\%$ and a sensitivity of $78.66\%$. Matsunaga et al. [41] addressed one task of the ISIC 2017 challenge to classify skin lesion images. The ISIC 2017 dataset was used with additional 409,969 and 66 images for the classes of melanoma, nevus and seborrheic keratosis, respectively. A binary ResNet-based classifier detected melanoma with an AUC of $92.4\%$. González-Díaz [42] addressed the same task using the CNN-based DermaKNet framework that includes networks for lesion segmentation, structure segmentation and diagnosis. This framework resulted in an AUC of $87.3\%$. Esteva et al. [43] created a large collection of 129,450 dermoscopic images with 2,032 different diseases. This collection was used to train CNN architectures for two key binary classification problems: keratinocyte carcinoma versus benign seborrheic keratosis; and malignant melanoma versus benign nevi. For the second problem, an AUC of $94\%$ and an accuracy of $72.10\%$ were achieved. Brinker et al. [44] compared the performance of a CNN architecture against the performance of nine dermatologists on the classification of malignant melanoma and benign nevi images. Indeed, the CNN outcomes appeared to be clearly superior to those obtained by both junior and board-certified dermatologists.

While some approaches for automated melanoma detection are based on global lesion features [45–47], other approaches are based on local lesion features [48–50] defined at selected keypoints. Such keypoints are typically based on a regular grid subdivision of the lesion image. Each of these keypoints is associated with a feature descriptor that represents the local information in a window centered at that keypoint. For example, Barata et al. [50] evaluated and compared the performance of a bag-of-features (BoF) approach versus a global-feature approach for melanoma detection. The two approaches demonstrated similar performance outcomes with a slight advantage for the local BoF approach at the expense of a higher computational cost.

Moreover, network analysis approaches have also been proposed for automated skin cancer diagnosis. For instance, Sadeghi et al. [29] analyzed the characteristics of dermoscopic images in order to construct pigment networks and their associated graphs, based on hole and net detection. As well, Jaworek-Korjakowska et al. [30] carried out superpixel segmentation of pigmented skin lesions using the simple linear iterative clustering (SLIC) algorithm [28]. Then, a region adjacency graph (RAG) was constructed for each dermoscopic image where the graph nodes and edges represent the generated superpixels and their neighborhood relationships, respectively. The edges are undirected and weighted by a function of the difference between features of the connected superpixel nodes. Thus, hierarchical superpixel merging was performed to get the cancerous lesions separated from the healthy regions.

Dataset Description and Preprocessing

Dataset Description

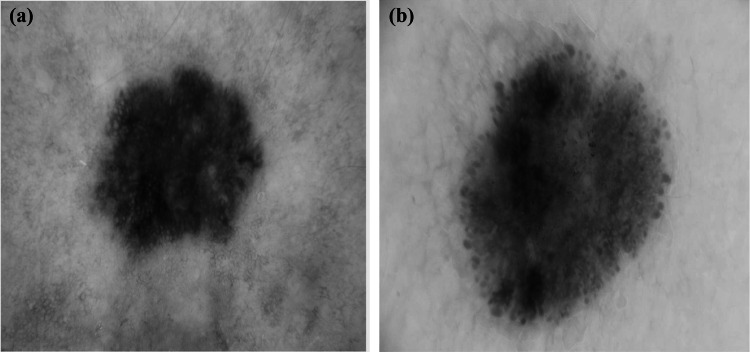
In our investigations, we consider two datasets. The first one is the $2600-$image ISIC 2017 dataset, a publicly available skin lesion image dataset released by the International Skin Imaging Collaboration in 2017 [51]. The lesion in each image was manually segmented by medical experts through manual tracing of the lesion contour to produce a binary mask where the pigmented skin lesion is the foreground and the other area is the background. The class proportions in the training data are $82\%$ and $18\%$ for the benign and melanoma lesions, respectively. To alleviate class imbalance, we created a second dataset formed by augmenting the first ISIC 2017 dataset with 250 melanoma images from the ISIC archive [41]. For the rest of this paper, we denote the two datasets by ISIC 2017 and the augmented ISIC 2017. Since the image resolutions show wide variations ranging from $42\times 34$ to $6427\times 4371$ pixels, all images were resampled to $750\times 750$ pixels (the average image resolution) for normalization and reduction of computational cost [52]. Figure 1 gives two examples of the pigmented skin lesions. In order to extract better lesion features and enhance the performance of the proposed system, a preprocessing step is applied. In this step, we applied hair and gel removal techniques to the skin images for better visualization of the pigmented skin lesions. After that, we performed contrast adjustment and average normalization for the images [52].

Fig. 1.

Pigmented skin samples from the ISIC 2017 dataset (a) a melanoma lesion (b) a benign lesion

Superpixel Graph Construction

We describe here in detail our approach to build a superpixel graph for each skin lesion image. Tentatively, an image might be considered as a regular lattice, where every pixel is connected to its neighboring pixels with periodic boundary conditions [53]. However, such a pixel-level approach leads to a huge computational complexity, especially in extracting the graph features, both in the spatial and spectral domains. Instead, we follow a more intuitive and practical approach where the input image is clustered into a set of superpixels and hence a graph representation is built on top of the generated superpixels. The stages of the superpixel graph construction are presented in Fig. 2 and Fig. 3 for melanoma and benign lesion images, respectively. There are four main stages for this construction process which are superpixel generation, superpixel merging, graph nodal signal assignment and graph connectivity assignment. In the next subsections, we will fill out the details of each step.

Fig. 2.

Stages of graph construction from a dermoscopic melanoma image. (a) Original skin lesion image. (b) Skin lesion segmentation output using the binary mask. (c) Superpixel clustering using the SLIC technique [54]. The color level of each superpixel is represented by the average throughout the whole superpixel. (d) Graph construction before superpixel merging. (e) Superpixel merging output. (f) Final graph construction

Fig. 3.

Stages of graph construction from a dermoscopic non-melanoma image. (a) Original skin lesion image. (b) Skin lesion segmentation output using the binary mask. (c) Superpixel clustering using the SLIC technique [54]. The color level of each superpixel is represented by the average throughout the whole superpixel. (d) Graph construction before superpixel merging. (e) Superpixel merging output. (f) Final graph construction

Superpixel Generation

Clustering individual pixels which have similar characteristics into a superpixel is an important preprocessing step that has been applied in many image processing and computer vision tasks [55–58]. If the number of superpixels is distinctly fewer than the number of individual pixels of the image, the superpixel representation can significantly minimize the complexity of the later image processing steps. While there are several ways to split an image into superpixels (see, e.g., [59]), we chose to segment skin lesion images into superpixels using the simple linear iterative clustering (SLIC) algorithm [28, 54]. Figure 2 (c) illustrates the superpixels constructed from a sample melanoma lesion image, and Fig. 3 (c) shows another example of constructed superpixels for a benign lesion image. In both figures, each cluster region is represented by its mean color in the CIELAB color space.

Superpixel Merging

Since the SLIC superpixel algorithm may produce superpixel maps with different numbers of superpixels for different images, the superpixel merging technique, introduced in [60], is performed to reduce the number of superpixels to a desired fixed number of superpixels.

Figure 2 (e) presents an example of melanoma skin lesion image superpixels after merging the original superpixels constructed in Fig. 3 (c). The superpixels are reduced to 20 superpixels over all images in the dataset. Figure 3 (e) is another example of merging the superpixels to 20 superpixels for a benign lesion. Each new cluster region in both figures is represented by the mean color in the CIELAB color space.

Graph Nodal Signal Assignment

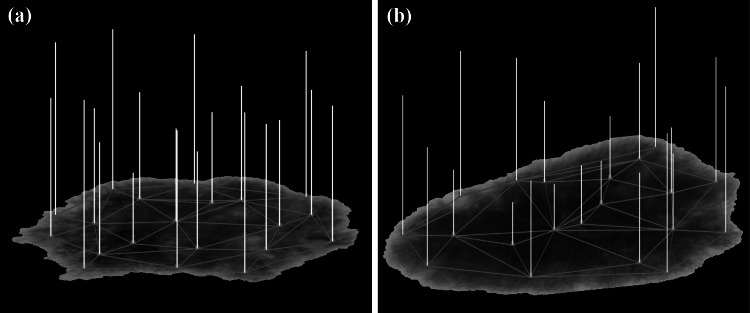
After determining the nodes (vertices) of the proposed graph, we connect each vertex to its neighboring ones to have a graph for each image. Before explaining our graph construction, we state basic graph definitions. A graph G consists of a set of vertices (nodes) ${\{v_i\}}_{i=1}^N=V$ and a set of edges $E\subseteq V\times V$. An edge $e_{\mathit{ij}}=(v_i,v_j)=(i,j)$ connects the vertices $v_i$ and $v_j$, $1\le i,j\le N$. For undirected graphs, $(v_i,v_j)$ is viewed as an unordered pair, i.e., $e_{\mathit{ij}}=e_{\mathit{ji}}=\{v_i,v_j\}=\{i,j\}$. The graphs in this paper are assumed to be connected and simple, so there are no loops $e_{\mathit{ii}}$. An unweighted graph is represented by the adjacency matrix $A=(a_{\mathit{ij}})$, where $a_{\mathit{ij}}=1$ if there is an edge $e_{\mathit{ij}}$ and zero otherwise. The degree of a vertex $v_i$ is the number of edges incident to $v_i$. This number is denoted by $k_i$. The degree matrix D is a diagonal matrix $D=(k_{\mathit{ij}})$, where $k_{\mathit{ii}}=k_i$. The shortest path between two connected vertices $v_i,v_j$ is denoted by $d_{\mathit{ij}}=d_{\mathit{ji}}$. If $v_i$ and $v_j$ are not connected, we set $d_{\mathit{ij}}$ to $\infty$. Since we want to transform an image into a graph signal, we have to assign a value to each vertex. This value may be chosen from a big variety of possible values associated to each superpixel. In our work, we defined the graph signal values based on color, texture or geometric features of each superpixel in the constructed graph. Figure 4 exhibits an example of graph signal values with the signal value (strength) on each node indicated by the length of the yellow bar. The graph signal values in this figure are based on the color features of the graph superpixels. Figure 4 (a) and (b) show the graph signals for melanoma and benign lesions, respectively.

Fig. 4.

Graph signals on the dermoscopic images. (a) Melanoma, (b) benign. The signal value at each node is the norm of a vector containing the maximum, minimum and median of CIELAB color values of the corresponding superpixel. The length of each bar represents the value (strength) of the signal

Graph Connectivity Assignment

Now, we move to the final stage in constructing the superpixel graph signals, which is defining the edges and their weights. First of all, we recall that the superpixel graphs are simple, connected and undirected and consist of $N=20$ vertices. The graph vertex of each superpixel is connected to vertices that correspond to the adjacent superpixels. See Fig. 2 (d),(f) and Fig. 3 (d),(f). We consider two types of superpixel graphs, namely weighted and unweighted graphs. For unweighted graphs, each graph edge $e_{\mathit{ij}}$ joins $v_i$ and $v_j$ with a weight of 1. In this case, the adjacency matrix corresponding to the graph will be $A=(a_{\mathit{ij}})$, where $a_{\mathit{ij}}$ is 1 if there is an edge $e_{\mathit{ij}}$, and zero otherwise. As for the weighted graphs, we consider three types of edge weights. In particular, an edge weight can be a function of differences in color, geometry, or texture features of the two connected superpixels. For color-based graph signals, we assign to each vertex (superpixel) $v_i$ a vector ${\mathbf{x}}_i$, whose components are the minimum, maximum, mean, median, standard deviation, variance and entropy values of the CIELAB components of the pixels inside the superpixel $v_i$.

The weight ${\omega }_{\mathit{ij}}$ assigned to an edge $e_{\mathit{ij}}$ is then defined to be

$$\begin{array}{c}\hfill {\omega }_{\mathit{ij}}=\frac{1}{\mathrm{\Omega }}exp\left[-,{\left(\frac{∥{\mathbf{x}}_i,-,{\mathbf{x}}_j∥-{\mu }_c}{{\sigma }_c}\right)}^2\right],\end{array}$$ 1

where ${\mu }_c$ is the mean of $\left\{∥{\mathbf{x}}_i,-,{\mathbf{x}}_j∥,:,e_{\mathit{ij}},\in ,E\right\}$ taken over all edges and ${\sigma }_c$ is the standard deviation. The number $\mathrm{\Omega }$ is a normalization factor, that is defined by

$$\begin{array}{c}\hfill \mathrm{\Omega }=\sum _{\begin{array}{c}\{i,j\}\in E\end{array}}exp\left[-,{\left(\frac{∥{\mathbf{x}}_i,-,{\mathbf{x}}_j∥-{\mu }_c}{{\sigma }_c}\right)}^2\right].\end{array}$$ 2

Notice that $\{i,j\}$ also denotes the edge $\{v_i,v_j\}$, or $e_{\mathit{ij}}$. This definition of weights generates higher connectivity between vertices with similar color levels. The intuition behind generating weighted graphs is that the human vision tends to focus on high contrast regions.

Geometry-based graph signals represent a second way to define the weights on the edges of the graph by considering the geometric features of each superpixel in the graph. We assign to each vertex (superpixel) $v_i$ a vector ${\mathbf{x}}_i$ whose components are the area, equivalent diameter, compactness, circularity, solidity, rectangularity, aspect ratio, eccentricity, major axis length and minor axis length of the superpixel [61].

A third way we consider in this paper to define the edge weights is based on superpixel texture features derived from the local binary patterns (LBP) [62] and the gray-level co-occurrence matrix (GLCM). In our work, we used the uniform rotation-invariant version of the LBP histograms [62], calculated from the gray-scale components of the skin lesion images. We computed the LBP features using 8 sampling points around the central pixel with a radius $R=1$ [62]. Thus, each superpixel (vertex) $v_i$ is described by a 10-dimensional LBP histogram. The GLCM is computed for each superpixel in 4 orientations $(0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ })$. Some statistical second-order features proposed by Haralick and Shanmugam [63] were calculated from those GLCMs. There are also other ways to define the weights on the edges. For instance, instead of using the Gaussian weighting function (1), we may consider other types of probability distributions. For instance, we may consider the exponential distribution

$$\begin{array}{c}\hfill f(x)=\frac{1}{2}{e}^{-|x|},x\in \mathbb{R}.\end{array}$$ 3

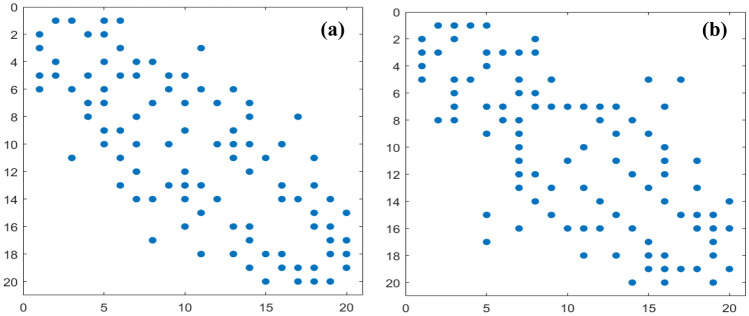
Figure 5 presents the adjacency matrices of the constructed unweighted graphs of two melanoma and benign samples, respectively. Each adjacency matrix is a 2D array $A=(a_{\mathit{ij}})$ of size $20\times 20$ as the graph is composed of 20 nodes, and this matrix is symmetric since the graph is undirected. The matrix elements $a_{\mathit{ij}}=1$ (colored with blue dots) indicate that there is an edge between vertex $v_i$ and vertex $v_j$. The slots $a_{\mathit{ij}}=0$ (with no blue dots) mean that there is no edge between the corresponding vertices. Figure 5 (a) shows the adjacency matrix of the unweighted graph for a sample melanoma image (ISIC_0010080), and Fig. 5 (b) shows the adjacency matrix of the unweighted graph for a sample benign image (ISIC_000000).

Fig. 5.

Visualization of the graph connectivity matrices of dermoscopic images. (a) Melanoma, (b) benign

Structural Graph Features

Different structural graph features were computed in the time and frequency domains in order to differentiate between benign and malignant skin lesions. The time-domain features measure both local and global graph aspects, while the frequency-domain features are derived from the graph Fourier transform (GFT). We recall that we have constructed two types of graph signals for skin lesion images, namely unweighted and weighted graph signals, with three types of weight values. Denote by $l_{\mathit{ij}}$ any of the weights between the graph nodes $v_i$ and $v_j$ as defined in Eq. (1). Recall also that our graphs are simple, connected and undirected. The shortest path length between $v_i$ and $v_j$, ${\gamma }_{\mathit{ij}}$, is defined in the case of an unweighted graph to be the number of edges of the shortest path that connects $v_i$ and $v_j$. In the case of a weighted graph, the shortest path distance between $v_i$ and $v_j$, ${\delta }_{\mathit{ij}}$, is defined to be the minimum sum of weights taken over all paths that connect $v_i$ and $v_j$. Since our graphs are connected, then $0<{\gamma }_{\mathit{ij}}$, ${\delta }_{\mathit{ij}}<\infty$. Define the inverse shortest-path length of a pair of graph nodes for unweighted and weighted graphs respectively as

$$\begin{array}{c}\hfill {ϵ}_{\mathit{ij}}=\frac{1}{{\gamma }_{\mathit{ij}}},{\epsilon }_{\mathit{ij}}=\frac{1}{{\delta }_{\mathit{ij}}}.\end{array}$$ 4

Features in the Time Domain

The time-domain (or vertex-domain) features of a graph are those directly extracted without applying any transforms. After constructing each graph, its structure is analyzed at two different levels ranging from characteristics that distinguish the whole graph at the global scale to characteristics of the basic graph components (nodes) at the local scale. The characterization of the graph structural features is of a major significance to understand and measure the complex graph dynamics. For each superpixel graph, 6 local measures and 5 global measures were computed. Each global feature measures only one value that captures specific information about the distribution of the superpixels, while the local features represent discriminative signatures having 20 values for each local feature corresponding to the $N=20$ nodes of the image graph. The full feature vector in the time domain contains 125 feature values corresponding to 20 superpixels $\times$ 6 local features in addition to 5 global features.

Local Graph Measures

The local features computed in our framework include the local efficiency (LE), local clustering coefficient (LCC), nodal strength (NS), nodal betweenness centrality (NBC), closeness centrality (CC) and eccentricity (Ecc) [64].

1. Local efficiency (LE): The local efficiency of each graph G is defined to be an N-dimensional vector ${(E_g(G_1),E_g(G_2),\cdots ,E_g(G_N))}^{\top }$ , where $G_i$ is the subgraph of G of the neighbors of the node $v_i$, and $E_g(·)$ is the global efficiency defined in Eq. (11) [65].

2. Local clustering coefficient (LCC): The local clustering coefficient of a graph node quantifies the extent to which node neighbors form a complete subgraph [65]. The LCC is an N-dimensional vector whose components are

   $$\begin{array}{c}\hfill C_{\mathit{loc}}(v_i)=\frac{2\times |E_{v_i}|}{k_i\times (k_i-1)},i=1,\cdots ,N,\end{array}$$ 5

   where $k_i$ is the degree of node $v_i$ and $|E_{v_i}|$ is the number of edges between the neighbors of node $v_i$.
3. Nodal strength (NS): The nodal strength measures the strength of each node $v_i$ as

   $$\begin{array}{c}\hfill N_s(v_i)=\left\{\begin{array}{cc}{k}_i,\hfill & \{G\}\text{is unweighted},\hfill \\ {\displaystyle \sum _{e_{\mathit{ij}}\in E}{l}_{\mathit{ij}},}\hfill & \{G\}\text{is weighted}.\hfill \end{array}\right)\end{array}$$ 6

   The nodal strength of the graph is the ${\mathbb{R}}^N$vector whose components are $N_s(v_i)$.

4. Nodal betweenness centrality (NBC): The nodal betweenness centrality is a centrality metric that measures the significance of the node $v_i$ in the graph G by counting the number of all shortest paths across the graph that pass through the node $v_i$ [66]. Let ${\displaystyle {\sigma }_{\mathit{mn}}}{\sigma }_{\mathit{mn}}$ be the total number of shortest paths from node ${\displaystyle m}m$ to node ${\displaystyle n}n$ and ${\displaystyle {\sigma }_{\mathit{mn}}(v_i)}{\sigma }_{\mathit{mn}}(v_i)$ and be the number of those paths that pass through ${\displaystyle v_i}{v}_i$. The betweenness centrality measure of the node $v_i$  within the graph G is defined in [66] as

   $$\mathcal{B}(v_i)=\sum _{m\ne n\ne i}\frac{{\sigma }_{\mathit{mn}}(v_i)}{{\sigma }_{\mathit{mn}}},$$ 7
5. Closeness centrality (CC): The closeness centrality of a graph node is the average length of the shortest path from that node to all other graph nodes. The components of the CC vector are defined to be

   $$\begin{array}{c}\hfill \mathcal{C}(v_i)=\frac{N}{{\displaystyle \sum _{j=1}^N{ϵ}_{\mathit{ij}}}},i=1,\cdots ,N.\end{array}$$ 8

   See [67].
6. Eccentricity (Ecc): The eccentricity of a graph node is the maximum distance between that node and any other node in G:

   $$\begin{array}{c}\hfill \mathcal{E}(v_i)=\left\{\begin{array}{cc}\underset{j\in G}{max}{\gamma }_{\mathit{ij}},\hfill & \{G\}\text{is unweighted},\hfill \\ \underset{j\in G}{max}{\delta }_{\mathit{ij}},\hfill & \{G\}\text{is weighted}.\hfill \end{array}\right)\end{array}$$ 9

We may also replace or augment the aforementioned 120 local graph features by other statistical measures. See the conclusions below. It should be noted that the local features are the ${\mathbb{R}}^{20}$ vectors defined above. Since there is no correspondence between nodes of lesion images, we may redefine these vectors by rearranging the components in an increasing order of different statistical values. However, in this paper, we consider these vectors as defined and still we can get good results. Likewise, the same process can be applied for the features defined in the frequency domain.

Global Graph Measures

The global graph features computed in our framework include the characteristic path length (CPL), global efficiency (GE), global clustering coefficient (GCC), density (D) and global assortativity (GA) [64].

1. Characteristic path length (CPL): The CPL is defined as the average shortest-path distance [68]:

   $$\begin{array}{c}\hfill L(G)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{N(N-1)}\sum _{i\ne j}{\gamma }_{\mathit{ij}},}\hfill & \{G\}\text{is unweighted},\hfill \\ {\displaystyle \frac{1}{N(N-1)}\sum _{i\ne j}{\delta }_{\mathit{ij}},}\hfill & \{G\}\text{is weighted}.\hfill \end{array}\right)\end{array}$$ 10
2. Global efficiency (GE): The global efficiency is the average inverse shortest-path distance [65, 69]:

   $$\begin{array}{c}\hfill E_g=\left\{\begin{array}{cc}{\displaystyle \frac{1}{N(N-1)}\sum _{i\ne j}{ϵ}_{\mathit{ij}},}\hfill & \{G\}\text{is unweighted},\hfill \\ {\displaystyle \frac{1}{N(N-1)}\sum _{i\ne j}{\epsilon }_{\mathit{ij}},}\hfill & \{G\}\text{is weighted}.\hfill \end{array}\right)\end{array}$$ 11
3. Global clustering coefficient (GCC): Let $C_{\mathit{loc}}(v_i)$ denote the local clustering coefficient defined in Eq. (5). The GCC is defined to be, [65],

   $$\begin{array}{c}\hfill C_g(G)=\frac{1}{N}\sum _{i=1}^N{C}_{\mathit{loc}}(v_i).\end{array}$$ 12

   This coefficient measures the average of the local clustering coefficients of an unweighted graph.
4. Density (D): Let |E| denote the total number of edges of an unweighted graph. The density is defined to be [65]

   $$\begin{array}{c}\hfill D(G)=\frac{2|E|}{N(N-1)}.\end{array}$$ 13
5. Global assortativity (GA): The global assortativity of a graph measures the tendency of the vertices to connect to similar vertices. In other words, [70, 71], it measures how much a node with a positive degree tends to connect to other correlated nodes, rather than its neighbors. The global assortativity can be expressed through the Pearson correlation coefficient as [70]

   $$\begin{array}{c}\hfill r=\frac{{\displaystyle \sum _{i=1}^{|E|}\left[\frac{j_i{k}_i}{|E|},-,{\left({\displaystyle \sum _{i=1}^{|E|}\frac{j_i+k_i}{{2|E|}^{3/2}}}\right)}^2\right]}}{{\displaystyle \sum _{i=1}^{|E|}\left[\frac{j_i+k_i}{2|E|},-,{\left({\displaystyle \sum _{i=1}^{|E|}\frac{j_i+k_i}{{2|E|}^{3/2}}}\right)}^2\right]}},\end{array}$$ 14

   where $j_i$ and $k_i$ represent the degrees of the vertices at the ends of the edge i. The assortativity r lies between $-1$ and 1, where $r=1$ represents perfect assortativity. For $0\le r\le -1$, the graph is non-assortative, and for $r=-1$, the graph is totally dis-assortative.

Features in the Frequency Domain

We present here two ways to define the graph Fourier transform (GFT) for a graph signal. Let A be the adjacency matrix for the graph. We define the associated Laplacian matrix to be

$$\begin{array}{cc}\hfill L=& D-A,\hfill \end{array}$$ 15

where $D=(d_{\mathit{ij}})$ is the diagonal degree matrix defined in Section 4. The Laplacian matrix L is a symmetric matrix which has a set of N real eigenvalues $\mathrm{\Lambda }=\{{\lambda }_0,{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_{N-1}\}$ with the corresponding set of orthonormal eigenvectors $U=\{u_0,u_1,\cdots ,u_{N-1}\}$. Hence, we have the orthogonal diagonalization relation

$$\begin{array}{cc}\hfill L=& U^{†}\mathrm{\Lambda }U.\hfill \end{array}$$ 16

According to [31, 72, 73], the GFT associated with L of a graph signal $f=\{f_0,f_1,\cdots ,f_{N-1}\}$ is defined to be

$$\begin{array}{c}\hfill \widehat{f}=Uf.\end{array}$$ 17

The inversion formula is merely

$$\begin{array}{c}\hfill f=U^{†}\widehat{f}.\end{array}$$ 18

Similar GFT pairs can be defined for weighted graphs. The other way to define the GFT established in [53, 74] is based on considering the diagonalization of the symmetric adjacency matrix only. In our work, we consider the GFT as defined in [72]. In addition to the vector $\widehat{f}$, other features we extract from the GFT of the graph signals are: energy, power, entropy and amplitude. In this paper, the total number of possible graph features in the frequency domain is 24 features.

Conventional Features

In addition to the graph-based features, we computed other conventional image features as well. The features are extracted from rectangular pixel windows instead of the superpixels as in the graph-based approach. The extracted conventional features are categorized into texture, color and geometrical features [36]. Because of the importance of color, we computed color features in different color spaces, namely, RGB, CIELAB, CIE LUV and HSV. These color representations exhibit robustness against uncontrolled imaging conditions [75].

For each skin lesion image, we extracted a total of 394 conventional features. As well, we extracted color, texture and geometric features for the associated superpixel graph signal. 

Melanoma Detection System

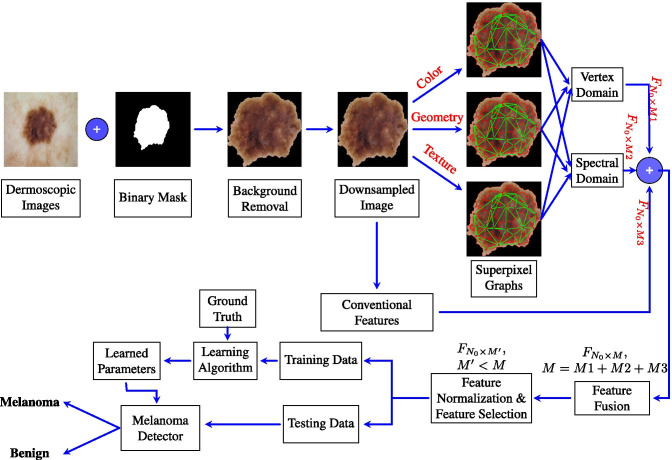
Figure 6 shows the overall design of the proposed melanoma detection system. For each input dermoscopic image of an $N_0-$image dataset, the associated binary mask is applied to remove the background. All of the images are resampled to a size of $750\times 750$. Then, graph-based and conventional features are computed for each image as described in Sections 5 and 6, respectively. For the graph-based features, a superpixel segmentation algorithm (Section 4) is applied and superpixel graphs are built based on color, geometry and texture. The graph-based features include $M1=125$ time-domain features and $M2=24$ spectral graph features. Other $M3=394$ conventional features are directly computed from the input image (Section 6). The overall set of $M=M1+M2+M3$ computed features is fused together to form the complete lesion image descriptor. The features are then normalized so that each feature contributes approximately proportionately to the final learning outcomes. Feature subset selection is performed to select the $M^{\prime }$ most discriminative features. The data are hence divided into training and test sets, where a learning algorithm is applied to the training set to train a melanoma detector which can then be applied to the test set to assess the classifier performance.

Fig. 6.

Block diagram of the proposed melanoma detection system

Results and Discussion

Experimental Setup

The proposed melanoma detection system was trained and tested using the two datasets described in Subsection 3.1. The results were compared with state-of-the-art methods [36]. We applied a 10-fold cross-validation scheme to each of the two datasets and computed the average performance metrics, namely the accuracy (AC), sensitivity (SN), specificity (SP) and the area under the receiver operating characteristics (ROC) curve. The following classifiers were trained and tested: support vector machines (SVM) [76, 77] with three different kernels (RBF, sigmoid, polynomial), K-nearest neighbors (KNN) [78], the multilayer perceptron (MLP) [77] and random forests (RF) [79].

Detection Performance Using the ISIC 2017 Dataset

First of all, we tested the detection performance on the ISIC 2017 dataset. The computed features were those of the color, geometry and texture features of unweighted superpixel graphs (Section 5) as well as conventional features (Section 6) of pigmented skin lesions. This leads to very low sensitivities, accuracies and AUCs, while the specificities are relatively high. Indeed, the best classifier in this case is the SVM with a sigmoid kernel which scored merely an AUC of $57\%$. The low sensitivity is due to the fact that the classifiers became biased toward the majority (benign) class and found it hard to learn the minority (melanoma) class due to the scarcity of the melanoma data samples.

Detection Performance Using the Augmented ISIC 2017 Dataset

To investigate classifier performance with relatively better class balance, we ran experiments on the augmented ISIC 2017 dataset. Table 2 gives the detection performance for two families of features, namely the conventional features (Section 6) and the combination of conventional and graph features. The best performance was obtained using the RF classifier and the combination of the conventional and graph features as shown in Table 2. There is a clear relative improvement using this feature combination over the case where conventional features only are used. In comparison to Table 1, using the augmented dataset, we obtained almost perfect performance metrics.

Table 2.

Melanoma detection performance using the augmented ISIC 2017 dataset. Performance is shown for seven classifiers and two feature types (conventional features (Conv) [36], and the best combination of conventional and unweighted graph features (Graph+Conv)). Performance metrics are the accuracy (AC), sensitivity (SN) and specificity (SP)

		SVM	SVM	SVM	KNN	MLP	RF
		(RBF)	(Sigmoid)	(Poly)
	AC	84.12	70.09	82.71	78.94	85.70	89.30
Conv	AUC	96.44	55.30	89.85	91.67	97.38	96.81
	SN	100.0	99.38	100.0	98.14	80.95	88.00
	SP	71.75	58.96	75.81	63.01	74.20	89.70
	AC	88.41	74.05	94.29	83.91	89.45	97.95
Graph	AUC	97.90	79.84	79.84	94.41	98.37	99.89
+Conv	SP	99.31	84.43	93.77	98.27	98.62	99.31
	SN	78.20	65.05	95.16	70.24	81.66	97.23

Table 1.

Melanoma detection performance using the ISIC 2017 dataset. Performance is shown for six classifiers and two feature types (conventional features (Conv) [36], and the combination of conventional and unweighted graph features (Graph+Conv)). Performance metrics are the accuracy (AC), sensitivity (SN) and specificity (SP)

		SVM	SVM	SVM	KNN	MLP	RF
		(RBF)	(Sigmoid)	(Poly)
	AC	54.53	61.40	52.51	52.32	56.76	47.30
Conv	AUC	56.26	57.01	57.00	46.53	52.09	49.68
	SN	40.15	64.48	23.94	39.77	38.22	1.93
	SP	72.20	60.62	83.40	66.80	77.99	94.59
	AC	50.58	61.97	52.51	52.53	51.54	48.07
Graph	AUC	53.52	50.00	50.03	49.59	53.55	53.84
+Conv	SN	34.36	67.18	13.13	35.52	25.87	1.02
	SP	72.54	59.46	93.82	71.81	80.69	96.14

Detection Performance Using Unweighted Superpixel Graph Features

Unweighted superpixel graph features can be broadly divided into two categories, namely features that depend on the graph structure only and features that depend on both of the graph structure and the graph nodal signal as well. The first category of features that are independent of the graph signal include local features (Eq. (5) – (9)) and global features (Eq. (10) – (14)). Table 3 shows the melanoma detection performance for this category of features using the local features, global features, local and global features and their combination with conventional features. The RF classifier outperforms all of the other classifiers on all performance metrics using the combination of all of the graph and convnetional features. Also, the detection results using local graph features are generally better than those of the global features. Moreover, the combined local and global features gave better results in comparison to either the local or the global features. In particular, the RF classifier achieved a $97.23\%$ accuracy, a $100\%$ sensitivity, a $95.5\%$ specificity and a $99.79\%$ AUC with the combination of conventional and graph features. The second category of features that are dependent on both graph structure and signal include the graph Fourier transform (GFT) coefficients (Eq. (17)) and GFT-based statistical measures. Tables 4, 5 and 6 show the detection performance for this category with graph features derived from color, geometry and texture information, respectively. In each table, the performance is shown for the GFT-based features, the GFT features combined with local and global features and finally the combination of all of these features with the conventional features. For color-based unweighted graph features of Table 4, the combination of the conventional and GFT features gives the best overall performance metrics: a $96.89\%$ accuracy, a $100\%$ sensitivity, a $94.81\%$ specificity and a $99.71\%$ AUC. Similarly, this combination of GFT and convnetional features gives the best overall performance for geometry-based and texture-based unweighted graph features of Tables 5, 6, respectively. In summary, in terms of the AUC metric, the texture-based unweighted graph features lead to the highest performance (AUC$=99.96\%$), followed by the color-based ones (AUC$=99.92\%$), and finally the geometry-based ones (AUC$=99.85\%$).

Table 3.

Melanoma detection performance using graph-signal-independent features of unweighted graphs. The skin lesion feature descriptors depend only on the graph structure and include local features (C), global features (G), local and global features (C+G) and their combination with conventional features (C+G+Conv)

		C	G	C+G	C+G+Conv
	AC	59.0	53.81	65.4	89.62
SVM	AUC	59.73	57.62	69.06	98.88
(RBF)	SN	53.63	43.6	65.4	100.0
	SP	68.86	68.51	71.28	81.66
	AC	55.71	59.0	59.86	71.11
SVM	AUC	51.72	54.56	49.58	79.33
(Sigmoid)	SN	64.36	59.52	68.86	83.04
	SP	56.4	74.05	52.25	62.28
	AC	55.88	50.17	55.36	93.25
SVM	AUC	51.72	54.56	49.58	79.33
(Poly)	SN	31.83	5.19	34.26	96.54
	SP	82.01	99.31	83.04	92.04
	AC	55.71	53.63	57.79	86.33
KNN	AUC	54.92	54.71	59.22	94.16
	SN	44.29	52.6	46.02	98.27
	SP	71.97	62.63	73.01	77.16
	AC	59.0	56.92	60.9	89.97
MLP	AUC	59.25	57.93	61.75	99.16
	SN	59.52	51.56	58.13	99.31
	SP	63.32	64.36	66.09	81.66
	AC	52.94	52.77	52.42	97.23
RF	AUC	61.37	53.2	63.69	99.79
	SN	8.304	27.34	8.304	100.0
	SP	98.96	79.93	97.58	95.5

Table 4.

Melanoma detection performance using color-signal-dependent features of unweighted graphs. The skin lesion feature descriptors include local features (C), global features (G), graph Fourier transform features (GFT), the combination of the three feature types (C+G+GFT) and their combination with conventional features (All)

		GFT	C+G+GFT	GFT+Conv	All
	AC	50.52	60.73	89.62	88.93
SVM	AUC	53.96	63.95	99.03	98.31
(RBF)	SN	50.17	56.75	99.65	100.0
	SP	54.67	65.4	81.31	79.93
	AC	52.08	55.54	77.34	77.68
SVM	AUC	54.54	49.99	89.21	87.13
(Sigmoid)	SN	57.09	62.63	93.43	91.7
	SP	51.21	54.67	66.44	63.67
	AC	52.25	58.13	91.18	92.73
SVM	AUC	54.54	49.99	89.21	87.13
(Poly)	SN	18.69	29.76	98.62	95.5
	SP	95.5	88.93	85.47	92.04
	AC	51.73	56.4	84.26	86.51
KNN	AUC	49.61	57.9	96.74	94.58
	SN	40.48	44.98	100.0	98.27
	SP	63.67	71.28	68.51	76.82
	AC	50.69	60.38	89.79	89.79
MLP	AUC	53.31	63.22	99.3	98.84
	SN	47.75	57.09	100.0	100.0
	SP	58.48	68.51	80.97	81.66
	AC	50.35	52.08	97.58	96.89
RF	AUC	53.85	62.94	99.92	99.71
	SN	4.498	5.882	100.0	100.0
	SP	98.62	99.65	95.16	94.81

Table 5.

Melanoma detection performance using geometry-signal-dependent features of unweighted graphs. The skin lesion feature descriptors include local features (C), global features (G), graph Fourier transform features (GFT), the combination of the three feature types (C+G+GFT) and their combination with conventional features (All)

		GFT	C+G+GFT	GFT+Conv	All
	AC	59.69	58.82	90.66	89.97
SVM	AUC	53.43	59.2	99.13	99.3
(RBF)	SN	36.33	47.75	99.65	100.0
	SP	91.35	73.7	82.01	80.97
	AC	55.54	56.06	78.55	75.09
SVM	AUC	52.44	51.78	87.35	85.96
(Sigmoid)	SN	55.36	61.94	96.54	92.04
	SP	63.67	50.87	67.13	62.98
	AC	51.73	55.88	88.24	92.39
SVM	AUC	52.44	51.78	87.35	85.96
(Poly)	SN	6.92	24.57	95.5	94.81
	SP	99.31	88.24	83.74	91.7
	AC	55.36	53.98	85.47	84.08
KNN	AUC	58.79	56.87	96.29	93.59
	SN	43.25	32.18	99.31	95.16
	SP	73.01	78.89	72.66	76.82
	AC	63.67	58.13	89.97	89.27
MLP	AUC	66.35	59.41	99.51	99.18
	SN	51.56	44.98	100.0	100.0
	SP	77.85	71.28	80.62	80.62
	AC	59.52	56.57	97.4	96.71
RF	AUC	67.91	68.88	99.85	99.78
	SN	31.49	19.03	100.0	100.0
	SP	89.62	94.81	94.81	96.19

Table 6.

Melanoma detection performance using texture-signal-dependent features of unweighted graphs. The skin lesion feature descriptors include local features (C), global features (G), graph Fourier transform features (GFT), the combination of the three feature types (C+G+GFT) and their combination with conventional features (All)

		GFT	C+G+GFT	GFT+Conv	All
	AC	52.6	59.86	89.27	87.72
SVM	AUC	52.03	61.11	98.89	98.44
(RBF)	SN	56.4	53.29	100.0	98.96
	SP	51.9	66.44	79.58	77.16
	AC	53.46	57.61	78.89	75.09
SVM	AUC	54.71	51.77	89.37	85.14
(Sigmoid)	SN	55.36	68.17	95.16	93.08
	SP	57.79	50.17	65.05	61.94
	AC	50.52	54.84	90.48	92.91
SVM	AUC	54.71	51.77	89.37	85.14
(Poly)	SN	15.22	24.91	97.58	94.81
	SP	93.77	88.93	85.12	92.39
	AC	53.81	57.09	84.6	85.99
KNN	AUC	51.41	58.82	97.49	94.65
	SN	53.63	48.44	99.65	98.27
	SP	54.33	65.74	69.9	74.74
	AC	52.42	60.9	90.48	89.97
MLP	AUC	54.65	61.18	99.73	98.67
	SN	54.67	57.44	100.0	99.65
	SP	52.94	68.17	80.97	81.31
	AC	53.29	53.46	97.23	96.89
RF	AUC	57.87	64.78	99.96	99.77
	SN	9.689	8.304	100.0	99.31
	SP	96.89	98.96	94.46	95.5

Detection Performance Using Weighted Graph Features

Weighted superpixel graph features account for the importance of the relations between superpixels through edge weight functions based on color, geometry and texture information (Eq. (1)). Tables 7, 8 and 9 show the detection performance for the weighted superpixel graph features derived from color, geometry and texture information, respectively. In each table, the performance is shown for the local features, global features, combined local and global features, the GFT-based features, the GFT features combined with local and global features, the conventional features combined with local and global features and finally the combination of all of these features.

Table 7.

Melanoma detection performance using color-based weighted graph features. The skin lesion feature descriptors include local features (C), global features (G), local and global features (C+G), graph Fourier transform features (GFT), local, global and GFT features (C+G+GFT), local, global and conventional features (C+G+Conv), GFT and conventional features (GFT+Conv) and the combination of all features (All). The performance metrics for each classifier are the accuracy (AC), specificity (SP) and sensitivity (SN)

		C	G	C+G	GFT	C+G+GFT	C+G+Conv	GFT+Conv	All
	AC	61.25	59.0	59.69	52.6	58.65	90.83	90.83	89.45
SVM	AUC	62.11	62.44	64.02	56.81	61.84	99.21	98.94	98.95
(RBF)	SN	63.32	53.63	56.4	56.4	56.75	100.0	100.0	100.0
	SP	59.86	65.4	64.71	58.48	64.71	82.35	82.01	79.58
	AC	59.52	59.52	58.48	52.08	59.69	77.68	78.89	75.61
SVM	AUC	52.45	62.38	47.65	53.1	46.06	87.95	86.54	86.66
(Sigmoid)	SN	70.59	50.52	68.17	57.44	69.55	95.16	92.73	95.85
	SP	52.94	68.86	55.36	54.67	56.06	66.44	66.09	61.94
	AC	52.25	50.0	52.94	50.35	51.9	94.46	89.97	94.29
SVM	AUC	52.45	62.38	47.65	53.1	46.06	87.95	86.54	86.66
(Poly)	SN	11.76	1.73	15.22	17.65	8.651	96.19	96.54	95.5
	SP	93.08	100.0	93.43	94.12	96.19	93.08	85.47	94.46
	AC	57.61	54.84	57.61	58.65	57.44	86.51	83.74	87.02
KNN	AUC	60.49	56.66	60.48	59.14	59.62	96.55	96.62	96.29
	SN	46.71	52.25	50.52	53.63	50.52	98.27	99.31	99.31
	SP	75.09	61.25	71.28	65.05	72.32	74.74	69.9	77.16
	AC	57.79	60.38	59.17	52.94	59.69	90.83	89.27	89.79
MLP	AUC	60.24	62.32	63.99	54.39	57.59	98.89	99.29	98.85
	SN	57.44	58.82	49.13	47.4	52.6	100.0	100.0	100.0
	SP	64.36	63.67	69.55	58.82	67.82	83.74	78.89	81.66
	AC	50.87	54.15	51.38	50.35	51.56	98.27	97.4	97.58
RF	AUC	61.82	60.52	64.54	55.97	63.82	99.86	99.89	99.8
	SN	2.076	26.99	3.46	3.114	3.46	99.65	100.0	98.96
	SP	100.0	85.12	100.0	99.31	100.0	97.58	96.19	96.89

Table 8.

Melanoma detection performance using geometry-based weighted graph features. The skin lesion feature descriptors include local features (C), global features (G), local and global features (C+G), graph Fourier transform features (GFT), local, global and GFT features (C+G+GFT), local, global and conventional features (C+G+Conv), GFT and conventional features (GFT+Conv) and the combination of all features (All). The performance metrics for each classifier are the accuracy (AC), specificity (SP) and sensitivity (SN)

		C	G	C+G	GFT	C+G+GFT	C+G+Conv	GFT+Conv	All
	AC	59.0	54.33	57.09	56.75	56.92	89.79	89.97	87.2
SVM	AUC	58.95	52.2	58.66	50.47	58.25	98.14	98.96	98.14
(RBF)	SN	56.4	45.33	51.56	25.95	53.98	99.31	99.65	99.65
	SP	63.67	67.47	65.74	90.31	65.4	81.66	81.66	76.12
	AC	59.86	52.6	59.52	59.34	56.4	75.78	74.74	74.39
SVM	AUC	52.02	53.21	49.83	51.79	49.86	81.69	86.91	79.41
(Sigmoid)	SN	67.13	38.06	69.55	51.9	68.86	91.35	92.73	87.2
	SP	52.6	79.93	54.67	66.78	53.29	64.36	62.28	65.05
	AC	53.81	50.87	54.15	51.73	51.56	94.81	90.31	92.73
SVM	AUC	52.02	53.21	49.83	51.79	49.86	81.69	86.91	79.41
(Poly)	SN	16.26	2.422	16.96	6.228	10.73	94.81	97.92	94.12
	SP	92.04	100.0	91.35	98.27	95.5	94.81	84.78	93.77
	AC	52.94	52.6	52.6	60.21	50.35	87.2	86.68	85.29
KNN	AUC	51.97	52.93	54.56	63.31	51.49	95.35	96.72	93.05
	SN	37.72	49.48	45.67	51.56	27.68	97.58	99.65	93.77
	SP	68.51	57.79	67.47	69.55	77.85	78.89	74.74	78.2
	AC	56.92	53.81	57.79	63.67	56.4	89.97	89.27	89.1
MLP	AUC	59.54	53.22	59.63	64.07	57.73	99.14	99.48	98.51
	SN	52.94	53.29	50.87	51.56	48.79	99.31	100.0	99.31
	SP	64.71	61.94	67.13	76.47	67.13	81.31	80.97	80.97
	AC	51.04	55.36	51.73	57.61	52.77	98.62	97.58	97.4
RF	AUC	59.28	52.94	59.51	68.78	68.01	99.86	99.91	99.83
	SN	3.114	29.07	4.498	27.68	11.76	100.0	100.0	99.65
	SP	100.0	84.08	100.0	88.58	95.85	97.23	95.16	95.16

Table 9.

Melanoma detection performance using texture-based weighted graph features. The skin lesion feature descriptors include local features (C), global features (G), local and global features (C+G), graph Fourier transform features (GFT), local, global and GFT features (C+G+GFT), local, global and conventional features (C+G+Conv), GFT and conventional features (GFT+Conv) and the combination of all features (All). The performance metrics for each classifier are the accuracy (AC), specificity (SP) and sensitivity (SN)

		C	G	C+G	GFT	C+G+GFT	C+G+Conv	GFT+Conv	All
SVM (RBF)	AC	59.34	55.36	58.65>	52.08	58.82	87.54	89.45	88.41
	AUC	61.76	54.88	58.66	51.84	60.38	98.28	98.79	97.9
	SN	57.79	49.13	52.94	55.36	58.82	98.96	99.31	99.31
	SP	65.74	68.86	66.44	55.71	64.71	78.89	79.93	78.2
SVM (Sigmoid)		57.96	55.54	55.02	52.42	57.96	77.85	75.78	74.05
	AUC	50.04	55.78	51.89	53.26	45.97	82.94	87.55	79.84
	SN	68.51	43.25	64.36	56.4	67.82	87.54	92.73	84.43
	SP	49.13	84.08	51.56	54.67	54.67	68.17	64.71	65.05
SVM (Poly)	AC	54.5	50.35	54.67	47.58	51.9	93.43	89.62	94.29
	AUC	50.04	55.78	51.89	53.26	45.97	82.94	87.55	79.84
	SN	16.26	2.076	19.38	9.689	10.73	95.5	96.19	93.77
	SP	94.81	100.0	92.73	92.04	95.5	94.12	84.43	95.16
KNN	AC	52.94	53.98	55.19	55.71	54.15	84.43	83.04	83.91
	AUC	53.12	53.53	55.82	56.64	54.57	94.75	96.51	94.41
	SN	33.56	49.13	39.1	64.01	44.64	97.92	100.0	98.27
	SP	75.09	58.82	71.97	54.67	67.13	73.7	67.82	70.24
MLP	AC	56.92	54.33	56.57	53.29	56.4	89.79	90.48	89.45
	AUC	59.93	57.79	60.26	52.8	59.47	98.68	99.25	98.37
	SN	51.9	54.67	52.25	51.21	48.44	99.65	99.65	98.62
	SP	66.44	60.9	65.74	56.06	67.82	82.35	81.66	81.66
RF	AC	50.35	53.63	51.21	53.46	51.21	97.23	98.44	97.75
	AUC	59.01	55.41	58.61	58.76	60.68	99.86	99.89	99.89
	SN	2.768	26.64	2.422	12.46	2.768	98.96	100.0	99.31
	SP	100.0	85.12	100.0	96.89	100.0	96.19	96.89	97.23

For color-based weighted graph features of Table 7, the combination of the conventional and GFT features gives the best overall performance metrics: a $97.4\%$ accuracy, a $100\%$ sensitivity, a $96.19\%$ specificity and a $99.89\%$ AUC. Similarly, this combination of GFT and convnetional features gives the best overall performance for geometry-based and texture-based weighted graph features of Tables 8, 9, respectively.

Several remarks are in order. First, we realize that the geometry-based weighted features lead to the best reported AUC ($99.91\%$). However, both of the texture- and color-based weighted graph features lead to a very close result (AUC$=99.89\%$). Secondly, the RF classifier generally gives the best performance among other classifiers. Thirdly, the performance with unweighted graph features is generally slightly better than that of the weighted graph features. This might hint at the need for better methods for graph weight selection. Fourthly, the local graph features are essentially better than global ones for melanoma detection. Generally, small improvements occur if the two types are combined together. Finally, the spectral GFT features lead to the best performance if they are combined with the conventional features (but not with the structural graph features).

ROC Performance Analysis

Figure 7 shows the receiver operating characteristic (ROC) curves for the proposed melanoma detection system for the aforementioned unweighted and weighted graph models. Figure 7 (a), (b) and (e) shows the ROC curves and the areas under the curve (AUC) for classifiers based on unweighted graph features using color, geometric and texture graph signals, respectively. The best performing classifiers are the RF, MLP and SVM with the RBF kernel. Figure 7 (b), (d) and (f) shows corresponding curves for the weighted graph features based on color, geometry and texture information. Again, the best performance classifiers are the RF, MLP and SVM with the RBF kernel.

Fig. 7.

ROC curves of all features (local, global and GFT of constructed graphs and conventional skin lesion features) using different classifiers. The mean and uncertainty of the area under the curve (AUC) are shown in parentheses for each classifier. Results are shown for 6 graph models: (a) Unweighted graph with color signal. (b) Weighted graph with color signal. (c) Unweighted graph with geometric signal. (d) Weighted graph with geometric signal. (e) Unweighted graph with texture signal. (f) Weighted graph with texture signal

Comparison with State-of-the-Art Melanoma Detection Methods

We compare the performance of our proposed graph-theoretic approach against the state-of-the-art methods listed in Table 10. For the first four methods [27 ,36 ,39 ,40], the proposed systems were trained and tested on the ISIC 2016 dataset. Although the method of Oliveira et al. [36] is based merely on hand-crafted features, this method still clearly outperforms the other three deep learning methods on the accuracy, sensitivity and specificity metrics. In particular, the methods in [39] and [27] have modest sensitivity scores. This shows that deep learning methods are not necessarily better than conventional ones. Compared to the four methods, our method shows even better performance metrics on the more challenging augmented ISIC 2017 dataset.

Table 10.

Performance comparison of different automated melanoma detection methods. The performance metrics for each classifier are the area under the curve (AUC) the accuracy (AC), specificity (SP) and sensitivity (SN)

Author	Year	Dataset	Features	Classifier	AUC	AC	SP	SN.
Majtner et al. [59]	2016	ISIC2016	RSurf, LBP, CNN-based	SVM	0.78	$82.60\%$	$89.80\%$	$53.30\%$
Gutman et al. [42]	2016	ISIC2016	Deep features	Deep Networks	0.80	$85.50\%$	$94.10\%$	$50.70\%$
Oliveira et al. [74]	2017	ISIC2016	Texture, color, geometric features	Ensemble of classifiers	−	$94.30\%$	$96.70\%$	$91.80\%$
Lopez et al. [54]	2017	ISIC2016	Deep features	VGG16 CNN	−	$81.33\%$	$84.00\%$	$78.66\%$
González-Díaz [39]	2018	ISIC2017	Deep features	CNN	0.87	−	−	−
Menegola et al. [62]	2017	ISIC2017	Deep features	VGG16 network	0.91	$72.10\%$	$95.00\%$	$54.70\%$
Esteva et al. [30]	2017	Images from ISIC, the Edinburgh Dermofit Library and the Stanford Hospital	Deep features	CNN	0.94	$72.10\%$	−	−
Matsunaga et al.[61]	2017	ISIC2017 + 1444 ISIC images	Deep features	CNN Ensemble	0.92	−	−	−
Reboucas Filho et al.[78]	2018	ISIC2017	GLCM, LBP, Hu moments	SVM	0.89	$89.93\%$	$89.90\%$	$92.15\%$
		ISIC2016	GLCM, LBP, Hu moments	SVM	0.92	$94.50\%$	94.57	$95.23\%$
		PH2	GLCM, LBP, Hu moments	SVM	0.99	$99.00\%$	99.20	$99.40\%$
Mahbod et al. [81]	2019	ISIC2017	Deep features (AlexNet, VGG16, ResNet-18)	SVM	0.84	−	−	−
Brinker et al. [18]	2019	ISIC Dermoscopic Archive	Deep features	CNN	−	−	$77.90\%$	$82.30\%$
Proposed Approach	2020	ISIC2017+ 250ISIC melanoma images	Superpixel graph features	Random forests	0.99	$97.50\%$	$95.10\%$	$100.00\%$

The methods of Menegola et al. [80], Matsunaga et al. [41] and González-Díaz [42] exploit the ISIC 2017 dataset to create CNN-based melanoma detectors. In particular, the top AUC score for melanoma detection in the ISBI 2017 challenge was achieved by Menegola et al. [80]. Still, the AUC scores of these detectors are clearly lower than that of our method (which was trained and tested on the augmented ISIC 2017 dataset with additional training data of 250 ISIC melanoma images). Although Matsunaga et al. [41] used more ISIC samples to supplement the ISIC 2017 training data, our method obviously demonstrates a better AUC score.

Also, Esteva et al. [43] and Brinker et al. [44] trained CNN models for melanoma detection with larger datasets of dermoscopic images, the reported metrics are clearly lower than those of our method. As well, the results reported by Reboucas Filho et al. [52] show promising performance of using features of GLCM, LBP and Hu moments. Nevertheless, our melanoma detection results are visibly better.

Conclusions

In this study, we have introduced a graph signal processing approach to detect malignant melanoma via dermoscopic images. We transform each dermoscopic image into a graph of superpixel vertices. The graph signals, as well as weighted edges, are defined using color, geometric and texture features. Several graph features are extracted in both time (125 features) and frequency (GFT) (24 features) domains. In addition, we extracted 394 conventional features based on the ABCD criteria. The experimental results demonstrated several conclusions:

• The best results were obtained using the texture-based unweighted graph features ($99.96\%$ AUC). The other graph features gave similar but slightly lower results.

• The use of the GFT coefficients and statistical measures based on them clearly improves the results.

• In general, local graph features computed over small vertex neighborhoods outperform global graph features.

• Most importantly, the performance using the graph representations is clearly better than that of conventional features (compare Table 2 and Tables (3 – 9)).

The approach presented in this work can be implemented and extended in many directions. A big variety of features and/or statistical measures can be applied to enrich the machine learning algorithms. For instance, we may add other statistical measures of local graph-based features.

Compliance with Ethical Standards

Conflict of interest

All authors have no conflict of interest and contributed equally in this work for conceptualization, methodology, formal analysis, investigation, and writing.

Ethical approval

The datasets used in this work (ISBI 2016 and ISBI 2017) are publically available.