On the Verge of Life: Distribution of Nucleotide Sequences in Viral RNAs

Abstract

The aim of the study is to analyze viruses using parameters obtained from distributions of nucleotide sequences in the viral RNA. Seeking for the input data homogeneity, we analyze single-stranded RNA viruses only. Two approaches are used to obtain the nucleotide sequences; In the first one, chunks of equal length (four nucleotides) are considered. In the second approach, the whole RNA genome is divided into parts by adenine or the most frequent nucleotide as a “space”. Rank–frequency distributions are studied in both cases. The defined nucleotide sequences are signs comparable to a certain extent to syllables or words as seen from the nature of their rank–frequency distributions. Within the first approach, the Pólya and the negative hypergeometric distribution yield the best fit. For the distributions obtained within the second approach, we have calculated a set of parameters, including entropy, mean sequence length, and its dispersion. The calculated parameters became the basis for the classification of viruses. We observed that proximity of viruses on planes spanned on various pairs of parameters corresponds to related species. In certain cases, such a proximity is observed for unrelated species as well calling thus for the expansion of the set of parameters used in the classification. We also observed that the fifth most frequent nucleotide sequences obtained within the second approach are of different nature in case of human coronaviruses (different nucleotides for MERS, SARS-CoV, and SARS-CoV-2 versus identical nucleotides for four other coronaviruses). We expect that our findings will be useful as a supplementary tool in the classification of diseases caused by RNA viruses with respect to severity and contagiousness.

Introduction

Studies of genomes based on linguistic approaches date a few decades back (Brendel et al. 1986; Pevzner et al. 1989; Searls 1992; Botstein and Cherry 1997; Gimona 2006; Faltýnek et al. 2019; Ji 2020). An interplay with methods of statistical physics as well as theory of complex systems brought new insights into biology (Dehmer et al. 2009; Qian 2013). Studies range from attempted n-gram-based classification of genomes (Tomović et al. 2006; Huang and Yu 2016) to algorithms for optimal segmentation of RNAs in secondary structure predictions (Licon et al. 2010) and analysis of substitution rates of coding genes during evolution (Lin et al. 2019), just to mention a few. Various types of sequences in genomes are related to multiple genetic codes (Trifonov et al. 2012) and can be studied both using quantitative linguistic point of view (Ferrer-i-Cancho et al. 2013; Ferrer-i-Cancho et al. 2014) and from a wider perspective, within more abstract approaches (Neuman and Nave 2008; Barbieri 2012). Recently, neural networks and deep learning algorithms emerged as new tools to analyze nucleotide sequences (Fang et al. 2019; Singh et al. 2019; Melkus et al. 2020; Ren et al. 2020) offering wider prospects for studies of genomes. Viruses, balancing on the fuzzy border between non-alive and alive, hence remaining on the verge of life (Villarreal 2004; Kolb 2007; Carsetti 2020), are within the most interesting subjects of studies.

The aim of the present Letter is to draw attention to simple treatments of nucleotide sequences in viral RNAs by means of new parameters, which can be immediately extracted from genome data. We expect that such parameters can be potentially used as an auxiliary tool in the classification of viruses (cf., in particular, Wang 2013). The idea of this study is linked to the recent COVID-19 outbreak, and the analysis started from comparing human coronaviruses (Su et al. 2016; Wu et al. 2020) and some other viruses. To achieve relative homogeneity of the material, we restrict our sample to single-stranded RNA viruses only. Both positive- and negative-sense RNAs are considered. For future reference, we also include two retroviruses, HIV-1 and HIV-2.

The paper is organized as follows. Summary of data and description of methods are given in “Data and Methods” section. Results are presented in “Results” section. Finally, brief discussion is given in “Discussion” section.

Data and Methods

The viral genomes are taken from the databases of the National Center for Biotechnology Information (NCBI, https://www.ncbi.nlm.nih.gov); the complete list is given in Table 1. Note that coronaviruses have rather long RNA genomes of ca. 30 kilobases (kba), which might bias the values of calculated parameters. To study the effect of RNA sizes, we also include some very short genomes, namely, Hepatitis D virus with 1682 ba (Saldanha et al. 1990) and Phage MS2 virus with 3569 ba (de Smit and van Duin 1993), as well as two longest known RNA viruses, Ball python nidovirus with 33452 ba (Gorbalenya et al. 2006) and Planidovirus with 41178 ba (Saberi et al. 2018). Still, the sizes of RNA viruses are much more homogeneous (the difference is up to 25 times) than those of DNA ones, which may vary by about four orders of magnitude (Campillo-Balderas et al. 2015).

Table 1.

Viruses analyzed in the work

No.	Short name	Full name	Typea	Size (bases)	NCBI sourceb
1	A/H1N1	Influenza A virus (A/swine/La Habana/ 130/2010(H1N1))	(−)	13371	HE584753.1 … HE584760.1
2	Ball python nidovirus	Ball python nidovirus 1	(+)	33452	674660326
3	Dengue	Dengue virus 2	(+)	10723	158976983
4	Ebola	Zaire ebolavirus	(−)	18962	MK672824.1
5	Feline-CoV	Feline infectious peritonitis virus	(+)	29355	315192962
6	HCoV-229E	Human coronavirus 229E	(+)	27317	12175745
7	HCoV-HKU1	Human coronavirus HKU1	(+)	29926	85667876
8	HCoV-NL63	Human coronavirus NL63	(+)	27553	49169782
9	HCoV-OC43	Human coronavirus OC43	(+)	30741	1578871709
10	Hepatitis A	Hepatovirus A	(+)	7478	NC_001489.1
11	Hepatitis C	Hepatitis C virus genotype 1	(+)	9646	22129792
12	Hepatitis D	Hepatitis delta virus	(−)	1682	13277517
13	Hepatitis E	Hepatitis E virus	(+)	7176	NC_001434.1
14	HIV-1	Human immunodeficiency virus 1	(retro)	9181	9629357
15	HIV-2	Human immunodeficiency virus 2	(retro)	10359	9628880
16	HRV-A	Human rhinovirus A1	(+)	7137	1464306962
17	HRV-B	Human rhinovirus B3	(+)	7208	1464306975
18	HRV-C	Human rhinovirus NAT001	(+)	6944	1464310212
19	Marburg	Lake Victoria marburgvirus - Ravn	(−)	19114	DQ447649.1
20	Measles	Measles virus strain Edmonston	(−)	15894	AF266290.1
21	MERS	Middle East respiratory syndrome coronavirus	(+)	30119	667489388
22	Norovirus	Norovirus Hu/GI.1/ CHA6A003_20091104/	(+)	7600	KF039737.1
		2009/USA
23	Phage MS2	Enterobacteria phage MS2	(+)	3569	176120924
24	Planidovirus	Planarian secretory cell nidovirus	(+)	41178	1571803928
25	Polio	Poliovirus (Enterovirus C)	(+)	7440	NC_002058.3
26	Rabies	Rabies virus strain SRV9	(−)	11928	AF499686.2
27	SARS	Severe acute respiratory syndrome coronavirus	(+)	29751	30271926
28	SARS-CoV-2	Severe acute respiratory syndrome coronavirus 2	(+)	29903	NC_045512
29	Yellow fever	Yellow fever virus	(+)	10862	NC_002031.1 g-max
30	Zika	Zika virus	(+)	10794	226377833 g-max

a Negative-sense RNA (−), positive-sense RNA (+) or retro

b All addresses should be prefixed by https://www.ncbi.nlm.nih.gov/nuccore/

We use two approaches to define nucleotide sequences. The first one is based on cutting an RNA genome into chunks of equal length of n nucleotides. The second approach is rooted in linguistics, so that the most frequent nucleotide is treated as a “space” dividing a RNA into “words” of different lengths (Rovenchak 2018). Note also distantly related units applied in the analysis of the human DNA, so called motifs (Liang 2014).

To demonstrate the first approach, with equal-length chunks, let us consider the Ebolavirus genome, starting with the following nucleotide sequence:

$$\text{GGACACACAAAAAGAAAGAAGAATTTTTAGGATCTTTTGT…}\mathrm{.}$$ 1

Choosing the chunk length n = 4, we obtain:

$$GGACACACAAAAAGAAAGAAGAATTTTTAGGATCTTTTGT\text{…}\mathrm{.}$$ 2

Eventually, for RNA length not being multiples of four, the last chunk can have one to three nucleotides. Obviously, the number of all possible 4-nucleotide combinations is 4⁴ = 256. Note that longer chunks would yield much higher variety of combinations with frequencies being distributed very smoothly. On the other hand, we would like to avoid studies of shorter chunks, like three-nucleotide sequences corresponding to codons. So, the length n = 4 seems optimal for our analysis.

In the second approach, the same Ebolavirus sequence (1) can be split using the most frequent nucleotide – adenine – as a “space” into the following:

$$GGCCCXXXXGXXGXGXTTTTTGGTCTTTTGT\text{…}\mathrm{.}$$ 3

The “X” stands for a zero-length element inserted between two consecutive “A”s.

We have also applied peculiar treatment of the Influenza A virus (H1N1) by adding spaces between each of eight segments of its RNA in the first and second approaches.

In both approaches, we calculate the frequencies of obtained nucleotide chunks within a given genome split in the respective manner and compile the rank–frequency distributions. The latter are obtained in a standard manner as follows: the most frequent item has rank 1, the second most frequent one has rank 2 and so on. Items with equal frequencies are given consecutive ranks in a random order, which is not relevant.

Results

The rank–frequency distributions obtained using the first approach – with 4-nucleotide chunks – were analyzed using a special software, AltmannFitter 2.1 (Altmann 2000). We found that two discrete distributions describe the obtained data with the highest precision, so called 1-displaced negative hypergeometric distribution (Grzybek 2007; Wilson 2013):

$$p_r=\frac{\left(\begin{array}{c}M+r-2\\ r-1\end{array}\right)\left(\begin{array}{c}K-M+n-r-2\\ n-r+1\end{array}\right)}{\left(\begin{array}{c}K+n-1\\ n\end{array}\right)},r=1,2,3,\dots \mathrm{.}$$ 4

and Pólya distribution (Wimmer and Altmann 1999; Johnson et al. 2005):

$$p_r=\frac{\left(\begin{array}{c}-p/s\\ r-1\end{array}\right)\left(\begin{array}{c}(p-1)/s\\ n-r+1\end{array}\right)}{\left(\begin{array}{c}-1/s\\ n\end{array}\right)},r=1,2,3,\dots \mathrm{.}$$ 5

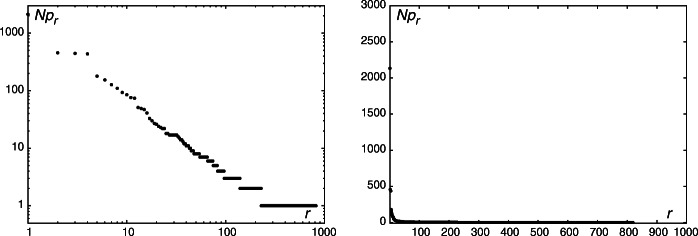
Absolute frequencies are obtained by multiplying p_r by the sample size N. In most cases, the discrepancy coefficient C = χ²/N is smaller than 0.02, which is considered a good fit (Mačutek 2008). Typical rank–frequency distributions and respective fits are shown in Fig. 1. Complete data are summarized in Table 2 and visualized in Fig. 2.

Fig. 1.

Typical rank–frequency distributions of four-nucleotide chunks and respective fits. The left panel shows the data for MERS and the fit with the hypergometric distribution, which is one of the best (C = 0.0011). The right panel demonstrated the worst fit obtained for the Hepatitis D virus data fit with the Pólya distribution (C = 0.0342)

Table 2.

Fitting parameters for the distributions of four-nucleotide chunks

Virus	Entropy	Size	Negative hypergeometric distribution	Pólya distribution
	S4	(chunks)	K	M	n	C	s	p	n	C
A/H1N1	5.3515	3345	2.4536	0.7918	258	0.0057	0.4156	0.3209	259	0.0060
Ball python nidov.	5.3385	8363	2.1873	0.7087	256	0.0043	0.4711	0.3227	256	0.0050
Dengue	5.3219	2681	2.3958	0.7561	256	0.0051	0.4270	0.3144	256	0.0055
Ebola	5.4002	4741	2.3911	0.8336	256	0.0008	0.4154	0.3462	256	0.0010
Feline-CoV	5.3357	7339	2.7359	0.8759	257	0.0011	0.3647	0.3186	257	0.0011
HCoV-229E	5.2899	6830	2.6172	0.7907	256	0.0014	0.3772	0.3007	257	0.0013
HCoV-HKU1	5.1491	7482	2.7836	0.7153	260	0.0057	0.3707	0.2506	261	0.0070
HCoV-NL63	5.1738	6889	2.7545	0.7344	256	0.0035	0.3754	0.2644	255	0.0042
HCoV-OC43	5.2854	7686	2.6510	0.7918	258	0.0027	0.3879	0.2975	257	0.0031
Hepatitis A	5.1923	1870	2.7578	0.8180	239	0.0079	0.3546	0.2877	243	0.0075
Hepatitis C	5.3871	2412	2.4158	0.8378	254	0.0029	0.4173	0.3454	254	0.0030
Hepatitis D	4.9309	421	2.1249	0.6739	178	0.0333	0.4566	0.3217	178	0.0342
Hepatitis E	5.3405	1794	2.3837	0.7811	254	0.0070	0.4297	0.3251	254	0.0077
HIV-1	5.2425	2296	2.5090	0.7853	239	0.0060	0.4090	0.3099	239	0.0066
HIV-2	5.3114	2590	2.5607	0.8015	256	0.0030	0.3892	0.3112	256	0.0029
HRV-A	5.2618	1785	2.7530	0.8492	248	0.0081	0.3418	0.2981	254	0.0077
HRV-B	5.2793	1802	2.6419	0.8706	238	0.0043	0.3774	0.3262	239	0.0042
HRV-C	5.3165	1736	2.5766	0.8688	243	0.0033	0.3890	0.3353	243	0.0033
Marburg	5.3418	4779	2.5061	0.8225	252	0.0020	0.4025	0.3267	253	0.0021
Measles	5.4293	3974	2.3932	0.8767	256	0.0022	0.4186	0.3655	256	0.0022
MERS	5.4040	7530	2.4687	0.8665	256	0.0011	0.4020	0.3498	257	0.0013
Norovirus	5.4015	1900	2.3835	0.8461	253	0.0046	0.4244	0.3536	254	0.0045
Phage-MS2	5.3680	893	2.3100	0.8084	249	0.0107	0.4436	0.3496	249	0.0114
Planidovirus	5.0360	10295	3.0466	0.7017	261	0.0183	0.2449	0.1863	315	0.0161
Polio	5.3837	1860	2.4300	0.8423	254	0.0044	0.4172	0.3452	254	0.0047
Rabies	5.3802	2982	2.4359	0.8425	252	0.0027	0.4148	0.3443	253	0.0028
SARS	5.3825	7438	2.6599	0.9058	256	0.0020	0.3716	0.3395	257	0.0019
SARS-CoV-2	5.3330	7476	2.8260	0.9014	258	0.0022	0.3546	0.3168	258	0.0021
Yellow fever	5.3430	2716	2.6168	0.8421	258	0.0050	0.3962	0.3206	257	0.0059
Zika	5.3377	2699	2.2919	0.7300	257	0.0081	0.4142	0.3181	258	0.0053

Note: Entropies S₄ are calculated for the distributions of four-nucleotide chunks using (6)

Fig. 2.

Location of viruses on the K − M plane (negative hypergeometric fit, left panel) and s − p plane (Pólya fit, right panel)

Note that the abovementioned goodness-of-fit condition comes from quantitative linguistic domain, where it is an “empirical rule of thumb” (Antić et al. 2019), and might not be directly applicable in the studies of genomes. However, it is used for various language levels, including letters and words (Antić et al. 2019; Mačutek 2008), and the observed distribution of four-nucleotide chunks are very similar to those of letters or syllables (cf, Wilson 2013; Rovenchak et al. 2018).

The first immediate observation from Fig. 2 is that the length of genomes has no special influence on the fitting parameters. Indeed, both the shortest Hepatitis D genome and two longest – Ball python nidovirus and Planidovirus – genomes have close values of M or s parameters. On the other hand, for genomes of similar lengths (coronaviruses) a clear separation is seen with respect to M and p parameters. It is even more pronounced in the former case corresponding to the negative hypergeometric distribution: lower values for HCoV viruses (229E, HKU1, NL63, and OC43) and higher ones for MERS, SARS, and SARS-CoV-2.

Rank–frequency distributions were also compiled for nucleotide “words” obtained using the second approach and used to calculate certain parameters, like entropy, mean length (first central moment), length dispersion (second central moment) and some others. A typical rank–frequency distribution is shown in Fig. 3. Comparing it to Fig. 1 we can easily see qualitatively different behavior, in particular, significantly longer plateaus at high ranks / low frequencies, which makes such distributions close to those of words in human languages. The differences between the distribution shapes of nucleotide “words” and n-grams are pronounced especially well in samples of rather short sizes, like several kba or a few dozen kba, and thus properties of “word-like” sequences might give new data for studies of such material, including mitochondrial DNA and viral RNA.

Fig. 3.

Typical rank–frequency distribution of nucleotide “words” (the data for the Marburg virus are shown). The left panel shows the plot in the log–log scale while in the right panel linear scales over axes are used

Previous studies (Rovenchak 2018) showed that entropy and mean lengths of such “word-like” nucleotide sequences in the mitochondrial DNA can be used to distinguish species and genera of mammals. It appears, however, that even better results are achieved with the “entropy – length dispersion” pair of variables, cf. Fig. 4.

Fig. 4.

Grouping of mammal species on the m₂ − S plane. Red-shaded area corresponds to Felidae, the blue one denotes Ursidae, and the green-one corresponds to Hominidae. Calculations are made using mitochondrial DNAs with adenine as a “space”

The parameters are defined as follows. Entropy is given by

$$S=-\sum _{r=1}^{r_{\max }}{p}_{r}ln{p}_r,$$ 6

where the upper summation limit corresponds to the total number of different “words” in the list and relative frequencies p_r are

$$p_r=f_r/N,\text{where}N=\sum _r{f}_r$$ 7

and f_r are absolute frequencies at rank r. Mean length and length dispersion are

$$m_1=\frac{1}{N}\sum _i{x}_i,m_2=\frac{1}{N}\sum _i{(x_i-m_1)}^2\mathrm{.}$$ 8

where the summations run over all the “words” of the analyzed genome. Lengths x_i of a particular word are counted as the number of nucleotides except for “X” having length zero.

One should note that from similarity of species one can expect proximity of points but not vice versa: it would be too bold to expect species distinguishability from only two parameters.

This second approach can be divided into two sub-branches: (a) adenine, which is the most frequent nucleotide in most species studied in the present work, is used as a “space”; (b) the most frequent nucleotide is used as a “space”. The latter is mostly relevant for RNAs, where low frequencies of adenine yield too long “words” thus significantly distorting the expected dependencies. The respective results are shown in Figs. 5–7. All the data are summarized in Table 3.

Fig. 5.

Location of viruses on the m₂ − S plane. Calculations are made using RNAs with adenine as a “space”, hence entropy is denoted S_A

Fig. 7.

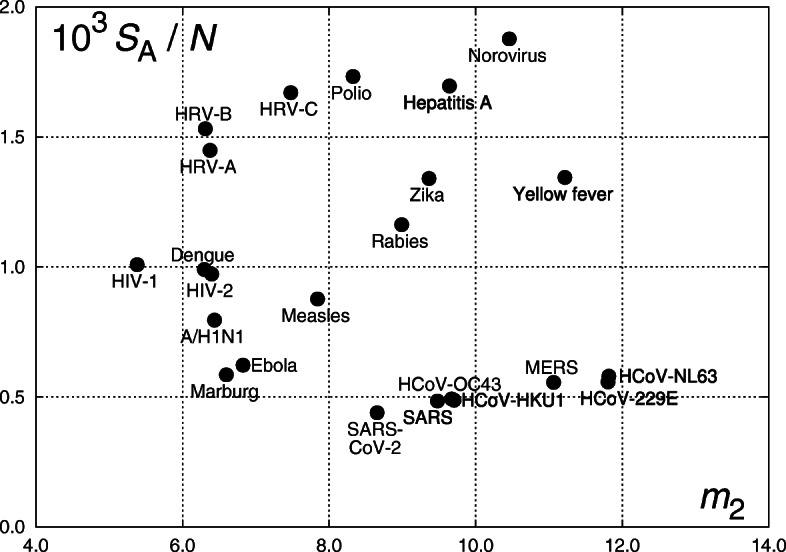
Location of viruses on the m₂ − S/N plane. Calculations are made using RNAs with adenine as a “space”, hence entropy is denoted S_A. The vertical axis thus represents the entropy divided by the number of nucleotide sequences separated by adenine in the respective genome

Table 3.

Parameters for the distributions of nucleotide sequences separated by a specific nucleotide

Virus	Entropy S	Size (“words”)	Size (bases)	Mean length m1	Length dispersion m2
A considered a “space” even if not being the most frequent:
A/H1N1	3.5446	4456	13371	2.0025	6.4378
Ball python nidov.	3.6911	11118	33452	2.0089	5.6785
Dengue	3.5204	3554	10723	2.0174	6.2980
Ebola	3.7703	6056	18962	2.1313	6.8261
Feline-CoV	4.0381	8572	29355	2.4246	8.8222
HCoV-229E	4.1411	7421	27317	2.6812	11.8059
HCoV-HKU1	4.0653	8332	29926	2.5918	9.7058
HCoV-NL63	4.2082	7254	27553	2.7985	11.8171
HCoV-OC43	4.1871	8503	30741	2.6154	9.6729
Hepatitis A	3.7125	2189	7478	2.4166	9.6428
Hepatitis C	4.7418	1890	9646	4.0349	23.7224
Hepatitis D	3.7600	340	1682	3.9500	30.1122
Hepatitis E	4.9569	1231	7176	4.8302	30.5829
HIV-1	3.3022	3273	9181	1.8054	5.3819
HIV-2	3.4121	3507	10359	1.9541	6.3979
HRV-A	3.4610	2389	7137	1.9879	6.3770
HRV-B	3.5822	2339	7208	2.0821	6.3131
HRV-C	3.6362	2177	6944	2.1902	7.4778
Marburg	3.6623	6256	19114	2.0555	6.5991
Measles	4.0685	4639	15894	2.4264	7.8423
MERS	4.3936	7901	30119	2.8122	11.0646
Norovirus	3.9312	2094	7600	2.6299	10.4595
Phage MS2	4.1385	836	3569	3.2703	15.0130
Planidovirus	3.0356	16361	41178	1.5169	3.6413
Polio	3.8237	2207	7440	2.3715	8.3277
Rabies	3.9758	3419	11928	2.4890	8.9910
SARS	4.1112	8482	29751	2.5077	9.4794
SARS-CoV-2	3.9369	8955	29903	2.3394	8.6559
Yellow fever	3.9853	2964	10862	2.6650	11.2174
Zika	4.0105	2992	10794	2.6080	9.3647
C is the most frequent:
Hepatitis C	3.8192	2894	9646	2.3334	8.7827
Hepatitis D	3.1128	505	1682	2.3327	13.0101
Hepatitis E	3.4866	2305	7176	2.1137	8.2778
Phage MS2	4.0693	934	3569	2.8223	9.9534
G is the most frequent:
Yellow fever	3.8711	3088	10862	2.5178	10.0036
Zika	3.8499	3140	10794	2.4379	9.3213
T is the most frequent:
Feline-CoV	3.7072	9588	29355	2.0617	6.4845
HCoV-229E	3.4910	9446	27317	1.8920	5.9998
HCoV-HKU1	3.0233	12002	29926	1.4935	3.7750
HCoV-NL63	3.0976	10806	27553	1.5499	4.0621
HCoV-OC43	3.4081	10931	30741	1.8124	5.5669
MERS	3.7682	9800	30119	2.0735	6.4379
SARS	3.8944	9144	29751	2.2537	7.9013
SARS-CoV-2	3.7307	9595	29903	2.1166	7.3059

In Fig. 7, we can observe in particular that α-coronaviruses, HCoV-229E and HCoV-NL63, have very close values of the parameters (the respective point nearly overlap). A similar situation is with β-corovaniruses HCoV-OC43 and HCoV-HKU1. Two other β-corovaniruses, SARS and SARS-CoV-2, are located close to HCoV-OC43 and HCoV-HKU1, while MERS occupies an intermediate position. The latter virus also significantly differs in the entropy value, see Fig. 5. On the other hand, calculations with the most frequent nucleotide used as a space (T for the analyzed coronaviruses) do not exhibit such a grouping, see Fig. 6.

Fig. 6.

Location of viruses on the m₂ − S plane. Calculations are made using RNAs with the most frequent nucleotide as a “space”, hence entropy is denoted S_m.f.

Similarly to the case of fixed-length chunks (four-nucleotide sequences analyzed above), one can expect close points for similar species but should not deduce that close points mean related species. Figures 4–6 demonstrate only one pair of parameters obtainable from rank-frequency distributions of nucleotide “words”, while Table 3 contains additional data. Further analysis can be done by processing the complete raw dataset used for calculations, which is freely available at 10.5281/zenodo.4045875.

When looking in detail into the rank–frequency distributions corresponding to coronaviruses we have discovered the following pattern: the first rank is always occupied by “X” followed by three single-nucleotide “words” with ranks 2–4, while the fifth ranks are occupied by a two-nucleotide sequence with either the same (4-same) or different (4-diff) nucleotides, see Table 4. Curiously, different nucleotides correspond to coronaviruses causing much more severe diseases. This observation is yet to be extended onto a wider material, but the preliminary data for the analyzed human viruses are as follows:

• 4-same: Dengue, HCoV-229E, HCoV-HKU1, HCoV-NL63, HCoV-OC43, HIV-1, HIV-2, HRV-A, HRV-B, HRV-C, Polio;

• 4-diff: A/H1N1, Ebola, Hepatitis A, Hepatitis C, Hepatitis E, Marburg, Measles, MERS, Norovirus, Rabies, SARS, SARS-CoV-2.

Three other viruses, Hepatitis D, Yellow fever, and Zika, do not follow either pattern having a two-nucleotide sequence with as low ranks as 3 or 4.

Table 4.

Top-ranked nucleotide sequences in the genomes of the human coronaviruses

	MERS		SARS		SARS-CoV-2		HCoV-229E		HCoV-HKU1		HCoV-NL63		HCoV-OC43
r	“word”	fr	“word”	fr	“word”	fr	“word”	fr	“word”	fr	“word”	fr	“word”	fr
1	X	3098	X	2845	X	3215	X	3380	X	4694	X	4272	X	3895
2	G	876	G	795	G	858	G	1033	A	1183	G	1149	G	1105
3	A	701	C	568	A	623	A	615	G	1151	A	814	A	963
4	C	668	A	567	C	542	C	458	C	581	C	521	C	468
5	GC	256	GC	316	GC	255	GG	288	AA	399	GG	387	AA	324
6	GG	234	GA	217	GG	245	GC	284	GA	339	AA	318	GA	322
7	GA	223	GG	202	AA	218	AA	211	GG	338	GA	296	GG	293
8	AA	214	AC	196	AC	214	GA	210	AC	271	GC	232	GC	269
9	AC	194	AA	167	GA	208	AC	156	AG	227	AG	194	AC	190
10	AG	134	CA	154	AG	138	AG	128	GC	223	AC	190	AG	171
11	CC	131	AG	102	CA	127	CA	105	AAA	117	CA	107	CA	96
12	CA	126	CC	81	CC	79	CC	56	CA	113	CC	69	CC	86
13	CG	80	CG	74	AAA	64	GAC	52	CC	104	CG	58	AAA	76

The abovementioned feature can be viewed with respect to (dis)similarity in the frequency structure of viral RNA and RNA or DNA of infected species. For instance, the fifth most frequent sequence of human mtDNA split by the most frequent C nucleotide is TA. Interestingly, it coincides with a sequence composed of nucleotides paring with G and C – and the GC sequence is the fifth most frequent in, e.g., MERS, SARS, SARS-CoV-2, see Table 4.

Discussion

We have presented several possible approaches to simple parametrization of RNA viruses based on the analysis of nucleotide sequences in viral genomes. They are based on discrete distributions (negative hypergeometric and Pólya) for equal-length (4-nucleotide) chunks and on the pair “entropy – length dispersion” for distributions of sequences separated by adenine or another most frequent nucleotide. Close values of parameters calculated from rank-frequency distributions of various nucleotide sequences are characteristic for related viruses, which is connected to similar structures of viruses and thus might reflect similarities in their functional properties. In some cases, however, close values are also obtained for unrelated viruses. This is not surprising as representing viruses on a plane means a two-parametric projection of points that are certainly described by more than two variables. We consider our study as preliminary steps in discovering such variables.

The structure of rank–frequency distributions of sequences of both types suggest an analogy with two text levels. Namely, equal-chunk sequences approach to letters or syllables while nucleotide “words” obtained using certain nucleotide as a separator are similar to ordinary words. Here, we should stress that these data correspond to rather short molecules, viral RNA and previously studied mtRNA (Rovenchak 2018), so the correlations might differ when dealing with larger nucleotide strings (cf. Gimona 2006; Ferrer-i-Cancho et al. 2013; Faltýnek 2019). Such an interpretation corresponds to the biosemiotic analogy between natural language texts and strings of biopolymers.

Observations regarding peculiarities of rank–frequency distributions, with the fifth most frequent sequence containing two either the same or different nucleotides (4-same vs 4-diff), support the fact that 4-diff cases correspond to viruses causing potentially more severe diseases when dealing with seven human coronaviruses. This tendency is generally preserved if the analyzed set is expanded by other viruses studied in this work. Some precautions concern, in particular, the two HIV types, which fall into the 4-same category while certainly being extremely dangerous. However, HIV are not strictly RNA viruses but retroviruses, so we suggest that the reported peculiarities might be specific for RNA viruses only. “False-positive” alerts (cf. Norovirus in the 4-diff category) are not problematic, but the rate of “false-negative” results (severe diseases in the 4-same category) is yet to be identified. Expansion of the analyzed material in future studies would help to clarify the relevance of this observation. To establish relations between peculiarities of the rank–frequency distributions in virus genomes and disease severity, a formalization of the latter is required. Initially we planned using the case fatality rate (CFR) indicator (Reich et al. 2012; Kim et al. 2020) but where not able to find a study with data for different viruses based on a unified approach, similar, e.g., to (GBD 2017).

The main expected outcome of our reported analysis is a call for collaboration to expand the dataset and consistently classify diseases caused by RNA viruses, in particular with respect to severity and contagiousness. If some simple patterns could be established in the nucleotide distributions, this might help alerting healthcare systems, which seems to become a very topical issue from this year on.

Declarations

Ethics approval and consent to participate

This article does not contain any studies with human participants or animals performed by any of the authors.

Conflict of Interests

The authors, Mykola Husev and Andrij Rovenchak, declare that they have no conflict of interest.