Skin Doctor CP: Conformal Prediction of the Skin Sensitization Potential of Small Organic Molecules

Abstract

Skin sensitization potential or potency is an important end point in the safety assessment of new chemicals and new chemical mixtures. Formerly, animal experiments such as the local lymph node assay (LLNA) were the main form of assessment. Today, however, the focus lies on the development of nonanimal testing approaches (i.e., in vitro and in chemico assays) and computational models. In this work, we investigate, based on publicly available LLNA data, the ability of aggregated, Mondrian conformal prediction classifiers to differentiate between non- sensitizing and sensitizing compounds as well as between two levels of skin sensitization potential (weak to moderate sensitizers, and strong to extreme sensitizers). The advantage of the conformal prediction framework over other modeling approaches is that it assigns compounds to activity classes only if a defined minimum level of confidence is reached for the individual predictions. This eliminates the need for applicability domain criteria that often are arbitrary in their nature and less flexible. Our new binary classifier, named Skin Doctor CP, differentiates nonsensitizers from sensitizers with a higher reliability-to-efficiency ratio than the corresponding nonconformal prediction workflow that we presented earlier. When tested on a set of 257 compounds at the significance levels of 0.10 and 0.30, the model reached an efficiency of 0.49 and 0.92, and an accuracy of 0.83 and 0.75, respectively. In addition, we developed a ternary classification workflow to differentiate nonsensitizers, weak to moderate sensitizers, and strong to extreme sensitizers. Although this model achieved satisfactory overall performance (accuracies of 0.90 and 0.73, and efficiencies of 0.42 and 0.90, at significance levels 0.10 and 0.30, respectively), it did not obtain satisfying class-wise results (at a significance level of 0.30, the validities obtained for nonsensitizers, weak to moderate sensitizers, and strong to extreme sensitizers were 0.70, 0.58, and 0.63, respectively). We argue that the model is, in consequence, unable to reliably identify strong to extreme sensitizers and suggest that other ternary models derived from the currently accessible LLNA data might suffer from the same problem. Skin Doctor CP is available via a public web service at https://nerdd.zbh.uni-hamburg.de/skinDoctorII/.

Introduction

Skin sensitizers are substances that have the potential to cause allergic contact dermatitis (ACD) during repeated exposure.¹ ACD is a major cause of occupational illnesses^2,3 and can severely diminish the quality of life of affected individuals. Therefore, thorough safety assessment is required prior to market release of new substances to prevent the induction of occupational or product exposure-based ACD. Moreover, in case of a skin sensitization hazard, potency information (i.e., the concentration required to induce skin sensitization) is key to determine safe use concentrations that do not result in the induction of skin sensitization.⁴

Historically, the skin sensitization potential and potency of substances have been mainly assessed by in vivo studies on animals and, rarely, complemented by confirmatory studies using safe doses on humans. The local lymph node assay (LLNA),⁵ conducted in mice, is today considered the most advanced animal testing system for skin sensitization potential and potency.⁶ In contrast to other animal assays, the LLNA assesses solely the induction phase and delivers potency information in the form of an EC3 value, which is considered to be a quantitative measure of the skin sensitization potency.⁷ The EC3 value represents a concentration required to derive a point of departure for quantitative risk assessment. However, the predictive capacity of animal testing for humans is limited (in general⁸ and also with regard to skin sensitization prediction⁹), and ethical and practical considerations as well as regulatory constraints have led to the development of alternatives to animal testing. These alternatives comprise in chemico and in vitro testing methods,¹⁰⁻¹³ as well as in silico tools that predict a compound’s skin sensitization potential based on its chemical structure or properties calculated therefrom.¹²⁻¹⁵ Nevertheless, the reliability and coverage of the individual alternative approaches is still limited, primarily due to the scarcity of available high-quality data for the development and validation of methods. For this reason, researchers have been exploring strategies for the combination of multiple nonredundant assays to achieve or exceed the level of predictive hazard or potency information provided by animal model data.¹⁶ These combined approaches are known as defined approaches (DAs) and as integrated approaches for testing and assessment (IATAs) and have been recently reviewed in ref (9). For the qualification of cosmetic compounds, in silico predictions can contribute to the prioritization of chemicals for efficacy testing and, subsequently, to early phases of (tiered) safety assessment strategies. For the latter, predictions can be used in “weight of evidence” considerations for risk assessment such as the dermal sensitization threshold approach¹⁷ or as input for DAs and IATAs. For a computational model to be accepted within a regulatory context, it should fulfill the five validation principles outlined by the OECD:¹⁸ a defined end point, an unambiguous algorithm, a defined applicability domain (AD), appropriate measures of goodness-of-fit, robustness, and predictivity, and, if possible, a mechanistic interpretation.

In the context of in silico prediction tools, the AD of a method defines the chemical space within which a method produces results with a defined reliability.^19,20 Most AD definitions include a more or less arbitrary or user-defined threshold to differentiate between reliable and unreliable predictions based on similarity to training data or the class probability returned by the modeling algorithm.²¹

An alternative for defining the reliability of a model for a certain compound of interest, without the definition of an AD, is offered by conformal prediction (CP).²²⁻²⁴ Whereas classical, standalone machine learning models based on support vector machines (SVMs), random forests (RFs), or other methods return a distinct prediction for a compound of interest (or, in the case of RF, a class probability, if desired), a CP model returns statistically justified class membership probabilities for each of the classes. Users may select a desired confidence level, 1−ε, and CP will return an observed error equal to, or very close to, the chosen error rate ε, as long as the randomness assumption of the samples (an assumption that is also made for classical machine learning models) holds true. On the basis of the class probabilities and the selected confidence level, the model determines whether a compound is within the AD of the model. If it is within the AD, one or more class labels will be assigned to the compound; if it is outside the AD, no class label will be assigned (or, more precisely, the compound will be assigned to the empty (null) class). As with the AD of classical machine learning models, different measures of the reliability of a prediction (conformity measures) may be selected for the model. However, the CP model offers the advantage that the manual selection of a cutoff value for this measure is not required. Instead, it is deduced in a straightforward mathematical way from the selected confidence level.

Different variants of CP support different needs regarding the characteristics of the modeling data, and the computational effort that should be invested.²⁵ A CP variant that has been shown to perform favorably on imbalanced data is Mondrian CP, because it treats each class independently of all other(s), thereby ensuring the validity of each individual class without the need for over- or under-sampling.²⁶⁻²⁸ An additional type of CP is aggregated CP, which repeats the workflow several times so that each training compound could be used as a proper training and calibration compound.²⁹ Aggregated CP is therefore favorable for small data sets. The combination of Mondrian CP and aggregated CP works particularly well on small, imbalanced data sets.

In this study, we apply aggregated, Mondrian CP to develop classifiers for the prediction of the skin sensitization potential of small molecules. We start with the development of a binary classifier that distinguishes nonsensitizers from sensitizers and then explore strategies to obtain a differentiation of weak to moderate sensitizers from strong to extreme sensitizers. The performance of the models is determined with thorough validation protocols and compared to the performance of existing in silico models. The final classifier, called “Skin Doctor CP”, is available as a web service, free of charge for academic use.

Methods

Data Sets

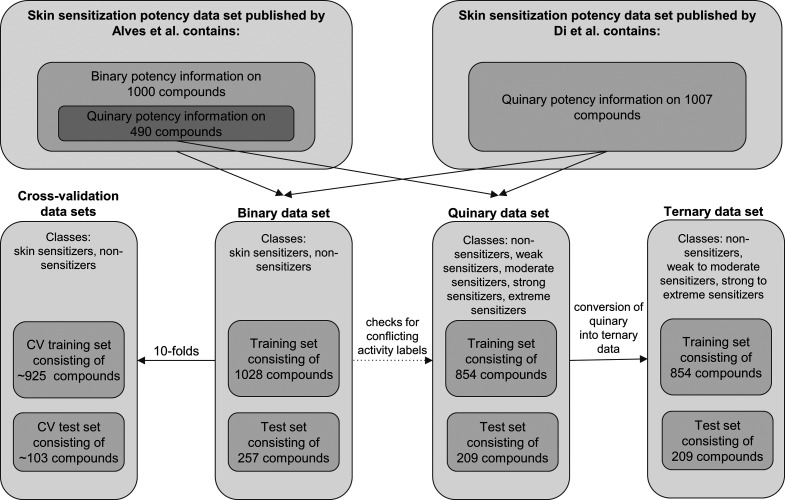
For the purpose of model development and evaluation, LLNA data sets on the skin sensitization potential of small organic compounds (Figure 1) were derived from the data published by Alves et al.³⁰ and Di et al.³¹ (all data are provided as Supporting Information, SI). The data set was prepared following a protocol described previously,³² which includes the removal of counterions, neutralization, standardization of tautomers, removal of stereochemical information, and removal of duplicate compounds and compounds with conflicting activity data based on canonical SMILES. For the current work, we refined this protocol by discarding any entries for which, based on the information provided by Alves et al. and Di et al., the exact molecular structure of the compound in question could not be conclusively confirmed. More specifically, we discarded any entries that match at least one of the following criteria:

• the CAS number provided refers to a polymer, an unspecified substance, or an incompletely defined substance (this concerns 49 and 60 entries of the data sets of Alves et al. and Di et al., respectively)

• the CAS number provided refers to a multicomponent substance for which the relevant component could not be unequivocally identified (this concerns 2 and 0 entries, respectively)

• the CAS number provided refers to a metal complex (this concerns 1 and 7 entries, respectively) or a metal salt (this concerns 1 and 1 entries, respectively)

• the CAS number provided refers to a substance with a molecular structure that is not consistent with the SMILES notation provided (this concerns 5 and 5 entries, respectively)

• the CAS number, EC number, compound name, and any further information provided did not allow to confirm the molecular structure of the substance in question (this concerns 2 and 40 entries, respectively)

Figure 1.

Overview of LLNA data sets and subsets employed in this study.

Further, multicomponent mixtures that have been tested negative and for which the least represented component accounts for at least one-third of the proportion of the major component were split into separate entries, each assigned to the “nonsensitizer” class (this concerns 7 and 15 entries of the data sets of Alves et al. and Di et al., respectively). In the case of two-component mixtures that (i) have been tested positive, (ii) for which one component is listed as a known nonsensitizer in the data sets of Alves et al. or Di et al., and (iii) for which the known nonsensitizer accounts for at least one-third of the mixture, the class label “sensitizer” was assigned to the other component (this concerns 1 entry derived from the data set compiled by Di et al.). The curated data set (Table SI_1) as well as the substances removed by the manual data curation process (Table SI_2) can be found in the SI published with this article.

Binary Data Set

The binary class labels of the data set were retrieved by a protocol identical to the one published in ref (32).

Multiclass Data Sets

All compounds included in the data set of Di et al.³¹ and approximately half of the compounds included in the data set of Alves et al.³⁰ are annotated with quinary LLNA data (Figure 1). The quinary potency information was used to derive a ternary data set (for the development of a ternary classifier) and a quinary data set (for the evaluation of the binary classifier with regard to quinary class memberships) following the identical data processing protocol of Wilm et al.³²

Compounds originating from the work of Alves et al. were assigned class labels based on the “LLNA class” property, whereas compounds sourced from the work of Di et al. were assigned class labels according to the “Classes” property. Compounds labeled as “Nonsensitizer” (Alves et al.) or “Negative” (Di et al.) were assigned the class label “non-sensitizer”. For the compilation of the quinary data set, the class labels “Weak”, “Moderate”, “Strong”, and “Extreme” sensitizers from both sources were preserved. For the compilation of the ternary data set, the quinary data were converted according to the following rules: “Weak” and “Moderate” skin sensitizers from both sources were assigned to the class “weak to moderate sensitizers”, whereas “Strong” and “Extreme” skin sensitizers from both sources were assigned to the class “strong to extreme sensitizers”. Compounds without data on their skin sensitization potential were removed (220 compounds). Following the conversion of the activity labels, three compounds were removed from the data set because of conflicting class labels.

Determination of Functional Groups for Data Set Analysis

The binary data set was analyzed with respect to the prevalence of the functional groups in organic chemistry encoded by 309 SMARTS patterns.³³ SMARTS pattern matching was performed with RDKit.³⁴ Any patterns matched by at least 20 out of the investigated compounds (1285 in the case of data set analysis, 275 in the case of performance analysis of the binary classifier) were included in the analysis.

Descriptor Calculation

Skin Doctor CP uses MACCS keys (166 bits), which have been identified as the most suitable descriptors during the development of Skin Doctor.³² These descriptors are calculated with RDKit.

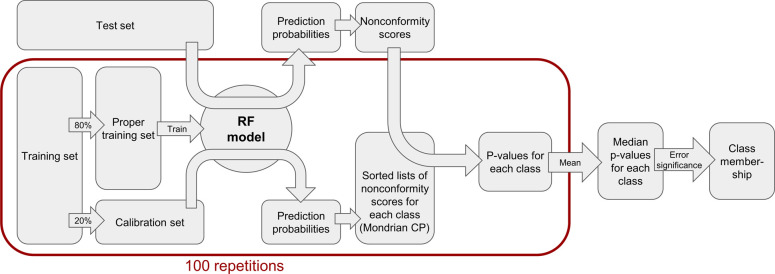
Model Generation with Aggregated Mondrian Conformal Prediction

Definition of Training and Test Sets

The binary data set was divided into a training set (80% of the data) and a test set (20% of the data). To maximize the comparability of the current study with our previous work,³² we preserved the data set split. However, because of the data set refinements described above (first and foremost, the removal of potentially problematic compounds), this means that the test set for the current study is effectively a subset of the previous work (test set present work: 257 compounds; test set previous work: 284 compounds). The 14 additional compounds that resulted from the splitting of two-component mixtures were added to the training set (training set present work: 1028 compounds; training set previous work: 1132 compounds). For both multiclass data sets, the same split into training and test sets was performed as on the binary data set. Thus, the training and test sets of the multiclass data sets are subsets of the training and test sets of the binary data set.

Each training set was divided into a proper training set (80%) and a calibration set (20%) by stratified random splitting with the train_test_split function of the model_selection module of scikit-learn³⁵ (data shuffling prior to data set splitting enabled), as shown in Figure 2. A random forest model was derived with scikit-learn from each proper training set (hyperparameters adopted from Wilm et al.,³² with n_estimators = 1000, max_features = “sqrt”, random_state = 43) and applied to the calibration set.

Figure 2.

Schematic workflow of the aggregated Mondrian CP model.

Model Development Approach

Two binary aggregated Mondrian CP models based on RF estimators were generated (technical details of the CP approach are provided in the next subsection): one classifier to distinguish nonsensitizers from sensitizers, and one classifier to distinguish weak to moderate sensitizers from strong to extreme sensitizers. The initial version of the classifier distinguishing nonsensitizers from sensitizers was evaluated on the respective training set within a 10-fold cross-validation framework. The second and final version of this classifier was trained on the full training set and evaluated on the corresponding test set. The performance of the final binary classifier was also evaluated on the quinary test set with regard to the quinary class membership. The classifier distinguishing weak to moderate sensitizers from strong to extreme sensitizers was trained and tested on all sensitizers included in the ternary training and test sets, respectively.

Finally, both classifiers were combined in a two-step workflow. First, the model distinguishing nonsensitizers from sensitizers (in its final version) is applied to each compound of interest. Compounds classified by that model as sensitizers (independent of the predicted class membership of the nonsensitizing class) are then subjected to predictions with the second classifier to distinguish weak to moderate sensitizers from strong to extreme sensitizers. The two-step workflow was evaluated by applying it to the ternary test set.

Technical Aspects of Conformal Prediction

Nonconformity scores (α-values) for the calibration and test data were calculated based on the following nonconformity function for each class i:

with P̂(y_i|x_i) being the class probability for class i returned by the RF model, and max_y≠yiP̂(y|x_i) being the maximum class probability for any other class returned by the RF model.

The α-values for each class (nonsensitizers and sensitizers, or weak to moderate sensitizers and strong to extreme sensitizers) from the calibration set were sorted, and p-values for each class were derived for each test compound based on the rank of the corresponding α-value of the test compound.

This procedure to derive p-values for each compound of the test set by developing a RF model on the proper training data and applying it to the calibration and test sets was repeated 100 times with different splits into proper training and calibration data to achieve aggregated CP. This was realized by random states (ranging from 0 to 99) assigned to the function used to split the data into a proper training and a calibration set. All 100 models were applied to the test data, and the median p-values from all 100 runs were used as the final p-values for the test data.

If the p-value of a test compound for a given class exceeded the selected significance level ε, the compound was assigned to that class. A compound may be assigned to a single class, to several classes, or to no class, depending on the p-values and significance level.

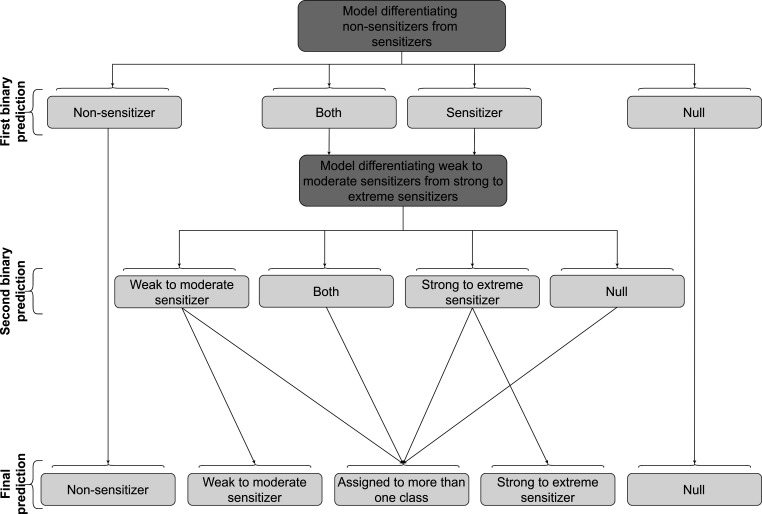
Combined Workflow for Prediction of Ternary Skin Sensitization Potential

Finally, the two binary models were integrated into a workflow for the ternary classification of the skin sensitization potential of compounds (Figure 3).

Figure 3.

Schematic overview of the workflow underlying the ternary prediction of the skin sensitization potential of compounds. In the first step, the binary model differentiating nonsensitizers from sensitizers (as described in the subsection “Development of Binary Classifier for Predicting Skin Sensitization Potential”) is applied to a compound. Depending on the p-values and the selected significance level (a compound is considered to belong to a certain class if the corresponding p-value exceeds the selected error significance), the compound is labeled “sensitizer”, “non-sensitizer”, “both”, or “null”. For compounds labeled “non-sensitizer” or “null”, these predictions are final. Compounds labeled “sensitizer” or “both” are forwarded to a second model for the discrimination of weak to moderate from strong to extreme sensitizers. Note that compounds labeled by the first binary classifier as “both” and labeled by the second binary classifier as “weak to moderate sensitizer” or “strong to extreme sensitizer” assigned to more than one class. Compounds labeled “sensitizer” by the first model and not assigned to any potency class by the second model are automatically labeled as both weak to moderate sensitizers and as strong to extreme sensitizers. This procedure is to ensure consistent predictions of the binary and the ternary classifiers. Note that this procedure increases the validity and decreases the efficiency of the second model (the performance measures validity and efficiency are explained in the section “Performance metrics”).

Within the workflow, the binary model is first applied to distinguish nonsensitizers from sensitizers. If this model assigns a compound to the sensitizer class (note that the compound may, in addition, be assigned to the nonsensitizer class), it is forwarded to the second classifier to differentiate weak to moderate from strong to extreme sensitizers. To result in a ternary prediction, the predictions of the two classifiers are combined in an array of three values (Booleans), one for each potency class. The selection rules of this process are illustrated in Figure 3.

Performance Metrics

For all models, the CP-specific measures validity and efficiency were used for evaluation. In the context of CP, validity is defined as the percentage of predictions that include the true class of a compound. For a binary model, this includes distinct predictions (i.e., predictions that predict exactly one class to be true) for the true class as well as predictions that state both classes are true. Analogous to a classical model, which returns correct predictions with a defined reliability only for compounds that are within the AD of the model, predictions made by a CP model can be considered valid as long as the correct label is part of the returned prediction set. The percentage of compounds for which a distinct prediction is obtained is quantified as efficiency. As such, efficiency is equivalent with the definition of coverage found for most non-CP models in the field of toxicity prediction (and also consistent with the definition of coverage used for the non-CP version of Skin Doctor).³² Analogous to the definition of the AD in classical models, validity and efficiency were calculated based on all predictions. In addition, the values of the general performance measures accuracy (ACC), Matthews correlation coefficient (MCC),³⁶ correct classification rate (CCR, also known as balanced accuracy), sensitivity (SE), specificity (SP), positive predictive value (PPV) and negative predictive value (NPV) were calculated based on all distinct predictions (i.e., all predictions that assigned a compound to exactly one activity class). For the binary as well as for the ternary model, class-wise validity and efficiency are the validity and efficiency measured on a subset of the tested compounds that have been experimentally determined to belong to the particular potency class.

For the ternary model, we consider both overall and class-wise performance, whereby overall performance refers to the mean values for each of the performance measures from the three potency classes. Class-wise performance measures are calculated individually for each potency class. In the cases of the non-CP performance measures (ACC, MCC, CCR, SE, SP, NPV, and PPV), class-wise performance values are calculated by combining all experimental and predicted class labels not belonging to the class of interest so that the performance measure can be calculated as if defined for two classes.

Results

Development of Binary Classifier for Predicting Skin Sensitization Potential

The processed and refined data sets of Alves et al. and Di et al. comprise binary activity data for a total of 946 and 909 substances, respectively. Among those, 562 substances are listed in both data sets. After duplicate removal (during which 7 unique substances, distributed over 15 entries, were removed because of conflicting class labels), the (final) binary data set comprises 760 nonsensitizers and 525 sensitizers. The prepared data set was divided into a training set (610 nonsensitizers and 418 sensitizers) and a test set (150 nonsensitizers and 107 sensitizers) for model development and evaluation, respectively (Table 1).

Table 1. Composition of Binary Training and Test Data Sets.

	training set	test set
nonsensitizers	610	150
sensitizers	418	107
total no. compounds	1028	257

Generation of Initial Binary Classifier and Its Performance during Cross-validation

An initial binary classifier was trained on a set of 610 nonsensitizers and 418 sensitizers and tested within a 10-fold cross-validation framework. The model was valid at all of the four tested significance levels (ε = 0.05, 0.10, 0.20 and 0.30), meaning that the validity was equal or close to 1−ε. The standard deviations of the model validity and efficiency were all below 0.04 and 0.05 (Table 2). The highest standard deviation for each value was generally observed for ε = 0.05. This observed trend is related to the comparably small number of compounds for which the model returns unambiguous results at this significance level.

Table 2. Overall Performance during 10-Fold Cross-validation of Binary Aggregated Mondrian CP Classifier Differentiating Nonsensitizers from Sensitizers¹.

ε	validity	efficiency	ACC	MCC	CCR	SE	SP	NPV	PPV
0.05	0.96 (0.02)	0.28 (0.05)	0.88 (0.07)	0.73 (0.15)	0.87 (0.08)	0.86 (0.13)	0.89 (0.09)	0.93 (0.06)	0.80 (0.14)
0.10	0.91 (0.02)	0.51 (0.05)	0.83 (0.03)	0.66 (0.06)	0.84 (0.03)	0.84 (0.07)	0.83 (0.06)	0.89 (0.05)	0.76 (0.05)
0.20	0.82 (0.03)	0.83 (0.04)	0.78 (0.03)	0.56 (0.07)	0.78 (0.04)	0.78 (0.09)	0.78 (0.05)	0.84 (0.05)	0.71 (0.04)
0.30	0.73 (0.04)	0.96 (0.02)	0.76 (0.03)	0.51 (0.06)	0.76 (0.03)	0.76 (0.06)	0.76 (0.05)	0.82 (0.04)	0.69 (0.05)

¹Standard deviation in brackets next to the values.

Some of the models were overconservative (i.e., the validity was higher than 1−ε), which is a known phenomenon of aggregated CP classifiers at low significance levels (ε ≤ 0.40) and is caused by an insufficient ability to properly rank the compounds of interest based on the selected nonconformity measure or one of the factors (modeling algorithm, type of descriptors, etc.) contributing to it. Overconservativeness of the model does not call into question the validity of the model and might, on the contrary, be favorable with respect to the reliability of predictions. Nevertheless, due to the trade-off between error rate and efficiency with regard to choice of significance level, overconservativeness coincides with an unnecessarily low efficiency for the selected significance level.³⁷

At a significance level of 0.05, the model obtained an ACC of 0.88 and an MCC of 0.73 during cross-validation, with an efficiency of 0.28. At a significance level of 0.30, predictions could be made for almost all test compounds (96%), at the cost of a reduced ACC and MCC (0.76 and 0.51, respectively). Predictions of compounds being nonsensitizers were very reliable. For significance levels from 0.05 to 0.30, the NPVs were between 0.93 and 0.82, indicating that the model could be particularly valuable in a regulatory context where harmful properties of substances in question should be ruled out with high reliability.³⁸ While for the four investigated significance levels only minor differences were observed for SE (between 0.76 and 0.86) and SP (between 0.76 and 0.89), the PPV (between 0.69 and 0.80) was lower than the NPV (between 0.82 and 0.93). Therefore, a negative prediction (nonsensitizer) made by the model seems to be more reliable than a positive prediction (sensitizer).

We also investigated model efficiency as a function of the selected significance level (Figure 4). Efficiency is found to increase steeply with low significance levels, reflecting the ability of the model to make distinct, single label predictions for an increasing amount of compounds (if we allow an increasing amount of erroneous predictions). Maximum efficiency is reached at a significance level of 0.28. Beyond this significance level, efficiency again decreases. This reflects the fact that the CP model will always guarantee an error rate close to the significance level. If, for example, a significance of 0.5 is desired (which in the binary case corresponds to a random model), predictions must be assigned to the empty class to fulfill this criterion (since the underlying model would have a better predictivity than 0.5).

Figure 4.

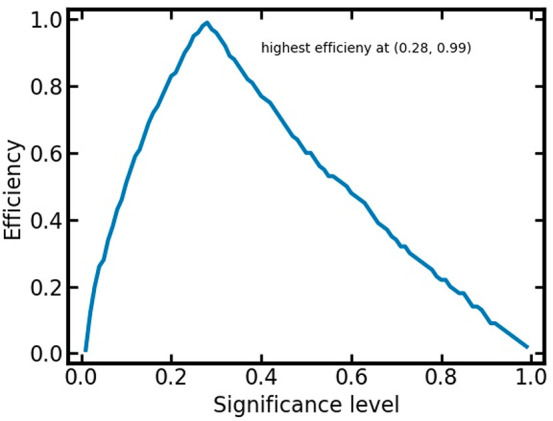
Efficiency of the binary classifier differentiating nonsensitizers from sensitizers within 10-fold CV in dependence of the significance level.

Generation of Final Binary Classifier and Its Performance on the Test Set

Following the CV studies, a final binary classification model, which we call “Skin Doctor CP”, was trained on the full training set and evaluated on a test set of 150 nonsensitizers and 107 sensitizers (Figure 1). The final p-values of the test set compounds can be found in Table SI_4.

Overall Performance on the Test Set

The model was valid for all four significance levels (Table 3). Although the validity at the significance level of 0.3 was only 0.69, which is 0.01 lower than the expected validity of 1−ε, this value is within the standard deviation observed for validities within CV. Therefore we assume that this slight under-predictivity is caused by statistical fluctuations and consider the model to be valid. The validity and efficiency of the final model were comparable to the values for the initial model (Table 3). The NPV (0.94 to 0.84) and SE (0.91 to 0.81) were higher than the PPV (0.83 to 0.65) and SP (0.88 to 0.70) for all of the four significance levels. While SE and NPV only slowly decreased with increasing error significance (ΔSE = 0.10 and ΔNPV = 0.10 between significance levels 0.05 and 0.30), SP and PPV decreased more drastically (ΔSP = 0.18 and ΔPPV = 0.18 over the range of significance levels). Therefore, negative predictions produced by this model can be considered reliable at all significance levels investigated, while positive predictions should be considered less reliable at high significance levels.

Table 3. Overall Performance of Binary Aggregated Mondrian CP Classifier, Differentiating Nonsensitizers from Sensitizers, on the Test Set.

ε	validity	efficiency	ACC	MCC	CCR	SE	SP	NPV	PPV
0.05	0.96	0.32	0.89	0.78	0.89	0.91	0.88	0.94	0.83
0.10	0.91	0.49	0.83	0.66	0.84	0.90	0.78	0.92	0.72
0.20	0.82	0.79	0.77	0.55	0.78	0.84	0.72	0.88	0.65
0.30	0.69	0.92	0.75	0.51	0.76	0.81	0.70	0.84	0.65

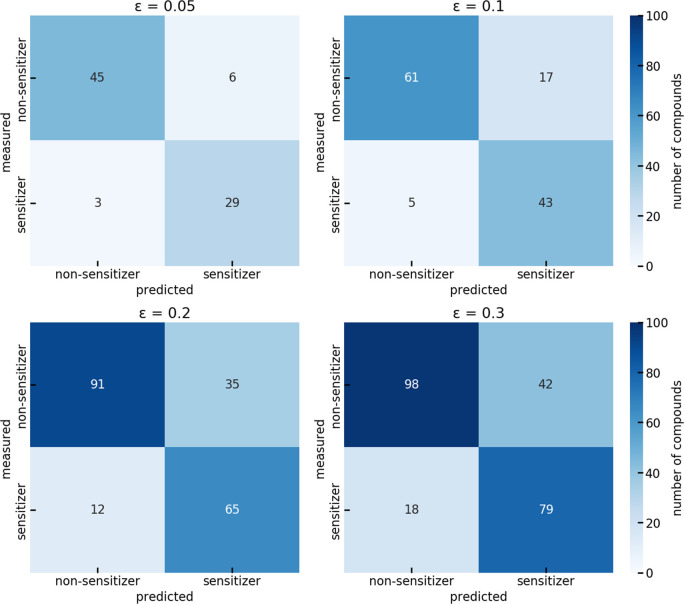
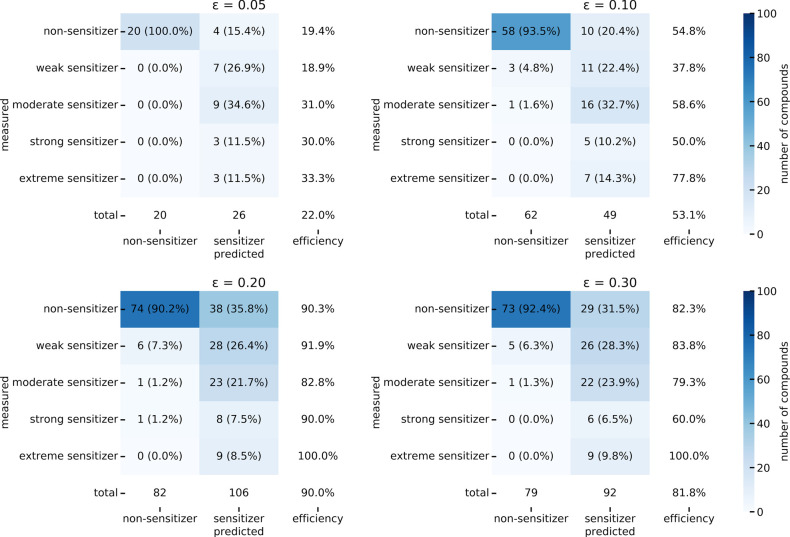
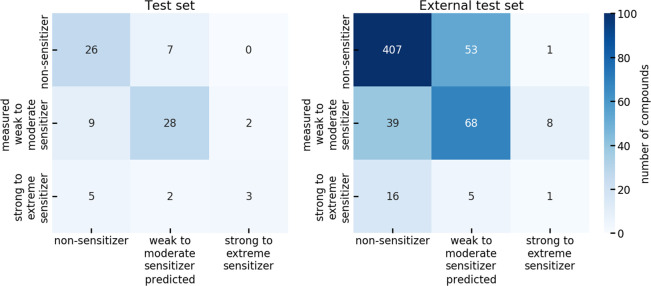
The confusion matrices of the model (Figure 5) reveal that the decrease in PPV observed with increasing error significance originates from an increasing tendency of the model to predict a compound to be a sensitizer (42%, 48%, 49%, and 51% of the molecules were predicted to be sensitizers at an significance level of 0.05, 0.10, 0.20, and 0.30, respectively), while the percentage of experimentally determined sensitizers remained comparably stable, between 38% and 41%.

Figure 5.

Confusion matrices reporting the classification results for the final binary classifier on the test set.

Class-Wise Performance on the Test Set

To better understand the performance of the model within the CP setting, the class-wise validity and efficiency (i.e., the model’s validity and efficiency calculated separately for each class of compounds, nonsensitizers and sensitizers, in the test set) of the binary classifier were analyzed for the selected significance levels (Table 4).

Table 4. Class-Wise Performance of Binary Classifier Differentiating Nonsensitizers from Sensitizers on the Test Set.

ε	class	validity	efficiency
0.05	nonsensitizer	0.96	0.34
	sensitizer	0.97	0.30
0.10	nonsensitizer	0.89	0.52
	sensitizer	0.95	0.45
0.20	nonsensitizer	0.77	0.84
	sensitizer	0.89	0.72
0.30	nonsensitizer	0.65	0.93
	sensitizer	0.74	0.91

The validity of the model was higher for sensitizers than for nonsensitizers at all significance levels. A slight preference of the model to produce positive predictions was observed that increased proportionally with the significance level. Nevertheless, the difference in model validity between nonsensitizers and sensitizers was relatively small and was highest (0.12) at the significance level of 0.20.

The model was valid for the sensitizer class at all four significance levels. For the nonsensitizer class, the model was valid at the significance level of 0.05 and only slightly under-predictive at the significance levels of 0.10 and 0.20. Since the deviation from the expected validity is only 0.01 and 0.03, which is within the standard deviations observed for the validity of the models during cross-validation, we nevertheless consider the model as valid for both classes at the significance levels of 0.10 and 0.20. At the significance level of 0.30, the validity of the nonsensitizing class was only 0.65. Because the deviation from the expected validity of 0.70 is not within the standard deviation observed during cross-validation (0.04), we assume that this might not only be caused by statistical fluctuations but might also originate from an underlying systemic problem of the model. We therefore suggest that predictions of sensitizer at this significance level be handled with care.

Differences in efficiency between both classes were similar to the differences observed for validity. The maximum difference in efficiency (0.12) was found at the significance level of 0.20.

Analysis of Performance of Final Binary Classifier Based on Quinary LLNA Data

False predictions are of varying degrees of concern, depending on the specific application scenario. In the regulatory context, false negative predictions will be of primary concern, whereas false positive predictions during the discovery phase may lead to a costly false deprioritization of compounds. Moreover, there is a distinction to be made between the false prediction of a weak skin sensitizer as nonsensitizer, and the false prediction of an extreme sensitizer as nonsensitizer. These types of distinction were examined using the quinary LLNA data (Figure 6).

Figure 6.

Distribution of the five potency classes among compounds predicted as nonsensitizers or sensitizers by the final binary classifier differentiating nonsensitizers from sensitizers. The percentages reported in parentheses refer to the total number of compounds reported in each column.

Quinary LLNA data are available for 124 nonsensitizers, 37 weak sensitizers, 29 moderate sensitizers, 10 strong sensitizers, and 9 extreme sensitizers in the test set. At the significance levels of 0.05, 0.10, 0.20, and 0.30, a distinct prediction could be made for 22%, 53%, 90%, and 82% of compounds in this subset of the binary test set, respectively.

The PPV of the quinary subset ranges from 85% at the significance level of 0.05 to 64% and 68% at the significance levels of 0.20 and 0.30. Compounds predicted as nonsensitizers are correctly classified in 90% to 100% of the cases (NPV). At all significance levels investigated, the majority of sensitizers falsely predicted to belong to the nonsensitizing class belong to the class of weak sensitizers. One moderate sensitizer (CAS No. 5205–93–6, an amino functional methacrylamide monomer that is a known skin irritant) was falsely predicted as nonsensitizers at the significance levels of 0.10 or higher. In addition, a strong sensitizer (CAS No. 106359–91–5, a complex naphthalenetrisulfonic acid dye and known skin irritant) has been misclassified as a nonsensitizer at the significance level of 0.20. No extreme sensitizers have been misclassified. Thus, there seems to be an inverse trend between the potency of a sensitizer and the likelihood of it being falsely predicted as a nonsensitizer, which is an encouraging result.

Analysis of Performance of Final Binary Classifier with Respect to Functional Groups Present in the Test Compounds

Using a collection of 309 SMARTS patterns representing functional groups in organic chemistry, we identified 35 such groups that are presented in at least 20 compounds of the test set (Table SI_5). At the significance level 0.3, the binary classifier was found to perform particularly well (ACC values between 0.83 and 0.90) on compounds that contained at least one of the following functional groups: 1,5-tautomerizable moiety, amide, phenol, ketone, primary alcohol, secondary amide, sulfonic acid (derivative), or carboxylic acid (derivative). Among those, phenols are a particularly interesting case as the number of nonsensitizers and sensitizers among this group is nearly balanced (59% vs 41%). The model correctly identified 10 nonsensitizers and 9 sensitizers while only assigning three nonsensitizers and no sensitizer to the wrong activity class. Note that the model assigns 19% of the phenols to the empty class, which is the highest percentage of empty predictions among the 35 selected functional groups.

In contrast, we found low rates of prediction accuracies (between 0.56 and 0.67) for compounds comprising a heteroaromatic ring system with a nonbasic nitrogen atom, carboxylic esters, and dialkylethers (for the individual groups of compounds the ratio between nonsensitizers and sensitizers is well balanced).

The tendencies observed for the significance level of 0.3 could also be recognized for the other significance levels that we investigated but are based on weaker statistics.

Comparison of Model Performance with Skin Doctor

The binary classifier enveloped in the CP framework presented in this work was developed using the identical machine learning method and hyperparameters as in one of the previously reported “Skin Doctor” models.³² However, Skin Doctor CP is trained on a modified training set and tested on a subset of the test set compared to the original Skin Doctor models. This limits direct comparability between the two approaches. Nevertheless, a qualitative comparison was performed here to estimate the main differences between the two approaches. Whereas the CP model allows the definition of the error significance level, the Skin Doctor model (“non-CP model”) features an AD definition that is based on the Tanimoto coefficient, calculated using Morgan2 fingerprints and averaged over the five nearest neighbors in the training set. Any compound with a Tanimoto coefficient below a threshold (usually 0.5) is considered to be outside of the AD.

When a Tanimoto coefficient of 0.5 is applied as the threshold for the AD, the classical Skin Doctor model yields a coverage of 0.96 for the test set (Table 5), which is comparable to the efficiency of the CP model at a significance level of 0.3 (efficiency 0.92). In this setting, the classical Skin Doctor model obtained an ACC of 0.73 and an MCC of 0.43, which is comparable to the performance of the CP model (ACC = 0.75, MCC = 0.51). When increasing the threshold of the AD to 0.75, the classical Skin Doctor model yielded a coverage of 0.28. This is comparable to the efficiency of the CP model at a significance level of 0.05 (efficiency 0.32). In this setup, the CP model clearly outperformed the non-CP model by obtaining an ACC of 0.89 (vs 0.78) and an MCC of 0.78 (vs 0.59). At a significance level of 0.2, the performance of the CP model is comparable to that of the non-CP model with the strict definition of the AD (ACC 0.77 vs 0.78 and MCC 0.55 vs 0.59), despite superior efficiency/coverage (0.79 vs 0.28).

Table 5. Overall Performance of Corresponding Non-CP Model “Skin Doctor”, Differentiating Nonsensitizers from Sensitizers, on the Test Set.

AD cutoff1	coverage2	ACC	MCC	CCR	SE	SP	NPV	PPV
0	1.0	0.72	0.41	0.70	0.57	0.82	0.74	0.69
≥0.5	0.96	0.73	0.43	0.71	0.60	0.82	0.75	0.69
≥0.75	0.28	0.78	0.59	0.81	0.89	0.73	0.92	0.64

¹Defined as the mean Tanimoto similarity to the five nearest neighbors.

²Coverage of the classical Skin Doctor is defined as the percentage of compounds in the test set that lie within the AD (i.e., for which a reliable prediction can be made by the model). This can be considered comparable to the definition of efficiency applied in this work, which is defined as the percentage of distinct predictions.

In-depth analysis of model performance showed that for the non-CP model the NPV increases with a stricter definition of the AD, whereas the PPV does not. This means that a stricter definition of the AD improves the reliability of the negative predictions but not of the positive ones. Within Skin Doctor CP, an increase in NPV from 0.84 to 0.94 and in PPV from 0.65 to 0.83 with decreasing error significance from 0.3 to 0.05 was found. Therefore, the use of Skin Doctor CP should in general be advantageous over the use of the non-CP models of Skin Doctor.

Development of Ternary Classifier for Predicting Skin Sensitization Potential

In an attempt to extend the capabilities of the machine learning approach to distinguish between three potency classes (nonsensitizer, weak to moderate sensitizer, and strong to extreme sensitizer), the feasibility of a two-step ternary model was explored, in which the (final) binary classifier forwards all compounds predicted as sensitizers to a downstream binary classifier to discriminate weak to moderate sensitizers from strong to extreme sensitizers. To ensure the validity of the two-step approach, the downstream binary model as well as the combined workflow was evaluated separately using (a subset of) the ternary data set. The composition of the full ternary training and test sets is shown in Table 6.

Table 6. Composition of Ternary Training and Test Data Sets.

	training set1	test set2
nonsensitizer	510	124
weak to moderate sensitizer	279	66
strong to extreme sensitizer	65	19
total no. compounds	854	209

¹Compared to the binary training set, 173 compounds have been removed because of missing multiclass labels and one compound has been rejected because of conflicting ternary class labels.

²Compared to the binary test set, 47 compounds have been removed because of missing multiclass labels and one compound has been rejected because of conflicting ternary class labels.

The binary classifier distinguishing weak to moderate sensitizers from strong to extreme sensitizers was developed following the same protocol and identical hyperparameters as described for the binary model distinguishing nonsensitizers from sensitizers (RF with 1000 estimators, enveloped by aggregate Mondrian CP; see Methods for details). This second model was trained and evaluated on subsets of the ternary training and test sets that comprise only sensitizing compounds. Within these subsets, 81% and 78% of the compounds in the training and test set belong to the class of weak to moderate sensitizers, respectively, while 19% and 22% of the compounds belong to the class of strong to extreme sensitizers, respectively. Unfortunately, the number of compounds in the training set (344) and test set (85) was relatively small and not sufficient to produce statistically solid evidence. The exact numbers in the following section should therefore not be considered reliable results. Rather, they should be considered as a proof of concept and an indication of a route that could be followed in the future with a larger database when more data become available.

Binary Classifier Distinguishing Weak to Moderate Sensitizers from Strong to Extreme Sensitizers

The binary model differentiating between weak to moderate sensitizers and strong to extreme sensitizers (for p-values see Table SI_4) was overconservative at all significance levels investigated (Table 7; validity = 0.94, 0.88, and 0.75 at significance levels of 0.10, 0.20, and 0.30; note that the significance level of 0.05 was not investigated since the efficiency of the model on the test set was 8%). As expected for an overconservative model, the efficiency of the model was comparably low (0.45, 0.71, and 0.98). At the three significance levels investigated, reasonably high values for SE (between 0.79 and 1.00) and SP (between 0.73 and 0.84) were found. The prediction that a compound is a weak to moderate sensitizer was highly reliable (NPV between 0.92 and 1.00) for all significance levels investigated, while a compound predicted to be a strong or extreme sensitizer could belong with almost equal probability to each of the two classes (PPV between 0.47 and 0.58). This strongly limits the model’s applicability in any use case, but the model could be improved by a larger data set that includes a higher number of strong to extreme sensitizers when such data become available.

Table 7. Overall Performance of Binary Model Distinguishing Weak to Moderate Sensitizers from Strong to Extreme Sensitizers on the Test Set.

ε	validity	efficiency	ACC	MCC	CCR	SE	SP	NPV	PPV
0.10	0.94	0.45	0.87	0.70	0.92	1.00	0.84	1.00	0.58
0.20	0.88	0.71	0.83	0.63	0.87	0.92	0.81	0.97	0.57
0.30	0.75	0.98	0.75	0.45	0.76	0.79	0.73	0.92	0.47

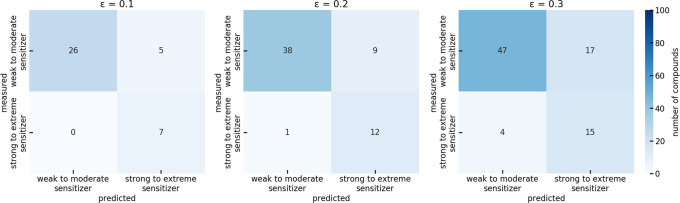
The observation of low PPV was also supported by the confusion matrices shown in Figure 7. The confusion matrices revealed that only 18% to 23% of the distinct predictions were made on strong to extreme sensitizers, which is the minority class.

Figure 7.

Confusion matrix of the binary model distinguishing weak to moderate sensitizers from strong to extreme sensitizers on the test set.

The classifier is overall overconservative, which is also reflected in the class-wise validities, all of which are higher than 1−ε (Table 8). Class-wise validities and efficiencies are almost balanced between both classes, with a maximum difference of 0.09 and 0.10 in validity and efficiency, respectively.

Table 8. Class-Wise Performance of Binary Model Distinguishing Weak to Moderate Sensitizers from Strong to Extreme Sensitizers on the Test Set.

ε	class	validity	efficiency
0.10	weak to moderate sensitizers	0.92	0.47
	strong to extreme sensitizers	1.00	0.37
0.20	weak to moderate sensitizers	0.86	0.71
	strong to extreme sensitizers	0.95	0.68
0.30	weak to moderate sensitizers	0.74	0.97
	strong to extreme sensitizers	0.79	1.00

Combined Workflow for Ternary Classification of Skin Sensitization Potential

Finally we combined, as a proof of concept, the two binary models in one workflow for the prediction of ternary skin sensitization potential and passed the resulting boolean array (storing the class membership of each compound to the three potency classes investigated) to our evaluation workflow. Within our test set, there was no case observed in which the first binary model predicted a compound to be a sensitizer but the second binary model predicted the compound to be neither a weak to moderate nor a strong to extreme sensitizer. We therefore believe there is no risk of artificially increasing the validity on this test set by reporting the validity and efficiency of the combined workflow.

Overall Performance on the Test Set

The combined workflow was valid overall, that is, in terms of the mean values among the three potency classes (overall validity = 0.92 and 0.80), at the significance levels of 0.10 and 0.20. At the error significance level of 0.30, the overall validity was only 0.66, which is 0.04 below the expected validity of 0.70. Although this value is still within the standard deviation observed for the significance level of 0.30 during 10-fold CV, it is larger than the deviations observed for other models and error significances within this work. We therefore cannot be sure that this under-predictiveness is only caused by statistical fluctuations and consider the validity of the model at the significance level of 0.30 as questionable.

The efficiency of the combined workflow (values between 0.42 and 0.90) was lower than or equal to the efficiency of the binary classifier differentiating between nonsensitizers and sensitizers (values between 0.49 and 0.92) at the three investigated significance levels (comparability of the two models is limited since the combined workflow is evaluated on only a subset of the data used for evaluation of the binary classifier) and lower than the efficiency of the binary classifier differentiating between weak to moderate and strong to extreme sensitizers (values between 0.45 and 0.98).

Satisfactory ACC values (from 0.90 to 0.73 for the significance levels investigated) and MCC values (from 0.78 to 0.54 for the significance levels investigated) were achieved on the ternary test set (Table 9).

Table 9. Overall Performance of Combined Workflow for Ternary Prediction of Skin Sensitization Potential on the Test Set¹.

ε	validity	efficiency	ACC	MCC	CCR	SE	SP	NPV	PPV
0.10	0.92	0.42	0.90	0.78	0.91	0.91	0.93	0.92	0.84
0.20	0.80	0.71	0.80	0.63	0.79	0.79	0.89	0.87	0.71
0.30	0.66	0.90	0.73	0.54	0.70	0.70	0.86	0.84	0.64

¹All performance measures are reported as the mean of the corresponding performance measure over all classes investigated.

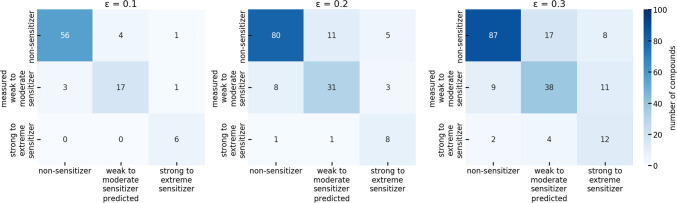
Analysis of the confusion matrices of the combined workflow on the test set (Figure 8) revealed that, at a significance level of 0.10 and 0.20, only 7% (6 out of 88 and 10 out of 148, respectively) of the compounds with distinct predictions were experimentally assigned as strong or extreme sensitizers. Thus, we expect the model to have limited impact on the prediction of strong to extreme sensitizers.

Figure 8.

Confusion matrix obtained with the combined workflow for the ternary prediction of the skin sensitization potential of all compounds of the ternary test set.

At a significance level of 0.30, which covers 90% of the test data, only 10% (18 out of 188) of the compounds were experimentally labeled as strong or extreme sensitizers. At the same time, 31 compounds were predicted to belong to this potency class. The likelihood of a compound predicted as being a strong or extreme sensitizer to belong to any of the three potency classes under investigation is almost equal for all three classes. A prediction with such a high false positive rate is not generally useful.

Class-Wise Performance on the Test Set

Since the low efficiency and the high false positive rate of strong to extreme sensitizers was not reflected by the overall performance measures, class-wise performance measures for each class of compounds were evaluated and summarized in Table 10.

Table 10. Class-Wise Performance of Combined Workflow for Ternary Prediction of Skin Sensitization Potential on the Test Set.

ε	class	validity	efficiency	SE	SP	PPV	NPV
0.10	nonsensitizer	0.93	0.49	0.92	0.89	0.95	0.83
	weak to moderate sensitizer	0.88	0.32	0.81	0.94	0.81	0.94
	strong to extreme sensitizer	1.00	0.32	1.00	0.98	0.75	1.00
0.20	nonsensitizer	0.81	0.77	0.83	0.83	0.90	0.73
	weak to moderate sensitizer	0.74	0.64	0.74	0.89	0.72	0.90
	strong to extreme sensitizer	0.89	0.53	0.80	0.94	0.50	0.98
0.30	nonsensitizer	0.70	0.90	0.78	0.86	0.89	0.72
	weak to moderate sensitizer	0.58	0.88	0.66	0.84	0.64	0.84
	strong to extreme sensitizer	0.63	0.95	0.67	0.89	0.39	0.96

At the significance levels of 0.10 and 0.20, the model was class-wise valid to over-predictive for nonsensitizers and strong to extreme sensitizers. With validities of 0.88 and 0.74, the model was slightly under-predictive for weak to moderate sensitizers at the significance levels of 0.10 and 0.20, respectively. We assume that the model can nevertheless be considered valid within the expected fluctuations on such a small data set. At a significance level of 0.30, the model was under-predictive for all classes investigated except nonsensitizers. With the validities for weak to moderate sensitizers and strong to extreme sensitizers being 0.58 and 0.63, the model must be considered invalid for these classes at the significance level of 0.30.

At all three significance levels, we observed a decrease in the PPV and an increase in the NPV from nonsensitizers to extreme sensitizers. These trends are related to the number of samples of each class in the training and test sets. The more samples of one class are present in a training set, the more reliable positive predictions and the less reliable negative predictions for that particular class become. While the PPV becomes unacceptably low (0.50 and 0.39) for strong to extreme sensitizers at significance levels of 0.2 and 0.3, respectively, the NPV stays reasonably high for all classes investigated (0.83 to 1.00 at ε = 0.10; 0.73 to 0.98 at ε = 0.20; 0.72 to 0.96 at ε = 0.30). Thus, a compound predicted to be a strong to extreme sensitizer most likely does not belong to that class, while the prediction that a compound is not a strong to extreme sensitizer can be considered reliable at all significance levels. This finding is supported by the reasonably high SE of strong to extreme sensitizers, indicating that 98%, 94%, and 89% of the strong and extreme sensitizers are correctly identified at the significance level of 0.10, 0.20, and 0.30, respectively. These tendencies also reflect the prevalence of the potency classes within the test set.

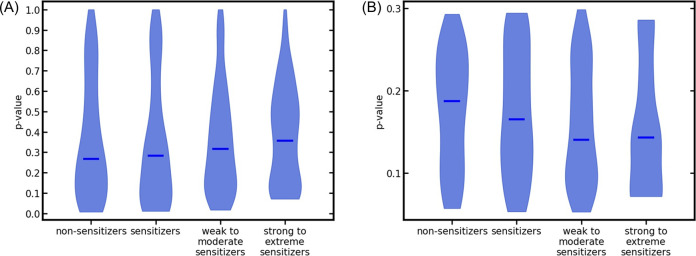
Within CP, a compound is assigned to a certain potency class if the corresponding p-value exceeds the selected significance level. Therefore, compounds with p-values in between the significance levels investigated will alter class membership when the significance level is altered. A prediction will be constant throughout all significance levels investigated, as long as the corresponding p-values are smaller than 0.10 (the lowest significance level investigated for the combined workflow) or larger than 0.30 (the highest significance level investigated in this work). The violin plots of the p-values returned by the two binary classifiers (Figure 9) visualize the distribution of p-values for each of the predicted classes within the ternary test set. All four distributions of p-values investigated show highest densities below 0.5. Compared with the two p-value distributions returned by the classifier that differentiates between nonsensitizers and sensitizers, the two distributions returned by the classifier differentiating between weak to moderate sensitizers and strong to extreme sensitizers comprise a lower percentage of compounds with p-values in extreme regions (below 0.05 or above 0.8). Thus, predictions are more likely to change depending on the significance level. The low-populated class of strong to extreme sensitizers intensifies this tendency compared to the weak to moderate sensitizing class.

Figure 9.

Violin plots of the distribution of p-values obtained for the ternary test set for the different classes of compounds as returned by the binary classification models: (A) complete test set; (B) detailed view of the p-value distributions close to the investigated significance levels, only considering p-values equal to or between 0.05 and 0.30. The median of the p-values for each potency class is indicated by a blue horizontal line.

Comparison of Ternary Classifier with Recently Published Model by Di et al

The data set of Di et al.³¹ is one of the two data resources employed for the testing and development of Skin Doctor and Skin Doctor CP. Di et al. derived ternary in silico models for the prediction of the skin sensitization potential of compounds from their data. The model that they selected as their best model uses MACCS keys just like ours, but their modeling algorithm differs (CP+RF vs SVM), and although similar, the data sets used for training and testing by Di et al. and by us are not identical. This makes a direct comparison of both models difficult. Indicators suggest that the overall performance of both models is comparable. With a coverage of 98% of the compounds of the test set, the model of Di et al. was reported to obtain an ACC of 0.71, whereas our model, at a significance level of 0.30, obtained an ACC of 0.73 on our test set (see Table 11 for details). At this significance level, the efficiency of our model (90%) is lower than the coverage of the Di et al. model (98%; recall that we consider the efficiency of a CP classifier to represent a similar concept to the coverage of a non-CP model). The efficiency of our model decreases further at lower significance levels, to 42% and 71% at the significance levels of 0.10 and 0.20, respectively. However, at the significance levels of 0.10 and 0.20, our combined workflow exhibits higher overall performance (ACC = 0.90 and 0.80, respectively) than the Di et al. model (ACC = 0.71).

Table 11. Comparison of Overall Performance Measures of Best Ternary Model Reported by Di et al. and Our Combined CP Workflow for Ternary Classification Applied.

	ACC	SE	SP	NPV	PPV	coverage/efficiency
Di et al.	0.71	0.61	0.83	0.84	0.68	98%
combined CP workflow at significance level of 0.3	0.73	0.70	0.86	0.84	0.64	90%
our reconstruction of the model reported by Di et al. (without AD applied)	0.70	0.60	0.83	0.83	0.67	100%

From our investigations of the class-wise performance of our own ternary classifier, we know that its capacity to discriminate weak to moderate from strong to extreme sensitizers is insufficient. Since this limitation is mainly caused by a lack of LLNA data, we found it surprising that the ternary classifier of Di et al. seems to not suffer from this problem. Therefore, we reconstructed the ternary model published by Di et al. using the identical training and testing data, the identical type of descriptors (MACCS keys fingerprint) and the same modeling algorithm (SVM, probability = True, gamma = 0.125). For this reconstructed model, we found similar overall performances as reported by Di et al., who did not publish any values pertaining to the class-wise performance of their model. Like the original model of Di et al., the reconstructed model achieved an ACC of 0.80 on the external test set. On the test set, the reconstructed model achieved an ACC of 0.70 (further indicators: SE = 0.60, SP = 0.83, NPV = 0.83, and PPV = 0.67). Since we did not apply any AD, the reconstructed model has a coverage of 100%. Di et al. report a coverage of 98% on the test set and similar but slightly better performance measures (see above). Differences in performance might originate from our not applying any AD definition (in contrast to Di et al.) and the usage of different modeling software with perhaps different default values.

Of particular interest, however, is how the class-wise performance of the reconstructed model compares to that of our ternary classifier. This experiment reveals that the reconstructed Di et al. model suffers from class-wise unreliability just as our own ternary classifier does (Tables 12 and 13). The SE of the reconstructed Di et al. model is unsatisfyingly low for strong to extreme sensitizers (0.30 on the test set and 0.05 on the external test set). The confusion matrices (Figure 10) show that the model only very rarely predicts that a compound belongs to the class of strong to extreme sensitizers. This is a similar finding to what we observed with our own CP-based ternary classifier (see above; Table 10). These results indicate that also our reconstructed Di et al. model is unable to properly differentiate between the two classes of skin sensitizers.

Table 12. Class-Wise Performance of Reconstructed Non-CP SVM MACCS Model on the Di et al. Test Set.

class	SE	SP	PPV	NPV	number of compounds
nonsensitizer	0.79	0.71	0.65	0.83	33
weak to moderate sensitizer	0.72	0.79	0.76	0.76	39
strong to extreme sensitizer	0.30	0.97	0.60	0.91	10

Table 13. Class-Wise Performance of Reconstructed Non-CP SVM MACCS Model on the Di et al. External Test Set.

class	SE	SP	PPV	NPV	number of compounds
nonsensitizer	0.88	0.6	0.88	0.60	461
weak to moderate sensitizer	0.59	0.88	0.54	0.90	115
strong to extreme sensitizer	0.05	0.98	0.10	0.96	22

Figure 10.

Confusion matrices of the reconstructed model of Di et al.

Conclusion

In this work, we explored the scope and limitations of aggregated Mondrian CP in the development of approaches for the binary and ternary classification of compounds with respect to their skin sensitization potential. First, we developed and evaluated a binary classifier to differentiate nonsensitizers from sensitizers. The CP model was found to be valid for all classes at nearly all significance levels investigated and revealed to be favorable in terms of the portion of compounds for which a distinct or reliable prediction could be made compared to our previously published non-CP RF model that was trained and tested on the identical descriptors and a similar but slightly larger data set.

Second, we developed and tested a binary classifier that differentiates weak to moderate sensitizers from strong to extreme sensitizers based on a data set containing all sensitizing compounds with ternary class information from our ternary data set. Although the model was valid both overall and class-wise, and resulted in reasonable efficiencies, the model must be taken with caution due to the low quantity of data available for development and testing. The model was found to be not sufficiently reliable when being applied to strong to extreme sensitizers.

Finally, we integrated both binary classifiers within a combined workflow to result in a ternary prediction of the skin sensitization potential. We showed that the combined workflow, which was overall valid at the significance levels of 0.10 and 0.20, suffered from poor PPV for strong and extreme sensitizers at the significance levels of 0.20 and 0.30. This limits the ability of the model to correctly identify compounds belonging to that class. Investigation of a recent ternary model published by others³¹ indicated that a low class-wise performance despite satisfying overall performance might also be a problem elsewhere and should be further investigated when publishing models developed using the currently available LLNA data.

From our studies, we conclude that aggregated Mondrian CP is a favorable approach for small and imbalanced data sets such as the LLNA data used in this work. This CP approach seems to be capable of improving the reliability and efficiency/coverage of binary classifiers for skin sensitization potential compared to non-CP approaches. In addition, CP offers the advantage of defined error rates that differentiate reliable from unreliable predictions without the need for a manually set threshold for a possible AD cutoff.

The ternary prediction of sensitizing potential would be highly relevant in a real-world setting. Our analysis has indicated that aggregated Mondrian CP provides benefits in efficiency and performance compared to the non-CP approach in this case as well. However, the amount of data currently available is unfortunately too small to properly distinguish different classes of sensitizing compounds, which strongly limits the applicability and reliability of the model. For better modeling, as well as for a statistically more solid evaluation of the model, more data (especially on strong and extreme sensitizers) are urgently needed.

Skin Doctor CP is available via a public web service at https://nerdd.zbh.uni-hamburg.de/skinDoctorII.

Glossary

Abbreviations

ACC

accuracy

AD

applicability domain

CCR

correct classification rate

CP

conformal prediction

MCC

Matthews correlation coefficient

NPV

negative predictive value

PPV

positive predictive value

RF

random forest

SE

sensitivity

SP

specificity

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemrestox.0c00253.

• Full Skin Doctor CP data set, including class labels and declaration of which substances were used for model training and for model testing; set of substances removed from original data set during manual data curation process; list of most common functional groups in data set and distribution of nonsensitizers and sensitizers within molecules containing this functional group; final p-values returned by two binary classifiers on binary and ternary test set; analysis of prediction accuracy for substances containing most common functional groups among test set (XLSX)

A.W. is supported by Beiersdorf AG through HITeC e.V. C.d.B.K. is funded by a PhD completion scholarship from the Universität Hamburg. C.S. and J.Ki. are supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - project number KI 2085/1–1. M.I.A. is supported by the Ministry of Education, Youth and Sports of the Czech Republic - project number LM2018130.

The authors declare the following competing financial interest(s): A.W. is funded by Beiersdorf AG through HITeC e.V. and J.K. is employed at Beiersdorf AG. A.W. and J.K. were involved in the design of the study, the interpretation of the data, the writing of the manuscript, and the decision to publish the results.