Abstract

Progress in immunotherapy has resulted in explosively increased new therapeutic interventions and they have shown promising results in the treatment of cancer. Animal testing is performed to provide preliminary efficacy and safety data for drugs under development prior to clinical trials. However, translational challenges remain for preclinical studies such as study design and the relevance of animal models to humans. Hence, only a small fraction of cancer patients showed response. The explosion of drug candidates and therapies makes preclinical assessment of every plausible option impossible, but it can be easily tested using Quantitative System Pharmacology (QSP) models. Here, we developed a QSP model for humanized mice. Tumor growth dynamics, T cell dynamics, cytokine release, immune checkpoint expression, and drug administration were modeled and calibrated using experimental data. Tumor growth inhibition data were used for model validation. Pharmacokinetics of T cell engager (TCE), tumor growth profile, T cell expansion in the blood and infiltration into tumor, T cell dissemination from primary tumor, cytokine release profile, and expression of additional PD-L1 induced by IFN-γ were modeled and calibrated using a variety of experimental data and showed good consistency. Mouse-specific response to T cell engager monotherapy also showed the key features of in vivo efficacy of TCE. This novel QSP model, designed for human peripheral blood mononuclear cells (PBMC) engrafted xenograft mice, incorporating the most critical components of the mouse model with key cancer and immune cells, can become an integral part of preclinical drug development.
Keywords: immuno-oncology, computational biology, mathematical model, immunocompromised mice, patient-derived xenograft, PBMC humanized mice
The recent success of immunotherapies represents “the silver lining in a dark cloud” for many cancer patients. However, favorable responses were achieved in only less than 15% of all cancer patients.1 Preclinical studies are critical in determining drug safety and efficacy; however, rodent models used in preclinical drug development cannot recapitulate human biology with sufficient accuracy, and allometric scaling methods can be misleading when key physiological or biochemical differences between species are not considered rigorously. Better animal models are emerging to represent the human immune system and tumor microenvironment.2 The development of humanized mouse models enables better human immune cell reconstitution, sheds light on the interactions between human immune cells and tumors of human origin, and shows better representation of human cancer pathologies, which may provide translation of drug safety and efficacy information when moving from bench to bedside.3
Humanized mouse models are typically generated using either human peripheral blood mononuclear cells (PBMC) or hematopoietic stem cells (HSC) engrafted into immunodeficient mice.4 Note that all abbreviations are described in Table S1. Human PBMC-engrafted mice provide a high level of functional and educated human T cell populations in mice, but show poor reconstitution of myeloid derived cells and NK cells due to the lack of important cytokines. Thus, PBMC humanized mouse is an attractive model for therapies targeting T cells such as bispecific antibodies (bsAbs), immune checkpoint inhibitors (ICIs), and CAR-T cell therapy. Unlike the PBMC humanized mouse model, human CD34+ HSCs-engrafted mice are developed by inoculating human hematopoietic cells into immunocompromised mice. Stable reconstitution of B, T, NK and myeloid cell lineages can be achieved providing long-term use for assessing agents that require multilineage immunity.5
Despite the success of humanized mouse models, limitations still exist.6 Even though humanized mouse models are close to human in terms of their immune response, the intrinsic properties of animals are never exactly the same as human. As for the PBMC humanized mouse model, which is the main focus of this study, major histocompatibility complex (MHC) in the tumor graft does not match the PBMCs from other healthy donors. The sources of PBMCs are also diverse, leading to large uncertainty and viability. In addition, only T cell populations are well reconstituted in PBMC humanized mouse model, whereas, essential human cytokines are missing, leading to dysfunctional human B cells and myeloid cells. Expansion of human T cells in mice is also observed due to the xeno-reactivity of human PBMC and host MHC class I and II, resulting in rapid development of Graft-versus-host disease (GvHD), which limits the therapeutic observational window to only 4–6 weeks.3 Importantly, costs of animal studies are substantial but provide limited information in some cases, causing a high failure rate in clinical trials. Alternative techniques are thus needed to improve the quality and predictive power of mouse models with reduced cost.7
In recent years, QSP modeling has demonstrated its value in complementing preclinical and clinical cancer research.8−12 Different QSP models have been developed for early discovery and clinical trial design of drug candidates to help identify feasible targets, predict efficacy and safety, optimize dosing, and provide precision medicine.13−15 Jafarnejad et al. developed a human QSP model to investigate the response of non-small cell lung cancer (NSCLC) patients to anti-PD-1 blockade, and to determine the most sensitive parameters as potential biomarkers.16 On this basis, Sové et al. improved the model and designed a modularized QSP modeling platform to help users construct mechanistic models for immuno-oncology applications.17 Virtual clinical trials were performed using an extended model by Wang et al. to explore the efficacy of combining an epigenetic modulator and ICIs in HER2-negative breast cancer patients.18 Ma et al. further improved this model by incorporating T cell engager (TCE) and ICIs to study TCE monotherapy and combination therapy with TCE and ICIs for colorectal cancer patients.19,20 Besides using human QSP models, Betts et al. developed a translational QSP model for CD3 Bispecific antibodies to understand its in vivo pharmacokinetics and pharmacodynamics (PK/PD) relationship with P-cadherin and translated this model to human for the prediction of clinical efficacy.21 Finley et al. have published a series of papers using a computational systems biology model to study the efficacy of antiangiogenic therapy in tumor-bearing mice.22−24 However, there is still a lack of a comprehensive QSP model for mouse models to predict immunotherapies in early discovery and improve translational power of these mouse models.
In this work, we have developed a QSP model for human PBMC-engrafted mouse models, with several key features including tumor growth, T cell expansion, ICIs dynamics, and drug induced cytokine release, to explore therapies targeting T cells. All model equations (eq 1–23) are described in Methods section. First, the outline of the model and governing equations for all mechanistic modules as well as module calibration are described, followed by a case study of TCE to demonstrate how to apply this model to certain therapies and how this model reproduces experimental data from in vivo studies of TCE. TCEs are a class of engineered bispecific monoclonal antibodies that can simultaneously bind to a tumor-selective cell surface antigen and receptor (TCR)-associated protein CD3 to activate T cells in an MHC I independent pathway. The detailed mechanism of action and QSP models of TCEs have been introduced in detail by Ma et al.19,20 Finally, we discuss how this mouse QSP model enables the establishment of a platform to provide insights into in vivo activities of T cell-targeted therapeutic agents and to bridge the gap between preclinical and clinical studies in cancer research.
Results
Case Study with T Cell Engager Cibisatamab
1. Model Calibration
1.1. Tumor Growth Calibration
Tumor growth in individual NOG female mice (NOD/Shi-scid/IL-2Rγnull) was measured by Bacac et al.25 using 1 × 106 LS174T-fluc2 cells. On this basis, Cinj in eq 1 was set to 1 × 106 and the values of K_growth and K_dec were derived from the tumor growth profiles (Figure 1). Black lines in Figure 1 are in vivo tumor growth measured by Bacac et al. for the tumor/PBMC cografting setting with E/T = 5:1 (Figure 1A) and 1:1 (Figure 1B). K_growth and K_dec were determined by fitting the model to the mean tumor growth, and the ranges were estimated by simulating 100 virtual (in silico) mice to match the experimental tumor growth profiles to determine 95% confidence intervals (CI) for the tumor growth profiles. Thus, the model was able to reproduce the overall trends in experimental tumor growth profiles in the absence of TCE treatment. Tumor growth following intraperitoneal PBMC transfer was also fitted, and showed a similar trend and mean as compared with the observations of Bacac et al. (Figure S2).
Figure 1.
Model predictions and observed data for in vivo tumor growth in NOG mice. Global optimization using a pattern search algorithm implemented in Matlab was used to optimize model parameters included in tumor growth using a consistent set of published data. This method was also applied to other calibrations in each section of the Methods section and parameters in each section were optimized separately. Model results are compared to experimental measurements from Bacac et al.25 for E:T (PBMC: tumor cells) ratio of 5:1 (A) and 1:1 (B). Experimental data (black lines) are shown as mean ± SD (red dots and vertical lines), n = 11 and 8 for 5:1 and 1:1, respectively. Simulation results are presented by mean ± SD (solid green line and green shading, n = 100). Purple shading indicates 95% confidence interval of simulated tumor growth. Data points were digitized from Bacac et al.25
1.2. T Cell Dynamics
1.2.1. T Cell Dynamics When Cografted with Cancer Cells
Significant T cell dissemination from the primary tumor was observed by Bacac et al.25 and quantified by Lehmann et al.26 The T-cell-positive tumor area fraction was calculated based on the skinfold chamber mouse model, indicating a significant decrease of T-cell-positive area fraction from 0.065 ± 0.013 on day 4 to 0.043 ± 0.007 on day 5, which means only 66% of T cells were remaining after 24 h (Table S2). To capture this feature, we assumed that the fold change of T-cell-positive area fraction corresponded to the fold change in absolute T cell numbers. The dissemination rate K_dis in eq 2 was estimated by generating 100 virtual mice, and K_death in eq 2 was already known based on several studies.16,17 Five hundred thousand T cells were cografted with cancer cells at day 1, and on average there were 354 380 ± 9588 and 182 960 ± 6234 T cells remaining on days 4 and 5 in the tumor site due to the dissemination of T cells to blood and other tissues based on our model predictions, corresponding to a 48% T cell reduction from day 4 to day 5. The results showed good consistency compared with the experimental range of fold change (Figure 2A, Table S2).
Figure 2.
Model predictions and observed data for T cell density for cografting (A and B) or i.p. transfer (C and D) of human T cells. (A) Predicted T cell number in primary tumor sites without TCE treatment. (B) Predicted T cell number in primary tumor sites with 2 mg/kg TCE treatment. Simulation results of 100 virtual mice are shown as solid color lines, number of T cells at Day 4 and 5 are shown as means ± SEM (red dots with red arrows, n = 100). Values are summarized in Table S2 as well as data points from Lehmann et al.26 (C) T cell expansion in mouse blood is compared with experimental measurements (color dotted lines with circles); data points were digitized from Søndergaard et al.28 (D) Intratumoral T cell density with TCE treatment following experimental dosing regimen by Griessinger et al.29 Simulation results are shown as solid color lines and presented by mean ± SEM (solid green line and green shading, n = 100). Direct comparison of simulated intratumoral density with data from Griessinger et al. is available in Table S3.
However, in the presence of TCE, T cells undergo significant proliferation. A 4.5 fold increase in T cells was observed on day 5 compared to day 4 for the CEA TCB treated group (Table S2). Parameters in eq 13 including K_T_pro, EC50_C exp, and EC50_TCE exp were estimated based on this observation. One hundred virtual mice were used to predict the number of T cells with TCE treatment. The results showed 349 940 ± 10 190 and 1 775 500 ± 147 073 T cells remaining on days 4 and 5, respectively, consistent with experimental data (Figure 2B, Table S2).
1.2.2. T Cell Dynamics When Engrafted by i.v. or i.p
In contrast to the cografting setting, T cells undergo significant expansion in blood after being engrafted by intravenous (i.v.) or intraperitoneal (i.p.) injection. The expansion has been quantified by Søndergaard et al. and Liu et al.27,28 The expansion of T cells in mouse determined by Søndergaard et al. is summarized in Figure 2C. One hundred virtual mice were used to estimate the values and ranges of K_C_pro and K_T_dec in eq 3. Expansion trends coincided with experimental measurements, and the mean and standard error for T cell expansion were within a reasonable range (Figure 2C).
On the basis of the works by Hipp et al. and Griessinger et al.29,30 only a small fraction of T cells in the blood infiltrate tumor sites with a density of ∼2 cells/mm2, which can be neglected compared with the TCE treated group. Thus, we assumed that q_T_in in eq 4 was close to 0. Q_T_in in eq 14 was estimated based on 2-D T cell density with TCE treatment determined by Hipp et al. and Griessinger et al. (Table S3). A 3-D T cell density was converted from 2-D density according to Mi et al.;31 the conversion is detailed in the Supporting Information. For direct comparison, we followed the same dose regimen used in Griessinger et al. and calculated the T cell density at the same end point. The results showed that the model prediction of T cell density was 21 264 ± 2551 cells/mm3, which was within the observed range (21 580 ± 9019 cells/mm3).
1.3. Cytokine Release Calibration (In Vitro, In Vivo)
Immunotherapies are prone to varying degrees of toxicities, of which cytokine release syndrome (CRS) is a common dose-dependent adverse event caused by TCEs.32 IL-6 plasma concentration is highly associated with the occurrence of CRS and can be used as a predictive biomarker to forecast CRS in advance.33−35 IFN-γ is also a cytokine of interest in our study due to its correlation with the efficacy of immunotherapies and immune escape mechanism. The release of both cytokines was modeled using the same method following eqs 5–11.
BL in eq 5 was directly obtained based on baseline IL-6 and IFN-γ concentrations measured by Godbersen-Palmer et al.,34cK_deg, Ktr, cImax, and cIC50 in eqs 5–11 were provided by Xiaoying et al.36 and were assumed identical for both cytokines. cEmax and cEC50 were fitted to in vitro cytokines released into culture supernatants with CEA TCB treatment (Figure S3) and then adjusted using in vivo data provided by Godbersen-Palmer et al. One hundred virtual mice were generated with varied BL, cEmax, and cEC50 for IL-6 and IFN-γ, respectively, to estimate the ranges of these three parameters following the same dose regimen used by Godbersen-Palmer et al.34 Boxplots of model predictions and experimental observations of control and TCE-induced plasma cytokine concentrations showed good agreement (Figure 3), indicating a reliable prediction of cytokine release by the mouse QSP model.
Figure 3.
Model predictions and observed data for cytokine concentration with TCE treatment for plasma IL-6 (A) and plasma IFN-γ (B). Experimental data from Godbersen-Palmer et al.34 are plotted as red boxes and simulation results are presented as blue boxes for both baseline concentrations (Exp_IL6_BL, Sim_IL6_BL, Exp_IFNg_BL, and Sim_IFNg_BL) and TCE induced concentrations (Exp_IL6, Sim_IL6, Exp_IFNg, and Sim_IFNg) following the same dosing regimen. Data points were digitized from Godbersen-Palmer et al.34
1.4. IFN-γ – PD-L1 Overexpression
PD-L1 surface expression is upregulated by IFN-γ, and the
mean fluorescent intensity (MFI) of PD-L1 expression has been measured
by Shin et al.37 for selected
melanoma cell lines by flow cytometry upon IFN-γ exposure. Here,
we assumed that MFI is equivalent to PD-L1 surface density defined
in eq 12. The initial
PD-L1 density, 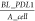 , prior to increased IFN-γ exposure
was set to 900 molecule/μm2 based on Jafarnejad et al.16 From experimental observations,
the density of PD-L1 increased significantly and reached an apex within
24 h of treatment, which was around 2 to 6 fold higher than the baseline
density. Thus, F in eq 12 was defined between 2 and 6 to set the upper
limit for PD-L1 upregulation. Afterward, the PD-L1 density of most
cell lines began to decline. However, none of the cell lines had PD-L1
density lower than the baseline. Based on this, we defined the lower
limit of PD-L1 density by adding
, prior to increased IFN-γ exposure
was set to 900 molecule/μm2 based on Jafarnejad et al.16 From experimental observations,
the density of PD-L1 increased significantly and reached an apex within
24 h of treatment, which was around 2 to 6 fold higher than the baseline
density. Thus, F in eq 12 was defined between 2 and 6 to set the upper
limit for PD-L1 upregulation. Afterward, the PD-L1 density of most
cell lines began to decline. However, none of the cell lines had PD-L1
density lower than the baseline. Based on this, we defined the lower
limit of PD-L1 density by adding 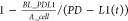 to the decline term in eq 12 to ensure that the decline
rate
was zero when real-time PD-L1 density approached the baseline value.
to the decline term in eq 12 to ensure that the decline
rate
was zero when real-time PD-L1 density approached the baseline value.
Similar to the tumor growth profiles, the mean model predicted PD-L1 densities for 100 virtual mice were fitted to mean experimental values. Then, we varied the values of k_PDL1 and k_dec_PDL1 to reproduce the experimental PD-L1 profiles to determine their ranges. The results showed that the simulated PD-L1 density reproduced the experimental data very well (Figure 4).
Figure 4.

Model predictions and observed data for IFN-γ and PD-L1. Experiment data from Shin et al.37 are shown as black lines and presented as means ± SEM (red dots and vertical lines, n = 9). Simulation results are presented by mean ± SD (solid green line and green shading, n = 100). Purple shading indicates 95% confidence intervals of simulated PD-L1 density. Data points were digitized from Shin et al.37
2. Model Validation
2.1. Tumor Growth Inhibition with TCE
After calibrating unknown parameters, we further validated the model by computing tumor regression with TCE treatment, since these data were not used during the fitting process. All parameters were fitted as described above, and we simulated the treatment following the dose regimens used by Bacac et al.25 For the cografting setting, 2.5 mg/kg cibisatamab was administered twice a week i.v. 1 or 7 days after tumor and T cells were cografted. For the mouse model with i.p. transfer of PBMC, T cells were injected 7 days after tumor cell injection, and 2.5 mg/kg cibisatamab was injected twice weekly i.v., beginning 3 days after PBMC transfer. Better inhibition of tumor growth was achieved when starting the treatment on day 1 compared with day 7, which was consistent with experimental observations (Figure 5A,B) by Bacac et al.25 More interesting, even though the treatment was given on day 10 following i.p. transfer of PBMCs, most tumor regression was experimentally observable on days 14 to 15, which was also reproduced by this model (Figure 5C), indicating a reliable estimation and calibration of T cell dynamics in this model. Overall, the model did an excellent job of reproducing inhibitory effect of cibisatamab on tumor progression.
Figure 5.
Model predictions for in vivo tumor growth in NOG mice with TCE treatment (2.5 mg/kg, i.v., twice/week) starting day 1 (A), day 7 (B) after cografting of human T cells and cancer cells or Day 10 after i.p. transfer of human T cells (C). For panels A and B, simulation results are presented by mean ± SD (solid green line and green shading, n = 100). Purple shading indicates 95% confidence intervals of simulated PD-L1 density. For panel C, individual tumor volume was plotted as solid color lines (n = 100) and presented as means ± SEM (solid green line and green shading) to show that the delayed response occurred around Day 15.
3. Model Application and Prediction
3.1. Dose Optimization
Cytokine release syndrome is a life-threatening complication associated with T cell-engaging therapies, and circulating IL-6 can be used as a biomarker to predict potential toxicity. Here, we computed the tumor volume on day 20 and associated plasma IL-6 concentration to identify an appropriate therapeutic window and to determine the best dose regimen to achieve a therapeutic benefit with the lowest increase in plasma IL-6.
When treatment started 1 day after cografting, similar tumor regression was observed for different doses ranging from 0.1 mg/kg to 10 mg/kg (Figure 6A). Elevated plasma IL-6 concentrations were found (Figure 6B). To ensure low plasma IL-6 concentration, 0.1 mg/kg, i.v., twice/week should be chosen. Similarly, 0.1 mg/kg was also the best dosing regimen for treatment that started 7 days after cografting (Figure 6C,D). Unlike cografting, i.p. transfer of T cells with treatment 3 days after that, had a most efficacious dose at 0.5 mg/kg, whereas 0.1 mg/kg showed a limited inhibitory effect. Higher doses lead to high plasma IL-6 without significant improvement of treatment outcomes (Figure 6E,F). To explore the mechanism, we compared intratumoral T cell density and the functional trimer (CEACEA_TCE_TeffCD3 in eq 19). When the dose was above 2.5 mg/kg, significant T cell infiltration was observed (Figure S5A). However, due to the bell-shaped concentration relationship of TCE,19,21 higher doses would lead to a less functional trimer being formed in the immunological synapse. Hence, we compared the number of functional trimers for the five doses and found that 0.1 and 0.5 mg/kg cibisatamab resulted in more functional trimers than did higher doses (Figure S5B). The 0.1 mg/kg dose had the highest number of functional trimers; however, due to its low T cell infiltration, the efficacy was not as good as that for the 0.5 mg/kg group.
Figure 6.
Tumor growth inhibition in NOG mice with different doses. Tumor volumes and plasma IL-6 concentration are shown at Day 20 of NOG mice with TCE treatment starting day 1 (A and B), day 7 (C and D) after cografting of human T cells and cancer cells or Day 10 after i.p. transfer of human T cells (E and F). No TCE was administrated for control groups and five doses were investigated and compared (0.1, 0.5, 2.5, 5, or 10 mg/kg, i.v., twice/week).
Discussion
Translating data from animal models to human is a critical biomedical challenge. Frequently disappointing results have been observed when translating results from rodents to human, indicating an urgent need for reliable and affordable alternatives to understand discrepancies between different species and improve the translational power of current animal models. Here, we developed a QSP model to study the in vivo activity of T cell-targeting therapies, such as bispecific antibodies and immune checkpoint inhibitors, in human PBMC engrafted xenograft mice. Development of a mouse QSP model, aligned with our previous published human QSP models, could potentially provide a more comprehensive understanding crucial for improving translational research and thus improve clinical efficiency with reduced cost.
Key features of PBMC humanized mice have been included in this model and calibrated using a variety of in vivo experimental data. The Gompertz model has shown excellent goodness-of-fit in all circumstances that we explored. T cell density and distribution were consistent with experimental measures, for all administration routes employed. Moreover, validation of this model using data following TCE treatment has proven the success of modeling T cell dynamics, by reproducing the immediate tumor regression when injected s.c. and delayed response when injected i.p. Cytokine release was modeled following published literature and the predicted concentrations of IL-6 and IFN-γ were at similar levels compared with in vivo measurements. However, the in vivo measurements of IL-6 and IFN-γ by Godbersen-Palmer et al. were based on immunocompetent mice and used a different bispecific antibody. Owing to the lack of data, we can only assume that bispecific antibodies have a similar effect on inducing cytokine release, and the differences between immunocompetent and immunocompromised mice need to be validated when more data become available. In addition, even though the transit compartment model has shown its ability to model cytokine release38 cytokine internalization was not considered and modeled explicitly. This process involves the cytokine-receptor binding, internalization, degradation or recycling, downstream signaling pathways that increase the expression of receptors or release of cytokines, etc. These procedures should be assessed and incorporated in future versions of the model. Upregulation of PD-L1 induced by IFN-γ was also successfully captured by this model, and this mechanism is responsible for acquired resistance to ICIs. Understanding the role of upregulated PD-L1 is critical for overcoming potential resistance and allowing patients to have long-term and stable benefits from ICIs. Plasma IL-6, as an important biomarker for predicting immune-related adverse events (irAE), provided information on potential toxicity and could help optimize the dose regimen. In addition, since we have T cell proliferation and PD-L1 upregulation in the QSP model, we can further explore how the intratumoral T cell’s density affects efficacy and how drug resistance develops with upregulated PD-L1.
Parameter sensitivity analysis determined the most influential parameters involved in certain processes (Figure S4). Unlike human QSP, most parameters showed little effect on the tumor volume because all mice responded to TCE treatment. However, CEA expression was still a very sensitive parameter in all cases, and this observation was consistent with human QSP, indicating a good translational power to predict human response from mouse studies. On this basis, mouse QSP could be a reliable model to determine potential biomarkers and study how target expression, target binding, and immediate downstream events affect patients’ response to different modalities when translated to human. In the future, when additional immune mechanisms are incorporated into the model, and additional data are available for model validation, a direct comparison of our mouse and human QSP models could help further improve the translational power and lower the high failure rates in drug discovery. Parameters that affect IL-6, IFN-γ release, Hill equation of PD-1, and TCE were also summarized in a PRCC heatmap (Figure S4).
Even though the QSP model successfully captured all experimental systems that we investigated here, there are several limitations that can be addressed with more experimental data or when necessary. In the first version of a mouse QSP, we did not include CD4+ T cells and regulatory T cells because Liu et al. did not observe regulatory T cells in tumor,27 and CD4+ T cells were not the key antitumor cells. Upregulation of PD-L1 by IFN-γ is semimechanistic without considering the details of associated pathways such as protein kinase D isoform 2 (PKD2)39 and IFN-γ-JAK1/JAK2-STAT1/STAT2/STAT3-IRF1 axis.40 There is also a lack of mapping of plasma IL-6 to toxicity categories. Van der Stegen et al. observed rapid weight loss and deaths for mice with high plasma IL-6 concentration above 1000 pg/mL.35 More in vivo data are needed to confirm the correlation between plasma IL-6 concentration and toxicity level. Furthermore, investigations should be done to translate preclinical toxicity predictions to clinical trials to determine an appropriate and safe dosing regimen. IL-6 alone is likely insufficient, and additional toxicity biomarkers should be combined to achieve more reliable predictions as done by Lim et al.41
In addition, for clinical trials design, a lower than necessary starting dose and/or a conservative dose escalation protocol can lead to prolonged delays before patients achieve efficacious concentrations, whereas a high starting dose is not preferred due to safety concerns. To help determine the right dose for first-in-human trials, solid validation should be performed to ensure the reliability and predictive power of QSP models to avoid misestimating caused by insufficient validation. Besides the dose, a less frequent dose is also always desired. Interestingly, for TCE, Hipp et al. observed sustained tumor regression for the tumors from day 15 until day 36 even though the treatment was stopped at day 22, indicating a potential less frequent dosing regimen.30 Thus, a comprehensive evaluation of dose as well as dosing frequency is essential to make the right decision. Although this topic was not well explored in the current study, dose optimization in the results section 3.1 presents an example showing how to utilize this model to predict the best dose regimen. More data and biomarkers will be incorporated for a comprehensive toxicity assessment, to find a balance between efficacy and toxicity.
Overall, the model was first fitted to a variety of experimental data without TCE treatment and was able to reproduce data with treatment, showing its ability to model tumor growth kinetics and predict treatment outcomes. All parameters included in this model can be further calibrated and validated with additional data and extended to other treatments and cancer types. With future updates, more mechanisms can be added to the current model, and the framework can be readily adapted for other therapies, indications, and in vivo mouse pharmacology models, for example, in HSC humanized mice, and immunocompetent mice. Using these models, the connection between mouse and human QSP models will be established, and these mechanistic models will be leveraged to improve the success rate of preclinical to clinical translation.
In summary, BsAbs and ICIs are complex modalities and every step from preclinical discovery to clinical trials and postmarketing analysis is full of unknowns and challenges. QSP modeling approaches are powerful tools to aid in drug development at each stage to understand the complexities of bsAbs and ICIs including prediction of efficacy, determination of dose regimen, assessment of immune-related adverse events (irAE), strategies to reduce toxicity, translation of animal data into optimal clinical studies, clinical trial design, and postapproval assessment. The mouse QSP model was able to reproduce in vitro data and in vivo behavior of tumor, T cells, TCE, and other key variables, providing a comprehensive framework to determine the efficacy of bsAbs, ICIs, and predict potential toxicity. More preclinical data and new features implemented in the next versions of the mouse QSP model, will enable the prediction of the first-in-human safe starting dose for various TCEs, ICIs, combinations and other drug modalities for a variety of indications. The model can further be used to alleviate the problems of translation from animals to humans along with our previously published human QSP models.
Methods
Model Diagram
The mouse QSP developed in this study has similar structure compared with our previous human QSP models for ICIs and T cell engager (TCE).16,19,20 The model contains three major compartments including central (blood), peripheral (other tissues and organs), and tumor and one minor tumor-draining lymph node (TdLN) compartment (Figure 7). For immunocompromised mice, TdLN is typically negligible in terms of its size and function.42 Even though TdLN’s function is interrupted, inclusion of the TdLN compartment can help develop the QSP model for immunocompetent mouse easily and would not affect other compartments for immunocompromised mouse. The model was modularized to several submodules including a cancer module, T cell module, immune checkpoint module, antibody pharmacokinetics (PK) module, and TCE module. The dynamics of the major species in each module will be described in detail in the next sections. Forty-three ordinary differential equations (ODEs) and 51 algebraic equations were used to model all biological processes involved in the model. Compartments, species, reactions, rules, events, and all model parameters as well as their references, have been summarized in an Excel spreadsheet in the Supporting Information. After model calibration, cibisatamab (RO6958688, RG7802) was presented as a case study and compared to its in vivo activity. Mouse PK parameters for cibisatamab have been reported, and PK parameters were fitted to experimental data.25 Observed and simulated serum concentrations of cibisatamab following intravenous doses of 0.5 and 2.5 mg/kg are provided in the Supporting Information (Figure S1). The pharmacodynamics of cibisatamab has been calibrated and described in our published human QSP models and was assumed to be the same in mouse.19,20 All simulations and sensitivity analyses were performed using the SimBiology platform in MATLAB R2020a (MathWorks, Natick, MA).
Figure 7.

Diagram of the main cellular and molecular interactions implemented in the mouse QSP model.
Model Equations
Tumor Growth
Different mathematical models have been applied to represent in vivo tumor growth kinetics. Classical models such as exponential, logistic, and Gompertz have proven their ability to fit experimental data. However, by comparing the descriptive power of the three models to the same population, the Gompertz model has shown superior goodness-of-fit properties compared to the other two models.43 Hence, in our mouse QSP model, the evolution of cancer cells is described by
 |
1 |
Here in eq 1, C(t) indicates the number of cancer cells at time point t, Cinj denotes the number of cancer cells injected into the mouse, which is known based on experimental methods, K_growth is the specific cancer cell proliferation rate, also known as tumor growth rate, followed by an exponential decrease rate K_dec of the proliferation rate. The tumor volume was calculated as the sum of volume of all cancer cells and tumor infiltrating immune cells. The pattern search function implemented in Matlab was used to fit the model and estimate the optimal parameter values of K_growth and K_dec in eq 1 by minimizing the error between the model predictions and the experimental measurements.
T Cell Dynamics When Cografted with Cancer Cells
The PBMC humanized mouse model can be developed by cografting cancer cells and PBMCs and injected subcutaneously (s.c.) in mouse. However, the majority of T cells would soon disseminate from the primary tumor via tumor associated blood or lymphatic vessels without being activated by tumor antigens due to the quick proliferation of cancer cells based on the intravital two-photon (2P) microscopy results reported by Bacac et al.25 Fewer T cells were observed 4 days after cografting, and no T cells were detected 10 days after cografting. The first-order dissemination of T cells is described by
| 2 |
where TT and K_dis represent the number of effector T cells in the tumor compartment and the dissemination rate of T cells from the primary tumor. The first-order death term, K_death represents a basal death rate of T cells in the tumor, which was derived from the lifespan of T cells as introduced by Jafarnejad et al. and Sové et al.16,17
T Cell Dynamics When Engrafted i.v. or i.p
PBMCs can also be engrafted by i.v. or i.p. injection to an immunodeficient mouse.7 Within this setting, a significant expansion of human T cells in mouse blood which causes severe GvHD was observed by several studies.27,28 Despite significant expansion in blood, only a few T cells were detected in tumors by Hipp et al. and Griessinger et al.,29,30 indicating poor T cell infiltration, in the absence of treatment. The expansion of T cells in the blood follows the Gompertz function
| 3 |
Similar to tumor growth, T cell expansion also follows a sigmoid growth curve observed by Søndergaard et al.28K_C_pro here denotes the proliferation/expansion rate and K_T_dec denotes the exponential decrease rate of K_C_pro. TC is the number of effector T cells in the blood and TCi is the number of initial T cells injected into mouse. The basal death rate of T cells in the blood is described as K_death. Note that the basal death term in the Gompertz law can be neglected in the current analysis. The basal death rate is too slow to affect the expansion rate but it would be beneficial to account for when we consider additional factors that may affect T cell death such as activation-induced cell death, extrinsic cell-death-receptor- and caspase-dependent apoptosis. Then this term can be modified accordingly to represent T cell death explicitly.
T cells in the blood will eventually be recruited into the tumor sites. The infiltration of T cells into tumor follows
| 4 |
where q_T_in denotes the infiltration rate of T cells from blood and VT is the volume of tumor.
Cytokine Release
TCE induced cytokine release was characterized using a modeling framework by Xiaoying et al.36 for both hematological malignancies and solid tumor. Since our mouse QSP model focuses on solid tumors, a transit compartmental model was used to represent the lag time of cytokines to be transported from release compartment to circulation. The cytokine PD model applied to IL-6 and IFN-γ in this study follow
 |
5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
Here, Cy_n (n = 1, 2, 3, 4, 5, 6) represents cytokine concentration in the tumor compartment (n = 1) and in five transit compartments (n = 2–6), CyC represents plasma cytokine concentration; BL, cK_deg, and Ktr denote baseline plasma cytokine concentration, cytokine degradation rate, and cytokine transit rate between compartments, respectively; cEmax and cEC50 in the second term of eq 5 represent maximum cytokine release rate induced by drug and exposure of active drug species to achieve the half-maximum cytokine release rate. The index n_c defines the sensitivity of cytokine release to drug stimulation. In addition, cytokine release is inhibited by a negative feedback mechanism, which is time variant and related to the overall exposure over a defined time interval. cImax is the maximum inhibition, which is equal to 1 indicating no cytokine release when maximum inhibition is achieved. cIC50 is the cumulative cytokine exposure to achieve half-maximum inhibition.
IFN-γ Induced PD-L1 Expression
Previous studies have demonstrated the ability of immune checkpoint blockade therapies and TCEs to increase IFN-γ production to eliminate cancer cells.25,44,45 However, a high concentration of IFN-γ could in turn induce more PD-L1 expression in cancer cells to promote the escape of tumor cells from immune surveillance and help develop resistance to immunotherapies.39 Quantifying the relationship between IFN-γ and PD-L1 upregulation is critical for identifying strategies that amplify tumor cell killing while reducing potential resistance to immunotherapies. Time and dose-dependent upregulation of IFN-γ-induced PD-L1 surface expression has been determined by Shin et al. and Chen et al.37,39 On the basis of their measurements, upregulation of PD-L1 was observed within a few hours with a certain concentration of IFN-γ, and the upregulation had an upper limit followed by a downregulation. The process is described as
 |
12 |
where the density of initial PD-L1
was calculated
from baseline PD-L1 number, BL_PDL1 divided by the
surface area of cancer cell, A_cell. k_PDL1 represents the upregulation rate of PD-L1 and is controlled by a
Hill equation of IFN-γ; in this Hill equation, IFN-γ
_T indicates the intratumoral IFN-γ concentration and ifngEC50 represents the concentration of IFN-γ
to achieve 50% of the maximum upregulation rate. The fourth term on
the right of the equation provides the upper limit of PD-L1 upregulation,
when the density of PD-L1 is close to the upper limit defined as 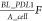 , the expression rate will be close to 0.
F represents the fold change of PD-L1 with respect to the initial
PD-L1 density and was estimated based on the experimental data. K_dec_PDL1 represents the decrease rate of PD-L1 downregulation
and there is also a lower limit defined as
, the expression rate will be close to 0.
F represents the fold change of PD-L1 with respect to the initial
PD-L1 density and was estimated based on the experimental data. K_dec_PDL1 represents the decrease rate of PD-L1 downregulation
and there is also a lower limit defined as 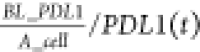 , which ensures that the PD-L1 density will
not be lower than the initial density.
, which ensures that the PD-L1 density will
not be lower than the initial density.
T Cell Activation, Proliferation, and Exhaustion in Tumor with TCE Treatment
PBMCs can be engrafted in immunodeficient mice either subcutaneously with cancer cells or intraperitoneally and follow distinct distribution profiles as described by eqs 2–4. Little T cell activation and proliferation were found without treatment;25,26 therefore, we assumed no T cell activation and proliferation. Independent of the engraftment method, T cells show completely different dynamics with drug treatment aimed at improving their antitumor activity. When cografted with cancer cells, only a few T cells remain in tumor sites, leading to limited efficacy against a tumor. However, in the presence of TCE, T cells will soon be activated by TCE and proliferate based on Bacac et al. and Lehmann etal.25,26 Significantly higher T cell density was observed 1 day after administration of TCE compared with control groups without any treatment or with nonbinding control TCE. The proliferation of T cells is described by
| 13 |
The first term on the right represents the proliferation rate of intratumoral T cells, the proliferation depends on number of T cells at time point t, number of cancer cells, and the concentration of TCE in the tumor. Two Hill equations were used here to represent the sensitivity of T cell proliferation to cancer cell numbers and TCE concentration. For example, if all cancer cells are killed by T cells or no treatment was given, we assume that no proliferation of T cells occurs. Here, EC50_C exp and EC50_TCE exp are the number of cancer cells and concentration of intratumoral TCE to achieve the half-maximum T cell proliferation rate.
For PBMCs engrafted by i.p. or i.v. injection, the expansion of T cells in mouse blood was observed and modeled by eq 3. With the administration of TCE, only intratumoral T cells displayed an activated phenotype, increased T cell activation was not observed in blood, indicating TCE-induced T cell activation was restricted to tumor sites with the formation of T cell target—TCE—cancer cell target ternary structure.25,29 According to this, eq 3 remains the same for treatment conditions. However, more evidence has shown improved T cell infiltration in the presence of TCE.29,30
| 14 |
Similar to eq 4, Q_T_in here denotes the infiltration rate of T cells with TCE treatment and EC50_Ttrans represents concentration of intratumoral TCE to achieve half-maximum T cell infiltration rate. Significant proliferation of intratumoral T cells was also detected, which follows the same proliferation rule described in eq 13.
Prolonged antigen stimulation and an immunosuppressive tumor microenvironment would cause significant T cell exhaustion. T cell exhaustion from cancer cells has been described by Jafarnejad et al. and Sové et al.16,17 as
| 15 |
| 16 |
| 17 |
Here, K_Tcell represents the T cell exhaustion rate caused by cancer cells and the density of bound PD1-PDL1/PDL2 molecules in immune synapse between cancer cells and T cells was translated to Teff exhaustion using a Hill equation (eqs 16 and 17).
Accelerated exhaustion was achieved by stimulation of TCE, which is described by
| 18 |
| 19 |
K_death_TCE represents the T cell exhaustion rate caused by TCE stimulation. The number of bound CEACEA_TCE_TeffCD3 was translated to the T cell exhaustion rate by TCE using a Hill equation (eqs 18 and 19), which has been described in detail by Ma et al.19,20
TCE Dynamics and Mouse PK for Cibisatamab Case Study
The PK/PD of TCE was described in our previous publications19,20 and summarized here. The antibody PK module in human QSP models has been adjusted for mouse with appropriate compartment volumes. The PK of cibisatamab was added to the recalibrated antibody PK module. In vivo PK profiles following 0.5 mg/kg i.v. bolus administration of cibisatamab in NOG mice were reported and fitted to a 2-compartmental model by Bacac et al.25 as well as the prediction of PK profile of 2.5 mg/kg i.v. administration. Simulated plasma concentrations of cibisatamab in this 4-compartment model following i.v. bolus administration of 0.5 and 2.5 mg/kg were fitted to the in vivo PK profiles and standard 2-compartment PK model to calibrate PK parameters in eq 23 of cibisatamab in the mouse QSP model (Figure S1).
 |
20 |
| 21 |
| 22 |
| 23 |
TCEP, TCEC, TCELN, and TCET indicate TCE concentration in the peripheral, central, TdLN, and tumor compartments, respectively. Vi and qi (i = C, P, T, LN) indicates the compartment volume and intercompartmental transport constants, respectively.
TCE Induced Teff Killing
The Teff killing rate (TKR) is expressed as an inverse Hill equation of ICIs and TCEs as follows, which has been reported by Ma et al.20
| 24 |
Here kC,death,Teff is the basal cancer killing rate by Teff and kC,death,TCETeff is the additional cancer killing rate by Teff activated by TCE, C is the total number of cancer cells in the tumor compartment, Teff is total number of Teff in the tumor, and Ttot is total number of T cells in the tumor. H_PD1 and H_CEA have been introduced in eqs 16 and 19, respectively. Details of this equation were provided by Ma et al.19,20
Parameter Estimation
All parameters included in this mouse QSP model are summarized in the Supporting Information with their references. They come from a diverse set of experiments. Some of them are directly provided in the literature and the rest of them have been derived from relevant data. Estimation and calibration of these parameters are provided in detail in the Results section. To present the application of this mouse QSP model to TCE, most parameters were estimated based on in vitro and in vivo experiments of TCE, and the model could be reparameterized when applied to other treatments and indications in the future when necessary. However, most experimental data have only a few data points, resulting in a certain degree of uncertainty and error of parameter estimation, which can be further validated when more data become available in the future.
Statistical Analysis
Parameter sensitivity analysis (PSA) was performed to assess the sensitivity of a set of parameters in the mouse QSP model using the Latin Hypercube Sampling (LHS) technique. The range and distribution of these parameters are provided in Supplementary Excel spreadsheet in the PSA tab. Partial rank correlation coefficient (PRCC) analysis was performed to identify the most influential parameters from the simulation results by using the Statistics and Machine Learning Toolbox.
Statistical analysis was performed for virtual mice populations (VMPs). The Wilcoxon test was used to analyze the differences between VMPs receiving different doses of cibisatamab using the ggpubr package embedded in RStudio v1.2.
Acknowledgments
This work was supported by a grant from Boehringer Ingelheim Pharmaceuticals, Inc. and NIH Grants R01CA138264 and U01CA212007.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsptsci.0c00178.
Author Contributions
H.M., C.G., and A.S.P. designed the project; A.S.P. and C.G. directed the project; H.M. built and modified the model; H.M. performed all simulations, collected the data, did all analyses, and drafted the manuscript; A.S.P., C.G., M.P., and J.W. revised the manuscript critically; all authors have read and approved the final manuscript.
The authors declare no competing financial interest.
Notes
Availability of data and material. The authors confirm that the data supporting the findings of this study are available within the article and the Supporting Information. The model code and script to fully implement and reproduce the results will be shared by the corresponding author in the GitHub repository to any qualified researcher on request.
Supplementary Material
References
- Haslam A.; Prasad V. (2019) Estimation of the Percentage of US Patients With Cancer Who Are Eligible for and Respond to Checkpoint Inhibitor Immunotherapy Drugs. Jama Network Open 2 (5), e192535 10.1001/jamanetworkopen.2019.2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brubaker D. K.; Lauffenburger D. A. (2020) Translating preclinical models to humans. Science 367 (6479), 742–743. 10.1126/science.aay8086. [DOI] [PubMed] [Google Scholar]
- De La Rochere P.; Guil-Luna S.; Decaudin D.; Azar G.; Sidhu S. S.; Piaggio E. (2018) Humanized Mice for the Study of Immuno-Oncology. Trends Immunol. 39 (9), 748–763. 10.1016/j.it.2018.07.001. [DOI] [PubMed] [Google Scholar]
- Okada S.; Vaeteewoottacharn K.; Kariya R. (2019) Application of Highly Immunocompromised Mice for the Establishment of Patient-Derived Xenograft (PDX) Models. Cells 8 (8), 889. 10.3390/cells8080889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson T.; Greiner D. L.; Shultz L. D. (2008) Creation of “humanized” mice to study human immunity. Curr. Protoc. Immunol. 81 (1), 15–21. 10.1002/0471142735.im1521s81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akkina R.; Allam A.; Balazs A. B.; Blankson J. N.; Burnett J. C.; Casares S.; Garcia J. V.; Hasenkrug K. J.; Kashanchi F.; Kitchen S. G.; Klein F.; Kumar P.; Luster A. D.; Poluektova L. Y.; Rao M.; Sanders-Beer B. E.; Shultz L. D.; Zack J. A. (2016) Improvements and Limitations of Humanized Mouse Models for HIV Research: NIH/NIAID “Meet the Experts” 2015 Workshop Summary. AIDS Res. Hum. Retroviruses 32 (2), 109–119. 10.1089/aid.2015.0258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito R.; Takahashi T.; Ito M. (2018) Humanized mouse models: Application to human diseases. J. Cell. Physiol. 233 (5), 3723–3728. 10.1002/jcp.26045. [DOI] [PubMed] [Google Scholar]
- Mentre F.; Friberg L. E.; Duffull S.; French J.; Lauffenburger D. A.; Li L.; Mager D. E.; Sinha V.; Sobie E.; Zhao P. (2020) Pharmacometrics and Systems Pharmacology 2030. Clin. Pharmacol. Ther. 107 (1), 76–78. 10.1002/cpt.1683. [DOI] [PubMed] [Google Scholar]
- Coletti R.; Leonardelli L.; Parolo S.; Marchetti L. (2020) A QSP model of prostate cancer immunotherapy to identify effective combination therapies. Sci. Rep. 10 (1), 9063. 10.1038/s41598-020-65590-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassidy T.; Craig M. (2019) Determinants of combination GM-CSF immunotherapy and oncolytic virotherapy success identified through in silico treatment personalization. PLoS Comput. Biol. 15 (11), e1007495. 10.1371/journal.pcbi.1007495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosinsky Y.; Dovedi S. J.; Peskov K.; Voronova V.; Chu L. L.; Tomkinson H.; Al-Huniti N.; Stanski D. R.; Helmlinger G. (2018) Radiation and PD-(L)1 treatment combinations: immune response and dose optimization via a predictive systems model. J. Immunother. Cancer 6, No.17 10.1186/s40425-018-0327-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klinke D. J. (2015) Enhancing the discovery and development of immunotherapies for cancer using quantitative and systems pharmacology: Interleukin-12 as a case study. Jo. Immunother. Cancer 3, 27. 10.1186/s40425-015-0069-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betts A.; van der Graaf P. H. (2020) Mechanistic Quantitative Pharmacology Strategies for the Early Clinical Development of Bispecific Antibodies in Oncology. Clin. Pharmacol. Ther. 108 (3), 528–541. 10.1002/cpt.1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates J. W. T.; Byrne H.; Chapman S. C.; Chen T.; Cucurull-Sanchez L.; Delgado-SanMartin J.; Di Veroli G.; Dovedi S. J.; Dunlop C.; Jena R.; Jodrell D.; Martin E.; Mercier F.; Ramos-Montoya A.; Struemper H.; Vicini P. (2017) Opportunities for Quantitative Translational Modeling in Oncology. Clin. Pharmacol. Ther. 6 (7), 418–429. 10.1002/cpt.1963. [DOI] [PubMed] [Google Scholar]
- Chelliah V.; Lazarou G.; Bhatnagar S.; Gibbs J. P.; Nijsen M.; Ray A.; Stoll B.; Thompson R. A.; Gulati A.; Soukharev S.; Yamada A.; Weddell J.; Sayama H.; Oishi M.; Wittemer-Rump S.; Patel C.; Niederalt C.; Burghaus R.; Scheerans C.; Lippert J.; Kabilan S.; Kareva I.; Belousova N.; Rolfe A.; Zutshi A.; Chenel M.; Venezia F.; Fouliard S.; Oberwittler H.; Scholer-Dahirel A.; Lelievre H.; Bottino D.; Collins S. C.; Nguyen H. Q.; Wang H. Q.; Yoneyama T.; Zhu A. Z. X.; van der Graaf P. H.; Kierzek A. M. (2020) Quantitative Systems Pharmacology Approaches for Immuno-Oncology: Adding Virtual Patients to the Development Paradigm. Clin. Pharmacol. Ther. 1987 10.1002/cpt.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jafarnejad M.; Gong C.; Gabrielson E.; Bartelink I. H.; Vicini P.; Wang B.; Narwal R.; Roskos L.; Popel A. S. (2019) A Computational Model of Neoadjuvant PD-1 Inhibition in Non-Small Cell Lung Cancer. AAPS J. 21 (5), 79. 10.1208/s12248-019-0350-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sové R. J.; Jafarnejad M.; Zhao C.; Wang H.; Ma H.; Popel A. S. (2020) QSP-IO: A quantitative systems pharmacology toolbox for mechanistic multi-scale modeling for immuno-oncology applications. CPT: Pharmacometrics Syst. Pharmacol. 9 (9), 484–497. 10.1002/psp4.12546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H. W.; Sove R. J.; Jafarnejad M.; Rahmeh S.; Jaffee E. M.; Stearns V.; Torres E. T. R.; Connolly R. M.; Popel A. S. (2020) Conducting a Virtual Clinical Trial in HER2-Negative Breast Cancer Using a Quantitative Systems Pharmacology Model With an Epigenetic Modulator and Immune Checkpoint Inhibitors. Front. Bioeng. Biotechnol. 8, 141 10.3389/fbioe.2020.00141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma H.; Wang H.; Sove R. J.; Jafarnejad M.; Tsai C.-H.; Wang J.; Giragossian C.; Popel A. S. (2020) A Quantitative Systems Pharmacology Model of T Cell Engager Applied to Solid Tumor. AAPS J. 22 (4), 85. 10.1208/s12248-020-00450-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma H.; Wang H.; Sové R. J.; Wang J.; Giragossian C.; Popel A. S. (2020) Combination therapy with T cell engager and PD-L1 blockade enhances the antitumor potency of T cells as predicted by a QSP model. Journal for Immuno Therapy of Cancer 8 (2), e001141 10.1136/jitc-2020-001141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betts A.; Haddish-Berhane N.; Shah D. K.; van der Graaf P. H.; Barletta F.; King L.; Clark T.; Kamperschroer C.; Root A.; Hooper A.; Chen X. Y. (2019) A Translational Quantitative Systems Pharmacology Model for CD3 Bispecific Molecules: Application to Quantify T Cell-Mediated Tumor Cell Killing by P-Cadherin LP DART((R)). AAPS J. 21 (4), 66. 10.1208/s12248-019-0332-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finley S. D.; Dhar M.; Popel A. S. (2013) Compartment model predicts VEGF secretion and investigates the effects of VEGFTrap in tumor-bearing mice. Front. Oncol. 3, 196. 10.3389/fonc.2013.00196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaddy T. D.; Wu Q. H.; Arnheim A. D.; Finley S. D. (2017) Mechanistic modeling quantifies the influence of tumor growth kinetics on the response to anti-angiogenic treatment. PLoS Comput. Biol. 13 (12), e1005874 10.1371/journal.pcbi.1005874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Q. H.; Arnheim A. D.; Finley S. D. (2018) In silico mouse study identifies tumour growth kinetics as biomarkers for the outcome of anti-angiogenic treatment. J. R. Soc., Interface 15 (145), 20180243. 10.1098/rsif.2018.0243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacac M.; Fauti T.; Sam J.; Colombetti S.; Weinzierl T.; Ouaret D.; Bodmer W.; Lehmann S.; Hofer T.; Hosse R. J.; Moessner E.; Ast O.; Bruenker P.; Grau-Richards S.; Schaller T.; Seidl A.; Gerdes C.; Perro M.; Nicolini V.; Steinhoff N.; Dudal S.; Neumann S.; von Hirschheydt T.; Jaeger C.; Saro J.; Karanikas V.; Klein C.; Umana P. (2016) A Novel Carcinoembryonic Antigen T-Cell Bispecific Antibody (CEA TCB) for the Treatment of Solid Tumors. Clin. Cancer Res. 22 (13), 3286–3297. 10.1158/1078-0432.CCR-15-1696. [DOI] [PubMed] [Google Scholar]
- Lehmann S.; Perera R.; Grimm H. P.; Sam J.; Colombetti S.; Fauti T.; Fahrni L.; Schaller T.; Freimoser-Grundschober A.; Zielonka J.; Stoma S.; Rudin M.; Klein C.; Umana P.; Gerdes C.; Bacac M. (2016) In Vivo Fluorescence Imaging of the Activity of CEA TCB, a Novel T-Cell Bispecific Antibody, Reveals Highly Specific Tumor Targeting and Fast Induction of T-Cell-Mediated Tumor Killing. Clin. Cancer Res. 22 (17), 4417–4427. 10.1158/1078-0432.CCR-15-2622. [DOI] [PubMed] [Google Scholar]
- Liu X.; Li H. L.; Liu J.; Guan Y. B.; Huang L. Y.; Tang H. L.; He J. X. (2014) Immune reconstitution from peripheral blood mononuclear cells inhibits lung carcinoma growth in NOD/SCID mice. Oncol. Lett. 8 (4), 1638–1644. 10.3892/ol.2014.2379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sondergaard H.; Kvist P. H.; Haase C. (2013) Human T cells depend on functional calcineurin, tumour necrosis factor-alpha and CD80/CD86 for expansion and activation in mice. Clin. Exp. Immunol. 172 (2), 300–310. 10.1111/cei.12051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griessinger C. M.; Olafsen T.; Mascioni A.; Jiang Z. K.; Zamilpa C.; Jia F.; Torgov M.; Romero J. M.; Marchioni F.; Satpayev D.; Lee C. Y.; Zhang G.; Nayak T. K.; Pincha M.; Amann M.; Mohan P. L. B.; Richard M.; Nicolini V. G.; Sam J.; Claus C.; Ferrara C.; Brunker P.; Bacac M.; Umana P.; Ruttinger D.; Wilson I. A.; Gudas J.; Klein C.; Tessier J. J. L. (2020) The PET-Tracer (89)Z -Df-IAB22M2C Enables Monitoring of Intratumoral CD8 T-cell Infiltrates in Tumor-Bearing Humanized Mice after T-cell Bispecific Antibody Treatment. Cancer Res. 80 (13), 2903–2913. 10.1158/0008-5472.CAN-19-3269. [DOI] [PubMed] [Google Scholar]
- Hipp S.; Voynov V.; Drobits-Handl B.; Giragossian C.; Trapani F.; Nixon A. E.; Scheer J. M.; Adam P. J. (2020) A Bispecific DLL3/CD3 IgG-like T-cell Antibody induces anti-tumor responses in Small Cell Lung Cancer. Clin. Cancer Res. 26, 5258. 10.1158/1078-0432.CCR-20-0926. [DOI] [PubMed] [Google Scholar]
- Mi H. Y.; Gong C.; Sulam J.; Fertig E. J.; Szalay A. S.; Jaffee E. M.; Stearns V.; Emens L. A.; Cimino-Mathews A. M.; Popel A. S. (2020) Digital Pathology Analysis Quantifies Spatial Heterogeneity of CD3, CD4, CD8, CD20, and FoxP3 Immune Markers in Triple-Negative Breast Cancer. Front. Physiol. 11, 583333 10.3389/fphys.2020.583333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maude S. L.; Barrett D.; Teachey D. T.; Grupp S. A. (2014) Managing Cytokine Release Syndrome Associated With Novel T Cell-Engaging Therapies. Cancer J. 20 (2), 119–122. 10.1097/PPO.0000000000000035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu M.; Kratzer A.; Johnson J.; Holland C.; Brandl C.; Singh I.; Wolf A.; Doshi S. (2018) Blinatumomab Pharmacodynamics and Exposure-Response Relationships in Relapsed/Refractory Acute Lymphoblastic Leukemia. J. Clin. Pharmacol. 58 (2), 168–179. 10.1002/jcph.1006. [DOI] [PubMed] [Google Scholar]
- Godbersen-Palmer C.; Coupet T. A.; Grada Z.; Zhang S. C.; Sentman C. L. (2020) Toxicity Induced by a Bispecific T Cell-Redirecting Protein Is Mediated by Both T Cells and Myeloid Cells in Immunocompetent Mice. J. Immunol. 204 (11), 2973–2983. 10.4049/jimmunol.1901401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Stegen S. J. C.; Davies D. M.; Wilkie S.; Foster J.; Sosabowski J. K.; Burnet J.; Whilding L. M.; Petrovic R. M.; Ghaem-Maghami S.; Mather S.; Jeannon J. P.; Parente-Pereira A. C.; Maher J. (2013) Preclinical In Vivo Modeling of Cytokine Release Syndrome Induced by ErbB-Retargeted Human T Cells: Identifying a Window of Therapeutic Opportunity?. J. Immunol. 191 (9), 4589–4598. 10.4049/jimmunol.1301523. [DOI] [PubMed] [Google Scholar]
- Chen X. Y.; Kamperschroer C.; Wong G.; Xuan D. W. (2019) A Modeling Framework to Characterize Cytokine Release upon T-Cell-Engaging Bispecific Antibody Treatment: Methodology and Opportunities. Clin. Transl. Sci. 12 (6), 600–608. 10.1111/cts.12662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin D. S.; Zaretsky J. M.; Escuin-Ordinas H.; Garcia-Diaz A.; Hu-Lieskovan S.; Kalbasi A.; Grasso C. S.; Hugo W.; Sandoval S.; Torrejon D. Y.; Palaskas N.; Abril-Rodriguez G.; Parisi G.; Azhdam A.; Chmielowski B.; Cherry G.; Seja E.; Berent-Maoz B.; Shintaku I. P.; Le D. T.; Pardoll D. M.; Diaz L. A.; Tumeh P. C.; Graeber T. G.; Lo R. S.; Comin-Anduix B.; Ribas A. (2017) Primary Resistance to PD-1 Blockade Mediated by JAK1/2 Mutations. Cancer Discovery 7 (2), 188–201. 10.1158/2159-8290.CD-16-1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krzyzanski W. (2011) Interpretation of transit compartments pharmacodynamic models as lifespan based indirect response models. J. Pharmacokinet. Pharmacodyn. 38 (2), 179–204. 10.1007/s10928-010-9183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.; Feng Y.; Lu L. B.; Wang H.; Dai L. N.; Li Y.; Zhang P. (2012) Interferon-gamma-induced PD-L1 surface expression on human oral squamous carcinoma via PKD2 signal pathway. Immunobiology 217 (4), 385–393. 10.1016/j.imbio.2011.10.016. [DOI] [PubMed] [Google Scholar]
- Garcia-Diaz A.; Shin D. S.; Moreno B. H.; Saco J.; Escuin-Ordinas H.; Rodriguez G. A.; Zaretsky J. M.; Sun L.; Hugo W.; Wang X. Y.; Parisi G.; Saus C. P.; Torrejon D. Y.; Graeber T. G.; Comin-Anduix B.; Hu-Lieskovan S.; Damoiseaux R.; Lo R. S.; Ribas A. (2019) Interferon Receptor Signaling Pathways Regulating PD-L1 and PD-L2 Expression. Cell Rep. 19 (6), 1189–1201. 10.1016/j.celrep.2017.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim S. Y.; Lee J. H.; Gide T. N.; Menzies A. M.; Guminski A.; Carlino M. S.; Breen E. J.; Yang J. Y. H.; Ghazanfar S.; Kefford R. F.; Scolyer R. A.; Long G. V.; Rizos H. (2019) Circulating Cytokines Predict Immune-Related Toxicity in Melanoma Patients Receiving Anti-PD-1-Based Immunotherapy. Clin. Cancer Res. 25 (5), 1557–1563. 10.1158/1078-0432.CCR-18-2795. [DOI] [PubMed] [Google Scholar]
- Seymour R.; Sundberg J.P.; Esch H. H. (2006) Abnormal lymphoid organ development in immunodeficient mutant mice. Vet. Pathol. 43 (4), 401–423. 10.1354/vp.43-4-401. [DOI] [PubMed] [Google Scholar]
- Vaghi C.; Rodallec A.; Fanciullino R.; Ciccolini J.; Mochel J. P.; Mastri M.; Poignard C.; Ebos J. M. L.; Benzekry S. (2020) Population modeling of tumor growth curves and the reduced Gompertz model improve prediction of the age of experimental tumors. PLoS Comput. Biol. 16 (2), e1007178 10.1371/journal.pcbi.1007178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni L.; Lu J. (2018) Interferon gamma in cancer immunotherapy. Cancer Med. 7 (9), 4509–4516. 10.1002/cam4.1700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian J. W.; Wang C.; Wang B.; Yang J.; Wang Y. D.; Luo F. F.; Xu J. Y.; Zhao C. J.; Liu R. H.; Chu Y. W. (2018) The IFN-gamma/PD-L1 axis between T cells and tumor microenvironment: hints for glioma anti-PD-1/PD-L1 therapy. J. Neuroinflammation 15 (1), 1–13. 10.1186/s12974-018-1388-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







