A Novel Cluster Sampling Design that Couples Multiple Surveys to Support Multiple Inferential Objectives

Abstract

In the United States the number of health systems that own practices or hospitals have increased in number and complexity leading to interest in assessing the relationship between health organization factors and health outcomes. However, the existence of multiple types of organizations combined with the nesting of some hospitals and practices within health systems and the nesting of some health systems within larger health systems generates numerous analytic objectives and complicates the construction of optimal survey designs. An objective function that explicitly weighs all objectives is theoretically appealing but becomes unwieldy and increasingly ad hoc as the number of objectives increases. To overcome this problem, we develop an alternative approach based on constraining the sampling design to satisfy desired statistical properties. For example, to support evaluations of the comparative importance of factors measured in different surveys on health system performance, a constraint that requires at least one organization of each type (corporate owner, hospital, practice) to be sampled whenever any component of a system is sampled may be enforced. Multiple such constraints define a nonlinear system of equations that “couples” the survey sampling designs whose solution yields the sample inclusion probabilities for each organization in each survey. A Monte Carlo algorithm is developed to solve the simultaneous system of equations to determine the sampling probabilities and extract the samples for each survey. We illustrate the new sampling methodology by developing the constraints and solving the ensuing systems of equations to obtain the sampling design for the National Surveys of United States Health Care Systems, Hospitals and Practices. We illustrate the virtues of “coupled sampling” by comparing the proportion of eligible systems for whom the corporate owner and both a hospital and a practice that are expected to be sampled to that expected under alternative sampling designs. Comparative and descriptive analyses that illustrate features of the sampling design are also presented.

1. Introduction

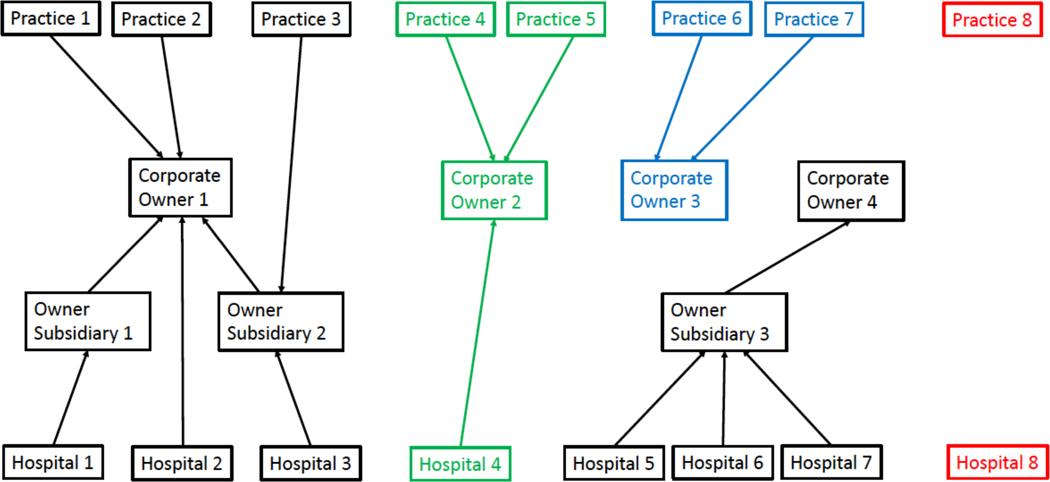
This paper describes novel methodology developed for a suite of surveys used to help characterize the structure, ownership, leadership, and care delivery procedures of United States health systems, hospitals and (physician) practices as part of an Agency for Healthcare Research and Quality (AHRQ) funded initiative (AHRQ 2019). The structure of US health care is complex as hospitals and practices may be nested within health systems and some health systems may be nested within larger health systems, leading to a mix of single, double and triple-tiered ownership structures (Figure 1). Systems may contain clusters of hospitals and practices of varying number and structure (“simple” or single-tiered systems; “complex” or double-tiered systems) while independent hospitals and practices are standalone entities. Simple systems are corporate entities including multiple hospitals or practices while complex systems are corporate entities that also include other systems. Hospitals and practices can be viewed as being in system (corporate owned) versus independent strata with the system stratum containing multiple substrata. The corporate owner is the corporate entity in the part of a system directly above a hospital or practice; they are known as a corporate parent if they head the entire system and as an owner subsidiary otherwise. Because they contain distinct features, different surveys must be used for corporate owners than for hospitals and practices.

Figure 1:

Layout of example health systems in the United States showing complex systems (black), a simple system (green), a simple system comprising only of hospitals also known as a medical group (blue), and an independent practice and independent hospital (red). Hospitals and practices are related to their owner (corporate parent or owner subsidiary) via directed edges while owner subsidiaries are related to their corporate parent also via directed edges. The complex system on the far left illustrates that a corporate parent can directly own hospitals and practices as well as owning owner subsidiaries that in turn own hospitals and/or practices. The other complex system illustrates that a corporate parent need not directly own any health units. Systems can also consist entirely of hospitals or practices while the later can be independent.

A simplistic sampling scheme would draw distinct stratified-cluster samples of systems, hospitals and practices. Organizations (e.g., a hospital) sampled in one survey would not affect the sampling of any organization (e.g., a corporate owner or a practice) in the other surveys. However, the joint inclusion (or selection) probability of the owner, a hospital, and a practice within a system in their respective surveys is the product of the three sample inclusion probabilities and hence could be very small. Regression analyses that estimate the simultaneous effect of system, hospital and practice characteristics measured in the surveys would then encounter an abundance of observations with missing values for some predictors. To overcome this concern, we seek a sampling design that requires each of the types of organizations in a system (the owner, some of the hospital(s) and some of the practice(s)) to be sampled if any part of the system is sampled. That is, the sampling designs are “coupled”.

Statistical design challenges arise due to the tremendous heterogeneity in the numbers of owner subsidiaries (in triple-tiered systems), hospitals and practices within a system. Although differences between organizations can be accounted for in statistical analyses once the data are collected, it is important to design a survey so that sufficient sample is expected for each type of organization. Otherwise, estimators of population totals and regression coefficients of key predictors may have large standard errors. Therefore, we sought a design that strategically allocated sample size across the organizations of different types and sizes. The level of correlation between the parts of a system may be depend on its size. Therefore, a sampling scheme under which the number of units sampled increases sub-linearly with the total number of units of that type in the system is warranted. However, if different numbers of surveys of each type (owner, hospital and practice) will be expended on different systems, the total number of units of each type cannot be determined in advance and so the sampling probabilities also cannot be determined. Furthermore, the sampling of units from one survey clearly impacts the sampling of units in the other surveys. Thus, unlike traditional survey designs, an optimal coupled sampling design and its associated sampling probabilities are unable to be solved in closed form or by numerical solution of an explicit equation.

Because Figure 1 presents configurations that have the form of a graph, one might think of applying methods for sampling networks. However, the structure of a health system involving a corporate owner, owner subsidiaries and hospitals and practices is perfectly hierarchical. A health system with a hierarchical structure is much less amenable to sampling methods for networks such as snowball sampling (Goodman 1961) and respondent-driven sampling (Heckathorn 1997). These chain referral sampling methods are better utilized for web-based sampling or searching (Cohen, Havlin et al. 2003, Boldi, Santini et al. 2004, Stutzbach, Rejaie et al. 2009, Maiya and Berger-Wolf 2011) and for sampling hard-to-reach populations (Handcock and Gile 2011).

We have not come across any existing methodologies for sampling multipart, connected organizations such as those depicted in Figure 1 in a feasible manner. However, hierarchically structured survey populations are commonly encountered in sociology, economics, public health, education and epidemiology. For example, social scientists are often interested in the impact of a community to life opportunities of its residents (Faber and Sharkey 2015) and public health researchers are interested in the relationship of geography to specific health outcomes (Diez Roux 2001). In educational studies, some big educational programs may have centers nested within them and the centers may have students classrooms in turn nested within them (Currie 2001). Neighborhood effects may be defined as latent variables that impact observed measurements (Garner and Raudenbush 1991, Durlauf 2004). However, what is unique in our study is the interest in sampling units at each level of these hierarchies and the fact that there are multiple units at each level. We sought to develop a coupled sampling methodology to distribute sample-size across that a diverse range of organizations to support a wide-range of inferences.

One approach to determining an optimal coupled sampling design is to specify a function that quantifies the extent to which each objective of interest is satisfied along with relative importance weights. The sampling design and sampling probabilities that optimize the function is a multiple-objective optimal design. While appealing, there are several challenges with this approach, including deciding which objectives to include and their importance weights. The number of objectives may be reduced by replacing some objectives with constraints ensuring a desired level of attainment and optimizing a function of the remaining objectives subject to these constraints (Cohen 1998, Moerbeek and Wong 2002). In some cases the constrained problem may be easier to solve and the two approaches (optimization over all objectives and constrained optimization over some) may be equivalent (Cook and Wong 1994).

Building on the idea of using constraints, we propose specifying heuristics that characterize desired properties of the coupled sample as constraints. An example heuristic is the constraint that at least one of each type of organization (corporate owner, hospital, practice) in a system is sampled if any sampling is performed on that system. Clearly, such an heuristic couples their sampling designs. Because an objective function isn’t being optimized when the goal is to satisfy heuristics, “sampling scheme” might be used interchangeably with “sampling design”.

Coupling the sampling designs via heuristics addresses challenges involving multiple populations and targets of inference beyond those in traditional survey sampling designs. The involvement of heuristics resembles a form of stratified sampling in which an heuristic function is used for the purpose of predicting the performance of tree searching algorithms in computer science, referred to as Heuristic Sampling (Chen 1992). It also shares traits with purposive and criterion sampling – widely used in qualitative research (Palinkas, Horwitz et al. 2015) – in that the objective function is difficult to define and the sampling scheme seeks to obtain a sample with pre-specified properties. Purposive sampling is often performed in studies seeking to learn what to focus on in a subsequent study. Hence, it is premature to specify an objective function due to a lack of population information and one prioritizes obtaining a diverse sample to ensure a wide spectrum of subjects are represented (Patton 2002, Etikan, Musa et al. 2016). Although coupled (heuristic) sampling yields probability samples while purposive sampling is nonprobabilistic, neither has an objective function and constraints or other criteria define the sampling design implicitly.

Another key contribution of this paper is the development of a computational algorithm for finding the sampling probabilities that simultaneously solve the nonlinear system of heuristic constraint equations to find the sampling probabilities and draw the sample. We derive an iterative (Monte Carlo) algorithm that mimics the sampling procedure and captures the characteristics of the population represented by the sampling frame. Previously, Monte Carlo methods have been adapted to sampling techniques to reduce statistical error, e.g. Importance Sampling (Harbitz 1983), Adaptive Sampling (Bucher 1988), Adaptive-Rejection Sampling (Gilks 1992, Gilks and Wild 1992). Several of these techniques are used for computation of Bayesian inferences. In contrast, our Monte Carlo algorithm solves a study design problem, not an estimation problem.

Our Monte Carlo algorithm for sample allocation in coupled surveys seeks to satisfy multiple objectives for learning about possibly inter-connected study units as opposed to maximizing the precision in relation to a single objective as in Neyman allocation (Neyman 1934), the traditional determinant of an optimal stratified sampling design. Neyman allocation yields the sampling design with the smallest variance given a fixed sample size assuming equal costs per unit for all strata. In related work, optimal allocation has been achieved in balanced sampling (Tille and Favre 2005) while alternative allocation criteria have been obtained under adaptive sampling with multiple objectives over which to optimize the sample allocation (Kaminska and Lynn 2017).

In the remainder of this paper, the CoE study is described in detail including using mathematical notation to formerly define the survey design problem, the specification of heuristics, and the representation of heuristics as constraints (Section 2). We then develop the sampling design problem in general terms using the CoE study for illustration and derive and implement an algorithm for computing the sampling design. The properties of the resulting sampling design are studied in Section 3. This includes the methodology for drawing the samples of organizations to be surveyed and determining the sampling probabilities under coupled sampling. Section 4 applies the computational procedure to the sampling frame and evaluates its statistical properties. The paper concludes in Section 5 while the relationship of our coupled sampling approach to a multiple-objectives optimal design is analyzed in the Appendix. The Appendix also shows how the complex sampling design is specified in the statistical software package Stata (StataCorp 2017) and then taken account of in subsequent analyses to enable population representative inferences.

2. National Survey of Health Systems and Organizations (NSHOS)

The NSHOS sampling frame was based on the IQVIA OneKey database. OneKey contains a vast array of information about health systems, hospitals, practices and physicians in the United States (AHRQ 2019, IQVIA 2019). The 2015 version contained information on 239,881 healthcare businesses (including 1,216,957 healthcare professionals) and relationships between businesses.

Eligible hospitals for the sampling frame contained at least 3 primary care physicians (PCPs) and were defined as critical access and general acute care. They were required to not have a reference to a specialty (e.g. cancer) in their business name. There were 6,030 hospitals in OneKey of which 4388 (73%) met this definition. Likewise, practices in the sampling frame consisted of those labelled as family, internal or geriatric medicine, or general and multispeciality group practices again with at least 3 PCPs. There were a total of 153,916 practices in OneKey and about 15,510 (10%) met this definition.

Systems include a corporate owner and a total of at least two qualifying hospitals or practices. Like hospitals and practices they could not reference a specialty in their business name. Systems with only a single hospital or practice were considered to be independent organizations. After first applying the qualifying rules to hospitals and practices and then applying the qualifying rules for systems, a total of 1,511 systems consisting of 164 complex systems, 390 owner subsidiaries (owned by the complex systems) and 957 simple systems remained.

2.1. Analytic Targets and Statistical Models Motivating Design

The types of analytic targets of the surveys include:

• (i)Descriptive analyses estimating population counts and proportions for each type of health organization.
• (ii)System-level regression analyses with predictors including summary measures of hospitals, practices and other owner-subsidiaries within the system (e.g., how many of each) and the system’s own characteristics.
• (iii)Hospital, practice, and combined hospital-practice regression analyses with predictors reflecting ownership structure (whether they are independent vs corporate owned vs multitiered corporate owned), summary measures of their sibling organizations, and characteristics of their owners.

Optimal designs for the analyses in (i) typically minimize the variance of an estimator of the population target of interest subject to cost or other resource constraints with the solution a form of Neyman allocation. In contrast, the comparative analyses in (ii) and (iii) simultaneously involve variables/information collected from each type of survey. These analyses benefit from sampling designs that aid the estimation of hierarchical regression models including predictors evaluated on the focal unit and predictors evaluated on the other units within the system (e.g., for the corporate parent, owner subsidiaries, and other hospitals and practices within the same system).

To illustrate how data from across the surveys may be combined in a statistical model and the breadth of inferences possible, consider the relationship of a hospital quality measure (an individual variable or a scale variable) to its own characteristics, those of its corporate owner (if applicable), those of other hospitals and practices within the immediate system (if applicable) and those of the greater system (if applicable). Each group of predictors is measured from the corresponding owner, hospital or practice surveys. Let y_ijk denote the quality measure outcome for the kth hospital in the jth owner subsidiary of corporate parent i while vectors of predictors for the highest-level corporate parent, mid-level corporate parent (the owner-subsidiary) and the hospital are denoted by the vectors x_i, x_ij, and x_ijk, respectively. The vector of predictors x_i may include summary measures of $(x_{i1},x_{i2},\dots ,x_{i{n}_i})$ and include an indicator of whether the system is complex or simple while x_ijk may include an indicator of whether the hospital is an independent hospital. In addition, the vectors ${\overline{h}}_{ij}\text{or}{\overline{p}}_{ij}$ denote summary measures of hospital and practice characteristics for the ij’th system while vectors ${\overline{h}}_{ij(k)}\text{and}{\overline{p}}_{ij(k)}$ are analogous except they exclude the k’th hospital or practice. A general hierarchical linear model for this analysis has the form

$$y_{ijk}={\beta }_0+{\beta }_1{x}_{ijk}+{\beta }_2{\overline{h}}_{ij(k)}+{\beta }_3{\overline{p}}_{ij(k)}+{\beta }_4{x}_{ij}+{\beta }_4{x}_i+{\theta }_i+{\lambda }_{ij}+{\epsilon }_{ijk}$$ (1)

where θ_i~normal(0, τ²), λ_ij~normal(0, τ²) and ε_ijk~normal(0, σ²). The generalized linear mixed model counterpart is analogous except for the possible absence of ε_ijk and addition of a nonlinear link function.

The model in (1) contains four vectors of predictors $(x_i,x_{ij},{\overline{h}}_{ij(k)}\text{and}{\overline{p}}_{ij(k)})$ but these are not applicable if the hospital is independent while x_i is redundant for simple systems. All organizations may be analyzed under a single model by defining indicator variables so that predictors fall out of the model if they are not applicable. For example, let the subscripts take values $i\in \{0,\dots ,n^s\};j\in \{0,\dots ,n_i^S\}$ for corporate parent i; and $k\in \{1,\dots ,n_{ij}^t\}$ for hospital (t = h) or practice (t = p) k in system ij. The subscript 0 denotes the absence of an element of the three-level data structure. Observations on systems with no owner-subsidiaries have (i > 0, j = 0) and include a dummy variable for simple system in place of x_ij. Hospitals and practices directly under a complex system also have (i > 0, j = 0) and include a dummy variable indicating such status in place of x_ij. Independent hospitals and practices have i = j = 0 and include indicator variables in place of predictors evaluated on corporate-parents and peer organizations.

Although simple systems have a two-level hierarchy, they can be extended to a three-level hierarchy and are represented in (1) by introducing a pseudo owner subsidiary that is sampled with probability 1 if the system is sampled. Likewise, independent hospitals and practices can be given pseudo corporate parents and owner subsidiaries that are both sampled with probability 1. These pseudo organizations allow statistical software to account for the sampling probabilities when comparing organizations across structures (e.g., comparing independent hospitals to those in complex and simple systems).

System-level counterparts to (1) would include ${\overline{h}}_{ij}\text{or}{\overline{p}}_{ij}$ as predictors as opposed to ${\overline{h}}_{ij(k)}\text{or}{\overline{p}}_{ij(k)}.$ This motivates use of a sampling design that attains data under which (1) and other models of interest are estimable and sufficiently precise estimates are obtained. We next develop the heuristics representing desired features of the NSHOS sampling design.

2.2. Sampling Design Constraints and Implicit Sampling Design

In Section 1 the heuristic that at least one of each type of organization (corporate owner, hospital, practice) in a system is sampled if any sampling is performed on that system was given as an example of a constraint. There are several other heuristics that appeal as logically beneficial to impose as constraints. To support analyses that seek to distinguish the impact of top-level (“corporate parent”) versus mid-level (“owner subsidiary”) ownership, it is advantageous to ensure sampling of the corporate parent if any of its owner subsidiaries are sampled and viceversa. Another appealing heuristic is that multiple hospitals and multiple practices within a system should be sampled whenever possible to aid the attainment of multiple responses within a system and thus support statistical analyses that seek to partition variation between the components of a system. We now formalize these heuristics as constraints along with traditional constraints such as ensuring that the allowable cost of the survey is not exceeded.

Suppose that the budget for the survey was fixed at N surveys (sampling costs of all types of organizations considered equal). Let s_ij denote the sample inclusion indicator (1 = included, 0 = not included) of the ij’th system (jth owner subsidiary of the ith corporate parent), and h_ijk and p_ijk the sample inclusion status of the kth hospital and practice, respectively, in system ij. The total sample size constraint is then:

$${\sum }_{i=0}^{n^s}{\sum }_{j=0}^{n_i^s}\left(s_{ij}+{\sum }_{k=1}^{n_{ij}^h}{h}_{ijk}+{\sum }_{k=1}^{n_{ij}^p}{p}_{ijk}\right)=N$$

A strongly desired feature of the sampling design is that it strongly supports estimation of hierarchical regression models like those in Section 2.1 seeking to determine which organization types and features thereof associate the most with an outcome. Therefore, if any surveys are expended on a system every type of organization (corporate parent, owner subsidiary, hospital, practice) within the system should be sampled. For example, if the corporate parent is sampled at least one owner subsidiary must be sampled (if any). Conversely, if an owner subsidiary is sampled its corporate parent must also be sampled. The constraints are represented as:

$$s_{i0}\left({\sum }_{j=1}^{n_i^s}{s}_{ij}\right)>0\text{if}{s}_{i0}>0\text{or}{\sum }_{j=1}^{n_i^s}{s}_{ij}>0\text{for}i\in \{0,\dots ,n^s\}$$

Analogous constraints ensure that hospitals and practices are sampled if their corporate owner is sampled and vice-versa:

$$\begin{gathered} s_{ij}\left({\sum }_{k=1}^{n_{ij}^h}{h}_{ijk}\right)>0\text{if}{s}_{ij}>0\text{or}{\sum }_{j=1}^{n_{ij}^h}{h}_{ijk}>0\text{for}i\in \{0,\dots ,n^s\}\text{and}j\in \{0,\dots ,n_i^s\} \\ {s}_{ij}\left({\sum }_{k=1}^{n_{ij}^p}{p}_{ijk}\right)>0\text{if}{s}_{ij}>0\text{or}{\sum }_{j=1}^{n_{ij}^p}{p}_{ijk}>0\text{for}i\in \{0,\dots ,n^s\}\text{and}j\in \{0,\dots ,n_i^s\} \\ \left({\sum }_{k=1}^{n_{ij}^h}{h}_{ijk}\right)\left({\sum }_{k=1}^{n_{ij}^p}{p}_{ijk}\right)>0\text{if}{\sum }_{j=1}^{n_{ij}^h}{h}_{ijk}>0\text{or}{\sum }_{j=1}^{n_{ij}^p}{p}_{ijk}>0\text{for}i\in \{0,\dots ,n^s\}\text{and}j\in \\ \{0,\dots ,n_i^s\} \end{gathered}$$

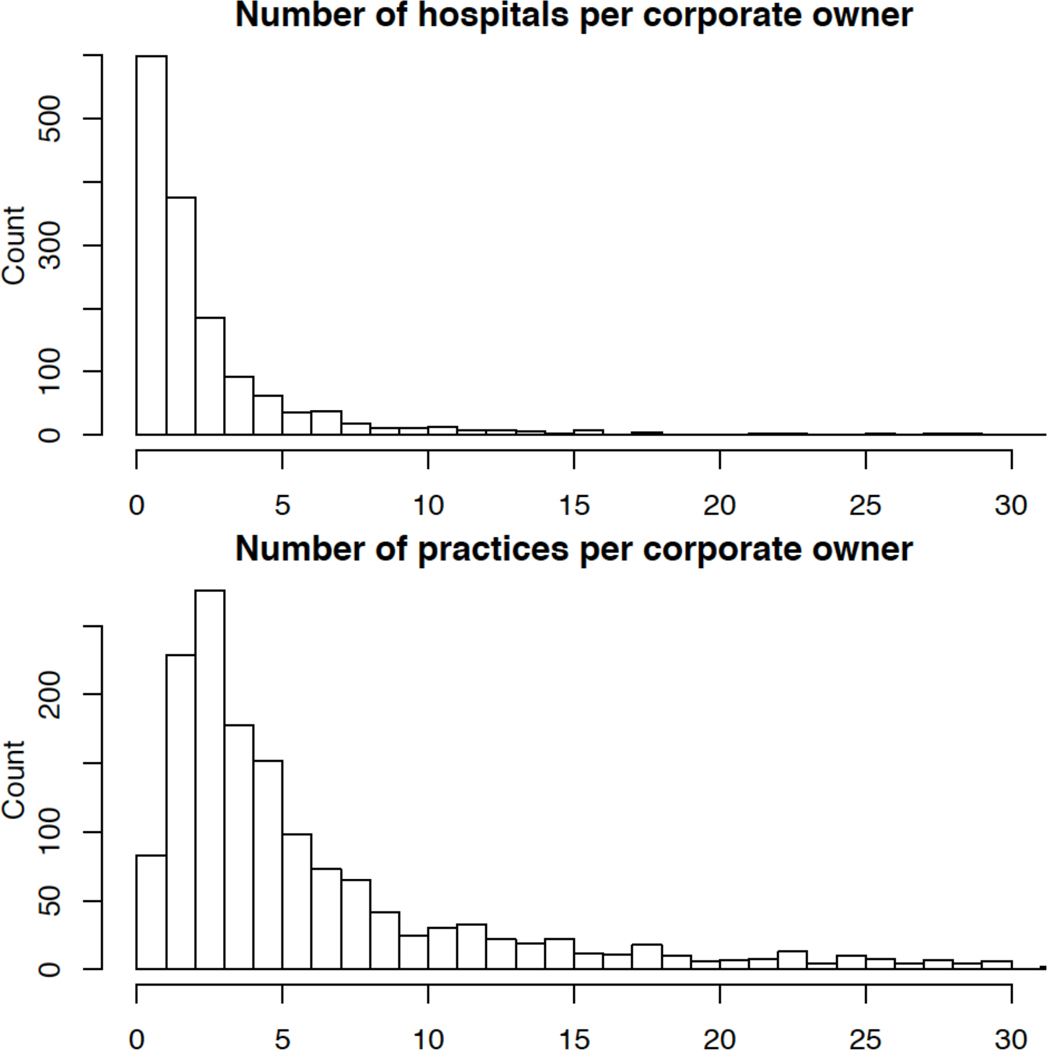
If within-system clustering was invariant to the size of the system, the optimal sampling design would sample the fewest number of sub-units within each system up to a common bound. In the absence of clustering, the expected sub-unit sample-size increases in proportion to the number of sub-units. In the NSHOS, it was believed that the correlation between the hospitals or practices within systems would lie between these extremes so that the optimal number of hospitals and practices to survey increases but only at a sub-linear rate. Because the distribution of the number of hospitals and practices directly under a corporate owner is left-skewed (Figure 2), this led to the specification that the number of surveys to expend on a system follow a logarithmic function beyond the threshold at which all hospitals or practices are sampled. Therefore, the survey allocation quantity constraints are:

$$\begin{gathered} f\left(n_{ij}^h\right)={\sum }_{j=1}^{n_{ij}^h}{h}_{ijk} \\ \text{where}f\left(n_{ij}^h\right)=\left[\min \left\{L,n_{ij}^h\right\}+lo{g}_B\left(n_{ij}^h/L\right)I\left(n_{ij}^h>L\right)\right]\text{and} \\ f\left(n_{ij}^m\right)={\sum }_{j=1}^{n_{ij}^p}{m}_{ijk} \end{gathered}$$

where $f\left(n_{ij}^p\right)=\left[\min \left\{L,n_{ij}^p\right\}+{\mathit{log}}_B\left(n_{ij}^p/L\right)I\left(n_{ij}^p>L\right)\right]$ and [x] denotes the floor of x, the largest integer not greater than x. The values of L = 4 and B = 1.9 were decided upon for NSHOS according to the following twofold rationale. In the case of corporate parents (organizations with i > 0 and j = 0), $n_{i0}^h\text{and}{n}_{i0}^p$ represent the numbers of hospitals and practices directly under the corporate parent (no owner subsidiary as an intermediate owner). To aid estimation of the amount of explained and unexplained variation at each level of a system, it is helpful to sample multiple sub-units of each type whenever possible. In the motivating study we anticipated a response rate of 50%; hence, L = 4 corresponds to an expected yield of 2 returned surveys. The log function with base 1.9 was used because it led to 10 hospitals or 10 practices being included in the sample for the largest system – 10 was an upper limit imposed by health care organization experts on our team – and interpolates 4 if there are only 4 hospitals or 4 practices.

Figure 2:

Histograms of the number of hospitals (top) and practices (bottom) per corporate owner. The number of corporate owners with 30 or more hospitals equals 13 (0.86%) while the number with 30 or more practices equals 36 (2.38%).

Although a number of constraints are deterministic, it is important to realize that the deterministic part only applies if a condition is met. Because the constraints are conditional, all marginal sampling probabilities lie strictly between 0 and 1. A marginal sampling probability of 1 can only occur if the entire sampling frame is to be sampled.

3. Estimation Algorithm

The nonlinearity of the above constraints makes extraction of a compliant three-way coupled sample and determination of the corresponding sampling probabilities a nonlinear, discretevalued system of equations requiring a computational solution. The following pseudo-codes describe the Monte-Carlo algorithms we developed to estimate the sampling probabilities (Algorithm 1) and draw the survey sample (Algorithm 2).

#Algorithm 1:

Generate sampling probabilities

Input:	$n_{ij}^h$ = Number of hospitals
	$n_{ij}^p$ = Number of practices
	$n_{i0}^{OS}$ = Number of owner subsidiaries
	C = Total number of surveys (4800 after independent organizations)
Output:	Sampling Frame Augmented with sampling probabilities (jcps-joss-2017-02-26prob1.csv)
Preliminary steps; for all $(i=1,\dots ,n^s;j=0,\dots ,n_i^S)$
1)	Compute the expenditure functions $f\left(n_{ij}^h\right)\text{and}f\left(n_{ij}^p\right)$ for corporate parent or owner subsidiary ij
2)	Evaluate the complexity score $C{S}_{ij}=1+f\left(n_{ij}^h\right)+f\left(n_{ij}^p\right);$ the total number of surveys to be expended on that system if sampled.
3)	Compute the desirability of sampling each organization
	$D{S}_{ij}=\frac{1}{D}\left(\frac{1+n_{ij}^h+n_{ij}^p}{1+I\left(n_{i0}^{OS}>0\right)}\right)$
	where $D={\sum }_{i,j}\left(\frac{1+n_{ij}^h+n_{ij}^p}{1+I\left(n_{i0}^{OS}>0\right)}\right)\text{and}{n}_{i0}^{OS}$ is the number of owner-subsidiaries in the ith system.
4)	Set Sij = 0.
Iterative (Monte-Carlo) phase; for i = 1: nsim:
1)	Randomize order of organizations by sampling them without replacement
2)	Apply order constraints to complex systems. If the first owner subsidiary occurs before its corporate parent
	a. Move corporate parent immediately in front of owner subsidiary
	b. Otherwise, move a randomly selected owner subsidiary immediately after corporate parent
3)	Use a bisection search algorithm to find the position, Nsamp, in the ordered list of organizations at which the number of surveys used first exceeds C.
4)	Compute Sampij = I(Posij ≤ Nsamp), where Posij denotes ordered position of organization ij
5)	Update Sij = Sij + Sampij
End
Closing
1)	Compute PrSampij = Sij/nsim, the estimated sample inclusion probability for organization ij
2)	Return sampling frame data including estimated sampling probabilities. Output: jcps-joss-2017-02-26prob1.csv

#Algorithm 2:

Extract sample

Input:	jcps-joss-2017-02-26prob1.csv
	$n_{ij}^h$ = Number of hospitals
	$n_{ij}^p$ = Number of practices
	$n_{i0}^{OS}$ = Number of owner subsidiaries
	$C_{sys}$ = Total number of surveys (= 4800 after independent organizations)
	$C_{00}^h$ = Total number of independent hospitals to sample (= 100)
	$C_{00}^p$ = Total number of independent practices to sample (= 800)
	$C_{\mathit{\text{tot}}}=C_{\mathit{\text{sys}}}+C_{00}^h+C_{00}^p$ is the total number of surveys afforded (= 5,700)
Generate sample indicators for each system
1)	Begin at the end of the preliminary steps of Algorithm 1
2)	Perform one iteration of the Iterative phase
3)	Output Sij for all (i = 1, ..., ns; j = 0,..., $n_i^s$)
Generate hospital and practice sample indicators
1)	For (i = 1, ..., ns; j = 0,..., $n_i^s$):
	a. Randomly order the hospitals within system ij; the first $f\left(n_{ij}^h\right)$ are sampled
	Randomly order the practices within system ij; the first $f\left(n_{ij}^p\right)$ are sampled
2)	For the independent hospitals and practices (i = j = 0):
	a. Randomly order the independent hospitals; the first $C_{00}^h$ are sampled
	b. Randomly order the independent practices; the first $C_{00}^p$ are sampled
Closing: Output the sample indicator for each system, hospital and practice

3.1. Illustration of Re-Ordering of Sampling Order of Organizations to Satisfy Constraints

The following list is an example of what might result after step (1) of the Iterative phase of Algorithm 1. We use the nomenclature ssss_oo to denote a 4-digit corporate owner ID supplemented with a two digit owner subsidiary ID, where the case oo = 00 denotes a corporate parent. Suppose the ordering of the first 10 owner organizations after the initial randomization is: 0123_00, 273_02, 056_02, 375_00, 0123_04, 0123_01, 945_00, 056_01, 945_03, 004_00. In addition, let and 375_02 be the first owner subsidiaries of corporate parent 375_00 to appear in the initial ordering. After applying the constraints in the Iterative phase, the new first 10 ordered organizations is: 0123_00, 0123_04, 273_00, 0273_02, 056_00, 056_02, 375_00, 375_02, 0123_01, 945_00. The new order reflects the shuffling needed to have every system in which either a corporate parent or an owner subsidiary is sampled have both the corporate parent and at least one owner subsidiary included in the sample.

The remaining elements of the Algorithm 1 and the entirety of Algorithm 2 involved standard operations. Deterministic functions are evaluated to determine the original likelihood of sampling a given organization or the number of hospitals or practices within a system to sample. For example, unconstrained randomization is used to order the hospitals and practices within a system and repeated iterations of the Iteration phase are used to compute a Monte-Carlo estimate of the probability of sampling each organization.

3.2. Theoretical Properties of the Sampling Design and the Use of Weights

Because the corporate parent is always sampled if an owner subsidiary is sampled, the inclusion probability of a corporate parent must exceed that of each of its owner subsidiaries. Hence, the inclusion probabilities for the owner subsidiaries can be divided by the inclusion probability of their corporate parent to yield conditional inclusion probabilities at the owner subsidiary level. Therefore, for complex systems the sampling scheme presented above contains three levels: first sample corporate parents, then sample owner subsidiaries within corporate parents, then sample hospitals and practices within owner subsidiaries.

The random ordering in step 1) of the iterative phase is based on probabilities given by the desirability of sampling each organization. A unit with a higher desirability score is expected to appear earlier in the ordered list. The subsequent shuffling of some corporate parents and owner subsidiaries ensures that whenever a complex system is sampled both its corporate parent and at least one of its owner subsidiaries are also sampled.

Marginal inclusion probabilities for the hospitals and practices within each system may be determined by multiplying their corporate-parent’s inclusion probability by the conditional inclusion probability of their owner subsidiary (if any) and their own conditional inclusion probability. The inverses of these marginal inclusion probabilities of sampling a given unit may be used to obtain unbiased estimates of totals and means of variables for the finite populations of owners, hospitals, and practices defined by the sampling frame (Kish 1990, Little 1991, Pfeffermann 1993, Pfeffermann 1996, Biemer and Christ 2008, Lohr 2009).

A plethora of possibilities exist for using the weights in comparative (e.g., regression) analyses. In standard regression analyses (those not involving random effects), the marginal weights for the units at a given level can be used (Sarndal, Swensson et al. 1992). In hierarchical or mixed-effect regression models the inverses of the marginal inclusion probabilities for corporate owners and the conditional sampling probabilities for hospitals and practices may be used as weights at the respective levels of the model with pseudo-likelihood methods used for estimation (Pfeffermann, Skinner et al. 1998). However, the use of weights for regression analyses, especially hierarchical regression analyses, is controversial due to debates on the use of design-based versus model-based inference (Little 2004, Gelman 2007, Rao, Verret et al. 2013, Yi, Rao et al. 2016). Furthermore, there has been some consideration of an empirical test to determine when the use of survey weights is justified (Bollen, Biemer et al. 2016). In the context of regression models, if the relationship between a predictor and an outcome is homogeneous then the use of weights in a regression analysis appears less important. However, if the effect is heterogeneous and inferences are to apply to the population defined by the sampling frame, using weights has the potential to yield unbiased estimates of the average effect of the predictor on the outcome even if the interacting variable is not available.

The joint inclusion probability of two units of the same type may be positively or negatively correlated depending on whether they are under the same or a different owner. However, the inclusion of hospitals (or practices) directly under a corporate parent will be positive correlated, particularly for a small organization, due to the fact that all hospitals (or practices) are sampled if there are fewer than 4. However, hospitals (or practices) under different corporate parents will have negative inclusion probabilities due to the finiteness of the sampling frame (the usual situation in design-based inference).

4. Empirical Results and Properties of the NSHOS Complex Survey Design

The study investigators stipulated that approximately 10% of the independent hospitals and practices in the sampling frame should be sampled leading to the decision to sample 100 of 1,034 hospitals and 800 of 7,710 practices. A total of 4,800 surveys remained to be allocated to corporate owners and the hospitals and practices under them. We apply the above algorithms to the sampling frames of the 1,121 systems including 164 complex and 957 simple systems, and comprising a total of 11,068 hospitals and practices, and examine the properties of the resulting sampling design.

4.1. Expected Features of Sample at the Whole System Level

The system characteristics segment of Table 1 summarizes the average number of units (hospitals, practices and owner subsidiaries) sampled in a system while the corporate parents, owner subsidiary and hospitals and practices segments summarize the total utilization of surveys of that type. The independent hospitals and practices are the entirety of their organization and so if sampled each consume a single survey. The sampling of the 957 simple systems leads to surveys being expended on themselves (the owner), hospitals and practices but no owner subsidiaries (hence the 0s in the owner subsidiary segment of the table). The 164 complex systems each have at least one owner subsidiary.

Table 1:

Characteristics of Sampling Design Across the Four Major Types of Organizations

Organization Type	System Characteristics			Surveys to Expend	Corporate Parent		Owner Subsidiary		Hospital & Practice
	N Hospitals	N Practices	N Own Sub		N	% Sampled	N	% Sampled	N	% Sampled
Indep Hospital	1	0	0	1	1034	9.7	0	0	1034	9.7
Ind. Practice	0	1	0	1	7710	10.4	0	0	7710	10.4
Simple System	1.3	4.3	0	5.2	957	45.7	0	0	5422	40.7
Complex System	12.6	21.8	2.4	21.7	164	68	390	45.4	5646	33

The expected sampling rate of complex systems (67.4%) is greater than that of simple systems (45.7%) and owner subsidiaries (45.2%). The inclusion probability of complex systems is bolstered by the requirement that they must be sampled whenever any of their owner subsidiaries are sampled (Objective 3), which results in many of them (and especially those with multiple owner subsidiaries) being moved up the sampling order (see Section 3.1). An owner subsidiary receives an increased inclusion probability if their corporate parent is sampled. However, the benefit to a given owner subsidiary of this constraint is less because they compete against other owner subsidiaries under the same corporate parent. In the absence of adjusting the randomized order to satisfy constraints, simple systems would have a higher inclusion probability than owner subsidiaries as their desirability score is greater (mean 6.67 versus 4.72). The lower desirability score for owner subsidiaries is overcome due to movements up the sampling order in complex systems, whose higher mean complexity score of 7.69 meant that movements were quite common, making their average marginal inclusion probabilities similar.

The proportions of hospitals and practices sampled across the different types of systems is revealing. Because the number of hospitals and practices per system is relatively small (1.3 and 4.3, respectively, for simple systems and 12.6 and 21.8, respectively, for complex systems) and the sampling constraints mandate 100% sampling of hospitals and practices in systems having up to 4 if the system is sampled, the proportion sampled within systems exceeds that for independents. In particular, the proportion sampled within simple systems is highest (40.8% overall; 49.3% of hospitals and 38.2% of practices) reflecting that they are smaller on average than complex systems (32.9% overall; 34.2% of hospitals and 32.2% of practices).

To study the sampling design from the perspective of corporate parents in more detail, complex systems are partitioned into deciles based on their complexity score (1 = least complex, 10 = most complex) and described in terms of numbers of hospitals, practices and owner subsidiaries (Table 2). Due to ties in the complexity score, the number of systems in each decile varies (see N for corporate parent). The probability of being selected for a corporate parent increases with the number of owner subsidiaries, hospitals and practices. The first two deciles are comprised of systems with a single owner subsidiary. The average inclusion probability for the owner subsidiaries are almost the same as for corporate parents with the slight discrepancy for decile 1 due to the rare occasion when the owner-subsidiary is the first organization not sampled at Step 4 of Algorithm 1. More complex systems tend to have more owner subsidiaries but the relationship is non-monotone as one system may have more hospitals and practices but fewer owner subsidiaries than another. The most complex systems have a large number of owner subsidiaries (171 owner subsidiaries across 18 corporate parents in decile 10, average 9.5). The trends for the percentages of owner subsidiaries and the percentages of hospitals and practices sampled are quadratic. The trend is initially increasing because the desirability of sampling the system increases and the constraints ensure that the owner subsidiaries and hospitals/practices in the system are highly likely to be sampled if the system is sampled. However, as the system’s complexity increases, the conditional inclusion probability of a given owner subsidiary, hospital or practice declines to the point that its marginal inclusion probability also declines.

Table 2:

Characteristics of Sampling Design for Complex Systems Across Deciles of Their Complexity Score

System Decile	System Characteristics			Surveys to Expend	Corporate Parent		Owner Subsidiary		Hospital & Practice
	N Hospitals	N Practices	N Own Sub		N	% Sampled	N	% Sampled	N	% Sampled
1	1.3	3.1	1	6.3	14	29.1	14	29.1	62	28.7
2	1.6	5.8	1	8	12	38.6	12	38.5	88	31.5
3	2.7	6.1	1.1	9.3	19	44.8	21	41	166	35.7
4	3.5	10	1.1	11.7	21	54.4	23	50.1	282	38.1
5	6.6	12.3	1.2	13.8	14	66	17	55.4	264	39
6	9.4	16.4	1.2	15.5	12	77.9	15	64.1	310	38.8
7	8.3	19.8	1.3	17.7	19	80.3	24	67.9	534	42.2
8	10.9	23.3	2.1	21.8	19	85.6	40	50.7	650	39.7
9	13.4	43.1	3.3	30.3	16	93.8	53	45.4	903	32
10	62.3	70.3	9.5	74.4	18	98.5	171	40.2	2387	27.5

4.2. Expected Features of Sample at the Owner (Corporate Parent – Owner Subsidiary) Level

Rather than considering systems in their entirety, we may also evaluate the sampling design considering all corporate owners (the direct part of the system under a corporate parent, simple systems and owner subsidiaries) as units. The results are partitioned based on the component of the complexity score for hospitals and practices in Tables 3A and 3B, respectively. Complexity scores ranged from 0 to 10, as described in Section 3. In Table 3A the number of hospitals increases by design with the desirability score but the number of practices and owner subsidiaries does not necessarily increase and likewise for practices in Table 3B. Because the combined sum of hospitals and practices had to be at least two for an organization to be a system, the least complex systems from the perspective of a hospital (those with 0 hospitals) and a practice (those with 0 practices) had to have at least two practices and two hospitals, respectively. This led to organizations with 0 hospitals having a larger average number of practices than organizations with 1 hospital and likewise for organizations with 0 and 1 practices. As the number of hospitals increased, the positive correlation with the number of practices is seen by the increasing numbers of practices until the sample sizes get very large at high values of hospital desirability. Systems comprising only practices have been referred to as Practice Groups (Fisher, Shortell et al. 2019). The probability that a given hospital or practice is sampled falls substantially in very large systems and may eventually fall below that for sampling independent hospitals and practices. The lone system in stratum 9 with respect to the number of hospitals does not have any owner subsidiaries; it is an outlier as it contains 81 hospitals as well as 4 practices but no owner subsidiaries.

Table 3A:

Characteristics of Sampling Design by Complexity Score Contribution from Hospitals

Number of Hospitals	System Characteristics			Surveys to Expend	Corporate Parent		Hospital & Practice
	N Hospitals	N Practices	N Own Sub		N	% Sampled	N	% Sampled
0	0	6.1	0	4.8	602	45.3	3681	32.1
1	1	2.8	0.1	4.2	377	37.8	1421	37
2	2	3.2	0.2	5.2	196	44.3	1019	42.4
3	3	4.8	0.2	6.7	92	51.9	717	42.2
4	4.4	5.7	0.5	8.2	100	63.4	1006	48.4
5	7.4	8.5	1.2	10.1	90	73.4	1431	43.8
6	13.7	9.7	1.3	11.2	39	81.9	914	36.2
7	27.6	13.1	4.9	13.2	11	96.5	448	29
8	54.5	12.5	6.5	14.5	2	99	134	20
9	81	4	0	14	1	100	85	15.3
10	179	33	13	18	1	100	212	8

Note: The component of the complexity score for hospitals is a monotone function of the number of hospitals

Table 3B:

Characteristics of Sampling Design by Component Score Contribution from Practices

Number of Practices	System Characteristics			Surveys to Expend	Corporate Parent		Hospital & Practice
	N Hospitals	N Practices	N Own Sub		N	% Sampled	N	% Sampled
0	3	0	0.4	3.7	125	37.5	372	49.3
1	2	1	0.1	3.7	246	33.3	740	45.1
2	0.8	2	0.2	3.8	284	33.7	806	48
3	1.5	3	0.1	5	177	41.3	788	49.6
4	2	4.4	0.2	6.1	251	49.2	1597	50.1
5	2.4	7.5	0.3	7.6	232	62.5	2302	49.7
6	3.7	13.9	0.6	9.1	139	78.3	2440	41.6
7	7.3	25.2	0.8	10.4	52	89	1695	28.7
8	9.3	42.7	0	11.7	3	95	156	21.5
9	7.5	78.5	1.5	13	2	99	172	15
10					0

Note: The component of the complexity score for practices is a monotone function of the number of practices

4.3. Whole system sampling properties

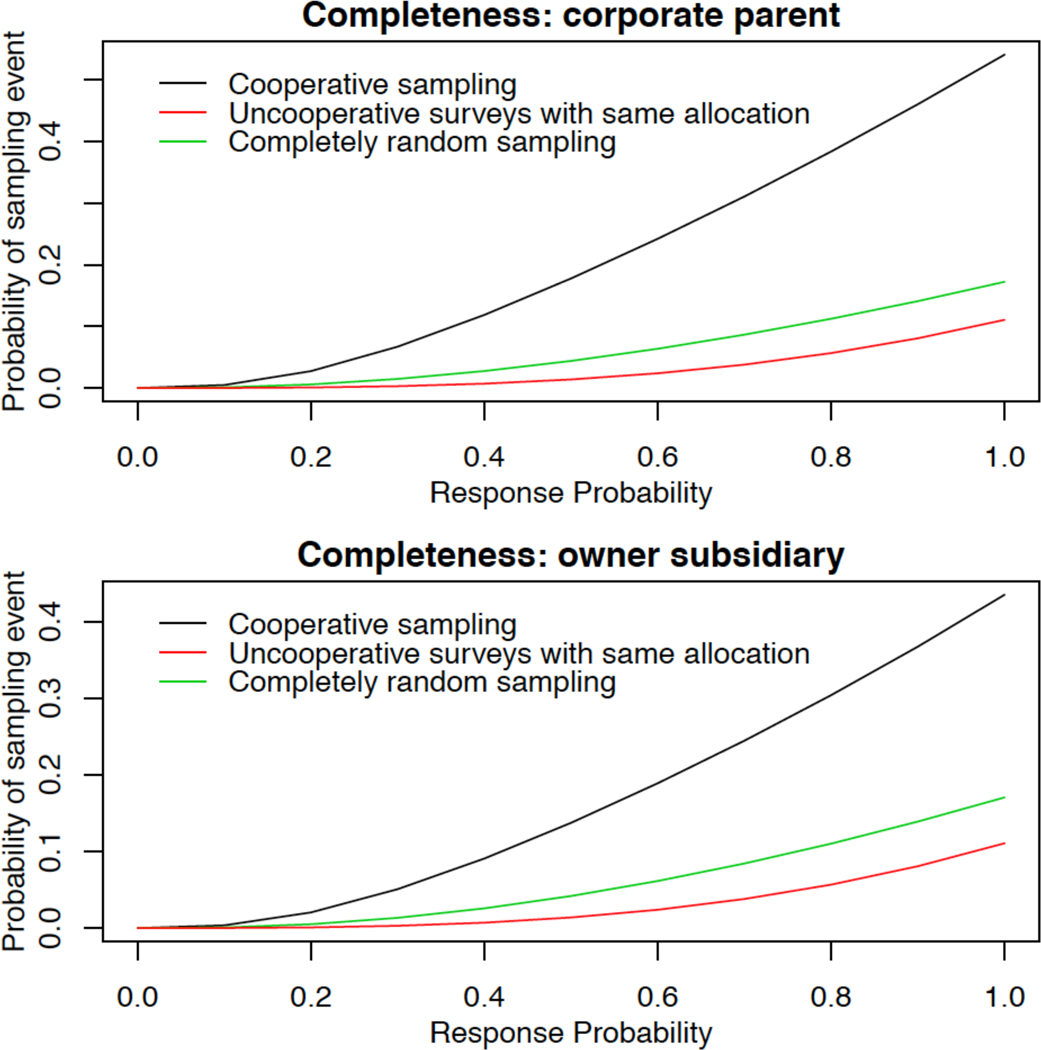
The nadir of the NSHOS study is the attainment of a completed survey from a corporate owner and at least one hospital and one practice directly under it – a “complete sample” in the sense that each aspect of the system is sampled. As such, the proportion of systems for which the three types of surveys are returned is a key metric for quantifying the extent to which the design supports statistical analyses involving measures from each survey. We compute the complete sample proportion for the coupled design, a design without coupling (i.e., no constraints between types of surveys) but the same overall survey allocation to each type of organization, and a design with the same overall sampling rate but complete independence in the selection of units. The ratio of the complete sample proportion for the coupled design to the other designs quantifies the extent to which coupling the surveys offers better support for these kinds of analyses. The individual probabilities and ratios of them can be expressed as a function of an assumed non-response probability. In the case of the NSHOS sampling frame, the proportions of complete samples expected for corporate parents and owner subsidiaries are similar to each other with both far surpassing those for the comparator sampling schemes (Figure 3).

Figure 3:

The probability of survey responses from each of the corporate owner [corporate parent (top), owner subsidiary (bottom)] and at least one hospital and one practice directly under it as a function of the response rate. The sampling schemes are the coupled sampling strategy and two comparator schemes: non-coupled sampling with the same overall organization-type allocation as for coupled sampling and equal probability completely random sampling of all units.

Analyses comparing corporate parents and owner subsidiaries are best supported by complex systems with complete samples from both the component directly under the corporate parent and at least one owner subsidiary. The relative likelihood of this event occurring is relatively much greater for coupled sampling than the comparator sampling schemes on the NSHOS sampling frame (Figure 4). At a 50% response rate, the probability under coupled sampling is 0.058, which is 115 and 10 times greater than for uncooperative but otherwise identical sampling and for completely random sampling, respectively. This example illustrates how coupled sampling simultaneously increases the expected sample-size (and thus reduces the estimation variance) for a wide range of analyses that might be performed given the data.

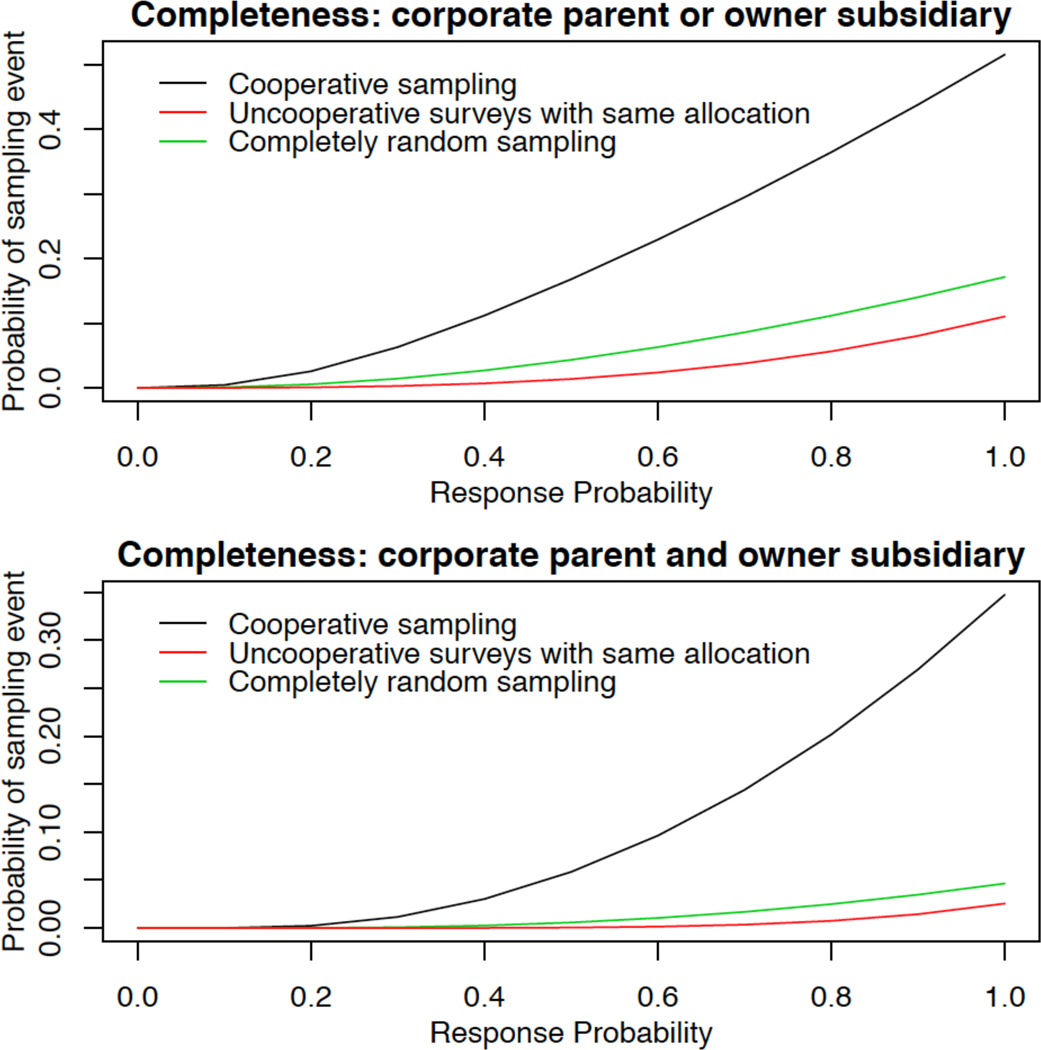
Figure 4:

The probability of survey responses from each of the corporate owner and at least one of its hospitals and at least one of its (top) and the same but from both the corporate parent and at least one of its owner subsidiaries (bottom) as a function of the response rate. The sampling schemes are the coupled sampling strategy and two comparator schemes: non-coupled sampling with the same overall organization-type allocation as for coupled sampling and equal probability completely random sampling of all units.

The probability of obtaining a complete sample from any part of the system has the least difference in performance between the sampling designs. At a 100% response rate, coupled sampling yields a complete response probability of nearly 0.5 whereas the complete response probability for other designs are between 0.1 and 0.2.

These results suggest that analyses involving measures from across the different surveys are substantially more viable under coupled sampling. At the same (returned survey) response rate, coupled sampling can bolster the fraction of completed surveys from all types of sub-organizations within the system from between 1–2% to between 10–30% depending on the response rate. This elevates the feasibility of such analyses from virtually impossible to able to provide useful information.

4.4. Owner subsidiary-corporate parent sampling properties

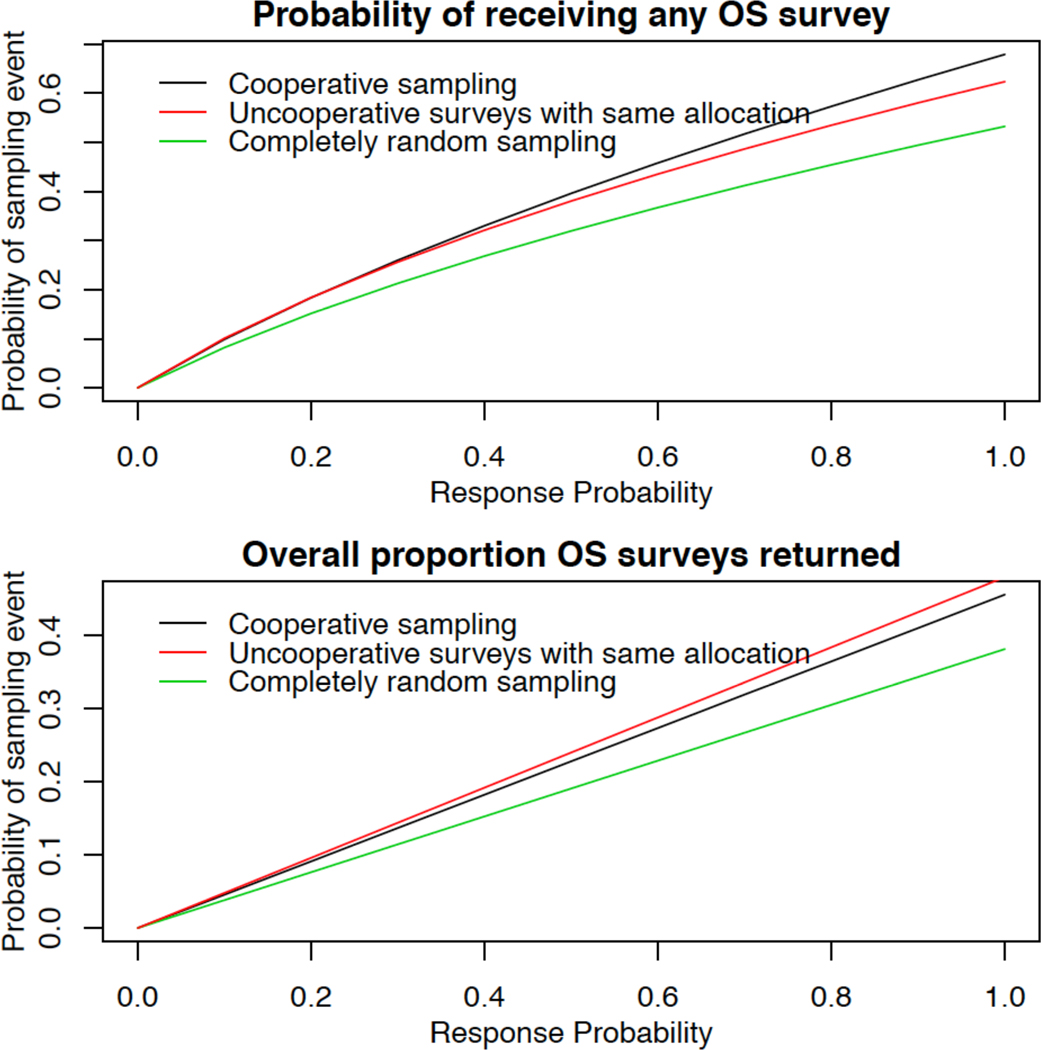
The proportion of complex systems for which a completed survey is obtained from both the corporate parent and at least one owner subsidiaries is a key metric of the ability of the sampling scheme to support ownership-level comparative analyses of corporate parents and their owner subsidiaries. The upper segment of Figure 5 reveals that the coupled sampling design yields a higher expected proportion of systems with these surveys returned. At our anticipated non-response fraction of 0.5, if the proportion of corporate parents to owner subsidiaries sampled is fixed at the same fraction as for the coupled sampling design, the inter-design returned survey ratio is 1.04 for coupled sampling compared to uncooperative sampling and 1.24 compared to completely random sampling. The ratios increase as the survey response rate increases to 1.09 and 1.27, respectively, at 100% response. Insight into the reason for the monotone increase of the ratio as the sampling fraction increases is given by the probability of obtaining at least one returned survey from n owner subsidiaries under equal probability sampling, which equals 1 − (1 − p_sampp_resp)ⁿ where p_samp is the probability of being sampled and p_resp is the probability of response conditional on being sampled. The probability rapidly approaches 1 as n → ∞. Therefore, coupled sampling is protective against sampling corporate parents without also sampling an owner subsidiary under them, and vice-versa, in complex systems.

Figure 5:

The probability of a survey response from at least one OS (top) of a CP and the overall proportion of OS surveys returned (bottom) as a function of the response rate for three different sampling schemes. The sampling schemes are coupled sampling and two null or control schemes: non-coupled sampling with the same overall organization-type allocation as for coupled sampling and equal probability completely random sampling of all units.

The lower segment of Figure 5 shows the proportion of owner subsidiaries expected to be sampled. Despite sampling a substantially greater number of corporate parent – owner subsidiary dyads, the coupled sampling design does not have the highest overall proportion of sampled owner subsidiaries. This occurs because under coupled sampling, the probability of including additional owner subsidiaries conditional on sampling at least one is lower than the inclusion probability for owner subsidiaries under uncooperative sampling.

5. Conclusion

In this paper we described the development of a novel coupled sampling design for the NSHOS surveys. The number of surveys expended on a system was determined by a system complexity score. Heterogeneity in the relative merit of sampling systems of various size and composition led to a second score known as a desirability score that was a major contributor to the sampling probabilities. However, the actual sampling probabilities of the coupled sampling design are not able to be expressed explicitly. Computation of the sampling weights and extraction of the sample was enabled using a sophisticated Monte Carlo algorithm. We developed the algorithm and used it to evaluate key features of the sampling design for the motivating NSHOS study. A key finding was that the sample-size of complete observations for the estimation of regression models involving measures from across the different surveys is substantially (e.g., 10-fold) greater under coupled sampling compared to the under independent sampling designs. Therefore, the coupled sampling design facilitates a wider range of statistical analyses than is feasible under traditional survey designs.

The above gain in statistical feasibility and efficiency of subsequent analyses was achieved by avoiding the scenario in which a system does not have any surveys from its hospitals or its practices and conversely of a hospital or practice being surveyed when their corporate owner is not surveyed. This led to the adoption of heuristics expressed as constraints that mandated that each aspect of a system would be sampled if any component of it was sampled and 100% sampling of up to 4 hospitals and practices for each owner. Thus, hospitals and practices at the largest systems were under-sampled while those at the smallest systems were over-sampled. By coupling the sampling designs through constraints such as these that aid obtaining surveys from all organization-types within a system, enabling all predictors in a statistical regression model to be measured, we enhance statistical efficiency.

Our survey design has the potential to support various types of analyses not directly discussed in the paper. Because systems may span areas (e.g., states, health referral regions), we did not directly incorporate geographic area-based cluster sampling or stratified sampling. However, due to the randomness of sampling, our sample has a wide coverage of systems, hospitals and practices in different geographies. Therefore, our sampling design would naturally support the estimation of hierarchical models that perform small area estimation with respect to geography. The coupled sampling methodology may also be applied to any situation in which a population of organizations that contains sub-organizations of multiple types and/or may contain forms of themselves (i.e., owner subsidiaries) as sub-units is tailor-made for coupled sampling. Such a study would benefit from the ability of the coupled sampling design to support multiple objectives including, as noted above, those involving analyses that simultaneously incorporate variables measured using the survey for the over-arching organization (the system survey) and those for each sub-organization (hospitals and practices).

In future work, more elements of the design could be incorporated in the procedure developed herein including hybrid designs that maximize precision subject to the constraints. For example, the fraction of independent organizations sampled could be a parameter that is optimized over to find the design that minimizes the variance of a comparison between independent and system-based hospitals. Likewise, a decay function that depends on an unknown parameter or parameters could be optimized over to find the optimal form for the complexity function for hospitals and/or practices.

Appendix

A.1. Multiple-Objectives Optimal Designs

Classical survey designs often involve some form of Neyman allocation. For example, the objective is often minimization of the variance of an unbiased estimator of the quantity being estimated subject to a budgetary or sample-size constraint. With multiple targets of inference within a single regression model the situation is more complicated, let alone the case when multiple regression models will be estimated. When one is interested in evaluating the effects of multiple factors in one or more regression models, a multiple objectives design problem obtains. If the success of meeting K objectives is quantified by statistical efficiency measures denoted Eff_k(Y, X, n), a multiple objectives optimizing function that combines them additively is:

$$\text{Eff}(Y,X,n)=\sum _{k=1}^K{w}_k{\text{Eff}}_k(Y,X,n)$$

where $w_k\ge 0\text{and}{\sum }_{k=1}^K{w}_k=1.$

The design-efficiency of a standard cluster randomized design with equal sample-sizes per cluster is 1 + (m − 1)ρ, where m is the number of within unit samples, $\rho ={\sigma }_b^2/\left({\sigma }_b^2+{\sigma }_w^2\right)$ is the intraclass correlation coefficient, ${\sigma }_b^2$ and ${\sigma }_w^2$ are the between-unit and within-unit variance components. Let n be the number of clusters. If the cost of sampling a cluster is C_u and the cost of sampling a unit within the cluster is C_k, the total cost is C = n(C_u + mC_k). The optimal design for estimating the coefficient of a within-cluster predictor (e.g., β₄ in the first regression model) maximizes the total number of observations, which for C_u > 0 occurs when n = 1 and m = (C − C_u)/C_k. Note the indifference of the solution to ρ. However, the optimal design for estimating a cluster-level predictor (e.g., β₁ in the first regression model) is given by

$$m=\max \left\{1,{\left(\frac{C_u(1-\rho )}{C_k\rho }\right)}^{0.5}\right\}$$

and

$$n=\frac{C}{C_u+m{C}_k}$$

If ρ ≈ 0 the optimal designs are essentially equivalent. Yet if ρ ≈ 1 they are polar opposites. Furthermore, if ρ and C_u are large there is a great loss of statistical efficiency from using the β₄ optimal design to estimate β₁ while in general using the β₁ optimal design fails to identify let alone estimate β₄ efficiently. Therefore, even in this simple case, different objectives lead to drastically different optimal designs. If the above two objectives were combined, the relative weight of each would have a substantial impact. However, the specification of such weights might be arbitrary.

To avoid the above predicament, we favor the specification of the design by directly specifying the type of solution that is known to be amenable to the analytic scenarios of interest, such as the estimability of complex hierarchical models. The paper develops a novel computational procedure that solves a system of equations to yield a numerical solution for the optimal sampling design (i.e., determining the sampling probabilities) that satisfy the constraints for the design. This approach essentially specifies the weights w_k for each objective implicitly (i.e., in the sense of being inversely-defined from the specified optimal-solution constraints) as opposed to being specified upfront and held fixed while the optimal-design (and thus its form) is determined. However, making a formal connection between the two approaches (i.e., establishing a primal problem – dual problem) was not an objective of this paper.

A.2. GitHub site and Code

The code used to perform the calculations in this paper is an R script available at the GitHub site maintained by the first author: https://github.com/kiwijomalley/Novel-Sampling-DesignAlgorithm. The script takes as an input data that contains summary information about health systems and owner subsidiaries and their underlying hospitals and physician practices. The data set provided on the GitHub site is made up because the Data Use Agreement for the project prohibits sharing the actual data. However, it allows the computations performed in the paper to be fully illustrated.

A.3. Accounting for Sampling Design in Statistical Analyses in Stata

Statistical analyses that use the survey weights can be operationalized with relative ease. The sampling design may be accounted for in advance by using the svyset command in Stata. The presence of hospitals and practices nested within a corporate owner and of owner subsidiaries nested within corporate parents, leads to a three-level hierarchical data structure. The appropriate svyset command has the form:

svyset CP_ID, weight(CP_weight) || OS_ID, weight(OS_weight) || HP_ID, weight(HP_weight) where CP_ID, OS_ID and HP_ID denote the identification codes for the corporate parent, owner subsidiary and the hospital or practice and CP_weight, OS_weight and HP_weight denote the inverses of the inclusion probability of the corporate parent and the conditional inclusion probabilities of the owner subsidiary, hospital and practices. As noted in Section 3.2, the conditional inclusion probabilities for owner subsidiaries equal the inclusion probability determined by Algorithm 1 divided by the inclusion probability of their corporate parent. The conditional inclusion probability for hospitals and practices are determined from the sampling design used within systems and owner subsidiaries to select hospital and practices. For example, under simple random sampling (SRS) these sampling probabilities equal the number of surveys allocated to hospitals (practices) divided by the number of hospitals (practices) within the organization. Expanding on Section 2.1, to allow for the fact that survey designs with three different structures (CP – OS – HP, CP – HP and independent HP) may be combined in a single analysis, we set OS_ID = HP_ID if OS_ID is not defined and CP_ID = HP_ID if HP_ID is not defined (e.g., as for an independent hospital or practice). This ensures that the IDs are defined for all hospitals and practices allowing statistical models and procedures to be applied to the combined data.

The meglm command in Stata allows for the estimation of mixed effects models with survey weights. For a binary valued outcome, the code

svy: melogit {model} || CP_ID: || OS_ID:

or

meglm {model} [pweight=HP_weight] || CP_ID:, pweight(CP_weight) || OS_ID:, pweight(OS_weight), family(binomial) link(logit)

could be used. The difference between the two specifications is that the latter does not rely on the sampling design having been specified via svyset. In general, it is best to set the design in advance as some procedures do not allow sampling design weights.