Using artificial intelligence techniques for COVID-19 genome analysis

Abstract

The genome of the novel coronavirus (COVID-19) disease was first sequenced in January 2020, approximately a month after its emergence in Wuhan, capital of Hubei province, China. COVID-19 genome sequencing is critical to understanding the virus behavior, its origin, how fast it mutates, and for the development of drugs/vaccines and effective preventive strategies. This paper investigates the use of artificial intelligence techniques to learn interesting information from COVID-19 genome sequences. Sequential pattern mining (SPM) is first applied on a computer-understandable corpus of COVID-19 genome sequences to see if interesting hidden patterns can be found, which reveal frequent patterns of nucleotide bases and their relationships with each other. Second, sequence prediction models are applied to the corpus to evaluate if nucleotide base(s) can be predicted from previous ones. Third, for mutation analysis in genome sequences, an algorithm is designed to find the locations in the genome sequences where the nucleotide bases are changed and to calculate the mutation rate. Obtained results suggest that SPM and mutation analysis techniques can reveal interesting information and patterns in COVID-19 genome sequences to examine the evolution and variations in COVID-19 strains respectively.

Introduction

The Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) virus, also known as COVID-19, was first identified in a patient with pneumonia in Wuhan, capital city of Hubei province, China in December 2019 [1]. The World Health Organization (WHO) declared that COVID-19 is a World Emergency on January 30, 2020 [2] and later a pandemic on March 11, 2020 [3]. According to the latest report of WHO [4], more than 65 million people have been infected by the COVID-19, with approximately 1.5 million deaths worldwide and this disease has spread to more than 200 countries. An effective therapeutic or vaccine has not emerged yet, due to novelty of the virus and its behavior. Countries and health bodies are taking, and recommending, preventive and isolation measures to reduce the transmission and reproduction rate. To develop effective therapeutics or vaccines that produce long-term immunity, it is necessary to understand the genome of the SARS-CoV-2 and its functionalities.

Genome of an organism is the total sum of its entire genetic potential, stored as an encoded sequence consisting of four nucleotide bases (Adenine-A, Guanine- G, Cytosine-C and Thymine-T) that make up its nucleic acids. The COVID-19 genome sequence is made from single-stranded sequence of nucleotides called RNA and is approximately 30 Kb long [5]. Identifying the sequence of nucleotides in a genome is called genome sequencing. Genome of SARS-CoV-2 has been sequenced by different groups around the world which revealed multiple strains of the virus and showed that its genome is 79% similar to the SARS-CoV-1 and 50% to the MERS-CoV (Middle East Respiratory Syndrome Coronavirus), respectively [6]. Identification of genome characteristics helps biomedical experts to produce hypotheses about the effect of these characteristics on the disease manifestations in the population. However, this is often a slow and resource intensive process that largely depends on domain expertise. For example, for COVID-19 pandemic, the early sequencing of the genome of different strains of SARS-CoV-2 did not turn into timely actionable insights and still many aspects of disease behavior are unknown. The use of artificial intelligence methods including sequential pattern mining (SPM), has the potential to accelerate the process of finding actionable insights and eventually contribute to a better global response.

The pattern analysis field provides efficient computer-based techniques that enable humans, particularly bioinformaticians, to analyze complex and large genetic and genomic data [7]. SPM [8], a special case of structured data mining, has been applied in genomics to find patterns of specific elements in genes [9], to analyze gene expression [10], to mine maximal contiguous frequent patterns from DNA sequence datasets [11], to discover motifs in DNA sequences [12], to predict protein function [13] and diseases [14], to discover gene interactions and their characterizations [15], to interpret patterns extracted from DNA microarrays [16], to mine k-mers [17] and to construct the phylogenetic tree [18]. Using SPM on sequential genome data can provide new insight about virus mutations, virulence and the various disease manifestations. Moreover, discovering important hidden information in genomes by using SPM can help speed up the process of biological research and is of great significance to the biological world.

The general goal of this paper is to explore the use of artificial intelligence techniques for COVID-19 genome analysis. More specifically, three contributions are made to address three subgoals.

• To evaluate if interesting patterns can be found in COVID-19 genome sequences, we apply SPM on these sequences. For this, the genome sequences are first converted into a corpus that is suitable for learning. Then, SPM techniques are applied on the corpus to find frequent nucleotide bases (nucleotides) and their patterns in the genome sequences. Moreover, relationships of nucleotides/patterns with each other are discovered through sequential rule mining.

• Second, to evaluate if the next nucleotide bases(s) can be predicted in COVID-19 genome sequences, state-of-the art prediction models are trained and applied on the corpus.

• Third, to analyze mutations in genome sequence, we propose an algorithm to find the mutations that takes place in genome sequences as well as the mutation rate. The algorithm is applied to the COVID-19 genome sequences.

The rest of this paper is organized as follows. Section 2 provides a detailed background on SARS-CoV-2 and its genomic structure. Related work on using artificial intelligence (AI)-based techniques for studying COVID-19 are also discussed in Section 2. Section 3 presents the SPM-based learning approach that is used to discover nucleotides and their frequent patterns in genome sequences, their relationships, and to predict next nucleotides bases(s). Evaluation of the proposed approach and obtained results are discussed in Section 4. Then, Section 5 describes the proposed mutation analysis technique. Finally, the paper is concluded with some remarks in Section 6.

Background on SARS-CoV-2 and related work

This section first introduces the background about SARS-CoV-2 and then how it has been studied using AI techniques.

SARS-CoV-2

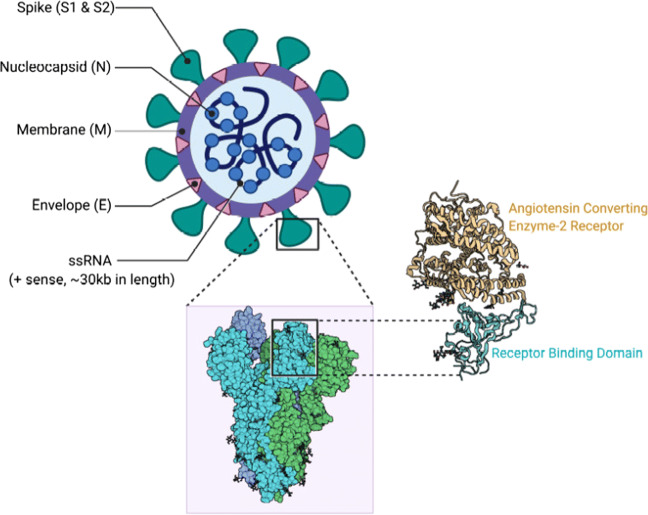
SARS-CoV-2 is a betacoronavirus with enveloped, single-stranded (positive-sense) RNA genomes of zoonotic origin. Their shapes are spherical to pleomorphic and their lengths are between 80-160 nm [19]. SARS-CoV-2 contains four structural proteins: (1) Spike (S), (2) Envelope (E), (3) Membrane (M) and (4) Nucleocapsid (N) (shown in Fig. 1). The S, M, and E proteins make the envelope of this virus. The E protein, which is the smallest structural protein, also plays a role in the production and maturation of SARS-CoV-2 [20]. The S and M proteins are also involved in the process of virus attachment during replication. The N proteins remain associated with the RNA to form a nucleocapsid inside the envelope. N is also involved in other aspects of the virus replication cycle (such as assembly and budding) and the host cellular response to viral infection. This virus is named coronavirus due to the crown-like appearance of the S protein when seen under microscope.

Fig. 1.

SARS-CoV-2 Structure [21]

SARS-CoV-2 can be contracted from animals such as bats and humans. This virus can enter the human body through its receptors, ACE2, which are present in various organs such as lungs, heart, kidneys and gastrointestinal tract. Thus, ACE2 facilitates the entry of the virus into target cells [22]. The process of CoV entering into the host cell begins when the S protein, that comprises S1 and S2 sub-units, binds itself to the ACE2 receptor in the host cells [23]. Therefore, infected patients not only experience respiratory problems such as pneumonia leading to Acute Respiratory Distress Syndrome (ARDS), but also experience heart, kidneys disorders and digestive tract [22]. The compact ridgeness of the S protein makes the virus to attach more strongly than other viruses of the same origin to host cells. After the S protein binds itself with the receptor in the target cell, the viral envelope fuses with the cell membrane and releases the viral genome into the target cell.

The genomic material released by this virus is mRNA. In its genome range, this virus is complemented by about six to twelve open reading frames (ORFs). The genome size of the SARS-CoV-2 varies from 29.8 kb to approximately 30 kb and its genome structure follows the specific gene characteristics of known CoVs. At the 5’UTR (terminal region), more than two-thirds of the genome comprises ORF1ab that encodes ORF1ab polyproteins. Whereas at the 3’UTR, one third consists of genes that encode structural proteins (S, E, M and N) (Fig. 2). SARS-CoV-2 also contains six accessory proteins that are encoded by ORF3a, ORF6, ORF7a, ORF7b, ORF8 and ORF10 genes [24]. Note that the untranslated regions (5’UTR and 3’UTR) are responsible for inter- and intra-molecular interactions, RNA-RNA interactions and for binding the viral and cellular proteins [25].

Fig. 2.

Structure of the SARS-CoV-2 genome [24]

Related work

Recent work done on the use of AI-based techniques for the diagnosis, detection, forecasting and prediction of COVID-19 is discussed in this section.

A review [26] provided a comprehensive overview on the use of mathematical models and AI-based techniques in COVID-19 studies. AI (machine learning, data mining and deep learning) techniques have been used mostly for medical imaging (such as X-ray and computed tomography (CT)) segmentation and diagnosis [27]. For example, COVID-19 diagnosis and detection from CT scans and X-ray images were done using deep learning techniques in [28–33], using supervised learning techniques such as support vector machine (SVM) in [34–36], using logistic regression (LR) in [37, 38], and using decision trees (DT), random forest (RF) in [39, 40] and ARIMA models [41].

For text based COVID-19 related data, the study [42] conducted a thematic analysis of COVID-19 related tweets with the VOSviewer software to examine general public reactions related to the COVID-19 outbreak. Moreover, SPM techniques were used to find frequent words/patterns and their relationship in tweets. The mutation rate was studied in [43] in genomic sequences gathered from COVID-19 patients data from GenBank. The missense nucleotide mutation rate and codon mutation rate were first found in genomes. After that, a recurrent neural network-based long short-term memory (LSTM) model was used to predict the future mutation rate of this virus. In the study, authors focused on the base substitution mutation rates and does not consider the insertion and deletion rates. Some tools were also developed in [44–46] to track SARS-CoV-2 genomic variations. Additionally, the modeling and forecasting of COVID-19 spread in top 5 worst-hit countries (Brazil, India, Peru, Russia and USA) was done in [47] by proposing a WCGFVL network which is a wavelet-coupled random vector functional link (RVFL) network.

Most of the mathematical modeling studies for COVID-19 focus mainly on the dynamics of COVID-19 and exploring the effect of prevention methods like travel restriction, lockdowns, and studying the effect of climate on the COVID-19 propagation. Similarly, AI-based techniques perform very well on test data. However, it is a known fact that good performance of an algorithm on test data does not guarantee that the algorithm will also perform similarly when deployed on the field. The main reason for this is that the real-life data is more prone to noise and other artefacts that are not usually present in the training and test data. On the other hand, in the image based analysis, there is a lack of diverse annotated images that can be used in experiments [26]. Wynants et al. [48] reviewed and critically evaluated studies that described prediction models for COVID-19. They argued that proposed models are reported badly, highly biased and models performance is probably optimistic. Authors suggested that rigorous prediction models require participant data from COVID-19 studies that are well-documented. Additionally, new studies and research should follow methodological guidance for developing reliable prediction models, as unreliable predictions models can cause more harm than good in guiding clinical decisions.

Analyzing COVID-19 Genome sequences with SPM and sequence prediction techniques

This section presents the proposed approach to address the two first sub-goals of this paper, which are to evaluate if pattern mining can reveal interesting patterns in COVID-19 genome sequences and if sequence prediction models can predict nucleotide bases from previous ones.

Generally, to find interesting patterns in data, several pattern mining techniques have been designed and applied on different types of datasets ranging from transactions to graphs, strings and sequences [49]. These techniques have been utilized in many different applications. However traditional pattern mining techniques do not work well on data that is time-based or sequentially ordered such as genome sequences. For such data, they fail to find patterns describing sequential relationships between events or elements. To address this limitation, techniques for SPM have been designed that can mine patterns in structured sequential data [8]. SPM consists of identifying important subsequences (patterns) in a set of discrete sequences, where the importance of a subsequence can be measured using different measures such as the occurrence frequency of a subsequence, its profit, and length. Because genome sequences are a form of discrete sequences, we have thus selected SPM techniques to analyze them.

For the second sub-goal of this paper, state-of-the art sequence prediction models are applied to see if the next nucleotide bases can be predicted from previous ones in a genome sequence. The considered models are Compact Prediction Tree (CPT) [50], CPT+ [51], Dependency Graph (DG) [52], All-K-Order-Markov (AKOM) [53], Transition Directed Acyclic Graph (TDAG) [54] and LZ78 [55].

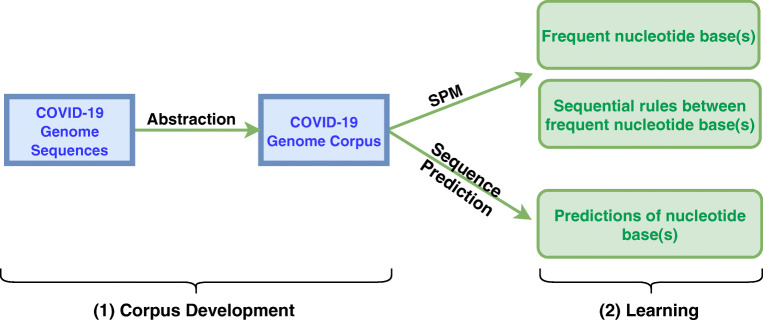
The overall proposed approach for analyzing COVID-19 genome sequences using SPM and sequence prediction models is depicted in Fig. 3. It consists of two main parts:

1. Corpus development: COVID-19 genome sequences are transformed into a corpus of discrete sequences, where each whole genome sequence is converted into a sequence of nucleotides.

2. Learning using SPM and Sequence Prediction Techniques: SPM algorithms are applied on the corpus to discover frequently occurring nucleotides, sequential relationships between nucleotides, and to predict the next nucleotides base(s) of a sequence.

These two parts are explained in more details in the next two subsections. Then, the next section presents results.

Fig. 3.

Proposed SPM and sequence prediction approach for analyzing COVID-19 genome sequences

Corpus development

The genome sequence database GenBank [56] was used to acquire sequencing data for strains of SARS-CoV-2. GenBank a popular online public database of nucleotide sequences that also supports bibliographical and biological annotation. It is maintained by the National Center for Biotechnology Information (NCBI) and is built primarily by submissions from individual laboratories and large-scale sequencing centers. In the last two decades, GenBank has grown exponentially with the number of sequence records doubling approximately every 18 months [56]. Such online databases allow research scientists throughout the world to immediately analyze any particular viral structure, its function, and the molecular basis. The genome sequenced data for virus obtained from online database is also crucial in global efforts to develop vaccines, antiviral drugs and particularly in accurate, sensitive diagnostic tests. At the time of writing this paper, the NCBI database for SARS-CoV-21 contains 43,779 COVID-19 nucleotide records and 112,477 SRA (Sequence Read Archive) runs. For computer scientists and bioinformaticians, the amount of COVID-19 related data stored in GenBank is enormous and is freely available online. COVID- 19 genome sequences can be considered as a computer-understandable corpus.

To apply SPM or sequence prediction models on genome sequence data, it must be first transformed into an appropriate electronic format that satisfies two main requirements that make it suitable for learning:

• Data must be converted into long sequences of items (symbols) to obtain discrete sequences that allow discovering interesting patterns in the corpus and performing accurate prediction.

• The set of symbols used for representing the data as discrete sequences must be carefully selected to provide a suitable abstraction such that irrelevant information can be left out while preserving all the meaningful information.

To perform this transformation, the “nucleotides to integers” abstraction is employed. It consists of converting each nucleotide into a distinct item (symbol), represented as a positive integer. This abstraction is quite general and allows applying various SPM algorithms, as well as sequence prediction models, as it will be explained.

The corpus of COVID-19 genome sequences obtained from GenBank [56] represents each genome sequence as a file in FASTA format containing the names of genes, followed by a sequence of nucleotides (A, C, G and T). This means that after removing the genes field, the complete genome sequence is a sequence of nucleotides (denoted as Ns). Combining all these nucleotides sequences can produce a corpus of discrete sequences. Formally, this corpus is defined as follows.

Definition 1 (Nucleotide base set)

Let NB = {A,C,G,T} be the set of all distinct nucleotide bases. The notation |NB| denotes the set cardinality. Hence, |NB| = 4 as there are 4 distinct nucleotides.

Based on the definition of nucleotide base set, a COVID-19 genome sequence corpus is represented as follows.

Definition 2 (COVID-19 genome sequence)

A COVID-19 genome sequence is an ordered list of nucleotides bases, CGS = 〈NB₁,NB₂,...,NB_n〉, such that $N{B}_i\subseteq$ NB (1 ≤ i ≤ n).

Definition 3 (COVID-19 genome sequence corpus)

A COVID-19 genome sequences corpus CGSC is a list of genome sequences CGSC = 〈 CGS₁, CGS₂, ..., CGS_p〉, where each genome sequence has a unique identifier (ID). For example, Table 1 shows a CGSC that contains four lines (genome sequences) with IDs 1, 2, 3 and 4.

Table 1.

A sample of a CGSC

ID	Sequence
1	〈....AATAACTCTATTGCCATACCCACAAATT.....〉
2	〈....TGCAGCAATCTTTTGTTGCAATATGGC.....〉
3	〈....CAGGTGCTGCATTACAAATACCATTTG.....〉
4	〈....CCCTAATGTGTAAAATTAATTTTAGTA.....〉

Note that a codon in the genome sequence represents a sequence of three nucleotide bases. There are 4³ = 64 different codons, in which 61 represent different amino acids that make up proteins. The remaining three codons represent the stop signals. As there are only 20 different amino acids and 61 possible codons, most amino acids (except Tryptophan and Methionine) are encoded by more than one codon. For example, the codons GGC, GGA and GGG encode the amino acid known as Glycine. The genetic code defines a mapping between codons and amino acids; such that every three nucleotide bases (codon) encodes one amino acid [57].

The final step is to convert the genome sequences into sequence of integers so that common SPM algorithms can be applied to the corpus. Before this step, each row contains a sequence of nucleotides found in a genome. Each nucleotide in the sequence is replaced by a positive integer. For example, the nucleotide A is replaced by 1. Similarly, C, G and T are encoded as 2, 3 and 4 respectively. Additionally, to apply some SPM algorithms, separator characters must be added between nucleotides such as a negative integer -1, and a negative integer -2 at the end of each row (line) [58].

Learning using SPM and sequence prediction techniques

SPM

After preparing the corpus, various SPM techniques can be applied to find patterns (subsequences of nucleotides) that appear in genome sequences. But to select interesting patterns, an appropriate measure must be used. The most common measure to evaluate patterns in pattern mining is the support measure (occurrence frequency) [8, 49]. This measure is relevant for this study as it allows to find subsequences of nucleotide bases that appear in numerous genome sequences, and thus to reveal their similarities. SPM using the support measure is known as the task of frequent SPM. Generally, it consists of enumerating all frequent subsequences in a set of discrete sequences [8]. Frequent SPM has been applied to analyze various types of data such as text documents and sequences of clicks on webpages. For the context of analyzing COVID-19 genome sequences, frequent SPM is defined as follows.

Definition 4 (Genome sequence containment)

A genome sequence S_α = 〈 α₁, α₂, ...,α_n 〉 is present (or contained) in another genome sequence S_β = 〈β₁, β₁,...,β_m〉 iff there exist integers 1 ≤ i₁ < i₂ < ... < i_n ≤ m, such that ${\alpha }_1\subseteq {\beta }_{i1},$ α₂ $\subseteq {\beta }_{i2},\mathrm{...},{\alpha }_n\subseteq {\beta }_{im}$ (denoted as $S_{\alpha }⊑S_{\beta }$). If S_α is contained in S_β, then S_α is said to be a subsequence of S_β.

Definition 5 (Support)

The support of a genome (sub-) sequence S_α in a corpus CGSC is the total number of sequences that contain S_α. It is denoted as sup(S_α) and defined as: $sup\left(S_{\alpha }\right)=\left|\right\{S|S_{\alpha }⊑S\wedge S\in CGSC\}|$.

Definition 6 (Frequent SPM in a genome sequence corpus)

Let there be a genome sequence corpus CGSC and a user-defined minimum support threshold minsup, such that minsup > 0. The task of frequent SPM in a CGSC is to enumerate all frequent genome subsequences. A genome subsequence S is frequent if sup(S) ≥ minsup.

For instance, consider the sample corpus of Table 1. The subsequence 〈AAT〉 has a support of 4 because it is contained in four lines (genome sequences).

Mining frequent sequential patterns in a corpus of COVID-19 genome sequences is not an easy task as sequences can be very long and similar. A sequence containing n items (nucleotides) can have up to 2ⁿ − 1 distinct subsequences. This makes the naive approach of calculating the support of all subsequences infeasible. In recent years, several efficient algorithms have been developed that apply various optimizations to find the exact solution to a SPM problem without exploring all the search space.

SPM algorithms explore the search space of patterns by first identifying all frequent subsequences each containing 1 item (nucleotide), called 1-sequences. Then, an algorithm recursively appends items to these subsequences to find larger subsequences. This is done by two basic operations, namely s-extensions and i-extensions. These operations are used to generate a (k + 1)-sequence from one or more k-sequences. It is important to point out that SPM can be applied to a more general case than what is described in this paper, where simultaneous items are allowed in a sequence. However, this paper does not discuss this case as nucleotides in genome sequences are always totally ordered.

For the purpose of speeding up the discovery of sequential patterns and to avoid finding duplicate sequences, SPM algorithms require to define a total order relation ≺ on items. Any total order can be used and it does not affect the final result produced by SPM algorithms. In the context of this paper, the order ≺ is thus simply defined on nucleotide bases from NB as the lexicographical order, that is A ≺ C ≺ T ≺ G.

SPM algorithms either employ a breadth-first search or a depth-first search. A breadth-first search algorithm first scans the dataset to find the frequent sequential patterns that contain a single item (1-sequences). Then, the algorithm produces 2-sequences by performing s-extensions and i-extensions of 1-sequences. Similarly, 3-sequences are produced by using 2-sequences and so on. This pattern generation process continues until no sequences can be generated. Whereas depth-first search algorithms discover patterns with a different approach. A depth-first search algorithm starts from sequences containing single items and then recursively performs i-extensions and s-extensions with one of these sequences to create larger sequences. When a pattern is no longer extendable, the algorithm backtracks to extend other patterns.

To avoid exploring the whole search space, SPM algorithms utilize a search space reduction property called the Apriori property or anti-monotonicity property. It states that for any two sequence s_α and s_β, if s_α is a subsequence of s_β, then s_β must have a support that is equal or less than that of s_α. For instance, if a sequence 〈A〉 has a support of 2, the sequence 〈AC〉 cannot have a support greater than 2. The Apriori property is helpful to reduce the search space since if a sequence occurs infrequently, then all the extensions of such sequences are also infrequent and therefore are not sequential patterns. For example, if minsup = 3, it is unnecessary to consider any extensions of 〈A〉 as they are all infrequent.

The main difference between SPM algorithms are in the following aspects:

1. Whether a breadth-first or depth-first search is used,

2. The type of database representation (vertical or horizontal) and internal data structures,

3. How the support of patterns is counted to find those satisfying the minsup constraint set by the user.

Some representative and efficient SPM algorithms are SPAM [59], TKS [60] and CM-SPAM [61]. SPAM is a depth-first search algorithm that relies on a vertical database representation to find all sequential patterns. Using a vertical representation allows to efficiently calculate the support of patterns without performing many costly database scans. The CM-SPAM [61] algorithm is an improved version of SPAM that utilizes a data structure named CMAP (Co-occurrence MAP) to reduce the search space and efficiently discover sequential patterns. This structure stores information about item co-occurrences. However, setting the minsup threshold to apply SPAM or CM-SPAM on a new dataset is not intuitive. Setting the minsup too high may result in finding no patterns, while setting it too low may result in finding millions of patterns. To address this limitation, an extension of CM-SPAM called TKS (Top-k Sequential) was proposed that directly let the user set the number of patterns k to be found. Then, TKS outputs the top-k most frequent sequential patterns in the input dataset. TKS applies various strategies to reduce the search space. Developing SPM algorithms is an active research area. An overview of SPM algorithms can be found in a recent survey [8].

Besides SPM, it is sometimes also interesting to find sets of nucleotides that frequently appear in genome sequences without considering the sequential ordering. For this purpose, the task of frequent itemset mining (FIM) is considered [49], which can be viewed as a special case of SPM. In the context of this paper, FIM is defined as follows.

Definition 7 (Frequent itemset mining)

Let there be a genome sequence corpus CGSC and a user-defined minimum support threshold minsup such that minsup > 0. Let NBS represents a nucleotide bases set, such that $NBS\subseteq NB$. The support of NBS in a corpus CGSC is the total number of sequences that contain nucleotides from NBS. It is denoted as sup(NBS) and defined as: sup(NBS) = |{S|∃x ∈ S ∀x ∈ NBS}|. The task of frequent itemset mining in CGSC is to enumerate all frequent nucleotide bases sets. A NBS is said to be frequent if sup(NBS) ≥ minsup.

For example, in Table 1, the nucleotide bases set {A,C,G,T} is frequent as they appear in all four genome sequences.

The first and most famous algorithm for FIM is Apriori [62]. It is designed to find frequent itemsets in large databases. It proceeds by discovering common items that can be extended to larger itemsets that appear sufficiently often. Itemsets (NBS in this work) extracted by Apriori can also be used to identify association rules (relationships) between items. Over the years, several fast and memory efficient FIM algorithms have been proposed [49].

Another type of patterns that is considered in this study to analyze a corpus of genome sequences is sequential rules. The motivation to search for these patterns is the following. Although frequent sequential patterns can reveal frequent subsequences of nucleotide bases, some patterns may be spurious since sequential patterns are found without assessing the confidence or probability that some nucleotide bases follow others. Thus, in some cases, sequential patterns may be misleading. Algorithms for sequential rule mining discover patterns by considering not only their support but also their confidence [63]. For genome sequences, the sequential rule mining task is defined as follows.

Definition 8 (Sequential rule)

A sequential rule $X\to Y$ is a relationship between two NB s $X,Y\subseteq NB$, such that X ∩ Y = ∅ and X,Y ≠∅. A rule $r:X\to Y$ means that if items of X occur in a sequence, items of Y will occur afterward in the same sequence.

Definition 9 (Support and confidence of a sequential rule)

An X is contained in S_α (written as $X⊑S_{\alpha }$) iff $X\subseteq {\bigcup }_{i=1}^n\left\{{\alpha }_i\right\}$. A rule $r:X\to Y$ is contained in S_α ($r⊑S_{\alpha }$) iff there exists an integer k such that 1 ≤ k < n, $X\subseteq {\bigcup }_{i=1}^k\left\{{\alpha }_i\right\}$ and $Y\subseteq {\cup }_{i=k+1}^n\left\{{\alpha }_i\right\}$. The confidence and support of a rule r in a corpus CGSC are defined as:

$$con{f}_{CGSC}\left(r\right)=\frac{\left|\right\{S|r⊑S\wedge S\in CGSC\}|}{\left|\right\{S|X⊑S\wedge S\in CGSC\}|}$$

$$su{p}_{CGSC}\left(r\right)=\frac{\left|\right\{S|r⊑S\wedge S\in CGSC\}|}{\left|CGSC\right|}$$

Definition 10 (Sequential rule mining)

Let there be a genome sequence corpus CGSC and user-defined minimum support and minimum confidence threshold minsup > 0 and minconf ∈ [0,1]. A rule r is a frequent sequential rule iff sup_CGSC(r) ≥ minsup and r is a valid sequential rule iff it is frequent and conf_CGSC(r) ≥ minconf. Mining sequential rules in a corpus is to find all the valid sequential rules.

A representative sequential rule mining algorithm is ERMiner (Equivalence class based sequential Rule Miner) [63]. It relies on a concept of equivalence classes of rules having the same antecedent and consequent and a vertical database representation to explore the search space of rules. ERMiner employs two operations (left and right merges) to generate larger rules from smaller rules and reduces the search space using a Sparse Count Matrix (SCM) technique. It was shown that ERMiner is more efficient than several previous sequential rule mining algorithms [63].

Sequence prediction techniques

Another learning task performed in this study is to build sequence prediction models using the COVID-19 genome sequences to see if the arrangement of nucleotide bases is predictable. Several popular models are applied to determine which one performs best. The applied models include CPT+ [51], CPT [50], DG [52], AKOM [53], Mark1 [64], TDAG [54] and LZ78 [55]. DG [52] is a Markov based lightweight model that takes as input a set of training sequences and calculates the probabilities that each symbol is followed by each symbol. A limitation of DG is that only the last symbol is considered to predict the next one. The AKOM [53] model addresses this issue by taking the last k symbols into account for prediction (where k is user-defined). Mark1, a first-order Markov prediction model, predicts the next symbol or item on the basis of current symbol of item. The LZ78 [55] and TDAG [54] use data compression approaches for sequence prediction.

The Compact Prediction Tree (CPT) and its improved version CPT+ are complex models. They not only takes more than one symbol into account but also consider different orderings and apply noise removal strategies. However, a drawback is that the CPT and CPT+ models typically requires a large amount of memory. CPT+ takes a set of training sequences as input and generates three data structures: a prediction tree, a lookup table and an inverted index. These three structures are built incrementally by considering each sequence one by one during training. For a genome sequence S_α of n elements, the suffix of S_α of size y where 1 ≤ y ≤ n is defined as P_y(S_α) = 〈α_n−y+ 1,α_n−y+ 2,...,α_n〉. Predicting the next nucleotides base(s) of S_α is done by finding those sequences that are similar to P_y(S_α) in any order. For prediction, CPT+ uses the consequent of each sequence that is similar to S_α. Let S_β be another genome sequence similar to S_α. The consequent of S_β with respect to S_α is the longest subsequence 〈β_v,β_v+ 1,...,β_m〉 of S_β such that ${\bigcup }_{k=1}^{v-1}\left\{{\beta }_k\right\}\subseteq P_y\left(S_{\alpha }\right)$ and 1 ≤ v ≤ m. Each nucleotides base(s) discovered in the consequent of a similar genome sequence of S_α is stored in the count table (CT) data structure. Finally, CPT+ returns as prediction the most supported nucleotides base(s) in the CT.

Experiments and results

This section presents results obtained by applying the techniques presented in the previous section on the COVID-19 genome sequences obtained from the NCBI GenBank. All the experiments were performed on an HP laptop with a fifth generation Core i5 processor and 8 GB RAM. Statistics about the collected genome sequences are presented in Table 2, where ID is the accession number of the genome sequence. The NCBI GenBank offers to download each sequence in the form of nucleotide, coding region or protein. We downloaded the genome sequences in nucleotide form.

Table 2.

Characteristics of COVID-19 genome taken from NCBI

ID	Release Date	Length	Location	Collection Date
MT745584	2020-07-13	29860	Bahrain	2020-06-22
MT750057	2020-07-13	29782	USA:Illinois	2020-06-17
MT750058	2020-07-13	29782	USA: Wisconsin	2020-06-09
MT291827	2020-04-06	29858	China: Wuhan	2019-12-30
MT291828	2020-04-06	29858	China: Wuhan	2019-12-30

The SPMF data mining library [58], developed in JAVA, is used to analyze the genome sequences. SPMF is an open-source and cross-platform framework that is specialized in pattern mining tasks. It offers implementations of more than 180 data mining algorithms. Results obtained by applying algorithms on the corpus are presented in the following subsections.

Frequent nucleotide sets

The Apriori algorithm for FIM was first applied on the corpus to find the frequently occurring nucleotide base sets. Apriori takes a corpus and a minsup threshold as input and outputs the frequent nucleotide base sets. A post-processing step was then performed to keep only frequent itemsets containing a single nucleotides or having a multiple of three nucleotides (the length of a codon). The sets extracted by Apriori from the MT745584 genome sequence for various minsup values are listed in Table 3. For minsup values in the range of 40% to 100%, Apriori generated only four frequent patterns. By decreasing minsup to 1%, Apriori generated 15 patterns.

Table 3.

Frequent nucleotide base sets discovered by Apriori

Pattern(s)	Support	Min. Support	Pattern(s)	Support	Min. Support
A	8915	100%	AGT	52	10%
C	5487	100%	ACT	48	5%
G	5859	100%	CGT	32	5%
T	9599	100%	ACG	12	1%

The first four patterns show that all the nucleotides appeared in all the lines of the sequence, which was expected. A and T make up for 62% of the genome sequence (approximately 30% for A and 32% for T). The four frequent nucleotide sets discovered by Apriori can be considered as uninteresting for biologists due to two reasons. First, the frequent nucleotide sets are unordered. This means that they do not follow any specific order. For example, AGT can represents eight (3³ − 1) different codons such as TGA, GAT, and GTA, that have a total support of 52. Second, Apriori does not ensure that nucleotides from a nucleotide set appear contiguously in a genome sequence. In other words, a nucleotide set can be considered as appearing in a sequence if all its nucleotides appears in it, although the nucleotides may be separated from each other by some other subpatterns (called gaps here). For example, the nucleotide set CGT is considered as appearing both in ACAAGT and TAACCGGT. In those examples, Apriori ignores the subpatterns of nucleotides between C, G, and T. Hence, Apriori increments the support value of CGT by one for each of such sequence where the nucleotides do not occur consecutively. The next subsections present results from the application of SPM algorithms that overcome the above two drawbacks of Apriori, and thus reveal more meaningful patterns.

The support (occurrence frequency) of nucleotides in four other COVID-19 genome sequences is listed in Table 4. The number of two nucleotides (A and G) in two strains (MT291827 and MT291828) are different. MT291828 has one less A and one extra G as compared to MT291827. The mutation analysis of these two strains in Section 5 also identifies that an A in MT291827 is replaced by G in MT291828.

Table 4.

Nucleotides percentage in COVID-19 genomes

ID	A (%)	C (%)	G (%)	T (%)
MT750057	8891 (29.853)	5470 (18.311)	5849 (19.639)	9572 (32.140)
MT750058	8891 (29.853)	5470 (18.311)	5849 (19.639)	9572 (32.140)
MT291827	8932 (29.914)	5482 (18.360)	5859 (19.622)	9585 (32.101)
MT291828	8931 (29.911)	5482 (18.360)	5860 (19.626)	9585 (32.101)

Frequent sequential patterns

Then, SPM algorithms were applied to find hidden sequential relationships between nucleotides. The CM-SPAM algorithm was executed, which requires to set a minsup threshold. CM-SPAM was configured to find only contiguous sequential patterns since patterns that skip nucleotides would be hard to interpret, and patterns that are not a multiple of three nucleotides (the size of a codon) were filtered out. Table 5 lists some of the frequent patterns discovered in MT745584 by CM-SPAM. The ten patterns on the left side appear for a minsup of at least 33% of the lines in the sequence. For instance, the frequent pattern AATAAC, with a support of 511 appeared in approximately 164 lines of the sequence, represents two codons that encodes the Asparagine amino acid. Similarly, the eight patterns on the right side appeared in at least 25% of lines and the remaining two patterns appeared in at least 15% of lines in the sequence. For example, the pattern ATTATCATA shows three frequent codons that encode the amino acid Isoleucine having a support of 416 and which appeared in 124 lines of the sequence. Similarly GTTGTGGTAGTG shows three codons where one codon (GTG) appears twice.

Table 5.

Frequent nucleotides extracted by CM-SPAM

Pattern	Support	Min. Sup	Pattern	Support	Min. Sup
AATAAC	511	33%	AATAAC	511	25%
AAAAAG	530	33%	ATTATCATA	416	25%
ACTATG	510	33%	AGTAGCTAC	369	25%
CAAAAG	510	33%	CAAAAG	510	25%
CTTTGT	523	33%	CAATGTCTA	392	25%
GTATTA	508	33%	GACTATGTT	392	25%
GTATGA	503	33%	GTTGTGGTAGTG	227	15%
CAACAA	499	33%	TACTAGAAT	403	25%
TTAACG	499	33%	ACCTTAAACTAA	243	15%
TCAGTG	502	33%	TCAGTG	502	25%

In terms of performance, the pattern mining process was quite fast. Table 6 indicates the performance of CM-SPAM for different minsup threshold values. It is observed that by decreasing minsup, more frequent patterns can be discovered by CM-SPAM, while the runtime and the memory usage increases.

Table 6.

Performance of CM-SPAM with varying minsup

Min. Sup %	Time (Sec)	Patterns	Memory (Mb)	Min. Sup.
33%	2	3549	45.839	493
25%	42	194361	49.256	374
20%	231	1372868	48	299

The TKS algorithm for top-k sequential pattern mining was also applied. It takes a corpus and a user specified parameter k as input and returns the top-k most frequent sequential patterns as output. The parameter k is used in place of minusp due to following reasons:

1. Selection of a proper minsup value to discover the desired amount of useful patterns has an effect on the performance of SPM algorithms.

2. The process of minimum support fine-tuning is hard and time consuming.

To overcome these drawbacks, the parameter k puts a bound on the total number of patterns discovered by the algorithm. Some top frequent nucleotides patterns discovered in MT745584 by the TKS algorithm of different lengths are shown in Table 7. Note that patterns discovered by CM-SPAM algorithm are almost similar to the results obtained with the TKS algorithm.

Table 7.

Frequent nucleotides sequential patterns extracted by TKS

Pattern	Length	Support	Pattern	Length	Support
ACG	3	594	GTATTA	6	508
AGT	3	611	AAATTT	6	537
CGT	3	594	ATTATCATA	9	416
CTA	3	597	CTAGGTAAA	9	396
TAC	3	604	GATAAAGCT	9	396
GTC	3	589	TACTAGAAT	9	403
CAAAAG	6	510	CAATGTACG	9	372
TCAGTG	6	502	AATAAC	6	510

Sequential rules

Then, the ERMiner algorithm was applied to find sequential rules. Figure 4 shows some rules found by ERMiner in MT745584, indicating strong relationships between nucleotides. The confidence (minconf ) threshold was set to 80%, which means that rules having a confidence of at least 80% were found (a rule $X\to Y$ has a confidence of 80% if the set of nucleotides in X is followed by the set of nucleotides in Y at least 80% of the times when X appears in a genome sequence). The minimum support threshold was also set to 80% and ERMiner generated 43 sequential rules in total. In that figure, the value above an arrow is the support, while the value below indicates the confidence (probability). For example, the first rule in Fig. 4 indicates that 93.5% of the time, the A nucleotide is followed by the C nucleotide. Using ERminer, some interesting relationships were discovered between nucleotides and codons. For example, nucleotides CG is followed by A89.6% of the time to form the codon CGA that encodes the Arginine amino acid. Similarly, the codon CGT follows and is followed by the nucleotide A 86.3% and 89% of the time respectively.

Fig. 4.

Sequential rules discovered in a genome sequence by ERMiner

Some sequential rules indicate the particular order of occurrence between specific nucleotides and codons and vice versa. For examples, the rules $CGT\to A$ and $A\to CGT$ and the rules $ACT\to G$ and $G\to ACT$. It was also observed so far that the total number of nucleotides in a sequence (abstraction simplicity) directly influences the efficiency of SPM algorithms.

Sequence prediction

Predicting the next nucleotides in a genome sequence was done to see how predictable a sequence is. Several models were compared for predicting the next nucleotides and their patterns. Each model is first trained on nucleotides and their patterns in sequences. Then, a prediction model is used to predict the next nucleotides and their patterns in a sequence. Prediction of the next nucleotides and their patterns is based on the scores calculated by the model for each nucleotide. For example, CPT+ predicted {T} for the sequence {A,C}, and ACT is a frequent codon that encodes the Threonine amino acid.

We compared the performance of CPT+ with other popular prediction models such as Dependency Graph (DG), Transition Directed Acyclic Graph (TDAG), CPT (the predecessor of CPT+), Mark1, AKOM (All-K-Order-Markov) and LZ78. Each model is trained and tested with 10-fold cross-validation. The cross-validation technique characterizes the performance of each model by evaluating the generalization of independent set over statistical results provided by the model. In k-fold cross-validation, the dataset is randomly partitioned into k sub-datasets. One sub-dataset is then selected as validation set for model testing and the remaining k − 1 sub-datasets are used for model training. This process is applied k times and each sub-dataset is used exactly once as the validation set. Single estimation of the result is obtained by taking the average of k results. The main reason to use 10-fold cross-validation is to achieve low variance in each run. Details about the dataset that only contains MT745584 are shown in Table 8.

Table 8.

Corpus statistics for sequence prediction

parameter	Value
Number of Sequences	1492
Number of distinct items	5
Itemsets item ID	4
Distinct item per sequence	20.42
Occurrence for each item	4.66
Corpus size in MB	5968

To evaluate prediction models, three measures are used. The result of a prediction can be:

• a success if the model predicts accurately,

• a failure if the model predicts inaccurately and

• no match if the model cannot perform a prediction.

The success, failure, no match are expressed as percentage for all predictions. The table also include information about the training time and testing time for each model, in seconds. On overall, the accuracy is the most important measure to compare the models as it represents the ability to make good predictions.

Results are shown in Table 9 for each compared model on MT745584. To put the results into perspective, Table 9 also include results for a baseline, which is a sequence prediction model that randomly predicts the next nucleotide of a sequence. This baseline model is called Random. Several observations are made from the results. First, it is found that No Match is always zero, meaning that predictions could always be performed using all models. Second, the testing and training times of models were quite similar for most models, and remained very low (lest than 1 second in all cases). Third, AKOM, where k = 3, provided the highest accuracy (20.71%) as compared to other prediction models, followed by DG. CPT+ had the highest number of failures, while CPT+, CPT and TDAG had similar performance. CPT, the predecessor of CPT+ performed slightly better than CPT+. A reason why CPT and CPT+ do not perform particularly well is because they consider that the ordering of previous nucleotides is not important to predict the next one. The most accurate models (DG, Mark1 and AKOM) consider a strict ordering of nucleotide(s) to perform predictions.

Table 9.

Accuracy of prediction models

Models	DG	TDAG	CPT+	CPT	Mark1	AKOM	LZ78	Random
Success	20.643	18.901	18.035	18.298	20.174	20.71	19.722	16.1
Failure	79.357	81.099	81.965	81.702	79.826	79.29	80.228	83.9
No Match	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Train Time	0.011	0.081	0.039	0.002	0.005	0.057	0.021	–
Test Time	00.001	00.000	0.305	0.469	0.001	00.000	0.002	–

Overall, the accuracy of models for nucleotide base(s) prediction in genome sequences was low. This may be due to the fact that sequences only contain four distinct items (nucleotides) and their distribution in the genome sequence is not uniform (A and T generally make 60-64% of the total genome sequence). Despite having low accuracy, all models achieved better performance than the Random prediction model, which had an accuracy of 16.1%.

A limitations of these prediction models is that they can predict only one item (nucleotide in this work) for a sequence of items. The genetic code that maps codons to amino acids follows the redundancy (or degeneracy) property [65]. This means that two different codons can encode the same amino acid. The redundancy is generally found in the third nucleotide in codons. One practical consequence of redundancy is that a single nucleotide substitution (called synonymous substitution) or an error at the third position usually leads to no alteration in amino acids in the encoded protein. Due to the redundant nature of genetic code, one may argue that predicting only one nucleotide in a codon is not that significant and useful.

However, codons can be organized into 9 families and 13 pairs on the basis of frequent patterns of redundancy. In 9 codon families, the first two nucleotides are enough to encode a unique amino acid. Adding any third nucleotide (say X) will generate the same amino acid. For example the two codon families (patterns) CGX and GCX encode two amino acids Arginine and Alanine respectively. Whereas in 13 codon pairs, the first two nucleotides are enough to encode two different amino acids. Adding a third purine (that contains either A or G) nucleotide (say Y ) generates one amino acid, and adding a third pyrimidine (containing either the C or T) nucleotide (say Z) generates another different amino acid. For example, the Leucine amino acid is encoded by a codon family (CTX) and a codon pair (TTY ). Thus, an interesting research possibility is to take advantage of redundant frequent patterns found by SPM algorithms to predict codon families and pairs. Another interesting direction would be to integrate domain knowledge in prediction models to further guide prediction.

COVID-19 Genomes mutation analysis

This section presents the proposed approach for the third sub-goal of this paper, which is to identify mutations in the COVID-19 genome sequences.

At this moment, it is still quite unclear how COVID-19 causes a variety of diseases that can range from asymptomatic to fatal respiratory failure. As many other organisms that divide and spread, the SARS-CoV-2 virus is constantly evolving by changing a few letters (nucleotides) at a time, to better adapt to new environments. The evolution process is not completely known as it changes slowly [66] compared to other viruses, thus, giving less mutations to study. On average, the coronavirus accumulates about two changes per month in its genome [67]. Most of the changes in the COVID-19 genome structure may not affect how the virus behaves, but a few may influence the disease’s transmissibility or severity. For example, Korber et al. [46] claimed that a mutation (D614G) appears to be more transmissible between people than the previous one (D614). However, that study received criticism because the scientists had not proved that the mutation itself was responsible for its domination; it could have benefited from other factors or from chance. Nevertheless, it is very important to understand the pattern in the virus mutates as well as its mutation rate.

The mutation rate of any virus is a critical parameter to understand viral evolution [68]. It is also the most important factor to assess the risk of emergent infectious disease and its accurate estimation is of great significance [69]. Additionally, for developing proper drugs/vaccines against COVID-19, genomic sequence and mutation analysis are crucial [70] and accurate information on the mutation rate can play a vital role in the assessment of possible drugs/vaccination strategies. In this regard, we propose an algorithm that can be used to analyze genome sequences for variations and also to study the mutation rate. The focus in this work is on substitution mutation, also known as point mutation. Algorithm 1 presents the pseudocode for point mutation analysis in genome sequences.

Algorithm 1 takes two COVID-19 genome sequences (GN₁ and GN₂) and compares the nucleotides in the two sequences line by line. The locations and lines number where nucleotides are different are stored in a set called V ec. Moreover, the changed nucleotides values are also stored in V ec. Mutation rate (MR) is calculated by the following formula:

$$MR=\frac{TM}{TNB}\times 100$$ 1

where TM is the total mutation taking place in the two sequences and TNB is the total number of nucleotides.

We have developed this algorithm in Python and the code along with genome sequences can be found at [71]. We have run the algorithms on two genome sequences (MT750057 and MT750058) from Table 2. The algorithm returns the lines number and locations where the nucleotides in genome sequence have changed (shown in Table 10). Moreover, the fourth and eight columns in Table 10 provide information about replacement of nucleotide bases. For example, the first entry in the fourth column shows that G (in MT750057) was replaced by T (in MT750058).

Table 10.

Point mutation analysis results

Line	Location	Position	Change	Line	Location	Position	Change
3	29	149	G → T	130	42	7,782	C → A
70	31	4,171	T → C	139	55	8,335	A → G
94	37	5,617	T → C	328	2	19,662	T → G
115	11	6,851	C → T	415	31	24,871	G → T

It is interesting to observe that the occurrence frequency of each nucleotide base (A, C, G and T) is the same in the two strains MT750057 and MT750058 (as observed in Table 4), despite that mutations occurred. The designed algorithm found that the MT750058 strain has eight more changes (listed in Table 10) than MT750057. The reason why the occurrence frequency of nucleotides remains the same despite these mutations is that for each mutation that changed a nucleotide by another, there was another mutation that changed another nucleotide by the former. More precisely, mutations have removed one A, two C, two G and three T, but have added the same number of each nucleotide. Hence, the total occurrence frequency of each nucleotide is the same in both strains.

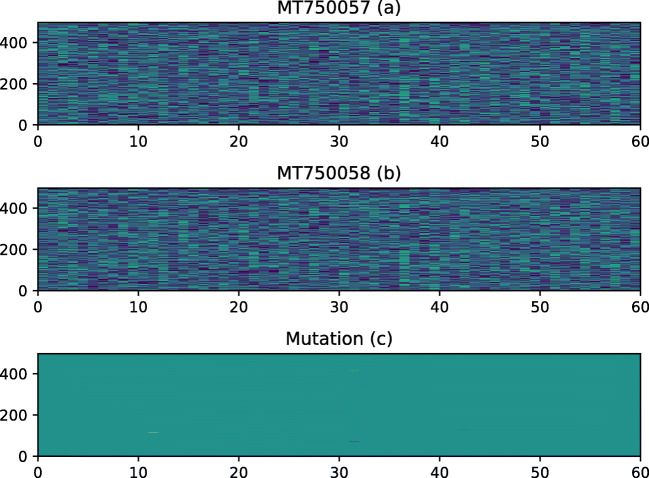
The matplotlib library was used to generate the plots for two genome sequences and the mutated sequence (Fig. 5). If there is any mutation in the two genome sequences (Fig. 5a,b), then the mutated sequence (Fig. 5c) will have bright spots. If there is no mutation, then the Fig. 5c will be dark with no bright spots. Both sequences were 497 lines long and each line contains 60 nucleotide except for the last line, that contain 22 nucleotide. The X-axis represents the location in the line where nucleotide bases are changed and Y-axis represents the line number where two sequences are changed.

Fig. 5.

COVID-19 genome mutation in whole sequences

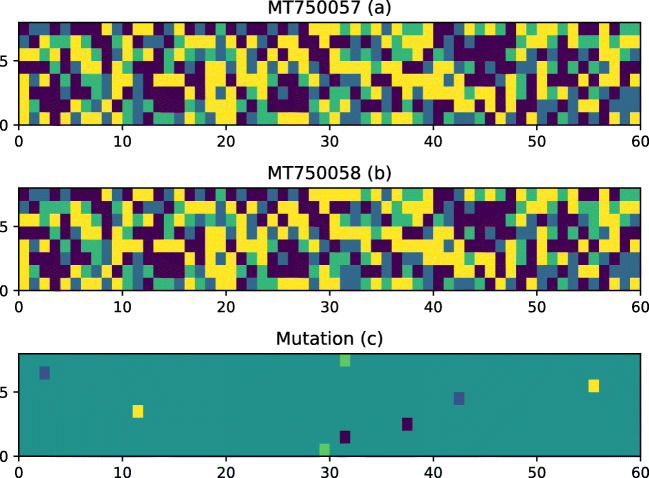
Figure 5 does not provide a very clear picture for the mutation. Some spots can be seen in Fig. 5(c) that show the place of mutations. To make the results clearer, we plot the mutation analysis for only those lines where the mutation take place instead of displaying the plots for all the lines in the sequences. Obtained results are shown in Fig. 6, that contain only 8 lines from two sequences where mutations took place.

Fig. 6.

COVID-19 genome mutation

The mutation rate comes out to be 0.0268% for the MT750057 and MT750058 genome sequences. Similarly the mutation rate for other two genome sequences (MT-291827, MT291828) comes out to be 0.0003% (one nucleotide base changed (A (in MT291827) → G (in MT291828)) at line 405, location 48, position 24,288). Table 4 that lists the total occurrence frequency of four nucleotides in MT291827 and MT291828 also indicated that MT291828 has one less A and one more G than MT291827. It is important to point out there that China genome sequences were reported earlier than USA genome sequences. Moreover, the genome sequences are from the same city. Whereas, the genome sequences for USA are from different cities. This shows that COVID-19 genome sequences mutation rate is different and increased with the passage of time. Moreover, genome sequences for different locations (cities) in the same country have high mutation rate. With this developed procedure, one can analyze:

• The point mutation and mutation rate in different genome sequences.

• How COVID-19 genome sequences are evolving as it spread in different locations.

With such information, one can investigate how the mutations vary from place to place and from country to country. Moreover, COVID-19 strains from different locations can be analyzed to investigate whether they coexist with each other or not. In this regard, one study [72] finds that European, North American and Asian COVID-19 strains might coexist.

This preliminary technique has some limitations. First, a requirement is that both genome sequences should have equal length. If length is not equal then some nucleotides in the longest genome sequence will not be considered in the analysis. For example, let the length of the shorter genome sequence (say X) be 85 and the length of longer genome sequence (say Y) be 95. Then, nucleotides in Y from position 86 to 95 will be ignored as the maximum length of X is 85. One possible solution is to add dummy values in X. However, this solution suffers from the problem of how to compare dummy values with nucleotides. Another solution is to make the length of X equal to that of Y by appending those nucleotides at the tail of X that are taken from Y. However, this will make the two sequences the same at appended locations and mutation analysis at these points will be useless. It is important to point out here that SPM-based learning approach in Section 3 does not suffer from genome sequence length issue and works well for genome sequences of any length.

The second limitation is that the procedure for mutation analysis considers the whole genome sequence without ORFs and proteins information. The technique can be improved in this regard by comparing nucleotides in the genome sequences ORFs wise. This will help in finding the mutation in particular ORFs and plotting the mutation analysis results for each ORF [73]. We believe that this technique still needs some improvements and in the future, we plan to work on the aforementioned limitations. The goal is to develop a generic technique that can find mutation and mutation rate ORFs wise and can work on genome sequences of different lengths without losing important information.

Conclusion

This paper proposed two approaches to investigate and analyze COVID-19 genome sequences. In the first approach, pattern mining techniques are used to find frequent nucleotide bases in the sequences, their frequent patterns and the sequential relationship between such patterns. Moreover, various sequence prediction models were evaluated on genome sequences, where AKOM (All-K-Order-Markov) performed better than other state-of-the-art algorithms. In the second approach, an algorithm was proposed to analyze mutations in COVID-19 genome sequences. The algorithm finds the location(s) in COVID-19 strains where the nucleotide bases are changed to calculate the mutation rate. The approaches presented in this paper are not limited to the SARS-CoV-2 virus. They could be used for the analysis of other human viruses too. The proposed approaches lead to several directions for future work, some of which are:

• To use of emerging patterns mining or contrast set mining techniques [74] on the COVID-19 genome sequences to discover emerging (or contrasting) trends in genome sequences that shows a clear and useful difference (or contrast) between two classes or disjoint features.

• To investigate the applicability of pattern mining and deep learning techniques [75] for the prediction of codon families and codon pairs in genome sequences.

• To find specific codons that are followed by specific codons. This will allow us to find codon signatures that indicate stickiness/preference between codons of amino acids.

• To take advantage of redundant frequent patterns in COVID-19 genomes discovered by SPM algorithms to predict codon families and pairs.

• To improve the mutation analysis approach to make it more general. For example, to propose some strategies that can be used to overcome the sequence length limitation and considering genes information in the genome sequences. Moreover, performing the indels (insertion or deletion of nucleotides bases) [76] mutation analysis along with point (substitution) mutation.

• The point mutation technique can be extended to compare a new genome sequence with a dataset of COVID-19 genomic sequences. The ultimate goal is to develop a technique that can work well on genome sequences of various length, perform indels and point mutation with gene information.

Compliance with ethical standards

Conflict of Interests

The authors declare that they have no conflict of interest.

Ethical Approval

This paper does not contain any studies with human participants or animals performed by any of the authors.