A Bayesian Approach for the Analysis of Panel-Count Data with Dependent Termination

Summary.

We consider modeling and Bayesian analysis for panel-count data when the termination time for each subject may depend on its history of the recurrent events. We propose a fully specified semiparametric model for the joint distribution of the recurrent events and the termination time. For this model, we provide a natural motivation, derive several novel properties, and develop a Bayesian analysis based on a Markov chain Monte Carlo algorithm. Comparisons are made to other existing models and methods for panel-count data. We demonstrate the usefulness of our new models and methodologies through the reanalysis of a data set from a clinical trial.

1. Introduction

Grouped recurrent event times data, popularly called panel-count data, occur when a subject, inspected over time only at scheduled time points 0 = a₀ < a₁ < ⋯ < a_J, may experience repeated occurrences of an important but possibly nonfatal event. Suppose N_i(t) denotes the number of nonfatal events experienced by subject i up to time t. The number of new recurrent events N_ij = N_i(a_j) – N_i(a_j−1) to subject i occuring in the inspection interval I_j = (a_j−1, a_j] is recorded until the termination time T_i, when the subject is removed from observation either due to an adverse response such as detection of a relapse to malignancy or due to a positive response such as cure. We are assuming that the inspection times are the same for all subjects and T_i is discrete and take values only a₁, … , a_J. Let x_i be the explanatory variable for subject i. We use the notation D = {N_ij : j = 1, … , T_i; x_i; T_i : i = 1, … , n} to denote the observed panel-count data.

See Gail, Santner, and Brown (1980), Oakes (1982), Sinha (1993), Scheike and Zhang (1998), Sun and Wei (2000), and the references therein for different examples of panel-count data from various clinical trials and animal experiments. Earlier works on modeling panel-count data often assumed that given the covariate x of the subject, the risk of termination at any time point t does not depend on the past history of nonfatal events $\mathcal{N}\left(t\right)$. But, this assumption will not be valid when, say, the termination is caused by either a significant positive response (say, cure or discharge from the treatment) or a negative response (such as relapse to malignancy). This risk of termination is often associated with the history of nonfatal events. For the bladder cancer data example (Sun and Wei, 2000) from the Veterans Administration Cooperative Urological Research Group (VACURG), the time-independent covariates available for each patient are a binary variable indicating treatment (1 for treatment thiotepa and 0 for placebo), number of tumors at entry, and the size of the largest tumor at entry. After the surgery to remove his/her primary tumor, each patient was monitored every month during scheduled clinic visit for number of new (since the previous clinic visit) superficial bladder tumors. A patient was terminated from further observation during a particular clinic visit probably due to clinically significant improvement of his/her disease symptoms. As the treatment (thiotepa and placebo) had to be instilled in the bladder, we can expect that a patient who is very prone to superficial bladder tumors is also expected to take longer than usual time to termination. A previous analysis of this data ignored the possible association between the risk of termination and the history of superficial tumors. Unlike the previous analysis, we treat both the event of termination (cure) and the recurrent events of superficial tumors as important responses.

Various methods of panel-count data and recurrent event times data, published so far, have put high emphasis on partially specified models. In such work, the model and associated inferential procedure depend on the particular underlying inferential objective, which can be of the following four types: (1) inference about N(t) (e.g., Sun and Wei, 2000), under the assumption that given x, the process N(t) is independent of T; (2) marginal inference about N(t) unconditional on the past history of events (e.g., Wang, Qin, and Chang, 2001); (3) inference about T given the history of N(·); and (4) inference about the termination modulated process N(t)l_[T≤t] (e.g., Ghosh and Lin, 2000), where 1_A is the indicator function.

In many applications, it may be desirable to have a fully specified model which can be used for addressing all four objectives together within a unified statistical analysis and also perform prediction, model diagnostic, simultaneous inferences on multiple parameters, etc. Especially when both the nonfatal events and the termination are deemed as important responses, and the termination depends on the history of nonfatal events, addressing each objective through separate analysis may be misleading. The results of the analysis of different partially specified models focusing on different objectives may conflict with each other and may be difficult to unify. Our aim is to develop and analyze a fully specified stochastic model of the joint distribution of the nonfatal events and the termination time. This new model also allows us to understand the prognostic values of the history of nonfatal events for evaluating the risk of termination.

A fully parametric model by Lancaster and Intrator (1998), here onward referred to as the LI model, allows only positive dependence between a subject’s history of nonfatal events and risk of termination. Our model represents a much broader class than the LI model and we can incorporate a negative association between N(t) and T. The data example discussed in this article may require a negative association between N(t) and T. The details of the comparison between our model and the LI model are given later. Recently introduced class of models for panel-count data in animal carcinogenicity experiments (e.g., Dunson, 2000) also do not incorporate the association between T and N(t).

In Section 2, we present a fully specified stochastic model for panel-count data with a dependent termination process. We present novel properties of our model and relationship of our model to other existing models for recurrent events data. Existing Bayesian literature on panel-count data is very limited. See Ibrahim, Chen, and Sinha (2001) for a current literature survey on Bayesian survival analysis. One of our goals is to demonstrate the use and advantages of the Bayesian paradigm for such problems. In Section 3, we present the likelihood of our model and associated Bayesian methods for analyzing such data. In Section 4, our methodology is illustrated with the analysis of panel-count data from the bladder cancer study from Sun and Wei (2000). In Section 5, we conclude our article with some closing remarks.

2. Model for Panel-Count Data

We assume that each N_i(t) is a realization of a compound nonhomogeneous Poisson process (Karlin and Taylor, 1981). Given the subject-specific unobservable frailty w_i, the cumulative number of nonfatal events to the subject i, under observation at time t (that is, T_i ≥ t) is given by

$$N_i\left(t\right)\mid x_i,w_i~\text{Poi}\left\{{\mu }_0\left(t\right)\text{exp}\left({\beta }_1{x}_i\right)w_i\right\},$$ (1)

where μ₀(t) is the baseline cumulative intensity and β₁ is the regression parameter of the covariate effect on the conditional intensity in (1). Here w₁, … , w_n are assumed to be independent Ga(η, η) with common density g(w | η) = η^ηw^η−1e^−ηw/Γ(η). The mean of w_i is taken to be unity to assure the identifiability of the model parameters and the variance of w_i is κ = η⁻¹. We assume that κ > 0 to exclude the oversimplified situation when, within the same subject, the increments of N(t) in disjoint intervals are independent. A finite mean frailty distribution is warranted here to assure a finite expected number of events within any finite time interval.

The model further assumes that the hazard of T_i at time t depends on the history of point process ${\mathcal{N}}_i\left(t\right)=\left\{N_i\left(s\right):s<t\right\}$ via the unobservable frailty w_i. We use a discretized version of the Cox model (Cox, 1972),

$$P\left[T_i=a_j\mid x_i,w_i,{\mathcal{N}}_i\left(a_j\right),T_i>a_{j-1}\right]=1-{\pi }_j^{\text{exp}\left({\beta }_2{x}_i\right)w_i^{\alpha }},$$ (2)

where β₂ is the regression parameter and ${\pi }_j=P\left[T=a_j\mid x=0,w=1,\mathcal{N}\left(t\right),T>a_{j-1}\right]$ is the discretized baseline conditional hazard rate.

Here, −∞ < α < + ∞ quantifies the nature of dependence between ${\mathcal{N}}_i\left(t\right)$ and the hazard of T_i. When α = 0, we have $P\left\{T_i=a_j\mid x_i,T_i>a_{j-1},{\mathcal{N}}_i\left(t\right)\right\}$ free of ${\mathcal{N}}_i\left(t\right)$ and we get the model of Sinha (1993), where the hazard of T_i at time t is assumed independent of ${\mathcal{N}}_i\left(t\right)$. When α > 0, there is positive association between N_i and T_i, that is, given the same value of x_i, a subject with a higher rate of nonfatal events has a higher risk of termination than another with a lower rate of nonfatal events. Similarly, α < 0 indicates a negative relationship between T_i and N_i. When α > 1, the variability of termination times are more than the heterogeneity of subjects in terms of their rates of nonfatal events and 0 < α < 1 implies the opposite. Again, α = 1 implies that the heterogeneity among subjects in terms of rates of nonfatal events is the same as the heterogeneity in terms of their termination times. When α = 1 and π_j = exp[−ρ{μ₀(a_j) – μ₀(a_j−1)}], we get the LI model (Lancaster and Intrator, 1998). This shows that the LI model allows only positive association and has a restrictive assumption of a very precise algebraic relationship between π_j and μ₀. We investigate some further useful and desirable properties of our model.

Theorem 1.

The conditional risk of termination, $P\left[T_i=a_j\mid {\mathcal{N}}_i\left(a_j\right),x_i,T_i>a_{j-1}\right]$, depends on the events history ${\mathcal{N}}_i\left(a_j\right)$ only through the cumulative number of events N_i(a_j). For the special case α = 1,

$$\begin{gathered} P\left[T_i=a_j\mid {\mathcal{N}}_i\left(a_j\right),x_i,T_i>a_{j-1}\right] \\ =1-{\left[1-\frac{{\pi }_j^{\text{exp}\left({\beta }_2{x}_i\right)}}{\text{exp}\left({\beta }_1{x}_i\right){\mu }_0\left(a_j\right)-\text{exp}\left({\beta }_2{x}_i\right)\text{log}\left(S_j\right)}\right]}^{\eta +N\left(a_j\right)}, \end{gathered}$$ (3)

where $S_j={\prod }_{k=1}^j{\pi }_k$.

The proof of Theorem 1 is given in the Appendix. Please note that Theorem 1 is very different from Implications 1–3 in Lancaster and Intrator (1998). When α ≠ 1, we can numerically evaluate the quantities $P\left[T_i=a_j\mid {\mathcal{N}}_i\left(a_j\right),x_i,T_i>a_{j-1}\right]$ and P[T_i = a_j | x_i, T_i > a_j−1], but no closed form expressions of these quantities are available. Unlike the model of Wang et al. (2001), P(T_i = a_j | x_i, T_i, > a_j−1) in our model does not follow a discretized Cox structure. We present the following theorem about the conditional distribution of nonfatal events in any interval given past history of events.

Theorem 2.

The conditional distribution of N_ij | x_i, ${\mathcal{N}}_i\left(a_{j-1}\right)$, T_i > a_j−1 depends on ${\mathcal{N}}_i\left(a_{j-1}\right)$ only through the N_i(a_j−1). For the case α = 1, this distribution is a generalized negative binomial with conditional expectation

$$\begin{gathered} E\left[N_{ij}\mid {\mathcal{N}}_i\left(a_{j-1}\right),x_i,T_i>a_{j-1}\right] \\ =\left\{\eta +N_i\left(a_{j-1}\right)\right\}\left[\frac{\text{exp}\left({\beta }_1{x}_i\right)\left\{{\mu }_0\left(a_j\right)-{\mu }_0\left(a_{j-1}\right)\right\}}{\eta +\text{exp}\left({\beta }_1{x}_i\right){\mu }_0\left(a_j\right)}\right]. \end{gathered}$$ (4)

The proof is given in the Appendix. The result in (4) is similar to the property of the model proposed by Oakes (1982). These two theorems also demonstrate that our model is very different from the modulated renewal process of Oakes and Cui (1994). For α ≠ 1, no such simple expression exists for $E\left[N_{ij}\mid {\mathcal{N}}_i\left(a_{j-1}\right),x_i,T_i>a_{j-1}\right]$, but, these can be numerically computed given the parameter values. Following the steps similar to the derivation of (4), we can also numerically evaluate E[N_ij | x_i, T_i > a_j−1]. The details are omitted here. These demonstrate that through our fully specified model along with Bayesian analysis, we can estimate different important model quantities of interest using a single unified inference procedure.

3. Likelihood and Posterior

It follows from (1) that, given w_i, N_ij for j = 1, … , J are independent Poi{w_iexp(β₁x_i)/μ_j}, where μ_j = μ₀(a_j) – μ₀(a_j−1) and Poi(γ) denotes the Poisson distribution with mean γ. The likelihood based on the sampling distributions of the N_ij is

$$L_1\left({\beta }_1,{\mu }_0,w\mid D\right)\propto \prod _{i=1}^n\prod _{j\in M_i}{\left[e^{{\beta }_1{x}_i}{w}_i{\mu }_j\right]}^{N_{ij}}\text{exp}\left[-e^{{\beta }_1{x}_i}{w}_i{\mu }_j\right],$$ (5)

where M_i, is the set of inspection intervals when the subject i is under observation. Using (2), we obtain the likelihood based on the sampling distributions of the T₁, … , T_n as

$$L_2\left({\beta }_2,\pi ,w\mid D\right)\propto \prod _{i=1}^n\left[1-{\pi }_{\left(i\right)}^{w_i^{\alpha }\text{exp}\left({\beta }_2{x}_i\right)}\right]S_{\left(i\right)}^{\text{exp}\left({\beta }_2{x}_i\right)w_i^{\alpha }},$$ (6)

where t_i = a_(i) ∈ {a₁, … , a_J} is the termination time of the subject i and $S_{\left(i\right)}={\prod }_{k=1}^{\left(i\right)-1}{\pi }_k$. In (2), we use a discretized Weibull baseline hazard rate ${\pi }_j=\text{exp}\left\{-{\lambda }_j\left(a_j^{\nu }-a_{j-1}^{\nu }\right)\right\}$, with unknown parameter vector ϕ = (λ, ν). This model on π_j allows for a very wide class for the hazard. In principle, it is possible to use a more flexible model with completely unspecified π_j.

The observed data likelihood L₀(β₁, β₂, α, ϕ, η | D) is obtained via the multiple integration $L_0\left({\beta }_1,{\beta }_2,\alpha ,\varphi ,\eta \mid D\right)\propto \int L_1\times L_2\times g\left(w\mid \eta \right)\prod _{i=1}^{n}d{w}_i$, where g(w | η) is the joint density of w = (w₁, … , w_n) given η. We present a semiparametric Bayes survival analysis approach (e.g., Sinha and Dey, 1997; Ibrahim et al., 2001) using a prior process to summarize the prior information on μ₀(·) and a prior distribution for the rest of the parameters. We assume that the prior information about μ₀(t) is independent of the prior information about the rest of the parameters, π(μ, β, η, ϕ, α) = π(μ) × π(β, η, ϕ, α). As (5) involves μ₀ only through (μ₁, … , μ_J), we only need the joint prior density of the increments (μ₁, … , μ_J). Using an independent increment gamma process prior (Kalbfleisch, 1978) on μ₀(t) we have the prior distribution μ_j ~ Ga(cγ_j, c) with independence for j = 1, … , J. The joint prior density of the increments is given by

$$\pi \left(\mu \right)=\prod _{j=1}^J\frac{c^{c{\gamma }_j}{\mu }_j^{c{\gamma }_j-1}}{\Gamma \left(c{\gamma }_j\right)}\text{exp}\left(-c{\mu }_j\right).$$ (7)

The hyperparameters, c and γ_j’s, assumed to be known here, are determined by the prior expectation (mean) and the precision of the prior expectation of μ₀(t). But, it is possible to put another level of hierarchy in this model using a hyperprior for (c, γ).

The joint posterior for our model is given by

$$p\left(\beta ,w,\eta ,\varphi ,\alpha \mid D\right)\propto L_1\left({\beta }_1,\mu ,w\mid D\right)\times L_2\left({\beta }_2,\varphi ,w\mid D\right)\times g\left(w\mid \eta \right)\times \pi \left(\beta ,\varphi ,\eta ,\alpha \right)\times \pi \left(\mu \right),$$ (8)

where $g\left(w\mid \eta \right)={\prod }_i\left[{\eta }^{\eta }{w}_i^{\eta -1}\text{exp}\left(-w_i\eta \right)/\Gamma \left(\eta \right)\right]$ is the product of gamma frailty densities and π(β, ϕ, η, α) is given below. Instead of dealing with complicated L₀((β₁, β₂, α, ϕ, η | D), we use popular MCMC tools (e.g., Chen, Ibrahim, and Shao, 2000) to sample from (8) and then use those samples to do the posterior inference. For practical convenience, we further assume that

$$\pi \left(\beta ,\eta ,\varphi ,\alpha \right)=\pi \left({\beta }_1\right)\times \pi \left({\beta }_2\right)\times \pi \left(\varphi \right)\times \pi \left(\eta \right)\times \pi \left(\alpha \right).$$ (9)

This assumption is reasonable, as β₁ and β₂ are the parameters associated with effects of covariate x, respectively, on N(t) and on T. In many practical applications, the priors on β₁ and β₂ will be very noninformative to balance both the skeptical and the enthusiastic views about the effects of covariates such as assigned treatments. It is also a common practice to assume priors on baseline functions μ and π to be independent of the rest of the parameters. As we can expect to have independent expert opinions about two different types of events N(·) and T, we have the assumption of mutual independence between the set of parameters associated with N(·) and the set associated with T. The prior belief on α, the parameter quantifying the association between the two types of events, is expected to be obtained independently from others. The parameter π(α) is assumed to be N(α₀, σ₃) with α₀ = 0 as we do not know a priori whether the association between the two classes of events should be either positive or negative. For further convenience we use N(β₁₀, σ₁) for π(β₁), N(β₂₀, σ₂) for π(β₂), and Ga(λ | A₁, B₁) × Ga(ν | A₂, B₂) for the density of π(ϕ). We are choosing the forms of the priors that are flexible, yet facilitate easy-to-sample conditional posteriors at each iteration of the MCMC. We would like to emphasize that if needed, MCMC is very capable of handling more complicated prior structures such as a multivariate π(β, η, ϕ, α) inducing prior dependencies among the parameters.

The full conditional distributions for the MCMC steps are given as follows using the notation [θ | rest] to denote the conditional distribution of ϕ given all other parameters:

1. $\left[{\mu }_j|\mathit{\text{rest}}\right]~Ga\left\{\tau {\Lambda }_j+{\sum }_i{N}_{ij}{V}_{ij},\tau +{\sum }_i{w}_i\text{exp}\left({\beta }_1{x}_i\right)V_{ij}\right\}$

2. $\left[\lambda \mid \mathit{\text{rest}}\right]~Ga\left\{m+1+A_1,B_1+{\sum }_i{t}_i^{\nu }{w}_i^{\alpha }\text{exp}\left({\beta }_2{x}_i\right)\right\}$

3. $\left[\nu \mid \mathit{\text{rest}}\right]\propto {\prod }_i\nu t_i^{\nu -1}\text{exp}\left\{-\lambda t_i^{\nu }{w}_i^{\alpha }\text{exp}\left({\beta }_2{x}_i\right)\right\}\times \pi \left(\nu \right)$

4. $\left[{\beta }_1\mid \mathit{\text{rest}}\right]\propto \text{exp}\left\{{\sum }_i{\beta }_1{x}_i{\sum }_j{N}_{ij}{V}_{ij}-{\sum }_i{w}_i\text{exp}\left({\beta }_1{x}_i\right){\sum }_j{\mu }_j{V}_{ij}\right\}\times \pi \left({\beta }_1\right)$

5. $\left[{\beta }_2\mid \mathit{\text{rest}}\right]\propto \text{exp}\left\{{\sum }_i{\beta }_2{x}_i-\lambda t_i^{\nu }{w}_i^{\alpha }\text{exp}\left({\beta }_2{x}_i\right)\right\}\times \pi \left({\beta }_2\right)$

6. $\left[\eta \mid \mathit{\text{rest}}\right]\propto {\prod }_i\left[\left\{{\eta }^{\eta }/\Gamma \left(\eta \right)\right\}{w}_i^{\eta -1}\text{exp}\left(-\eta w_i\right)\right]\times \pi \left(\eta \right)$

7. $\left[w_i\mid \mathit{\text{rest}}\right]\propto w_i^{{\Sigma }_j{N}_{ij}{V}_{ij}+\alpha +\eta -1}\times \text{exp}\left[-w_i\left\{\text{exp}\left({\beta }_1{x}_i\right){\sum }_j{\mu }_j{V}_{ij}+\eta \right\}-\lambda w_i^{\alpha }{t}_i^{\nu }\text{exp}\left({\beta }_2{x}_i\right)\right]$

8. $\left[\alpha \mid \mathit{\text{rest}}\right]\propto {\prod }_i{w}_i^{\alpha }\text{exp}\left\{-\lambda w_i^{\alpha }{t}_i^{\nu }\text{exp}\left({\beta }_2{x}_i\right)\right\}\times \pi \left(\alpha \right)$.

Here V_ij is the indicator variable of whether subject i is examined at time a_j. Except for μ_j and λ, all other conditional densities are not in standard form. Fortunately, the conditional densities for β₁, β₂, η, v, and α are log concave. So, a readily available software program for the adaptive rejection sampling method (Gilks and Wild, 1992) has been used to sample from these log-concave densities. To avoid lengthening the article, the proofs of their log concavities are omitted. Notice that the conditional density of each w_i is proportional to f(w) × h(w), where f(w) is proportional to gamma density function and h(w) is a bounded function. To sample w_i’s, we have used a Metropolis-Hastings algorithm with acceptance probability r(w_old, w_new) = min[{h(w_new)/h(w_old)}, 1]. Here, w_new is the candidate value simulated from f(w) and w_old is the current value of w_i at this iteration. In particular we have used 10 Gibbs chains with 20,000 iterations in each chain. To monitor the convergence of MCMC, we have checked that the estimated scale reduction factor $\widehat{R}$ of Gelman and Rubin (1992) is less than 1.2 for each of the parameters. This is a very popular and easy method to monitor the convergence of the MCMC algorithm. We have also checked several other convergence diagnostics of the MCMC using the publicly available software package CODA (Best, Cowles, and Vines, 1995).

4. Analysis of the Bladder Cancer Data

We reanalyze the bladder cancer data from the VACURG (Sun and Wei, 2000), allowing a possible association between the history of superficial tumor occurrences and the risk of termination. The data set is available at the website www.blackwellpublishers.co.uk/rss. We use only the binary regression variable treatment in our model. For each patient, some of the monthly clinic visits (before termination) have missing observations as the patients have missed some of their clinic visits. We assume here that patterns of missed clinic visits are noninformative in the sense that the probability of a patient missing a particular clinic visit does not depend on the unobserved number of tumors in that month. This assumption of missing at random (Little and Rubin, 1987) may not be valid for this data example, but the patterns of missing data and methodologies dealing with them are beyond the scope of this article. To accommodate missing counts in some of the months, the set M_i in (5) should contain only those months when subject i has been observed to have his/her scheduled clinic visits.

Hyperprior specification:

We have used zero mean and high variance (1000) for the regression parameters β₁ and β₂ to reflect our prior opinions of no covariate effects on the rate of nonfatal events as well as on the risk of termination. Because we do not have prior input from any expert, we are using diffuse priors for β₁ and β₂ and similar diffuse priors later for other parameters. We have noticed that our analysis is not sensitive to the choice of the values of the hyperparameters as long as the priors remain sufficiently diffuse.

For hyperparameters τ = 1/c and γ₁, … , γ_J associated with the gamma process in (7), we take τ = 5.0 and ${\gamma }_j={\gamma }_0\left(a_j\right)-{\gamma }_0\left(a_{j-1}\right)=0.01\times \left({\sqrt{a}}_j-{\sqrt{a}}_{j-1}\right)$. These choices imply that the prior guess for μ_j is $0.01\times \left({\sqrt{a}}_j-{\sqrt{a}}_{j-1}\right)$ and the precision of the prior guess is very low, c = 0.2 (or variability of the prior guess is 5.0). Our choice of the hyperparameters reflects our prior belief, although a very weak one, that the overall rate of superficial tumors is slightly higher than 0.01 per unit time. The selection of such a diffuse prior process allows the conclusion to be driven by the likelihood.

Table 1 presents the results of our data analysis. The posterior estimate of β₂ is 0.0427, indicating a slight increase in risk of drop-out due to cure (positive response). There is not much evidence for the treatment effect on termination time because the 95% credible interval for β₂ contains zero. There is, however, good evidence that thiotepa reduces the rate of superficial tumors as the 95% credible interval of β₁ is (0.538, 2.77). Please note that the posterior standard deviation (0.507) of β₁ is around 10% larger than the standard error of the corresponding estimate of Sun and Wei (2000). But, unlike the previous analysis, the standard deviation of the marginal posterior does take care of the additional uncertainty in the posterior estimate of a parameter due to the presence of the rest of the parameters of the model.

Table 1.

Summary of posterior analysis

Parameter	Mean	SE	95% Credible interval
β1	−1.491	0.507	(−0.538, −2.77)
β2	0.0427	0.229	(−0.401, 0.580)
α	−0.0137	0.0295	(−0.081, 0.037)
η	0.1313	0.0298	(0.0817, 0.1968)
ν	2.192	0.1849	(1.778, 2.546)
λ	0.0006	0.0005	(0.0001, 0.0019)

The posterior mean of α is negative, indicating some evidence of negative association between {N(t)} and T. So, the patients who are more prone to superficial tumors are likely to be terminated later (longer follow-up times). But, the evidence for negative α is not strong as the 95% credible interval for α contains zero. There is also strong evidence that the baseline hazard rate for the termination is increasing over time (that is, ν is positive). The results of our Bayesian analysis are in general agreement with the findings of Sun and Wei (2000).

Model validation:

Model validation diagnostics are very important in Bayesian survival analysis (Sinha and Dey, 1997; Ibrahim et al., 2001). We developed a method for model validation for panel-count data via a Bayesian cross-validated residual called the conditional predictive ordinate (CPO). The cross-validated posterior predictive probability evaluated at the observed data from patient i is given as

$$\begin{gathered} CP{O}_{\left(i\right)}=P\left[N_i=N_{i,obs},T_i=t_i\mid D_{\left(-i\right)}\right] \\ ={\left[E\left\{P{\left(N_i=N_{i,obs},T_i=t_i\mid \theta \right)}^{-1}\mid D\right\}\right]}^{-1}, \end{gathered}$$ (10)

where D_(−i) is the observed data with the patient i removed, θ = (μ, β₁, β₂, η, α, λ, ν) is the set of parameters of the model, and $N_i=\left(N_{i1},\dots ,N_{i{T}_i}\right)$. The final expression of the CPO in (10) follows from a result of Gelfand, Dey, and Chang (1992). This expression actually enables us to use the samples from the posterior p(θ | D) to compute the CPO using the following Monte Carlo integration algorithm:

• Step 1: Simulate from ${\left\{{\theta }_l\right\}}_{l=1}^M$ from p(θ | D) MCMC;

• Step 2: For each θ_l, simulate ${\left\{w_{ib}\right\}}_{b=1}^B$ from p(w_i | θ_l, D) for i = 1, … , n;

• Step 3: For l = 1, … , M, compute P(N_i = N_i,obs, T_i = t_i | θ_l) using $\frac{1}{B}\sum _{b=1}^{B}P\left(N_i=N_{i,obs}\mid \theta ,w_{ib}\right)P\left(T=t_i\mid {\theta }_i,x_i,w_i\right)$;

• Step 4: Finally, compute $CP{O}_{\left(i\right)}\text{=}{\left[\left\{1/M\right\}{\sum }_{i=1}^M\{1/P\left(N_i=N_{i,obs},T_i=t_i\mid {\theta }_l\right)\right]}^{-1}$.

As they are probabilities, the CPOs lie between 0 and 1 and a higher value of the CPO implies a better agreement between the model and the observation. Typically, CPOs are plotted against their covariate values to check whether the CPO values have any relationship with the covariates. Figure 1 presents the plot of the CPO of each subject versus the corresponding termination time. Figure 1 also uses separate symbols for 47 subjects corresponding to the placebo group and the rest corresponding to the treatment group. From this plot, there appears to be neither evidence of any possible outlier nor evidence of a treatment-dependent pattern. The pattern of CPOs does not appear to depend on the termination times. This plot suggests that our model fits the data adequately.

Figure 1.

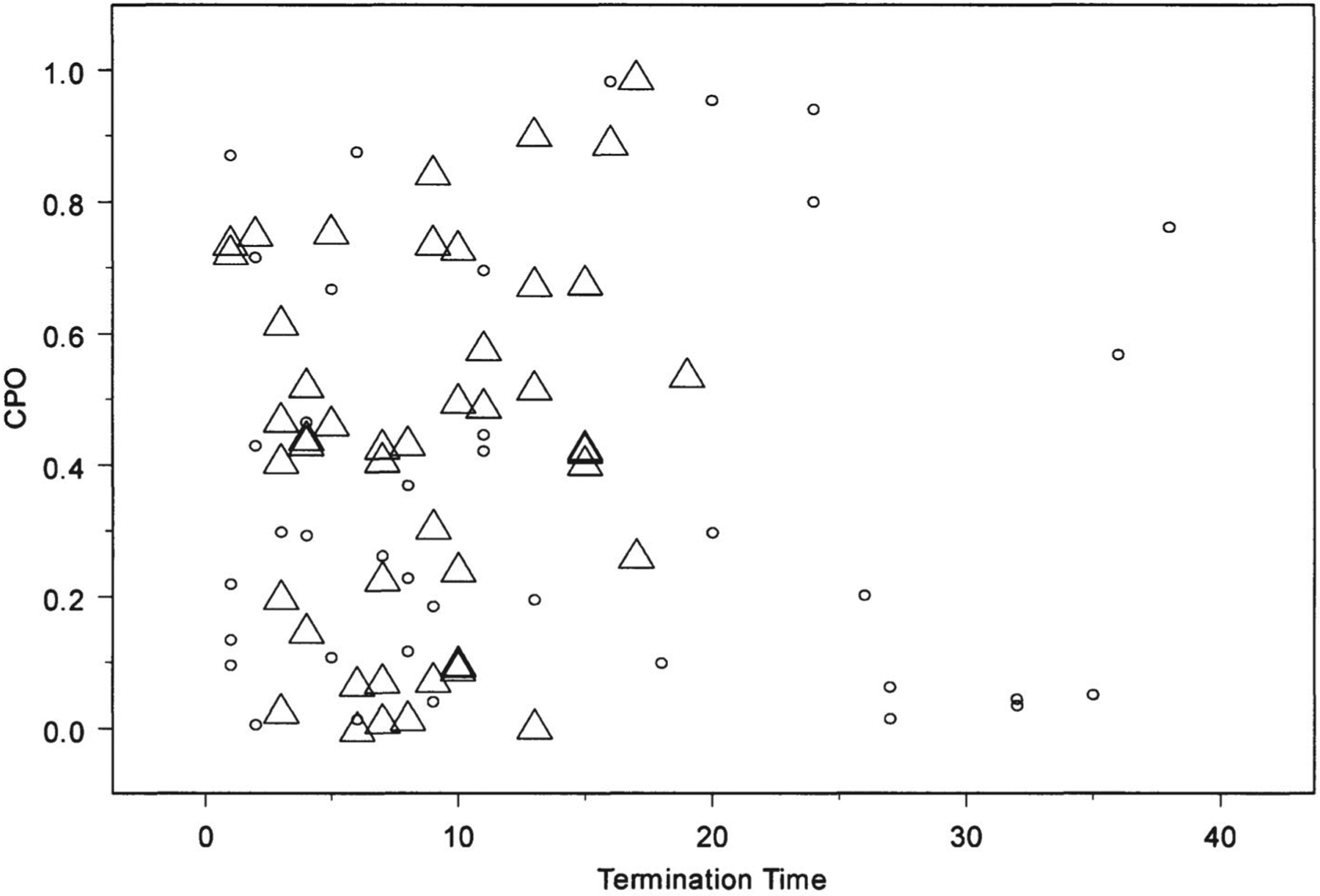
Plot of termination time versus CPO for each patient: ○ for treatment and Δ for placebo.

Prediction:

Please note that one of the major advantages of a Bayesian analysis is that one can compute the predictive distributions of nonfatal events and termination time of a future patient given the values of his/her covariate x. The steps for simulating termination time T and number of events until termination N(T) of a future patient are very similar to the computation of CPO in the last paragraph:

• Step 1: Simulate ${\left\{{\theta }_l\right\}}_{l=1}^M$ from p(θ | D) using MCMC;

• Step 2: For each θ_l, simulate w_l from Ga(w | η_l);

• Step 3: For l = 1, … , M, simulate T_l using $P\left[T_l=a_j|x,w_l,{\theta }_l\right]=1-{\pi }_{jl}^{\text{exp}\left({\beta }_{2l}x\right)w_l}$;

• Step 4: Finally, simulate N(T_l) from Poi{μ_0l(T_l)exp(β_1lx)w_lx}.

These {T₁, N(T₁)}, … , {T_M, N(T_M)} are MCMC samples from the bivariate predictive distribution of {T, N(T)} of a future patient with covariate value x. Now these MCMC samples can be used to compute different quantities (e.g., mean, median, standard deviation, prediction interval, etc.) related to the predictive distributions of T and N(T).

5. Remarks

5.1. Censoring of the Termination

In many data examples encountered in practice, the termination time T_i may be subjected to right-censoring. Typically, the censoring time C_i is assumed independent of T_i and we further assume that risk of C_i does not depend on events history. To allow possible right-censoring, we need a straight-forward modification of L₂ in (6) as

$$\begin{gathered} L_2\left({\beta }_2,\pi ,w\mid D\right) \\ \propto \prod _{i=1}^n{\left[1-{\pi }_{\left(i\right)}^{w_i^{\alpha }\text{exp}\left({\beta }_2{x}_i\right)}\right]}^{{\delta }_i}{\pi }_{\left(i\right)}^{\left(1-{\delta }_i\right)w_i^{\alpha }\text{exp}\left({\beta }_2{x}_i\right)}{S}_{\left(i\right)}^{\text{exp}\left({\beta }_2{x}_i\right)w_i^{\alpha }}, \end{gathered}$$ (11)

where the observed t_i = a_(i) ∈ {a₁, … , a_J} is the minimum of termination time T_i and censoring time C_i, and ${\delta }_i=1_{\left[t_i=T_i\right]}$ is the indicator of censoring of termination for subject i. Our methodology can accommodate this case with this minor modification of the likelihood and without any major modification of the MCMC tool.

A potentially serious censoring problem may arise when T_i is actually continuous, but only observed as interval censored within the grid intervals a₁ < a₂ < ⋯ < a_J. Treating T_i as discrete when T_i is in reality only interval censored may give us biased inference, and the level and direction of bias in the inference are, at this point, unknown.

5.2. Comparison to LI Model

The LI model (Lancaster and Intrator, 1998), developed in the context of modeling the joint distribution of hospitalization rate and death in AIDS patients, assumes that the counting process N(t) (hospitalizations) occurs as a compound Poisson process and each hospitalization has a fixed (but unknown) probability of causing the termination (death). Due to the structure of the LI model, only positive association between rate of N(·) and risk of T is allowed. The assumption of discrete T is not very credible when the termination event is death. In Lancaster and Intrator (1998), T was assumed to be equal to one of a₁, … , a_J. For a patient with T ∈ I_j = (a_j−1, a_j], the increment N_j = N(a_j) – N(a_j−1) is informative about T – a_j–1 (length of interval-censored part of T) and ignoring the difference a_j – T in the likelihood may bias the inference. Neither the LI model nor our model can describe accurately a situation with continuous termination time, as we need to use an approximation where the termination time is interval censored and the number of hospitalizations in the last observation interval can be informative about the exact termination time within the interval. For many data examples including the VACURG data, the termination event is not necessarily a random consequence of a nonfatal event, and there are cases when a history of higher rates of nonfatal events implies an expected delay in the favorable termination event such as the cure or discharge from hospital. The LI cannot accommodate this kind of negative relationship between recurrent events history and risk of termination.

Appendix

Proof of Theorem 1.

The conditional discrete hazard of the termination event given the nonfatal events history $\mathcal{N}\left(a_j\right)$ is given by

$$\begin{gathered} P\left[T=a_j\mid \mathcal{N}\left(a_j\right),x,T>a_{j-1}\right]=\frac{P\left[T=a_j,\mathcal{N}\left(a_j\right)\mid x\right]}{P\left[T>a_{j-1},\mathcal{N}\left(a_j\right)\mid x\right]} \\ =\frac{\int S_{j-1}^{w^{\alpha }\text{exp}\left({\beta }_{2}x\right)}\left[1-{\pi }_j^{w^{\alpha }\text{exp}\left({\beta }_{2}x\right)}\right]w^{N\left(a_j\right)}\text{exp}\left\{-w{\mu }_0\left(a_j\right)e^{{\beta }_{1}x}\right\}g\left(w\mid \eta \right)dw}{\int S_{j-1}^{w^{\alpha }\text{exp}\left({\beta }_{2}x\right)}{w}^{N\left(a_j\right)}\text{exp}\left\{-w{e}^{{\beta }_{1}x}{\mu }_0\left(a_j\right)\right\}g\left(w\mid \eta \right)dw}, \end{gathered}$$

where g(w | η) is the Ga(η, η) density of the frailty w. The above integral expressions are derived from the sampling distribution of $\mathcal{N}\left(a_j\right)$ in (1) and the conditional hazard in (2). The rest of the proof follows from here.

Proof of Theorem 2.

Let us define the vector (N₁, … , N_j)—the vector of number of nonfatal events to a subject in first j intervals. Also, note that N(a_j−1) = N₁ + ⋯ + N_j−1. Then,

$$\begin{gathered} P\left[N_j=m\mid \mathcal{N}\left(a_{j-1}\right),T>a_{j-1},x\right] \\ =\frac{P\left[N_j=m,T>a_{j-1},\mathcal{N}\left(a_{j-1}\right)\mid x\right]}{P[T>a_{j-1},\mathcal{N}\left(a_{j-1}\mid x\right]} \\ \propto {\int }_0^{\infty }P\left[N_j=m,\mathcal{N}\left(a_{j-1}\right)=\left(N_1,\dots ,N_{j-1}\right)\mid w\right]P\left(T>a_{j-1}\mid w\right)g(w\mid \eta )dw \\ \propto {\int }_0^{\infty }{S}_{j-1}^{w^{\alpha }\text{exp}\left({\beta }_{2}x\right)}\frac{w^{N\left(a_{j-1}\right)+m}}{m!}\times \text{exp}\left\{-w{\mu }_0\left(a_j\right)e^{{\beta }_{1}x}\right\}g(w\mid \eta )dw. \end{gathered}$$

Note that the above probability needs to be evaluated only up to the normalizing constant as a function of m. The rest of the proof follows from here.