Abstract
The paper is concerned with the vibration characteristics of the Coronavirus family. There are some 25–100 receptors, commonly called spikes protruding from the envelope shell of the virus. Spikes, resembling the shape of a hot air balloon, may have a total mass similar to the mass of the lipid bi-layer shell. The lipid proteins of the virus are treated as homogeneous elastic material and the problem is formulated as the interaction of thin elastic shell with discrete masses, modeled as short conical cross-sectional beams. The system is subjected to ultrasonic excitation. Using the methods of structural acoustics, it is shown that the scattered pressure is very small and the pressure on the viral shell is simply the incident pressure. The modal analysis is performed for a bare shell, a single spike, and the spike-decorated shell. The predicted vibration frequencies and modes are shown to compare well with the newly derived closed-form solutions for a single spike and existing analytical solutions for thin shells. The fully nonlinear dynamic simulation of the transient response revealed the true character of the complex interaction between local vibration of spikes and global vibration of the multi-degree-of-freedom system. It was shown that harmonic vibration at or below the lowest resonant modes can excite large amplitude vibration of spikes. The associated maximum principal strain in a spike can reach large values in a fraction of a millisecond. Implications for possible tearing off spikes from the shell are discussed. Another important result is that after a finite number of cycles, the shell buckles and collapses, developing internal contacts and folds with large curvatures and strains exceeding 10%. For the geometry and elastic properties of the SARS-CoV-2 virus, these effects are present in the range of frequencies close to the ones used for medical ultrasound diagnostics.
Keywords: Ultrasound excitations, Coronavirus family, Collapse of lipid bi-layer envelope, Resonant and transient vibrations of spikes, Large tensile strains, Disruption of life-cycle of coronaviruses
1. Introduction
Nature has endowed viruses with a beautiful and dangerous feature – the crown. Many enveloped viruses including influenza, HIV, and SARS belong to this family. The crown is composed of densely packed receptors, commonly named spikes. They are not just for decoration. The receptors play an essential role in the reproductive cycle of the virus. They bind with their counterparts of the invaded cell and initiate the mechanism of injecting the deadly genome into the cell.
For decades, the interface between the virus and host cell has become a battlefield of modern science. Tremendous efforts have been made by the medical and biological communities to deactivate the interface by pharmacological means or by boosting the natural immune response, as is the case with the new vaccine. This is not the place to review the enormous literature on this subject. Instead, we will look at the effect of the receptors from the point of view of rigorous laws of continuum mechanics and structural dynamics. In the case of the influenza A virus, the spikes are massive structures protruding through the apparently thin and smooth membrane. The estimated total mass of the spikes in the viral envelope similar to the mass of the bare lipid bi-layer shell itself.
The objective of the reported work is to identify the most probable damage scenario of the family of coronaviruses, subjected to harmonic excitation. In the language of mechanics, the problem is formulated as an interaction of vibration of a thin elastic shell with a large set of attached, but much smaller elastic objects, randomly distributed over the surface. The specific geometry of spikes and the presence of large concentrated masses would render the resonant and transient response of the viral shell different than in the case of the spike-free liposome and justifies the title of the paper.
This paper does not report on any new constitutive models or other advances in theoretical and computational mechanics. On the contrary, it uses simple concepts of the mechanics and physics of solids, which are commensurate with the incomplete knowledge of the geometry and material properties of the viruses. Instead, the paper is contributing to the solution of the most urgent problem facing the nation and the world. In this article, we construct a practical geometrical and computational model of the viral shell decorated with spikes, based on the limited information in the literature. The scattering problem of the shell with the acoustic harmonic wave is solved to determine the spatial and temporal variation of pressures on the surface of the shell. Closed-form solutions are derived for the resonant vibrations of the shell and individual spikes in the realm of continuum mechanics. Then, a numerical simulation is performed on the static and dynamic response. A fully nonlinear simulation of the complex assembly of the viral envelope heavily armed with spikes follows the modal analysis. Finally, the possibility of permanently damaging the shell and/or spikes by a short burst of the ultrasound wave is discussed. The paper poses three questions pertinent to the present pandemic:
-
(i)
Under what condition will the ultrasound pulse excite large-amplitude resonant vibrations of the viral envelope with the crown?
-
(ii)
Can the life cycle of the SARS-CoV-2 virus be disrupted by the ultrasound excitations without damaging healthy cells?
-
(iii)
By what mechanism can the spikes and the viral shell be permanently damaged?
The paper is answering the above questions and building the computational model step-by-step using the tools of modern acoustics, structural mechanics, and dynamics. Neuman et al. (2006) and Beniac et al. (2006) were the first to determine the most probable geometry of the spikes. The relative contribution of lipid bilayer shell and the S-receptors proteins of the influenza virus in the process of static indentation was studied experimentally by Schaap et al. (2012) under the Atomic Force Microscope (AFM). Compared with the bare viral membrane, the spike-decorated virus was found to be twice as stiff, due to membrane-attached spikes. This conclusion was independently confirmed by Li (2012). The Cryo-Electron Tomography (CT) is a powerful tool to scan and visualize the architecture of a virus. In the second half of 2020 alone five papers were published, disclosing various silent features of the SARS-CoV-2 virus, its spikes, and the way it is connected to the envelope shell. Wrapp et al. (2020), Srinivasan et al. (2020), Yao et al. (2020), Ke et al. (2020), and Turoňová et al. (2020) provided a complete 3D models of the virus, now circulating in the media. Low-cycle fatigue in the nanoindentation tests on the SARS-CoV-2 virus was reported by Kiss et al. (2021).
The dynamic responses of liposomes have been extensively studied by the drug delivery industry. Liposomes are tiny man-made smooth spherical vesicles that transport a given drug to the infected cell. There is an enormous literature on this subject accumulated over the past 30 years. Excellent review articles on this subject were published by Schroeder et al. (2009) and Sirsi and Borden (2014). A practical solution to the drug release issue is offered by poromechanics, Ma et al. (2018). The theory of sonoporation uses the concept of ultrasound-induced cavitations and the collapse of micro-bubbles in order to induce opening in the liposome shells. It is interesting that the new vaccine developed by Pfizer is delivered to the body by means of a liposome.
Molecular Dynamics offers many tools to model and visualize the process of the assembly of the viruses. There are several degrees of resolution from the atomic level, through the particle level, all the way to the coarse grain. A critical review of the vast literature on this subject (600+ papers) is available in the recent paper by Marrink et al. (2019) who is also behind the development of the popular Martini model (Arnarez et al., 2015). The images of the virus generated by molecular dynamics were very helpful for choosing the geometry of the virus in Section 2. Hu and Buehler (2020) constructed the multi-degree-of-freedom model of the spike at the scale of molecules connected by tiny springs. Their model predicts a spectrum of vibration modes within the spike itself. They found that the lowest mode is critical for a successful binding with the receptors of the invaded cell.
Parallel to the molecular dynamics, homogenized continuum models of the virus were proposed, based on the information provided by the nanoindentation tests under the Atomic Force Microscope (AFM) (De Pablo, 2020; Klug et al., 2006). This approach goes back to the work of late Tony Evens at UCSB, who introduced the concept of area compressibility and bending stiffness of the viral shell (Evans et al., 1976). Last year, low-cycle fatigue in the nanoindentation tests on the SARS-CoV-2 virus was reported by Kiss et al. (2021). The continuum formulation and molecular dynamics to model the geometry and properties of viruses are two complementary tools rather than competing theories. Each is based on a certain set of assumptions and has its advantages and limitations.
Our team was encouraged by the approach taken by a group of researchers at Caltech led by Ortiz. They predicted by purely analytical and numerical methods a spectral gap between resonant harmonic frequencies of healthy and cancerous cells (Heyden and Ortiz, 2016). Guided by this work, the first successful trial to kill breast, colon, and leukemia cancer cells was announced by the same team, (Mittelstein et al., 2020).
Several challenges were encountered in the course of the present research. The main difficulty has come from a lack of experimental data in the literature on damage and fracture of the envelope and S-spike materials at the scale of continuum mechanics. Buehler and Ackbarow (2007) offer a description of differences in fracture mechanisms at the scale of atoms and molecules, as compared with ductile and brittle fracture of engineering materials. They emphasize the importance of covalent and hydrogen bonds at the atomic level. At the molecular scale, different forces operate. For example, the heads and tails in the lipid bi-layer membrane are held together by the hydrophobic, Van der Waals, electrostatic, and other long- and short-range forces. This is not the avenue that is taken in this article. We have to rely on limited test configurations that can be performed at a scale of 10–100 nanometers. Several assumptions had to be made in lieu of the experimental data. More discussion on this topic is presented in Section 13. It is ironic that much more useful information exists in the literature on critical interaction forces at the atomistic and molecular scale than at the scale of a continuum. Still, several techniques such as the RVE method exists in mechanics to homogenize the discrete molecular models and determine the average elastic properties (Young modulus and Poisson ratio). To the best of our knowledge, this has not been done.
The present paper summarizes the results of the feasibility study and indicates a plan for follow-up research. It is directed to all audiences and is intended to initiate a discussion and collaboration across several disciplines of microbiology, physics, and mechanics. The results obtained are surprising and at the same time very promising.
2. Geometry of the SARS-CoV-2
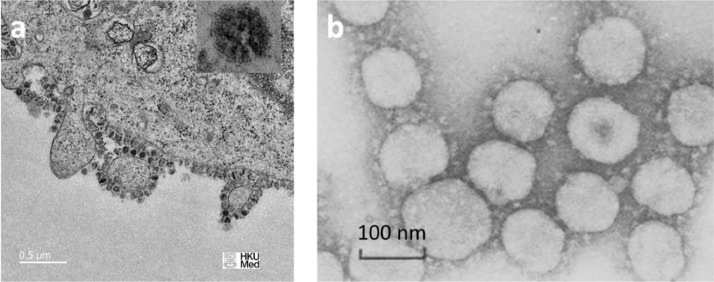
Topology. There is an abundance of photographic coverage of the coronaviruses such as influenza and SARS-CoV-2 on the websites. The photograph of the SARS-CoV-2 during the budding process and the sister TGEV pig virus are shown in Fig. 1. A virus does not make an exact copy of itself in the reproduction cycle. In the coronavirus family, the size, shape, and distribution of the receptors vary considerably across the surface of the virus and from one virus to the other (Neuman et al., 2006). What a virus does extremely well is to copy exactly its RNA genome. It is difficult to determine the size and number of receptors (spikes) on the surface of the virus from the planar 2D, low-resolution photographs. Counting the number of spikes on the periphery of the viral shell of the TGEV virus in Fig. 1 returns the numbers between 12 and 22 with an average of 16. Some assumptions must be made to develop the 3D model of the virus with receptors. There is a vast literature on geometrical modeling of smooth capsid viruses, see for example (Twarock and Luque, 2019). Assuming perfect triangulation on a sphere, the total number of vertices (spikes) on the surface of the virus, can be determined with the help of the Euler formula in topology
| (1) |
where stands for the number of the equilateral triangles on the surface of a sphere. The side length of a triangle can be found from the 2D photos by counting the number of spikes on the circumference, . Then, the area of one triangle times the number of triangles must be equal to the area of the virus . The total number of spikes on the sphere is then found from simple geometrical consideration and Eq. (1).
| (2) |
Fig. 1.
The image of the budding process of the SARS-CoV-2 (source University of Hong Kong) and the family of TGEV viruses (courtesy of Pedro de Pablo). Note, the identical size and a very similar crown of both types of viruses.
Eq. (2) appears to predict correctly the number of spikes on the sphere, even though the spikes are randomly distributed on the surface. For example, taking = 16 for the TGEV virus, the total number of spikes is = 96., in agreement with the value given by Srinivasan et al. (2020). Schaap et al. (2012), and others reported on a similar number for the influenza A virus. Most recently Yao et al. (2020) and independently Ke et al. (2020) reported on a much smaller number of spikes, = 24–25 for the SARS-CoV-2. From the Cryo-EM photos in the above papers, the average number of sparsely distributed spikes on the periphery of the shell is = 8. The Euler formula predicts again correctly the total number if spikes. = 26. In the present computational model, a densely populated virus with 96 spikes is considered because the experimental validation will be performed on the TGEV pig virus.
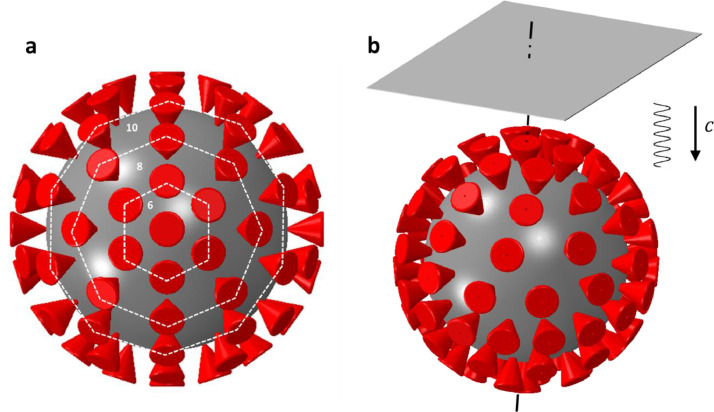
Guided by the above results, the distribution of spikes on the sphere was defined by making several cuts at different parallels and an increasing number of spikes was evenly distributed over the circumference of each of the respective circles. In the present, densely populated virus, the numbers of spikes on the respective cuts are taken to be 1–6–8–10–14–20–14–10–8–6–1, giving a total of 98 spikes, see Fig. 2 . Such a model preserves a rotational symmetry, but perfect triangulation was intentionally not achieved. Spikes are staged at all cross-sections, except the main equator, with an average solid angle of 22.5°.
Fig. 2.
Reconstruction of the 3D model of the spike-decorated Influenza A virus from 2D photographs. Top view (a) and side 3D image. The plane ultrasound harmonic wave is perpendicular to the axis of the sphere joining the North and South Poles.
Spike geometry. Determination of the exact shape of spikes and the way that they are attached to the lipid bilayer and to the M protein below has become one of the main challenges in the course of this research. In most of the existing photos, only a shade of the receptor is seen. Compared with the radius of the virus, the spikes are small but compact structures, resembling a hot air balloon from the side view. It is generally agreed that the spike is composed of three proteins twisted together, giving the appearance of a clove from above. The early photographs published by Beniac et al. (2006) and Neuman et al. (2006) were too crude to serve as prototypes of computational models. A more precise geometry of the SARS-CoV-2 spike is reconstructed based on the image provided by the Cryo-EM photographs and molecular dynamics simulation, shown in Fig. 3 (Wrapp et al., 2020). Still, the shape of the spike, constructed by the molecular dynamic simulation varies across recent literature (Hu and Buehler, 2020; Srinivasan et al., 2020). Very recently Turoňová et al. (2020) presented the most detailed pictures and models of the spike and its connection to the SARS-CoV-2 viral shell. They found that the connecting stalk is composed of three very flexible cables that can be modeled as a three-hinge system of rods. The bending flexibility is then very small allowing the virus to more easily find and connect to the receptors of the infected cell. The present model is representative to the influenza and TGEV virus and is different.
Fig. 3.
Three-dimensional reconstruction of the SARS-CoV-2 virus from Cryo-EM photos. Side view (a, and b) and top view (c). The connection of the spike with the membrane shell is not shown in the original picture. The various dimensions of the spike were scaled up from its known total height H.
The information on the total height of the spike of = 16 nm (160 A), is consistent across the literature. All other dimensions can then scaled-up from the image in Fig. 3. The spike is assumed of the shape of the truncated cone with the radius at the bottom and at the top. The top radius , shown in Fig. 3b is different in the side view and the top view. Taking = 8 nm, the volume of the cone is about 1072 nm3. This is almost three times larger than the volume of the tributary area of each spike on the shell is = 320 nm3. The same radius, estimated from the aerial view is = 5.5 nm, reduces the volume to 506 nm3. These numbers already suggest that spikes will dominate the vibration response of the virus. There is a short cylindrical part of the spike at the bottom, called a stalk in the biomedical literature. The radius of the bottom part will control the bending stiffness of the spike and so its natural vibration frequency. In the present paper, it is assumed that the spike is fixed into the shell. A modified model of SARS-CoV-2 with a fewer number of spikes and the 3-hinge connection at the base will be the subject of the follow-up publication (Nonn and Wierzbicki, 2021)
Mechanical properties. The mechanical properties of viruses, available in the literature are by far incomplete for performing rigorous analysis. The review article by Buehler and Yung (2009), provided a wealth of information on deformation and failure of protein materials in general, with no reference to the spike S-protein. For the purpose of the present paper, we follow the assumption of mainstream research in microbiology that the viral envelope is an elastic continuum. This leaves of course several unanswered questions about the symmetry of elastic properties in tension and compression, viscosity and strain rate sensitivity, multi-axial response, failure or rupture of the spike material, and effect of different properties of the shell and spikes, etc. The state-of-the-art is that Young modulus is determined by matching measured and numerically predicted force-displacement curves in the nanoindentation tests under the Atomic Force Microscope (AFM). An excellent overview of methods and results on the mechanics of viruses can be found in the monograph edited by Mateu (2013) who also contributed several key chapters of the book. In the present paper the specific values of the geometrical and loading parameters, Young modulus and Poisson ratio of the influenza A virus, taken from Schaap et al. (2012) are given in Table 1 ,
Table 1.
Input parameters of the present modal and transient analysis.
| 98 | 16 nm | 50 nm | 2 nm | 8 nm | 4 nm |
| 0.1–1.0. MPa | 1300 g/m3 | 0.45 | 30 or 60 MPa | 30 or 60 MPa |
3. Wave scattering
The plane longitudinal harmonic wave introduces a time variable pressure on the surface of the virus. The total pressure is the sum of the incident pressure and scattered pressure. In general, the pressure field of the plane incident acoustic wave generated by the ultrasound transducer can be written in the separable form in space and time. Due to the spherical symmetry, the pressure is axisymmetric, depending only on the polar angle but not on the azimuth ,
| (3) |
where is the incident pressure amplitude, is time, is the circular frequency measured in rad/s, is the wavenumber, and is the direction of the propagating plane acoustic wave. In the spherical coordinate system . The circular frequency is related to the linear frequency , measured in Hz, . The wavenumber is , where is the sound speed in the medium.
The present analysis starts with the simplest uncoupled model of the smooth rigid sphere. Then, a more complex model will be constructed and discussed. The reference solution of a rigid sphere is important because it is exact and does not depend on the material properties of the virus shell. There are two physical parameters controlling the total pressure acting on the virus, the radius of the sphere and the wave number , which form a single dimensionless parameter , where is the wavelength. The next step in complexity is the consideration of the receptors or spikes on the surface of the virus, still keeping the material as rigid. Viruses, especially the SARS-CoV-2, are highly deformable and the surface pressure generated by the interaction with the incoming wave at the nano-scale is a formidable problem and has not been studied in the literature. Finally, the effect of the elasticity on the scattered pressure will be discussed.
4. Scattering of the rigid shell
For the general body geometry, numerical approaches must be employed to solve for the scatted pressure. One efficient and effective numerical approach is the boundary element method, which has been well developed and widely applied in many problems of structural acoustics (Jensen et al., 2011). In this method, the solution of the boundary-value problem for the unknown scattered pressure field was formulated as boundary integrals in terms of the free-space Green function and pressure and normal pressure gradient on the object surface. On the object surface, the normal pressure gradient is known from the boundary condition while the scattered pressure is unknown. The unknown pressure on the object surface was solved from the boundary integral equation by the use of numerical boundary element discretization. In principle, the application of this numerical method can provide an accurate evaluation of the effect of the spikes in scattering. The input parameters of the problem are the body geometry, the wavenumber , and the amplitude of the ultrasound wave . The output is the spatial and temporal variation of the incident, scattered and total pressure acting on the body.
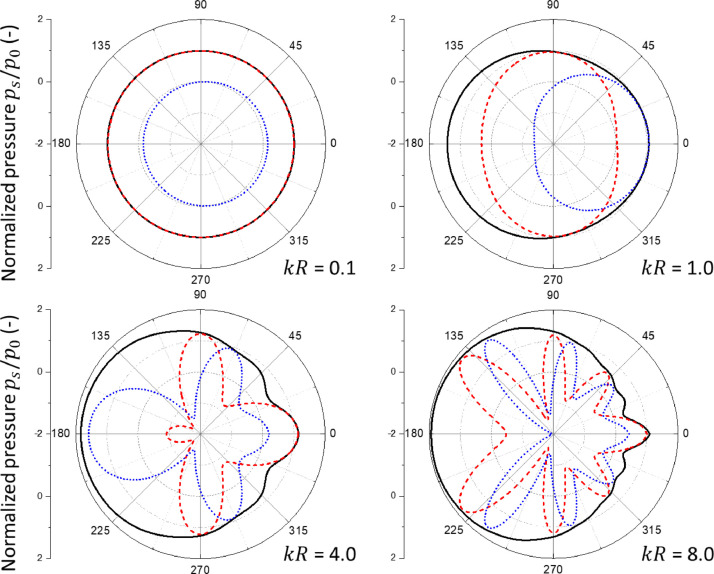
The scattering problem considered in this work is linear. The amplitude of the scattered pressure (t) is linearly proportional to the incident pressure amplitude . In general, the total pressure field consists of the and components, i.e. with and with . In the case of a rigid sphere or spherical shell, an analytic solution of the scattered pressure is known (Morse and Ingard, 1986). A subroutine was developed to determine the total pressure on the shell. As an illustration, Fig. 4 shows the distributions of the incident, scattered, and total pressures on the surface of the rigid sphere for a sample value of = 4. The three curves on each sub-figure respectively represent , , and for the component and , , and for the component. At this value of for which the acoustic wavelength is comparable to sphere's radius , the scattered pressures are comparable to the incident pressures in amplitude. The total pressures over the sphere surface, and , are represented by a small number of Fourie-Legendre functions of , which enable a straightforward determination of the associated pressure excitations for the normal mode vibrations of the deformable spherical object or shell.
Fig. 4.
The distributions of the incident (red dashed line), scattered (blue dotted line), and total (black solid line) pressures over the rigid sphere, plotted as a function of polar angle , for fixed . (a) is for the component while (b) is for the component.
Fig. 5 shows the variation of the component and the component of the total pressure on the surface of the sphere for different values of . In the case of small , the scattering is weak so that the scattered pressure is negligible. The total pressure is dominated by the incident pressure with and . This pressure distribution is effective for exciting the resonant motions of lower normal modes such as the breathing and bouncing modes. In the case of large , both and oscillate with the polar angle on the sphere surface with a phase shift and strong scattering from the front surface of the sphere while weak scattering from the back surface due to the shadowing effect. The resulting pressure distribution is effective in producing resonant motions of relatively higher normal modes of the deformable body. The present solution is valid for both media, the air and water.
Fig. 5.
The pressure distributions of the component (red deashed line) and the component (blue dotted line) as well as the amplitude of the total pressure (black solid line) on the sphere surface due to scattering of plane acoustic waves by the rigid sphere for (a) , (b) , (c) , and (d) 0.
Scattering in water is similar to that in the air since the solution of the scattering problem depends on the single parameter only. Since the sound speed in water is about four times larger than in air, the value of in water is about four times smaller than in air for the same sound frequency. As a result, it may be easier to induce the resonant motions of lower normal modes in water than in air. Another effect is associated with the added mass effect in the motion of normal modes. The added mass in water is significant while it is negligible in the air since the density of water is much larger than that of air (Lamb, 1931). The consideration of the added mass effect in the motion of the deformable body generally lowers the resonant frequency of the normal modes. The correction factor on the natural vibration frequencies of the bare shell is given in Section 11. A similar analysis of the effect of water on the vibration frequency of a single spike is provided in Section 10.
5. Scattering into a deformable elastic shell
In the case of a deformable object, the action of the time-varying pressure, including the scattering effect will excite vibrations of the surface of the object. This will change the Neumann boundary condition for the normal pressure gradient on the object surface. The coupled fluid-solid interaction problem will become quite complicated. The vibration of the object surface radiates sound waves, propagating away from the object, causing acoustic energy dissipation that limits the amplitude of the vibration. The amplitude of induced resonant vibration of a normal mode is generally given by the ratio between the pressure excitation and the acoustic impedance at the associated resonant frequency.
Significant simplifications are obtained in the case of the uniform breathing vibration mode, to be derived in the next section, because the unit normal vector to the spherical surface remains the same. In the case of small values, a simple analytic solution of the acoustic impedance for the breathing (or bouncing) mode is obtained as the radiation of a monopole (or dipole) source (Lamb, 1931).
6. Effect of spikes on the scattering
Determination of the effect of the spikes on the process of scattering and surface pressure generated by the harmonic wave is a very challenging task. The shape of the spike-decorated model is too complicated to perform an exact scattering analysis. Instead, we assessed the scattering effect of a spike by means of two approximate models. Since the size of the individual spike is much smaller compared to the viral shell, the scattering from the spike is negligibly small in the cases with much less than 1. With this model, the incident pressure dominates the total pressure on each spike, and then the resulting pressure on the viral shell is simply the known incident pressure. The second model is to treat the spike as a small rigid sphere that is connected to the viral shell by a thin rod. The scattering of the spike is then approximately represented by the scattering of the small sphere and the pressure acting on the surface of the spike is self-equilibrated and uniform. The solution of the scattering by a sphere is analytically known. In particular, in the case of small values of , the pressure on the sphere is nearly uniform exciting only radial extensions and compressions within the volume of the spike. This type of response is then fully uncoupled from the global vibration of the viral shell. In either case, the spikes make only the second-order effect on the pressure distribution on the surface of the virus. At the same time, spikes dominate the eigenvalue and transient response because of their large mass.
7. Fourier/Legendre expansion of the spatial pressure distribution
In the present formulation, the spatial and temporal distribution of pressure is represented in the multiplicative form. The temporal variation is the same as the incident harmonic wave. The spatial distribution of the pressure, and , depends on the single parameter .
In the case of a sphere, and are given by a summation of the Fourier-Legendre series of the polar angle with the amplitude coefficient decaying rapidly with the order of the Fourier-Legendre function. The first term in the series is independent of , representing a uniform pressure over the body surface. It excites the breathing vibration of the elastic spherical shell. The second term excites the bouncing vibration. In the case of small values of, these two terms are dominant. In the large values of , in addition to these two terms, higher terms also become important, which can excite high normal mode vibrations.
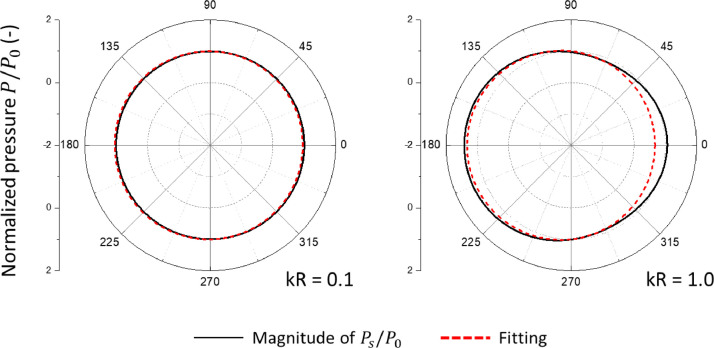
Guided by the above mathematical formulation, a simple analytical fit of the numerical pressure distribution is proposed in the form
| (4) |
where is the total pressure acting on the surface of the shell. The exact numerically determining pressure distribution is shown by a solid black line in Fig. 6 for two values of the parameter . The prediction of the simplified Eq. (4), is denoted by the red line. The pressure given by Eq. (4) is seen to capture the first-order effects with good accuracy for less than or equal to order one. It will be introduced in Section 14 as a forcing term in the transient analysis of vibration
Fig. 6.
The comparison of the exact numerical solution for the total pressure amplitude with a simple analytical fit of Eq. (4) for = 0.1 and = 1.0.
8. Reynolds number, cavitation, and viscosity
It is instructive to check the magnitude of the Reynolds number. For large Reynolds numbers, there is a danger of cavitation. Very small Reynold numbers bring the necessity of considering viscous effects. From the definition, the Reynolds Number , where is the characteristic fluid particle velocity, is the kinematic viscosity of the fluid. The flow velocity is defined from the harmonic vibration. If represents the amplitude of resonant motion of the spherical shell, then , where and being the sound speed. The Renolds number can then be transformed into the form
| (5) |
The associated Womersley number, which is the ratio of transient inertial force to the viscous force can also be calculated. The magnitude of and the associated number for the representative vibration amplitude of = 10 nm are given in Table 2 .
Table 2.
Input values to the calculation of the Reynolds and Womersley numbers.
| Medium | (m/s) | (m2/s) | Womersley number | ||
|---|---|---|---|---|---|
| Water | 0.023 - 0.23 | 1372 | 1.8 × 10−6 | 0.23 - 2.3 | 104 - 103 |
| Air | 0.1 - 1.0 | 343 | 1.5 × 10−5 | 0.1 - 1.0 | 102 - 10 |
The calculated numbers fall within a safe middle range. It can be concluded that the viscous and cavitation effects can be neglected in the estimate of harmonic forces. Since the Reynold number measures the viscous flow effect on the mean force on the shell, it does not affect the assumption in solving the (transient) harmonic motion problem. The above viscous effect should not be confused with the viscoelastic properties of the envelope which brings the issue of damping of resonant vibration. This effect will be considered in the subsequent publication.
9. Resonant vibrations of the smooth shell
Determination of the spectrum of free frequencies of shells of the revolution was the subject of extensive research since the classical treatise of (Lamb, 1882). The spectrum of natural frequencies consists of two infinite sets of modes spaced within a finite frequency interval. The upper-frequency spectrum corresponds to a purely radial motion. The lowest frequency, corresponding to the so-called breathing mode is given by
| (6a) |
When additional degrees of freedom in the form of tangential displacements are allowed, the membrane energy is considerably reduced, giving rise to the lower frequency spectrum. However, the purely inextensional deformation modes can never be achieved within the membrane theory for the spherical shell. The inextensional modes are developed only for structures with zero Gaussian curvature, such as a cylindrical shell. Baker (1961) presented the most general solution of the membrane response in the form
| (6b) |
where is the dimensionless frequency parameter of the vibratory mode of order . Four cases of particular interest are compared in Table 3 .
Table 3.
The frequency parameter in Baker's (1961) solution.
| Mode | [MHz] | ||
|---|---|---|---|
| Breathing mode | 0 | 914 | |
| Rocking mode | 1 | 0 | 0 |
| Bouncing mode | 2 | 0.6 | 343 |
| Asymptotic solution | 1.0 | 572 |
The frequency corresponding to the breathing = 0 mode, involving uniform extension and compression of the shell is 2–4 times higher than all the others. The rocking mode = 1 is the rigid body translation and is not present. The bouncing mode, = 2, and all higher modes do not depend on the Poisson ratio . This is an important result because the exact value of is unknown for the viral lipid bilayer. The dimension of the term is 1/s, so the frequency is in Hz. It should be noted that, except = 0, all frequencies of the lower branch have an asymptotic value. Taking the input parameters gathered in Table 1, the predicted frequencies are shown in the last column of 3. The comparison of the analytical prediction with the FE simulation is presented in Section 11.
10. Stiffness and strain localization in the single spike
A simple beam bending analysis of the spike provides a wealth of information about the mechanics of the cone-like spikes, refer to Fig. 12. The authors were unable to find the solution for the cone-like cantilever in the literature. The solution for the Euler-Bernoulli beam theory is summarized below. The correction for the shear effect (Timoshenko beam) is discussed later. The geometry is fully characterized by the height , the bottom, reference radius the top radius or the ratio of the radii . The moment inertia of a circular cross-section is , where is the current radius. Denote by the reference moment of inertia of a prismatic beam of a constant radius . The spike is loaded by the force at its tip and fully clamped at the bottom. The bending moment equilibrium equation is
| (7) |
where is the transverse deflection of the beam. For the fully clamped beam, both deflections and slopes are zero at the base. In the conical geometry, the radius is a linear function of the x-coordinate,
| (8) |
Fig. 12.
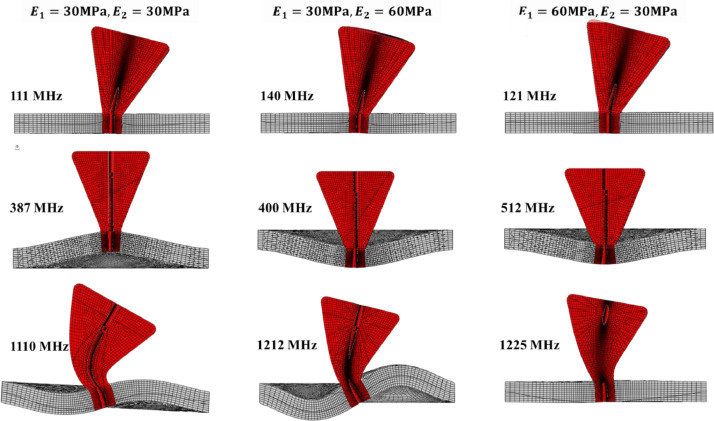
The effect of the elastic properties of the spikes and shell on the mode of vibration. Spikes vibrate around the apparently rigid base at the low frequencies of 111–140 MHz. At the intermediate frequencies of 387–513 MHZ, the spikes move in the radial direction, together with the vibrating shell. Finally, there is a complex interaction between the vibration of the flexible spike and shell at the high end of the frequency spectrum 1110–1225 MHz. Some vibration modes are on different planes.
Care should be taken when solving Eqs. (7) and (8) because of a singularity at = 1. After some cumbersome algebra, the solution of the ordinary differential equation yields the relation between the tip load and deflection , , where the stiffness of the structure is
| (9) |
The subscript 1 indicates the solution for the stiffness of the spike. For a uniform thickness beam, = 1 and Eq. (9) reduces to the classical solution for a cantilever beam. The normalized deflection profile of the axis of the cone, is
| (10) |
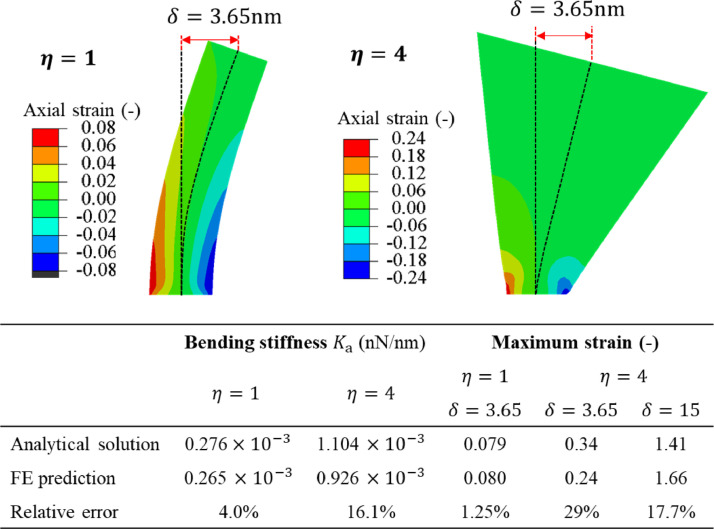
where . The plots of the normalized deflection profiles of the analytical and numerical solutions for the two limiting cases = 1 uniform cross-section) and = 4 (truncated cone) are shown in Fig. 7 . In both cases, the predicted deflected shapes are very close to the numerical results. The present solution proves that deformations are localized in a short region of the length equal approximately to the bottom radius of the spike. The spike responds then mostly as a rotation around a generalized “elastic” hinge.
Fig. 7.
The normalized shapes for the analytical and numerical solutions are almost identical for both cylindrical ( = 1) and, conical ( = 4) beams.
Comparison of the prediction of Eq. (9) with the numerically calculated stiffness is presented in the table in Fig. (8). Two effects might be responsible for the 16% error in the case of = 4. One is the transverse shear and the other one the clamped boundary condition of the spike. The solution of the Timoshenko cone-like beam is too complex to be presented in a closed-form. At the same time, the effect of the boundary condition can be assessed.
The above analysis is valid for the model with large stiffness, inducing flexural vibration of the spike. In the other limiting case, of flexible connection, applicable to the SARS-CoV-2 (Turoňová et al., 2020), the spike will undergo axial tension-compression vibration mode.
The local stiffness of the shell is large compared with the spike bending stiffness but is finite. Consider the tributary area of the spike as a square section of the shell × subjected to a local point bending moment. By disregarding the local curvature, the approximate solution provides the following expression for the local bending stiffness of the shell . For the present geometry, and = , the solution is = 27. The combined bending stiffness of two springs in series can be calculated from
| (11) |
By comparing with it is seen that correction is small and lowers the total bending stiffness by 5%, leaving still an error of 11%. It can be concluded that the error comes mainly from the transverse shear strains not included in the Euler beam theory.
Knowing the beam stiffness and the deflected shape, it is possible to calculate the maximum curvature at the hinge from Eqs. (9) to (10), in terms of the tip deflection
| (12) |
The corresponding maximum strain at the extreme fiber, located at = from the middle axis of the beam is
| (13) |
For example, taking the amplitude of vibration = 3.65 nm from Fig. 8 , the strain will reach 0.35. At the maximum amplitude of vibration, = 15 nm (see Section 13 for explanation), the strain will increase to 1.41. The prediction of Eq. (13) is close but underestimates the values of the FE simulation, shown by the color-coded plots in Fig. 8. The present values should be compared with the fracture strain of the S-protein spike, which is the subject of the future study. In any case, tearing off the spike from the shell at such large tensile strains is a real possibility.
Fig. 8.
The error analysis of the analytical solution for the uniform section beam and the truncated conical beam. Comparison of the analytically predicted stiffness and maximum strains.
11. Natural period of vibration of a single spike
Vibration in the vacuum (or air). Knowing the bending stiffness of the spike, a close-form solution on the natural vibration frequency of the spike can be easily calculated. In the one-degree-of–freedom model, the vibration frequency is
| (14) |
where is the equivalent spring constant, defined by Eq. (11) and is the total mass of the spike For a given , two parameters of the spike, and , are controlling the frequency. The mass of the truncated cone is
| (15) |
The final expression for the frequency is
| (16) |
Taking the reference values of all parameters from Table 2, the closed-form solution predicts the frequency of the spike to be = 123.8 MHz. By replacing the analytically derived stiffness = 1104 nN/nm with the more exact numerically calculated stiffness = 926 nN/nm, the one-degree-of-freedom model predicts the resonant vibration of the spike at 112 MHz, almost identical to the FE value of 110 MHz.
Vibration in water. The shape of a spike is too complicated to attempt an exact solution involving fluid-solid interaction. The concept of the added mass should be used instead. There are several publications on the vibration of the cantilever beam in water that is based on this concept. Of particular interest is the article by Weigert et al. (1996) because it provides an experimental validation on the beams of only 200 micrometers length. The correction factor is given by a simple expression
| (17) |
The above equation was shown by Weigert et al. to reproduce the experimentally determine frequencies in the first eight modes with good accuracy. Assuming that the mass density of the spike is approximately equal to the mass density of water , the correction factor of frequencies becomes = 0.71. Thus, the fundamental frequency of the spike will be reduced from 112 MHz to 79 MHz. This result is further discussed in Section 14.
12. Finite element simulation
The geometry of the viral envelope with spikes is complicated and numerical methods must be used to determine resonant and transient vibration of the system. The lipid bilayer shell with = 12.5 is of intermediate thickness and solid finite elements were used throughout. Two Finite Element models were developed; the full 3D model for the shell with spikes and the 2D axisymmetric model for the smooth shell.
The purpose of the axisymmetric model is to cross-check the accuracy of the numerical and analytical solution. Baker's solution (Baker, 1961) presented in Section 9 was based on the membrane theory for very thin shells. It was necessary to assess the limitations of this theory and for that purpose, five elements were used through the thickness of the shell for both models. Simulations of the full virus with spike were done using a one-eighth 3D model with the appropriate symmetry, in order to reduce computation time. The general-purpose Finite Element code Abaqus/standard was used. Eight-node brick elements with reduced integration (C3D8R) were used across the thickness of the shell, and six-node wedge elements (C3D6) were used for the spikes. There were 9610 elements in one spike; 40,920 elements in the shell; and 159,202 elements in total. The explicit time integration algorithms must satisfy the Courant stability criterion. Abaqus is automatically adjusting the time step to satisfy this criterion. For the smallest size of the finite element of a fraction of the nm and the wave speed of 150 m/s in the virus material, the time step is set up to be 0.0001 ns.
12.1. Natural frequencies for the shell without spikes in the air
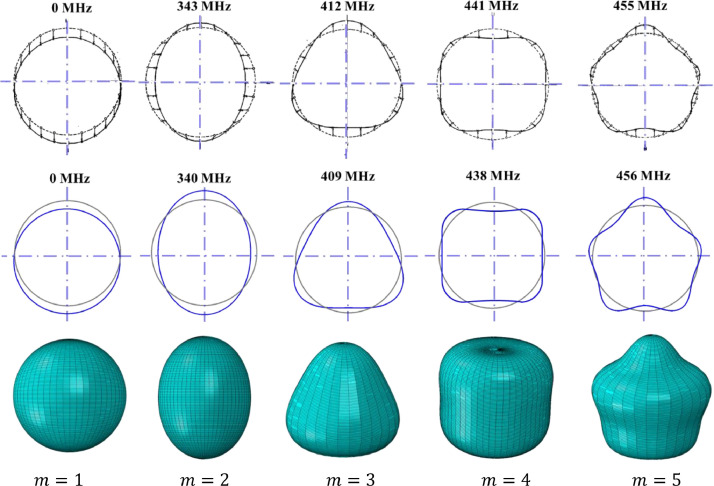
12.1 Natural frequencies for the shell without spikes in the air are presented in Fig. 9 . The eigenmodes and the associated eigenfrequencies in the Baker closed-form solution are depicted in the first row. The second and third rows show the Abaqus numerical results for the cross-sectional shape and the 3D view. The first mode = 1 (first column) is a rigid body rocking motion. It will never be generated under the plane harmonic wave and its frequency is zero. The second mode, = 2 is the so-called bouncing node, sometimes referred to as the wineglass four-node mode. Then, there are higher modes with increasing frequencies. The frequencies predicted by the analytical and numerical solutions are almost identical and this high level of correlation is valid up to the ninth mode. Up to that point, the membrane action dominates the response. For still higher modes the local curvature increases and bending action comes into play. The numerical model with eight elements through the thickness is able to predict both membrane and bending strains. The frequencies continue to increase, as opposed to the Baker solution that predicts the asymptotic value of about 572 MHz. This feature was pointed out by Silbiger (1962) in his discussion of Baker's solution.
Fig. 9.
Comparison of Baker's analytical solution (top row) with the results of the numerical simulation, (bottom rows). Both models were axisymmetric, smooth, and spike-less. A perfect correlation is observed in both mode shapes and natural frequencies.
So, where is the breathing mode? Searching through higher modes, it was found between the 16th and 18th modes, vibrating respectively at frequencies of 895 MHz and 977 MHz, see Fig. 10 . Abaqus detected the purely radial motion at 913 MHz as the 17th mode. In the Baker analysis, the breathing mode belongs to a different branch and vibrates at 923 MHz, for the Poisson ratio of = 0.45. The insert in Fig. 10 illustrates the locally distorted mesh as a combination of local shear and bending strains. These two components, which are absent from the Baker solution, increase substantially the stiffness of the shell and its vibration frequency.
Fig. 10.
The breathing vibration mode is predicted by the numerical analysis. It sits rather strangely in the company of two higher modes, n = 17 and n = 19 dominated by bending and the through-thickness shear. Still, the agreement between the analytical and numerical solutions in terms of vibration frequencies is remarkable.
It is concluded that the breathing mode is important mainly because of its mathematical simplicity. In reality, it must be an unstable mode. A small disturbance in the pure spherical geometry or uniform loading will cause a jump to a different mode. There is here an analogy with buckling of a thin spherical shell, where the pre-buckling uniform compression bifurcates into higher modes with combined bending and membrane action (Hutchinson, 2016).
12.2. Natural frequencies for the shell without spikes in water
Sonstegard (1969) extended Baker's modal analysis in the air to the shells surrounded by water. The problem was solved using the energy method, including both membrane and bending strain terms. By analogy with Baker's analysis, there are two branches. The upper-frequency spectrum is extensional, purely membrane modes. The lower frequency spectrum includes both membrane and bending action and are called composite modes. It was found that the difference between the incompressible and compressible fluid was negligible. Comparison of the frequencies in the air and water was shown in Fig. 3 of the above publication for the first eight frequencies. The reduction factor for the breathing mode = 1 was equal approximately to 0.5. The corresponding reduction in the bouncing mode is only 0.7. Baker expressed his solution in the dimensionless form while Sonstegard presented an example only for a steel shell with an aspect ratio of 20, not the same as the present case of = 12.5.
The concept of the added mass provides a simple approximate method of calculating the effect of water on natural frequencies. The validity of the added mass approach was discussed in Section 8. The ratio of frequencies is, Jensen et al. (2011),
| (18) |
where is the added mass and is the mass of the shell made of the protein material. The added mass in the breathing mode is . The added mass in the bouncing mode is half of it. Taking the present aspect ratio = 12.5, the result of the above estimates is
| (19) |
| (20) |
The above closed-form solution provides comparable estimates to the exact fluid/solid interaction solution by Sonstegard (Sonstegard, 1969). The magnitude of the Reynold numbers, calculate in Section 8 proves that the added mass approach is applicable to the range of frequencies considered in the present paper.
12.3. Vibration analysis of a single spike
A full eigenvalue analysis of the viral shell with spikes reveals a complex interaction of the bending of spikes and vibration of the shell. To better interpret this interaction, the bending stiffness of a single spike and its local vibration must be determined. In the first step the spike with a surrounding square section × of the shell is isolated, in a similar way as in the closed-form solution in the previous section. A horizontal force was applied to the end of the spike and the load-displacement relation was calculated using Abaqus explicit code.
Five different combinations of the elastic modulus of the spike and the shell were considered, defined in Fig. 11 . The default value is = = 30 MPa. The bending stiffness of the spike increase linearly for a range of = 1.5 – 200 MPa, in perfect agreement with the closed-form solution. The numerical simulation confirms the stiffness predicted by the analytical solution. This means that the frequency of vibration of the spike given by the closed-form solution, Eq. (11), 123 MHz should be correct. Indeed, the lowest period of vibration in the numerical analysis of the system returns the value of 111 MHz.
Fig. 11.
Stiffness of the spike, modeled as an inverted truncated cone fixed into the shell. Five different combinations of the elasticity modulus of spike and shell were considered. The numerical simulation confirms that the shell is an order of magnitude stiffer than the cantilever beam.
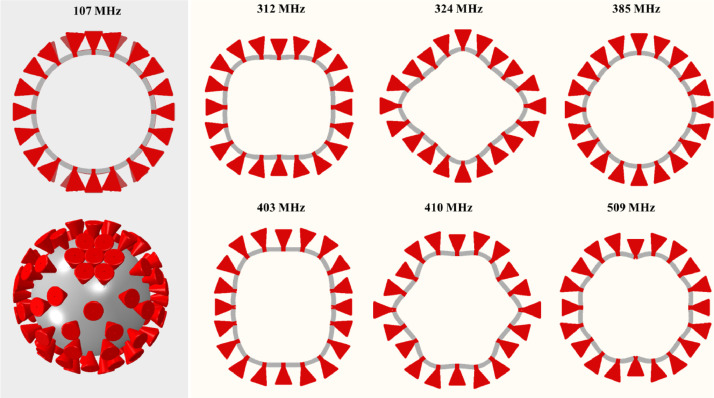
The authors could not find in the literature information on the relative difference between the elastic properties of the bilayer lipid membrane and protein. Therefore, a parametric study of the effect of the elastic properties of spikes and shell was also performed. The numerically predicted natural frequencies of spikes for three ratios in the first three modes are shown in Fig. 12 . In the lowest range of the frequencies (111, 121, and 140 MHz) spikes vibrate around the stationary rigid shell. A strong interaction between the local spike and global shell vibrations are clearly seen for the intermediate range (378, 400, 512 MHz) and higher frequencies (1110, 1212, 1225 MHz). The above close-up images will be helpful in explaining a complex vibration of the spike-infested virus to be discussed in the next sub-section.
12.4. Natural vibration of the shell with spikes
In the last step of the eigenvalue analysis, the first seven vibration modes were selected from the output of the Abaqus code. Several features of the response can be distinguished from Fig. 13 .
-
(i)
At the lowest frequency of 107 MHz, the spikes vibrate around a stationary shell, as evidence by the first column. In the 3D view, six spikes swing back and forth with respect to the North and South Pole spikes (lower left). The next row of spikes vibrates out of phase from the first row. The frequency is very close to the frequency of 111 MHz predicted earlier for a single spike.
-
(ii)
There is a large spectral gap between the lowest vibration frequency and all higher six frequencies, starting at 312 MHz.
-
(iii)
The mode shapes of the virus with spikes differ from the spike-less virus, described in previous sections due to a large mass of spikes. Still, there is a similarity of the second-lowest mode with the bouncing mode in Fig. 9.
-
(iv)
There is a complex interaction between local spike vibration and global vibration of the shell.
Fig. 13.
The first seven vibration modes and the associated frequencies of the full model of the virus with spikes. The large inertia of spikes changes the mode of vibration as compared with the smooth shell in Fig. 7. The spike can move radially or swing to the left and right.
The results of the eigenfrequency analysis of the virus with spikes prove that the spikes will swing around the neutral position at several well-defined frequencies.
13. Transient response at resonance
Input and output parameters. This section is built on the results of all previous results of the paper and demonstrates the growth of the vibration amplitude of the harmonic ultrasound excitation at or around resonant frequencies. The shell-spikes system is subjected to the pressure varying in space and time, according to Eq. (4). In both cases, the pressure acting on the virus shell will excite the breathing as well as the bouncing modes. The presence of spikes will disturb this nice symmetry and will generate all modes with different amplitudes.
In the forcing term, given by Eq. (4), both the temporal and spatial variation of pressure depends on the imposed circular frequency or liner frequency . The parameter is defined as , where is the wave speed in the air, = 343 m/s and is the wavelength. The simulation will be done for three values of resonant frequencies, for a virus suspended in the air. The fourth case = 0 corresponds to uniform pressure. The input to loading for the numerical analysis is summarized in Table 4 .
Table 4.
Spatial and temporal variation of the pressure on the surface of the shell.
| 0 | |||
| = 110 MHz | = 691 × 106 | 0.1 | |
| = 340 MHz | = 2136 × 106 | 0.311 | |
| = 910 MHz | = 5718 × 106 | 0.866 |
The pressure is applied to the surface of the shell as well as the top surface of the truncated cone spikes. The pressure on the lateral surface of spikes is self-equilibrated and does not contribute to the deformation of the system. The maximum intensity of the harmonic wave is taken to be 1.0 MPa in all calculations.
The objective of this section is to provide both a qualitative analysis of the complex interaction of different vibration modes of the shell and coupling of the local spike vibrations and the global vibration of the shell. Zero displacement and velocities were taken as initial conditions.
The value of all ten input parameters on the geometry, material, and loading were given in Table 1, Section 2.
The output of the numerical simulation is the vertical displacement at the base of the spike and horizontal displacement at the top of the spike. In particular, the amplitude of the shell vibration at the North (and South) Poles is plotted. The 3D view is also shown in some cases. The default values of input parameters are , , = 110 MHz and = . In order to reduce the number of combinations, the effect of and is discussed first.
14. Results of transient vibrations
Effect of water. The solution of the transient vibrations of the viral envelope with spikes in water formulated as the fluid/solid interaction will be too complicated to attempt. It was shown that resonant frequencies of individual spikes (Section 11.1) and the spike-free or “bold” shell (Section 11.2) in water are reduced by approximately 50%. The added mass approach for the modal analysis can be extended to get an approximate solution for transient problems. The magnitude of the inertia force to move the column of water around the shell is equivalent to increasing the mass density of the shell or decrease the Young modulus. To reduce the vibration frequency by a factor of two, as predicted by Eqs. (16)–(20), the mass density should be increased four times. Alternatively, the Young modulus could be reduced by the same amount. The analysis of the effect of Young's modulus ratio on transient vibration, shown in Fig. 14 confirms that qualitatively, the response is similar to the shell in the air but shifted in time. Lowering frequencies will bring analysis closer to the safe range in ultrasound diagnostics, as discussed in the next sections.
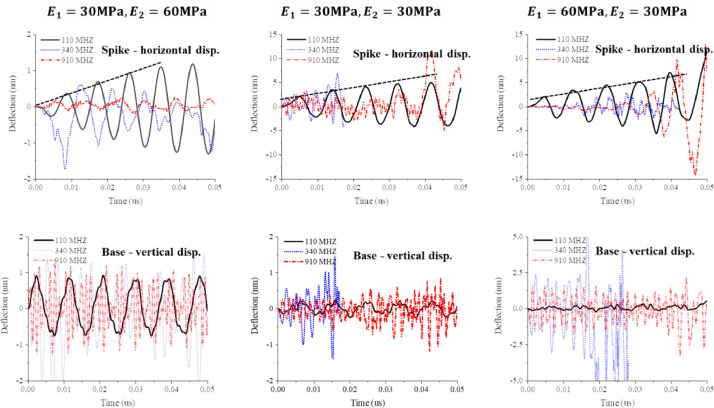
Fig. 14.
Illustration of the initial liner growth of the horizontal and vertical vibration amplitudes. Note, that the scale of the first plot in the first row is different from the remaining two plots. The large initial effect of the ratio disappears for later time.
Effect of the wavenumber. The wavenumber or the dimensionless parameter , controls the spatial distribution of pressure. It was shown in the previous section that for small values of less than 1.0, the scattered pressure is very small and can be neglected. For the viral shell, is always smaller than unity both in the air and water. Transient simulations run at = 0, 0.01, 0.1 and, 1.0 yield almost identical results. At = 0 the pressure is uniformly distributed over the surface. Small imperfections are needed to facilitate the initiation of the second, bouncing vibration mode and eventual transition to the dynamic buckling. There are two types of imperfections. Large structural imperfections to the uniform thickness shell are introduced by the concentrated masses of spikes. The non-uniformity in the pressure loading, however small it might be acts as initial loading imperfections. In this respect, Eq. (3) should be used for the input forcing term, even for smaller values of .
Effect of the ratio. It was shown in Sections 9 and 10 that the stiffness and natural frequency of a single spike depend on the relative values of Yong modulus and mass densities of the spike and membrane proteins. Simulations were performed at three values of = 0.5, 1.0, and 2.0. The ratio is controlling the interaction between the spikes and the shell. The growth of the maximum displacement of the spike in time for three values and three resonant frequencies is shown in Fig. 14. The initial growth under the resonant frequency of spike of 110 MHz is linear, and the growth rate, measured by the slope of the straight-line fit, is inversely proportional to the frequencies, as predicted by Heyden and Ortiz (2016).
At the beginning of the vibration process, the horizontal swinging of the top of spikes is almost an order of magnitude larger than vertical displacement at the spike/shell interface, shown in the second row. Numerical simulation was run up to 0.05 µs, or 50 ns. For an undamped system, the amplitude will grow to infinity at a resonant frequency. Each column in Fig. 14 corresponds to a different ratio of elastic moduli. Large horizontal amplitudes are reached at any of the three resonant frequencies, an indication of a strong and complex coupling of the local spike vibration and global shell vibration.
The 3D visualization of the vibration modes is presented in Fig. 15 for one-quarter of the shell. One can clearly see the process of swinging spikes which appear to be random and out of phase. The spike touches the shell, developing a new self-contact point or contact line. The red color at the bottom of the most severely deformed spikes denotes the magnitude of the principal (tensile) strain, ε = 1.66. The maximum horizontal amplitude of a spike is = 15 nm. According to Eq. (7), the analytically predicted strain is ε = 1.41 giving the error of 15%. This reasonably good correlation is building confidence in the engineering accuracy of the analytical solution.
Fig. 15.
Numerical study on the effect of resonant frequencies and the ratio of elastic properties on the vibration amplitudes of the shell and spike. The arrows indicate the location of maximum bending strains.
It can be concluded that at later times the response becomes independent of . Therefore, all other simulations in this section were done for the default value = = 30 MPa. It should be noted that the effect of includes indirectly a possible difference in mass densities between the spike protein and the lipid bi-layer envelope. Strictly speaking, the resonant frequency depends on the ratio .
Effect of pressure amplitude. The parametric study is then reduced to the effect pressure and frequency , because of their relation to the application of ultrasound transducers used for medical imaging. Those two parameters are strongly inter-related which makes the analysis interesting but difficult to present in a clear way.
According to O'Brien (2007), the range of the intensity generated by the present generation of transducers is W/cm2. This corresponds to the range of pressure = 0.1–5MPa. For the resonant vibration, low magnitude of pressure amplitude will delay but not prevent reaching large amplitudes for the undamped system. Increasing vibration amplitude at the North and South Pole will eventually lead to a global buckling and collapse. As a reference, we took the critical buckling pressure of a perfect thin spherical shell loaded quasi-statically (Hutchinson, 2017),
| (21) |
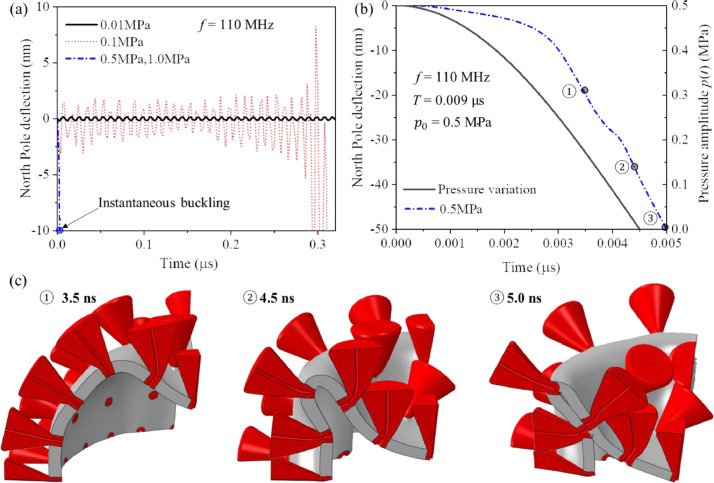
For the present geometry and elastic properties, (refer to Table 3), the critical buckling pressure is = 0.25MPa. At that pressure, the uniformly compressed shell buckles into the dimple-like shape. Under a quasi-static loading, the shell should not buckle at 0.1 MPa. But it does under harmonic excitation, in accord with the Lyapunov concept of dynamic buckling, involving the growth of amplitude in the presence of imperfections.
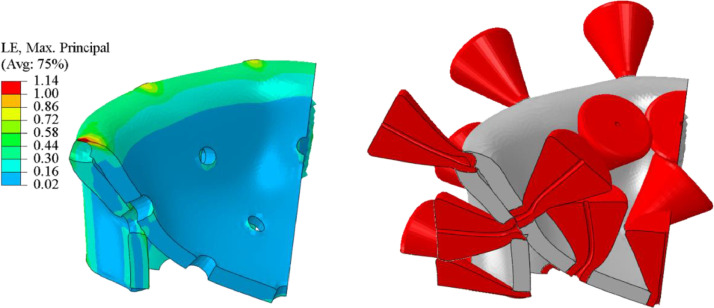
Numerical simulation was run at four values of the pressure, = 0.01, 0.1, 0.5, and 1.0 MPa. The growth of the North Pole amplitude of the shell is shown in Fig. 16 a. Under the lowest values of the pressure 0.01 MPa, the amplitude is constant in the considered time interval = 0.3 µs. The response changes at the pressure amplitude equal to 0.1 MPa giving rise to the growth of the amplitude of the bouncing mode that culminates with buckling and total collapse at = 0.31 µs, Fig. 16a. At the higher pressures of 0.5 MPa, the shell buckled almost instantaneously, shown as a blue curve in Fig. 16b. The snapshots of the deforming shell at 3.5 ns, 4.5 ns, and 5.0 ns are shown in Fig. 16c for the quarter model. The period of vibration at the frequency of 110 MHz is = 9 ns. It is interesting to compare the response with the time variation of the forcing term, depicted in Fig 16b by a solid black line. So, the collapse occurs during the half of the first cycle vibration. The shell is collapsing and crumpling until internal contact is established to reach the next equilibrium state, (Hutchinson and Thompson, 2017). To further reinforce the present conclusion, the cross-sectional view of the damaged shell is shown in Fig. 17 . The color-coded profile of the maximum principal strain (on the left) has an average of 0.75 with one point exhibiting the strain of 1.14. The spikes were removed for clarity. On the 3D view and the cross-section section view (right figure), one can see large deflections of spikes, some of them touching the deformed shell.
Fig. 16.
The plot of the North Pole deflection amplitude versus time for four pressures, (a). Deflection versus time curve for 0.5 MPa pressure (b). Deformation sequence under 0.5 MPa pressure at the extended time scale of the initial 0.005 µs, (c). The numerical simulation stops when the dimple amplitude caused internal contacts, giving rise to large tensile strain at the high-curvature crease.
Fig. 17.
The 3D view and the maximum principal strains in the collapsed viral shell. Spikes were removed from the color-coded plot for clarity.
The above scenario might be modified because the viral shell is not empty. The average mass density of the interior is however much smaller than that of the lipid bi-layer shell. The internal pressure caused by the “implosion” of the viral shell may in fact help to eject the deadly RNA to the surrounding.
Effect of harmonic frequency. The modal analysis in Section 9 has identified three reference vibration modes. A single pike vibrates with respect to the stationary shell at 110 MHz. The resonant vibration of spikes in the entire shell is 107 MHz, refer to Fig. 13. The resonant frequencies of the spike-free shell in the bouncing mode is 340 MHz and in the shell, with spikes, it reduces to 312 MHz. Transient simulations were performed at these three distinct frequencies, in the time interval 1- 0.05 µs and the results are shown in Fig. 14. Any of these frequencies are inducing all vibration modes, consistent with what we know about coupling effects in two-degree-of-freedom and multi-degree-of-freedom systems. The amplitude is initially increasing linearly and the rate of growth is inversely proportional to the frequency, as predicted by Heyden and Ortiz (2016). The maximum deflections of 15 nm are reached very early, within 0.05 ms. The base of the spikes moves vertically 1 nm around the neutral position in the initial 0.05 µs time interval but eventually grow much bigger if the simulation is carried out three times longer. Abaqus simulations always stopped automatically when the “excessive” distortion of an element was detected.
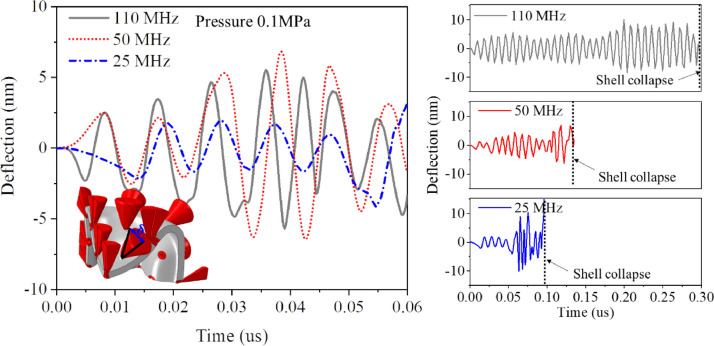
To bring the present analysis closer to practical applications, simulations were run at = 110 MHz, = 50 MHz and = 25 MHz. The comparison of the spike amplitude versus time at these three frequencies is shown in Fig. 18 . In all three cases, the amplitude reaches high and comparable values.
Fig. 18.
Evolution of the lateral deflections of spikes for three harmonic frequencies. Initial growth is shown on the left. Simulation at a longer time until buckling, right. The deflections were plotted for the spike marked with a blue triangle.
The most interesting result is shown on the right of Fig. 18. Here, the simulation was run until Abaqus terminates due to excessive deformation at the collapse of one or several finite elements. This happens at 0.35 µs for 110 MHz, at 0.13 µs for 50 MHz, and at 0.1 µs for 25 MHz. Such an order is counter-intuitive. The present results demonstrate that large, potentially damaging vibration of spikes, as well as the collapse of the viral shell, are present at frequencies and powers, routinely used in medical imaging diagnostics.
15. Implication for the life cycle of the coronavirus
Ultrasound is known to cause shattering of wineglass at about 620 Hz, Skeldon et al. (1998) and Prikhodko et al. (2011) breaking of kidney stones, and opening the lipid shell of liposome for drug delivery. Can the application of the same technique disrupt the reproductive cycle of SARS CoV-2? At this stage of research, it is still premature to say definitely yes.
Damage of spikes or viral shell? There are two competing mechanisms in transient vibration of the lipid membrane with a crown: large amplitude flexural (or axial) vibrations of individual spikes and buckling and collapse of the entire shell. In either case, large tensile strains are developed, potentially resulting in the formation of cracks and rupture. The release of RNA from the viral envelope could then disrupt the life cycle of a virus. The results of the parametric study, summarized in Figs. 14 and 18 proved that strains are localized in the high curvature zones of the local buckles and folds, reaching 10%. At the same time, the spikes vibrate at an ever-increasing amplitude. At the maximum amplitude of 15 nm, the tensile strain at the base of the spile can get as high as 1.66. Both mechanisms could be equally damaging to the virus. The similarity of the quasi-static and dynamic dimple formation, discussed extensively by Hutchinson (2016) and Hutchinson and Thompson (2017) was demonstrated. These results bring us to the most important conclusion of the paper:
Large, potentially damaging deformation of the viral shell with spikes can be achieved at the frequencies and powers routinely used in ultrasound imaging and diagnostics.
Our findings effectively eliminate safety concerns of applying ultrasound vibration at frequencies of 1–50 MHz to or around humans. Additionally, it was shown that large vibration amplitudes and strains are generated under the relatively small value of pressure = 0.1 MPa.
The authors were unable to find consistent information in the literature on the critical fracture properties of glycoprotein spike material, treated as a continuum. Several authors provided estimates on the indentation depth of the envelope at failure under AFM tests but not the fracture strain (Klug et al., 2006). Luque (2011) estimated the fracture strain of the capsid viral shell to be 0.05. The spike S-protein is also lipid-made and must have its limit on elongation. In any case, the strains in the viral shell and spikes may by far exceed these values. In the absence of any fracture theory of the lipid and protein material and the relevant experimental data, a quantitative fracture analysis was not carried any further in the present study. Still, the possibility of disrupting the reproduction cycle of coronaviruses is clearly laid out.
Another important piece of information is that the amplitude of resonant vibration reaches large values within only 0.3 microseconds under a broad range of frequencies. It will thus be possible to program the pulse generated by the transducers of the harmonic waves, to sweep over a broader range of frequencies in a fraction of a second. This finding will remove one of the shortcomings of the present state-of-the-art where the geometry and material properties are not precisely known.
16. Conclusions and outlook
An attempt is made in this paper to formulate the response of the virus to the ultrasound excitations as a problem is mechanics and dynamics. It is the small size of the viral envelope and even smaller dimensions of a spike that makes the formulation and solution difficult but at the same time interesting. The general procedure applies to both the virus suspended in the air or floating in body fluids and the effect of water was shown to substantially lower the frequency spectrum. Spikes with their large masses act as randomly distributed seeds for the process of buckling and total collapse of the viral shell.
It was shown that the pressure distribution on the viral shell depends on a single parameter and, is dominated by the first two terms in the Taylor-Legendre series expansions. Higher components are also present, especially for large frequencies. A great deal of effort was devoted to the determination of natural vibration modes and frequencies, using both analytical and numerical methods. The availability of closed-form solutions is important due to uncertainties in the geometry and mechanical properties of the viral material. In this way, the effect of elastic parameters, mass densities, spike geometry, etc. can be readily assessed. The eigenvalue analysis confirmed the existence of three distinct resonant frequencies of 111 MHz for the individual spike, and 340 MHz for the bouncing mode, and 910 MHz for the breathing modes of the spike-free shell.
The fully nonlinear simulation of the forced vibration revealed the true character of the viral response to harmonic waves. Even though the system consisted of a hundred-degrees-of-freedom (98 spikes), a general pattern emerges. First, harmonic excitation of the system at any of the three distinct natural frequencies induced coupled vibrations of both shell and the spikes. Secondly, large amplitudes are reached at a fraction of a microsecond as initial imperfection grows in time. The amplitude of the bouncing mode increases, leading to the buckling and collapse of the viral shell. The analysis of the color-coder strain fields proved the development of large tensile strains under low frequencies, spanning a safe range of 25–50 MHz. This conclusion is valid for the set of input parameters defining vibration in the air-suspended viral shell. According to the analysis in Sections 10 and 11, natural frequencies of the vibration of the viral shell in water (body fluids) are 50% smaller.
Before moving into preventive or therapeutic applications, the validation study must be performed. The present research has identified two ways of reaching this goal. One will be to provide more precise information on the input of the finite element simulation. Research should focus on the effect of damping on the amplitude of resonant vibration in order to calculate more precisely the needed power of the ultrasound pulse and pressure amplitude. The analysis of the vibration of the viscoelastic structure will be straightforward but was not performed yet.
A critical step will be to develop the fracture theory of the lipid bi-layer shell and spike material. It will then be relatively easy to predict the failure sequence of spikes. A possible sequence of events is that a crack would first initiate at the bottom of the spike and propagate until the spike is teared-off. Alternatively, the shell itself could rupture first. The general-purpose FE codes have reached a high degree of accuracy and in many fields of engineering and design are replacing physical testing. The task of providing improved mechanical properties of the viral envelope with spikes rests on the shoulders of experimental microbiology. That also includes measuring the more exact geometry of the spike-membrane interface.
Our team decided to take a more direct approach to validate the present prediction. Now, it is feasible to conduct ex Vitro experiments with frequencies (range: 1–50 MHz), ultrasonic pressures ( range: 0.1–5 MPa; corresponding intensity range: 0.3–800 W/cm2) and pulse durations (typically 1 µs which is greater than shell collapse times in Fig. 18) generated by laboratory-based ultrasound equipment available commercially (O'Brien, 2020). We have teamed up with the experimental lab of Professor Pedro de Pablo of the Universitat Autonoma de Madrid (De Pablo, 2020). Ex Vitro tests on the TGEV pig virus (inactive to humans) are being planned to see under what combination of ultrasound parameters and exposure times, damage to the virus will be detected under the Atomic Force Microscope.
Considering the enormous attempts of the scientific community around the globe to develop new weapons for the fight against the present pandemic, our results should be looked at from a proper perspective. The acquired immunity provided by the vaccine recently developed by Pfizer and Moderna would be an ideal solution to fight SARS-CoV-02. But it would be just temporary because the emergence of new mutations or strains would require the development of new vaccines, as occurs seasonably with the influenza virus, with an investment of time of one year. In this paper, we presented a new concept of using ultrasound and mechanical resonance to target SARS-CoV-2 and other enveloped viruses that do not have this time limitation. Currently, we have only outlined the promising first step of this ambitious project that would require more profound interdisciplinary research.
Author contributions
Conceptualization: T.W.; Formal analysis: T.W.; Investigation: T.W., W.L., and Y.L.; Methodology: T.W.; Model development: W.L.; Visualization: W.L. and J.Z.; Writing - original draft: T.W.; Writing - review & editing: all co-authors.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
The leading author (T.W.) would like to express his deep gratitude to his co-workers at MIT for using their private time over the past six months for conducting together with the present study. Thanks are due to Ian Schapp and Tony Luque for many helpful discussions on the properties of the coronavirus. The comments received from William D. O'Brien on the availability of commercial ultrasound equipment to conduct the validation study is greatly appreciated.
References
- Arnarez C., Uusitalo J.J., Masman M.F., Ingólfsson H.I., de Jong D.H., Melo M.N., Periole X., de Vries A.H., Marrink S.J. Dry Martini, a coarse-grained force field for lipid membrane simulations with implicit solvent. J. Chem. Theory Comput. 2015;11:260–275. doi: 10.1021/ct500477k. [DOI] [PubMed] [Google Scholar]
- Baker W.E. Axisymmetric modes of vibration of thin spherical shell. J. Acoust. Soc. Am. 1961;33:1749–1758. doi: 10.1121/1.1908562. [DOI] [Google Scholar]
- Beniac D.R., Andonov A., Grudeski E., Booth T.F. Architecture of the SARS coronavirus prefusion spike. Nat. Struct. Mol. Biol. 2006;13:751–752. doi: 10.1038/nsmb1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buehler M.J., Ackbarow T. Fracture mechanics of protein materials. Mater. Today. 2007;10:46–58. doi: 10.1016/S1369-7021(07)70208-0. [DOI] [Google Scholar]
- Buehler M.J., Yung Y.C. Deformation and failure of protein materials in physiologically extreme conditions and disease. Nat. Mater. 2009;8:175–188. doi: 10.1038/nmat2387. [DOI] [PubMed] [Google Scholar]
- De Pablo P.J., 2020. Private communication.
- Evans E.A., Waugh R., Melnik L. Elastic area compressibility modulus of red cell membrane. Biophys. J. 1976;16:585–595. doi: 10.1016/S0006-3495(76)85713-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyden S., Ortiz M. Oncotripsy: targeting cancer cells selectively via resonant harmonic excitation. J. Mech. Phys. Solids. 2016;92:164–175. doi: 10.1016/j.jmps.2016.04.016. [DOI] [Google Scholar]
- Hu Y., Buehler M.J. Comparative analysis of nanomechanical features of coronavirus spike proteins and correlation with lethality and infection rate. Matter. 2020:1–11. doi: 10.1016/j.matt.2020.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchinson Imperfections and energy barriers in shell buckling John. Int. J. Solids Struct. 2017:1–27. doi: 10.1016/j.ijsolstr.2018.01.030. [DOI] [Google Scholar]
- Hutchinson J.W. Buckling of spherical shells revisited. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016;472 doi: 10.1098/rspa.2016.0577. [DOI] [Google Scholar]
- Hutchinson J.W., Thompson J.M.T. Nonlinear buckling interaction for spherical shells subject to pressure and probing forces. J. Appl. Mech. Trans. ASME. 2017;84 doi: 10.1115/1.4036355. [DOI] [Google Scholar]
- Marrink J., Corradi V., Souza C.T., Ingólfsson I., Tieleman P., Sansom S.P. Computational modeling of realistic cell membranes. Chem. Rev. 2019;119:6184–6226. doi: 10.1021/acs.chemrev.8b00460. S.P.H.D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen F.B., Kuperman W.A., Porter M.B., Schmidt H. Springer Science & Business Media; 2011. Computational Ocean Acoustics. [Google Scholar]
- Ke Z., Oton J., Qu K., Cortese M., Zila V., McKeane L., Nakane T., Zivanov J., Neufeldt C.J., Cerikan B., Lu J.M., Peukes J., Xiong X., Kräusslich H.G., Scheres S.H.W., Bartenschlager R., Briggs J.A.G. Structures and distributions of SARS-CoV-2 spike proteins on intact virions. Nature. 2020;588:498–502. doi: 10.1038/s41586-020-2665-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss B., Kis Z., Pályi B., Kellermayer M.S.Z. Topography, spike dynamics, and nanomechanics of individual native SARS-CoV-2 virions. Nano Lett. 2021 doi: 10.1021/acs.nanolett.0c04465. acs.nanolett.0c04465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klug W.S., Bruinsma R.F., Michel J.-.P., Knobler C.M., Ivanovska I.L., Schmidt C.F., Wuite G.J.L. Failure of viral shells. Phys. Rev. Lett. 2006;97 doi: 10.1103/PhysRevLett.97.228101. [DOI] [PubMed] [Google Scholar]
- Lamb H. Edward Arnold; 1931. The Dynamical Theory of Sound. [Google Scholar]
- Lamb H. On the vibrations of a spherical shell. Proc. Lond. Math. Soc. 1882;s1-14:50–56. doi: 10.1112/plms/s1-14.1.50. [DOI] [Google Scholar]
- Li S. Georg-August-Universität Göttingen; 2012. Atomic Force Microscopy Study on the Mechanics of Influenza Viruses and Liposomes. [Google Scholar]
- Luque A. Universitat de Barcelona; 2011. Structure, Mechanical properties, and Self-Assembly of Viral Capsids. [Google Scholar]
- Ma J., Hsiao C.-.T., Chahine G.L. Numerical study of acoustically driven bubble cloud dynamics near a rigid wall. Ultrason. Sonochem. 2018;40:944–954. doi: 10.1016/J.ULTSONCH.2017.08.033. [DOI] [PubMed] [Google Scholar]
- Mateu M.G. Springer Netherlands; Dordrecht: 2013. Structure and Physics of Viruses, Subcellular Biochemistry. [DOI] [Google Scholar]
- Mittelstein D.R., Ye J., Schibber E.F., Roychoudhury A., Martinez L.T., Fekrazad M.H., Ortiz M., Lee P.P., Shapiro M.G., Gharib M. Selective ablation of cancer cells with low intensity pulsed ultrasound. Appl. Phys. Lett. 2020;116 doi: 10.1063/1.5128627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morse P.M., Ingard K.U. Princeton University Press; 1986. Theoretical Acoustics. [Google Scholar]
- Neuman B.W., Adair B.D., Yoshioka C., Quispe J.D., Orca G., Kuhn P., Milligan R.A., Yeager M., Buchmeier M.J. Supramolecular architecture of severe acute respiratory syndrome coronavirus revealed by electron cryomicroscopy. J. Virol. 2006;80:7918–7928. doi: 10.1128/JVI.00645-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nonn A., Wierzbicki T. A feasibility study on tearing off spikes and rupturing the SARS-CoV-2 viral shell by an ultrasound pulse. Extrem. Mech. Lett. 2021 to be submitted to. 2021. To be Submitt. to Extrem. Mech. Lett. [Google Scholar]
- O'Brien W.D.J. Pulse receiver UTEX scientific instruments inc. Priv. Commun. 2020 [Google Scholar]
- O'Brien W.D.J. Ultrasound–biophysics mechanisms☆. Prog. Biophys. Mol. Biol. 2007;93:212–255. doi: 10.1016/j.pbiomolbio.2006.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prikhodko I.P., Zotov S.A., Trusov A.A., Shkel A.M. Microscale glass-blown three-dimensional spherical shell resonators. J. Microelectromechanical Syst. 2011;20:691–701. doi: 10.1109/JMEMS.2011.2127453. [DOI] [Google Scholar]
- Schaap I.A.T., Eghiaia F., Des George A., Veigel C. Effect of envelope proteins on the mechanical properties of influenza virus. J. Biol. Chem. 2012;287:41078–41088. doi: 10.1074/jbc.M112.412726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder A., Kost J., Barenholz Y. Ultrasound, liposomes, and drug delivery: principles for using ultrasound to control the release of drugs from liposomes. Chem. Phys. Lipids. 2009;162:1–16. doi: 10.1016/J.CHEMPHYSLIP.2009.08.003. [DOI] [PubMed] [Google Scholar]
- Silbiger A. Nonaxisymmetric modes of vibration of thin spherical shells. J. Acoust. Soc. Am. 1962;34:862. doi: 10.1121/1.1918210. –862. [DOI] [Google Scholar]
- Sirsi S.R., Borden M.A. State-of-the-art materials for ultrasound-triggered drug delivery. Adv. Drug Deliv. Rev. 2014;72:3–14. doi: 10.1016/J.ADDR.2013.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skeldon K.D., Nadeau V.J., Adams C. The resonant excitation of a wineglass using positive feedback with optical sensing. Am. J. Phys. 1998;66:851–860. doi: 10.1119/1.19031. [DOI] [Google Scholar]
- Sonstegard D.A. Effects of a surrounding fluid on the free, axisymmetric vibrations of thin elastic spherical shells. J. Acoust. Soc. Am. 1969;45:506–510. doi: 10.1121/1.1911402. [DOI] [Google Scholar]
- Srinivasan S., Cui H., Gao Z., Liu M., Lu S., Mkandawire W., Narykov O., Sun M., Korkin D. Structural genomics of SARS-CoV-2 indicates evolutionary conserved functional regions of viral proteins. Viruses. 2020;12:360. doi: 10.3390/v12040360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turoňová B., Sikora M., Schürmann C., Hagen W.J.H., Welsch S., Blanc F.E.C., von Bülow S., Gecht M., Bagola K., Hörner C., van Zandbergen G., Landry J., de Azevedo N.T.D., Mosalaganti S., Schwarz A., Covino R., Mühlebach M.D., Hummer G., Krijnse Locker J., Beck M. In situ structural analysis of SARS-CoV-2 spike reveals flexibility mediated by three hinges. Science (80-.) 2020;370:203–208. doi: 10.1126/science.abd5223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Twarock R., Luque A. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat. Commun. 2019;10:4414. doi: 10.1038/s41467-019-12367-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigert S., Dreier M., Hegner M. Frequency shifts of cantilevers vibrating in various media. Appl. Phys. Lett. 1996;69:2834–2836. doi: 10.1063/1.117334. [DOI] [Google Scholar]
- Wrapp D., Wang N., Corbett K.S., Goldsmith J.A., Hsieh C.-.L., Abiona O., Graham B.S., McLellan J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science. 2020;1263:1260–1263. doi: 10.1126/science.abb2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao H., Song Y., Chen Y., Wu N., Xu J., Sun C., Zhang J., Weng T., Zhang Z., Wu Z., Cheng L., Shi D., Lu X., Lei J., Crispin M., Shi Y., Li L., Li S. Molecular Architecture of the SARS-CoV-2 Virus. Cell. 2020;183:730–738. doi: 10.1016/j.cell.2020.09.018. .e13. [DOI] [PMC free article] [PubMed] [Google Scholar]