A Novel Utility to Correct for Plate/Batch/Lot and Nonspecific Binding Artifacts in Luminex Data

Abstract

Cytokines and other secreted soluble proteins are routinely assayed as fluorescence intensities on the Luminex (Luminex, Austin, TX) platform. As with any immunoassay, a portion of the measured Ab binding can be nonspecific. Use of spiked-in microbead controls (e.g., AssayChex Process, Control Panel; Radix Biosolutions, Georgetown, TX) can determine the level of nonspecific binding on a per specimen basis. A statistical approach for correction of this assay’s nonspecific binding artifact was first described in earlier work. The current paper describes a novel utility written in the R language (https://www.r-project.org), that refines correction for nonspecific binding in three important ways: 1) via local polynomial regression, the utility allows for curvature in relationships between soluble protein median fluorescence intensities and nonspecific binding median fluorescence intensities; 2) to stabilize correction, the fit of the nonlinear regression function is obtained via repeated cross-validation; and 3) the utility addresses possible bias due to technical error in measured nonspecific binding. The utility first logarithm transforms and then removes plate/batch/lot artifacts from median fluorescence intensities prior to correction for nonspecific binding, even when plates/batches/lots are unbalanced with respect to experimental factors of interest. Continuous (e.g., age) and categorical (e.g., diagnosis) covariates are accommodated in plate/batch/lot artifact correction. We present application of the utility to a panel of 62 cytokines in a sample of human patients diagnosed with systemic sclerosis and to an experiment that examined multiple lots of a human 51-cytokine panel. The R script for our new utility is publicly available for download from the web.

Cytokines and other secreted soluble proteins (SPs) are routinely assayed as fluorescence intensities on the Luminex (Luminex, Austin, TX) platform using multiplexed microbead arrays. Median fluorescence intensity (MFI) readings are estimated across a sample of microbeads (usually at least 50) for each analyte. The MFI readings are subject to various artifacts, prominently including plate/batch/lot (PBL) effects and nonspecific binding. On the Luminex platform, nonspecific binding can be quantified along with other instrument and assay parameters using spiked-in control microbeads, such as those from Radix Biosolutions (AssayChex Process Control Panel; Radix Biosolutions). Specifically, nonspecific binding is quantified by fluorescence intensities from Radix Biosolutions’ AssayChex Process Control Panel Magnetic Control Microbead 100, made with a custom bead address for the Stanford Human Immune Monitoring Center (Microbead Fluorescent Control, nonspecific control [NC] microbeads).

A statistical approach for correction for nonspecific binding artifact was first described earlier (1). Since then, the nature of this artifact and its correction have been further evaluated by members of our research team. This paper describes a novel utility written in the R language (https://www.r-project.org) that refines correction for nonspecific binding in three important ways.

To begin with, the utility is designed to allow for nonlinear relationships between SP and NC MFIs. Montoya et al. (1) employed NC MFIs as a linear (i.e., straight-line) regression covariate to adjust for variation in cytokine MFIs associated with nonspecific binding. Use of regression has the advantage of employing all available sample MFI data as constraints to estimate the appropriate correction, which should result in a correction of low variance (i.e., low SE). A possible drawback to using a linear covariate is that this first-order approximation may introduce bias if the relationship between SP MFI and NC MFI is not accurately described by a straight line. The novel utility provided in this study uses a form of nonlinear local regression, which allows for estimation of and correction for curvature in the relationship between SP MFI and NC MFI.

If the regression method is too local, meaning that it uses too few MFI data to estimate each subinterval of the curve, bias will be low but the variance (instability) of the estimated correction curve will be high. To find an optimal balance between bias and variance, we apply a method wherein the bandwidth (“window”) of the MFI data used for locally estimating the regression function is chosen via cross-validation (in the sense used in Ref. 2). Cross-validation randomly partitions the sample of data into subsets of approximately equal quantities of observations, fits the regression model to the data in all subsets but one, and tests performance (mean squared prediction error, which is the average squared difference between the observed MFI and predicted MFI, as reviewed on page 312 of Ref. 3) of the fitted regression model in the held-out subset. This process is continued until each subset is used as the held-out test subset. The entire cross-validation process is then repeated multiple times, each time with a new random partitioning of the data into the same quantity of subsets. This repeated cross-validation, although more computationally-intensive and time-consuming, reduces instability (e.g., figure 6 in Ref. 4). Our novel utility employs repeated 5-fold cross-validation, randomly partitioning the data into five subsets separately for each repeat.

Standard regression methods, including ordinary least squares, assume that predictor variables are measured with little to no technical error. When predictor variables do contain substantial amounts of technical error relative to that in the response variable, these standard regression methods tend to yield inconsistent estimates of the relationship between predictors and response (5), with bias often being in the direction of underestimating the slope of the relationship (i.e., slope biased toward zero). The utility presented in this study mitigates possible bias due to technical error-in-variables in the predictor (NC MFI).

The core of our new utility is the R package lpme that employs the method of Huang and Zhou (3), which offers local, errors-in-variable regression with bandwidth selection via cross-validation. The contribution of the present work is to package and extend Huang and Zhou’s (3) regression procedure within a user-friendly R utility that will streamline workflow for immunologists. This utility first preprocesses the data, including removal of PBL artifacts, fits the nonspecific binding artifact-correction regression models, plots the data at every processing step to permit visual inspection of the full process, and terminates by generating an output file (in a standard format) of MFI values for each SP that are detrended for artifacts related to PBL and nonspecific binding. Importantly, our novel utility corrects for PBL artifacts, even when the assay experiment is unbalanced across PBLs (e.g., when the ratio of treated to untreated participants varies among PBLs). This is crucial so that removal of PBL artifact does not remove the experimental factor(s) of interest (e.g., the effect of medical treatment). The output from the utility can be used for further analyses of SP MFIs (e.g., comparison of treatment conditions in a randomized trial). Use of this novel utility requires an introductory-level understanding of the R language and interface. The method of Huang and Zhou (3) employs simulation of technical error and cross-validation. Our utility extends their method by introducing repeated cross-validation to reduce instability of estimates of MFI values that are corrected for nonspecific binding artifacts.

Materials and Methods

Nomenclature

We distinguish between specimen and sample. We use “specimen” to refer to a single specimen of tissue (e.g., serum) from a single observational unit (e.g., research participant) at a single point in time; and “sample” to refer collectively to a subset of such specimens drawn from the full population of all such specimens. Although immunologists can use sample to denote a single specimen of tissue, the method presented in this study is built on a statistical foundation in formal sampling theory. To be consistent with the established body of sampling theory, sample must be defined as a collection and subset of specimens drawn from a population.

The terms plate, batch, lot, kit, and experiment are defined as follows. A “plate” constitutes a set of specimens run together on the same microtiter plate (e.g., a 96-well plate). A typical setup is 10–12 wells for standards plus the common control, leaving up to 86–88 wells with specimens. Plates are not always full. A “batch” is a set of specimens from which MFIs are acquired at the same time (or possibly immediately following one another in time) but potentially spanning more than one microtiter plate. A “lot” is a single build of reagents or kits, usually identified by a vendor lot number. A “kit” is a specific product from one vendor. A kit will generally have multiple lots over time. Multiple types of kits exist with the same or different panels of analytes and from different vendors. Comparison of results across kits from different vendors is generally inadvisable, even if the same SPs are tested. An “experiment” is a single study that may encompass multiple plates, batches, lots, and/or kits arranged according to the specific a priori experimental design for that specific study.

Luminex assay for Pulmonary Hypertension Assessment and Recognition of Outcomes in Scleroderma

All Luminex assays were performed in the Human Immune Monitoring Center, Stanford University School of Medicine. Human 62-plex custom ProcartaPlex Kits were purchased from Thermo Fisher Scientific (Santa Clara, CA) and used according to the manufacturer’s recommendations with modifications as follows. Briefly, custom assay control microbeads by Radix Biosolutions (AssayChex Process Control Panel; Radix Biosolutions) were added to all wells of a 96-well plate along with cytokine-specific microbeads. The plates were then washed in a BioTek ELx405 washer (BioTek Instruments, Winooski, VT). Serum specimens (≥250 μl) were diluted 3-fold with kit-supplied assay buffer, added to the plate containing the mixed Ab-linked microbeads, and incubated at room temperature for 1 h, followed by overnight incubation at 4°C. Room temperature and 4°C incubation steps were performed on an orbital shaker at 500–600 rpm. Following the overnight incubation, plates were washed in a BioTek ELx405 washer (BioTek Instruments) and then kit-supplied biotinylated detection Ab mix was added and incubated for 60 min at room temperature with shaking. Each plate was washed as above, and kit-supplied streptavidin–PE was added. After incubation for 30 min at room temperature, wash was performed as described above, and kit-supplied Reading Buffer was added to the wells. Each specimen was measured in two technical replicates (i.e., two wells). Four specimens had only one replicate each and were excluded. Plates were read using a FlexMap 3D Instrument (Luminex). Wells with a bead count <50 were flagged, and data with a bead count <20 were excluded.

Luminex assay for lot experiment

Specimens were run simultaneously on three lots of a custom 51-plex kit (ProcartaPlex; Thermo Fisher Scientific). Assays were run according to the manufacturer’s recommendations with modifications as described. Briefly, specimens were mixed with Ab-linked polystyrene beads in a 96-well filter-bottom plate and incubated at room temperature for 2 h followed by overnight incubation at 4°C. Room temperature incubation steps were performed on an orbital shaker at 500–600 rpm. Plates were vacuum filtered and washed twice with wash buffer followed by incubation with biotinylated detection Ab for 2 h at room temperature. Plates were vacuum filtered and washed twice as above, and streptavidin–PE was added. After incubation for 40 min at room temperature, two additional vacuum washes were performed, and vendor supplied Reading Buffer was added. Each specimen was measured in two replicate wells. Plates were read on a Luminex 200 instrument (Luminex). Wells with a bead count <35 were flagged, and wells with a bead count <20 were excluded. AssayChex Process Control Panel microbeads (Radix Biosolutions) were included in all wells within each lot.

The novel utility

The R script for our utility is available for public download at http://iti.stanford.edu/himc/new-statistical-consultation-service.html. The utility performs four steps for the user.

Step 1: preprocessing.

PBL artifacts in MFI means per PBL are removed using the method of population marginal means (6) via R package emmeans (7) from the fit of a linear mixed model [R package nlme (8)], in which the latter accounts for the nested design (sampling of specimens and technical replicate wells within each specimen). The utility’s use of population marginal means is designed to permit removal of PBL artifacts with minimal removal of variation associated with specified experimental factors of interest (e.g., treatment condition), even when sample sizes per level of a factor of interest are unbalanced on one or more PBL(s). That is, means are estimated as if each PBL is balanced with respect to sample sizes for all levels of a factor of interest. For simplicity of estimating population marginal means, the utility assumes a “without interaction” model [reviewed in Section 4.1 of (6)]. Advanced users could directly revise the R script to allow for interactions [reviewed in Section 4.2 of (6)] that are specific to their applications. PBL artifacts are removed at the mean levels of all continuous covariates (e.g., body mass index). Altogether this procedure yields preprocessed MFI (pMFI) values. Removal of PBL artifacts precedes removal of nonspecific binding artifacts to allow for the possibility that means of NC MFI values may vary among PBLs because of the PBL artifact. The utility assumes that each specimen occurs in only one PBL. If not, the user should concatenate the specimen and PBL identifiers to create a new per PBL specimen identifier. Also, for single-plate studies, users will need to create two “pseudo-plates” by partitioning the data in balanced fashion with respect to any experimental factors of interest, a feature that may be automated in subsequent releases of the utility. Linear mixed models assume that the outcome variable is approximately normally distributed (9) so MFI data are logarithm transformed by the utility prior to fitting the linear mixed model.

Step 2: regression on nonspecific binding.

Using the exponentiated “PBL-detrended” MFI data for each SP and the NC microbeads, our utility averages over technical replicate wells and logarithm transforms these averages. Separately for each SP, the utility fits a curve to the pMFI data for that SP regressed on the pMFI data for the NC microbeads. Because NC pMFI contains technical errors, the meanreg function in R package lpme is employed to correct for possible bias in the estimated regression curve due to technical errors in the predictor variable (NC pMFI). Use of lpme requires an estimate of the technical variance in NC pMFI values. Our utility estimates NC pMFI technical variance by using the δ method (see pp 149–154 in Ref. 10) for logarithm transformation of averages over technical replicate wells. (See the Theory for estimating technical variance section for details.) Our utility does require that at least some, and preferably all, specimens have at least two technical replicates. Estimation of NC pMFI technical error is performed after removal of PBL artifacts, so in this context, our utility does not absolutely require that technical replicate wells for each specimen all occur on the same PBL; however, keeping all technical replicate wells per specimen on the same PBL is highly desirable as a precaution against imperfect removal of PBL artifacts. As detailed in the Introduction section, local regression estimation (3) requires an estimate of the optimal bandwidth. Our utility allows the user to choose a span and granularity of potential bandwidths to be assessed as well as the quantity of repeated 5-fold cross-validations. The final and stabilized estimate of the optimal bandwidth is the average of the optimal values per each repeat from the repeated cross-validations. For advanced users who wish to modify our utility for their own purposes, Dr. H. Zhou (personal communication) suggests “the default choices” in function mean-regbwSIMEX for “h₁ and h₂ for the purpose of bandwidth selection.”

Step 3: plot results.

Our utility generates four panels of figures. Each panel contains one figure per SP (and NC within two panels). In the first and second panels, data points are colored uniquely by PBL, and these first two panels are the only panels that display MFI of NC microbeads in a separate figure within the panel. The first panel displays the MFI data prior to any processing on the vertical axis and sequential well order (with respect to PBL) on the horizontal axis. The second panel displays the MFI data after removal of PBL artifacts (pMFI) on the vertical axis and sequential well order (with respect to PBL) on the horizontal axis. The third panel displays pMFI for each SP on the vertical axis and pMFI of NC microbeads on the horizontal axis along with the fitted line that is used to correct for nonspecific binding. The fourth panel displays MFI data after removal of PBL artifacts and nonspecific binding artifacts (detrended pMFI [dpMFI]) for each SP on the vertical axis and sequential specimen order (with respect to PBL) on the horizontal axis. Each panel of figures generated by our utility is designed to be visually clear, including automatic scaling of each axis to be inclusive of all data. Each panel is written to a user-specified external file (.png format).

Step 4: output of fully processed MFI data.

Separately for each SP, the vertical departures of observed values from the fit of the regression curve (third panel) are the estimates of pMFI values corrected for nonspecific binding (dpMFI), which are displayed in the fourth panel. The utility writes these dpMFI data to a comma-delimited text file (.csv format). Variables in this output file are named “SP”; “NCpMFI” for pMFI of nonspecific binding; “SPFit” for fit of local, error-in-variables regression of SP pMFI on NC pMFI; “SPpMFI” for pMFI for the SP; “dpMFI” for MFI for the SP with PBL artifacts and nonspecific binding artifacts removed; and “Specimen” for input specimen identifier.

To reduce computation time, using the parallel package in R (11), processing is distributed across multiple logical processors on the user’s computer. Specifically, the utility detects the total quantity of logical processors available, divides that quantity by three, and rounds up to the nearest integer. Division by three is designed to minimize thermal stress on computer hardware.

Example applications

For fitting the regression curve of the third panel, bandwidth selection employed 10 repeats of 5-fold cross-validation and two iterations of simulation of technical error (see Ref. 3, page 31) per repeat for 20 simulations in total. A Laplace distribution (see Ref. 12, pages 200–201) was assumed for the technical error, per Huang and Zhou (see Ref. 3, page 323), in NC pMFI.

Pulmonary Hypertension Assessment and Recognition of Outcomes in Scleroderma.

Pulmonary Hypertension Assessment and Recognition of Outcomes in Scleroderma (PHAROS) is a prospective registry (13) that includes systemic sclerosis patients at risk for pulmonary arterial hypertension (PAH) based on a pulmonary function test and echocardiographic parameters (at risk) and with incident PAH based on right heart catheterization. The study was conducted in accordance with the Declaration of Helsinki. Institutional Review Board approval was obtained at 20 sites throughout the United States, and all patients provided written informed consent prior to enrollment into the registry. Serum was available from a total of 85 patients. The data analyzed in this study consisted of 45 at-risk specimens and 48 incident PAH specimens, with two patients providing multiple longitudinal specimens. Incident cases were included if the patient met criteria for World Health Organization Group I PAH by right heart catheterization within 6 mo of serum collection. Fluorescence intensities were acquired from four assay plates with the following at-risk/incident PAH specimen ratios: 11:12, 15:12, 8:11, and 11:13.

Lot experiment.

The lot experiment was designed to isolate lot effects (different custom builds of the same Luminex kit), with all other technical variables held constant. Lot comparisons were performed in parallel on eight prevaccine sera specimens from eight healthy participants from an influenza vaccination study (14). Specimens were from a previous cohort run and stored in −80°C. Therefore, samples underwent a second thaw cycle. The study (14) was conducted in accordance with the Declaration of Helsinki and was approved by the Stanford University Institutional Review Board. All patients provided written informed consent prior to enrollment.

Theory for estimating technical variance

Theory for local, error-in-variables regression is detailed in Huang and Zhou (3), theory for population marginal means is detailed in Searle et al. (6), and theory for linear mixed models is detailed in Pinheiro and Bates (9). This section will thereby focus on the derivation of the estimate of technical variance in NC pMFI values used in our utility.

Technical variance is observed in pMFI values. Separately by each SP and NC, these pMFI values are “processed” by averaging across technical replicate wells per specimen, followed by taking the natural logarithm of each resultant mean. Local, error-in-variables regression is performed on these pMFI values, and the error-in-variables regression method requires an estimate of the technical variance in the predictor variable, which in this study is processed NC pMFI. Hereafter, we denote a realization of a processed NC pMFI value by x, and ${\mathbb{Z}}^{+}$ denotes the positive integers.

Assumption 1.

Sampling is two-stage, with a sampling of n specimens and a sampling of m_i technical replicates within each specimen in the sample, $n\in {\mathbb{Z}}^{+}$ and $m_i\in {\mathbb{Z}}^{+}$, i ∈ [1, … , n]. The volume of the specimen is not infinite, so the total possible quantity of technical replicates that can be performed per specimen is finite at ${\tau }_i,{\tau }_i\in {\mathbb{Z}}^{+}$, i ∈ [1, … , n]. Specifically, it is ${\tau }_i\stackrel{\text{ def }}{=}\left(V_i\times f\right)/v$ infinite, where V_i is the initial volume of specimen available for assay, f is the fold dilution, and v is the pipetted volume (H. Darby, Luminex, personal communication).

Assumption 2.

Sampling is simple random without replacement within each specimen i, i ∈ [1, … ,n]. Following terminology and notation in Thompson (see Chapter 2 in Ref. 15), let ${\left\{Z_{ij}\in \{0,1\}\right\}}_{j=1}^{{\tau }_i}$ be identically distributed Bernoulli random variables with side constraint $m_i=\sum _{\forall j\in i}{Z}_{ij}$ and $\text{E }〚Z_{ij}〛=m_i/{\tau }_i$, where E is conventional statistical notation for expectation and m_i/τ_i is the inclusion probability of x_ij.

Typically, experiments are designed with the same quantity of technical replicates per specimen such that m_i = m ∀ i ∈ [1, … , n]. To keep formulation completely general, however, we retain the subscript in m_i.

Per Rice (see pages 196–197 in Ref. 10) with some changes in notation and addition of the ${\left\{Z_{ij}\in \{0,1\}\right\}}_{j=1}^{{\tau }_i}$, consider the following unbiased estimates:

$${\widehat{\sigma }}_i^2〚x_{ij}〛\stackrel{\text{ def }}{=}\frac{{\tau }_i-1}{\left(m_i-1\right){\tau }_i}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{\left(x_{ij}-{\overline{x}}_i\right)}^2,{\overline{x}}_i=\frac{1}{m_i}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{x}_{ij},$$ (Eq. 1)

where ${\widehat{\sigma }}_i^2〚x_{ij}〛$ is the estimated technical variance and ${\overline{x}}_i$ is the estimated mean for the i^th specimen on a sample size of 1 < m_i < τ_i, where τ_i is defined in Assumption 1. Statistics ${\widehat{\sigma }}_i^2〚x_{ij}〛$ and ${\overline{x}}_i$ are each a random variable because of Assumption 2. An unbiased estimate of the variance in the sample mean per specimen is

$${\widehat{\sigma }}_i^2〚{\overline{x}}_i〛\stackrel{\text{ def }}{=}\frac{\left(1-\frac{m_i}{{\tau }_i}\right)}{m_i\left(m_i-1\right)}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{\left(x_{ij}-{\overline{x}}_i\right)}^2,$$ (Eq. 2)

(see p. 197 in Ref. 10), where ${\widehat{\sigma }}_i^2〚{\overline{x}}_i〛$ is also a random variable per Assumption 2. Further,

$$\begin{gathered} \underset{m_i\to {\tau }_i}{\text{lim}}〚\frac{{\tau }_i-1}{\left(m_i-1\right){\tau }_i}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{\left(x_{ij}-{\overline{x}}_i\right)}^2〛 \\ =\frac{1}{{\tau }_i}\sum _{j=1}^{{\tau }_i}{\left(x_{ij}-{\overline{x}}_i\right)}^2={\sigma }_i^2〚x_{ij}〛, \end{gathered}$$ (Eq. 3)

$$\underset{m_i\to {\tau }_i}{\text{lim}}〚\frac{\left(1-\frac{m_i}{{\tau }_i}\right)}{m_i\left(m_i-1\right)}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{\left(x_{ij}-{\overline{x}}_i\right)}^2〛=0,$$ (Eq. 4)

where ${\sigma }_i^2〚x_{ij}〛$ is the population variance. Eq. 3 and, especially, Eq. 4 are important because, although m_i is small (e.g., m_i = m = 2), in practice, τ_i may not be excessively large compared with m_i. For example, for the PHAROS study, V_i ≈ V ≈ 250 μl, v = 250 μl, f = 3, and τ_i ≈ τ ≈ (250 × 3)/25 = 30; so, the sampling fraction was m/τ = 1/15. For the lot experiment, V_i ≈ V ≈ 50 μl specimen in 100 μl assay buffer for 150 μl, v = 25 μl, f = 3, and τ_i ≈ τ ≈ (150 × 3)/25 = 18; so, the sampling fraction was m/τ = 1/9.

What Eqs. 1–4 overlook is that we are not directly interested in the technical variance of processed NC pMFI but instead in the technical variance of

$$\text{ln}〚\frac{1}{m_i}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{x}_{ij}〛=\text{ln}〚\frac{S}{m_i}〛,$$ (Eq. 5)

for $S_i\stackrel{\text{ def }}{=}\sum _{j=1}^{{\tau }_i}{Z}_{ij}{x}_{ij}$. It can be shown that

$$\text{Var}〚\text{ln}〚\frac{S_i}{m_i}〛〛\approx \frac{{\sigma }_i^2〚{\overline{x}}_i〛}{{\mu }_i^2}.$$ (Eq. 6)

Var is conventional statistical notation for “variance.” Eq. 6 is a known, useful result (e.g., see Ref. 16); the ratio ${\sigma }_i^2〚{\overline{x}}_i〛/{\mu }_i^2$ is the squared coefficient of variation of the mean of the technical replicates in specimen i. Many laboratories apply a threshold and exclude (and possibly replace) observations for any specimen for which $\sqrt{{\sigma }_i^2〚x_{ij}〛/{\mu }_i^2}\ge c$, for some scalar, real constant c, such that 0 < c < 1. Because ${\sigma }_i^2〚{\overline{x}}_i〛/{\mu }_i^2<{\sigma }_i^2〚x_{ij}〛/{\mu }_i^2\forall m_i\in \left(1,{\tau }_i\right]$,

$$c^2>\frac{{\sigma }_i^2〚x_{ij}〛}{{\mu }_i^2}>\frac{{\sigma }_i^2〚{\overline{x}}_i〛}{{\mu }_i^2}.$$ (Eq. 7)

For example, a generous threshold on technical error of c = 0.3 gives

$$\frac{9}{100}>\frac{{\sigma }_i^2〚x_{ij}〛}{{\mu }_i^2}>\frac{{\sigma }_i^2〚{\overline{x}}_i〛}{{\mu }_i^2},$$ (Eq. 8)

where c < 0.3 should make Eq. 6 an accurate approximation (16).

This process of taking the logarithm of the mean of technical replicates per specimen is performed for NC and all SPs. As such, the variance, as given by Eq. 6, is of similar scale for NC and all SPs. Hence, there is need for error-in-variables regression.

In practice, ${\sigma }_i^2〚{\overline{x}}_i〛/{\mu }_i^2$ is unknown and must be estimated from the observed data. From Eqs. 1 and 2,

$${\widehat{\sigma }}_i^2〚{\overline{x}}_i〛\stackrel{\text{ def }}{=}\frac{\left(1-\frac{m_i}{{\tau }_i}\right)}{m_i\left(m_i-1\right)}\sum _{j=1}^{m_i}{\left(x_{ij}-{\overline{x}}_i\right)}^2,{\overline{x}}_i=\frac{1}{m_i}\sum _{j=1}^{m_i}{x}_{ij}.$$ (Eq. 9)

We employ the first-order approximation $\text{Var}〚\text{ln}〚{\overline{x}}_i〛〛\approx {\widehat{\sigma }}_i^2〚{\overline{x}}_i〛/{\overline{x}}_i^2$ in our utility. Our pooled estimate across all specimens of the technical variance for NC MFI transformed, per Eq. 5, is

$$\frac{1}{\stackrel{⌣}{n}}\sum _{i=1}^{\stackrel{⌣}{n}}\frac{{\widehat{\sigma }}_i^2〚{\overline{x}}_i〛}{{\overline{x}}_i^2},$$ (Eq. 10)

where $\stackrel{⌣}{n},0<\stackrel{⌣}{n}<n$ is the quantity of specimens with at least two replicate wells.

Results

PHAROS

Using our 62-plex custom Luminex kits for serum cytokine analysis, MFI values were acquired for each cytokine in each specimen of the PHAROS example data set, except for two specimens that had some missing values. Those two specimens were excluded from processing by the utility. The unprocessed MFI data are shown in Fig. 1. The preprocessed, pMFI of Step 1 are displayed in Fig. 2. In Fig. 2, the blue and red lines are estimates of the trend in the mean across plates before and after removal of plate effects, respectively. The largest adjustment was for the fourth plate (at right in each figure), although a few cytokines (TGFA) also demonstrated marked adjustment in the third plate. This illustrates the importance of correcting for plate effects separately for each SP.

FIGURE 1.

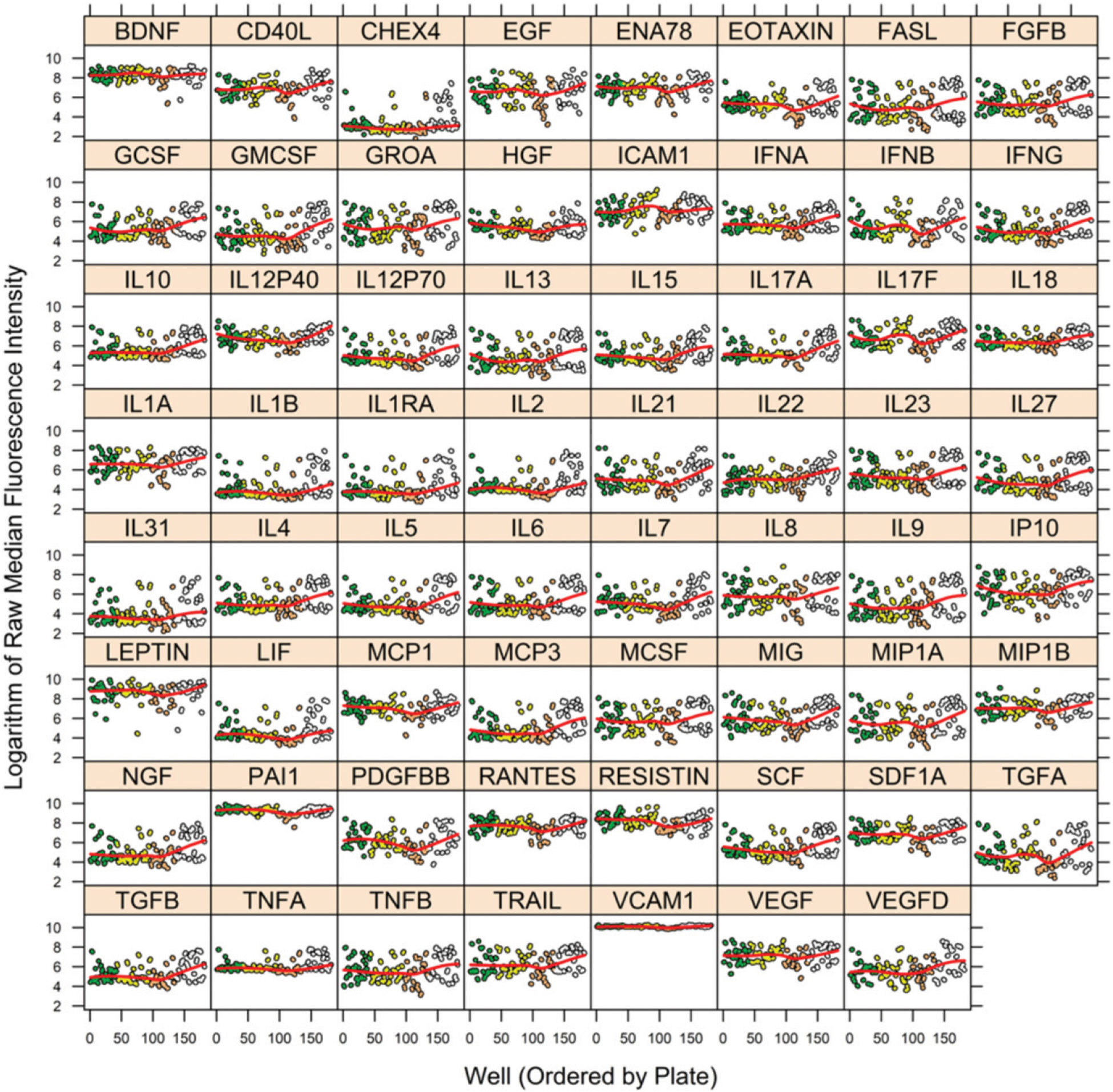
MFI per well by cytokine before removal of plate and nonspecific binding artifacts for PHAROS study. The vertical axis is MFI before removal of plate and nonspecific bindings artifacts, and the horizontal axis is the ordering of wells (across plates). A separate figure is shown for each cytokine and for the NC microbeads (labeled “CHEX4”). Color coding of circles distinguishes wells from different plates. Red line within each figure is a spline smooth of trend in mean. Figure was prepared in R package lattice (19).

FIGURE 2.

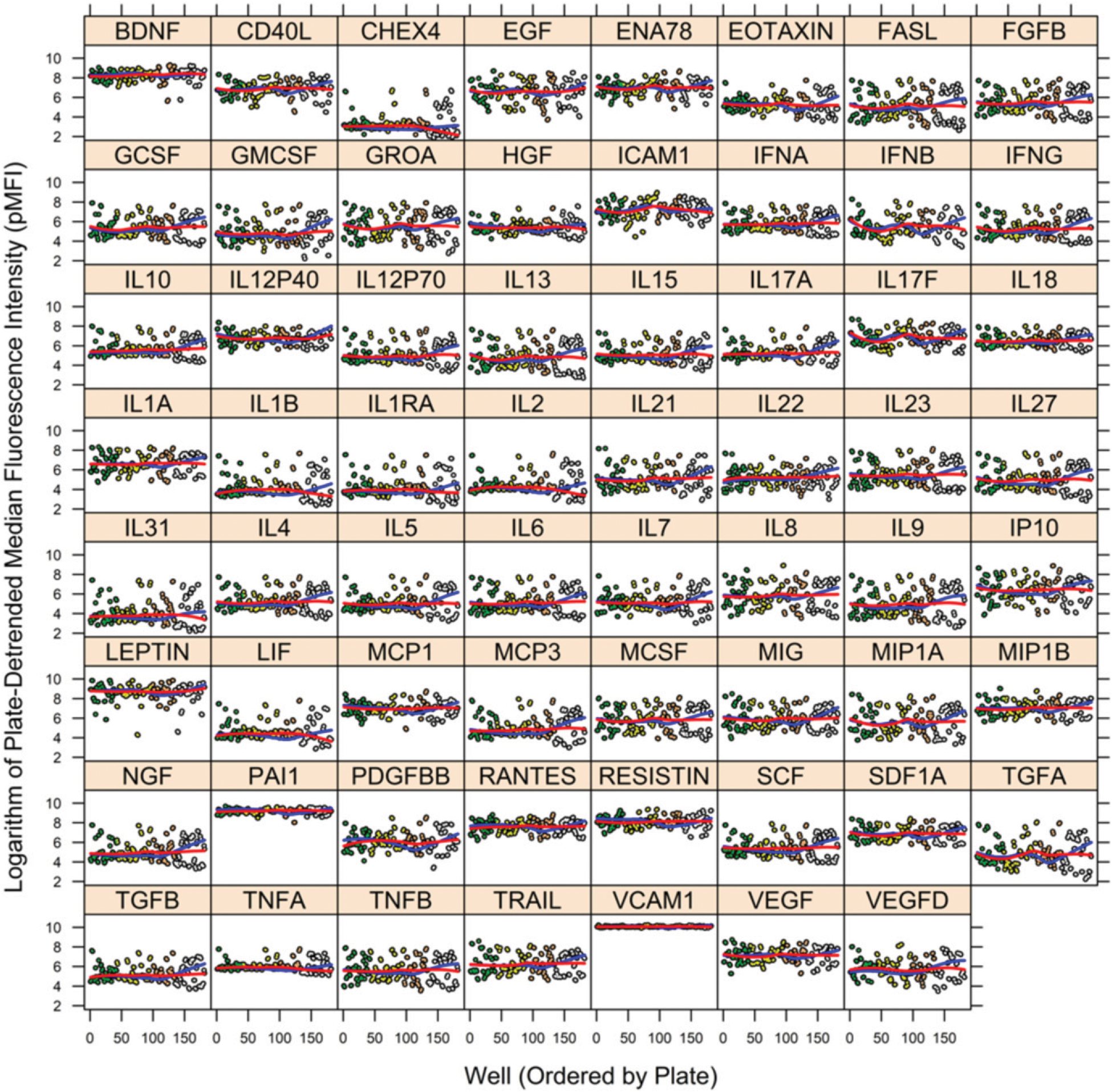
MFI per well by cytokine after removal of plate artifact (pMFI) for PHAROS study. The vertical axis is MFI after removal of plate artifact (pMFI), and the horizontal axis is the ordering of wells (across plates). A separate figure is provided for each of the 62 cytokines plus the NC microbeads (labeled “CHEX4”). Color coding of circles distinguishes wells from different plates. Blue and red lines within each figure are spline smooths of trends in mean before and after removal of plate artifact, respectively. The largest adjustment was for the fourth plate (at right in each figure); although a few cytokines (TGFA) demonstrated adjustment in the third plate as well. Compare to the unprocessed data of Fig. 1. Figure was prepared in R package lattice (19).

The pMFI data of Step 1 along with the fit of the regression curve (Step 2) are shown in Fig. 3 (Step 3). The fit of the regression curve is used to remove the variation in each cytokine’s pMFI values associated with nonspecific binding pMFI, which results in the fully detrended data (Step 4, Fig. 4). Estimated regression functions are generally linear, with little to no curvature. Fig. 5 shows an example of the sequential removal of plate effects and nonspecific binding effects on a highly affected cytokine, VEGFD.

FIGURE 3.

Fit of regression model to pMFI data by cytokine for removal of nonspecific binding artifact for PHAROS study. Vertical axis is pMFI for cytokine, and horizontal axis is pMFI for NC microbeads (nonspecific binding). Black circles are observed pMFI data, and red line is estimated local, error-in-variables regression curve. A separate figure is provided for each of the 62 cytokines. The vertical departures of observed pMFI values (black) from the regression curve (red) are estimates of pMFI corrected for nonspecific binding (dpMFI) where dpMFI is shown in Fig. 4. The large gaps in the sample distribution of NC pMFI values ≥4 necessitated assessment of large bandwidths for the local regression estimator. Figure was prepared in R package lattice (19).

FIGURE 4.

Final output dataset for PHAROS study. Vertical axis is MFI after removal of plate and nonspecific binding artifacts (dpMFI) for each cytokine, and horizontal axis is the ordering of specimens (across plates). A separate figure is provided for each of the 62 cytokines. Red line within each figure is a spline smooth of trend in mean. Compare with the data (pMFI) prior to removal of nonspecific binding artifact (Fig. 2). Figure was prepared in R package lattice (19).

FIGURE 5.

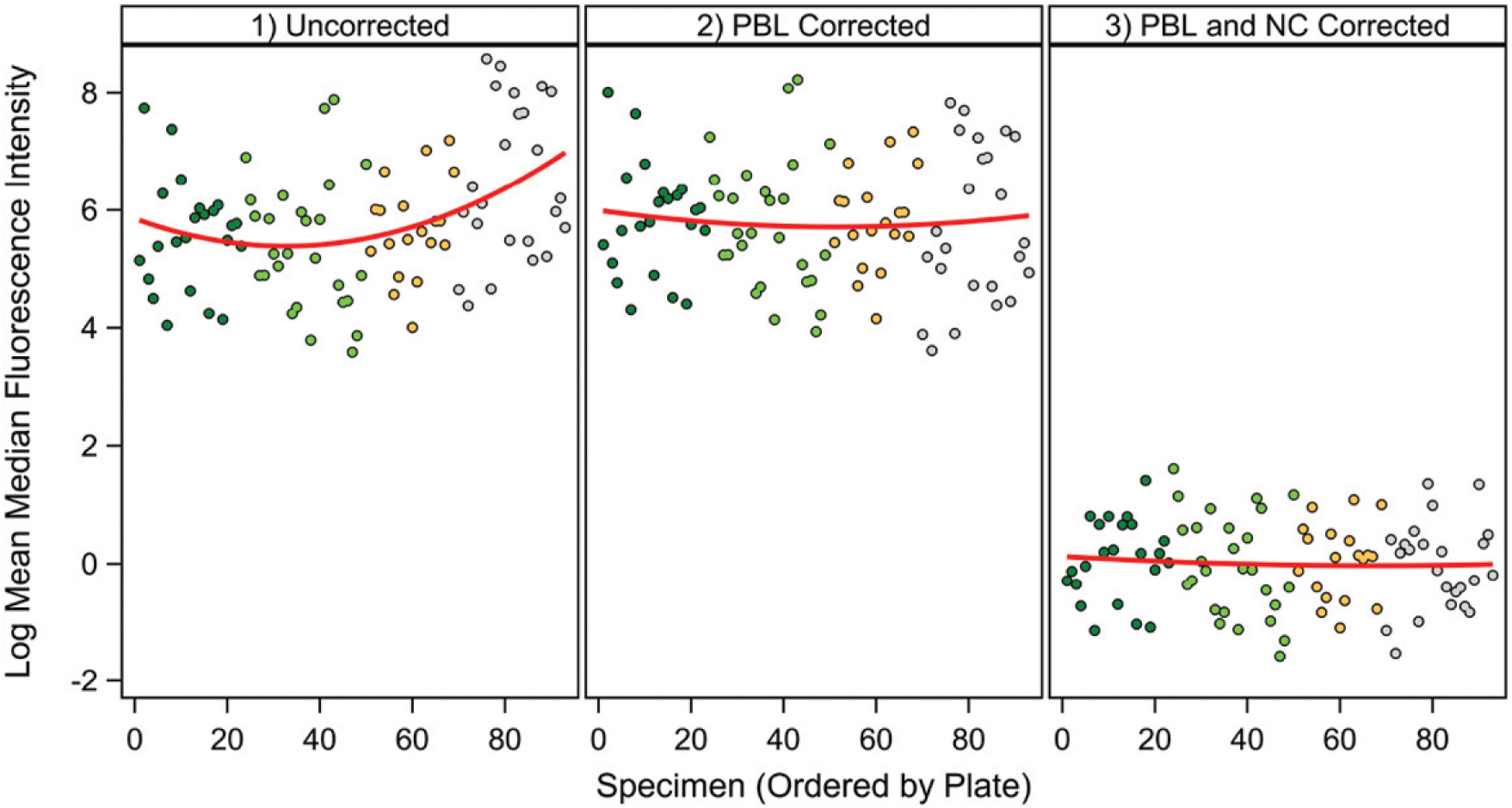
Example of changes with plate artifact removal and nonspecific binding artifact removal. VEGFD was chosen as a cytokine that showed significant plate and nonspecific binding artifacts. Left panel, Uncorrected data; middle panel, data with plate artifact removal; right panel, data with removal of plate and nonspecific binding artifacts. Figure was generated in SAS ODS Graphics (SAS Institute, Cary, NC).

The large gaps in the sample distribution of NC pMFI values ≥4 necessitated assessment of large bandwidths for the local regression estimator (Step 2 and Fig. 3), which may have limited detection of curvature. Fig. 4 illustrates that following removal of plate and nonspecific binding artifacts a few cytokines have some outlying individual dpMFI values (e.g., BDNF and ICAM1). These outlying data may require closer scrutiny to determine if they are the result of another assay artifact or other error. That scrutiny is made possible through the output file generated by the utility, which contains the specimen identifiers and their dpMFI values. The R utility ran for ~4252.50 s on three logical processors (3.5 GHz Intel Xeon; Intel, Santa Clara, CA).

Lot experiment

Supplemental Figs. 1–4 provide results for the lot experiment. The utility removed very pronounced lot-specific artifacts (Supplemental Fig. 2). Note also the curvature in some of the estimated regression functions (e.g., TGFB) of Supplemental Fig. 3. The artifact removal function ran for ~2678.8 s on three logical processors (3.5 GHz Intel Xeon; Intel).

Effect of detrending on variance and biological findings

Supplemental Fig. 5 shows the percentage of interspecimen variance reduced by detrending for nonspecific binding by cytokine in the PHAROS study. There tends to be a higher percentage variance reduction for low-abundance cytokines, such as TNFA or IL-2, compared with high-abundance cytokines, such as ICAM1 or LEPTIN. This likely reflects the fact that nonspecific binding tends to be a lower proportion of interspecimen variance when the specific cytokine signal is high, although there are also inherent differences in the level of nonspecific binding by cytokine.

To determine the extent to which our utility might reveal or improve detection of biological findings, we looked for age-associated cytokines in the PHAROS data set. With correction for plate artifact alone, we saw no significant associations at p < 0.05 (Supplemental Fig. 6). However, additional detrending for nonspecific binding revealed two significant age associations, IP10 and TNFA, both proinflammatory cytokines that have been shown to increase with age (17).

Discussion

With the widespread use of Luminex assays, PBL and nonspecific binding artifacts can impact research in a wide variety of settings. Our novel utility provides a standardized way to illustrate the extent of and correct MFI values for these artifacts, even when assay experiments are unbalanced as PBLs. As indicated in the Materials and Methods section, removal of PBL artifacts precedes removal of variation associated with nonspecific binding to allow for the possibility that means of NC MFI vary among PBLs because of PBL artifact.

The novel utility proposed in this study, which sequentially corrects for artifacts of PBL and nonspecific binding separately for each SP, expands the investigator’s ability to detect artifacts that vary widely among SPs. For instance, for the PHAROS data, correction for nonspecific binding in IL-1B is strong, but correction for nonspecific binding is clearly more modest for LEPTIN (Fig. 3). The level of nonspecific binding may also depend on details of the kit protocol, such as specimen incubation time, which may or may not include an overnight step.

The lot experiment illustrates the importance of using a regression method that allows for curvature, given that the fitted regression lines showed curvature for some cytokines (Supplemental Fig. 3). As explained in the Introduction, this allowance for curvature yields dpMFI values that are local to each subinterval of the observed dynamic range of NC pMFI values.

The current version of the utility employs a single value for specimen volume for all specimens, V_i = V ∀ i ∈ [1, … , n]. Future versions of the utility may allow users to specify the volume of specimen on a per specimen basis in the input data set. The current utility also requires more than one PBL per experiment and requires that most specimens have more than one replicate (well). Further work is required to allow the utility to analyze single-PBL and single-replicate experimental designs.

The utility is designed to be applied to data sets of sample sizes at least as large as those presented in the worked examples of this paper. Future work could extend the utility for application to samples containing small quantities of specimens.

We have carefully designed our utility to provide correction for PBL artifacts and nonspecific binding artifacts, as detailed in the Materials and Methods section. That said, not every user will agree with every assumption that we have built into our utility. Some users may wish to try workflows with and, separately, without applying our utility prior to further statistical analyses (e.g., comparison of treatment means). Certainly, final findings that are consistent with or without applying our utility may be especially robust. That said, final findings should be more accurate regarding the biological processes being studied when appropriately corrected for possible assay artifacts. We have not tested our utility’s capacity to correct for artifacts due to different vendors/kits.

Our utility yields sample estimates of dpMFI because they are obtained from an estimated regression curve. As such, the output dpMFI values (Step 4) contain sampling error (i.e., random variation across different samples of specimens of the same sample size drawn from the same population). A rigorous workflow would propagate this sampling error throughout any subsequent statistical analyses of the estimated dpMFI values. In theory, the entire procedure, dpMFI estimation (Steps 1–4) plus subsequent statistical analysis using dpMFI estimates (e.g., comparing means between treatment groups), could be performed on many resamples using applicable sample reuse procedures. The current version of the utility will require further refinement to reduce computation times before incorporation in sample reuse procedures becomes feasible.

Specifically, even with parallel processing, our utility’s R script can take some time to run because of repeated cross-validation. The improved stability of dpMFI estimates are worth the additional computation time required for repeated cross-validation. For example, the regression function (Step 2) produced a very poor fit to the data for a few cytokines when we tried five instead of 10 repeated cross-validations, so we used 10 repetitions for Fig. 3. That said, the user does have full control over run times through choice of quantity of repeated cross-validations.

Users should regard results from the utility with caution for superabundant SPs. Superabundant SPs are those of concentrations above the optimal dilution of the majority of SPs in the analyte panel and thereby above linear range. Superabundant SPs are readily distinguished by pronounced left skewness in their sample distribution and with mean high within the dynamic range of the assay. See, for instance, VCAM1 in Fig. 1. For removal of PBL artifacts via linear mixed models, departure from a normal distribution will be worsened by logarithmic transformation for SPs with distributions of left skewness. Future releases of the utility might replace logarithmic transformation with the more flexible Box–Cox transformation (18) to accommodate right or left skewness. Whether this revision to the utility would be prudent is unclear. The assay artifact of suboptimal dilution causes acquired MFIs for superabundant SPs to fall above linear range, so their usefulness for investigating association with biological factors of interest will necessarily be limited. Investigators may wish to exclude superabundant SPs from their panels or redesign their assays (e.g., different dilutions for different sets of SPs) to ensure that all SPs encompass linear range.

Although PBL artifacts are well-known for Luminex and other biological assays, nonspecific binding may be underappreciated as a source of variance. We specifically showed (Supplemental Fig. 5) that percentage variance reduction with nonspecific binding correction varies by cytokine, meaning that this artifact does not affect all measurements equally. Furthermore, we showed that nonspecific binding correction revealed age associations for two cytokines, which were NS (p ≥ 0.05) with removal of PBL artifact alone (Supplemental Fig. 6); thus, these corrections can have important consequences for biological findings.

This novel utility may be relevant in research on predictive serum biomarkers and generally in research, including clinical trials. Indeed, accurate measurements of cytokine levels are paramount to the identification of cytokine signatures that correlate with disease activity or outcomes. The ultimate goal is to discover easily accessible serum biomarkers that accurately predict disease activity or outcomes in individual research participants to predict clinical trial outcomes with accuracy, such as the clinical outcome of PAH in the PHAROS sample of patients.

Abbreviations used in this article:

dpMFI

detrended pMFI

MFI

median fluorescence intensity

NC

nonspecific control

PAH

pulmonary arterial hypertension

PBL

plate/batch/lot

PHAROS

Pulmonary Hypertension Assessment and Recognition of Outcomes in Scleroderma

pMFI

preprocessed MFI

SP

soluble protein