Quantitative Assessment of Weight-Bearing Fracture Biomechanics Using Extremity Cone-Beam CT

Abstract

Purpose:

We investigate an application of multisource extremity Cone-Beam CT (CBCT) with capability of weight-bearing tomographic imaging to obtain quantitative measurements of load-induced deformation of metal internal fixation hardware (e.g. tibial plate). Such measurements are desirable to improve the detection of delayed fusion or non-union of fractures, potentially facilitating earlier return to weight-bearing activities.

Methods:

To measure the deformation, we perform a deformable 3D-2D registration of a prior model of the implant to its CBCT projections under load-bearing. This Known-Component Registration (KC-Reg) framework avoids potential errors that emerge when the deformation is estimated directly from 3D reconstructions with metal artifacts. The 3D-2D registration involves a free-form deformable (FFD) point cloud model of the implant and a 3D cubic B-spline representation of the deformation. Gradient correlation is used as the optimization metric for the registration. The proposed approach was tested in experimental studies on the extremity CBCT system. A custom jig was designed to apply controlled axial loads to a fracture model, emulating weight-bearing imaging scenarios. Performance evaluation involved a Sawbone tibia phantom with an ~4 mm fracture gap. The model was fixed with a locking plate and imaged under five loading conditions. To investigate performance in the presence of confounding background gradients, additional experiments were performed with a pre-deformed femoral plate placed in a water bath with Ca bone mineral density inserts. Errors were measured using eight reference BBs for the tibial plate, and surface point distances for the femoral plate, where a prior model of deformed implant was available for comparison.

Results:

Both in the loaded tibial plate case and for the femoral plate with confounding background gradients, the proposed KC-Reg framework estimated implant deformations with errors of <0.2 mm for the majority of the investigated deformation magnitudes (error range 0.14 - 0.25 mm). The accuracy was comparable between 3D-2D registrations performed from 12 x-ray views and registrations obtained from as few as 3 views. This was likely enabled by the unique three-source x-ray unit on the extremity CBCT scanner, which implements two off-central-plane focal spots that provided oblique views of the field-of-view to aid implant pose estimation.

Conclusion:

Accurate measurements of fracture hardware deformations under physiological weight-bearing are feasible using an extremity CBCT scanner and FFD 3D-2D registration. The resulting deformed implant models can be incorporated into tomographic reconstructions to reduce metal artifacts and improve quantification of the mineral content of fracture callus in CBCT volumes.

1. INTRODUCTION

Longitudinal follow-up of fractures could benefit from methods to quantify mechanical stability of the healing bone. Recently introduced multisource extremity cone-beam computed tomography (CBCT, Fig. 1) provides a promising platform for such measurements, as it enables 3D tomographic imaging under physiological weight-bearing^1,2. However, for complex fractures involving metal fixation hardware, motion of fracture fragments and deformation of the hardware might be challenging to measure directly from the CBCT reconstruction domain due to metal-induced artifacts. To address this issue, we propose to deploy the Known Component Registration (KC-Reg) framework^3-5. KC-Reg utilizes a prior model of an undeformed fixation implant obtained from CAD data or the reconstruction of a high-dose, high-tube-potential CT scan. The load-induced deformation of the implant is then estimated by performing spline-based Free-Form Deformable⁶ (FFD) 3D-2D registration^3-5 of this model to the CBCT projections. Previously, a similar approach was investigated in imaging of flexible hardware such as K-wires³ or cochlear implants⁷. Compared to these earlier works, the application of deformable KC-Reg to fracture hardware is challenged by the complex 3D structure of such implants that requires a relatively large number of control points to capture their transformations. To enable efficient 3D-2D registrations in this scenario, we propose to progressively increase the number of independently moving control point groups during the registration process.

Figure 1.

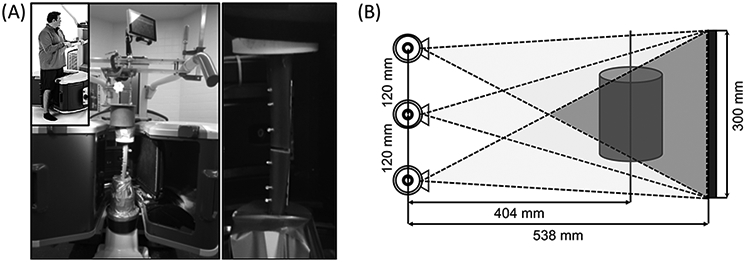
(A) The extremity CBCT in weight-bearing configuration. A custom jig was designed to apply controlled loads (emulating weight-bearing) to fracture models inside the gantry. A model of LCP-fixed tibial fracture under load is shown on the right. (B) Multisource configuration and system geometry of the extremity CBCT. Darker region indicates the cone that all three beams can cover.

The proposed algorithm (termed FFD-KC-Reg) is not only useful in quantifying the deformation of internal fixation hardware under physiological loads. The deformed implant model obtained using FFD-KC-Reg can be also incorporated into model-based CBCT image reconstruction or material decomposition algorithms to reduce metal-induced artifacts (e.g. Known-Component Reconstruction^7,8, KC-Rec), and improve quantitative accuracy of bone mineral density (BMD) measurements in fracture callus in the vicinity of the internal fixation implants⁹.

In this work, we investigated the feasibility of comprehensive quantitative assessment of fracture healing using the multisource extremity CBCT combined with FFD-KC-Reg and KC-Rec algorithms. In particular, we evaluated the accuracy and robustness of FFD-KC-Reg in application to the experimental models of instrumented tibial fractures under realistic weight-bearing conditions.

2. METHOD

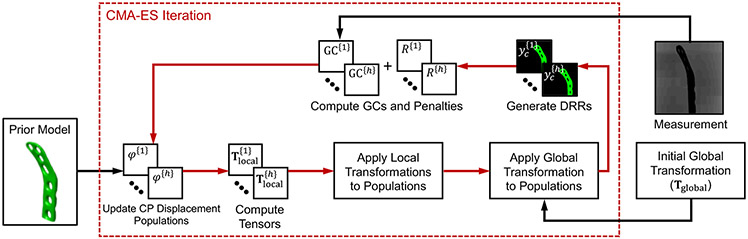
Fig. 2 illustrates the general workflow of the proposed FFD-KC-Reg for the quantification of weight-bearing deformations of internal fixation implant. We use a prior model of the undeformed implant as an initial template for the algorithm. The model is 3D-2D deformably registered to a subset of projection views of the weight-bearing fracture acquired using the multisource extremity CBCT scanner. The scanner is described in Sec. 2.1. The 3D-2D registration framework includes: i) a point cloud parameterization of the implant (in Sec. 2.2), ii) a deformation model based on control points and 3D cubic B-splines (in Sec. 2.2), and iii) an error metric to compare simulated projections of the deformed implant to the measured CBCT views (in Sec. 2.3).

Figure 2.

Flowchart for the proposed spline-based free-form deformable known-component 3D-2D registration approach to detect the deformation of an internal fixation implant under weight-bearing. Red arrows denote the iterative loops for CMA-ES optimization, and black arrows indicate the iteration-independent inputs.

2.1. Multisource Extremity CBCT for Weight-Bearing Imaging of Fractures

The multisource extremity CBCT scanner is shown in Fig. 1. Its gantry configuration enables 3D imaging of a standing subject¹, thus provides a unique capability for volumetric visualizations of weight-bearing lower limb from approximately mid-femur. The scanner has a source-axis distance (SAD) of 404 mm, a source-detector distance (SDD) of 538 mm, and a detector size of 300 × 300 mm² (flat-panel detector with a 0.6 mm CsI scintillator)^1,2.

The scanner incorporates an innovative multisource x-ray unit designed to minimize cone-beam artifacts. Three x-ray focal spots are arranged vertically, parallel to the axis of rotation (i.e. along the length of the lower extremity in Fig. 1A) at an approximately 120 mm spacing. Such multisource configuration may aid 3D-2D registration by providing additional oblique views of the subject, compared to using only different azimuthal views in a traditional single-source CBCT acquisition. In this study, we denote the superior focal spot as T1, the middle one as T2, and the inferior one as T3 (Fig. 1B). We apply the following rapid source-switching acquisition sequence: T1, T2, T3, T2, T1, …, T2, for a total of 200 projection views (i.e. including 50 for T1, 100 for T2, and 50 for T3)⁹.

2.2. Free-Form Deformable Point Cloud Model of Internal Fixation Hardware

The 3D-2D registration step in FFD-KC-Reg implements a 3D spline-based deformable framework to represent deformations of the internal fixation implant. For each implant in the field-of-view, we first use prior design data to parameterize an undeformed version of the implant using a point cloud model. The complete transformation of the point cloud of the hth implant (T^{h}) at any given Cartesian coordinate (x, y, z) can be then written as a summation of global and local transformations:

$${\mathbf{T}}^{\{h\}}(x,y,z)≔{\mathbf{T}}_{\text{global}}^{\{h\}}(x,y,z)+{\mathbf{T}}_{\text{local}}^{\{h\}}(x,y,z,\phi ).$$ (1)

where T_global is a six degree-of-freedom (DoF) global rigid alignment, and T_local is the local transformation operator that described the deformation of the point cloud model due to weight-bearing. A rough global transformation (any errors in global transformation will likely be corrected during the estimation of local transformation) can be obtained prior to FFD-KC-Reg by various reported rigid-body registration techniques^4,10,11. For estimating local transformation, we adopt a 3D cubic B-spline-based FFD model⁶ given by:

$${\mathbf{T}}_{\text{local}}^{\{h\}}(x,y,z,\phi )=\sum _{l=0}^3\sum _{m=0}^3\sum _{n=0}^3{B}_3^{\{l\}}({\eta }_x)B_3^{\{m\}}\left({\eta }_y\right)B_3^{\{n\}}({\eta }_z)\phi (c_x+l,c_y+m,c_z+n),$$ (2a)

$$c_x≔\lfloor \frac{x}{{\delta }_x}\rfloor -1,c_y≔\lfloor \frac{y}{{\delta }_y}\rfloor -1,c_z≔\lfloor \frac{z}{{\delta }_z}\rfloor -1,{\eta }_x≔\frac{x}{{\delta }_x}-\lfloor \frac{x}{{\delta }_x}\rfloor ,{\eta }_y≔\frac{y}{{\delta }_y}-\lfloor \frac{y}{{\delta }_y}\rfloor ,{\eta }_z≔\frac{z}{{\delta }_z}-\lfloor \frac{z}{{\delta }_z}\rfloor .$$ (2b)

where φ denotes the transformation of the 3D control point (CP) map with a dimension of n_x × n_y × n_z. The CPs are non-isotropically distributed along the x, y and z axes with spacings δ_x, δ_y and δ_z, respectively. The CP closest to a point cloud node (x, y, z) is represented by the index (c_x, c_y, c_z). (η_x, η_y, η_z) is the 3D vector between (c_x, c_y, c_z) and (x, y, z) normalized by the spacing of control points (δ_x, δ_y, δ_z). Eq. 2 interpolates the displacement field of the CP map (φ) to the entire point cloud model. A relatively smooth, C² continuous, and locally controllable interpolated displacement for every node of the point cloud is obtained using a 3D tensor product of three 1D cubic B-spline functions B₃(η) (indexed by l, m and n):

$$\{\begin{array}{c}{B}_3^{\{0\}}(\eta )=(1-\eta {)}^3∕6\hfill \\ B_3^{\{1\}}(\eta )=(3{\eta }^3-6{\eta }^2+4)∕6\hfill \\ B_3^{\{2\}}(\eta )=(-3{\eta }^3+3{\eta }^2+3\eta +1)∕6\hfill \\ B_3^{\{3\}}(\eta )={\eta }^3∕6\hfill \end{array}\phantom{\}}$$ (3)

2.3. Deformable 3D-2D Known-Component Registration

Global and local transformations of the fixation implant are estimated iteratively using 3D-2D registration. The current guess of combined transformation is applied to the point cloud model of the undeformed fixation implant, and digital reconstructed radiographs (DRRs) of deformed model are then generated. DRRs are compared to measured CBCT projection data based on a similarity metric to compute an updated transformation of the point cloud^3-5. In this work, we utilize gradient correlation (GC) as the similarity metric during 3D-2D registration³:

$$\text{GC}(y_{\ast },y_c)=\frac{1}{2}\left(\text{NCC}({\nabla }_u{y}_{\ast },{\nabla }_u{y}_c)+\text{NCC}({\nabla }_v{y}_{\ast },{\nabla }_v{y}_c)\right),$$ (4a)

$$\text{NCC}(y_{\ast },y_c)=\frac{{\sum }_u{\sum }_v(y_{\ast }(u,v)-\text{mean}\{y_{\ast }\})(y_c(u,v)-\text{mean}\{y_c\})}{\sqrt{{\sum }_u{\sum }_v(y_{\ast }(u,v)-\text{mean}\{y_{\ast }\}{)}^2}\sqrt{{\sum }_u{\sum }_v(y_c(u,v)-\text{mean}\{y_c\}{)}^2}}.$$ (4b)

where u and v are the projection coordinates, and NCC is the normalized cross correlation between DRRs of the fixation implant y_c and measured projections y_*. Additionally, we incorporate a 3D diffusion penalty R to regularize the smoothness of CP displacements written as:

$$R(\phi )=\frac{1}{n_x{n}_y{n}_z}\sum _i\sum _j\sum _k\left(\Vert {\nabla }_x\phi {\Vert }^2+\Vert {\nabla }_y\phi {\Vert }^2+\Vert {\nabla }_z\phi {\Vert }^2\right){\delta }_x{\delta }_y{\delta }_z.$$ (5)

In this study, covariance matrix adaptation evolution strategy (CMA-ES) was applied to solve the 3D-2D registration of the point cloud by minimizing the sum of negative GC and the penalty term³. The population size for CMA-ES was set to 40, and a maximum number of 400 iterations was performed to obtain an optimized transformation. To accelerate the convergence, the nearby CPs were grouped together and each of the groups was defined to undergo a single rigid transformation (to be determined by the registration). In addition, a ‘multiresolution’ scheme to group CPs was implemented, where the number of CP groups (thus the level of details captured by the resulting combined deformation) was increased as the registration progressed.

2.4. Experimental Validations

Digital models of the undeformed fixators were obtained by acquiring high-dose, high-resolution CBCT scans of the fixators using an experimental test-bench. The scans were reconstructed via FDK using 250 × 250 × 250 μm³ voxels, and each reconstructed volume was then converted into a point cloud using the vertices of the original voxel grid.

We first validated the accuracy of predicted bone deformations under realistic loading conditions. A compression jig was developed to apply axial loads (mimicking weight-bearing patient scans) to phantoms and cadaveric specimens (Fig. 1A). The experiments involved a biomechanically accurate Sawbone tibia phantom with a 4 mm fracture gap at the center. The tibia was fixed using a Synthes ten-hole stainless-steel locking compression plate (LCP) and six stainless-steel locking screws. Two groups of four stainless-steel reference BBs were rigidly attached to the superior and inferior ends of the LCP using ~1 cm spacers. BBs were sufficiently far from the fixator to be visible in the reconstructions without any interference from the metal artifacts. Such setup ensured that the BBs could be segmented out from the FDK reconstructed volumes to calculate ground truth deformations of the implant. The phantom was placed in the compression jig, and six CBCT scans were acquired under increasing amount of loading (including one unloaded scan).

The proposed FFD-KC-Reg algorithm was performed on small subsets of the CBCT projection views. We compared two scenarios: i) 12 projections extracted at a 15° interval starting from the 15° gantry rotation angle, which resulted in 4 views for each of the three sources, and ii) 3 neighboring projections, one view for each source at the angles of 91° (T1), 92° (T2) and 93° (T3). Deformation of the prior point cloud were parameterized using a 6 × 6 × 10 CP map with spacings of 8.75 mm, 8.75 mm and 25 mm along the x, y and z directions, respectively. During FFD-KC-Reg, the number of CP groups was increased from 2 to 10.

We computed the estimated deformation of the fixator in each loading scenario based on registered point clouds. The bottom portions of undeformed and deformed point clouds were first rigidly registered, and the Euclidian distance between the two clouds at every note was then calculated. To evaluate the accuracy of the proposed algorithm in the axial loading experiment, we computed root-mean-squared errors (RMSEs) of BB locations. Specifically, the ground truth BB positions were obtained by segmenting the BBs from FDKs of the unloaded and loaded phantom scans. To estimate BB locations precited by FFD-KC-Reg in each loading scenario, the estimated displacement vector field was applied to the BB positions of the unloaded scan. RMSE was then computed between those predicted and ground truth BB locations.

In addition, we tested the robustness of the proposed algorithm to confounding background gradients and more complex implant shapes. In this experiment, the phantom involved a titanium femoral plate inside a water bath with three bone-mimicking calcium inserts (50 mg/mL, 100 mg/mL and 200 mg/mL calcium concentrations) and two stainless-steel locking screws. The plate was pre-deformed before placed in the phantom. FFD-KC-Reg was performed using the same CPs arrangement as in the previous experiment and projection views acquired via the same protocol.

A high-resolution reference point cloud model of the deformed femoral plate was obtained using the same benchtop protocols as for generating the undeformed model. To evaluate the accuracy of registration in the experiment with confounding gradients, the rigid coherent point drift (CPD)¹² algorithm was applied to map the reference point cloud onto the one estimated by registration. RMSEs were computed between the closest nodes (determined by the KNN algorithm) of estimated and reference point clouds.

We also illustrated the potential benefits of incorporating implant knowledge in model-based CBCT reconstruction using KC-Rec. Monoenergetic penalized-weighted least-squares (PWLS) reconstructions¹³ with and without the estimated implant model were applied to the CBCT dataset of the femoral plate phantom with three calcium inserts using 500 iterations, 20 subsets and a quadratic regularization.

3. RESULTS

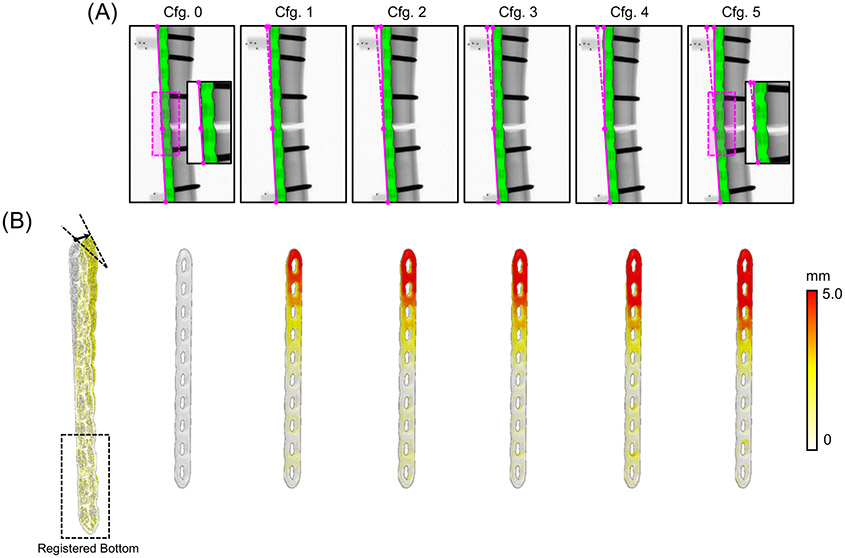
Fig. 3 shows the results using the proposed FFD-KC-Reg algorithm for unloaded (Cfg.0) and loaded Sawbone phantoms (Cfg. 1 to 5 with increasing amount of load). Fig. 3A overlays the simulated DRRs of the deformed LCP (registered using only three views) onto the measured projections from Cfg.0 to Cfg.5. There is a good match between 3D-2D registered DDRs and the measurements. Estimated displacements with respect to the undeformed LCP point cloud are illustrated in Fig. 3B for all six configurations. Increased amount of displacement was measured on the superior fragment of the Sawbone, consistent with where the load was applied experimentally. RMSEs of the reference BBs locations are listed in Table 1. The displacements were estimated with ~0.2 mm or better accuracy, independent from magnitude of the load. Errors were slightly smaller for the reference BBs in the inferior section of the implant, likely due to the less pronounced deformation of the implant in that region. In addition, registrations using only 3 neighboring views had similar RMSEs as the ones obtained using 12 views, suggesting that the oblique T1 and T3 projections provided fairly rich spatial information that could minimize the need for additional azimuthal views.

Figure 3.

(A) CBCT projections of the instrumented tibia phantom for a range of axial loading conditions. Amount of load increases from Cfg.0 to 5. The green overlays are DRRs of the estimated deformed implant obtained with FFD-KC-Reg from three projection views. (B) Estimated displacement of the deformed point cloud relative to the point cloud of the undeformed implant model. The white point cloud in the left image is the undeformed prior model, and the yellow point cloud is the estimated deformed model.

Table 1.

RMSEs of BB locations obtained using the deformation field from FFD-KC-Reg compared to their positions estimated by 3D segmentations of FDK reconstructions.

BBs Location	Number of Views	Cfg. 1 (mm)	Cfg. 2 (mm)	Cfg. 3 (mm)	Cfg. 4 (mm)	Cfg. 5 (mm)
Superior	12	0.140	0.217	0.208	0.226	0.238
	3	0.141	0.201	0.214	0.215	0.250
Inferior	12	0.166	0.153	0.166	0.184	0.202
	3	0.108	0.112	0.151	0.220	0.206

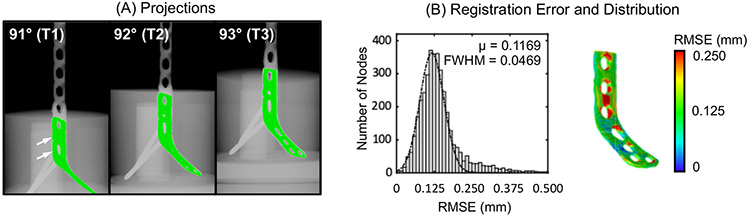
Fig. 4 shows overlaid projections and distribution of registration errors for the femoral plate phantom with complex background gradients. DRRs obtained using FFD-KC-Reg matched well with the measured projections of the deformed plate (Fig. 4A). Fig. 4B investigates the registration RMSEs, computed between the point cloud of a high-resolution, high-dose reference scan of the deformed implant and the result of registration as explained in the previous section. Similar to the previous tibial LCP experiment results, errors were typically less than 0.2 mm. The largest RMSE was observed around the holes where locking screws were inserted (arrows in Fig. A), most likely due to the confounding gradients (i.e. locking screws and calcium inserts) existing in that region. Inclusion of the locking screws into the prior implant model may help to mitigate this error.

Figure 4.

(A) Projections with overlaid DDRs of estimated deformed implant from three projection views. (B) Registration errors (mean and FWHM) and error distributions across the implant surface for the phantom with the deformed femoral plate and confounding background gradients.

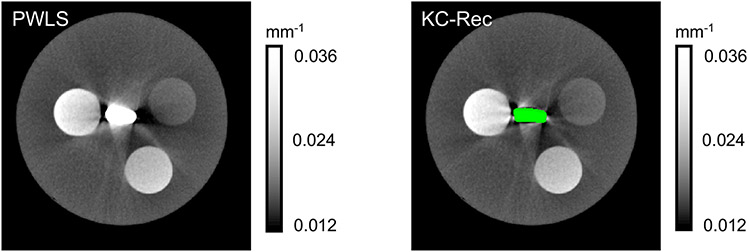
Improvement in image quality around the fixation implant achieved by model-based CBCT reconstruction with the knowledge of deformed implant is illustrated in Fig. 5. Glare pre-correction and fast Monte Carlo scatter compensation¹⁴ were applied during KC-Rec. Reduction of streaks and blooming effects around the implant model is apparent in the KC-Rec image. We anticipate further improvement in the image quality by optimizing settings for pre-corrections and reconstruction (e.g. using a finer reconstruction voxel grid in the vicinity of the implant).

Figure 5.

Model-based iterative reconstructions for the phantom with pre-deformed femoral plate and calcium inserts. The left image is the reconstruction without incorporating the deformed implant, the right one is reconstructed using the monoenergetic Known Component framework (KC-Rec).

4. DISCUSSION & CONCLUSION

Proposed deformable 3D-2D registration using an FFD model yielded <0.2 mm accuracy in the estimation of metal fixator deformation for a broad range of loading conditions. The unique three-source configuration of the CBCT system was able to achieve this accuracy using only three x-ray views by exploiting the oblique projections from the superior and inferior sources. Ongoing studies include further assessment of the effect of projection sampling on the performance of proposed deformable 3D-2D registration algorithm. Furthermore, we are also investigating alternative deformation models based on finite-element analysis (FEA) of the weight-bearing internal fixation implants¹⁵.

The work reported here focused on the quantification of the biomechanical stability of the healing fracture. In a parallel effort, we are investigating improved measurements of BMD in fracture callus by a dual energy (DE) technique, where the three sources of the system are operated at different x-ray potentials. Similar to the approach presented in this work, a Known Component model of the implant is utilized during the model-based DE decomposition to improve robustness in the presence of fixation hardware. Ongoing research includes the integration of proposed FFD-KC-Reg into the recently developed DE Known-Component Model-Based Material Decomposition (KC-MBMD) algorithm⁹.