Lunar rhythms in growth of larval fish

Abstract

Growth and survival of larval fishes is highly variable and unpredictable. Our limited understanding of this variation constrains our ability to forecast population dynamics and effectively manage fisheries. Here we show that daily growth rates of a coral reef fish (the sixbar wrasse, Thalassoma hardwicke) are strongly lunar-periodic and predicted by the timing of nocturnal brightness: growth was maximized when the first half of the night was dark and the second half of the night was bright. Cloud cover that obscured moonlight facilitated a ‘natural experiment’, and confirmed the effect of moonlight on growth. We suggest that lunar-periodic growth may be attributable to light-mediated suppression of diel vertical migrations of predators and prey. Accounting for such effects will improve our capacity to predict the future dynamics of marine populations, especially in response to climate-driven changes in nocturnal cloud cover and intensification of artificial light, which could lead to population declines by reducing larval survival and growth.

1. Introduction

The ocean is a dangerous place for larval fish because of the risk of starvation [1–3], predation [4,5] and/or advection away from suitable habitat [6–8]. Cumulative estimates of mortality during the pelagic larval stage often exceed 99% [9], which adult fishes commonly offset via high fecundities [10,11], and by spawning at locations or times that increase offspring survival [12,13]. Small reductions in risks to offspring can yield large increases in fitness when combined with high fecundity [14]. When scaled-up to populations, these small changes in larval mortality combined with high fecundity will lead to large changes in the recruitment of young fishes, which can facilitate boom-and-bust dynamics and severely challenge the effective conservation, management and sustainability of fisheries [15].

Improved understanding of factors that drive variation in larval performance could therefore lead to: (i) improved forecasts of boom-and-bust dynamics, (ii) better predictions of how fish populations might respond to future environmental change, and (iii) more sustainable fisheries. More than 100 years of research on larval fish ecology has highlighted important environmental conditions that affect variation in larval performance (e.g. food [1,3,16], predators [5,17], temperature [18–20], hydrodynamics [7,21–23]); and yet, the accuracy of forecasts remains limited [15,24–26]. What are we missing?

Nocturnal ecology—the missing piece of the puzzle? Most ecological studies ignore the night [27,28]. This may reflect a cognitive bias that shapes our conceptual frameworks and the data that we choose to collect [29]. Half of the lives of larval fishes—and important events shaping their growth and survival—occur at night [30–33]. Over the typical lifespan of a larval fish (1–10 weeks [34–36]), the night-time ocean environment may be far more variable than the day-time environment. Fortunately, night-time conditions change in somewhat predictable ways. Over a 29.5 day lunar cycle, there is tremendous variation in the intensity and timing of nocturnal illumination: nights close to the new moon are perpetually dark; nights close to the full moon are perpetually bright; nights in the intervening periods (e.g. ‘first quarter’ and ‘last quarter’ moons) are illuminated by only a portion of the lunar disc, and for opposing halves of the night. Variation in the intensity and timing of nocturnal illumination affects diel vertical migrations of zooplankton [31,37] (e.g. copepods, a primary food source for larval fishes [38–40]) and micronekton [41–45] (e.g. myctophid ‘lanternfishes’ that prey on larval fishes in large numbers [45–47]). In short, moonlight suppresses the flux of predators and prey into the surface waters where larval fishes reside [48,49]. A ‘moving window’ of lunar illumination (owing to the timing of moonrise and set across a lunar month), coupled with the influence of cloud cover that obscures moonlight, probably creates a dynamic landscape of potential risks and rewards for larval fish. From a forecasting perspective, the lunar cycle fortuitously makes this dynamic landscape predictable. The knowledge gap we still need to fill is how that lunar periodic landscape affects larvae. Consequently, we hypothesized that growth of larval fish will vary with the lunar cycle, and that temporal patterns of growth should therefore further depend on a fish's birthdate. To quantify these patterns, we: (i) used otoliths [50] (ear stones) to reconstruct size-at-age of young coral reef fish (sixbar wrasse, Thalassoma hardwicke); (ii) fit an appropriate growth model to capture age-related patterns of growth during the larval stage; (iii) interpreted daily change in residual size as a measure of age-independent growth rate (hereafter we refer to these residuals as ‘growth’); and (iv) evaluated patterns of variation in age-independent growth rate across the lunar cycle.

2. Methods

(a). Study system

We reconstructed birthdates and larval growth trajectories of recently settled sixbar wrasse, T. hardwicke, sampled from the island of Mo'orea, French Polynesia. Sixbars are coral reef fish, commonly found on shallow fringing reefs and lagoons throughout much of the Indo-Pacific region. Spawning is observed on most days of the lunar cycle [51,52], but reproductive output peaks near the new moon and is lowest near the full moon [53]. Spawning activity is also concentrated near reef edges (e.g. breaks in the reef), and during times of day when offshore water flow is maximal [52]. These reproductive patterns probably facilitate rapid transport of propagules off the reef and into the adjacent pelagic habitat where initial predation risk may be reduced [12,54]. Pelagic larvae develop for an average of approximately 47 d (range approx. 37–63 d [34,53]), before settling back to the reef at night. Larvae systematically alter developmental durations (i.e. they exhibit accelerated or delayed maturation) to settle on a darker night of the lunar cycle than is predicted by their birthdates [53]. Selection in the pelagic habitat favours individuals born close to the full moon (fish born at this time incur a mortality rate that is approximately one-fifteenth that of individuals born during the new moon [53]). This pattern of selection on birthdates and systematic developmental plasticity leads to maximal settlement near the new moon, despite the low production of eggs at a time that would lead to settlement near the new moon (i.e. approx. 47 d prior, which corresponds to the full moon [13]). As a further consequence of selection and developmental plasticity, traits of successful settlers (e.g. size and/or age) vary as a function of their birthdates and developmental histories, and these traits probably influence competitive interactions [55–57], and survival and reproduction (i.e. via carry-over effects [53]).

(b). Reconstructing larval developmental histories

We used hand nets and clove oil anaesthetic to collect recently settled sixbars (i.e. fish less than 15 mm total length, TL) from focal reefs distributed across eight locations on the north shore of Mo'orea. All activities were conducted with permission from the French Polynesian government, and in strict accordance with Victoria University of Wellington animal ethics permits (AEC22038, AEC26378). Descriptions of collection sites and details of sampling effort are presented in Shima et al. [53] which used these collections to quantify survival patterns. Briefly, we collected approximately 10 settlers per location at weekly intervals from February to June 2017 (957 settlers total), and we randomly selected a subsample of approximately five fish per location per week (n = 490) for further analysis (we subsampled owing to cost and time constraints).

We extracted sagittal otoliths, cleaned them following methods of Shima & Swearer [58], and sent them to CEAB's Otolith Research Laboratory (www.ceab.csic.es/en/otolith-research-lab-2), where they were mounted sulcus-side down and polished along the sagittal plane to expose daily growth increments along the postrostral axis (validated in Shima 1999 [59]). Daily increment widths from the otolith core to the conspicuous settlement mark were tagged and measured along this axis using the ‘calliper tool’ of ImagePro Premier.

We estimated each settler's larval age (i.e. pelagic larval duration in days) from the number of tagged daily growth increments counted from the core to the settlement mark plus two (to account for the lag between spawning and the initiation of otolith increments [34]). We estimated post-settlement age from the number of daily increments counted from the settlement mark to the otolith edge. We estimated the calendar date of an individual's birth by taking the known date of collection and subtracting the estimated age of the fish (i.e. age = number of larval increments + 2 + number of post-settlement increments). We successfully reconstructed complete otolith growth histories and calendar dates of birth (and, by extension, dates associated with each growth increment) for 411 settlers (of 490 attempted; 79 samples were either damaged during preparation or otherwise yielded growth sequences that could not be resolved and/or assigned to calendar dates with certainty).

(c). Estimating body size from otoliths

We reconstructed each settler's size (TL, mm) at each day of its larval life, from the record of daily otolith increments across the larval stage, using the modified-Fry method [60]:

$$\begin{array}{rl}{L}_i& =a+\text{exp}(\ln (L_{0p}-a)+(\ln (L_{\mathrm{cpt}}-a)-\ln (L_{0p}-a))\\ & \times \frac{(\ln (R_i)-\text{ln}(R_{0p}))}{(\ln (R_{\mathrm{cpt}})-\text{ln}(R_{0p}))}),\end{array}$$ 2.1

where L_i and R_i are fish length (TL) and otolith radius at age i, L_cpt and R_cpt are fish length and otolith radius at capture, L_0p and R_0p are fish length and otolith radius at biological intercept (which were assumed to be 1.5 mm and R_0p = 2.5 µm, respectively, based upon values from the published literature [36,61], and our own qualitative observations), and a, b and c are parameters estimated by fitting data to other relationships.

Specifically, b and c were estimated from the nonlinear regression using the nls function in R v. 4.0.2 [62]:

$$\hspace{0.17em}{L}_{\mathrm{cpt}}=\hspace{0.17em}{L}_{0p}-\hspace{0.17em}b{R}_{0p}^c+b{R}_{\mathrm{cpt}}^c,$$ 2.2

a was then defined as:

$$\hspace{0.17em}a=L_{0p}-b{R}_{0p}^c.$$ 2.3

We took this approach because Wilson et al. [63] suggested that back-calculated estimates of size provide a better proxy of fish length-at-age than otolith radius-at-age, and the modified-Fry method for back-calculating size-at-age minimized bias in estimated size.

(d). Detrending growth trajectories

We removed age-related trends in larval growth by fitting a growth model and obtaining residuals. We evaluated five candidate growth models (von Bertalanffy, logistic, Gompertz, quadratic and an unrestricted model of size as a function of age) to capture the general relationship between larval size (TL, in mm) and larval age (in days). We fitted each model (using the nls function in R for nonlinear models, lm for the unrestricted model (L_i ∼ ‘age’, modelled as a factor); [63]) to the full set of data (i.e. growth trajectories of the 411 individuals) and used Akaike's information criterion adjusted for small sample size (AICc) to determine the best model (using the MuMIn package [64]).

The relationship between size and age of sixbar larvae was best described by an unrestricted model (electronic supplementary material, figure S1, red line), although the von Bertalanffy function described length at age better than the other growth models (electronic supplementary material, figure S1, black line, shown for comparison). Despite a severe penalty for having many more parameters, the unrestricted model greatly outperformed the von Bertalanffy model (ΔAICc = 1284; electronic supplementary material, figure S2). The von Bertalanffy growth function failed to capture the size-at-age patterns of the youngest and oldest larvae (electronic supplementary material, figure S3). Thus, we use the unrestricted model in our subsequent growth analyses, which had the added advantage of generating residuals for each age with a mean of 0.

Using the unrestricted model, we obtained residuals for each observation as a measure of de-trended size-at-age. We interpreted a change in residual size as a measure of ‘growth’. Because estimates of residual size were dependent upon the sample at age i (and this varied between time-steps as individuals settled and were therefore absent from the sample at age ‘i + 1’), we estimated residual growth for successive days in the larval life of each individual as:

$$\text{residual}\hspace{0.17em}\text{siz}{\text{e}}_{(i+1)}\text{–residual}\hspace{0.17em}\text{siz}{\text{e}}_{(i^{\mathrm{\prime }})},$$ 2.4

where the subscript i′ indicates the subset of individuals at age i that remained in the pelagic until at least age i + 1. Thus, this difference in residuals provides the growth of a fish (in mm d⁻¹) during its ith day relative to all fish whose growth was measured on their ith day. Note that the average residual growth among fish at each age was = 0.

(e). Lunar patterns of larval growth

Because we previously observed strong effects of birth date on survival, we visually examined residual growth trajectories of larvae born in different quarters of an approximately 29.5 d lunar month. As an exploratory exercise, we re-expressed each larva's calendar date of birth as a lunar day (LD, where 0 corresponds to the new moon, 14 to the full moon, etc.), and then binned fish into lunar quarters of birth (i.e. centred on the new moon, first quarter moon, full moon and last quarter moon). We visualized residual growth trajectories (i.e. residual growth plotted against larval age) for each lunar cohort using smoothed conditional means (span = 3, generated from generalized additive models (GAMs)). These visualizations strongly suggested a pattern of lunar periodicity in residual growth.

We then formally evaluated lunar periodicity in residual growth using periodic regression, following methods of deBruyn & Meeuwig [65]. More specifically, we evaluated a set of candidate models that included fixed effects for lunar periodicity (using sin θ and cos θ (where θ is an angular representation of LD)), and random intercepts and slopes associated with each individual (i.e. a variable called ‘FishID’, coded as a factor with unique levels corresponding to the 411 individuals in our sample) and calendar date (modelled using the lm4e package [66]). These random effects were included to account for non-independence among multiple estimates of residual growth obtained from (i) individual fish and (ii) the same calendar dates. We fitted candidate random effects structures (using restricted maximum likelihood (REML), and a single fixed effect: sin θ), and used AICc to identify the best random effect structure (i.e. with the lowest AICc; MuMIn package [64]). We evaluated competing models of lunar periodicity that included the best random effects structure and either sin θ alone, or sin θ and cos θ (fitted using maximum likelihood; AICc to determine the best model). Finally, we re-fitted the best mixed effects model using REML to obtain unbiased parameter estimates [67].

(f). Sources of variation in lunar periodicity

Following the results of the previous analyses, we hypothesized that lunar periodicity in growth may be related to intensity and timing of nocturnal brightness. Nocturnal brightness is shaped by predictable attributes of the lunar cycle (e.g. moon phase, timing of moonrise and moonset) and by an additional component induced by the masking effects of cloud cover. This ‘natural experiment’, enabled us to formulate a statistical model that captured the two components of nocturnal brightness (the lunar cycle and cloud cover), and allowed us to quantify how growth responded to cloud cover across the lunar month (i.e. to evaluate if nocturnal brightness, per se, was causally linked to variation in growth).

We obtained estimates of lunar parameters (including times of moonrise and moonset at our study site) from https://www.timeanddate.com, and used these values to calculate ‘early night illumination’ (i.e. the proportion of time from 18.00 to 0.00 when the moon was above the horizon) and ‘late night illumination’ (i.e. the proportion of time from 0.00 to 6.00 when the moon was above the horizon) on each calendar day. In addition, we estimated ‘moon brightness’ on each calendar day as the proportion of the lunar disc illuminated (new moon = 0, full moon = 1). We estimated ‘early night brightness’ as the product of ‘early night illumination’ and ‘moon brightness’. Similarly, we estimated ‘late night brightness’ as the product of ‘late night illumination’ and ‘moon brightness’.

We obtained available records of nocturnal cloud cover data estimated by the Atmospheric Infrared Sounder [68]. We estimated ‘cloud cover’ at our study location from the proportion of an area of night sky within a bounding box (3° latitude × 3° longitude centred on Mo'orea) that was obscured by clouds (i.e. irrespective of cloud type or altitude). Where nocturnal cloud cover observations were missing (19 of 126 records), we infilled with adjacent day-time observations. Finally, we logit transformed cloud cover to meet statistical assumptions.

We modelled growth as a function of (i) early night brightness, (ii) late night brightness, (iii) cloud cover nested within early night brightness, and (iv) cloud cover nested within late night brightness. We also included a random intercept for FishID, and we evaluated a set of autoregressive error structures to account for temporal autocorrelation in our data. Specifically, we evaluated a first-order autoregressive error structure (AR1) and an autoregressive-moving-average error structure (ARMA; p = 1, q = 1), and used AICc to identify the best model. Because the lme4 package does not currently support autoregressive error structures, we fitted these models using lme (nlme package [69]).

If growth of larval sixbars is mediated by patterns of nocturnal illumination (e.g. brightness at particular times of night), then we predicted that the effects of increasing cloud cover should differ qualitatively with the phase of the moon. Specifically: (i) at the new moon (when the moon is below the horizon throughout the entire night), increasing cloud cover should have no effect; (ii) during the lunar phase when growth is below average, increasing cloud cover should be beneficial (i.e. growth should converge to levels observed for a darker night, i.e. the new moon); and (iii) during the lunar phase when residual growth is above average, increasing cloud cover should be costly (again, residual growth should converge to levels observed for a darker night, i.e. the new moon). We used the ‘effects’ package [70] to visualize parameter estimates.

3. Results

(a). Lunar patterns of larval growth

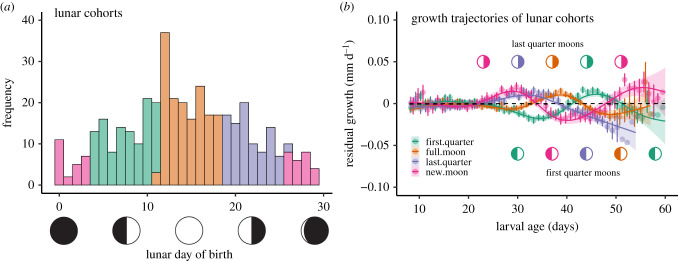
Larval fish had birthdates across the entire lunar cycle, although more fish in our sample were born close to the full moon than during other lunar phases (figure 1a). Larval sixbars, like most reef organisms, develop in a pelagic environment before settling back to the reef, where they remain through adulthood. Pelagic larval durations ranged from 37 to 61 d. Growth was relatively invariant over the first 25 d of larval life, but growth patterns became more pronounced (and variation appeared to be a function of the lunar cycle) after day 25 (figure 1b). The shift in these growth trajectories was related to the timing of a fish's birth relative to the lunar cycle, with each cohort's trajectory offset by approximately 7 d (i.e. an interval similar to the offset between lunar cohorts), suggestive of lunar periodicity in larval growth. All lunar cohorts experienced at least one episode of accelerating growth that appeared to coincide with the last quarter of the moon, and a minimum near the first quarter.

Figure 1.

Lunar cohorts of larval sixbar wrasse and their residual growth trajectories. (a) Frequencies of sampled larvae (n = 411) born on each LD. Colour identifies ‘lunar cohort’ determined by birthdate on a lunar calendar (estimated from otoliths). Birthdates from LD ∼ 26 to LD 3 = ‘new moon’; 4 ≤ LD ≤ ∼11 = ‘first quarter’; approximately 12 ≤ LD ≤ 18 = ‘full moon’; 19 ≤ LD ≤ ∼25 = ‘last quarter’ (note that variation assignments at day 11 and 26 is owing to uneven durations of lunar months). (b) Residual (i.e. age-independent) growth trajectories of larvae assigned to four lunar cohorts. Given are mean ± 1 s.e. residual growth per day (points are offset for presentation) and fitted lines are predicted by a GAM (span = 3). Dashed line indicates average growth. Symbols indicate the timing of the last quarter moons (top) and first quarter moons (bottom) for each lunar cohort (i.e. for median lunar birthdates of each lunar cohort). (Online version in colour.)

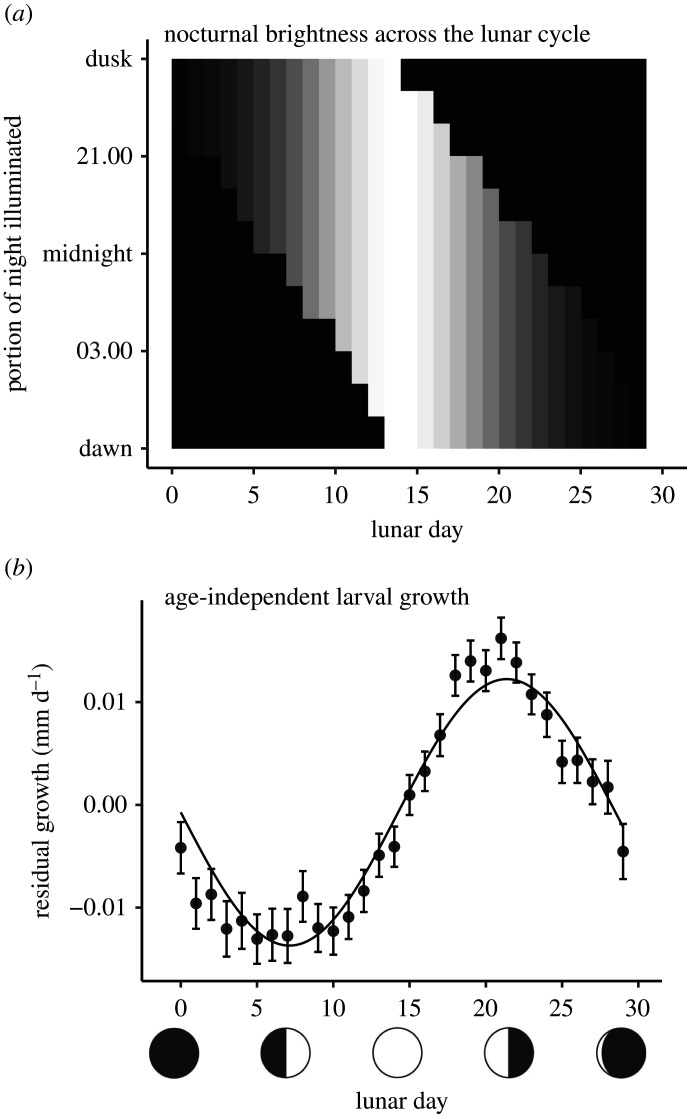
We used periodic regression to formally quantify lunar periodicity in growth. We constrained our formal analyses to observations of residual growth derived from larvae aged 25–50 d because growth trajectories appeared to diverge after 25 d of age (figure 1b) and nearly all fish had completed their larval development by 50 d of age (see the electronic supplementary material, figure S4 for a presentation with all ages). We evaluated a set of competing statistical models and settled on a random effect structure that included both random intercepts and slopes associated with FishID and calendar date (ΔAICc for the next best model = 8.11; electronic supplementary material, table S1). Inclusion of cos θ did not improve model fit (ΔAICc = 0.56; i.e. ΔAICc < 2); consequently we considered the simplified model (with periodicity modelled by sin θ alone) to be the best model. The parameter estimate for sin θ was −0.0130 (s.e. = 0.0014, t-value = −9.30), and the intercept was −0.000731 (s.e. = 0.000982, t-value = −0.74), indicating the following lunar periodicity: growth was lowest near the first quarter moon (LD approx. 7), increased through the full moon, and peaked near the last quarter moon (LD approx. 21; figure 2).

Figure 2.

Lunar pattern of (a) nocturnal brightness and (b) residual growth of larval sixbar wrasse. Nocturnal brightness is expressed as intensity (i.e. proportion of lunar disc illuminated: greyscale, black = 0, white = 1) and timing (moonrise and moonset, averaged over the sampled months, rounded to the nearest hour) of moonlight across lunar nights. Residual (i.e. age-independent) growth is mean ± 1 s.e., fit by periodic regression (note our formal analyses included a set of random effects not represented by this fitted line). y-axis in panel (a) ranges from 18.00 (approx. dusk, y-axis maximum) to 6.00 the following morning (approx. dawn, y-axis minimum). x-axis of both panels is date expressed on a 29.5 d lunar cycle (0 = new moon, 14 = full moon, etc.).

(b). Sources of variation in the magnitude of lunar periodicity

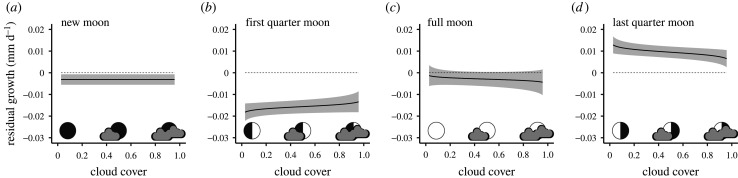
Temporal variation in nocturnal cloud cover facilitated a ‘natural experiment’ that enabled us to test a hypothesis that growth-related effects were mediated by moonlight, as opposed to other sources of variation occurring on a lunar schedule (e.g. tides). Temporal autocorrelation in larval growth was best captured by an ARMA (q = 1, p = 1) error structure. This model outperformed a competing model with an AR1 error structure (ΔAICc = 380.94), and effectively eliminated temporal autocorrelation in the residuals. Our model suggests that cloud cover modifies the effect of nocturnal lunar illumination on growth of larval fish, and it provides support for our hypothesis that nocturnal brightness mediates growth of larval fish (electronic supplementary material, table S2). The effect of cloud cover depends on the timing of lunar illumination: when the early portion of the night is bright, cloud cover tends to increase growth of larval fish (0.00143, s.e. = 0.00099, t = 1.44). By contrast, when the latter half of the night is bright, cloud cover reduces growth of larval fish (−0.00189, s.e. = 0.00089, t = −2.11). Importantly, these parameter estimates indicate that the effect of cloud cover varies qualitatively with the state of the moon. Nocturnal cloud cover has no effect on larval growth when the moon is not visible (figure 3a) or is full (figure 3c), which is when we observed average growth of larvae. However, cloud cover increases larval growth during portions of the lunar month when growth is normally low, presumably because nocturnal brightness is deleterious for growth (figure 3b, cf. figure 2b), but cloud cover reduces larval growth during portions of the lunar month when growth is normally high, presumably because nocturnal brightness enhances growth (figure 3d, cf. figure 2b).

Figure 3.

Predicted residual growth of larval sixbar wrasse as a function of nocturnal cloud cover, conditional on lunar parameters set to (a) the new moon, (b) the first quarter moon, (c) the full moon, and (d) the last quarter moon. Given are predicted values (black lines) ± 95% CI (shaded envelopes). X-axis is the proportion of night sky (in a 3° latitude × 3° longitude region centred on Mo'orea) shrouded in cloud, back-transformed to the original scale (0 = clear night, 1 = fully cloudy night). Predictions falling above the dashed line indicate better-than-average growth; values below the dashed line indicate worse-than-average growth.

4. Discussion

Our study demonstrates strong lunar periodicity in growth rates of larval fish. On the best nights of the lunar month (i.e. near the last quarter moon) larval sixbars grew approximately 0.012 mm d⁻¹ more than average, but on the worst nights (i.e. near the first quarter moon), they grew approximately 0.014 mm d⁻¹ less than average. Thus, for a typical larval sixbar (calculated for an individual 37.5 d in age), its growth is 24% greater on the best night relative to the worst. This matters because larval growth is inextricably linked to larval survival, recruitment and fisheries productivity [1–6].

Larval growth was not maximal on the brightest nights of a lunar cycle, as would be expected if growth was simply driven by vision of larval fish [71,72]. Instead, growth was maximized when the first half of the night was dark and the second half of the night was bright (i.e. during the last quarter moon when the moon rises around midnight). Conversely, larval growth was minimized when the first half of the night was bright and the second half of the night was dark (i.e. during the first quarter moon). Nocturnal cloud cover moderated these effects, making the worst nights for growth better and the best nights for growth worse. Importantly, these effects were estimated from a natural experiment that decoupled moonlight from other aspects of the lunar cycle, and suggested that moonlight per se is the environmental mechanism that mediates growth. This is notable because it suggests that nocturnal illumination drives an important component of the productivity of marine ecosystems.

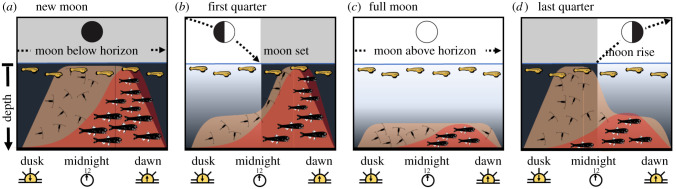
We hypothesize that these lunar patterns of growth are ultimately linked to the effect of moonlight on organisms that vertically migrate and enter surface waters at night. These diel vertical migrants (DVMs) are suppressed by moonlight [31,37,41–45,73], although the component species (or functional groups) that comprise this mobile community may vary in their sensitivities and/or responses to moonlight [74]. Zooplankton (potential prey) respond rapidly to the onset of darkness [37,74]. By contrast, micronekton (e.g. myctophids that prey on larval fishes) may initiate nightly migrations from much deeper depths and reach surface waters to hunt larval fishes later at night, and with a significant delay relative to vertically migrating zooplankton [45–47]. Consequently, prey availability in surface waters may be suppressed by early nocturnal brightness while predator densities may be suppressed by late nocturnal brightness (figure 4). We hypothesize that these effects result in the lunar patterns of growth for larval sixbars. Influxes of both prey and predators may be relatively high during the new moon, and predation risk may prevent larval fish from capitalizing on increased prey biomass [75] (figure 4a). Predator and prey DVMs may both be suppressed during the full moon, leading larval fish to be relatively free of risk, but with relatively little food in the surface waters, resulting in no net growth advantage (figure 4c). Growth may be worst at the first quarter moon because prey are suppressed but predators are not (figure 4b), whereas growth may be best at the last quarter because predators are suppressed and prey are not (figure 4d). The more we know about how marine organisms respond to the lunar cycle and night-time illumination, the more reliably we can make predictions about the future of marine ecosystems.

Figure 4.

A schematic hypothesis of how nocturnal illumination may shape larval growth of a reef fish. The lunar cycle is represented as four discrete panels for simplicity: (a) new moon, (b) first quarter moon, (c) full moon, and (d) last quarter moon. Each panel shows a cross section of the atmosphere (white = moon above horizon; grey shading = moon below horizon) and the water column (light blue line = sea level, depth gradient from epipelagic to mesopelagic) through time (from dusk to dawn). Moon phase, moonrise and moonset times create variation in nocturnal illumination that affects the water column. Larval sixbar wrasse (shown in yellow) remain in surface waters; their prey (copepod icons/brown shading) and their predators (myctophid icons/red shading) undergo diel vertical migrations that are sensitive to nocturnal illumination. Prey can respond quickly to changes in light; predators migrate from deeper depths and therefore respond with a time lag. (Online version in colour.)

We note that our sampling can only account for growth of larval fish that survived to settlement. We speculate that interactions between larvae of reef organisms and the DVM community may also contribute to changing patterns of selective predation across the lunar cycle. These effects, mediated by nocturnal illumination, are likely to affect the composition of larval communities that survive to settle back to the reef. We also note that the behaviour patterns of larvae of reef organisms themselves may be mediated by nocturnal illumination, and such effects may further contribute to observed patterns. Lastly, lunar periodicity in spawning of other reef associated organisms could increase prey availability for larval fishes and thus contribute to variation in growth rates during particular phases of the lunar cycle. None of these possibilities are mutually exclusive with our hypothesis of an important interaction between the DVM and the surface-dwelling larvae of marine reef fishes (a similar hypothesis has also been proposed for pelagic fisheries [27]).

Our data suggest that growth rates of young larvae (i.e. less than 25 d of age) are relatively invariant (figure 1b; see also the electronic supplementary material, figure S4). Early stages of development are primarily fuelled by maternal provisioning (i.e. yolk) but this intrinsic energy source is unlikely to account for homogeneous growth beyond the first few days of larval life. We speculate that younger (and therefore smaller) larvae may be relatively unaffected by the DVM community (i.e. they may be sufficiently small to escape increased predation risk and/or unable to capitalize on prey sources that are affected by nocturnal processes). Younger larvae may simply experience a more homogeneous prey and predator environment.

Periodic variation in lunar illumination has remained a constant environmental feature through the history of all life on Earth, and has probably shaped the evolution of life-history strategies that relate to spawning and larval development in the sea. Indeed, many marine organisms reproduce [12] and complete their pelagic larval stage [13,76,77] on a lunar schedule, and this may indicate an evolutionary response to periodic moonlight and its associated effects (e.g. facilitation and/or suppression of the DVM community). Sixbars spawn disproportionately on the days near the new moon [53], even though survival is lowest for fish born at the new moon. Part of the explanation for this seemingly paradoxical spawning pattern may lie in the observed lunar pattern of growth. Spawning at the new moon is the only time that provisions offspring with two episodes of beneficial growth in the pelagic larval stage (with the second episode occurring immediately prior to settlement; figure 1b). For the growth advantage to reconcile the paradox, we note that the growth advantage associated with spawning on a new moon would need to compensate for the reduced survival of larvae by greatly increasing the fitness of post-settlement juveniles and/or adults (e.g. via a carry-over effect). Our previous work [53] suggests that such fitness advantages do accrue to fish that settle to the reef at older ages and larger sizes (i.e. traits that are probably associated with larvae that were spawned on the new moon).

The magnitude of lunar periodic larval growth that we quantified for sixbars rivals documented effects of food and climate [20], both currently used to improve forecasting that informs management decisions for important fisheries [25]. Our results suggest that changes in nocturnal illumination (attributable to the lunar cycle and cloud cover) could explain some of the notoriously high variability in stock-recruitment relationships observed in many fisheries. This is good news because the lunar cycle is predictable, and global patterns of cloud cover (that modify lunar effects) are routinely measured by satellites; hence, such effects could be incorporated into existing management frameworks with little additional cost or effort. What we need is more research quantifying these lunar effects on marine populations. Our work also suggests that other factors which can contribute to variation in nocturnal illumination in the sea, including artificial light sources (e.g. overspill and/or cloud reflection from coastal cities [78–80]), suspended sediments [81], and/or climate change that is predicted to alter geographical distributions of cloud cover [82–84], have the potential to disrupt marine ecosystems. Accounting for such effects may greatly improve forecasts that inform future management and conservation efforts.

Ethics

All research was conducted under protocols approved by Victoria University of Wellington's Animal Ethic's Committee (permit numbers: 22038, and 26378). Field work in French Polynesia was conducted under research permits issued by the Delegation a la Recerche (de la Polynesie Francaise).

Data accessibility

All data and R code for analyses and figures are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.zgmsbcc93 [85].

Authors' contributions

All authors contributed to the conceptualization and design of this research. J.S.S. coordinated the data collection with assistance from S.E.S. J.S.S. analysed the data with essential input from all authors; J.S.S. wrote the initial draft of the manuscript, with essential input from all authors.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Royal Society of New Zealand–Marsden Fund (VUW1503), the U.S. National Science Foundation (OCE-1130359), and Victoria University of Wellington.