An Agent-Based Modeling of COVID-19: Validation, Analysis, and Recommendations

Abstract

The coronavirus disease 2019 (COVID-19) has resulted in an ongoing pandemic worldwide. Countries have adopted non-pharmaceutical interventions (NPI) to slow down the spread. This study proposes an agent-based model that simulates the spread of COVID-19 among the inhabitants of a city. The agent-based model can be accommodated for any location by integrating parameters specific to the city. The simulation gives the number of total COVID-19 cases. Considering each person as an agent susceptible to COVID-19, the model causes infected individuals to transmit the disease via various actions performed every hour. The model is validated by comparing the simulation to the real data of Ford County, KS, USA. Different interventions, including contact tracing, are applied on a scaled-down version of New York City, USA, and the parameters that lead to a controlled epidemic are determined. Our experiments suggest that contact tracing via smartphones with more than 60% of the population owning a smartphone combined with city-wide lockdown results in the effective reproduction number (R_t) to fall below 1 within 3 weeks of intervention. For 75% or more smartphone users, new infections are eliminated, and the spread is contained within 3 months of intervention. Contact tracing accompanied with early lockdown can suppress the epidemic growth of COVID-19 completely with sufficient smartphone owners. In places where it is difficult to ensure a high percentage of smartphone ownership, tracing only emergency service providers during a lockdown can go a long way to contain the spread.

Supplementary Information

The online version contains supplementary material available at (10.1007/s12559-020-09801-w)

Introduction

COVID-19 is a highly transmissible disease that was declared a global pandemic on March 11, 2020, by the World Health Organization (WHO) [1]. The disease is caused by a strain of coronavirus, namely, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [2], and is highly infectious, resulting in more than 56 million cases worldwide as of November 19, 2020 [3]. While originating in Wuhan, China, in December 2019 [4], the disease has spread to more than 200 countries of the world by now [3]. Countries have taken non-clinical restrictive measures (e.g., lockdown) as the primary approach to contain the virus’s outbreak since effective clinical measures are yet to be found [5, 6]. This disease has heavily affected the economies of most countries, leading to the global coronavirus recession or the Great Shutdown [7].

The SARS-CoV-2 virus spreads through close contacts, i.e., when a susceptible person inhales droplets coming from an infected individual through coughing or sneezing [8]. It can also infect people if they touch their eyes, nose, or mouth after having physical contact with contaminated surfaces [8]. This nature of transmission has given rise to various preventive practices, referred to as non-pharmaceutical interventions (NPI), such as wearing masks, personal protective equipment (PPE), washing hands frequently, staying home, and avoiding gatherings [9].

In order to model the transmission of this disease, many mathematical models have been reported in the literature. For example, Kermack and McKendrick have proposed a Susceptible-Infected-Recovered (SIR) epidemic model in [10] and Hethcote has proposed a Susceptible-Infected-Susceptible (SIS) epidemic model in [11]. On the other hand, in [12], a microsimulation model has been applied to assess the impact of NPIs for COVID-19. In parallel to the abovementioned models and variants thereof, there are attempts to develop agent-based models (ABM) in the literature with different aims and goals. In fact, agent-based models have been used to model various diseases for a long time (e.g., [13–17]). Thus, agent-based models have become rather popular to model the spread of COVID-19 and analyze various ways to approach the issue [18–21]. Notably, many research works have experimented with contact tracing and its impacts on the spread of COVID-19 [22–25].

In this paper, we present an ABM intending to simulate the disease dynamics and transmission of COVID-19 among the inhabitants of a city. Our approach involves validating our agent-based model by running simulations on Ford County, KS, USA. Various parameters of our ABM are fitted to validate the model. Later, these parameters are used for running all experiments for a scaled-down version of New York City, USA.

Our model can be adapted for any realistic scenario by incorporating appropriate parameters specific to the city under consideration. We also examine the impacts of protective measures and city-wide lockdown on the infection spread and determine the suitable parameters that help to contain the spread. Our experiments further explore the conditions under which the so-called digital herd immunity [26, 27] can be achieved by applying contact tracing approach via smartphones.

Our results suggest that, with lockdown in effect, if more than 60% of the population in a city are traceable through smartphones, effective reproduction number (R_t) falls below 1 within 3 weeks of intervention. Moreover, 75% or more of the population owning smartphones results in R_t < 1 sooner, and the new infections are eliminated entirely within 3 months of intervention.

Methods

Data and Assumptions

We use two categories of data in our model as follows (see Supplementary Sections 1–3 for details):

1. Location-specific data

   1. We use the demographics of the inhabitants in a particular city (i.e., education, employment, life expectancy, percentage of individuals having different professions, and the nature and timing of various tasks performed by the people) and the data related to the number of transports and the average family size.
   2. We also use the data related to COVID-19 disease, its spread among the population, and the intervention measures taken by the authorities. These include the number of infections in the city and the day of the announcement of restrictive policies or awareness measures.

   To conduct our simulations, we have collected the above data for Ford County, KS [28–36], and New York City [37–42], of USA.

2. Physiological data

   The probability of a person coughing and sneezing, touching contaminated objects, coming into physical contact with others, or washing hands is also an important parameter of our model, which would differ based on whether a person is at work, home, or hospitalized.

As an abstraction, we ignore the changes in the city’s population within the period of our simulation, i.e., we ignore births, deaths, and migrations.

The Agents

In our ABM, each person is an agent and each agent is susceptible to COVID-19. We consider five possible states for a person at any particular time as follows:

1. Not-infected or healthy (H)

2. Infected, not contagious, asymptomatic (N)

3. Infected, contagious, and asymptomatic (A)

4. Infected, contagious, and symptomatic (S)

5. Dead or recovered (D)

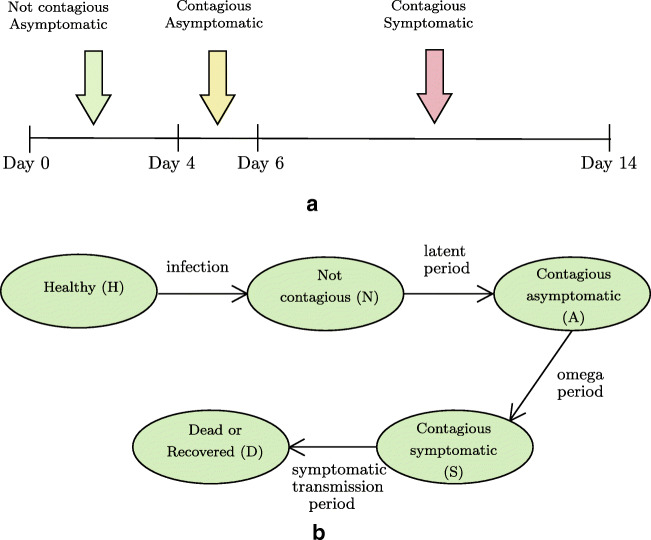
Figure 1a presents the time interval between different stages of infection [43, 44], and Fig. 1b demonstrates the state transitions.

Fig. 1.

Stages of COVID-19 infection (a) and state transitions in our model (b)

Each agent is associated with a family and is assigned to one of four generic professions: doctors and nurses (healthcare workers), students, service holders, and the unemployed. For each profession, the behaviors or tasks of the agents can be summarized through a set as follows:

• Tasks for students, T_s = {Stay Home, Go to School, Study, Return Home, Attend Event}

• Tasks for doctors, nurses, healthcare workers, T_d = {Stay Home, Go to Hospital, Treat Patients, Return Home, Attend Event}

• Tasks for service holders, T_w = {Stay Home, Go to Work, Work, Return Home, Attend Event}

• Tasks for unemployed people, T_u = {Stay Home, Go outside, Attend Event, Return Home}

Each task is controlled by some dynamic parameters, as mentioned below.

• i.min_start_time, max_start_time Determine when a particular task should begin in the day.
• ii.min_duration, max_duration Control the duration of a particular task.
• iii.min_prob, max_prob Determine the probability with which an agent should perform the task.

Each agent performs several actions irrespective of the profession (s)he belongs to. This can be represented by the following set.

• Set of actions for agents, A = {Sneeze, Contaminate thing, Physical contact, Wash hands}

Note carefully that we distinguish the term “action” from the term “task” in our context: the latter refers to professional tasks (already described above for different professions), whereas, here, we discuss the former. Only the action of washing hands has a positive (in the context of disease spread) impact on the person himself who is performing the action, whereas the rest affect others, and the effect is negative. Sneeze and physical contact cause human to human transmission. On the other hand, the action Contaminate thing realistically signifies an agent touching fomite, which in turn infects other agents. For simplifying the model, we have implemented them under a common framework. Each such action is controlled by some dynamic parameters as follows:

• i.min_time_gap, max_time_gap Determine the interval between two consecutive occurrences of an action.
• ii.min_prob_affect, max_prob_affect Determine the probability with which the action would have an effect in general.
• iii.min_prob, max_prob Determine the probability with which an agent should perform the action.
• iv.min_effect_others, max_effect_others Determine the probability with which the action would affect others.
• v.min_effect_self, max_effect_self Determine the probability with which the action would affect oneself.

Each person has a protection_level. As (and when) awareness is increased in the city, this value is improved with varying degrees. For doctors and healthcare professionals, a higher degree of protection is apportioned. The real-life significance of protection_level lies in the use of protective face shields, masks, maintaining hygiene, etc. When an agent reaches state S (infected, contagious, and symptomatic state), (s)he may or may not be hospitalized which, in our model, has been determined through probabilistic means. If and when hospitalized, all activities of the agent (i.e., patient) are halted, and he stays at the hospital throughout the day.

Interaction Between Agents and Transmission

Agents/persons in our model are associated with groups (depending on the person’s task) for interaction at every time unit (i.e., hour).

The set of groups in our model is given by G = {F, T, W, E, H} as defined below.

• F = Stay home

• T = Commute

• W = Work or attend school

• E = Attend event

• H = Stay at the hospital

Each agent at any period of time belongs to one of these five groups for an hour before being allocated to another group (based on Supplementary Tables 3 and 8).

For transportation, at first, our model calculates the total number of free seats by multiplying the number of transports with the passenger capacity. Then, it assigns a free seat to a new agent. Every time an agent is given a free seat, the seat becomes occupied, and the number of free seats in that transport is decremented.

Within a group, agents can remain in different proximity with one another. Our model, at first, generates every possible pair of individuals in a group. Each pair then receives a numerical value (i.e., representing the proximity) chosen from one out of ten predefined ranges. Each range satisfies the relation 0 ≤ B_low < B_high ≤ 1, where B_low and B_high are lower and upper bounds of the range respectively.

The actions that lead to infection of another person will only matter when those are being executed by an infected person in the contagious stage of the disease. Equation (1) calculates the infection value of a susceptible person due to negative impacts of actions performed by an infected agent.

$$infection=(1-protection\text{\_}level)\times E\times proximity$$ 1

Here, 0 ≤ O_min ≤ E ≤ O_max ≤ 1; O_min and O_max represent lower and upper limits of the impacts of an infected person’s actions on others respectively.

On the other hand, Eq. (2) calculates the infection value due to the positive effects of actions, i.e., washing hands.

$$infection=(-1)\times (1-protection\text{\_}level)\times E$$ 2

Here, − 1 ≤ S_min ≤ E ≤ S_max ≤ 0; S_min and S_max are, respectively, the lower and upper limits of the impacts of an action on oneself.

This infection value is then compared with an action_infect_threshold. Exceeding this threshold would cause the susceptible person’s infection_level to be incremented (or decremented in case of actions with a positive impact) by an amount equal to the infection value calculated above. By the end of the day, based on an infection_threshold, whether a person will be infected or not will be determined by this infection_level.

Even after a specific action has been performed, it is not guaranteed that it will indeed have an effect on others. Besides, an action may have an effect, but it may not directly contribute to the spread of infection. This is why we have introduced multiple layers of probabilities and thresholds in the model.

Environment

Awareness and Lockdown

A city may declare lockdown policies and awareness measures on the X^th and Y^th days of community transmission respectively. For the latter, a person’s awareness_level is incremented from day Y. For a realistic simulation, we allow some individuals to continue working or leaving their residences for different necessary tasks during lockdown.

Contact Tracing and Quarantine

Contact tracing is the process of identifying the people who came within the close proximity of an infected person and subsequently quarantining them before they can infect others. Since new infections are only found due to the onset of symptoms, it is likely that some people who came into contact with the infected person during the omega period (see Fig. 1) have been infected as well. Traditional contact tracing through interviewing infected patients is not feasible [26]. Leveraging smartphones through appropriate contact tracing apps [45] for tracking is a more reasonable option. This may be referred to as digital contact tracing.

Here, we consider a scenario where all smartphone users would have contact tracing apps installed and will be brought under the umbrella of such an intervention. Our model traces (and subsequently quarantines for 14 days) someone who was in a group with an infected patient for a number of days prior to the onset of symptoms.

Digital Herd Immunity

When most people in a population become immune to an infectious disease (via vaccines or mass infection), the disease cannot spread anymore. This condition is called herd immunity [46]. In such a scenario, even if someone comes in contact with infected patients, he will not fall sick, i.e., the disease will be defeated by his immune system. However, even without making the population biologically immune to an infectious disease, the population can be made immune to epidemic growth with the use of technology [26]. This condition is known as digital herd immunity (DHI).

By digital contact tracing and quarantining potentially infected people even before they show any symptoms during their latent period, the spread of the disease can be significantly lowered, eventually leading to the elimination of any further epidemic growth, thereby achieving digital herd immunity. In a nutshell, digital herd immunity suggests that there is always a critical fraction 0 ≤ ϕ_c < 1 of app ownership, such that subscribing to contact-tracing apps by a fraction ϕ > ϕ_c of the population is sufficient to prevent epidemic spread [26].

Code and Availability

We have implemented our ABM using Python3 programming language [47]. The experiments have been conducted in the following machines: (i) a desktop computer having intel core i7-7700 processor (3.6 GHz, 8 MB cache) CPU, 16 GB RAM, and NVIDIA TITAN XP (12 GB, 1582 MHz) GPU; (ii) a virtual private server (16-core CPU), 64 GB RAM, and 200 GB Storage; (iii) a cloud computing platform Galileo from Hypernet (https://galileoapp.io/). All code and data can be found at the following link: https://github.com/s-shamil/agent-based-modeling-covid-19.

Results

An Overview of Our Experiments

The simulations that we ran can be divided into two categories. Firstly, we validated the model for Ford County by running the simulations for a period of 60 days. Secondly, we conducted our experiments to examine the effects of lockdown, contact tracing, and a combination thereof on a scaled-down version of the New York City, USA.

We chose Ford County for the availability of data and a high number of COVID-19 tests performed by the county. Although an initial case of infection was identified in Ford County on March 17, 2020, the infected individual was effectively isolated [48]. Thus, we have run the simulation from April 8 with 2 initial cases with lockdown imposed from day 1 [29]. On the other hand, New York City was chosen due to the massive COVID-19 hit in this city.

Through our experiments, we have examined the impacts of protective measures and city-wide lockdown on the infection spread and determined the suitable parameters to contain the disease spread.

We infer the factors that lead to digital herd immunity and, finally, apply these parameters to the simulation of Ford County. We further compute and assess the parameter called effective reproduction number (R_t) [49], following the method given by Venkatramanan et al. [50]. If R_t < 1 can be sustained, it would signify that the number of new cases will gradually terminate among the population [49, 51].

For the sake of validating the model, we have first shown that the output generated from our model with Ford County’s parameters nicely follows the real data. For the experiments on New York City, we ran multiple simulations and reported the respective mean accompanied by the confidence interval of 95% in the graphs. Since the graphs reporting the effective reproduction number (R_t) contain overlapping curves, for clarity, we have shown the mean curves only.

Model Validation Using Ford County Data

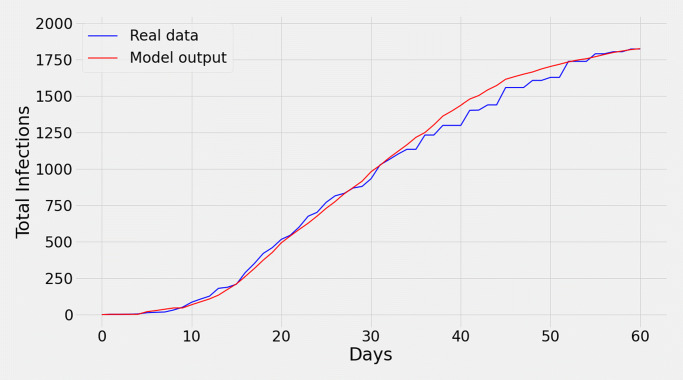
We ran the simulation for the full population (size = 33,619) of Ford County (Fig. 2). The blue curve in Fig. 2 represents real data of total cases. Our simulation results, represented by the red one, have a root mean square error (RMSE) of 50.23 approximately. The resulting curve is obtained by applying varying degrees of protection_level (defined in “The Agents” section), action_infect_threshold, and infection_threshold (defined in “Interaction Between Agents and Transmission” section) for different segments, i.e., ranges of days (Tables 1 and 2).

Fig. 2.

Validation of the model. The blue (red) curve represents the real (simulated) total cases. The red curve nicely follows the blue curve with an RMSE of around 50.23

Table 1.

Variation of protection_level: protection_level on different days for inhabitants of Ford County

	Days 0–15	Days 16–20	Days 21–38	Days 39–60
Healthcare workers	0.2	0.22	0.8	0.95
Others	0.1	0.12	0.75	0.9

These values have been obtained through extensive experiments. Healthcare workers include all doctors, nurses, and people working in the health sector. Others include students, service holders, and unemployed people

Table 2.

Variation of action_infect_threshold and infection_threshold: action_infect_threshold and infection_threshold on different days for inhabitants of Ford County. These values have been obtained through extensive experiments

	Days 0–8	Days 9–20	Days 21–38	Days 39–45	Days 46–60
action_infect_threshold	0.5	0.65	0.665	0.675	0.7
infection_threshold	0.5	0.65	0.65	0.65	0.65

Simulations on Ford County

Effect of Lesser Interventions

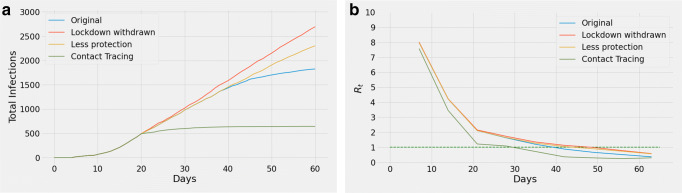
We simulated to check how the outcome would change with a lesser degree of intervention. Firstly, protection_level of the last segment (days 39–60) was lowered (yellow curve) by keeping it the same as the previous segment (days 21–38). This resulted in a significant increase of daily incidence as compared to the blue curve (i.e., the curve representing the total cases simulated by the model), whereas lifting movement restrictions from day 21 (red curve), as opposed to continuing the lockdown, results in an even worse situation (Fig. 3a). The variations of R_t for these changes are illustrated in Fig. 3b.

Fig. 3.

Effect of (i) removing lockdown from day 21 (red curve), (ii) allowing the protection_level of days 21–38 to continue until day 60 (yellow curve), and (iii) the simulation of total cases (blue curve) are shown in (a). Contact tracing from day 21 (green curve) with 75% smartphone users results in fewer infections (with respect to the total population) compared to the blue curve by the end of day 60. Corresponding R_t curves are reported in (b)

Effect of Contact Tracing

Figure 3a compares the impact of contact tracing implemented from day 21 (green curve) with the simulation of total cases (blue curve). In this simulation, we consider 75 % of the population to be smartphone holders. However, not everyone in a group remains close enough (to the infected person) to allow smartphone applications to record their data. Considering 30% people in a group within reachable range and 90% group records being available, the simulation is continued until day 60 by tracing the contacts for the previous 2 days. Although infections continue to rise extensively in case of the blue curve, the green curve starts to flatten and the spread terminates (Fig. 3a). As for the variation of R_t (Fig. 3b), both the blue and green curves proceed to fall below 1 but the green one (i.e., involving contact tracing) does so sooner.

Simulation on New York City: a Scaled-Down Version

Simulation on New York City for a period of 120 days is done considering a population of 10,000; parameters specific to New York City in the input are accommodated for the smaller population to ensure the appropriate scaling (see Supplementary Table 10).

As a basic validation of this scaled-down version, the R_t values for the full population using an SIR model [10], and the same for the (scaled-down) ABM model have been compared, and the calculated RMSE was found to be 0.4626 for 90 days of simulation (see Section 4 of Supplementary file for more details).

Effect of Interventions

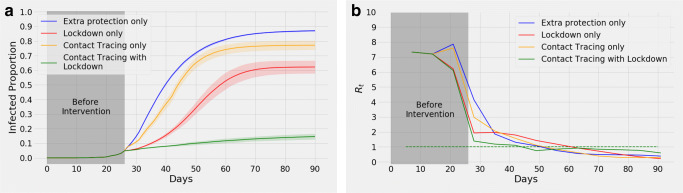
We have simulated four different scenarios with different intervention combinations, namely, no intervention (NI; blue), only contract tracing (CT; yellow), only lockdown (LD; red), and a combination of CT and LD (CT+LD; green). For all scenarios, the parameters are the same as NI until day 27, up to when around 5% people are infected.

We consider 75% of the agents to be traceable as smartphone owners [52]. In a realistic scenario, lockdown policies and movement restrictions do not ensure that everyone will stay home. Thus, we consider that the lockdown will be effective on all students and on 50% of the service holders; among them, to simulate a practical lockdown, we keep 70% individuals strictly within their homes and allow the rest (30%) to go out for different reasons. Evidently, CT+LD results in the least number of infections (Fig. 4a). The relative trends of R_t also support this (Fig. 4b) as R_t drops below 1 much faster for CT+LD.

Fig. 4.

a illustrates the effects of interventions imposed since day 27: introducing added protection (blue curve), contact tracing (CT) alone (yellow curve), lock down (LD) alone (red curve), both contact tracing and lock down (CT+LD) in combination (green curve). The shaded portion represents confidence interval. Corresponding means of R_t curves are illustrated in (b)

Varying the Percentage of Smartphone Users for Contact Tracing

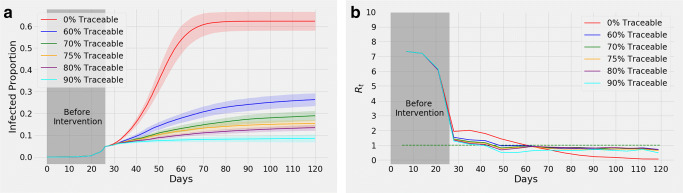
Figure 5a illustrates a comparison considering different percentages of the population to be smartphone owners. In all these cases, we consider 30% people in a group associated with a person to be in close proximity and traceable only if they own smartphones. Moreover, among all the groups that a person stays in throughout the day, we assume 90% of their records to be available. Figure 5b illustrates the corresponding variation in R_t. As the percentage of smartphone owners increases, R_t falls below 1 more rapidly. Furthermore, Fig. 5a demonstrates that the total percentage of the population infected becomes much less with more “traceability,” i.e., with higher fractions of smartphone users. Evidently, contact tracing with more than 60% smartphone users leads to R_t < 1 within 3 weeks of intervention. Moreover, new infections are eliminated completely among the population with more than 75% smartphone users, as shown in Fig. 5a, within only 3 months of intervention.

Fig. 5.

Introducing contact tracing with a different percentage of the population being smartphone users from day 27. (a) shows, with higher percentage of smartphone owners, less portion of the population are infected by the end of day 120. The shaded portion represents confidence interval. Variation of means of R_t is illustrated in (b)

Combined Impact of Lockdown and Contact Tracing

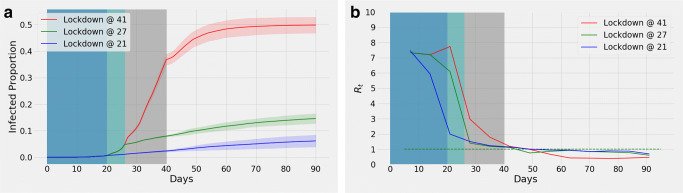
Simulations were run to observe the impact of lockdown being initiated on different days while introducing contact tracing from day 27 in all cases (Fig. 6a). By the end of 90 days, the curves having lockdown introduced on the 21st (blue curve), 27th (green curve), and 41st (red curve) days result in 6.18% (95% confidence interval, 3.93%, 8.43%), 14.63% (95% confidence interval, 12.77%, 16.49%), and 49.85% (95% confidence interval, 46.82%, 52.88%) infections respectively. Clearly, an early imposition of lockdown regulation causes R_t to fall more quickly (Fig. 6b).

Fig. 6.

With contact tracing from day 27, a shows effects of lock-down from day 21 (blue), 27 (green), and 41 (red). The shaded portion represents confidence interval. Variation of means of R_t is illustrated in (b)

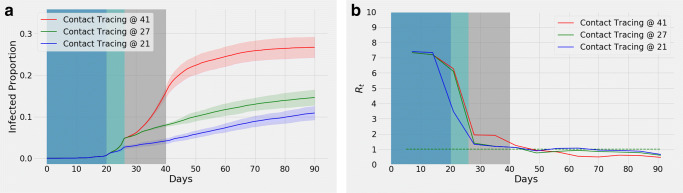
Also, simulations were run to comprehend the effects of introducing contact tracing on different days with lockdown being declared on day 27 in all cases (Fig. 7a). By the end of 90 days, the curves having contact tracing introduced on the 21st (blue curve), 27th (green curve), and 41st (red curve) days result in 10.89% (95% confidence interval, 9.23%, 12.55%), 14.63% (95% confidence interval 12.77%, 16.49%), and 26.7% (95% confidence interval 24.21%, 29.19%) infections respectively. The corresponding R_t curves are shown in Fig. 7b that show similar results as in Fig. 6b.

Fig. 7.

With lockdown from day 27, a shows effects of contact tracing from day 21 (blue), 27 (green), and 41 (red). The shaded portion represents confidence interval. Variation of means of R_t is illustrated in (b)

Some More Variations

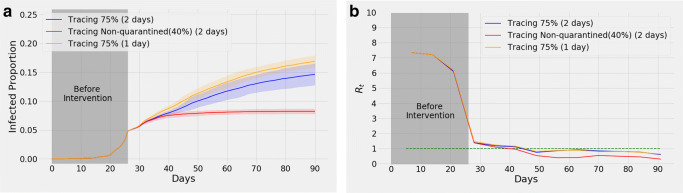
• i.Tracing certain categories of people: Lockdown regulations only apply to all students and 50% of service holders. The rest of the people, i.e., doctors, nurses, healthcare workers, and the remaining 50% of service holders amount to about 40% of the population (referred to as group $\mathcal{A}$ for brevity in what follows). Figure 8a illustrates a simulation where only the people belonging to group $\mathcal{A}$ are traced (red curve) from day 27. Compared to the blue curve that illustrates tracing 75% of the entire population, tracing the people from group $\mathcal{A}$ causes 8.24% (95% confidence interval 7.80%, 8.68%) infections by the end of day 90, with the mean being less by 6.39% compared to the blue curve. In both cases, contacts of the previous 2 days are traced for every infected person.
• ii.Effect of tracing for different number of days: In Fig. 8a, we show a comparison of our simulations where we again have 75% smartphone users but the tracing is done for the previous day’s contacts only (yellow curve) as opposed to the previous 2 days (blue curve). This results in 16.87% (95% confidence interval 15.85%, 17.89%) infections (of the total population) by the end of day 90, with the mean being 2.2% greater compared to the blue curve.

Fig. 8.

a shows effects of tracing 75% of entire population (blue) as opposed to only the doctors, nurse, healthcare workers, and 50% service holders (red) from day 27. Both of these curves result from tracing the contacts of the previous 2 days. The yellow curve shows the effect of tracing 75% of the population for the previous day only. The shaded portion represents confidence interval. The means of their R_t curves are given in (b)

Assessing Contact Tracing Against Service Holders Observing Lockdown

We have varied the percentage of smartphone users (while applying contact tracing) as well as the percentage of service holders who stay at home (during a lockdown), where both are implemented from day 27. The results are presented in a heatmap in Fig. 9. As can be seen from the heatmap, the performance of 100% smartphone ownership alone is quite close to that of a lockdown of 100% service holders. This means that a substantial strength of contact tracing with nearly everyone being traced can virtually mantle the necessity of lockdown imposed on service holders. However, although 100% traceability can be difficult to achieve, the heatmap demonstrates that maintaining a high level of smartphone ownership—if not 100%—can still lower the total cases significantly. In essence, if the concept of digital herd immunity (i.e., more than 75% smartphone ownership) can be realized, then even a very relaxed lockdown (even 50%) can ensure a flattening of the curve with only 14.63% (95% confidence interval 12.77%, 16.49%) of the population being infected.

Fig. 9.

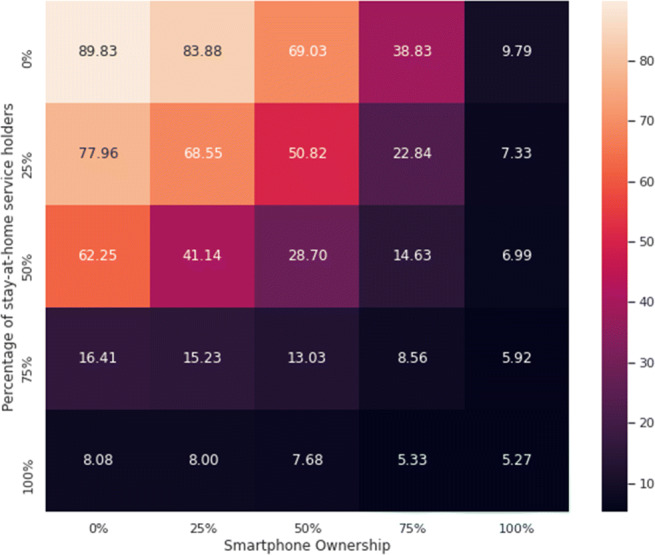
Heatmap representing the effects of varying the percentage of smartphone users (horizontal axis) and the percentage of service holders staying in their homes during a lockdown (vertical axis). Each entry denotes the percentage of total infections (by the end of day 90)

Discussions

We found that lockdown regulations alone can result in fewer people being infected in total compared to contact tracing approaches, but it takes more time to reach R_t < 1. However, the success of combining lockdown and contact tracing surpasses all the other interventions significantly. This is evident from Fig. 4a which shows that the red curve (lockdown alone) causes 62.25% (95% confidence interval 57.96%, 66.54%) infections (with respect to the total population). On the other hand, the yellow curve (contact tracing alone) causes 77.20% (95% confidence interval 74.17%, 80.24%) infections (with respect to the total population). Although the red curve (mean) causes 14.95% fewer infections than the yellow one (mean), the green curve (mean) representing the combination causes 47.62% less infections than the red one.

Implementing contact tracing early will only work best if lockdown regulations follow shortly. With the increasing delay in introducing these restrictions, the rate of infection rises more rapidly. This can be seen from Fig. 6: although contact tracing has begun since day 27, the longer it takes to introduce lockdown following it, the greater is the increase in new infections every day.

Lockdown regulations are the most effective when implemented early. Even if contact tracing measures are introduced late (red curve in Fig. 7), they work well when supplemented with early lockdown as opposed to early contact tracing with delayed lockdown (red curve in Fig. 6). This suggests that as long as lockdown is initiated early, delayed contact tracing will still work reasonably well. Ford County had issued movement restrictions from the beginning of community transmission [29]; therefore, contact tracing works well in our simulation of the county (Fig. 3).

Tracing a certain category of people may have a more profound effect on the overall disease spread. Effectively tracing individuals who go to their workplaces, avail transport facilities, and attend small gatherings after lockdown regulations had already begun (i.e., doctors, nurses, healthcare workers, and about half of the service holders in our simulation reported in Fig. 8) contains the spread with fewer total infections even if they represent a smaller fraction (only 40% in our simulation) of the susceptible population.

Owning smartphones (at varying percentage of the susceptible population) and ensuring (effective) contact tracing thereby ensures R_t < 1. Although not immediately, it does stop the spread of COVID-19 gradually. This will be quicker if lockdown is maintained. However, lockdown cannot be imposed for an indefinite period of time as it comes with economic repercussions. Therefore, it is important to know the fraction of smartphone owners in the susceptible population necessary to quickly eliminate new infections. While having 60% or more smartphone owners in the susceptible population can slow down the spread, in order to completely contain it within a short period of time, this percentage should be maintained at 75% or more.

It can be seen from Fig. 9 that when 100% service holders go to work, having no movement restrictions, the infection spread can still be maintained at 9.79% (95% confidence interval 9.07%, 10.5%) with maximum contact tracing, i.e., 100% smartphone owners. Even with 75% smartphone owners and 0% service holders under lockdown, the spread can be limited to 38.83% (95% confidence interval 34.3%, 43.36%) by the end of day 90. Thus, even a relaxed lockdown (possibly due to its economic repercussions and other difficulties) can contain the disease spread if effective contact tracing can be ensured.

Conclusion

Our model can be adapted for simulating the spread of COVID-19 in any city by supplying suitable parameters as input. This can be used to observe what percentage of people in the city needs to remain traceable and for how many days in order to flatten the curve. This can also help gain insight into the curve’s future trend if current conditions persist for that city.

We have analyzed the effectiveness of digital herd immunity by exploring the impact of contact tracing and finding the parameters that lead to the termination of the epidemic within the city. Our results suggest that it is possible to achieve digital herd immunity soon and with few new infections by implementing contact tracing as soon as possible if lockdown regulations had been implemented already. We have found from our experiments that ensuring 75% smartphone owners in the population with at least 90% of the records being available in each person’s phone can completely contain the spread in a city within 3 months of intervention. Moreover, a more effective approach can be tracing all of the emergency service providers (who go to their workplaces) during the lockdown. Although they constitute only 40% of the population in our simulation, tracing only this category of people can flatten the curve within a short period of time.

The agents’ interaction in our model is done at the granularity of an hour. Also, a detailed agent interaction has been implemented. This makes our model quite realistic and stable albeit at the cost of being computationally intensive. We are now working toward making a more scalable version of the model. Another immediate research direction is to explore different probability distributions to model the disease dynamics. Informatively, different studies in the literature used different kinds of distributions (i.e., normal, Gamma, Poisson, etc.) for this purpose [21, 22, 24]. Although our current model is threshold-based (similar to the model developed in [21]), with multiple layers of probabilities and thresholds, it implicitly mimics a Bernoulli-like distribution. We plan to explicitly employ Bernoulli trial in modeling the infection as our future work.

Authors’ Contributions

Shamil: Implemented the model, planned and designed the experiments, conducted the experiments, analyzed and interpreted the results, drafted the manuscript. Farheen: Implemented the model, planned and designed the experiments, conducted the experiments, analyzed and interpreted the results, drafted the manuscript. Ibtehaz: Implemented the model, planned and designed the experiments, analyzed and interpreted the results. Khan: Conducted some experiments. Rahman: Conceived the study, planned and designed the experiments, analyzed and interpreted the results, supervised the research work.

Compliance with Ethical Standards

Conflict of interest

The authors declare that they have no conflict of interest.