Predicting likelihood of in vivo chemotherapy response in canine lymphoma using ex vivo drug sensitivity and immunophenotyping data in a machine learning model

Abstract

We report a precision medicine platform that evaluates the probability of chemotherapy drug efficacy for canine lymphoma by combining ex vivo chemosensitivity and immunophenotyping assays with computational modelling. We isolated live cancer cells from fresh fine needle aspirates of affected lymph nodes and collected post‐treatment clinical responses in 261 canine lymphoma patients scheduled to receive at least 1 of 5 common chemotherapy agents (doxorubicin, vincristine, cyclophosphamide, lomustine and rabacfosadine). We used flow cytometry analysis for immunophenotyping and ex vivo chemosensitivity testing. For each drug, 70% of treated patients were randomly selected to train a random forest model to predict the probability of positive Veterinary Cooperative Oncology Group (VCOG) clinical response based on input variables including antigen expression profiles and treatment sensitivity readouts for each patient's cancer cells. The remaining 30% of patients were used to test model performance. Most models showed a test set ROC‐AUC > 0.65, and all models had overall ROC‐AUC > 0.95. Predicted response scores significantly distinguished (P < .001) positive responses from negative responses in B‐cell and T‐cell disease and newly diagnosed and relapsed patients. Patient groups with predicted response scores >50% showed a statistically significant reduction (log‐rank P < .05) in time to complete response when compared to the groups with scores <50%. The computational models developed in this study enabled the conversion of ex vivo cell‐based chemosensitivity assay results into a predicted probability of in vivo therapeutic efficacy, which may help improve treatment outcomes of individual canine lymphoma patients by providing predictive estimates of positive treatment response.

1. INTRODUCTION

Lymphoma is one of the most common cancers in dogs and represents the most common haematopoietic malignancy. ¹ Dogs develop lymphoma at a higher incidence rate compared to people (114 per 100 000 dogs compared to 20 per 100 000 humans). ¹ The most common form of canine lymphoma is the multicentric form, which manifests as generalized lymphadenopathy. Approximately 75% of canine lymphoma cases develop as multicentric lymphoma, with other forms being less common (6.9% alimentary and less than 5% mediastinal). ² In terms of the immunophenotype, the B‐cell subtype comprises 58% of newly diagnosed cases, and the T‐cell subtype comprises 35%. ³ Survival rates differ significantly between immunophenotypes—approximately 9 and 6 months for the most common B‐ and T‐cell subtypes, respectively. ¹

Chemotherapy is considered the treatment of choice, and the highest response rates and remission durations are achieved with multi‐agent chemotherapy. Treatment regimens typically combine cyclophosphamide, doxorubicin, vincristine, and prednisone—collectively known as CHOP—which results in a clinical remission rate of 73% to 96% and overall survival time of 275 to 344 days for high‐grade lymphomas. ⁴ , ⁵ Recently, a novel antineoplastic drug called rabacfosadine (TANOVEA‐CA1) has also become available; an overall response rate of 87% and median progression free interval of 122 days were reported for naïve canine multicentric lymphoma treated with single agent rabacfosadine. ⁶ With the failure of first‐line protocols or relapse, rescue treatments are considered, with lomustine being a key component of many rescue protocols. ⁷ , ⁸ Rescue protocols typically result in lower response rates and shorter remission durations than first‐line protocols. ⁷ , ⁹ , ¹⁰ Treatment outcomes also differ between different subtypes of canine lymphoma, with most T‐cell subtypes having poorer treatment response than B‐cell subtypes. ¹¹ , ¹²

The significant variance in treatment responses in various clinical scenarios implies a critical need to predict treatment response accurately, especially in patients with rare lymphoma subtypes or subtypes with low remission rates. Addressing this need may improve treatment outcomes by enabling clinicians to select the most effective drugs and exclude ineffective ones for each patient.

Cell‐based ex vivo drug sensitivity assays have been widely studied as a precision medicine tool to recapitulate the tumour microenvironment in vitro and predict in vivo responses in human lymphoproliferative disorders. ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ For canine lymphoma, Pawlak et al. reported an in vitro chemosensitivity assay that measures the cytotoxicity of various anticancer reagents in high‐grade primary lymphoma cells. ¹⁸ This previous work showed that drug sensitivity varies among individual patients and that a direct measurement of drug response in primary cancer cells is a potential predictor of actual response in the body. However, parameters derived from the outcome of a drug sensitivity assay alone can be insufficient when predicting in vivo response. Adding other phenotypic information such as the immunophenotype of a patient's cancer cells as determined by flow cytometry may enhance the predictive value of ex vivo drug sensitivity testing. ¹⁸ , ¹⁹

Individualized patient outcome modelling is another core feature of precision medicine. In human oncology, personalized predictive modelling has many clinical applications, especially those related to diagnostic and prognostic decisionmaking. ²⁰ Machine learning is a particularly popular modern approach for predicting patient outcomes in human oncology, ²¹ and machine learning strategies have been successfully applied to a variety of human cancers and treatment regimens. ²² , ²³ , ²⁴ One of the most promising avenues of this research is related to direct prediction of drug response ²⁵ ; however, despite the popularity and promise of predictive machine learning in human oncology, it remains relatively uncommon in veterinary oncology.

Clinical models are typically assessed strictly on predictive accuracy. However, the choice of output format is critical for maximizing clinical utility. Many traditional modelling approaches output some categorical value such as “good response” because categorical model outputs have a variety of convenient performance assessment methods. ²⁶ However, these traditional models are not calibrated to accurately assess the likelihood of a good response, meaning a patient with a 55% likelihood of positive response and a patient with a 95% likelihood of positive response would both be classified as “positive responders”. Clearly, important information is lost in the conversion from likelihood scores to categorical reporting. ²⁷ One less common modelling approach that represents major gains in clinical utility is to develop models that directly report the likelihood of positive response for a patient. ²⁰ , ²¹ , ²⁷ This is especially important when there may be multiple treatment options available for a given case.

However, the development of probabilistic models that directly and accurately report likelihood scores is associated with significant challenges, such as more complex performance assessments. ²⁸ Because probabilistic models report both a response and the likelihood of that response (eg, a 95% likelihood of positive response), many traditional performance metrics used for categorical models, such as sensitivity and specificity, must be extended to address this likelihood. For example, in categorical models, a model that predicts a positive response in a patient that fails to response is simply wrong, whereas in probabilistic models, a model that predicts a 90% likelihood of positive response in a patient that fails to respond must be penalized more harshly than a model that predicts a 30% likelihood of positive response in the same patient. This difference leads to natural, if less well known, extensions of popular modelling metrics. Probabilistic models can be assessed using metrics such as the Brier score, which penalizes inaccuracy as in the example above, or calibration curves (as seen in Figure 1), which graph the predictions of a probabilistic model against the actual frequency of positive or negative outcomes in a dataset. ²⁸ For a likelihood model to have good performance, among all patients predicted to have a 70% likelihood score, roughly 70% of them would have positive responses and 30% of them would have negative responses.

FIGURE 1.

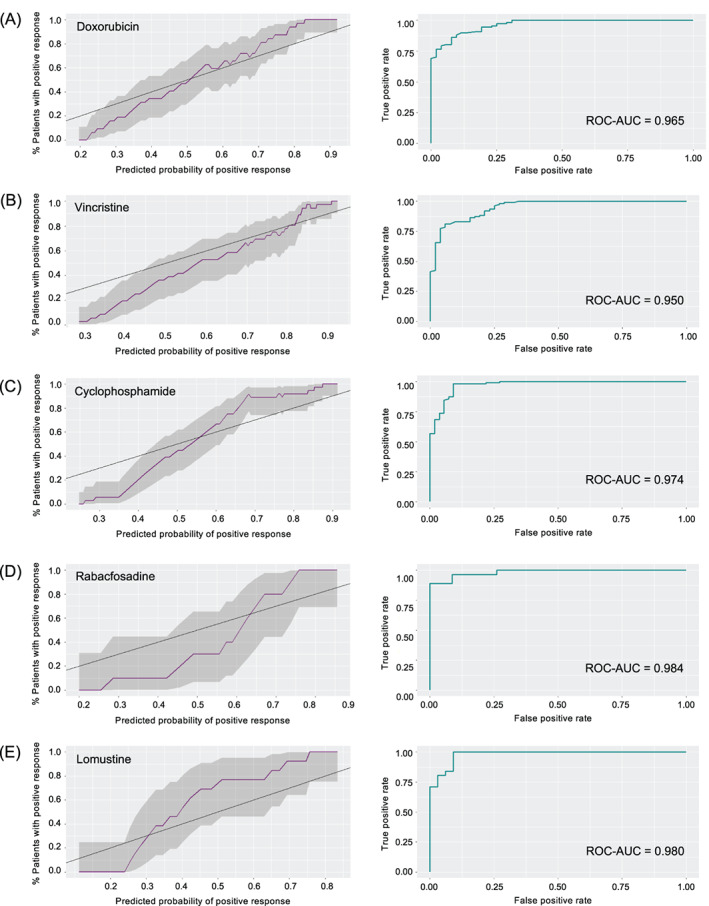
Performance metrics for probabilistic random forest models of drug responses. Sliding‐window calibration graphs (left) of predicted probability of positive response vs percentage of patients experiencing a positive response (window size = 20% of sample size; purple line = prediction; shaded region = 95% prediction interval; black line = perfect calibration) and ROC curves (right) of probabilistic random forest model for A, doxorubicin; B, vincristine; C, cyclophosphamide; D, rabacfosadine and E, lomustine [Colour figure can be viewed at wileyonlinelibrary.com]

In this study, we present a machine learning approach for predicting treatment response in canine lymphoma. Rather than reporting discrete classifications of positive or negative response, we sought to use random forest models ²⁹ , ³⁰ to accurately predict the likelihood of positive responses to individual chemotherapies. We hypothesized that the combination of direct drug sensitivity measurements and flow cytometry data could accurately predict treatment outcomes in a machine learning model of treatment response in canine lymphoma.

2. METHODS

2.1. Case selection

The study included 261 canine patients with confirmed diagnosis of lymphoma who received at least one dose of the modelled drugs (Supplementary Table S1). All dog owners provided informed consent for participation in this study. Cell and molecular assays were conducted on fine needle aspiration (FNA) samples that were submitted to a clinical laboratory (ImpriMed, Inc., Palo Alto, CA) between April 2018 and October 2019. A sample was considered neoplastic if it met the following criteria: cytological or histological diagnosis of lymphoma plus flow cytometric findings that >80% of the lymphocytes had either B‐ or T‐cell immunophenotype or >60% of the lymphocytes had a single phenotype and positive clonality by PCR for antigen receptor rearrangements. Data extracted from submitted medical records included patient age, weight, sex, clinical stage, date of diagnosis, date of initiation of treatment, treatment protocol, time to treatment response, time to disease progression and date of death.

2.2. Flow cytometry

FNA samples from patient lymph nodes were shipped overnight in Transport Media (ImpriMed, Inc., Palo Alto, CA) with ice packs, and most samples arrived with high cell viability (Supplementary Figure S1). Flow cytometry was performed within 48 hours of sample collection. Directly conjugated antibody combinations consisting of fluorescein isothiocyanate (FITC), phycoerythrin (PE), alexa fluor 647 (AF647) and allophycocyanin (APC) were used for surface staining cell suspensions. When an abnormal lymphocyte population was identified on routine analysis, the following antibodies (with specific clones in parentheses) were included in the flow cytometry panel for immunophenotyping: anti‐canine CD21 PE (CA2.1D6), CD3 FITC (CA17.2A12), CD4 PE (YKIX302.9), CD8 AF647 (YCATE55.9), CD5 PE (YKIX322.3), CD45 FITC (YKIX716.13), class II MHC APC (YKIX.334.2), CD34 FITC (1H6), and anti‐human CD14 AF647 (TUK). The class II MHC antibody was purchased from Thermo Fisher Scientific (Waltham, MA), and all other antibodies from Bio‐Rad Laboratories (Hercules, CA). Aliquots of cells at concentrations ranging from 0.2 to 1.0 × 10⁶ cells/mL were labelled with antigen‐specific antibodies or isotype controls at a concentration of 2 to 10 μg/mL in phosphate‐buffered saline (PBS) with 1% bovine serum albumin. Labelled cells were incubated at 4°C in the dark for 45 minutes and then washed repeatedly. Cytometric analysis was performed using Guava easyCyte 8HT (Luminex, Austin, TX) and FCS Express 6 (De Novo Software, Pasadena, CA) was used to analyse data. Lymphocyte populations were gated to exclude dead cells based on forward scatter vs side scatter plots. When the antigen fluorescence was higher than that of an antibody isotype control, the antigen was considered positive.

2.3. Drug sensitivity testing

Ex vivo drug sensitivity assays were conducted on freshly isolated primary cells derived from the patients' FNA samples. Red blood cells (RBC) in the FNA samples were lysed in RBC Lysis Buffer (Thermo Fisher Scientific, Waltham, MA). The RBC‐lysed samples were washed twice with PBS and resuspended in Optimum Culture Media (ImpriMed), which maintained high cell viability over the timespan of the assay (Supplementary Figure S2). Each well in a 384‐well micro‐titre plate (Corning, Corning, NY) was seeded with 30 000 cells. The tested chemotherapeutic drugs were purchased from commercial vendors as follows: Selleckchem (Houston, TX) for doxorubicin, vincristine sulfate, and lomustine, and Niomech‐IIT GmbH (Bielefeld, Germany) for mafosfamide cyclohexylamine. Chemically stable mafosfamide cyclohexylamine was selected as a cyclophosphamide analog, which does not require hepatic activation to produce its active metabolite 4‐hydroxy‐cyclophosphamide in vitro. ³¹ Rabacfosadine (TANOVEA‐CA1) was generously provided by the manufacturer (VetDC, Fort Collins, CO). All drugs were prepared in PBS containing 10% DMSO. Cells in the micro‐titre plates were treated in duplicate with the drug compounds in seven different concentrations per drug, covering approximately a 100 000‐fold concentration range (1.3 nM to 100 μM), in addition to seven untreated control wells. The cells were incubated for 72 hours at 37°C in a 5% CO₂‐charged incubator. After the incubation, cell viability was assessed using alamarBlue (Thermo Fisher Scientific) and the plates were read with the Spark multimode microplate reader (Tecan, Männedorf, Switzerland) following the manufacturer's instructions. The dose‐response curves were analysed in GraphPad Prism 7 (GraphPad Software, San Diego, CA), which was used to generate IC₅₀ and AUC values. Maximum cytotoxicity was defined as the maximum percentage of cells killed in any well treated with a given drug.

2.4. Response annotation

Patient responses were annotated using retrospective medical record review and heuristics derived from the VCOG Response Evaluation Criteria for Peripheral Nodal Lymphoma. ³² For model training and testing, an automated response annotation approach was used. If a patient received multiple therapies in a combination regimen such as CHOP, response to each drug was assessed individually at the most proximal post‐treatment visit, typically 1 to 2 weeks after administration.

Our weekly response annotations were further modified confidence weighting approach, which was an attempt to address confounding factors related to multidrug regimens. Because patient samples represent a “snapshot” of disease state, which changes over time as a result of both mutation and selective forces exerted by chemotherapy, weekly responses were adjusted by a weighting factor scaled by the time elapsed since the sampling date. This annotation strategy was calibrated to assess the most likely “true” response within 90 days of the sample acquisition date. In cases of pre‐treated patients (including relapse), responses were annotated both before and after the sampling date, which allowed us to effectively annotate patients who showed resistance to therapy before we received their samples.

The base selection equation was:

$$R=\max \left(\left\{r_{\mathit{CR}},r_{\mathit{PR}},r_{\mathit{SD}},r_{\mathit{PD}}\right\}\right)$$

where R represents the final annotated response for a drug, and each response category's weight was formulated as:

$$r_{\text{RECIST}}=\sum _{i=0}^{n}1-\frac{\left|t_i-14\right|}{76}$$

where n is the number concordant weekly responses for a given drug in a patient and t_i is the time elapsed between the sample date and response i, with t₀ = 90 to ensure responses with no valid annotations were assigned a weight of 0. In cases of discordant annotations within a month of the sampling date, the later response was granted a further upward weighting adjustment to deemphasize transient responses. As an example, a patient that shows complete response after a single dose of cyclophosphamide immediately after sampling is weighted as a “more confident” response (ie, has a higher weighting value) than a patient who achieves complete response after 3 weeks of intermittent cyclophosphamide therapy, as in CHOP. Similarly, a patient who maintained durable complete response over several weeks of doxorubicin alone would be weighted as a “more confident” than a patient who only received doxorubicin once or twice over a period of months. The automated annotation was calibrated for a 95% concordance rate when compared to unanimous annotation consensus among three blinded independent reviewers (Raghavendra Sumanth Pudupakam, Hye‐Ryeon Lee and Sungwon Lim).

2.5. Predictive modelling

Models were trained and tested based on responses to single drugs. The selected drugs represented some of the most common cytotoxic drugs used for treatment of canine lymphoma and included doxorubicin, vincristine, cyclophosphamide, lomustine and rabacfosadine. Parameters included drug response variables (either area under the drug response curve or IC₅₀ and maximum cytotoxicity ³³ ) and the percentage of the sampled cell population expressing a variety of flow cytometry markers, including percent of lymphocytes, percent of large lymphocytes, forward scatter, side scatter, and percentages of cells expressing CD21, class II MHC, CD3, CD8 and CD34. All variables were formulated as continuous values, and the same input variables were used for each model unless otherwise noted.

Each drug response cohort was split into model training and testing cohorts using random selection, with 70% of samples being used for training and 30% being used for testing. All data were centred and scaled based on means and standard deviations derived from the training set. In samples missing data for four or fewer variables, data were imputed using a k‐nearest neighbours approach with k = 5 and all nearest neighbours derived from the training set. ³⁴

The pre‐processed training data was used as input to tune and train drug‐specific random forest models. ²⁹ Tuning was performed using repeated cross‐validation with 10 repeats of 4 random folds each and a log loss optimization function over 500 trees for each run. Tuning parameters included minimum leaf node size, number of variables assessed per split, and splitting criteria (maximum Gini coefficient ³⁵ or random selection, otherwise known as extremely randomized trees ²⁹ ). Expected model outputs were probability of a positive response to a specific drug. Variable importance was assessed using mean decrease in node impurity. ³⁵

2.6. Model performance assessment

Model performance was assessed by applying the tuned and trained models to the testing cohort for each drug and scored using a combination of ROC‐AUC and Brier score. Because each model's training set had a different rate of positive responses, we also assessed test set performance using Brier skill score calibrated to a reference model of the positive response rate in the entire cohort for a given drug. Models were further assessed by visual inspection of their performance across the whole dataset using rolling calibration curves with binomial confidence intervals and boxplots.

2.7. Time‐to‐response analysis

Response data for time to response analysis were collected from patient medical records. Time to complete response was assessed from the time of sample acquisition to the time of first documented complete response for a patient. Patients that did not achieve a documented complete response were censored at the time of last follow‐up or death.

2.8. Statistical methods

All machine learning models were developed in R 3.6.1. Data pre‐processing was performed using the caret package. ³⁶ The random forest model was generated using the ranger package. ³⁰ Performance assessments were performed using the ROCR package ³⁷ and custom R code. Time to complete response analyses were performed using R's survival package. ³⁸ An unpaired t test was used to assess the statistical significance of the differences in the mean probability score among various patient subgroups.

2.9. Cell line validation statement

No cell lines were used in this study.

3. RESULTS

3.1. Patient demographics

Table 1 presents the demographic information for all 261 dogs in the study. Intermediate to large‐sized B‐lymphocytes expressing high levels of class II MHC were the most common immunophenotype in the study. CD4‐positive lymphocytes with low levels of class II MHC were the frequently identified immunophenotype among T‐cell lymphomas.

TABLE 1.

Patient characteristics

Parameter	Total study population (N = 261)	Doxorubicin study population (N = 159)	Vincristine study population (N = 163)	Cyclophosphamide study population (N = 166)	Rabacfosadine study population (N = 50)	Lomustine study population (N = 64)
Age
Median ± SD	9 ± 3.1	9 ± 3.1	9 ± 3.1	9 ± 3.1	9 ± 2.7	9 ± 3.2
Range	1 to 16 years	1 to 16 years	1 to 16 years	1 to 16 years	3 to 15 years	2 to 16 years
Weight
Median ± SD	27 ± 11.9	27 ± 12.4	27 ± 11.4	27 ± 11.7	25.5 ± 12.9	27 ± 11.5
Sex
Male	18 (6.9%)	13 (8.1%)	10 (6.1%)	9 (5.4%)	2 (4.0%)	5 (7.8%)
Female	8 (3.0%)	5 (3.1%)	4 (2.4%)	4 (2.4%)	2 (4.0%)	5 (7.8%)
Male neutered	127 (48.6%)	81 (50.9%)	79 (48.4%)	79 (47.5%)	24 (48.0%)	28 (43.7%)
Female spayed	97 (37.1%)	53 (33.3%)	62 (38.0%)	66 (39.7%)	19 (38.0%)	21 (32.8%)
Unknown	11 (4.2%)	7 (4.4%)	8 (4.9%)	8 (4.8%)	3 (6.0%)	5 (7.8%)
Clinical stage
2	6 (2.2%)	3 (1.9%)	2 (1.2%)	1 (0.6%)	0 (0.0%)	2 (3.1%)
3	97 (37.1%)	60 (37.7%)	62 (38.0%)	61 (36.7%)	16 (32.0%)	27 (42.2%)
4	48 (18.3%)	27 (17.0%)	26 (16.0%)	26 (15.7%)	15 (30.0%)	7 (10.9%)
5	15 (5.7%)	7 (4.4%)	6 (3.7%)	6 (3.6%)	3 (6.0%)	1 (1.6%)
NS a	95 (36.3%)	62 (39%)	67 (41.1%)	72 (43.4%)	16 (32.0%)	27 (42.2%)
a	101 (61.2%)	66 (68%)	57 (59.4%)	56 (59.6%)	25 (73.5%)	30 (81%)
b	34 (20.6%)	13 (13.4%)	17 (17.7%)	17 (18.0%)	8 (23.5%)	4 (10.8%)
NSS b	30 (18.2%)	18 (18.6%)	22 (22.9%)	21 (22.3%)	1 (3.0%)	3 (8.1%)
Immunophenotype
B	171 (65.5%)	103 (64.7%)	100 (61.3%)	101 (60.8%)	35 (70.0%)	29 (45.3%)
T	46 (17.6%)	27 (16.9%)	32 (19.6%)	29 (17.4%)	8 (16.0%)	26 (40.6%)
Others c	30 (11.4%)	17 (10.6%)	19 (11.6%)	23 (13.8%)	2 (4.0%)	7 (10.9%)
N d	14 (5.3%)	12 (7.5%)	12 (7.3%)	13 (7.8%)	5 (10.0%)	2 (3.1%)

^a Not staged.

^b Not substaged.

^c Dual immunophenotype, inconclusive, non‐B/non‐T, and immature phenotypes.

^d Not immunophenotyped.

3.2. Optimum model parameters varied despite relatively consistent optimum input variables

Model tuning parameters were broadly comparable across drugs, but there were slight differences between models. All models showed the best tuning performance with minimum leaf node size equal to 1 and the number of variables per split equal to 2. The doxorubicin and cyclophosphamide models were most performant when splitting criteria were based on the maximum Gini coefficient, whereas the other three models were optimized using the extremely randomized trees approach, which randomly selects splitting variables among a selected subset. ²⁹ Most of the tested drugs showed better predictive power when the drug response was formulated as a combination of IC₅₀ and maximum cytotoxicity rather than the area under the drug response curve. The only exception was cyclophosphamide, which showed significantly better performance when using the area under the drug response curve.

3.3. Model performance

Test set performance was measured using the area under the receiver operating characteristic curve (ROC‐AUC) for positive response (clinical response or partial response), Brier score, and Brier skill score. The doxorubicin predictive model showed the best performance with a test set ROC‐AUC of 0.702, Brier score of 0.188, and Brier skill score of 0.09. The cyclophosphamide model was similarly performant with an ROC‐AUC of 0.697 but a less performant Brier score of 0.21 and Brier skill score of 0.05. Vincristine had an ROC‐AUC of 0.603, Brier score of 0.239, and Brier skill score of 0.02. Rabacfosadine had an ROC‐AUC of 0.714, Brier score of 0.248, and Brier skill score of 0.008. Lomustine had an ROC‐AUC of 0.63, Brier score of 0.246, and Brier skill score of 0.032.

Most models showed good calibration across the entire dataset, although the models tended to underforecast in samples with lower probabilities of positive response (Figure 1, left). When models were back‐applied to the whole dataset for each drug, the ROC‐AUC was universally above 0.95, indicating high resolution (Figure 1, right). Figure 2 indicates high sharpness in the drug response forecasts as well. Finally, back‐calculated Brier scores were also similarly low, with all models below 0.095.

FIGURE 2.

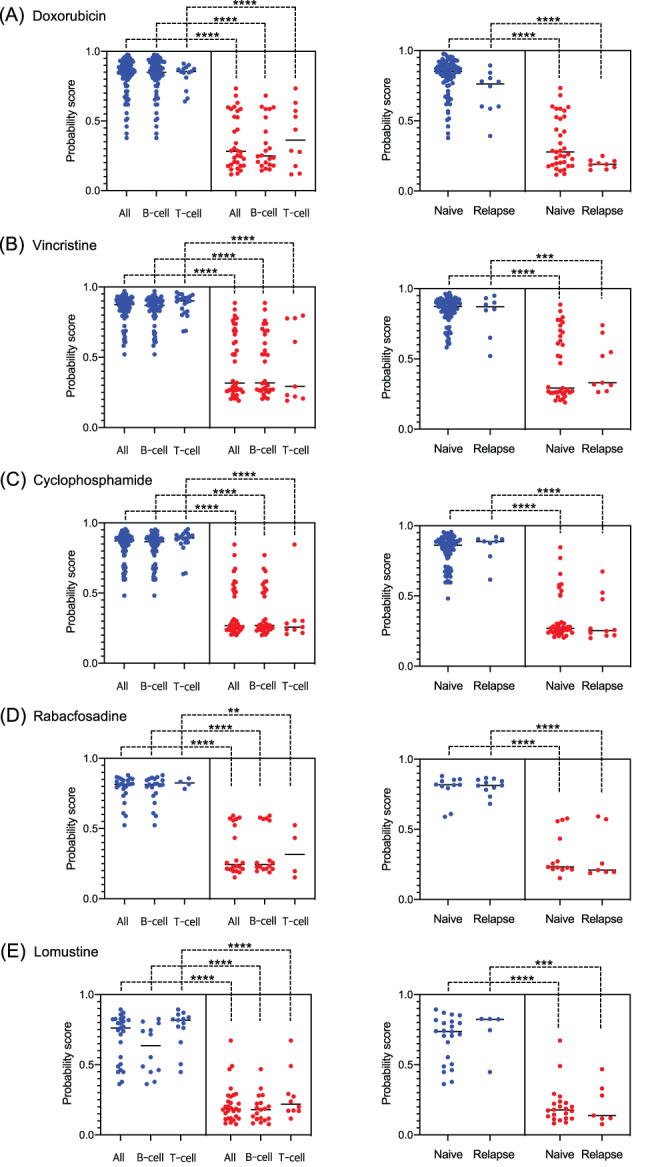
Discrimination between positive and negative scores among patient subpopulations. Comparison of the predictive probability scores for A, doxorubicin; B, vincristine; C, cyclophosphamide; D, rabacfosadine and E, lomustine across the patient subgroups (B‐ vs T‐cell patients [left] and naïve vs relapse patients [right]) showing positive responses (blue; complete response or partial response) and negative responses (red; stable disease or progressive disease). Lines indicate unpaired t‐tests, and asterisks represent significance levels (****P < .0001; ***P < .001; **P < .01) [Colour figure can be viewed at wileyonlinelibrary.com]

3.4. Predictive scores accurately distinguish between positive and negative responses among different immunophenotypes and relapse status

We next assessed the model performance by analysing the distribution of the predictive scores, namely probabilities of positive response for each drug, among different biological subgroups. The results demonstrate a clear difference in the mean predictive score between the patients with positive response (complete response or partial response) and negative response (stable disease or progressive disease). P values were less than .001 for all drugs when the number of patients was larger than 10 (Figure 2, left). Our models performed well for both B‐ and T‐cell subtypes; distributions were the most dichotomized for rabacfosadine. The same level of significance was observed when comparing the distribution and mean predictive scores of naïve and relapsed patients for each drug (Figure 2, right). Notably, the dichotomization was more pronounced among the relapsed patients.

3.5. Time to complete response is significantly better for patients with higher prediction scores

We also analysed time to complete response for each model when samples were dichotomized into patients with predictive scores >50% and patients with predictive scores <50% (Figure 3). The doxorubicin, vincristine and cyclophosphamide models all showed significant differences in time to complete responses (log‐rank P < .05), with patients with higher scores responding more quickly. The rabacfosadine and lomustine models did not show significant differences in time to complete response (log‐rank P = .2 for rabacfosadine and .3 for lomustine). However, we note that both the rabacfosadine and lomustine datasets contained significantly smaller numbers of patients than the other three drugs.

FIGURE 3.

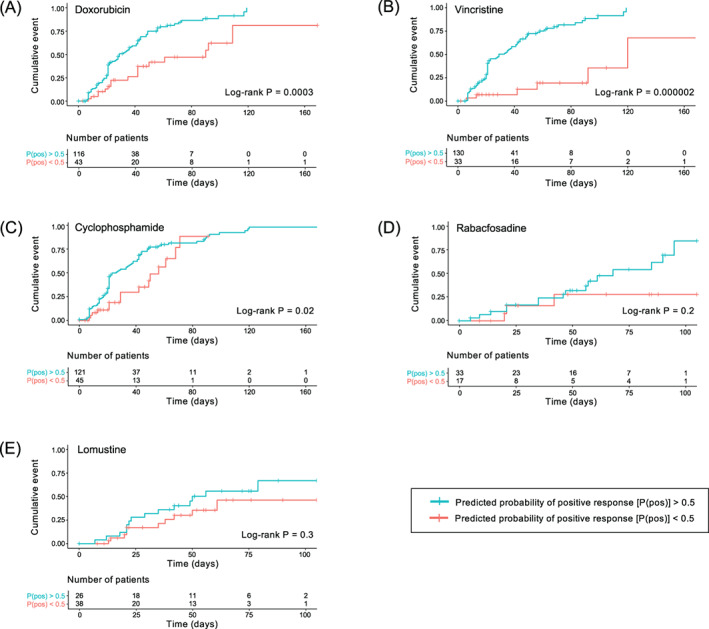
Cumulative incidence curves of time to complete response. All patients received at least one dose of A, doxorubicin; B, vincristine; C, cyclophosphamide; D, rabacfosadine and E, lomustine after the ex vivo chemosensitivity assay sampling date. Patient groups were dichotomized at 50% predicted probability of positive response. The bottom tables show number of patients who have not achieved complete response or been censored at a given time point [Colour figure can be viewed at wileyonlinelibrary.com]

4. DISCUSSION

In this study, we showed that drug sensitivity data and flow cytometry data acquired from primary canine lymphoma samples were sufficient to generate accurate probabilistic models of positive responses to individual chemotherapeutic agents. This finding addresses the current need for predictive models of treatment response to minimize the treatment burden in canine lymphoma. Our modelling approach features a variety of strengths, including the ability to informatively predict the likelihood of positive treatment response in individual canine lymphoma patients as well as close association with improved time to complete response in patients with positive predictions.

We modelled in vivo drug responses to five common chemotherapeutic agents that have direct cytotoxic effects in canine lymphoma cells: doxorubicin, vincristine, cyclophosphamide, lomustine, and rabacfosadine. ¹ , ⁶ Model performance was evaluated with a variety of measures, including ROC‐AUC, representing a model's ability to discriminate between positive and negative responses; Brier score, a proper scoring function that represents the error between probabilistic predictions and actual outcomes; and Brier skill score, which compares the Brier score for a drug response model to the prevalence of positive responses in our data set. Test set ROC‐AUC was above 0.6 for all drugs, and overall ROC‐AUC was above 0.95 for all drugs, indicating good discrimination between positive and negative responses in our data set. ³⁹ Brier scores varied between drugs, but because Brier score is dependent on prevalence of positive responses, we also evaluated Brier skill score to normalize all Brier scores to the prevalence of positive responses for a given drug in our data set. Brier skill scores varied, but all models showed positive Brier skill scores, indicating improved predictive value over positive response prevalence alone.

Probabilistic predictions of treatment response and survival in human oncology represent powerful tools to improve patient outcomes and have shown success in a wide variety of diseases. ⁴⁰ , ⁴¹ , ⁴² We have applied the concept of probabilistic treatment response prediction to canine lymphoma. However, the identification of relevant features is a challenge in any biological model. Direct measurements of treatment response in primary tumour samples are almost certainly relevant to treatment response in patients. ¹⁸ However, ex vivo assessments of chemosensitivity may not fully capture the behaviour of drugs or cells in vivo, which may render these measures insufficient to fully predict individual treatment responses alone. Because many immunophenotypic subtypes with diverse treatment response profiles have been described in canine lymphoma, ⁴³ we sought to use common immunophenotypic markers as additional variables for our models.

Although we used the same immunophenotypic markers for each drug model in this study, response prediction values varied significantly between drugs for each patient, which implies significant differences in variable importance. Drug sensitivity parameters were highly important for doxorubicin, vincristine, and rabacfosadine models, whereas flow cytometry variables were more important in the cyclophosphamide and lomustine models. However, the importance of IC₅₀ vs maximum cytotoxicity varied depending on the model in question. Percentage of CD21+ cells was also commonly in the top three most important variables, and it was particularly important for the cyclophosphamide and lomustine models. Although our cyclophosphamide model was optimized by using AUC of the drug response curve rather than IC₅₀ and maximum cytotoxicity as variables, that variable was still only of moderate importance in the final random forest. This may indicate that the AUC‐based cyclophosphamide model's superior predictive accuracy was related to a reduction of treatment‐response variables among the total variable set rather than any predictive superiority of AUC over IC₅₀ and maximum cytotoxicity. This difference seen in the cyclophosphamide model may also be related to our response annotation strategy since cyclophosphamide frequently occurs later in a variety of combination chemotherapy regimens (eg, after doses of doxorubicin and vincristine in CHOP).

The cases that were modelled in this study were broadly representative of the cases seen in community practice, with similar distributions of immunophenotypes and disease stage at presentation. ¹ We do note some differences between each individual drug cohort, however. Most notably, patients treated with lomustine were more likely to have T‐cell disease (40% vs 16%‐20% in the other treatment cohorts; Table 1), which is representative of lomustine‐based regimens being a common alternative to CHOP chemotherapy in this immunophenotype. ⁷ , ⁴⁴ , ⁴⁵ Patients treated with rabacfosadine in our study were also more likely to have stage 4 or higher disease (36% vs 19%‐24% in other treatment cohorts; Table 1). This prevalence of high‐stage disease in our rabacfosadine cohort translated to a positive response rate lower than that reported in clinical trials (54% vs 74%‐87%). ⁶ , ⁹

A core assumption made in this study is the decision to ascribe responses to individual drugs, even in the case of multi‐agent chemotherapies. Although we recognize that there are likely significant interactions between drugs in multi‐agent regimens, the strength of these synergistic or antagonistic interactions remains to be fully understood. ⁴⁶ , ⁴⁷ We have attempted to mitigate the effects of this assumption using a confidence weighting approach that is heavily influenced by rapid changes in response status, whether positive or negative. It is difficult to derive any meaningful information from sustained responses across multiple drugs in a chemotherapy regimen (ie, there is little meaningful information regarding response to cyclophosphamide if a patient is in complete response, receives cyclophosphamide, and remains in complete response), but the combination of weekly or biweekly response assessments and a confidence weighting scale does allow our method to capture any sudden changes in response status, such as a patient with complete response to CHOP after receiving vincristine and doxorubicin suddenly experiencing progressive disease after receiving cyclophosphamide. Despite this, we do note that it is especially difficult to fully dissect the role of individual therapeutic agents in survival analyses for patients treated with multi‐agent regimens.

Although our modelling approach reliably distinguished between positive and negative responses and showed clear advantages in time to complete response for drugs with larger sample sizes, we note that there were differences between test set performance depending on the drug in question. This may indicate that drugs with different mechanisms of action necessitate different measures of treatment response or secondary model variables or it may be related to a confounding factor between drugs that are commonly combined (eg, cyclophosphamide is often administered in the second week of a CHOP protocol, which may influence in vivo drug sensitivity in a way that is not captured by individual drug sensitivity measurements). The incorporation of additional variables, such as genomic sequencing data or interaction terms between combination therapies, into our models may increase predictive performance. For example, certain breed‐specific mutations, such as MDR1, can have significant impacts on chemotherapy efficacy and patient outcomes. ⁴⁸ These data are not currently captured in our models, and their addition may enhance the predictive accuracy of the models presented here. Furthermore, the models of rabacfosadine and lomustine showed relatively good performance by a variety of metrics and clearly dichotomized positive and negative treatment responses in all the tested subgroups, but there was no significant difference in time to complete response. This observation may be the result of relatively small sample sizes for these drugs in our study, and more patients may be necessary to completely model treatment responses in these patients.

Our results show that drug sensitivity parameters and common flow cytometry markers used for immunophenotyping are sufficient to develop probabilistic models of chemotherapy response in canine lymphoma. It is highly likely that larger sample sizes and the inclusion of other variables may enhance the predictive power of the models described here. We believe that these and other predictive models of treatment outcome may empower veterinarians to make personalized therapy recommendations for canine lymphoma, which may lead to reduced treatment burden and increased survival.

CONFLICT OF INTEREST

All authors except Chantal Tu, Wendi Velando Rankin and Douglas H. Thamm are employees of ImpriMed, Inc. Deanna Swartzfager is an independent contractor for ImpriMed, Inc. Wendi Velando Rankin and Douglas H. Thamm are shareholders and members of the scientific advisory board of ImpriMed, Inc.

Supporting information

Supplementary Figure 1 Cell viability in the Transport Media 24 hours post sampling. Fine needle aspirates from patient lymph nodes were shipped overnight in the Transport Media with ice packs. Red blood cells in the FNA samples were lysed in RBC Lysis Buffer. The RBC‐lysed samples were then washed twice with phosphate‐buffered saline (PBS). Cell viability was measured by the number of live cells' ratio to the total number of cells after trypan blue staining.

Supplementary Figure 2. (A) Cell viability changes over time in the Optimum Culture Media during 4‐day incubation at 37°C in 5% CO2. (B) Representative flow cytometry scatter plots at Day 0 (the date of sampling) and Day 4 of the incubation. FNA samples from patient lymph nodes were transported with ice packs on the same day of sampling. The RBC‐lysed samples were washed twice with PBS and resuspended in the Optimum Culture Media. Each well in a 96‐well micro‐titre plate was seeded with 100 000 cells. On each day, cell viability was measured as the percentage of lymphocytes gated in the flow cytometry scatter plots. Samples from two independent patients were used and all the data points were duplicated for each patient.

Table S1 Clinical responses

Bohannan Z, Pudupakam RS, Koo J, et al. Predicting likelihood of in vivo chemotherapy response in canine lymphoma using ex vivo drug sensitivity and immunophenotyping data in a machine learning model. Vet Comp Oncol. 2021;19:160–171. 10.1111/vco.12656

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are not publicly available due to privacy restrictions.