A framework for defining FLASH dose rate for pencil beam scanning

Abstract

Purpose

To develop a method of (a) calculating the dose rate of voxels within a proton field delivered using pencil beam scanning (PBS), and (b) reporting a representative dose rate for the PBS treatment field that enables correspondence between multiple treatment modalities. This method takes into account the unique spatiotemporal delivery patterns of PBS FLASH radiotherapy.

Methods

The dose rate at each voxel of a PBS radiation field is approximately the quotient of the voxel’s dose and “effective” irradiation time. Each voxel’s “effective” irradiation time starts when the cumulative dose rises above a chosen threshold value, and stops when its cumulative dose reaches its total dose minus the same threshold value. The above calculation yields a distribution of dose rates for the voxels within a PBS treatment field. To report a representative dose rate for the PBS field, we propose a user‐selectable parameter of pth percentile of the dose rate distribution, such that (100 − p) % of the field is above the corresponding dose rate. To demonstrate the method described above, we design FLASH transmission fields using 250 MeV protons and calculate the PBS dose rate distributions in both two‐dimensional (2D) and three‐dimensional (3D) models. To further evaluate the formalism, we provide an example of a clinical PBS treatment field.

Results

With the 2D PBS transmission field, it is demonstrated that the time to accumulate the total dose at a voxel is limited to a fraction of the delivery time of the entire field. In addition, the spatial distributions of dose and dose rate are quite different within the field. For the 10 × 10 cm² PBS field irradiating a 3D water phantom, the prescribed dose of 10 Gy at 10 cm depth is delivered in 1.0 s. The dose rate decreases in the irradiated volume with increasing depth (until the Bragg peak) due to increase of beam spot size by Coulomb scattering. For example, 95% of the irradiated volume between 0 and 10 cm depth receive >40 Gy/s, whereas between 0–20 cm and 0–30 cm depth, 95% of the irradiated volume received >36 Gy/s and >24 Gy/s, respectively. For the clinical PBS treatment field, the scanning pattern conforms to the PTV. PBS dose rate data are presented for the PTV and adjacent normal organs.

Conclusion

We have developed a method of calculating the dose rate distribution of a PBS proton field and have recommended nomenclature for reporting PBS treatment dose rate. We believe that standardizing the method for calculating and reporting PBS treatment dose rates, in a manner that corresponds with other treatment modalities, will advance the research and potential application of PBS FLASH radiotherapy.

1. INTRODUCTION

The interest in the biological effects of ultrahigh dose rate irradiation has grown significantly in the last half decade, starting with the publication of Favaudon et al., ¹ in which significant sparing of normal tissue with iso‐effective tumor growth delay was demonstrated through irradiation at dose rates on the order of 40 Gy/s. The normal tissue sparing effect, which was dubbed the FLASH effect, has resulted in a large number of radiobiology experiments, most of which have been performed using broad beams of electrons or protons (bbFLASH). ¹ , ² , ³ , ⁴ , ⁵ , ⁶ In these experiments, the dose is pulsed in the time domain, with the entire field delivery happening simultaneously within each pulse. This mode of dose delivery has two characteristic dose rates. The first is the instantaneous dose rate, which is the dose per pulse divided by the pulse duration. The second is the average dose rate which is the total dose divided by the entire delivery duration.

Most FLASH studies thus far have reported both average and instantaneous dose rates since the mechanism of the FLASH effect is as yet not fully understood. A proposed mechanism which has gained traction in the literature is based on the radiolytic depletion of oxygen in the irradiated normal tissue, causing hypoxia‐induced radioresistance. ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² In summarizing the influence of dose rate on the FLASH effect, the review article of Vozenin et al. stated that empirical evidence suggests “the dominant variable for response was the overall duration of the dose.” ⁹ Their opinion is consistent with that of Petersson et al., in evaluating the oxygen depletion hypothesis, concluding that “… the total dose rate across the entire exposure, rather than the instantaneous dose rate, … is of particular relevance in driving oxygen depletion relevant to FLASH effects.” ¹⁰ Therefore, the consensus is that the average dose rate seems to be the most relevant for FLASH.

Proton therapy using pencil beam scanning (PBS), or spot scanning, introduces additional considerations for defining dose rate since the dose at each point in the field is the sum of contributions from multiple asynchronous spots. While each beam spot will have instantaneous and average dose rates analogous to those discussed above for broad beams, the dose rate of any voxel within a PBS field is more difficult to characterize. Up to now, proton FLASH studies have been conducted using static pencil beam passing through a set of beam modifying devices to deliver broad beam type FLASH with average dose rates on the order of 70–100 Gy/s. ² , ⁴ , ¹³ , ¹⁴ , ¹⁵ In one experiment by Montay‐Gruel et al., a high intensity x‐ray beam was delivered to a very narrow rectangular field, and the irradiation area was increased by scanning the sample through the beam. ⁷ The only study to use PBS delivery is by Girdhani et al., with all beam spots delivered in a scanned pattern to a 1.2 × 1.8 cm² field in <0.5 s. ¹⁴ For this study, the field dose rate, defined as the ratio of the field dose to the total delivery time, was used. ¹⁴ While appropriate for this small field size, the field dose rate may not adequately describe the local dose rate of a larger PBS field. For example, clinical cyclotron with an output of 800 nA ¹⁶ could deliver 40 Gy/s to the plateau (normal tissue) region of a ~7 × 7 cm² field, with a field uniformity of 95%. In this case, it may be necessary to consider local (voxel‐wise) dose rate in the context of the oxygen depletion hypothesis.

The importance of considering the dose accumulation in a local region (or voxel) of a PBS field as a function of time is illustrated by the following example. For simplicity, consider a monoenergetic field delivery (i.e., no layer switching) as illustrated in Fig. 1. Figures 2(a) and 2(c) show the dose accumulation and instantaneous dose rate as a function of time for three selected points ($a$, $\overrightarrow{b}$, and $\overrightarrow{c}$) from Fig. 1, demonstrating that the time to accumulate the total dose at a given point is limited to a fraction of the total field delivery time. Figures 2(b) and 2(d) compare the characteristics of the time‐dependent dose accumulation for the same point $\overrightarrow{a}$ from Fig. 1 with that of a similar point in an electron bbFLASH field delivered in a series of pulses. These figures show that the intra‐spot dose rate for pencil beam scanning is analogous to the instantaneous dose rate for bbFLASH. In the paper of van Marlen et al., studying the use of PBS FLASH proton therapy for stereotactic treatment of the lung, they acknowledged the contribution of dose at each voxel from different beam spots. ¹⁷ However, “Scanning time has not been included in the definition of T,” with T being the “location specific irradiation time.” Van de Water et al. investigated the PBS FLASH therapy for head and neck cancer and calculated the “3D dose‐averaged dose rate” for each voxel which represented the instantaneous dose rate averaged over all spots (weighted by their dose contribution). ¹⁸ They also did not take into account the scanning time of PBS delivery. By neglecting the scanning time, these reports lack consideration of the temporal separation between spots, and as a result will provide the same dose rate estimate from an array of spots regardless of the time period required to accumulate the dose. The techniques used in both of these planning studies consider the instantaneous dose rate contributions to each voxel. To formulate a biological analog to the bbFLASH dose rate for PBS, scanning time must be take into account.

Fig. 1.

Illustration of a PBS proton field. (a) pencil beam dose delivered in the first 10 ms. (b) dose delivered after 92.5 ms. (c) dose delivered after 237.5 ms. The scanning pattern is shown as a black dotted line and spot locations are shown as black circles. The color‐coded points labeled $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, and $\overrightarrow{\mathrm{c}}$ in the field are referred to in later figures. [Color figure can be viewed at wileyonlinelibrary.com]

Fig. 2.

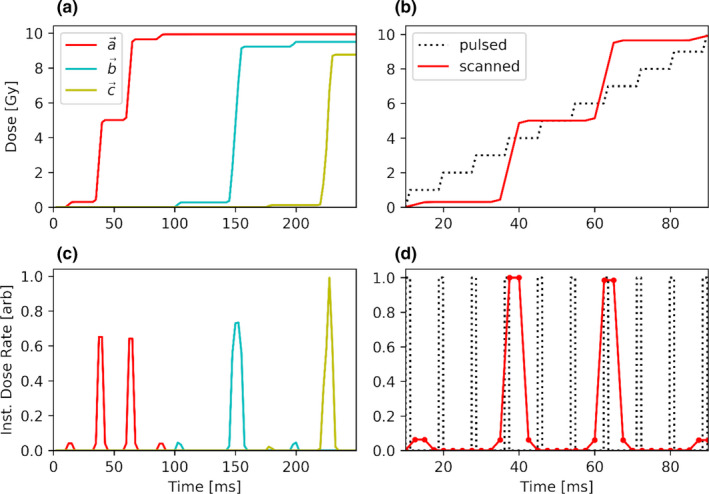
The panels in the left column show cumulative dose (a) and instantaneous dose rate (c) plotted for the three color‐coded points of interest identified in Fig. 1. The panels on the right column show an example electron bbFLASH (black dotted curve) and PBS (solid red line) delivery. Panels b and d display the cumulative dose and the instantaneous dose rate, respectively, for the red point $\overrightarrow{\mathrm{a}}$ in Fig. 1 as a function of time. [Color figure can be viewed at wileyonlinelibrary.com]

In this paper, we present a mathematical framework to derive the dose rate at a point or voxel in a PBS field. In the methods section, we present the PBS dose rate formalism. We then illustrate our method using both two‐dimensional (2D) and three‐dimensional (3D) models. To further evaluate the formalism, we provide an example of a clinical PBS treatment field. In the Discussion section, we relate the proposed PBS dose rate definition to a biological hypothesis of the FLASH effect, discuss the PBS dose rate properties, and recommend the standardization of nomenclature for reporting the dose rate of PBS FLASH delivery.

2. MATERIALS AND METHODS

For illustrative purposes, we consider a 2D plane near the surface of a PBS field as shown in Fig. 1. This illustration sufficiently describes all the fundamental parameters in defining PBS FLASH dose rate. We can express the total dose, $D$, delivered to location $\overrightarrow{x}$ within the full field application time $t_f$ as: $D\left(\overrightarrow{x}\right)=d\left(\overrightarrow{x},t_f\right),$with the corresponding average or “field” dose rate computed as

$${\dot{D}}_{\text{field}}\left(\overrightarrow{x}\right)=\frac{\mathrm{D}\left(\overrightarrow{\mathrm{x}}\right)}{t_f}.$$

However, as shown in Fig. 2, most of the dose accumulation at $\overrightarrow{x}$ occurs only during a fraction of $t_f$. Figure 3(b) illustrates that the dose accumulated at the red cross in panel A occurs between 10.0 and 92.5 ms of the 250 ms PBS field delivery. The formalism proposed in this work aims at defining the PBS dose rate which accounts for this situation. Consider for this purpose an effective irradiation time,

$$T\left(\overrightarrow{x}\right)=t_1‐t_0,$$

where $t_0$ and $t_1$ are defined in terms of $d\left(\overrightarrow{x},t\right)$ by the expressions:

$$d\left(\overrightarrow{x},t_0\right)=d^{†},\text{and}$$

$$d\left(\overrightarrow{x},t_1\right)=D\left(\overrightarrow{x}\right)‐d^{†}.$$

Fig. 3.

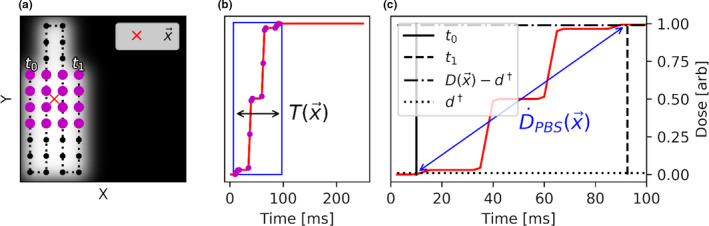
Illustration of dose accumulation at the position of the red cross in panel a. Panel b plots $d\left(\overrightarrow{x},t\right)$ as a function of t, showing that most of the dose accumulation is within a narrow window of time (blue rectangle). Panel A displays the PBS spots which contribute significant dose to $\overrightarrow{x}$ (magenta dots); most of the dose is delivered between 10.0 and 92.5 ms of the PBS field delivery. A graphical example of $T\left(\overrightarrow{x}\right)=t_1‐t_0$ and $d^{†}$ for the point in the PBS field is illustrated in panels a, c. [Color figure can be viewed at wileyonlinelibrary.com]

In other words, the effective irradiation time starts at $t_0$ when the accumulated dose at $\overrightarrow{x}$ exceeds a threshold dose of $d^{†}$, and ends at t ₁ when the accumulated dose comes within $d^{†}$ of the total dose, $D\left(\overrightarrow{x}\right)$. Figure 3(c) highlights the above graphically for the voxel at the red cross in Fig. 3(a). In Fig. 3(b), we plot $d\left(\overrightarrow{x},t\right)$ as a function of time during the PBS field delivery, with the blue box representing the dose accumulation at the voxel between $t_0$ and t ₁. Figure 3(c) shows a graphical example of how $T\left(\overrightarrow{x}\right)$ can be computed. The PBS dose rate at point $\overrightarrow{x}$ is the quotient of $[D\left(\overrightarrow{x}\right)‐$2 $d^{†}]$ and $T\left(\overrightarrow{x}\right)$:

$${\dot{D}}_{\text{PBS}}\left(\overrightarrow{x}\right)=\frac{D\left(\overrightarrow{x}\right)‐2d^{†}}{T\left(\overrightarrow{x}\right)}.$$

The applicability of the above formalism to potential clinical treatment with PBS fields is illustrated with the following example. A hypothetical multifield optimized (MFO) lung SBRT plan was designed, following the clinical dosimetric guidelines of the RTOG 0915 SBRT lung trial, but optimized for ultrahigh dose rate delivery, namely, transmission fields with single energy layers were used. We then calculated the dose and dose rate distributions of the treatment fields using the proposed method; the results of one of the treatment fields is presented in the Results section. We note that the purpose of this exercise is not to create a clinically acceptable FLASH plan, nor to imply the applicability of FLASH in this use case, but only to demonstrate our PBS dose rate computation framework in a clinically relevant scenario.

3. RESULTS

The dose and dose rate distributions for the example shown in Figs. 1, 2, 3 are calculated with a dose grid spacing of 0.5 cm in all dimensions and shown as color‐wash displays in Figs. 4(a) and 4(b). The first notable observation is the dissimilarity of the dose and PBS dose rate distributions. The uniform dose distribution is by design. In the PBS dose rate distribution two salient features are apparent, namely, a discrete and continuous variation of the dose rate.

Fig. 4.

Plot of the dose distribution (a) and the PBS dose rate distribution (b) for a matrix of 113 × 113 points just below the surface of a 5 by 5 cm monoenergetic PBS field. The 50% isodose line is plotted with a dashed magenta line. The scanning pattern and spot locations are plotted with black dotted line and circles, respectively. Panel C shows the dose rate volume histogram for the area enclosed by the dashed magenta line (where dose is greater than or equal to 50% of the 10 Gy prescription dose) in panel b. As indicated by the cyan rectangle in Panel C, 95% of the points have an effective dose rate exceeding 100 Gy/s. [Color figure can be viewed at wileyonlinelibrary.com]

The discrete behavior can be understood as follows. Practically, $T\left(\overrightarrow{x}\right)$ reflects the time required to traverse the scanning path between the spots delivered at $t_0$ and $t_1$, as illustrated in Fig. 3(a). In this diagram, the point of interest, $\overrightarrow{x}$ requires inclusion of just over three lines of spots. However, considering voxels along the X‐axis in Fig. 4(b), the total number of scan lines could vary between two and four depending on the relative position of a voxel to a scan line, the spot spacing, and the spot radius (interaction range). As a result, $T\left(\overrightarrow{x}\right)$ would increase or decrease substantially, thereby drastically changing the dose rate. The discrete nature of both the delivery pattern and spot interaction range (imposed by $d^{†}$) result in dose rate discontinuities in this situation.

Figure 4(c) displays the dose rate volume histogram. To understand the continuous variation of the PBS dose rate across the field [gradients along Y‐axis in Fig. 4(b)], consider the delivery path lengths required to deliver contributing spots as a function of Y position in the field. Generally speaking the number of scan lines that influence $T\left(\overrightarrow{x}\right)$ will decrease as $\overrightarrow{x}$ approaches an edge where the spot pattern is not connected (opposite a u‐turn in the pattern), with the extreme minimum being at the corners opposite the beginning and end of the pattern. This is exemplified by the lower dose rate for a central voxel than that for a voxel at the edge, with maxima at two of the corners. The reason for the dose rate being high in only two lower corners has to do with the nature of the scanning pattern. Specifically, those points in the upper corners include scan‐time contribution from many more spots than the points in the lower corners which has only a few neighboring lines contributing to $T\left(\overrightarrow{x}\right)$.

To illustrate the fundamental characteristics of the PBS dose rate in 3D, we calculate the ${\dot{D}}_{\text{PBS}}\left(\overrightarrow{x}\right)$ distribution for a 250 MeV monoenergetic 10 × 10 cm² proton field delivering 10 Gy to isocenter placed at 10 cm depth in a water phantom with an in‐air spot sigma of approximately 3.3 mm. For simplicity, but without loss of generality, a quasi‐static spot delivery was assumed in which the dose is deposited to points on a 5 mm square grid assuming 2 ms spot delivery time with 10 mm/s scanning speed. These parameters are nominally representative of modern scanning systems. ¹⁹ , ²⁰ Based on these values, the total dose delivery plus beam traversal time is 2.5 ms per spot, for a total field delivery time of 1000 ms, and a ${\dot{D}}_{\text{field}}$ of 10 Gy/s.

For a prescribed dose of 10 Gy, a reasonable threshold value of 0.1 Gy is chosen for $d^{†}$. The ${\dot{D}}_{\text{PBS}}\left(\overrightarrow{x}\right)$ distribution was calculated with a grid spacing of 2.5 mm in all dimensions with the aid of the Eclipse^TM Treatment Planning System (Varian Medical Systems, Inc. Palo Alto, CA) using PyESAPI, the Python extension to the Eclipse^TM Scripting API. ²¹ Figure 5(a) shows a color‐wash display of the PBS dose rate in a water phantom along the central plane. An apparent feature is the decrease in dose rate with depth, which is displayed quantitatively in Fig. 6(a). This behavior can be understood in terms of the increase in pencil beam radius (and the radius of influence) with depth due to multiple coulomb scattering. As a result, the spot size relative to the scanning pattern dimension grows leading to an increase of $T\left(\overrightarrow{x}\right)$ with depth, and hence, a corresponding decrease in dose rate. Figure 5(b) shows a dose rate volume histogram to quantify the decrease in dose rate with increasing depth. Specifically, 95% of the irradiated volume (defined as the region receiving >= 50% of the prescription dose) between 0 and 10 cm depth receive >40 Gy/s, whereas between 0–20 cm and 0–30 cm depth, 95% of the irradiated volume received >36 Gy/s and >24 Gy/s, respectively.

Fig. 5.

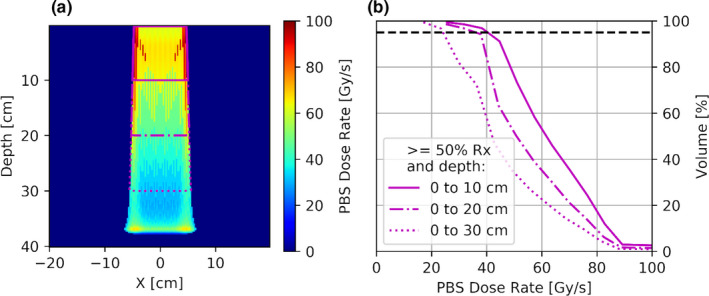
A color‐wash display of the axial view of 3D PBS dose rate distribution in water phantom for a 10 by 10 cm field (a). PBS dose rate vs volume histogram for regions receiving >50% of prescription dose and extending to various depths (b). [Color figure can be viewed at wileyonlinelibrary.com]

Fig. 6.

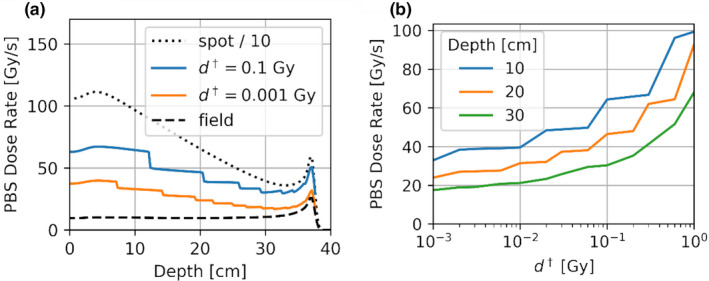
Panel a shows PBS dose rate as a function of depth at the center of the 10 by 10 cm field. Also shown for comparison purposes is the average field dose rate (dashed) and the scaled instantaneous spot dose (dotted). The dose rate decreases as the threshold $d^{†}$ is decreased, and approaches the field dose rate when $d^{†}$ nears zero. The abrupt changes in dose rate for the middle two curves are due to the sudden increase in $T\left(\overrightarrow{x}\right)$ when the spot size becomes larger to include more dose contributing spots. Panel b shows ${\dot{D}}_{\mathit{PBS}}$ for a single voxel along central axis at 10, 20, and 30 cm depths for values of $d^{†}$ spanning three order of magnitude. [Color figure can be viewed at wileyonlinelibrary.com]

The behavior of the dose rate with depth can be modulated by choice of $d^{†}$. Figure 6(a) shows representative depth dose rate (DDR) curves for two values of $d^{†}$, together with average spot (dotted) and field (dashed) dose rate depth curves. As expected, the PBS DDR trends toward that of a single spot with increasing values of $d^{†}$, and that of a uniform field with decreasing values of $d^{†}.$ The abrupt changes in dose rate for the two PBS dose rate curves are due to the sudden increase in $T\left(\overrightarrow{x}\right)$ when the spot size becomes larger resulting in more contributing spots. To analyze the dependence of ${\dot{D}}_{\mathit{PBS}}$ on $d^{†}$, Fig. 6(b) shows the PBS dose rate for a single central voxel at 10, 20, and 30 cm depth for a range of $d^{†}$ values from 0.001 to 1 Gy. The sensitivity of PBS dose rate on the $d^{†}$ value will be discussed later.

3.A. Clinical FLASH planning scenario

The dose and dose rate distributions of a single field of a hypothetical multifield optimized (MFO) lung FLASH SBRT plan are shown as color‐wash displays in Figs. 7(a) and 7(b). These are in the plane of the beam isocenter. Overlaid are the target and other structures. The PBS dose rate is calculated using $d^{†}$ = 0.01 Gy. The corresponding dose rate volume histograms, for irradiated volume above 0.1 Gy, are shown for the PTV, the lungs, and the esophagus in Fig. 7(c). Figure 7(d) shows the positions and MU of each spot, together with the scanning pattern. These results demonstrate the usefulness of the proposed PBS dose rate calculation in providing a framework for the evaluation of clinical PBS FLASH dose rates.

Fig. 7.

Color‐wash displays of dose (panel a) and dose rate (panel b) distributions for a single field from a hypothetical MFO FLASH SBRT lung plan. Panel C shows the dose rate volume histograms for >0.1 Gy irradiated volumes of the PTV, lungs, tracheobronchial tree, and esophagus. Panel D shows the positions and MUs of the spots in beam coordinates on isocenter plane, along with the scanning path (dotted line). [Color figure can be viewed at wileyonlinelibrary.com]

4. DISCUSSION

4.A. Connecting PBS dose rate formalism to the FLASH effect

In the first FLASH paper by Favaudon et al, ¹ they defined FLASH dose rate as being >40 Gy/s. Since then there have been many radiobiology studies on this topic, as noted in the review paper by Vozenin, Hendry, and Limoli, ⁹ The sum of the findings from these studies is that the dose rate must be >30 Gy/s for the FLASH effect. To date, only one study has used PBS to study the FLASH effect, ¹⁴ but the definition of dose rate used in that reference may not be generally appropriate for larger PBS treatment fields. Thus, for future study of the FLASH effect with PBS, there is a need to develop a method for calculating and reporting the dose rate of a PBS treatment field.

The mechanism of the FLASH effect is as yet not fully understood. A working hypothesis has been suggested by Spitz et al. ⁸ based on the radiolytic depletion of oxygen in the irradiated normal tissue, causing hypoxia‐induced radioresistance. This working hypothesis has now been embraced by others. ¹⁰ The phenomenon of radiolytic oxygen depletion have also been studied by Ling et al., ¹² and others (see the references in the review paper by Vozenin, Hendry, and Limoli ¹⁰ ). In the study of Ling et al., the oxygen diffusion coefficient in mammalian cells was measured experimentally to be 2 × 10⁻⁵ cm /s. Collectively, these experiments suggest that if enough dose is delivered to deplete the physiological oxygen, and if the delivery time is sufficiently short, temporary hypoxia will be induced prior to oxygen rediffusion into the irradiated normal tissue, therefore, resulting in radioresistance. In this context, a meaningful description of dose rate of the radiation field is needed. In the paper of Vozenin, Hendry, and Limoli, ⁹ they considered different physical parameters of FLASH delivery with electrons and concluded that “the dominant variable for response was the overall duration of the dose.” To the best of our knowledge, the study presented herein is the first to accurately account for the time‐dependent dose accumulation of a voxel, taking into account the scanning time, and report the dose rate of a PBS treatment field.

Over the many decades of radiation studies, the time scales of the various steps in the radiophysical, radiochemical, and radiobiological events are reasonably well known. This knowledge is elegantly summarized in Fig. 2 of the review paper by Vozenin, Hendry, and Limoli. ¹⁰ In brief, physical energy deposition occurs in <10⁻¹⁵ s, physical‐chemical interactions between 10⁻¹⁵ and 10⁻¹² s, various chemical interactions between 10⁻¹² and 10⁻⁵ s. As the lifetime of free radicals is approximately 10⁻⁵ s, radiolytic depletion of oxygen likely occurs in <10⁻⁵ s time scale. Important for the FLASH effect is that, subsequent to the oxygen depletion in the irradiated volume, rediffusion requires a much longer time than the irradiation time of <1 s. To date, all positive findings of the FLASH effect in the literature have been performed with <1 s total irradiation time. Therefore, considering the local dose accumulation time (also being on the order of <1 s) for large PBS fields seems justified.

4.B. PBS dose rate parameter dependencies

In this paper, we proposed a novel method to calculate the dose rate at each voxel of a scanned pencil beam taking into account the relationship of dose accumulation and irradiation time at that voxel. While the chosen example is for discrete spot delivery, it can be applied to continuous scanning so long as $d\left(\overrightarrow{x},t\right)$ is known, with the beam flux and scanning speed as input parameters. In addition, the formalism can be extended to PBS delivery using the extended Bragg peak [see Fig. 6(a)] or any other PBS‐like dose delivery.

In our formulation of calculating the dose rate at each voxel, there is a user selectable parameter, that is, the threshold of accumulated dose $d^{†}$ which, when exceeded, starts the clock for deriving the effective irradiation time for that voxel. The same threshold applies in ending the irradiation time, when the delivered dose comes within the total dose minus $d^{†}$. We emphasize that this user selectable parameter is essential for calculating a meaningful PBS dose rate. To assess the dependence of the PBS dose rate on $d^{†}$, we performed the sensitivity analysis shown in Fig. 6(b), with the value of $d^{†}$ ranging three orders of magnitude. As can be seen, the magnitude of change in ${\dot{D}}_{\mathit{PBS}}$ with $d^{†}$ depends on both the value of $d^{†}$ and the position of the voxel in the field. Take for example the central voxel at 10 cm depth; for our selection of 0.1 Gy, which is 1% of the prescription dose, an increase by a factor of two to 0.2 Gy incurs a negligible change in ${\dot{D}}_{\mathit{PBS}}$, whereas a decrease by a factor of two to 0.05 Gy would decrease ${\dot{D}}_{\mathit{PBS}}$ by ~30%, which would not alter the FLASH effect based on data from Montay‐Gruel, P., et al. ³ The appropriate choice of $d^{†}$ is a bit arbitrary at this point, and will require further experiments which correlate bbFLASH and PBS FLASH biological outcomes to determine the appropriate value. Wilson et al., in considering the various dose delivery characteristics, concluded that the “range of variables and outcomes seen to date warrants further investigation to confirm that these are the key parameters for inducing the FLASH effect.” ⁹

As there is a distribution in the calculated dose rate ${\dot{D}}_{\text{PBS}}\left(\overrightarrow{x}\right)$ [see Fig. 4(b)] for a PBS field, consideration is needed to meaningfully and succinctly characterize a representative “PBS dose rate.” Such choices include the average, mean, median, and minimum dose rates. For FLASH therapy, since biological effect seems to be present only above a certain dose rate, ³ selecting the minimum might seem logical. However, this choice may be skewed by outliers. We therefore propose a user‐selectable parameter of pth percentile of the ${\dot{D}}_{\text{PBS}}\left(\overrightarrow{x}\right)$ distribution, such that (100 − p)% of the field is above the corresponding dose rate. In Fig. 4(c), we selected the 5th percentile, such that 95% of the field is above the dose rate of 100 Gy/s.

4.C. Practical use of ${\dot{D}}_{\text{PBS}}$

The selection of values for $d^{†}$ and p influences the reported PBS dose rate. To the extent that the FLASH phenomenon is dose rate dependent, there may be implications in correlating the reported PBS dose rate with radiobiological observations. For instance, in selecting the 5th percentile as the representative dose rate, there is 5% of the treatment volume receiving less than the desired FLASH dose rate. One may ask if such an “under‐dose rate” will influence the radiobiological outcome. That said, as the radiobiological basis for the FLASH effect remains largely unknown, any discussion of this nature is by and large speculative.

For reporting the representative or effective dose rate of a PBS proton field, it may be of importance to standardize the nomenclature. First, a region of interest needs to be identified: per our definition only voxels with accumulated doses $D>2\times d^{†}$ get a dose rate assigned (and if the accumulated dose is only marginal larger than $2\times d^{†}$ the usefulness of the assigned dose rate value might be arguable). In our case (Figs. 4, 5, 6), we chose the 50% isodose line. For this region of interest, we suggest the use of ${\dot{D}}_{d^{†}\text{,p}}$ to denote that the dose rate is for a threshold ($d^{†}$), and p the percentile in the dose rate distribution selected for the representative dose rate. For the example given in Fig. 5, one would have ${\dot{D}}_{0\text{.1,5}}$ = 40 Gy/s for the volume between 0 and 10 cm [see Fig. 5(b)], meaning that 95% of the volume has >40 Gy/s dose rate when 0.1 Gy is selected as the threshold.

4.D. General applicability of the PBS dose rate formalism

While the motivation of this study was the formulation of a dose rate definition for pencil beam delivery, and our examples have focused on the plateau region of the depth dose curve (where most normal tissue sparing should occur), our proposed dose rate formalism applies to the entire PBS field volume, including the Bragg peak (as shown in Figs. 5 and 6). We have also demonstrated successful application to a PTV‐shaped field with modulated spot intensity and variable spot spacing. The examples presented in this work successfully demonstrate the application of the described formalism to cases relevant both for preclinical and clinical investigations.

We also point out that while our discussion of ${\dot{D}}_{\mathit{PBS}}$ has been in the context of PBS delivery, the formalism can be extended to other modes of dose delivery, including but not limited to multi‐energy‐layer and spread out Bragg peak modalities. In the case of bbFLASH, the dependency on $d^{†}$ will not be as marked as with PBS. In the extreme case of continuous beam bbFLASH, the ${\dot{D}}_{\mathit{PBS}}$ will be independent of $d^{†}$. Slight variation of ${\dot{D}}_{\mathit{PBS}}$ with selection $d^{†}$ will be introduced with pulsed delivery. Additionally, ${\dot{D}}_{\mathit{PBS}}$ for a bbFLASH field should be identical to the field dose rate distribution.

In terms of PBS delivery, the introduction of discrete features into the resulting dose rate distribution seems numerically inconvenient. However, this is simply a (perhaps unavoidable) mathematical artifact arising from the selection of a finite dose cutoff combined with dose delivery to points on a discrete lattice. In reality, biological systems will likely not experience such extreme variation (i.e., factor of two difference from one voxel to the next). A possible solution would be the introduction of a sigmoid (rather than a step function) in the threshold definition. While such a definition may help to smooth out some of the discrete behavior (and maybe make use of ${\dot{D}}_{\mathit{PBS}}$,in optimization algorithms more convenient) we contend that the fundamental formalism presented here will still apply. It is also important to point out that FLASH works above a threshold, with no apparent upper limit. ³ Therefore, a plan optimization would try to achieve a minimum threshold dose rate for as large a volume as possible, therefore, any dose rate variations within the volume, yet, still above the minimum dose rate threshold, would still be in the FLASH regime, and therefore, likely have little further effect. To our knowledge, ${\dot{D}}_{\mathit{PBS}}\left(\overrightarrow{x}\right)$ is the only definition of dose rate which could allow cross comparison of FLASH outcomes for different mode of dose delivery.

5. CONCLUSION

We have developed a method of calculating the dose rate distribution of a PBS proton field and have recommended nomenclature for reporting PBS treatment dose rate. This provides a framework for describing PBS dose rate in a precise and consistent manner, a necessary requirement for cross‐investigational comparison of FLASH results. We believe that standardizing the method for calculating and reporting PBS treatment dose rates will advance the research and potential application of PBS FLASH radiotherapy.

CONFLICT OF INTEREST

All authors were employees of Varian Medical Systems at the time of writing this paper.