Measuring and compensating for ocular longitudinal chromatic aberration

Abstract

It is well known that the eye’s optics and media introduce monochromatic and chromatic aberration unique to each individual. Once monochromatic aberrations are removed with adaptive optics (AO), longitudinal chromatic aberrations (LCA) define the fidelity for multi-wavelength, high-resolution vision testing and retinal imaging. AO vision simulation systems and AO scanning laser ophthalmoscopes (AOSLOs) typically use the average population LCA to compensate for focus offsets between different wavelengths precluding fine, individualized control. The eye’s LCA has been characterized extensively using either subjective (visual perception) or objective (imaging) methods. Classically, these have faced inconsistencies due to extraneous factors related to depth of focus, monochromatic aberration, and wavelength-dependent light interactions with retinal tissue. Here, we introduce a filter-based Badal LCA compensator that offers the flexibility to tune LCA for each individual eye and demonstrate its feasibility for vision testing and imaging using multiple wavelengths simultaneously. Incorporating the LCA compensator in an AOSLO allowed the first objective measurements of LCA based on confocal, multi-wavelength foveal cone images and its comparison to measures obtained subjectively. The objective LCA thus obtained was consistent with subjective estimates in the same individuals and hence resolves the prior discrepancies between them. Overall, the described approach will benefit applications in retinal imaging and vision testing where the focus of multiple wavelengths needs to be controlled independently and simultaneously.

1. INTRODUCTION

Adaptive optics (AO) technology has played an increasingly important role in vision science since its introduction in the eye by Liang et al. in 1997 [1]. By measuring and correcting the ocular higher-order aberrations in addition to defocus and astigmatism, AO allows for imaging the retina at diffraction-limited resolution [1-3], controlling and targeting visual stimulus on the retina with spatiotemporal precision [4], and investigating visual performance under aberration-free and optically manipulated conditions [5-7]. More broadly, applications of AO for the eye have spanned the range from high-resolution retinal imaging to vision testing/simulation with no imaging. More recently, concomitant AO imaging and stimulus delivery has allowed relating retinal structure with visual perception at the scale of individual cone photoreceptors [8-12].

A feature common to most AO systems is that the wavefront sensing beam is obtained from a pseudo-monochromatic or narrow-bandwidth light source. Consequently, the deformable mirror corrects aberrations for a single wavelength band alone. To deliver aberration-corrected light stimuli or to image at wavelengths different from that used for wavefront sensing, one must account for the eye’s native longitudinal chromatic aberration (LCA). These chromatic aberrations have a considerable effect on visual performance [5,13,14] and retinal imaging quality [15]. Moreover, as the eye ages, a complex interaction between chromatic and monochromatic aberrations may govern visual performance under polychromatic viewing [16,17]. Furthermore, it is of great interest to understand how vision is affected by new multifocal lens designs for presbyopia that contain their own native chromatic aberration [18].

When the application demands imaging and/or vision testing with a single wavelength, the chromatic offset is often simply compensated for by an extra vergence induced by the deformable mirror in addition to that measured at the wavefront sensing wavelength. However, when multiple wavelengths are required, different strategies are employed to overcome the LCA.

In retinal imaging systems, two optical methods are commonly used to compensate for LCA: (1) an achromatizing lens [19-24] and (2) repositioning the light source and detector to account for the vergence difference between imaging and wavefront sensing wavelengths [3,25]. The achromatizing lens introduces the opposite wavelength-dependent power that matches the average LCA in a human population but suffers from an introduction of extraneous aberrations when slightly misaligned with respect to the optical axis of the eye [26]. Zhang et al. [26] reported that as little as 0.4 mm of misalignment of an achromatizing lens relative to the eye’s pupil can sufficiently nullify the visual performance benefit provided by the lens. Even with the best optical design and careful alignment, the achromatizing lens can still only correct a fixed amount of aberration based on the population average and does not account for inter-subject variability in LCA. The second approach, that of repositioning the light source, entails introducing equal and opposite defocus between the imaging wavelength and the reference wavelength (either the wavefront sensing or other, depending on application) at the entrance pupil of the instrument. In practice, this is typically achieved by translating the fiber tip axially in the light delivery apparatus by a predefined amount based on average population measures, such that the optimal dioptric offset is obtained at the system entrance pupil. The detection path, in turn, is also displaced axially to accommodate LCA in light collection and achieve optical conjugacy with the imaging planes. Light beams propagating through spherical mirror telescopes in modern ophthalmoscopes [i.e., optical coherence tomography (OCT) and scanning laser opthalmoscope (SLO)] with vergences as large as 2.2 D (400–700 nm) introduce extraneous aberrations that need to be minimized via sophisticated optical design strategies [27,28].

In AO vision testing instruments, light from an external display, a cathode-ray tube (CRT) monitor, digital light projector (DLP), or similar is focused on the retina via AO correction. For monochromatic stimuli, subjects typically adjust the defocus either via a Badal optometer, trial lenses, or the defocus state of the deformable mirror to achieve subjective sharpness of image quality. This process then needs to be repeated for each wavelength separately, and no one state of the apparatus simultaneously corrects two or more visible wavelengths together. This precludes studies of color vision that require, say, a red and a green target to be simultaneously focused on the retina. An alternative approach is where two separate displays are used, one each for red and green targets, respectively, placed at different focal distances to optimize image quality for each [29]. An elegant combination of a diffractive liquid crystal on silicon spatial light modulator (LCoS-SLM) and a tunable lens was recently demonstrated to provide control of LCA [30]. In this paradigm, the tunable lens compensated for the wavelength-dependent defocus phase variations in the LCoS-SLM caused due to diffraction. However, it was not possible to compensate for higher-order aberrations simultaneously with LCA.

For these existing approaches described above, a detailed analysis of native human LCA in the population is desired. To this end, LCA has been measured extensively, both subjectively [31-33] (using different psychophysical techniques) and objectively [34-36] (using reflectometric or imaging techniques). Vinas et al. [37] described the first measures of LCA taken under AO correction, in both a subjective and objective manner in the same subjects. As described in Vinas et al., there are two methods commonly used for objective LCA measurements—double-pass retinal aerial images and wavefront sensing. Subjective LCA measures rely on subjects finding the best image focus for targets created by different wavelengths. More importantly, these two measures (objective and subjective) of LCA produce inconsistent results, in a large part due to the poor axial resolution of the objective methods. That the retinal layer(s) responsible for the backscattered light remain ambiguous in case of both aerial images and wavefront sensing necessitates the axial localization of the retinal backscatter source to harmonize objective and subjective measures of LCA.

Here, we demonstrate a filter-based Badal LCA compensator that can be applied to both AO vision simulation (AOSIM) (with no imaging) and AO retinal imaging systems to compensate for LCA across different subjects and wavelength bands in an individualized manner. To assess the LCA compensation performance, the luminance contrast sensitivity function (CSF) at 526 and 661 nm was measured in a custom AOSIM system, and cone photoreceptor images were acquired at the foveal center in multiple wavelengths in an AO scanning laser ophthalmoscope (AOSLO). The sources of inconsistencies typically observed between LCA measures obtained in an objective and subjective manner were revealed when the imaging plane of cone photoreceptors was chosen as the focal plane reference for estimating LCA.

2. MATERIALS AND METHODS

A. Optical Setups

1. Filter-Based Badal LCA Compensator

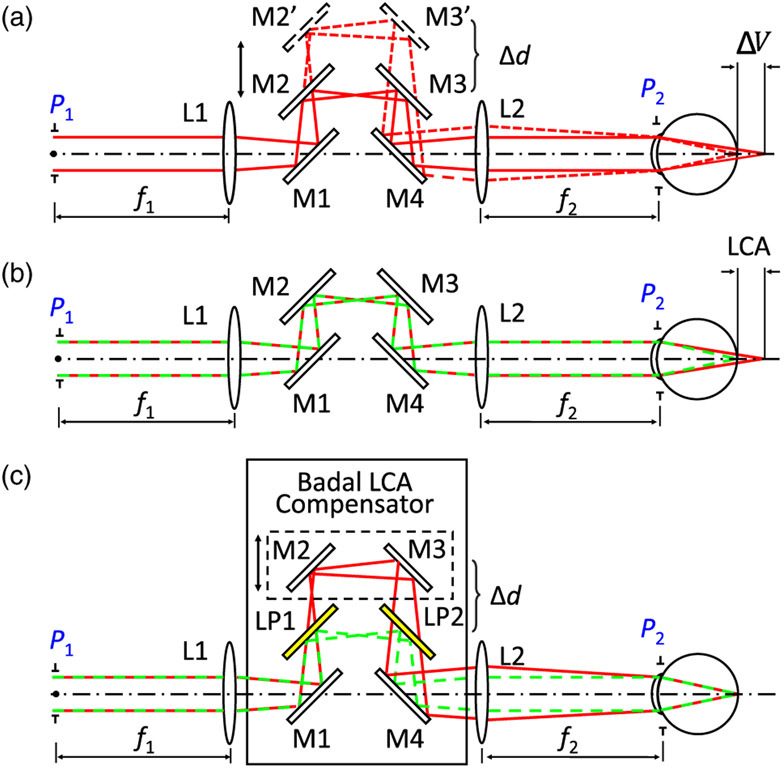
A Badal optometer typically consists of an afocal telescope, the distance between whose focusing elements can be altered in order to introduce relative defocus between the entrance and exit pupils (P₁ and P₂ in Fig. 1). Practically, a Badal optometer is often realized by placing two mirrors [M2 and M3 in Fig. 1(a)] on a translational stage so that the location of the entrance and exit pupils can be kept constant relative to the focusing elements. A key feature that makes Badal optometers attractive in studies of vision science is that they introduce vergence without altering image magnification. When two wavelengths share a common path as in a traditional Badal optometer, the eye’s native LCA forces them to be defocused relative to one another [Fig. 1(b)]. Here, we introduced a pair of long-pass filters (LP1, LP2) statically between the mirrors (M1 and M2, M3 and M4) and the lenses (L1, L2) [Fig. 1(c)]. Finely altering the distance (Δd) between the mirrors and the filters introduces dynamic defocus control between the transmitted longer wavelength relative to the reflected shorter wavelength channel and thus offers customizable LCA compensation between the two channels.

Fig. 1.

(a) Typical Badal optometer consists of two focusing elements (L1 and L2) and flat mirrors (M1–M4) that are together used to form an afocal telescope. M2 and M3 are placed on a translation stage. Moving the stage (Δd) can alter the physical distance between L1 and L2 (M2’, M3’ and the dashed line) introducing extra vergence (ΔV) at the exit pupil P₂ (dashed line), which leads to a focal plane change in the eye (ΔV). Note that ΔV here shows the defocus change in diopters and not physical distance. (b) When two wavelengths (say, a red and a green) are used together in a Badal system, the eye’s LCA forces the two wavelengths to be defocused relative to each other. (c) Two long-pass filters (LP1 and LP2) inserted between the mirror pairs M1, M2 and M3, M4 separate the longer and shorter wavelengths so that they can have tunable relative defocus at P₂ as a function of Δd. L, lens; M, mirror; LP, long-pass filter; LCA, longitudinal chromatic aberration; P, pupil plane; ΔV, vergence change; Δd, distance change in (a) the afocal telescope and (c) in the transmitted beam.

The distance Δd [Figs. 1(a) and 1(c)] changes the object distance u of the second lens L2 as follows:

$$u=f_2+2\Delta d.$$ (1)

Using the thin lens formula, the image distance v is defined by

$$v=\frac{f_2^2}{2\Delta d}+f_2.$$ (2)

The chromatic change in vergence (ΔV) at the exit pupil is

$$\Delta V=\frac{1}{v-f_2}=\frac{2\Delta d}{f_2^2}.$$ (3)

Units are meters in all equations above.

2. Multi-Wavelength AO Vision Simulator with the Filter-Based Badal LCA Compensator

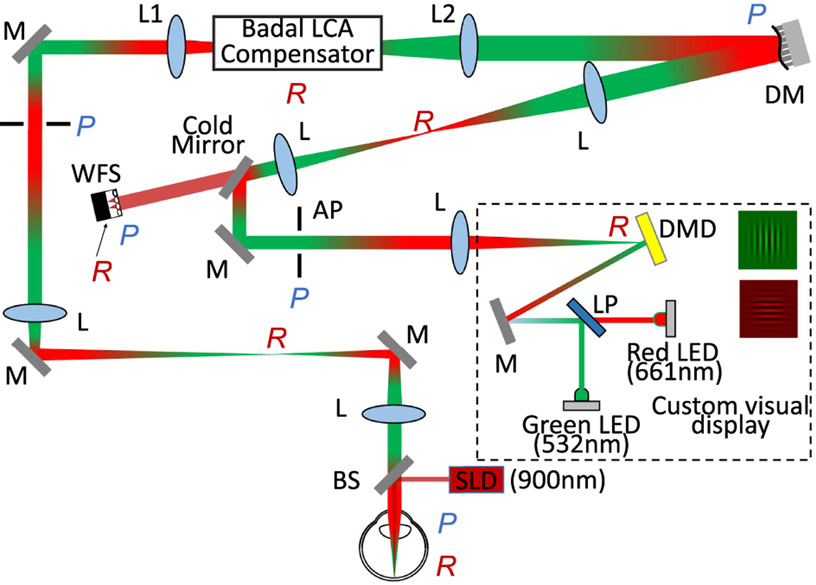
The filter-based Badal LCA compensator was first introduced into a multi-wavelength AOSIM system whose schematic diagram is shown in Fig. 2. The main components of the system are: (1) a wavefront sensing/compensating path; (2) a psychophysical channel that has a custom-developed multi-wavelength DLP as a visual display; (3) a filter-based Badal LCA compensator as described above.

Fig. 2.

Optical layout of the multi-wavelength adaptive optics vision simulation (AOSIM) system. The wavefront beacon was introduced into the eye by a pellicle beamsplitter (BS). The backscattered light was relayed to the deformable mirror (DM) and the wavefront sensor camera (WFS) by several afocal telescopes. The custom visual display consisted of a digital micrometer device (DMD) and two LEDs centered at 532 nm and at 661 nm combined together via a long-pass filter (LP). Example isochromatic grating stimuli are shown. The stimuli light was coupled into the wavefront sensing/correction path through a cold mirror. The artificial pupil (AP) ensured the vision testing was performed through a controllable 6 mm pupil. L, lens; M, mirror; LP, long-pass filter; BS, beamsplitter; DM, deformable mirror; WFS, wavefront sensor; SLD, superluminescent diode; DMD, digital micrometer device; P, pupil plane; R, retinal plane; AP, artificial pupil.

A superluminescent diode (SLD) centered at 906 ± 8 nm (Inphenix, California) was collimated, spatially filtered with a 500 μm pinhole, and then introduced into the eye via a 92/8 (transmission/reflection) pellicle beamsplitter as the wavefront sensing beacon. The light scattered from the retina was imaged onto the deformable mirror (Mirao52d, Imagine Eyes, Orsay, France) and the Shack–Hartmann wavefront sensor via image relay optics constructed using a train of achromatic doublets. An extra conjugate pupil plane was accommodated to allow the insertion of trial lenses to compensate for sphere and cylinder.

The multi-wavelength DLP system consisted of a digital micromirror device (DMD) and two interchange-able, narrowband, light-emitting diodes (LED) centered at 532 nm (27 nm FWHM) and 661 nm (14 nm FWHM) as illumination. The DMD provided a 1° field of view (FOV) based on the system magnification. The DMD and LEDs were placed in free space and aligned as such to eliminate artifacts due to chromatic fringing and diffraction due to the DMD sub-apertures. An artificial pupil (AP) in the vision testing channel ensured an optimal pupil size for psychophysics. For all experiments described here, aberrations were corrected dynamically for a 6.5 mm eye’s pupil, while vision testing was performed over an artificial 6 mm pupil.

The filter-based Badal LCA compensator was inserted between the two lenses (L1, L2). It included two long-pass filters with a 600 nm cutoff wavelength (Semrock, Rochester, New York) placed statically as described in Fig. 1(c). The wavefront sensing light and the 661 nm LED light went through the transmission path, while the 532 nm LED was reflected. Prior to visual psychophysics, calibration of the spatial scale in pixels per degrees was performed independently for both channels to account for any residual non-common path errors and chromatic difference of magnification originating due to the system’s optics. If left uncompensated, these factors have the potential to confound the CSF measurements.

3. AOSLO with the Filter-Based Badal LCA Compensator

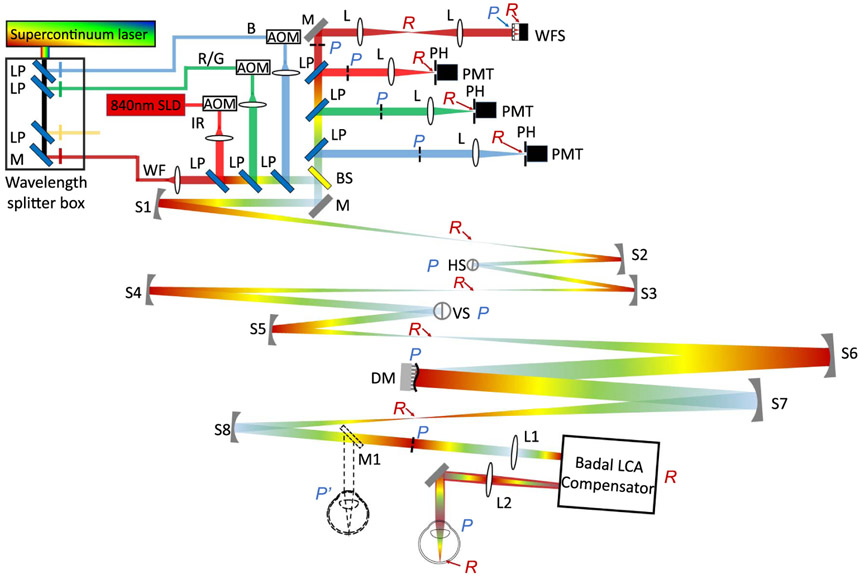
The schematic of the multi-wavelength AOSLO used for demonstrating LCA compensation is shown in Fig. 3.

Fig. 3.

Layout of the multi-wavelength AOSLO with the filter-based Badal LCA compensator. The dashed line at the eye’s pupil, mirror M1, and eyeball show the traditional scenario without the LCA compensator. The eye’s pupil in traditional operation was replaced by the entrance pupil of the LCA compensator. S, spherical mirror; L, lens; M, mirror; HS, horizontal scanner; VS, vertical scanner; LP, long-pass filter; BS, beamsplitter; SLD, superluminescent diode; AOM, acousto-optic modulator; WF, wavefront sensing channel; IR, infrared channel; R/G, red/green channel; B, blue channel; WFS, wavefront sensor; DM, deformable mirror; PH, pinhole; PMT, photomultiplier tube; P, pupil plane; R, retinal plane.

A supercontinuum laser source (SuperK Extreme, NKT Photonics, Denmark) provided broadband illumination. Using a network of long-pass and narrowband interference filters, four wavelength bands for retinal illumination were separated and coupled into single-mode fibers. These were 450–500, 500550, 550–740, and 740–970 nm. Each band was then further filtered with narrowband interference filters (25 nm FWHM) mounted in removable optomechanical mounts for ease of switching wavelengths. Of these, the near-IR band with a 900 ± 16 nm narrowband filter was used for wavefront sensing. For the experiments described here, the remaining three bands were used for retinal imaging and stimulation in the visible range, with narrowband filters centered at either 470, 496, 520, 543, 578, 598, 623, or 640 nm. A superluminescent diode with 840 ± 15 nm (Superlum Diodes Ltd., Ireland) provided near-IR illumination for imaging. At one given time, four wavelength channels—a short wavelength (blue, B in Fig. 3), a middle/long wavelength (red/green, R/G in Fig. 3), an infrared imaging wavelength (near-infrared, IR in Fig. 3), and a wavefront sensing beam (WF in Fig. 3)—were launched into the AOSLO using a light delivery network consisting of long-pass filters. The first three supported imaging and retinal stimulation simultaneously with the help of acousto-optic modulators (AOM, Brimrose Corp, Baltimore, Maryland) [38]. The light collection assembly mirrored the delivery arm of the system. Each illumination channel had a dedicated imaging channel consisting of a focusing lens, confocal pinhole, and photomultiplier tube (PMT). In all, there were three imaging channels, one each for B, R/G, and IR. The final light collection arm housed the Shack–Hartmann wavefront sensor.

The entrance pupil of the optical system was optically conjugated with a resonant scanner (Electro-Optical Products Corp., Fresh Meadows, New York), a galvanometer scanner (Cambridge Technology, Bedford, Massachusetts), a large-stroke magnetic membrane deformable mirror (DM97-15, ALPAO, Montbonnot-Saint-Martin, France), and the eye’s pupil using a train of afocal spherical mirror-based telescopes. Following principles put forth by Gómez-Vieyra et al. [28], the optical system was initially designed in ZEMAX optical design software to ensure diffraction-limited performance over an extended dioptric range and field of view. The former is needed to account for the eye’s native LCA for multiple wavelengths extending across the visible to near-infrared wavelengths. In traditional operation, the B, R/G, and WF channels are all defocused by the population average LCA [39] with respect to the IR channel such that they are all focused at the optimal (and same) axial plane in the retina. Here, we sought to investigate the feasibility of using the filter-based Badal LCA compensator to achieve the same. Therefore, we purposely reset all wavelength channels to have zero defocus at the system entrance pupil instead of the population average LCA. The light collection assembly in each detection channel was also correspondingly adjusted axially to achieve optical conjugacy with the light delivery. A 6.5 mm diameter eye’s pupil was used for wavefront measurement and compensation.

The filter-based Badal LCA compensator [Fig. 1(c)] was inserted at the eye’s pupil with the help of an additional lens-based telescope (L1 and L2). The two long-pass filters had 660 nm cutoff wavelength, and the two flat mirrors were placed on a precise translation stage with a micrometer drive. The IR and WF channel beams passed through the long-pass filters, while the visible wavelengths were reflected by them. The distance between the mirrors and the filters could be adjusted continuously to compensate for the LCA between the IR and the visible channels.

B. Subjects

Three color-normal subjects were involved in the AOSIM experiments where we measured isochromatic luminance CSFs centered at 532 nm and 661 nm. Four color-normal subjects were involved in the LCA measurement and compensation experiments in the AOSLO. The age range of the subjects is 23–39 yo. Subjects S1, S2, and S3 were emmetropes, and S4 was a −2.75 D myope. Subjects were cyclopleged in both cases. The research was approved by the University of Washington institutional review board, and all subjects signed an informed consent before their participation in this study. All procedures involving human subjects were in accordance with the tenets of the Declaration of Helsinki.

C. Experiments

1. Isochromatic Luminance Contrast Sensitivity Function with LCA Correction

We measured isochromatic (or monochromatic) CSFs in three subjects using the quickCSF paradigm [40]. This measurement was aimed at testing the optical performance of the filter-based Badal LCA compensator. If it were functioning as designed, the isochromatic CSFs measured at two different wavelength bands would (a) align with respect to each other and (b) have substantially high spatial frequency cutoffs with AO and chromatic aberration correction, and together these would denote optimal optical performance. The experimental protocol began with the subjects optimizing their image quality with AO correction for the red (661 nm LED) channel to minimize the LCA between the wavefront sensing (900 nm) and the red stimulus. This was done by placing a static correction in the form of a trial lens at the artificial pupil (AP) outside of the wavefront sensing path. Next, the subjects optimized their image quality for green (532 nm LED) by translating the mirrors in the filter-based Badal LCA compensator. When the AO loop was closed, the DM had an equal and opposite defocus as the filter-based Badal LCA compensator’s transmission path and thus optimized the wavefront sensing path to have minimum defocus. Altering the distance between the long-pass filters and movable mirrors changed the defocus generated by the DM, which introduced the extra defocus for the reflection path to compensate for the LCA between 532 and 661 nm channels. In this manner, with the same optical and vergence states of the system, both wavelength channels (532 and 661 nm) were focused together in an optimal fashion.

For vision testing, a Gabor stimulus with luminance modulations created by either the red or green LED were shown to the subject via the AO and LCA correction. The subject responded to the orientation (horizontal or vertical) via a two-alternate forced paradigm. The spatial frequency and contrast in each presentation were varied according to the quickCSF (qCSF) approach consisting of 150 total presentations per run. A total of four runs were obtained for each wavelength.

2. Multi-Wavelength Retinal Images with LCA Correction

Images at the foveal center were taken through both transmitted and reflected channels of the filter-based Badal LCA compensator. These included one IR wavelength (840 nm, transmitted channel) and six visible wavelengths (520, 543, 578, 598, 623, and 640 nm, reflected channel). Macular pigment absorption impeded foveal imaging with <10 μW of power at 470 and 496 nm. Supplement 1 shows results from 470 nm at 2.5 deg temporal eccentricity. Imaging powers at the cornea were: <8 μW for 520–598 nm and <20 μW for 623 and 640 nm for an 0.8 deg FOV. Note that the confocal pinhole in the visible light detection channel was kept relatively large, equal to 1.8 Airy disk diameter. We chose to use a relatively large pinhole to maximize light collection for the low light levels used at the cornea. More importantly, we aimed to test the optical performance of the filter-based Badal LCA compensator to determine how far it degrades the quality of the illumination point-spread function. Increasing the pinhole size reduces the advantages it provides for lateral resolution in detection; hence, in this case, the lateral resolution is dictated to a larger extent by the optical quality of illumination. Again, two criteria were used to gauge the optical performance of the filter-based Badal LCA compensator. If it were functioning optimally, (a) optimized image quality for both the transmitted (IR) and reflected (visible) wavelengths would be obtained with the same vergence state of the optical system and (b) image quality would be sufficiently optimal to reveal the smallest cones in the foveal center at both wavelengths simultaneously. Recall that the filter-based Badal LCA compensator here is responsible for compensating for the entire LCA of the human eye and that the illumination and detection channels are aligned to have zero vergence.

The experiment protocol included first optimizing the IR (840 nm) image by imposing a static defocus offset on the DM. This static offset stayed the same across all visible imaging. Next, for each visible wavelength, the filter-based Badal LCA compensator was translated until the image was focused. Similar to the AOSIM case, this vergence state of the optical system optimized image quality for both the transmitted (IR) and reflected (visible) wavelength channels together. Ten-second videos were recorded in each case and registered offline. When the images appeared best focused to the operator, the corresponding micrometer readings on the compensator were recorded and converted to spherical defocus in diopters [Eq. (3)] to obtain a measure of objective LCA. The chromatic difference in focus was obtained with the 543 nm imaging wavelength as the reference. The sensitivity of the objective measurement was assessed by a set of through focus retinal images (details in Supplement 1).

3. Objective versus Subjective Measures of LCA

The objective LCA measurements were compared against the subjective estimates of LCA in the same AOSLO platform for the same subjects. Eight visible wavelengths bands (470, 496, 520, 543, 578, 598, 623, and 640 nm) were used for this measurement. For 470 and 496 nm, because foveal retinal images were not feasible, objective measures were not available.

For each wavelength, a 20/20 Snellen “E” was generated in the center of the scanning raster using the AOM and delivered to the retina with monochromatic AO correction. Next, the subject determined the point of best focus by translating the filter-based Badal LCA compensator while the AO loop was closed. This was repeated four times for each wavelength, and the micrometer reading at the best focal plane was recorded during each run. The averaged micrometer readings were converted to spherical defocus in diopters using Eq. (3) and used to estimate the chromatic difference of focus with the 543 nm wavelength as the reference.

3. RESULTS

A. Isochromatic AO-Corrected Luminance CSFs

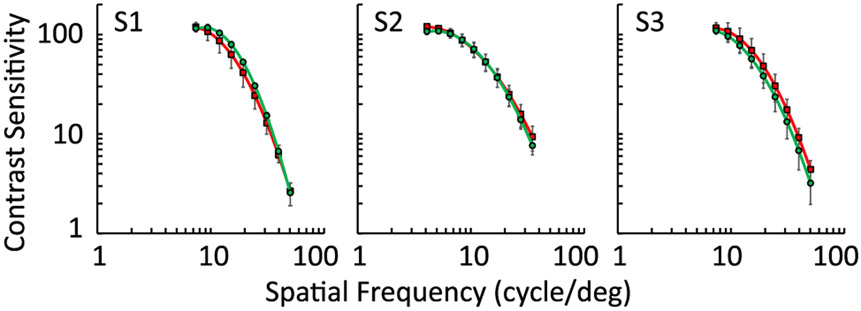
The averaged CSFs for isochromatic red (661 nm) and green (532 nm) for the three subjects is shown in Fig. 4. The spatial frequencies ranged from 5 to 63 c/deg. At lower spatial frequencies, the limited field of view did not allow sufficient cycles to be generated. In general, the CSFs follow known estimates from previous work across the subjects and for the two wavelengths. Two observations are important to note. First, isochromatic CSFs at both red and green wavelengths align with each other, when ocular LCA is compensated. Paired student’s t-tests confirmed no significant differences between both wavelengths (p > 0.05 for all spatial frequencies). In the scenario where there is no LCA compensation, only one of the two wavelengths would be optimized in retinal image quality, and hence such equivalency in isochromatic CSFs would not be possible. Second, the CSFs showed a high spatial frequency cutoff above 50 c/deg for all subjects, indicating that performance was excellent when monochromatic and chromatic aberrations were corrected and that it was ultimately close to the limit imposed by the foveal cone photoreceptor mosaic. If the filter-based Badal LCA compensator were adversely affecting the system’s optical quality, such high spatial frequency cutoffs would not have been achievable. Together, these observations confirm that the filter-based Badal LCA compensator achieved optimal performance in correcting chromatic aberration without sacrificing retinal image quality.

Fig. 4.

Averaged contrast sensitivity functions (CSFs) for 661 and 532 nm channels for three subjects, S1, S2, and S3, after the LCA compensation. Red and green curves represent the 661 nm and 532 nm channels, respectively. Both channels achieved an excellent and similar contrast sensitivity performance, indicating the optimal correction of LCA.

B. Objective and Subjective Estimates of LCA

1. Multi-Wavelength Images after LCA Compensation

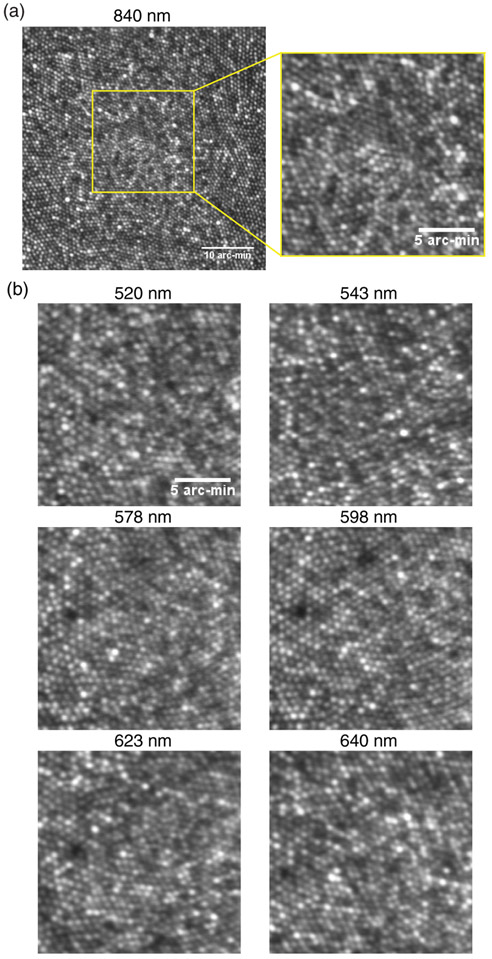
Figure 5 shows example retinal images taken with the filter-based Badal LCA compensator incorporated into an AOSLO. All images shown here were obtained from the fovea. Figure 5(a) shows the image obtained from the transmission path (840 nm IR) with 0.8 deg FOV and a zoomed-in view of the central 0.3 deg. Figure 5(b) shows 0.3 deg FOV zoomed-in images for the six visible wavelengths, all obtained at the fovea and using the reflected path of the filter-based Badal LCA compensator. In these images, purposely magnified to reveal fine spatial detail, one can notice that sufficient resolution is available to count individual cones in the foveal center. Furthermore, imaging at the visible wavelengths comes at no cost to the near-IR 840 nm image, i e., the same vergence state of the system optimizes image quality for both the visible and IR wavelengths simultaneously. Given how the individual visible and near-IR beams traverse the system with zero relative defocus between each other, the onus of compensating for the entire ocular LCA relies on the filter-based Badal LCA compensator. The high-resolution images obtained here demonstrate that chromatic difference in focus at least as large as 1.15D (LCA between the 520 and 840 nm wavelength) can be compensated for with this approach. Further, this approach provides comparable resolution to the conventional approach in AOSLO instruments, where the population average LCA is introduced at the system entrance pupil. However, the current approach described here provides substantially increased flexibility for tuning the LCA to each subject and to each wavelength band in a customized manner.

Fig. 5.

Representative multi-wavelength cone images at fovea taken through (a) the transmitted channel and (b) the reflected channel. The FOV of the 840 nm image on the top left is 0.8°. The rest of the zoom-in images all have a 0.3° FOV. The scale bar in the zoom-in images is 5 arc-min. The imaging wavelengths are denoted at the top of each panel.

2. Comparing Objective and Subjective Estimates of LCA

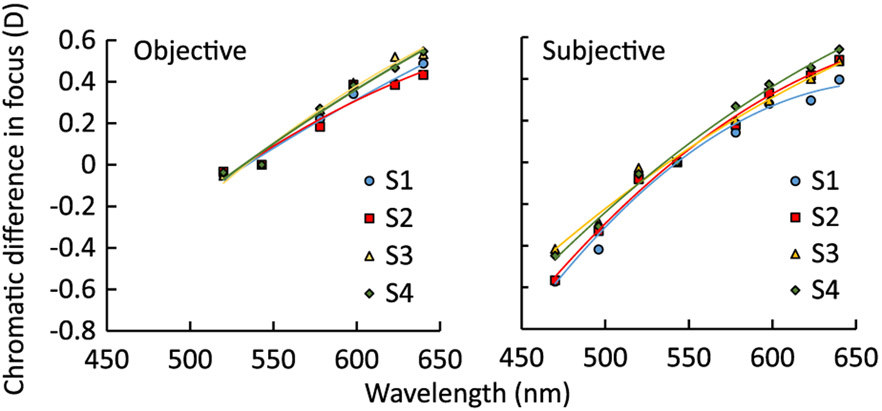
The defocus required to optimize the image quality of foveal cones was considered as the objective estimate of LCA and is shown in Fig. 6(a) for all subjects. Similarly, the best subjective focus obtained across the visible wavelengths is shown in Fig. 6(b). In both plots, the LCA is referenced to 543 nm wavelength. A second-order polynomial fit is also shown in both cases.

Fig. 6.

Objective (left) and subjective (right) chromatic difference of focus relative to the 543 nm wavelength as the reference for four subjects (S1–S4). The objective LCAs were measured from 520 to 640 nm, while the subjective LCAs were from 470 to 640 nm.

Both objective and subjective measurements show inter-subject variations, with slightly larger variability observed in the subjective method. We used the standard deviation to describe these variabilities. For the objective measurements, the mean inter-subject variation was 0.03 D, and the maximum variability was 0.07 D at 623 nm. For the subjective measurements, the mean inter-subject variability was 0.05 D, and the maximum was 0.08 D at 470 nm.

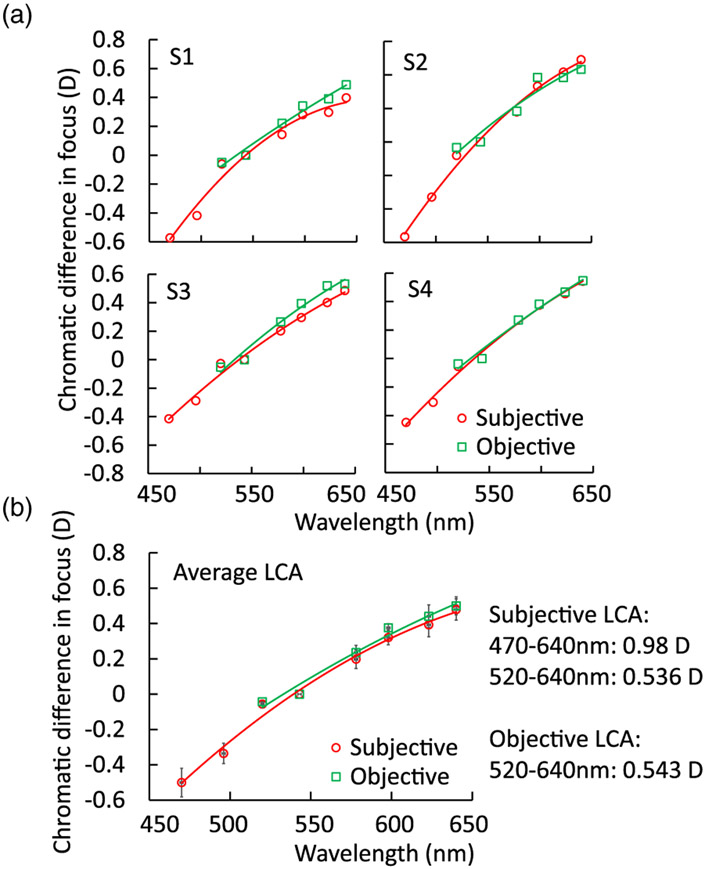
The comparisons of objective and subjective LCA measurements are plotted in Fig. 7. Figure 7(a) shows the individual comparisons for the four subjects. S1 and S3 had slightly larger differences than S2 and S4 when comparing the objective and subjective measures. The maximum differences were 0.09 D for S1 and 0.12 D for S3, both at 623 nm. Figure 7(b) shows the averaged LCA for the four subjects where the largest difference was 0.06 D observed at 598 nm. For the six wavelengths between 520 and 640 nm, where both subjective and objective measures were available, the difference was only 0.01 D on average between subjects. The student’s t-test was applied on each wavelength from 520 to 640 nm to compare the objective and subjective LCAs, and no significant differences were found.

Fig. 7.

Objective versus subjective chromatic difference measurements for individual subjects (a) S1–S4 and (b) average. The subjective and objective estimates of the total LCA for the wavelength range 520–640 nm have no significant differences.

4. DISCUSSION AND CONCLUSIONS

Here we demonstrated a strategy for compensating for LCA that can be applied to AO vision simulation and imaging systems to achieve individualized compensation for each subject and across different wavelength bands. Incorporating the filter-based Badal LCA compensator in an AOSLO allowed the first objective measurements of LCA based on confocal, high-resolution, foveal cone images and its comparison to measures obtained subjectively. Together, the objective and subjective LCA thus obtained from the same subjects harmonizes previous estimates of LCA obtained using a wide range of modalities.

A. Benefits and Limitations of the Filter-Based Badal LCA Compensator

The filter-based Badal LCA compensator provides an opportunity to address questions in vision testing and imaging where two wavelengths need to be focused in conjunction. A prime example is studies of color vision, where wavelengths are typically chosen to preferentially isolate one specific cone photoreceptor type or color-opponent mechanism. An isoluminant red-green grating, for instance, has been used routinely to characterize the red-green axis of color vision. Such stimuli are traditionally rendered using two separate displays, each tuned to optimize different wavelength bands. However, achieving pixel-level alignment between both displays to enable extremely high spatial frequencies proves challenging. Our method of using a single display with the filter-based Badal LCA compensator allows for high spatial frequencies at different wavelengths to be displayed with high fidelity, as evidenced by the excellent visual performance obtained in the isochromatic CSFs. Similarly, measures of high spatial frequency detection thresholds for red-green or blue-yellow isoluminant gratings are now possible using the same apparatus, which have been thus far accessible only by using dual-laser interference fringes to bypass the eye’s optics [41,42].

For studies where one aims to associate specific features of the cone spectral topography and the early visual system to visual perception [10-12], simultaneous imaging and retinal tracking in near-infrared wavelengths is required alongside visible light stimulation in order to target stimuli on the retina at the spatial scale of individual cells. While precompensating for the eye’s LCA based on the population average has so far been used to achieve the simultaneous focus of the visible and near-infrared wavelengths, small departures from the population need to be accounted for by trading-off the optimality in imaging and/or stimulation. It is therefore highly desirable to have fine control of focus at different wavelengths and for different subjects as is provided by the filter-based Badal LCA compensator described here.

The filter-based Badal LCA compensator is not free of limitations. As it is currently presented here, many applications would benefit from just two wavelengths focused simultaneously on the retina. The design can be modified to further realize LCA corrections across more wavelength bands, only limited by optomechanical considerations. For instance, incorporating a third channel would require another translation stage and two additional long-pass filters. Second, the strategy that we describe here is not suitable for applications where LCA for a large continuous wavelength band needs to be corrected, such as OCT. Finally, the transmitted and reflected paths of the compensator are essentially faced with dissimilar aberrations, leading to non-common path wavefront errors in the imaging and wavefront sensing paths. As evidenced by the CSFs and foveal cone images however, these non-common path errors seem to play a minor role in retinal image quality. Furthermore, the traditional realization of multi-wavelength AO systems with a dedicated wavefront sensing channel faces similar limitations due to non-common path errors. Other than vision testing, such dual-wavelength imaging instruments are also used for imaging the intrinsic and extrinsic fluorophores in the retina using variations of auto-, single- or two-photon fluorescence microscopy in humans and in animal models [43-46]. The eye’s native LCA between the excitation and emission bands needs to be compensated for to optimize signal efficiency [47]. By providing an independent control of the excitation and emission wavelength bands, the filter-based Badal LCA compensator can prove to be an effective tool for obtaining high efficiency in imaging fluorescence.

B. Improved Technology for Subjective and Objective LCA Measurements

Estimates of LCA obtained subjectively are confounded to some extent due to the finite depth of focus of the human eye. Without monochromatic aberration compensation, the native optical errors in the human eye extend the depth of focus to the extent that a static correction of LCA without accounting for the inter-subject variability in LCA may be sufficient. With AO correction of monochromatic aberrations, however, the depth of focus is reduced considerably [48]. Vinas et al. [37] provided the first subjective estimates of LCA with AO correction and concluded that the inter-subject variability in LCA is small (<0.10 D). In their study, because the wavefront sensor path was shared with the visible wavelengths, the subjects optimized subjective image quality in open loop by using a traditional Badal optometer. Here, subjective optimization of image quality was performed under dynamic AO control. Vinas et al. used a Maltese cross as their visual stimuli that presumably had a broader spatial frequency spectrum than the 20/20 Snellen letter ‘E’ used here, which may affect the defocus that the subjects needed to optimize image quality. Despite these differences, the subjective LCAs obtained in Vinas et al. aligned with that measured here.

Previous methods of objective assessments of LCA via imaging —the reflectometer [34,35,37] and wavefront sensor [35,37]— are faced with an ambiguity in determining the retinal layer from which the light is scattered back. This ambiguity has been attributed as the key factor for why the objective measures of LCA are smaller than the subjective ones. The majority of the signals detected in the imaging sensor in these cases originate from the strongest scattering layer, which is not the same across different wavelengths. Delori and Pflibsen studied light reflectance from different intraocular tissues using fundus reflectometry [49]. They concluded that for red light, the majority of the signal originated from the choroid, while in green and blue light, the contribution of the choroidal reflections is smaller compared to other layers. Rynders et al. [34] and Vinas et al. [37] compared the subjective and objective LCA measurements quantitatively and confirmed the finding of Delori et al. It is important to clarify here the definition of LCA we use in our measurements. Light of different wavelengths focusing at different retinal depths can be attributed to a combination of dispersion in the anterior chamber and vitreous as well as differential absorption and hence penetration for multi-wavelength light due to the retinal tissue itself. By treating the plane of cone photoreceptors as the focal reference and imaging them with the known axial sectioning capabilities of an AOSLO, our goal was to overcome the latter and report LCA measurements as governed only by that arising in the anterior eye. Imaging the plane of cone photoreceptors thus provided an excellent resolution for the ambiguities in previous objective measures of LCA. That the subjective estimates of LCA now align with the objective measures as obtained from foveal cone images indicates that the subjects chose to introduce defocus to optimize the visual stimuli to fall on cone photoreceptors and thus initiate the cascade of vision.

C. Our LCA Measurements Compared with Previous Studies

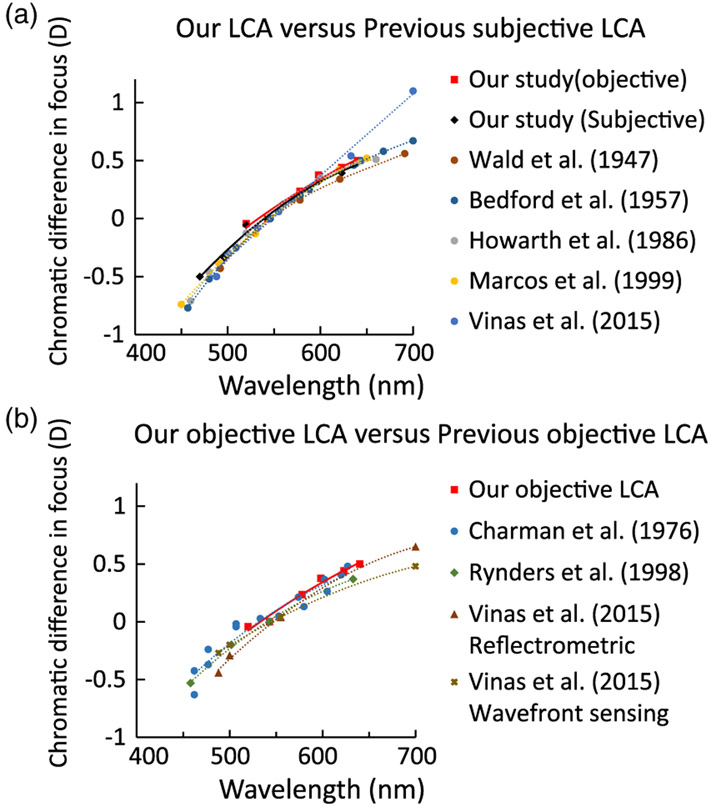
Figure 8 shows our LCA measurement compared with previous subjective [31-33,36,37] and objective [34,35,37] studies. These previous studies were chosen because of either a large data pool or similar wavelength range as our study. Here we only showed the data from 450 to 700 nm range for both subjective and objective measurements. As seen in Fig. 8(a), both our subjective and objective LCA measurements showed good agreement with previous subjective studies, which is consistent with the hypothesis that the subjective focal plane was optimized to be at the photoreceptor layer. Figure 8(b) indicates that above the reference wavelength of 543 nm (0 D LCA position), our objective LCA is higher compared with other studies. This confirms that at the longer wavelengths, the strongest scattering layers in the previous studies were distal to the photoreceptors, resulting in an LCA that was smaller than the subjective measures.

Fig. 8.

(a) Comparison of previous subjective LCA estimations and our subjective (black solid line) and objective (red solid line) measurements. All the LCA estimations, including our objective one, agree well with each other. (b) Comparison of previous objective LCA studies with our objective measurements.

One caveat for our objective LCA is that a relatively shorter wavelength range (520–640 nm) was feasible compared to other reports. High macular pigment density impedes foveal cone imaging with safe light levels at shorter wavelengths. However, subjective LCA was measured under the same shorter wavelengths at the fovea and showed good agreement with previous reports. To overcome this limitation, we imaged the retina at 2.5 deg temporal eccentricity where macular pigment density is reduced [50] and subjective LCA is similar to the fovea [34] (See Supplement 1). The consistency between objective and subjective estimates of LCA obtained at 470 nm denotes that the agreement between them observed in the longer wavelength range is maintained for this shorter wavelength also.

In summary, this study demonstrates a filter-based Badal LCA compensator applied to adaptive optics vision testing and imaging systems that offers the flexibility to tune LCA for each individual eye. This approach will benefit color vision research, cone-targeted vision testing, as well as intrinsic and extrinsic fluorescence imaging. Using the AOSLO, we objectively assessed the LCA for the first time by visualizing the fine detail in the foveal cone image across multiple wavelengths and showed that the objective LCA thus measured aligns extremely well with subjective LCA estimates in the same subjects.