Abstract
Purpose:
To introduce a novel framework to combine deep-learned priors along with complementary image regularization penalties to reconstruct free breathing & ungated cardiac MRI data from highly undersampled multi-channel measurements.
Methods:
Image recovery is formulated as an optimization problem, where the cost function is the sum of data consistency term, convolutional neural network (CNN) denoising prior, and SmooThness regularization on manifolds (SToRM) prior that exploits the manifold structure of images in the dataset. An iterative algorithm, which alternates between denoizing of the image data using CNN and SToRM, and conjugate gradients (CG) step that minimizes the data consistency cost is introduced. Unrolling the iterative algorithm yields a deep network, which is trained using exemplar data.
Results:
The experimental results demonstrate that the proposed framework can offer fast recovery of free breathing and ungated cardiac MRI data from less than 8.2s of acquisition time per slice. The reconstructions are comparable in image quality to SToRM reconstructions from 42s of acquisition time, offering a fivefold reduction in scan time.
Conclusions:
The results show the benefit in combining deep learned CNN priors with complementary image regularization penalties. Specifically, this work demonstrates the benefit in combining the CNN prior that exploits local and population generalizable redundancies together with SToRM, which capitalizes on patient-specific information including cardiac and respiratory patterns. The synergistic combination is facilitated by the proposed framework.
Keywords: alternating minimization, free breathing cardiac MR, learned prior, model-based, non-local prior, subject specific prior
1 |. INTRODUCTION
Breath-held cardiac cine MRI is a key component in cardiac MRI exams, which is used for the anatomical and functional assessment of the heart. Unfortunately, several subject groups (e.g. children and chronic obstructive pulmonary disease (COPD) patients1) cannot hold their breath and hence are excluded from breath-held MRI studies. In addition, breath-held protocols are also associated with long scan times. Several methods were introduced to reduce the breath-holding requirements or enable free breathing cardiac MRI protocols, including parallel MRI,2,3 approaches that exploit the structure of x-f space,4–6 compressed sensing schemes,7,8 low-rank methods,9,10 blind compressed sensing,11,12 motion compensated methods,13,14 and kernel low-rank methods.15 Motivated by recent deep learning frameworks for static imaging applications,16–18 deep-learning based breath-held cardiac cine acceleration methods were also introduced.19,20 Recently, several researchers have proposed to estimate cardiac and respiratory phases from the central k-space regions using band-pass filtering; the data are then binned to the respective phases, followed by reconstruction using compressed sensing21,22 or low-rank tensor methods.23,24 These methods depend on the accurate estimation of phases using prior information about the cardiac and respiratory rates, which may degrade with irregular respiration or arrhythmia. We have recently introduced the SToRM25–28 framework as an alternative to explicit motion resolved strategies.21–23 SToRM assumes that the images in the free-breathing dataset lie on a smooth and low-dimensional manifold parameterized by cardiac & respiratory phases. SToRM acquisition relies on navigator radial spokes, which are used to compute the manifold Laplacian matrix, to capture the structure of the manifold. Once the Laplacian matrix is available, the estimation of the dataset simplifies to a quadratic regularization scheme. SToRM can provide reliable free breathing reconstructions from around 40 seconds/slice of scan time, which ensures that the image manifold is well-sampled.
The main focus of this work is to further reduce the scan time of SToRM by combining the patient-specific SToRM prior with deep-learned priors, which are population generalizable. While the direct deep learning approaches17,18 that estimate the images directly from the measured k-space data are computationally efficient, it is not straight forward for them to ensure data consistency or incorporate patient-specific priors. We hence rely on our recent model-based deep learning (MoDL) framework, which formulates the image recovery as an optimization scheme,29,30 where the cost function is the combination of a data consistency term with a deep learned prior; the unrolling of an iterative algorithm to solve the above cost function translates to a deep network. This main difference of this scheme with other model based methods16,19,31 is the use of embedded conjugate gradient (CG) blocks and the sharing of network parameters between iterations; our results in29,30 show that sharing of trainable parameters across iterations reduces the training data requirement significantly, while the use of CG blocks within the deep network translates to improved results for a specified number of iterations. Note that the use of CG blocks results in a slightly longer run time compared to direct learning approaches.17,18 However, the proposed framework still provides significantly shorter run times than classical compressed sensing strategies, thanks to the reduced number of iterations and reduced number of CG steps per iterations. In this work, we use this optimization-based framework for the seamless integration of the forward model (coil sensitivity information, sampling pattern) with SToRM priors and deep learning priors.
The proposed MoDL-SToRM cost consists of a data consistency term, a deep learned prior that learns population generalizable information, and the SToRM prior; the framework may also be used with other regularizers such as.32–34 The CNN-based prior exploits local image redundancies of the 2D+time dataset.
By contrast, the SToRM prior exploits non-local redundancies between images in the dataset, which are specific to the cardiac and respiratory patterns of the subject. The regularization parameters that weigh the individual contributions of each term are also optimized during the training phase, eliminating the need for image-specific tuning of parameters. The combination of deep learning with other complementary priors in the context of free-breathing image reconstruction is not reported in the literature, to the best of our knowledge. These complementary priors enable the recovery from highly undersampled measurements, thus reducing the acquisition time by 5-10-fold over SToRM. While our focus is on free-breathing applications in this work, the algorithm may also provide good reconstructions of relatively less challenging breath-held applications.
2 |. METHODS
2.1 |. Acquisition scheme
Four healthy volunteers instructed to breathe normally were scanned at the Siemens Aera scanner in the University of Iowa hospitals to generate prospectively undersampled free-breathing ungated radial dataset. The data were acquired using a FLASH sequence with a 32 channel cardiac array. The scan parameters were TR/TE = 4.2/2.2 ms, number of slices = 5, slice thickness = 5 mm, FOV = 300 mm, spatial resolution = 1.17 mm. A temporal resolution of 42 ms was obtained by binning 10 consecutive lines of k-space per frame, including 4 uniform navigator lines. Each slice comprised of 10 000 radial lines of the k-space binned to 1000 frames, resulting in an acquisition time of 42s.
The raw k-space data were interpolated to a Cartesian grid and 7 virtual coils were approximated out of the initial 32 using a SVD-based coil-compression technique. The coil sensitivity maps were estimated from the compressed data using ESPIRiT.35 The SToRM25 reconstructed images were used as the reference to train the deep networks. We use subsets of the above data to demonstrate the utility of the proposed scheme.
2.2 |. MoDL-SToRM: formulation
We generalize the model-based deep learning framework (MoDL) by adding a SToRM prior:
| (1) |
Here, is the multi-channel Fourier sampling operator, which includes coil sensitivity weighting. is a 3-D CNN-based estimator that estimates the noise and alias patterns in the dataset from local neighborhoods of the 2D+time dataset; is a measure of the alias/noise contribution in the dataset X.29 The denoised signal can thus be estimated from the data X as
| (2) |
Note that we can also express , where is the denoised version of X, when it is corrupted with noise and/or artifacts. However, we expect when X is an image free from noise and artifacts; i.e, in this case. The above relation allows us to rewrite the second term in Equation (1) as the norm of the differences between the original and denoised images. The SToRM prior tr (XTLX), exploits the similarities beyond the local neighborhood. The manifold Laplacian, L = D–W is estimated from the k-space navigators.25 The diagonal matrix D is specified as D(i,i) = Σj W(i,j), where W is a weight matrix, such that, the weight W(i,j) is high when xi and xj have similar cardiac and/or respiratory phase. tr is the trace operator.
2.3 |. Alternating minimization algorithm
We expand the SToRM penalty as
We consider temporary variables and Q = WX and rewrite Equation (1) as:
| (3) |
We note that Equation (3) is equivalent to Equation (1) when and Q = WX. Minimizing the objective with respect to X, assuming variables Y and Q to be fixed and determined from the previous iterations yields:
| (4) |
where is the adjoint of . This can be solved as
| (5) |
As D is diagonal, can be implemented on a frame-by-frame basis. We solve for Equation (5) for each frame of X using conjugate gradients algorithm. This provides us with an alternating algorithm:
| (6) |
| (7) |
| (8) |
| (9) |
Once the number of iterations is fixed, the network can be unrolled to yield a deep network as in Figure 1A. The parameters of and the optimization parameters λ1 and λ2 are trainable and shared throughout the iterations.
FIGURE 1.
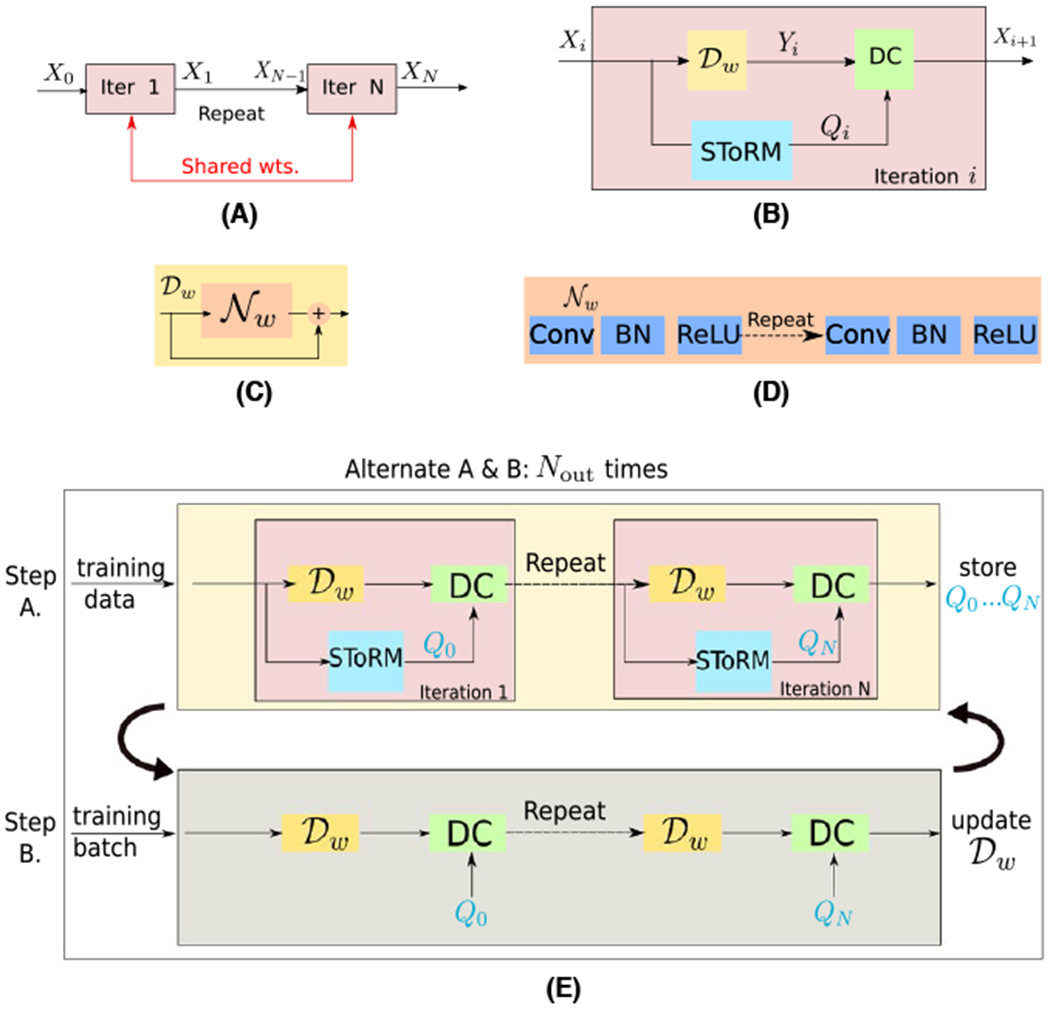
Illustration of the proposed MoDL-SToRM framework. The proposed scheme is obtained by unrolling the iterations specified by Equations (6)–(9) as shown in (A). Each iteration consists of CNN denoiser , specified by Equation (6), SToRM update specified by Equation (7), and data-consistency enforcement specified by Equation (9), as shown in (B). The CNN denoiser is implemented as a residual network as shown in (C), where the architecture of is shown in (D). Here, , the noise extractor operator. The main differences between this scheme and other model-based deep-learned schemes is the sharing of the weights across iterations as shown in (A) and the use of CG blocks to enforce the data-consistency in (B), when complex forward models such as multi-channel sampling is used. Note that unlike DC and that involves local operations, the update of Qn is global in nature; the direct implementation of the unrolled network in (A) is associated with high memory demand and is not feasible on current GPU devices. We use the training strategy in (E), where we use the lagged update of Qn. Specifically, we perform a forward pass through the network to determine Qn for all the frames in each training dataset. These Qn parameters are stored. Batches of seven frames of X0 and Qn are fed into the network to update the network weights, which can be performed on the GPU. We propose to precompute Qn in an outer-loop and update it less frequently than the network parameters
We initialize the iterations with the SToRM solution:
| (10) |
where η is fixed and chosen manually to produce the best SToRM results.
2.4 |. Network and training details
We note that the unrolled network described by Equations (6)–(9) is dependent on the weight matrix W, which captures the non-local similarities between image frames. For each training/testing dataset, we estimate W from navigators; the dataset and the corresponding W are used for training/testing. The rest of the variables including the regularization parameters λ1, λ2, and the weights of Nw are learned during training. Specifically, we train the unrolled network in an end-to-end fashion using different sets of {X0, Xg, W} . Here Xg is the ground-truth, while W is fixed during training and is different for each training and test dataset. The CNN captures the local redundancies, which is independent from the non-local information in W. Since the end-to-end network sees different sets of training data, each with different W matrices, it learns the network parameters that are invariant/independent of the specific W.
2.4.1 |. Lagged update of Qn
The training scheme requires the storage of Yn, Qn, and Xn. The straightforward training of the unrolled architecture in Figure 1A requires all these intermediate variables to be available on the GPU memory, which is often not feasible. We propose a lagged approach shown in Figure 1E, where Qn is updated less frequently during training. We update Qn iby making a forward pass through the network, assuming known network parameters. The Qn, each corresponding to 200 frames, are then stored in the computer memory and assumed to be fixed during the inner iterations. The trainable network parameters specified by w, λ1 and λ2 are optimized in the inner loop on the GPU. We form batches of seven frames and the corresponding frames of the pre-computed Qn for training. Following convergence of Equation (3) (inner-loop) for a fixed Qn, we update Qn and re-train the network, assuming the network parameters from the previous outer iteration as the initialization. We need multiple outer iterations for the training procedure to converge.
2.4.2 |. Training dataset
The data were acquired on four healthy volunteers, each but one with two different views–short axis and four chamber view–resulting in a total of seven datasets. We used the data from four datasets for training and remaining three for testing. We extracted three non-overlapping groups of 200 frames each from the above datasets, which were used for training. The SToRM reconstruction of the datasets from 1000 frames are considered as reference data, whereas, the input to the network was X0, the solution to Equation (10) computed with reduced number of frames (200).
2.4.3 |. Trainable parameters of the network
The CNN block specified by consists of a 6 layer CNN with 64 filters of dimensions 3 × 3 × 3 in the first five layers, followed by two 3 × 3 filters in last layer. To deal with complex data, the real and imaginary part of the frames were passed as two channels of the input tensor. The total number of trainable parameters in the network is 151666 real variables. The sharing of the parameters across iterations provides good performance, while significantly reducing training data demand as shown in.29
2.4.4 |. Training strategy
The network was trained with the Adam optimizer on mean squared error loss, implemented on TensorFlow and trained on a NVIDIA P100 GPU. We pre-trained the to denoise various versions of SToRM-1000 reconstructions corrupted with different levels of noise, which took 18 hours (1200 epochs). Next, we trained a MoDL-SToRM with N = 1. Following a single iteration training, we considered a multiiteration model (N > 1), with the parameters initialized by the ones learned with N = 1.
We observed that a network with two iterations was sufficient to provide good reconstructions; the performance saturated beyond two repetitions. The total training time was 35 hours. The final inference for 8.4 s of data was from a single forward pass containing N = 2 repetitions, which takes around 28 second for all 200 frames. This is significantly faster than most compressed sensing reconstructions.
We also compare the proposed MoDL-SToRM reconstruction scheme against (a) SToRM alone and (b) Tikhonov-SToRM shown in Equation (11).
| (11) |
We consider reconstructions from 200 frames, corresponding to 8.4 seconds of acquisition time. All comparisons are made with SToRM reconstructions from 1000 frames (42 seconds) using the signal to error ratio metric (in addition to the standard PSNR and SSIM) defined as
| (12) |
where X1000 denotes the SToRM-reconstruction from 1000 frames and X is the specific reconstruction. The visual comparisons of the reconstructed images, their time profiles, and error images with SToRM reconstructions from 1000 frames as ground truth, are shown in Figures 2–4.
FIGURE 2.
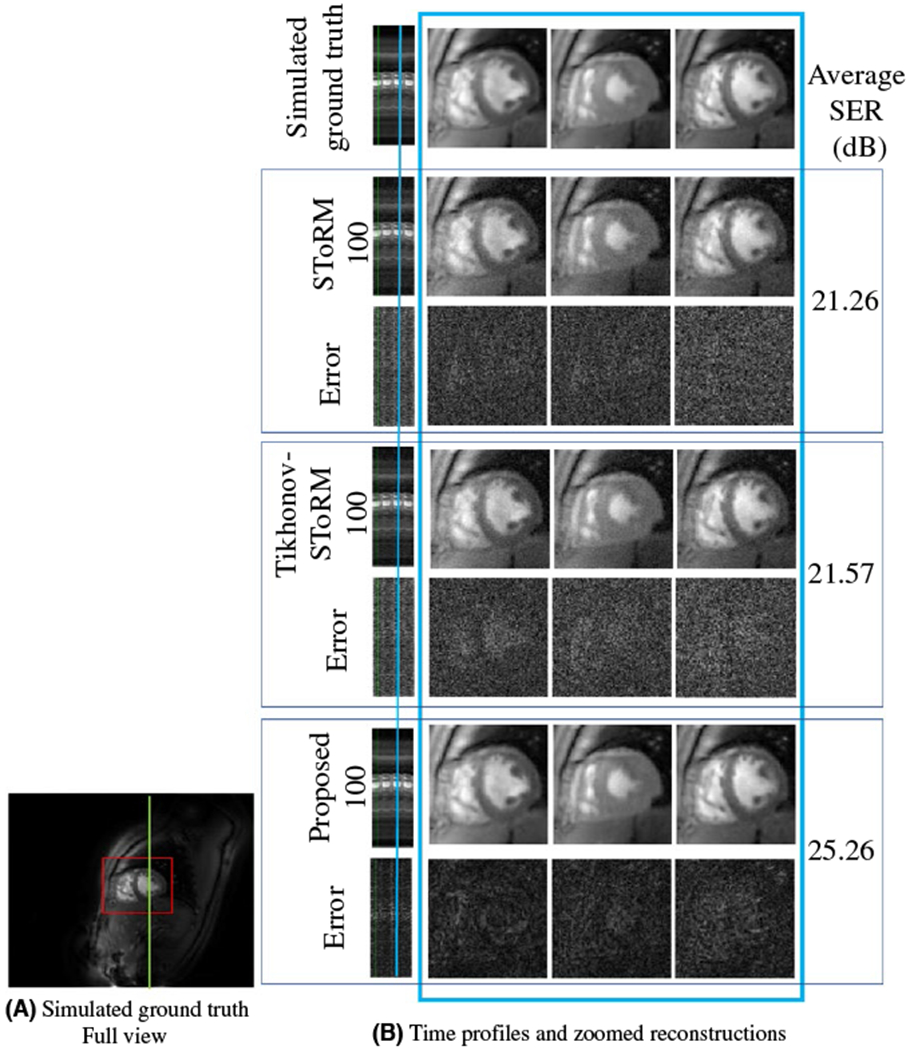
Comparisons on the simulated dataset: A, Full view of a single frame from the simulated ground truth time series of 500 frames. Only (red) cropped myocardium region is shown in (B). B, Top row: Simulated ground truth time series of 500 frames. Following six rows are three sets of competing reconstructions and corresponding error (w.r.t to top row) images: (i) SToRM reconstruction with 100 frames, (ii) Tikhonov-SToRM reconstruction with 100 frames and (iii) proposed with 100 frames. First column is the time profile along a vertical cut across the myocardium shown in green in (A). Following three columns show three cardiac states at one respiratory stage. The position of the respiratory stage is marked blue on the time profile, in the first column. Three cardiac states are neighboring frames near the marked time point. The SER (dB) reported in the figure corresponds to the myocardium area
FIGURE 4.
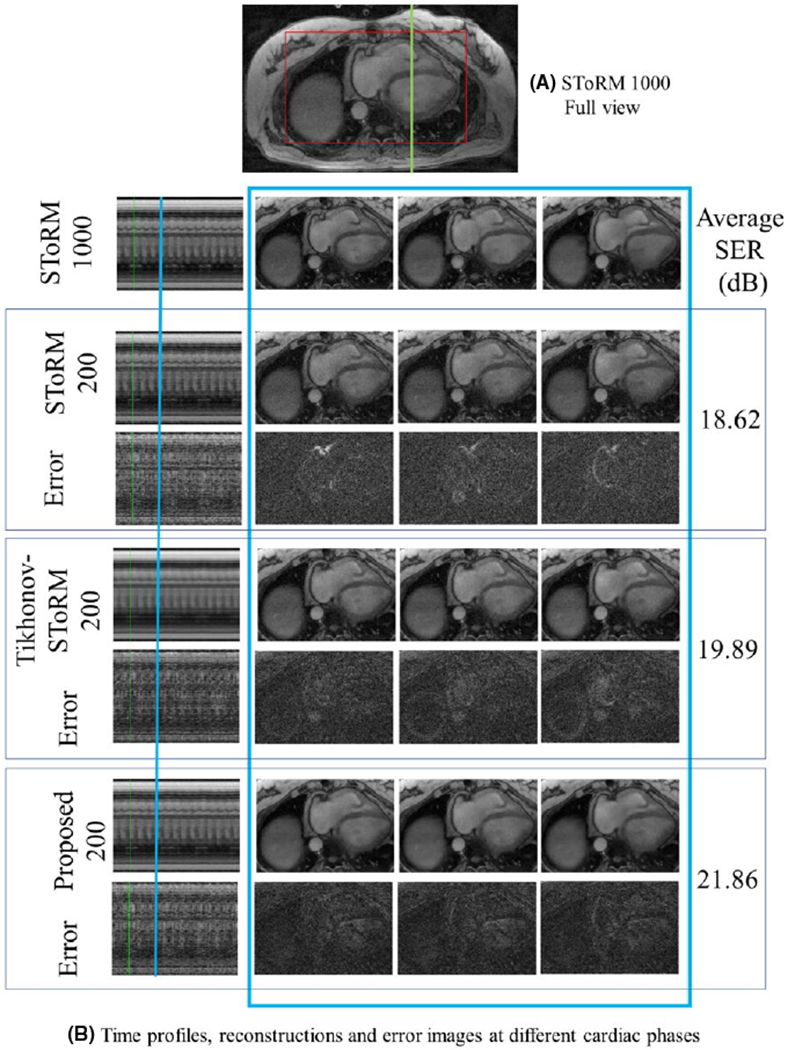
Dataset 2: A, Full view of a single frame from the SToRM reconstruction using 1000 frames. Only (red) cropped myocardium region is shown. B, Top row: SToRM reconstruction using 1000 frames. Following six rows are three sets of competing reconstructions and corresponding error (w.r.t to top row) images: (i) SToRM reconstruction with 200 frames, (ii) Tikhonov-SToRM reconstruction with 200 frames and (iii) proposed with 200 frames. First column is the time profile along a vertical cut across the myocardium shown in green in (A). Following three columns show three cardiac states at one different respiratory stage. The position of the respiratory stage is marked blue on the time profile, in the first column. Three cardiac states are neighboring frames near the marked time point. The SER (dB) reported in the figure corresponds to the myocardium area
2.5 |. Simulated data
We generated simulated free breathing datasets by extracting three cardiac cycles of a SToRM-1000 reconstruction and deforming (using Bspline interpolation) them in space and time to generate six synthetic datasets. These simulated datasets (four training & two testing) were retrospectively undersampled using six golden angle radial lines & four uniform radial navigators. The results on a test dataset is shown in Figure 2, while quantitative comparisons are in Table 1.
TABLE 1.
Quantitative comparison of the methods on simulated dynamic datasets
| Dataset | Method | SER (dB) | PSNR (dB) | SSIM |
|---|---|---|---|---|
| SToRM | 16.31 | 37.31 | 0.8868 | |
| Subject 1 | Tikhonov-SToRM | 18.78 | 39.77 | 0.9021 |
| Proposed | 20.36 | 41.36 | 0.9386 | |
| SToRM | 14.54 | 33.33 | 0.8161 | |
| Subject 2 | Tikhonov-SToRM | 16.55 | 35.40 | 0.8783 |
| Proposed | 20.12 | 38.97 | 0.9114 | |
| SToRM | 17.09 | 34.19 | 0.8345 | |
| Subject 3 | Tikhonov-SToRM | 19.02 | 36.17 | 0.8484 |
| Proposed | 20.73 | 37.83 | 0.9021 | |
| SToRM | 15.04 | 34.60 | 0.6880 | |
| Simulated | Tikhonov-SToRM | 15.29 | 34.85 | 0.6968 |
| dataset 1 | Proposed | 23.43 | 42.98 | 0.9602 |
| SToRM | 21.63 | 36.03 | 0.8641 | |
| Simulated | Tikhonov-SToRM | 21.92 | 36.92 | 0.8696 |
| dataset 2 | Proposed | 26.82 | 41.23 | 0.9721 |
We report the signal to error ratio (SER), peak signal to noise ratio (PSNR), and structural similarity index (SSIM). These metrics are reported for the entire field of view. By contrast, the SER (dB) metrics reported in the Figures are reported only for the myocardium area.
3 |. RESULTS
3.1 |. Selection of parameters
We first discuss how the parameters of the algorithm was selected.
3.1.1 |. Number of iterations N
We observe that the performance of MoDL-SToRM saturates with N. For example, for test dataset 1, we obtained PSNR of 37.13 dB, 40.68 dB, and 41.36 dB, with N=0, 1, and 2, respectively. The change in performance from N=2 to N=3 was negligible; we choose N=2 in the rest of the experiments.
3.1.2 |. Number of outer iterations in training Nout
We observe that few outer iterations were sufficient for the training to converge. We obtained PSNR of 40.62 dB 41.36 dB and 41.37 dB, when the number of outer iterations is 1, 2, and 3, respectively. We choose this setting for the rest of the experiments since the performance saturates at Nout = 2.
3.2 |. Comparisons with other methods
The comparisons on the simulated datasets in Figure 1 show that the proposed method provides the best reconstructions, which is also confirmed by the quantitative results shown in Table 1. The comparisons of the reconstructions from 200 frames in Figure 3 show that the proposed algorithm provides the most accurate reconstructions, revealed by the reduced errors and improved SER. We observe that the performance of SToRM suffers when the number of frames are reduced, evidenced by the high amount of noise like alias artifacts. Comparison of the proposed method with MoDL29 (explained in Supporting Information Figure S1), is provided in the Supporting Information (Figure S3–S5, Table S1). MoDL only uses local information and is hence not able to provide high quality reconstructions for such high accelerations; however, we expect the MoDL to work well in breath-held applications such as.19 This signifies the need of the additional SToRM prior, which can exploit the non-local redundancy a simple CNN model cannot capture. The comparisons on prospective data shows that the proposed reconstruction from 8.4 seconds scan time is most comparable with SToRM from 42s of scan time, while the SToRM-alone reconstructions from 8.4 seconds scan time results in noise amplification.
FIGURE 3.
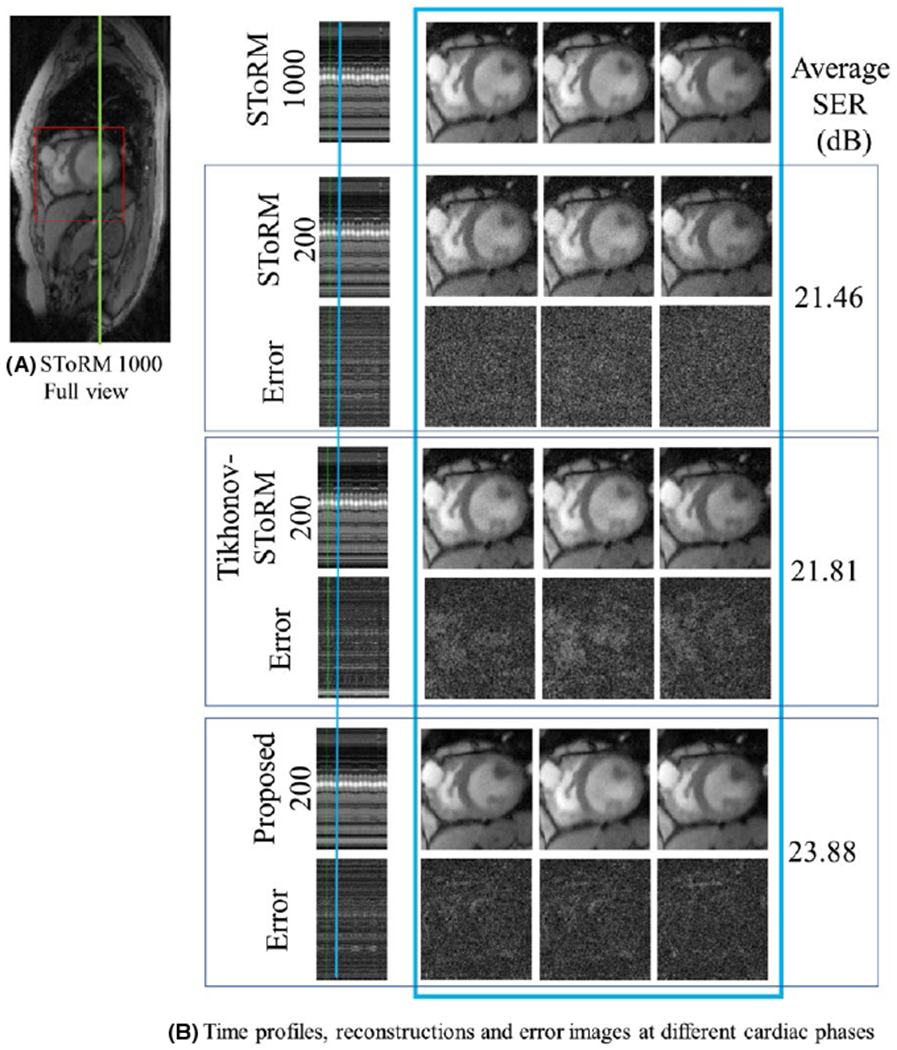
Comparisons on Dataset 1: A, Full view of a single frame from the SToRM reconstruction using 1000 frames. Only (red) cropped myocardium region is shown. B, Top row: SToRM reconstruction using 1000 frames. Following six rows are three sets of competing reconstructions and corresponding error (w.r.t to top row) images: (i) SToRM reconstruction with 200 frames, (ii) Tikhonov-SToRM reconstruction with 200 frames and (iii) proposed with 200 frames. First column is the time profile along a vertical cut across the myocardium shown in green in (A). Following three columns show three cardiac states at one respiratory stage. The positions of the respiratory stage is marked blue on the time profile, in the first column. Three cardiac states are neighboring frames near the marked time point. The SER (dB) reported in the figure corresponds to the myocardium area
4 |. DISCUSSION & CONCLUSION
We introduced a model-based framework, which can accommodate learnable CNN priors along with conventional SToRM regularizers, for the recovery of free breathing and ungated cardiac MRI data from radial acquisitions. The CNN exploits local population-generalizable redundancies, while the SToRM prior enables the use of patient specific nonlocal redundancies that depend on the cardiac and respiratory patterns. Our experiments show that very few iterations of Equations (6)–(9) is sufficient to provide good reconstructions. The fast saturation of performance with iterations is mainly due to the use of CG algorithm within the network. The improved performance in the context of limited training data can be attributed to the trainable parameters in the network, shared across iterations. The proposed scheme also provides a fast reconstruction time of around 30 seconds on a P100 GPU for the reconstruction of 200 frames.
We observe that from the error images in Figures 2 and 3 that the proposed approach results in reduced overall errors compared to competing methods, there are relatively higher residual errors around the image edges. Nevertheless, we note that the residual error is comparable or lower in magnitude than the ones obtained by other methods at all spatial locations, including at edges. The results also show that the MoDL-SToRM approach outperforms Tikhonov-SToRM, demonstrating the use of learnable priors. We observe from the figures in the supplementary information (S.3 & S.4) that the use of MoDL alone provides poor quality reconstructions, while its combination with SToRM provides improved results. We note that the undersampling factor needed to enable free breathing and ungated cardiac MRI is quite high (≈50 fold undersampling), compared to most deep learning-based acceleration schemes. MoDL uses local redundancies to recover these images, which results in poor reconstructions in this highly undersampled setting. The SToRM scheme facilitates the combination of information from different image frames. The reduced effective sampling resulting from reduced acquisition time causes increased errors, which the added MoDL regularization reduces. Although the CNN network architecture is same for MoDL and MoDL-SToRM, the two networks are trained to minimize different cost functions and hence the learned weights are expected to be different. We note that the size of the CNN in the proposed scheme is significantly smaller than those available in the literature; as shown in,29,30 the sharing of weights between iterations allows us to significantly reduce the data demand required to avoid overfitting. The decay of validation error with training iterations as shown in the supplementary material also confirms that the model is not overfitting the data. This is also confirmed by the validation curves shown in the Supporting Information (Figure S2).
We rely on the alternating minimization strategy specified by Equations (6)–(9) to solve Equation (3). We have not rigorously studied the convergence of this algorithm to the objective in Equation (3), which is beyond the scope. Similarly, we have not studied the impact of the sampling pattern (e.g numbers of spokes) on the quality of the reconstructions in this note. The data were acquired using a sequence with four uniform radial navigators and six golden angle radial lines. This will be the focus of our future work. Each image is only sampled with 10 radial lines, which translates to 50 fold undersampling. MoDL-SToRM simultaneously exploits local and global redundancies to yield improved results. The SToRM scheme facilitates the combination of information from different image frames. With low number of frames, the SToRM-alone regularization results in increased errors, which the added MoDL regularization reduces significantly. MoDL and MoDL-SToRM share the network architecture (except for λ2) but the learned weights differ significantly. In this work, we restricted our attention to L2 loss metric to train the network. Several researchers have recently proposed alternate metrics for network training with improved results. We had experimented with L2–L1 losses with little improvement in quality. The performance of the algorithm may be improved using sophisticated training strategies including GAN, but is beyond the scope of this work.
Supplementary Material
Acknowledgments
Funding information
NIH, Grant/Award Number: 1R01EB019961-01A1
REFERENCES
- 1.Gay SB, Sistrom CL, Holder CA, Suratt PM. Breath-holding capability of adults. Implications for spiral computed tomography, fast-acquisition magnetic resonance imaging, and angiography. Investigative Radiol. 1994;29:848–851. [PubMed] [Google Scholar]
- 2.Huang F, Akao J, Vijayakumar S, Duensing GR, Limkeman M. k-t grappa: A k-space implementation for dynamic MRI with high reduction factor. Magn Reson Med. 2005;54:1172–1184. [DOI] [PubMed] [Google Scholar]
- 3.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. Sense: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 4.Liang ZP, Jiang H, Hess CP, Lauterbur PC. Dynamic imaging by model estimation. Int J Imaging Syst Technol. 1997;8:551–557. [Google Scholar]
- 5.Sharif B, Derbyshire JA, Faranesh AZ, Bresler Y. Patient-adaptive reconstruction and acquisition in dynamic imaging with sensitivity encoding (paradise). Magn Reson Med. 2010;64:501–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tsao J, Boesiger P, Pruessmann KP. k-t blast and k-t sense: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med. 2003;50:1031–1042. [DOI] [PubMed] [Google Scholar]
- 7.Jung H, Sung K, Nayak KS, Kim EY, Ye JC. k-t focus: a general compressed sensing framework for high-resolution dynamic MRI. Magn Reson Med. 2009;61:103–116. [DOI] [PubMed] [Google Scholar]
- 8.Lustig M, Santos J, Donoho D, Pauly J. k-t SPARSE: high frame rate dynamic MRI exploiting spatio-temporal sparsity. Proceedings of the 14th Annual Meeting of ISMRM, Seattle, WA, 2006. p. 2420. [Google Scholar]
- 9.Zhao B, Haldar JP, Christodoulou AG, Liang ZP. Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints. IEEE Trans Med Imaging. 2012;31:1809–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR. IEEE Trans Med Imaging. 2011;30:1042–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging. 2013;32:1132–1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lingala SG, Jacob M. A blind compressive sensing framework for accelerated dynamic MRI. In IEEE International Symposium on Biomedical Imaging, 2012a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Asif MS, Hamilton L, Brummer M, Romberg J. Motion-adaptive spatio-temporal regularization for accelerated dynamic MRI. Magn Reson Med. 2013;70:800–812. [DOI] [PubMed] [Google Scholar]
- 14.Mohsin YQ, Lingala SG, DiBella E, Jacob M. Accelerated dynamic MRI using patch regularization for implicit motion compensation. Magn Reson Med. 2017;77:1238–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nakarmi U, Wang Y, Lyu J, Liang D, Ying L. A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI. IEEE Trans Med Imaging. 2017;36:2297–2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Diamond S, Sitzmann V, Heide F, Wetzstein G. Unrolled optimization with deep priors. In arXiv:1705.08041, 2017:1–11. https://arxiv.org/abs/1705.08041. [Google Scholar]
- 17.Jin KH, McCann MT, Froustey E, Unser M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans Image Process. 2017;29:4509–4522. [DOI] [PubMed] [Google Scholar]
- 18.Lee D, Yoo J, Ye JC. Deep residual learning for compressed sensing MRI. In IEEE International Symposium on Biomedical Imaging 2017:15–18. ISBN 9781509011728. [Google Scholar]
- 19.Qin C, Schlemper J, Caballero J, Price A, Hajnal JV, Rueckert D. Convolutional recurrent neural networks for dynamic MR image reconstruction. ArXiv e-prints, December 2017. [DOI] [PubMed] [Google Scholar]
- 20.Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging. 2018;37:491–503. [DOI] [PubMed] [Google Scholar]
- 21.Feng L, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72:707–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. Xd-grasp: golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med. 2016;75:775–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Christodoulou AG, Hitchens TK, Wu YL, Ho C, Liang ZP. Improved subspace estimation for low-rank model-based accelerated cardiac imaging. IEEE Trans Biomed Eng. 2014;61:2451–2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Christodoulou AG, Shaw JL, Nguyen C, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2:215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Poddar S, Jacob M. Dynamic MRI using smoothness regularization on manifolds (storm). IEEE Trans Med Imaging. 2016;35:1106–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Poddar S, Lingala SG, Jacob M. Joint recovery of under sampled signals on a manifold: application to free breathing cardiac MRI. In 2014, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE; 2014:6904–6908. [Google Scholar]
- 27.Poddar S, Jacob M. Low-rank recovery with manifold smoothness prior: theory and application to accelerated dynamic MRI. In 2015, IEEE 12th International Symposium on Biomedical Imaging (ISBI), IEEE; 2015:319–322. [Google Scholar]
- 28.Poddar S, Jacob M. Recovery of noisy points on band-limited surfaces: kernel methods re-explained. CoRR, 2018;abs/1801.00890 http://arxiv.org/abs/1801.00890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Aggarwal HK, Mani MP, Jacob M. MoDL: model-based deep learning architecture for inverse problems. IEEE Trans Med Imaging. 2018a:1–1. ISSN 0278-0062. doi: 10.1109/TMI.2018.2865356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Aggarwal HK, Mani MP, Jacob M. Model-based image reconstruction using deep learned priors (MODL). In 2018, IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), IEEE; 2018b:671–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018;79:3055–3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lingala SG, Jacob M. A blind compressive sensing framework for accelerated dynamic MRI. In Proceedings/IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE International Symposium on Biomedical Imaging, NIH Public Access; 2012b:1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hu Y, Ongie G, Ramani S, Jacob M. Generalized higher degree total variation (HDTV) regularization. IEEE Trans Image Process. 2014;23:2423–2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Goud S, Hu Y, Jacob M. Real-time cardiac MRI using low-rank and sparsity penalties. In 2010, IEEE International Symposium on Biomedical Imaging: From Nano to Macro, IEEE; 2010:988–991. [Google Scholar]
- 35.Uecker M, Lai P, Murphy MJ, et al. Espirit—an eigenvalue approach to autocalibrating parallel MRI: where sense meets grappa. Magn Reson Med. 2014;71:990–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


