Abstract
Purpose
To investigate the stress-strain behaviour of 9 soft contact lens materials, that are commonly used in the market, under uniaxial compression loading.
Methods
Seven types of hydrogel and two types of silicone-hydrogel soft contact lens materials were hydrated in phosphate-buffered saline (PBS) solution then subjected to uniaxial compression loads. The load rate was set to 16.0 N/min starting with two consecutive initial 5.0 N loading cycles followed by three relaxation periods of 4.0 min within which there were two more 5.0 N loading cycles and eventually, a full loading cycle that stopped at a load of 49.0 N. The load and contraction data obtained experimentally were analysed to derive the stress-strain behaviour. Finite Element (FE) analysis was then utilised to evaluate the performance of soft contact lenses on the human eye and handling lenses off the eye.
Results
Unlike tensile tests, all tested materials showed nonlinear behaviour when tested under compression. When fitted to first-order Ogden hyperelastic model, parameter μ was found to be varying in the range 0.12 to 0.74 MPa and material parameter α was found to be varying in the range 8.2 to 20.326 among the nine tested materials. Compression modulus of elasticity was 2.2 times higher than the tensile modulus of elasticity on average. FE simulation with nonlinear Ogden constitutive model showed a limited change (8%~12%) in the optical performance when compared to other material models, however, it predicted higher stress when the lens was simulated under bending during off-eye handling.
Conclusions
Compression tests revealed slightly nonlinear behaviour when materials were strained under compression stress down to 15% ~ 30% of their nominal heights. Considering the physiological compression loading range of 8 mmHg, secant moduli of elasticity were 1.5% to 6.9% higher than the tension moduli of elasticity depending on the material. Tensile-based moduli of elasticity could be used in FE analysis as a step towards simulating the optical performance of soft contact lenses on-eye. However, nonlinear compression-based material models are recommended for FE analysis of soft contact lenses when lens-handling is investigated off-eye.
Introduction
Material stiffness was not of particular interest when contact lenses first became widely commercially available [1, 2]. This is because lenses were manufactured from polymethyl methacrylate (PMMA) and various gas permeable materials that were, to all intents and purposes, rigid. Once soft contact lenses were developed by Otto Wichterle [2] in the 1960s, the physical properties and characteristics of hydrogel materials were of more interest, as they draped and moulded to the corneal shape. As a result, lenses manufactured in materials with different properties would, in theory, perform differently on the eye [1].
However, as soft contact lenses became more commercially successful, the main driver in terms of physical characteristics was oxygen permeability (DK) [3, 4] in a bid to maintain a healthy corneal metabolism. It was to this end that silicone hydrogel materials were developed, which provided higher DK values [5]. The downside of this development was that silicone hydrogel materials had much higher moduli of elasticity than hydrogels and this then brought up issues of comfort and decreased wettability, as silicon is hydrophobic [6, 7].
Since then, contact lens designers and material manufacturers have been balancing the demand from practitioners for excellent oxygen transmission with material properties that allow excellent comfort and fitting characteristics [1]. For daily disposable contact lenses, now the world’s largest selling modality, there is little the practitioner can do in terms of fit, as lenses are generally supplied with one base curve and diameter and the manufacturers have optimised the trade-off between comfort, fit and oxygen transmission. However, in the specialist contact lens market, where practitioners are fitting eyes that are outside the disposable range in terms of corneal shape and power, material stiffness is of more importance.
Such contact lenses are available in a wide variety of designs and materials, spanning hydrogels and silicone hydrogels and it is in this area where modulus becomes of interest [8]. If a practitioner changes material in order to reduce lipid deposit rates, it is useful to know how this would affect the fit of the lens and whether any adjustment is necessary. It is at this juncture that moving to a material with a similar modulus becomes important. However, in practice, soft materials with similar linear elastic moduli may not behave in the same way [1]. Thus, investigating the full range of physical characteristics and the relationship between them would be of use to specialist practitioners [9, 10].
In linear elastic materials, the modulus of elasticity (E), which is also called Young’s modulus, can be defined as the ratio of the applied stress (σ) to resulting strain (ε), [1] Eq 1.
| (1) |
A low modulus material is more deformable on the eye and offers less resistance against the eyelid [11]. On the other hand, a material with high modulus is comparatively stiffer and is easier to handle by wearers [12].
During normal use, a soft contact lens is subjected to bending during handling off the eye and a combination of compression due to eyelid load and shear due to tear surface tension while on the eye. Previous studies described the stress-strain behaviour of both hydrogel and silicone-hydrogel materials as linear elastic materials [13–17] based on tensile testing. However, the eyelid pressure on contact lenses cannot be described as tensile stress. Instead, it could be described as compression stress as the eyelid pushes the contact lens down towards the anterior surface of the cornea, which offers resistance due to the intraocular pressure and corneal stiffness.
Compression modulus of elasticity can be determined using the spherical indentation technique [18, 19], however, the understanding of the numerical values of the modulus of elasticity determined by indentation is underpinned by a complex combination of theoretical and experimental work [20]. Furthermore, indentation measurements consistently result in lower moduli values compared with uniaxial measurements [21], which makes indentation measurements incomparable with the moduli values that material manufacturers use to characterise their hydrogels for the contact lens industry.
Consequently, this study aimed to investigate the compressive stress-strain behaviour of 9 materials, that are commonly used in the specialist contact lens market, under uniaxial loading. The study estimates various linear and nonlinear material models for these hydrogel and silicone-hydrogel materials. In addition to the lab-based experiments, the study utilises Finite Element (FE) analysis to predict the geometry of the soft lens on the eye. Then further analysis of the resulting geometry was performed to evaluate the optical performance of these soft contact lenses. Finally, an off-eye simulation was carried out to investigate the effect of handling contact lenses made of the investigated nine materials on the maximum stress generated as a result of wearers’ Taco test that is usually carried out before each wear to check that the soft lens is not inside out.
Materials and methods
Uniaxial unconfined compression testing
Uniaxial compression tests were performed on nine different materials, Table 1. The material samples used in this study were provided by UltraVision CLPL (Leighton Buzzard, UK), part of the SEED group, (Tokyo, Japan).
Table 1. Raw data of tested materials.
| Lab code | Commercial name and ISO* Classification | Base material | Manufacturer | Colour | Water Content at 20°C (%) | Oxygen permeability DK (mL O2 cm-2 s-1 mmHg-1) | Wet refractive index |
|---|---|---|---|---|---|---|---|
| B# 09 | CONTAFLEX 77 Clear | Hydrogel | Contamac Ltd | Clear | 77 | 45 | 1.3739 |
| filcon 2 (45) [77%] | |||||||
| B# 02 | DEFINITIVE (V3) 74 Blue UV | Silicone-Hydrogel | Contamac Ltd | Blue | 74 | 60 | 1.3753 |
| efrofilcon A 5B (60) [74%] | |||||||
| B# 05 | DEFINITIVE (V3) 74 Clear | Silicone-Hydrogel | Contamac Ltd | Clear | 74 | 60 | 1.3749 |
| efrofilcon A 5B (60) [74%] | |||||||
| B# 03 | CONTAFLEX 67 Clear | Hydrogel | Contamac Ltd | Clear | 67 | 30 | 1.392 |
| filcon 2 (30) [67%] | |||||||
| B# 06 | CONTAFLEX 58 Clear | Hydrogel | Contamac Ltd | Clear | 58 | 21 | 1.406 |
| filcon 2 (21) [58%] | |||||||
| B# 08 | CONTAFLEX GM3 58 Clear | Hydrogel | Contamac Ltd | Clear | 58 | 26 | 1.416 |
| acofilcon A2 (26) [58%] | |||||||
| B# 04 | CONTAFLEX 55 Blue | Hydrogel | Contamac Ltd | Blue | 55 | 19 | 1.4086 |
| methafilcon A 4 (19) [55%] | |||||||
| B# 07 | BENZ-G3X 49 Blue | Hydrogel | Benz Research & Development | Clear | 49 | 15 | 1.425 |
| hioxifilcon B 1 (15) [49%] | |||||||
| B# 01 | CONTAFLEX 38 Clear UV | Hydrogel | Contamac Ltd | Clear | 38 | 8 | 1.4381 |
| filcon 1 (8) [38%] |
*ISO stands for the International Organization for Standardisation.
Contact lens materials are supplied in a dry form to allow lathing, therefore, the testing procedure involved taking 6 cylindrical blanks of each material, measuring their dry dimensions before hydrating them for 8 hours in 0.9% phosphate-buffered saline (PBS) solution (Sigma Aldrich, UK). Initial hydrated dimensions were measured just before the test using a digital Vernier calliper (D00352, Duratool, Taiwan). These measurements for both length and diameter were taken at three different locations each along the sample axial and radial directions respectively and then averaged.
A special custom-made test rig was designed by Biomechanical Engineering Group (BioEG) using R7.0 PTC Creo software (Parametric Technology Corporation, Boston, Massachusetts, US) and manufactured at the School of Engineering, University of Liverpool, Fig 1. The rig consists of two flat platens to allow the tested samples to sit between them and a relatively heavy base to add more rigidity to the rig structure. The rig was enveloped in a perspex container to allow a hydration fluid to be used during the test. A black O-ring rubber seal was used to prevent the fluid from leaking to the base. Most of the main rig components were cut from golden coloured brass round bars which came as a 60 mm diameter raw material.
Fig 1. The custom-made compression test rig that was designed and manufactured at the School of Engineering, University of Liverpool, UK.

The compression tests were conducted at room temperature (approx. 20°C) in the Biomechanics Laboratory at the School of Engineering, University of Liverpool (Liverpool, UK) using an Instron 3366 dual-column, table-top testing machine. This was equipped with a calibrated 50 N load cell and BlueHill 3 control software (Instron, MA, UK), Fig 2. The software allowed the design of specific test profiles and to pre-set the exact test sequence with every specimen through its automated controlled TestProfiler module. The test protocol was defined to ensure the maximum load of the loadcell is not reached.
Fig 2. Compression test experimental setup showing the main components and the Instron machine.
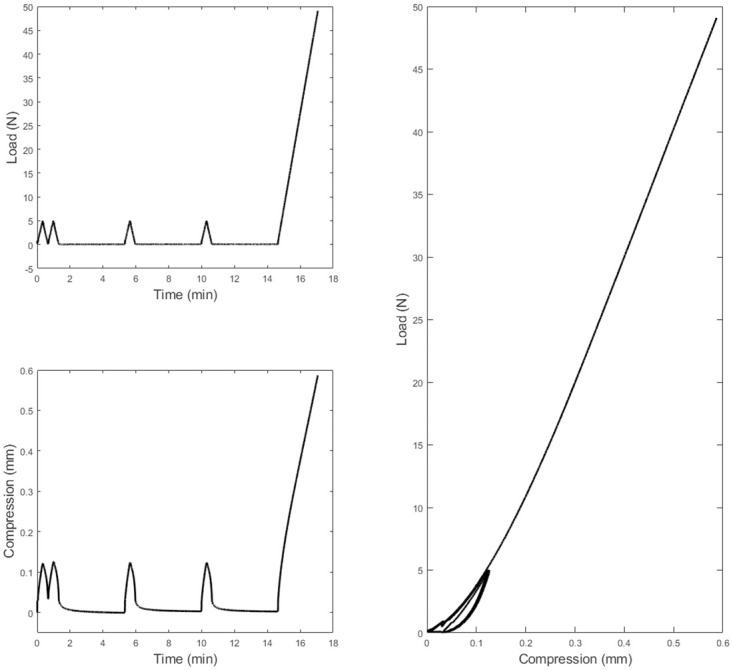
Load rate was set to 16.0 N/min starting with two consecutive initial 5.0 N loading cycles followed by three relaxation periods of 4.0 min within which there were two more 5.0 N loading cycles and eventually a full loading cycle that stopped at a load 49.0 N just before the maximum loading range of the load cell, Fig 3. These values were found experimentally to be optimum for hydrogel testing under compression, enabling sufficient recovery and repeatable measurements. The samples were secured between a set of mechanical platens made of brass and specially designed for use with the Instron testing machine. A thin layer of oil-based lubricant was applied on the surfaces of the platens to reduce any restraint to the lateral sample expansion during the compression test. With the aim of maintaining hydration throughout the testing procedure, samples were submerged in a perspex chamber filled with PBS solution. The compression forces F at specified time increments were recorded and converted into compression stress σE values through dividing them by the hydrated samples’ initial cross-section area A0 (Eq 2) [22, 23].
Fig 3. Raw compression test data as collected from the Instron BlueHill 3 control software for a hydrated Contaflex 38 Clear UV sample with 5.91 mm initial length.
| (2) |
At the same time increments, the change in sample length ΔL = L0 − L1 was recorded by measuring the instantaneous length L1 and dividing ΔL by the initial length of the strip L0 to calculate the strain ε (Eq 3).
| (3) |
Secant modulus of elasticity at any point (σ,ε) on the stress-strain curve can then be determined as at this point.
For nonlinear material modelling, a first-order (N = 1) Ogden hyperelastic material model [24] was used to fit and simulate the nonlinear stress-strain behaviour of the tested materials. The Ogden constitutive strain energy equation can be expressed in terms of the principal stretches as
| (4) |
[24]
Where U is the strain energy; μi and αi, are material parameters; are the deviatoric principal stretches (ratio between the deformed length L1 and the initial length L0) in principal directions. Since no lateral forces were applied during the compression tests conducted in the current study, principal stretches can be simplified to , hence
| (5) |
| (6) |
| (7) |
where
| (8) |
Therefore, the stress-strain relationship can be described in uniaxial mode as:
| (9) |
The parameters of the Ogden material model (Eq 9) were estimated using the particle swarm optimisation (PSO) algorithm available in MATLAB’s Global Optimization Toolbox. Lower boundaries of μ and α were set to 10−6 and -5 while upper boundaries were set to 10 and 50 respectively with a swarm size of 40, and a maximum number of iterations of 1000. The objective function (err) was set to:
| (10) |
where σexp is the experimental stress, σpre is the model predicted stress and N is the number of strain data points. Limits of PSO optimisation were set based on the authors’ bast knowledge of inverse analysis of soft materials [13, 26–28].
Finite element modelling
In this study, eight-node first-order continuum solid hybrid brick elements “C3D8H” were used in two-layers of elements to the averaged eye model and soft contact lens models in ABAQUS (Dassault Systèmes, Vélizy-Villacoublay, France) FE software package licenced to the University of Liverpool, UK.
The FE mesh convergence study of the eye’s model was carried out through applying internal pressure of 15 mmHg on the internal surface of 14 eye models with node numbers varying between 804 and 750,006 nodes, half of them are in two layers, then monitoring the relevant anterior eye’s apex displacement. The outcomes showed that the number of the elements equal to 28,800 arranged in rings of 43,206 nodes in two layers has converged to the displacement of 421.14 μm at the apex node and selected as an optimal number of elements for this simulation. Likewise, the contact lenses mesh was tested by 10 Plano lenses models, five of them were in two layers with a number of nodes varying between 20166 and 53529 nodes. All contact lenses models were tested when being fitted to the selected 43206-node eye model while lenses apex displacement was recorded. The outcomes demonstrated that the model with the number of the elements equal to 30480 arranged in rings of 45969 nodes in double layers has converged to the displacement of 205.21 μm at the apex node and selected as an optimal number of elements for this simulation. During the mesh conversion study, the maximum recorded central processing unit (CPU) time for running a single model was 4.7 h in a quad-core processor 64-bit operating system.
Typically, the in-vivo human eye globe geometry is quantified whilst the eye is stressed due to the intraocular pressure (IOP) hence, geometries cannot be used directly for modelling without pre-processing. To achieve the eye’s stress-free configuration at 0 mmHg IOP, the eye globe model was initially built with the inflated dimensions, then a stress-free adjustment of the eye model was determined by following the iterative method presented in [29]. The eye’s stress-free model was computed by considering an average IOP of 15 mmHg [30] and a maximum node position error of 0.1 μm. Once the stress-free eye model was obtained, it was pressurised to 15 mmHg through a uniformly distributed static pressure on the internal surfaces of the eye globe model to mimic the aqueous and vitreous effect on the eyewall. ABAQUS nonlinear geometry option “NLGEOM” was activated during the inflation step and subsequent analysis. This option allows loads to be applied incrementally whilst updating the stiffness matrix in each increment. Hence the ABAQUS solver allows nonlinear materials to be used for certain parts without altering linear FE formulation for linear materials of other parts of the model.
The averaged eye model came as a result of secondary analysis in a collection of fully anonymised data that has been used in several previous studies [31–34] where only healthy eyes were selected to be processed. The averaged eye model’s central corneal thickness is 0.57 mm, peripheral corneal thickness is 0.63 mm, equatorial scleral thickness is 0.79 mm and posterior pole thickness 0.83 mm, S1 Data. According to the University of Liverpool’s Policy on Research Ethics, ethical approval was unnecessary for studies that solely involve the secondary analysis of fully anonymised data. Nevertheless, the study followed the tenets of the Declaration of Helsinki. Anterior eye’s topography measurements were levelled before the removal of edge artefacts following the methods detailed in our previous studies [35, 36]. Model central corneal thickness is 0.57 mm, peripheral corneal thickness is 0.63 mm, the equatorial scleral thickness is 0.79 mm and the posterior pole thickness is 0.83 mm.
In the FE simulation, Ogden material models [24] were used to represent the eye tissue’s mechanical behaviour under loading conditions following earlier experimental studies [26, 37, 38]. The eye was modelled as hyperelastic soft tissue with a water-like density of 1000 kg/m3 and four regions including the cornea (μc = 0.07, αc = 110.8), anterior, intermediate and posterior sclera separated at elevation angles of 55°, 7.5°, -47.5° measured from the centre of the sclera [26], Fig 4a and 4b. The purpose of splitting the sclera into three regions was to consider regional mechanical properties of scleral tissue using circumferential regions of isotropic elements to replicate macroscale sclera displacements. Scleral materials were characterised as μs1 = 0.441, αs1 = 124.5, μs2 = 0.349, αs2 = 138.5, μs3 = 0.308 and αs3 = 162.2.
Fig 4.
(a) Typical FE model for averaged eye and soft contact lens used in the simulation where different colours represent different material models. (b) the interaction between the soft contact lens and the eye demonstrated in displacement distribution across the anterior part of the eye. (c) typical FE model for a CONTAFLEX 77 Clear soft contact lens in no load position. (d) the stress on the soft contact lens as a result of being held between the thumb and the forefinger during handling.
Soft contact lens models (S2 Data) were built with four material models (based on the manufacturers’ tensile modulus of elasticity, physiological compression modulus of elasticity obtained at σ = 8 mmHg, compression moduli of elasticity obtained at ε = 0.05, and compression-based nonlinear Ogden model) for each of the nine materials included in this study. Therefore, a total of 36 soft lenses were investigated, in the simulation, on an eye model representing an averaged eye geometry.
When a soft contact lens is fitted to a cornea, it deforms [39]. Any deformation of the optic zone will affect the optical power profile. This change in lens power is termed effective power change (EPC). It is simply the refractive power of the lens post fit minus the originally designed refractive power pre-fit, which is Plano in this study. The light raytracing technique outlined in our previous study [13] was employed to measure the EPC that incurred by the fitting of each soft contact lens to the cornea. A custom-built MATLAB script performing light raytracing across the lens optic zone was written and validated using the AutoCAD software ® (Autodesk, Inc., San Rafael, California, USA) [39, 40].
In the current study, a Plano (zero) powered corrective lens was used in simulating the soft contact lens’s material behaviour on the eye. By determining the lens’s power after being fitted to the eye, this power built during the fit is representing the lens’s effective power change EPC as the initial lens’s off-eye power was zero. The lens’s geometrical profile was generated via a custom-built MATLAB software before being further processed to build a FE model for the lens. The stabilisation design, commonly known as prism ballast or gravity-based stabilisation, was used in the design of the peripheral zone of soft lenses. The lens diameter was set to 14.5 mm, with base curve 8.2 mm, and central thickness 0.11 mm. Details about soft contact lens design procedures are published in our previous studies [13, 39]. Eyelid interaction was simulated by applying the eyelid pressure dynamically as a function of time. This function is based on the palpebral aperture measurement, as reported in [41]. The effect of the tear layer was simplified and simulated by applying the surface tension of the tear fluid of 43.6 mPa [42] to the back surface of the contact lens as no fluid-structure interaction analysis has been carried out in this study. Steps of the FE modelling process are listed in Table 2.
Table 2. Finite element simulation parameters.
| Model | Step | Description | Integration scheme | Loading condition | Time |
|---|---|---|---|---|---|
| Eye | 1 | Stress-free iterations [29] | Implicit | Static | Normalised increments (0:1) |
| Eye | 2 | Inflation, IOP = 15 mmHg [30] | Implicit | Static | Normalised increments (0:1) |
| Lens on-eye | 3 | Eyelid pressure 8.0 mmHg [43] | Implicit | Dynamic | 0.6 s, see [41] |
| 4 | Surface tension 43.6 mPa [42] | Implicit | Static | Normalised increments (0:1) | |
| Lens off-eye | 5 | Bending while held between the thumb and the forefinger’s pressure 200 Pa [44] | Implicit | Static | Normalised increments (0:1) |
Soft contact lenses off-eye handling was simulated as if the lens is held between the thumb and the forefinger during a ‘Taco’ test to check if a lens is inside-out, Fig 4c and 4d. To ensure their lenses are the correct way around, wearers are usually advised to gently squeeze the lens as if they were trying to fold it in half, then look at the edge of the lens. if edges are pointing upwards and appear to meet, then the lens is in the correct way around. This test is needed before every wear as wearing a contact lens the wrong way around makes it ineffective at correcting vision (blurry vision) and may cause complications to the eye (eye pain, red eye, itchy eye) if worn inside-out for a long time. The Taco test generates bending stress on the soft lens by stretching the front surface of the lens and compresses the back surface around the bending line when the lens is being tested when it is the correct way around.
In the current study, the Taco test was simulated via a linearly increasing pressure of 200 Pa [44] applied on the external surface of the lens while the lens nodes on Y-axis were fixed. As a result, the soft lens bends, and stresses build on the lens surface. Each run ended just before any of the model iso-parametric elements got distorted by producing a negative volume. The maximum von-Mises stress was exported at this stage of simulation as the maximum possible deformation was achieved without failure.
Results
Compression tests revealed slightly nonlinear behaviour when materials were strained under compression stress down to 15%~30% of their nominal heights. The secant modulus of elasticity E was determined for each material at the physiological loading stress 8 mmHg (10.8 kPa), which corresponds to the mean eyelid pressure as reported by Shaw et al. [43].
All materials tested revealed physiological compressive moduli of elasticity higher than the tensile moduli of elasticity as reported by their manufacturer with an average ratio of 2.2, Fig 5. This average ratio increased to 2.7 when moduli were calculated at ε = 0.05, Table 3.
Fig 5. Moduli of elasticity of tested materials as reported by the manufacturer and as measured experimentally in the current study at 8 mmHg stress and 0.05 strain.
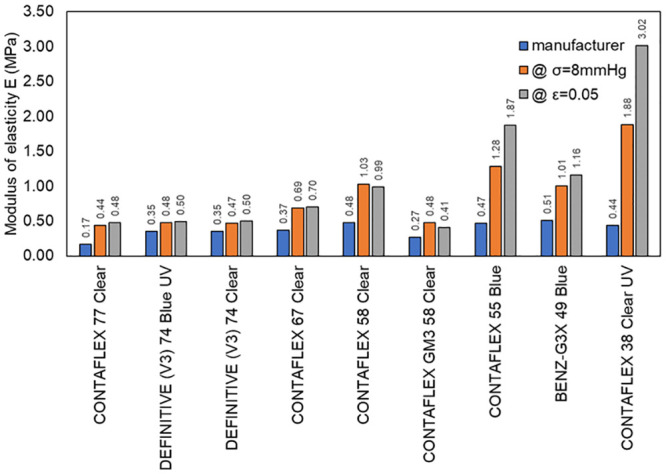
Table 3. Material parameters as provided, measured, or determined.
| Load | Tension | Tension | No-load | No-load | No-load | No-load | Compression | Compression | Compression | Compression | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data source | Manufacturer | Reported in [13] | Measured | Measured | Measured | Measured | Determined | Determined | Determined | Determined | |
| Lab code | Commercial name \Material parameters | E (MPa) | E (MPa) | Dry length (mm) | Wet length (mm) | Dry diameter (mm) | Wet diameter (mm) | μ (MPa) | α | E (MPa) @ σ = 8mmHg | E (MPa) @ ε = 0.05 |
| B# 09 | CONTAFLEX 77 Clear | 0.17 | 0.20 | 5.01±0.01 | 6.78±0.09 | 12.71±0.01 | 16.04±0.29 | 0.157 | 10.506 | 0.442 | 0.479 |
| filcon 2 (45) [77%] | |||||||||||
| B# 02 | DEFINITIVE (V3) 74 Blue UV | 0.35 | 0.28 | 4.72±0.02 | 7.70±0.07 | 12.72±0.01 | 20.31±0.10 | 0.16 | 9.878 | 0.477 | 0.496 |
| efrofilcon A 5B (60) [74%] | |||||||||||
| B# 05 | DEFINITIVE (V3) 74 Clear | 0.35 | 0.28 | 4.70±0.02 | 7.61±0.10 | 12.69±0.00 | 20.26±0.22 | 0.17 | 9.036 | 0.469 | 0.5 |
| efrofilcon A 5B (60) [74%] | |||||||||||
| B# 03 | CONTAFLEX 67 Clear | 0.37 | 0.46 | 5.01±0.01 | 7.31±0.04 | 12.70±0.01 | 18.47±0.05 | 0.221 | 9.214 | 0.691 | 0.703 |
| filcon 2 (30) [67%] | |||||||||||
| B# 06 | CONTAFLEX 58 Clear | 0.48 | - | 5.01±0.03 | 6.74±0.04 | 12.70±0.01 | 16.24±0.04 | 0.308 | 8.76 | 1.028 | 0.989 |
| filcon 2 (21) [58%] | |||||||||||
| B# 08 | CONTAFLEX GM3 58 Clear | 0.27 | - | 5.01±0.01 | 8.05±0.06 | 12.71±0.01 | 19.18±0.06 | 0.122 | 9.93 | 0.481 | 0.406 |
| acofilcon A2 (26) [58%] | |||||||||||
| B# 04 | CONTAFLEX 55 Blue | 0.47 | - | 5.03±0.00 | 6.02±0.03 | 12.77±0.00 | 14.07±0.10 | 0.718 | 8.185 | 1.284 | 1.872 |
| methafilcon A 4 (19) [55%] | |||||||||||
| B# 07 | BENZ-G3X 49 Blue | 0.51 | - | 5.00±0.00 | 6.35±0.05 | 12.71±0.01 | 14.59±0.03 | 0.367 | 9.558 | 1.005 | 1.163 |
| hioxifilcon B 1 (15) [49%] | |||||||||||
| B# 01 | CONTAFLEX 38 Clear UV | 0.44 | - | 5.00±0.01 | 5.98±0.04 | 12.69±0.01 | 13.70±0.08 | 0.732 | 20.326 | 1.884 | 3.015 |
| filcon 1 (8) [38%] |
Some of the results obtained from this study can be compared with a previous study [13] where the modulus of elasticity under tensile load was tested experimentally for four particular materials (CONTAFLEX 77 Clear, DEFINITIVE (V3) 74 Blue UV, DEFINITIVE (V3) 74 Clear, CONTAFLEX 67 Clear). The average ratio of the physiological compressive moduli of elasticity as obtained in this study to the experimentally obtained tensile moduli of elasticity reported in [13] was 1.8. Unlike the uniaxial tensile test [13], all the materials showed nonlinear behaviour when under compression, therefore when fitted to the first-order Ogden hyperelastic model [24] material parameter μ was found to be 0.33±0.22 MPa on average and material parameter α was found to be 10.6±3.5 on average, Fig 6.
Fig 6. Stress σ verses strain ε for the 9 types of materials. Moduli of elasticity at 8 mmHg stress and 0.05 strain were marked in red and blue markers, respectively.
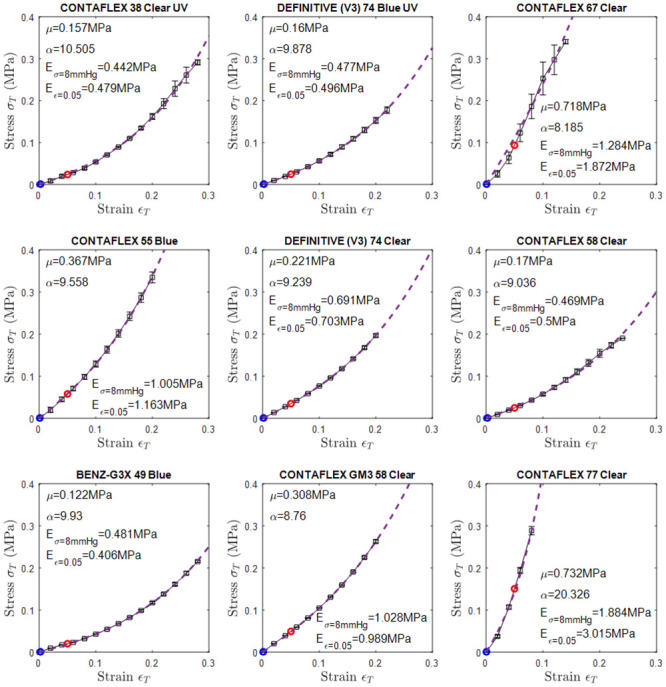
The blue dashed line represents the Ogden model that fitted to the stress-strain curve.
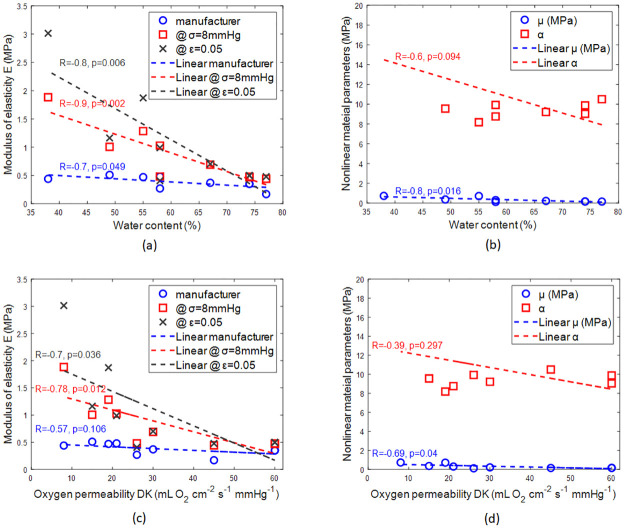
When the stiffness of the soft material was investigated against their water contents while being hydrated, it was clear that there was a reverse linear relationship between the water content and the material stiffness. Secant moduli of elasticity in the physiological loading range (σ = 8mmHg) were strongly and inversely correlated to the water content (R = -0.88, p = 0.002), then secant moduli of elasticity at 5% strain loading range (ε = 0.05) comes second with R = -0.83, p = 0.006 and finally, the manufacturers’ moduli of elasticity with a moderate reversed linear relationship (R = -0.67, p = 0.049), Fig 7a.
Fig 7. Effect of water content on the (a) moduli of elasticity, (b) nonlinear material parameters.
Effect of Oxygen permeability DK on the (c) moduli of elasticity, (d) nonlinear material parameters which were used to fit the Ogden first-order model to each material.
The nonlinear first-order model parameters were investigated against the material water contents. The same reverse linear relationship was noted with the parameter μ (R = -0.77, p = 0.016) at a higher correlation than α (R = -0.59, p = 0.016). This indicates the overall stiffness is more significantly changing in comparison to nonlinearity behaviour of the material.
Likewise, the stiffnesses of the materials were reversely correlated with DK through moderate correlation (R = -0.57, p = 0.106) when the manufacturers’ moduli were considered, strong correlation (R = -0.78, p = 0.012) when the moduli of elasticity in the physiological loading range (σ = 8mmHg) were considered, and finally, strong correlation (R = -0.7, p = 0.036) when the moduli of elasticity 5% strain loading range (ε = 0.05) were considered Fig 7.
Nonlinear first-order model parameters were also inversely correlated with DK. Moderate reverse correlation (R = -0.69, p = 0.04) was noticed between parameter μ and DK and weak reverse correlation (R = -0.39, p = 0.297) was noticed between parameter α and DK.
In this statistical analysis, following Rumsey [45], the correlation coefficients have been interpreted as a moderate linear relationship when R = 0.5~0.69 and strong linear relationship when R = 0.7~0.99, with R = 1 indicating a perfect linear relationship. Negative R values indicate reverse linear relationships where the dependent variable on the vertical axis decreases with the increase of the independent variable on the horizontal axis.
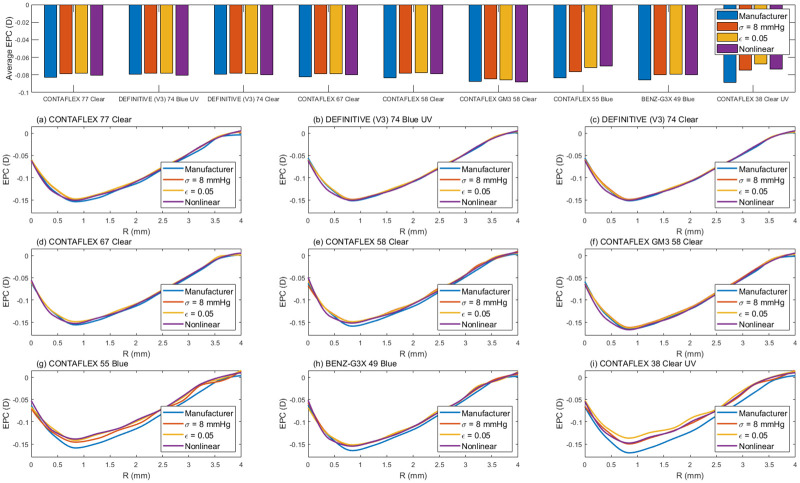
On one hand, in terms of the contact lenses’ performance on the eye, FE simulation showed that two of the investigated materials (CONTAFLEX 55 Blue & CONTAFLEX 38 Clear UV) are more susceptible to the type of the material model used to describe their behaviour under loading conditions than other materials, however, no significant differences were found, Fig 8. CONTAFLEX 55 Blue showed higher negative EPC at 0.8 mm radius when modelled either by the manufacturers’ modulus or the physiological modulus, while CONTAFLEX 38 Clear UV optical performance showed higher negative EPC when modelled by either the manufacturers’ modulus or the ε = 0.05 modulus. Compared to other models, the nonlinear model showed limited change in the max EPC with an average of 6% and range 8 to 12%.
Fig 8. Simulated effective optical power change (EPC) of soft contact lenses models as a result of being fitted to an averaged eye model.
On the other hand, in terms of the contact lenses’ performance off-the-eye, Stresses generated as a result of bending during handling lenses between the thumb and the forefinger showed that stresses in the range 16.3 kPa to 312.8 kPa depending on the material and the material model used in the simulation process. Consistently, models based on the tensile moduli of elasticity were recording less von-Mises stress than the linear compression-based material models and nonlinear material models. The biggest difference in the stress caused by bending was noticed in CONTAFLEX 38 Clear UV hydrogel with von-Mises stress of 312.8 kPa when the nonlinear Ogden material model was used, compared to 42.2 kPa when the linear tensile-based material model was used. Similarly, CONTAFLEX 55 Blue recorded 252.2 kPa and 45.1 kPa with nonlinear Ogden material model compared to the linear tensile-based material model, respectively, Fig 9.
Fig 9. Simulated maximum von-Mises stress on the soft contact lens as a result of being held between the thumb and the forefinger during handling.
Discussion
Currently, the stiffness of soft contact lens materials reported by their moduli of elasticity is the only way that researchers or manufacturers can evaluate material behaviours in the literature or the market. These moduli always come as a result of uniaxial tensile testing of thin strips of the material and are quite useful when evaluating the durability of the material during user handling. However, they are not accurate if they were used to predict the performance of the contact lenses on the eye. This is because, in this state, lenses are mostly subject to compressive loading.
It was clear from the results obtained from this study that the compressive stress-strain behaviour of the investigated soft contact lenses materials is nonlinear. This is evidently distinct from the relatively smooth linear stress-strain behaviour researchers reported for the same materials under tensile testing. Although it was expected that these soft materials resist compression more than tension in the physiological loading range, it was surprising that some materials like CONTAFLEX 38 Clear UV have recorded a compression modulus almost five times higher than its tensile modulus of elasticity. This indicates that such material behaviour could not be correctly predicted by the tensile modulus only. Some other investigated materials like batches of CONTAFLEX 55 Blue, CONTAFLEX 58 Clear, and BENZ-G3X 49 Blue also experienced a substantial difference (more than double) between the compressive and tensile modulus of elasticity, Table 3.
The misleading effect of using the tensile modulus of elasticity exclusively to estimate either the contact lens comfort or its optical performance on the eye can be anticipated clearly through the results of the current study. The results suggest that most contact lens materials are stiffer than it might have been estimated when they are subject to the eyelid pressure. This is a crucial finding as complications like the formation of conjunctival flaps were correlated to the stiff performance of contact lenses on the eye [46–49]. In terms of optical performance, the flexibility of soft contact lenses results in more deformation on the eye and hence possible significant alteration in dimensions and refractive powers from the desired specification [13, 39], hence poor optical performance, and failure to correct the refractive error effectively.
Water contents were always inversely correlated to the moduli of elasticity under compression regardless of the loading range, Fig 7a. The same observation is valid even when nonlinear modelling of the material behaviour was considered, Fig 7b. This indicates that the material water content could be used as an indicator to the material behaviour on the eye as it was either strongly correlated with the compressive moduli of elasticity or in the worst cases moderately correlated. On the other hand, a stiffer contact lens material may achieve excellent optical performance because of its dimensional stability on the eye but this may be achieved at the expense of user comfort as such lenses resists the eyelids’ pressure and pushes both the cornea and the eyelid with every blink. As humans blink 15 to 20 times per minute on average [50], the user’s pain accumulates during the wearing of the lens as they feel a little knock on their eye with every blink. Moreover, the fact that humans’ blink rate is several times more than required for ocular lubrication [51, 52] adds to the pain accumulation problem.
It is important here to notice the contact lenses user comfort is not exclusively dependant on the lens’s stiffness, but other factors are involved too [53]. These comfort factors include the geometric design [54] and the Oxygen permeability DK [55].
The results of DK and water content investigations showed that the nonlinear material parameter α reduce with both DK and water content, which means the material becomes more linear in behaviour while the stiffness parameter μ remained approximately the same.
On the other hand, when the soft lenses handling was investigated, the nonlinear material model was showing that the material develops maximum stress of 1.5 (DEFINITIVE (V3) 74 Blue UV) to 7.4 times (CONTAFLEX 38 Clear UV) more than the linear tensile based material model. This indicated that using compression-based material models is necessary when investigating the handling of soft contact lenses. As the nonlinear material model was giving the highest von-Mises stress among the other material models in most of the cases, considering the worst-case scenario in design nonlinear Ogden model is recommended for modelling the handling for soft contact lenses off-eye.
The study has two limitations. Since hydrogels can absorb water up to 90% of their volume or even more, their mechanical properties exhibit hyperelastic and poroelastic behaviour. The poroelasticity can be predicted by using a biphasic model [56] assuming the hydrogel is composed of a fluid phase and a solid phase. Nevertheless, in this study, the poroelasticity was not considered and the hydrogels were assumed to be composed of a single solid phase and behave as hyperelastic materials. The assumption was based on the experience that during instantaneous loading the biphasic and incompressible hyperelastic models predict equivalent stress distribution [57, 58]. Furthermore, modelling the tear film as an extra layer was not considered in this simulation, as the focus was given to the contact lens deformation in order to calculate the lens EPC.
Knowledge of commonly used contact lens materials’ behaviour under compression is essential when it comes to evaluating or optimising their performance on the ocular surface [11]. Although the contact lens market is still far from generating the ideal lens concept [59], it can benefit considerably by considering these properties in their designs. In addition, there is a need to develop comparable standardised techniques to measure soft contact lens material stiffness and other related properties as emphasised in previous studies [1, 60–62]. Unfortunately, this is currently not the case, and essential aspects of material behaviour are not considered in commercial designs [61].
Supporting information
(XLSX)
(XLSX)
Acknowledgments
The authors would like to thank Mr Jijimon Mathew at the School of Engineering, University of Liverpool, UK for his assistance in designing and manufacturing the compression rig components (Fig 1). Authors also thank Miss Arwa Fathy from Wirral Grammar School for Girls, UK for the digital drawings of human fingers associated with Fig 4 of this research paper. Thanks are extended to Mr John Clamp, the Joint CEO and CTO of UltraVision CLPL, UK for providing the raw materials that have been used in this study.
Data Availability
All relevant data are within the manuscript and its Supporting information files.
Funding Statement
Ultravision CLPL provided support in the form of a salary for LW and raw materials used for the study. The specific roles of this author are articulated in the ‘author contributions’ section. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. No additional external funding was received for this study.
References
- 1.Bhamra Tarnveer Singh T BJ. Mechanical properties of contact lenses: The contribution of measurement techniques and clinical feedback to 50 years of materials development. Contact Lens and Anterior Eye. 2017;Volume 40, Issue 2:Pages 70–81. 10.1016/j.clae.2016.11.005 [DOI] [PubMed] [Google Scholar]
- 2.Wichterle O, Lím D. Hydrophilic Gels for Biological Use. Nature. 1960;185:117 10.1038/185117a0 [DOI] [Google Scholar]
- 3.Fonn D, Bruce AS. A review of the Holden-Mertz criteria for critical oxygen transmission. Eye Contact Lens. 2005;31(6):247–51. Epub 2005/11/15. 10.1097/01.icl.0000182488.70745.1d . [DOI] [PubMed] [Google Scholar]
- 4.Fatt I, Lin D. Oxygen tension under a soft or hard, gas-permeable contact lens in the presence of tear pumping. Am J Optom Physiol Opt. 1976;53(3):104–11. Epub 1976/03/01. 10.1097/00006324-197603000-00002 . [DOI] [PubMed] [Google Scholar]
- 5.Sweeney DF. Have silicone hydrogel lenses eliminated hypoxia? Eye Contact Lens. 2013;39(1):53–60. Epub 2012/12/29. 10.1097/ICL.0b013e31827c7899 . [DOI] [PubMed] [Google Scholar]
- 6.Guillon M. Are Silicone Hydrogel Contact Lenses More Comfortable Than Hydrogel Contact Lenses? Eye & Contact Lens. 2013;39(1):86–92. 10.1097/ICL.0b013e31827cb99f [DOI] [PubMed] [Google Scholar]
- 7.Dumbleton K. Adverse events with silicone hydrogel continuous wear. Cont Lens Anterior Eye. 2002;25(3):137–46. Epub 2005/11/24. 10.1016/s1367-0484(02)00009-7 . [DOI] [PubMed] [Google Scholar]
- 8.Snyder C. Modulus and its Effect on Contact Lens Fit. Contact Lens Spectrum. 2007;(1). [Google Scholar]
- 9.Sulley A, Lorenz KO, Wolffsohn JS, Young G. Theoretical fitting characteristics of typical soft contact lens designs. Contact Lens & Anterior Eye. 2017;40:248–52. 10.1016/j.clae.2017.04.001 [DOI] [PubMed] [Google Scholar]
- 10.Stapleton F, Tan J. Impact of Contact Lens Material, Design, and Fitting on Discomfort. Eye & Contact Lens. 2017;43(1):32–9. 10.1097/ICL.0000000000000318 . [DOI] [PubMed] [Google Scholar]
- 11.Kim EPDS, Mou M.Sc.;, Klaus Ehrmann Ph.D. Mechanical Properties of Contact Lens Materials. Eye & Contact Lens: Science & Clinical Practice 44 (Supplement 2):S148–S156, November 2018. 2018. 10.1097/ICL.0000000000000442 [DOI] [PubMed] [Google Scholar]
- 12.Jones LS, Lakshman & Rogers, R. & Dumbleton, Kathryn. Surface treatment, wetting and modulus of silicone hydrogels. Surface treatment, wetting and modulus of silicone hydrogels Optician 232 28–34 2006:28–34.
- 13.Moore J, Lopes BT, Eliasy A, Geraghty B, Wu R, White L, et al. Simulation of the Effect of Material Properties on Soft Contact Lens On-Eye Power. Bioengineering (Basel, Switzerland). 2019;6(4). Epub 2019/10/12. 10.3390/bioengineering6040094 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim E, Saha M, Ehrmann K. Mechanical Properties of Contact Lens Materials. Eye Contact Lens. 2018;44 Suppl 2:S148–s56. Epub 2017/11/09. 10.1097/ICL.0000000000000442 . [DOI] [PubMed] [Google Scholar]
- 15.Young G, Garofalo R, Peters S, Harmer O. The effect of temperature on soft contact lens modulus and diameter. Eye Contact Lens. 2011;37(6):337–41. Epub 2011/09/10. 10.1097/ICL.0b013e31822e8c3b . [DOI] [PubMed] [Google Scholar]
- 16.Horst CR, Brodland B, Jones LW, Brodland GW. Measuring the modulus of silicone hydrogel contact lenses. Optom Vis Sci. 2012;89(10):1468–76. Epub 2012/09/18. 10.1097/OPX.0b013e3182691454 . [DOI] [PubMed] [Google Scholar]
- 17.Young G, Garofalo R, Harmer O, Peters S. The effect of soft contact lens care products on lens modulus. Cont Lens Anterior Eye. 2010;33(5):210–4. Epub 2010/08/03. 10.1016/j.clae.2010.06.002 . [DOI] [PubMed] [Google Scholar]
- 18.Lin DC, Shreiber DI, Dimitriadis EK, Horkay F. Spherical indentation of soft matter beyond the Hertzian regime: numerical and experimental validation of hyperelastic models. Biomechanics and modeling in mechanobiology. 2009;8(5):345–58. Epub 2008/11/02. 10.1007/s10237-008-0139-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gabler S, Stampfl J, Koch T, Seidler S, Schuller G, Redl H, et al. Determination of the viscoelastic properties of hydrogels based on polyethylene glycol diacrylate (PEG-DA) and human articular cartilage. International Journal of Materials Engineering Innovation. 2009;1(1):3–20. 10.1504/IJMatEI.2009.024024 [DOI] [Google Scholar]
- 20.Mesarovic SD, Fleck NA. Spherical indentation of elastic-plastic solids. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences. 1999;455(1987):2707–28. 10.1098/rspa.1999.0423 [DOI] [Google Scholar]
- 21.McKee CT, Last JA, Russell P, Murphy CJ. Indentation versus tensile measurements of Young’s modulus for soft biological tissues. Tissue Eng Part B Rev. 2011;17(3):155–64. Epub 2011/03/21. 10.1089/ten.TEB.2010.0520 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Davis J. Tensile Testing: ASM International; 2004.
- 23.Mayah AA. Biomechanics of Soft Tissues: Principles and Applications: CRC Press; 2018.
- 24.Ogden RW, Hill R. Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proceedings of the Royal Society of London A Mathematical and Physical Sciences. 1972;326(1567):565–84. 10.1098/rspa.1972.0026 [DOI] [Google Scholar]
- 25.Bower AF. Applied Mechanics of Solids: CRC Press; 2009.
- 26.Geraghty B, Abass A, Eliasy A, Jones SW, Rama P, Kassem W, et al. Inflation experiments and inverse finite element modelling of posterior human sclera. Journal of biomechanics. 2020;98:109438 Epub 2019/11/05. 10.1016/j.jbiomech.2019.109438 . [DOI] [PubMed] [Google Scholar]
- 27.Magalhães R, Elsheikh A, Büchler P, Whitford C, Wang J. Application of particle swarm optimization in inverse finite element modeling to determine the cornea´s mechanical behavior. Acta Scientiarum-technology. 2017;39:325–31. [Google Scholar]
- 28.Zhou D, Abass A, Eliasy A, Studer HP, Movchan A, Movchan N, et al. Microstructure-based numerical simulation of the mechanical behaviour of ocular tissue. Journal of The Royal Society Interface. 2019;16(154):20180685 10.1098/rsif.2018.0685 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Elsheikh A, Whitford C, Hamarashid R, Kassem W, Joda A, Buchler P. Stress free configuration of the human eye. Med Eng Phys. 2013;35(2):211–6. Epub 2012/10/09. 10.1016/j.medengphy.2012.09.006 . [DOI] [PubMed] [Google Scholar]
- 30.Wang YX, Xu L, Wei WB, Jonas JB. Intraocular pressure and its normal range adjusted for ocular and systemic parameters. The Beijing Eye Study 2011. PLoS One. 2018;13(5):e0196926 Epub 2018/05/18. 10.1371/journal.pone.0196926 . patent holder with Biocompatibles UK Ltd. (Franham, Surrey, UK) (Title: Treatment of eye diseases using encapsulated cells encoding and secreting neuroprotective factor and / or anti-angiogenic factor; Patent number: 20120263794), and has a patent application with University of Heidelberg (Heidelberg, Germany) (Title: Agents for use in the therapeutic or prophylactic treatment of myopia or hyperopia; Europaische Patentanmeldung 15 000 771.4). This does not alter our adherence to PLOS ONE policies on sharing data and materials. All other authors declare that no other competing interests exist. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Consejo A, Llorens-Quintana C, Radhakrishnan H, Iskander DR. Mean shape of the human limbus. J Cataract Refract Surg. 2017;43(5):667–72. 10.1016/j.jcrs.2017.02.027 [DOI] [PubMed] [Google Scholar]
- 32.Consejo A, Radhakrishnan H, Iskander DR. Scleral changes with accommodation. Ophthalmic & physiological optics: the journal of the British College of Ophthalmic Opticians. 2017;37(3):263–74. Epub 2017/04/26. 10.1111/opo.12377 . [DOI] [PubMed] [Google Scholar]
- 33.Consejo A, Llorens-Quintana C, Bartuzel MM, Iskander DR, Rozema JJ. Rotation asymmetry of the human sclera. Acta Ophthalmol. 2018. Epub 2018/08/28. 10.1111/aos.13901 . [DOI] [PubMed] [Google Scholar]
- 34.Consejo A, Wu R, Abass A. Anterior Scleral Regional Variation between Asian and Caucasian Populations. J Clin Med. 2020;9(11). Epub 2020/10/30. 10.3390/jcm9113419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Abass A, Lopes BT, Eliasy A, Wu R, Jones S, Clamp J, et al. Three-dimensional non-parametric method for limbus detection. PLOS ONE. 2018;13(11):e0207710 10.1371/journal.pone.0207710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Abass A, Lopes BT, Eliasy A, Salomao M, Wu R, White L, et al. Artefact-free topography based scleral-asymmetry. PLOS ONE. 2019;14(7):e0219789 10.1371/journal.pone.0219789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Elsheikh A, Wang D, Brown M, Rama P, Campanelli M, Pye D. Assessment of Corneal Biomechanical Properties and Their Variation with Age. Current Eye Research. 2007;32(1):11–9. 10.1080/02713680601077145 [DOI] [PubMed] [Google Scholar]
- 38.Elsheikh A, Geraghty B, Rama P, Campanelli M, Meek KM. Characterization of age-related variation in corneal biomechanical properties. Journal of the Royal Society Interface. 2010;7(51):1475–85. 10.1098/rsif.2010.0108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Abass A, Stuart S, Lopes BT, Zhou D, Geraghty B, Wu R, et al. Simulated optical performance of soft contact lenses on the eye. PLOS ONE. 2019;14(5):e0216484 10.1371/journal.pone.0216484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Doll T, Moore J, Shihab AH, Lopes BT, Eliasy A, Maklad O, et al. Which feature influences on-eye power change of soft toric contact lenses: Design or corneal shape? PLOS ONE. 2020;15(11):e0242243 10.1371/journal.pone.0242243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kwon K-A, Shipley RJ, Edirisinghe M, Ezra DG, Rose G, Best SM, et al. High-speed camera characterization of voluntary eye blinking kinematics. Journal of The Royal Society Interface. 2013;10(85):20130227 10.1098/rsif.2013.0227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhao G, Wollmer P. Surface activity of tear fluid. Acta Ophthalmol Scand. 1998;76:438–41. 10.1034/j.1600-0420.1998.760409.x [DOI] [PubMed] [Google Scholar]
- 43.Shaw AJ, Collins MJ, Davis BA, Carney LG. Eyelid pressure and contact with the ocular surface. Investigative ophthalmology & visual science. 2010;51(4):1911–7. 10.1167/iovs.09-4090 . [DOI] [PubMed] [Google Scholar]
- 44.Bretz K, Jobbágy Á, Bretz K. Force measurement of hand and fingers. Biomechanica Hungarica. 2010. 10.17489/biohun/2010/1/07 [DOI] [Google Scholar]
- 45.Rumsey DJ. Statistics For Dummies: Wiley; 2016.
- 46.Lin MC, Yeh TN. Mechanical complications induced by silicone hydrogel contact lenses. Eye Contact Lens. 2013;39(1):115–24. Epub 2012/12/29. 10.1097/ICL.0b013e31827c77fd . [DOI] [PubMed] [Google Scholar]
- 47.Graham AD, Truong TN, Lin MC. Conjunctival epithelial flap in continuous contact lens wear. Optom Vis Sci. 2009;86(4):e324–31. Epub 2009/02/20. 10.1097/OPX.0b013e318199d1f7 . [DOI] [PubMed] [Google Scholar]
- 48.Alba-Bueno F, Beltran-Masgoret A, Sanjuan C, Biarnés M, Marín J. Corneal shape changes induced by first and second generation silicone hydrogel contact lenses in daily wear. Cont Lens Anterior Eye. 2009;32(2):88–92. Epub 2009/02/03. 10.1016/j.clae.2008.11.002 . [DOI] [PubMed] [Google Scholar]
- 49.Maïssa C, Guillon M, Garofalo RJ. Contact lens-induced circumlimbal staining in silicone hydrogel contact lenses worn on a daily wear basis. Eye Contact Lens. 2012;38(1):16–26. Epub 2011/12/08. 10.1097/ICL.0b013e31823bad46 . [DOI] [PubMed] [Google Scholar]
- 50.Nakano T, Kato M, Morito Y, Itoi S, Kitazawa S. Blink-related momentary activation of the default mode network while viewing videos. Proceedings of the National Academy of Sciences. 2013;110(2):702–6. 10.1073/pnas.1214804110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Doane MG. Interactions of eyelids and tears in corneal wetting and the dynamics of the normal human eyeblink. Am J Ophthalmol. 1980;89(4):507–16. Epub 1980/04/01. 10.1016/0002-9394(80)90058-6 . [DOI] [PubMed] [Google Scholar]
- 52.Karson CN. Spontaneous eye-blink rates and dopaminergic systems. Brain. 1983;106 (Pt 3):643–53. Epub 1983/09/01. 10.1093/brain/106.3.643 . [DOI] [PubMed] [Google Scholar]
- 53.Dumbleton K, Woods CA, Jones LW, Fonn D. The Impact of Contemporary Contact Lenses on Contact Lens Discontinuation. Eye & Contact Lens. 2013;39(1):93–9. 10.1097/ICL.0b013e318271caf4 [DOI] [PubMed] [Google Scholar]
- 54.Vidal-Rohr M, Wolffsohn JS, Davies LN, Cerviño A. Effect of contact lens surface properties on comfort, tear stability and ocular physiology. Cont Lens Anterior Eye. 2018;41(1):117–21. Epub 2017/09/21. 10.1016/j.clae.2017.09.009 . [DOI] [PubMed] [Google Scholar]
- 55.Dillehay SM. Does the level of available oxygen impact comfort in contact lens wear?: A review of the literature. Eye Contact Lens. 2007;33(3):148–55. Epub 2007/05/16. 10.1097/01.icl.0000245572.66698.b1 . [DOI] [PubMed] [Google Scholar]
- 56.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. Journal of biomechanical engineering. 1980;102(1):73–84. 10.1115/1.3138202 [DOI] [PubMed] [Google Scholar]
- 57.Ateshian GA, Ellis BJ, Weiss JA. Equivalence between short-time biphasic and incompressible elastic material responses. Journal of biomechanical engineering. 2007;129(3):405–12. Epub 2007/06/01. 10.1115/1.2720918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Harris MD, Anderson AE, Henak CR, Ellis BJ, Peters CL, Weiss JA. Finite element prediction of cartilage contact stresses in normal human hips. J Orthop Res. 2012;30(7):1133–9. Epub 2011/12/30. 10.1002/jor.22040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kamath PM. Physical and chemical attributes of an ideal contact lens. Contacto. 1969;13:29–34. [Google Scholar]
- 60.Y G G R, Harmer O., Peters S. The effect of soft contact lens care products on lens modulus, Contact Lens and Anterior Eye. 2010;Volume 33, Issue 5:Pages 210–4. 10.1016/j.clae.2010.06.002 [DOI] [PubMed] [Google Scholar]
- 61.Young GMP, Ph.D., Optom F.C.; Garofalo Renee O.D; Peters Shaun B.Sc.; Oliver Harmer B.Sc. The Effect of Temperature on Soft Contact Lens Modulus and Diameter. Eye & Contact Lens: Science & Clinical Practice 37(6):337–341, November 2011. November 2011: 337–41. 10.1097/ICL.0b013e31822e8c3b [DOI] [PubMed] [Google Scholar]
- 62.Tranoudis Ioannis E N. Tensile properties of soft contact lens materials. Contact Lens and Anterior Eye. 2004;Volume 27, Issue 4:Pages 177–91. 10.1016/j.clae.2004.08.002 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(XLSX)
(XLSX)
Data Availability Statement
All relevant data are within the manuscript and its Supporting information files.