MetaClean: a machine learning-based classifier for reduced false positive peak detection in untargeted LC–MS metabolomics data

Abstract

Introduction

Despite the availability of several pre-processing software, poor peak integration remains a prevalent problem in untargeted metabolomics data generated using liquid chromatography high-resolution mass spectrometry (LC–MS). As a result, the output of these pre-processing software may retain incorrectly calculated metabolite abundances that can perpetuate in downstream analyses.

Objectives

To address this problem, we propose a computational methodology that combines machine learning and peak quality metrics to filter out low quality peaks.

Methods

Specifically, we comprehensively and systematically compared the performance of 24 different classifiers generated by combining eight classification algorithms and three sets of peak quality metrics on the task of distinguishing reliably integrated peaks from poorly integrated ones. These classifiers were compared to using a residual standard deviation (RSD) cut-off in pooled quality-control (QC) samples, which aims to remove peaks with analytical error.

Results

The best performing classifier was found to be a combination of the AdaBoost algorithm and a set of 11 peak quality metrics previously explored in untargeted metabolomics and proteomics studies. As a complementary approach, applying our framework to peaks retained after filtering by 30% RSD across pooled QC samples was able to further distinguish poorly integrated peaks that were not removed from filtering alone. An R implementation of these classifiers and the overall computational approach is available as the MetaClean package at https://CRAN.R-project.org/package=MetaClean.

Conclusion

Our work represents an important step forward in developing an automated tool for filtering out unreliable peak integrations in untargeted LC–MS metabolomics data.

1. Introduction

A commonly used tool for untargeted metabolomics analyses is liquid chromatography paired with high-resolution mass spectrometry (LC–MS), which generates raw data for chemicals in three dimensions: mass-to-charge ratio (m/z), retention time (rt) and abundance. Prior to downstream analyses, these data are generally pre-processed using software to identify peaks representing chemicals in each sample, perform retention time correction, and then group similar peaks across all the samples. This process yields a table of features, or peaks, (of specific m/z and rt), and their respective abundances in every sample (Dunn et al. 2011; Smith et al. 2006). A variety of pre-processing software exist for LC–MS data, including both commercial, such as MassHunter Profinder (Agilent), Progenesis QI (Waters), and Compound Discoverer (Thermo), as well as open-source, such as XCMS (Smith et al. 2006), MZmine (Pluskal et al. 2010), and apLCMS (Yu et al. 2009), software. However, despite the availability and diversity of pre-processing software, significant challenges in detecting and integrating peaks persist. These include large variations in peak detection across software, high prevalence of false positive peaks, and poor integration of identified peaks (Coble and Fraga 2014; Myers et al. 2017; Rafiei and Sleno 2015). Subsequent filtering strategies based on pre-determined thresholds on metrics, such as mean/median value across samples, variability across biological samples, and levels of missing values, are routinely employed to remove noisy peaks (Chong et al. 2019; Want et al. 2010). In particular, the most common filtering method, relative standard deviation (RSD) calculated on peaks in a routinely injected pooled quality control (QC) sample, retains peaks that are within a typical threshold, e.g., RSD < 30% (Broadhurst et al. 2018). While this reduces the total number of peaks to a few thousand, and improves the ratio of high-quality peaks to low-quality ones in the final dataset, the latter still usually remain in large numbers (Schiffman et al. 2019). Particularly for RSD filtering, integration of noise, multiple peaks, or partial peak integrations can be reproducible in sequential measurements of the same sample, but they may not be reliable across many independent biological samples. The result is that pre-processed output tables, even after traditional filtering approaches, can still contain incorrect abundance values. This can lead to spurious conclusions from downstream data analyses, if the peaks are not manually curated.

Several tools have been developed to reduce the number of low-quality integrations in LC–MS metabolomics data mainly through optimizations of the pre-processing software mentioned above. For example, IPO optimizes XCMS parameters using isotope data (Libiseller et al. 2015), xMSanalyzer improves peak detection by merging multiple datasets produced by varying the parameters of methods from XCMS and apLCMS (Uppal et al. 2013), and warpgroup utilizes subregion and consensus integration bound detection (Mahieu et al. 2016). Each of these tools improves the performance of pre-processing software in various ways, such as increasing the number of “reliable” peaks (Libiseller et al. 2015) and enhancing the detection of low abundance metabolites (Chong et al. 2019), but they do not provide a means to evaluate the integration quality following pre-processing. Currently, WiPP (Borgsmüller et al. 2019) is the only available tool that assesses integration quality and automatically filters any poorly integrated peaks. However, WiPP is only applicable to GC–MS data, and does not consider shifts in retention time that are common to untargeted data generated with LC. Without a way to automatically and objectively assess integration quality in LC–MS data, manual quality assessment, which is both time-consuming and subjective, is the only way to ensure that poor peak integrations do not propagate to downstream analyses (Schiffman et al. 2019).

Some computational methods have been developed to directly assess peak integration. Zhang et al. (2014) proposed and evaluated the effectiveness of six quantitative LC–MS peak quality metrics in filtering out low-quality peaks. However, this evaluation was limited in several ways. First, it utilized a small set of only 12 peaks (6 high- and 6 low-quality), which likely don’t capture the large variation in peak quality observed in LC–MS metabolomics data (Coble and Fraga 2014; Myers et al. 2017; Rafiei and Sleno 2015). To scale up this evaluation, the “ground truth” quality of the peaks was determined by a consensus method, namely defining peaks identified by two out of three peak-picking tools as high-quality, and the others as low-quality. However, this consensus method does not sufficiently address the limitations of these tools in identifying low-quality peaks described above (Schiffman et al. 2019). The study also did not provide recommendations for how to threshold the proposed quality metrics to classify peaks as high- or low-quality. Thus, this work did not yield an objective, automated method for identifying low-quality LC–MS peaks. In the related field of proteomics, Eshghi et al. (2018) developed the R package TargetedMSQC, which combines quantitative peak quality metrics and machine learning techniques (Alpaydin 2014) for the automatic flagging of low-quality peaks in targeted LC–MS data. However, targeted data are generally less complex than untargeted data as they focus on only a limited number of compounds. Furthermore, the methods in this package rely heavily on an internal standard for each peak, which is not used in untargeted data. Thus, there is an urgent need for methods that can automatically detect and filter poor peak integrations in untargeted LC–MS datasets.

In this paper, we propose a novel computational framework that accomplishes this goal by employing a combination of machine learning techniques and peak quality metrics. Specifically, we evaluated the performance of three sets of metrics, namely, the set proposed by Zhang et al. (2014), one set consisting of metrics from TargetedMSQC (Eshghi et al. 2018) repurposed for untargeted metabolomics, and a combination of the two sets. We paired each metric set with a diverse set of machine learning algorithms (Alpaydin 2014) to develop multiple classifiers that can distinguish high-quality peaks from low-quality ones. High-quality peaks defined here were those that were visually distinct from background, and had a well-integrated single-peak area, thereby correlating well with analyte concentration. We used an untargeted metabolomics data set, a rigorous cross-validation framework, and appropriate classification evaluation measures and statistical tests to determine the best-performing classifier. We then evaluated the performance of the framework on multiple validation data sets, both with and without RSD-based filtering. Our framework, as well as the best-performing classifiers, are available as the MetaClean R package at https://CRAN.R-project.org/package=MetaClean for integration into untargeted metabolomics pipelines.

2. Materials and methods

2.1. Untargeted LC–MS metabolomics datasets

Four publicly available untargeted LC–MS metabolomics datasets, two from Metabolomics Workbench (MW) (Sud et al. 2016), and two from MetaboLights (ML) (Haug et al. 2019), were utilized in this study. One of these was the development dataset used to evaluate and select the peak quality classifiers (with and without RSD filtering), while the other test sets were used for the external validation of these classifiers.

The development dataset (MW id ST000726) (Metabolomics Workbench 2017a) included 89 blood plasma samples analyzed on an Agilent 6530 QTOF with a Waters Acquity HSS T3 (50 × 2.1 mm, 1.8 μm) column in reversed phase positive mode. The Test 1 dataset (MW id ST000695) (Metabolomics Workbench 2017b) included LC–MS data from 100 blood serum samples analyzed in the same laboratory on the same platform as the development set. The Test 2 dataset (ML id MTBLS354) (MetaboLights 2016a) consisted of LC–MS data from 204 plasma samples analyzed on a different Agilent 6540 QTOF instrument with an ACQUITY UPLC BEH C18 (1.7 μm, 2.1 mm × 100 mm; Waters) column in reversed phase negative mode at a different laboratory. A fourth dataset (ML id MTBLS306) (MetaboLights 2016b) included LC–MS data from 109 urine samples analyzed on a Thermo Scientific Exactive (Orbitrap) instrument with a ZIC-pHILIC column run in alternating mode. This dataset was split into the Test 3 (positive mode) and Test 4 (negative mode) datasets. Evaluation on these various test sets provided a cross-platform estimate of the performance of the peak quality classifiers. Further details of these datasets are summarized in Table 1.

Table 1.

Details of the datasets utilized in this study

Basic details of datasets							#Labeled peaks in original dataset			#Labeled peaks after RSD filtering
Data set (Database ID)	# Samples/QCsa	Total # Peaks	Matr ix	Instrument	Column	Modeb	# Passc	# Failc	# Total	# Passd	# Faild	# Totald
Development (ST000726)	89/13	5423	Plasma	Agilent 6530 QTOF	Waters Acquity HSS T3	Pos	303	197	500	244	155	399
Test 1 (ST000695)	100/10	4204	Serum	Agilent 6530 QTOF	Watters Acquity HSS T3	Pos	360	140	500	301	116	417
Test 2e,f (MTBLS354)	203/35	14,903	Plasma	Agilent 6540 QTOF	Acquity UPLC BEH C18	Neg	367	133	500	51	24	75
Test 3g (MTBLS306)	109/10	14,492	Urine	Thermo Scientific Exactive (Orbitrap)	ZIC-pHILIC	Pos	275	225	500	94	78	172
Test 4g (MTBLS306)	109/10	12,712	Urine	Thermo Scientific Exactive (Orbitrap)	ZIC-pHILIC	Neg	272	228	500	89	80	169

^aThe “# Samples/QCs” column refers to the number of LC–MS samples and pooled QCs, respectively, processed in each dataset

^bElectrospray ionization mode, “Pos” for positive and “Neg” for negative

^c“# Pass” and “# Fail”, respectively, are the numbers of expert-defined high- and low-quality peaks out of the 500 sampled randomly from each dataset

^d“# Pass” and “# Fail”, respectively, are the numbers of expert-defined high- and low-quality peaks among the original 500 with RSD < 30%

^eFiles used for RSD filtering in Test 2 were named with a “CC”. QC samples for all other datasets were clearly indicated with a “QC” in the filename

^fFor additional information regarding Test 2, refer to the associated publication (To et al. 2016)

^gFor additional information regarding Test 3 and Test 4, refer to the associated publication (Muhsen Ali et al. 2016)

2.2. Pre-processing of datasets

For each dataset, peak-picking, retention time correction, and grouping of the peaks across the samples and QCs was performed using XCMS (version 3.6.3), with parameters optimized for each dataset using IPO (version 1.8.1; details in Supplementary Table 1). After pre-processing, 500 peaks were randomly selected from each dataset. A figure was printed for each peak using the getEIC function from XCMS for a visual assessment of its distinction from the background and other peaks, overall shape, and the quality of integration under the peak for all samples taken together. An expert (Petrick) then assigned a label of Pass (high-quality) or Fail (low-quality) to each peak (see Fig. 1 for examples). The fraction of Fail peaks in our study datasets ranged from 27.4 to 39.6% (Table 1).

Fig. 1.

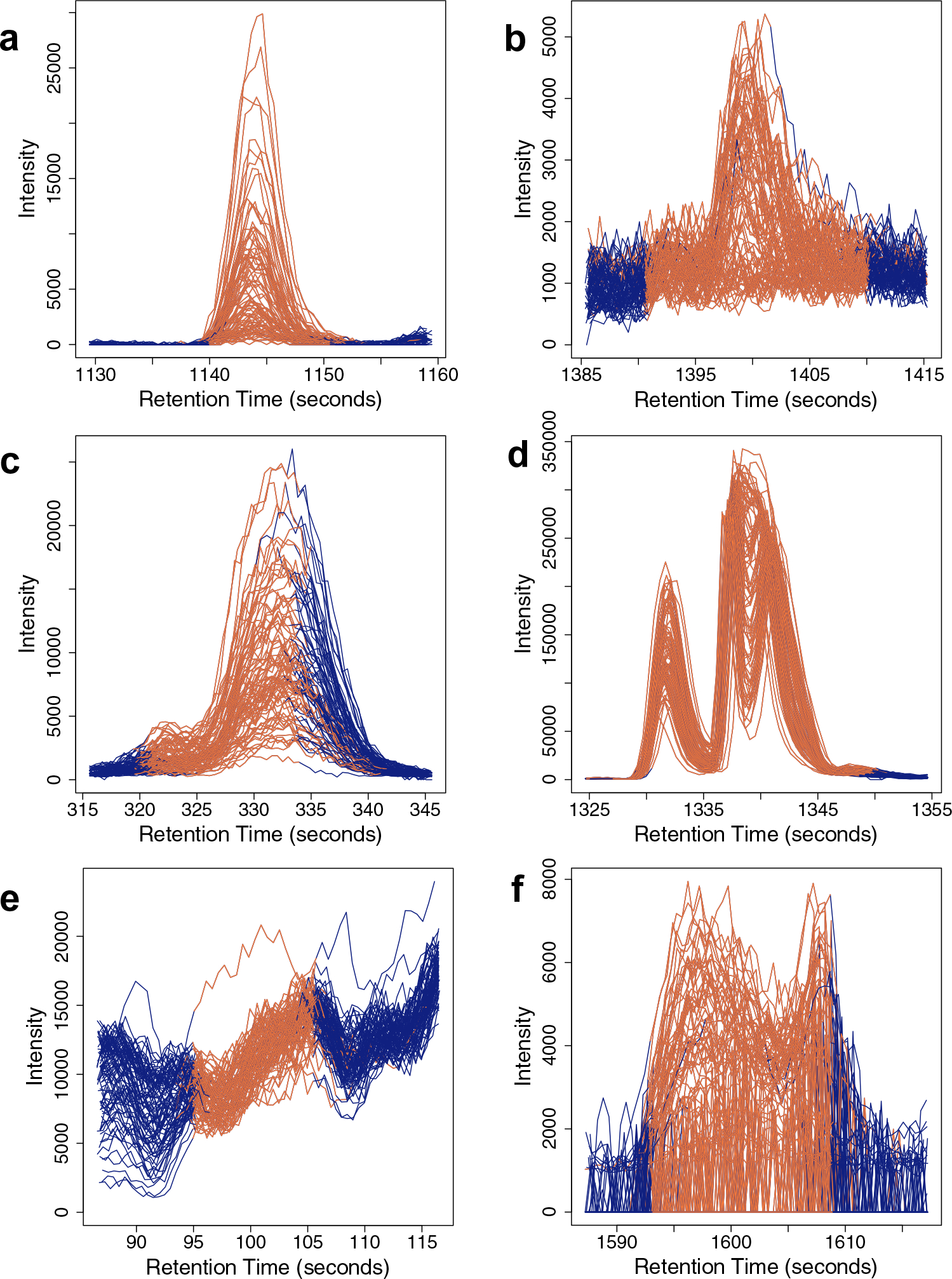
Examples of peaks labeled Pass (a, b) and Fail (c–f). The X- and Y-axes of these plots, generated using XCMS, denote the aligned retention time and intensity of the identified peak respectively. a An ideal peak—excellent shape, well-aligned samples, clearly distinguishable from the background signal, and its assigned boundaries capture the entire peak shape. The peak in b is also labeled Pass, since its shape is reasonably well-defined, although its intensity is close to the baseline, and it is slightly over-integrated. The Fail class has a lot more variation. Examples c–e are labeled Fail for the following reasons: c partial integration of the peak, d integration of multiple peaks into one, and e integration of noise. Example (f), like (b), depicts a low-intensity peak, but the shape is considerably worse. The intensity of the right boundary is high, and the peak has a large central dip that gives it an “M” shape rather than the expected Gaussian curve-like shape

2.3. Peak integration quality metrics

Three sets of peak integration quality metrics were evaluated in this study. The first set of metrics were adapted from the TargetedMSQC package (version 0.99.1, Eshghi et al. 2018), which utilized a total of 52 metrics developed from variations of 9 main metric groups. However, a majority of these variations, as well as main similarity and area ratio metric groups, were dependent on either internal standards or requirements for fragmentation data, which aren’t always available for untargeted LC–MS data. Thus, we were only able to adapt a single metric from each of the seven remaining metric groups utilized by TargetedMSQC. These adapted metrics included apex-boundary ratio, jaggedness, symmetry, modality, FWHM2base, elution shift, and retention time consistency (referred to as the M7 metric set; see Table 2).

Table 2.

Names, descriptions, formulas, and interpretations of the 11 peak integration quality metrics used in our study, categorized into the sets they were obtained/adapted from

Name	Description	Formulaa	Interpretationb
M7 (Eshghi et al.)
Apex-Boundary Ratio (ABR)	Uses boundary-over-apex intensity ratio to assess completeness of integration	$ABR=\frac{\mathit{\text{max}}\left(I_1,I_N\right)}{I_A}$	LV ⇒ HQ HV ⇒ LQ Range: (0,1]
Elution Shift (ES)	Assesses retention time shift of samples by comparing time-position of peak apex	$ES=\frac{abs\left(t_{A,s}-med\left(t_{A,1},\dots ,t_{A,S}\right)\right)}{PB}$ $PB=\mathit{\text{avg}}\left(t_{N,1},\dots ,t_{N,S}\right)-\mathit{\text{avg}}\left(t_{1,1},\dots ,t_{1,S}\right)$	LV ⇒ HQ HV ⇒ LQ HV ⇒ HQ
FWHM2Base (F2B)	Assesses separation of peaks by measuring peak-width at half-max vs. peak-width at base	$F2B=\frac{t_{HA,2}-t_{HA,1}}{t_N-t_1}$ If tHA,2 does not exist, F2B=0	LV ⇒ LQ Range: (0,1]
Jaggedness (J)	Captures shape quality by calculating the number of changes in direction over length of intensity vector	D = diff ([I1,…,IN]) D′ = {sign(d), d ∈ D, ifd > ff * IA0, d ∈ D, ifd < ff * IA $J=\frac{\mathit{\text{sum}}(D^{\prime })}{N}$	LV ⇒ HQ HV ⇒ LQ
Modality (M)	Measures the first unexpected change in direction of intensity to detect splitting and integration of multiple peaks	M = maxDip/IA maxDip = Ilr − Iff	LV ⇒ HQ HV ⇒ LQ
RT Consistency (RTC)	Assesses retention time alignment of samples by comparing the time at the center index of the time vector	$RTC=\frac{abs\left(\mathit{\text{avg}}\left({\mathit{\text{ct}}}_1,\dots ,c{t}_S\right)-c{t}_s\right)}{\mathit{\text{avg}}\left(c{t}_1,\dots ,c{t}_S\right)}$ cts = tN,s − (tN,s − t1,s)/2	LV ⇒ HQ HV ⇒ LQ
Symmetry (SY)	Measures correlation between left and right halves of a peak	$SY=\mathit{\text{cor}}([I_1,\dots ,I_{\frac{N}{2}}],[I_{\frac{N}{2}},\dots ,I_N])$	HV ⇒ HQ LV ⇒ LQ Range: [−1,1]
M4 (Zhang et al.)
Gaussian Similarity (GS)	Measures similarity of a peak to Gaussian-fitted curve	$\mathit{\text{GaussianSimilarity}}=\frac{C\cdot G}{\Vert C\Vert \cdot \Vert G\Vert }$ C = std([I,, .., IN]) G = std([GI1,…, GIN]) where GI equal to value of intensity of Gaussian fitted curve	HV ⇒ HQ LV ⇒ LQ Range: [0, 1]
Sharpness (SH)	Captures steepness of a peak by summing the ratio of the difference between neighboring points and the point within the pair expected to have the lower value	$SH={\sum }_{i=2}^A\frac{I_i-I_{i-1}}{I_{i-1}}+{\sum }_{i=A}^{N-1}\frac{I_i-I_{i+1}}{I_{i+1}}$	HV ⇒ HQ LV ⇒ LQ
Triangle Peak Area Similarity Ratio (TPASR)	Estimates shape quality by comparing peak area to area of triangle formed by the apex and boundaries	$\mathit{\text{TPASR}}=\frac{abs\left(t{r}_{-}\mathit{\text{area}}-p{k}_{-}\mathit{\text{area}}\right)}{\mathit{\text{t}}{r}_{-}\mathit{\text{area}}}$ tr_area = 0.5 * N * IA $\mathit{\text{pkarea}}={\sum }_{i=1}^N{I}_i$	LV ⇒ HQ HV ⇒ LQ
Zig-Zag Index (ZZ)	Captures shape quality by measuring the normalized variance between a point and its immediate neighbor on either side	$ZZ=\frac{{\sum }_{n=2}^{n=N-1}{\left(2I_n-I_{n-1}-I_{n+1}\right)}^2}{N*EP{I}^2}$$EPI=I_A-\mathit{\text{avg}}\left(I_1+I_2+I_{N-1}+I_N\right)$	LV ⇒ HQ HV ⇒ LQ

^aThe variables used in the formulae of the metrics are defined as follows: Ii represents the value within the intensity vector of a peak at position i, i = {1,2,…,N}. t_i represents the value within the retention time vector of a peak at position i, i = {1,2,…,N}. I_A and t_A represent the value of the maximum intensity (position A = { 1,2,…,N } and the retention time at the corresponding position, respectively; also, t_HA represents the retention time at the position of half the maximum intensity. For metrics that require information from multiple samples (e.g. Elution Shift), the second index represents the sample of interest s = {1,2,…, S}, where S is the total number of samples. The formulae also make use of the following functions: avg() stands for average, std() stands for standard normalization, med() stands for median, sign() returns the sign of a real number, diff () is the contiguous pairwise differences between values in a sequence, and abs() stands for absolute value. Each metric is calculated for every individual sample within a peak, and the overall metric value for the peak is calculated as the mean of the sample-level values. For more information on each of these sets of metrics, please refer to the original publications (Eshghi et al 2018 and Zhang et al. 2014), or our MetaClean package

^bIn this column, which indicates how the value of a metric indicates the quality of a peak, the abbreviations LV and HV stand for “Low Value” and “High Value” respectively, and LQ and HQ stand for “Low Quality” and “High Quality” respectively. Ranges are also specified for the metrics that are bounded; else, the range is (−∞, ∞)

The second set of metrics was obtained from the Zhang et al. (2014) study on quality assessment of peaks in untargeted LC–MS metabolomics data. Four of the six metrics proposed in that study, namely sharpness, Gaussian similarity, triangle peak area similarity ratio (TPASR), and local zigzag index (referred to as the M4 metric set; see Table 2), were used here. From the original study, the signal-to-noise ratio metric required additional signal information beyond the chromatographic peak data output by XCMS, and was therefore not included here. The peak significance metric was also not used, since its values for individual peaks were sensitive to even slight variations in XCMS’ parameters, and thus likely not robust across datasets and platforms.

Finally, we also considered a set of eleven metrics, referred to as the M11 set, that was a union of the TargetedMSQC (M7) and Zhang et al. (M4) metrics.

All metrics were calculated for each of the 500 selected peaks in all five datasets (Table 1) as described in Fig. 2. For a single peak, the metrics were calculated for each of the N individual samples, and the mean of those values was used to quantify the corresponding quality metric of that peak. This resulted in a matrix of 500 × M values, where M is equal to the number of peak quality metrics being calculated (4, 7, and 11, respectively for the M4, M7 and M11 sets). This matrix constituted the input for training and testing the candidate peak quality classifiers considered in our study. R implementations of these metrics were adapted from the TargetedMSQC package and Matlab code provided by the authors of the Zhang et al. (2014) study. These implementations for untargeted LC–MS metabolomic data, along with detailed documentation, are available in our MetaClean R package.

Fig. 2.

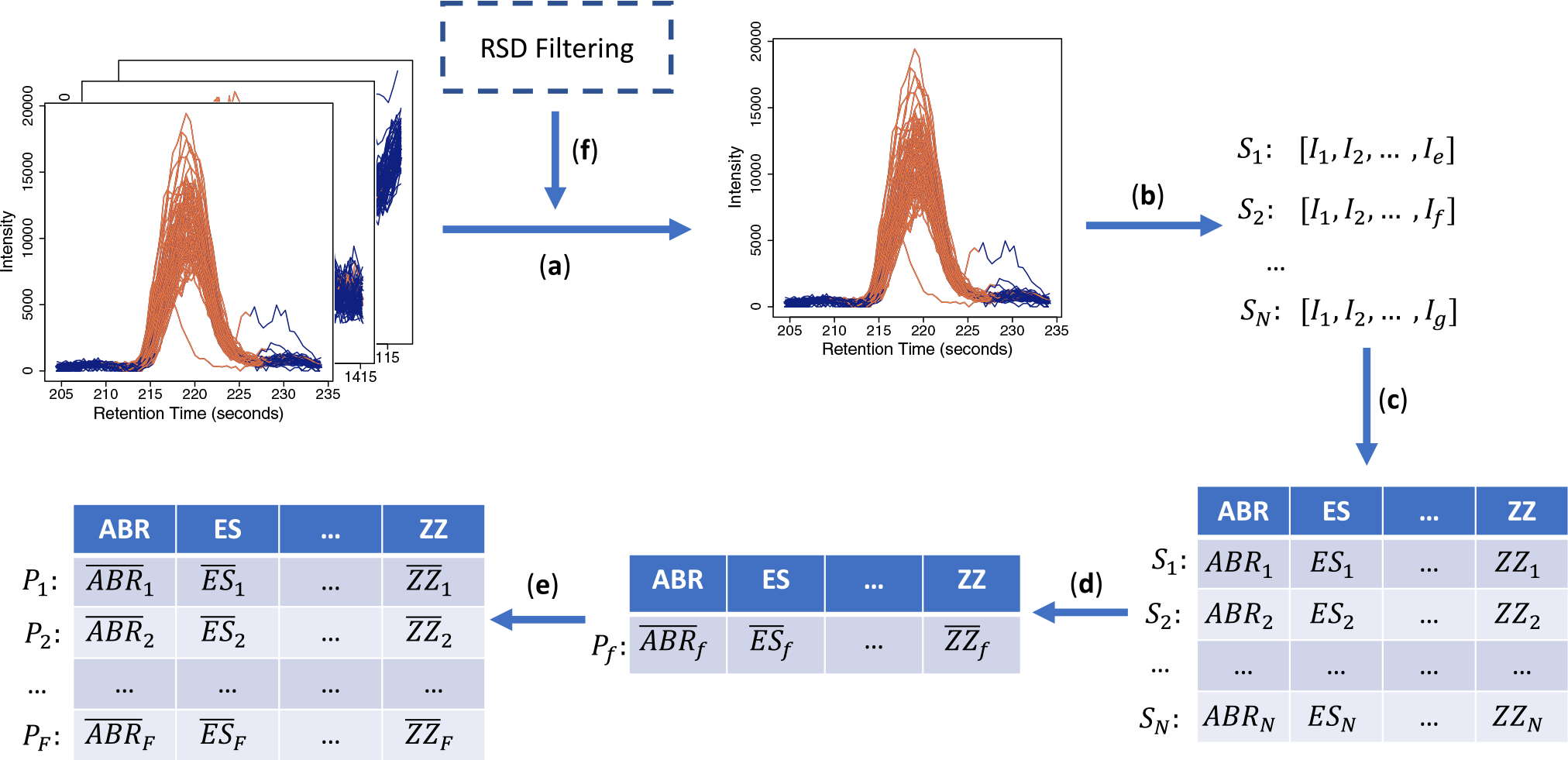
Schematic describing our calculation of the peak integration quality metrics. We use the same notation as in Table 2. a Intensity and retention time information is extracted for every peak in a dataset. b Vectors for intensity, I_i, and time (not shown here) are extracted for every sample, S_n (n = {1,2, … , N}, where N is the number of samples in a peak), P_f (f = {1,2, … , F}, where F is the total number of peaks). Note that the lengths of the intensity vectors (X, Y, … , Z) may or may not be equal. c The metrics listed in Table 2 are applied to these intensity (and the corresponding retention time) vectors to calculate the corresponding values for each sample. d The quality metric for a peak is calculated as the mean of the corresponding values (marked by horizontal bars) for the group of samples constituting the peak. e This process is repeated for all the peaks to obtain a matrix with integration quality metrics (11 total; detailed in Table 2) as columns, and peaks (the originally labeled 500 in each of our datasets described in Table 1) as rows. f Optionally, a dataset can first be pre-processed using RSD filtering, in which case the quality metric calculation and MetaClean are applied to the filtered subset of the original 500 peaks in each dataset (Table 1)

2.4. Development and performance assessment of peak quality classifiers

After the computation of metric sets M4, M7 and M11 for the given set of peaks, we developed classifiers to predict if a peak is high- or low-quality, referred to as Pass and Fail cases, respectively. Specifically, we used the metrics in each of the above sets as attributes of the peaks. Next, we used eight established classification algorithms (Alpaydin 2014) to develop peak quality classifiers based on these sets of attributes and available quality labels (Pass or Fail) in the development set. These algorithms were Decision Tree (DT), Logistic Regression (LR), Naive Bayes (NB), Neural Network (NN), SVM with the most commonly used linear kernel (SVM_L), AdaBoost (AB), Model Averaged Neural Network (MANN), and Random Forest (RF) (details in Supplementary Table 2). The caret R package (Kuhn 2008, version 6.0–84) was used for implementations of these algorithms, and integrated into our MetaClean package. The combination of three metric sets and eight classification algorithms yielded 24 candidate peak quality classifiers that were analyzed further.

We employed a rigorous fivefold cross-validation (CV) procedure (Arlot and Celisse 2010) for training and assessing the performance of these candidate classifiers (Fig. 3). In this procedure, each dataset, i.e., the peak × quality metric matrix, was split into five randomly selected, equally sized partitions, referred to as CV folds. Then, in each CV round, four of these partitions were used for training each of the 8 candidate classifiers for each metric set, and the remaining partition was used to generate CV test predictions. After all five CV rounds had been executed, the five disjoint prediction sets were concatenated to yield a prediction set of the same length as the original number of peaks in the development set. This vector was then evaluated against the true labels in the development set, using the measures described below, to assess the performance of the classifier (quality metric-classification algorithm combination) under consideration. To reduce the likelihood of obtaining over/under-optimistic results from a single CV execution, we executed this process ten times, and assessed each candidate classifier’s performance as the average of its measures’ values across all these executions.

Fig. 3.

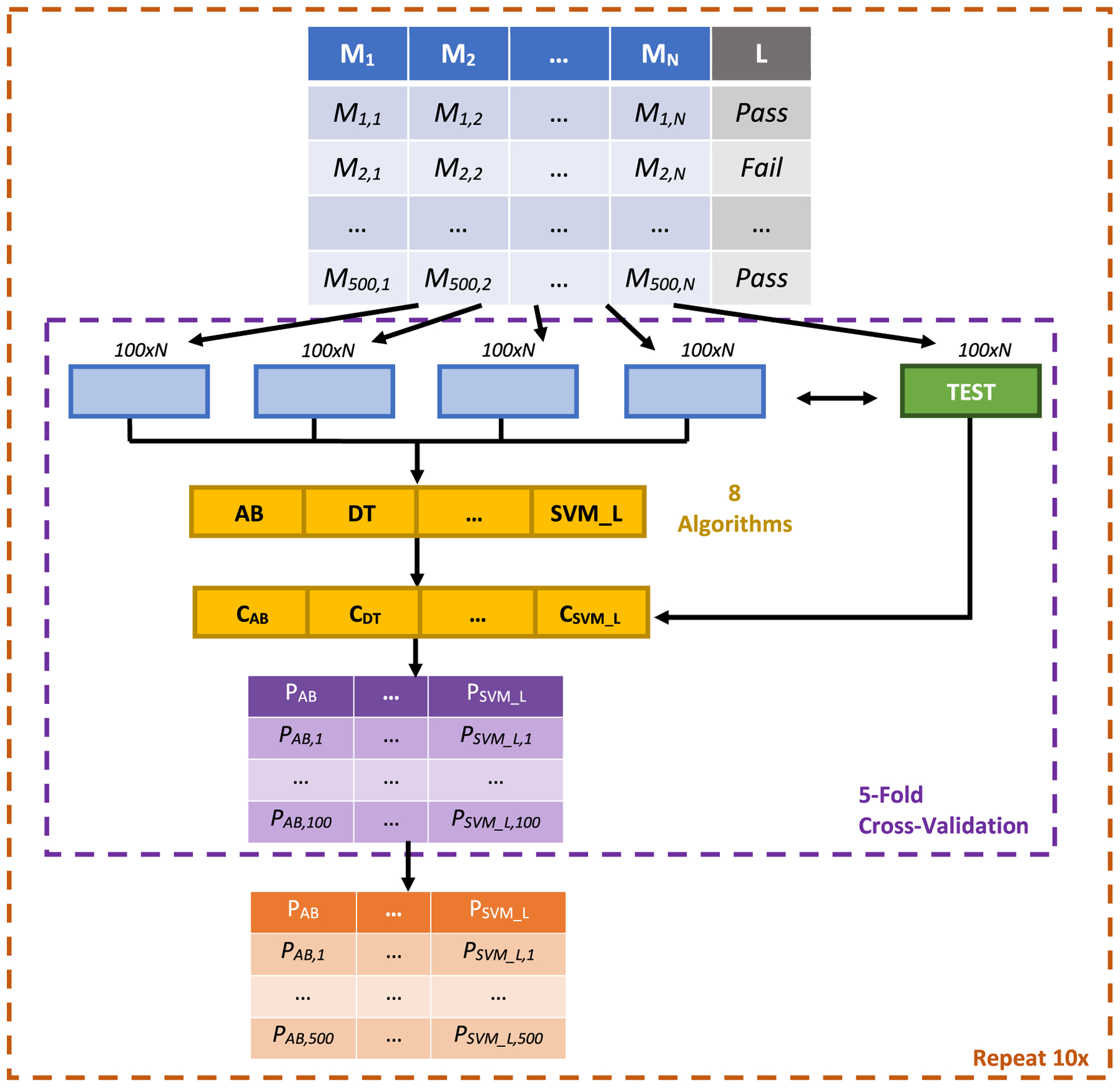
Schematic of the cross-validation-based machine learning framework utilized in this study and our MetaClean package. For each of the three metric sets M4, M7 and M11, calculated as illustrated in Fig. 2 and shown in the top table, the original development set consisting of 500 labeled peaks was randomly partitioned into five equally sized subsets. One of these subsets was selected to be a test set (green box in the second row), while the other four (blue boxes in the second row) were combined and used to train 8 candidate classifiers using as many established algorithms (denoted by yellow boxes in the third and fourth rows; described in Supplementary Table 2). The candidate classifiers then made predictions for each of the 100 peaks in the test set (purple box in penultimate row). The five sets of predictions at the end of each round of cross-validation were then concatenated into one prediction vector for each candidate classifier (orange box in final row). These concatenated predictions were then evaluated using the various measures described in the Sect. 2 and Supplementary Fig. 1. Finally, to reduce the bias that can result from an over- or under-optimistic random split of the data during cross-validation, we repeated the whole process ten times and averaged the resultant evaluation measures as the final performance assessment of each candidate classifier. The same process was applied for developing and evaluating candidate RSD-augmenting classifiers in the latter part of our study

2.5. Evaluation measures to assess the performance of peak quality classifiers

Several measures have been proposed to evaluate the performance of classifiers (Lever et al. 2016). While Accuracy, which is simply the proportion of all the examples that were predicted correctly by the classifier, is the most commonly used, it does not differentiate between (in)correct predictions in the two classes. Therefore, it may not be effective for performance assessment in situations where the classes are not balanced, as in our study (Table 1). Therefore, we also included evaluation measures designed for class-specific evaluation (Lever et al. 2016), namely sensitivity (recall_Pass), specificity (recall_Fail), positive predictive value (PPV, precision_Pass), and negative predictive value (NPV, precision_Fail). We also included composite measures, namely balanced accuracy, the average of sensitivity and specificity, and respective F-measures for the Pass and Fail classes, which are the harmonic means of the corresponding precision and recall values. See Supplementary Fig. 1 for detailed definitions of all these measures.

Specifically, since our final goal was to produce binary Pass or Fail classifications, we first scanned the full CV prediction vector generated by each classifier for the probability threshold at which the balanced accuracy measure was maximized. The probabilistic predictions were then binarized at this threshold, and the final evaluation of the classifier was conducted in terms of accuracy, and F-measures for the Pass and Fail classes, both in the CV setup and the test sets.

2.6. Statistical comparison of the candidate peak quality classifiers and selection of the final classifier

The above CV framework and evaluation procedure and measures generated a comprehensive assessment of the performance of the candidate classifiers. Using the scmamp R package (Calvo and Santafé 2016) (version 0.2.55), we then analyzed these performance statistics to identify the best-performing classifier for each of the three metric sets M4, M7 and M11, respectively, and then across all the metric sets. For this, we applied Friedman’s statistical test, followed by Nemenyi’s test, to the collected performance statistics (Demsar 2006). Friedman’s test ranks the performance of each classifier across each of the ten CV runs and compares the average rank of each classifier. Nemenyi’s test then performs multiple hypothesis correction to account for the comparison of multiple classifiers. The result of these tests is the critical difference (CD) value for each pair of classifiers, which represents the minimum distance between their ranks for their performance to be considered statistically different, as well as the corresponding p-value. These final results for all the tested classifiers can be visualized as a CD plot, such as those shown in Supplementary Fig. 2.

These tests were performed in an intra-metric set round followed by an inter-metric set round. During the intra-metric set round, the tests were applied to eight classifiers for each metric set (M4, M7 and M11) separately to determine the best performing classifier that was either ranked first or statistically tied for first across the F-measure assessments for the Pass and Fail classes. Next, in the inter-metric set round, the best-performing classifiers for each metric set were statistically compared with each other using the same procedure.

2.7. Development and evaluation of the global peak quality classifier

The above quality metric and classification framework was first applied to the full set of 500 peaks in the development and test datasets (Table 1). Specifically, this assessment yielded the best-performing combination of metric set and classification algorithm that was then used to train the global peak quality classifier on the entire development set. The performance of this classifier was then assessed on the four independent test sets listed in Table 1, one generated on the same LC–MS platform, and the other three with various differences from the development dataset. The same evaluation measures as used in the above CV-based framework were used to assess the performance of the global classifier on each of these test sets.

As another test, we assessed how much of the classifier’s performance could be attributed to random chance. For this, we generated random counterparts of the final classifier by randomly permuting the labels of the development dataset 100 times and training the best-performing classification approach on each of these randomized datasets. These counterparts were then evaluated on the four test sets in the same way as the real classifier, and the random performance measures calculated as the average of performance measure values of all the counterparts.

2.8. RSD filtering on pooled QCs and peak quality classification

For each dataset, RSD was calculated on the QC samples for all peaks in the XCMS-generated peak table. Using RSD < 30% as the threshold to identify reproducible peaks (Dunn et al. 2011; Want et al. 2010), we generated alternative high- (Pass) and low- (Fail) quality classifications for the 500 labeled peaks as in each dataset. We then assessed these classifications in terms of the evaluation measures mentioned in Sect. 2.5, and the performance of this RSD filtering method compared with that of the global classifier developed above.

The initial set of 500 peaks for each dataset was then subset to retain only those peaks with RSD < 30%. The numbers of peaks, as well as their distribution into the Pass and Fail classes, remaining in each of our study’s datasets after filtering are shown in Table 1. To assess if, and by how much, our approach can further improve peak quality classification after this filtering, we re-executed the entire MetaClean framework on these remaining subsets of peaks. Specifically, we developed an RSD-augmenting peak quality classifier from the 399 peaks in the development set, and evaluated it in the four test sets (417, 75, 172, and 169 peaks, respectively). All the steps in this process were carried out in exactly the same way as for the global classifier.

3. Results

3.1. Performance of candidate global peak quality classifiers assessed using the cross-validation framework

We first assessed the performance of the 24 classifiers, i.e., combinations of three metric sets and eight classification algorithms, obtained through the CV procedure applied to the full set of peaks in the development set. Specifically, the performance of the eight classifiers tested for each pair of metric sets was compared (scatter plots in Supplementary Fig. 3), and Wilcoxon Rank Sum test p-values calculated to determine the statistical significance of the difference in performance between each pair of compared metric sets. In general, we observed only moderately significant differences. Thus, the candidate classifiers developed from all the metric sets were used to identify the final peak quality classifier.

3.2. Determination of the global peak quality classification algorithm and metric set

As described, we identified the global peak quality classifier through two rounds of statistical comparison of candidate classifier performance, namely an intra-metric set round, followed by an inter-metric set one. In the first round, we compared the classifiers developed using each metric using Friedman’s and Nemenyi’s tests. As can be seen from the results in Supplementary Fig. 2A, across all metric sets and evaluation measures, several classifiers performed statistically equivalently, i.e., connected by horizontal lines in the corresponding CD plots. Therefore, we selected the classifier with the lowest average rank, i.e., the one represented by the leftmost vertical line in the CD plot, as the best performing candidate global classifier for each metric set. These classifiers were based on the AdaBoost, Random Forest and AdaBoost algorithms for M4, M7 and M11, respectively. This result is particularly interesting because both AdaBoost and Random Forest are ensemble classification algorithms that have shown superior performance in several biomedical applications (Whalen et al. 2016; Yang et al. 2010).

Next, in the inter-metric set round, we performed the same Friedman’s and Nemenyi’s test-based statistical comparison of these selected candidate classifiers. The results, shown again as CD plots in Supplementary Fig. 2B, show that AdaBoost with the M11 metric set model performed significantly better than the other candidate classifiers in terms of F-measure for both the Pass (Friedman-Nemenyi p = 0.001 and 0.005) and Fail (Friedman-Nemenyi p = 0.0023 and 0.0023) classes. Thus, the combination of the AdaBoost algorithm and the M11 metric set was selected to build the global peak quality classifier.

3.3. Performance of the global peak quality classifier in independent test sets

Finally, we assessed the performance of the global classifier in four independent test sets: one generated from the same platform as the development set (Test 1) and the other three from a different platform (Test 2, Test 3 and Test 4; see Table 1). These results are shown in red bars in Fig. 4. Notably, the classifier performed well on Test 1 in terms of Accuracy and Pass and Fail F-measures indicating that the classifier works very well on independent data from the same analytical platform that the development set was derived from (Agilent 6530, Reversed Phase Positive). To further validate this observation, MetaClean was reapplied to MTBLS306, which was split to create two of the test sets in each ionization mode (Table 1). These datasets were therefore from the same analytical platform. In this evaluation, Positive Mode data were first used as the development set and the Negative Mode data used as an independent test set and vice-versa. As we observed with Development and Test 1, these test sets also yielded results that compared well with those from their corresponding development sets (see Supplementary Fig. 4).

Fig. 4.

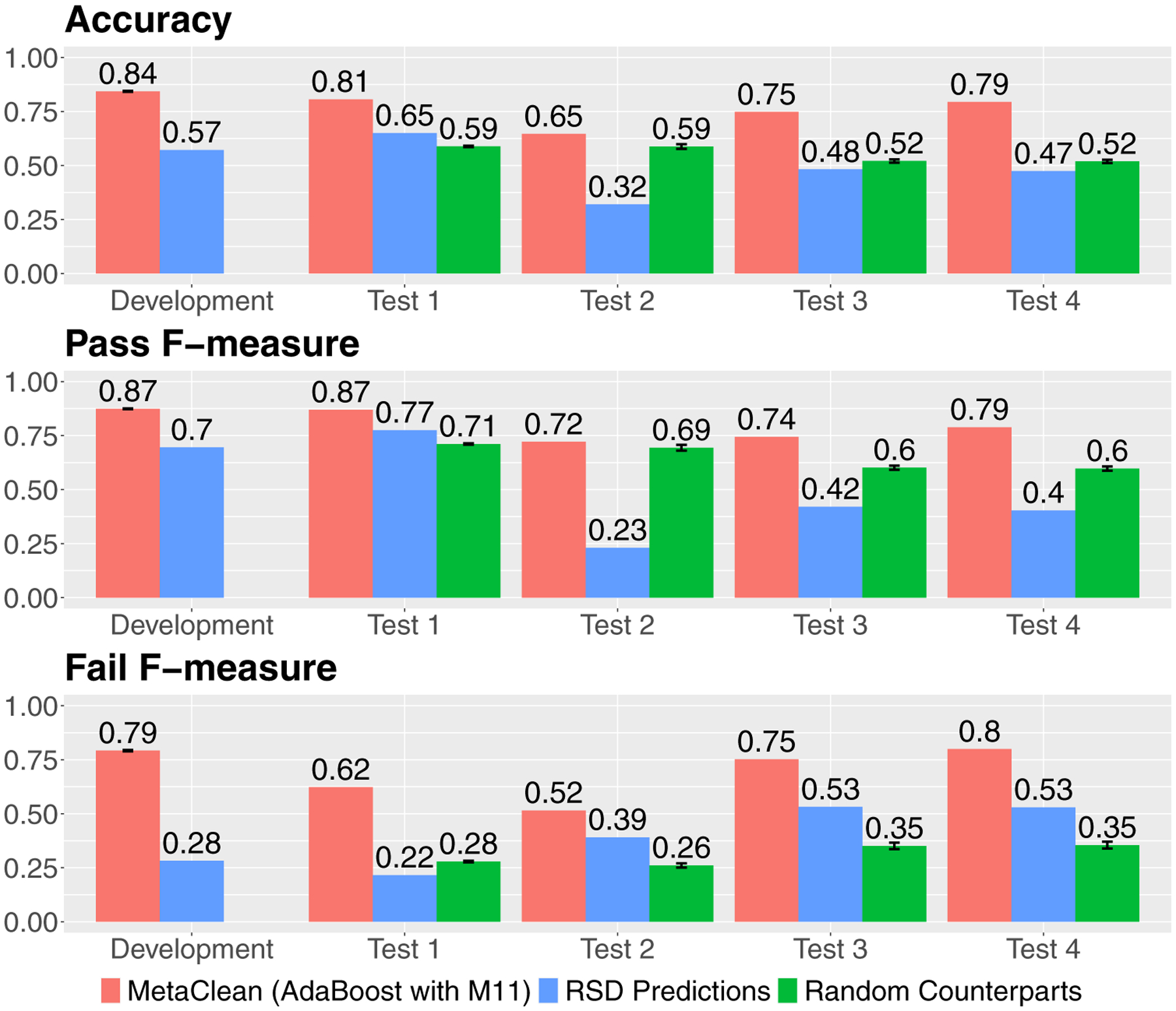
The performance of the global peak quality classifier on the development set and four independent test sets (Test 1–4), in terms of accuracy, and F-measures for the Pass and Fail classes. Shown here are the performances of the global AdaBoost with M11 classifier (red bars), pooled QC filtering by RSD < 30% (blue bars), and the random counterparts of the global classifier (green bars). These results show that the performance of the global classifier generalized very well to data generated from the same platform (Test 1), and reasonably well to data from other platforms (Test 2–4). The classifier also performed consistently better than filtering by RSD < 30%. In addition, across all these comparisons, the real global classifier performed much better than its random counterparts, indicating that the observed results weren’t due to random chance

In contrast, the global classifier performed slightly worse on datasets Test 3 and 4, and only moderately well on Test 2, which was expected due to the different analytical platforms these datasets were generated from. However, the evaluation measures were still high, e.g., accuracy of 0.65 to 0.79, indicating that the classifier generalized reasonably well across platforms.

We further compared the performance of our global classifier on each test set to those of its random counterparts (green bars in Fig. 4). Indeed, the real classifier performed consistently better than its random counterparts, demonstrating that the classifier captured a real relationship between the labels and peak quality metrics, and its results were not due to random chance.

3.4. Performance of MetaClean peak in comparison to and conjunction with RSD filtering

We also compared the performance of the MetaClean global classifier to the alternative approach of filtering peaks by RSD. We found that the latter performed worse than the former on all the test sets (Fig. 4, blue bars). This was consistent with the observation that several peaks that passed RSD filtering in the various datasets were labeled as Fail in terms of integration quality (Table 1), highlighting the complementary nature of the two approaches. Specifically, while RSD filtering focuses on removing random analytical error, MetaClean focuses on removing integration error to capture the most accurate correlate of analyte concentration.

Given this complementarity, we assessed the ability of MetaClean to complement RSD filtering using revised versions of our study datasets consisting only of labeled peaks with RSD < 30% (Table 1). Again, the best performing classifier for the 399 peaks with RSD < 30% was found to be AdaBoost with M11 in the development set (see Supplementary Figs. 5 and 6 for CD plots and scatter plots, respectively). The performance of the resultant RSD-augmenting classifier on Tests 1–4 was consistent with the performance of the global classifier prior to RSD filtering (see Supplementary Fig. 7), with high Accuracy and Pass and Fail F-measures for Tests 1, 3, and 4, and moderate performance in Test 2. This indicated that MetaClean is expected to be useful in combination with other pre-processing or filtering approaches as well.

4. Discussion

There are currently no tools for the automatic detection and removal of low-quality integrations from untargeted LC–MS metabolomics data. As such, studies utilizing metabolomics data risk reporting unreliable results, or must otherwise go through a process of reiterated statistical analysis and manual evaluation of peaks. In this study, we sought to build such a tool using a variety of machine learning techniques and peak quality metrics to automatically and accurately classify low-quality peaks in untargeted metabolomics data.

We ultimately built this global peak quality classifier using 11 previously published quality metrics (Zhang et al. 2014; Eshghi et al. 2018) and the AdaBoost algorithm (Alpaydin 2014). This classifier performed well on an independent test set generated on the same experimental platform as the development dataset (Accuracy = 0.81, F-measures for high- and low-quality peak classes = 0.87 and 0.62, respectively). It also performed reasonably well on independent test sets generated using different analytical platforms (Accuracy = 0.65, 0.75, and 0.79, F-measures for high-quality peak class = 0.72. 0.74, and 0.79, and F-measures for low-quality peak class = 0.52, 0.75, and 0.78, for Tests 2, 3, and 4 respectively).

MetaClean also performed better than pooled QC filtering at classifying single peak integration quality (Fig. 4), and can be integrated into metabolomics workflows in conjunction with QC filtering (Supplementary Fig. 7) to produce robust data for downstream analysis. Even with small sample sizes following filtering (Table 1), MetaClean performed well across all test datasets. The results of our study, as well as its companion MetaClean R package, provide an effective method for automatically and objectively flagging peaks with poor integration quality in untargeted metabolomics data.

Despite its good performance, our global classifier had some limitations. First, it was conservative and performed worse for the low-quality class (Fail) than the high-quality one (Pass) for Test 1 and 2, which can be partly attributed to the smaller number of peaks of the former class in the classifier development sets (Table 1). The overall decrement in performance of Test 2 may have been further influenced by its peaks’ characteristics. For example, many of the misclassified low-quality peaks in this dataset were low abundance, making them difficult to distinguish from background noise using an automated classifier that has not explicitly been trained on such cases; our development dataset indeed did not contain many examples of such low-abundance Pass peaks. Furthermore, Test 2 had a smaller number of peaks that passed the RSD < 30% filtering threshold and a smaller IPO peak width parameter (Supplementary Table 1), suggesting that this dataset may have been comparatively more dissimilar from the other datasets used in this study. Finally, since MetaClean requires an XCMS object input, it is not amenable in its current form to uniquely formatted vendor-processed outputs.

In summary, we showed that our peak quality classification methodology represents an effective way to post-process the results of peak-picking algorithms like XCMS to improve the quality of untargeted metabolomics data and the downstream analyses conducted on them. As expected, the characteristics of an LC–MS run, such as the ionization mode, analytical platform and method, and biological matrix will affect peak shape and size, and ultimately the quality of integrations. Therefore, these should be considered when applying the methodology or package to the target data set. In addition, studies with particular interests, such as environmental exposures or biological intermediates that may be low abundance compounds or with particular peak shapes, should include a sufficient number of relevant examples when retraining a peak quality classifier for such datasets.

Such a classifier can be integrated into a standard automated untargeted metabolomics pre-processing workflow, facilitated by our MetaClean package. If warranted by the study design, an additional layer of automated filtering using traditional approaches, such as RSD filtering, can also be implemented. While it is still recommended to manually assess shape and integrations of the predicted high-quality peaks, the use of our methodology/package facilitates an automated workflow for reduced spurious findings in untargeted LC–MS metabolomics data.