Multi-trait transcriptome-wide association studies with probabilistic Mendelian randomization

Summary

A transcriptome-wide association study (TWAS) integrates data from genome-wide association studies and gene expression mapping studies for investigating the gene regulatory mechanisms underlying diseases. Existing TWAS methods are primarily univariate in nature, focusing on analyzing one outcome trait at a time. However, many complex traits are correlated with each other and share a common genetic basis. Consequently, analyzing multiple traits jointly through multivariate analysis can potentially improve the power of TWASs. Here, we develop a method, moPMR-Egger (multiple outcome probabilistic Mendelian randomization with Egger assumption), for analyzing multiple outcome traits in TWAS applications. moPMR-Egger examines one gene at a time, relies on its cis-SNPs that are in potential linkage disequilibrium with each other to serve as instrumental variables, and tests its causal effects on multiple traits jointly. A key feature of moPMR-Egger is its ability to test and control for potential horizontal pleiotropic effects from instruments, thus maximizing power while minimizing false associations for TWASs. In simulations, moPMR-Egger provides calibrated type I error control for both causal effects testing and horizontal pleiotropic effects testing and is more powerful than existing univariate TWAS approaches in detecting causal associations. We apply moPMR-Egger to analyze 11 traits from 5 trait categories in the UK Biobank. In the analysis, moPMR-Egger identified 13.15% more gene associations than univariate approaches across trait categories and revealed distinct regulatory mechanisms underlying systolic and diastolic blood pressures.

Introduction

Transcriptome-wide association studies (TWASs) are widely applied to integrate genome-wide association studies (GWASs) with gene expression mapping studies for investigating the causal molecular mechanisms underlying diseases and disease-related complex traits.^1,2 While TWASs were originally proposed either as a weighted SNP set test² or a test for various relationships among SNPs, gene expression, and an outcome trait,¹ TWASs are closely related to Mendelian randomization (MR) analysis per its detailed algorithmic formulation, with one of the outcomes effectively testing the causal effect of a gene on the GWAS trait by treating the cis-SNPs of the gene as its instrumental variables.^3,4 Many statistical methods have been recently developed for TWASs and exemplary methods include PrediXcan,² TWAS,¹ DPR,⁵ TIGAR,⁶ SMR,⁷ PMR-Egger,⁴ FOCUS,⁸ and UTMOST,⁹ to name a few. Different TWAS methods differ in their ways of using cis-SNPs (i.e., some use one cis-SNP⁷ while others use all cis-SNPs), modeling SNP effects on gene expression (i.e., some make a sparse effect assumption⁷ while others make different polygenic modeling assumptions), fitting models (i.e., some use a likelihood-based algorithm⁴ while others use two-stage regression based algorithms), and accounting for horizontal pleiotropy (i.e., some account for it⁴ while others do not)—horizontal pleiotropy occurs when genetic variants affect the GWAS trait through pathways other than or in addition to the gene of focus and is particularly important to control for as it is widespread in TWAS applications.⁴

Despite the above technical differences, almost all existing TWAS methods are univariate in nature and analyze one GWAS trait at a time. However, GWASs often collect multiple correlated phenotypes¹⁰ that share a common genetic basis.¹¹ Indeed, many loci have been recently identified to have pleiotropic associations with multiple phenotypes. Exemplary pleiotropic gene associations include CACNA1C (MIM: 114205) for both bipolar disorder (MIM: 125480) and schizophrenia (MIM: 181500),¹² SLC39A8 (MIM: 608732) for schizophrenia and Parkinson disease (MIM: 168600),¹³ and RGS12 (MIM: 602512) for serum lipids and inflammatory bowel disease (MIM: 266600).¹⁴ Consequently, performing multivariate analysis to test gene associations with multiple traits jointly may lead to an appreciable power gain. The benefits of multivariate analysis over univariate analysis have been well documented in other analytic settings such as association tests in GWASs.15, 16, 17, 18 There, by modeling multiple traits together, multivariate analysis can increase power over univariate analysis in identifying pleiotropic loci that affect multiple traits simultaneously. In addition, by explicitly modeling phenotypic correlation, multivariate analysis can also increase power over univariate analysis to identify loci that affect only one trait, because of its ability to control for the other correlated traits. Therefore, it is appealing to develop statistical methods for analyzing multiple traits jointly for TWAS applications.

Here, we develop such a method to identify genes associated with multiple correlated traits in TWASs. Our method builds upon a previously developed likelihood inference framework for TWAS analysis⁴ and extends it to analyze multiple outcome traits. Our method explicitly accounts for the correlation structure among multiple traits, accommodates cis-SNPs that are in linkage disequilibrium (LD) with each other, relies on the widely used Egger assumption to model horizontal pleiotropic effects, and performs inference based on a maximum likelihood framework. We refer to our method as the multiple outcome probabilistic Mendelian randomization with Egger assumption (moPMR-Egger). With simulations and real data applications, we show that moPMR-Egger provides calibrated type I error control for both causal effects testing and horizontal pleiotropic effects testing, yields substantial power gain over univariate approaches, and is computationally efficient for biobank scale datasets.

Material and Methods

moPMR-Egger Overview

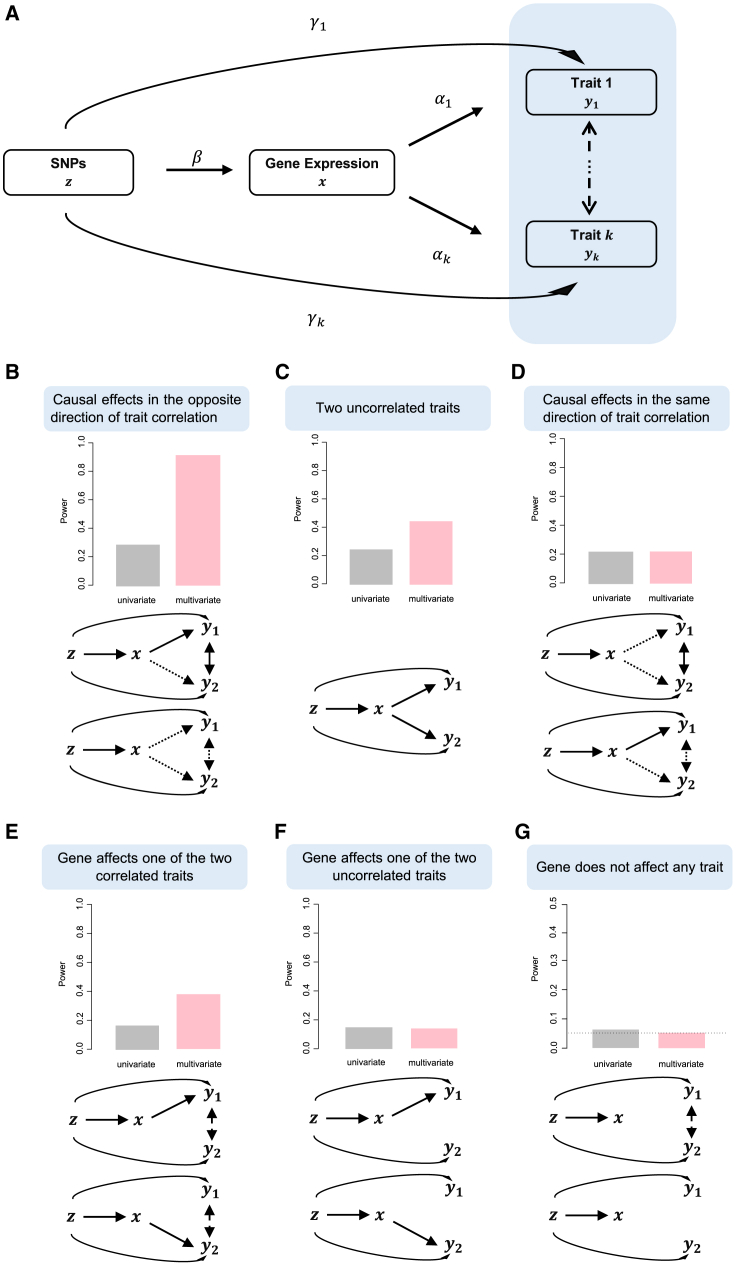
We provide an overview of moPMR-Egger here, with its details supplied in the Supplemental Material and Methods. moPMR-Egger is developed for identifying genes causally associated with multiple outcome traits in TWAS applications. moPMR-Egger builds upon the two-sample MR framework, which aims to estimate and test for the causal effect of an exposure on an outcome in the setting where the exposure and outcome are measured in two separate studies with no sample overlap. In the TWAS setting we consider here, the exposure is gene expression level that is measured in a gene expression study, while the outcomes are multiple correlated quantitative traits that are measured in a GWAS. In moPMR-Egger, we examine one gene at a time and treat its cis-SNPs as instrumental variables. With the instrumental variables, we estimate and test the causal effects of the gene on multiple outcome traits together. We do so by performing joint analysis of gene expression and multiple outcome traits in a likelihood framework while properly accounting for potential horizontal pleiotropic effects. An illustrative diagram of the moPMR-Egger model is displayed in Figure 1A.

Figure 1.

A method schematic for moPMR-Egger and illustration of its power as compared to the univariate counterpart in various scenarios

(A) moPMR-Egger applies to the TWAS setting and attempts to estimate the causal effects (α₁,…, α_k) of gene expression (x) on multiple traits of interest (y₁,…,y_k) in the presence of confounding factors (U, not shown) by using cis-SNPs (z) as instrumental variables. moPMR-Egger relies on a joint likelihood framework and effectively accounts for the horizontal pleiotropy (γ₁,…, γ_k) and the correlation among multiple traits.

(B–G) Multi-trait modeling with moPMR-Egger (pink) is beneficial under various scenarios as compared to univariate method PMR-Egger that analyzes one trait at a time (gray). Six scenarios are examined using simple illustrative simulations on two traits (y₁, y₂): gene affects two correlated traits, with its causal effects on the two traits in the opposite direction of trait correlation (B); gene affects two uncorrelated traits (C); gene affects two correlated traits, with its causal effects on the two traits in the same direction of trait correlation (D); gene affects one of the two correlated traits (E); gene affects one of the two uncorrelated traits (F); or gene does not affect any trait (G). In these scenarios, the gene has either non-zero causal effects on two traits (two arrows from gene to traits) or one trait (one arrow) or no trait (no arrow), with causal effects in the same direction (two dotted arrows) or in the opposite direction (one solid arrow and one dotted arrow) or in either directions (two solid arrows). The traits are positively correlated (solid double-head arrows) or negative correlated (dotted double-head arrows) or either (dashed double-head arrows) or uncorrelated (no double-head arrows). y axis shows power in (B)–(F) and type I error in (G). Type I error is calculated as the percentage of discoveries among 1 million null simulation replicates. Power is calculated as the percentage of discoveries among the 1,000 alternative simulation replicates. For power calculation, discoveries are declared based on a Bonferroni corrected p value threshold: 0.05/1,000 for the multivariate approach and 0.05/2,000 for the univariate approach that tested each of the two traits separately.

Technically, we follow existing TWAS approaches and use all cis-SNPs that are in LD with each other as instruments. We denote x as an n₁-vector of gene expression levels that are measured on n₁ individuals in the gene expression study and denote ${\mathit{Z}}_x$ as an n₁ by p matrix of genotypes for p instruments (i.e., cis-SNPs) in the same study. We denote $\mathit{Y}$ as a k by n₂ matrix of k outcome traits measured on n₂ individuals in the GWAS and denote ${\mathit{Z}}_Y$ as an n₂ by p matrix of genotypes for the same p instruments there. We assume x and each column of ${\mathit{Y}}^T$, ${\mathit{Z}}_x$, and ${\mathit{Z}}_Y$ have all been standardized to have a mean of zero and a standard derivation of one. We consider three linear regressions to model the two studies separately,

$$\mathbf{x}=1_{n_1}{\mu }_x+{\mathit{Z}}_x\mathbf{\beta }+{\mathbf{\epsilon }}_x,$$ (Equation 1)

$$\tilde{\mathbf{x}}=1_{n_2}{\mu }_x+{\mathit{Z}}_Y\mathbf{\beta }+{\mathbf{\epsilon }}_{\tilde{x}},$$ (Equation 2)

$$\mathit{Y}={\tilde{\mathbf{\mu }}}_Y{1}_{n_2}^T+\mathbf{\alpha }{\tilde{\mathbf{x}}}^T+\mathit{\Gamma }{\mathit{Z}}_Y^T+\tilde{\mathit{E}},$$ (Equation 3)

where Equation 1 is for the gene expression study and Equations 2 and 3 are for the GWAS. Above, both ${\mu }_x$ (a scalar) and ${\tilde{\mathbf{\mu }}}_Y$ (a k-vector) are intercepts; $\tilde{\mathbf{x}}$ is an unobserved n₂-vector of gene expression for GWAS individuals; $\mathbf{\beta }$ is a p-vector of SNP effect sizes on gene expression; $\mathbf{\alpha }$ is a k-vector and represents the k causal effects of gene expression on the k outcomes; $\mathit{\Gamma }$ is a k by p matrix of horizontal pleiotropic effects, representing the pleiotropic effects of p instruments on the k outcomes; ${\mathbf{\epsilon }}_x$ is an n₁-vector of residual error with each element independently and identically distributed from a normal distribution $\text{N}\left(0,{\sigma }_x^2\right)$; ${\mathbf{\epsilon }}_{\tilde{x}}$ is an n₂-vector of residual error with each element independently and identically distributed from the same normal distribution $\text{N}\left(0,{\sigma }_x^2\right)$; and $\tilde{\mathit{E}}$ is a k by n₂ matrix of residual error, with each column following a multivariate normal distribution $MV{N}_k\left(0,\mathrm{\Omega }\right)$, where Ω is a k by k covariance matrix that accounts for the correlation structure among k outcomes. Note that, while the above three equations are specified based on two separate studies, they are joined together with the common parameter $\mathbf{\beta }$ and the unobserved gene expression measurements $\tilde{\mathbf{x}}$. Equations 2 and 3 can also be combined into

$$\mathit{Y}={\mathbf{\mu }}_Y{1}_{n_2}^T+\mathbf{\alpha }{\left({\mathit{Z}}_Y\mathbf{\beta }\right)}^T+\mathit{\Gamma }{\mathit{Z}}_Y^T+\mathit{E},$$ (Equation 4)

where $\mathit{E}=\mathbf{\alpha }{\mathbf{\epsilon }}_{\tilde{x}}^T+\tilde{\mathit{E}}$ and ${\mathbf{\mu }}_Y=\mathbf{\alpha }{\mu }_x+{\tilde{\mathbf{\mu }}}_Y.$ Importantly, we emphasize that the above Equations 1, 2, 3, and 4 define a data generative model, which determines how gene expression and outcome traits are generated based on cis-SNPs. In addition, the inclusion of the horizontal pleiotropic effects term $\mathit{\Gamma }{\mathit{Z}}_Y^T$ in Equations 3 and 4, when further paired with the equal horizontal pleiotropic effects assumption made on $\mathit{\Gamma }$ detailed below, effectively extends the commonly used MR-Egger modeling framework¹⁹ toward accommodating multiple correlated instruments and multiple outcome traits.

Because p is often larger than n₁, we will need to make additional modeling assumptions on $\mathbf{\beta }$ to make the model identifiable. In addition, we will need to make additional modeling assumptions on $\mathit{\Gamma }$; otherwise the two instrumental effect terms defined in Equation 4—the vertical pleiotropic effects $\mathbf{\alpha }{\left({\mathit{Z}}_Y\mathbf{\beta }\right)}^T$ and the horizontal pleiotropic effects $\mathit{\Gamma }{\mathit{Z}}_Y^T$—are also not identifiable from each other. Here, we follow the standard omnigenic modeling assumption and assume that all elements in $\mathbf{\beta }$ are non-zero and each follows a normal distribution $\text{N}\left(0,{\sigma }_{\beta }^2\right)$. In addition, we follow the PMR-Egger assumption⁴ and assume equal horizontal pleiotropic effects across SNPs for each trait i: ${\Gamma }_{ij}={\mathit{\gamma }}_i$ for $j=1,\cdots ,p$, with ${\mathit{\gamma }}_i$ being a scalar of horizontal pleiotropic effect. The assumption on equal horizontal pleiotropic effects across SNPs on a trait is widely applied in other TWAS⁸ and robust MR studies^19,20 and is equivalent to assuming $\mathit{\Gamma }=\mathit{\gamma }{1}_p^T$, with $1_p$ being a p-vector of ones and $\mathit{\gamma }={\left({\gamma }_1,\cdots ,{\gamma }_k\right)}^T$.

Our key parameters of interest in the above joint model are the causal effects $\mathbf{\alpha }$ of the gene on multiple outcome traits. The causal interpretation and identification of $\mathbf{\alpha }$ can be derived based on the decision-theoretic framework of causal inference21, 22, 23, 24 (details in Supplemental Material and Methods). Such causal interpretation of $\mathbf{\alpha }$ requires at least two assumptions of MR to hold: (1) instruments are associated with gene expression; (2) instruments are not associated with any other confounders that may be associated with both gene expression and each outcome. moPMR-Egger no longer requires the general exclusion restriction condition of traditional MR (i.e., instruments only influence each outcome through the path of gene expression), as we make an explicit modeling assumption on the horizontal pleiotropy effects $\mathit{\Gamma }$. However, our explicit modeling assumption on $\mathit{\Gamma }$ follows (3) the InSIDE assumption that the instrument-gene expression effects and instrument-outcome effects are independent of each other, which is sometimes referred to as the weak exclusion restriction condition.¹⁹ Consequently, the causal effect interpretation of $\mathbf{\alpha }$ depends on MR assumptions as well as the other explicit modeling assumptions. Many of these assumptions are not testable in practice as an exhaust list of confounding factors is often unknown. Therefore, while we follow standard MR analysis and use the term “causal effect” throughout the text, we only intend to use this term to emphasize that the $\mathbf{\alpha }$ estimates here are more likely to be closer to the causal estimates than the effect size estimates from a standard multivariate regression of Y on $\tilde{\mathbf{x}}$.

In the above model, we are interested in estimating the causal effects $\mathbf{\alpha }$ and testing the null hypothesis ${\text{H}}_0:\mathbf{\alpha }=\mathbf{0}$ in the presence of the horizontal pleiotropic effects $\mathbf{\gamma }$. Rejecting the null hypothesis of $\mathbf{\alpha }=\mathbf{0}$ would suggest that the gene of focus has non-zero causal effects on at least one trait. In addition, we are interested in estimating the horizontal pleiotropic effect size $\mathbf{\gamma }$ and testing the null hypothesis ${\text{H}}_0:\mathbf{\gamma }=\mathbf{0}$. Rejecting the null hypothesis of $\mathbf{\gamma }=\mathbf{0}$ would suggest that the cis-SNPs have non-zero horizontal pleiotropic effects on at least one trait. We accomplish both tasks under the maximum likelihood inference framework, in direct contrast to the standard MR-Egger inference framework¹⁹ and most previous TWAS approaches^1,2,5 that use two-stage regression-based algorithms. Compared to the two-stage regression-based algorithms, maximum likelihood-based inference can properly account for the uncertainty in parameter estimates in the first regression stage, thus potentially improving statistical power.⁴ To enable maximum likelihood-based inference, we develop a parameter expansion version of the expectation maximization (EM) algorithm by maximizing the joint likelihood defined based on Equations 1 and 4 (details in the Supplemental Material and Methods). The EM algorithm allows us to obtain the maximum likelihood of the joint model, together with maximum likelihood estimates for both $\mathbf{\alpha }$ and $\mathbf{\gamma }$. In addition to the joint model, we apply the EM algorithm to two reduced models, one without $\mathbf{\alpha }$ and the other without $\mathbf{\gamma }$, to obtain the corresponding maximum likelihoods there. Afterward, we perform likelihood ratio tests for either ${\text{H}}_0:\mathbf{\alpha }=\mathbf{0}$ or ${\text{H}}_0:\mathbf{\gamma }=\mathbf{0}$, by contrasting the maximum likelihood obtained from the joint model to that obtained from each of the two reduced models, respectively.

We refer to our model and algorithm together as the two-sample probabilistic Mendelian randomization with Egger regression for multiple outcomes (moPMR-Egger). The term “mo” is referred to the modeling of multiple outcomes of interest. The term “probabilistic” is referred to the data generative nature of our model and the maximum likelihood inference procedure as explained above. The term “Egger” is referred to the horizontal pleiotropic assumption made on $\mathit{\Gamma }$ that effectively generalizes the MR-Egger regression assumption to both correlated instruments and multiple outcomes.

Extensions to summary statistics

While we have presented moPMR-Egger based on individual-level data, moPMR-Egger can be easily extended to perform inference using summary statistics only. To do so, we denote ${\mathit{\Sigma }}_1$ as the SNP-SNP correlation matrix (i.e., LDmatrix) among cis-SNPs of the gene of focus in the gene expression study. We denote ${\mathit{\Sigma }}_2$ as the corresponding SNP correlation matrix in the GWAS data. Both matrices are of dimensionality p by p and are positive semi-definite. Note that both ${\mathit{\Sigma }}_1$ and ${\mathit{\Sigma }}_2$ can be estimated using individuals of corresponding ethnicity from an LD reference panel (e.g., the 1000 Genomes project). With the definition of ${\mathit{\Sigma }}_1$ and ${\mathit{\Sigma }}_2$, we can re-express the moPMR-Egger model in terms of summary statistics as

$${\hat{\mathbf{\beta }}}_x={\mathit{\Sigma }}_1\mathbf{\beta }+{\mathbf{e}}_x,$$ (Equation 5)

$${\hat{\mathit{B}}}_y=\mathbf{\alpha }{\left({\mathit{\Sigma }}_2\mathbf{\beta }\right)}^T+\mathit{\Gamma }{\mathit{\Sigma }}_2+{\mathit{E}}_y,$$ (Equation 6)

where ${\hat{\mathbf{\beta }}}_x$is a p-vector of estimates for the standardized marginal SNP effect sizes on the gene expression; ${\hat{\mathit{B}}}_y$ is a k by p matrix of estimates for the standardized marginal SNP effect sizes on the k outcomes; ${\mathbf{e}}_x$ is a p-vector of estimation errors that follow a multivariate normal distribution $N\left(0,{\mathit{\Sigma }}_1{\sigma }_x^2/\left(n_1-1\right)\right)$; and ${\mathit{E}}_y$is a k by p matrix of estimation errors that follow a matrix normal distribution $MN\left(0,\mathbf{\Omega },{\mathit{\Sigma }}_2/\left(n_2-1\right)\right)$ with $\mathbf{\Omega }$ being a k by k row covariance matrix and ${\mathit{\Sigma }}_2/\left(n_2-1\right)$ being a p by p column covariance matrix. Again, the matrix $\mathbf{\Omega }$ is used to model the covariance structure among multiple correlated outcome traits. We adapt our EM algorithm for individual-level data to perform estimation and inference using summary statistics (details in the Supplemental Material and Methods). The estimation and inference procedures are all based on the maximum likelihood framework and are largely similar to what has been described in the previous section.

Simulations

We performed cross-gene based simulations to assess the performance of moPMR-Egger and compare it with existing approaches. To do so, we randomly selected 10,000 genes from GEUVADIS.²⁵ We extracted cis-SNPs for these 10,000 genes, obtaining a median of 576 cis-SNPs per gene (min = 11; max = 7,409). For each gene in turn, we simulated the gene expression level and the outcome traits using the genotype data obtained from the gene expression study and the GWAS, respectively. Specifically, we first obtained genotypes for p cis-SNPs of the gene of focus from the GEUVADIS data. We standardized the genotype vector of each SNP to have a zero mean and a unit standard deviation. With the standardized genotype matrix ${\mathit{Z}}_x$, we simulated the SNP effect sizes $\mathbf{\beta }$ from a normal distribution $N\left(0,PV{E}_{\text{zx}}/p\right)$, where $PV{E}_{\text{zx}}$ represents the proportion of gene expression variance explained by genetic effects. We summed the genetic effects across all cis-SNPs as ${\mathit{Z}}_x\mathbf{\beta }$. In addition, we simulated the residual errors ${\mathbf{\epsilon }}_x$ from a normal distribution $N\left(0,1-PV{E}_{\text{zx}}\right)$. We finally summed the genetic effects and residual errors to yield the simulated gene expression level.

Next, we obtained genotypes ${\mathit{Z}}_Y$ for the same p SNPs from 2,000 randomly selected control individuals in the Kaiser Permanente/UCSF Genetic Epidemiology Research Study on Adult Health and Aging (GERA).^26,27 We standardized the genotype vector of each SNP to have a zero mean and a unit standard deviation. With the standardized genotype matrix ${\mathit{Z}}_Y$, we simulated the causal effects of the gene of focus on four outcome traits. Specifically, we used the same SNP effect sizes $\mathbf{\beta }$ in the gene expression data and set the four causal effects ${\left({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\right)}^T=\sqrt{{\mathbf{PVE}}_{\text{zy}}/PV{E}_{\text{zx}}}$. Here, PVE_zy is a vector of size four and each of its elements represents the proportion of phenotypic variance explained by the causal effect of SNPs for the corresponding phenotype. Afterward, we simulated the residual errors for the four phenotypes for each individual from a multivariate normal distribution $MVN\left(0,\mathbf{\Omega }\right)$, where we used the correlation matrix of four lipid traits (total cholesterol [TC], low-density lipoprotein [LDL], high-density lipoprotein [HDL], and triglyceride [TG]) calculated in the NFBC1966 database²⁸ to serve as $\mathbf{\Omega }$. Specifically, the correlations are 0.13 between TC and HDL, 0.88 between TC and LDL, 0.41 between TC and TG, 0.09 between HDL and LDL, −0.44 between HDL and TG, and 0.29 between LDL and TG (Table S1). We also simulated the horizontal pleiotropic effects $\mathbf{\gamma }$ of these SNPs on the four traits, with details described in the next paragraph. We finally summed the horizontal pleiotropic effects, vertical pleiotropic effects, and residual errors to yield the four simulated traits.

In the simulations, we first examined a baseline simulation setting where we set n₁ = 465, n₂ = 2,000, $PV{E}_{\text{zx}}=10\text{\%}$, and PVE_zy = (0,0,0,0)^T, with all ${\Gamma }_{kj}=0\left(k=1,\cdots ,4;j=1,\cdots ,p\right)$. On top of the baseline setting, we varied one parameter at a time to examine the influence of various parameters. For $PV{E}_{\text{zx}}$, we set it to be either 1%, 5%, or 10%; the last value is close to the median gene expression heritability estimates across genes.^29,30 For $\mathbf{\beta }$, we examined alternative SNP effect size distributions that deviate from the omnigenic assumption. Specifically, we considered sparse settings where we randomly selected either one SNP or three SNPs to have non-zero effects on gene expression, as well as polygenic settings where 1% or 10% of the SNPs were randomly selected to have non-zero effects. Again, these non-zero effects were simulated from a normal distribution to explain a fixed $PV{E}_{\text{zx}}$. For the horizontal pleiotropic effects $\mathit{\Gamma }$, for each trait in turn, the trait-specific horizontal pleiotropic effect size is randomly selected for each gene among five choices: 0, small (1 × 10⁻⁴), moderate (5 × 10⁻⁴, 1 × 10⁻³), or large (2 × 10⁻³), which corresponds approximately to the 0%, 50%, 70%, 90%, or 95% quantiles of horizontal pleiotropic effect estimates from real data,⁴ respectively. Note that the large horizontal pleiotropic effect of 2 × 10⁻³ is also large in our real data applications: across 11 analyzed traits, on average, only 5.27 genes among 13,513 genes have an absolute horizontal pleiotropic effect size greater than 2 × 10⁻³ (Figure S1). The same trait-specific horizontal pleiotropic effect is assigned to all SNPs with non-zero horizontal pleiotropic effects. The proportion of non-zero effect SNPs for each trait is further determined randomly with replacement from five choices (0%, 10%, 30%, 50%, or 100%) and thus may vary across genes and traits. In addition, we examined directional pleiotropy setting (the ratio of SNPs with negative versus positive horizontal pleiotropic effects is 0:10), approximately directional pleiotropy settings (1:9 or 3:7), and balanced pleiotropy setting (5:5). For $\mathbf{\Omega }$, in addition to using the estimated $\mathbf{\Omega }$ from the real data, we also examined settings where $\mathbf{\Omega }$ is an identity matrix and where $\mathbf{\Omega }$ has an exponential covariance structure with each element ${\text{Ω}}_{i,j}={\rho }^{|i-j|}$ with $\rho$ being either 0.5, 0.7, or 0.9. The trait correlation in the exponential covariance structure ranges from 0.125 to 0.9, closely resembling the estimates obtained from real data (Table S1). We also examined the setting where $\mathbf{\beta }$ are correlated. In this setting, we simulated the SNP effects on gene expression from a multivariate normal distribution with covariance matrix $w\mathit{\Sigma }$. Here, $\mathit{\Sigma }$ is the LD matrix among SNPs and $w$ is a scalar that is chosen to ensure that $PV{E}_{\text{zx}}$ equals to 10%. For PVE_zy, in addition to the baseline setting with zero causal effects, we also examined homogeneous causal effect settings and heterogeneous causal effect settings. In the homogeneous causal effect settings, we set all elements of PVE_zy to the same value $v$, with $v$ being either 0.5%/4, 1%/4, 1.5%/4, or 2%/4 in different settings. In the heterogeneous causal effect settings, we set the first element of PVE_zy as $v$ and the other elements of PVE_zy as 0.15$v$, 0.85$v$, and 0.50$v$, respectively, with $v$ being either 0.5%, 1%, 1.5%, or 2% in different settings. In terms of causal effect size direction, we randomly selected one, two, three, or four traits to be affected by gene expression both in the homogeneous and heterogeneous causal effect settings. When the gene expression affected two phenotypes, its effect on one of the two traits was in the opposite direction of its effect on the other. When the gene expression affected three phenotypes, its effects on two randomly selected traits were in the opposite direction of its effect on the third trait. When the gene expression affected four phenotypes, its effects on two or three randomly selected traits were in the opposite direction of its effects on the other two or one trait.

For type I error control examination, we performed 10,000 simulation replicates for each simulation scenario described above. For power calculation, we examined two different approaches depending on the methods we compare to (more details in the next section). In the first approach, we performed 1,000 alternative simulations and compared power based on a Bonferroni corrected p value threshold (0.05/1,000 for the multivariate approach and 0.05/4,000 for the univariate approaches that tested each of the four traits separately). In the second approach, we performed 100 alternative simulations together with 900 null simulations for each simulation scenario and calculated power based on a false discovery rate (FDR) of 0.05. While we mainly focus on using individual-level data for simulations, we also validate the implementation of the summary statistics based moPMR-Egger in a subset of simulations (details in Discussion).

Besides the above comprehensive simulations, we also conducted a set of simple simulations on two traits to illustrate the benefits of multivariate modeling over univariate modeling. Here, we set n₁ = 465, n₂ = 2,000, $PV{E}_{\text{zx}}=10\text{\%}$, and $\mathit{\gamma }={\left(0.0001,0.0005\right)}^T$, and set the correlation between the two traits to be either 0.66 (correlated) or 0 (independent). The value 0.66 corresponds to the correlation estimate between systolic blood pressure (SBP) and diastolic blood pressure (DBP) in UK Biobank (Table S1). In the simulations, we examined three causal effect settings: a setting where the gene causally affects both traits with PVE_zy = (0.01,0.01)^T, with effect sizes either in the same direction or in the opposite direction; a setting where the gene causally affects one trait with PVE_zy = (0.01,0)^T; and a null setting where the gene affects neither traits causally with PVE_zy = (0,0)^T. In total, we examined six simulation scenarios that combine three causal effects settings and two trait correlation settings. We performed 1,000 simulation replicates for each alternative scenario for comparing power at the Bonferroni thresholds and performed 1 million simulation replicates for each null scenario for examining type I error control. We only compared moPMR-Egger with the univariate method PMR-Egger in these simple simulations for illustrative purposes.

Compared Methods

No other multivariate methods have been developed so far for analyzing multiple traits in TWAS applications. Therefore, we examined three univariate TWAS methods that include the following. (1) PMR-Egger, which tests and controls for horizontal pleiotropy using multiple correlated instruments, for which we used all cis-SNPs for the model and used PMR_individual function implemented in the R package PMR to test the causal effect and pleiotropic effect. (2) PrediXcan, which uses multiple correlated instruments but does not control for horizontal pleiotropy. For PrediXcan, we used all cis-SNPs for the model and used ElasticNet implemented in the R package glmnet to obtain the coefficient estimates for the cis-SNP effects on gene expression. (3) TWAS, which uses multiple correlated instruments but does not control for horizontal pleiotropy. For TWAS, we used all cis-SNPs for the model and used BSLMM³¹ implemented in the GEMMA³² software to obtain coefficient estimates for the cis-SNP effects on gene expression. All these methods are suitable for two-sample design and yield p values for testing the causal effects. These three methods differ in their prior assumptions on $\mathbf{\beta }$: PrediXcan relies on the ElasticNet assumption; TWAS relies on the BSLMM³¹ assumption; and PMR-Egger relies on the normal assumption. In addition, PrediXcan and TWAS rely on a two-stage regression procedure while PMR-Egger is based on maximum likelihood. In the analysis, we applied each univariate TWAS method to analyze one trait at a time. We then declared gene association significance based on a Bonferroni corrected p value threshold that adjusted for both the number of genes tested and the number of traits tested.

We also modified the above three univariate TWAS methods into ad hoc multivariate TWAS procedures for analyzing multiple outcome traits. Specifically, for each univariate method, we examined one gene at a time and obtained the minimal p value across multiple traits to serve as the association evidence for the gene of focus. Because the null distribution of minimum p values is not trivial to obtain, we compared the power of these minimal p value approaches based on FDR. Specifically, for simulations, we computed the power of different methods based on an FDR cutoff of 0.05. For real data applications, we first performed 10 random permutations on the individuals while maintaining the correlation among traits. We then applied each method on the permuted data to obtain the null distribution of minimum p values, with which we calculated empirical FDR and declared gene association significance based on an FDR cutoff of 0.05.

Besides the above methods, we also compared moPMR-Egger with TWMR³³ in simulations. TWMR is a two-stage based MR method that incorporates multiple genes as exposure variables. TWMR analyzes one outcome trait at a time and uses only independent SNPs to serve as instruments. Here, we considered both the standard univariate procedure of TWMR for analyzing one trait a time and the minimum p value procedure of TWMR similar to what is described above for multiple trait analysis. We examined the type I error control of TWMR in the baseline simulation settings, with parameters n₁ = 465, n₂ = 2,000, $PV{E}_{\text{zx}}=10\text{\%}$, PVE_zy = (0,0,0,0)^T, and $\mathit{\gamma }={\left(\mathrm{0,0,0,0}\right)}^T$ in the absence of horizontal pleiotropy or $\mathit{\gamma }={\left(1\times {10}^{-4},5\times {10}^{-4},1\times {10}^{-3},2\times {10}^{-3}\right)}^T$ in the presence of horizontal pleiotropy. We also assessed power of TWMR for testing causal effects in alternative simulation settings using the minimum p value approach of TWMR in the homogeneous causal effects settings where each element of PVE_zy is set to be 2%/4. In the TWMR analysis, we examined one gene at a time while controlling for its neighboring genes as covariates. To do so, following Porcu et al.,³³ for each gene in turn, we used PLINK software³⁴ (v.1.90b6.13) to perform linear regression analysis on its cis-SNPs and obtain cis-SNPs that are significantly associated with gene expression level at an FDR threshold of 0.05. We termed these significant cis-SNPs as cis-eQTLs. Next, we retained genes that have at least one cis-eQTL and retained SNPs that are cis-eQTLs for at least one of these genes for analysis. We further pruned these SNPs using PLINK (with $r^2<0.1$, which is the default setting recommended in TWMR) to retain an independent set of SNPs to serve as instruments. Due to these stringent filtering steps required by TWMR,³³ we were only able to analyze an average of 81.61% of genes in the simulations. TWMR results are described in the Discussion section.

Real data applications

We applied moPMR-Egger to perform multi-trait TWAS by integrating gene expression data from GEUVADIS²⁵ with GWASs from UK Biobank.³⁵ Specifically, we obtained the GEUVADIS data as the gene expression data and examined 11 traits from the UK Biobank. The traits were selected based on previous studies^36,37 and all traits have a SNP heritability greater than 0.2. These outcome traits can be roughly divided into the following five trait categories: (1) blood pressure (SBP and DBP), (2) physical measures including height (MIM: 606255), body mass index (BMI [MIM: 606641]), forced vital capacity (FVC), and FEV1-FVC ratio, (3) blood count (platelet count, red blood cell count, eosinophils count, and white blood cell count), (4) white blood cell indices (eosinophils count and white blood cell count), and (5) red blood cell indices (red blood cell count and red blood cell distribution width [RDW]). Note that the white blood cell indices category represents a subset of the blood count category. The correlations among all analyzed trait pairs within each category are listed in Table S1. For each of these five trait categories in turn, we applied moPMR-Egger and the univariate approach PMR-Egger to analyze the traits in the trait category. The detailed data processing steps for the GEUVADIS data and UK Biobank data are described below.

The GEUVADIS data²⁵ contains gene expression measurements for 465 individuals collected from five different populations that include CEPH (CEU), Finns (FIN), British (GBR), Toscani (TSI), and Yoruba (YRI). In the expression data, we only focused on protein coding genes and lincRNAs that are annotated in GENCODE (release 12).^38,39 Among these genes, we removed lowly expressed genes that have zero counts in at least half of the individuals to obtain a final set of 15,810 genes. We performed PEER normalization to remove confounding effects and unwanted variations following previous studies.^5,40 Afterward, following Zeng and Zhou,⁵ to remove the remaining population stratification, we quantile normalized the gene expression measurements across individuals in each population to a standard normal distribution, and then further quantile normalized the gene expression measurements to a standard normal distribution across individuals from all five populations. Besides the expression data, all individuals in GEUVADIS also have their genotypes sequenced in the 1000 Genomes Project. We obtained genotype data from the 1000 Genomes Project phase 3. We filtered out SNPs that have a Hardy-Weinberg equilibrium (HWE) p value < 10⁻⁴, a genotype call rate < 95%, or a minor allele frequency (MAF) < 0.01. We retained a total of 7,072,917 SNPs for analysis.

The UK Biobank data consists of 487,298 individuals and 92,693,895 imputed SNPs.³⁵ We followed the same sample QC procedure in Neale lab (Web Resources) to retain a total of 337,129 individuals of European ancestry. We filtered out SNPs with an HWE p value < 10⁻⁷, a genotype call rate < 95%, or an MAF < 0.001 to obtain a total of 13,876,958 SNPs. For each trait in turn, we regressed the resulting standardized phenotypes on sex and top ten genotype principal components (PCs) to obtain the residuals, standardized the residuals to have a mean of zero and a standard deviation of one, and finally used these scaled residuals to conduct TWAS analysis.

We integrated the GEUVADIS data with GWASs from UK Biobank for TWAS analysis. For each gene in turn in the GEUVADIS data, we extracted cis-SNPs that are within either 100 kb upstream of the transcription start site (TSS) or 100 kb downstream of the transcription end site (TES). We overlapped these SNPs in GEUVADIS with the SNPs obtained from UK Biobank to obtain common sets of SNPs. The mean number of the overlapped cis-SNPs between GEUVADIS and UK Biobank is 497 (median = 443, min = 1, max = 8,085). Afterward, for each pair of gene (from GEUVADIS) and trait category (from GWAS) in turn, we run the multivariate approach moPMR-Egger and the univariate approach PMR-Egger to examine the causal relationship between gene expression and multiple traits in the category. For comparison between moPMR-Egger and PMR-Egger, we declared significance based on the corresponding Bonferroni corrected thresholds: 0.05/15,810 for moPMR-Egger and 0.05/(15,810^∗k) for PMR-Egger, where k is the number of the outcome traits in the specific category.

Among the five trait categories, we focused on the blood pressure category further for an in-depth analysis. The blood pressure category contains two traits, SBP and DBP, with an estimated correlation of 0.66 between them. Blood pressure is a complex trait with heritability estimated in the range of 0.3–0.5.³⁶ Many large-scale GWASs have been conducted to investigate the genetic architecture underlying blood pressure.41, 42, 43, 44, 45 Elevated blood pressure is a strong and modifiable46, 47, 48, 49 driver for risk of stroke (MIM: 601367) and coronary artery disease (MIM: 608320), which are leading causes of mortality and morbidity globally.^50,51 For the blood pressure category, in addition to moPMR-Egger and PMR-Egger, we also applied the minimum p value approaches of PMR-Egger, TWAS and PrediXcan. For these minimum p value approaches, we applied each method to examine one gene at a time. For each gene in turn, we analyzed each trait in the trait category separately and obtained the minimum p value across these traits as the association evidence for the gene of focus. We performed 10 random permutations of individuals to obtain a null distribution of minimum p values, with which we calculated FDR. Note that the correlation between the two phenotypes remains after such permutation. In the moPMR-Egger analysis, we also divided the identified genes based on their effect sizes on the two traits into two gene groups: genes that have the same effect signs on both traits and genes that have opposite effect signs on both traits. We examined these two gene sets carefully by performing gene set enrichment analysis using the Gene Ontology (GO) and Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways with the clusterprofiler R package.⁵² We declared gene set significance based on a q-value threshold of 0.05.

For the in-depth analysis of the blood pressure category traits, we also considered two other TWAS methods: FOCUS⁸ and TWMR.³³ FOCUS is a TWAS fine mapping method and relies on a Bayesian framework to analyze genomic regions that contain at least one significant gene detected by any standard TWAS method. Therefore, we paired FOCUS with moPMR-Egger or each of the three univariate TWAS methods to analyze regions that contain at least one significant gene detected by the corresponding TWAS method. Following Mancuso et al.,⁸ we obtained a set of independent non-overlapping genomic regions termed as LD blocks from LDetect.⁵³ We removed genomic regions that overlap with the MHC region due to the extensive LD structure there. Also following Mancuso et al.,⁸ we conducted our analysis on a subset of regions that harbor at least one genome-wide-significant SNP (p < 5 × 10⁻⁸) and at least one significant TWAS gene identified by the corresponding TWAS method based on an FDR threshold of 0.05. Due to these stringent filtering steps required by FOCUS, we were able to analyze only 4,692 genes in 246 regions. We declared genes as significant if they are in the 90% credible set output from FOCUS. We then compared the performance of moPMR-Egger and each of the three univariate TWAS methods by examining how consistent the significant genes are before and after FOCUS analysis. For TWMR, we followed the same procedure described in the compared methods subsection to extract multiple independent cis-eQTLs to serve as instrument variables. We retained 398,996 cis-eQTLs and 5,573 genes for TWMR analysis. We analyzed the two blood pressure traits with the minimum p value approach of TWMR and declared gene significance based on a Bonferroni corrected threshold.

Results

Method overview

moPMR-Egger is described in the Material and Methods, with technical details provided in the Supplemental Material and Methods. For TWAS applications, moPMR-Egger examines one gene at a time and estimates and tests its causal effects on multiple outcome traits together. Different from many existing TWAS approaches, moPMR-Egger models multiple SNP instruments that are in LD with each other, performs TWAS in a maximum likelihood inference framework, is capable of testing and controlling for horizontal pleiotropic effects commonly encountered in TWAS, while jointly analyzing multiple outcome traits (Figure 1A). By modeling multiple correlated traits together, moPMR-Egger can improve the power of TWAS.

We first performed simple simulations to develop intuition and illustrate the benefits of modeling multiple traits together. Briefly, we relied on real genotype data and simulated gene expression along with two outcome traits (Material and Methods). We compared moPMR-Egger with its univariate counterpart PMR-Egger. In the simulations, we found that multi-trait modeling is particularly beneficial in the pleiotropic causal effects setting where the gene causally affects both traits, regardless whether the two traits are correlated (Figure 1B) or not (Figure 1C). The power gain brought by multi-trait modeling in the absence of trait correlation is presumably due to its ability to properly account for the correlation between test statistics on the two traits there—the univariate TWAS test statistics on the two traits remain correlated (correlation coefficient = 0.58) due to the shared underlying gene expression predictor, even though the two traits are not correlated with each other. The power gain brought by multi-trait modeling is especially apparent when the gene effects on the two traits are in the opposite direction as the trait correlation (Figure 1B), but becomes much less obvious when the gene effects on the two traits are in the same direction as the trait correlation (Figure 1D) where it becomes harder to disentangle the causal effects from the trait correlations.¹⁶ Multi-trait modeling is also beneficial in the case where the gene only affects one trait, as long as the two traits are correlated with each other (Figure 1E). Afterall, multivariate analysis can also improve power to detect genes associated with only one trait by effectively controlling for the other correlated traits and thus reducing error variance as previously shown in other settings.^15,16 Certainly, the power of multi-trait modeling is similar to or slightly lower than univariate trait modeling when the gene only affects one trait and when the two traits are also independent of each other (Figure 1F). The power gain brought by multivariate modeling across majority of simulation scenarios is accompanied with effective type I error control (Figure 1G).

Simulations: testing and estimating the causal effects

We performed comprehensive simulations to carefully examine the effectiveness of moPMR-Egger and compared it with existing TWAS approaches in realistic scenarios. Briefly, we relied on real genotype data and simulated gene expression along with four outcome traits (Material and Methods). We compared moPMR-Egger with three existing univariate TWAS methods that include PMR-Egger, PrediXcan, and TWAS. We examined type I error control and power of moPMR-Egger for both causal effects testing and horizontal pleiotropic effects testing across a total of 287 simulation scenarios (25 null and 152 alternative scenarios for causal effects testing; 22 null and 88 alternative scenarios for horizontal pleiotropic effects testing). These simulation scenarios are summarized in Table S2 and include both those simulated under the model and those simulated with various model misspecifications.

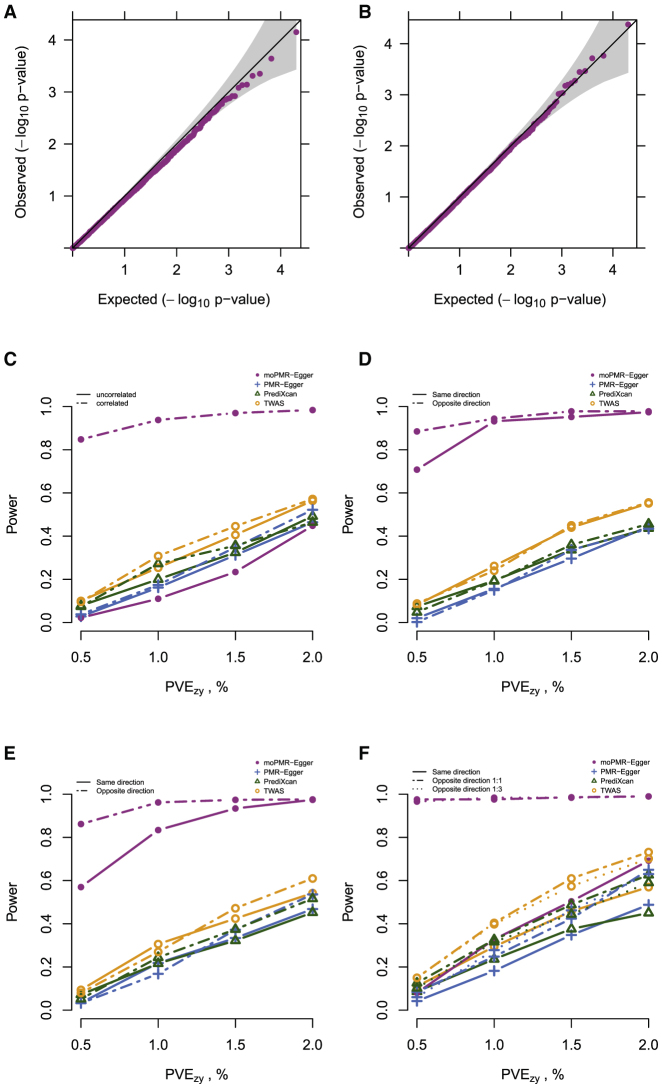
Our first set of simulations is focused on the causal effects test. We first examined type I error control of moPMR-Egger under the null, where the gene has no causal effects on any of the four traits. We found that moPMR-Egger provides well-calibrated type I error control both in the absence (Figure 2A) and presence (Figure 2B) of horizontal pleiotropic effects, regardless of the horizontal pleiotropic effect sizes. The null p value distribution from moPMR-Egger remains largely similar regardless whether the genetic architecture underlying gene expression is sparse or polygenic (Figure S2), regardless of the gene expression heritability (Figure S3), regardless whether the SNP effects on gene expression are simulated to be correlated with respect to LD or not (Figure S4), and regardless whether the multiple traits are correlated or not (Figure S5). Note that the p values of moPMR-Egger are slightly conservative when the gene expression heritability is low, likely due to the fact that the joint likelihood is no longer informative on the causal effects and thus cannot be approximated well by an asymptotic normal distribution (Figure S3).

Figure 2.

Type I error control and power for testing the causal effects under various simulation scenarios

(A and B) Quantile-quantile plot of −log10 p values for testing the causal effects either in the absence or in the presence of horizontal pleiotropic effects under null simulations. Null simulations are performed under different horizontal pleiotropic effect sizes: (A) $\mathbf{\gamma }={\left(\mathrm{0,0,0,0}\right)}^T$; (B) ${\gamma }_j$ randomly selected from (0, 1 × 10⁻⁴, 5 × 10⁻⁴, 1 × 10⁻³, 2 × 10⁻³), j = 1,2,3,4. p values from moPMR-Egger are on the expected diagonal line across a range of horizontal pleiotropic effect sizes.

(C–F) Power (y axis) at a Bonferroni adjusted threshold to detect the causal effects is plotted against different causal effect sizes characterized by PVE_zy for the first trait (x axis) in the heterogeneous causal effect settings, where the PVE_zy for the remaining traits are 15%, 85%, 50% of the PVE_zy for the first trait. Compared methods include moPMR-Egger (magenta), PMR-Egger (blue), PrediXcan (green), and TWAS (orange). Different line symbols represent whether the four traits are correlated or not in (C) and the direction of causal effects in (D)–(F). Simulations are performed under different number of affected traits being from one to four (C–F) in the absence of horizontal pleiotropic effect.

moPMR-Egger makes a relatively strong modeling assumption on the horizontal pleiotropy and assumes that for a given trait all SNPs have the same horizontal pleiotropic effects. Such horizontal pleiotropic modeling assumption follows that of the Egger regression. To examine the robustness of such assumption, we randomly selected a fixed proportion of SNPs, instead of all of them, to exhibit horizontal pleiotropic effects. We found that p values of moPMR-Egger remain calibrated regardless of the sparsity of the horizontal pleiotropic SNPs (Figure S6). Besides the directional pleiotropy settings where the ratio of SNPs with negative versus positive effects is set to be 0:10, we also examined two approximately directional pleiotropy settings (1:9 or 3:7) and one balanced setting (5:5) by randomly assigning the corresponding proportion of SNPs to have negative versus positive effects. We found that p values of moPMR-Egger remain calibrated in either the approximately directional pleiotropy settings or in the balanced setting when the horizontal pleiotropic effects for each trait is small or moderate (Figure S7A). However, when horizontal pleiotropic effect for one of the traits is large, as one might expect,⁴ moPMR-Egger p values become inflated (Figure S7B). Overall, the p values of moPMR-Egger for testing causal effects generally adhere to the diagonal line under the null with various moderate model misspecifications.

Next, we examined the power of moPMR-Egger and compared it with three univariate methods to identify non-zero causal effects. As expected, moPMR-Egger is more powerful than the univariate TWAS methods in most simulation scenarios. Specifically, across a total of 152 simulation scenarios, moPMR-Egger achieves an average of 53.12%, 42.40%, and 36.79% power gain as compared to PMR-Egger, PrediXcan, and TWAS, respectively. The power gain by moPMR-Egger remains substantial regardless whether the causal effects on different traits are homogeneous (Figures S8 and S9) or heterogeneous (Figures 2C–2F and S10), whether the gene affects one trait or multiple traits (Figure S11), how these traits are correlated with each other (Figure S12), and in the absence (Figures 2C–2F and S8) or presence of horizontal pleiotropic effects (Figures S9 and S10). The only exception is the simulation scenario where four traits are all independent of each other and where the gene is only associated with one of the four traits (Figures 2C and S8A–S10A). The lower power of moPMR-Egger in this scenario is presumably because moPMR-Egger uses extra parameters to model the non-zero causal effects on multiple correlated traits, thus suffering from a loss of degrees of freedom and subsequent loss of power there. However, even when the gene is associated with only one of the four traits, moPMR-Egger still has substantially more power than the other methods when traits are correlated with each other (Figures 2C, S8A, S9A, and S10A). Note that both moPMR-Egger and PMR-Egger control for horizontal pleiotropy while PrediXcan and TWAS do not. Consequently, in the presence of horizontal pleiotropy, the p values from PrediXcan and TWAS are known to be inflated and fail to control for type I error.⁴ As a result, PrediXcan and TWAS appear to have higher power than PMR-Egger if we treat all p values as calibrated and rely on a nominal p value threshold instead of the corrected type I error threshold. However, even in the presence of horizontal pleiotropy and inflated p values, the apparent power based on a nominal p value threshold for PrediXcan and TWAS is lower than that for moPMR-Egger, highlighting the importance of multi-trait modeling.

Power of different methods and the power gain brought by moPMR-Egger depend on several important parameters. First, the power of all methods reduces as the causal effects decrease, regardless whether the horizontal pleiotropy is absent or present. However, the power reduction of moPMR-Egger is the lowest among all methods, supporting its robust performance (Figure S11). Second, moPMR-Egger models multiple traits jointly and explicitly accounts for the trait correlations. Consequently, the power of moPMR-Egger increases as the correlation among the traits increases, while the power of the other methods does not change much (Figure S12). Third, as in illustrative simulations, the relative power gain brought up by modeling multiple traits depends on whether the causal effects on traits are in the same direction as the trait correlation or not. Specifically, when two traits are positively correlated with each other, then the power gain by moPMR-Egger is larger when the causal effect on one trait is in the opposite direction of that on the other as compared to being in the same direction, and vice versa (Figures 2D, S8B, S9B, and S10B). Finally, moPMR-Egger explicitly models the horizontal pleiotropic effects of SNPs on multiple traits separately. Consequently, moPMR-Egger remains powerful with an increased number of traits influenced by horizontal pleiotropy or with an increased horizontal pleiotropic effect size, whereas the other methods suffer (Figures S11C and S11D).

In the above simulations, we have primarily compared moPMR-Egger with the univariate approach of three existing TWAS methods. Here, we also compared moPMR-Egger with a minimum p value modification of these univariate methods for adapting them to analyze multiple traits together. Specially, we obtained the minimum p values across traits as the association evidence for the given gene and computed power of different methods based on an FDR of 0.05. Consistent with previous simulation results, the power improvement by moPMR-Egger over PMR-Egger, PrediXcan, and TWAS remains substantial regardless whether the causal effects on different traits are homogeneous (Figures S13A and S13C) or heterogeneous (Figures S13B and S13D) and whether there is an absence (Figures S13A and S13B) or presence (Figures S13C and S13D) of horizontal pleiotropy effects. Note that different from the above results under the Bonferroni adjusted threshold, both PrediXcan and TWAS display lower power in the presence of horizontal pleiotropy effect conditional on fixed FDR as one would expect (Figures S13C and S13D).

Finally, besides testing, moPMR-Egger produces accurate estimates of the causal effects, both under the null and under various alternatives, in the absence or presence of horizontal pleiotropic effects (Figure S14A).

Simulations: testing and estimating horizontal pleiotropic effects

Our second set of simulations is focused on horizontal pleiotropic effects testing. A benefit of moPMR-Egger, as compared to the usual TWAS/MR methods, is its ability to test whether SNPs exhibit non-zero horizontal pleiotropic effects on any outcome traits.

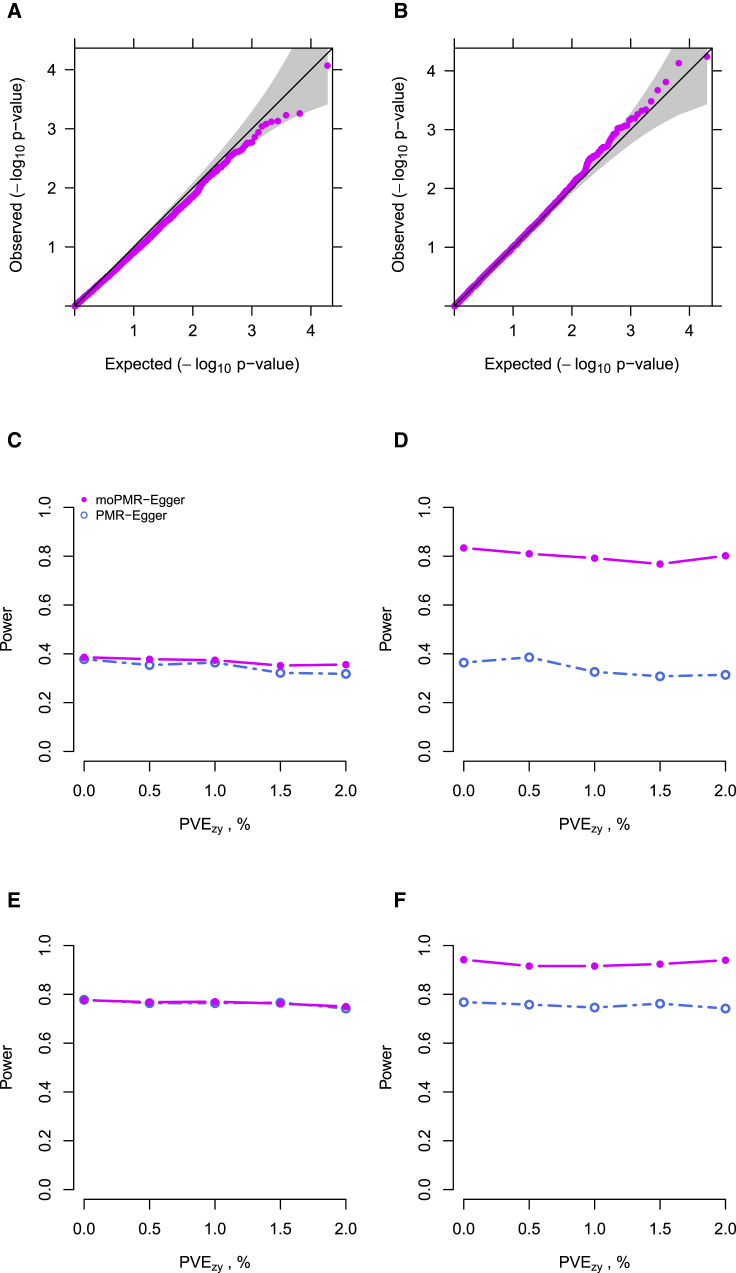
We first examined type I error control of moPMR-Egger on horizontal pleiotropic effects testing under the null, where no horizontal pleiotropic effect exists for any of the four traits. We found that the p values from moPMR-Egger on testing horizontal pleiotropy are well calibrated, either in the absence or presence of causal effects (Figures 3A and 3B), regardless of the correlation among multiple traits (Figure S15) and regardless whether the genetic architecture underlying gene expression is sparse or polygenic as long as causal effects are absent (Figure S16). The only setting where moPMR-Egger fails is when its modeling assumptions are violated in multiple ways. For example, when the genetic architecture underlying gene expression is sparse and when the gene affects more than two traits, then the p values of moPMR-Egger become inflated (Figures S16C and S16D). Overall, the p value of moPMR-Egger for testing horizontal pleiotropic effects under the null is well calibrated across the majority of scenarios.

Figure 3.

Type I error control and power for testing the horizontal pleiotropic effects under various simulation scenarios

(A and B) Quantile-quantile plot of −log10 p values from moPMR-Egger for testing the horizontal pleiotropic effects either in the absence or presence of causal effect under null simulations. Null simulations are performed under different causal effect sizes characterized by different PVE_zy: (A) $\mathbf{P}\mathbf{V}{\mathbf{E}}_{\text{zy}}={\left(\mathrm{0,0,0,0}\right)}^T$; (B) $\mathbf{P}\mathbf{V}{\mathbf{E}}_{\text{zy},j}$randomly selected from (0, 0.005, 0.01, 0.015, 0.02), j = 1,2,3,4. p values from moPMR-Egger are on the expected diagonal line across a range of causal effect sizes.

(C–F) Power (y axis) at a Bonferroni adjusted threshold to detect the pleiotropic effects is plotted against different causal effect sizes characterized by PVE_zy (x axis). Simulations are performed under either correlated traits (D and F) or independent traits (C and E), in the presence of horizontal pleiotropic effect with $\mathbf{\gamma }={\left(\mathrm{0,1}\times {10}^{-4},5\times {10}^{-4},1\times {10}^{-3}\right)}^T$ in (C) and (D) and $\mathbf{\gamma }={\left(1\times {10}^{-4},5\times {10}^{-4},1\times {10}^{-3},2\times {10}^{-3}\right)}^T$ in (E) and (F).

Next, we examined the power of moPMR-Egger in detecting non-zero horizontal pleiotropic effects. Here, we compared the performance of moPMR-Egger with PMR-Egger, which is the only existing method that can provide a calibrated test for horizontal pleiotropic effect.⁴ We first compared with the univariate approach of PMR-Egger. In the simulations, we found that the power of PMR-Egger and moPMR-Egger increases with increasing horizontal pleiotropy, with moPMR-Egger outperforming PMR-Egger across a range of settings (Figure 3C versus Figure 3E and Figure 3D versus Figure 3F). While moPMR-Egger has comparable power with PMR-Egger when all four traits are uncorrelated with each other (Figures 3C and 3E), moPMR-Egger outperforms PMR-Egger in the presence of trait correlation (Figures 3D and 3F). In addition, the power of both methods reduces with increasing sparsity of the horizontal pleiotropic effects, though moPMR-Egger remains more powerful than PMR-Egger across a range of sparsity levels either in the absence or presence of causal effects (Figure S17). Consistent with the simulations on causal effects testing, the power of both methods on pleiotropic effects testing suffers in the absence of directional pleiotropic effects (Figure S18). Besides the univariate approach of PMR-Egger, we also compared moPMR-Egger with the minimum p value approach of PMR-Egger and obtained consistent results (Figure S19).

Finally, moPMR-Egger can estimate the horizontal pleiotropic effects accurately in the presence of directional pleiotropic effects. However, in the absence of directional pleiotropic effects, as expected, the pleiotropic effect estimates become downward biased (Figure S14B).

Real data applications

We applied moPMR-Egger for TWAS analysis to integrate gene expression data from GEUVADIS with GWAS data on 11 traits from 5 trait categories in the UK Biobank (details in Material and Methods). The gene expression data from GEUVADIS study includes 15,810 genes. The five trait categories in UK Biobank include the blood pressure category, physical measures category, blood count category, white blood cell indices category, and red blood cell indices category. We examined one trait category at a time to identify genes associated with traits in the category.

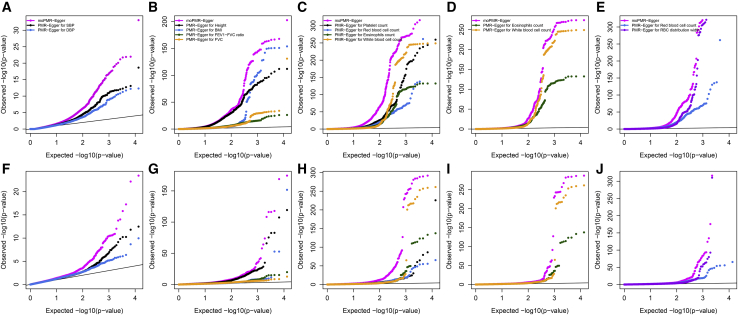
The p values for testing the causal effects of each gene on the traits from moPMR-Egger are displayed for each trait category, along with the p values from PMR-Egger for each trait in the category (Figures 4A–4E) as well as the corresponding minimum p values across traits in the category (Figure S20). We did not apply the univariate approaches of PrediXcan and TWAS as both do not control for horizontal pleiotropic effects that are prevalent in the data as demonstrated before.⁴ Indeed, both approaches produce inflated p values under the null simulations when the absolute horizontal pleiotropic effect exceeds 0.0001 (Figure S21), which happens on an average of 1,636.46 genes across 11 traits examined here (ranges from 1,320 for BMI to 2,632 for height; Figure S1). Therefore, instead, we compared the minimum p value approaches of these two methods in an in-depth analysis described in the next paragraph. Consistent with simulations, moPMR-Egger identified more genes than the univariate PMR-Egger at the corresponding Bonferroni corrected transcriptome-wide thresholds (Table S3). moPMR-Egger identified a total of 13.15% more genes as compared to PMR-Egger, highlighting the power of analyzing multiple traits jointly in TWAS. Majority of genes (89.29%) identified by PMR-Egger are also identified by moPMR-Egger but with increased association significance (Figure S22A). For example, TFRC (MIM: 190010) is identified to be associated with RDW (PMR-Egger p = 3.22 × 10⁻¹⁷), but with increased association evidence when all traits in the red blood cell indices category are modeled together (moPMR-Egger p = 5.72 × 10⁻²²). TFRC encodes the classical transferrin receptor that is involved in cellular iron uptake.⁵⁴ Multiple SNPs in TFRC have been established to be associated with various erythrocyte phenotypes in GWASs.⁵⁵ These associated erythrocyte phenotypes include the mean corpuscular hemoglobin (MCH) and mean corpuscular volume (MCV, the average volume of red blood cells) which is closely related to RDW.^54,55 The variants in TFRC likely lead to decreased iron availability for red cell precursors, as has been observed in mice deficient in Tfrc, thus resulting in a compensatory increase of red blood cell size as measured by RDW.⁵⁶ In addition, and perhaps more importantly, moPMR-Egger detected many likely causal genes that are missed by PMR-Egger. For example, EPHB4 (MIM: 600011) is identified by moPMR-Egger only in the blood pressure category (moPMR-Egger p = 1.41 × 10⁻⁸, PMR-Egger p = 0.98 for SBP and p = 5.33 × 10⁻⁴ for DBP). EPHB4 encodes the Ephrin type-B receptor 4 that binds to ephrin-B2 and plays an essential role in vascular development and angiogenesis.^57,58 Previous studies have demonstrated that deletion of Ephb4 in mice leads to hypotension,⁵⁹ supporting the causal role of EPHB4 in regulating blood pressure. We list the regional association plots for TFRC and EPHB4 in Figures S23–S25.

Figure 4.

TWAS analysis results for five trait categories in the UK Biobank using moPMR-Egger and PMR-Egger

Quantile-quantile plots of −log10 p values for testing the causal effects are shown for the blood pressure trait category (A), the physical measures trait category (B), the blood count trait category (C), the white blood cell indices trait category (D), and the red blood cell indices trait category (E). Quantile-quantile plot of −log10 p values for testing the horizontal pleiotropic effects are shown for the blood pressure trait category (F), the physical measures trait category (G), the blood count trait category (H), the white blood cell indices trait category (I), and the red blood cell indices trait category (J). Compared methods include the multi-trait method moPMR-Egger (magenta) and univariate method PMR-Egger (different colors for different traits). SBP, systolic blood pressure; DBP, diastolic blood pressure; BMI, body mass index; FVC, forced vital capacity; RBC, red blood cell count.

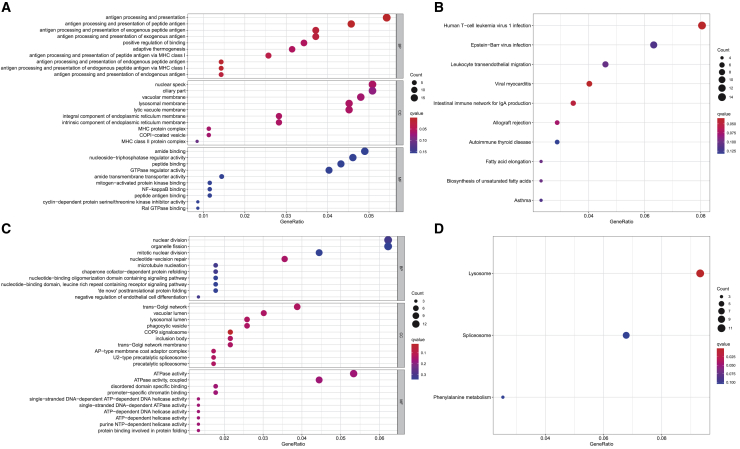
We performed an in-depth analysis on the blood pressure category, which contains only two traits (SBP and DBP) and is thus easy to explore in detail. Here, in addition to comparing with the univariate approach of PMR-Egger as described above, we compared moPMR-Egger with the minimum p value approaches of PMR-Egger, PrediXcan, and TWAS. We calculated the power of different methods based on an empirical FDR of either 0.01, 0.025, 0.05, 0.075, or 0.1 using permutations. Consistent with simulations, moPMR-Egger identified more genes than the other methods, highlighting the importance of multi-trait modeling (Figure S26). Specifically, the number of significant genes detected by moPMR-Egger, PMR-Egger, PrediXcan, and TWAS based on an empirical FDR of 0.05 are 765, 691, 90, and 83, respectively. The performance of moPMR-Egger is followed closely by PMR-Egger, supporting the previous observation that likelihood-based inference as used in these two methods is more powerful than the two-stage based inference used as in PrediXcan and TWAS.^4,60 Among the genes identified by moPMR-Egger, approximately 40% (301/765) of significant genes identified by moPMR-Egger have opposite causal effect directions on the two traits. GO and KEGG pathway enrichment analyses (Figure 5) show that genes with the same causal effect direction on the two traits are significantly enriched in the pathways of antigen processing and presentation (q = 1.96 × 10⁻⁴; Figure 5A), human T cell leukemia virus 1 infection (q = 0.03), viral myocarditis (q = 0.03), and intestinal immune network for IgA production (q = 0.04, Figure 5B). Such enrichment in inflammation and induced immune response pathways supports their recently revealed roles in regulating blood pressure.61, 62, 63 Indeed, inflammation activates innate and adaptive immune responses, resulting in alterations in the vasculature, kidneys, and sympathetic nervous system (SNS) that can eventually lead to chronically elevated blood pressures.⁶⁴ In contrast, genes with opposite causal effect directions on the two traits are significantly enriched in the pathways of COP9 signalosome (q = 0.02; Figure 5C) and lysosome (q = 5.14 × 10⁻⁴, Figure 5D). The enrichment in COP9 signalosome and lysosome pathways supports their critical functions in maintaining homeostasis and plasticity of vasculature and subsequent regulation of blood pressure. Indeed, both COP9 signalosome and lysosome control ubiquitination in the vasculature and the subsequent modulation of protein turnover.⁶⁵ Protein ubiquitination and turnover in the vasculature determine the vascular tone and stiffness, which can affect SBP and DBP differently during cardiac cycles of cell contraction and relaxation.⁶⁶

Figure 5.

GO function and KEGG pathway enrichment analysis on genes identified by moPMR-Egger and PMR-Egger in the blood pressure trait category

Dot plots show the top ten enriched GO BP, CC, and MF terms for identified genes that have the same causal effect direction on SBP and DBP (A) and that have the opposite causal effect directions on SBP and DBP (C). Dot plots show the top ten enriched KEGG pathway terms for genes that have the same causal effect direction on SBP and DBP (B) and that have the opposite causal effect directions on SBP and DBP (D). Dot color represents statistical significance of enrichment analysis based on q-value while dot size represents the fraction of genes annotated to each term. SBP, systolic blood pressure; DBP, diastolic blood pressure; GO, Gene Ontology; BP, biological process; CC, cellular component; MF, molecular function; KEGG, Kyoto Encyclopedia of Genes and Genomes.

Next, we shifted our focus to testing horizontal pleiotropic effects. The p values for testing the horizontal pleiotropic effects of each gene from moPMR-Egger and PMR-Egger are shown for the five trait categories (Figures 4F–4J). Consistent with simulations, moPMR-Egger detected a total of 17.10% more genes with horizontal pleiotropy than PMR-Egger (Table S3). Specifically, moPMR-Egger detected 56 genes in the blood pressure category, 275 in the physical measures category, 383 in the blood cell count category, 146 in the white blood cell indices category, and 153 in the red blood cell indices category, with gene overlaps showing in Figure S27. In contrast, PMR-Egger detected 26, 196, 266, 106, and 136, respectively. The majority of genes (71.53%) identified by PMR-Egger are also identified by moPMR-Egger (Figure S22B). Importantly, 36.16% of genes with significant horizontal pleiotropic effects identified by moPMR-Egger have significant causal effects, while 11.64% of genes with significant causal effects have horizontal pleiotropic effects. The noticeable overlap between genes with horizontal pleiotropic effects and genes with causal effects highlights the importance of modeling both effects in TWAS. In-depth analysis in the blood pressure category also revealed that genes with significant causal effects on DBP and SBP are enriched in pathways of antigen processing and presentation as well as protein refolding (Figures S28A and S28B), while genes with the significant horizontal pleiotropic effects are enriched in various metabolic processes and protein export (Figures S28C and S28D).

Finally, we note that moPMR-Egger is also computationally efficient, with similar computing time and physical memory requirement as existing TWAS methods (Table S4).

Discussion

We have presented moPMR-Egger, a method that extends the univariate PMR-Egger for analyzing multiple outcome traits in TWAS applications. moPMR-Egger accounts for the correlation structure among multiple traits, takes advantage of all cis-SNPs that are in LD with each other, tests and controls for horizontal pleiotropic effects, and performs inference under a likelihood framework. In both simulations and real data applications, moPMR-Egger yields calibrated p values across a wide range of scenarios and substantially improves power over existing univariate approaches.

One important modeling assumption we made in moPMR-Egger is that SNPs exhibit the same horizontal pleiotropic effect on the same trait. Such equal effect size assumption for each trait directly follows that of the Egger assumption^4,19,20 and is analogous to the burden effect size assumption commonly used for rare variant tests. Consistent with previous studies,^4,19,20 we found that the equal effect size assumption employed in moPMR-Egger appears to work reasonably robust for causal effect estimations and testing with respect to a range of model misspecifications and appears to be effective in the real data applications examined here. However, we do acknowledge that our equal effect size assumption in moPMR-Egger can be overly restrictive in many settings. Therefore, while we view moPMR-Egger as an important first step toward multi-trait TWAS applications, we emphasize that imposing more realistic modeling assumptions on the horizontal pleiotropic effects in the future will likely be beneficial.

We have primarily illustrated the benefits of moPMR-Egger for analyzing individual-level GWAS data. moPMR-Egger can be easily extended to take input in the form of summary statistics alone (details in Material and Methods). Specifically, the summary statistics version of moPMR-Egger requires standardized marginal SNP effect size estimates or marginal z-scores, both on the gene expression and on the multiple outcome traits of interest. Moreover, it requires an LD correlation matrix among cis-SNPs that can be constructed based on a reference panel. Note that when a reference panel is used to construct the LD correlation matrix, one needs to ensure that the ethnicity of the reference panel matches that of the study data to avoid potentially biased inference results.⁴ In addition, it requires an estimated correlation matrix among multiple traits. The trait correlation matrix can be easily estimated by using the marginal z-scores of genome-wide SNPs for each trait: because the correlation between two traits equals approximately to the correlation between the marginal z-scores for the two traits under the null where SNPs are not associated with any trait, we can select SNPs with a p value greater than a predefined significance threshold (e.g., 10⁻⁵) for any trait and use the correlation among these marginal z-scores as an estimate for the trait correlation.⁶⁷ We have validated the implementation of the summary statistics version of moPMR-Egger in the simulations and found that the results are largely consistent with that of moPMR-Egger fitted using individual level data (Figures S29, S30). Being capable of making use of summary statistics extends the applicability of moPMR-Egger to datasets where individual-level genotype or phenotype is not available.

We have mainly compared moPMR-Egger with three existing univariate TWAS methods that include PMR-Egger, PrediXcan, and TWAS. These three univariate TWAS methods and moPMR-Egger all examine one gene at a time. We note, however, that other univariate TWAS methods have been recently developed for modeling multiple genes jointly. For example, TWMR analyzes one gene at a time while controlling for its neighboring genes as covariates. In the null simulations, we found that the p values from the univariate approach of TWMR are overly conservative while the p values from the minimum p value approach of TWMR are inflated (Figure S31A), even in the absence of horizontal pleiotropy. The p values from both the univariate approach and the minimum p value approach of TWMR are overly inflated in the presence of horizontal pleiotropy (Figure S31B). In the alternative simulations, we found that TWMR is much less powerful than moPMR-Egger, resulting in an average of around 20-fold power loss across simulation scenarios: the power of TWMR is only around 0.08 in the absence of horizontal pleiotropy and only around 0.03 in the presence of horizontal pleiotropy. The low power of TWMR is likely due to the relatively small sample size in GEUVADIS as brought up by Porcu et al.³³ We also applied TWMR to analyze the two blood pressure traits. Due to the stringent filtering criteria recommend by Porcu et al.,³³ we analyzed a total of 5,573 genes. In the real data analysis, TWMR identified only 8 significant genes associated with at least one trait while moPMR-Egger identified 67 in the same analyzed gene set, supporting the low power of TWMR as observed in simulations. As another example, FOCUS⁸ is a TWAS fine mapping method that examines one genomic region at a time to identify the causal gene among a list of candidate ones in the region. FOCUS is commonly applied to only examine genomic regions that contain at least one significant gene detected by a standard TWAS method. Consequently, FOCUS can be effectively paired with any univariate TWAS method including moPMR-Egger as a pre-selection step. We followed Mancuso et al.⁸ to pair FOCUS with moPMR-Egger and each of the three univariate TWAS methods to analyze the two blood pressure traits. Due to the stringent filtering criteria recommend by Mancuso et al.,⁸ we analyzed a total of 246 genomic regions and 4,692 genes. In the analysis, we found that the significant genes identified by moPMR-Egger are largely consistent with those identified after FOCUS analysis, more so than the other methods (Figure S32), supporting the effectiveness of moPMR-Egger. Integrating multi-trait modeling with multi-gene modeling is an important future research direction.

Data and code availability

No data were generated in the present study. The GEUVADIS gene expression data are publicly available online. The GERA data is publicly available on dbGaP with accession number phs000788. The UK Biobank data is from UK Biobank resource under application number 30686.

The moPMR-Egger is implemented in the R package PMR, freely available on GitHub.

Declaration of Interests

The authors declare no competing interests.

Published: January 11, 2021

Web Resources

• dbGaP, https://www.ncbi.nlm.nih.gov/gap

• GEMMA, http://www.xzlab.org/software.html

• GEUVADIS, http://www.geuvadis.org

• moPMR-Egger, https://github.com/yuanzhongshang/PMR

• OMIM, https://www.omim.org/

• PLINK, https://www.cog-genomics.org/plink/

• Sample QC procedure in Neale lab, https://github.com/Nealelab/UK_Biobank_GWAS/tree/master/imputed-v2-gwas

• UK Biobank, https://www.ukbiobank.ac.uk/