Frustration and Direct-Coupling Analyses to Predict Formation and Function of Adeno-Associated Virus

Abstract

Adeno-associated virus (AAV) is a promising gene therapy vector because of its efficient gene delivery and relatively mild immunogenicity. To improve delivery target specificity, researchers use combinatorial and rational library design strategies to generate novel AAV capsid variants. These approaches frequently propose high proportions of nonforming or noninfective capsid protein sequences that reduce the effective depth of synthesized vector DNA libraries, thereby raising the discovery cost of novel vectors. We evaluated two computational techniques for their ability to estimate the impact of residue mutations on AAV capsid protein-protein interactions and thus predict changes in vector fitness, reasoning that these approaches might inform the design of functionally enriched AAV libraries and accelerate therapeutic candidate identification. The Frustratometer computes an energy function derived from the energy landscape theory of protein folding. Direct-coupling analysis (DCA) is a statistical framework that captures residue coevolution within proteins. We applied the Frustratometer to select candidate protein residues predicted to favor assembled or disassembled capsid states, then predicted mutation effects at these sites using the Frustratometer and DCA. Capsid mutants were experimentally assessed for changes in virus formation, stability, and transduction ability. The Frustratometer-based metric showed a counterintuitive correlation with viral stability, whereas a DCA-derived metric was highly correlated with virus transduction ability in the small population of residues studied. Our results suggest that coevolutionary models may be able to elucidate complex capsid residue-residue interaction networks essential for viral function, but further study is needed to understand the relationship between protein energy simulations and viral capsid metastability.

Significance

Adeno-associated virus is one of the most promising gene delivery vectors today and has been approved by the U.S. Food and Drug Administration for gene replacement therapies. Despite clinical advances, improvements to vector design are sorely needed to address many other unmet medical needs. Inspired by adjacent fields of research, in which models of protein fitness derived from molecular dynamics approaches and from sequence family modeling have been used to design protein variants, we explored the potential of these models for predicting virus formation and function. A reliable and predictive computational tool would be a tremendous addition to the vector development process, enabling the generation of functional adeno-associated virus variant panels at a faster pace and at lower cost.

Introduction

Adeno-associated virus (AAV) is widely favored as a gene therapy vector and, to date, has been tested in over 200 human clinical trials internationally. AAV was recently approved by the U.S. Food and Drug Administration as the first gene replacement therapy for an inherited genetic disorder, in part because of the vector’s nonpathogenicity and generally benign safety profile (1,2). AAV is an efficient delivery vector, capable of transducing both dividing and nondividing cells to produce sustained gene expression (3,4). However, further improvements to the vector are highly sought after to enhance delivery efficiency in targeted cell populations, which would minimize the vector doses required and reduce vector production costs as well as safety concerns because of dose-dependent immune responses to the vector (5, 6, 7, 8).

As a result of successful AAV biomining efforts (9, 10, 11), gene therapy developers have had access to hundreds of isolated AAV variants. Researchers have then employed a variety of design strategies to further engineer these AAV vectors for enhanced gene delivery. The three main approaches that have emerged are 1) rational design, 2) directed evolution, and 3) computationally driven design. Rational design approaches use current knowledge of vector biology to make targeted modifications to the capsid, whereas directed evolution conducts rounds of mutation and selection to explore the capsid functional space (12,13). Bioinformatics-driven strategies have recently emerged as a method, drawing upon large data sets of AAV capsid information and applying computational models to accelerate exploration of the viral fitness landscape (14). Initial studies in this space have yielded promising results, including AAV chimera populations designed using the SCHEMA algorithm to minimize structural disruption (15,16), mapping of AAV capsid amino acids important for structure and function using high-throughput studies (17,18), and the development of ancestral AAV vectors (19). Here, we explore data-driven computational approaches with varying degrees of complexity for predicting the fitness of capsid mutants, with the future goal of incorporating these in silico approaches into the AAV vector design pipeline.

The Frustratometer approach described in Ferreiro et al. (20), the first of the two computational approaches that we applied, is based on the energy landscape theory of protein folding (21). Naturally occurring proteins generally have a smooth, funnel-like energy landscape with minimal kinetic traps, promoting robust and rapid folding into a single native structure. The shape of the landscape arose and is maintained through evolutionary optimization by strengthening residue-residue contacts in the native structure and reducing the number of energetically favorable contacts outside of the native structure. The phenomenon of the evolutionary optimization of protein energy landscapes is known as the “principle of minimal frustration” (22,23). Residual localized frustration within protein structures may be retained during evolution to facilitate protein allostery and multimeric interactions (24). Previous studies have shown that the Frustratometer, which can be used to identify these localized patches of frustration, can provide insight into protein conformational changes and association. Frustration analysis of proteins that exhibit allostery indicates that known regions of conformational cracking are highly frustrated (23). The associative memory, water-mediated, structure and energy model (AWSEM), the optimized coarse-grained model that underlies the Frustratometer, has accurately predicted homodimer and heterodimer docking sites (25). Frustration analysis has also been applied fruitfully to the problem of mapping out structural reaction mechanisms (26). Here, we apply the Frustratometer to evaluate the change upon binding of the frustration level of residue-residue interactions that are formed during AAV capsid assembly.

Coevolutionary modeling, alternatively, seeks to identify residues with a structural or functional relationship in a protein or pair of proteins through analysis of the protein sequence family, which contains a record of the evolutionary constraints on protein function. Direct-coupling analysis (DCA) has emerged as a prominent statistical framework for identifying direct interactions of protein residues from genomic data (27,28). When applied to a family of protein sequences, this model can predict crucial pairs of interactions for protein structure and function and identify the effect of mutations by inferring the probability that a mutated sequence belongs to the family (29,30). DCA has accurately recapitulated known structural contacts in a variety of proteins and intermediate protein structures (27,28,31). DCA approaches were initially applied to the characterization of bacterial two-component system signaling networks and the design of libraries predicted to enhance signaling (32, 33, 34). More recently, DCA approaches have shown promise in identifying interacting residues in protein oligomers (35, 36, 37). Coevolutionary approaches previously applied to viruses have correctly identified interactions between viral proteins, but these models have not been evaluated for their ability to predict mutant AAV functionality (38, 39, 40). We aimed to evaluate DCA’s ability to capture patterns that identify functional members of the parvovirus family by predicting the formation and function of AAV mutants.

Here, we applied the Frustratometer to AAV2 monomer and assembled capsid structures to identify residues with large shifts in frustration index between these two states. We then mutated these residues to alanine and experimentally evaluated capsid assembly, thermal stability, and transduction efficiency. We compared these experimental results to predictions from the Frustratometer and DCA models. The frustration approach shows limited promise for predicting aspects of viral capsid structure and produced counterintuitive results with regards to stability. DCA supports the possibility of predicting capsid transduction ability in this small study.

Materials and Methods

Identifying residue contacts within and between AAV2 capsid subunits

The high-resolution crystal structure of AAV2 (Protein Data Bank, PDB: 1LP3) was visualized and analyzed in PyMol 2.2.0. Inter-residue contacts were identified as any pair of residues containing atoms within 4.5 Å of each other. Intrasubunit contacts were identified within an AAV2 subunit, and extrasubunit contacts were identified between AAV2 subunits.

Sequence conservation in the parvovirus sequence family

We used the hidden Markov model (HMM) from Pfam parvovirus coat protein VP2 family (PF00740) (Data S1) to search the UniProt database and obtained a multiple sequence alignment (MSA) with 8904 protein sequences (Data S2). Sequences with gaps greater than 50 amino acids were removed, leading to an MSA of 2569 sequences, and sequences with greater than 90% identity were reweighted as described previously (28), leaving 129.77 effective sequences. Conservation was then computed for all positions modeled in the Pfam HMM using Shannon entropy and reweighted from 0 to 1 so that a value of 1 indicates full conservation (41).

Frustratometer analysis of AAV capsid subunits

Using the crystal structure of AAV2, two types of constructs were created for analysis: a monomer form, consisting of a single AAV2 capsid subunit, and an assembly form, consisting of a central monomer and each monomer containing a residue with any atom within a radius of 4.5 Å around any of the central monomer residues. The AWSEM-MD Frustratometer Server with default parameters (sequence separation = 12 and no electrostatics) was used to calculate the single-residue frustration index (F) of the monomer and assembly structures (42). The Δ-frustration index was then calculated for each residue as F_assembly−F_monomer (20).

Computational alanine mutagenesis using AWSEM

To calculate the predicted change in energy between the monomer and multimer states for alanine mutants, we applied the AWSEM, a predictive protein coarse-grained model that combines terms from energy landscape theory and information from a database of known protein structures. The physical portion of the model focuses on hydrogen bonding, hydrophobic interactions, and water-mediated interactions between hydrophilic residues. Bioinformatic data are used to bias the structure of sequence fragments (nine residues or less) toward the structure of similar sequence fragments found in other proteins. The energy function of this model is described in Eq. 1 (43).

$$V_{AWSEM}=V_{backbone}+V_{contact}+V_{burial}+V_{helical}+V_{FM}$$ (1)

Then, the change in energy between alanine mutants and wild type (WT) was computed for monomer and multimer structures as described in Eq. 2.

$$\Delta E={V_{AWSEM}}_{Ala}-{V_{AWSEM}}_{WT}$$ (2)

The ΔΔE of alanine substitution was then computed as described in Eq. 3.

$$\Delta \Delta E=\Delta E_{Multimer}-\Delta E_{Monomer}$$ (3)

Alanine frequency in the parvovirus sequence family

The parvovirus sequence family was processed and reweighted as described for the sequence conservation calculation. The frequency of alanine at each position represented in the Pfam HMM was then calculated.

DCA of AAV2 capsid

DCA was applied to the preprocessed alignment of the parvovirus sequence family described in the sequence conservation calculation to infer a global statistical model of coevolved residue interactions. DCA infers a joint probability distribution to satisfy the statistical observations of protein family sequence, with parameters that include pairwise couplings e_ij(x_i, x_j) and local biases (fields) h_i(x_i) (28). Pairwise couplings may be restricted to occur within a certain spatial residue distance based on the structure of a given member of the sequence family (29). From this distribution, direct information values may be computed to quantify how two sites in the protein are directly coupled (28). The top 300 pairs by direct information score were plotted against measured residue-residue contacts from the AAV2 structure to assess this approach’s ability to identify residue interactions (although only 300 pairs were plotted, all contacts were considered in subsequent calculations). This joint probability distribution was also used to calculate the probability P_DCA(seq) that a given sequence is a member of the characterized sequence family, and this probability was converted into a unitless energy Hamiltonian H_DCA(seq) ∼logP_DCA(seq) (29,33,44). This Hamiltonian term was computed for AAV2 sequences with each residue position mutated to alanine. The Hamiltonian score of alanine mutants was compared to WT using the ΔH_DCA(Ala) metric described in Eq. 4.

$$\Delta H_{DCA\left(Ala\right)}={H_{DCA}}_{Ala}-{H_{DCA}}_{WT}$$ (4)

Site-directed mutagenesis of AAV2 cap gene

Site-directed mutagenesis of the AAV2 cap gene was performed to substitute selected residues with alanines. The pXX2 plasmid containing the wtAAV2 rep and cap genes was used as the template (45). Primers containing the desired alanine mutations were purchased from Integrated DNA Technologies. 18 cycles of PCR amplification were conducted according to the QuikChange protocol using Pfu Ultra polymerase (Agilent Technologies, Santa Clara, CA). After cycling was complete, template DNA was removed by digesting with DpnI (New England Biolabs, Ipswich, MA). Resulting plasmids were sequence verified through an external vendor (Genewiz, Morrisville, NC).

Virus production

Viruses containing the desired capsid mutations were prepared through a triple plasmid transfection of human embryonic kidney 293T (HEK293T) cells with the rep-cap encoding plasmid (pXX2 or pXX2-derived mutants), pSC-GFP (encodes a self-complementary GFP transgene flanked by inverted terminal repeats), and pXX6-80 (encodes adenoviral helper genes) using polyethylenimine. Cells were harvested 48 h post-transfection and lysed by three freeze-thaw cycles. 50 U/mL of benzonase (Sigma-Aldrich, St. Louis, MO) was added to the cell lysate to degrade free nucleic acids and the mixture was centrifuged to remove cell debris. The supernatant was then loaded into Quick-Seal Ultra Clear 25 × 89 mm centrifuge tubes (Beckman Coulter, Crea, CA) containing a 15–54% iodixanol step gradient. Tubes were sealed and spun in a Beckman Type 70Ti rotor at 48,000 rpm for 1 h 45 min at 18°C, and virus was extracted from the 40% iodixanol layer. For the differential scanning fluorescence assay, viruses were concentrated into gradient buffer (10 mM Tris (pH 7.6), 10 mM MgCl₂, 150 mM NaCl) using Amicon Ultra 100 kDa centrifugal filters (EMD Millipore, Burlington, MA).

Quantification of viral particles

Viral titers were quantified using quantitative polymerase chain reaction (qPCR). Briefly, viral capsids were denatured to release their genomes using incubation in 2 M NaOH at 56°C followed by neutralization with 2 M HCl. SYBR Green Power PCR Master Mix (Thermo Fisher Scientific, Waltham, MA) along with primers against the cytomegalovirus promoter (forward, 5′-TCACGGGGATTTCCAAGTCTC-3′ and reverse, 5′- AATGGGGCGGAGTTGTTACGA-3′) were used to detect viral genomes. Samples were analyzed on the Bio-Rad CFX96 qPCR machine (Hercules, CA) to obtain absolute titer values against a standard curve. Raw data are provided (Data S3).

Genome protection assay

Viruses were diluted 1:10 in endo buffer (1.5 mM MgCl₂, 0.5 mg/mL bovine serum albumin, 50 mM Tris (pH 8.0)) and incubated at the indicated temperature for 30 min. Samples were then split into 20 μL treatment fractions and treated with either 0.5 μL benzonase (1:10 dilution, 250 U/μL; Sigma-Aldrich), or sham buffer (50% glycerol, 50 mM Tris-HCl, 20 mM NaCl, 2 mM MgCl₂ (pH 8.0)). Samples were incubated at 37°C for 30 min, and then the benzonase was inactivated through the addition of 0.5 μL of 0.5 M EDTA. The number of viral genomes in benzonase and sham-treated fractions was then quantified using qPCR and genome protection calculated as the ratio of genomes in the benzonase-treated fraction to the sham-treated fraction. Raw data are provided (Data S3).

Differential scanning fluorescence assay

The differential scanning fluorescence assay was adapted from previous reports (46). Viruses were diluted to a concentration of 10¹² viral genomes/mL in gradient buffer (10 mM Tris (pH 7.6), 10 mM MgCl₂, 150 mM NaCl), and 45 μL virus sample was mixed with 5 μL 50× sypro orange (Thermo Fisher Scientific). Assays were conducted in a Bio-Rad CFX96 qPCR instrument using a melt curve protocol ramping from 25 to 95°C at a rate of 1° per min, with fluorescence reads every 0.2°. Lysozyme enzyme was analyzed as a control.

Quantification of virus transduction

HEK293T cells were seeded on 48-well tissue-culture-treated poly-L-lysine coated plates ∼24 h pre-transduction. At 95% confluency, cells were transduced with virus in media with serum at 1000 multiplicity of infection. 24 h after transduction, media was changed. 48 h after transduction, cells were harvested for flow cytometry analysis on a BD FacsCanto II (BD Biosciences, San Jose, CA). Virus transduction ability was quantified using the transduction index (TI), which is the product of the percentage of GFP+ cells and geometric mean fluorescence intensity. The transduction index is a linear indicator of viral transduction efficiency (47). Counts and gating thresholds are provided (Data S4).

Results and Discussion

Frustratometer analysis of AAV capsid

Frustration can be computationally quantified using the Frustratometer, which draws upon an optimized coarse-grained modeling that has been used to analyze protein energy landscapes (42). We applied the Frustratometer to AAV2 to predict residues that favor either the assembled capsid structure or the monomeric capsid protein. The AAV capsid consists of three capsid proteins, VP1, VP2, and VP3, that assemble in a 1:1:10 ratio to form a 60-mer capsid. Cryo-electron-microscopy-resolved structures of AAV2 do not include the unstructured VP1 and VP2 N-terminal domains, so this analysis focuses on the VP3 domain shared by all three VPs that forms the exterior capsid structure. Because it would be too computationally intensive to analyze the entire 60-mer capsid structure, we generated a multimer assembly substructure from the 60-mer capsid structure by selecting the seven VP3 subunits within 4.5 Å of a central monomer (Fig. S1). Then, mutational frustration was calculated for every residue-residue contact in the monomer and multimer structures (Fig. 1). Because the monomer structure is derived from cryo-electron microscopy conducted on the intact capsid, any differences in frustration index between the monomer and multimer are due to multimeric residue interactions and not structural changes in the monomer. The multimer structure contains more minimally frustrated residue pairs than the monomer, particularly at capsid subunit-subunit binding interfaces. This reduction in frustration is consistent with previously observed shifts in frustration at protein binding interfaces related to the burial of hydrophobic surfaces (20).

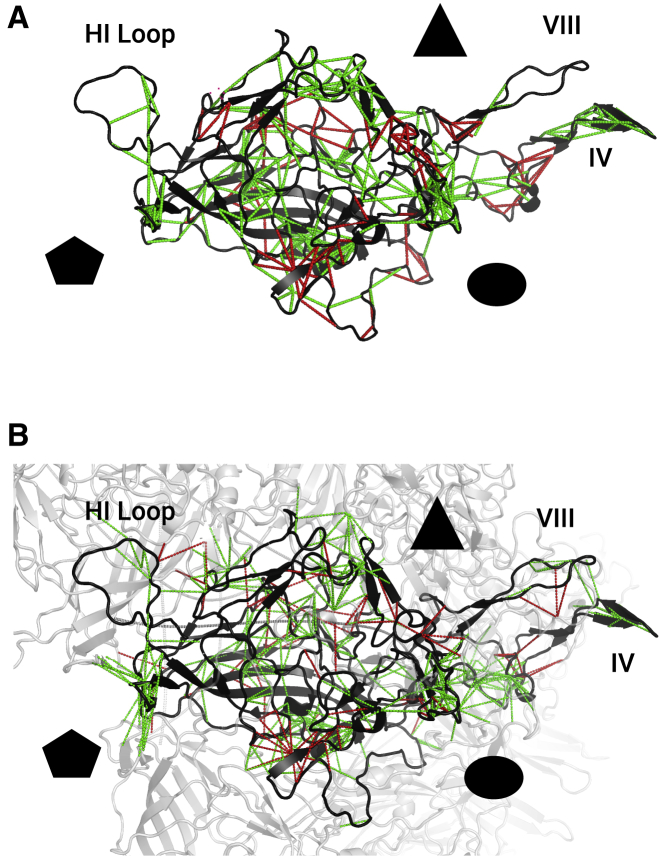
Figure 1.

Analysis of AAV capsid using mutational frustration. Mutational frustration of all possible residue interactions was computed using the Frustratometer for the AAV2 monomer and multimer. Minimally and highly frustrated interactions were plotted on crystal structures of AAV2. (A) Capsid residue interactions that are minimally (green) or highly (red) frustrated within the AAV2 monomer are indicated by connecting lines with the protein backbone in dark gray. (B) Capsid residue interactions that are minimally (green) or highly (red) frustrated within the AAV2 monomer and between the AAV2 monomer and the other subunits in the AAV2 multimer are indicated by connecting lines with the protein backbone in dark gray and other subunits in light gray. The icosahedral (T = 1) capsid fivefold (pentagon), threefold (triangle), and twofold (circle) axes of symmetry are indicated. Variable regions IV and VIII and the HI loop are labeled.

Single-residue mutational frustration indices (looking at the frustration of each residue as opposed to residue pairs) were also computed for the monomer and the multimer assembly. The AAV2 monomer has 30.6% minimally frustrated residues and 8.1% highly frustrated residues, whereas the AAV2 multimer has 30.3% minimally frustrated residues and 6.6% highly frustrated residues. Both configurations have more neutral residues than a set of 314 monomeric proteins previously curated and analyzed from the PDB, which have on average ∼40% minimally frustrated residues and >10% highly frustrated residues (20). Single-residue mutational frustration indices were then combined to generate a Δ-frustration index. This change in frustration upon protein-protein binding was previously computed for a benchmark of assemblies of homodimers and their subunits curated from the PDB (48). In a previous study employing the Frustratometer, 25% of residues found in protein-protein interaction domains exhibited an increase of ∼1.5 single-residue mutational frustration index units (i.e., a Δ-frustration index of 1.5) in the bound state, whereas 7% of residues exhibited a decrease in the single-residue mutational frustration index (i.e., a negative Δ-frustration index) (20). In AAV2, ∼6.0% of residues exhibit an increase in single-residue mutational frustration index in the multimer state greater than one unit (Δ-frustration index >1), whereas 3.7% of residues exhibit a decrease in single-residue mutational frustration index by more than one unit (Δ-frustration index <1) (Fig. S2). Molecular dynamics models of virus assembly have previously shown that interactions between viral subunits must be relatively weak to permit viral assembly while avoiding kinetic traps due to malformed structures; this property may result in a less dramatic shift toward minimal frustration upon binding than in smaller protein assemblies (49,50).

We hypothesized that this Δ-frustration index metric may highlight AAV capsid residues that shift in frustration upon subunit-subunit interaction, indicating they play key roles in stability of either the monomer or the multimer assembly. By this logic, positive values of the Δ-frustration index would identify residues that favor the multimer assembly state, whereas negative values identify residues that favor the monomer state.

We also compared the Δ-frustration index to other residue-level parameters. There was no correlation of the change in frustration upon capsid assembly with sequence conservation in the parvovirus family (Fig. 2 C) or distance from the capsid center (Fig. 2 D). There is a slight positive correlation (R² = 0.018, p = 0.0025) between the number of inter-residue contacts, defined as two residues having a pair of atoms with a distance of <4.5 Å, and the Δ-frustration index (Fig. 2 E). Residues with lower frustration in the multimer state tend to have more contacts with other residues, suggesting that essential capsid interactions take place in these domains that are conserved across the parvovirus family (51). Conversely, residues with lower frustration in the monomer state have fewer contacts with other capsid residues. These residues may play a role in capsid interactions with other proteins on the virus’s transduction pathway as opposed to intracapsid interactions. Indeed, mutation of R471 has previously been shown to reduce immune system interactions and K527 is known to be proximal to the AAV2 heparin binding pocket, although mutation does not impact heparin binding (52).

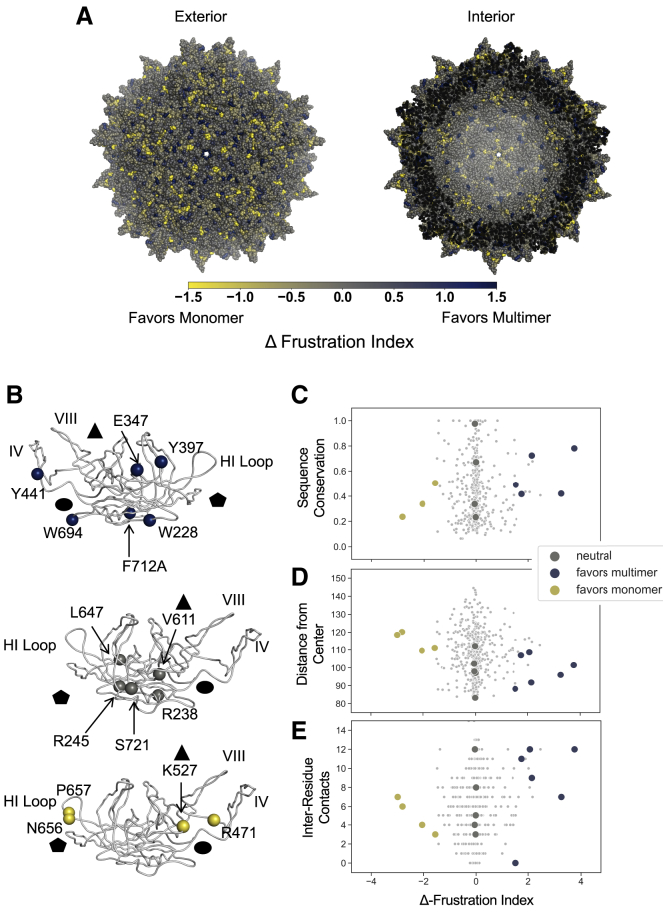
Figure 2.

AAV2 Δ-frustration index and capsid residues selected for experimental analysis. AAV2 Δ-frustration index was computed as the difference between monomer and multimer single-residue frustration indices. Residues with a positive Δ-frustration index are predicted to favor the multimer, whereas residues with a negative Δ-frustration index are predicted to favor the monomer. (A) AAV2 60-mer capsid crystal structure colored according to Δ-frustration index is given. Views of the capsid from exterior and interior are shown. (B) Residues selected for experimental analysis are shown. Residues favoring the multimer state (blue, Δ-frustration index >1.5), residues favoring the monomer state (yellow, Δ-frustration index <−1.5), and neutral residues (gray, Δ-frustration index >−0.1 and <0.1) were selected for further study. The capsid fivefold (pentagon), threefold (triangle), and twofold (circle) axes of symmetry are indicated. Top view shows interior face of the VP3 subunit, and middle and bottom views show exterior face. Δ-frustration index for AAV2 capsid residues was plotted against (C) sequence conservation in the parvovirus family computed using Shannon entropy of reweighted sequences normalized from 0 to 1 (1 indicates full conservation), (D) residue distance from center of AAV2 capsid (Å), and (E) number of residue-residue contacts according to a 4.5 Å heavy-atom distance threshold. Residues selected for mutation are large colored circles, and residues not selected are small gray dots.

A set of representative residues was selected based on the Δ-frustration index favoring the multimer, favoring the monomer, or neutral toward either state. Based on the threshold identified in Ferreiro et al. (20), Δ-frustration index values >1.5 were labeled as favoring the multimer and values <1.5 as favoring the monomer (20). Six residues from the 14 residues favoring the multimer were selected randomly, and all four residues that were predicted to favor the monomer were selected. Five neutral residues were selected randomly from the 229 residues with Δ-frustration indices >−0.1 and <0.1. These selected residues were experimentally mutated to alanine to evaluate their role in capsid formation, thermal stability, and transduction efficiency.

In addition to applying the Frustratometer, we used the coarse-grained protein force field on which the Frustratometer is based, the AWSEM (43), directly to predict the change in energy (ΔE) upon mutation of the selected residues to alanine. We developed a ΔΔE metric by subtracting the monomer ΔE from the multimer ΔE for each alanine mutant. Because a more negative ΔE-value indicates greater energetic stability, alanine mutants with a lower ΔΔE score than the WT are predicted to favor the multimer state, whereas alanine mutants with a higher ΔΔE score than WT are predicted to favor the monomer state. Whereas the Frustratometer measures the favorability of a particular interaction or set of interactions for a particular residue compared to a distribution of decoy interactions, the ΔΔE metric makes predictions about the specific change in stability upon mutating to alanine, which is what was done experimentally. Because the ΔΔE score is highly correlated with the Δ-frustration index in the studied mutants (R² = 0.79, p ≪ 0.001), we included comparisons of ΔΔE and experimental results in our supplemental data.

DCA of AAV capsid

We next applied DCA to make predictions about the fitness of the selected AAV2 alanine mutants. DCA is a global statistical model derived from a multiple sequence alignment of a protein family (28). In this case, we used the capsid sequences of parvoviruses drawn from Pfam (ID: PF00740) to construct the MSA that is used as input to DCA (53). We plotted the top 300 predicted residue-residue couplings from DCA against likely residue-residue interactions (including direct contacts, potential dynamic interactions, and ligand coordination interactions) defined as inter-residue distance <12 Å in the AAV2 crystal structure (Fig. 3; Table S1). The overlap between some DCA-predicted interactions and likely interactions identified in the AAV2 capsid crystal structure (60 monomeric pairs and eight multimeric pairs of interactions) suggests crucial pairs maintained through evolution that play important structural roles at the monomeric and oligomeric level. This model may also be able to identify interacting residue pairs that are not proximate in the AAV capsid but are functionally relevant, a strength of this approach over structure-based models.

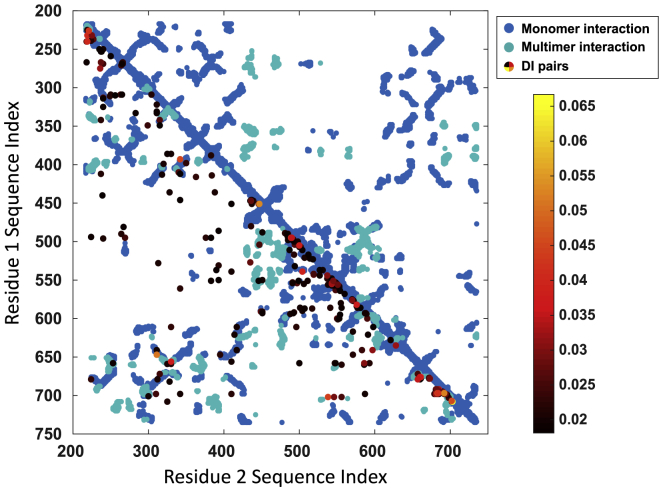
Figure 3.

AAV2 capsid residue-residue couplings inference by direct-coupling analysis (DCA). DCA was applied to a multiple sequence alignment of sequences identified as likely parvovirus coat proteins in Pfam. Predicted residue-residue couplings from DCA and likely residue-residue interactions (inter-residue distance <12 Å) identified in the AAV2 capsid crystal structure (1LP3) are plotted on a map. DCA-predicted pairs (colored by direct information score, with lighter colors suggesting stronger couplings), structurally determined monomeric interactions (blue), and structurally determined multimeric interactions (green) are plotted at the intersection of the two contacting residues’ AAV2 capsid sequence indices (VP1 numbering).

To investigate the capsid mutants with DCA, we computed the change in DCA Hamiltonian upon alanine mutation for each position in the AAV2 capsid. DCA estimates a joint probability distribution that is used to generate the family-specific DCA Hamiltonian parameters that describe a relative probability that any given sequence is a member of the sequence family. This probability can be log transformed to obtain a unitless quasienergy (DCA Hamiltonian energy H_DCA(Ala)) (29,44). Lower values of the DCA Hamiltonian energy correspond to sequences that are more likely to belong to the sequence family under consideration and thus more likely to be structurally and functionally similar to the family members. The change in the DCA Hamiltonian energy for alanine mutants as compared with the WT (ΔH_DCA(Ala)) was compared with other residue-level parameters (Fig. 4).

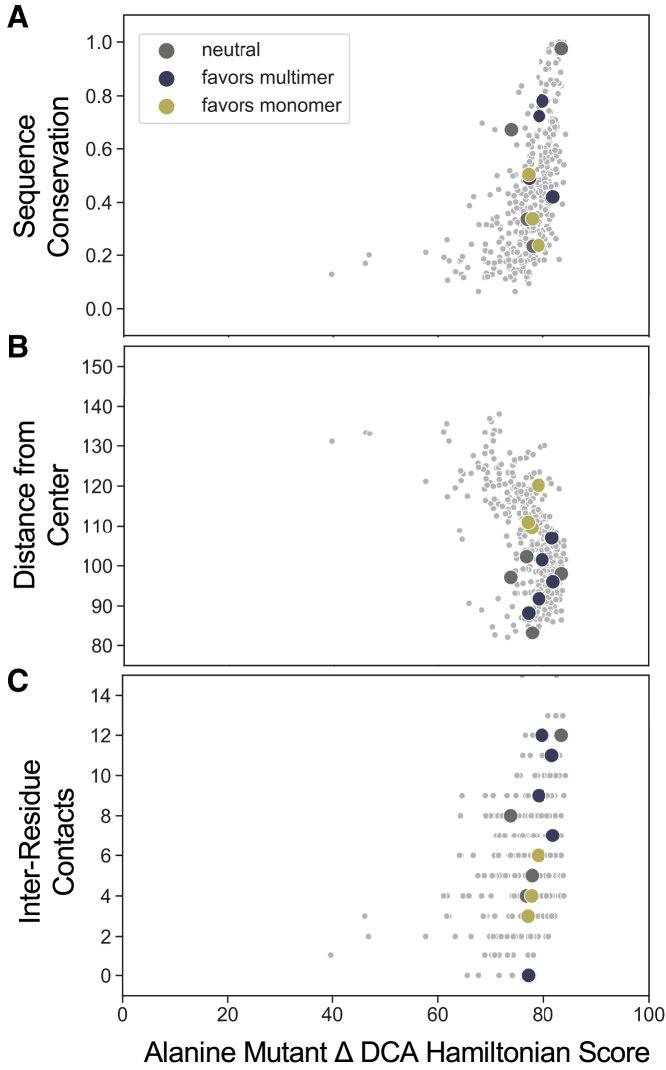
Figure 4.

Comparison of DCA energy changes upon mutation of the wild-type residue to alanine, H_DCA(Ala), to other residue-specific parameters. Plots of the ΔH_DCA(Ala) score against (A) sequence conservation in the parvovirus family, (B) three-dimensional distance of residue from center of the AAV2 capsid (Å), and (C) number of residue-residue contacts according to a 4.5 Å heavy-atom distance threshold are given. AAV2 capsid residues selected for mutation are plotted with large colored circles, and residues not selected for mutation are shown as small gray dots.

The energy change upon mutation of the wild-type residue to alanine, ΔH_DCA(Ala), is correlated with sequence conservation within the parvovirus family (R² = 0.30, p ≪ 0.001), indicating that locations with higher sequence conservation are more sensitive to mutation (Fig. 4 A). DCA generates a global model of the parvovirus sequence family and makes predictions of mutant virus fitness based on the prevalence of residue identities and residue interaction coupling strength in the family. Unsurprisingly, DCA predicts that mutations of a highly conserved residue will be detrimental to fitness. ΔH_DCA(Ala) is negatively correlated with residue distance from the capsid center (R² = 0.28, p ≪ 0.001). Residues further from the capsid center have lower (more favorable) ΔH_DCA(Ala) scores, suggesting that alanine mutations of these residues are more likely to be tolerated (Fig. 4 B). ΔH_DCA(Ala) has a low but significant correlation with the number of residue-residue contacts (R² = 0.13, p ≪ 0.001) (Fig. 4 C), suggesting that DCA is able to identify some residues that participate in a large number of interactions in capsid proteins. Correlations with capsid structural features were recovered despite the paucity of available parvoviral sequences for this analysis. The direct-coupling analysis joint probability distribution was inferred from an alignment of parvoviruses with 130 effective sequences (M_eff), 5.06% of the 2569 starting sequences after reweighting sequences to account for sequence homology. Although this M_eff is lower than the number that is thought to be necessary to produce high rates of true positive contact predictions, the inferred model nonetheless shows some promise in identifying interactions in the AAV2 capsid structure (28,54).

Whereas the AWSEM uses a protein force field to generate predicted energies of protein structures, DCA uses a global model of a sequence family to predict a quasienergy representing sequence fitness. To quantify the relationship between AWSEM energy and DCA quasienergy predictions for the selected alanine mutants, we computed the correlations between ΔE_Ala of the monomer and multimer, ΔΔE_Ala, and ΔH_DCA(Ala) (Fig. S3). These metrics were previously found to be highly positively correlated for protein monomers (29). In the mutants analyzed, the AWSEM monomer ΔE prediction actually has a high negative correlation with ΔH_DCA(Ala) (R² = 0.66, p = 0.001), whereas there is no significant correlation between the AWSEM multimer ΔE and ΔH_DCA(Ala) (R² = 0.24, p = 0.11) or the ΔΔE metric and ΔH_DCA(Ala) (R² = 0.053, p = 0.47). We also quantified the relationship between Δ-frustration index and ΔH_DCA(Ala). In the mutants analyzed, these metrics are not significantly correlated (R² = 0.12, p = 0.26). This surprising divergence between DCA- and AWSEM-derived predictions of the fitness of alanine mutants may be attributable to the many roles of viral proteins in transduction. This may also be a function of viral capsid metastability, as viruses must maintain stable structures to protect their genomes but also release their genomic cargo at its intended intracellular destination (49).

Formation of AAV2 capsid alanine mutants

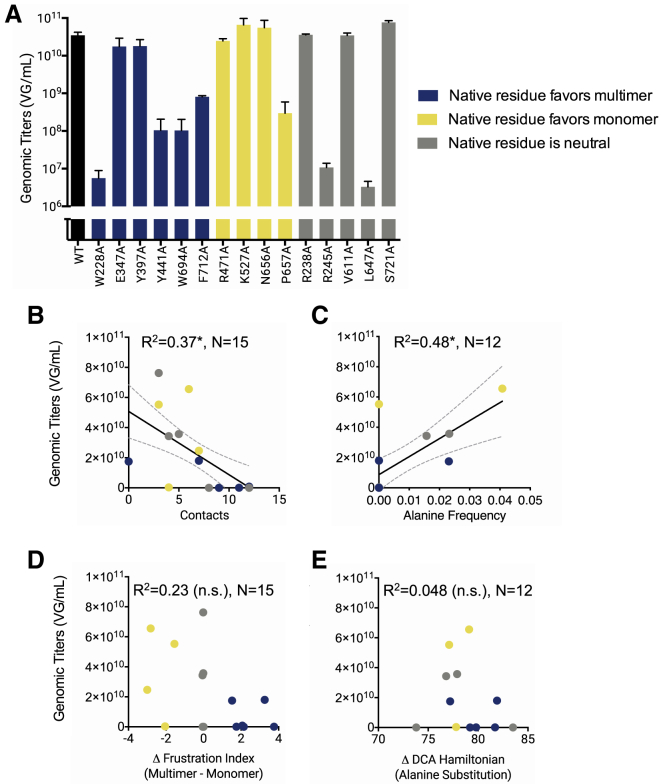
We mutated the selected AAV2 capsid residues to alanine and generated genome-packaging viruses (Fig. 5 A). Among the mutants of residues predicted to favor multimer formation, four out of six exhibit decreased genomic titers, with the remaining mutants exhibiting titers comparable to WT AAV2 capsid. Among the mutants of residues that were predicted to disfavor multimer formation, one (P657A) exhibits decreased genomic titers, whereas the other three exhibit titers comparable with the WT. Among mutants of residues predicted to be neutral with respect to multimer formation, two out of the five exhibit decreased genomic titer, whereas three exhibit titers comparable with the WT.

Figure 5.

Ability of alanine capsid mutants to form viruses with encapsidated genomes. Selected residues were mutated to alanine, and viruses were produced. Genomic titers of one-plate virus preps were determined through qPCR. (A) Genomic titers of alanine mutants expressed as viral genomes per mL (VG/mL) are given. N = 3 independent virus preps. Error bars are mean ± SE. One-way ANOVA was performed with Dunnett’s post hoc multiple comparison test to compare mutants to WT; no statistically significant differences were detected. Genomic titers are plotted against (B) number of residue-residue contacts in the native capsid structure, (C) alanine frequency in the parvovirus sequence family, (D) Δ-frustration index, and (E) ΔH_DCA(Ala). N = 15 mutants for structure-based analyses. N = 12 mutants for sequence-based analyses because R471A, F712A, and S721A do not exist in a majority of the sequence family (majority gaps at their alignment position). Regression lines with 95% confidence interval are plotted for statistically significant correlations. R²-values and significance levels are reported (^∗p < 0.05).

In an attempt to understand the factors that influence genomic titers in the alanine mutation variants, we first compared virus production titers against two simple metrics that were derived either from structural data on the AAV2 capsid (the number of contacts made by a particular residue) (Fig. 5 B) or from an MSA of parvovirus family sequences (the frequency at which alanine appears at the mutated site) (Fig. 5 C). Mutant virus production has a negative correlation with the number of residue-residue contacts made by the native residue in the capsid structure, i.e., the greater the number of native contacts a residue has, the lower the yield of virus formed when that residue is mutated to an alanine (Fig. 5 B). Additionally, virus production is positively correlated with the frequency of alanine residues observed at the native residue’s position in an MSA of parvovirus family sequences (Fig. 5 C). In other words, if an alanine is frequently found in a homologous capsid position in many other parvoviruses, the alanine mutation in the AAV2 capsid is better tolerated and yields higher virus production levels.

Mutant virus formation is not significantly correlated with the native residue’s Δ-frustration index (Fig. 5 D) and DCA-based ΔH_DCA(Ala) scores (Fig. 5 E). However, there appears to be a general trend in which mutants of residues with higher Δ-frustration indices have reduced formation. Proline has a unique influence on secondary structure that is not directly considered by the AWSEM Frustratometer, which can often result in challenges when attempting to predict mutational effects (55,56). If the P657A mutant is excluded from this analysis, then virus formation is correlated with the Δ-frustration index of native residues, but not ΔH_DCA(Ala) (Fig. S4). The results thus far demonstrate that the Δ-frustration index computed with AWSEM-MD is somewhat related to capsid formation but does not fully predict assembly.

We also considered the impact of coding mutations introduced in the assembly-activating protein (AAP) and X gene trans-encoded elements of the AAV genome that play a role in capsid assembly and viral DNA replication, respectively (57,58). The W228A, R238A, R245A, and E347A mutations also introduce coding mutations in AAP (Table S3). These modifications may play a role in W228A and R245A’s reduced viral formation because AAP is essential for AAV2 production (59). The V611A, L647A, N656A, P657A, W694A, and S721A mutations also introduce coding mutations in the X gene. These mutations may play a role in reduced viral titers for some of these mutants. However, removal of the X gene reduces AAV2 genomic titers by 33%, so X gene mutations are likely only a partial factor in L647A, P657A, and W694A’s reduced genomic titers (58).

AAV formation occurs via a multistep process involving first capsid protein production and assembly into a 60-mer capsid, then insertion of the viral genome into the capsid lumen via function of other protein factors (60,61). Our findings suggest that both simple structural contact information and sequence family residue frequency information can help to guide the design of variants with the goal of modulating complete virion yield. From these observations, it is unclear whether more sophisticated computational models provide better guidance in viral variant design than do relatively simple metrics derived from the capsid structure (residue-residue contacts) and the parvovirus sequence family alignment (Fig. 5, B and C). No single model appears to capture capsid formation (i.e., combination of capsid assembly and genome packaging) fully, perhaps because none of these approaches explicitly take into account interactions with other known AAV factors and helper virus proteins that are required for capsid assembly and viral genome packaging (57,62, 63, 64). The models may potentially perform better in prediction of AAV2 VP monomer formation and empty capsid assembly as opposed to complete genome-containing virion formation because these intermediate steps require fewer interactions with protein cofactors and viral genomic DNA (65). Quantification of VP monomer yield, capsid morphology, and the ratio of empty/full viral capsids would provide some measure of these earlier stages in viral vector production.

Thermal stability of AAV2 capsid alanine mutants

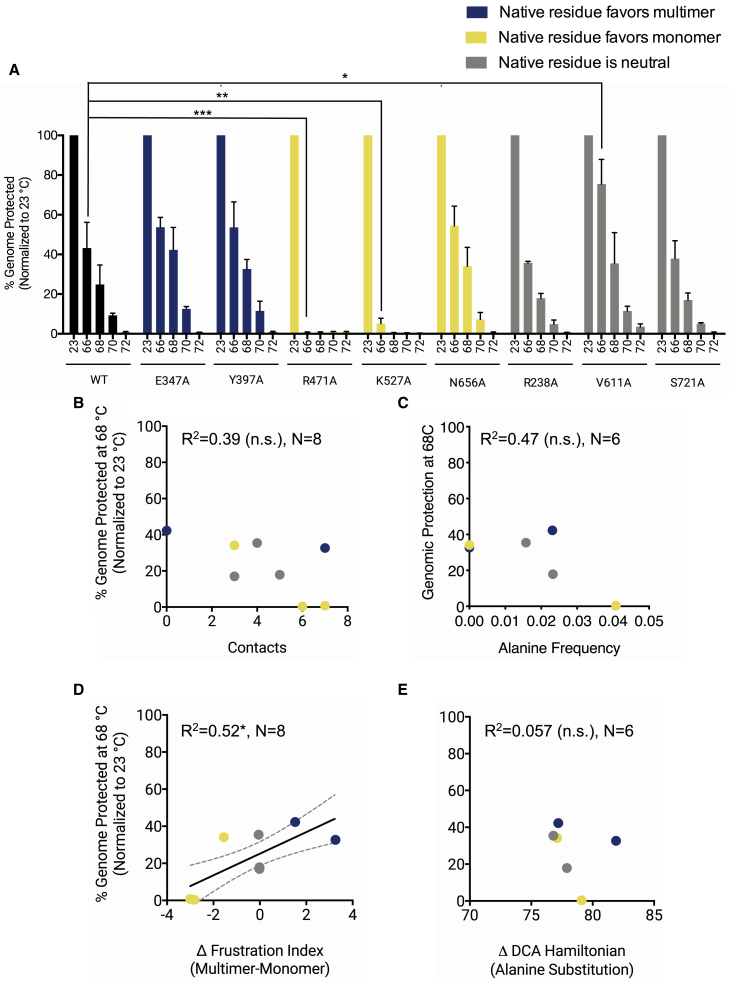
Viruses that formed with sufficient titers for further analysis (>10¹⁰ viral genomes/mL) were screened for thermal stability through a genomic protection assay. Specifically, viruses were incubated at a range of temperatures near the WT AAV2 capsid melting temperature, which was previously reported as 72.4°C (46). The virus samples were then treated with a nuclease to degrade any uncoated viral genomes. After nuclease inactivation, the samples were then assayed for the number of remaining genomes (i.e., genomes that are protected from nuclease digestion by an intact capsid). Most capsids exhibit thermal stability comparable with the WT, with the exception of the R471A and K527A mutants (Fig. 6 A). These two mutants appear to lose genomic protection after incubation at 66°C. To further characterize these mutants’ reduction in thermal stability, the melting points of these mutants were determined using a differential scanning fluorescence assay (Table S1. List of Top 300 Couplings Found Using DCA and their Direct Information Scores, Data S2. Multiple Sequence Alignment Generated by Using HMM to Query for Sequences in the Parvovirus Sequence Family, Document S2. Article plus Supporting Material; (46)). R471A exhibits a 6.8°C decrease in melting temperature compared with the WT, and K527A exhibits a 3.5°C decrease in melting temperature compared with the WT (Fig. S5 B).

Figure 6.

Thermal stability of alanine mutant capsids. Alanine mutants that formed at sufficient titers were exposed to various temperatures (°C) and then assayed for genomic protection. Temperature-treated samples were incubated with benzonase or sham buffer and genomes quantified using qPCR. (A) Genomic protection after incubation at elevated temperatures is shown. N = 3 independent experiments titered in duplicate. Error bars are mean ± SE. Two-way ANOVA was performed with Dunnett’s post hoc multiple comparison test to compare mutants with WT at each tested temperature. Percentage of genome protected is the fraction of genomes in the benzonase-treated sample as compared with the sham-treated sample. Genomic protection at 68°C is plotted against (B) number of residue-residue contacts in the native capsid structure, (C) alanine frequency in the parvovirus sequence family, (D) Δ-frustration index, and (E) ΔH_DCA(Ala). N = 8 mutants for structure-based analyses. N = 6 mutants for sequence-based analyses because these residues do not exist in a majority of the sequence family (these residues are considered as insertions in the hidden Markov model of the family). Regression lines with 95% confidence interval are plotted for statistically significant correlations. R²-values and significance levels are reported. ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001.

Capsid thermal stability at 68°C was compared to various computational metrics of fitness as described above. Virus thermal stability is not correlated with the number of residue-residue contacts made by the original residue in the WT structure (Fig. 6 B) or with the frequency of alanine in an alignment of parvovirus sequences (Fig. 6 C). Thermal stability is, however, correlated with the Δ-frustration index (Fig. 6, D and E). Interestingly, alanine mutants of native residues predicted to favor the monomer by Δ-frustration index have lower genomic protection at 68°C (Fig. 6 D). ΔH_DCA(Ala) shows no correlation with capsid thermal stability (Fig. 6 E). These results indicate that metrics derived from physical energy-based models such as the Δ-frustration index may capture information about thermal stability, although elucidating the reasons why capsid mutants predicted to favor the multimer have lower melting temperatures will require further studies. This relationship may be due to the stability of the capsid monomer playing an important role in overall capsid thermal stability. Indeed, parvovirus capsid denaturation or disassembly at high temperatures is thought to occur cooperatively as subunits lose tertiary structure and disassemble into trimer intermediates simultaneously; this denaturation mechanism has been demonstrated in minute virus of mice (66,67). In future work, these ideas about the relative importance of monomer and multimer stability can be evaluated by testing the melting point of mutant monomers synthesized in bacterial expression systems without other required components for capsid assembly. It is notable that this result is in contrast with capsid assembly, in which mutants of residues predicted to favor the multimer have generally higher genomic titers, in line with our initial expectations. This conflict may be resolved through a more detailed experimental examination of the stages of mutant capsid assembly, including monomer synthesis, trimer assembly, empty capsid formation, and genome packaging. It is also possible that the results observed in this study have some dependence on the size of genomic cargo and the use of a self-complementary transgene, as transgene size and self-complementarity have previously been shown to impact virion thermostability (68). This possibility may be examined by conducting thermostability assays on mutant virions packaging genomes of different sizes and single-stranded genomes.

Transduction efficiencies of AAV2 capsid alanine mutants

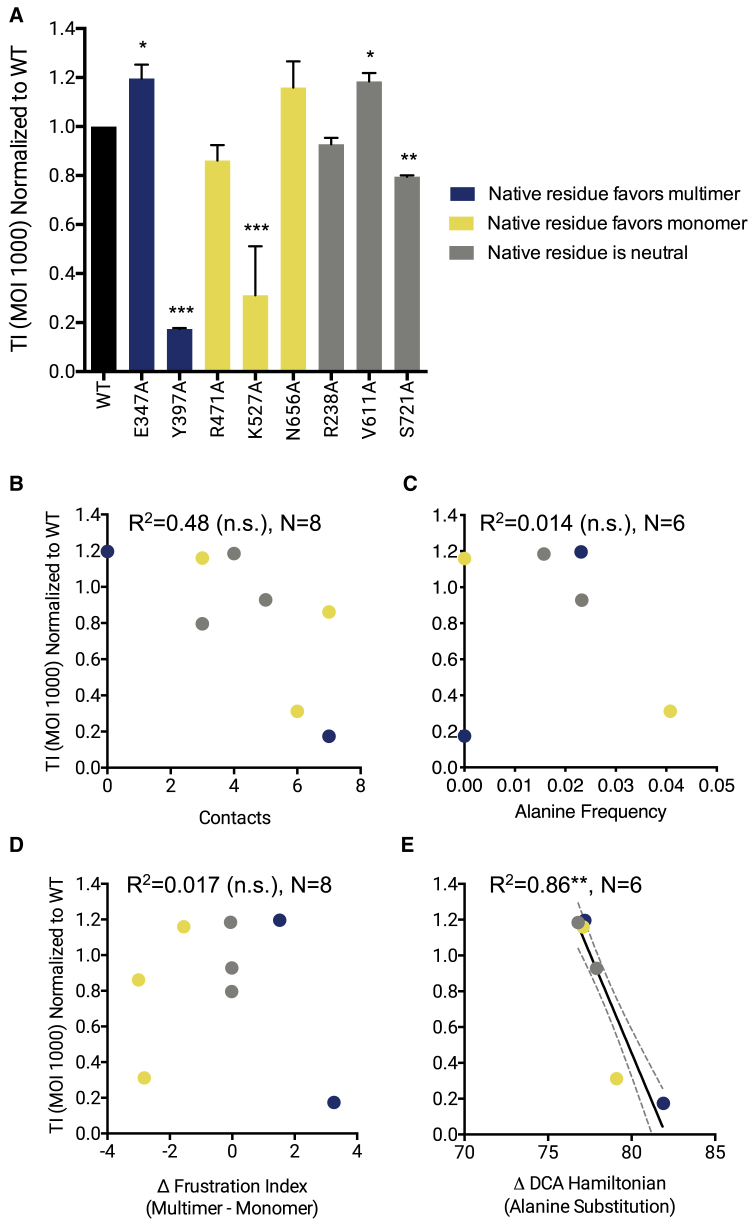
Lastly, the WT and mutant viruses were screened for their ability to transduce HEK293T cells. Variants with mutations that were predicted to favor multimer formation and variants with mutations that were predicted to disfavor multimer formation show a wide range of transduction levels, with some mutants severely deficient in transduction and others comparable to WT (Fig. 7 A). Mutants that were predicted to be neutral with respect to multimer formation all show transduction levels similar to WT. The number of residue-residue contacts (Fig. 7 B) and the Δ-frustration index (Fig. 7 D) are not correlated with virus transduction ability. Because these metrics are derived from the viral capsid structure and a physical energy function, they do not take into account the interactions the AAV capsid must successfully make with its cellular environment to transduce cells. The frequency of alanine at the site of the mutated residue in an alignment of parvovirus sequences is also not correlated with transduction (Fig. 7 C). The ΔH_DCA(Ala) score, however, is highly correlated with virus transduction (Fig. 7 E). Capsid alanine mutants that are predicted to have higher fitness in the DCA-derived model of parvovirus coat protein sequence are more successful at genome delivery into host cells.

Figure 7.

Transduction ability of alanine mutant capsids. HEK293T cells were transduced with viruses packaging scGFP transgene at a multiplicity of infection of 1000, and transgene expression was quantified at 48 h post-transduction using flow cytometry. (A) Transduction index (TI) of viruses. TI is the product of percentage of GFP+ cells and the geometric mean fluorescence intensity; metrics were obtained from flow cytometry. N = 3 independent experiments done in triplicate. Error bars are mean ± SE. One-way ANOVA was performed with Dunnett’s post hoc multiple comparison test to compare mutants with WT. TI of alanine mutants is plotted against (B) number of residue-residue contacts in the native capsid structure, (C) frequency of alanine in the parvovirus sequence family at the site of the mutated residue, (D) Δ-frustration index, and (E) ΔH_DCA(Ala) score. N = 8 mutants for structure-based analyses. N = 6 mutants for sequence-based analyses because R471A and S721A were excluded from these analyses because these residues do not exist in a majority of the sequence family (these residues are considered as insertions in the hidden Markov model of the family). Regression lines with 95% confidence interval are plotted for statistically significant correlations. R²-values and significance levels are reported. ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001.

AAV transduction is a complex, multistage process, requiring the capsid to interact with extracellular receptors, escape the endosome, traffic to and enter the cell nucleus, and disassemble to release the transgene for transcription (69). The ΔH_DCA(Ala) score is the only metric found to be highly correlated with transduction efficiency, although when the number-of-contacts metric is restricted to the same set of six residues analyzed for ΔH_DCA(Ala), this metric also exhibits a high correlation with transduction (Table S2). Because the DCA approach is based on a global model drawing on sequences from the parvovirus family, this model may be better able to predict which mutated sequences are able to traverse the virus’s infectivity pathway successfully. Although DCA is not likely to capture the wide range of receptor interactions that AAV and other parvoviruses undergo to initiate cell entry, this approach may capture features of alternate capsid conformations required for exposure of the viral endosomal escape and nuclear localization domains. This hypothesis may be evaluated by examining vector transduction of cell lines with different receptors, as well as specific stages of transduction such as cellular entry, endosomal escape, nuclear trafficking, and genome release. Furthermore, pairwise residue-residue interactions appear to be essential to this result, as the parvovirus family alanine frequency metric is not correlated with transduction efficiency. However, this result is derived from data collected on only six viral mutants. As a next step, the DCA approach should be applied to a larger capsid single-mutant library to validate this preliminary finding. Additionally, AAV in vitro transduction often differs significantly from in vivo gene delivery, so an assessment of the correlation of DCA predictions with in vivo infectivity is crucial for determining whether DCA has utility in informing capsid designs for gene therapy.

Conclusions

We evaluated two different computational approaches for their abilities to predict the formation and function of AAV capsid mutants (Fig. S7). To characterize the relationship between metrics derived from these approaches and viral formation and function, we generated a series of AAV2 capsid mutants and experimentally evaluated their assembly, thermal stability, and transduction (Table 1).

Table 1.

R²-Values of Linear Regression between Computational Metrics and Experimental Measures

	Titers	Genomic Protection	Transduction
Structural contacts	0.37∗, N = 15	0.39 (n.s.), N = 8	0.48 (n.s.), N = 8
Alanine frequency	0.48∗, N = 12	0.47 (n.s.), N = 6	0.014 (n.s.), N = 6
ΔF	0.23 (n.s.), N = 15	0.52∗, N = 8	0.017 (n.s.), N = 8
ΔHDCA(Ala)	0.048 (n.s.), N = 12	0.057 (n.s.), N = 6	0.86∗∗, N = 6

^∗p < 0.05, ^∗∗p < 0.01. n.s, not significant.

Viral intracapsid interactions are governed by the same thermodynamic principles at play in all protein-protein interfaces which are typically governed by weak noncovalent interactions (70). The predominant interaction in capsid assembly is the burial of hydrophobic regions between capsid monomer binding interfaces (66,71). We sought to capture these fundamental capsid interactions through the Frustratometer energy function derived from the energy landscape theory of protein folding. This energy function is computed using the AWSEM, a coarse-grained molecular dynamics force field that has been used for simulating protein folding and protein-protein interactions. Studies drawing upon such modeling have previously captured viral assembly pathways, suggesting that this approach may prove fruitful in identifying residues crucial for virus formation (72, 73, 74, 75, 76).

We also explored computational approaches for translating evolutionary information about fitness constraints from the AAV2 capsid sequence family into predictions about viral mutant function. DCA is a global statistical model of sequence families that infers the parameters of an energy function with terms representing single-residue identity and residue-residue pairwise couplings. By generating a global model of sequence families rather than a local model of each residue-residue interaction, DCA can isolate directly interacting pairs from indirect correlations that appear because of the intertwined networks of primary interactions (28,29).

Both the Frustratometer and DCA capture features of the protein energy landscape; whereas the Frustratometer simulates physical interactions within proteins, DCA incorporates information from the evolutionary pressures that have shaped all members of the sequence family to fold robustly and form functional proteins. DCA also incorporates other constraints on evolution for protein function in addition to folding and stability. These two computational approaches have been shown to be correlated in their predictions in prior studies on protein monomers, but when applied to a virus capsid, they appear to capture somewhat different information about capsid stability and function. This may be due to the complex energy landscape of the metastable viral capsid or the large number of protein-protein interactions AAV encounters in its infectivity pathway.

The results of this exploratory study hint at the potential of DCA for predicting viral transduction and raise interesting questions about the relationship between the Frustratometer-based metric and capsid stability. Correlations between these predictions and experimental results are comparable to those observed in studies evaluating modern state-of-the-art models for mutation prediction in a variety of proteins and experimental outcomes (77, 78, 79, 80). However, any conclusions are limited by the small number of mutants studied and the high propensity of AAV capsid mutations to reduce viral production yields, limiting further study. Analysis of the DCA approach is further limited by the need for coverage of each mutant position in a multiple sequence alignment. Residues that are insertions with respect to the profile hidden Markov model used to construct the multiple sequence alignment were not characterized because the DCA framework cannot make predictions about the fitness of regions that are not included in the input alignment.

This study was also limited by the selection of mutants using only one computational approach. To better understand the capacity of these models to make predictions about the AAV capsid, larger-scale mutational studies exploring a variety of mutation types are needed. Mutations should be selected that span the range of DCA mutation fitness predictions to ensure coverage of the 19% of possible alanine mutants with ΔH_DCA(Ala) scores more favorable than the mutants tested and 1.4% of possible alanine mutants with ΔH_DCA(Ala) scores less favorable than the mutants tested. Models should also be evaluated on a large range of random mutations of different designs, such as single mutants to nonalanine residues, protein chimeras, and multiresidue mutations. Prior attempts to build unbiased large libraries of AAV variants using DNA shuffling and error-prone PCR have been limited by the virus’s intolerance to mutants that impact capsid architecture (17,81,82). A detailed analysis of model performance on different mutation types will clarify the value of these computational approaches for aiding viral library design. Such data may also be used to develop supervised approaches incorporating features from DCA and the Frustratometer to predict specific experimental outcomes.

Overall, the results of this study suggest that computational frameworks relying on evolutionary sequence information and force-field-based predictions may provide guidance for specific elements of AAV structure and function, but do not on their own provide a complete picture of vector fitness. Hybrid approaches using DCA to infer likely residue-residue contacts that are given as input to constrain energy-based models may be powerful in developing a better understanding of capsid metastability (83,84). The performance of DCA may also be improved through integration of the growing body of AAV variant sequence data obtained through barcoded, directed-evolution experiments and biomining. Development and validation of these larger data-driven computational models will ideally lead to the development of an accurate in silico model of AAV fitness. The resulting refined model could then be used to prescreen engineered viruses, thereby accelerating the development of optimized vectors for more effective gene therapy.

Editor: Mark Alber.

Supporting Citations

Reference (85) appears in the Supporting Material.

Author Contributions

N.N.T., J.S., F.M., and P.G.W. conceived of the study. N.N.T., Q.Z., K.R.G., C.B., and N.P.S. conducted computational analyses. N.N.T., K.R.G., and S.B. planned and conducted experiments and collected and analyzed data. J.S., F.M., and P.G.W. supervised the project. N.N.T. wrote the manuscript, and all authors reviewed and edited the manuscript.