Short peptides as predictors for the structure of polyarginine sequences in disordered proteins

Abstract

Intrinsically disordered proteins and intrinsically disordered regions are frequently enriched in charged amino acids. Intrinsically disordered regions are regularly involved in important biological processes in which one or more charged residues is the driving force behind a protein-biomolecule interaction. Several lines of experimental and computational evidence suggest that polypeptides and proteins that carry high net charges have a high preference for extended conformations with average end-to-end distances exceeding expectations for self-avoiding random coils. Here, we show that charged arginine residues even in short glycine-capped model peptides (GRRG and GRRRG) significantly affect the conformational propensities of each other when compared with the intrinsic propensities of a mostly unperturbed arginine in the tripeptide GRG. A conformational analysis based on experimentally determined J-coupling constants from heteronuclear NMR spectroscopy and amide I′ band profiles from vibrational spectroscopy reveals that nearest-neighbor interactions stabilize extended β-strand conformations at the expense of polyproline II and turn conformations. The results from molecular dynamics simulations with a CHARMM36m force field and TIP3P water reproduce our results only to a limited extent. The use of the Ramachandran distribution of the central residue of GRRRG in a calculation of end-to-end distances of polyarginines of different length yielded the expected power law behavior. The scaling coefficient of 0.66 suggests that such peptides would be more extended than predicted by a self-avoiding random walk. Our findings thus support in principle theoretical predictions.

Significance

Intrinsically disordered proteins are rich in charged and deficient in hydrophobic residues. High net charges of disordered protein segments favor statistical coil ensembles, which are more extended than a self-avoiding random coil. It is unclear whether the chain extension solely reflects the avoidance of nonlocal interactions or if local nearest-neighbor interactions also provide significant contributions. The relevance of nearest-neighbor interactions, which are neglected in random coil models, has been emphasized in the literature but only sporadically considered in molecular modellings of disordered proteins and peptides. We determined the Ramachandran distributions of protonated arginine in GRRG and GRRRG peptides. Our results reveal the contribution of nearest-neighbor interactions to the extended conformations reported for a variety of polyarginine protein segments.

Introduction

Intrinsically disordered proteins (IDPs) exhibit a dynamic behavior that allows them to exist as an ensemble of energetically similar albeit structurally distinct conformations under physiological conditions. Although IDPs do not have a single well-defined native structure, they are involved in many life-sustaining biological processes (1, 2, 3, 4). This disconnect between structure and function has challenged the now-outdated central dogma of protein biophysics that a well-defined protein structure is necessary for function. Generally, the conformational ensembles of IDPs can be categorized by their conformational ensembles in terms of two states, i.e., collapsed globules (in poor solvents) and self-avoiding random coils (in good solvents) (2,5, 6, 7), where the goodness of the solvent depends on the amino acid composition of the protein. Moreover, NMR studies revealed the occurrence of local residual structure in the former that are stabilized by nonlocal interactions (8, 9, 10, 11). Because IDPs are generally rich in amino acid residues with charged or polar side chains (2,12,13), one might suspect that water would function as a good solvent and thus favor the more extended self-avoiding coil state. However, several lines of evidence reported in the literature show that IDPs and homopeptides with polar residues adopt collapsed conformations even in the presence of denaturing cosolvents (14,15). Even an excess of charges does not guarantee an extended state in that a preference for the coiled state requires that the net charge per residue of a polypeptide chain must exceed a certain value for moving the polymer above the theta point at a given temperature (15,16).

Conceptually, both the ideal Flory random coil model and the self-avoiding random walk model are based on the assumption that a polymer can be described as a freely jointed chain of subunits (16, 17, 18, 19). In the case of polypeptides/proteins, this would imply a nearly unhindered rotation with regard to the backbone torsions ϕ and ψ that connect the peptide groups. However, this idealization is at variance with reality in that steric hindrance and electrostatic interactions restrict the dihedral angles ϕ and ψ. This restriction is generally considered as mostly insignificant because the sterically allowed regions of the Ramachandran plot of individual amino acid residues are very similar, with the sole exception of glycine (more extended) and proline (more restricted) (20). Moreover, the radii of gyration of proteins and IDPs in denaturing solvents exhibit scaling exponents that cluster around 0.59, the expectation value for a self-avoiding random walk in a good solvent (21,22).

The above line of thinking can be questioned based on a variety of experimental and computational results. First of all, the sampled regions of the Ramachandran plot have been found to be more restricted by far more factors than just steric allowance. Backbone and side-chain interactions with the solvent cause the intrinsic conformational propensities of amino acids to differ significantly (23, 24, 25, 26). Residues preferably sample the upper-left quadrant of the Ramachandran plot (between 70 and 80%) (27, 28, 29, 30, 31). The remaining 20–30% are generally distributed over several turn-like conformations. Conformational distributions of amino acid residues differ mostly in terms of their sampling of poly-proline II (pPII) and β-strand-like conformations and also with regard to their conformational entropies (32,33). Second, the random coil model is based on the isolated pair hypothesis, which stipulates that the conformational sampling of each amino acid in a polypeptide chain is independent from each other (17). However, experimental as well as bioinformatical evidence strongly suggests that conformational distributions of residues are significantly modified by nearest-neighbor interactions (NNIs) (34, 35, 36, 37, 38, 39, 40).

Besides solvent-mediated effects, one possible source of NNIs could be the electrostatic interaction between charged side chains. Exploring the NNIs between charged groups seems to be of general relevance for IDPs owing to the common occurrence of charged residues in these proteins. Because many proteins are rarely fully disordered in their native state, some of the focus in the field has shifted to defining intrinsically disordered regions that exist in proteins that are otherwise well structured. These regions are often rich with charged amino acids that can drive interactions with other proteins or biomolecules. Patches of charged amino acids often exist as so-called linear motifs, which is a class of intrinsically disordered regions (41, 42, 43, 44), as well as in repeat segments of proteins (45). As indicated above, protein segments and polypeptides with a sufficiently high net charge per residue can be more extended than predicted by a self-avoiding random coil model (15).

The study described in this article was motivated by a recent investigation of 20 protamine sequences that are all very rich in arginine (15,18). The sequences differed with regard to their net charge and the distribution of arginine residues. Atomistic simulations of these polypeptides suggest that an increase in net charge above a certain threshold value can trigger a globule-to-coil transition. Scaling coefficients for peptides with very high net charges were predicted to exceed the canonical 0.59 value. Mao et al. described the extended backbone of the investigated polyarginine as a rod-like structure (15). They used the OPLS/AA/L (optimized potentials for liquid simulations/all atom)molecular mechanics force field and an implicit solvent model. To account for electrostatic interactions between side chains, a mean field electrostatic energy term was added to the total energy function.

To explore the contribution of charges to the NNIs between arginine residues, we combined vibrational and NMR spectroscopy to determine the Ramachandran plots of arginine in GRRG and GRRRG. A previously reported conformational analysis of arginine in the cationic model peptide GRG showed that this amino acid has a comparatively high propensity for the pPII structures with a smaller but still significant tendency to populate more extended β-strand and turn-like conformations (46). Recent density functional theory (DFT) calculations have provided evidence that the hydration shell around the peptide backbone of GRG stabilizes this conformational bias (47). Here, we use GRG as a reference system for the intrinsic structural propensities of arginine residues. Our experimentally based results are compared with distributions produced by molecular dynamics (MD) simulations with a CHARMM36m force field combined with a TIP3P water model (48). We relate our findings to the predictions of Mao et al. (15) by using them to predict the scaling law for a polyarginine chain of 25 residues.

Materials and Methods

Solution NMR experiments

For ¹H NMR experiments, peptides were purchased from Genscript. They were dissolved in an aqueous solution of 90% H₂O and 10% D₂O at a concentration of 100 mM, and the pH was adjusted to <2.0. The measurements were recorded with a 600-MHz Bruker AV600 spectrometer. For all other NMR experiments, isotopically labeled amino acids were purchased from Cambridge Isotopes, and the peptides of interest were synthesized using an Applied Biosystems 433A peptide synthesizer. Purification was performed via reverse-phase high pressure liquid chromatography (HPLC) before freeze drying. The product of the solid-phase peptide synthesis was checked using electrospray ionization and matrix-assisted laser desorption/ionization mass spectrometry. The labeled peptides were dissolved at a concentration of between 5 and 10 mM in an aqueous solution of 90% H₂O and 10% D₂O, and the pH was adjusted to <2.0. The measurements were recorded with a Bruker 800-MHz AV800 spectrometer. Table S1 lists the measured J-coupling constants with the homo- and heteronuclear NMR technique that was utilized as well as the technique employed for a specific J-coupling constant. A detailed description of the application of each individual technique to short model peptides is given in earlier articles (27,49). A list of J-coupling constants used for this study is given in Table S1.

Vibrational spectroscopy experiments

Peptides were dissolved in D₂O to either 100 (GRRG) or 70 (GRRRG) mM concentration. The pH was adjusted to <2.0 with deuterium chloride (DCl). The Raman spectra were obtained with the 514.5-nm radiation of a Spectra-Physics (Mt. View, CA) Argon laser (200 mW). The laser beam was directed into a Renishaw confocal microscope and focused onto a thin glass coverslip with a 20× objective. The scattered light was filtered with a 514.5 notch filter. Polarized Raman spectra were recorded using a Renishaw confocal microscope. The microscope is equipped with a linear polarizer and a λ/2 plate that rotates the y-polarized light into the x-direction. Polarized and unpolarized spectra were recorded between 1400 and 1800 cm⁻¹. A background spectrum of the D₂O/DCl mixture was recorded on the same day as and later subtracted from each peptide spectrum. The unpolarized spectra were recorded as an average of five measurements using the WiRE 3.3 Renishaw software, and the polarized spectra were an average of 10 total measurements. FTIR (Fourier transform infrared) and vibrational circular dichroism (VCD) spectra were recorded with a Chiral IR/VCD spectrometer from BioTools using a 48-μm cell and peptide concentrations of 150 and 175 mM for GRRRG and GRRG, respectively. All VCD spectra exhibited a highly nonlinear baseline even after the subtraction of the background. This was corrected for by fitting the baseline to a cubic polynominal function, which was then subtracted from the spectrum, followed by some minor adjustment of the baseline in the amide I′ region. For all spectroscopic measurements, pD values below 2 were achieved by the addition of DCl to ensure the protonation of the carboxylate group.

Data analysis

Both the NMR coupling constants and the amide I′ band profiles were analyzed using probability density distributions p(ϕ,ψ) of R residues of GRRG and GRRRG. Spectroscopic expectation values were calculated as the ensemble average over these distributions (50):

$$\langle O\rangle =\frac{{\int }_{-\pi }^{\pi }O\left(\varphi ,\psi \right)P\left(\varphi ,\psi \right)d\varphi d\psi }{Z},$$ (1)

where O represents the considered spectroscopic observable, i.e., J-coupling values as well as Raman intensity, IR molar absorptivity, and/or molar dichroism of amide I′ at a given wavenumber. Z is the partition sum.

For the analysis of the J-coupling constants, we utilized Ramachandran distributions of amino acid residues expressed in terms of linear combinations of weighted two-dimensional Gaussian subdistributions associated with known secondary structures:

$$P\left(\varphi ,\psi \right)=\sum _{j=1}^N\left(\frac{{\chi }_j}{2\pi \sqrt{\left|\widehat{V_j}\right|}}\right)e^{-0.5\cdot {\left(\overrightarrow{\rho }-{\overrightarrow{\rho }}_{j,0}\right)}^T{\widehat{V_j}}^T\left(\overrightarrow{\rho }-{\overrightarrow{\rho }}_{j,0}\right)},$$ (2)

where the index j represents the j^th conformation summed over N different subdistributions with their own statistical weights χ_j. The position vector ${\overrightarrow{\rho }}_j$ represents a coordinate pair in the Ramachandran plot, and ${\overrightarrow{\rho }}_{j,0}$ represents the coordinates of the maximum of the j^th distribution. The matrix ${\hat{V}}_j$ contains the standard deviations with regard to ϕ and ψ as on-diagonal and correlation coefficients as off-diagonal elements. The latter have been assumed to be zero for the analyses described in this article.

The construction of our Ramachandran plots started with five of the experimentally determined J-coupling constants listed in Table S1 (rows 1–5). These parameters have in common that the involved nuclei belong to the same residue. A sixth coupling constant, ²J(N_iC_α,i−1), reflects the spin-spin interaction between nearest-neighbor residues. It depends on the ψ-angle of the (i−1)^th residue (51). We only used the first five constants in Table S1 for the fitting procedure described below, but ²J(N_iC_α,i−1) values were calculated and compared with experimentally obtained values. The coupling parameters were selected because of their rather different dependencies on the dihedral angles ϕ and ψ of the peptide backbone. Each coupling constant can be related to one of these dihedral angles with a Karplus equation (49,52). These equations all take the form of Eq. S1, but the differences in phase and Karplus parameters cause each J-coupling constant to depend on the backbone angle in a vastly different manner. The measured coupling constants represent conformational averages that can be calculated by Eq. 1 and a given probability density distribution (Eq. 2) with the Karplus parameters listed in Table S2. We optimized the model by minimizing the difference between experimental and simulated J-coupling constants, which reflect the conformational average of the two dihedral angles of the peptide backbone (φ and ψ). The purpose of the fitting is to produce population statistics for five possible peptide conformations, which can be displayed as distinct regions on a Ramachandran plot. Each of these conformations is represented by a two-dimensional Gaussian distribution (Eq. 2). The initial distribution was taken from the already-reported Ramachandran plot of GRG (46). The corresponding conformations are pPII at (ϕ,ψ) = (−76.5°, 150°), β-strand at (ϕ,ψ) = (−110°, 150°), inverse γ-turn (iγ) at (ϕ,ψ) = (−80°, 70°), right-handed helical at (ϕ,ψ) = (−50°, −30°), and left-handed helical at (ϕ,ψ) = (55°, 30°). We omitted the weakly populated γ-turn. Because none of the fits indicated a population of left-handed helical conformation, we added instead the asx-turn at (ϕ,ψ) = (55°, 160°), which is populated by residues with hydrogen bonding capability (28,29). This measure was motivated by the relatively high value for ³J(H^NC^β) for R1 of GRRG. As we will show below, our fit to the GRRG data set yielded a population of the conformation for the first arginine peptide. The halfwidths of these distributions are listed in Table S3. The relative populations of these conformational subdistributions were used as free parameters subject to normalization in a nonlinear least-square fit using the lsquarefit module of MATLAB 2019b (The MathWorks, Natick, MA). In a second step, we slightly modified the ϕ- and ψ-positions of the subdistributions to optimize the fit. They were allowed to vary in the following intervals: 1) pPII with 85° < ϕ < −65° and 130° < ψ < 180°, 2) β-strand with −100° < ϕ < −180° and 140° < ψ < 180°, 3) right-handed helical with −80° < ϕ < −50° and −40° < ψ < 0°, 4) inverse γ-turn with −90° < ϕ < −70° and 70° < ψ < 80°, and 5) the asx-turn conformation with 60° < ϕ < −90° and 130° < ψ < 180°. The fit was repeated for every chosen set of dihedral angles. A comparison of the reduced χ² values of the fit allowed for a rather exact identification of the optimal solution for all ϕ-angles for which we found the uncertainty to vary between ±3° and ±8°. The situation is different for the ψ-values of pPII and β-strand, which can be varied over intervals of ±15° without causing a substantial change of the reduced χ² values. We also varied the halfwidths of the subdistributions. For none of them did that lead to a reduction of the reduced χ² value.

Amide I profiles (in particular the VCD signals) of this mode are excellent tools to reduce the uncertainty regarding the ψ-coordinates. The Raman and IR profile have a specific shape if the conformational ensemble is dominated by extended structures such as pPII and β-strand. In the pPII region of the Ramachandran plot, the strength of the VCD signal depends heavily on the ψ-coordinate (24), whereas ϕ and ψ affect the signal for ϕ-angles below −120°. Contrary to J-coupling constants, amide I profiles have to be calculated for a given conformation of the considered peptide, not for individual residue conformations. To reduce the computational time for achieving this task, we used the Ramachandran plots obtained from J-coupling fitting to construct a somewhat truncated model which regions of the Ramachandran plot which are not sampled by the peptides’ residues. Details of this model and the mathematics used to calculate the amide I′ band profiles are described in the Supporting materials and methods. For both peptides, φ- and ψ-angles of pPII and β-strand had to be modified to sufficiently reproduce the respective VCD signal. The new ϕ- and ψ-values were then used to refit the J-coupling parameters. This yielded a set of slightly modified mole fractions, which were used to recalculate the amide I profiles. The procedure generally converged after two to three loops.

Comparison of Ramachandran plots

To obtain a quantitative criterion for the comparison of Ramachandran distributions, we utilize the Hellinger distance (37,53):

$$H\left(P_{R_i}\left({\varphi }_i,{\psi }_i\right),P_{R_j}^{\prime }\left({\varphi }_j,{\psi }_j\right)\right)=\left|\right|\frac{1}{2}\underset{-\pi }{\overset{\pi }{\int }}\underset{-\pi }{\overset{\pi }{\int }}{\left(\sqrt{P_{R_i}\left({\varphi }_i,{\psi }_i\right)}-\sqrt{P_{R_j}^{\prime }\left({\varphi }_j,{\psi }_j\right)}\right)}^{2}d\varphi d\psi \left|\right|$$ (3)

The Hellinger distance measures the dissimilarity of two two-dimensional distributions. If the value is zero, the compared distributions are identical. A value of 1 indicates orthogonality. However, because individual residues sample a restricted space of the Ramachandran plot, H will never reach high values for statistical coil conformations. Here, we adopt the criteria of Schweitzer-Stenner and Toal (37), according to which two distributions are very similar if $H\le 0.1$. Values with 0.1 < H ≤ 0.25 and 0.25 < H ≤ 0.4 are moderately similar and dissimilar, respectively. Any larger value indicates significant dissimilarity.

In addition to our use of the Hellinger distance, we compared the Ramachandran distributions of the GRG and the investigated peptides by calculating their conformational entropy. For individual residues, it is calculated as

$$S=-R\sum _{\varphi =-\pi }^{\pi }\sum _{\psi =-\pi }^{\pi }P\left(\varphi ,\psi \right)\text{ln}\left[P\left(\varphi ,\psi \right)\right],$$ (4)

where R is the gas constant. In the absence of any nearest-neighbor interactions, the total entropy of a peptide would be the sum of individual entropies of the respective residues. If, as expected, nearest-neighbor interactions affect the conformational distributions of GRRG and GRRRG, the total conformational entropy of a peptide would reflect correlation effects, which can be accounted for by conditional probabilities (39,54). The calculation of such entropies is outside of the scope of this work.

Calculation of Debye length

To gauge the contribution of electrostatic interaction between charged groups (arginine side chains and the N-terminal in this case) could be of any significance for an understanding the results of our conformational analysis we have to estimate the Debye length for the solution conditions used in our study. To this end, we employ

$${\lambda }_D=\frac{\sqrt{8\pi e^2{N}_A}}{{10}^3\epsilon }\cdot \sqrt{\frac{c_0}{k_{B}T}},$$ (5)

where N_A is the Avogadro number, e is the elementary charge, k_B is the Boltzmann constant, T the absolute temperature, and c₀ is the molar ion concentration, which is very much determined by the peptide concentration.

MD simulations and mesostate calculations

MD simulations were performed using GROMACS 5.1.2 (55, 56, 57, 58) on single GRG, GRRG, and GRRRG peptides with a CHARMM36m force field and a TIP3P water model (59,60). Additional simulations using Amber ff14SB and OPLS-AA/M with TIP3P and TIP4P, respectively, were carried out for GRG. The effects of water models were explored by running simulations of GRG using the Amber ff14SB and CHARMM36m with the OPC water model for comparison (61). For the simulation with CHARMM36m, the peptides are capped with protonated NH₃⁺ termini and neutral C-termini (COOH) to mimic the influence of the acidic conditions used for the NMR and Raman experiments. For each simulation, a single peptide was solvated in a cubic box of 40 × 40 × 40 Å³. The energy minimization is performed using steepest descent minimization for 100,000 steps, followed by a pressure equilibrium for 20 ps at 300 K and a pressure of 1 bar. Stoichiometric amounts of Cl⁻ atoms are added to ensure electroneutrality. Each 500-ns-long trajectory is acquired using the velocity rescale thermostat (62) and the Berendsen barostat (63).

To assess the MD-based Ramachandran distributions, we calculated the occupation of mesostates that cover populated regions of the Ramachandran plot. They are visualized in Fig. S4. They are defined as follows: 1) pPII (−90° < ϕ < −42°, 100° < ψ < 180°), 2) antiparallel β-strand (aβ) (−180° < ϕ < −130°, 130° < ψ < 180°), 3) parallel β-strand (pβ) (−150° < ϕ < −130°, 100° < ψ < 128°), 4) the transition region between pPII and aβ (β_t) (−130° < ϕ < −90°, 130° < ψ < 180°), and 5) right-handed helical (−90° < ϕ < −32°, −60° < ψ < 14°). The mesostate populations were calculated from the MD trajectories using time frames 50–500 ns as the number of conformations within each mesostate region normalized by the total number of conformations. Eqs. 1 and S1 were used to calculate the J-coupling constants for each of the nonterminal residues of the investigated peptides.

Results and Discussion

Conformational analysis of GRRG and GRRRG

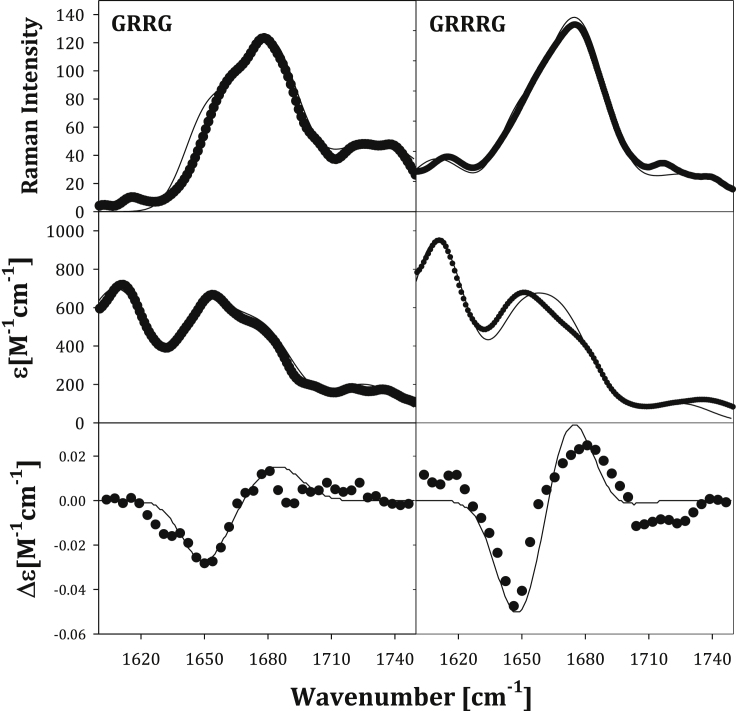
Fig. 1 shows the NMR spectra measured to determine the indicated coupling constants for GRRG. The respective spectra for GRRRG are shown in Fig. S1. The experimental values obtained from these spectra are listed in Table 1. The corresponding amide I′ band profiles in the Raman, IR, and VCD spectra are shown in Fig. 2. In addition to the overlapping amide I′ bands between 1640 and 1680 cm⁻¹, the Raman and IR spectra show weak contributions from the CO stretching mode of the C-terminal COOH group above 1700 cm⁻¹. Moreover, the IR spectrum depicts another band at approximately 1608 cm⁻¹, which is one of two IR-active CNC stretching modes. The underlying normal mode is not Raman active. Recently, Ghosh et al. provided experimental evidence for vibrational through-space coupling between symmetric and asymmetric CNC stretching modes and the two amide I′ modes of the arginine dipeptide (64). If excitonic coupling was substantial in the case of GRRG and GRRRG, it would occur between the high-wavenumber CNC mode and the amide I′ mode of the C-terminal peptide mode, the intrinsic wavenumber of which is closest to that of the CNC mode (1648 cm⁻¹). The intrinsic wavenumber of the nonterminal amide I′ modes is 1666 cm⁻¹. The wavenumber differences between these modes and the CNC modes at 1608 cm⁻¹ are too large for substantial mixing of wavefunctions, even in the presence of significant excitonic coupling. This notion applies even more to the amide I′ mode of the N-terminal at 1679 cm⁻¹. Because of the strong transition dipole moments of CNC and amide I modes, through-space coupling between the 1608 cm⁻¹ should produce a VCD spectrum with a detectable component at 1608 cm⁻¹. Such a component is not detectable in our spectra. It should be noted that the intrinsic wavenumber of blocked dipeptides is generally closer to the CNC position. This notion applies particularly to the respective N-terminal mode, which is generally in the 1630 cm⁻¹ region and thus much closer to the CNC mode position. The large difference between the N-terminal amide I wavenumbers of unblocked and blocked peptides reflects the influence of the positive charge on the N-terminal ammonium group (65). Taken together, we conclude that coupling between CNC and local amide I′ modes does not significantly affect the band profiles of the latter.

Figure 1.

NMR measurements to determine J-coupling constants, shown for GRRG. (A) Experimental doublets resulting from the ³J(H^N,H^α) coupling are shown. (B) Soft HNCA-COSY for determination of ³J(H^N,C′) is shown. (C) CO-coupled [H]NC_αH_α for the determination of ³J(H^α,C′) is shown. (D) HNHB[HB]-E.COSY for the measurement of ³J(H^N,C^β) is shown. (E) Intensities obtained from a J-modulated ¹H,¹⁵N-HSQC experiment and the fit to $I\left(\tau \right)=Acos\left({}^{1}J\left(N,C^{\prime }\right)\tau \right)cos({}^{2}J\left(N{C}^{\prime }\right)\tau exp\left(-\tau /T_2\right)$ to determine ¹J(N_i,C^α_i) or ²J(N_i,C^α_i−1) are shown in gray.

Table 1.

Experimental and computed J-coupling constants of the indicated arginine residues of GRG, GRRG, and GRRRG in aqueous solution

		GRGa	GRRG		GRRRG
		Ri	R1	R2	R1	R2	R3
3J(HNHα)	exp.	6.66 (0.01)	6.54 (0.017)	7.22 (0.035)	6.55 (0.040)	6.65 (0.044)	7.14 (0.052)
	Gaussian	6.47	6.51	6.95	6.66	6.63	7.03
	MD	6.74	6.28	6.8	6.2	6.53	7.45
3J(HNC′)	exp.	1.00 (0.08)	1.01 (0.067)	1.26 (0.151)	1.01 (0.067)	1.41 (0.403)	1.08 (0.201)
	Gaussian	0.98	0.96	1.22	1.14	1.53	1.11
	MD	1.11	1.26	1.08	1.25	0.97	0.94
3J(HαC′)	exp.	2.47 (0.05)	2.02 (0.067)	0.806 (0.201)	1.61 (0.269)	0.672 (0.067)	0.806 (0.067)
	Gaussian	2.36	2.02	1.88 (1.80)b	1.81	1.82 (1.7)b	1.93 (1.86)b
	MD	2.15	2.43	2.34	2.39	2.7	2.39
3J(HNCβ)	exp.	1.79 (0.15)	1.87 (0.220)	1.49 (0.660)	1.32 (0.220)	0.99 (0.330)	1.10 (0.440)
	Gaussian	1.75	1.81	1.43	1.61	1.35	1.46
	MD	1.61	1.69	1.60	1.73	1.79	1.40
1J(NCα)	exp.	11.02 (0.10)	11.79 (0.214)	11.60 (0.165)	11.92 (0.139)	11.82 (0.146)	11.59 (0.142)
	Gaussian	10.94	11.78	11.61	11.6	11.53	11.36
	MD	11.16	11.29	11.86	11.70	11.50	11.09
χpPII		0.58	0.69	0.45	0.69	0.39	0.53
χβ		0.20	0.16	0.33	0.29	0.44	0.38
Total extended		0.78	0.85	0.78	0.88	0.84	0.91
χrhHel		0.08	0.07	0.02	0.02	0.16	0.09
χiγ		0.03	0.08	0.2	0.00	0.00	0.00
χasx		0.08	0.006	0.00	0.00	0.00	0.00
Reduced χ2		0.05	0.16	1.43	1.01	1.46	0.99

Experimental uncertainties are listed in parenthesis. The theoretical values were calculated with a Gaussian distribution model described in the text (48). The mole fractions of the considered conformations are listed at the bottom of each column. The MD results were obtained from simulations with CHARMM36m/TIP3P as described in the text.

^aThe uncertainty of these propensities is ±0.1 because of large correlation effects.

^bBased on DFT calculations for alanine peptides.

Figure 2.

Raman (upper panel), FTIR (middle panel), and VCD (lower panel) spectra of GRRG (left) and GRRRG (right) in D₂O at pD 2 in the region between 1600 and 1750 cm⁻¹ region. The solid lines result from calculations described in the text.

Generally, the amide I′ band profiles show the characteristics of conformations associated with the upper-left quadrant in the Ramachandran plot. The Raman profile is dominated by isotropic scattering, for which the excitonic coupling leads to a substantial intensity redistribution from low- to high-wavenumber modes. The very opposite occurs for IR absorption. This leads to a large noncoincidence between the peak positions of Raman and IR, which is diagnostic of the preponderance of extended conformations (66). The negative couplet in the VCD spectrum indicates substantial sampling of pPII conformations (67,68).

Our conformational analysis of the nonterminal residues of GRRG and GRRRG is based on a model that describes the Ramachandran plot of individual residues as a superposition of two-dimensional Gaussian distributions associated with known secondary structures. The probability density distributions thus obtained are optimized to reproduce experimentally obtained J-coupling constants and amide I′ band profiles. Details of the model and the fitting procedure are described in the Materials and methods and sections of the Supporting materials and methods cited therein.

In a first round, we used the Karplus parameters reported by Wirmer and Schwalbe for ¹J(N,C^α) (51). Subsequently, we performed the fitting procedure with the parameter set for ¹J(N,C^α) reported by Ding and Gronenborn (69). Checking the performance of these different parameter sets was deemed important because the ¹J(N,C^α) values of GRRG and GRRRG were found to be systematically larger than that of GRG, thus indicating that NNIs cause an upshift of the distributions and/or a redistribution of mole fractions between turn-like and extended conformations. Assessing these changes correctly is of utmost importance to the specific aims of this study. Although both models produce comparable reduced χ² values for the two sets of ¹J(N,C^α) parameters, a better consistency between amide I′ simulations and J-coupling fits was obtained with the parameter set of Ding and Gronenborn. Simulation of the amide I′ VCD profile with the statistical weights and subdistribution positions obtained with the parameters of Wirmer and Schwalbe led to an overestimation of the rotation strength. This could be corrected for by reducing the ψ-values for pPII and β-strand, which in turn leads to a larger discrepancy between experimental and fitted ¹J(N,C^α) values. This discrepancy was reduced when we used the Karplus parameters of Ding and Gronenborn, because they yield slightly larger ¹J(N,C^α) than the Wirmer-Schwalbe set. It should be noted, however, that both parameter sets produce acceptable reduced χ² values.

The solid lines in Fig. 2 represent the result of the above iterative fitting procedure simulation of the respective amide I′ band profiles. The agreement between experimental and calculated profiles is quite satisfactory. Minor differences between, e.g., the IR profile of GRRRG are quantitative rather than qualitative in nature. It is of particular importance that we were able to reproduce the rotational strength of the amide I modes, which predominantly results from excitonic coupling between amide modes (70). Details of the spectroscopic parameters used for the amide I′ calculations are given in the Supporting materials and methods. The CNC band in the IR spectra as well as the CO bands in IR and Raman spectra have been accounted for by adding Gaussian band profiles with adjustable peak intensities and halfwidths.

J-coupling parameters and the respective reduced χ² (χ_J²) values are listed in Table 1. The latter were calculated as described by Zhang et al. (24). It should be stated again that ²J(N,C^α) was not incorporated in the fitting process. The reported values were calculated using the Ramachandran distributions obtained from the fit to the other coupling parameters. Generally, the fitting yielded J-coupling values very close to the experimental values. However, one exception is noteworthy. Our fits could not reproduce the surprisingly low ³J(H^α,C′) values observed for R2 of GRRG as well as for R2 and R3 of GRRRG. All these values are substantially different from those reported for GRG and also from the respective values obtained for the R1 residues of the two investigated peptides. The Karplus curves of these parameters in Fig. S2 suggest that the low values for ³J(H^α,C′) are due to conformational sampling around ϕ = −50° and/or −180°. The former would be to some extent compatible with the rather well-reproduced ³J(H^N,H^α) and ³J(H^N,C′) values but at variance with the values observed for ³J(H^N,C^β), which exhibits a maximum in this region. A ϕ-value of −180° is problematic because a major population in this region would totally jeopardize the calculation of ³J(H^N,H^α) and ³J(H^N,C′). A more fundamental difficulty arises from the fact that the lowest possible value that can be produced by the respective Karplus curve (1 Hz) is larger than our experimental values. Such low experimental values are actually not unusual for proteins, as documented by Hu and Bax (71). All these observations strongly suggest that the reported empirical parametrization of the Karplus curve for ³J(H^α,C′) becomes inaccurate at its minimum. We obtained a slightly better result with the Karplus parameters obtained from DFT calculations for alanine peptides, which are listed in Table S2 (72). It is more likely that the real Karplus curves become negative in this region. This is a result that the respective empirical Karplus scenarios do not account for (24). It is worth mentioning in this context that a similar problem arose with earlier attempts to reproduce the low values of the ³J(C′,C′) coupling constant of trialanine (49,73).

Generally, it should be noted that the utilized Karplus parameters do not differentiate between different amino acids with their different side chains. It is possible that the individual parameters of arginine residues would give rise to Karplus curves with more pronounced minima. Such data can, however, not yet be derived because the number of analyses measuring J-couplings for proteins with high-resolution structures are limited and also the DFT calculations have not yet been performed addressing this point.

Rather large reduced χ² values would be obtained for the residues indicated above if one considered the obtained values for ³J(H^α,C′). That would obfuscate the assessment of how well the remaining parameters were reproduced. Therefore, we omitted ³J(H^α,C′) from our calculation of the reduced χ² values for these residues. Thus, all obtained reduced χ² values listed in Table 1 are below 2, which indicates satisfactory agreement between theory and experiment.

To demonstrate the validity and significance of the obtained coupling parameter values, we created a correlation plot comparing the calculated J-coupling parameters with the corresponding experimental ones. As shown in Fig. S3, a nearly perfect linear correlation is reflected by a regression coefficient of 0.998, a slope of 0.98, and an axis value of 0.028.

The predicted values for ²J(N,C^α) are systematically lower than the corresponding experimental values. This is not surprising because the corresponding Karplus plots never exceed 8.7 Hz (49). It deserves to be noted that the Karplus parameters for ²J(N,C^α) might exhibit some significant side-chain dependence as well. However, the very fact that some of the measured values are even larger strongly corroborates the predominance of extended structures. Hence, the calculated values are as close to the experimental values as possible with the used Karplus parameters.

It should be noted that the ³J(H^NC^β) values obtained for GRRRG are systematically larger than the corresponding experimental values. This leads to the larger reduced χ² values listed in Table 1. The reason for this discrepancy is that, as for ³J(H^α,C′), the experimental coupling constants are unusually small. This moves them somewhat outside of the region reproducible by the corresponding Karplus function. However, these discrepancies are less pronounced than those obtained for ³J(H^α,C′). For GRRG, we obtained a much closer agreement between experimental and computed values.

The sensitivity analysis described in the Materials and methods showed that the uncertainties of our fitting parameters are rather limited. We estimated an uncertainty of ±0.05 for the reported pPII and β-propensity. The sole exceptions are the propensity values for R3 of GRRRG, for which we observed correlation effects between the pPII and right-handed helical propensities and the ψ-coordinate of the former. When we reduced the latter to simultaneously account for the observed ¹J(N,C′) and amide I VCD, we observed rather significant population redistributions from right-handed helical to pPII. Although the propensities listed in Table 1 represent optimums with regard to the reproduction of the experimental data, the respective uncertainties for pPII and right-handed helical are comparatively large (±0.1). Interestingly, the β-strand propensity is rather insensitive to ψ-variations.

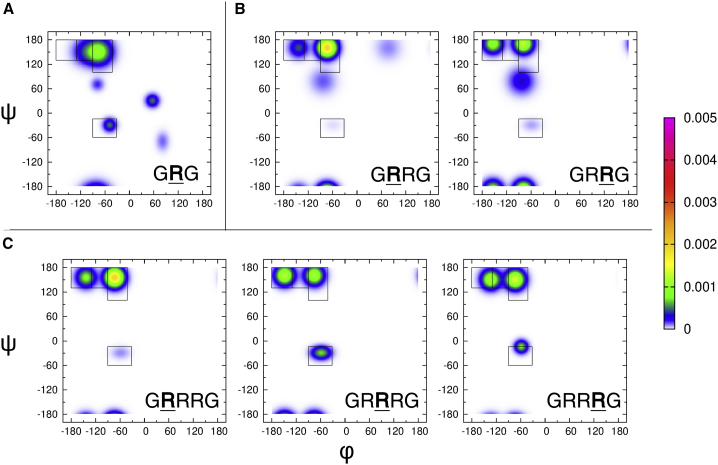
The Ramachandran plots of GRRG and GRRRG as well as the earlier reported plot for GRG (46) are shown in Fig. 3. It is reasonable to assume that the terminal glycine residues produce minimal NNIs to the conformational ensemble of arginine, so we can use it as a good model of the intrinsic propensities of arginine. We will therefore use “Ri” when referring to the “intrinsic arginine.” The Ramachandran plot nicely illustrates the previously reported strong intrinsic preference for pPII (46). Although the pPII basin is the most occupied one in the upper-left region of the Ramachandran plot, the broad population density actually reflects an overlap between pPII and β_t. Ri also exhibits a nearly equal propensity for right- and left-handed helical conformations and weak though not negligible population of γ-turn conformations. This Ramachandran plot, the corresponding Gaussian subdistributions, and their propensity values will be used as the basis to compare the Ramachandran plots of arginine residues in the model peptides GRRG and GRRRG (Fig. 3, b and c; Table 1). The comparison will reveal to what extent the propensities observed for Ri are altered because of the presence of neighboring arginines.

Figure 3.

Ramachandran plots for individual arginine residues in GRG, GRRG, and GRRRG derived from a conformational analysis of these peptides as described in the text. The bold capital R indicates the residue for which the conformational distribution is displayed. The rectangles in the figure mark the mesostates defined in the text. Note that the bright spot in the upper-left quadrant of GRG results from the overlap of the dominant pPII and a less pronounced β-strand basin. Both are clearly separated in the Ramachandran plots of GRRG and GRRRG. The basin below pPII is related the inverse γ-conformation. The rather large but not very pronounced basin in the upper-right quadrant of R1 of GRRG reflects the population of asx-like turn conformations. The color code used for the plots is indicated by the scale bar on the right.

We first assess the differences between the conformational distributions of each arginine by looking closely at the way the populations change. First, it should be noted that pPII propensities of the N-terminal arginines, R1, in both GRRG and GRRRG (0.69) are slightly above the value obtained for Ri (0.58). Generally, the differences between the Ramachandran plots of Ri and R1 are noteworthy for both GRRG and GRRRG. The β-strand conformation has shifted to the left toward more negative ϕ-values. pPII and β-strand have both shifted up to larger ψ-values, as reflected by the larger ¹J(NC^α) values. Moreover, the population of the left-handed helical structures in GRG has been replaced by some minor sampling of asx-turns in the distribution of R1 in GRRG.

Differences between Ri and R2 of GRRG and GRRRG seem to be even more pronounced. A fraction of the population is redistributed from pPII to β-strand in the latter. This effect is most pronounced for R2 of GRRRG, where the β-strand becomes the dominant basin. It is clearly shifted to more negative φ-values. This change is again particularly pronounced for R2, where the β-strand maximum is now at −155° in GRRG and at −150° in GRRG, which positions it in the aβ mesostate region. R2 and R3 do not show any population in the right half of the Ramachandran plot. Compared with all other arginine residues, the fraction of right-handed helical conformations is significantly larger for R2 of GRRRG. The total propensities for extended pPII and the β-strand conformations are on average higher (0.855) for GRRG and GRRR than the value obtained for GRG (0.78). Overall, the obtained results indicate that NNIs in GRRG and GRRRG produce distributions of more extended structures.

In addition to the above comparisons of statistical weights and positions of local maxima of the probability density distribution, we evaluated the dissimilarity between the conformational distributions of the doublet and triplet residues with the intrinsic propensities of Ri using the Hellinger distance (see Eq. 3 in the Materials and methods). This metric has been used previously to quantitatively compare two Ramachandran plots (37). Our calculated Hellinger distances are all summarized in Table 2. For both the doublet and triplet arginine residues, the Hellinger distance (for comparisons with Ri) ranges from 0.32 to 0.36, indicating that all arginines are moderately different from Ri (cf. the criteria in Materials and methods). A comparison of the arginine doublet yields a Hellinger distance of 0.08, suggesting that they are much more similar to each other than they are to Ri. For the arginine triplet, we obtained the following Hellinger distances: 0.1 for R1/R2, 0.15 for R1/R3, and 0.15 for R2/R3. All the values suggest that the compared distributions are moderately similar. These values reveal again that the changes produced by a single neighbor are more pronounced than the one induced by the presence of a second interacting neighbor. However, despite the rather low Hellinger distances for R1/R3 and R2/R3, the increased β-strand propensity of R2 is noteworthy and deserves further consideration (vide supra).

Table 2.

List of Hellinger distances comparing the Ramachandran plots of the indicated residues in the investigated peptides

		Ri	R1	R2
GRRG	R1	0.34	-	-
	R2	0.35	0.13	-
GRRRG	R1	0.33	-	-
	R2	0.35	0.1	-
	R3	0.33	0.15	0.13

Another parameter that can be used to illustrate the influence of NNIs is the conformational entropy. We used the obtained Gaussian model distributions in Eq. 4 to calculate the conformational backbone entropy for GRG as well as for R1R2 in GRRG and for R1R2 and R2R3 pairs in GRRRG. The observed entropy values are listed in Table S4. Because the calculated entropy depends on the mesh size chosen for the probability density distribution (2° for both dihedral angles in our case), a reference system is needed (32,33). We use the 77.7 J · mol⁻¹ · K⁻¹ value that we calculated for an artificially constructed Ramachandran distribution of random coil type conformation, which mimics the situation in which a residue samples the conformationally permissible space (32). As one can infer from the values in Table S4, the entropy values of all arginine-based peptides investigated are considerably lower. For GRG, the obtained value of 67.45 J · mol⁻¹ · K⁻¹ corresponds to a Helmholtz energy difference of approximately 3 kJ · mol⁻¹. We observed a reduction of the entropy by −2.26 with regard to GRG and −0.47 J · mol⁻¹ · K⁻¹ for R1 and R2 of GRRG, which corresponds to a Helmholtz energy loss of only 673 and 140 J · mol⁻¹ at room temperature. For the pentapeptide, the entropy losses are −4.48, −2.59, and −3.75 J · mol⁻¹ · K⁻¹, which correspond to a Helmholtz energy increase of 1.335, 0.772, and 1.118 kJ · mol⁻¹ at room temperature. Compared with the above random coil value, the corresponding entropy values indicate a reduction of the Helmholtz energy at room temperature by more than 4 kJ · mol⁻¹. We can conclude that the NNI-induced entropy reduction of arginine residues is significant in the pentapeptide but rather moderate in the tetrapeptide.

MD simulations of GRRG and GRRRG

We wondered whether the obtained NNIs could be at least qualitatively reproduced by MD simulations. Identifying combinations of peptide/protein force fields and water models that can reproduce particularly experimental J-coupling constants has been attempted by several groups over the last 10 years. Many of the canonical force fields have been optimized to account for the exceptionally high pPII propensity of alanine (48,74,75).

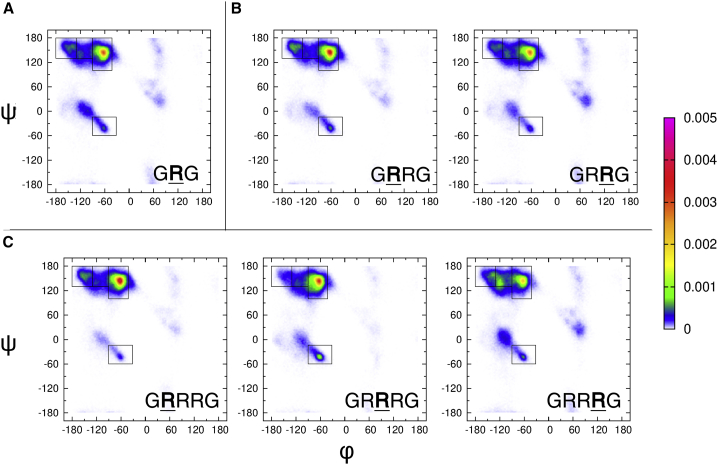
Recently, Zhang et al. showed that Amber ff14SB combined with TIP3P reproduces experimental J-coupling constants and amide I′ profiles for guest alanine in GAG better than other force fields under study (24). Here, we first used Amber ff14SB and CHARMM36m with TIP3P and OPLS-AA/M with TIP4P to produce the Ramachandran distribution of cationic GRG. To access the obtained distributions, we calculated the respective reduced χ² values for J-coupling constants and the VCD profile of amide I′, which are listed in Table S5. Fig. S5 shows the J-coupling constants of central arginine in GRG of these simulations as a function of time. Reduced χ² values and mesostate populations of each trajectory are then calculated using the time period 50–500 ns to account for some of the fluctuations. Of the three force fields examined, CHARMM36m produces by far the best agreement with the experimental data. Additional simulations were carried out using Amber ff14SB and CHARMM36m with the OPC water model. The reduced χ² values, also reported in Table S5, show that the OPC water model consistently and significantly worsens the reproduction of J-coupling constants but slightly improves the reproduction of the VCD profile of amide I′. We therefore used CHARMM36m and TIP3P to produce conformational distributions for cationic GRG, GRRG, and GRRRG. The corresponding Ramachandran plots are shown in Fig. 4, and the mesostate populations as a function of simulation time are shown in Fig. S6. Fig. S6 demonstrates that the mesostate populations remain relatively stable throughout the MD simulations. Fig. S5 shows J-coupling constants as a function of time of each arginine in GRRG and GRRRG. These values also remain relatively stable with the exception of two curves in Document S1. Supporting materials and methods, Figs. S1–S8, and Tables S1–S5, Document S2. Article plus supporting material c. To compare them with the distributions obtained with our Gaussian models, we calculated the occupation of the mesostates defined in Materials and methods to account for some of the fluctuations observed in Figs. S5 and S6. The mesostate populations are listed in Table 3. As already indicated by the respective χ² values (Table S5), the simulations capture the pPII and the overall β-strand propensities of GRG well. Contrary to the respective Gaussian distribution, however, the β-strand population is spread over a broader range of φ-values, thus covering β_t, β_a, and even β_p. The respective populations of the mesostate associated with right-handed helical/type III β-turn structure are comparable. The comparatively small differences between MD and Gaussian distributions are also reflected in the differences between calculated and experimental J-coupling constant (Table 1). The χ_J² value of 2.65 obtained for the MD distribution is larger than the Gaussian value, but the performance is very much comparable with what we observed for GAG.

Figure 4.

Ramachandran of arginine residues in GRG, GRRG, and GRRRG obtained from MD simulations with a CHARMM36m force field combined with a TIP3P water model. Details of the simulations are described in Materials and method. The color code used for the plots is indicated by the scale bar on the right.

Table 3.

Mesostate populations of arginine residues in the Ramachandran plots of the indicated peptides as obtained from MD simulations with a CHARMM36m force field and a TIP3P water model

		GRG	GRRG		GRRRG
		Ri	R1	R2	R1	R2	R3
pPII	Gaussian	0.54	0.27	0.3	0.42	0.21	0.3
	MD	0.46	0.53	0.46	0.59	0.55	0.35
βt	Gaussian	0.11	0.09	0.11	0.16	0.09	0.21
	MD	0.11	0.11	0.14	0.11	0.13	0.19
Aβ	Gaussian	0.11	0.22	0.25	0.14	0.34	0.21
	MD	0.12	0.13	0.11	0.12	0.06	0.12
Pβ	Gaussian	0.01	0.01	0.01	0	0	0.02
	MD	0.06	0.05	0.07	0.05	0.07	0.04
rh	Gaussian	0.01	0.01	0.04	0.13	0.19	0.14
	MD	0.05	0.05	0.03	0.02	0.07	0.04

An inspection of the MD Ramachandran plots of the arginine residues in GRRG and GRRRG (Fig. 4) already indicates that the respective differences between the conformational distributions are much less pronounced than between the respective Gaussian distributions. The Ramachandran plot seems to indicate an enhanced sampling of β-strand conformations only for R3 of GRRRG. This impression is confirmed by an inspection of mesostate populations. For GRRG, the total β-strand populations are 0.29 and 0.32. Corresponding values for GRRRG are 0.28, 0.26, and 0.43, indicating a significant increase of β-strand solely for R3. Not surprisingly, CHARMM36m produces much larger discrepancies between calculated and experimental J-coupling values, as indicated by the rather large χ_J² values (Table 1). Therefore, we must conclude that CHARMM36m, despite its capability to reproduce the experimental values of GRG comparatively well, significantly underestimates NNIs. This notion is further corroborated by Hellinger distances comparing Ri in GRG with the arginines in GRRG and GRRRG. They all lie between 0.11 and 0.18, indicating that the respective distributions are moderately similar.

Because NNIs inferred from our experimental data give rise to more extended conformations, one might well expect this to be caused by repulsive interactions between charged arginine residues. However, if this were the case, one would expect that MD simulations, which should fully account for this type of interaction, should reproduce our experimental results. This is apparently not the case. Therefore, the results of the MD simulations seem to suggest that the electrostatic interactions between positively charged arginine groups do not significantly contribute substantially to the NNIs.

Estimating the length of polyarginine peptides

The results of our Gaussian model-based analysis suggest that NNIs produce two effects. First, it eliminates the populations of the conformations situated in the right half of the Ramachandran plot. This alone reduces the probability that a longer arginine chain would form turns and loops that are a necessity for compact structures. Second, it causes a redistribution from pPII to β-strand and a shift of the latter toward more negative ϕ-values. If this occurs in poly-R segments as well, it will lead to an increase of the end-to-end distances. Overall, the propensities of GRRRG listed in Table 1 seem to suggest an anticorrelation between the β-strand and the pPII population of nearest neighbors, which Schweitzer-Stenner and Toal earlier reported for several GxyG tetrapeptides (76). We wondered to what extent polyarginine with the arginine distribution of R2 in GRRRG would exhibit a $\left|{\overrightarrow{r}}_{00}\right|\propto N^{\nu }$ dependence, where N is the number of residues and the exponent ν is indicative of the compactness/extension of the considered polymer. We calculated the r_oo as a function of the number of residues between the peptide groups using the formalism described in Supporting materials and methods. To this end, we used the truncated distribution employed for the modeling of Raman amide I′ profiles. As shown in Fig. 5, r_oo follows a power law with ν = 0.66 ± 0.02. The obtained statistical uncertainty suggests that the deviation from the 0.59 value for a self-avoiding random coil is significant. We performed the same calculation for poly-R segments assuming the conformational distribution of arginine in GRG. The corresponding plot is shown in Fig. S7. The corresponding exponent is 0.62 ± 0.05. Thus, the margin of error includes the canonical 0.59 value and the 0.66 value obtained with our NNI-based calculation. Hence, we can conclude that although our NNI-based model clearly predicts a scaling behavior for polyarginine that lies above the expectation for a self-avoiding random coil, it is likely that this reflects a combination of intrinsic propensities of R and the influence of NNI. Mao et al. (15) showed a scaling-law-like behavior for plots of residue distances (averaged over all atoms and all peptide segments, i.e., all pairs, triplets, etc.) versus chain separation, which is a measure of the number of considered residues, for a series of protamine sequences and polyarginine. They did not report the respective ν-values. We simulated their curves with MATLAB and found that the scaling exponent for their polyarginine calculation is close to 0.7. This is not too distinct from the above prediction based on our conformational analysis of GRRRG.

Figure 5.

End-to-end distance between the N-terminal and the C-terminal carbonyl oxygen calculated as a function of the difference between the number of residues of a hypothetical polyarginine peptide for which we assumed the Ramachandran distribution obtained for the central residue R2 of GRRRG. The solid line results from a fit of a power law to the calculated data. The scaling coefficient obtained from the fit is 0.66 ± 0.02.

Mao et al. related the extended structure of polyarginine to electrostatic interactions. Their calculations clearly showed that the slope of the above-described plots increases beyond the random coil level with increasing net charge of the considered peptide segment. However, in our case, electrostatic interactions are unlikely to be relevant. At the chosen acidic pH, the chloride concentration is approximately 10 mM. If we take this as the ionic strength, the Debye length would be close to 0.64 nm. The real ionic strength is higher because of the three counterions per peptide in the GRRG and four counterions per peptide in the GRRRG solution. The total value for the ionic strength therefore varied between approximately 280 mM (for the Raman experiments with GRRRG) and 25 mM (for the NMR experiments with GRRG). Hence, the Debye length will be significantly shorter. As shown in Fig. S8, representative distances between charged groups in the investigated peptides are above 1 nm, well outside of the range of electrostatic interactions. The corresponding difference between R1 and R3 is 0.96 nm and significantly larger than the above Debye length.

We would like to emphasize at this point that our findings do not invalidate the role of electrostatics for long polypeptides or even proteins. It is obvious that electrostatic repulsion adds to the excluded volume effect and destabilizes compact conformations formed by nonlocal interactions. However, as demonstrated by the above calculation, end-to-end distances depend on individual conformational distributions of residues, which are determined by intrinsic propensities and local nearest-neighbor interactions. Mao et al. reported a high probability that arginine samples the pPII conformation during MD simulations (15). For the polyarginine case, they report a probability of 0.23 for three or more arginine residues in a row to adopt a pPII conformation. This suggests an average pPII propensity of at least 0.61 for each residue. This value is very close to the pPII propensities that emerged from our analysis of GRG and of the R1 residues of GRRG and GRRRG (Table 1) but is significantly larger than respective values obtained for R2 and R3 of these peptides.

The corresponding counting of β-strand conformations starts with two consecutive residues. Thus, the 0.08 value reported for polyarginine correspond to a minimal propensity of 0.28. This value is higher than the 0.2 obtained from our Gaussian analysis of GRG but is very close to the values obtained for the R1 residues of GRRG and GRRRG and significantly lower than the β-strand propensities of R2 and R3 in both peptides. For right-handed helical conformations, Mao et al. reported that propensity values for helical trimers are negligibly low. This is not at odds with our own per-residue propensities. Even the obtained values for GRRRG would yield an average value of 0.006 for three helical conformations to exist in a row. Overall, we can conclude that the MD simulations of Mao et al. might overestimate the pPII content of polyarginines similarly to what we observed with our own MD simulations (vide supra). However, it deserves to be noted in this context that the pPII trough considered by Mao et al. is larger than ours (−120° < ϕ < −60°). Hence, it covers part of the β_t mesostate, which we count toward the β-strand sampling.

Conclusions

The Gaussian model analysis of J-coupling constants and amide I′ Raman band profiles of GRRG and GRRRG revealed a rather strong nearest-neighbor interaction between arginine residues, which eliminates conformations in the right half of the Ramachandran plot and redistributes conformational sampling from pPII to β-strand. Additionally, they shift the β-strand basin to more negative values. Thus, they cause a more extended average structure of the respective peptides. A Hellinger-distance-based analysis reveals that the R residues in both peptides differ more from that in GRG than they do among each other. However, a calculation of the conformational entropy shows a more significant reduction in GRRRG due to NNIs. A comparison of individual propensities in the latter suggests an anticorrelation between pPII and β-strand propensities, in line with earlier observations (76). In view of the ionic strength values of our samples, it is unlikely that the observed NNIs are electrostatic in nature. They are most likely solvent mediated, as predicted by Avbelj et al. (26,77) This notion is corroborated by much less pronounced NNI effects obtained with MD simulations using CHARMM36m + TIP3P. These calculations should fully account for any electrostatic effects but are likely to underestimate strongly cooperative interactions between solvent molecules, which give rise to solvent-mediated NNIs. We used the conformational distribution of R2 in GRRRG to predict the length of the polyarginine as a function of the number of residues and found that it follows a power law with a scaling coefficient of 0.66, which is statistically significantly larger than the 0.59 value expected for an ideal random coil with excluded volume. We argue that our results show the relevance of individual propensities and their dependence on NNIs for the conformational sampling of peptides and proteins in aqueous solutions, which do not adopt collapsed states (ν > 0.5). In line with an earlier suggestion of Scheraga and co-workers, we suggest using the term statistical coil for the conformational manifolds of such systems (78).

Finally, it is noteworthy that MD simulations of a single arginine residue in peptide segments of H4 histone tails produced a Ramachandran plot that bears some similarity with what we observed for the central residue of GRRRG (79). In both cases, pPII and β-strand basins are clearly separated and nearly equally populated. The population of right-handed helical conformations is still significant, though less pronounced, than the ones for pPII and β-strand. In the peptide, arginine is flanked by a lysine toward the N- and by a valine toward the C-terminus. The authors used an Amber99SB force field combined with the TIP3P water model for their calculations.

Associated content

The following tables and figures can be found in the Supporting materials and methods: Karplus plots for the utilized coupling parameters, a visualization of mesostates, a plot of the end-to-end distance between carbonyl oxygens of a hypothetical polyarginine peptide, visualizations of inter-residue distance in extended GRRG and GRRRG, and a table listing conformational entropies.

Author Contributions

B.M. performed the reported NMR, Raman, FTIR, and VCD experiments. B.A. performed the MD simulations. B.M. and R.S.-S. analyzed the experimental data and wrote most of the article. B.A. wrote part of the MD section of the article. H.S and B.U. supervised the NMR experiments and MD simulations and contributed to the discussion of the data.

Editor: Scott Showalter.