Torsional stress can regulate the unwrapping of two outer half superhelical turns of nucleosomal DNA

Significance

The torsional stress to chromatin structure plays an important role in eukaryotic cell where DNA-binding proteins such as RNA polymerase and chromatin remodeling complexes actively apply torsional stress. Under torsional stress, chromatin keeps balance between the integrity of the eukaryotic genome for storage of the genetic information and the accessibility of the DNA for gene expression. Using all-atom molecular dynamics simulations, we found that positive torsion facilitated asymmetric unwrapping of the DNA without a large extension of the DNA, while negative torsion suppressed unwrapping. Our results suggest that the stability of individual nucleosomes in chromatin can be changed or tuned by torsional stress, thereby DNA accessibility of regulatory proteins can be changed to regulate gene expression.

Abstract

Torsional stress has a significant impact on the structure and stability of the nucleosome. RNA polymerase imposes torsional stress on the DNA in chromatin and unwraps the DNA from the nucleosome to access the genetic information encoded in the DNA. To understand how the torsional stress affects the stability of the nucleosome, we examined the unwrapping of two half superhelical turns of nucleosomal DNA from either end of the DNA under torsional stress with all-atom molecular dynamics simulations. The free energies for unwrapping the DNA indicate that positive stress that overtwists DNA facilitates a large-scale asymmetric unwrapping of the DNA without a large extension of the DNA. During the unwrapping, one end of the DNA was dissociated from H3 and H2A-H2B, while the other end of the DNA stably remained wrapped. The detailed analysis indicates that this asymmetric dissociation is facilitated by the geometry and bendability of the DNA under positive stress. The geometry stabilized the interaction between the major groove of the twisted DNA and the H3 αN-helix, and the straightened DNA destabilized the interaction with H2A-H2B. Under negative stress, the DNA became more bendable and flexible, which facilitated the binding of the unwrapped DNA to the octamer in a stable state. Consequently, we conclude that the torsional stress has a significant impact on the affinity of the DNA and the octamer through the inherent nature of the DNA and can change the accessibility of regulatory proteins.

The genome DNA of eukaryotes is stored compactly in a nucleus and folded into a higher order structure called chromatin to protect the DNA from being damaged by radiation and so on. At the same time, decompaction of the chromatin structure is also required for the control of gene regulation in cellular processes for transcription, replication, repair, and recombination. Nucleosome is the fundamental structural unit of chromatin and is composed of histone proteins and DNA. Its crystal structure revealed that within the nucleosome, 146 or 147 base pairs of DNA wrap 1.75 times around an octameric histone core (1). Although the nucleosome is stable in physiological conditions, thermal fluctuations cause spontaneous partial unwrapping of nucleosomal DNA from the histone core. Experiments have found a dynamic motion between an open state with partially unwrapped DNA and a closed state with fully wrapped DNA (2, 3), which is often referred to as the breathing motion of the nucleosome. Förster resonance energy transfer (FRET) experiments (4–6) showed that in the absence of salt, the outer superhelical turn of nucleosomal DNA (hereinafter referred to as “the outer turn of DNA”) within the nucleosome repeatedly unwraps and rewraps.

In addition to the spontaneous unwrapping of the outer turn of DNA, some DNA-binding proteins, such as transcribing RNA polymerase (RNAP) (7, 8) and chromatin remodelers (9, 10), actively apply forces to unwrap or rewrap nucleosomal DNA. During transcription, RNAP moves along the DNA helix and generates positive stress on the DNA in front of the RNAP and negative stress behind it. Consequently, DNA downstream and upstream of the polymerization site are overwound (either overtwisted or positively supercoiled) and underwound (either undertwisted or negatively supercoiled), respectively (11). As nucleosome core particles prefer to bind negatively supercoiled DNA, overwound DNA ahead of the RNAP would destabilize the DNA–histone or histone–histone interactions in the nucleosome, and underwound DNA behind the RNAP would promote reassembly of nucleosomes (12, 13).

Single-molecule experiments have shown that torsional stress by mechanical force has a significant impact on the stability of the nucleosome (5, 14, 15). Another experiment by scanning force microscopy showed that overwound DNA led to larger nucleosome opening angles than relaxed or underwound DNA (16), suggesting that the overwound DNA facilitates the unwrapping of the outer turn of DNA.

However, the mechanism of unwrapping and rewrapping the outer turn of DNA is not well known at the atomic level. In order to understand how the torsional stress on the outer turn of DNA affects the stability of the nucleosome, we carried out all-atom molecular dynamics (MD) simulations of the nucleosome under torsional stress. Previously, we investigated unwrapping of two half superhelical turns of nucleosomal DNA from either end of the DNA (hereinafter referred to as “two outer half turns of DNA”) without torsional stress (17–20). The free energy under torsional stress in this article will give further insight into understanding the unwrapping of the outer turn of DNA.

Results

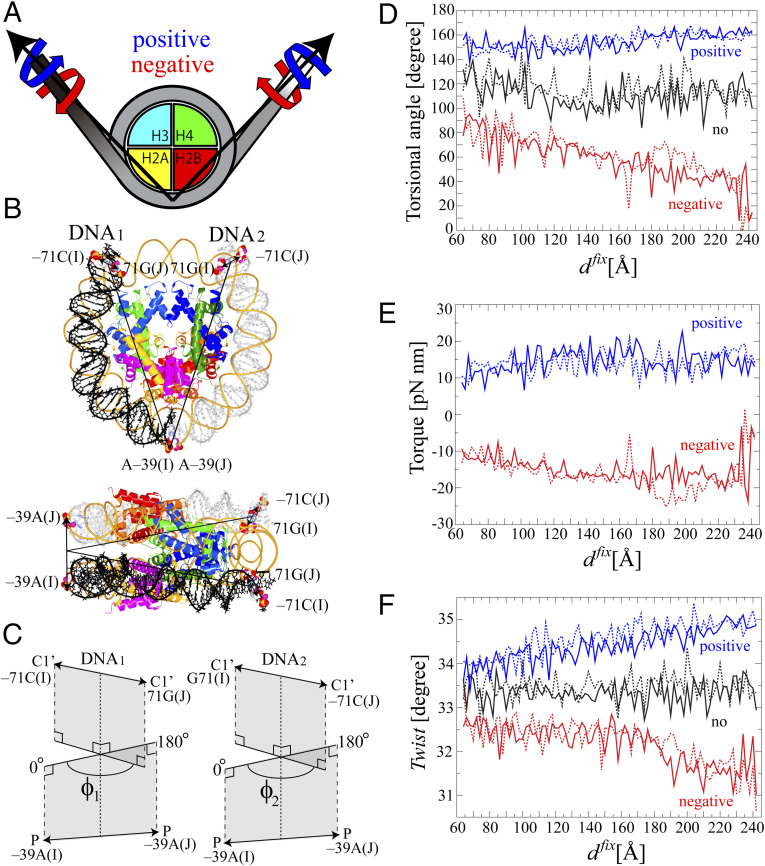
We applied positive or negative torsional stress at the third base pair from each end of the DNA to suppress base pair breakup at either end of the DNA as shown in Fig. 1 (see SI Appendix for the setup and the procedure of the simulations in SI Appendix, Fig. S1). Fig. 1A shows the schematic picture of the nucleosome with the direction of the positive and negative stress during the umbrella sampling simulations, while the atoms on which the stress was imposed are shown in the space-filled model (Fig. 1B). The definition of the torsion to describe the torsional stress is shown in Fig. 1C. As the unwrapping of the DNA proceeds, the torsion increased and decreased under positive and negative stress, respectively (Fig. 1D), according to the torsional stress imposed by Eq. 2. The magnitude of the applied torque was mostly within 10 to 20 pN nm (Fig. 1E), which is comparable with the Escherichia coli RNAP stall torque of ∼11 pN nm (8). DNA twist gradually increased and decreased upon addition of the torsional stress (Fig. 1F). The values of the twist, ∼33.0° ± 2.0°, were within the range where the elastic property of the DNA is maintained (21–23).

Fig. 1.

The system of the nucleosome for simulations under torsional stress. We used a crystal structure of a nucleosome with α-satellite palindromic 147 bp DNA (Protein Data Bank code: 1kx5) (46). The histone tails were truncated to facilitate the unwrapping of the DNA. Consequently, residues 46 to 132 in H3, 25 to the C terminal in H4, 16 to 114 in H2A, and 32 to 121 in H2B were used. (A) Schematic representation of the system of the nucleosome for torsional stress. The axes of the torsional stress are shown as arrows. The torques are applied to the ends of the DNA anticlockwise and clockwise along the axes under positive (blue) and negative (red) stress, respectively. (B) The initial structure of the nucleosome is shown in tube model with the view from top and side. The histone proteins, H3, H4, H2A, and H2B, are shown in blue, green, yellow, and red, respectively. DNA₁ and DNA₂ are shown in black and gray, respectively. The base pairs on which the torsional restraints were imposed, −71 C:G 71 in DNA_{1 or 2} and −39 A in DNA_{1 or 2} located opposite the dyad, are shown in the space-filled model. (C) The definition of the torsional angles of ϕ₁ and ϕ₂. The torsional angle of ϕ₁ is calculated using the positions of two pairs of atoms. The first pair is the two C1’ atoms of −71 C in chain I and 71 G in chain J, and the other pair is the two phosphorus atoms of −39 A in chain I and chain J located opposite the dyad. The axis of torsion was defined as the line passing through the two midpoints between the two C1’ atoms and between the two phosphorus atoms. Then, the torsional angle of ϕ₁ is defined as the angle between a plane which includes the two C1’ atoms and the axis and another plane which includes the two phosphorus atoms and the axis. The torsional angle of ϕ₂ is defined in a similar way to the torsional angle of ϕ₁. (D) Torsional angle, (E) torque, and (F) Twist in DNA₁ and DNA₂ are plotted against d^fix during the last 50 ns of the umbrella sampling simulations. These parameters show the structural response of each of 90 replicas to the torsional restraint. Twist of the base pair step parameter was analyzed for the third to 35th base pairs from the end of the DNA_{1 or 2}. The effect of the torsional stress on the DNA was incorporated as follows in a similar way to the procedure used by refs. 21, 22: $V_i^{stress}=k_{1i}{\left({\varphi }_1-{\varphi }_1^0\right)}^2+k_{2i}{\left({\varphi }_2-{\varphi }_2^0\right)}^2$ for the i-th window. Both ${\varphi }_1^0$ and ${\varphi }_2^0$ were set at 0° and 180° for the generation of positive and negative stress, respectively. Torque was calculated by $T_i^{stress}=2k_{1i}\left({\varphi }_1-{\varphi }_1^0\right)+2k_{2i}\left({\varphi }_2-{\varphi }_2^0\right)$. Details are given in Materials and Methods and SI Appendix, Supplementary Methods.

Free Energy for Unwrapping the DNA.

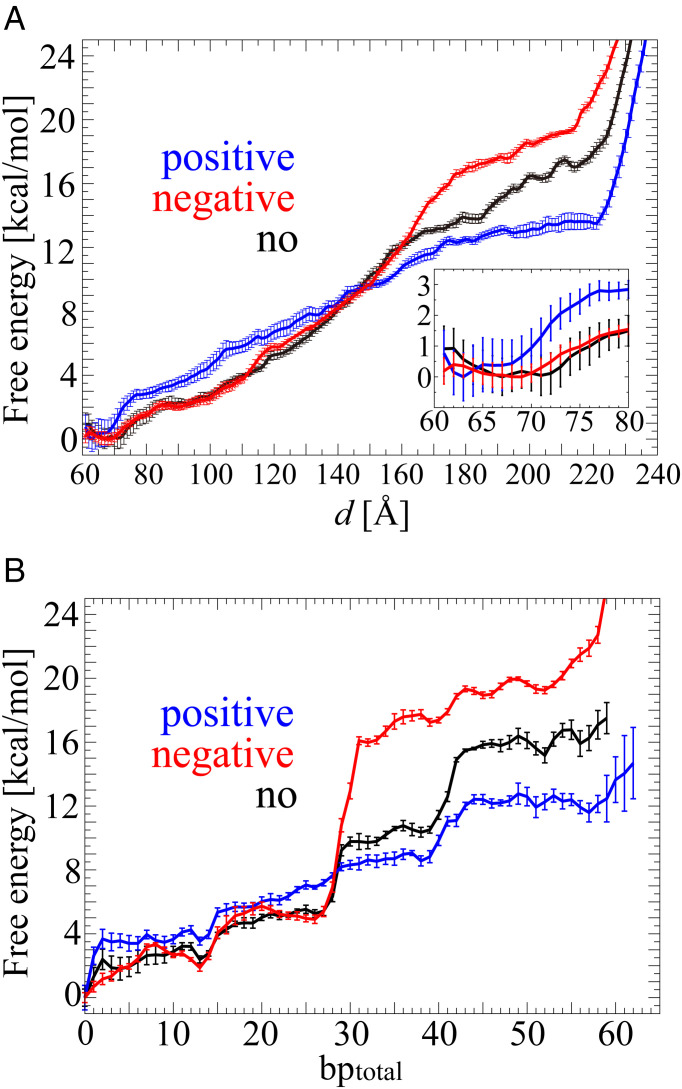
We calculated the free energy for unwrapping the DNA against the DNA end-to-end distance d using the weighted histogram analysis method (WHAM) algorithm (24, 25) (Fig. 2A). The free energies had a global minimum free energy of 0.0 kcal/mol when d = 63, 69, and 67 Å under positive, negative, and no stress, respectively. Up to d = 145 Å, the free energy under positive stress was larger than those under negative and no stress, indicating more free energy is required to extend the distance between two DNA ends under positive stress. In particular, the differences in the free energy up to that distance among the three torsional conditions come from the sharper rise of the free energy from d = ∼63 to 76 Å under positive stress compared with those from d = ∼70 to 85 Å under negative and no stress, where the DNA started to dissociate from the H3 αN-helix. This indicates that the interaction between the DNA and the H3 αN-helix was stronger under positive stress. A relatively moderate increase in the free energy followed the sharp rise. The gradient of the free energy under positive stress was nearly constant up to d = 170 Å, while those under negative and no stress gradually increased along d. Eventually, free energies became larger than that for positive stress at d = ∼150 Å. When two outer half turns of DNA were fully unwrapped, the free energies were 13.5 kcal/mol at d = 220 Å, 19.5 kcal/mol at d = 214 Å, and 17.0 kcal/mol at d = 214 Å under positive, negative, and no stress, respectively. After those distances, the free energies rapidly increased because the DNA started to be stretched.

Fig. 2.

Free energies for unwrapping the DNA against d (A) and bp_total (B) under positive (blue), negative (red), and no (black) torsional stress. The averages of the SEMs in the free energy along d (within the range of sufficient sampling data) were 0.41, 0.24, and 0.31 kcal/mol under positive, negative, and no stress, respectively. Inset: enlargement of the free energy from d = 60 to 80 Å. The averages of the SEMs in the free energy along bp_total were 0.45, 0.30, and 0.38 under positive, negative, and no stress, respectively. The SEMs are shown in error bars along the free energy.

To interpret the unwrapping process from a structural viewpoint, we changed the perspective of the free energy as a function of the total number of unwrapped base pairs (hereafter referred to as bp_total) using SI Appendix, Eqs. S7 and S8 (Fig. 2B). The nucleosome under positive, negative, and no stress had a global free energy minimum of 0.0 kcal/mol at bp_total = 0. In all cases, the free energies for positive, negative, and no stress reached 12.0, 19.3, and 15.2 kcal/mol at bp_total = ∼52, respectively, when the unwrapping of two outer half turns of DNA was completed. During the unwrapping, distinctive increases in the free energy were observed at bp_total = 0, ∼13, 26, 39, and 52 under all the three cases. A remarkably sharp increase in free energy was observed at bp_total = 26 under negative and no stress but not under positive stress.

Large-Scale Asymmetric Unwrapping of the DNA under Positive Stress.

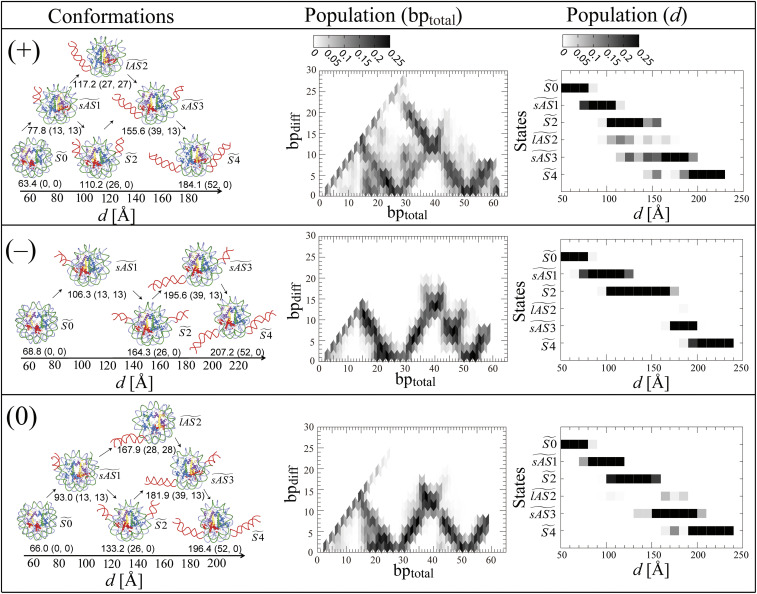
Next, we examined how the DNA unwrapping process advanced. To address it, we counted the difference in the number of unwrapped DNA base pairs, bp_diff, which is defined as |bp₁ − bp₂|, where bp₁ and bp₂ denote the number of unwrapped base pairs from DNA₁ and DNA₂, respectively (hereafter bp is used for the number of unwrapped base pairs from one end if it is not necessary to distinguish between the two ends of the DNA) (Fig. 3).

Fig. 3.

Unwrapping paths under positive (+), negative stress (−), and no stress (0). The left-hand column shows representative conformations observed with d and (bp_total, bp_diff) in parentheses. bp_total is the sum of bp₁ and bp₂, where bp₁ and bp₂ are numbers of unwrapped base pairs at the ends of DNA₁ and DNA₂, respectively. bp_diff is the difference between bp₁ and bp₂, defined as | bp₁ – bp₂ |. The unwrapped DNA is shown in red. The orientation of each conformation is different from the others for the sake of visual clarity. The arrows indicate possible small- and large-scale asymmetric unwrapping of the DNA from states $\stackrel{\sim }{S0}$ to $\stackrel{\sim }{S4}$ (see also Fig. 4A). The middle column shows the average population of conformations as a function of bp_total and bp_diff. The average was calculated according to SI Appendix, Eq. S8. The population is normalized to the total population of bp_diff with the same bp_total. The values of bp_diff more than 0.25 are set at 0.25. The right-hand column shows the average populations of six conformational states, $\stackrel{\sim }{S0}$, $\stackrel{\sim }{sAS1}$, $\stackrel{\sim }{S2}$, $\stackrel{\sim }{lAS2}$, $\stackrel{\sim }{sAS3}$ and $\stackrel{\sim }{S4}$, against d. The average was calculated according to SI Appendix Eq. S8 at the interval of 10 Å with d for each state and the remaining state. The population for each state is normalized to the total population of these states with the same d. The values of any population with more than 0.25 are set at 0.25.

We observed that there are small-scale and large-scale asymmetric paths (where one end is unwrapped a lot but the other end is not so much) for the unwrapping of the DNA in the figure. The branches of the transitional paths were observed at bp_total = ∼13, 26, 39, and 52, corresponding to bp_total where the free energy increases distinctively in Fig. 2B.

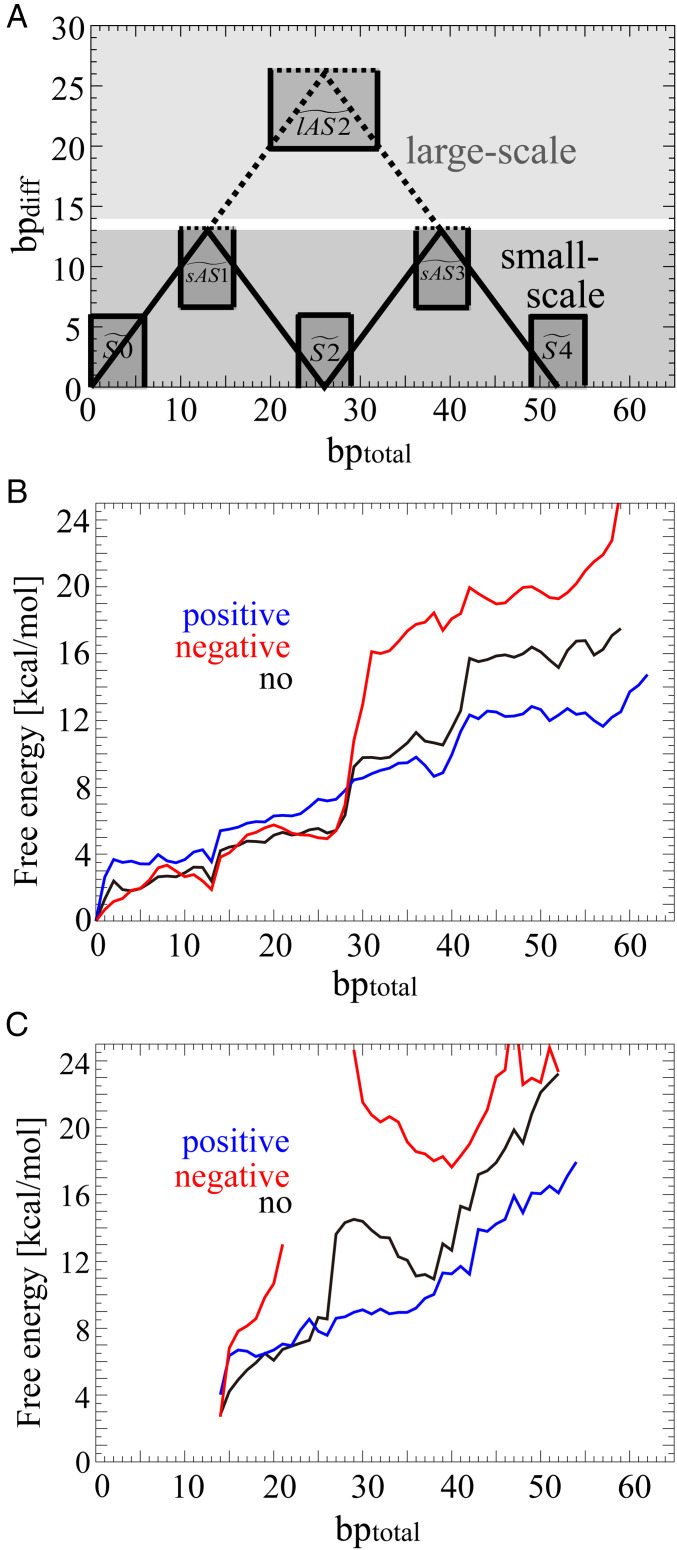
To understand the feature of these conformations at the branches of the transitional paths, six conformational states of $\stackrel{\sim }{S0}$, $\stackrel{\sim }{sAS1}$, $\stackrel{\sim }{S2}$, $\stackrel{\sim }{lAS2}$, $\stackrel{\sim }{sAS3}$, and $\stackrel{\sim }{S4}$ were defined according to bp_total and bp_diff as shown in Fig. 4A. The representative conformations, corresponding to these states under positive (+), negative (−), and no stress (0), are shown in the left-hand column of Fig. 3, respectively. $\stackrel{\sim }{S0}$ contains conformations around (bp_total, bp_diff) = (0, 0), the initial state where the DNA is tightly wrapped (symmetric 0); $\stackrel{\sim }{sAS1}$ is around (bp_total, bp_diff) = (∼13, ∼13), a state where one end of the DNA dissociates from H3 (small-scale asymmetric 1); $\stackrel{\sim }{S2}$ is around (bp_total, bp_diff) = (∼26, ∼0), a state where both ends of DNA_{1 or 2} disconnect from H3 (symmetric 2); $\stackrel{\sim }{lAS2}$ is around (bp_total, bp_diff) = (∼26, ∼26), a state where one end of the DNA dissociates from H3 and H2A-H2B, but the other end of the DNA remains unwrapped (large-scale asymmetric 2); $\stackrel{\sim }{sAS3}$ is around (bp_total, bp_diff) = (∼39, ∼13), a state where one end of the DNA dissociates from H3 and H2A-H2B, and the other end of the DNA dissociates from H3 (small-scale asymmetric 3); and $\stackrel{\sim }{S4}$ is around (bp_total, bp_diff) = (∼52, ∼0), the final state of the unwrapping of two outer half turns of DNA where both ends of the DNA dissociate from H3 and H2A-H2B (symmetric 4). $\stackrel{\sim }{sAS3}$ can be reached from $\stackrel{\sim }{lAS2}$ by unwrapping the other end of the DNA from H3 or from $\stackrel{\sim }{S2}$ by the continuous unwrapping of one end of the DNA from H2A-H2B.

Fig. 4.

Free energies for the small- and large-scale asymmetric unwrapping of the DNA against bp_total. According to the classification of the probability distribution (A), the free energies of the small- (B) and large-scale (C) unwrapping are shown in blue, red, and black under positive, negative, and no stress, respectively. The probability distribution calculated according to SI Appendix, Eq. S2 was classified as that in the small-scale asymmetric unwrapping of the DNA when bp_diff ≤ 13 (dark gray area) and as that in the large-scale asymmetric unwrapping of the DNA when bp_diff ≥ 14 (thin gray area). Definition of the six states of $\stackrel{\sim }{S0}$, $\stackrel{\sim }{sAS1}$, $\stackrel{\sim }{S2}$, $\stackrel{\sim }{lAS2}$, $\stackrel{\sim }{sAS3}$, and $\stackrel{\sim }{S4}$ are also shown to be (0 ≤ bp_total ≤ 6, 0 ≤ bp_diff ≤ 6), (0 ≤ bp_total ≤ 16, 7 ≤ bp_diff), (23 ≤ bp_total ≤ 29, 0 ≤ bp_diff ≤ 6), (20 ≤ bp_total ≤ 32, 20 ≤ bp_diff), (36 ≤ bp_total ≤ 42, 7 ≤ bp_diff), and (49 ≤ bp_total ≤ 55, 0 ≤ bp_diff ≤ 6), respectively. The solid lines connecting $\stackrel{\sim }{S0}$, $\stackrel{\sim }{sAS1}$, $\stackrel{\sim }{S2}$, and $\stackrel{\sim }{sAS3}$ and the dotted lines connecting $\stackrel{\sim }{sAS1}$, $\stackrel{\sim }{lAS2}$, and $\stackrel{\sim }{sAS3}$ denote representative transitional paths for small- and large-scale asymmetric unwrapping, respectively. Free energies of the small- and large-scale unwrapping were calculated according to SI Appendix, Eq. S7. The ranges of bp_total for the free energies of the large-scale unwrapping were considered to be 14 to 54 under positive, 14 to 21 and 29 to 52 under negative, and 14 to 52 under no stress.

The middle and right-hand columns of Fig. 3 show the populations of these conformational states against bp and d, respectively. The right-hand column of Fig. 3 shows that the populations of $\stackrel{\sim }{S2}$, $\stackrel{\sim }{lAS2}$, and $\stackrel{\sim }{sAS3}$ were remarkably different in the range of d = 100 to 180 Å among the three stress conditions. Under negative stress, the state from d = 120 to 170 Å is mainly located at $\stackrel{\sim }{S2}$, where (bp_total, bp_diff) is (∼26, ∼0). SI Appendix, Fig. S2 shows representative conformations in the range of d from 130 to 170 Å (free energy from 6.9 to 15.0 kcal/mol), where $\stackrel{\sim }{S2}$ is exclusively dominant. The exclusive existence of $\stackrel{\sim }{S2}$ in the wide ranges of d and the free energy is the cause of the remarkably sharp rise of the free energy with regard to bp_total under negative stress. In contrast to negative stress, the range of the exclusive existence of $\stackrel{\sim }{S2}$ was narrower from d = 120 to 130 Å under no stress, and there was no exclusive existence of $\stackrel{\sim }{S2}$ under positive stress.

Comparing the populations of the states among the three stress conditions, the large-scale asymmetric unwrapping of the DNA $\left(\stackrel{\sim }{lAS2}\right)$ clearly appeared only under positive stress. Furthermore, compared with no stress, the populations against d have shifted to the left under positive stress, while they have shifted to the right under negative stress. These results indicate that the process of unwrapping the DNA proceeded faster and slower against d under positive and negative stress, respectively. Under positive stress, it is possible to reach $\stackrel{\sim }{S4}$ conformation even at d = ∼150 Å. Moreover, the large-scale asymmetric unwrapping at $\stackrel{\sim }{lAS2}$ was observed in the wider region, d = ∼100 to 170 Å, under positive stress, while $\stackrel{\sim }{lAS2}$ was observed in two places, d = ∼160 to 190 Å, under no stress. Consequently, positive stress facilitated the unwrapping of the DNA, while negative stress suppressed it.

The Free Energies for the Small- and Large-Scale Asymmetric Unwrapping of the DNA.

We calculated free energies for the small- and large-scale asymmetric unwrapping of the DNA using SI Appendix, Eq. S8 (Fig. 4 B and C). The probability distribution for the small- and large-scale asymmetric unwrapping of the DNA were classified with bp_diff ≤ 13 and bp_diff ≥ 14 (Fig. 4A), respectively. ΔG_lAS2/S2, the difference between G_lAS2 (the free energy in $\stackrel{\sim }{lAS2}$) and G_S2 (the free energy in $\stackrel{\sim }{S2}$), decides the transitional paths for the large- and small-scale asymmetric unwrapping. ΔG_lAS2/S2 (= G_lAS2 − G_S2) were estimated to be about 2.0, no data, and 9.2 kcal/mol under positive, negative, and no stress, respectively (SI Appendix, Fig. S3), indicating that the large-scale asymmetric unwrapping of the DNA is facilitated under positive stress. It should be noted that positive stress makes ΔG_lAS2/S2 smaller by increasing G_S2 ($=\mathrm{\Delta }{\text{G}}_{\text{H}3\text{\_first}}^{\text{small}}+\mathrm{\Delta }{\text{G}}_{\text{H}3\text{\_second}}^{\text{small}}$, a higher value of 7.2 kcal/mol than that of 5.3 kcal/mol for no stress) and decreasing G_lAS2 ($=\mathrm{\Delta }{\text{G}}_{\text{H}3\text{\_first}}^{\text{small}}+\mathrm{\Delta }{\text{G}}_{\text{H}2\text{A}-\text{H}2\text{B\_first}}^{\text{large}}$, a lower value of 9.2 kcal/mol than that of 14.5 kcal/mol for no stress), which both facilitate the large-scale asymmetric unwrapping of the DNA.

Positive Stress Utilizes the Geometry of the DNA (Minor Groove) to Stabilize the DNA–H3 Interaction.

The crystal structure of the nucleosome (1) used as the initial atomic model shows the minor grooves of the DNA at superhelical location (SHL) = ±6.5 partially interact with the H3 αN-helix. Under positive stress, both of the minor grooves of the twisted DNA rotated and further strengthened the interaction with the H3 αN-helix from d = 63 to ∼76 Å (SI Appendix, Fig. S4 A–D) on both sides of the DNA. A sharp increase in the free energy of 3.6 kcal/mol from d = 63 to ∼76 Å (Fig. 2 A, Inset) would be required to break the stable interaction between the minor groove of the DNA and the H3 αN-helix. In contrast to positive stress, the frequency of simultaneous contact on both sides of the DNA was much smaller under negative stress (SI Appendix, Fig. S4 A and B).

Next, we measured how long contact between the DNA and the H3 αN-helix was maintained in the small-scale asymmetric unwrapping of the DNA from $\stackrel{\sim }{S0}$ to $\stackrel{\sim }{S2}$ through $\stackrel{\sim }{sAS1}$. From $\stackrel{\sim }{sAS1}$ to $\stackrel{\sim }{S2}$, contact was retained for the longest under positive stress (SI Appendix, Fig. S4E). This indicates that contact between the twisted minor groove of the DNA and the H3 αN-helix was stronger, and another high energy of 3.6 kcal/mol (Fig. 4B) (see also $\mathrm{\Delta }{\text{G}}_{\text{H}3\text{\_second}}^{\text{small}}$ in SI Appendix, Fig. S3) would be used for breaking the remaining interaction with H3 αN-helix when the small-scale asymmetric unwrapping advances.

Positive Stress Utilizes the Inherent Dynamic Nature of the DNA (Bendability and Flexibility) to Destabilize the DNA–H2A-H2B Interaction.

Not only the DNA–H3 interaction but also the DNA–H2A-H2B interaction should affect the free energies at the states of $\stackrel{\sim }{lAS2}$, $\stackrel{\sim }{sAS3}$, and $\stackrel{\sim }{S4}$. Here, we analyzed two physical quantities of the DNA as the enthalpic contribution: 1) the number of contacts between the DNA and the octamer and 2) the local bending angles for base pairs of DNA_{1 or 2}. One may expect that positive and negative stress change the pattern of the contact between the minor groove of the DNA at SHL = ± 5.5 and the H2A-H2B L1-L2 loops as was found in contact between the minor groove of the DNA at SHL ± 6.5 and the H3 αN-helix. However, the number of contacts did not show any clear difference (SI Appendix, Fig. S5). This is thought to be because the minor groove of the DNA at SHL = ± 5.5 has already been facing the H2A-H2B L1-L2 loops under no stress. This implies that the strength of the interfacial interaction between the DNA and the H2A-H2B L1-L2 loops did not change under stress and did not contribute to the difference in their free energies.

SI Appendix, Fig. S6 shows that the local bending angles decreased as the unwrapping of the DNA proceeded under positive stress, while they increased under negative stress. Compared with the bend angles under no stress, the bends of the base pair steps of −71 C:G 71/−70 A:T 70, −68 T:A 68/−67 A:T 67, −60 T:A 60/−59 G:C 59, −58 C:G 58/−57 A:T 57, and −51 T:A 51/−50 A:T 50 increased by ∼2.0° under negative stress and decreased by ∼1.0° under positive stress. The pyrimidine–purine steps such as TA and CA dinucleotide steps have been generally found to be more flexible and more easily bent than other steps (26, 27). Consequently, stress induces conformational changes at these dinucleotide steps; positive stress makes unwrapped DNA straighter, and negative stress makes it more bent.

As for the entropic contribution, we examined the conformational entropies of DNA against bp according to SI Appendix, Eq. S13 as shown in SI Appendix, Fig. S7. The entropy under positive stress was lower than under no stress, probably because the unwrapped DNA under positive stress is straightened, and the DNA became less flexible. In contrast, the entropy of the DNA under negative stress was larger than that under no stress. This indicates that the DNA became more flexible, probably due to the partial deformation of the DNA. These results indicate that the gain in the conformational entropy, which decreased the free energy for unwrapping the DNA, increased in order under positive, no, and negative stress, while the internal energy required to deform the DNA for unwrapping, which increased the free energy, increased in order under positive, no, and negative stress. For example, the DNA of the representative conformation at d = ∼164 Å under negative stress was sharply bent and partially underwound (the left-hand column of Fig. 3 for negative stress or SI Appendix, Fig. S2C). It should be noted that the conformation was located at a steep gradient of the free energy at d = ∼150 to 180 Å (or at the end of the state of $\stackrel{\sim }{S2}$), where the force to unwrap was estimated to be ∼17 pN (Fig. 2A). The maximum force was estimated to be 27 pN between d = 163 and 165 Å. This value corresponds to the force of ∼30 pN when a single DNA starts to unwind (28). The deformation at d = ∼165 Å under negative stress is thought to be because the increased flexibility of the DNA enabled the DNA to deform against the extension of d. In contrast to negative stress, maximum forces of 14 and 24 pN were also observed in the end of $\stackrel{\sim }{S2}$ at d = 155 and 159 Å under positive and no stress, respectively, where any DNA melting as was observed under negative stress was not observed.

Therefore, the internal energy of the DNA for unwrapping is mainly thought to cause the difference in the free energies of the states of $\stackrel{\sim }{lAS2}$, $\stackrel{\sim }{sAS3}$, and $\stackrel{\sim }{S4}$.

Discussion

Comparison with the Experimental and Computational Data.

The free energy had a local minimum at bp_total = 13, which can explain why the partially unwrapped nucleosome structures have been observed by cryogenic-electron microscope (cryo-EM) (29). The free energy for the entire unwrapping of two outer half turns of DNA was estimated to be ∼15 kcal/mol without torsional stress. This value is higher than the experimental values which range ∼5 to 12 kcal/mol; however, these values are likely to depend on how the experimental data were handled (4, 5, 30, 31).

The free energy in total indicates that positive torsion facilitated unwrapping the DNA, while negative torsion suppressed unwrapping (or facilitated rewrapping) the DNA. This is consistent with the experimental data which showed strong destabilization of the nucleosome under a positive torque (12, 13). This also supports the “twin-helix” domain model (11) that overtwisted DNA ahead of the RNAP disassembles the nucleosome, and undertwisted DNA behind the RNAP reassembles the nucleosome (12, 13).

Large-scale asymmetric unwrapping of nucleosomal DNA has been observed by experiments of time-resolved small-angle X-ray scattering (32, 33), FRET (34), high-speed atomic force microscopy (35), and cryo-EM (29). Large-scale asymmetric unwrapping was also observed in transcription (36) and remodeling (10) processes. Our previous all-atom MD simulation of the nucleosome without torsional stress (20) has observed small-scale asymmetric unwrapping of the DNA in $\stackrel{\sim }{sAS1}$ and $\stackrel{\sim }{sAS3}$. In addition to $\stackrel{\sim }{sAS1}$ and $\stackrel{\sim }{sAS3}$, MD simulations of the nucleosome using coarse-grained models have observed large-scale unwrapping in $\stackrel{\sim }{lAS2}$ (37, 38).

The increased bendability of the DNA under negative stress is likely to be a cause for the stabilization of the nucleosome. In general, the high-affinity sequences such as AT-rich sequences bend toward the minor groove and have higher bendability (34, 39, 40). Decrease and increase in the bending angle of a single DNA under positive and negative torsional stress, respectively, have been observed by all-atom MD simulations (21–23). These previous reports are consistent with our present results.

Interpretation of Experimental Data by Single-Molecule Experiments.

The stabilization of the nucleosome under positive and negative stress was experimentally studied (14, 41, 42). Sheinin et al. used an angular optical trapping method to measure the extension of the DNA with the mononucleosome under extension force and torque (14). The occurrence of the release of the outer turn of DNA increased under positive and negative stress and was interpreted as the interaction between the outer turn of DNA and H2A-H2B being stabilized under positive and negative stress (14). Bancaud et al. (41) applied the same technique to single nucleosome arrays to measure the extension of the arrays under extension force and rotation. The rotation-extension curve under positive and negative stress was interpreted as being caused by the positively and negatively crossed linker DNAs at the entry/exit of the nucleosomes in a tightly wrapped state (42). The studies by Sheinin et al. and Bancaud et al. are consistent with each other in terms of the stability of the nucleosome under stress. However, the cause of the stability was considered differently. Sheinin et al. (14) considered the stabilization of the DNA–H2A-H2B interaction along the reaction coordinate of the unwrapped base pairs of the DNA while Bancaud et al. (41) considered the stabilization of the crossed linker DNA along the reaction coordinate of the supercoil density.

Sheinin et al. (14) analyzed the number of released base pairs of the DNA (including a high-affinity 601-positioning element) on both ends from the force-extension curve by implicitly assuming that the nucleosome unwraps symmetrically. In a FRET experiment, however, Ngo et al. (34) showed asymmetric unwrapping of the nucleosome with a 601-positioning sequence (under no stress) and suggested that it was due to the difference in rigidity between the first and second halves of the DNA sequence. Asymmetric unwrapping of the nucleosome with the sequence of Windom 601L has also been observed (under no stress) at a high ionic concentration of more than 1 M MgCl₂ by all-atom MD simulations (43). Asymmetric unwrapping of DNA with an asymmetric sequence would be more likely to occur than for DNA with a symmetric sequence as was used in our study.

Consequently, the force-extension curves might need to be reinterpreted by taking into consideration other factors such as linker DNA crossing, the DNA–H3 αN-helix interaction, and asymmetric unwrapping of the nucleosome.

Proposed Model for Asymmetric Unwrapping of Nucleosomal DNA.

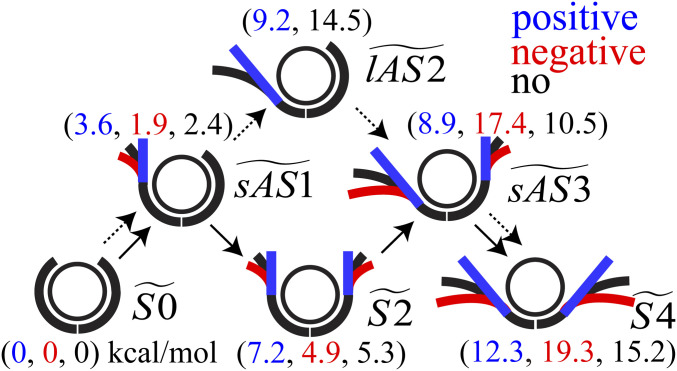
We propose a model for the small- and large-scale asymmetric unwrapping of nucleosomal DNA as follows (Fig. 5).

Fig. 5.

Schematic representation of the model of the transitional paths for the small- and large-scale asymmetric unwrapping of two outer half turns of DNA under torsional stress. The unwrapping of two outer half turns of DNA under positive, negative, and no stress is schematically shown in blue, red, and black, respectively. The transitional states are labeled by $\stackrel{\sim }{S0}$, $\stackrel{\sim }{sAS1}$, $\stackrel{\sim }{S2}$, $\stackrel{\sim }{lAS2}$, $\stackrel{\sim }{sAS3}$, and $\stackrel{\sim }{S4}$. The likelihood of the transition from wrapped to unwrapped DNA from $\stackrel{\sim }{S0}$ to $\stackrel{\sim }{S4}$ is schematically shown by the solid and dotted arrows for the small- and large-scale asymmetric unwrapping of the DNA, respectively. The values in parentheses are values of the free energies in each state.

First, the positive torsional stress overtwists the DNA, while the negative torsional stress undertwists the DNA. Second, the minor groove of the DNA at SHL = ± 6.5 rotates and further strengthens the interaction with the H3 αN-helix under positive stress, which stabilizes the nucleosome and suppresses the transition from $\stackrel{\sim }{sAS1}$ to $\stackrel{\sim }{S2}$. Third, the change in the bendability and flexibility of the DNA influences the free energy for the unwrapping of the DNA. Overtwisted DNA under positive stress is straightened. The straightened DNA would increase the bending energy if the DNA retained the bent form to maintain its contact with H2A-H2B. This high bending energy in the DNA would facilitate the unwrapping of the DNA to relax the bent form of the DNA from $\stackrel{\sim }{sAS1}$ to $\stackrel{\sim }{lAS2}$. In contrast, the DNA under negative stress is more bendable and would not require as much internal bending energy to wrap the DNA as under positive stress. It is notable that our simulation indicates that the change in the affinity of the DNA and H2A-H2B under positive and negative stress is not because of the change in the interfacial direct interaction between the DNA and H2A-H2B but because of the change in the inherent dynamic nature of the DNA with regard to its bendability and flexibility.

Finally, ΔG_lAS2/S2 decides the transitional path for the large- and small-scale asymmetric unwrapping. In terms of DNA–histone interactions, ΔG_lAS2/S2 can be regarded as ΔG_(H2A-H2B)/H3, the difference between G_H2A-H2B (the free energy for unwrapping one end of the DNA from H2A-H2B) and G_H3 (the free energy for unwrapping the other end of the DNA from H3). Under positive stress, ΔG_(H2A-H2B)/H3 is relatively small, 2.0 kcal/mol. Thus, after one end of the DNA unwraps from H3, further unwrapping of the same end of the DNA from the H2A-H2B is likely to occur within the thermal fluctuation of k_BT = ∼0.6 kcal/mol. In contrast to positive stress, ΔG_(H2A-H2B)/H3 for negative and no stress are so large that the large-scale asymmetric unwrapping of the DNA from H2A-H2B would be strongly suppressed. In fact, when one end of the DNA unwraps from H3, the other end of the DNA is more likely to start unwrapping. Consequently, the large- and small-scale asymmetric unwrapping of the DNA is facilitated under positive and negative stress, respectively.

The idea that the magnitude of the difference between G_H2A-H2B and G_H3, ΔG_(H2A-H2B)/H3, plays a role in the small- and large-scale asymmetric unwrapping would be applicable not only to the torsional stress but also other factors, such as the histone tails (19, 37, 44) (which we did not consider in this study), the DNA sequence (34), and histone modifications.

The Efficient Unwrapping of Nucleosomal DNA in Chromatin under Positive Stress.

The free-energy landscapes against d were similar under the three different stress conditions in the sense that the free energies gradually increased (Fig. 2). The populations of the transitional states from $\stackrel{\sim }{S0}$ to $\stackrel{\sim }{S4}$, however, were clearly different among the conditions as shown in Fig. 3. Under positive stress, the nucleosome can reach $\stackrel{\sim }{lAS2}$ even at d less than ∼100 Å. This indicates that the unwrapping of the DNA from H2A-H2B can occur without a large extension of the DNA under positive stress. This efficient unwrapping of the DNA would allow proteins to access the exposed DNA even when nucleosomes are in condensed chromatin.

Computational Limitation.

To check the reproducibility of our results, we compared the free-energy curve with a previously reported free energy (20). In the previous study, the MD simulation was carried out at a concentration of 120 mM NaCl in a simulation box of 150 Å × 150 Å × 150 Å to obtain the unwrapping free energy under no stress. The SD between these independent studies was calculated to be 0.40 kcal/mol (SI Appendix, Fig. S8). We also examined the deviations of the free energy in this study. SI Appendix, Fig. S9 shows the free-energy curves at intervals of 10 ns for the last 50 ns in the umbrella sampling simulation. The SDs for the five free-energy curves were calculated to be 0.91, 0.54, and 0.70 kcal/mol under positive, negative, and no stress, respectively. Consequently, the difference in the free energies in these studies under no stress, 0.40 kcal/mol, was within the SD of the sampled free-energy curves, 0.70 kcal/mol. These results suggest that the free energy in this study (at least under no stress) is reproducible within these error ranges.

As the DNA sequence used in our study was symmetric, the distribution of the unwrapped DNA should also be symmetric, which has been shown in the Monte Carlo simulation of the asymmetric unwrapping at the outer and inner turns of DNAs with a coarse-grained model (45). As shown in SI Appendix, Fig. S10, we measured (bp₁ − bp₂)/(bp₁ + bp₂) as an indicator of the extent of the asymmetry (0.0: completely symmetric and ±1.0: completely asymmetric). The figure shows that once the nucleosome unwrapping became asymmetric in one direction (e.g., bp₁ >> bp₂), it did not become asymmetric in the other direction (bp₁ << bp₂) within 100-ns simulations. This indicates that the 100-ns simulation per window may not be enough to sample asymmetric distribution in both directions. However, the overall distribution of conformations from all the replicas was fairly even on both ends, indicating that the conformation sampling along the reaction coordinate is sufficient at least to show the facilitating of the asymmetric unwrapping of the DNA under positive stress.

It should be noted that there is a difference between the systems studied in single-molecule experiments and our study. In our study, the linker DNA was not included; however, a long linker DNA was in principle included in the experiments. Simulation of the nucleosome with long linker DNA under torsional stress would enable direct comparison and give more detailed information about the unwrapping of the nucleosome.

Despite the limitation of not including linker DNA in the model to reduce the computational time, we believe the free-energy landscape of the unwrapping of two outer half turns of DNA in our study gives insight into the symmetric and asymmetric unwrapping of two outer half turns of DNA under torsional stress.

Conclusion

Our simulation showed that torsional stress can regulate the transitional paths of the small- and large-scale asymmetric unwrapping of two outer half turns of DNA through the geometry of the DNA (minor groove) and the inherent dynamic nature of the DNA (bendability and flexibility). We demonstrated that under positive stress, the strengthened interaction between the twisted minor groove of the DNA and the H3 αN-helix, and the weakened interaction between the straightened DNA and the H2A-H2B L1-L2 loops, both facilitated the large-scale asymmetric unwrapping of two outer half turns of DNA. In contrast, the undertwisted DNA generated by negative stress made the DNA bent and flexible, which suppressed unwrapping. Our data suggests that DNA accessibility in the chromatin can be regulated by enhancing or suppressing asymmetric unwrapping without a large extension of the DNA through torsional stress generated by proteins such as RNAP and chromatin remodeling complexes, which may explain why genes in condensed chromatin states can be expressed.

Materials and Methods

Atomic Model.

We used a crystal structure of a nucleosome with α-satellite palindromic 147 bp DNA (Protein Data Bank code: 1kx5) (46). The histone tails were truncated to facilitate the unwrapping of the DNA. Consequently, residues 46 to 132 in H3, 25 to the C terminal in H4, 16 to 114 in H2A, and 32 to 121 in H2B were used. As the nucleosome core particle contains two copies of each octamer and the DNA has two ends, we distinguish them with suffixes “a” and “b” for the octamer and “1” and “2” for the ends of the DNA. In this study, nucleotides from −73 A to −39 A of chain I and nucleotides from 73 T to 39 T of chain J were assigned to DNA₁, and nucleotides from 73 T to 39 T of chain I and nucleotides from −73 A to −39 A of chain J were assigned to DNA₂ according to the nucleotide sequence in 1kx5 (Fig. 1B).

MD Simulations of the Systems in Water.

Simulations were carried out using an MD simulation program called SCUBA (20, 47–52) with the AMBER ff14SB (53), bsc1 (54), and ff99ions08 (55) force-fields for the octamer, DNAs, and ions, respectively. The structure of nucleosome was placed in a rectangular box of ∼125 Å × 245 Å × 155 Å (SI Appendix, Fig. S1A). ∼148,000 TIP3P water molecules (56) were added to surround the system. To neutralize the charges of the system, sodium ions were placed in the box, and then additional sodium and chloride ions were added at a concentration of 150 mM NaCl. In total, the system comprised ∼465,000 atoms. The system was equilibrated at a constant pressure of one bar and a temperature of 300 K for 10 ns. Details are given in SI Appendix, Supplementary Methods.

Adaptively Biased MD Simulation of the System.

To generate a series of configurations of the unwrapping of the nucleosome from tightly wrapped to unwrapped, the adaptively biased MD (ABMD) method (57) combined with the multiple-walker method (58) was carried out for ∼30 ns at a constant volume and a temperature of 300 K with six walkers (replicas) of the nucleosome, which were selected from the equilibration simulation. The reaction coordinate d was defined as the DNA near end-to-end distance, or the distance between the two centers of mass of the third base pair from each end of the DNA, −71 C:G 71 in DNA₁ and 71 G:C −71 in DNA₂. The value of the reaction coordinate in the initial structure was 70.7 Å. After the ABMD simulation was carried out, a series of 90 conformations at intervals of about 2.0 Å with d between 64 and 242 Å were selected from the conformational ensembles of the replicas. Details are given in SI Appendix, Supplementary Methods.

Umbrella Sampling Simulations under Torsional Stress and No Stress.

Using a series of 90 conformations in the ABMD simulation, umbrella sampling simulations were carried out for 100 ns to obtain the free energy for the unwrapping of nucleosomal DNA with torsional stress and no stress. The umbrella potential for the i-th window (i = 1, ..., N_win = 90) used is

$$V_i^{\mathit{umb}}=k_i^{\mathit{umb}}{\left(d-d_i^{\text{fix}}\right)}^2,$$ [1]

where $d_i^{\text{fix}}$ is a fixed distance to maintain d within the range of 64 Å to 242 Å with intervals of 2 Å. $k_i^{\text{umb}}$ is an arbitrary harmonic force constant, which was set at 0.2 kcal/mol/Ų. The trajectory for the last 50 ns was used for the analysis. The WHAM (24, 25) was used to refine the free-energy landscape. Details are given in SI Appendix, Supplementary Methods.

Torsional Stress in the Umbrella Sampling Simulations.

The effect of the torsional stress on the DNA for the i-th window was incorporated as follows in a similar way to the procedure used by refs. 21, 22:

$$V_i^{stress}=k_{1i}{\left({\varphi }_1-{\varphi }_1^0\right)}^2+k_{2i}{\left({\varphi }_2-{\varphi }_2^0\right)}^2,$$ [2]

where the torsional angles of ϕ₁ and ϕ₂ are defined using the C1’ atoms of the third base pairs from the ends of the DNA and the phosphorus atoms located opposite the dyad (Fig. 1 B and C). Both ${\varphi }_1^0$ and ${\varphi }_2^0$ were set at 0° and 180° for the generation of positive and negative stress, respectively. As appropriate values of the force constants k_1i and k_2i to produce torque within 10 to 20 pN nm were not known in advance, the values of k_1i and k_2i were adjusted for the first ∼25 ns. Since then, both of the force constants k_1i and k_2i were set at 2.0 × 10⁻² × (i – 1) + 1.5 kcal/(mol rad²) for the positive stress and at 1.5 × 10⁻² × (i – 1) + 0.50 kcal/(mol rad²) for the negative stress. Details are given in SI Appendix, Supplementary Methods.

The Number of Unwrapped Base Pairs.

Base pairs were defined as being unwrapped when the center of each base pair at the end of the DNA continuously deviated more than 4 Å from the center of the corresponding base pair in the reference structure, where DNA was fully wrapped. The energy-minimized structure of the nucleosome in water medium was used as the reference structure.

The Number of Contacts between the DNA and the Octamer.

Contacts were counted when any pair of atoms of the DNA and the octamer was located within a distance of 4 Å of each other.

Conformational Analysis of the DNA.

The conformational change of the DNA was measured using the base pair step parameters using program called 3DNA (59). Twist, Tilt, and Roll of the base pair step parameters were analyzed for the third to 35th base pairs from the end of the DNA_{1 or 2}. The first and second base pairs at the end of DNA_{1 or 2} were not included in the analysis. The torsional stress would not influence these base pair steps because they behaved like a free end. The local bending angle was calculated as $\sqrt{{\left(Tilt\right)}^2+{\left(Roll\right)}^2}$.

Conformational Entropy of the DNA.

The conformational entropies of the two ends of DNA_{1 or 2} were calculated using the quasiharmonic approximation (60). Details are given in SI Appendix, Supplementary Methods.

Computational Time.

All the simulations, requiring a total time of 27 μs, were mainly performed on the Cray XC40 supercomputer at Kyoto University and the SGI ICE X supercomputer at the Japan Atomic Energy Agency. The total computational time was more than 20 million central processing unit core hours.

Data Availability.

Relevant conformations and trajectory files have been deposited in the Materials Cloud Archive 2020 (DOI:10.244335/materialscloud:r9-xt).