Crossed–uncrossed projections from primate retina are adapted to disparities of natural scenes

Significance

Many mammals with frontal eyes have robust binocular vision and stereoscopic depth perception. Here, we show that the organization of projections from the retinas to the central nervous system in these animals is quite effective in ensuring that the most common binocular disparities send signals directly to the same cortical hemisphere, thereby enabling fast and accurate depth estimation.

Abstract

In mammals with frontal eyes, optic-nerve fibers from nasal retina project to the contralateral hemisphere of the brain, and fibers from temporal retina project ipsilaterally. The division between crossed and uncrossed projections occurs at or near the vertical meridian. If the division was precise, a problem would arise. Small objects near midline, but nearer or farther than current fixation, would produce signals that travel to opposite hemispheres, making the binocular disparity of those objects difficult to compute. However, in species that have been studied, the division is not precise. Rather, there are overlapping crossed and uncrossed projections such that some fibers from nasal retina project ipsilaterally as well as contralaterally and some from temporal retina project contralaterally as well as ipsilaterally. This increases the probability that signals from an object near vertical midline travel to the same hemisphere, thereby aiding disparity estimation. We investigated whether there is a deficit in binocular vision near the vertical meridian in humans and found no evidence for one. We also investigated the effectiveness of the observed decussation pattern, quantified from anatomical data in monkeys and humans. We used measurements of naturally occurring disparities in humans to determine disparity distributions across the visual field. We then used those distributions to calculate the probability of natural disparities transmitting to the same hemisphere, thereby aiding disparity computation. We found that the pattern of overlapping projections is quite effective. Thus, crossed and uncrossed projections from the retinas are well designed for aiding disparity estimation and stereopsis.

In most vertebrates, optic-nerve fibers leaving either eye cross to the contralateral side of brain via the optic chiasm (1). Complete decussation refers to cases in which all fibers cross to the other side (i.e., all fibers from the left eye terminate in the right hemisphere of the central nervous system, while all from the right eye terminate in the left hemisphere). Partial decussation occurs in most mammals: many fibers project contralaterally, but some from the temporal retinas do not cross to the other hemisphere. Interestingly, the proportion of fibers that project ipsilaterally depends on the relative orientation of the eyes. If the eyes are directed laterally (i.e., large angle between the optic axes), a small proportion projects ipsilaterally. If the eyes are frontal (i.e., small angle between optic axes), a large proportion projects ipsilaterally. This relationship is codified by the Newton–Müller–Gudden Law that states that the ratio of uncrossed to crossed fibers is proportional to the width of binocular visual field, which in turn, depends on eye laterality (1–3).

Animals with large laterality (e.g., mouse, rat, rabbit, sheep, squirrel, chipmunk) have a narrow binocular field that is subserved by the temporal retinas of both eyes (4) (Fig. 1A). Animals with less laterality (e.g., cats, nonhuman primates, humans) have a wide binocular field (4) (Fig. 1B). In these animals, the proportion of ipsilaterally projecting fibers can be half of the total proportion. The boundary between ipsilateral and contralateral projections is near the vertical meridians of the eyes. The nasal retina of the left eye and temporal retina of the right eye represent the left visual field, which is, in turn, represented in the right visual cortex. The temporal retina of the left eye and nasal retina of the right eye are stimulated by the right visual field, which is represented in the left cortex.

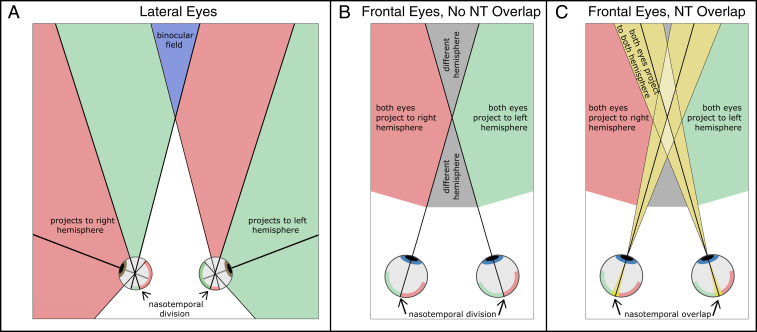
Fig. 1.

Projections to hemispheres in lateral- and frontal-eyed mammals. (A) Top view of lateral-eyed animal. Nasal retina and temporal retina in the left eye are represented by pink and green, respectively, and the opposite for the right eye. Pink regions in front of the animal represent points in the visual scene that produce signals that travel to the right hemisphere. Green regions represent points that produce signals to the left hemisphere. The blue region represents the binocular visual field where points stimulate both retinas. (B) Top view of a frontal-eyed mammal with no crossed–uncrossed nasotemporal (NT) overlap in the decussation pattern. The left and right halves of the retinas are represented by green and pink, respectively. Green and pink regions in front of the animal represent scene points that produce signals from both eyes to the left and right hemispheres, respectively. Gray regions represent scene points that would send signals from the two eyes to different hemispheres (i.e., regions for which there is no binocular integration through direct paths from the retinas to cortex). (C) Top view of frontal-eyed mammal with crossed–uncrossed overlap in the decussation pattern. Green and pink regions in the retina again represent regions for which both eyes project to one hemisphere. Yellow regions in the retinas represent the crossed–uncrossed overlap: the parts of the retinas that project to both hemispheres. Yellow regions in front represent scene points that produce signals to both hemispheres due to the overlapping projections. Light yellow represents regions where stimulation occurs in either the nasal retinas of both eyes or the temporal retinas of both eyes. Due to the crossed–uncrossed overlap, signals from both eyes would be sent to both hemispheres. Gray regions represent points in the scene that send signals from the two eyes to different hemispheres. They are much smaller than when there is no crossed–uncrossed overlap.

The nasotemporal division is the boundary in the retina that separates crossing and noncrossing fibers. As we said, the division in frontal-eyed mammals occurs near the vertical meridians. A significant problem for the neural computation of binocular disparity would arise if the nasotemporal division occurred precisely such that all retinal points to the left of the vertical meridian projected to one side of the brain, while all points to the right of the meridian projected to the opposite side (Fig. 1B). Small objects that were nearer or farther than current fixation would end up producing signals that traveled to opposite halves of the brain. For example, an object above fixation with uncrossed disparity (farther than fixation) would be imaged in the lower retina of the left eye just nasalward (i.e., rightward) from the vertical meridian and in the lower retina of the right eye just nasalward (leftward) from the vertical meridian; hence, the left eye’s signal would be sent to the right hemisphere, and the right eye’s signal would be sent to the left hemisphere. Combining the signals to estimate disparity would then require using pathways that cross from one hemisphere to the other via one of the commissures such as the corpus callosum. This would necessitate longer neural paths involving more synapses, which would surely adversely affect the speed and accuracy of computations required to estimate binocular disparity and the perception of depth from disparity (5–7). A solution is to have overlapping projections near the vertical meridian (i.e., some fibers in nasal retina near the meridian would project ipsilaterally, while most nasal fibers would still project contralaterally) (Fig. 1C). There is clear evidence for just this arrangement in cats and nonhuman primates and some evidence for this in humans.

In cats, there is a strip of retina encompassing the vertical meridian in which retinal ganglion cell axons project to both hemispheres in the central nervous system (5, 8–11). The strip is about $1.5^{○}$ wide.

There are analogous overlapping projections in nonhuman primates. Stone et al. (12) sectioned one optic tract in rhesus monkeys (Macaca mulatta). They then examined the two retinas to determine which ganglion cells had survived the ensuing retrograde degeneration. If the right optic tract was sectioned, one might expect to observe no surviving ganglion cells in the nasal retina of the left eye and temporal retina of the right eye. However, Stone et al. (12) observed such surviving cells as far as ${\mathrm{1}}^{○}$ from the vertical midline, which indicates an overlap in projections near the nasotemporal boundary. In long-tailed macaque monkeys (Macaca fascicularis), Bunt et al. (13) injected a retrograde labeler into the lateral geniculate nucleus (LGN) on one side of the brain and measured where the label appeared in the two retinas. They found a region near the vertical meridian where the label appeared in both retinas. The width of the overlapping region was $1^{○}$ to ${\mathrm{2}}^{○}$. Fukuda et al. (7) obtained similar results in Japanese macaques (Macaca fuscata). They injected different retrograde labelers into the left and right LGNs and observed clear crossed–uncrossed overlap near the vertical midline. The width of the overlap was roughly proportional to the distance from the fovea. They also observed an asymmetry. In the upper retina (lower visual field), more retinal axons on the nasal side of the midline projected ipsilaterally than axons on the temporal side of midline that projected contralaterally (14). To verify their observations, Fukuda et al. (7) also examined crossed–uncrossed projections in fluorescent dye experiments with injections in the optic tract and in physiological experiments employing antidromic responses in retinal ganglion cells due to stimulation of the left or right LGN. The results confirmed the asymmetry and the increasing width of the overlap region with eccentricity.

The effectiveness of the overlapping projections in nonhuman primates was demonstrated indirectly by Cowey and Wilkinson (15). They showed that severing the corpus callosum (thereby preventing binocular processing via interhemispheric communication) had no discernible effect on rhesus monkeys’ stereoacuity near the vertical midline. In contrast, sectioning the optic chiasm had a very deleterious effect on stereoacuity.

There is evidence for overlapping crossed–uncrossed projections in humans as well. Some investigators tested split-brain patients (i.e., commissurotomized patients) in an attempt to ascertain the parts of the visual field where intrahemispheric processing can occur. They asked whether such patients can make reliable same–different judgments of stimuli presented on opposite sides of vertical midline. Intrahemispheric processing is needed to make such judgments, so doing the task reliably would suggest the presence of some crossed–uncrossed overlap in projections from the retinas. Some reported obvious deficits (16–18), suggesting no projection overlap. One more recent study employed more careful monitoring of eye position, presented targets closer to the vertical midline, and reported very reliable same–different judgments (19). Thus, studies of split-brain patients offer some support in humans for crossed–uncrossed overlap in projections similar to that observed in nonhuman primates.

Other investigators tested patients with loss of a visual hemifield (homonymous hemianopia) due to loss of a cortical hemisphere. Consider a patient with no useable right cortical hemisphere. If the nasotemporal split in the retina was precise, their residual functional visual field should be the right hemifield with a precise boundary along the vertical meridian through the fovea. If instead, there was crossed–uncrossed overlap, the functional field should extend slightly leftward from the vertical meridian. In most of these perimetry experiments, the patient is told to maintain fixation on a point while small bright targets are presented at various positions on an otherwise dark background. The patient reports on each trial whether he/she saw the target. Of course, the target could be detected due to light scattered from the nominally tested location to another part of the retina. One must also be certain that the patient maintained accurate fixation. Reinhard and Trauzettel-Klosinski (20) solved both of these problems by presenting dark spots on a bright background and monitoring the stimulus position by using a scanning laser ophthalmoscope to view the stimuli directly on the retina. In nearly all of the eyes they tested, the border of the functional field was shifted slightly across the vertical meridian: clear evidence for crossed–uncrossed overlap in central projections. In most of the eyes, the border was shifted farther from the meridian at greater vertical eccentricities, which is consistent with the monkey data (7, 14). Wessinger et al. (21) obtained similar results in similar patients.

Here, we investigate the effectiveness of the crossed–uncrossed overlap. We first examine whether deficits in human stereopsis occur along the vertical meridian. We find no evidence for deficits. We next quantify the overlap from anatomical data from nonhuman primates and data from functional Magnetic Resonance Imaging (fMRI) from humans. We then calculate the proportion of common naturally occurring disparities that would send signals directly to the same cortical hemisphere given different patterns of overlap. We find that the pattern observed in humans and nonhuman primates is quite effective.

Stereoacuity in Different Parts of the Visual Field

As we said earlier, a decussation pattern with a precise split at the vertical meridian would cause signals from objects near the vertical midline, both farther and nearer than fixation, to project to different hemispheres. This, in turn, would seemingly create difficulty in estimating binocular disparity. Thus, we would expect to observe poorer stereopsis near the vertical meridian than near the horizontal meridian.

Mochizuki et al. (22) investigated stereoacuity in the peripheral visual field of humans. They measured the smallest disparity that elicits a reliable depth percept along eight meridians (including above, below, left, and right of the fovea) at eccentricities of $10^{○}$, $20^{○}$, and ${\mathrm{30}}^{○}$. They observed no deficits in the upper and lower fields relative to the left and right fields; indeed, stereoacuity was slightly better in the lower field than in other locations. They did not, however, explore areas farther or nearer than fixation. Such stimuli are more likely to generate signals to opposite hemispheres (Fig. 1B), so it is important to investigate those regions in space.

We explored those regions with a psychophysical experiment. Specifically, we measured stereoacuity with different disparity pedestals (e.g., farther or closer than fixation) to see if a deficit emerges in the regions of interest (ROIs).

Fig. 2 A and B illustrates the stimulus and procedure. We presented two small spots, one having a greater disparity than the other, on the upper and lower vertical meridians and on the left and right horizontal meridians. Subjects indicated the one that appeared nearer. Importantly, stereoacuity at each field location was measured for five disparity pedestals, which placed the stimuli nearer than, at, or farther than fixation. We also measured stereoacuity at the fovea using the same procedure. Details are in Materials and Methods.

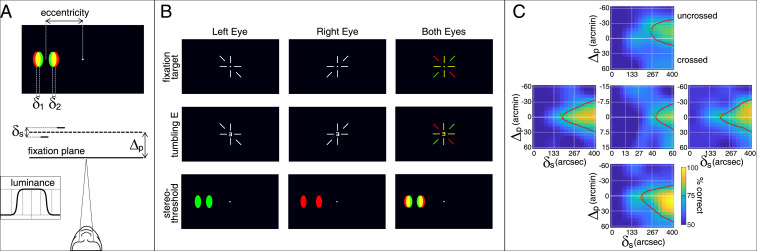
Fig. 2.

Stereoacuity experiment. (A) Schematic of the stimulus. Two bright spots were presented in either the central or peripheral visual field. One had a horizontal disparity of ${\delta }_1$, and the other had a horizontal disparity of ${\delta }_2$. Their relative disparity was ${\delta }_s$ = ${\delta }_1$ –${\delta }_2$. The average of the two disparities is the disparity pedestal, ${\mathrm{\Delta }}_P$. The pedestal caused the stimuli to appear nearer than, at, or farther than the fixation target. The luminance of each spot was a central plateau with Gaussian skirts (Inset). (B) Experimental stimuli and procedure. A dichoptic fixation target (Top) was presented to enable accurate fixation at the screen distance. Upon a button press, a stimulus was presented for 200 ms. Occasionally, it was a tumbling E shown at the fovea (Middle). Usually, it was the two spots (Bottom). Then, the subject indicated on the keyboard the orientation of the tumbling E or which of the two spots was closer. (C) Stereoacuities at different positions in the visual field. Data are averaged across subjects. Individual subject data are shown in SI Appendix, Fig. S1. Middle Center shows the data for the fovea. Top, Bottom, Middle Left, and Middle Right show the data from the upper, lower, left, and right visual fields, respectively. The horizontal axis in each panel is the relative disparity between the spots: ${\delta }_s$. The vertical axis is the disparity pedestal: ${\mathrm{\Delta }}_P$. Note the different scales for the fovea compared with the peripheral locations. Color represents percentage correct, which ranged from 50% (chance) to 100% (perfect). Red contours represent threshold (75%). Green dots represent the highest stereoacuity for each field location. Those values were 43.8 seconds of arc (arcsec) at the fovea (Middle Center), 188.2 in the left field (Middle Left), 260.3 in the upper field (Top), 204.3 in the right field (Middle Right), and 198.8 arcsec in the lower field (Bottom). Data and code to perform the experiment and the data analysis are publicly available (67).

Fig. 2C provides the results, averaged across subjects. (Individual subject data are provided in SI Appendix, Fig. S1.) The foveal data are in Fig. 2 C, Middle Center, and the left, upper, right, and lower field data are in Fig. 2 C, Middle Left, Top, Middle Right, and Bottom, respectively The horizontal axis in each panel is the relative disparity between the two dots, ${\delta }_s$. The vertical axis is the disparity pedestal, ${\mathrm{\Delta }}_P$, which is the overall disparity of the spots relative to the fixation distance. Positive values are nearer than fixation (crossed disparity), and negative values are farther (uncrossed). Color represents the percentage of correct responses for each combination of disparity pedestal and relative disparity: yellow for better performance and blue for worse. Red contours are the estimated stereoacuity (75% correct). Green dots are the best stereoacuity (the lowest discriminable disparity; values are reported in Fig. 2C).

Not surprisingly, stereoacuity was better in the fovea than in the periphery. Foveal acuity was also better with zero-disparity pedestals than with nonzero pedestals, as reported previously (23). Stereoacuity at the peripheral field locations was also affected by the disparity pedestal, somewhat differently at different field positions. We observed no deficit on the vertical meridian relative to the horizontal meridian. We assessed the statistical reliability of the various effects for the peripheral field locations using a repeated measures ANOVA supported by Kruskal–Wallis tests. The ANOVA revealed significant main effects of relative disparity (P < ${\mathrm{10}}^{-12}$; this occurred because performance was better with large disparities) and disparity pedestal (P < ${\mathrm{10}}^{-15}$; because performance was better with small pedestals). There was not a statistically reliable effect of peripheral field location (P = 0.29). There were significant interactions between relative disparity and pedestal (P = 0.028; this occurred because performance was better when relative disparity was large and the pedestal was small) and between pedestal disparity and field location (P = 0.0015; because performance was better with crossed disparity in the lower field and uncrossed disparity in the upper), and there was no significant interaction between relative disparity and field location (P = 0.91). The Kruskal–Wallis tests confirmed the reliability of the main effects observed in the ANOVA test. Details are provided in SI Appendix, Table S1.

The fact that performance was best with crossed disparity in the lower field and uncrossed in the upper field is consistent with the top-back pitch of the vertical horopter (24, 25, 26). However, the most important result is that we did not observe a deficit near the vertical meridian compared with the horizontal meridian even in regions nearer and farther than fixation. The results suggest that the problem of projections to opposite hemispheres that could occur with a precise split at the vertical meridian has been solved in the human visual system, perhaps by crossed–uncrossed overlap as in cat and monkey.

Crossed–Uncrossed Overlap

We determined the patterns of crossed–uncrossed overlap in monkeys from the anatomical data of Fukuda et al. (7) and in humans from the fMRI data of Benson et al. (27, 28) and Benson and Winawer (29, 30). The patterns are similar.

Monkeys.

Fig. 3 summarizes the findings of Fukuda et al. (7) in Japanese macaques. To generate this figure, we used the conversion that 1 mm of retina corresponds to $4^{○}$ of visual angle (31, 32). Fig. 3A plots some of their data in retinal coordinates. We assumed that the overlap was symmetric around the vertical meridian as defined by Fukuda et al. (7). Green represents retinal regions that project ipsilaterally, yellow represents regions that project contralaterally, and yellow–green represents regions that project both ipsilaterally and contralaterally. The width of the overlapping region increases from $\sim 0.6^{○}$ in the central retina to $\sim 2^{○}$ at $15^{○}$ above and below the fovea. These data are consistent with other observations (13, 14).

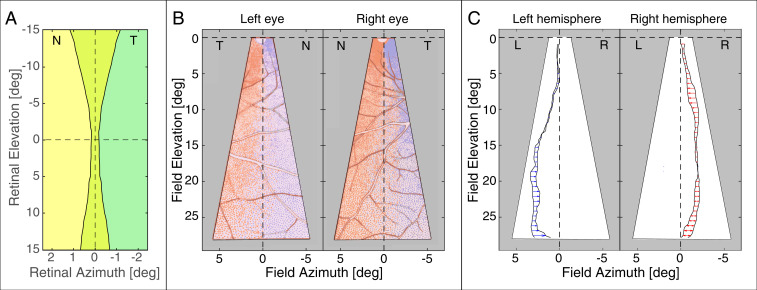
Fig. 3.

Overlap of crossed–uncrossed projections in monkey. (A) Width of overlap as a function of elevation. The data are from figure 2 of ref. 7, averaged across the three monkeys in that figure. The dashed lines represent the horizontal and vertical meridians of the retinas according to Fukuda et al. (7). The foveas of the two retinas are superimposed. The temporal edge of contralaterally projecting cells is superimposed with the nasal edge of ipsilaterally projecting cells. Temporal retinas are indicated by T, and nasal is indicated by N. The green region indicates ganglion cells that project to the ipsilateral LGN only, and the yellow region indicates cells that project to the contralateral LGN only. The crossed–uncrossed overlap is the yellow–green region. (B) Asymmetry of projections to the two hemispheres. The plot in Left is for the lower visual field of the left eye (i.e., superior retina); temporal field (T) is to the left, and nasal (N) is to the right. The plot in Right is for lower visual field of the right eye; temporal is to the right, and nasal is to the left. Blue dots represent ganglion cells labeled with tracer injected into the left LGN, and red dots represent ganglion cells labeled with tracer injected into the right LGN. The blue curves indicate where label from the left LGN ended, and red curves indicate where label from the right LGN ended. The differences in the curves between the two eyes show that the projections are not symmetric in the two retinas. The dashed vertical and horizontal lines represent their definitions of the vertical and horizontal meridians, respectively. Adapted from figure 5 of Fukuda et al. (7). (C) Differences in where the overlapping projections end in the two eyes. The plot in Left shows where label from the left LGN ended in the two eyes: arrowheads for the right eye relative to the left. L and R indicate the left and right halves of the visual field, respectively. Arrows point leftward, which means that the left hemisphere’s projection ended closer to the vertical meridian for the right eye than for the left eye. The plot in Right shows where label from the right LGN ended in the two eyes: arrowheads again for the right eye relative to the left. Arrows point leftward, which means that the right hemisphere’s projection ended farther from the vertical meridian in the right eye than in the left eye.

Fig. 3B is plotted in visual field coordinates. It shows an asymmetry in crossed and uncrossed projections reported by Fukuda et al. (7). The data are from the superior retina (i.e., inferior field). The blue and red dots represent retinal ganglion cells that were retrograde labeled from tracer injected into the left and right LGNs, respectively. The regions of crossed–uncrossed overlap in the left and right retinas are evident from the mixing of blue and red dots. The colored contours represent where the overlap regions ended in the two retinas. The cells marked with blue dots are farther from the vertical meridian than the ones marked with red. Fig. 3C shows the difference in positions of the terminations of the overlap regions in the left and right LGNs. Unfortunately, one cannot easily interpret this asymmetry relative to the vertical meridian because Fukuda et al. (7) were unable to unambiguously determine the orientation of the vertical meridian in their anatomical data.

Humans.

To determine the crossed–uncrossed overlap in humans, we reanalyzed data from the Human Connectome Project (HCP) 7-T retinotopy dataset (27, 28). This dataset provides whole-brain population receptive field (pRF) position and size estimates for 181 subjects. The estimates are based on high-resolution fMRI retinotopic mapping experiments performed as part of the HCP (28, 33). We used these pRF estimates to construct the pattern of crossed–uncrossed projections.

The results are shown in Fig. 4. For each subject, the pRF estimates were represented on the cortical surface (Fig. 4A) in order to identify the location of the boundary between the primary visual area (V1) and the secondary visual area (V2), which represents the vertical meridian of the visual field. These pRF measurements were combined with a prior, defined in terms of cortical surface anatomy, of the V1 and V2 retinotopic maps using Bayesian inference (29, 34). These inferred maps provide a good estimate of the location of the V1/V2 boundary, as well as a set of ${\mathrm{1}}^{○}$-wide eccentricity bands across V1 and V2 (Fig. 4 A, Lower). Within each eccentricity band, we examined the polar angle representation of the pRF estimates that were within 5 mm of the V1/V2 boundary. The value of 5 mm was chosen because it is the smallest value that encompasses most of the ipsilateral projections. These ROIs were examined for the upper (ventral) and lower (dorsal) visual field boundaries separately. The portion of cortex within these ROIs represents $46.8\pm 22.7^{○}$ of visual field from the vertical meridian for the upper visual field and $48.3\pm 14.2^{○}$ of visual field from the vertical meridian for lower visual field. For each ROI, we computed a smooth histogram of the polar angles weighted by cortical surface area. These histograms are shown as violin plots in the visual field in Fig. 4B. For a particular polar angle about the visual field, the thickness of the violin plot represents the relative fraction of the ROI’s total surface area for the given polar angle. Each violin is plotted with partial opacity such that the darker regions indicate where ipsilateral pRF centers are superimposed with the contralateral centers, thus illustrating the regions of overlap between the left and right hemispheres. Note that the histograms extend only $\pm$5 mm from the V1/V2 boundaries and thus, represent a small portion of the horizontal visual field around its vertical meridian [for instance, at ${\mathrm{7}}^{○}$ of eccentricity, it corresponds to $\pm {\mathrm{13}}^{○}$ (35)]. We computed the 75th percentile of the portion of each histogram representing the ipsilateral visual field to define the extent of the contralateral retinal projection, measured in degrees of rotation around the visual field from the vertical meridian (Fig. 4C). The 75th percentile was used as a conservative estimate of the maximum projected angle. Note that considering a larger area would include more contralateral projects, not affecting the ipsilateral ones and preserving the result.

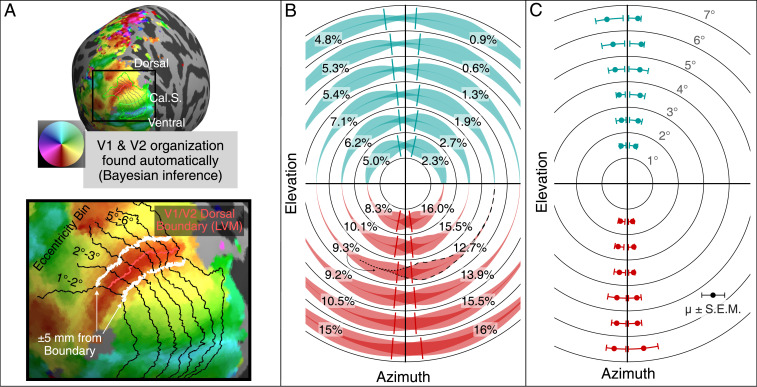
Fig. 4.

Ipsilateral representation of the visual field along the V1/V2 boundary (i.e., along the vertical meridian of the visual field). (A) ROIs for the upper and lower visual fields were calculated automatically for each of the 362 hemispheres. Isoeccentricity contours and the V1/V2 boundary were found using Bayesian inference (29, 34). Cortex was divided into eccentricity bins, each ${\mathrm{1}}^{○}$ wide. Within each bin, the upper and lower V1/V2 boundaries were extended by 5 mm in both directions. The map shows the position of the Calcarine Sulcus (Cal.S) as reference. Vertices within this region were examined for ipsilateral representation of the visual field. (B) The representation of the ipsilateral visual field near the V1/V2 boundary (i.e., LVM, the Lower Vertical Meridian). One smooth density violin plot is shown for each V1/V2 boundary ROI described in A. The violin plots show the density of pRF centers near the vertical meridian in V1 and V2 in terms of polar angle, weighted by cortical surface area. Darker colors indicate regions of overlap between the left and right hemisphere ROIs. Note that because the ROIs include only the parts of cortex within 5 mm of the vertical meridian representation, these ROIs contain little representation of the horizontal visual field. The numbers next to the histograms indicate the percentage of each ROI’s surface area that represents the ipsilateral visual field (i.e., 100 times the ROI’s ipsilateral surface area divided by the entire ROI’s surface area). Each hemisphere’s ipsilateral surface area percentages are printed in its ipsilateral visual field. For example, the “$9.3\%$” printed in the lower left visual field ($3^{○}$ to ${\mathrm{4}}^{○}$ of eccentricity) indicates that 9.3$\%$ of the surface area within 5 mm from the V1/V2 lower visual field boundary (dorsal boundary) of the left hemisphere is characterized by a pRF center in the left visual field. The violin plot associated with the 9.3$\%$ is highlighted: the contralateral part of the violin plot is outlined with dashed lines, while the ipsilateral part is outlined with dotted lines. A line is plotted in each eccentricity bin and quadrant indicating the estimated median ipsilateral representation plotted in C. (C) The ipsilateral polar angle representation of the ROIs described in A forms a propeller blade pattern around the vertical meridian. For each subject, the polar angle representations of the ROI were sorted by distance from the vertical meridian, and the 75th percentile polar angle value of the ipsilateral visual field was calculated for each subject. The median of this (75th percentile) value across subjects is plotted in the visual field in this panel (dots), together with the interquartile range. The median is also plotted as lines in B.

Fig. 4C shows the resulting boundaries of the contralateral projections of the ipsilateral fields. As in the monkey data, the width of the human crossed–uncrossed overlap increases with retinal eccentricity. The width grows from less than ${\mathrm{1}}^{○}$ near the fovea to $1^{○}$ to 1.${\mathrm{5}}^{○}$ at $\pm 5^{○}$ to ${\mathrm{7}}^{○}$ eccentric. The human data span ${\mathrm{14}}^{○}$ of visual angle, while the monkey data span ${\mathrm{30}}^{○}$. Where the two datasets superimpose, the human overlap is somewhat wider than the monkey; this could be due to the human’s larger interocular distance, which causes greater disparity for a given scene (36).

The ipsilateral data in Fig. 4C could be distorted if some subjects were placed in the MRI bore with their heads tilted slightly leftward or rightward. Such a tilt could cause ipsilateral representation to appear in the pRFs due to misalignment of the subject’s vertical meridian with that of the stimulus. If this happened, there would be especially strong ipsilateral representation in such subjects either along the right upper and left lower (for a subject whose head is tilted leftward) or along the right lower and the left upper (rightward). To check this possibility, we calculated the correlation between right upper and left lower and between right lower and left upper ipsilateral surface areas across subjects. The correlations were very small and statistically insignificant ($r=0.087$; $P\approx 0.1$), indicating that head tilt did not substantially affect the results.

Natural Disparity Statistics

To answer our research question—how effective is the crossed–uncrossed overlap in ensuring that signals from the environment project directly to the same hemisphere—we need to know the statistics of naturally occurring disparity. To this end, we used previous measurements of disparity statistics across the visual field while people engaged in everyday activities (25). The apparatus was a mobile scene-tracking and binocular eye-tracking apparatus that measures the three-dimensional (3D) structure of the scene and where subjects are fixating in those scenes as they engage in everyday activities. Materials and Methods has details on the apparatus and data analysis.

We could not measure ocular torsion directly, and this is potentially problematic because torsion, especially cyclovergence, affects the relationship between scene geometry and disparity at the retinas, particularly near the vertical midline. Thus, in our analysis we incorporated the most likely torsion based on Listing’s Law (L1) and Listing’s Extended Law (L2). These laws dictate the torsion of the eyes for all distances and directions of gaze. Unless the eyes are converged near, L1 is generally obeyed. With near convergence, L1 is not obeyed; the deviation is expressed by L2 (37). In L2, Listing’s plane for each eye is rotated temporally by $\pm$1/4 of the horizontal vergence angle, thereby affecting cyclovergence. The behavior is quantified by

$${\varphi }_L=-{\varphi }_R=\frac{\lambda }{2}{\sin }^{-1}\left(\frac{\sin \left(\nu /2\right)}{\cos \left(\gamma /2\right)}\right),$$ [1]

where ${\varphi }_L$ and ${\varphi }_R$ are the angles of rotation of the Listing’s planes and depend on the horizontal vergence angle $\nu$ and the binocular azimuth $\gamma$. $\lambda$ is a gain from 0 to 1 that defines the behavior between L1 and L2: $\lambda =0$ means that the rotation planes are coplanar as specified by L1; $\lambda =1$ means that the rotation planes are rotated in opposing directions by the amount specified by L2. The value of $\lambda$ varies somewhat across individuals. The average is 0.8 (38). We used that value in computing the natural disparity statistics at the retinas. However, we also investigated what the effects on disparity statistics would be if we assumed other biologically plausible values for $\lambda$.

Disparity Distributions.

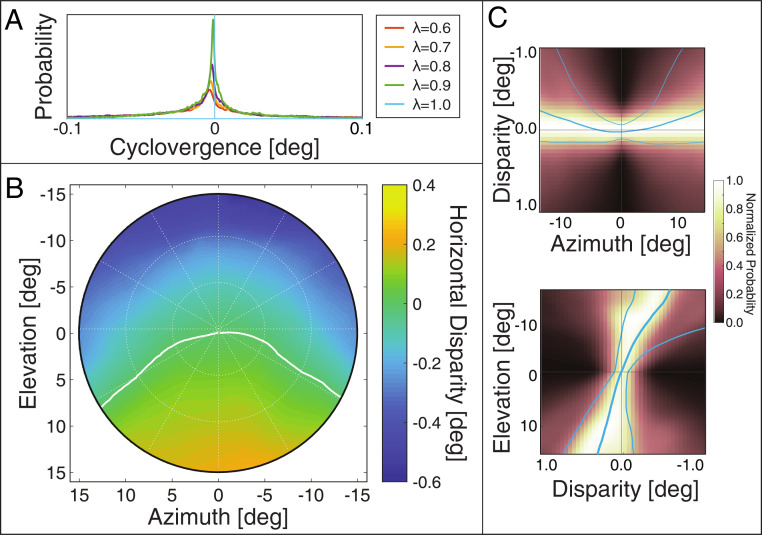
From the previous dataset (25), we computed the distribution of naturally occurring disparities in different parts of the visual field. We first needed to know how different assumptions about ocular torsion would affect the disparity distribution. From the eye-tracking data, we know the distributions of fixation distances and directions. We used those data to calculate the distribution of cyclovergence that would have occurred given different assumptions about the L2 gain ($\lambda$). Fig. 5A plots the probability of different cyclovergence values for $\lambda$ values of 0.6 to 1. Very few values greater than a few minutes of arc are observed for any value of $\lambda$. We then calculated the distribution of naturally occurring disparity for each of those values of $\lambda$ and found that there is essentially no effect even near the vertical meridian. Those results are provided in SI Appendix, Fig. S2. In summary, the distribution of disparity is essentially unaffected by variations in L2 gain from one individual to another.

Fig. 5.

Natural disparity statistics. The data from refs. 25 and 26 have been averaged across subjects and subjected to a weighted combination across tasks as in ref. 24. (A) Distributions of cyclovergence from ref. 25, weighted across tasks, for $\lambda$ = 0.6 to 1 (Eq. 1). Negative cyclovergence is extorsion. When $\lambda$ = 1, Listing’s Extended Law is precisely obeyed so all cyclovergence values are zero. (B) Median horizontal disparity at each position in the central $30^{○}$ of the visual field assuming $\lambda =0.8$. The abscissa and ordinate represent azimuth and elevation, respectively. Disparity values are indicated by color: darker blue corresponds to larger uncrossed disparity; darker yellow corresponds to larger crossed disparity. The white curve indicates where the median disparity changes sign from crossed to uncrossed. (C) Distributions of naturally occurring horizontal disparity along the horizontal and vertical meridians. Upper plots the normalized probability of different disparities along the horizontal meridian, and Lower plots those probabilities along the vertical meridian. The thick blue curves represent the median disparities at each eccentricity, while the thin curves represent the 25th and the 75th percentiles of the distribution.

Fig. 5B plots median disparity for the central $30^{○}$ assuming an L2 gain of 0.8. Along the vertical meridian, the central tendency of the disparity distribution is crossed in the lower visual field and uncrossed in the upper. These biases increase with increasing eccentricity. The data along oblique meridians indicate that the pattern of uncrossed disparity in the upper field and crossed disparity in the lower field generalizes to the whole visual field.

Fig. 5C provides closer looks at the distributions by showing the distributions along the horizontal and vertical meridians in Upper and Lower panels, respectively. The thick curves represent the median disparity, and the thin curves represent the 25th and 75th percentiles. The pattern of uncrossed disparity in the upper field and crossed disparity in the lower field is quite evident. These are strong biases: for instance, $10^{○}$ above the fovea (i.e., upper field), $71\%$ of the disparities are uncrossed.

Comparison of Crossed–Uncrossed Overlap and Disparity Statistics

As we argued earlier, it should be more effective (i.e., faster and more spatially precise) to integrate binocular signals from direct paths from both retinas to the cortex rather than from a direct path from one retina and an indirect path from the other. We next investigated how effective the observed overlap (Figs. 3 and 4) would be in maximizing the proportion of natural disparities that generate signals directly to the same hemisphere. We performed the analysis both with the monkey data from Fukuda et al. (7) and with the human data from Benson et al. (27, 28) and Benson and Winawer (29, 34).

Monkey Data.

To compare monkey and human data, we must take into account the difference in eye separation in the two species. Average interocular distance in Japanese macaques is 3.5 cm (39), while the average in humans is 6.3 cm [$\pm 0.4$ cm (40)]. To close approximation, disparity magnitude is proportional to interocular distance (36), so to compare the monkey and human data, we multiplied the width of the crossed–uncrossed overlap reported by Fukuda et al. (7) by the ratio of interocular distances ($6.3/3.5$). To account for variability in human interocular distance, we considered values within the $95\%$ CIs of the distribution.

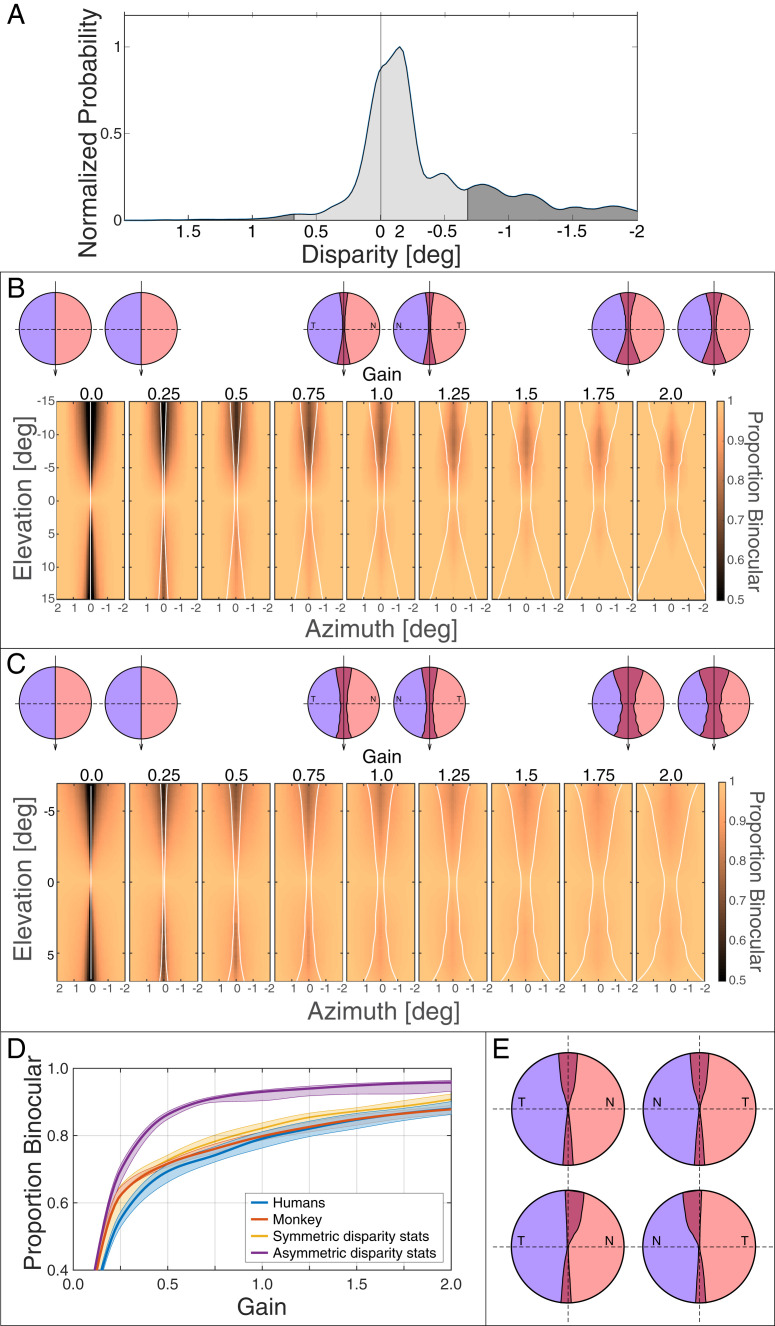
We then incorporated the statistics of naturally occurring disparities in humans. Fig. 6A shows an example distribution from $10^{○}$ in the upper visual field. Here, the median disparity is $-31$ minutes of arc (arcmin). We then applied the crossed–uncrossed overlap, corrected for interocular distance, to these distributions. We assumed that the overlap is symmetric (i.e., the same extent for crossed and uncrossed projections). The axis of symmetry was an earth-vertical line. We aligned the nominal vertical meridian in the Fukuda data on that line. The symmetric overlap at $10^{○}$ is represented in Fig. 6A by the light gray area between $-0.65$ and $+0.65^{○}$. After we identified the appropriate part of the disparity distribution, we calculated the proportion of the total disparities that fell within those bounds. Those values are plotted in Fig. 6B. Icons above the panels represent different widths. Each panel shows the proportion of naturally occurring disparities, at a given field location, that would project directly to the same hemisphere for different widths of the crossed–uncrossed overlap. The widths were varied by applying different multipliers—gains—to the widths reported by Fukuda et al. (7) (Fig. 3A). Gains of 0.5 and 2 yield half and twice the widths, respectively, they reported. As larger gains were used, the proportion of disparities projecting to the same hemisphere increased. We then found for each gain the position in the visual field with the lowest proportion of same-hemisphere projections (i.e., the worst case). Those proportions are represented by the orange curve in Fig. 6D. The proportion of same-hemisphere projections increases significantly for gains of 0.5 and higher. When the gain is 1, the proportion rises to 0.80. The proportion does not increase significantly for gains greater than 1. For example, when the gain is 2, the proportion increases to only 0.88. The reason for the small increase with larger gains is that the disparity distributions have long tails (Fig. 5C), so when the central mass of disparities is captured, there is little to be gained by increasing the bounds of the overlap further.

Fig. 6.

Distribution of natural disparities and how crossed–uncrossed projections affect binocular integration. (A) Proportion of natural disparities projecting to the same hemisphere assuming symmetric overlap. The distribution of horizontal disparity from the natural scene statistics (Fig. 5) is plotted for an elevation of $-10^{○}$ (i.e., upper visual field). From the data of Fukuda et al. (7) (Fig. 3A), we calculated the proportion of disparities that would produce signals traveling to the same hemisphere (light gray) and the proportion that would produce signals to different hemispheres (dark gray). (B) Overlap width and binocular integration in monkey. We varied the width of the crossed–uncrossed overlap assuming symmetry. The icons on top represent the overlap for gains of zero, one, and two. Blue and red represent the parts of the retina projecting to left and right LGN, respectively. The panels below the icons plot the proportions of disparities for each position in the visual field that would, according to different overlap widths, send signals to the same hemisphere. Upper visual field is at the top of each panel; left field is to the left. The crossed–uncrossed overlap assumed in each panel is represented by the thin white lines. Color indicates the proportion of disparities that send signals directly to the same hemisphere. The middle panel uses the overlap described by Fukuda et al. (7) (Fig. 3A). The others are the same pattern multiplied by different gains. (C) Overlap width and binocular integration in human. We again varied the width of the crossed–uncrossed overlap. Icons represent overlap for gains of zero, one, and two. The panels plot the proportions of disparities that would send signals to the same hemisphere. Color indicates the proportion of disparities that send signals directly to the same hemisphere. The assumed crossed–uncrossed overlap is represented by the thin white lines. The middle panel uses the overlap shown in Fig. 4C. (D) Proportion of disparities projecting to the same hemisphere. Proportion is plotted as a function of overlap width (gain). The span of elevations was different in the monkey and human data ($\pm 15^{○}$ and $\pm 8^{○}$, respectively), so here, we used $\pm 8^{○}$ for both species. The orange and blue curves represent the proportions based on the monkey and human data, respectively, assuming symmetric overlap. The yellow curve shows the proportion if the width was optimal for the natural disparity statistics. The purple curve shows the proportion if the width and asymmetry of the overlap were optimal for the natural disparity statistics. (E) The icons in Upper represent the optimal crossed–uncrossed overlap pattern assuming symmetry for the human interocular distance and elevation span of $\pm 8^{○}$. The overlap pattern would encompass 90% of the natural disparities at each field position (i.e., between the 5th and 95th percentiles of the disparity distribution at each eccentricity). N and T indicate nasal and temporal retina, respectively. The icons in Lower show the pattern if we relax the assumption about asymmetry.

Of course, the distribution of natural disparities is generally not centered on zero (Fig. 5). Most notably, it is centered on uncrossed disparities in the upper field and crossed disparities in the lower. An asymmetric pattern of crossed–uncrossed overlapping projections to the hemispheres would therefore be more effective by assuring that the most likely disparities generate signals sent directly to the same hemisphere. The needed asymmetry for crossed disparity is for fibers from nasal retina near the vertical meridian to project ipsilaterally along with the expected contralateral projection. This asymmetry would be adaptive because it would assure that likely disparities in that part of the visual field send signals directly to the same hemisphere. The needed asymmetry for uncrossed disparity is the reverse: temporal retina near the vertical meridian should project contralaterally along with the expected ipsilateral projection. Fukuda et al. (7) plotted horizontal and vertical lines in their anatomical data (e.g., their figure 5 A and B) to represent approximations to the horizontal and vertical meridians of the eyes, but they could not determine true horizontal nor true vertical. By true vertical, we mean how an earth-vertical line in the world would project onto the retina of an upright animal with the eyes in forward gaze (the same definition of vertical used in refs. 24 and 25). We investigated the significance of this by rotating the anatomical data in opposite directions in the two eyes and seeing how that affected the proportion of disparities that would send signals directly to the same hemisphere. We found that a rotation of −${\mathrm{3}}^{○}$ (meaning overlap extends to temporal upper retina and nasal lower retina) produces a somewhat greater proportion of same-hemisphere projection than no rotation (0.85 vs. 0.80). The opposite rotation (+${\mathrm{3}}^{○}$) produces a noticeably lower proportion of 0.67.

Human Data.

We next applied the same analysis to the human fMRI data. We first found the bounds of the contralateral projections of the ipsilateral fields for elevations of –$7^{○}$ to +${\mathrm{7}}^{○}$ (Fig. 4C) and then found the proportion of naturally occurring disparities that fall within those bounds. We assumed that the vertical meridian in the data corresponded to true vertical as defined earlier. This is a reasonable assumption because ocular torsion is very similar with the head upright and with body and head in supine position as adopted when the fMRI data were collected (41). Because the fMRI data were collected with binocular stimulation, we could not ascertain whether the crossed–uncrossed overlap is asymmetric, so we initially assumed symmetry. (A similar fMRI study with monocular stimulation would reveal if the overlap was asymmetric.) The results are shown in Fig. 6C. Each panel shows the proportion of naturally occurring disparities, at a given field position, that would project directly to the same hemisphere for different widths of the crossed–uncrossed overlap. The widths were varied by applying gains to the pattern in Fig. 4C. As larger gains were used, the proportion increased. We then found for each gain the position in the visual field with the lowest proportion of same-hemisphere projections. Those proportions are represented by the orange curve in Fig. 6D: again, the worst case. The proportion increases noticeably with increasing gain up to a value of about one where the proportion starts to asymptote. When the gain is one, the proportion is 0.79, so the great majority of naturally occurring disparities would send signals directly to the same hemisphere with a symmetric overlap of the size indicated by the fMRI data.

As we did in the analysis of the monkey data, we investigated the possible benefit of asymmetric overlap by rotating the anatomical data in opposite directions in the two eyes. Rotations of −${\mathrm{3}}^{○}$, ${\mathrm{0}}^{○}$, and +${\mathrm{3}}^{○}$ produce proportions of same-hemisphere projections of 0.83, 0.79, and 0.62, respectively.

Ideal Overlap Pattern.

We also conducted an analysis in which we allowed the overlap to have the width at each elevation that would encompass 90% (5th to 95th percentile) of the naturally occurring disparities at the corresponding elevation. The results for a gain of one are represented by the yellow curve in Fig. 6D. The proportion of direct projections increased from 0.80 to 0.88. We also examined the potential effect of asymmetric overlap. To do this, we assumed an asymmetry centered on the median natural disparity at each eccentricity and then, for each elevation, found the width and asymmetry of overlap that would encompass 90% of the observed disparities at that elevation. The results are represented by the purple curve in Fig. 6D. The proportion of disparities projecting to the same hemisphere increased significantly to 0.93 when gain = 1. Thus, there would be a clear benefit if the asymmetry of the crossed–uncrossed overlap were adjusted to be centered on the median of the natural disparity distribution.

The disparity statistics depend on the natural task. In SI Appendix, Fig. S3, we show how the task (make sandwich, order coffee, indoor walk, outdoor walk) would affect binocular integration for different decussation patterns. Interestingly, the proportion of disparities that would project to the same hemisphere is highest for the two tasks involving medium and far distances (indoor walk and outdoor walk). The decussation pattern has more effect in the two near tasks (make sandwich and order coffee).

Discussion

Summary of Results.

We first examined stereo performance psychophysically near the vertical meridian and nearer and farther than fixation to see if a deficit can be found. We did not observe one. We then investigated whether crossed–uncrossed overlap in decussation is effective in maximizing the proportion of naturally occurring disparities that project to the same hemisphere. We found that the increasing width of the overlap with increasing retinal eccentricity is well suited for ensuring that signals are sent directly from the two eyes to the same hemisphere. We also found that effectiveness would be increased if the overlap was asymmetric: biased toward uncrossed disparities in the upper visual field and toward crossed disparities in the lower field.

Lateral Eyes.

As we mentioned earlier, many mammalian species (e.g., rats, mice, horses, sheep, goats, squirrels, chipmunks, rabbits, tree shrews) have widely separated optic axes, and consequently, most of their visual field is monocular (4, 42). However, there is also a small binocular field straight ahead of the animal (Fig. 1A). That part of the field is imaged on a crescent in the temporal retina of both eyes.

In these animals, the entire retina projects to the contralateral hemisphere of the central nervous system. If those were the only projections, binocular interaction in the brain would have to occur via indirect communication from one hemisphere to the other. However, it has been reported in several lateral-eyed mammals that the temporal crescent of the retina also projects ipsilaterally: specifically, in the rat (43–45), mouse (46, 47), rabbit (48), chipmunk (49, 50), hamster (51, 52), goat (53), and sheep (53, 54). Thus, the temporal crescents of the retinas in these animals project both contralaterally and ipsilaterally so that stimuli in the binocular field can in principle produce signals that travel directly to the same hemisphere. This is the same pattern that is observed in cats and primates, suggesting that overlapping projections are a general principle in mammals regardless of the size of the binocular visual field.

Of course, the absolute disparities associated with stimuli in the binocular field of lateral-eyed animals would be enormous (if disparity is defined relative to the optic axes as it is in frontal-eyed animals), so the circuitry underlying disparity estimation would have to take such large disparities into account. There is indeed clear evidence from one of these animals—the mouse—that they have cortical neurons that respond selectively to binocular disparity (55) and that the animal can use responses from these neurons to perceive depth from disparity (56).

Development of Cross–Uncrossed Projections.

The development of most regions of mammalian central nervous system consists of an initial proliferation of neurons, many of which later die. Pruning by cell death yields an intricate pattern of neural connectivity (57). The overlap of crossed and uncrossed projections from the retina appears to result from such a developmental process.

In adult cats, retinal ganglion cells in temporal retina project to the ipsilateral hemisphere, and cells in the nasal retina project to the contralateral hemisphere; however, there is a region of crossed–uncrossed overlap near the vertical meridians (9–11). In newborn kittens, many ganglion cells in temporal retina project contralaterally. During the first weeks of life, most of these cells die, resulting in the small region of crossed–uncrossed overlap characteristic of adult cats (58, 59). The cell death is the by-product of competitive interactions between the axons of retinal ganglion cells. Evidence for this comes from the observation that sectioning the optic tract from one eye protects the proliferate contralateral projection from temporal retina of the other eye (58–60) (i.e., after sectioning, the exuberant contralateral projections persist into adulthood).

A similar developmental pattern is observed in rodents. At birth, ganglion cells in rats, mice, and hamsters project to all of the contralateral superior colliculus and sparsely to all of the ipsilateral colliculus (47, 52, 61). During the first couple of weeks, many ipsilaterally projecting cells die, the remaining ipsilateral projection becomes confined to a small part of the colliculus, and the axons from those cells arise from only the temporal crescent of the retina (47, 52, 61). As in the cat, putting an eye at a competitive disadvantage (by early enucleation or blocking of activity by tetrodotoxin) allows the exuberant ipsilateral projection from the other eye to persist.

We found that the pattern of crossed–uncrossed projections from the two eyes is well suited for ensuring that nearly all naturally occurring disparities will send signals to the same cortical hemisphere. The development of such projections in rodents and cats suggests strongly that the projection pattern is shaped by experience. Specifically, the axons of retinal ganglion cells from the left and right eyes that are frequently activated together retain their central connections, while the axons of cells that are not frequently activated together do not retain their connections due to death of exuberant contralaterally projecting cells. In this way, the decussation pattern eventually becomes most effective. The developmental story may be different in macaques because there is some evidence that the mature pattern of overlap is present soon after birth (62).

Conclusion

We know from previous work that the vertical horopter (i.e., where projections from corresponding retinal points near the vertical meridian intersect in the world) is well tuned to the distribution of naturally occurring disparities (24, 25). Specifically, corresponding points in the lower retina (upper field) are shifted toward uncrossed disparity, and corresponding points in the upper retina (lower field) are shifted toward crossed. Those shifts are commensurate with the most likely disparities in those parts of the visual field. We also know that biases in binocular vergence occurring with saccades are consistent with natural disparity statistics (25). We now suggest that the decussation pattern in monkeys and humans is another adaptation to regularities in the natural environment.

Materials and Methods

Stereoacuity Experiment.

Subjects.

Three adult males participated. One was naive to the experimental purpose. All had normal visual acuity and stereopsis. The study was approved by the Institutional Review Board at the University of California, Berkeley. All subjects gave informed consent before starting the experiment.

Apparatus.

Stimuli were presented dichoptically using a haploscope. Head position was stabilized with a head and chin rest. Two displays (LG 32UD99-W), one for each eye, were viewed via mirrors close to the eyes. Screen size was $69.6\times 39.3$ cm, and screen distance was 61 cm, resulting in a field of view of $59.4^{○}\times 35.7^{○}$. Screen resolution was $\mathrm{3,840}\times \mathrm{2,160}$, yielding $64.5\times 60.5$ pixels per degree. In our convention, crossed disparities are positive, and uncrossed disparities are negative.

Stimuli.

The stimuli were two bright spots on a dark background. They were presented at the fovea or ${\mathrm{8}}^{○}$ above, below, left, and right of the fovea. The luminance of the spots was constant in the middle with Gaussian skirts on all sides (Fig. 2A). The length of the plateau was 6 arcmin in the foveal condition and 60 arcmin in the peripheral. The SDs of the skirts were 2 and 8 arcmin, respectively. The foveal spots were circular, and the peripheral ones were elliptical with a 2:1 aspect ratio. Spot separation was 4.5 arcmin in the foveal condition and 15 arcmin in the peripheral in order to maximize discriminability (63). In the foveal measurements, the two spots were presented one above the other. In the peripheral measurements, they were presented radially (i.e., one to left and the other to the right along the horizontal meridian and one above and one below along the vertical meridian). In this way, we equated any crowding effects along the horizontal and vertical meridians (64), but more importantly, we also limited the horizontal extent of the two spots when testing along the vertical meridian. A pink noise texture was applied to each spot to aid disparity estimation. Antialiasing was employed to allow subpixel displacements of the spots.

Procedure.

The stimuli were presented for 200 ms. After each presentation, subjects made a forced choice judgment of which spot was closer (Fig. 2B). Auditory feedback was provided. We presented five disparity pedestals between −15 and +15 arcmin at the fovea and between −60 and +60 arcmin in the periphery. The relative disparity between the two spots was varied in nine steps between −60 and +60 arcsec at the fovea and in seven steps between −400 and +400 arcsec in the periphery. The pedestal values were chosen to encompass most natural disparities at each retinal location (24, 25). Each condition was presented 25 times for a total of 1,125 trials at the fovea and 875 for each of the four sampled locations in the periphery: a grand total of 4,425 trials per subject. We used the method of constant stimuli to vary relative disparity from trial to trial.

Occasionally, a tumbling E (1.5-arcmin stroke width; 20/30 equivalent) was presented instead of the two-spot stimulus, and the subject indicated which of four orientations had been presented in a forced choice judgment with feedback. These trials were incorporated to make sure that the subject accurately fixated the dichoptic fixation target. All subjects performed at or near ceiling on this task, which means that they did in fact maintain accurate fixation.

Threshold estimation.

The psychometric data were fitted with cumulative Gaussians using Psignifit (version 2.5.6; https://github.com/wichmann-lab/psignifit/wiki), a Matlab toolbox that implements maximum likelihood fitting (65). From the fits, we determined the relative disparity yielding 75% performance for each field position, pedestal, and subject. We also computed 95% CIs.

Natural Disparity Statistics.

Subjects.

Four adult males participated. All had normal visual acuity and stereopsis. The study was approved by the Institutional Review Board at the University of California, Berkeley. All subjects gave informed consent before starting the experiment.

Apparatus.

The apparatus was a head-mounted binocular eye tracker: SR Research Eyelink II with sampling frequency 250 Hz and accuracy 0.${\mathrm{5}}^{○}$. The apparatus was customized with a stereoscopic scene camera with field of view $75^{○}\times 58^{○}$, resolution of $640\times 480$ pixels, and frame rate of 30 Hz. More details are provided in ref. 25.

Procedure.

Subjects performed four tasks chosen as representative of everyday activities, encompassing different fixation ranges from near (making sandwich) to midrange (order coffee and indoor walk) to far (outdoor walk). An in-house calibration was used to estimate the translation and rotation of viewpoints from the stereo camera to the eyes. More details are in ref. 25.

Postprocessing.

The torsion of the eyes, particularly cyclovergence, affects horizontal disparity at the retinas, especially near the vertical meridian. Torsion can therefore affect our estimates of natural disparity statistics (Fig. 5). The eye tracker we used provides estimates of gaze azimuth and elevation for each eye but no information about torsion. We incorporated the expected effects of torsion by using well-documented models. Listing’s Law (L1) specifies the 3D orientation of the eyes (i.e., vertical, horizontal, and torsional) for different gaze directions. According to L1, the final orientation of an eye is determined by a single rotation from primary gaze position (straight ahead at long distance) about an axis that lies within the plane orthogonal to the primary orientation’s gaze direction: Listing’s plane.

When the eyes are converged near, L1 is not exactly obeyed; the deviation is expressed by Listing’s Extended Law (L2) (37). In L2, the Listing’s plane for each eye is rotated temporally by $\pm 1/4$ of the horizontal vergence angle. This affects cyclovergence. The behavior is quantified in Eq. 1 as a function of $\lambda$. The parameter $\lambda$ is a gain from 0 to 1 that defines the interplay between L1 and L2: $\lambda =0$ means that the rotation planes are coplanar as specified by L1, and $\lambda =1$ means that the rotation planes are rotated in opposing directions as specified by L2. We incorporated L2 in the analysis with $\lambda$ = 0.8 (24, 25, 66) because 0.8 is a typical value for adults with normal binocular vision (37, 38). We also examined potential effects on disparity statistics by assuming $\lambda$ values from 0.6 to 1 (Fig. 5A and SI Appendix, Fig. S2).

Data Availability.

The Human Connectome Project 7 Tesla Retinotopy Dataset stores fully-processed pRF model parameters for 181 subjects from the HCP. These data can be found on the Open Science Framework: https://osf.io/bw9ec/ (28). The Human Connectome Project stores images and preprocessed structural data from 3T MR scans. These data are available at https://db.humanconnectome.org/ (30). The Visual Performance Fields stores retinotopic maps predicted by Bayesian inference and distances along the cortical surface. These data are available on the Open Science Framework: https://osf.io/5gprz/ (34). The BORIS Dataset stores statistics of retinal disparities and gaze direction for subjects performing everyday tasks in the natural environment. These data are available on the Open Science Framework: https://osf.io/t9qg5 (26). The Peripheral Stereo-Threshold Project data about stereoscopic threshold measured at fovea and in periphery in humans, together with the code to run the experiment and to analyze the data. The project and data can be found on the Open Science Framework: https://osf.io/74hgx (67).