Abstract
The inbreeding coefficient (F) of individuals can be estimated from molecular marker data, such as SNPs, using measures of homozygosity of individual markers or runs of homozygosity (ROH) across the genome. These different measures of F can then be used to estimate the rate of inbreeding depression (ID) for quantitative traits. Some recent simulation studies have investigated the accuracy of this estimation with contradictory results. Whereas some studies suggest that estimates of inbreeding from ROH account more accurately for ID, others suggest that inbreeding measures from SNP‐by‐SNP homozygosity giving a large weight to rare alleles are more accurate. Here, we try to give more light on this issue by carrying out a set of computer simulations considering a range of population genetic parameters and population sizes. Our results show that the previous studies are indeed not contradictory. In populations with low effective size, where relationships are more tight and selection is relatively less intense, F measures based on ROH provide very accurate estimates of ID whereas SNP‐by‐SNP‐based F measures with high weight to rare alleles can show substantial upwardly biased estimates of ID. However, in populations of large effective size, with more intense selection and trait allele frequencies expected to be low if they are deleterious for fitness because of purifying selection, average estimates of ID from SNP‐by‐SNP‐based F values become unbiased or slightly downwardly biased and those from ROH‐based F values become slightly downwardly biased. The noise attached to all these estimates, nevertheless, can be very high in large‐sized populations. We also investigate the relationship between the different F measures and the homozygous mutation load, which has been suggested as a proxy of inbreeding depression.
Keywords: coancestry, deleterious recessive mutations, genetic drift, identity by descent, inbreeding load
1. INTRODUCTION
Inbreeding depression, the change in the mean of a quantitative trait with inbreeding (a reduction in fitness in the case of life‐history traits), is a main factor for the extinction of endangered species (Allendorf, Luikart, & Aitken, 2013; Frankham, Ballou, & Briscoe, 2010; O’Grady et al., 2006) and the management of livestock (Leroy, 2014). Regarding fitness components, inbreeding depression is generally assumed to occur because of the increased homozygosity of partially recessive deleterious alleles (Charlesworth & Willis, 2009; Hedrick, 2012), although some unknown depression may also occur by reduced heterozygosity at loci presenting heterozygote advantage (Charlesworth, 2015).
For quantitative traits, the rate of inbreeding depression (ID) is usually quantified by the slope of the linear regression of the individual phenotypic values on their inbreeding coefficient, F (Lynch & Walsh, 1998). The inbreeding coefficient of an individual, the probability of identity by descent of alleles, that is, alleles of an individual in a locus that come from a common ancestor to its parents, can be obtained from pedigree data (Wright, 1969) but also inferred from genome homozygosity (Li & Horvitz, 1953; Malécot, 1948; Toro et al., 2002), mainly using highly dense molecular markers, such as SNPs. Genomic or molecular measures of F have the advantage of providing estimates of realized inbreeding values, which are often more precise than pedigree ones (Curik, Ferenčaković, & Sölkner, 2014; Keller, Visscher, & Goddard, 2011; Wang, 2016), and do not require a knowledge of the genealogical relationships of individuals. They, however, measure overall homozygosity, which includes not only identity by descent of alleles but also identity in state, that is, identical alleles coming from different ancestors.
Different metrics are available to obtain the estimates of genomic inbreeding, either based on maximum likelihood (e.g., Milligan, 2003; Wang, 2007), methods of moments (e.g., Purcell et al., 2007; Ritland, 1996), the diagonal elements of a genomic relationship matrix (VanRaden, 2008; Yang, Lee, Goddard, & Visscher, 2011), homozygosity measures (e.g., Bjelland, Weigel, Vukasinovic, & Nkrumah, 2013; Szulkin, Bierne, & David, 2010), genotypic correlations (Ackerman et al., 2017) or the proportion of the genome within runs of homozygosity (ROH) (Ceballos, Joshi, Clark, Ramsay, & Wilson, 2018; Ferenčaković et al., 2013; Ferenčaković, Sölkner, Kapš, & Curik, 2017; McQuillan et al., 2008) or homozygosity‐by‐descent genomic segments (Druet & Gautier, 2017). Multiple empirical comparisons have been made between the estimates of ID with alternative inbreeding measures (Bjelland et al., 2013; Goudet, Kay, & Weir, 2018; Kardos, Taylor, Ellegren, Luikart, & Allendorf, 2016; Pryce, Haile‐Mariam, Goddard, & Hayes, 2014; Santure et al., 2010; Saura et al., 2015; Zhang, Calus, Guldbrandtsen, Lund, & Sahana, 2015), but without the knowledge of the true ID, it is difficult to make conclusions about which genomic F measure provides more appropriate estimations.
An assessment of the accuracy of some of the F measures in the estimation of ID can be made with computer simulations (e.g., Kardos, Luikart, & Allendorf, 2015; Keller et al., 2011), where the true parameters are known, even though simulated scenarios are always a simplified view of the natural processes. Thus, Keller et al. (2011) studied the correlation between different F measures and the homozygous mutation load (HML) of each individual, defined as the number of homozygous loci for rare alleles (MAF < 0.05) carried by an individual. This is assumed to be a proxy of the individual overall load of homozygous (partially) recessive deleterious mutations and, thus, of inbreeding depression. Using this approach, Keller et al. (2011) showed that ROH‐based F measures are the most powerful to detect ID. Kardos et al. (2015) rather considered the correlation between the F measures and the proportion of the genome which is identical by descent (IBD), concluding that both ROH‐based and SNP‐by‐SNP‐based F measures can explain a large amount of the genomic IBD variation if the number of SNPs is sufficiently large (tens of thousands). However, these previous simulation studies did not consider ID of a quantitative trait in itself, but addressed the issue in an indirect way by considering some proxies of it.
More recently, Yengo et al. (2017) used data on true genotypes for several millions of human SNPs and simulated ID by ascribing phenotypic effects to a sample of the SNPs under different scenarios. They then investigated the accuracy in the estimation of ID using different measures of individual F. The main conclusion was that the most accurate estimations were obtained with a measure of genomic inbreeding based on the correlation between uniting gametes (FUNI; previously called FIII by Yang et al., 2011), a statistic based on the deviation of SNP homozygosity from their expected values giving a larger weight to rare alleles than to common alleles. In contrast, ROH‐based measures of inbreeding (FROH) were shown to provide very large overestimations of ID. Yengo et al. (2017) thus explicitly recommended the use of FIII to estimate ID with molecular data. This generated some debate, though, as it was argued that the simulations performed by Yengo et al. (2017) were not carried out with explicit simulated individuals subjected to genetic processes (Kardos, Nietlisbach, & Hedrick, 2018). Rather, trait values had been simulated as a function of the inbreeding coefficient which was calculated in a similar way as FIII, perhaps biasing the conclusions in favour of this F measure (Kardos et al., 2018; see also reply by Yengo et al., 2018). More recently, Nietlisbach, Muff, Reid, Whitlock, and Keller (2019) performed a set of genetically explicit simulations concluding that, in contrast to Yengo et al. (2017) results, FROH provided the most accurate estimates of ID, whereas FIII (called Falt by Nietlisbach et al., 2019) produced substantial upwardly biased estimates. Thus, these sets of simulations showed contradictory results.
The scenarios considered by Yengo et al. (2017) and Nietlisbach et al. (2019), however, were also very different in terms of population sizes and intensities of selection. For example, Nietlisbach et al. (2019) considered a subdivided population consisting of 30 demes of 200 individuals each connected by migration, assuming deleterious mutations with homozygous fitness effects exponentially distributed with mean −0.03. In contrast, Yengo et al. (2017) used in their simulations real human genotypic data from 10,000 unrelated individuals, and dominance effects were simulated assuming they were inversely proportional to the allele frequency variance and, therefore, with a potentially very large value.
Here, we carried out another set of genetic explicit simulations considering simplistic scenarios to evaluate the relative performance of different genomic marker F measures on the estimation of the rate of inbreeding depression. Our results show that, for low effective population sizes (N = 100), where individuals are expected to be more related to each other and where natural selection is, in general, relatively less intense, FROH provides the most accurate estimates of ID, whereas FIII provides overestimations, in full agreement with the results of Nietlisbach et al. (2019). However, for large effective population sizes (N ≥ 1,000), where individuals tend to be less related and deleterious alleles are expected to be at lower frequencies, FIII provides almost unbiased average estimations of ID, in agreement with the results of Yengo et al. (2017), although with a great noise, whereas FROH can produce slightly downwardly biased average estimates of ID, also with a great noise.
2. METHODS
2.1. Simulation procedure and parameters
Time‐forward individually based simulations were carried out of a diploid monoecious population of constant size N (100, 500, 1,000, 5,000 and 10,000) individuals with random mating. A modified version of the program SLIM (Messer, 2013) was used in which mutations with effect on fitness have a pleiotropic effect on a quantitative trait (Caballero, Tenesa, & Keightley, 2015). A single genome sequence of 100 Mb, initially devoid of variation, was assumed where mutations appear at a rate U per haploid genome and generation chosen to produce about 30,000 SNPs in the final generation for all population sizes. The rate of recombination between consecutive positions was assumed to be c = 10−8, which implies an average rate of recombination of 1 cM per Megabase. Thus, the genome length sequence (100 Mb) and the genetic length (1 M) are typical of a mammalian chromosome. Simulations were run for 10N discrete generations (5N in the case of N = 10,000). Ninety‐five per cent of mutations were assumed to be neutral, the remainder having an effect on a quantitative trait (QTL) and a pleiotropic effect on fitness. The genotypic values for the wild‐type homozygote, the heterozygote and the mutant homozygote were 0, ah and a for the quantitative trait, and 1, 1 + sh and 1 + s for fitness, where a constant dominance coefficient of h = 0.2 was assumed. Multilocus genotypic values assumed a multiplicative model for fitness and an additive model for the quantitative trait across loci. To minimize the noise, phenotypic values for the quantitative trait were assumed to equal genotypic values; that is, no environmental error was added to the phenotypic values. Values of a and s were obtained from a bivariate gamma distribution with mean effect −0.03 and shape parameter β = 1 (i.e., following an exponential distribution). A correlation (ρ) between a and s values was generally assumed to be one, that is, the trait is fitness itself, but a values were scaled so that the amount of ID was about the same for all population sizes considered (about 1% decrease in the mean per 1% increase in inbreeding or an inbreeding load of about one haploid lethal equivalent). Because mutations always reduced the value of the trait and were partially recessive, the model implied directional dominance, that is, homozygous recessive genotypes always reduced the trait value, thus generating ID for the trait. Except for the impact of purifying selection on deleterious mutations, the simulated populations were Wright–Fisher ideal populations so that the population size (N) approximately equals the effective population size.
For the population sizes of N = 100, 1,000 and 10,000, additional simulations were run considering all previous parameters (default scenario) with the following changes: (a) a one‐order higher (c = 10−7) or lower (c = 10−9) recombination rate between consecutive genomic positions. (b) A density of SNPs one quarter of that assumed previously, obtained by reducing to a quarter the mutation rate per generation, that is U/4. (c) A percentage of 10% (instead of 5%) of mutations affecting the trait and fitness. (d) An average effect of mutations on fitness of s = −0.1 instead of −0.03. (e) A distribution of effects for fitness and the trait with shape parameter for the gamma distribution of β = 0.1 or 2 instead of one. (f) A coefficient of dominance of mutations of h = 0 (complete recessive) instead of 0.2. (g) A correlation between fitness (s) effects and effects for the quantitative trait (a) of ρ = 0.5 instead of one. For these scenarios, the rate of inbreeding depression widely varied between 0.2% and 12% decrease in the mean per 1% increase in inbreeding, depending on the scenario and population size.
For all scenarios, the genotypes of all individuals of the population in the last simulated generation were obtained and the expected ID was quantified by the sum of 2dpq values for all segregating QTLs (Morton, Crow, & Muller, 1956), where p and q are the frequencies of the wild and mutant allele, respectively, and d = a (h–½) is the dominance effect. An estimate of the rate of inbreeding depression was also obtained by making all individuals homozygous (inbreeding coefficient F = 1) and calculating the change in the mean of the trait relative to that in the original individuals. The obtained values of ID coincided almost perfectly with their expectations.
The homozygous mutation load (Keller et al., 2011) was obtained as the number of homozygous mutations carried by individuals. Three different measures were obtained: (a) HML, the total number of homozygous mutations for neutral SNPs, that is, excluding QTLs; (b) HMLMAF, the number of homozygous mutations for neutral SNPs with minor allele frequency lower than or equal to 0.05 (this is the definition applied by Keller et al., 2011); (c) HMLQTL, the number of homozygous mutations for QTLs.
2.2. Measures of inbreeding coefficients and estimates of the rate of inbreeding depression
From the last generation of each simulation, the files map and ped were generated with all individuals of the population (to avoid the confounding effect of sampling) and all neutral segregating SNPs (i.e., QTLs were removed). No MAF pruning was made to the data. The following measures of the coefficient of inbreeding of each individual were then obtained with the programs PLINK (Purcell et al., 2007) and GCTA (Yang et al., 2011):
Estimators FI, FII, and FIII provided by GCTAv1.93.0 with the –ibc option:
| (1) |
| (2) |
| (3) |
where S is the total number of markers, xk is the number of minor alleles of marker k (i.e., 0, 1 or 2 copies), and pk is the current frequency of the minor allele in the population.
The estimator FI is that proposed by VanRaden (2008) and referred to as VanRaden2. The estimator FIII was called Falt by Keller et al. (2011) and Nietlisbach et al. (2019), FGRM by Huisman, Kruuk, Ellis, Clutton‐Brock, and Pemberton (2016) and FUNI by Yengo et al. (2017) and Alemu et al. (2020). For this measure of F, homozygous genotypes are weighted by the inverse of their allele frequencies (Yang et al., 2011), thus giving more weight to rare alleles. FIII can also be obtained as (Keller et al., 2011) (with opposite sign), where δ equals 1/pk for homozygotes of the minor allele, 1/(1 – pk) for homozygotes of the major allele and zero for the heterozygotes, thus explicitly showing the larger weight given to rare rather than to common alleles.
The estimator FHOM is a measure of the deviation from Hardy–Weinberg proportions and is obtained by PLINK1.9 with the –het option.
| (4) |
Both FHOM and FII are based on the scaled difference between the observed (O[H]) and expected (E[H]) frequency of homozygotes, that is, (O[H] – E[H])/ (1 – E[H]), although the summation over markers is made differently in each case.
Finally, the estimator based on runs of homozygosity (FROH) was obtained using PLINK1.9 with the default options: a minimum of 100 SNPs, at least 1 SNP per 50 Kb, and a scanning window of 50 SNPs. We considered runs of lengths larger than 0.1 Mb (FROH ‐0.1), 1 Mb (FROH ‐1) or 5 Mb (FROH ‐5), after removing highly linked SNPs (r 2 > .9) with the ‐‐indep‐pairwise 50 5 0.9 PLINK option, as recommended by Howrigan, Simonson, and Keller (2011).
An explanation of the rationale and relationship between the estimators FI, FII, FIII and FHOM is given in the Supplementary Appendix. The inbreeding coefficient of an individual (F), that is, the probability of identity by descent of the two alleles at a locus, is a concept relative to a (sometimes arbitrary) reference base population (e.g., an earlier generation of the population). If the allele frequencies of the reference generation are considered in the estimators, these are expected to measure the inbreeding coefficient (IBD) relative to that reference generation, at least when all loci are at linkage equilibrium (see Supplementary Appendix). Unfortunately, the reference generation frequencies are usually unknown and the estimates are obtained assuming the current generation allele frequencies. In this case, the measures of F from (1), (2), (3), (4) refer to the deviations of the frequencies of homozygotes from those expected under Hardy–Weinberg expectations or the correlation between the alleles carried by individuals. Thus, they take positive or negative values, generally implying an excess or a defect, respectively, of homozygotes. In contrast, the measures obtained by FROH take only positive values (from zero to one) as they are expected to include genomic segments of homozygosity produced by IBD.
The estimated ID was obtained as the slope of the linear regression of the phenotypic values (Phe) of individuals on their different F measures. All individuals of the population were used in this regression to avoid biases due to sampling errors. In addition, as was mentioned above, phenotypic values were taken with no error, so that any deviation of the estimated ID from its true value should be ascribed to the different properties of the molecular measures of F.
Simulations were repeated between 100 and 1,000 times depending on the population size considered. For each replicate, the estimated ID obtained with each F measure was compared with the expected (true) ID, calculating the distribution of deviations from the expected value and the root‐mean‐square error (RMSE), a combined measure of accuracy and precision. Pearson correlations between all F values and between these and the phenotypic values of individuals (Phe) and the different homozygous mutations loads (HML, HMLMAF and HMLQTL) were also obtained and averaged across replicates.
2.3. Alternative set of simulations
To double‐check the main results obtained, additional time‐forward individually based simulations were performed with an in‐house C program alternative to SLIM, modified from Caballero, Bravo, and Wang (2017). In this case, populations of size N = 100, 1,000 and 5,000 were run for 1,000 (N = 100) or 10,000 (N ≥ 1,000) discrete generations, assuming a 60 Kb genome sequence of 1 Morgan genetic length and a mutation rate adjusted to produce up to 30,000 SNPs. Thus, the number of SNPs and the genetic length were similar to those of the previous simulations. A 10% proportion of mutations were assumed to be deleterious with average selection and dominance coefficients of s = −0.03 and h = 0.2, respectively. Selection coefficients for mutations were obtained, as before, from an exponential distribution, but dominance coefficients were assumed to be variable, with an inversely proportional relationship with selection coefficients following the model proposed by Caballero and Keightley (1994) (see also Caballero, 2020, p. 159). Values of the true ID and those estimated with the different F values were obtained from each of the last 200 generations of each replicated simulation, considering the whole population. Given the short genome sequence assumed in these simulations, ROH segments larger than 1 Kb were considered.
3. RESULTS
Table 1 shows the mean and variance of all F measures in the default scenario for three population sizes. SNP‐by‐SNP‐based F measures using Hardy–Weinberg deviations or correlations between alleles (FI, FII, FIII and FHOM) have virtually the same mean, as expected (see Supplementary Appendix), but FIII and FHOM show a lower variance, particularly FIII. Mean and variances of FROH estimates are lower for increasing fragment lengths. Table 2 presents the average correlations between F measures. FI has a strong negative correlation with FII, as suggested from their different subtracting terms (see Equations 1 and 2), and generally low correlations with the other F measures. FII also shows intermediate (for small N) or low correlations (for large N) with the other measures, but larger than those for FI. Measures FIII, FHOM and FROH show rather large correlations with one another, decreasing for larger population sizes.
Table 1.
Mean and variance of different genomic measures of the inbreeding coefficient (F; see text for definitions), averaged over replicates, for different population sizes (N)
| FI | FII | FIII | FHOM | FROH− 0.1 | FROH −1 | FROH− 5 | |
|---|---|---|---|---|---|---|---|
| Mean | |||||||
| N= 100 | −0.0057 | −0.0053 | −0.0053 | −0.0052 | 0.1398 | 0.1120 | 0.0430 |
| N = 1,000 | −0.0006 | −0.0005 | −0.0005 | −0.0006 | 0.1720 | 0.0712 | 0.0108 |
| N = 10,000 | −0.00004 | −0.00004 | −0.00004 | −0.00004 | 0.0784 | 0.0072 | 0.0010 |
| Variance | |||||||
| N = 100 | 0.0424 | 0.0435 | 0.0077 | 0.0250 | 0.0130 | 0.0130 | 0.0110 |
| N = 1,000 | 0.0264 | 0.0266 | 0.0011 | 0.0039 | 0.0025 | 0.0026 | 0.0018 |
| N = 10,000 | 0.0660 | 0.0660 | 0.0002 | 0.0007 | 0.0005 | 0.0003 | 0.0002 |
Standard errors of means and variances are below 0.002 (N = 100) and 0.003 (N = 1,000 and 10,000).
[Correction added on 19 January 2021, after first online publication: table 1 has been modified.]
Table 2.
Correlation between different genomic measures of the inbreeding coefficient (F; see text for definitions), averaged over replicates, for different population sizes (N)
| FII | FIII | FHOM | FROH −0.1 | FROH −1 | FROH −5 | |
|---|---|---|---|---|---|---|
| N = 100 | ||||||
| FI | −0.6438 | 0.3922 | 0.1544 | 0.2038 | 0.2083 | 0.2206 |
| FII | 0.4279 | 0.5661 | 0.5193 | 0.5091 | 0.4500 | |
| FIII | 0.8786 | 0.8775 | 0.8694 | 0.8046 | ||
| FHOM | 0.8526 | 0.8244 | 0.6946 | |||
| FROH −0.1 | 0.9868 | 0.8507 | ||||
| FROH −1 | 0.8785 | |||||
| N = 1,000 | ||||||
| FI | −0.9171 | 0.1933 | 0.0690 | 0.0829 | 0.1000 | 0.1172 |
| FII | 0.2076 | 0.2754 | 0.2555 | 0.2450 | 0.2144 | |
| FIII | 0.8587 | 0.8427 | 0.8577 | 0.8190 | ||
| FHOM | 0.8810 | 0.8192 | 0.6576 | |||
| FROH −0.1 | 0.8893 | 0.6845 | ||||
| FROH −1 | 0.7607 | |||||
| N = 10,000 | ||||||
| FI | −0.9946 | 0.0501 | −0.0160 | 0.0114 | 0.0324 | 0.0316 |
| FII | 0.0525 | 0.0932 | 0.0619 | 0.0512 | 0.0450 | |
| FIII | 0.7506 | 0.7125 | 0.8102 | 0.7366 | ||
| FHOM | 0.7138 | 0.6075 | 0.4879 | |||
| FROH −0.1 | 0.6747 | 0.5240 | ||||
| FROH −1 | 0.7681 | |||||
Standard errors are below 0.005 (N = 100), 0.003 (N = 1,000) and 0.006 (N = 10,000).
Figure 1 shows the proportional deviations of the estimated ID values obtained with different neutral molecular F measures with respect to the true values, that is, (EstID – TrueID)/ TrueID, where EstID and TrueID are the estimated and true ID, respectively. Thus, a value of, say + 1, implies an overestimation of ID by 100% and a value of −1 an underestimation of ID by 100%. The bars exclude 2.5% of the extreme deviations at each side and the dot is the arithmetic mean of the deviations. The measures FI and FII provide always very biased estimates (underestimations) of ID, and this is also the case, although to a less extent, for FHOM. For small population size (N = 100), FIII produces upwardly biased estimates whereas estimates with FROH are unbiased, irrespective of the ROH minimum length assumed. However, as the population size N is increased, FROH estimates of ID can become underestimations, particularly if short fragment lengths are included in the analysis, whereas those from FIII become more and more accurate on average, although with a large variation across replicates. For the largest population size (N = 10,000), both FROH and FIII incur in a slight underestimation of ID on average, but with a great variation. Thus, FIII transits from providing overestimations of ID for small population sizes to slight underestimations for large ones. A representation of the particular deviations observed for each simulated replicate with different population sizes is shown in Figure S1.
Figure 1.
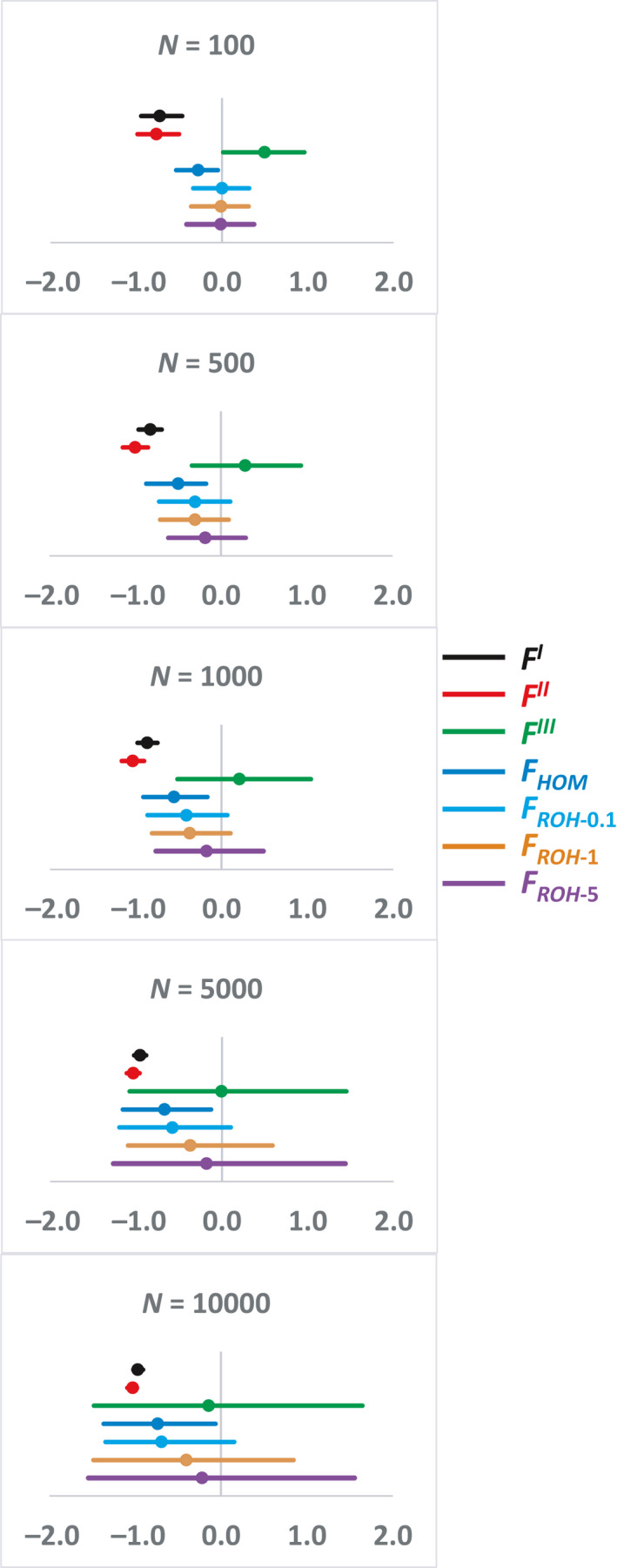
Proportional deviation of the estimates of the rate of inbreeding depression (ID) obtained with different measures of the inbreeding coefficient with marker data (see text), with respect to the true simulated ID. The dot is the mean deviation, and the bar indicates the 95% of the distribution of simulated replicates. Simulated parameters: population size N; genome sequence of 100 Mb run for 10N discrete generations (5N in the case of N = 10,000); rate of recombination between consecutive positions c = 10−8; mutation rate per haploid genome and generation U chosen to produce about 30,000 SNPs in the final generation for all population sizes; 95% of mutations assumed to be neutral, the remainder having an effect on a quantitative trait (QTL) and a pleiotropic effect on fitness; homozygous effects for the trait (a) and fitness (s) obtained from a bivariate gamma distribution with mean effect −0.03 and shape parameter β = 1; the mean homozygous effect for the trait (a) was adjusted to obtain a true inbreeding depression rate of about 1 (one per cent decline in mean per one per cent increase in inbreeding or an inbreeding load of about one haploid lethal equivalent) for all population sizes; dominance coefficient h = 0.2; correlation ρ = 1 between a and s values
For N = 100, the average root‐mean‐square error (RMSE) of the estimates of ID obtained with FROH ‐5 (0.216 ± 0.047) is lower than that obtained with FIII (0.597 ± 0.097) (Figure 2). However, for larger population sizes, this difference disappears, for example for N = 10,000, RMSE FROH ‐5 = 0.837 ± 0.255 and RMSE FIII = 0.772 ± 0.231.
Figure 2.
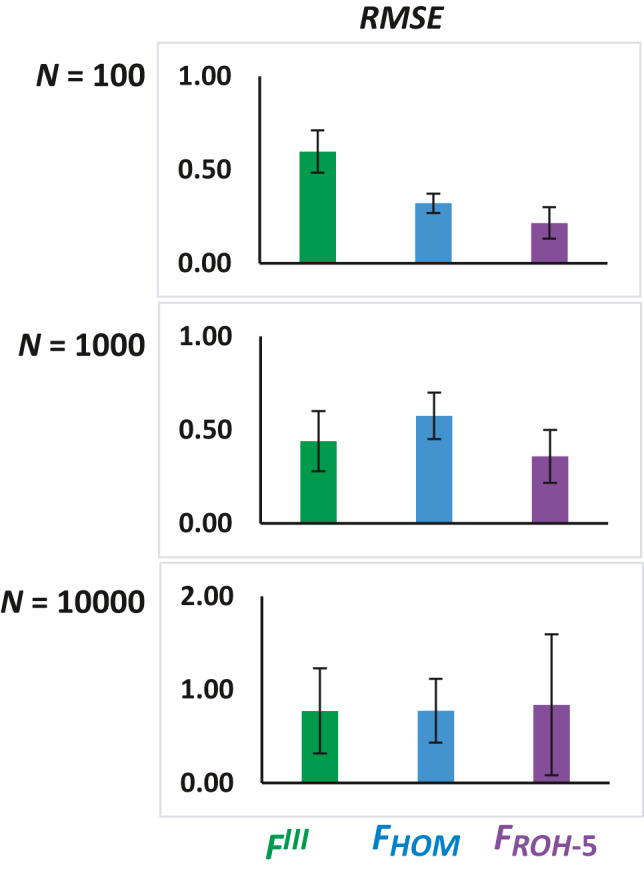
Root‐mean‐square error (RMSE) of estimates of the rate of inbreeding depression obtained from three measures of the individual inbreeding coefficient (FIII, FHOM and FROH‐5; see text). Results refer to the default parameters as in Figure 1. Bars indicate one standard error of the mean
Figure 3 shows results analogous to those of Figure 1 for different parameters alternative to those of the default scenario. These include different recombination rates, density of SNPs, intensity of selection, distribution of allelic effects and degree of recessiveness. Rates of inbreeding depression obtained using FI and FII give underestimations for all scenarios and are not shown. Thus, results are only given in the figure for FIII, FHOM, FROH ‐1 and FROH ‐5. Although some quantitative differences can be observed for the different scenarios, the main conclusions reached above generally hold. FIII gives overestimations of ID in all scenarios for N = 100, becoming almost unbiased, on average, for N = 10,000. FHOM usually underestimates ID. FROH ‐5 provides generally good estimates of ID with a tendency to a slight underestimation. Averaging results from all scenarios gives an outcome very similar to that of the default scenario (cf. Figure 1 and Figure S2). In addition, the corresponding results using a simulation program alternative to SLIM (Figure S3) gives the same general picture. Estimates of ID from FROH (with ROH > 1 Kb) are nearly unbiased for N = 100 but imply underestimations for larger N, whereas the overestimation incurred by FIII is reduced as N is increased. In this case, the error bars are very short because each simulated value obtained is the average of 200 estimations carried out in the last 200 generations of each simulation.
Figure 3.
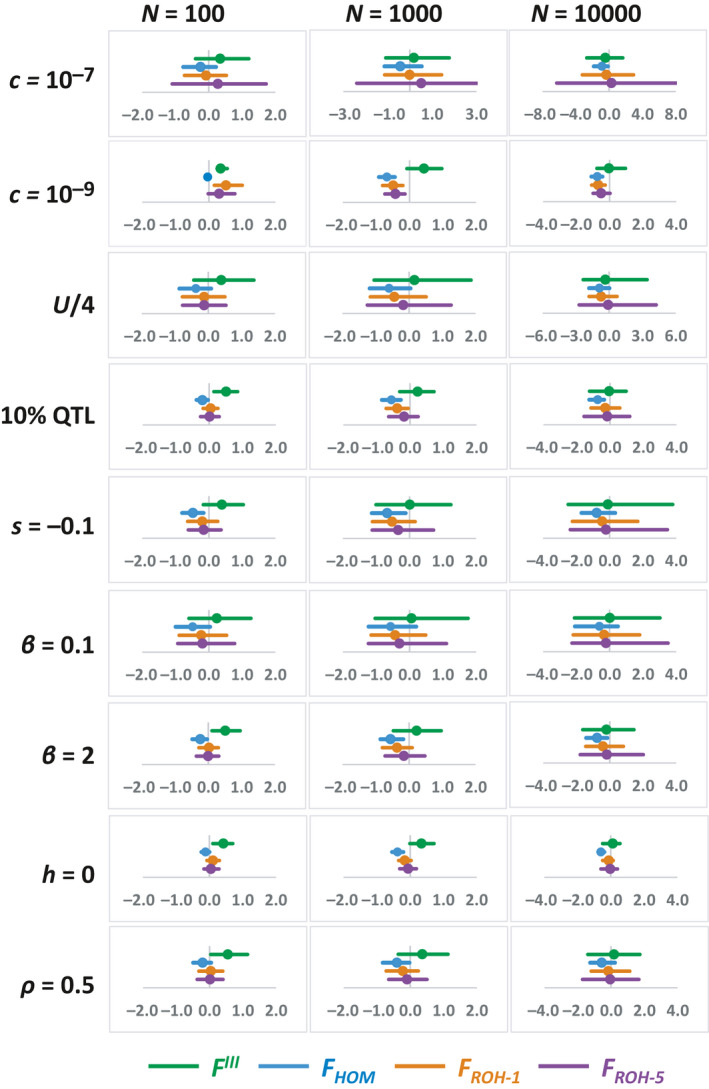
Proportional deviation of the estimates of the rate of inbreeding depression (ID) obtained with different measures of the inbreeding coefficient with marker data (see text), with respect to the true simulated ID. Simulations assume different population sizes (N). The dot is the mean deviation and the bar indicates the 95% of the distribution of simulated replicates. The simulation parameters are the same as for Figure 1 (default parameters), with the following changes: (Row 1) recombination rate between positions c = 10−7. (Row 2) recombination rate between positions c = 10−9. (Row 3) density of SNPs one quarter of that assumed in Figure 1. (Row 4) 10% of mutations affecting the trait and fitness. (Row 5) Average effect of mutations on fitness of −0.1. (Row 6) Distribution of effects for fitness and the trait with shape parameter for the gamma distribution of β = 0.1. (Row 7) Distribution of effects for fitness and the trait with shape parameter for the gamma distribution of β = 2. (Row 8) coefficient of dominance of mutations of h = 0. (Row 9) correlation between fitness (s) effects and effects for the quantitative trait (a) of ρ = 0.5
Table 3 gives the correlation between the phenotypic values of individuals (Phe) and the different measures of the homozygous mutation load (HML). All correlations are diminished as the population size is increased, as expected. In all cases, also as expected, Phe has the largest correlation with HMLQTL. For small population sizes (N = 100), Phe has a larger correlation with HML than with HMLMAF. In contrast, for larger N, Phe is more correlated with HMLMAF than with HML, suggesting that the phenotype of individuals can be ascribed more strongly to rare homozygous alleles. In fact, as shown in Figure S4, the larger the population size, the lower the QTL frequencies and the larger the contribution to ID by rare alleles, as would be expected. Nevertheless, for large N (particularly for N = 10,000), all correlations between the different values of HML and Phe are rather low, indicating that the homozygous mutation load is a poor proxy of fitness in large populations.
Table 3.
Correlation between phenotypic values (Phe) for the quantitative trait and the homozygous mutation load, obtained as the number of mutant homozygotes carried by individuals considering all neutral SNPs (HML), neutral SNPs with MAF < 0.05 (HMLMAF), and quantitative trait loci (HMLQTL), for different population sizes (N)
| HML | HMLMAF | HMLQTL | |
|---|---|---|---|
| N = 100 | |||
| Phe | 0.6652 | 0.4538 | 0.7930 |
| HML | 0.4711 | 0.8949 | |
| HMLMAF | 0.4771 | ||
| N = 1,000 | |||
| Phe | 0.1237 | 0.1723 | 0.3020 |
| HML | 0.6226 | 0.3694 | |
| HMLMAF | 0.3270 | ||
| N = 10,000 | |||
| Phe | 0.0107 | 0.0158 | 0.0712 |
| HML | 0.5018 | 0.0600 | |
| HMLMAF | 0.0663 | ||
Standard errors are below 0.005 (N = 100) and 0.002 (N = 1,000 and 10,000).
Finally, Figure 4 shows the correlation between the F measures and the phenotypic value (Phe) of individuals and the homozygous mutations loads (HML). FIII has the largest correlation with Phe and HMLMAF for all values of N and with HMLQTL for N ≥ 1,000. The largest correlation with HML is achieved by FHOM, as expected.
Figure 4.
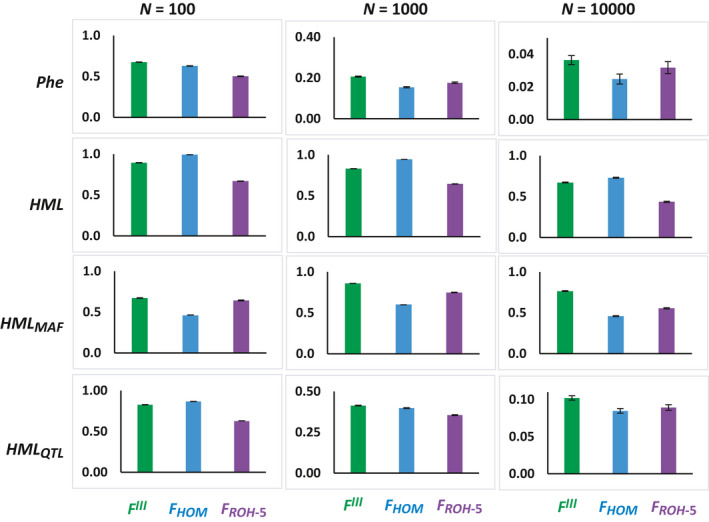
Correlation between the individual values of the genomic measures of the inbreeding coefficient (FIII, FHOM and FROH‐5; see text) and the individual phenotypic value for the quantitative trait (Phe), the total homozygous load for neutral SNPs (HML), the homozygous load for neutral SNPs with MAF ≤ 0.05 (HMLMAF) and the homozygous load for QTLs (HMLQTL). Bars indicate one standard error of the mean
4. DISCUSSION
Inbreeding depression is a key issue for explaining the evolution of populations and to carry out the management and conservation of wild and domestic species (Lynch & Walsh, 1998). The increasing availability of dense molecular markers (SNPs) for many species has allowed the prediction of the relationships among individuals in the absence of pedigree records. In fact, genomic measures of F can be more useful than pedigree estimates, as they provide realized rather than expected genomic relationships (Kardos et al., 2016; Keller et al., 2011). These estimates of genomic inbreeding can, in turn, be used to estimate the rate of inbreeding depression. If the allele frequencies of many loci at Hardy–Weinberg and linkage equilibrium were known without error at a given previous generation of the population and these frequencies were included in the different SNP‐by‐SNP F measures in the current generation, their expected values would provide the true mean inbreeding coefficient (IBD) referred to that previous generation (i.e., the F value that would be obtained from the pedigree) (see Supplementary Appendix). The usual scenario, however, is that only the current allele frequencies are available to be used in the different SNP‐by‐SNP F measures and these provide deviations of the genotypic frequencies from their HW expectations. Estimates from genomic segments of homozygosity (FROH) are intended to look for events of IBD. However, not all ROH involve IBD and the measures obtained strongly depend on the length of the fragments considered. Thus, it is unclear which F measures from molecular data are the most appropriate to estimate the rate of inbreeding depression. While the simulation results of Yengo et al. (2017) supported the use of SNP‐by‐SNP‐based F estimates with more weight for rare alleles, those of Nietlisbach et al. (2019) pointed towards the use of ROH‐based F estimates. Our results seem to reconcile these contrasting results and suggest that the recommendation to be made strongly depends on the particular population considered.
Nietlisbach et al. (2019) compared different F measures carrying out genetically explicit simulations of a metapopulation under purifying selection against deleterious mutations. The metapopulation included 30 demes of 200 individuals each connected by migration (1.2 migrants per deme and generation) and was run for 5,000 discrete generations. Viability selection was considered on a genome mimicking that of the great tit, with around 50,000 neutral loci and 2,500 deleterious loci acting multiplicatively. Homozygous effects were exponentially distributed with mean s = −0.03 and a mean dominance coefficient of h = 0.18 (following estimated parameters from Wang, Hill, Charlesworth, & Charlesworth, 1999). To perform their simulations, they used a binary viability model and compared the different methods that can be used to estimate ID in this type of models. Deleterious variants were excluded from the analysis of genomic inbreeding and apparently no filtering for MAF was applied to the data. ROH with length > 1 Mb were obtained using sliding windows of 50 SNPs with steps of 5, allowing up to one heterozygote per segment and removing SNPs with high linkage disequilibrium (r 2 > .9). The main conclusion obtained by Nietlisbach et al. (2019) was that, under their simulated scenario, FROH provides unbiased average estimations of ID, whereas FIII gives severe average overestimations (about +0.7 in the scale given in our Figure 1), and FHOM a slight underestimation (about −0.2). Their results also showed that the variation between the estimates of ID was smaller by using FROH than by using FIII and those from FHOM had the lowest variation (see Nietlisbach et al., 2019, Figure 2). In addition, the RMSE of ID estimates obtained from FHOM, FROH and FIII were 0.86, 1.01 and 2.02, respectively. Thus, FIII estimates of ID showed about twice as large RMSE as FROH ones.
Yengo et al. (2017), in contrast, used a different simulation approach, by considering human genotypic data of 10,000 unrelated individuals (pairwise genetic relationship < 0.05) and assigning phenotypic values with a model for which dominance effects were assumed to be constant or a function of the inverse of the variance of the allele frequency. In these simulations, therefore, a much larger population size was assumed than for the individual demes of Nietlisbach et al. (2019), and dominance effects could be very substantial for loci with rare alleles. The analysis of inbreeding measures was carried out assuming a MAF of 0.05 and ROH fragments were obtained either pruning high linkage disequilibrium (LD) SNPs or considering only fragments > 1.5 Mb. Yengo et al. (2017) considered different scenarios, such that causal variants could be enriched in random, high‐ or low‐LD genome regions. In the random LD scenario (the causal variants are a random subset of all SNPs) with dominance effects inversely related to the variance of the allele frequencies, FIII was found to provide unbiased estimates of ID, FHOM a slight underestimation and FROH (with ROH lengths > 1.5Mb) a large average overestimation of about 90% of ID (see Yengo et al., 2017, Figure 1b), that is, a value of about +0.9 in the scale of our Figure 1. They also found that the estimates of ID from FROH had about a threefold larger standard error than those from FIII. Additionally, they found that both FIII and FHOM produced overestimates of ID when QTLs are enriched in high‐LD regions, and underestimates of ID when enriched in low‐LD regions, and that these biases could be corrected or reduced if LD score and MAF stratification were applied. Population stratification also produced biases in estimates of ID from FHOM and FROH, which were not observed in those from FIII. In accordance with their simulated results, the estimations of ID over 25 human quantitative traits were consistently larger when obtained from FROH measures than from FIII ones. However, more significant cases of ID were detected with FIII than with FROH.
Our simulations consider some parameters similar to those assumed by Nietlisbach et al. (2019), such as the average selection coefficient and dominance, but assume a single undivided population of varying size. We also considered a simple additive multilocus model for a quantitative trait rather than a binary viability model, so that a log scale is not necessary to be applied and the regression of raw phenotypic values on the predicted F provides a direct estimate of the inbreeding depression rate. Our simulations for N = 100 show no bias of the average ID when FROH is used, irrespective of whether short (>0.1 or >1 Mb) or long (>5 Mb) ROH are considered (Figure 1). FHOM underestimates ID by a fraction of about −0.3, whereas FIII overestimates it by a fraction of about +0.5. These results are actually very similar to those obtained by Nietlisbach et al. (2019), that is −0.2 and +0.7, respectively. In addition, for N = 100 we found that the RMSE of ID estimates from FIII measures were three times larger than those from FROH ones (Figure 2), in concordance with a twofold difference in the same direction observed by Nietlisbach et al. (2019). We observed, however, that estimates of ID from FHOM for N = 100 had a RMSE larger than those from FROH (Figure 2), whereas Nietlisbach et al. (2019) results showed a RMSE for FHOM slightly lower than that from FROH. We should note, however, that apparently, Nietlisbach et al. (2019) did not consider estimates of ID below zero (see their Figure 2), what may explain this difference between both studies.
In contrast, our results are rather different from those of Nietlisbach et al. (2019) when larger population sizes are assumed. In this scenario, estimates of ID by FROH can become downwardly biased in our simulations, particularly if short ROH are considered (Figure 1). For example, with ROH of length > 1 Mb the underestimation of ID is in a fraction of about −0.01, −0.30, −0.37, −0.37 and −0.40 for increasing population sizes, from 100 to 10,000. If large fragments are used in the calculations (>5 Mb), the bias is lower (−0.01, −0.18, −0.17, −0.18 and −0.22 for increasing N). The increased underestimation of ID when short ROH are considered may occur because some short ROH may not reflect IBD, as suggested by Pryce et al. (2014), and thus, FROH overestimates the true genomic inbreeding (cf. mean values of FROH ‐0.1, FROH ‐1 and FROH ‐5 in Table 1). However, it can also be argued that long ROH only account for recent inbreeding whereas measures of F including also short ROH would incorporate more ancient inbreeding, what may contribute to values of short‐ROH‐F measures larger than those from long ones.
The increase in population size also results in a reduction of the average bias of the estimated ID using FIII, whose bias becomes 0.5, 0.28, 0.21, −0.002 and −0.14 for increasing values of N. Thus, average estimates of ID with FIII for large population sizes are basically unbiased or slightly so, in agreement with the main result obtained by Yengo et al. (2017). Our results do not agree with those of Yengo et al. (2017), however, in relation with the estimation of ID using FROH, as they obtained overestimations by a fraction +0.9 whereas we obtained almost unbiased estimates or slight underestimations for large N. In fact, Yengo et al. (2017) found generally much larger estimates of ID for 25 human quantitative traits when FROH was used than when FIII was used. Kardos et al. (2018) argued that the FROH measures considered by Yengo et al. (2017) only accounted for long ROH and, thus, for only recent inbreeding. If short ROH and thus more ancient inbreeding would have been incorporated, this could have resulted in larger estimates of F and lower ID values. Nevertheless, the larger the population size, the larger the noise in the estimates of ID both from FIII and FROH, pointing towards the difficulties of estimating the rate of inbreeding depression in large outbred populations. We observed that variation in the estimates of ID from FIII and FROH were similar in the case of N = 10,000 (see Figure 1) and that the RMSE of these estimates were also about the same for these two F measures (see Figure 2 for N = 10,000). This contrasts with the result of Yengo et al. (2017), which indicated that the estimates of ID from FROH had a threefold larger standard error than those from FIII. It must be noted, however, that our simulations refer to a simplistic model of a constant population size, with uniform LD along the genome and without any source of stratification, which can differ from the complex structure of the human genomes and populations analysed by Yengo et al. (2017). Thus, there may be a source of unknown factors that could be contributing to the differences between the results of both studies.
We obtained estimates of the mean, variance and correlation between the different genomic F measures and between these and the homozygous mutation load (HML), suggested to be a proxy of ID (Keller et al., 2011). The mean of the genomic measures FI, FII, FIII and FHOM is basically the same (Table 1) and close to the value of the deviation from Hardy–Weinberg proportions expected in a panmictic population, −1/2N (Kimura & Crow, 1963; Robertson, 1965). The correlation results indicate that FI (VanRaden2) and FII measures of inbreeding are poorly correlated with the other measures (Table 2) and are poor estimators of ID (Figure 1 and Figure S3). They should therefore be disregarded in the estimation of ID. In addition, these estimators show a larger variance than the other SNP‐by‐SNP‐based measures of inbreeding, FHOM and FIII. The latter shows the lowest variance, as demonstrated by Yengo et al. (2018). Correlations between FIII, FHOM and FROH, however, are generally high, as observed in empirical studies (e.g., Bérénos, Ellis, Pilkington, & Pemberton, 2016). Estimates of ID from FHOM, however, are also generally biased (Figure 1 and Figures S3), so this F measure should not be used either to estimate ID.
We found that FIII is the measure of genomic inbreeding showing the largest correlation with the phenotypic values of individuals (Figure 4), as well as with HMLMAF (the definition of homozygous mutation load from Keller et al., 2011), and the HML applied to QTLs (HMLQTL) for large populations. Thus, our results suggest that FIII is the F statistic more related with the load of deleterious recessive mutations, as also suggested by the analysis of genomic cattle data by Alemu et al. (2020). Some of these results contrast with those of Keller et al. (2011), who found that FROH had the largest correlation with HMLMAF, followed by FIII and then FHOM (see Figure 7 of Keller et al., 2011), whereas we observed that the largest correlation is for FIII, followed by FROH and then FHOM (see Figure 4). However, the simulations of Keller et al. (2011) did not consider selection of any type. Purifying selection, as applied in our simulations, would imply some reduction in genetic variability across the genome, so that rare allele frequencies would get more relevance in the HML.
Regarding FROH, we found that the lowest bias in the estimation of ID occurred when large ROH were considered (Figure 1 and Figure S3). This could be explained, as mentioned above, because short ROH may not fully reflect IBD, overestimating the true genomic inbreeding, but also because short ROH are less enriched in QTLs. Szpiech et al. (2013) showed that ROH in the human genome are enriched in deleterious mutations and that long ROH are more enriched than short ones. In cattle, however, the result is the opposite, with short ROH more enriched in deleterious mutations than long ones (Zhang et al., 2015). Our simulations show that, for the smallest population size (N = 100), the correlation between the phenotypic values (Phe) and FROH is 0.66 ± 0.003 for FROH ‐0.1 and 0.58 ± 0.004 for FROH ‐5, in line with the cattle results. In contrast, for the largest population size (N = 10,000) the corresponding correlations are 0.012 ± 0.001 for FROH ‐0.1 and 0.017 ± 0.001 for FROH ‐5, in agreement with the human genome results. It is expected that cattle populations, heavily subjected to selection, have lower effective population sizes than human populations, so our results are consistent with the observations.
The F measure showing the largest correlation with the overall homozygosity mutation load (HML, considering all allele frequencies) was FHOM. Multilocus heterozygosity has been traditionally related to overall fitness, although with a poor correlation (Grueber, Waters, & Jamieson, 2011; Slate & Pemberton, 2002). This, however, has been mainly focused on few markers (e.g., microsatellites) and the possibility to explore the multilocus heterozygosity—fitness correlation with highly dense markers using FHOM or other measures of F opens new research areas.
In summary, our simulation results indicate that estimates of the rate of inbreeding depression from FROH measures of inbreeding are appropriate for populations with low effective sizes but may lead to some underestimation for large ones, unless the ROH fragments considered are sufficiently long. Estimates of the rate of inbreeding depression from rare‐SNP‐by‐SNP‐based F measures (FIII) are severely biased in populations of small effective size, but nearly unbiased in large ones, showing the largest relationship with the phenotypic values of individuals and the homozygous mutation load. This different performance of the F measures depending on the population size can respond to the expectation that small populations are subjected, in general, to less intense selection than large ones, although purging selection of the inbreeding load can be more effective in the former (García‐Dorado, 2012; López‐Cortegano, Vilas, Caballero, & García‐Dorado, 2016). The use of FI and FII measures of genomic inbreeding and, to a lesser extent FHOM, cannot be advised to estimate ID. For large effective population sizes, however, the estimation of the rate of inbreeding depression becomes rather difficult as all estimations are subjected to a high error.
CONFLICT OF INTEREST
None declared.
Supporting information
Supplementary Material
ACKNOWLEDGEMENTS
We are grateful to Miguel Toro, Aurora García‐Dorado and three anonymous referees for helpful comments on the manuscript. This work was funded by Agencia Estatal de Investigación (AEI) (CGL2016‐75904‐C2), Xunta de Galicia (ED431C 2016‐037) and Fondos Feder: “Unha maneira de facer Europa.” Tom Druet is Senior Research Associate from the F.R.S.‐FNRS and was supported by Grants T.1053.15 and J.0154.18 from the F.R.S.‐FNRS. We acknowledge the support by UVigo Marine Research Centre funded by the “Excellence in Research (INUGA)” Programme from the Regional Council of Culture, Education and Universities, with co‐funding from the European Union through the ERDF Operational Programme Galicia 2014‐2020.
Caballero A, Villanueva B, Druet T. On the estimation of inbreeding depression using different measures of inbreeding from molecular markers. Evol. Appl..2021;14:416–428. 10.1111/eva.13126
DATA AVAILABILITY STATEMENT
All software and scripts used in the simulations are available in GitHub: https://github.com/armando‐caballero/Caballero‐et‐al.‐Evol‐Appli‐2020.
REFERENCES
- Ackerman, M. S. , Johri, P. , Spitze, K. , Xu, S. , Doak, T. G. , Young, K. , & Lynch, M. (2017). Estimating seven coefficients of pairwise relatedness using population‐genomic data. Genetics, 206, 105–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alemu, S. W. , Kadri, N. K. , Harland, C. , Faux, P. , Charlier, C. , Caballero, A. , & Druet, T. (2020). An evaluation of inbreeding measures using a whole genome sequenced cattle pedigree. Heredity, submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allendorf, F. W. , Luikart, G. H. , & Aitken, S. N. (2013). Conservation and the genetics of populations. Chichester, UK: John Wiley and Sons. [Google Scholar]
- Bérénos, C. , Ellis, P. A. , Pilkington, J. G. , & Pemberton, J. M. (2016). Genomic analysis reveals depression due to both individual and maternal inbreeding in a free‐living mammal population. Molecular Ecology, 25, 3152–3168. 10.1111/mec.13681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjelland, D. W. , Weigel, K. A. , Vukasinovic, N. , & Nkrumah, J. D. (2013). Evaluation of inbreeding depression in Holstein cattle using whole‐genome SNP markers and alternative measures of genomic inbreeding. Journal of Dairy Science, 96, 4697–4706. 10.3168/jds.2012-6435 [DOI] [PubMed] [Google Scholar]
- Caballero, A. (2020). Quantitative genetics. Cambridge, UK: Cambridge University Press. [Google Scholar]
- Caballero, A. , Bravo, I. , & Wang, J. (2017). Inbreeding load and purging: Implications for the short‐term survival and the conservation management of small populations. Heredity, 118, 177–185. 10.1038/hdy.2016.80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero, A. , & Keightley, P. D. (1994). A pleiotropic nonadditive model of variation in quantitative traits. Genetics, 38, 883–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero, A. , Tenesa, A. , & Keightley, P. D. (2015). The nature of genetic variation for complex traits revealed by GWAS and regional heritability mapping analyses. Genetics, 201, 1601–1613. 10.1534/genetics.115.177220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceballos, F. C. , Joshi, P. K. , Clark, D. W. , Ramsay, M. , & Wilson, J. F. (2018). Runs of homozygosity: Windows into population history and trait architecture. Nature Reviews Genetics, 19, 220–234. 10.1038/nrg.2017.109 [DOI] [PubMed] [Google Scholar]
- Charlesworth, B. (2015). Causes of natural variation in fitness: evidence from studies of Drosophila populations. Proceedings of the National Academy of Sciences U.S.A., 112, 1662–1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, D. , & Willis, J. H. (2009). The genetics of inbreeding depression. Nature Reviews Genetics, 10, 783–796. 10.1038/nrg2664 [DOI] [PubMed] [Google Scholar]
- Curik, I. , Ferenčaković, M. , & Sölkner, J. (2014). Inbreeding and runs of homozygosity: A possible solution to an old problem. Livestock Science, 166, 26–34. 10.1016/j.livsci.2014.05.034 [DOI] [Google Scholar]
- Druet, T. , & Gautier, M. (2017). A model‐based approach to characterize individual inbreeding at both global and local genomic scales. Molecular Ecology, 26, 5820–5841. 10.1111/mec.14324 [DOI] [PubMed] [Google Scholar]
- Ferenčaković, M. , Hamzić, E. , Gredler, B. , Solberg, T. R. , Klemetsdal, G. , Curik, I. , & Sölkner, J. (2013). Estimates of autozygosity derived from runs of homozygosity: Empirical evidence from selected cattle populations. Journal of Animal Breeding and Genetics, 130, 286–293. 10.1111/jbg.12012 [DOI] [PubMed] [Google Scholar]
- Ferenčaković, M. , Sölkner, J. , Kapš, M. , & Curik, I. (2017). Genome‐wide mapping and estimation of inbreeding depression of semen quality traits in a cattle population. Journal of Dairy Science, 100, 4721–4730. 10.3168/jds.2016-12164 [DOI] [PubMed] [Google Scholar]
- Frankham, R. , Ballou, J. D. , & Briscoe, D. A. (2010). Introduction to conservation genetics. Cambridge, UK: Cambridge University Press. [Google Scholar]
- García‐Dorado, A. (2012). Understanding and predicting the fitness decline of shrunk populations: Inbreeding, purging, mutation, and standard selection. Genetics, 190, 1461–1476. 10.1534/genetics.111.135541 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudet, J. , Kay, T. , & Weir, B. S. (2018). How to estimate kinship. Molecular Ecology, 27, 4121–4135. 10.1111/mec.14833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grueber, C. E. , Waters, J. M. , & Jamieson, I. G. (2011). The imprecision of heterozygosity‐fitness correlations hinders the detection of inbreeding and inbreeding depression in a threatened species. Molecular Ecology, 20, 67–79. 10.1111/j.1365-294X.2010.04930.x [DOI] [PubMed] [Google Scholar]
- Hedrick, P. W. (2012). What is the evidence for heterozygote advantage selection? Trends in Ecology and Evolution, 27, 698–704. 10.1016/j.tree.2012.08.012 [DOI] [PubMed] [Google Scholar]
- Howrigan, D. P. , Simonson, M. A. , & Keller, M. C. (2011). Detecting autozygosity through runs of homozygosity: A comparison of three autozygosity detection algorithms. BMC Genomics, 12, 460 10.1186/1471-2164-12-460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huisman, J. , Kruuk, L. E. , Ellis, P. A. , Clutton‐Brock, T. , & Pemberton, J. M. (2016). Inbreeding depression across the lifespan in a wild mammal population. Proceedings of the National Academy of Sciences U.S.A., 113, 3585–3590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kardos, M. , Luikart, G. , & Allendorf, F. W. (2015). Measuring individual inbreeding in the age of genomics: Marker‐based measures are better than pedigrees. Heredity, 115, 63–72. 10.1038/hdy.2015.17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kardos, M. , Nietlisbach, P. , & Hedrick, P. W. (2018). How should we compare different genomic estimates of the strength of inbreeding depression? Proceedings of the National Academy of Sciences U.S.A., 115, E2492–E2493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kardos, M. , Taylor, H. R. , Ellegren, H. , Luikart, G. , & Allendorf, F. W. (2016). Genomics advances the study of inbreeding depression in the wild. Evolutionary Applications, 9(10), 1205–1218. 10.1111/eva.12414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller, M. C. , Visscher, P. M. , & Goddard, M. E. (2011). Quantification of inbreeding due to distant ancestors and its detection using dense single nucleotide polymorphism data. Genetics, 189, 237–249. 10.1534/genetics.111.130922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M. , & Crow, J. F. (1963). The measurement of effective population number. Evolution, 17, 279–288. 10.1111/j.1558-5646.1963.tb03281.x [DOI] [Google Scholar]
- Leroy, G. (2014). Inbreeding depression in livestock species: Review and meta‐analysis. Animal Genetics, 45, 618–628. 10.1111/age.12178 [DOI] [PubMed] [Google Scholar]
- Li, C. C. , & Horvitz, D. G. (1953). Some methods of estimating the inbreeding coefficient. American Journal of Human Genetics, 5, 107–117. [PMC free article] [PubMed] [Google Scholar]
- López‐Cortegano, E. , Vilas, A. , Caballero, A. , & García‐Dorado, A. (2016). Estimation of genetic purging under competitive conditions. Evolution, 70, 1856–1870. 10.1111/evo.12983 [DOI] [PubMed] [Google Scholar]
- Lynch, M. , & Walsh, B. (1998). Genetics and analysis of quantitative traits. Sunderland, MA: Sinauer. [Google Scholar]
- Malécot, G. (1948). Les mathématiques de l’hérédité. Paris, France: Masson et Cie. [Google Scholar]
- McQuillan, R. , Leutenegger, A.‐L. , Abdel‐Rahman, R. , Franklin, C. S. , Pericic, M. , Barac‐Lauc, L. , … Wilson, J. F. (2008). Runs of homozygosity in European populations. American Journal of Human Genetics, 83, 359–372. 10.1016/j.ajhg.2008.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messer, P. (2013). SLiM: Simulating evolution with selection and linkage. Genetics, 194, 1037–1039. 10.1534/genetics.113.152181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milligan, B. G. (2003). Maximum‐likelihood estimation of relatedness. Genetics, 163, 1153–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morton, N. E. , Crow, J. F. , & Muller, H. (1956). An estimate of the mutational damage in man from data on consanguineous marriages. Proceedings of the National Academy of Sciences U.S.A., 42, 855–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nietlisbach, P. , Muff, S. , Reid, J. M. , Whitlock, M. C. , & Keller, L. F. (2019). Nonequivalent lethal equivalents: Models and inbreeding metrics for unbiased estimation of inbreeding load. Evolutionary Applications, 12(2), 266–279. 10.1111/eva.12713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Grady, J. J. , Brook, B. W. , Reed, D. H. , Ballou, J. D. , Tonkyn, D. W. , & Frankham, R. (2006). Realistic levels of inbreeding depression strongly affect extinction risk in wild populations. Biological Conservation, 133, 42–51. 10.1016/j.biocon.2006.05.016 [DOI] [Google Scholar]
- Pryce, J. E. , Haile‐Mariam, M. , Goddard, M. E. , & Hayes, B. J. (2014). Identification of genomic regions associated with inbreeding depression in Holstein and Jersey dairy cattle. Genetics Selection Evolution, 46, 71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell, S. , Neale, B. , Todd‐Brown, K. , Thomas, L. , Ferreira, M. A. R. , Bender, D. , … Sham, P. C. (2007). PLINK: A tool set for whole‐genome association and population‐based linkage analyses. American Journal of Human Genetics, 81, 559–575. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritland, K. (1996). Estimators for pairwise relatedness and individual inbreeding coefficients. Genetical Research Cambridge, 67, 175–185. 10.1017/S0016672300033620 [DOI] [Google Scholar]
- Robertson, A. (1965). The interpretation of genotypic ratios in domestic animal populations. Animal Science, 7(3), 319–324. 10.1017/S0003356100025770. [DOI] [Google Scholar]
- Santure, A. W. , Stapley, J. , Ball, A. D. , Birkhead, T. R. , Burke, T. , & Slate, J. O. N. (2010). On the use of large marker panels to estimate inbreeding and relatedness: Empirical and simulation studies of a pedigreed zebra finch population typed at SNPs. Molecular Ecology, 19, 1439–1451. [DOI] [PubMed] [Google Scholar]
- Saura, M. , Fernández, A. , Varona, L. , Fernández, A. I. , de Cara, M. Á. , Barragán, C. , & Villanueva, B. (2015). Detecting inbreeding depression for reproductive traits in Iberian pigs using genome‐wide data. Genetics Selection Evolution, 47, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slate, J. , & Pemberton, J. M. (2002). Comparing molecular measures for detecting inbreeding depression. Journal of Evolutionary Biology, 15, 20–31. 10.1046/j.1420-9101.2002.00373.x [DOI] [Google Scholar]
- Szpiech, Z. A. , Xu, J. S. , Pemberton, T. J. , Peng, W. P. , Zollner, S. , Rosenberg, N. A. , & Li, J. Z. (2013). Long runs of homozygosity are enriched for deleterious variation. American Journal of Human Genetics, 93, 90–102. 10.1016/j.ajhg.2013.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szulkin, M. , Bierne, N. , & David, P. (2010). Heterozygosity‐fitness correlations: A time for reappraisal. Evolution, 64, 1202–1217. 10.1111/j.1558-5646.2010.00966.x [DOI] [PubMed] [Google Scholar]
- Toro, M. , Barragán, C. , Óvilo, C. , Rodrigañez, J. , Rodriguez, C. , & Silió, L. (2002). Estimation of coancestry in Iberian pigs using molecular markers. Conservation Genetics, 3, 309–320. [Google Scholar]
- VanRaden, P. M. (2008). Efficient methods to compute genomic predictions. Journal of Dairy Science, 91, 4414–4423. 10.3168/jds.2007-0980 [DOI] [PubMed] [Google Scholar]
- Wang, J. (2007). Triadic IBD coefficients and applications to estimating pairwise relatedness. Genetical Research Cambridge, 89, 135–153. 10.1017/S0016672307008798 [DOI] [PubMed] [Google Scholar]
- Wang, J. (2016). Pedigrees or markers: Which are better in estimating relatedness and inbreeding coefficient? Theoretical Population Biology, 107, 4–13. 10.1016/j.tpb.2015.08.006 [DOI] [PubMed] [Google Scholar]
- Wang, J. , Hill, W. G. , Charlesworth, D. , & Charlesworth, B. (1999). Dynamics of inbreeding depression due to deleterious mutations in small populations: Mutation parameters and inbreeding rate. Genetical Research Cambridge, 74, 165–178. [DOI] [PubMed] [Google Scholar]
- Wright, S. (1969). Evolution and the genetics of populations, Vol. 2 The theory of gene frequencies. Chicago, IL: University of Chicago Press. [Google Scholar]
- Yang, J. , Lee, S. H. , Goddard, M. E. , & Visscher, P. M. (2011). GCTA: A tool for genome‐wide complex trait analysis. American Journal of Human Genetics, 88, 76–82. 10.1016/j.ajhg.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yengo, L. , Zhu, Z. , Wray, N. R. , Weir, B. S. , Yang, J. , Robinson, M. R. , & Visscher, P. M. (2017). Detection and quantification of inbreeding depression for complex traits from SNP data. Proceedings of the National Academy of Sciences U.S.A., 114, 8602–8607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yengo, L. , Zhu, Z. , Wray, N. R. , Weir, B. S. , Yang, J. , Robinson, M. R. , & Visscher, P. M. (2018). Estimation of inbreeding depression from SNP data. Proceedings of the National Academy of Sciences U.S.A., 115, E2494–E2495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Q. , Calus, M. P. , Guldbrandtsen, B. , Lund, M. S. , & Sahana, G. (2015). Estimation of inbreeding using pedigree, 50k SNP chip genotypes and full sequence data in three cattle breeds. BMC Genetics, 16, 88 10.1186/s12863-015-0227-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Data Availability Statement
All software and scripts used in the simulations are available in GitHub: https://github.com/armando‐caballero/Caballero‐et‐al.‐Evol‐Appli‐2020.


