Development of a Cadence-Based Metabolic Equation for Walking

Abstract

PURPOSE:

To develop cadence-based metabolic equations (CMEs) for predicting intensity of level walking and evaluate these CMEs against the widely adopted ACSM Metabolic Equation, which predicts walking intensity from speed and grade.

METHODS:

235 adults (21–84 years of age) completed 5-min level treadmill walking bouts between 0.22–2.24 m/s, increasing by 0.22 m/s for each bout. Cadence (steps/min) was derived by dividing directly-observed steps by bout duration. Intensity (oxygen uptake; mL/kg/min) was measured using indirect calorimetry. A simple CME was developed by fitting a least-squares regression to the cadence-intensity relationship and a full CME was developed through best subsets regression with candidate predictors of age, sex, height, leg length, body mass, BMI, and percent body fat. Predictive accuracy of each CME and the ACSM Metabolic Equation was evaluated at normal (0.89–1.56 m/s) and all (0.22–2.24 m/s) walking speeds through k-fold cross-validation and converted to metabolic equivalents (METs; 1 MET=3.5 mL/kg/min).

RESULTS:

On average, the simple CME predicted intensity within ~1.8 mL/kg/min (~0.5 METs) at normal walking speeds and with negligible (<0.01 METs) bias. Including age, leg length, and BMI in the full CME marginally improved predictive accuracy (≤0.36 mL/kg/min [≤0.1 METs]), but may account for larger (up to 2.5 mL/kg/min [0.72 MET]) deviations in the cadence-intensity relationships of outliers in age, stature, and/or BMI. Both CMEs demonstrated 23–35% greater accuracy and 2.2–2.8 mL/kg/min [0.6–0.8 METs] lower bias than the ACSM Metabolic Equation’s speed-based predictions.

CONCLUSION:

While the ACSM Metabolic Equation incorporates a grade component and is convenient for treadmill-based applications, the CMEs developed herein enable accurate quantification of walking intensity using a metric that is accessible during overground walking, as is common in free-living contexts.

INTRODUCTION

Physical activity (PA) intensity is a central component of public health PA guidelines (1, 2), as higher intensity levels (e.g., minimally moderate to vigorous) are generally associated with greater improvements in health (2, 3). Additionally, performing activities at a higher intensity is a more time efficient approach to reach recommended volumes of PA. Conversely, inappropriately high PA intensities increase risk for injury and adverse events (2, 4). Prescribing PA intensities that are too high can also decrease affect response (i.e., enjoyment) (5) and reduce adherence to exercise programs (6). Considering that walking is the most commonly reported leisure-time PA in adults (7), developing simple and more practical methods of measuring and prescribing walking intensity has substantial value for public health.

Since 1980, the American College of Sports Medicine (ACSM) has published a metabolic equation for predicting walking intensity in terms of oxygen uptake (VO₂; mL/kg/min) from speed (Speed; m/min) and incline (Grade; decimal form) as follows: (8, 9)

$$V{O}_2=\left[0.1•\mathit{\text{Speed}}\right]+\left[1.8•\mathit{\text{Speed}}•\mathit{\text{Grade}}\right]+3.5$$ [1]

While the ACSM Metabolic Equation provides a simple method for estimating walking intensity during treadmill walking, its utility in the free-living setting is inherently limited by the difficulty of measuring and prescribing speed during overground walking.

Conversely, walking cadence (steps/min) can easily be assessed with accelerometry or through direct observation (by dividing observed step counts by elapsed time), and readily prescribed by synchronizing foot-strikes to music and metronome tempos (10). Moreover, cadence combines with step length to determine walking speed and displays a strong correlation (r = 0.93) with absolutely-defined walking intensity (METs) (11). Therefore, developing a metabolic equation based on cadence could provide a simple and accessible tool for monitoring and prescribing walking intensities.

Studies examining the cadence-intensity relationship have consistency supported ≈100 steps/min as a heuristic threshold associated with absolutely-defined moderate intensity (3 METs) in ostensibly healthy adults (12). While this evidence-based, broadly representative heuristic is useful for public health messaging, differences in demographic and anthropometric factors may contribute to inter-individual variability in the cadence-intensity relationship. For example, prior studies have reported higher walking intensities at a given cadence in 75- versus 65-year-old adults (13), men versus women (14), taller versus shorter adults (15), and those with lower versus higher body mass indices (BMIs) (16). Data from the CADENCE-Adults Study’s (17) large sample of men and women across the adult lifespan provide an unique opportunity to examine the practical relevance of individual characteristics such as these in the cadence-intensity relationship. Furthermore, accounting for any such effects in a cadence-based metabolic equation may enable the individualization of walking intensity estimations and prescriptions.

The primary aims of this study were to use treadmill walking data collected from a large, heterogeneous sample of adults to: 1) develop cadence-based metabolic equations (CMEs) that predict walking intensity (VO₂; mL/kg/min) from cadence alone (a simple CME) and with additional individual characteristics (a full CME), potentially including any of: age, sex, height, leg length, body mass, BMI, and/or percent body fat; and 2) compare the predictive accuracies of these CMEs to that of the ACSM Metabolic Equation. A secondary aim of this study was to examine the effects of these individual characteristics on the cadence-speed relationship in order to explore a potential mechanism underlying their associations with walking intensity.

METHODS

This study was a secondary analysis of the NIH/NIA funded R01 CADENCE-Adults study (NCT02650258). More details regarding specific methods and data collection procedures are published elsewhere (17).

Participants

The original sample included 260 ostensibly healthy and ambulatory adults, comprised of 10 men and 10 women from each 5-year age group between 21–84 years of age (e.g., 21–25 years, 26–30 years, etc.). The study protocol was approved by the University of Massachusetts Amherst Institutional Review Board. All participants provided written informed consent.

Metabolic Testing Procedure

Participants arrived after having fasted for at least 4 hours. The metabolic testing protocol consisted of up to ten 5-min treadmill walking bouts at 0% grade separated by 2-min standing rests. Treadmill speed was set at 0.22 m/s (0.5 mph) for the first bout and increased by 0.22 m/s for each bout thereafter. The protocol was terminated following the completion of a bout where participants: 1) naturally selected to run; 2) exceeded 75% of their age-predicted maximum heart rate (i.e., 220-age); or 3) reported a Borg rating of perceived exertion (RPE) (18) > 13.

Measures

Sex and age were self-reported. Standing and seated height were measured with a stadiometer and sub-ischial leg length was calculated by subtracting seated height from standing height. A Tanita scale (DC-430U; Tanita Corporation, Tokyo, Japan) was used to measure body mass and body fat percentage through bioelectrical impedance (19). Cadence (steps/min) was derived by dividing directly-observed (i.e., hand counted [or tallied]) step counts by bout duration (total steps / 5 min). Oxygen uptake (VO₂; mL/kg/min), the criterion measure of PA intensity, was measured using a validated (20) portable indirect calorimeter (Oxycon Mobile, Vyaire Medical Inc, Höchberg, Germany) and averaged across time-stamped data collected between 2:45–4:45 of each 5-min bout, to coincide with steady-state oxygen uptake (21).

Analytic Sample

The ACSM Metabolic Equation for Walking is stated to be most accurate at ambulatory speeds of 0.83–1.67 m/s (1.9–3.7 mph) (9). This range of speeds encompasses normal walking speeds of ostensibly healthy men and women across the adult lifespan (22). Therefore, an analytic sample comprised of bouts completed at 0.89, 1.12, 1.34, and 1.56 m/s (2.0, 2.5, 3.0, and 3.5 mph; hereafter referred to as the normal speeds dataset) was used for calibrating the simple and full CMEs and for their initial cross-validation, as described below. Data were excluded for participants whose tests were terminated prior to reaching the slowest speed (0.89 m/s; n = 24). An analytic sample comprised of all walking bouts performed by the same participants regardless of speed (hereafter referred to as the all speeds dataset) was also used to evaluate the generalizability of these equations to a wider range of walking speeds.

Statistical Analysis

All statistical analyses were performed using R-Studio (version 3.5.1, R Foundation for Statistical Computing, Vienna, Austria). Statistical significance was set at α < 0.05.

The simple CME, which predicts VO₂ from cadence alone, was developed by fitting a least-squares regression model to the normal speeds dataset. This equation included a quadratic cadence term (cadence²) if doing so significantly improved model fit, as determined using a likelihood-ratio test with mixed modeling to account for the random effect of participant (23).

The full CME, which includes individual characteristics as additional predictors of VO₂, was developed using best subsets regression analysis (24) in the normal speeds dataset. This analysis considers every model possible with the specified predictor terms and selects the model with the best performance according to a pre-specified selection criteria, and has shown to out-perform stepwise regression procedures (25). Predicted residual sum of squares (PRESS; a cross-validated measure of sum of squares) was used as the model selection criterion. Candidate predictor terms included cadence, cadence², age, sex, height, leg length, body mass, BMI, and percent body fat (main effects and all two-way interactions). Age was also included as a binary variable (age ≥ 65 or < 65 years) because prior studies have reported age-related differences in walking intensity between young/middle-aged and older adults but not between young and middle-aged adults (26, 27). Variance inflation factors (VIFs) were calculated for each predictor and verified to be < 5 to confirm that multicollinearities did not exist. The predictive accuracies of the simple and full CMEs were evaluated using repeated k-fold cross-validation (k = 5, 10 repetitions) to calculate root mean square error (RMSE), mean absolute error (MAE), and mean bias (28). These measures of predictive error are presented in units of VO₂ (mL/kg/min) and METs (1 MET = 3.5 mL/kg/min).

Our intent to develop metabolic equations for public health applications places a high value on producing a parsimonious full CME while maintaining its predictive accuracy. We therefore attempted to refine the full CME (i.e., remove inconsequential variables) by removing single predictor terms and repeating the k-fold cross validation analysis in the normal speeds dataset. If removing a predictor term resulted in no change in RMSE and MAE (rounded to 0.01 mL/kg/min), then that term was excluded from the final full CME. Additionally, if the full CME included leg length and/or percent body fat, we tested another full CME that instead included a more easily attained indicator of stature and/or obesity (i.e., height and/or BMI, respectively).

We also evaluated the generalizability of the simple and full CME to a wider range of walking speeds through a similar k-fold cross-validation in the all speeds dataset. However, to reflect the performance of the CME’s reported herein, only bouts with speeds within the range of the normal speeds dataset were included when fitting equations in training fold participants. Trained equations were then cross-validated in all bouts performed by testing fold participants.

The method of cross-validation used to assess predictive error influences the error values that are observed (29). Therefore, to maintain methodological consistency, a similar repeated k-fold cross-validation procedure was used to evaluate the predictive capacity of the ACSM Metabolic Equation. Specifically, participants were divided into training and testing folds in the same manner. Then, instead of fitting an equation with the training fold data and applying that equation to the testing fold, the ACSM Metabolic Equation (Eq. 1) was applied to each testing fold. This analytical procedure enabled direct comparisons of the resulting RMSE, MAE, and mean bias values to those obtained with the simple and full CMEs.

To examine the effect of each individual characteristic included in the full CME on walking speed at a given cadence, linear mixed modeling was used to describe treadmill walking speed (outcome) while controlling for cadence (fixed effect) and participant (random effect) in the normal speeds dataset. F-tests with Satterthwaite approximations for denominator degrees of freedom (30) were then performed when an individual characteristic was added to this model. A similar analysis was also performed while including all additional predictor terms of the full CME as fixed effects in order to examine their effects in combination (i.e., while controlling for each other). The slope of each significant term was examined to determine direction of effect.

RESULTS

Of the 260 participants who completed the treadmill walking protocol, data were excluded for 4 who experienced metabolic testing equipment failure (17) and 21 whose tests were terminated prior to reaching the slowest speed of the normal speeds dataset (0.89 m/s). The normal speeds dataset was therefore comprised of 235 participants who completed 872 treadmill walking bouts at 0.89 m/s up to a maximum of 1.56 m/s (2.0–3.5 mph). The all speeds dataset included 1,747 walking bouts performed by the same 235 participants at 0.22 m/s up to a maximum of 2.24 m/s (0.5–5.0 mph). Participant descriptive characteristics are summarized in Table 1 and Supplement File 1 provides a summary of the cadences, step lengths, and walking intensities observed at each treadmill walking speed.

Table 1:

Participant Characteristics.

Variable	All (N = 235)	Young Adults (n = 76)	Middle-Aged Adults (n = 78)	Older Adults (n = 81)
Female (%)	47.2	50.0	48.7	43.2
Age (years)	51.1 [17.8] 21–84	30.4 [5.8] 21–40	50.1 [5.9] 41–60	71.4 [6.4] 61–84
Height (cm)	169.9 [9.0] 149.1–194.1	170.7 [9.3] 149.1–194.1	171.2 [9.1] 150.1–190.1	167.8 [8.4] 151.0–188.3
Body Mass (kg)	74.1 [13.6] 46.3–128.8	72.8 [14.1] 51.6–119.0	76.1 [13.9] 47.8–128.8	73.5 [12.7] 46.3–103.3
BMI (kg/m2)	25.6 [3.6] 18.6–37.6	24.8 [3.4] 19.4–36.9	25.9 [3.8] 19.0–37.6	26.0 [3.5] 18.6–36.0
Leg Length (cm)	80.2 [5.4] 65.7–94.8	79.7 [5.8] 65.7–94.5	80.8 [5.3] 66.6–92.0	80.1 [5.1] 70.3–94.8

Values are presented as mean [SD] min-max

Cadence Metabolic Equation Development

Including a quadratic term significantly improved the fit of a linear mixed regression model to the cadence-intensity relationship (p < 0.001). The simple CME was therefore developed by fitting a quadratic least-squared regression model to the relationship between cadence and VO₂ in the normal speeds dataset (Table 2). The fits of this equation to the treadmill walking data in the normal and all speeds datasets are shown in Figures 1A and 1B, respectively. For comparison, the fits of the ACSM Metabolic Equation to the normal and all speeds datasets are displayed in Figures 1C and 1D, respectively.

Table 2.

Simple and Full CME Predictor Terms and Coefficients

CME	Intercept	Cadence	Cadence2	Age × Cadence	BMI × Cadence2	Leg Length × Age	Age × Height
Simple	1.811	0.02014	7.427 E-4	--	--	--	--
Full	−0.1172	--	1.400 E-3	−1.362 E-3	−8.288 E-6	1.541 E-03	--
Fullht	−0.4367	--	1.430 E-3	−1.455 E-3	−9.012 E-6	--	8.086 E-4

Example: Simple CME Predicted VO₂ (mL/kg/min) = 1.811 + [0.02014*Cadence] + [7.427 E-4*Cadence²]

Predictor (units); Cadence (steps/min); Leg Length (cm); Age (years); BMI (kg/m²)

× indicates interaction

CME, cadence-based metabolic equation; BMI, body mass index; Full_ht, Full CME including height instead of leg length

Figure 1:

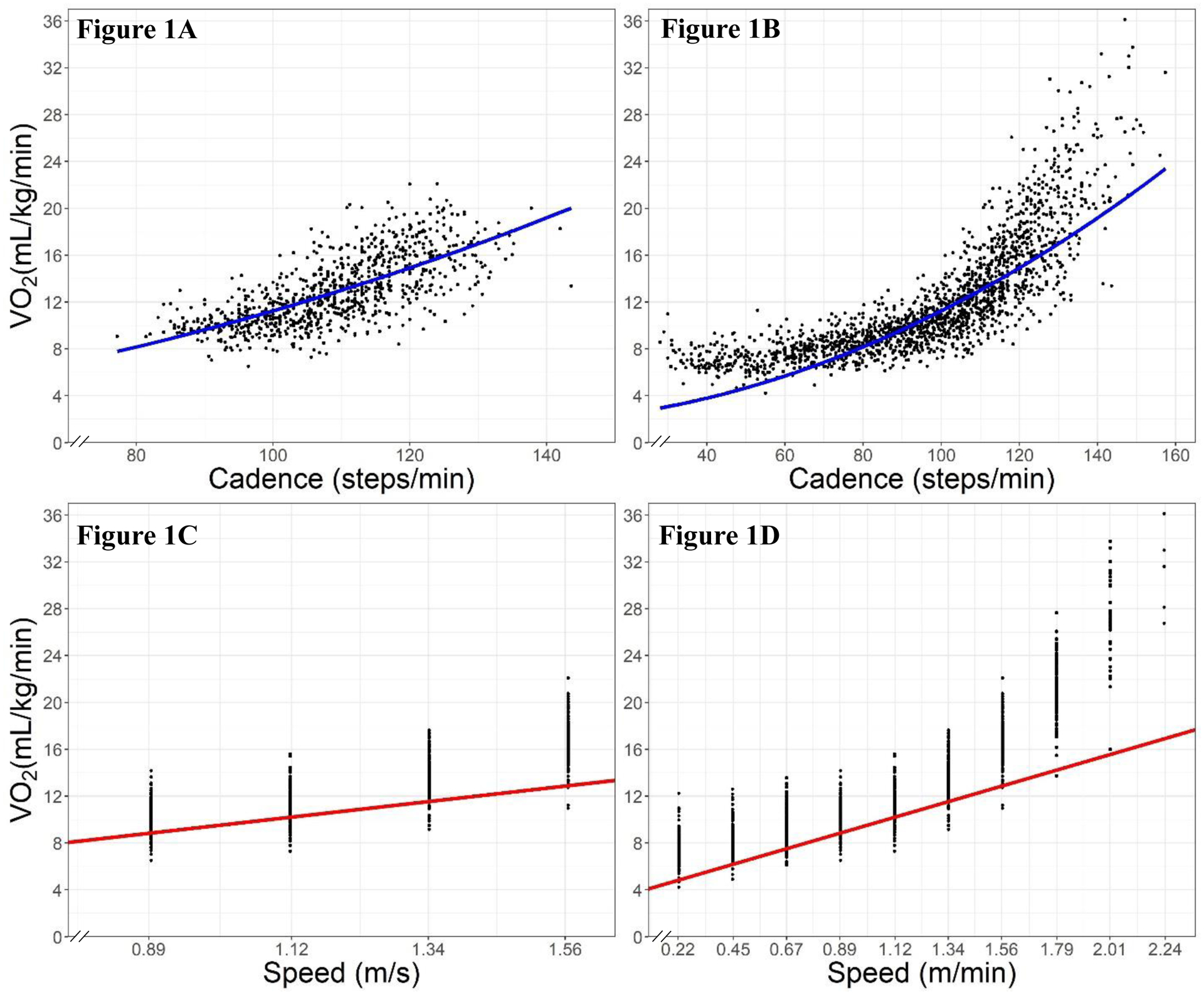
Fits of the simple CME (Figures 1A and 1B) and the ACSM Metabolic Equation (Figures 1C and 1D) to the normal speeds dataset (Figures 1A and 1C) and data from all treadmill walking bouts (Figures 1B and 1D)

CME = cadence-based metabolic equation

The best subsets regression analysis for developing the full CME selected a model with the following predictor terms: cadence², age*cadence, sex*cadence², BMI*cadence², and leg length*age (with age only being included as a continuous variable). However, removing the interaction between sex and cadence² did not change the full CME’s predictive error so this predictor term was not ultimately included. An equation including height instead of leg length (hereafter referred to as the full_ht CME) was also developed (Table 2). All VIF values were < 5.

To demonstrate the effect of each individual characteristic on predicted walking intensities, Table 3 provides predicted VO₂ values at 80, 100, and 120 steps/min when one characteristic (either age, BMI, leg length, or height) was set to the sample minimum or maximum, while all others were set to the corresponding sample means (reported in Table 1). For example, the effect of age was examined by using the full CME to predict walking intensity for two individuals: one with the youngest and the other with the oldest age of participants in the study sample, while both had BMIs and leg lengths equal to the sample means. This same analysis was used to derive the cadence thresholds associated with 3, 4, and 5 METs. Predictions at cadence > 120 steps/min and > 6 METs were not calculated to avoid extrapolation.

Table 3:

Walking intensities at a given cadence (top rows) and cadence thresholds associated with walking intensities (bottom rows) predicted by the simple and full CMEs

	Simple CME	Full CME						Fullht CME
		Min Age	Max Age	Min BMI	Max BMI	Min LL	Max LL	Min Ht	Max Ht
Cadence*
80 steps/min	8.18	7.79	8.71	8.60	7.59	7.09	9.38	7.46	9.32
100 steps/min	11.25	11.49	10.69	11.69	10.12	9.97	12.26	10.29	12.15
120 steps/min	14.92	16.15	13.63	15.78	13.52	13.8	16.09	14.08	15.94
Intensity†
3 METs	95	95	98	93	103	89	103	101	89
4 METs	115	111	122	112	122	110	121	120	110
5 METs	132	125	140	127	139	126	136	135	127
6 METs	143	137	143	140	143	140	143	143	141

Full CME predictions calculated with one characteristic input as indicated (min or max) and all others set to study sample means

^*Units of values are mL/kg/min

^†Units of values are steps/min

CME, cadence-based metabolic equation; LL, leg length; Min, characteristic set to study sample minimum; Max, characteristic set to study sample maximum; Full_ht, Full CME including height instead of leg length

Metabolic Equation Cross-Validation

The measures of predictive error resulting from k-fold cross-validation of the simple and full CMEs and ACSM Metabolic Equation are reported in Table 4. The simple CME had RMSE and MAE values of 2.09 and 1.63 mL/kg/min (0.60 and 0.46 METs), respectively, in the normal speeds dataset and 2.85 and 2.06 mL/kg/min (0.81 and 0.59 METs), respectively, in the all speeds dataset. The full CME demonstrated marginally better predictive accuracy (0.13–0.36 mL/kg/min [0.04–0.10 METs] lower RMSE and MAE) than the simple CME in both datasets (Table 4). Both CMEs demonstrated approximately no bias (mean biases = 0.01 mL/kg/min) in the normal speeds dataset. Additionally, the inclusion of height instead of leg length in the full_ht CME resulted in the same predictive error values as the original full CME (Table 4).

Table 4:

Predictive Error of the Simple and Full CME and ACSM Metabolic Equations from Repeated K-Fold Cross-Validation in the Normal and All Speeds Datasets.

Equation	Normal	All	0.89 m/s	1.12 m/s	1.34 m/s	1.56 m/s
	(N = 872)	(N = 1747)	(n = 235)	(n = 228)	(n = 219)	(n = 190)
RMSE
Simple	2.09 [0.18]	2.85 [0.23]	1.72 [0.17]	1.86 [0.20]	1.88 [0.22]	2.84 [0.34]
Full	1.96 [0.17]	2.49 [0.16]	1.57 [0.15]	1.74 [0.15]	1.81 [0.19]	2.66 [0.35]
Fullht	1.97 [0.17]	2.49 [0.16]	1.58 [0.16]	1.74 [0.15]	1.81 [0.19]	2.67 [0.35]
ACSM	2.79 [0.18]	3.70 [0.24]	1.70 [0.17]	1.86 [0.17]	2.69 [0.21]	4.44 [0.26]
MAE
Simple	1.63 [0.14]	2.06 [0.2]	1.35 [0.15]	1.46 [0.17]	1.47 [0.18]	2.35 [0.31]
Full	1.50 [0.13]	1.80 [0.11]	1.20 [0.12]	1.34 [0.14]	1.41 [0.16]	2.16 [0.29]
Fullht	1.51 [0.12]	1.79 [0.11]	1.22 [0.12]	1.34 [0.14]	1.41 [0.16]	2.17 [0.29]
ACSM	2.25 [0.17]	2.75 [0.19]	1.38 [0.13]	1.54 [0.15]	2.34 [0.20`]	4.11 [0.24]
Bias*
Simple	−0.01 [0.30]	−0.91 [0.40]	0.72 [0.27]	0.77 [0.28]	−0.02 [0.34]	−1.86 [0.38]
Full	−0.01 [0.29]	−0.69 [0.28]	0.58 [0.26]	0.66 [0.27]	−0.02 [0.32]	−1.56 [0.38]
Fullht	−0.01 [0.29]	−0.66 [0.28]	0.60 [0.25]	0.67 [0.27]	−0.03 [0.32]	−1.58 [0.38]
ACSM	−2.11 [0.18]	−2.66 [0.20]	−1.21 [0.15]	−1.33 [0.17]	−2.22 [0.22]	−4.07 [0.24]

Values are presented as mean [SD]

^*Bias calculated as (Measured VO2 - Predicted VO2)

All units are mL/kg/min

CME, cadence-based metabolic equation

The ACSM Metabolic Equation demonstrated lower predictive accuracy than the simple and full CMEs in the normal speeds dataset, with 0.62–0.83 mL/kg/min (0.18–0.24 MET) greater RMSE and MAE values (Table 4). Differences in metabolic equation accuracy were larger in the all speeds dataset, where the ACSM Metabolic Equation had an RMSE of 3.70 mL/kg/min (1.05 METs) and MAE of 2.75 mL/kg/min (0.79 METs). These values were 0.69–1.21 mL/kg/min (0.20–0.34 METs) greater than the RMSE and MAE of the simple and full CMEs (Table 4). The mean bias values of the ACSM Metabolic Equation in the normal and all speeds datasets (2.11 and 2.66 mL/kg/min, respectively) were also greater in magnitude than those of the simple and full CMEs.

Effects of Individual Characteristics on Cadence-Speed Relationship

F-tests in mixed models that described walking speed while controlling for cadence demonstrated there was a significant main effect of age (p = 0.046) on walking speed and significant interactions between cadence and leg length/height (p-values < 0.001). The corresponding regression coefficients indicated that walking speed at a given cadence was inversely related to age and directly related to leg length/height (Table 5). There were no significant effects of BMI on walking speed (p = 0.90 for main effect; p = 0.53 for BMI-cadence interaction). These results were consistent with those observed when modeling the effects of all full CME predictor terms on walking speed in a single mixed model (Table 5)

Table 5:

F-Tests and Mixed Regression Model Coefficients for Effects of Individual Characteristics on Walking Speed at a Given Cadence

Test/Model†	Variable/Predictor Term	p-value	Coefficient [95% CI]
Main Effect	Age	0.046*	−0.0788	[−0.156, −0.00175]
	BMI	0.90	--	--
	Leg Length	<0.001*	1.05	[0.830, 1.265]
	Height	<0.001*	0.633	[0.504, 0.762]
Interaction with Cadence†	Age	0.89	--	--
	BMI	0.53	--	--
	Leg Length	<0.001*	0.0136	[0.00844, 0.0187]
	Height	<0.001*	0.00783	[0.00476, 0.0109]
Full CME‡	Cadence*Age	<0.001*	−0.00279	[−0.00367, −0.000383]
	Cadence2*BMI	0.17	--	--
	Age*Leg Length	0.003*	0.00330	[0.0000411, 0.00466]

All tests/models also include main effect of cadence

^†Tests for interaction also include main effects

^‡Full CME tests simultaneously include all predictor terms in the model

^*p <0.05

CME = cadence-based metabolic equation; BMI = body mass index

DISCUSSION

Using an age- and sex-balanced sample of 235 adults ranging in age from 21–84 years, we have developed metabolic equations (Table 2) that demonstrate the capacity to predict walking intensity from cadence within ~1.8 mL/kg/min (~0.5 METs) on average at normal walking speeds (0.89–1.56 m/s). Evaluating these CMEs against the ACSM Metabolic Equation (Eq. 1) further demonstrated that they perform with 23–35% lower RMSE and MAE and ~2.2 mL/kg/min (~0.6 MET) lower bias than a current, widely recognized metabolic equation for walking. The sample used to develop these CMEs inherently suggests that they are generalizable to men and women across the adult lifespan. Furthermore, the use of cadence in these metabolic equations enables their application as simple and accessible tools for monitoring and prescribing walking intensity during overground walking, as is common in the free-living setting.

The Cadence Metabolic Equations

The simple CME predicted walking intensity with an RMSE and MAE of 2.09 and 1.63 mL/kg/min (0.60 and 0.46 METs), respectively, in the normal speeds dataset and approximately no bias. The full CME included age, leg length, and BMI as additional predictors and, as hypothesized, demonstrated better predictive accuracy than the simple CME (Table 5). However, the marginal reduction in error (≤ 0.36 mL/kg/min [≤ 0.10 MET] lower RMSE and MAE) that resulted from including these additional predictors, on average, is likely to have negligible practical significance. For example, according to their MAE values in the normal speeds dataset, we would expect most people to have a metabolic intensity of 3.54–4.46 METs when walking at the simple CME’s 4 MET cadence threshold, versus 3.57–4.43 METs when walking at that determined by the full CME. Furthermore, as illustrated by this example, both CMEs demonstrate the capacity to predict cadences associated with absolutely-defined moderate intensity walking (3.0–5.9 METs) because their predictive error values were < 1 MET. Therefore, the simple CME can predict the intensity of walking with reasonable accuracy and performs comparably to the full CME for the average individual, while limiting user burden and being more practical for public health applications.

The cadence corresponding to 3.0 METs in the simple CME was 95 steps/min, and that for the full CME when using the sample average age, height/leg length, and BMI was 96 steps/min. At 100 steps/min, both equations predict a walking intensity of 3.2 METs (using the same demographic/anthropometric values for the full CME). These values are consistent with 100 steps/min as a heuristic cadence threshold for absolutely-defined moderate intensity (12).

Effects of Individual Characteristics on Walking Intensity and Speed

Although accounting for age, leg length, and BMI in the full CME did not appreciably improve the average predictive accuracy, these characteristics appeared to result in more substantial differences in predictions of walking intensity between some individuals. Specifically, at a given cadence of 80, 100, and 120 steps/min and while controlling for the other variables, walking intensity predictions differed between the oldest and youngest individuals by up to 2.52 mL/kg/min (0.72 METs), the shortest and longest-legged individuals by up to 2.29 mL/kg/min (0.65 METs), the shortest and tallest individuals by up to 1.86 mL/kg/min (0.53 METs), and those with the lowest and highest BMI by up to 2.26 mL/kg/min (0.65 METs; Table 3). These findings indicate that large (but biologically plausible) differences in age, stature, and BMI can have meaningful influences on the individual cadence-intensity relationship. The full CME may therefore be advantageous for predicting walking intensity when an individual has more extreme demographic and/or anthropometric characteristics (e.g., with older adults and very tall and/or obese individuals).The choice of which CME to use will depend on these characteristics, in addition to the cadence/intensity being examined (due to the age- and BMI-cadence interactions), desired level of precision, and user resources and expertise.

The effect of age on walking intensity in the full CME was modified by both leg length (positive age-leg length interaction) and cadence (negative cadence-age interaction; Table 5). Therefore, increases in age were associated with higher walking intensities in individuals with long leg lengths and/or at slow cadences (e.g., ≥ 88 cm when walking at 100 steps/min) but lower intensities when walking with faster cadences and/or shorter leg lengths (e.g., ≥ 92 steps/min with the sample average leg length [80 cm]). Prior studies (26, 31) have reported that older adults have higher absolutely-defined walking intensities than younger adults walking at the same speed due to age-related declines in coordination and motor strategies for preserving balance and stability (e.g., increases in antagonist muscle contraction and step width). Similarly, Peacock et al. (13) examined the cadence-intensity relationship in 29 older adults (≥ 60 years) and reported that 75-year-olds required 10 steps/min lower cadences to attain the same MET levels as 65-year-olds. The positive effect of age on walking intensity at slow cadences and/or with longer leg lengths aligns with these prior reports while additionally suggesting that the effect of age on walking intensity increases with increasing stature. However, while the shorter step lengths of older adults reportedly contribute to their elevated walking intensities at a given speed (26, 31), these shorter step lengths would theoretically lead older adults to have slower walking speeds at a given cadence. Therefore, the negative effect of age on walking intensity at faster cadences and/or with shorter leg lengths may be due to older adults walking with shorter step lengths and reduced walking speeds and rates of external work (i.e., work for accelerating the body’s center of mass) at a given cadence. Our results provide direct support for this negative influence of age on walking speed (p = 0.046; Table 5). Peacock et al. (13) did not provide any information pertaining to participants’ step lengths or cadences at a given speed. However, because their sample was smaller and consisted exclusively of physically-active older adults, they may not have observed the same age-related differences in step length.

The positive effect of leg length/height included in the full and full_ht CME (Tables 2 and 3) is likely related to positive associations between leg length/height and step length (32), which lead taller individuals to walk faster and perform more external work at a given cadence. In the present study, participant leg length and height were directly related to walking speed at a given cadence (p-values < 0.001; Table 5). Furthermore, at each treadmill walking speed in the normal speeds dataset, correlations between step length (derived by [speed/cadence]) and leg length/height ranged from 0.43–0.64. The leg length-age interaction in the full CME resulted in a greater effect of leg length on predicted walking intensity in older individuals. This may indicate that increasing leg length attenuated the age-related decreases in step length and walking intensity discussed above. Rowe et al. (15) and Peacock et al. (13) similarly reported that 10 cm (4 in) increases in height were associated with 0.93 and 2.45 mL/kg/min (0.27 and 0.70 MET) greater intensities at a given cadence, respectively, which is greater than that observed herein when inputting the mean ages of their samples in the full CME (0.51 and 1.10 mL/kg/min with a mean sample ages of 33 and 71 years, respectively). Nonetheless, Peacock et al. observed a greater effect of height with an older sample than Rowe et al., which is consistent with the positive age-leg length interaction in the full CME.

BMI demonstrated a negative effect on the cadence-intensity relationship with a greater effect at higher cadences (Tables 2 and 3), which would result in obese individuals requiring a higher cadence to attain a given intensity. The non-significant effect of BMI on walking speed at a given cadence (p = 0.90; Table 5) indicates that this association was not the result of obesity-related differences in gait parameters. Beets et al. (16) similarly reported that individuals with a higher BMI required higher cadences than those with lower BMIs to reach the same intensity, at least within the range of intensities they observed (< 5 METs). Marshall et al. (33) also observed an effect of BMI on the cadence-intensity relationship. However, they reported that the cadence thresholds associated with 3 METs for normal weight, overweight, and obese individuals in their multiple regression analysis were 127, 94, and 103 steps/min, respectively, and 106, 103, and 110 steps/min, respectively, in their Receiver Operating Characteristic (ROC) curve analysis. These conflicting results may be related to Marshall et al. observing larger differences in mean cadences at a given speed between BMI categories (differences 6.0–6.8 steps/min at 0.89–1.56 m/s with overweight < normal weight < obese) compared to herein (differences 2.2–2.9 steps/min). Future studies are needed to further examine BMI’s effect on the cadence-intensity relationship and whether such potential effects are related to differences in gait parameters.

The ACSM Metabolic Equation

The earliest dissemination of the ACSM Metabolic Equation we could identify was in the second edition of the ACSM Guidelines for Exercise Testing and Prescription in 1980 (8). The speed component of this equation ([0.1•Speed] in Eq. 1) was developed using data collected from three trained men during level treadmill walking (34). Nonetheless, the conditions in which the ACSM Metabolic Equation is intended to be applied (i.e., treadmill walking at 0.89–1.56 m/s) (8, 9) are consistent with those used in the primary analyses herein.

In these data, the ACSM Metabolic Equation had an RMSE of 2.79 mL/kg/min (0.80 METs and MAE of 2.25 mL/kg/min (0.64 METs). Additionally, its bias (−2.11 mL/kg/min [−0.60 METs]) indicates that it tended to underpredict walking intensity, which is visually apparent in Figures 1C and 1D and has been reported in prior studies (35, 36). These underpredictions may be related to the small sample used to develop the ACSM Metabolic Equation’s speed component (34), its use of the standardized resting metabolic rate (3.5 mL/kg/min) as an intercept (which does not account for the additional metabolic costs for balance and posture (35, 37), or its use of a linear form when the speed-intensity relationship of walking has shown to be curvilinear (35, 37, 38).

Nonetheless, the ACSM Metabolic Equation also has several strengths: 1) the simplicity of this equation makes it easily remembered and applied, 2) the ACSM Metabolic Equation incorporates a grade component to account for the vertical cost of inclined walking, 3) it is convenient to use during treadmill walking, where walking speed and grade are easily prescribed and monitored, and 4) an ACSM Metabolic Equation is available for predicting running intensity, with the same form as that for walking but different coefficients for the horizontal (speed) and vertical (grade) components (9). Therefore, the CMEs developed herein do not provide a replacement for the ACSM Metabolic Equation for walking – they are instead additional tools for use in applications where cadence is more practical to monitor or prescribe than walking speed (e.g., during overground walking). Similarly, the purpose of evaluating the ACSM Metabolic Equation’s performance in these data was not to discourage its use – we instead used this equation to set a benchmark for the CMEs developed herein, on the basis that the ACSM Metabolic Equation has already been adopted and disseminated by many, including the ACSM (9).

Strengths and Limitations

A primary strength of this study was its inclusion of a large, age- and sex-balanced sample of 21- to 84-year-old adults for the development of the simple and full CMEs. This sample represents all participants in the CADENCE-Adults study (NCT02650258) with valid data at treadmill walking speeds of at least 0.89 m/s. Of note, the original sample included 85 year olds but none of these individuals met our analytical inclusion criteria. The use of this adult lifespan sample suggests that these equations, and the predictive accuracies reported herein, will be broadly generalizable. Additionally, previous studies (11, 12, 39) have highlighted the importance of accounting for anthropometric and demographic characteristics when using cadence to predict walking intensity. Our analyses explored the effects of these variables using a large and heterogeneous sample that contained sufficient variability (Table 1) in these characteristics to identify any existing effects. Finally, the cross-validated measures of predictive error we have used to develop the full CME and evaluate metabolic equation performance (i.e., the PRESS statistic and k-fold cross-validation) reflect out-of-sample error, as is directly relevant to using these equations in research and health applications.

The CMEs developed herein do not account for the grade of inclined walking and future studies are needed to verify their generalizability to overground walking. Additionally, the methods available for conducting best subsets regression analysis did not allow the random effect of participants to be included when developing the CMEs. However, our approaches to model selection and equation evaluation are based on predictive error, as opposed to significance testing or R² values, and therefore remain valid. The random effect of participants was included in all models used for significance testing (i.e., the likelihood ratio test and F-tests). Lastly, the simple and full CMEs demonstrated RMSE and MAE values of 1.50–2.09 mL/kg/min [0.43–0.60 METs] in the normal speeds dataset. While we maintain that this level of accuracy is satisfactory for a simple and accessible tool used in public health applications, the practical significance (e.g., health implications, effects on PA program adherence) of exhibiting this or any level of predictive error is difficult to determine empirically. For this reason, we concurrently tested the ACSM Metabolic Equation in these data and demonstrated that the metabolic equations developed herein exceed a benchmark set by a metabolic equation that has already been disseminated and adopted (9).

Conclusions

Performing activities at an appropriate intensity is an important component of improving health through PA (1–3) while still establishing sustainable PA behaviors (2, 4–6). However, PA intensity can be difficult to quantify and convey to the general public. Therefore, we have developed a simple CME (Table 2) that can predict walking intensity within ~1.8 mL/kg/min (~0.5 METs) on average from cadence alone. The average predictive capacity of this equation was not substantially improved by including age, leg length, and BMI as additional predictors in the full CME, indicating the simple CME would perform with comparable accuracy in public health applications while being easier and more practical to use. However, the full CME may have utility in adults who are outliers in terms of age, stature, and/or BMI. The choice of which CME to use will depend on these characteristics, in addition to the cadence/intensity being examined (due to the age- and BMI-cadence interactions), desired level of precision, and user resources and expertise. These CMEs also predicted walking intensity with 23–35% greater accuracy and ~2.2 mL/kg/min (~0.6 METs) less bias than the ACSM Metabolic Equation. Furthermore, while the ACSM Metabolic Equation is advantageous for applications where walking speed can be easily set and monitored (e.g., treadmill walking), cadence can be directly observed (i.e., manually counted) during overground walking or assessed using a number of contemporary wearable technologies, and entrained by synchronizing foot-strikes to the tempo of music or a metronome (10). Therefore, the CMEs provided herein will enable accurate quantification and prescription of walking intensity while employing a metric that is accessible to researchers, health professionals, and members of the general public in the free-living setting.