Digital Image Processing Features of Smartwatch Photoplethysmography for Cardiac Arrhythmia Detection

Abstract

The aim of our work is to design an algorithm to detect premature atrial contraction (PAC), premature ventricular contraction (PVC), and atrial fibrillation (AF) among normal sinus rhythm (NSR) using smartwatch photoplethysmographic (PPG) data. Novel image processing features and two machine learning methods are used to enhance the PAC/PVC detection results of the Poincaré plot method. Compared with support vector machine (SVM) methods, the Random Forests (RF) method performs better. It yields a 10-fold cross validation (CV) averaged sensitivity, specificity, positive predicted value (PPV), negative predicted value (NPV), and accuracy for PAC/PVC labels of 63%, 98%, 83%, 94%, and 93%, respectively, and a 10-fold CV averaged sensitivity, specificity, PPV, NPV, and accuracy for AF subjects of 92%, 96%, 85%, 98%, and 95%, respectively. This is one of the first studies to derive image processing features from Poincaré plots to further enhance the accuracy of PAC/PVC detection using PPG recordings from a smartwatch.

I. Introduction

Atrial Fibrillation (AF) is the most common type of cardiac arrhythmia among people over 50, with evidence suggesting an increasing prevalence and incidence worldwide [2]. It is believed that the natural history of AF is progressive and that it is induced at the early stage by a trigger activity that causes paroxysmal AF [3]. Recent advances in wearable devices have allowed for combining portable heart rate monitoring with location information and connectivity, which has prompted the hypothesis of replacing implantable loop recorders with a noninvasive device to continuously monitor silent arrhythmias such as AF [4]. However, other types of cardiac arrhythmia, like premature ventricular contraction (PVC) and premature atrial contraction (PAC), often occur during long term paroxysmal AF monitoring among elderly people. A study in healthy normal volunteers has found the prevalence of PVC between the ages of 46 to 65 is 73.1% in a 24 hour Holter ECG recording [5]. Another large population-based study of individuals aged at least 50 years has found that 99% of all participants did have at least 1 PAC during 24-hour Holter monitoring [6].

Currently, AF detection using photoplethysmogram (PPG) data is mainly using the pulse-to-pulse interval [7], which easily gives false AF alerts in the presence of PAC and PVC. Thus, a combined AF detection plus PAC/PVC detection is necessary to reduce false positives. However, there is scant literature on detecting PAC/PVC from PPG-based data. Many established algorithms have been published for AF detection using PPG data, however, none of them have a clear PAC/PVC detector in parallel. A study by Sološenko et al. [8] suppressed non-AF rhythms like premature pulses and sinus arrhythmia to reduce false AF alarms, but the accuracy of non-AF rhythm suppression is not mentioned in the paper. A simple PAC detection criterion is mentioned in Kwon et al. [9] using Deep Learning methods for AF detection, which consider a beat as PAC when the interval with the previous beat was less than 85% of the average interval. The reported sensitivity and specificity for this PAC indicator are 92.55% and 98.18%, respectively [9]. However, this simple PAC detector is only used for measuring PAC burden, and with higher PAC burden (24%-28% of samples), the specificity of the Deep Learning models drop to around 90%. Recently, our lab has published a method for PAC and PVC detection from AF data using a Poincaré plot method applied to fingertip video PPG data acquired from a smartphone [10]. It should be noted, however, that video PPG signal quality, as well as the pulse oximetry PPG signal used by [8] and [9], have much higher signal fidelity than does signal from a wrist, as the skin is thinner on the fingertip. Moreover, motion artifacts are less severe for video PPG and pulse oximetry PPG than for smartwatch PPG data, as long as the finger makes constant good contact with the smartphone’s camera.

In this paper, we developed novel machine learning models using smartwatch PPG data as an input to distinguish PAC/PVC from AF based on features derived from Poincaré plots [10] with image processing tools. To the best of our knowledge, this is one of the first studies to accomplish this.

II. Materials and Methods

A. Dataset

35 participants (28 male and 7 female) ranging in age from 50 – 91 years old participated in the smartwatch study at the ambulatory cardiovascular clinic at the University of Massachusetts Medical Center (UMMC) [11]. Among the 35 participants, 23 participants were identified as being in normal sinus rhythm (NSR), 5 participants had PAC or PVC, and 9 subjects exhibited AF. This study was approved by the University of Massachusetts Medical School (UMMS) Institutional Review Board (UMMS IRB #H00009953). Reference ECG and smartwatch data were measured simultaneously from the chest and a wrist using a 7-lead Holter monitor (Rozinn RZ153+ Series, Rozinn Electronics Inc., Glendale, NY, USA) and a smartwatch (Simband 2, Samsung Digital Health, San Jose, CA, USA (henceforth referred to simply as Simband)) [1], respectively. One channel of the 3-channel Holter ECG signals was used as the reference for estimation of heart rates, which was sampled at 180 Hz. Only the 5th PPG channel (green LED color, wave length 520–535 nm) among all 8 channels of Simband PPG signals was used for data analysis since it consistently provided the best signal quality. Three-axis accelerometer (ACC) signals were also recorded on Simband, and both PPG and ACC signals were originally sampled at 128 Hz and were then down-sampled to 50 Hz and 20 Hz, respectively. All signals were segmented to a 30-second length with no overlap for peak detection analysis.

B. Experiment Protocol

The study protocol was designed to simulate activities of daily living during smartwatch use and consisted of the following sequences: sit still for 2 minutes, walk slowly for 2 minutes, stand still for 30 seconds, walk quickly for 2 minutes, stand still for 30 seconds, move arms randomly for 2 minutes, and stand still for 30 seconds. Participants were then asked to sit and stand repetitively for 1 minute followed by climbing stairs for 1 additional minute. The last procedure required participants to sit for 1 minute.

C. Preprocessing of Poincaré plot

For each 30-sec PPG segment shown in panel (a) of Figure 1, a peak detection algorithm [12] was first performed to detect HR, which is shown in panel (c) of Figure 1. Then, the difference of HR (diff-HR) was calculated and used as the x and y coordinate for plotting the Poincaré plot. Poincaré plots in panel (d) of Figure 1 are generated by connecting all coordinates in the diff-HR sequence with a straight line, called the trajectory, and the starting point for each line consists of the current diff-HR beat as x coordinate and the previous diff-HR beat as y coordinate, and the ending point consists of the next diff-HR beat as x coordinate and the current diff-HR beat as y coordinate. The range of x and y axes for each Poincaré plot is set to [−80, 80] BPM, which represents the maximum change of heart rate a person could have. In our previous study, we only used binary Poincaré plots to detect repeated patterns for trajectories that fell inside certain marked regions [10]. However, binary Poincaré plots will miss-detect PAC/PVCs if trajectories do not fall inside the marked regions due to a slight HR difference between PAC/PVC beats. Hence, we propose a new “density” Poincaré plot to increase the trajectory overlapping and also reduce the effect of motion artifact on PAC/PVC detection. Resolution for each density Poincaré plot is predefined as 1000 × 1000 zero-valued pixels, as shown in panel (e) of Figure 1. This resolution is not optimized yet but is simply set for a higher resolution (equals 0.16 BPM per pixel). The line width for trajectories is set to 20 pixels (equals 0.32 BPM) to increase the overlap with nearby trajectories. The key different between density Poincaré plot and the original Poincaré plot is that each new density Poincaré plot trajectory is drawn on top of all previous trajectories.

Fig. 1.

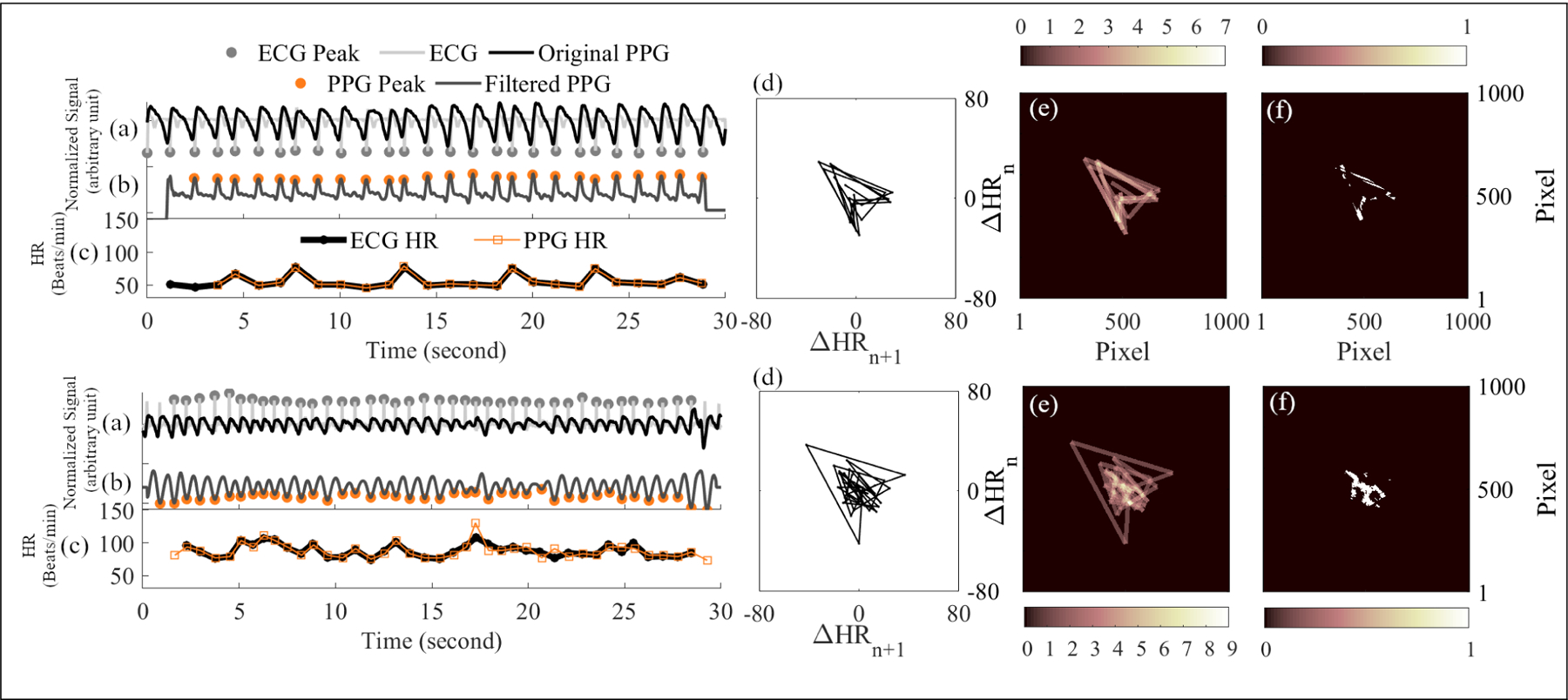
Example signals, Poincaré plots, and density Poincaré plots for PAC/PVC (top panels) and AF (bottom panels). Each panel shows (a): reference ECG overlapped with original PPG; (b): filtered PPG with detected peaks; (c): HR from reference ECG and filtered PPG; (d): Poincaré plot from PPG HR; (e): density Poincaré plot from PPG HR; (f): segmentation of density Poincaré plot for Zernike moments from a 30-sec segment.

D. Image Processing Features from Density Poincaré Plots

70 features are calculated from below image processing methods:

• Statistical Moments: image moments are useful to describe the phase span of objects, which can be used for PAC/PVC and AF detection because AF trajectories encompasses a bigger region due to rapid changes of heart rate when compared with the trajectories of PAC/PVC data. Since the zeroth order central moment is 1, and the first-order central moment is 0, we only include the first-order non-central moment, and the second-, third- and fourth- order central moments [13] as our features, which are also called the variance, skewness, and kurtosis, respectively. Since our input is a 2-D image, we first calculate different order moments based on row and column direction of image. After receiving the 1-D vector of moments, we apply two criteria—mean and variance—to generate one feature for each 1-D vector. In this way, we collect 13 features from statistical moments.

• 2-D Cross-correlation with Templates: cross-correlation can be helpful for PAC/PVC and AF detection if representative templates are chosen and can reflect the difference between density Poincaré plots of PAC/PVC and AF. After checking all 292 density Poincaré plots, we selected 5 representative templates from all segments: two templates from two AF subjects, one template from one NSR subject, and two templates from two PAC/PVC subjects. These 5 segments were then excluded when we built the machine learning classifier. Both templates and the input images are first self-normalized to [0, 1] value, and then the 2-D cross-correlation value is calculated between template images and input data. 5 features are collected from this method.

• Zernike Moments: segmentation of density Poincaré plots is needed before calculating Zernike moments, as they require binary images as inputs [14]. Zernike moments can describe the smoothness of object boundaries, and a PAC/PVC density plot after segmentation should have smoother boundaries, since most of its trajectories are overlapped with each other. The threshold of segmentation was selected as >3 to set a given pixel value as true, and this threshold was optimized based on removing low density background noise while preserving useful repeated patterns. 14 features from Zernike moments were calculated based on 14 different order combinations in Zernike polynomials [14].

• Discrete Wavelet Transform Features: frequency domain information in density Poincaré plots can be measured by discrete wavelet transform. A density Poincaré plot is first down-sampled to 256 × 256 to save computation time for wavelet transform, and then two-level wavelet decomposition of the density plot is performed using Daubechies 4 (DB4) wavelets. From the two-level wavelet decomposition, we found four features that were useful for later classification: entropy of level 1 approximation and horizontal coefficients, energy of level 1 approximation coefficients, and energy of level 2 diagonal coefficients.

• Hough Transform Features: since our density Poincaré plot only consists of lines, the Hough transform as an edge detector should provide useful features [15]. As the starting and ending points for each trajectory are already known, edge detection is skipped, and it is easy to calculate the angle θ of the line with the x axis and the distance ρ between the midpoint of the line and bottom left corner of the image which is the origin of the Hough Transform:

  $$\theta =\mathit{\text{arctan}}\left(\frac{x_0-x_1}{y_1-y_0}\right),\rho =x_0\mathit{\text{cos}}\left(\theta \right)+y_0\mathit{\text{sin}}\left(\theta \right)$$ (1)

  where x₀ and y₀ stand for the x and y coordinate of the starting point for each line, and x₁ and y₁ stand for the x and y coordinate of ending point for each line.

E. Machine Learning Models

• Random Forest (RF) Classifier: to examine the variability of proposed machine learning models, we used a k-fold (k=10) cross validation (CV) method to randomly partition the dataset into 90% training set and 10% testing set, and then we perform the analysis on the training set and validate it on the testing set. Averaged results from the above 10 folds on the testing set are reported as the validation results. Random Forest models use a boot-strapping technique [16], in which the original data sets are randomly sampled using 67% of samples for model training (in-bag), while the rest of the data (out-of-bag set of 33%) are used for internal cross-validation. Using Bayesian optimization as the hyperparameter tuning, the final hyperparameters for Random Forests classification are: number of trees = 500, minimum leaf size = 1, number of predictors to sample = 20, and maximum number of splits = 195.

• Support Vector Machine (SVM) Classifier: the polynomial kernel function provides one of the best result on SVM multiclass classifiers [17]. During the training of the SVM model, standardization of input data is performed.

III. Results

Human adjudication of motion and noise determined that 287 30-sec segments from 35 subjects were clean data after removing 5 clean segments as cross-correlation templates. Evaluation of our proposed machine learning models is based on three classes: AF, NSR and PAC/PVC. Table I shows the results from our proposed RF model and proposed SVM model. The first row in Table I shows 191, 52, and 44 segments associated with NSR, AF, and PAC/PVC labels, respectively. The added-up confusion matrix from 10-fold CV for the proposed RF and SVM models are shown in the left and right columns, respectively, from row 2 to 5. The 10-fold CV averaged sensitivity, specificity, PPV, NPV, and accuracy for PAC/PVC detection using the proposed RF model are 63.00%, 97.89%, 83.33%, 93.67%, and 92.57%, respectively. The sensitivity, specificity, PPV, NPV and accuracy for PAC/PVC detection using the SVM method are lower: 61.00%, 92.80%, 63.50%, 92.94% and 87.88%.

TABLE I.

Classification Results for AF, PAC/PVC and NSR labels

Classifier	Random Forests			SVM
Class	NSR	AF	PAC/PVC	NSR	AF	PAC/PVC
Ground Truth	191	52	44	191	52	44
TP	185	48	28	174	46	27
TN	86	213	233	84	201	220
FP	2	9	5	3	9	17
FN	6	4	16	17	6	17
Sensitivity (%)	96.84	92.33	63.00	91.05	88.33	61.00
Specificity (%)	97.57	95.99	97.89	96.67	95.78	92.80
PPV (%)	98.97	85.29	83.33	98.36	85.02	63.50
NPV (%)	93.79	98.24	93.67	83.61	97.20	92.94
Accuracy (%)	97.11	95.32	92.57	92.80	94.30	87.88

The AF detection sensitivity, specificity, PPV, NPV, and accuracy from 10-fold CV for the RF model are 92.33%, 95.99%, 85.29%, 98.24%, and 95.32%, respectively, which are all higher than the AF detection results of the SVM model, which has sensitivity, specificity, PPV, NPV, and accuracy as 88.33%, 95.78%, 85.02%, 97.20%, and 94.30%, respectively.

IV. Discussion

In this work, we illustrated the Random Forests approach and the SVM approach to detect PAC/PVC from NSR and AF data segments. We have shown that our PAC/PVC detection model using the RF method improved the sensitivity, specificity, PPV, NPV, and accuracy by 2.00%, 5.10%, 19.83%, 0.73% and 4.69%, respectively, when compared to SVM. Since the SVM model cannot address the imbalanced data issue, it requires fine tuning the cost matrix for better classification results.

Given the low 90% sensitivity and 95% specificity of AF detection for the models, we can conclude that giving higher class weights for false AF detection is inevitable for machine learning algorithms to outperform the traditional statistical AF detection methods, which usually reach a high 98% sensitivity and 99% specificity [7].

The insufficient amount of PAC/PVC data could be the reason for our low sensitivity for PAC/PVC detection. Although we have 35 subjects, there are only 5 PAC/PVC subjects and 9 AF subjects with 44 PAC/PVC segments and 52 AF segments, which are not enough to fully encapsulate PAC/PVC patterns, especially given the noisy nature of wristwatch PPG data. In the future, we will need to collect more PAC/PVC data to make sure the training set fully captures all possible dynamics in the testing set.

V. Conclusions

The importance of this work is we used a new image processing method to extract features from the density Poincaré plot that was generated by the beat-to-beat heart rate from PPG signals, and performed three-class discrimination consisting of AF, PAC/PVC, and NSR. The Random Forests model showed better PAC/PVC detection results when compared to the SVM method. The AF detection accuracy remains to be improved on both models, and a penalty weight for false AF detection will be added in the future.

Clinical relevance—

By detecting PACs and PVCs, the proposed methods can reduce false positive detection of AF, especially for those NSR subjects with frequent episodes of PAC/PVC.